Finite Difference–Collocation Method for the Generalized Fractional Diffusion Equation

Abstract

In this paper, an approximate method combining the finite difference and collocation methods is studied to solve the generalized fractional diffusion equation (GFDE). The convergence and stability analysis of the presented method are also established in detail. To ensure the effectiveness and the accuracy of the proposed method, test examples with different scale and weight functions are considered, and the obtained numerical results are compared with the existing methods in the literature. It is observed that the proposed approach works very well with the generalized fractional derivatives (GFDs), as the presence of scale and weight functions in a generalized fractional derivative (GFD) cause difficulty for its discretization and further analysis.

1. Introduction

Fractional calculus (FC) is an important branch of applied mathematics, which deals with the arbitrary order derivative and integration [1,2,3,4,5]. Its applications in different fields are seen in biophysics [6], engineering [7], fluid mechanics and bioengineering [8,9] and other areas including image processing [10,11,12,13]. Most of these studies are mainly based on the traditional fractional derivatives, such as the Riemann–Liouville fractional derivative and the Caputo fractional derivative, etc. Recently, in [14] Agrawal discussed a new GFD, which generalized the traditional derivatives using weight and scale functions. The scale functions were used to compress and enlarge the domain for the close observation of physical phenomena, while the weight functions provide flexibility for the researchers to assess physical events at different times. Due to such behaviors of the scale and weight functions, the study of fractional partial differential equations (FPDE) using a GFD has attracted researchers in recent years. Several authors have developed numerical schemes for solving FPDEs involving GFDs. Here, we cite only few of them. In [15,16], Agrawal and coauthors presented the numerical solutions to the Berger’s equation and the fractional advection–diffusion equation (FADE) with a generalized time-fractional derivative for the first time. The numerical solutions to these problems were obtained using the finite difference method. Further, the authors of [17,18], studied the time-fractional telegraph equations and fractional advection–diffusion equations in terms of GFDs and developed the higher order schemes to solve such equations. Kumar et al. [19] presented two numerical schemes to approximate the GFDs and obtained the convergence orders as $(2-\alpha )$ and $(3-\alpha )$, respectively. Further, these schemes were applied to solve the fractional integro-differential equations defined in terms of GFDs. In [20], Kumari and Pandey proposed an approximation method with a $(4-\alpha )th$ order of convergence to approximate GFDs and applied it to solve the fractional advection–diffusion equations. Li and Wong [21] discussed a numerical scheme to find the solution of the generalized subdiffusion equation. Here, the authors used the generalized Grunwald–Letnikov approximation method to solve the problem. Some other recently presented methods for solving different types of fractional diffusion equations are summarized as follows: in [22], the authors discussed the matrix method for the reaction–diffusion equation that involved the Mittag–Leffler kernel. Duan et al. [23] solved the convection–diffusion equations using the Shannon–Runge–Kutta–Gill method. In [24], the authors discussed the solution to the fractional subdiffusion and the reaction–subdiffusion equations with a nonlinear source term using the Legendre collocation method. Lin and Xu [25] solved the time-fractional diffusion equation (TFDE) using the spectral method and finite difference method (FDM). In [26], Murio solved the time-fractional advection–diffusion equation (TFADE) by using implicit FDM. Sweilam et al. [27] developed the Crank–Nicolson FDM to solve a linear TFDE defined with a Caputo fractional derivative. In [28], Luchko solved the initial value and boundary value multi-term TFDE using the Fourier series method. Dubey et al. [29] proposed a residual power series method to obtain the solution of homogeneous and nonhomogeneous nonlinear fractional order partial differential equations.

In this paper, we study the generalized fractional diffusion equation (GFDE) obtained from the standard diffusion equation by replacing the first-order time derivative term with a fractional derivative of order $\gamma ,0<\gamma <1$, given as,

$$*{\mathcal{D}}_t^{\gamma }v(x,t)=\frac{{\partial }^{2}v(x,t)}{\partial x^2}+g(x,t),x\in [0,1],t\in [0,\tau ],$$

(1)

with initial and boundary conditions,

$$\left\{\begin{array}{c}v(x,0)={\eta }_1\left(x\right),0\le x\le 1,\hfill \\ v(0,t)={\eta }_2\left(t\right),v(1,t)={\eta }_3\left(t\right),0\le t\le \tau ,\hfill \end{array}\right.$$

(2)

where $g(x,t)$ is the source/sink function.

The motive of this paper is to construct an efficient method to obtain the numerical solution to the GFDE. The present method is based on the finite difference and collocation methods with Jacobi polynomials as the basis function. The outline of the paper is as follows: In Section 2, we discuss some basic facts about FC and Jacobi polynomials, which are needed throughout this paper. In Section 3, first, the finite difference method is used to discretize the time derivative. Second, on the space variable, we use the collocation method for numerical approximation. Further, we estimate the error and convergence analysis analytically, which ensures the numerical applicability of the proposed method. In Section 5, we present two numerical examples to validate the proposed method. Furthermore, we compare our results with a few other methods from the literature, which are presented in Section 5. Finally, in Section 6, the conclusions are discussed.

2. Preliminaries of Fractional Calculus and Jacobi Polynomials

In this section, we discuss some preliminary facts and basic properties of generalized fractional calculus and Jacobi polynomials [1,30].

2.1. Generalized Fractional Calculus

Definition 1

([14]). The Caputo derivative of a function $v\left(\tau \right)$ of order γ is defined as

$$\left({\mathcal{D}}_{0+}^{\gamma }v\right)\left(\tau \right)=\left({\mathcal{I}}^{\delta -\gamma }{\mathcal{D}}^{\delta }v\right)\left(\tau \right)=\frac{1}{\mathrm{\Gamma }(\delta -\gamma )}{\int }_0^{\tau }{(\tau -s)}^{\delta -\gamma -1}{v}^{\left(\delta \right)}\left(s\right)ds,\tau >0,$$

(3)

where $\delta -1<\gamma \le \delta$ and $\delta \in {\mathbb{Z}}^{+}$.

Definition 2

([14]). A generalized fractional derivative of order $\gamma >0$ of a function $v\left(\tau \right)$ with respect to weight function $\omega \left(\tau \right)$ and scale function $z\left(\tau \right)$ is defined as

$$\left({\mathcal{D}}_{[z;\omega ;L]}^{\gamma }v\right)\left(\tau \right)={\left[\omega \left(\tau \right)\right]}^{-1}\left[{\left(\frac{D_t}{z^{{}^{\prime }}\left(\tau \right)}\right)}^{\gamma }\left(\omega \left(\tau \right)v\left(\tau \right)\right)\right].$$

(4)

Definition 3.

A generalized fractional integral of a function $v\left(\tau \right)$ of fractional order $\gamma >0$ is defined as

$$\left({\mathcal{I}}_{[z;\omega ]}^{\gamma }v\right)\left(\tau \right)=\frac{{\left[\omega \left(\tau \right)\right]}^{-1}}{\mathrm{\Gamma }\left(\gamma \right)}{\int }_0^{\tau }\frac{\omega \left(s\right)z^{{}^{\prime }}\left(s\right)v\left(s\right)}{{[z\left(\tau \right)-z\left(s\right)]}^{1-\gamma }}ds.$$

(5)

Definition 4

([14]). The left/forward generalized Caputo fractional derivative of order $\gamma >0$ of function $v\left(\tau \right)$ with respect to weight function $\omega \left(\tau \right)$ and scale function $z\left(\tau \right)$ is defined by

$$(*{\mathcal{D}}_{0+}^{\gamma }v)\left(\tau \right)={\mathcal{I}}_{0+;[z;\omega ]}^{\delta -\gamma }{\mathcal{D}}_{0+;[z;\omega ;L]}^{\delta }=\frac{{\left[\omega \left(\tau \right)\right]}^{-1}}{\mathrm{\Gamma }(\delta -\gamma )}{\int }_0^{\tau }\frac{{\left(\omega \left(s\right)v\left(s\right)\right)}^{\left(\delta \right)}}{{(z\left(\tau \right)-z\left(s\right))}^{\gamma +1-\delta }}ds,$$

(6)

where $\delta -1<\gamma \le \delta ,\delta \in {\mathbb{Z}}^{+}$.

For a particular choice of the weight and scale functions $\left(z\right(\tau )=\tau ,\omega (\tau )=1)$, Equation (6) reduces to the Caputo derivative. We have considered the weight and scale sufficiently good such that the integral exists in GFD.

2.2. Jacobi Polynomials

Definition 5.

The Jacobi polynomials [31] ${\mathcal{J}}_n^{\alpha ,\beta }\left(z\right)$ for indices $\alpha ,\beta >-1$ and degree n are the solutions of the Sturm–Liouville problems. These are orthogonal polynomials with respect to the Jacobi weight function $\omega \left(z\right)={(1-z)}^{\alpha }{(1+z)}^{\beta }$ in interval $[-1,1]$, defined as follows:

$${\mathcal{J}}_n^{\alpha ,\beta }\left(z\right)=\frac{\mathrm{\Gamma }(\alpha +n+1)}{n!\mathrm{\Gamma }(\alpha +\beta +n+1)}\sum _{m=0}^n\left(\frac{n}{m}\right)\frac{\mathrm{\Gamma }(\alpha +\beta +n+m+1)}{\mathrm{\Gamma }(\alpha +m+1)}{\left(\frac{z-1}{2}\right)}^m.$$

(7)

The kth derivative of Jacobi polynomials defined as

$$\frac{d^k}{d{z}^k}{\mathcal{J}}_n^{\alpha ,\beta }\left(z\right)=\frac{\mathrm{\Gamma }(\alpha +\beta +n+1+k)}{2^k\mathrm{\Gamma }(\alpha +\beta +n+1)}{\mathcal{J}}_{n-k}^{(\alpha +k,\beta +k)}\left(z\right),k\in \mathbb{N},$$

(8)

satisfy the recurrence relation

$${\mathcal{J}}_{n+1}^{\alpha ,\beta }\left(z\right)=({\mathcal{A}}_{n}z-{\mathcal{B}}_n){\mathcal{J}}_n^{\alpha ,\beta }\left(z\right)-{\rho }_n{\mathcal{J}}_{n-1}^{\alpha ,\beta }\left(z\right),n\ge 1,$$

(9)

where

$${\mathcal{J}}_0^{\alpha ,\beta }\left(z\right)=1,{\mathcal{J}}_1^{\alpha ,\beta }\left(z\right)=\frac{1}{2}(\alpha +\beta +z)+\frac{1}{2}(\alpha -\beta ),$$

$${\mathcal{A}}_n=\frac{(2n+\alpha +\beta +1)(2n+\alpha +\beta +2)}{2(n+1)(n+\alpha +\beta +1)},{\mathcal{B}}_n=\frac{(2n+\alpha +\beta +1)({\alpha }^2-{\beta }^2)}{2(n+1)(n+\alpha +\beta +1)(2n+\alpha +\beta )},$$

and

$${\rho }_n=\frac{(2n+\alpha +\beta +2)(n+\alpha )(n+\alpha )}{(n+1)(n+\alpha +\beta +1)(2n+\alpha +\beta )}.$$

For the transformation of the interval $[-1,1]$ to $[0,1]$, we use the relation, $z=2x-1$. The recurrence relation (9) becomes

$${\mathcal{J}}_{n+1}^{\alpha ,\beta }\left(x\right)=({\xi }_{n}x-{\mathcal{K}}_n){\mathcal{J}}_n^{\alpha ,\beta }\left(x\right)-{\rho }_n{\mathcal{J}}_{n-1}^{\alpha ,\beta }\left(x\right),n\ge 1,$$

(10)

where

$$\begin{array}{cc}\hfill {\xi }_n& =\frac{(2n+\alpha +\beta +1)(2n+\alpha +\beta +2)}{(n+1)(n+\alpha +\beta +1)},\hfill \\ \hfill {\mathcal{K}}_n& =\frac{(2n+\alpha +\beta +1)(2n^2+(1+\beta )(\alpha +\beta )+2n(\alpha +\beta +1))}{(n+1)(n+\alpha +\beta )(2n+\alpha +\beta )}.\hfill \end{array}$$

It satisfies the orthogonality relation

$${\int }_0^1{\mathcal{J}}_n^{\alpha ,\beta }\left(x\right){\mathcal{J}}_m^{\alpha ,\beta }\left(x\right)w_1^{\alpha ,\beta }\left(x\right)dx={\delta }_{n,m}{\mathcal{H}}_n^{\alpha ,\beta },\alpha ,\beta >-1,$$

(11)

where ${\delta }_{n,m}$ is the Kronecker delta function, $w_1^{\alpha ,\beta }\left(x\right)=x^{\beta }{(1-x)}^{\alpha }$ is the weight function, and

$${\mathcal{H}}_n^{\alpha ,\beta }=\frac{\mathrm{\Gamma }(n+1+\beta )\mathrm{\Gamma }(n+\alpha +1)}{(2n+1+\alpha +\beta )n!\mathrm{\Gamma }(n+1+\alpha +\beta )}.$$

(12)

The summation form of the Jacobi polynomials ${\mathcal{J}}_n^{\alpha ,\beta }\left(x\right)$ is written as

$${\mathcal{J}}_n^{\alpha ,\beta }\left(x\right)=\sum _{k=0}^j{(-1)}^{k+j}\frac{\mathrm{\Gamma }(k+j+1+\alpha +\beta )\mathrm{\Gamma }(j+1+\beta )}{k!\mathrm{\Gamma }(j+1+\alpha +\beta )\mathrm{\Gamma }(k+1+\beta )},$$

(13)

and the pth derivative of Equation (13) in $[0,1]$, can be further rewritten in terms of x as

$$\frac{d^p}{d{x}^p}{\mathcal{J}}_n^{\alpha ,\beta }\left(x\right)=\frac{\mathrm{\Gamma }(\alpha +\beta +n+1+p)}{\mathrm{\Gamma }(\alpha +\beta +n+1)}{\mathcal{J}}_{n-p}^{(\alpha +p,\beta +p)}\left(x\right),p\in \mathbb{N}.$$

(14)

The value of the shifted Jacobi polynomials at the end points are given as

$${\mathcal{J}}_n^{\alpha ,\beta }\left(0\right)={(-1)}^n\frac{\mathrm{\Gamma }(1+n+\beta )}{\mathrm{\Gamma }(1+\beta )n!},{\mathcal{J}}_n^{\alpha ,\beta }\left(1\right)=\frac{\mathrm{\Gamma }(1+n+\alpha )}{\mathrm{\Gamma }(1+\alpha )n!}.$$

(15)

Let $v\left(x\right)$ be a square integrable function defined on $[0,1]$, then

$$v\left(x\right)=\sum _{i=0}^{\infty }{c}_i{\mathcal{J}}_i^{\alpha ,\beta }\left(x\right),$$

(16)

where $c_i$ are the unknown coefficients $(c_i,i=0,1,2\dots )$ determined by the relation

$$c_i=\frac{1}{{\mathcal{H}}_i^{\alpha ,\beta }}{\int }_0^{1}v\left(x\right)w^{\alpha ,\beta }\left(x\right){\mathcal{J}}_i^{\alpha ,\beta }\left(x\right)dx,i=0,1,2\dots .$$

(17)

Truncating the series in Equation (16) up to $(m+1)$ terms, the approximation of $v\left(x\right)$ is given as

$$v_m\left(x\right)=\sum _{i=0}^m{c}_i{\mathcal{J}}_i^{\alpha ,\beta }\left(x\right).$$

(18)

3. Numerical Scheme and Stability Analysis

3.1. Discretization in the Time Direction

For the discretization of the GFD, we follow the discretization process as discussed in Refs. [19,32]. We split the time interval $[0,\tau ]$ into $\mathcal{M}$ equal parts having step size $\Delta t=\frac{\mathcal{T}}{\mathcal{M}}$, $\mathcal{M}\in {\mathbb{Z}}^{+}$, and choose the node points as $t_r=r(\Delta t),r=0,1,2,\dots ,\mathcal{M},$ with starting point $t_0=0$. Assuming $w\left(t\right)>0,\gamma \in (0,1)$, and $z\left(t\right)$ is a monotonic increasing function on $[0,\mathcal{T}]$, such that $\eta =z\left(s\right)$; then, $s=z^{-1}\left(\eta \right)$. The discretization of the GFD of $v\left(t\right)$ at node $t_r$ is given as

$$\begin{array}{cc}\hfill *{\mathcal{D}}_t^{\gamma }v\left(t_r\right)& =\frac{{\left[w\left(t_r\right)\right]}^{-1}}{\mathrm{\Gamma }(1-\gamma )}\sum _{l=1}^r{\int }_{t_{l-1}}^{t_l}\frac{{\left[w\left(s\right)v\left(s\right)\right]}^{{}^{\prime }}}{{[z\left(t_r\right)-z\left(s\right)]}^{\gamma }}ds,\hfill \\ \hfill & =\frac{{\left[w\left(t_r\right)\right]}^{-1}}{\mathrm{\Gamma }(1-\gamma )}\sum _{l=1}^r{\int }_{z\left(t_{l-1}\right)}^{z\left(t_l\right)}\frac{1}{{[z\left(t_r\right)-\eta ]}^{\gamma }}.\frac{d\left[w\left(z^{-1}\left(\eta \right)\right)v\left(z^{-1}\left(\eta \right)\right)\right]}{d{z}^{-1}\left(\eta \right)}d{z}^{-1}\left(\eta \right),\hfill \\ \hfill & =\frac{{\left[w\left(t_r\right)\right]}^{-1}}{\mathrm{\Gamma }(1-\gamma )}\sum _{l=1}^r\frac{w\left(t_l\right)v\left(t_l\right)-w\left(t_{l-1}\right)v\left(t_{l-1}\right)}{z\left(t_l\right)-z\left(t_{l-1}\right)}{\int }_{z\left(t_{l-1}\right)}^{z\left(t_l\right)}\frac{1}{{[z\left(t_r\right)-\eta ]}^{\gamma }}d\eta +{\mathcal{R}}_r,\hfill \\ \hfill & =\frac{{\left[w\left(t_r\right)\right]}^{-1}}{\mathrm{\Gamma }(2-\gamma )}\sum _{l=1}^r{q}_l[w\left(t_l\right)v\left(t_l\right)-w\left(t_{l-1}\right)v\left(t_{l-1}\right)]+{\mathcal{R}}_r,\hfill \end{array}$$

(19)

where

$$q_l=\frac{{[z\left(t_r\right)-z\left(t_{l-1}\right)]}^{1-\gamma }-{[z\left(t_r\right)-z\left(t_l\right)]}^{1-\gamma }}{z\left(t_l\right)-z\left(t_{l-1}\right)},l=1,2,\dots r,$$

(20)

and ${\mathcal{R}}_r$ is the truncation error given by

$$\begin{array}{c}\hfill {\mathcal{R}}_r=\frac{{\left[w\left(t_r\right)\right]}^{-1}}{\mathrm{\Gamma }(1-\gamma )}\sum _{l=1}^r{\int }_{z\left(t_{l-1}\right)}^{z\left(t_l\right)}\frac{1}{{[z\left(t_r\right)-\eta ]}^{\gamma }}[\frac{d\left[w\left(z^{-1}\left(\eta \right)\right)v(x,z^{-1}\left(\eta \right))\right]}{d\eta }\\ \hfill -\frac{w\left(t_l\right)v\left(t_l\right)-w\left(t_{l-1}\right)v\left(t_{l-1}\right)}{z\left(t_l\right)-z\left(t_{l-1}\right)}]d\eta .\end{array}$$

(21)

Lemma 1.

The coefficient $q_l,l=1,2,\dots ,r,$ given by Equation (20), satisfies $q_r>q_{r-1}>\dots >q_0>0.$

Proof. 

For the proof of Lemma 1, see Ref [32].

3.2. Approximation in Space Direction

We apply the collocation method to approximate the spatial domain of Equation (1) with Jacobi polynomials. We consider the approximate solution $v_{\mathcal{N}}(x,t)$ of the form,

$$v_{\mathcal{N}}(x,t)=\sum _{s_1=0}^{\mathcal{N}}{c}_{s_1}\left(t\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x\right).$$

(22)

From Equations (22) and (1), we obtain

$$*{\mathcal{D}}_t^{\gamma }{v}_{\mathcal{N}}(x,t)=\frac{{\partial }^2{v}_{\mathcal{N}}(x,t)}{\partial x^2}+g(x,t),t\in [0,\tau ],$$

(23)

with the initial and boundary conditions of Equation (1),

$$\begin{array}{cc}\hfill v_{\mathcal{N}}(x_0,t)& =\sum _{s_1=0}^{\mathcal{N}}{c}_{s_1}\left(t\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x_0\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill v_{\mathcal{N}}(x_{\mathcal{N}},t)& =\sum _{s_1=0}^{\mathcal{N}}{c}_{s_1}\left(t\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x_{\mathcal{N}}\right).\hfill \end{array}$$

(25)

From Equations (1), (19), and (22), we have the semi-discretized scheme as follows

$$\begin{array}{cc}\hfill \sum _{s_1=0}^{\mathcal{N}}\left[\frac{{\left[w\left(t_r\right)\right]}^{-1}}{\mathrm{\Gamma }(2-\gamma )}\sum _{l=1}^r{q}_l[w\left(t_l\right)c_{s_1}\left(t_l\right)-w\left(t_{l-1}\right)c_{s_1}\left(t_{l-1}\right)]\right]{\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x\right)& \hfill \\ \hfill =\sum _{s_1=0}^{\mathcal{N}}{c}_{s_1}\left(t_r\right)\frac{\mathrm{\Gamma }(\alpha +\beta +s_1+3)}{\mathrm{\Gamma }(\alpha +\beta +s_1+1)}{\mathcal{J}}_{s_1-2}^{(\alpha +2,\beta +2)}\left(x\right)\\ \hfill +{\mathcal{R}}_r+{\mathcal{R}}_s+g(x,t_r),r=1,2,\dots ,\mathcal{M},\end{array}$$

(26)

where ${\mathcal{R}}_s$ denotes the error term in the space direction arising due to replacing $v(x,t)$ with $v_{\mathcal{N}}(x,t)$.

Neglecting the error part, we obtain the fully discretized scheme of Equation (1) by the collocation method [32,33]. We choose the collocation points such that the stability is unchanged. So, we choose the collocation point of the form $x_i,i=1,2,\dots \mathcal{N}-1$, which are the roots of the nth degree Jacobi polynomials, and $x_0$, $x_{\mathcal{N}}$ are the boundary conditions. Thus, for $(x_i,t_r)\in (0,1)\times [0,\tau ],i=1,\dots ,\mathcal{N};r=1,\dots \mathcal{M},$ it holds that

$$\begin{array}{c}\hfill \sum _{s_1=0}^{\mathcal{N}}\left[\frac{{\left[w\left(t_r\right)\right]}^{-1}}{\mathrm{\Gamma }(2-\gamma )}\sum _{l=1}^r{q}_l[w\left(t_l\right)c_{s_1}\left(t_l\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x_i\right)-w\left(t_{l-1}\right)c_{s_1}\left(t_{l-1}\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x_i\right)]\right]\\ \hfill =\sum _{s_1=0}^{\mathcal{N}}{c}_{s_1}\left(t_r\right)\frac{\mathrm{\Gamma }(\alpha +\beta +s_1+3)}{\mathrm{\Gamma }(\alpha +\beta +s_1+1)}{\mathcal{J}}_{s_1-2}^{(\alpha +2,\beta +2)}\left(x_i\right)+g(x_i,t_r),r=1,2,\dots ,\mathcal{M},\end{array}$$

(27)

and the initial and boundary conditions become

$$\left\{\begin{array}{c}{v}_{\mathcal{N}}(x_i,0)=\sum _{s=0}^{\mathcal{N}}{c}_{s_1}\left(0\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x_i\right)={\eta }_1\left(x_i\right),\hfill \\ v_{\mathcal{N}}(x_0,t_r)=\sum _{s_1=0}^{\mathcal{N}}{c}_{s_1}\left(t_r\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x_0\right)={\eta }_2\left(t_r\right),\hfill \\ v_{\mathcal{N}}(x_{\mathcal{N}},t_r)=\sum _{s_1=0}^{\mathcal{N}}{c}_{s_1}\left(t_r\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x_{\mathcal{N}}\right)={\eta }_3\left(t_r\right).\hfill \end{array}\right.$$

(28)

In this way, from Equations (27)–(28) we have a system of $(\mathcal{N}+1)$ linear difference equations in unknown coefficients $c_{s_1},s_1=0,1,2\dots \mathcal{N}$. We can find the value of the unknown coefficients by solving the system of linear equations using any standard method. Hence, the approximate solution can be found from Equation (22).

4. Error and Convergence Analysis

In this section, we discuss the error and convergence analysis of the proposed numerical method for Equation (1). We prove the error and convergence analysis analytically with the help of the following lemma and theorems.

Lemma 2

([32]). The truncation error ${\mathcal{R}}_r$ defined by Equation (21) satisfies

$${\mathcal{R}}_r\le \left[\frac{1}{8w_r\mathrm{\Gamma }(1-\gamma )}+\frac{\gamma }{2w_r\mathrm{\Gamma }(3-\gamma )}\right]\underset{t_0\le \eta \le t_r}{max}\left|{\mathcal{U}}^{″}\left(\eta \right)\mathcal{L}\right|\Delta t^{2-\gamma },$$

(29)

where $\mathcal{U}\left(\eta \right)$ is the approximating function, $w_r$ is the weight function at node $t_r$ for $r=1,2\dots \mathcal{M}$, and $\mathcal{L}$ is the Lipschitz constant on the interval $[t_{l-1},t_l]$.

Proof. 

For the detailed proof of this lemma, we refer to [32].

Theorem 1.

The error in approximation of the function $v\left(x\right)$ by the first m terms of the series in Equation (16) is bounded by the sum of the absolute values of all the neglected coefficients in the series, i.e.,

$${\mathcal{E}}_{\tau }\left(\mathcal{N}\right)=|v\left(x\right)-v_{\mathcal{N}}\left(x\right)|\le \sum _{i=m+1}^{\infty }\left|c_i\right|,$$

(30)

$\forall v\left(x\right),\forall m,$ and $x\in [0,1].$

Proof. 

The proof is trivial since $|{\mathcal{J}}_i^{\alpha ,\beta }\left(x\right)|\le 1,\forall x\in [0,1]$ and $i\ge 0$.

Theorem 2.

Let $v\left(x\right)$ be the square integrable function defined on $[0,1]$ and $\left|v\left(x\right)\right|\le {\mathcal{M}}_1$, where ${\mathcal{M}}_1$ is constant. Then, the $v\left(x\right)$ can be expanded with an infinite sum of Jacobi polynomials, and the infinite series converges to $v\left(x\right)$ uniformly, i.e.,

$$v\left(x\right)=\sum _{i=0}^{\infty }{c}_i{\mathcal{J}}_n^{\alpha ,\beta }\left(x\right),$$

(31)

where

$$|c_i|\le \frac{{\mathcal{M}}_1\mathrm{\Gamma }(1+\beta )}{\mathrm{\Gamma }(2+\alpha +\beta )}\frac{1}{i^3},i>1,$$

and ${\mathcal{E}}_m\to$ 0.

Proof. 

From Equations (16) and (18), we have

$$v_m\left(x\right)=\sum _{i=0}^m{c}_i{\mathcal{J}}_i^{\alpha ,\beta }\left(x\right),$$

(32)

where $c_i$ are the unknown coefficients. Furthermore, from Equation (17), we obtain

$$\begin{array}{cc}\hfill c_i& =\frac{1}{{\mathcal{H}}_i^{\alpha ,\beta }}{\int }_0^1{\left(x\right)}^{\beta }{(1-x)}^{\alpha }v\left(x\right){\mathcal{J}}_i^{\alpha ,\beta }\left(x\right)dx,\hfill \\ \hfill |c_i|& =\left|\frac{1}{{\mathcal{H}}_i^{\alpha ,\beta }}{\int }_0^1{\left(x\right)}^{\beta }{(1-x)}^{\alpha }v\left(x\right){\mathcal{J}}_i^{\alpha ,\beta }\left(x\right)\right|dx,\hfill \\ \hfill & \le \frac{{\mathcal{M}}_1}{{\mathcal{H}}_i^{\alpha ,\beta }}{\int }_0^1\left|{\left(x\right)}^{\beta }{(1-x)}^{\alpha }{\mathcal{J}}_i^{\alpha ,\beta }\left(x\right)\right|dx,\hfill \\ \hfill & \le \frac{{\mathcal{M}}_1}{{\mathcal{H}}_i^{\alpha ,\beta }}\frac{\mathrm{\Gamma }(\alpha +i+1)}{i!\mathrm{\Gamma }(\alpha +\beta +i+1)}\sum _{m=0}^i\left(\genfrac{}{}{0pt}{}{i}{m}\right)\frac{\mathrm{\Gamma }(\alpha +\beta +i+m+1)}{\mathrm{\Gamma }(\alpha +m+1)}{\int }_0^1\left|x^{\beta }{(1-x)}^{\alpha }{(x-1)}^m\right|dx,\hfill \\ \hfill & \le \frac{{\mathcal{M}}_1(2i+1+\alpha +\beta )\mathrm{\Gamma }(i+1+\alpha +\beta )\mathrm{\Gamma }(1+\beta )}{\mathrm{\Gamma }(i+1+\beta )\mathrm{\Gamma }(2+\alpha +\beta )}\frac{1}{i^4},\hfill \\ \hfill & \le \frac{{\mathcal{M}}_1\mathrm{\Gamma }(1+\beta )}{\mathrm{\Gamma }(2+\alpha +\beta )}\frac{1}{i^3}.\hfill \end{array}$$

(33)

Hence, the series $v_m\left(x\right)$ converges to $v\left(x\right)$ uniformly.

Theorem 3.

Let $h\left(t\right)$ be $\mathcal{N}$ times differentiable function defined on interval $[0,\tau ]$. Let $v_{\mathcal{N}}\left(t\right)={\sum }_{j_1}^{\mathcal{N}}{c}_{j_1}{\mathcal{J}}_{j_1}^{\alpha ,\beta }\left(t\right)$ be the approximation of $h\left(t\right)$, then

$$\parallel h\left(t\right)-v_{\mathcal{N}}\left(t\right)\parallel \le \frac{\mathcal{M}{\mathcal{S}}^{n+1}}{\left(\right(\mathcal{N}+1)!)}\sqrt{{\mathcal{B}}_{\tau }(1+\alpha ,1+\beta )},$$

(34)

where $\mathcal{M}={max}_{t\in [0,\tau ]}{h}^{\mathcal{N}+1}\left(t\right)$, $\mathcal{S}=max\{\tau -t_0,t_0\}$ and ${\mathcal{B}}_{\tau }(1+\alpha ,1+\beta )$ denote the incomplete Beta function. At $\tau =1$, it reduces to the standard Beta function.

Proof. 

By the Taylor series expansion, we have

$$h\left(t\right)=h\left(t_0\right)+h^{{}^{\prime }}\left(t_0\right)(t-t_0)+\dots +h^{\mathcal{N}}\left(t_0\right)\frac{{(t-t_0)}^{\mathcal{N}}}{\mathcal{N}!}+h^{\mathcal{N}+1}\left(t\right)\frac{{(t-t_0)}^{\mathcal{N}+1}}{(\mathcal{N}+1)!},$$

(35)

where $t_0\in [0,\tau ]$ and $\zeta \in [t_0,t]$. Let

$${\mathcal{P}}_{\mathcal{N}}\left(t\right)=f\left(t_0\right)+f^{{}^{\prime }}\left(t_0\right)(t-t_0)+\dots +\frac{f^{\mathcal{N}}\left(t_0\right){(t-t_0)}^{\mathcal{N}}}{\mathcal{N}!},$$

(36)

then

$$|h\left(t\right)-{\mathcal{P}}_{\mathcal{N}}\left(t\right)|=\left|h^{\mathcal{N}+1}\left(t\right)\frac{{(t-t_0)}^{\mathcal{N}+1}}{(\mathcal{N}+1)!}\right|.$$

(37)

Since, we assume that $v_{\mathcal{N}}\left(t\right)$ is the best square approximation of $h\left(t\right)$, we have

$$\begin{array}{cc}\hfill \parallel h\left(t\right)-v_{\mathcal{N}}{\left(t\right)\parallel }^2& \le \parallel h\left(t\right)-{\mathcal{P}}_{\mathcal{N}}{\left(t\right)\parallel }^2,\hfill \\ \hfill & ={\int }_0^{\tau }w\left(t\right){[h\left(t\right)-{\mathcal{P}}_{\mathcal{N}}\left(t\right)]}^{2}dt,\hfill \\ \hfill & ={\int }_0^{\tau }{\left[h^{\mathcal{N}+1}\left(t\right)\frac{{(t-t_0)}^{\mathcal{N}+1}}{(\mathcal{N}+1)!}\right]}^{2}dt,\hfill \\ \hfill & \le \frac{{\mathcal{M}}^2}{{((\mathcal{N}+1)!)}^2}{\int }_0^{\tau }{(t-t_0)}^{2n+2}w\left(t\right)dt,\hfill \\ \hfill & \le \frac{{\mathcal{M}}^2{\mathcal{S}}^{2n+2}}{{((\mathcal{N}+1)!)}^2}{\int }_0^{\tau }{\left(t\right)}^{\beta }{(1-t)}^{\alpha }dt,\hfill \\ \hfill & =\frac{{\mathcal{M}}^2{\mathcal{S}}^{2n+2}}{{((\mathcal{N}+1)!)}^2}{\mathcal{B}}_{\tau }(1+\alpha ,1+\beta ).\hfill \end{array}$$

(38)

Hence,

$$\parallel h\left(t\right)-v_{\mathcal{N}}\left(t\right)\parallel \le \frac{\mathcal{M}{\mathcal{S}}^{n+1}}{\left(\right(\mathcal{N}+1)!)}\sqrt{{\mathcal{B}}_{\tau }(1+\alpha ,1+\beta )}.$$

(39)

Theorem 4.

Let $v(x,t)$ be a continuous function satisfying the conditions (2) for any t, and $g(x,t)$ is continuous. Assuming $v_{\mathcal{N}}(x,t_r)=v_{\mathcal{N}}^r\left(x\right)={\sum }_{s_1=0}^{\mathcal{N}}{c}_{s_1}\left(t_r\right){\mathcal{J}}_{s_1}^{\alpha ,\beta }\left(x\right)$ is the numerical approximation of the scheme (27), then the scheme (27) is unconditionally stable, and for any $r\ge 0$, it holds that

$$\parallel v_{\mathcal{N}}^r{\left(x\right)\parallel }_{L^2}\le \frac{w_0}{w_r}\parallel v_{\mathcal{N}}^0{\left(x\right)\parallel }_{L^2}+\sum _{l=1}^{r-1}\frac{h_l}{w_r}\parallel g^l{\parallel }_{L^2}+\frac{{\eta }_r}{q_r{w}_r}{\parallel g^r\parallel }_{L^2},$$

(40)

where $g(x,t_r)=g^r\left(x\right)$, and $h_l=\left(\frac{1}{q_l}-\frac{1}{q_{l+1}}\right){\eta }_l,l=1,2,\dots r-1$.

Proof. 

The proof of this theorem is similar to the Theorem 1 of [32]. In [32], the authors proved the stability for the time-fractional KdV equation. Here, we extend the proof for the time-fractional diffusion equation. To prove Theorem 4, we first rewrite Equation (26) over the summation up to time step $t_{r-1}$ in discrete form. Thus, we have

$$\begin{array}{c}\hfill \frac{1}{{\eta }_r}{q}_r{w}_{r}v(x,t_r)=\frac{1}{{\eta }_r}\left[\sum _{l=1}^{r-1}(q_{l+1}-q_l)w_{l}v(x,t_l)+q_1{w}_{0}v(x,t_0)\right]+v^{″}(x,t_r)+g(x,t_r),\end{array}$$

(41)

where $r=1,2,..\mathcal{M}$, and ${\eta }_l=w_l\mathrm{\Gamma }(2-\gamma )$.

Let $w^{\alpha ,\beta }\left(x\right)=x^{\beta }{(1-x)}^{\alpha }$, and $u_{\mathcal{N}-2}^r\left(x\right)=u_{\mathcal{N}-2}(x,t_r)$ is the polynomial of $\mathcal{N}-2$ degree satisfying $v_{\mathcal{N}}^r\left(x\right)=u_{\mathcal{N}-2}^r\left(x\right)w^{\alpha ,\beta }\left(x\right)$. Multiplying both sides of Equation (41) by $u_{\mathcal{N}-2}(x_i,t_r)w^{\alpha ,\beta }\left(x_i\right)$, and taking the summation on i from 0 to $\mathcal{N}$, we have

$$\begin{array}{cc}\hfill \sum _{i=0}^N\left[\frac{1}{{\eta }_r}{q}_r{w}_{r}v(x_i,t_r)\right]u_{\mathcal{N}-2}(x_i,t_r)w^{\alpha ,\beta }\left(x_i\right)& =\sum _{i=0}^N\frac{1}{{\eta }_r}\left[\sum _{l=1}^{r-1}(q_{l+1}-q_l)w_{l}v(x_i,t_l)+q_1{w}_{0}v(x_i,t_0)\right]\hfill \\ \hfill & +\frac{1}{{\eta }_r}\left[v^{″}(x_i,t_r)+g(x_i,t_r)u_{\mathcal{N}-2}(x_i,t_r)w^{\alpha ,\beta }\left(x_i\right)\right],\hfill \end{array}$$

(42)

where $w^{\alpha ,\beta }\left(x_i\right)$ is the corresponding weight function. Since the degree of $v_{\mathcal{N}}^r$(x) does not exceed $\mathcal{N}+1$, then from Equation (11),

$${(v_{\mathcal{N}}^r,u_{\mathcal{N}-2}^r)}_{w^{\alpha ,\beta }\left(x\right)}=(v_{\mathcal{N}}^r,v_{\mathcal{N}}^r).$$

(43)

It can be easily shown that

$${\int }_0^1{v}^{″}(x,t_r)u_{\mathcal{N}-2}(x,t_r)w^{\alpha ,\beta }(x,t_r)dx={\int }_0^1{v}^{″}(x,t_r)v(x,t_r)w^{\alpha ,\beta }(x,t_r)dx=0.$$

(44)

Now, the discrete form of the Equation (42) at the nodes $x_i$ can be rewritten as

$$q_r{w}_r\parallel v_{\mathcal{N}}^r{\left(x\right)\parallel }_{L^2}\le \sum _{l=1}^{r-1}(q_{l+1}-q_l)w_l\parallel v_{\mathcal{N}}^l\left(x\right){\parallel }_{L^2}+q_1{w}_0\parallel v_{\mathcal{N}}^0\left(x\right){\parallel }_{L^2}+{\eta }_r{\parallel g^r\left(x\right)\parallel }_{L^2},$$

(45)

by using the Cauchy–Schwartz inequality and Lemma (1). The remaining part of the proof can be completed following similar steps to those shown in Theorem 1 of [32].

5. Numerical Results

In this section, we provide two numerical examples to validate the presented finite difference–collocation method. In the given examples, we calculate the maximum absolute error (MAE), absolute error (AE), and the order of convergence (CO) for each example. With the help of the MAE and CO, we analyze the error and convergence analysis numerically. Furthermore, we have plotted the graphs of the numerical solutions by changing the various parameters of $\gamma ,\alpha ,\beta$, and scale function $z\left(t\right)$. For the numerical simulations, we take the weight function $w\left(t\right)=1$. All numerical simulations were performed with Mathematica software.

The MAE at time t is given by

$${\mathcal{E}}_n\left(t\right)=\underset{0\le x\le 1}{max}|v(x,t)-v_{\mathcal{N}}(x,t)|,$$

(46)

and the order of convergence is defined by

$$CO=\frac{log\left(\frac{{\mathcal{E}}_{n_1}\left(t\right)}{{\mathcal{E}}_{n_2}\left(t\right)}\right)}{log\left(\frac{n_2}{n_1}\right)},$$

(47)

where $v(x,t)$ and $v_{\mathcal{N}}(x,t)$ are the exact and approximate solutions, respectively. ${\mathcal{E}}_{n_1}\left(t\right)$ and ${\mathcal{E}}_{n_2}\left(t\right)$ are the MAEs for two consecutive values $n_1$ and $n_2$.

Example 1.

Here, we consider the generalized version of the problem given in [34] as

$$*{\mathcal{D}}_t^{\gamma }v(x,t)-\frac{x^2}{2}\frac{{\partial }^{2}v(x,t)}{\partial x^2}=0,t\in [0,\tau ],$$

(48)

the initial and boundary conditions are given by

$$\left\{\begin{array}{c}v(x,0)=x^2,0\le x\le 1,\hfill \\ v(0,t)=0,v(1,t)=e^{t+\gamma },0\le t\le \tau .\hfill \end{array}\right.$$

(49)

The exact solution of Example (1) is $x^2{e}^{t+\gamma }.$ This problem is solved for various values of $\mathcal{N},\gamma ,z\left(t\right)$, and t. In Table 1 and Table 2, we compare the results obtained by our technique to the given methods in [35,36,37] at $\gamma =0$. We observed that the results obtained by the present method (PM) provided a better approximation for this problem. In Table 3, we have discussed the MAE and CO for various values of $\gamma$ and $\mathcal{M}$. Further, in Figure 1, we plotted the AE comparison graphs for different values of $\gamma$ and observe that the numerical approximation showed good agreement with the exact solution. Figure 2 shows the behavior of the AEs for various values of $\mathcal{N}$ with a fixed $\gamma =0.2$. We observe from Figure 2 that the numerical solution at $\mathcal{N}=6,8$ showed good agreement with the exact solution at $\gamma =0.2$. Finally, in Figure 3, we plotted the numerical solutions for the various values of $\gamma =0.1,0.3,0.5,0.7,0.9$ for a fixed value of $\mathcal{N}=5$.

Table 1. Comparison of MAE for Example 1 with $\gamma =0.75,z\left(t\right)=t$.

t	x	Method of [35]	Method of [36]	Method of [37]	Present Method
0.25	0.3	$1.312\times {10}^{-1}$	$1.346\times {10}^{-1}$	$1.293\times {10}^{-1}$	8.009 $\times {10}^{-2}$
.	0.6	$4.957\times {10}^{-1}$	$5.385\times {10}^{-1}$	$5.175\times {10}^{-1}$	1.313 $\times {10}^{-2}$
.	0.9	$1.055\times {10}^{-1}$	$1.211\times {10}^0$	$1.164\times {10}^0$	6.041 $\times {10}^{-2}$
0.5	0.3	$1.685\times {10}^{-1}$	$1.795\times {10}^{-1}$	$1.695\times {10}^{-1}$	6.342 $\times {10}^{-2}$
.	0.6	$6.303\times {10}^{-1}$	$7.183\times {10}^{-1}$	$6.780\times {10}^{-1}$	9.543 $\times {10}^{-2}$
.	0.9	$1.352\times {10}^0$	$1.616\times {10}^{-1}$	$1.525\times {10}^{-1}$	5.315$\times {10}^{-2}$
0.75	0.3	$2.118\times {10}^{-1}$	$2.313\times {10}^{-1}$	$2.154\times {10}^{-1}$	5.242 $\times {10}^{-2}$
.	0.6	$7.962\times {10}^{-1}$	$9.255\times {10}^{-1}$	$8.618\times {10}^{-1}$	6.875 $\times {10}^{-2}$
.	0.9	$1.733\times {10}^0$	$2.082\times {10}^0$	$1.939\times {10}^0$	4.891 $\times {10}^{-2}$
1	0.3	$2.645\times {10}^{-1}$	$2.909\times {10}^{-1}$	$2.687\times {10}^{-1}$	4.349 $\times {10}^{-2}$
.	0.6	$9.745\times {10}^{-1}$	$1.163\times {10}^0$	$1.075\times {10}^0$	4.802 $\times {10}^{-2}$
.	0.9	$2.014\times {10}^0$	$2.618\times {10}^0$	$2.419\times {10}^0$	1.048 $\times {10}^{-2}$

Table 2. Comparison of MAE for Example 1 with $\gamma =0.9,z\left(t\right)=t$.

t	x	Method of [35]	Method of [36]	Method of [37]	Present Method
0.25	0.3	$1.122\times {10}^{-1}$	$1.218\times {10}^{-1}$	$1.210\times {10}^{-1}$	9.795 $\times {10}^{-2}$
.	0.6	$4.762\times {10}^{-1}$	$4.872\times {10}^{-1}$	$4.841\times {10}^{-1}$	1.543 $\times {10}^{-1}$
.	0.9	$1.046\times {10}^0$	$1.096\times {10}^0$	$1.089\times {10}^0$	5.303 $\times {10}^{-3}$
0.5	0.3	$1.564\times {10}^{-1}$	$1.588\times {10}^{-1}$	$1.567\times {10}^{-1}$	7.852 $\times {10}^{-2}$
.	0.6	$6.086\times {10}^{-1}$	$6.355\times {10}^{-1}$	$6.268\times {10}^{-1}$	1.129 $\times {10}^{-1}$
.	0.9	$1.342\times {10}^0$	$1.429\times {10}^0$	$1.410\times {10}^0$	9.122 $\times {10}^{-2}$
0.75	0.3	$1.9948\times {10}^{-1}$	$2.041\times {10}^{-1}$	$1.998\times {10}^{-1}$	6.677 $\times {10}^{-2}$
.	0.6	$7.761\times {10}^{-1}$	$8.165\times {10}^{-1}$	$7.992\times {10}^{-1}$	9.517 $\times {10}^{-2}$
.	0.9	$1.722\times {10}^0$	$1.837\times {10}^0$	$1.798\times {10}^0$	5.475 $\times {10}^{-2}$
1	0.3	$2.529\times {10}^{-1}$	$2.588\times {10}^{-1}$	$2.517\times {10}^{-1}$	5.719 $\times {10}^{-2}$
.	0.6	$9.938\times {10}^{-1}$	$1.035\times {10}^0$	$1.007\times {10}^0$	6.471 $\times {10}^{-2}$
.	0.9	$2.144\times {10}^0$	$2.329\times {10}^0$	$2.265\times {10}^0$	1.964 $\times {10}^{-2}$

Table 3. The CO and MAE for Example 1 with various values of $\gamma$ and $z\left(t\right)=t^2$.

	$\mathit{\gamma }=0.3$		$\mathit{\gamma }=0.5$		$\mathit{\gamma }=0.7$
$\mathcal{M}$	MAE	CO	MAE of PM	CO	MAE of PM	CO
50	$2.637\times {10}^{-1}$	⋯	$4.921\times {10}^{-1}$	⋯	$7.994\times {10}^{-1}$	⋯
100	$9.246\times {10}^{-2}$	$1.617$	$1.839\times {10}^{-1}$	$1.419$	$3.310\times {10}^{-1}$	$1.263$
200	$2.919\times {10}^{-2}$	$1.663$	$6.782\times {10}^{-2}$	$1.439$	$1.380\times {10}^{-1}$	$1.270$
400	$9.186\times {10}^{-3}$	$1.667$	$2.464\times {10}^{-2}$	$1.460$	$5.677\times {10}^{-2}$	$1.282$
800	$2.850\times {10}^{-3}$	$1.688$	$8.878\times {10}^{-3}$	$1.473$	$2.344\times {10}^{-2}$	$1.275$

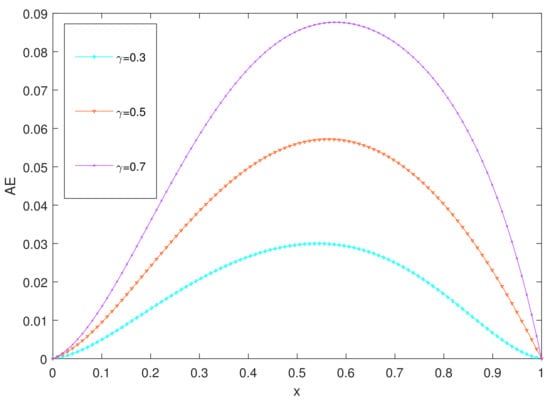
Figure 1. Comparison of AE at $t=0.5,\mathcal{N}=5,z\left(t\right)=t$, and different values of $\gamma$ for Example 1.

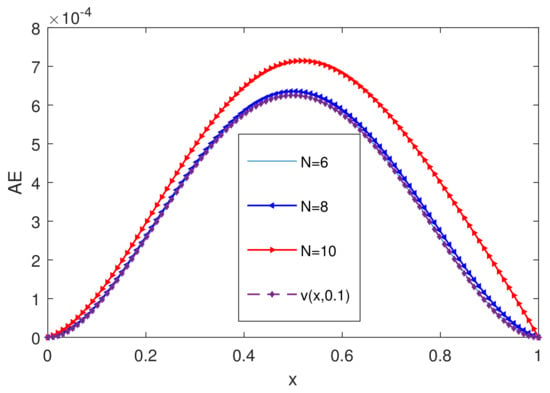
Figure 2. Plot of AE for different values of $\mathcal{N}$ at $t=0.1$ and $z\left(t\right)=t$ for Example 1.

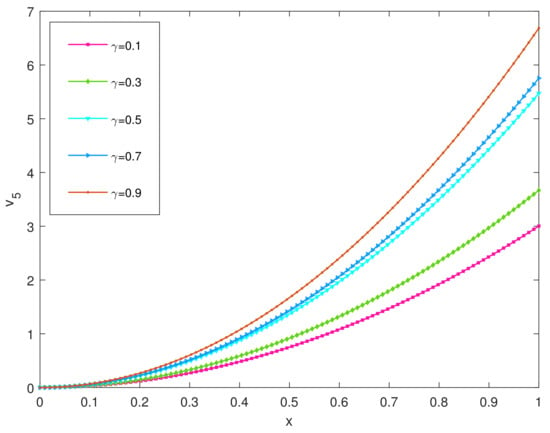
Figure 3. Comparison of the numerical solution for different values of $\gamma$ at $t=1$ and $z\left(t\right)=t^2$ for Example 1.

Example 2.

Consider the following Example [34],

$$*{\mathcal{D}}_t^{\gamma }v(x,t)=\frac{{\partial }^{2}v(x,t)}{\partial x^2}+g(x,t),t\in [0,\tau ],$$

(50)

where

$$g(x,t)=4{\pi }^2{t}^{2}sin\left(2\pi x\right)+\frac{2t^{2-\gamma }sin\left(2\pi x\right)}{(2-3\gamma +{\gamma }^2)\mathrm{\Gamma }(1-\gamma )},$$

with the initial and boundary conditions given by,

$$\left\{\begin{array}{c}v(x,0)=0,\hfill \\ v(0,t)=0,v(1,t)=0.\hfill \end{array}\right.$$

(51)

The exact solution for this Example (2) is $t^{2}sin\left(2\pi x\right)$.

We shall apply the numerical scheme (26) to solve this problem (2) for different values of $\mathcal{N}$ with $z\left(t\right)=t$ varying the fractional order $\gamma =0.1,0.3,0.5,0.7$. We obtain the AEs at the grid points in the given domain, which are shown in Table 4 and Table 5, respectively. The results presented in Table 4 and Table 5 establish the convergence of the proposed method for different values of $\gamma$. In Table 6, we show the MAE by varying the different values of $\gamma =0.3,0.5,0.7$ and $\mathcal{M}$. Further, we show the CO for each value of $\gamma$, which proves the accuracy of the present method. In Figure 4, we compared the numerical solutions for various choices of $\gamma$ with the exact solution known at $\gamma =0.2$. In Figure 5, the solution graphs for different values of $\mathcal{N}$ and plot of the exact solution (for $\gamma =0.2$) are shown. From Figure 4 and Figure 5, we conclude that the numerical solution obtained by the proposed method converges to the exact solution. Finally, we compared our results with the existing method [34] in Table 7. We see that the proposed method gives better accuracy in approximating the numerical solutions.

Table 4. Comparison of AE for Example 2 at $\gamma =0.1,0.3$ and various values of $\mathcal{N}$.

	$\mathit{\gamma }=0.1$			$\mathit{\gamma }=0.3$
$\mathbf{x}$	$\mathcal{N}=\mathbf{5}$	$\mathcal{N}=\mathbf{7}$	$\mathcal{N}=\mathbf{9}$	$\mathcal{N}=\mathbf{5}$	$\mathcal{N}=\mathbf{7}$	$\mathcal{N}=\mathbf{9}$
0.1	$5.899\times {10}^{-4}$	$4.786\times {10}^{-5}$	$2.407\times {10}^{-6}$	$5.801\times {10}^{-4}$	$4.707\times {10}^{-5}$	$2.352\times {10}^{-6}$
0.2	$3.927\times {10}^{-4}$	$3.174\times {10}^{-5}$	$1.694\times {10}^{-6}$	$3.801\times {10}^{-4}$	$3.074\times {10}^{-5}$	$1.618\times {10}^{-4}$
0.3	$2.403\times {10}^{-4}$	$2.173\times {10}^{-5}$	$1.126\times {10}^{-6}$	$2.296\times {10}^{-4}$	$2.087\times {10}^{-5}$	$1.058\times {10}^{-6}$
0.4	$1.376\times {10}^{-4}$	$1.057\times {10}^{-5}$	$5.571\times {10}^{-6}$	$1.315\times {10}^{-4}$	$1.008\times {10}^{-5}$	$5.174\times {10}^{-7}$
0.5	$1.051\times {10}^{-18}$	$7.952\times {10}^{-20}$	$3.281\times {10}^{-19}$	$1.233\times {10}^{-4}$	$1.067\times {10}^{-18}$	$5.225\times {10}^{-19}$
0.6	$1.436\times {10}^{-4}$	$1.045\times {10}^{-5}$	$5.560\times {10}^{-7}$	$1.246\times {10}^{-4}$	$1.000\times {10}^{-5}$	$5.186\times {10}^{-7}$
0.7	$2.313\times {10}^{-4}$	$2.343\times {10}^{-5}$	$1.344\times {10}^{-6}$	$2.378\times {10}^{-4}$	$2.066\times {10}^{-4}$	$1.077\times {10}^{-6}$
0.8	$3.567\times {10}^{-4}$	$3.164\times {10}^{-5}$	$1.678\times {10}^{-6}$	$3.875\times {10}^{-4}$	$3.099\times {10}^{-5}$	$1.623\times {10}^{-6}$
0.9	$5.679\times {10}^{-4}$	$4.567\times {10}^{-5}$	$2.457\times {10}^{-6}$	$5.112\times {10}^{-4}$	$4.888\times {10}^{-5}$	$2.399\times {10}^{-6}$

Table 5. Comparison of AE for Example 2 at $\gamma =0.5,0.7$ and various values of $\mathcal{N}$.

	$\mathit{\gamma }=0.5$			$\mathit{\gamma }=0.7$
$\mathbf{x}$	$\mathcal{N}=\mathbf{5}$	$\mathcal{N}=\mathbf{7}$	$\mathcal{N}=\mathbf{9}$	$\mathcal{N}=\mathbf{5}$	$\mathcal{N}=\mathbf{7}$	$\mathcal{N}=\mathbf{9}$
0.1	$3.386\times {10}^{-5}$	$4.579\times {10}^{-5}$	$2.194\times {10}^{-6}$	$5.350\times {10}^{-4}$	$4.407\times {10}^{-5}$	$2.406\times {10}^{-6}$
0.2	$6.886\times {10}^{-4}$	$2.914\times {10}^{-5}$	$1.387\times {10}^{-6}$	$3.230\times {10}^{-4}$	$2.717\times {10}^{-5}$	$1.694\times {10}^{-6}$
0.3	$8.617\times {10}^{-4}$	$1.953\times {10}^{-5}$	$8.399\times {10}^{-7}$	$1.815\times {10}^{-4}$	$1.800\times {10}^{-5}$	$1.126\times {10}^{-6}$
0.4	$5.455\times {10}^{-4}$	$9.335\times {10}^{-6}$	$3.863\times {10}^{-7}$	$1.047\times {10}^{-4}$	$8.528\times {10}^{-6}$	$5.570\times {10}^{-7}$
0.5	$1.191\times {10}^{-18}$	$1.087\times {10}^{-18}$	$5.186\times {10}^{-18}$	$6.447\times {10}^{-19}$	$3.683\times {10}^{-18}$	$3.280\times {10}^{-19}$
0.6	$5.575\times {10}^{-4}$	$9.435\times {10}^{-6}$	$3.789\times {10}^{-7}$	$1.046\times {10}^{-4}$	$8.546\times {10}^{-6}$	$5.580\times {10}^{-7}$
0.7	$8.637\times {10}^{-4}$	$1.944\times {10}^{-6}$	$8.457\times {10}^{-7}$	$1.824\times {10}^{-4}$	$1.890\times {10}^{-5}$	$1.136\times {10}^{-6}$
0.8	$6.745\times {10}^{-4}$	$2.879\times {10}^{-5}$	$1.478\times {10}^{-6}$	$3.320\times {10}^{-4}$	$2.654\times {10}^{-5}$	$1.794\times {10}^{-6}$
0.9	$3.378\times {10}^{-4}$	$4.543\times {10}^{-5}$	$2.148\times {10}^{-6}$	$5.458\times {10}^{-4}$	$4.568\times {10}^{-5}$	$2.451\times {10}^{-6}$

Table 6. The MAE and CO for Example 2 for various values of $\gamma$ and $\mathcal{M}$.

	$\mathit{\gamma }=0.3$		$\mathit{\gamma }=0.5$		$\mathit{\gamma }=0.7$
$\mathcal{M}$	MAE	CO	MAE of PM	CO	MAE of PM	CO
50	$1.475\times {10}^{-6}$	⋯	$1.718\times {10}^{-6}$		$3.746\times {10}^{-6}$	⋯
100	$4.636\times {10}^{-6}$	$1.667$	$6.336\times {10}^{-6}$	$1.439$	$1.553\times {10}^{-6}$	$1.271$
200	$1.425\times {10}^{-6}$	$1.701$	$2.300\times {10}^{-6}$	$1.461$	$6.385\times {10}^{-7}$	$1.282$
400	$4.459\times {10}^{-7}$	$1.676$	$8.228\times {10}^{-7}$	$1.483$	$2.613\times {10}^{-7}$	$1.289$
800	$1.387\times {10}^{-7}$	$1.685$	$2.938\times {10}^{-7}$	$1.485$	$1.065\times {10}^{-7}$	$1.296$

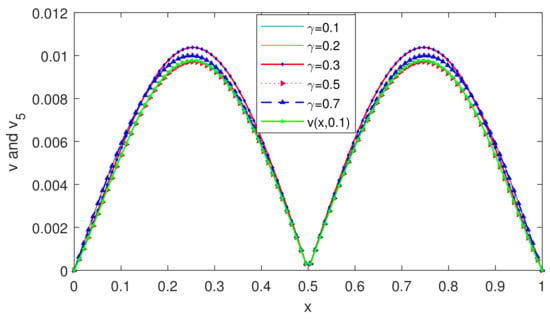
Figure 4. Comparison of the numerical and the exact solution at $t=0.1$ and different values of $\gamma$ for Example 2.

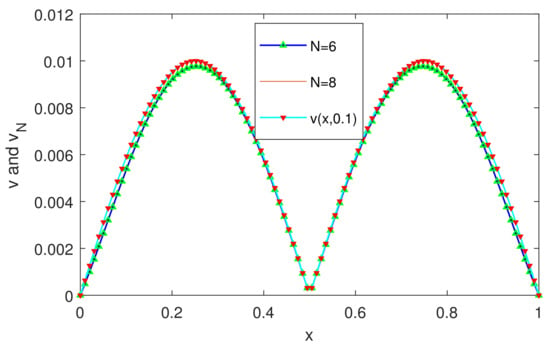
Figure 5. Plot of the numerical solutions for different values of $\mathcal{N}$ at $t=0.1$ for Example 2.

Table 7. Comparison of the MAE of Example 2 with $\gamma =0.5$.

$\mathcal{M}$	Present Method	Method [34]
2	$1.061\times {10}^{-4}$	$1.627\times {10}^{-1}$
4	$3.879\times {10}^{-5}$	$3.101\times {10}^{-2}$
6	$2.103\times {10}^{-5}$	$1.140\times {10}^{-2}$
8	$1.342\times {10}^{-5}$	$5.378\times {10}^{-3}$
10	$3.925\times {10}^{-6}$	$2.726\times {10}^{-3}$
12	$7.953\times {10}^{-7}$	$1.461\times {10}^{-3}$
14	$1.047\times {10}^{-6}$	$8.187\times {10}^{-4}$
16	$1.252\times {10}^{-6}$	$4.755\times {10}^{-4}$

6. Conclusions

A numerical scheme for a new class of fractional diffusion equation was studied in this paper in which the time derivative was considered as the generalized fractional derivative. The scheme used the finite difference and collocation methods to find the numerical solution. The theoretical error and convergence analysis were also validated numerically. The numerical examples showed that the proposed method achieved high accuracy in comparison to other methods [34,36,37,38] presented recently.