Exponential Stability of Highly Nonlinear Hybrid Differently Structured Neutral Stochastic Differential Equations with Unbounded Delays

Abstract

This paper mainly studies the exponential stability of the highly nonlinear hybrid neutral stochastic differential equations (NSDEs) with multiple unbounded time-dependent delays and different structures. We prove the existence and uniqueness of the exact global solution of the new stochastic system, and then give several criteria of the exponential stability, including the $q_1$th moment and almost surely exponential stability. Additionally, some numerical examples are given to illustrate the main results. Such systems are widely applied in physics and other fields. For example, a specific case is pantograph dynamics, in which the delay term is a proportional function. These are widely used to determine the motion of a pantograph head on an electric locomotive collecting current from an overhead trolley wire. Compared with the existing works, our results extend the single constant delay of coefficients to multiple unbounded time-dependent delays, which is more general and applicable.

1. Introduction

The neutral stochastic delay differential equations with Markov switching (the hybrid NSDDEs) are widely used in many fields such as physics, engineering, biology and finance, especially mechanics. The control theory, stability analysis and applications of NSDDEs, not only integer-order differential equations but also fractional-order differential equations, have attracted the attention of researchers recently. In the paper [1], the authors studied the approximate controllability of a semi-linear stochastic control system with nonlocal conditions in a Hilbert space. In the paper [2], the authors dealt with the complete controllability of a semi-linear stochastic system with delay under the assumption that the corresponding linear system is completely controllable. The paper [3] investigated the approximate controllability of fractional stochastic Sobolev-type Volterra–Fredholm integro-differential equation of order $1<r<2$. The paper [4] studied the time fractional system in the Caputo sense of fluid-conveying single-walled carbon nanotubes (SWCNT). In the applications, the papers [5,6] proposed stochastic delay differential models to investigate the dynamics of the transmission of COVID-19 and the prey–predator system with hunting cooperation in predators, respectively. In the current collection systems for an electric locomotive, there is a pantograph on the train roof collecting current from the overhead trolley wire suspended by regularly spaced stiff springs. The pantograph has two masses with a connecting spring and two velocity dampers. With the train moving at a constant speed, a contact force is exerted on the wire, so that the displacement of the wire can determine the motion of the pantograph head. The literature [7] modeled the above system by a pantograph differential equation in which the delay function is unbounded. Further, in [8], the authors discussed the exponential stability criteria of highly nonlinear neutral stochastic pantograph differential equations (NPSDEs) as a specific case of the NSDDEs with unbounded delay. Therefore, in this paper, it is of theoretical and practical significance to consider a more general and applicable system: the highly nonlinear hybrid differently structured NSDDE with unbounded delays. It will be introduced step by step below.

The hybrid NSDDEs are usually used to describe the stochastic systems depending on not only the present state but also the past state with its changing rate, and may encounter some abrupt changes. They are often modeled on ${\mathbb{R}}^d$ with the stochastic differential equation

$$d\left[x\right(t)-U(x(t-\tau )\left)\right]=F\left(x\right(t),x(t-\tau ),t,r(t\left)\right)dt+G\left(x\right(t),x(t-\tau ),t,r(t\left)\right)dW\left(t\right)$$

(1)

with the initial

$$\{x\left(\theta \right):-\tau \le \theta \le 0\}=\xi \in C_{{\mathcal{F}}_0}^b([-\tau ,0];{\mathbb{R}}^d),r\left(0\right)=i_0\in S,$$

(2)

where ${\left\{W\left(t\right)\right\}}_{t\ge 0}$ is an m-dimensional standard Brownian motion in a filtered complete probability space $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$. ${\left\{r\left(t\right)\right\}}_{t\ge 0}$ is a right continuous homogeneous Markovian chain with the finite state space $S=\{1,2,\cdots ,N\}$ and generator $\Gamma ={\left({\gamma }_{ij}\right)}_{N\times N}.$ Additionally, it is independent of ${\left\{W\left(t\right)\right\}}_{t\ge 0}.$ $U\left(x\right):{\mathbb{R}}^d\to {\mathbb{R}}^d$ is the neutral term. $\tau$ is the constant time delay. $F:{\mathbb{R}}^d\times {\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S\to {\mathbb{R}}^d$ and $G:{\mathbb{R}}^d\times {\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S\to {\mathbb{R}}^{d\times m}$ are drift and diffusion coefficients, respectively. ${\mathbb{R}}_{+}=[0,\infty ).$ For the given $\tau \ge 0,$$C([-\tau ,0];{\mathbb{R}}^d)$ denotes the family of all continuous function $\xi :[-\tau ,0]\to {\mathbb{R}}^d$ with the norm $\parallel \xi \parallel ={sup}_{-\tau \le \theta \le 0}\left|\xi \left(\theta \right)\right|.$$C_{{\mathcal{F}}_0}^b([-\tau ,0];{\mathbb{R}}^d)$ denotes the set of all bounded and ${\mathcal{F}}_0$-measurable $C([-\tau ,0];{\mathbb{R}}^d)$-valued random variables. The authors in [9,10] studied the exponential stability of the exact solution and numerical solution for NSDDEs. In [11], the authors investigated the almost surely asymptotic stability of NSDDEs.

In many practical situations, the hybrid NSDDEs often have multiple delays. The delay term “$x(t-\tau )$” is replaced by “$x(t-{\tau }_1),\cdots ,x(t-{\tau }_n)$”, where ${\tau }_1,\cdots ,{\tau }_n$ are positive constants. The authors in [12,13] established the stability criteria of hybrid multiple-delay NSDDEs. In [14], the authors studied the boundedness and mean square exponential stability of the exact solution of highly nonlinear hybrid NSDDEs with multiple delays.

Additionally, the delay terms in NSDDEs may be bounded functions of time t. Such as in [15], the exponential stability in $p(p>1)$th-moment for NSDDEs with time-varying delay was investigated. The authors in [16] studied the mean-square exponential stability of uncertain neutral linear stochastic time-varying delay systems. In [17], the robust mixed $H_2/H_{\infty }$ globally linearized filter design problem was investigated for a nonlinear stochastic time-varying delay system.

Furthermore, the delay functions in stochastic systems need to be generalized from the bounded case to unbounded case in many application models whose evolutions depend on all of the historical states. Thus, the systems become more complex and the unboundedness of delay terms may make the systems no longer stable. The fractional-order stochastic differential equations (FSDEs) are also used alternatively to model this kind of system and have received increasing attention due to their wide applications in many disciplines. Therefore, the theoretical analysis of stochastic systems with unbounded delay is necessary. In the paper [18], the authors discussed existence for a class of fractional neutral stochastic systems with infinite delay. The paper [19] investigated the approximate controllability results of Atangana–Baleanu fractional neutral stochastic systems with infinite delay by using the Bohnenblust–Karlin fixed-point theorem. The paper [20,21,22] studied the existence and uniqueness of Caputo fractional SDEs, SDDES and NSDDES. Additionally, in [23,24], the p-moment exponential stability of Caputo fractional differential equations with random impulses was established by the application of Lyapunov functions. In [25], the authors established existence and uniqueness theorem of neutral stochastic functional differential equations with infinite delay and the almost certain robust stability. More research on NSDDEs with unbounded delay can be found in [26,27].

However, in most of the above studies, the coefficients F and G grow linearly. This condition is too strict to be satisfied in many practical systems. In [28], the authors investigated the stability of the highly nonlinear hybrid SDDEs under the Khasminskii-type conditions instead of linear growth conditions. In [29,30], the stability of the highly nonlinear hybrid NSDDEs and the approximate solutions are also discussed. More results can be found in [31,32].

All the systems mentioned above have the same structures, only with different parameters in the switching spaces. For example, in two states, $S\left(1\right)$ and $S\left(2\right)$, the system is, respectively, modeled as $d\left[x\right(t)-U(x(t-\tau )\left)\right]=\left(ax\right(t)-bx(t-\tau \left)\right)dt+cx(t-\tau )dW\left(t\right)$ and $d[x\left(t\right)-U\left(x(t-\tau )\right)]=(\tilde{a}x\left(t\right)-\tilde{b}x(t-\tau ))dt+\tilde{c}x(t-\tau )dW\left(t\right),$ where $a,b,c,\tilde{a},\tilde{b},\tilde{c}$ are constants with $a\ne \tilde{a},b\ne \tilde{b},c\ne \tilde{c}$. When the equation in $S\left(2\right)$ becomes $d[x\left(t\right)-U\left(x(t-\tau )\right)]=(\widehat{a}x\left(t\right)-\widehat{b}{x}^3\left(t\right)-\widehat{c}x(t-\tau ))dt+\widehat{d}{x}^2(t-\tau )dW\left(t\right)$, we can see that the system has quite different structures in two states. There are a few articles investigating such systems. In [33], the authors studied the robust stability of SDDEs whose structures are different in subsystems. The authors in [34] studied the exponential stability of the corresponding neutral versions. The authors in [35] further studied the highly nonlinear stochastic systems with different structures and multiple constant-bounded delays. As far as we know, there is no study on the highly nonlinear hybrid differently structured NSDDEs with multiple unbounded delays yet. Motivated by the above mentioned research, the current work focuses on filling this gap.

In this article, we discuss the following highly nonlinear hybrid differently structured NSDDEs with multiple unbounded time-dependent delays:

$$\begin{array}{cc}\hfill d[x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)]=& F(x\left(t\right),x(t-{\delta }_1\left(t\right)),\cdots ,x(t-{\delta }_n\left(t\right)),t,r\left(t\right))dt\hfill \\ \hfill & +G(x\left(t\right),x(t-{\delta }_1\left(t\right)),\cdots ,x(t-{\delta }_n\left(t\right)),t,r\left(t\right))dW\left(t\right).\hfill \end{array}$$

(3)

The system (3) has the initial value

$$\{x\left(\theta \right):-\delta \left(0\right)\le \theta \le 0\}=\xi \in C_{{\mathcal{F}}_0}^b([-\delta \left(0\right),0];{\mathbb{R}}^d);r\left(0\right)=i_0\in S,$$

(4)

where

$$\begin{array}{cc}\hfill & F:{\mathbb{R}}^d\times {\mathbb{R}}^d\times \cdots \times {\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S\to {\mathbb{R}}^d(\mathrm{the\; number\; of} {\mathbb{R}}^d \mathrm{in\; the\; domain\; is} n+1),\hfill \\ \hfill & G:{\mathbb{R}}^d\times {\mathbb{R}}^d\times \cdots \times {\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S\to {\mathbb{R}}^{d\times m}(\mathrm{the\; number\; of} {\mathbb{R}}^d \mathrm{in\; the\; domain\; is} n+1),\hfill \\ \hfill & U:{\mathbb{R}}^d\times {\mathbb{R}}_{+}\to {\mathbb{R}}^d\left(\mathrm{the\; neutral\; term}\right),\hfill \\ \hfill & {\delta }_l:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+},l=1,\cdots ,n\left(\mathrm{the\; delay\; functions}\right)\hfill \end{array}$$

are all Borel-measurable. For a fixed $t\ge 0,$ set $\delta \left(t\right)={max}_{1\le l\le n}{\delta }_l\left(t\right).$ We also assume that $F(0,\cdots ,0,t,i)=0,$$G(0,\cdots ,0,t,i)=0,$$U(0,t)=0.$ Other notations are the same as that in Equation (1).

This paper studies the existence, uniqueness, $q_1$th moment asymptotical boundedness of the global solution of the system (3) and investigates the criteria of the $q_1$th moment and almost surely exponential stability of the system (3). Based on this motivation [34], the main contribution of this work is generalizing the corresponding stability results of the highly nonlinear hybrid differently structured NSDDEs from one constant delay to multiple unbounded time-varying delay situation. The unboundedness of the delay functions ${\delta }_l\left(t\right)(l=1,2,\cdots ,n)$ makes our model more applicable and meaningful, but it also improves the difficulty of theoretical analysis. The results of this paper were obtained mainly by the Lyapunov function method, M-matrix method, Generalized $It\widehat{o}$ formula and other mathematical tools. In particular, we used the factor $e^{-\zeta \delta \left(t\right)}$ to overcome the main problem caused by the unbounded delays effectively. Here, $\zeta$ is a positive constant. As in [28] and other existing researche, Khasminskii’s condition needs to be given when studying the stability of highly nonlinear stochastic systems. However, when the systems are generalized to the unbounded delay situation, the stability may be broken by the unboundedness. So, we added the factor $e^{-\zeta \delta \left(t\right)}$ in the corresponding Khasminskii condition in this paper to control the growth of unbounded delay functions. It is worth mentioning that when we take $n=1$ and unbounded function $\delta \left(t\right)=\theta t(0<\theta <1)$, the system (3) becomes a stochastic pantograph system.

The rest of this article is arranged as follows: the preliminaries and assumptions are presented in Section 2. Section 3 shows the main results of this article, including the existence, uniqueness and boundedness of the exact solution and the exponential stability of the new system. Three numerical examples are presented in Section 4 to illustrate the results. The conclusions are presented in Section 5.

2. Preliminaries and Assumptions

The notations in the above section are working throughout this paper without specification. Additionally, denote the Euclidean norm for any $y\in {\mathbb{R}}^d$ by $\left|y\right|$. For the matrix $B,$${\left|B\right|}^2=trace\left(B^{T}B\right)$ denotes the trace norm of $B,$ and $B^T$ is the transpose. The nonsingular M-matrix $A={\left(a_{ij}\right)}_{H\times H}$ means it is a square matrix that can be described as $A=rI-T$ with all elements of T being non-negative and $r>\rho \left(T\right),$ where $\rho \left(T\right)$ is the spectral radius of T and I is the identity matrix. More details of the M-matrix can be seen in [36].

The family of continuous non-negative functions $V(x,t,i):{\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S\to {\mathbb{R}}_{+}$, ensuring that for each $i\in S,$ they are continuously twice differentiable in x and once in t, is denoted by $C^{2,1}({\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S;{\mathbb{R}}_{+}).$ For a given function $V(x,t,i)\in C^{2,1}({\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S;{\mathbb{R}}_{+}),$ the operator $LV:{\mathbb{R}}^d\times {\mathbb{R}}^d\times \cdots \times {\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S\to \mathbb{R}$ is defined as (see, e.g., [36]):

$$\begin{array}{cc}\hfill LV(x-U(& y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill & =V_t(x-U(y_1,t),t,i)+V_x(x-U(y_1,t),t,i)F(x,y_1,\cdots ,y_n,t,i)\hfill \\ \hfill & +\frac{1}{2}trace\left[G^T(x,y_1,\cdots ,y_n,t,i)V_{xx}(x-U(y_1,t),t,i)G(x,y_1,\cdots ,y_n,t,i)\right]\hfill \\ \hfill & +\sum _{j=1}^N{\gamma }_{ij}V(x-U(y_1,t),t,j),\hfill \end{array}$$

(5)

where

$$\begin{array}{c}\hfill V_t(x,t,i)=\frac{\partial V(x,t,i)}{\partial t},V_x(x,t,i)=\left(\frac{\partial V(x,t,i)}{\partial x_1},\cdots ,\frac{\partial V(x,t,i)}{\partial x_d}\right),V_{xx}(x,t,i)={\left(\frac{{\partial }^{2}V(x,t,i)}{\partial x_j\partial x_k}\right)}_{d\times d}.\end{array}$$

The following assumptions are necessary to obtain the main results of this work.

Assumption 1

(${\mathcal{A}}_1$). For any $x,y_1,\cdots ,y_n,\widehat{x},\widehat{y_1},\cdots ,\widehat{y_n}\in {\mathbb{R}}^d$ and each integer $h>0$ with $\left|x\right|\vee |y_1|\vee \cdots \vee |y_n|\vee |\widehat{x}|\vee |\widehat{y_1}|\vee \cdots \vee |\widehat{y_n}|\le h,$ and all $t\ge 0,i\in S,$ there exists a constant $K_h>0,$ such that

$$\begin{array}{cc}\hfill \left|F\right(& x,y_1,\cdots ,y_n,t,i)-F(\widehat{x},\widehat{y_1},\cdots ,\widehat{y_n},t,i){|}^2\vee {|G(x,y_1,\cdots ,y_n,t,i)-G(\widehat{x},\widehat{y_1},\cdots ,\widehat{y_n},t,i)|}^2\hfill \\ \hfill & \le K_h\left(\right|x-\widehat{x}{|}^2+\sum _{1\le l\le n}|y_l-\widehat{y_l}{|}^2).\hfill \end{array}$$

(6)

The assumption (${\mathcal{A}}_1$) is the local Lipschitz condition. It is one of the important conditions to ensure the uniqueness and existence of the solution of the system (3), which can be seen, for example, in [36].

Assumption 2

(${\mathcal{A}}_2$). For $l=1,\cdots ,n,$ the delay function ${\delta }_l:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ is differentiable, and there exists a constant $\overline{\delta }>0$ such that

$${\delta }_l^{{}^{\prime }}\left(t\right)\le \overline{\delta }<1.$$

For $t\in {\mathbb{R}}_{+},$ let ${\delta }_l^{*}\left(t\right)=t-{\delta }_l\left(t\right),$ noticing that ${\delta }_l^{{*}^{\prime }}\left(t\right)\ge 1-\overline{\delta }>0,$ so ${\delta }_l^{*}\left(t\right)$ is an increasing function of $t,$ and then $t-{\delta }_l\left(t\right)\ge -{\delta }_l\left(0\right)\ge -\delta \left(0\right).$

Assumption 3

(${\mathcal{A}}_3$). (Khasminskii’s condition) For convenience, we divide the state space $S=\{1,\cdots ,N\}$ into $S_1=\{1,2,\cdots ,N_1\}$ and $S_2=\{N_1+1,\cdots ,N\},$ where $1\le N_1<N$. The system (3) has different structures in $S_1$ and $S_2$.

For two given constants $q_1$ and $q_2$ with $q_2>q_1\ge 2$, and for any $i\in S_1,$ there exist constants $\zeta >0,{\alpha }_{i1},{\alpha }_{i2},{\alpha }_{i3l}\in {\mathbb{R}}_{+},l=1,\cdots ,n,$ such that for $x,y_1,\cdots ,y_n\in {\mathbb{R}}^d,$ and $t\ge 0,$

$$\begin{array}{cc}\hfill & {(x-U(y_1,t))}^{T}F(x,y_1,\cdots ,y_n,t,i)+\frac{q_2-1}{2}{\left|G(x,y_1,\cdots ,y_n,t,i)\right|}^2\hfill \\ \hfill \le & {\alpha }_{i1}-{\alpha }_{i2}|x-U(y_1,t){|}^2+e^{-\zeta \delta \left(t\right)}\sum _{l=1}^n{\alpha }_{i3l}{\left|y_l\right|}^2,\hfill \end{array}$$

(7)

and for $i\in S_2,$ there exist additional constants ${\alpha }_{i4},{\alpha }_{i5l}\in {\mathbb{R}}_{+},l=1,\cdots ,n,$ satisfying that for $x,y_1,\cdots ,y_n\in {\mathbb{R}}^d,$ and $t\ge 0,$

$$\begin{array}{cc}\hfill & {(x-U(y_1,t))}^{T}F(x,y_1,\cdots ,y_n,t,i)+\frac{q_1-1}{2}{\left|G(x,y_1,\cdots ,y_n,t,i)\right|}^2\hfill \\ \hfill \le & {\alpha }_{i1}-{\alpha }_{i2}|x-U(y_1,t){|}^2+e^{-\zeta \delta \left(t\right)}\sum _{l=1}^n{\alpha }_{i3l}{\left|y_l\right|}^2\hfill \\ & -{\alpha }_{i4}|x-U(y_1,t){|}^{q_2-q_1+2}+e^{-\zeta \delta \left(t\right)}\sum _{l=1}^n{\alpha }_{i5l}{\left|y_l\right|}^{q_2-q_1+2}.\hfill \end{array}$$

(8)

Moreover, assume that

$$\mathcal{A}:=diag(q_1{\alpha }_{12},\cdots ,q_1{\alpha }_{N2})-\Gamma$$

(9)

and

$$\mathcal{S}:=diag(q_2{\alpha }_{12},\cdots ,q_2{\alpha }_{N_{1}2})-{\left({\gamma }_{ij}\right)}_{i,j\in S_1}$$

(10)

are nonsingular M-matrices.

Equations (7) and (8) in assumption (${\mathcal{A}}_3$) show that the structures of the system (3) are quite different, and the coefficients of the system (3) are highly nonlinear.

Define

$${({\theta }_1,\cdots ,{\theta }_N)}^T={\mathcal{A}}^{-1}{(1,\cdots ,1)}^T$$

(11)

and

$${({\eta }_1,\cdots ,{\eta }_{N_1})}^T={\mathcal{S}}^{-1}{(\omega \cdots ,\omega )}^T,$$

(12)

where $\omega$ is the positive constant that can be chosen to satisfy the assumption (${\mathcal{A}}_4$) below ([33] showed a selecting method of $\omega$). By the assumption (${\mathcal{A}}_3$) we know $\mathcal{A}$ and $\mathcal{S}$ are nonsingular M-matrices(see, e.g., [36]), so that ${\theta }_i>0,i\in S$ and ${\eta }_j>0,j\in S_1.$

Assumption 4

(${\mathcal{A}}_4$). The following conditions are necessary and important for the stability of the system (3).

$$\delta :=\underset{i\in S,1\le l\le n}{max}\left({\alpha }_{i3l}{\theta }_i\right)<\frac{{(1-\sigma )}^{q_1}(1-\overline{\delta })}{(1-\overline{\delta })n(q_1-2){(1-\sigma )}^{q_1}+2n},$$

(13)

$$\begin{array}{cc}\hfill \widehat{\omega }:=& \left(\underset{i\in S_1,1\le l\le n}{max}{q}_2{\alpha }_{i3l}{\eta }_i\right)\vee \left(\underset{i\in S_2,1\le l\le n}{max}{q}_1{\alpha }_{i5l}{\theta }_i\right)<\frac{q_2{(1-\sigma )}^{q_2}(1-\overline{\delta })}{n(q_2-q_1+2)+(1-\overline{\delta })n(q_2-2){(1-\sigma )}^{q_2}}\omega ,\hfill \end{array}$$

(14)

$$\underset{i\in S_2}{min}(q_1{\alpha }_{i4}{\theta }_i-\sum _{j\in S_1}{\gamma }_{ij}{\eta }_j)\ge \omega .$$

(15)

The similar assumptions also can be seen in the Theorem 3.1 of [34].

For convenience of derivation, denote by ${\omega }_2:=\frac{q_2-q_1+2}{q_2}\widehat{\omega }.$ From condition (14), we have

$$\omega -\frac{q_2-2}{q_2}n\widehat{\omega }>\left(1-\frac{(1-\overline{\delta })(q_2-2){(1-\sigma )}^{q_2}}{(q_2-q_1+2)+(1-\overline{\delta })(q_2-2){(1-\sigma )}^{q_2}}\right)\omega ,$$

and

$$\omega -\frac{q_2-2}{q_2}n\widehat{\omega }-\frac{n}{(1-\overline{\delta }){(1-\sigma )}^{q_2}}{\omega }_2=\omega -\frac{(1-\overline{\delta }){(1-\sigma )}^{q_2}(q_2-2)n+(q_2-q_1+2)n}{q_2(1-\overline{\delta }){(1-\sigma )}^{q_2}}\widehat{\omega }>0.$$

So, there exists $0<\frac{(q_2-q_1+2){(1-\sigma )}^{-q_2}n\widehat{\omega }}{(1-\overline{\delta })(q_2\omega -(q_2-2)n\widehat{\omega })}<{\alpha }_0<1$ such that

$${\omega }_1:={\alpha }_0(\omega -\frac{q_2-2}{q_2}n\widehat{\omega })>\frac{n}{(1-\overline{\delta }){(1-\sigma )}^{q_2}}{\omega }_2.$$

(16)

We also define two functions $F_i:{\mathbb{R}}_{+}\to \mathbb{R},i=1,2,$ as follows:

$$\begin{array}{cc}\hfill F_1\left(\eta \right)=& \eta c_2{(1+\sigma )}^{q_2}+\frac{n{\omega }_2}{1-\overline{\delta }}-{\omega }_1{(1-\sigma )}^{q_2},\hfill \\ \hfill F_2\left(\eta \right)=& \eta c_2{(1+\sigma )}^{q_1}+\frac{2n\delta }{1-\overline{\delta }}-(1-n\delta (q_1-2)){(1-\sigma )}^{q_1},\hfill \end{array}$$

(17)

where $c_2=\left({max}_{i\in S}{\theta }_i\right)\vee \left({max}_{i\in S_1}{\eta }_i\right)$ is a constant. Notice that for $i=1,2$, $F_i\left(\eta \right)$ is strictly increasing in $\eta ,$ and ${lim}_{\eta \to \infty }{F}_i\left(\eta \right)=+\infty .$ Based on (16) and (13), we know

$$\begin{array}{cc}\hfill & F_1\left(0\right)=\frac{n{\omega }_2}{1-\overline{\delta }}-{\omega }_1{(1-\sigma )}^{q_2}<0,\hfill \\ \hfill & F_2\left(0\right)=\frac{2n\delta }{1-\overline{\delta }}-(1-n\delta (q_1-2)){(1-\sigma )}^{q_1}<0.\hfill \end{array}$$

(18)

So, there is the unique positive root ${\eta }_i^{*}(i=1,2)$ of the equation $F_i\left(\eta \right)=0,$ and $F_i\left(\widehat{\zeta }\right)<0$ for any $\widehat{\zeta }<{\eta }_i^{*}.$

Assumption 5

(${\mathcal{A}}_5$). For any $y\in {\mathbb{R}}^d,y^{*}\in {\mathbb{R}}^d,t\ge 0,$ and the same ζ in the assumption (${\mathcal{A}}_3$), there is a constant $\overline{\sigma }\in (0,1-\overline{\delta })$ such that

$$|U(y,t)-U(y^{*},t)|\le \overline{\sigma }{e}^{-\zeta \delta \left(t\right)}|y-y^{*}|.$$

(19)

Recalling that $U(0,t)=0,$ (19) implies $\left|U(y,t)\right|\le \overline{\sigma }{e}^{-\zeta \delta \left(t\right)}\left|y\right|.$

Some classical inequalities used in this paper are listed as follows while their proofs are omitted. The details of Lemma 1 can be found in, for example, [36,37].

Lemma 1.

Classical inequalities.

(1)

For $x,y,\alpha ,\beta \ge 0,$

$$x^{\alpha }{y}^{\beta }\le \frac{\alpha x^{\alpha +\beta }+\beta y^{\alpha +\beta }}{\alpha +\beta }.$$

(20)

(2)

For $a,b\ge 0,\nu >0,p\ge 1,$

$${(a+b)}^p\le {(1+\nu )}^{p-1}{a}^p+{(1+{\nu }^{-1})}^{p-1}{b}^p.$$

(21)

(3)

For $p\ge 1,t\ge 0,$

$$\begin{array}{cc}\hfill & {(1-\sigma )}^{p-1}{\left(\right|x|}^p-e^{-\zeta \delta \left(t\right)}(1-\overline{\delta }){\sigma \left|y\right|}^p)\le |x-U(y,t){|}^p;\hfill \\ \hfill & {|x-U(y,t))|}^p\le {(1+\sigma )}^{p-1}{\left(\right|x|}^p+e^{-\zeta \delta \left(t\right)}(1-\overline{\delta }){\sigma \left|y\right|}^p).\hfill \end{array}$$

(22)

Let $\sigma =\overline{\sigma }/(1-\overline{\delta })$ so that $\overline{\sigma }<\sigma \in (0,1)$. Based on the assumption (${\mathcal{A}}_5$), we can obtain the first inequality of (22) from (21) by taking $\nu =\frac{\sigma }{1-\sigma },a=x-U(y,t)$$b=U(y,t);$ and letting $a=x,b=-U(y,t),$ and $\nu =\sigma ,$ we obtain the second inequality in (22).

3. Main Results

Two theorems are given in this section to discuss the exponential stability of system (3). Theorem 1 establishes the existence, uniqueness and the $q_1$th moment asymptotical boundedness of the exact global solution. Theorem 2 shows the $q_1$th moment and almost sure exponential stability of system (3).

Theorem 1.

Let Assumptions (${\mathcal{A}}_1$)–(${\mathcal{A}}_5$) hold; then, system (3), with any initial condition (4), has a unique global solution $x\left(t\right)$ on ${\mathbb{R}}_{+}$ satisfying the following properties:

$$\underset{t\to \infty }{lim\; sup}\frac{1}{t}{\int }_0^t\mathbb{E}{\left|x\left(s\right)\right|}^{q_2}ds\le K_1,$$

(23)

$$\underset{t\to \infty }{lim\; sup}\mathbb{E}{\left|x\left(t\right)\right|}^{q_1}\le K_2,$$

(24)

where the constant $K_1>0$ and $K_2>0$ are only related with the initial data.

Proof. 

To investigate system (3) with different structures, We define the new Lyapunov function $V:{\mathbb{R}}^d\times {\mathbb{R}}_{+}\times S\to {\mathbb{R}}_{+}$ as:

$$V(x,t,i)=\left\{\begin{array}{cc}{\theta }_i{\left|x\right|}^{q_1}+{\eta }_i{\left|x\right|}^{q_2},\hfill & i\in S_1\\ {\theta }_i{\left|x\right|}^{q_1},\hfill & i\in S_2.\end{array}\right.$$

(25)

where ${\theta }_i$ and ${\eta }_i$ are defined in (11) and (12). Then,

$$c_1{\left|x\right|}^{q_1}\le V(x,t,i)\le c_2{\left(\right|x|}^{q_1}+{\left|x\right|}^{q_2}),$$

(26)

where $c_1={min}_{i\in S}{\theta }_i$ and $c_2$ is the same as in (17).

Letting ${\tilde{x}}_t=x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t),$ and by the generalized $It\widehat{o}$ formula, we have

$$V({\tilde{x}}_t,t,r\left(t\right))=V({\tilde{x}}_0,0,r\left(0\right))+{\int }_0^{t}LV({\tilde{x}}_s,x(s-{\delta }_1\left(s\right)),\cdots ,x(s-{\delta }_n\left(s\right)),s,r\left(s\right))ds+M\left(t\right),$$

(27)

where $M\left(t\right)$ is a martingale with $M\left(0\right)=0.$

Now, we estimate the operator $LV$. For $i\in S_1,t\ge 0,$

$$\begin{array}{cc}\hfill LV(& x-U(y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill =& q_1{\theta }_i{|x-U(y_1,t)|}^{q_1-2}{(x-U(y_1,t))}^{T}F(x,y_1,\cdots ,y_n,t,i)\hfill \\ \hfill & +\frac{1}{2}{q}_1(q_1-2){\theta }_i|x-U(y_1,t){|}^{q_1-4}{|{(x-U(y_1,t))}^{T}G(x,y_1,\cdots ,y_n,t,i)|}^2\hfill \\ \hfill & +\frac{1}{2}{q}_1{\theta }_i|x-U(y_1,t){|}^{q_1-2}{\left|G(x,y_1,\cdots ,y_n,t,i)\right|}^2\hfill \\ \hfill & +q_2{\eta }_i{|x-U(y_1,t)|}^{q_2-2}{(x-U(y_1,t))}^{T}F(x,y_1,\cdots ,y_n,t,i)\hfill \\ \hfill & +\frac{1}{2}{q}_2(q_2-2){\eta }_i|x-U(y_1,t){|}^{q_2-4}{|{(x-U(y_1,t))}^{T}G(x,y_1,\cdots ,y_n,t,i)|}^2\hfill \\ \hfill & +\frac{1}{2}{q}_2{\eta }_i|x-U(y_1,t){|}^{q_2-2}{\left|G(x,y_1,\cdots ,y_n,t,i)\right|}^2\hfill \\ \hfill & +\sum _{j=1}^N{\gamma }_{ij}{\theta }_j|x-U(y_1,t){|}^{q_1}+\sum _{j=1}^{N_1}{\gamma }_{ij}{\eta }_j{|x-U(y_1,t)|}^{q_2}.\hfill \end{array}$$

By $|x^T{g|}^2\le {\left|x\right|}^2{\left|g\right|}^2,$ and (7), we can derive

$$\begin{array}{cc}\hfill & LV(x-U(y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill \le & q_1{\theta }_i{|x-U(y_1,t)|}^{q_1-2}\left({(x-U(y_1,t))}^{T}F(x,y_1,\cdots ,y_n,t,i)+\frac{q_1-1}{2}{\left|G(x,y_1,\cdots ,y_n,t,i)\right|}^2\right)\hfill \\ \hfill & +q_2{\eta }_i{|x-U(y_1,t)|}^{q_2-2}\left({(x-U(y_1,t))}^{T}F(x,y_1,\cdots ,y_n,t,i)+\frac{q_2-1}{2}{\left|G(x,y_1,\cdots ,y_n,t,i)\right|}^2\right)\hfill \\ \hfill & +\sum _{j=1}^N{\gamma }_{ij}{\theta }_j|x-U(y_1,t){|}^{q_1}+\sum _{j=1}^{N_1}{\gamma }_{ij}{\eta }_j{|x-U(y_1,t)|}^{q_2}\hfill \\ \hfill \le & q_1{\theta }_i{|x-U(y_1,t)|}^{q_1-2}\left({\alpha }_{i1}-{\alpha }_{i2}|x-U(y_1,t){|}^2+e^{-\zeta \delta \left(t\right)}\sum _{l=1}^n{\alpha }_{i3l}{\left|y_l\right|}^2\right)\hfill \\ \hfill & +q_2{\eta }_i{|x-U(y_1,t)|}^{q_2-2}\left({\alpha }_{i1}-{\alpha }_{i2}|x-U(y_1,t){|}^2+e^{-\zeta \delta \left(t\right)}\sum _{l=1}^n{\alpha }_{i3l}{\left|y_l\right|}^2\right)\hfill \\ \hfill & +\sum _{j=1}^N{\gamma }_{ij}{\theta }_j|x-U(y_1,t){|}^{q_1}+\sum _{j=1}^{N_1}{\gamma }_{ij}{\eta }_j{|x-U(y_1,t)|}^{q_2}.\hfill \end{array}$$

From (9)–(12), we have

$$-q_1{\alpha }_{i2}{\theta }_i+\sum _{j=1}^N{\gamma }_{ij}{\theta }_j=-1,i\in S,$$

(28)

and

$$-q_2{\alpha }_{i2}{\eta }_i+\sum _{j=1}^{N_1}{\gamma }_{ij}{\eta }_j=-\omega ,i\in S_1.$$

(29)

From (20), (28) and (29), we have that for any $i\in S_1,$

$$\begin{array}{cc}\hfill & LV(x-U(y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill \le & q_1{\theta }_i{\alpha }_{i1}|x-U(y_1,t){|}^{q_1-2}-|x-U(y_1,t){|}^{q_1}+e^{-\zeta \delta \left(t\right)}{q}_1{\theta }_i\sum _{l=1}^n{\alpha }_{i3l}(\frac{q_1-2}{q_1}|x-U(y_1,t){|}^{q_1}+\frac{2}{q_1}|y_l{|}^{q_1})\hfill \\ \hfill & +q_2{\eta }_i{\alpha }_{i1}|x-U(y_1,t){|}^{q_2-2}-\omega |x-U(y_1,t){|}^{q_2}+e^{-\zeta \delta \left(t\right)}{q}_2{\eta }_i\sum _{l=1}^n{\alpha }_{i3l}(\frac{q_2-2}{q_2}|x-U(y_1,t){|}^{q_2}+\frac{2}{q_2}|y_l{|}^{q_2})\hfill \\ \hfill \le & q_1{\theta }_i{\alpha }_{i1}|x-U(y_1,t){|}^{q_1-2}-(1-\sum _{l=1}^n{\theta }_i{\alpha }_{i3l}(q_1-2))|x-U(y_1,t){|}^{q_1}+e^{-\zeta \delta \left(t\right)}2{\theta }_i\sum _{l=1}^n{\alpha }_{i3l}{\left|y_l\right|}^{q_1}\hfill \\ \hfill & +q_2{\eta }_i{\alpha }_{i1}|x-U(y_1,t){|}^{q_2-2}-(\omega -\sum _{l=1}^n{\eta }_i{\alpha }_{i3l}(q_2-2))|x-U(y_1,t){|}^{q_2}+e^{-\zeta \delta \left(t\right)}2{\eta }_i\sum _{l=1}^n{\alpha }_{i3l}{\left|y_l\right|}^{q_2}.\hfill \end{array}$$

(30)

Based on (8)–(12), (15) and (20), we can similarly find that for $i\in S_2,$

$$\begin{array}{cc}\hfill & LV(x-U(y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill \le & q_1{\theta }_i{\alpha }_{i1}|x-U(y_1,t){|}^{q_1-2}-(1-\sum _{l=1}^n{\theta }_i{\alpha }_{i3l}(q_1-2))|x-U(y_1,t){|}^{q_1}+e^{-\zeta \delta \left(t\right)}2{\theta }_i\sum _{l=1}^n{\alpha }_{i3l}{\left|y_l\right|}^{q_1}\hfill \\ \hfill & -(\omega -\frac{q_1(q_1-2){\theta }_i}{q_2}\sum _{l=1}^n{\alpha }_{i5l})|x-U(y_1,t){|}^{q_2}+e^{-\zeta \delta \left(t\right)}\frac{q_1(q_2-q_1+2){\theta }_i}{q_2}\sum _{l=1}^n{\alpha }_{i5l}{\left|y_l\right|}^{q_2}.\hfill \end{array}$$

(31)

Letting $c_3:=\left({max}_{i\in S}{q}_1{\theta }_i{\alpha }_{i1}\right)\vee \left({max}_{i\in S_1}{q}_2{\eta }_i{\alpha }_{i1}\right),$ recalling conditions (13) and (14), and combining with (30) and (31), we have that for all $i\in S,$

$$\begin{array}{cc}\hfill & LV(x-U(y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill \le & c_3\left(\right|x-U(y_1,t){|}^{q_1-2}+|x-U(y_1,t){|}^{q_2-2})+2e^{-\zeta \delta \left(t\right)}\delta \sum _{l=1}^n|y_l{|}^{q_1}+\frac{q_2-q_1+2}{q_2}{e}^{-\zeta \delta \left(t\right)}\widehat{\omega }\sum _{l=1}^n{\left|y_l\right|}^{q_2}\hfill \\ \hfill & -(1-n\delta (q_1-2))|x-U(y_1,t){|}^{q_1}-(\omega -\frac{q_2-2}{q_2}n\widehat{\omega }){|x-U(y_1,t)|}^{q_2}.\hfill \end{array}$$

(32)

Substituting (16) into (32), it follows that

$$\begin{array}{cc}\hfill & LV(x-U(y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill \le & c_3\left(\right|x-U(y_1,t){|}^{q_1-2}+|x-U(y_1,t){|}^{q_2-2})-\frac{1-{\alpha }_0}{{\alpha }_0}{\omega }_1{|x-U(y_1,t)|}^{q_2}\hfill \\ \hfill & -(1-n\delta (q_1-2))|x-U(y_1,t){|}^{q_1}+2e^{-\zeta \delta \left(t\right)}\delta \sum _{l=1}^n|y_l{|}^{q_1}+e^{-\zeta \delta \left(t\right)}{\omega }_2\sum _{l=1}^n|y_l{|}^{q_2}-{\omega }_1{|x-U(y_1,t)|}^{q_2}.\hfill \end{array}$$

As $c_3>0$ and ${\omega }_1>0,$ define the function

$$\Theta \left(u\right)=c_3(u^{q_1-2}+u^{q_2-2})-\frac{1-{\alpha }_0}{{\alpha }_0}{\omega }_1{u}^{q_2}.$$

Then, $\Theta \left(u\right)$ has finite supremum value on ${\mathbb{R}}_{+}$, and can be denoted by $c_4:={sup}_{u\in [0,+\infty )}\Theta \left(u\right)<\infty .$ So,

$$\begin{array}{cc}\hfill & LV(x-U(y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill \le & c_4-(1-n\delta (q_1-2))|x-U(y_1,t){|}^{q_1}+2e^{-\zeta \delta \left(t\right)}\delta \sum _{l=1}^n|y_l{|}^{q_1}+e^{-\zeta \delta \left(t\right)}{\omega }_2\sum _{l=1}^n|y_l{|}^{q_2}-{\omega }_1{|x-U(y_1,t)|}^{q_2}.\hfill \end{array}$$

By (22), the final estimation for $LV$ is as follows:

$$\begin{array}{cc}\hfill & LV(x-U(y_1,t),y_1,\cdots ,y_n,t,i)\hfill \\ \hfill \le & c_4-(1-n\delta (q_1-2)){(1-\sigma )}^{q_1-1}{\left|x\right|}^{q_1}+(1-n\delta (q_1-2))\sigma {(1-\sigma )}^{q_1-1}(1-\overline{\delta })e^{-\zeta \delta \left(t\right)}{\left|y_1\right|}^{q_1}\hfill \\ \hfill & -{\omega }_1{(1-\sigma )}^{q_2-1}{\left|x\right|}^{q_2}+{\omega }_1\sigma {(1-\sigma )}^{q_2-1}(1-\overline{\delta })e^{-\zeta \delta \left(t\right)}{\left|y_1\right|}^{q_2}\hfill \\ & +2e^{-\zeta \delta \left(t\right)}\delta \sum _{l=1}^n|y_l{|}^{q_1}+e^{-\zeta \delta \left(t\right)}{\omega }_2\sum _{l=1}^n{\left|y_l\right|}^{q_2}.\hfill \end{array}$$

(33)

Now, we prove the main results of Theorem 1 based on those we obtained in the above.

By the existing conditions, we see that on $[-\delta \left(0\right),{\sigma }_{\infty }),$ system (3) has the unique maximal local solution $x\left(t\right),$ where ${\sigma }_{\infty }$ is the explosion time [36]. For bounded $\xi$, there is a positive constant ${\gamma }_0$ such that $\parallel \xi \parallel <{\gamma }_0.$ For each $\gamma \ge {\gamma }_0,$ the stopping time ${\tau }_{\gamma }$ is defined by

$${\tau }_{\gamma }=inf\{t\ge 0:|x\left(t\right)|\ge \gamma \},inf\varnothing =\infty .$$

(34)

as $\gamma \to \infty ,{\tau }_{\gamma }$ is increasing. Denote by ${\tau }_{\infty }:={lim}_{\gamma \to \infty }{\tau }_{\gamma }\le {\sigma }_{\infty },a.s.$ To prove that in finite time the solution $x\left(t\right)$ of system (3) does not explode, we need to show ${\tau }_{\infty }=\infty ,a.s.,$ which implies ${\sigma }_{\infty }=\infty ,a.s.$

From (27), by taking expectation and combining with (33), we have that for $t\ge 0,$

$$\begin{array}{cc}\hfill & \mathbb{E}V({\tilde{x}}_{t\wedge {\tau }_{\gamma }},t\wedge {\tau }_{\gamma },r(t\wedge {\tau }_{\gamma }))\hfill \\ \hfill =& \mathbb{E}V({\tilde{x}}_0,0,r\left(0\right))+\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}LV({\tilde{x}}_s,x(s-{\delta }_1\left(s\right)),\cdots ,x(s-{\delta }_n\left(s\right)),s,r\left(s\right))ds\hfill \\ \hfill \le & \mathbb{E}V({\tilde{x}}_0,0,r\left(0\right))+c_{4}t-(1-(q_1-2)n\delta ){(1-\sigma )}^{q_1-1}\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_1}ds\hfill \\ \hfill & +(1-(q_1-2)n\delta )\sigma {(1-\sigma )}^{q_1-1}(1-\overline{\delta })\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x(s-{\delta }_1\left(s\right))\right|}^{q_1}ds\hfill \\ \hfill & -{\omega }_1{(1-\sigma )}^{q_2-1}\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_2}ds+{\omega }_1\sigma {(1-\sigma )}^{q_2-1}(1-\overline{\delta })\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x(s-{\delta }_1\left(s\right))\right|}^{q_2}ds\hfill \\ & +2\delta \sum _{l=1}^n\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}|x(s-{\delta }_l\left(s\right)){|}^{q_1}ds+{\omega }_2\sum _{l=1}^n\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x(s-{\delta }_l\left(s\right))\right|}^{q_2}ds.\hfill \end{array}$$

(35)

It follows from assumption (${\mathcal{A}}_2$) that for any $l=1,\cdots ,n,$

$$\begin{array}{cc}\hfill \mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x(s-{\delta }_l\left(s\right))\right|}^{q_1}ds& \le \frac{1}{1-\overline{\delta }}\mathbb{E}{\int }_{-\delta \left(0\right)}^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_1}ds\hfill \\ \hfill & =\frac{1}{1-\overline{\delta }}\mathbb{E}{\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_1}ds+\frac{1}{1-\overline{\delta }}\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_1}ds,\hfill \end{array}$$

(36)

and

$$\begin{array}{cc}\hfill \sum _{l=1}^n\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x(s-{\delta }_l\left(s\right))\right|}^{q_1}ds& \le \sum _{l=1}^n\mathbb{E}\frac{1}{1-\overline{\delta }}{\int }_{-\delta \left(0\right)}^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_1}ds\hfill \\ \hfill & =\frac{n}{1-\overline{\delta }}\mathbb{E}{\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_1}ds+\frac{n}{1-\overline{\delta }}\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_1}ds.\hfill \end{array}$$

(37)

Substituting (36) and (37) into (35), together with (26), we have

$$\begin{array}{cc}\hfill c_1\mathbb{E}{\left|{\tilde{x}}_{t\wedge {\tau }_{\gamma }}\right|}^{q_1}\le & K_3+c_{4}t+\left(\frac{2n\delta }{1-\overline{\delta }}-(1-(q_1-2)n\delta ){(1-\sigma )}^{q_1}\right)\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_1}ds\hfill \\ \hfill & +\left(\frac{n{\omega }_2}{1-\overline{\delta }}-{\omega }_1{(1-\sigma )}^{q_2}\right)\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_2}ds,\hfill \end{array}$$

(38)

where

$$\begin{array}{cc}\hfill K_3=& \mathbb{E}V({\tilde{x}}_0,0,r\left(0\right))+\left(\frac{2n\delta }{1-\overline{\delta }}+(1-n\delta (q_1-2))\sigma {(1-\sigma )}^{q_1-1}\right)\mathbb{E}{\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_1}ds\hfill \\ \hfill & +\left(\frac{n{\omega }_2}{1-\overline{\delta }}+{\omega }_1\sigma {(1-\sigma )}^{q_2-1}\right)\mathbb{E}{\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_2}ds.\hfill \end{array}$$

Recalling (18), it follows from (38) that

$$c_1\mathbb{E}{\left|{\tilde{x}}_{t\wedge {\tau }_{\gamma }}\right|}^{q_1}\le K_3+c_{4}t.$$

(39)

From (22), we obtain

$$\begin{array}{cc}\hfill {(1-\sigma )}^{q_1-1}\mathbb{E}{\left|x(t\wedge {\tau }_{\gamma })\right|}^{q_1}& \le \mathbb{E}|{\tilde{x}}_{t\wedge {\tau }_{\gamma }}{|}^{q_1}+\sigma {(1-\sigma )}^{q_1-1}(1-\overline{\delta })\mathbb{E}{\left|x(t\wedge {\tau }_{\gamma }-{\delta }_1(t\wedge {\tau }_{\gamma }))\right|}^{q_1}.\hfill \end{array}$$

By (39), we can further derive that

$$\begin{array}{cc}\hfill c_1{(1-\sigma )}^{q_1-1}\underset{0\le s\le t}{sup}\mathbb{E}{\left|x(s\wedge {\tau }_{\gamma })\right|}^{q_1}& \le K_3+c_{4}t+c_1\sigma {(1-\sigma )}^{q_1-1}(1-\overline{\delta })\underset{0\le s\le t}{sup}\mathbb{E}{\left|x(s\wedge {\tau }_{\gamma }-{\delta }_1(s\wedge {\tau }_{\gamma }))\right|}^{q_1}\hfill \\ \hfill & \le K_3^{{}^{\prime }}+c_{4}t+c_1\sigma {(1-\sigma )}^{q_1-1}\underset{0\le s\le t}{sup}\mathbb{E}{\left|x(s\wedge {\tau }_{\gamma })\right|}^{q_1},\hfill \end{array}$$

where $K_3^{{}^{\prime }}=K_3+c_1\sigma {(1-\sigma )}^{q_1-1}{sup}_{-\delta \left(0\right)\le s\le 0}\mathbb{E}{\left|\xi \left(s\right)\right|}^{q_1}.$ Consequently,

$$c_1{(1-\sigma )}^{q_1}\mathbb{E}{\left|x(t\wedge {\tau }_{\gamma })\right|}^{q_1}\le K_3^{{}^{\prime }}+c_{4}t.$$

(40)

Recalling ${\tau }_{\gamma }$ defined in (34), it follows from (40) that

$$c_1{(1-\sigma )}^{q_1}{\gamma }^{q_1}\mathbb{P}({\tau }_{\gamma }\le t)\le K_3^{{}^{\prime }}+c_{4}t.$$

Letting $\gamma \to \infty ,$ $\mathbb{P}({\tau }_{\infty }\le t)=0$ for $t\ge 0.$ This means $\mathbb{P}({\tau }_{\infty }\ge t)=1.$ Because t is arbitrary, we obtain ${\tau }_{\infty }=\infty$ a.s..

Next, we show the properties (23) and (24).

Firstly, (38) yields

$$0\le c_1\mathbb{E}|{\tilde{x}}_{t\wedge {\tau }_{\gamma }}{|}^{q_1}\le K_3+c_{4}t+\left(\frac{n{\omega }_2}{1-\overline{\delta }}-{\omega }_1{(1-\sigma )}^{q_2}\right)\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_2}ds,$$

namely,

$$\left({\omega }_1{(1-\sigma )}^{q_2}-\frac{n{\omega }_2}{1-\overline{\delta }}\right)\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{\left|x\left(s\right)\right|}^{q_2}ds\le K_3+c_{4}t.$$

Bearing in mind that $\left({\omega }_1{(1-\sigma )}^{q_2}-\frac{n{\omega }_2}{1-\overline{\delta }}\right)>0,$ and letting $\gamma \to \infty ,$ the monotone convergence theorem gives that

$$\underset{t\to \infty }{lim\; sup}\frac{1}{t}{\int }_0^t\mathbb{E}{\left|x\left(s\right)\right|}^{q_2}ds\le \frac{c_4(1-\overline{\delta })}{{\omega }_1{(1-\sigma )}^{q_2}(1-\overline{\delta })-n{\omega }_2}=:K_1,$$

which verifies that (23) is true.

To show (24), fix ${ϵ}_0<\zeta \wedge {\eta }_1^{*}$ so that $F_1\left({ϵ}_0\right)<0.$ By the generalized $It\widehat{o}$ formula,

$$\begin{array}{cc}\hfill e^{{ϵ}_{0}t}V({\tilde{x}}_t,t,r\left(t\right))=& V({\tilde{x}}_0,0,r\left(0\right))+M_1\left(t\right)\hfill \\ \hfill & +{\int }_0^t{e}^{{ϵ}_{0}s}\left({ϵ}_{0}V({\tilde{x}}_s,s,r\left(s\right))+LV({\tilde{x}}_s,x(s-{\delta }_1\left(s\right)),\cdots ,x(s-{\delta }_n\left(s\right)),s,r\left(s\right))\right)ds,\hfill \end{array}$$

where $M_1\left(t\right)$ is another martingale with $M_1\left(0\right)=0.$

It follows after taking expectation to $e^{{ϵ}_0(t\wedge {\tau }_{\gamma })}V({\tilde{x}}_{t\wedge {\tau }_{\gamma }},t\wedge {\tau }_{\gamma },r(t\wedge {\tau }_{\gamma }))$ that

$$\begin{array}{cc}\hfill & \mathbb{E}\left(e^{{ϵ}_0(t\wedge {\tau }_{\gamma })}V({\tilde{x}}_{t\wedge {\tau }_{\gamma }},t\wedge {\tau }_{\gamma },r(t\wedge {\tau }_{\gamma }))\right)\hfill \\ \hfill =& \mathbb{E}V({\tilde{x}}_0,0,r\left(0\right))+\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{e}^{{ϵ}_{0}s}\left({ϵ}_{0}V({\tilde{x}}_s,s,r\left(s\right))+LV({\tilde{x}}_s,x(s-{\delta }_1\left(s\right)),\cdots ,x(s-{\delta }_n\left(s\right)),s,r\left(s\right))\right)ds.\hfill \end{array}$$

Just as the same discussion as above, by (33), (35)–(38), and using (22), we can derive that

$$\begin{array}{cc}\hfill & \mathbb{E}\left(e^{{ϵ}_0(t\wedge {\tau }_{\gamma })}V({\tilde{x}}_{t\wedge {\tau }_{\gamma }},t\wedge {\tau }_{\gamma },r(t\wedge {\tau }_{\gamma }))\right)\hfill \\ \hfill \le & K_4+\frac{c_4}{{ϵ}_0}{e}^{{ϵ}_{0}t}+F_2\left({ϵ}_0\right)\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{e}^{{ϵ}_{0}s}|x\left(s\right){|}^{q_1}ds+F_1\left({ϵ}_0\right)\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{e}^{{ϵ}_{0}s}{\left|x\left(s\right)\right|}^{q_2}ds,\hfill \end{array}$$

(41)

where

$$\begin{array}{c}\hfill K_4=\mathbb{E}V({\tilde{x}}_0,0,r\left(0\right))+\left({ϵ}_0{c}_2{(1+\sigma )}^{q_2-1}\sigma +\frac{n{\omega }_2}{1-\overline{\delta }}+{\omega }_1\sigma {(1-\sigma )}^{q_2-1}\right)\mathbb{E}{\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_1}ds\\ \hfill +\left({ϵ}_0{c}_2{(1+\sigma )}^{q_1-1}\sigma +\frac{2n\delta }{1-\overline{\delta }}+(1-n\delta (q_1-2))\sigma {(1-\sigma )}^{q_1-1}\right)\mathbb{E}{\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_1}ds.\end{array}$$

Now, we see a new function $\Xi \left(u\right):{\mathbb{R}}_{+}\to \mathbb{R}:$

$$\Xi \left(u\right)=c_4+F_2\left({ϵ}_0\right)u^{q_1}+F_1\left({ϵ}_0\right)u^{q_2}.$$

Because $F_1\left({ϵ}_0\right)<0$ and $q_2>q_1,$ function $\Xi \left(u\right)$ has the finite supremum value that can be denoted as $c_5:={sup}_{u\ge 0}\Xi \left(u\right)<\infty .$ Letting $\gamma \to \infty$ in (41), and with (26), we obtain

$$c_1{e}^{{ϵ}_{0}t}\mathbb{E}|{\tilde{x}}_t{|}^{q_1}\le K_4+\mathbb{E}{\int }_0^t{e}^{{ϵ}_{0}s}\Xi \left(\right|x\left(s\right)\left|\right)ds\le K_4+\frac{c_5}{{ϵ}_0}(e^{{ϵ}_{0}t}-1).$$

(42)

Using inequality (21) by setting $a={\tilde{x}}_t,b=U(x(t-{\delta }_1\left(t\right)),t)$ and $\nu ={\theta }_0>{({\sigma }^{\frac{-q_1}{q_1-1}}-1)}^{-1},$ then by (42) we obtain

$$\begin{array}{cc}\hfill {\mathbb{E}\left|x\left(t\right)\right|}^{q_1}& \le {(1+{\theta }_0)}^{q_1-1}\mathbb{E}|{\tilde{x}}_t{|}^{q_1}+{(1+{\theta }_0^{-1})}^{q_1-1}\mathbb{E}{\left|U(x(t-{\delta }_1\left(t\right)),t)\right|}^{q_1}\hfill \\ \hfill & \le {(1+{\theta }_0)}^{q_1-1}\frac{K_4+\frac{c_5}{{ϵ}_0}(e^{{ϵ}_{0}t}-1)}{c_1{e}^{{ϵ}_{0}t}}+{(1+{\theta }_0^{-1})}^{q_1-1}{\sigma }^{q_1}(1-\overline{\delta })\mathbb{E}{\left|x(t-{\delta }_1\left(t\right))\right|}^{q_1}.\hfill \end{array}$$

(43)

For any $t\ge 0,$ (43) gives

$$\begin{array}{cc}\hfill & \underset{0\le s\le t}{sup}\mathbb{E}{\left|x\left(s\right)\right|}^{q_1}\hfill \\ \hfill \le & {(1+{\theta }_0)}^{q_1-1}(\frac{K_4}{c_1}{e}^{-{ϵ}_{0}t}+\frac{c_5}{c_1{ϵ}_0})+{(1+{\theta }_0^{-1})}^{q_1-1}{\sigma }^{q_1}\left(\underset{-\delta \left(0\right)\le s\le 0}{sup}{\mathbb{E}\left|\xi \left(s\right)\right|}^{q_1}+\underset{0\le s\le t}{sup}\mathbb{E}{\left|x\left(s\right)\right|}^{q_1}\right).\hfill \end{array}$$

Considering that $1-{(1+{\theta }_0^{-1})}^{q_1-1}{\sigma }^{q_1}>0,$ then

$$\underset{0\le s\le t}{sup}\mathbb{E}{\left|x\left(s\right)\right|}^{q_1}\le \frac{{(1+{\theta }_0)}^{q_1-1}(\frac{K_4}{c_1}{e}^{-{ϵ}_{0}t}+\frac{c_5}{c_1{ϵ}_0})+{(1+{\theta }_0^{-1})}^{q_1-1}{\sigma }^p\mathbb{E}{\parallel \xi \parallel }^{q_1}}{1-{(1+{\theta }_0^{-1})}^{q_1-1}{\sigma }^{q_1}},$$

and so

$$\underset{t\to \infty }{lim\; sup}\mathbb{E}{\left|x\left(t\right)\right|}^{q_1}\le \frac{c_5{(1+{\theta }_0)}^{q_1-1}+c_1{ϵ}_0{(1+{\theta }_0^{-1})}^{q_1-1}{\sigma }^p\mathbb{E}{\parallel \xi \parallel }^{q_1}}{c_1{ϵ}_0(1-{(1+{\theta }_0^{-1})}^{q_1-1}{\sigma }^{q_1})}=:K_2,$$

which implies that (24) is satisfied. Thus, the proof is completed. □

Theorem 2.

Let Assumptions (${\mathcal{A}}_1$)–(${\mathcal{A}}_5$) hold. Denote by ${\lambda }_0:=min\{{\eta }_1^{*},{\eta }_2^{*},\zeta \}.$ Additionally, if ${\alpha }_{i1}=0$ for $i\in S,$ then for any initial condition (4), the global solution $x\left(t\right)$ of system (3) has the following properties:

$$\underset{t\to \infty }{lim\; sup}\frac{ln{\mathbb{E}\left|x\left(t\right)\right|}^{q_1}}{t}\le -\zeta ,$$

(44)

$$\underset{t\to \infty }{lim\; sup}\frac{ln\left|x\right(t\left)\right|}{t}\le -\frac{\zeta }{q_1},a.s..$$

(45)

Proof. 

Recalling (17) and (18), ${\eta }_1^{*}$ and ${\eta }_2^{*}$ are, respectively, the unique positive root of equations $F_1\left(\eta \right)=0$ and $F_2\left(\eta \right)=0.$ So, we know ${\lambda }_0>0,$ and that for any $0<\overline{\lambda }<{\lambda }_0,$ $F_1\left(\overline{\lambda }\right)<0,F_2\left(\overline{\lambda }\right)<0.$

By the generalized $It\widehat{o}$ formula, it follows that

$$\begin{array}{cc}\hfill e^{\overline{\lambda }t}V({\tilde{x}}_t,t,r\left(t\right))=& V({\tilde{x}}_0,0,r\left(0\right))+M_2\left(t\right)\hfill \\ \hfill & +{\int }_0^t{e}^{\overline{\lambda }s}\left(\overline{\lambda }V({\tilde{x}}_s,s,r\left(s\right))+LV({\tilde{x}}_s,x(s-{\delta }_1\left(s\right)),\cdots ,x(s-{\delta }_n\left(s\right)),s,r\left(s\right))\right)ds,\hfill \end{array}$$

(46)

where $M_2\left(t\right)$ is a martingale with $M_2\left(0\right)=0.$

Then taking expectation to $e^{\overline{\lambda }t(t\wedge {\tau }_{\gamma })}V({\tilde{x}}_{t\wedge {\tau }_{\gamma }},t\wedge {\tau }_{\gamma },r(t\wedge {\tau }_{\gamma })),$ where ${\tau }_{\gamma }$ is given in (34), we obtain

$$\begin{array}{cc}\hfill & \mathbb{E}\left(e^{\overline{\lambda }(t\wedge {\tau }_{\gamma })}V({\tilde{x}}_{t\wedge {\tau }_{\gamma }},t\wedge {\tau }_{\gamma },r(t\wedge {\tau }_{\gamma }))\right)\hfill \\ \hfill =& \mathbb{E}V({\tilde{x}}_0,0,r\left(0\right))+\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{e}^{\overline{\lambda }s}\left(\overline{\lambda }V({\tilde{x}}_s,s,r\left(s\right))+LV(x\left(s\right),x(s-{\delta }_1\left(s\right)),\cdots ,x(s-{\delta }_n\left(s\right)),s,r\left(s\right))\right)ds.\hfill \end{array}$$

Just as the same discussion as above, by (33), (35)–(38) and (22), we have that for ${\alpha }_{i1}=0,$

$$\mathbb{E}\left(e^{\overline{\lambda }(t\wedge {\tau }_{\gamma })}V({\tilde{x}}_{t\wedge {\tau }_{\gamma }},t\wedge {\tau }_{\gamma },r(t\wedge {\tau }_{\gamma }))\right)\le K_5+F_2\left(\overline{\lambda }\right)\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{e}^{\overline{\lambda }s}|x\left(s\right){|}^{q_1}ds+F_1\left(\overline{\lambda }\right)\mathbb{E}{\int }_0^{t\wedge {\tau }_{\gamma }}{e}^{\overline{\lambda }s}{\left|x\left(s\right)\right|}^{q_2}ds,$$

where

$$\begin{array}{c}\hfill K_5=\mathbb{E}V({\tilde{x}}_0,0,r\left(0\right))+\left(\overline{\lambda }{c}_2{(1+\sigma )}^{q_2-1}\sigma +\frac{n{\omega }_2}{1-\overline{\delta }}+{\omega }_1\sigma {(1-\sigma )}^{q_2-1}\right)\mathbb{E}{\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_2}ds\\ \hfill +\left(\overline{\lambda }{c}_2{(1+\sigma )}^{q_1-1}\sigma +\frac{2n\delta }{1-\overline{\delta }}+(1-n\delta (q_1-2))\sigma {(1-\sigma )}^{q_1-1}\right)\mathbb{E}{\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_1}ds.\end{array}$$

As $F_1\left(\overline{\lambda }\right)<0,F_2\left(\overline{\lambda }\right)<0$ and from (26), we have that

$$c_1\mathbb{E}\left(e^{\overline{\lambda }(t\wedge {\tau }_{\gamma })}{\left|{\tilde{x}}_{t\wedge {\tau }_{\gamma }}\right|}^{q_1}\right)\le K_5.$$

when $\gamma \to \infty ,$ we obtain

$$e^{\overline{\lambda }t}\mathbb{E}{|x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)|}^{q_1}\le \frac{K_5}{c_1}.$$

Using inequality (21) by setting $a={\tilde{x}}_t,b=U(x(t-{\delta }_1\left(t\right)),t)$ and $\nu =\frac{\sigma }{1-\sigma },$ it becomes

$$\begin{array}{cc}\hfill e^{\overline{\lambda }t}\mathbb{E}{\left|x\left(t\right)\right|}^{q_1}& \le {(1-\sigma )}^{1-q_1}{e}^{\overline{\lambda }t}\mathbb{E}|{\tilde{x}}_t{|}^{q_1}+{\sigma }^{1-q_1}{e}^{\overline{\lambda }t}\mathbb{E}{\left|U(x(t-{\delta }_1\left(t\right)),t)\right|}^{q_1}\hfill \\ \hfill & \le \frac{K_5}{c_1}{(1-\sigma )}^{1-q_1}+\sigma (1-\overline{\delta })\left(e^{\overline{\lambda }(t-{\delta }_1\left(t\right))}\mathbb{E}{\left|x(t-{\delta }_1\left(t\right))\right|}^{q_1}\right).\hfill \end{array}$$

(47)

So,

$$\underset{0\le s\le t}{sup}{e}^{\overline{\lambda }s}{\mathbb{E}\left|x\left(s\right)\right|}^{q_1}\le \frac{K_5}{c_1}{(1-\sigma )}^{1-q_1}+{\sigma \mathbb{E}\parallel \xi \parallel }^{q_1}+\sigma \underset{0\le s\le t}{sup}{e}^{\overline{\lambda }s}\mathbb{E}{\left|x\left(s\right)\right|}^{q_1}.$$

Then, we have

$$\underset{0\le s\le t}{sup}{e}^{\overline{\lambda }s}\mathbb{E}{\left|x\left(s\right)\right|}^{q_1}\le \frac{1}{1-\sigma }\left(\frac{K_5}{c_1}{(1-\sigma )}^{1-q_1}+\sigma \mathbb{E}{\parallel \xi \parallel }^{q_1}\right),$$

which implies

$$\underset{0\le t\le \infty }{sup}{e}^{\overline{\lambda }t}\mathbb{E}{\left|x\left(t\right)\right|}^{q_1}\le \left(\frac{K_5}{c_1}{(1-\sigma )}^{-q_1}+\frac{{\sigma \mathbb{E}\parallel \xi \parallel }^{q_1}}{1-\sigma }\right),$$

and

$$\underset{t\to \infty }{lim\; sup}\frac{{\mathbb{E}\left|x\left(t\right)\right|}^{q_1}}{t}\le -\overline{\lambda }.$$

By (46), we can similarly derive

$$e^{\overline{\lambda }t}V({\tilde{x}}_t,t,r\left(t\right))\le K_6+F_2\left(\overline{\lambda }\right){\int }_0^t{e}^{\overline{\lambda }s}|x\left(s\right){|}^{q_1}ds+F_1\left(\overline{\lambda }\right){\int }_0^t{e}^{\overline{\lambda }s}{\left|x\left(s\right)\right|}^{q_2}ds+M_2\left(t\right),$$

where

$$\begin{array}{c}\hfill K_6=V({\tilde{x}}_0,0,r\left(0\right))+\left(\overline{\lambda }{c}_2{(1+\sigma )}^{q_2-1}\sigma +\frac{n{\omega }_2}{1-\overline{\delta }}+{\omega }_1\sigma {(1-\sigma )}^{q_2-1}\right){\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_2}ds\\ \hfill +\left(\overline{\lambda }{c}_2{(1+\sigma )}^{q_1-1}\sigma +\frac{2n\delta }{1-\overline{\delta }}+(1-n\delta (q_1-2))\sigma {(1-\sigma )}^{q_1-1}\right){\int }_{-\delta \left(0\right)}^0{\left|\xi \left(s\right)\right|}^{q_1}ds.\end{array}$$

From $F_1\left(\overline{\lambda }\right)<0,F_2\left(\overline{\lambda }\right)<0$ and the inequality (26), we obtain

$$c_1{e}^{\overline{\lambda }t}{|x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)|}^{q_1}\le K_6+M_2\left(t\right).$$

Then, the non-negative semi-martingale convergence theorem gives

$$\underset{t\to \infty }{lim\; sup}\left(e^{\overline{\lambda }t}{|x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)|}^{q_1}\right)<\infty ,a.s.$$

So, there exists a positive finite random variable $\tilde{\zeta }$ such that

$$\underset{0\le t<\infty }{sup}\left(e^{\overline{\lambda }t}{|x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)|}^{q_1}\right)\le \tilde{\zeta },a.s.$$

Similarly, with the procedure as in (47), it follows that for $t\ge 0,$

$$\underset{0\le s\le t}{sup}{e}^{\overline{\lambda }s}{\left|x\left(s\right)\right|}^{q_1}\le \frac{1}{1-\sigma }\left({(1-\sigma )}^{1-q_1}\tilde{\zeta }+\sigma {\parallel \xi \parallel }^{q_1}\right),a.s.$$

Then

$$\underset{0\le t<\infty }{sup}{e}^{\overline{\lambda }t}{\left|x\left(t\right)\right|}^{q_1}\le \frac{1}{1-\sigma }\left({(1-\sigma )}^{1-q_1}\tilde{\zeta }+\sigma {\parallel \xi \parallel }^{q_1}\right),a.s.$$

and consequently,

$$\underset{t\to \infty }{lim\; sup}\frac{ln\left|x\right(t\left)\right|}{t}\le -\frac{\overline{\lambda }}{q_1},a.s.$$

Thus, we see that (44) and (45) hold by the arbitrariness of $\overline{\lambda }$ as required. The proof is completed. □

Remark 1.

In papers [23,24], the p-moment exponential stability of the Caputo fractional differential equations with a single structure were investigated by the application of Lyapunov functions. In Theorem 2 of this work, the Lyapunov function method is used to establish the $q_1$th moment and almost sure exponential stability of the differently structured stochastic system (3). Moreover, If the Caputo fractional derivatives of the Lyapunov functions are applied, the results of this work will make sense in the corresponding Caputo fractional version driven by the standard Brownian motion as well.

4. Example

This section will show three numerical examples to illustrate the main results.

Example 1.

We discuss the following neutral stochastic pantograph differential equation on $\mathbb{R}$:

$$\begin{array}{cc}\hfill & d[x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)]\hfill \\ \hfill =& F(x\left(t\right),x(t-{\delta }_1\left(t\right)),x(t-{\delta }_2\left(t\right)),t,r\left(t\right))dt+G(x\left(t\right),x(t-{\delta }_2\left(t\right)),t,r\left(t\right))dW\left(t\right),\hfill \end{array}$$

(48)

$x\left(0\right)=-1,$${\delta }_1\left(t\right)=0.1t,{\delta }_2\left(t\right)=0.2t$ and $U(y_1,t)=0.24e^{-0.3t}{y}_1.$ $W\left(t\right)$ is a 1-dimensional standard Brownian motion. $r\left(t\right)$ is the right continuous Markov chain with state space $S=\{1,2,3\}$ and the generator

$$\begin{array}{cc}\hfill & \Gamma =\left(\begin{array}{ccc}-2& 1& 1\\ 1.2& -3& 1.8\\ 0.5& 0.5& -1\end{array}\right).\hfill \end{array}$$

S is divided into $S_1=\{1,2\}$ and $S_2=\left\{3\right\}$. For $i\in S,$ set

$$\begin{array}{cc}\hfill & F(x,y_1,y_2,t,1)=-5x+1.2e^{-0.3t}{y}_1;G(x,y_1,y_2,t,1)=0.2e^{-0.3t}{y}_2;\hfill \\ \hfill & F(x,y_1,y_2,t,2)=-12x+1.92e^{-0.3t}{y}_1-0.3e^{-0.3t}{y}_2;G(x,y_1,y_2,t,2)=x+0.1e^{-0.3t}{y}_2;\hfill \\ \hfill & F(x,y_1,y_2,t,3)=-8x^3-6x-0.6912e^{-0.6t}x{y}_1^2-0.055296e^{-0.9t}{y}_1^3;G(x,y_1,y_2,t,3)=0.1e^{-0.6t}{y}_2^2.\hfill \end{array}$$

(49)

Equation (49) shows that system (48) has different structures in the subspaces $S_1$ and $S_2.$ Now, the Assumptions (${\mathcal{A}}_1$), (${\mathcal{A}}_2$) and (${\mathcal{A}}_5$) hold with $d=1,n_1=2,n=2,\delta \left(t\right)=0.2t,$ $\overline{\delta }=0.2,\overline{\sigma }=0.24,\sigma =0.3,\zeta =2.$ Then, it can be verified that

$$\begin{array}{cc}\hfill (x-U(y_1,t))F(x,y_1,y_2,t,1)+\frac{3}{2}{\left|G(x,y_2,t,1)\right|}^2\le & -5|x-U(y_1,t){|}^2+0.01e^{-0.6t}{y}_1^2+0.06e^{-0.6t}{y}_2^2;\hfill \\ \hfill (x-U(y_1,t))F(x,y_1,y_2,t,2)+\frac{3}{2}{\left|G(x,y_2,t,2)\right|}^2\le & -10|x-U(y_1,t){|}^2+0.1512e^{-0.6t}{y}_1^2+0.051e^{-0.6t}{y}_2^2;\hfill \\ \hfill (x-U(y_1,t))F(x,y_1,y_2,t,3)+\frac{3}{2}{\left|G(x,y_2,t,3)\right|}^2\le & -3|x-U(y_1,t){|}^2+0.1728e^{-0.6t}{y}_1^2+0.002e^{-0.6t}{y}_2^2\hfill \\ \hfill & -2|x-U(y_1,t){|}^4+0.02e^{-1.2t}{y}_1^4+0.01e^{-1.2t}{y}_2^4.\hfill \end{array}$$

so that for $q_1=2,q_2=4,$ the Assumption (${\mathcal{A}}_3$) is satisfied with

$$\begin{array}{cc}\hfill & {\alpha }_{11}=0;{\alpha }_{12}=5;{\alpha }_{131}=0.01;{\alpha }_{132}=0.06;{\alpha }_{21}=0;{\alpha }_{22}=10;{\alpha }_{231}=0.1512;{\alpha }_{232}=0.051;\hfill \\ \hfill & {\alpha }_{31}=0;{\alpha }_{32}=3;{\alpha }_{331}=0.1728;{\alpha }_{332}=0.02;{\alpha }_{34}=2;{\alpha }_{351}=0.02;{\alpha }_{352}=0.01.\hfill \end{array}$$

Then, we obtain

$$\mathcal{A}=\left(\begin{array}{ccc}12& -1.& -1\\ -1.2& 23& -1.8\\ -0.5& -0.5& 7\end{array}\right);\mathcal{S}=\left(\begin{array}{cc}22& -1\\ -1.2& 43\end{array}\right).$$

Taking $\omega =3$, we have

$$({\theta }_1,{\theta }_2,{\theta }_3)=(0.1013,0.0608,0.1544);({\eta }_1,{\eta }_2)=(0.0466,0.0246),$$

Thus, the conditions in the Assumption (${\mathcal{A}}_4$) all hold.

By solving the equation $F_1\left(\eta \right)=0$ and $F_2\left(\eta \right)=0$, we obtain ${\lambda }_0=0.94133.$ Then, by Theorems 1 and 2, we see that the unique global solution $x\left(t\right)$ of Equation (48) is exponentially stable as follows:

$$\underset{t\to \infty }{lim\; sup}\frac{ln{E\left|x\left(t\right)\right|}^{q_1}}{t}\le -{\lambda }_0=-0.94133$$

and

$$\underset{t\to \infty }{lim\; sup}\frac{ln\left|x\right(t\left)\right|}{t}\le -\frac{{\lambda }_0}{2}=-0.470665,a.s.$$

(50)

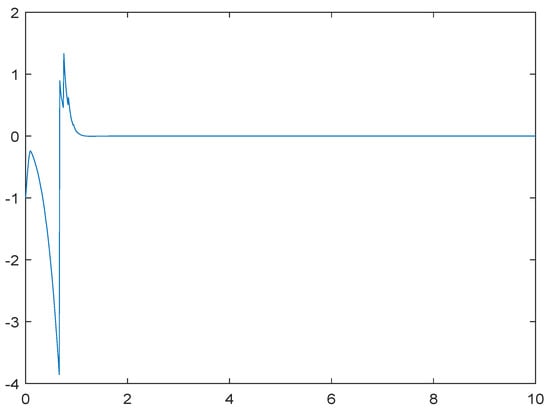
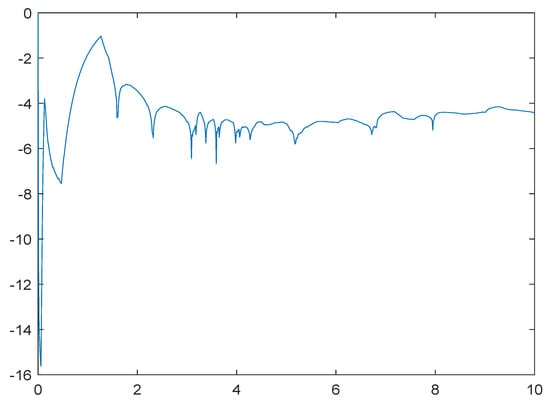
Figure 1 and Figure 2 show the computer simulations of the solution $x\left(t\right)$ of the system (48) and the stability (50), respectively, by the Euler–Maruyama method with a step size of 0.01 and initial data $x\left(0\right)=-1,r\left(0\right)=2$ for 1000 samples. Figure 1 indicates that the highly nonlinear differently structured hybrid NSDEs with multiple unbounded time-varying delays (48) are asymptotically stable, while Figure 2 shows that it is almost surely exponential stable, which illustrates the results accurately.

Figure 1. Computer simulation of the solution x(t) of Equation (48).

Figure 2. Computer simulation of the $ln\left|x\right(t\left)\right|/t$ of the solution x(t) of Equation (48).

Example 2.

We give two differently structured NSDEs with bounded and with unbounded delays on $\mathbb{R}$, respectively, and discuss the differences in the asymptotic behaviors of them.

Case 1 (with bounded delay):

$$\begin{array}{cc}\hfill & d[x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)]\hfill \\ \hfill =& F(x\left(t\right),x(t-{\delta }_1\left(t\right)),x(t-{\delta }_2\left(t\right)),t,r\left(t\right))dt+G(x\left(t\right),x(t-{\delta }_2\left(t\right)),t,r\left(t\right))dW\left(t\right),\hfill \end{array}$$

(51)

where $x\left(0\right)=-1,$ ${\delta }_1\left(t\right)=sint,{\delta }_2\left(t\right)=cost$ $U(y_1,t)=0.24y_1.$

Case 2 (with unbounded delay):

$$\begin{array}{cc}\hfill & d[x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)]\hfill \\ \hfill =& F(x\left(t\right),x(t-{\delta }_1\left(t\right)),x(t-{\delta }_2\left(t\right)),t,r\left(t\right))dt+G(x\left(t\right),x(t-{\delta }_2\left(t\right)),t,r\left(t\right))dW\left(t\right),\hfill \end{array}$$

(52)

where $x\left(0\right)=-1,$ ${\delta }_1\left(t\right)=0.8t,{\delta }_2\left(t\right)=0.5t,$ $U(y_1,t)=0.24y_1.$

For comparison, we set all the other terms in Equations (51) and (52) to be the same. $W\left(t\right)$ is a 1-dimensional standard Brownian motion. $r\left(t\right)$ is the same Markov chain as that in Example 1. We set

$$\begin{array}{cc}\hfill & F(x,y_1,y_2,t,1)=-0.5x+1.2y_1;G(x,y_1,y_2,t,1)=0.2y_2;\hfill \\ \hfill & F(x,y_1,y_2,t,2)=-1.2x+1.92y_1-0.3y_2;G(x,y_1,y_2,t,2)=x+0.1y_2;\hfill \\ \hfill & F(x,y_1,y_2,t,3)=-0.8x^3-6x-0.6912x{y}_1^2-0.055296y_1^3;G(x,y_1,y_2,t,3)=0.1y_2^2.\hfill \end{array}$$

Obviously, two equations have quite different structures in the subspaces of $r\left(t\right),$ and both of them do not satisfy the condition (${\mathcal{A}}_3$) of Theorem 2. Now we simulate the solutions of Equations (51) and (52) respectively by the Euler–Maruyama method with step size 0.01 and initial data $x\left(0\right)=-1,r\left(0\right)=2$ for 1000 samples.

Figure 3 indicates that the highly nonlinear differently structured hybrid NSDDE (51) with multiple bounded time-varying delays is asymptotically stable, though the conditions of Theorem 2 are not met. Figure 4 shows that when the delay terms become unbounded, the solution of the NSDDE (52) is no longer stable. Further with the Example 1, it can be seen that when the conditions of Theorem 2 are satisfied in unbounded delay case, the solution is asymptotically stable and almost surely exponential stable.

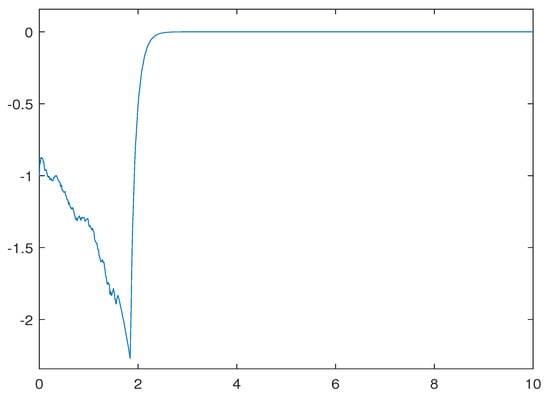
Figure 3. Computer simulation of the solution $x\left(t\right)$ of Equation (51).

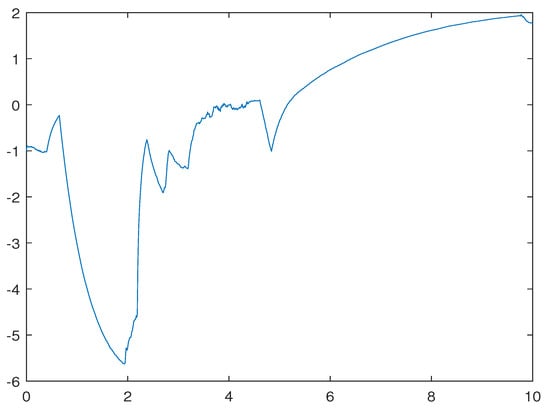
Figure 4. Computer simulation of the solution $x\left(t\right)$ of Equation (52).

The Example 2 shows not only the differences in the asymptotic behavior of the systems with bounded and with unbounded delays, but also the effectiveness of the conditions of Theorem 2 in the unbounded delay case.

Example 3.

Now we show the following neutral stochastic differential delay equation on ${\mathbb{R}}^2$:

$$\begin{array}{cc}\hfill & d[x\left(t\right)-U(x(t-{\delta }_1\left(t\right)),t)]\hfill \\ \hfill =& F(x\left(t\right),x(t-{\delta }_1\left(t\right)),x(t-{\delta }_2\left(t\right)),t,r\left(t\right))dt+G(x\left(t\right),x(t-{\delta }_2\left(t\right)),t,r\left(t\right))dW\left(t\right),\hfill \end{array}$$

(53)

where $x\left(t\right)={(x_1\left(t\right),x_2\left(t\right))}^T\in {\mathbb{R}}^2,x\left(0\right)={(-1,-1)}^T,$${\delta }_1\left(t\right)=0.1t,{\delta }_2\left(t\right)=0.2t.$ For $y\in {\mathbb{R}}^2,$ we set $U(y,t)=0.24e^{-0.3t}y.$ $F={(F_1,F_2)}^T,G={(G_1,G_2)}^T.$ $F_1,F_2,G_1,G_2$ will be defined later.

$W\left(t\right)$ is a 1-dimensional standard Brownian motion. $r\left(t\right)$ is the same Markov chain as that in Examples 1 and 2. For $i\in S,z_1,z_2,z_3\in \mathbb{R},$ set

$$\begin{array}{cc}\hfill & F_1(z_1,z_2,z_3,t,1)=-2.4z_1+5e^{-0.3t}{z}_2;G_1(z_1,z_2,z2,t,1)=0.2e^{-0.3t}{z}_3;\hfill \\ \hfill & F_2(z_1,z_2,z_3,t,1)=-z_1+3.9e^{-0.3t}{z}_2;G_1(z_1,z_2,z,t,1)=0.06e^{-0.3t}{z}_3;\hfill \\ \hfill & F_1(z_1,z_2,z_3,t,2)=-2.5z_1+1.6e^{-0.3t}{z}_2-0.3e^{-0.3t}{z}_3;G_1(z_1,z_2,z,t,2)=1.58z_1+0.1e^{-0.3t}{z}_3;\hfill \\ \hfill & F_2(z_1,z_2,z_3,t,2)=-3z_1+0.85e^{-0.3t}{z}_2-0.5e^{-0.3t}{z}_3;G_2(z_1,z_2,z,t,2)=2.7z_1+0.3e^{-0.3t}{z}_3;\hfill \\ \hfill & F_1(z_1,z_2,z_3,t,3)=-5z_1^3-6z_1-0.6912e^{-0.6t}{z}_1{z}_2^2-0.05e^{-0.9t}{z}_2^3;G_1(z_1,z_2,z,t,3)=0.5e^{-0.6t}{z}_3^2;\hfill \\ \hfill & F_2(z_1,z_2,z_3,t,3)=-1.7z_1^3-5z_1-0.7e^{-0.6t}{z}_1{z}_2^2-0.2e^{-0.9t}{z}_2^3;G_2(z_1,z_2,z,t,3)=1.32e^{-0.6t}{z}_3^2.\hfill \end{array}$$

Obviously, the system (53) has different structures in the subspaces. Similarly with the calculation in Example 1, it can be verified that the conditions in Theorem 2 hold with $d=2,$ $n_1=2,n=2,\delta \left(t\right)=0.2t,\overline{\delta }=0.2,\overline{\sigma }=0.24,\sigma =0.3,\zeta =2.$ We now show the computer simulations of the solution $x\left(t\right)$ of the system (53) by the Euler-Maruyama method with step size 0.01 and initial data $x\left(0\right)={(-1,-1)}^T,r\left(0\right)=2$ for 1000 samples.

Figure 5 indicates that the highly nonlinear differently structured hybrid NSDE with multiple unbounded time-varying delays (53) is asymptotically stable, which illustrates the results accurately.

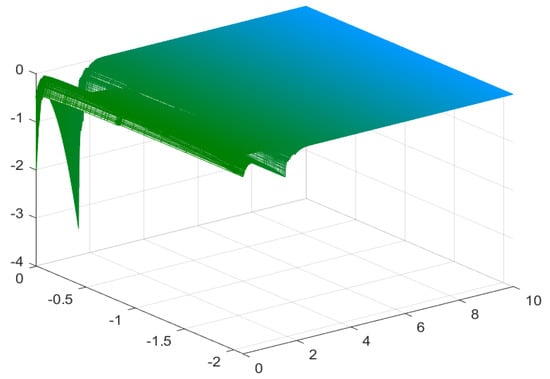
Figure 5. Computer simulation of the solution $x\left(t\right)$ of the Equation (53).

5. Conclusions

In this paper, we study the highly nonlinear hybrid differently structured NSDDEs with multiple unbounded time-varying delays. The existence, uniqueness and $q_1$th moment asymptotical boundedness of the exact global solution of the new system were investigated. The criteria of the $q_1$th moment and almost surely exponential stability are established. Based on existing works, this paper’s main contribution is extending the exponential stability results of highly nonlinear hybrid differently structured NSDDEs from the single constant delay to more general multiple unbounded time-varying delays. We used the M-matrix, generalized $It\widehat{o}$ formula, non-negative semi-martingale convergence theorem and Lyapunov function methods to obtain the results. The factor $e^{-\zeta \delta \left(t\right)}$ was fully used to overcome the difficulty caused by the unbounded delay functions. The new system we discussed in this paper is more general and applicable. A specific case of the application is the pantograph dynamics, in which the unbounded delay is a proportional function. Three numerical examples are also given to illustrated the results of this paper.