Fractional Dynamics of Typhoid Fever Transmission Models with Mass Vaccination Perspectives

Abstract

In this work, we formulate and mathematically study integer and fractional models of typhoid fever transmission dynamics. The models include vaccination as a control measure. After recalling some preliminary results for the integer model (determination of the epidemiological threshold denoted by ${\mathcal{R}}_c$, asymptotic stability of the equilibrium point without disease whenever ${\mathcal{R}}_c<1$, the existence of an equilibrium point with disease whenever ${\mathcal{R}}_c>1$), we replace the integer derivative with the Caputo derivative. We perform a stability analysis of the disease-free equilibrium and prove the existence and uniqueness of the solution of the fractional model using fixed point theory. We construct the numerical scheme and prove its stability. Simulation results show that when the fractional-order $\eta$ decreases, the peak of infected humans is delayed. To reduce the proliferation of the disease, mass vaccination combined with environmental sanitation is recommended. We then extend the previous model by replacing the mass action incidences with standard incidences. We compute the corresponding epidemiological threshold denoted by ${\mathcal{R}}_{c\star }$ and ensure the uniform stability of the disease-free equilibrium, for both new models, when ${\mathcal{R}}_{c\star }<1$. A new calibration of the new model is conducted with real data of Mbandjock, Cameroon, to estimate ${\mathcal{R}}_{c\star }=1.4348$. We finally perform several numerical simulations that permit us to conclude that such diseases can possibly be tackled through vaccination combined with environmental sanitation.

1. Introduction

Typhoid fever, caused by a salmonella bacterium (Salmonella typhi), is a tropical disease transmitted by the ingestion of food or/and water contaminated with feces. It is most prevalent in countries located below the equator, in Southeast Asia, and in the Indian subcontinent, where hygiene conditions are poor [1,2]. The principal symptoms of typhoid fever are insomnia, fever, generalized fatigue, headaches, stomach ache, anorexia, constipation or diarrhea, and vomiting. These symptoms can last several weeks. Without effective treatment, typhoid fever can lead to death. According to the World Health Organization (WHO), the number of cases of typhoid fever is estimated to be between 11 and 21 million, with 128,000 to 161,000 deaths annually due to the severity of the disease [1,2]. Vaccination, sanitary measures, and hygiene measures are the best ways to prevent the spread of the disease [2].

Since the work of Sir Ronald Ross on malaria [3], mathematical tools such as differential equations have usually been used to understand and describe the dynamics of infectious diseases [4,5,6,7,8,9,10,11,12]. In [7], the authors proposed a $SVI{I}_{c}R$ that takes into account some control mechanisms (treatment, education campaigns, and vaccination). Quarantining the infected individuals and their treatment are the main control measures studied in [8]. The author used optimal control methods to conclude that the outbreak can be eliminated or controlled if the control strategies are combined to their highest levels. The same conclusions are given in [10,11]. Recently, Olumuyiwa James et al. [9] formulated and studied an optimal control model for typhoid fever that takes into account both indirect and direct transmission. They compared various proposed strategies using numerical simulations and concluded that the disease burden can be controlled if all the available control measures are combined.

Very recently, many authors have proposed fractional-order models in mathematical epidemiology (ref. [13]), ecology (ref. [14]), plant epidemiology (refs. [15,16]), and psychology (ref. [17]). Indeed, the necessity of the use of fractional derivatives in epidemiology, for example, comes from the fact that these operators have many properties, such as their different types of kernels and the crossover behavior in the model, which can only be described using these operators. Moreover, any real data that have zigzag dynamics (mostly many) that cannot be projected by an integer-order derivative can be solved by a fractional model more clearly.

The principal disadvantage of models with integer derivatives is that they do not permit the definition of memory effects. Replacing integer derivatives with fractional derivatives makes it possible to remedy this problem. Indeed, they offer different ways to forecast data by varying the fractional-order parameter [12,18,19]. Several fractional operators have been defined so far. The most popular are the fractional operators of Caputo, the fractional Caputo–Fabrizio operator, and the fractional operator of Atangana–Baleanu. Each operator explores the dynamics of the studied phenomenon differently, thus helping us to predict more variations in the evolution of the phenomenon. The advantages and disadvantages of each fractional operator and their application domains can be found in [20,21,22].

To the best of our knowledge, there are few mathematical works on typhoid fever using fractional operators [6,12]. In [12], the authors used the Caputo–Fabrizio operator to extend the model proposed in [23]. They provided existence, uniqueness, and stability criteria for the proposed fractional-order typhoid model. More recently, Abboubakar et al. [6] formulated a $SIR$-B-type compartmental model with both integer and Caputo derivatives. The only control measure was vaccination. They computed the control reproduction number, $R_c$, and performed stability analysis of the disease-free equilibrium point for both models. The present contributions are listed as follows:

• Using a fractional derivative in place of an integer derivative, as used in our previous model [5], we formulate a new model. To prove the existence and uniqueness of the solutions, we use fixed point theory. The corresponding numerical scheme is obtained through the Adams–Bashforth–Moulton method [24,25]. The stability of this numerical scheme is also proven. Finally, several numerical simulations are carried out from the real values of parameters estimated with real data of Mbandjock, in Cameroon (see [5]).
• Secondly, we extend the previous models by replacing the mass action incidence law with the standard incidence law. For these new models, we compute the corresponding control reproduction number, ${\mathcal{R}}_{c\star }$, and ensure the uniform stability of the equilibrium point without disease. As in [6], model parameters are estimated. With these new parameter values, we finally perform several numerical simulations that permit us to compare the quantitative dynamics of the two types of models.

The rest of the work is organized as follows. We devote Section 2 to preliminary definitions of the fractional derivative in the sense of Caputo and useful results. Formulation of the models with mass incidence law and standard incidence, as well as their mathematical analysis (computation of control reproduction numbers, asymptotic stability analysis of the disease-free equilibrium, existence as well as the uniqueness of solutions, construction of the numerical scheme with its stability), is also described in this section. The calibration of the model with standard incidences and several numerical results is given in Section 3. We end the paper with a discussion and conclusions.

2. Materials and Methods

2.1. Useful Definitions and Results

For over ten years, fractional derivatives have captured the attention of researchers, who use these fractional operators to model physical, chemical, and biological processes. One can cite the dynamics of transmissible diseases [26,27,28]. Before the formulation of the fractional models, it is important to recall their definition, as well as two results that will be used later in the fractional model analysis.

Definition 1.

Let $f\in C_{-1}^l$, and we have the following relation:

$$D_{\tau }^{\nu }f\left(\tau \right)=\left\{\begin{array}{cc}\frac{d^{r}f\left(\tau \right)}{d{\tau }^r},\hfill & \hfill \nu =r\in \mathbb{N}\\ \frac{1}{\Gamma (r-\nu )}{\int }_0^{\tau }{(\tau -\iota )}^{r-\nu -1}{f}^{\left(r\right)}\left(\iota \right)d\iota ,\hfill & \hfill -1+r<\nu <r,r\in \mathbb{N},\end{array}\right.$$

(1)

which represents the Caputo derivative of f.

Lemma 1.

Assume that $\chi ,\mathbf{Q},\mathbf{h},\mathbf{Y}>0$, $\mathbf{k}\mathbf{h}\le \mathbf{Y}$ with $\mathbf{k}\in \mathbb{N}$, and

$${\mathbf{y}}_{q,m}=\left\{\begin{array}{cc}{(m-q)}^{\chi -1}\hfill & q=1,2,\dots ,m-1,\hfill \\ 0\hfill & q\ge m.\hfill \end{array}\right.$$

Let ${\sum }_{q=\mathbf{k}}^{q=i}{\mathbf{y}}_{q,m}|{\mathbf{e}}_q|=0$ for $\mathbf{k}>m\ge 1$.

If

$$|{\mathbf{e}}_m|\le \mathbf{Q}{\mathbf{h}}^{\chi }\sum _{q=1}^{m-1}{\mathbf{y}}_{q,m}|{\mathbf{e}}_q|+|{\eta }_0|,m=1,2,\dots ,\mathbf{k},$$

then

$$|{\mathbf{e}}_k|\le \mathcal{M}|{\eta }_0|,\mathbf{k}\in \{1,2,\dots \}$$

where $\mathcal{M}\in {\mathbb{R}}_{+}$ does not depend on $\mathbf{h}$ and $\mathbf{k}$.

Lemma 2.

If $0<\chi <1$ and $\mathbf{d}\in \mathbb{N}$, then there exist positive constants $W_{\chi ,1}$ and $W_{\chi ,2}$ only dependent on $\chi ,$ such that

$${(1+\mathbf{v})}^{\chi }-{\mathbf{v}}^{\chi }\le {\mathcal{W}}_{\chi ,1}{(1+\mathbf{v})}^{\chi -1}\mathit{and}{(2+\mathbf{v})}^{\chi +1}-2{(1+\mathbf{v})}^{\chi +1}+{\mathbf{v}}^{\chi +1}\le {\mathcal{W}}_{\chi ,2}{(1+\mathbf{v})}^{\chi -1}.$$

2.2. Model Dynamics with Mass Action Incidence Law

2.2.1. Model Formulation in ODE Sense and Its Analysis

In a previous work [5], we formulated and analyzed a new mathematical model for the transmission dynamics of typhoid fever with application to the town of Mbandjock, in the central region of Cameroon. The model is divided into seven compartments: susceptible individuals $S\left(t\right)$, vaccinated individuals $V\left(t\right)$, infected individuals in latent stage $E\left(t\right)$, infected individuals without any sign of the disease $C\left(t\right)$, symptomatic infected individuals $I\left(t\right)$, recovered individuals $R\left(t\right)$, and the density of bacteria in the environment $B\left(t\right)$. Each individual in each compartment naturally dies at a rate ${\mu }_h$. Susceptible humans are recruited at a constant rate ${\Lambda }_h$. The population in compartment $S_h$ decreases either by vaccination at a rate $\xi$, or by infection at an incidence rate $\nu B\left(t\right)S\left(t\right)$, where $\nu$ is the contact rate. We denote by $\theta$ the rate at which vaccinated individuals lose their immunity. The vaccine efficacy is denoted by $ϵ$. The compartment E of latent individuals, which include infected susceptible individuals and vaccinated individuals, progresses either to the carriers compartment C at a rate $q{\gamma }_1$ or to the compartment I at the rate $(1-q){\gamma }_1$. Asymptomatic individuals become symptomatic at the rate $(1-p){\gamma }_2$ or recover at the rate $p{\gamma }_2$. $\delta$ denotes the disease-induced death rate of symptomatic individuals. Recovered individuals become susceptible at a rate $\alpha$. With this brief description, the mathematical formulation of the model studied in [5] is presented as follows:

$$\begin{array}{cc}\hfill \dot{S}\left(t\right)& ={\Lambda }_h-(k_1+\nu B\left(t\right))S\left(t\right)+\theta V\left(t\right)+\alpha R\left(t\right),\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& =-\left[k_2+(1-ϵ)\nu B\left(t\right)\right]V\left(t\right)+\xi S\left(t\right),\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)& =-k_{3}E\left(t\right)+\nu \left[\pi V\left(t\right)+S\left(t\right)\right]B\left(t\right),\hfill \end{array}$$

(2c)

$$\begin{array}{cc}\hfill \dot{C}\left(t\right)& =q{\gamma }_{1}E\left(t\right)-k_{4}C\left(t\right),\hfill \end{array}$$

(2d)

$$\begin{array}{cc}\hfill \dot{I}\left(t\right)& =q_1{\gamma }_{1}E\left(t\right)+p_1{\gamma }_{2}C\left(t\right)-\left[k_5+\sigma \right]I\left(t\right),\hfill \end{array}$$

(2e)

$$\begin{array}{cc}\hfill \dot{R}\left(t\right)& =p{\gamma }_{2}C\left(t\right)+\sigma I\left(t\right)-k_{6}R\left(t\right),\hfill \end{array}$$

(2f)

$$\begin{array}{cc}\hfill \dot{B}\left(t\right)& =p_{c}C\left(t\right)+p_{i}I\left(t\right)-{\mu }_{b}B\left(t\right),\hfill \end{array}$$

(2g)

where $k_1=\xi +{\mu }_h$, $k_2=\theta +{\mu }_h$, $k_3={\gamma }_1+{\mu }_h$, $k_4={\mu }_h+{\gamma }_2$, $k_5=\delta +{\mu }_h$, $k_6=\alpha +{\mu }_h$, $\pi =-1+ϵ$, $q_1=1-q$, $p_1=-p+1$, $k_7=k_1{k}_2-\theta \xi ={\mu }_h(k_2+\xi )>0$, $k_8=k_5+\sigma$.

Model (2) is defined in the following set:

$$\mathcal{W}=\left\{{\left(S,V,E,C,I,R,B\right)}^{\prime }\in {\mathbb{R}}_{+}^7:N=V+S+C+E+I+R\le {\displaystyle \frac{{\Lambda }_h}{{\mu }_h}};B\le {\displaystyle \frac{(p_i+p_c){\Lambda }_h}{{\mu }_h{\mu }_b}}\right\},$$

in which a dynamical system is defined, and where N denotes the human population.

Without disease, model (2) has the following equilibrium: ${\mathcal{Q}}_0={\left(S_0,V_0,0,0,0,0,0\right)}^{\prime }$, where $S_0={\Lambda }_h{k}_2/\left({\mu }_h(k_2+\xi )\right)$ and $V_0={\Lambda }_h\xi /\left({\mu }_h(k_2+\xi )\right)$. Using the same approach developed in [29], we obtain the control reproduction number given by

$$\begin{array}{c}\hfill {\mathcal{R}}_c=\sqrt{{\displaystyle \frac{\nu {\Lambda }_h(k_2+\pi \xi ){\gamma }_1\left[p_{c}q(\sigma +k_5)+p_i(k_4(1-q)+{\gamma }_{2}q(1-p))\right]}{{\mu }_b{\mu }_h{k}_3{k}_4(k_2+\xi )(\sigma +k_5)}}}.\end{array}$$

(3)

Considering the model without vaccination, $R_c$ is equal to the basic reproduction number:

$${\mathcal{R}}_0=\sqrt{{\displaystyle \frac{\nu {\Lambda }_h{\gamma }_1\left[p_{c}q(\sigma +k_5)+p_i(k_4(1-q)+{\gamma }_{2}q(1-p))\right]}{{\mu }_b{\mu }_h{k}_3{k}_4(\sigma +k_5)}}}.$$

(4)

Thus, it follows that

$$\begin{array}{c}\hfill {\mathcal{R}}_c={\mathcal{R}}_0\sqrt{{\displaystyle \frac{(k_2+\pi \xi )}{(k_2+\xi )}}}.\end{array}$$

Since $\pi \xi =(1-ϵ)\xi \le \xi$, we have ${\displaystyle \frac{(k_2+\pi \xi )}{(k_2+\xi )}}\le 1$, which means that ${\mathcal{R}}_c\le {\mathcal{R}}_0$. This proves that mass vaccination is a useful tool that can be used to effectively tackle this kind of tropical disease.

For typhoid model (2) in the ODE sense, the following results were proven in [5].

Proposition 1

([5]). For model (2), ${\mathcal{Q}}_0$ is locally and globally asymptotically stable in $\mathcal{W}$ if ${\mathcal{R}}_c<1$ and unstable if ${\mathcal{R}}_c>1$.

Proposition 2

([5]). Let us define the following coefficients:

$$\begin{array}{cc}\hfill {\mathbf{a}}_2& ={\mathcal{R}}_c^4{k}_3^2{k}_4^2{k}_8^2{\mu }_h^2{(\xi +k_2)}^2\pi \times \hfill \\ & \times ({\mu }_h{\gamma }_1\alpha (k_5+\sigma q)+{\gamma }_2{\mu }_h{k}_8(\alpha +{\gamma }_1)+{\gamma }_1{\gamma }_2\alpha (1-pq)k_5+[{\mu }_h^2+(\alpha +{\gamma }_2+{\gamma }_1){\mu }_h]{\mu }_h{k}_8),\hfill \\ \hfill {\mathbf{a}}_1& =-{\mathcal{R}}_c^2{k}_3^2{k}_4^2{k}_8^2{\mu }_h^2{(\xi +k_2)}^2{\gamma }_1{\Lambda }_h{k}_6\pi (k_4{q}_1+{\gamma }_2{p}_{1}q)({\mathcal{R}}_c^2-{\mathcal{R}}_b^2),\hfill \\ \hfill {\mathbf{a}}_0& =-{\gamma }_1^2{\mu }_h{\Lambda }_h^2{k}_3{k}_4{k}_6{k}_8{(k_4{q}_1+{\gamma }_2{p}_{1}q)}^2{(\pi \xi +k_2)}^2(\xi +k_2)({\mathcal{R}}_c^2-1).\hfill \end{array}$$

Model (2) with the integer derivative either has (1) only one endemic equilibrium whenever (${\mathbf{a}}_0<0⟺{\mathcal{R}}_c>1$) or (${\mathbf{a}}_1<0$ and ${\mathbf{a}}_0=0$ or ${\mathbf{a}}_1^2-4{\mathbf{a}}_2{\mathbf{a}}_0=0$), (2) two endemic equilibrium points if (${\mathbf{a}}_0>0({\mathcal{R}}_c<1)$, ${\mathbf{a}}_1<0({\mathcal{R}}_c>{\mathcal{R}}_b)$ and $a_1^2-4{\mathbf{a}}_2{\mathbf{a}}_0>0$), or (3) no equilibrium otherwise.

Theorem 1

([5]). Model (2) exhibits a supercritical bifurcation at ${\mathcal{R}}_c=1$, which implies that whenever ${\mathcal{R}}_c>1$, the endemic equilibrium is locally asymptotically stable.

Remark 1.

Proposition 1 combined with Theorem 1 implies that Proposition 2 (iii) will never hold true for model (2). Thus, the condition ${\mathcal{R}}_c<1$ is sufficient to eradicate the disease.

2.2.2. Fractional-Order Typhoid Model

The following model is obtained when we replace the integer derivative operator in (2) with the non-integer operator in the Caputo sense.

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }S\left(t\right)& ={\Lambda }_h-(k_1+\nu B\left(t\right))S\left(t\right)+\theta V\left(t\right)+\alpha R\left(t\right),\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }V\left(t\right)& =-\left[k_2+(1-ϵ)\nu B\left(t\right)\right]V\left(t\right)+\xi S\left(t\right),\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }E\left(t\right)& =-k_{3}E\left(t\right)+\nu \left[\pi V\left(t\right)+S\left(t\right)\right]B\left(t\right),\hfill \end{array}$$

(5c)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }C\left(t\right)& =q{\gamma }_{1}E\left(t\right)-k_{4}C\left(t\right),\hfill \end{array}$$

(5d)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }I\left(t\right)& =q_1{\gamma }_{1}E\left(t\right)+p_1{\gamma }_{2}C\left(t\right)-\left[k_5+\sigma \right]I\left(t\right),\hfill \end{array}$$

(5e)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }R\left(t\right)& =p{\gamma }_{2}C\left(t\right)+\sigma I\left(t\right)-k_{6}R\left(t\right),\hfill \end{array}$$

(5f)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }B\left(t\right)& =p_{c}C\left(t\right)+p_{i}I\left(t\right)-{\mu }_{b}B\left(t\right).\hfill \end{array}$$

(5g)

with $S\left(0\right)\ge 0$, $V\left(0\right)\ge 0$, $B\left(0\right)\ge 0$, $E\left(0\right)\ge 0$, $I\left(0\right)\ge 0$, $C\left(0\right)\ge 0$, and $R\left(0\right)\ge 0$.

Asymptotic Stability of the Disease-Free Equilibrium

Before investigating the stability of the disease-free equilibrium point, we consider the fractional-order system (5) as follows:

$${}_{t_0}^C{D}_t^{\eta }\mathbf{x}\left(t\right)=\mathcal{F}\left(\mathbf{x}\left(t\right)\right),$$

(6)

where $\mathbf{x}\left(\zeta \right)\in {\mathbb{R}}^7$, $\mathcal{F}\in {\mathbb{R}}^7\times {\mathbb{R}}^7$, $0<\eta <1$. The characteristic equation of the matrix $\mathcal{F}$ evaluated at any equilibrium (see [30]) is given by

$$det\left(s(\mathbf{I}-(1-\eta \left)\mathcal{F}\right)-\eta \mathcal{F}\right)=0.$$

(7)

For the fractional model (5), the asymptotic stability of ${\mathcal{Q}}_0$ is claimed in the following result.

Theorem 2.

The disease-free equilibrium ${\mathcal{Q}}_0$ is uniformly asymptotically stable if ${\mathcal{R}}_c<1$, and unstable otherwise.

Proof. 

The Jacobian matrix of system (5) evaluated at the disease–free equilibrium ${\mathcal{Q}}_0$ is given by

$$J\left({\mathcal{Q}}_0\right)=\left(\begin{array}{ccccccc}-k_1& \theta & 0& 0& 0& \alpha & -\nu S_0\\ \xi & -k_2& 0& 0& 0& 0& -\nu \pi V_0\\ 0& 0& -k_3& 0& 0& 0& \nu (S_0+\pi V_0)\\ 0& 0& q{\gamma }_1& -k_4& 0& 0& 0\\ 0& 0& q_1{\gamma }_1& p_1{\gamma }_2& -(k_5+\sigma )& 0& 0\\ 0& 0& 0& p{\gamma }_2& \sigma & -k_6& 0\\ 0& 0& 0& p_c& p_i& 0& -{\mu }_b\end{array}\right)=\left(\begin{array}{cc}{J}_1& J_2\\ J_3& J_4\end{array}\right),$$

where $J_1=\left(\begin{array}{cc}-k_1& \theta \\ \xi & -k_2\end{array}\right)$, $J_2=\left(\begin{array}{ccccc}0& 0& 0& \alpha & -\nu S_0\\ 0& 0& 0& 0& -\nu \pi V_0\end{array}\right)$, $J_3=O_{{\mathbb{R}}^{5\times 2}}$, and

$J_4=\left(\begin{array}{ccccc}-k_3& 0& 0& 0& \nu (S_0+\pi V_0)\\ q{\gamma }_1& -k_4& 0& 0& 0\\ q_1{\gamma }_1& p_1{\gamma }_2& -(k_5+\sigma )& 0& 0\\ 0& p{\gamma }_2& \sigma & -k_6& 0\\ 0& p_c& p_i& 0& -{\mu }_b\end{array}\right)$.

The characteristic Equation (7) of the typhoid fractional model (5) becomes

$$\left\{\begin{array}{c}det\left(s({\mathbf{I}}_2-(1-\eta )J_1)-\eta J_1\right)=0\hfill \\ det\left(s({\mathbf{I}}_5-(1-\eta )J_4)-\eta J_4\right)=0,\hfill \end{array}\right.$$

(8)

which is equivalent to

$$\left\{\begin{array}{c}{a}_2{s}^2+a_{1}s+a_0=0,\hfill \\ \left\{s\left[(1-\eta )k_6+1\right]+k_6\eta \right\}\left(s^4+\frac{A_1}{A_5}{s}^3+\frac{A_2}{A_5}{s}^2+\frac{A_3}{A_5}s+\frac{A_4}{A_5}\right)=0,\hfill \end{array}\right.$$

(9)

where $a_2={(1-\eta )}^2{k}_7+(1-\eta )(k_1+k_2)+1$, $a_1=2\eta (1-\eta )k_7+\eta (k_1+k_2)$, $a_0={\eta }^2{k}_7$,

$$\begin{array}{cc}\hfill A_5& ={\eta }_1^3{k}_3{k}_4{k}_8{\mu }_b\left({\eta }_1{k}_9+q_1{p}_i+p_{c}q\right)(1-{\mathcal{R}}_c^2)\hfill \\ & +{\eta }_1^3{\mu }_b\left[k_3{k}_8\left(k_8{p}_{c}q+p_1{\gamma }_2{p}_{i}q\right)+k_3{k}_4\left(q_1{k}_4{p}_i+p_1{\gamma }_2{p}_{i}q\right)+k_4{k}_8{k}_9\right]\hfill \\ & +{\eta }_1^2{\mu }_b\left(k_8{k}_9+k_4{k}_9+k_3{k}_9\right)+{\eta }_1{k}_9{\mu }_b\hfill \\ & +\left(\left(\left({\eta }_1^3{k}_3+{\eta }_1^2\right)k_4+{\eta }_1^2{k}_3+{\eta }_1\right)k_8+\left({\eta }_1^2{k}_3+{\eta }_1\right)k_4+{\eta }_1{k}_3+1\right)k_9,\hfill \end{array}$$

$$\begin{array}{cc}\hfill A_1& =\left\{4k_3{k}_4{k}_8{k}_9{\mu }_b{\eta }_1^3\eta +3{\eta }_1^2{k}_3{k}_8{\mu }_b\eta q_1{k}_4{p}_i+3{\eta }_1^2\eta k_3{k}_4{\mu }_b{k}_8{p}_{c}q\right\}(1-R_c^2)\hfill \\ & +3{\eta }_1^2\eta k_3{k}_4{\mu }_b\left(q_1{k}_4{p}_i+p_1{\gamma }_2{p}_{i}q\right)+3{\eta }_1^2{k}_3{k}_8{\mu }_b\eta \left[k_8{p}_{c}q+p_1{\gamma }_2{p}_{i}q\right]\hfill \\ & +2{\eta }_1{k}_4{k}_9{\mu }_b\eta +(2{\eta }_1{k}_3+1)k_9{\mu }_b\eta +3{\eta }_1^2{k}_4{k}_8{k}_9{\mu }_b\eta +2{\eta }_1{k}_8{k}_9{\mu }_b\eta \hfill \\ & +\left(\left(\left(3{\eta }_1^2{k}_3+2{\eta }_1\right)k_4+2{\eta }_1{k}_3+1\right)k_8+\left(2{\eta }_1{k}_3+1\right)k_4+k_3\right)k_9\eta ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill A_2& =\left[6{\eta }_1^2{k}_3{k}_4{k}_8{k}_9{\mu }_b{\eta }^2+3{\eta }_1{k}_3{k}_4{k}_8{\mu }_b{\eta }^2\left(p_{c}q+q_1{p}_i\right)\right](1-{\mathcal{R}}_c^2)\hfill \\ & +3{\eta }_1{\eta }^2\left[k_3{k}_8{\mu }_b\left(k_8{p}_{c}q+p_1{\gamma }_2{p}_{i}q\right)+k_4{k}_8{k}_9\left({\mu }_b+k_3\right)+k_3{k}_4{\mu }_b\left(q_1{k}_4{p}_i+p_1{\gamma }_2{p}_{i}q\right)\right]\hfill \\ & +\left(k_4{k}_8+k_3{k}_8+k_3{k}_4+k_8{\mu }_b+k_4{\mu }_b+k_3{\mu }_b\right)k_9{\eta }^2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill A_3& ={\mu }_b{\eta }^3{k}_3{k}_4{k}_8\left[4k_9{\eta }_1+q_1{p}_i+p_{c}q\right](1-{\mathcal{R}}_c^2)\hfill \\ & +({\mu }_b+k_3)k_4{k}_8{k}_9{\eta }^3+k_3{\mu }_b{\eta }^3\left\{k_{8}q(k_8{p}_c+p_1{\gamma }_2{p}_i)+k_4{p}_i(q_1{k}_4+p_1{\gamma }_{2}q)\right\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill A_4& =\left(1-{\mathcal{R}}_c^2\right){\eta }^4{k}_3{k}_4{k}_8{\mu }_b\stackrel{k_9}{\overbrace{\left[q_1{k}_4{p}_i+k_8{p}_{c}q+p_1{\gamma }_2{p}_{i}q\right]}},\hfill \end{array}$$

and ${\eta }_1=1-\eta$.

Since both coefficients of the first equation of (9) are positive, it follows that the real parts of the solution of (9) are negative. From the second equation of (9), we have that $s_1=-\frac{k_6\eta }{\left[(1-\eta )k_6+1\right]}$ is one solution, and the other solutions are the root of $\mathcal{T}\left(s\right):=A_5{s}^4+A_1{s}^3+A_2{s}^2+A_{3}s+A_4$. Note that $A_4>0⟺{\mathcal{R}}_c<1$, and ${\mathcal{R}}_c<1⟹\left(A_1>0,A_2>0,A_3>0,\mathrm{and}{A}_5>0\right)$. Then, it follows that, if ${\mathcal{R}}_c<1$, then the disease-free equilibrium ${\mathcal{Q}}_0$ is asymptotically stable whenever the following Routh–Hurwitz criteria $\frac{A_1{A}_2}{A_5^2}-\frac{A_3}{A_5}>0$ and $\frac{A_1{A}_2{A}_3}{A_5^3}-\frac{A_1^2{A}_4}{A_5^3}-\frac{A_3^2}{A_5^2}>0$ are satisfied for polynomial $\mathcal{T}\left(s\right)$.

For uniform stability, we use the Lyapunov function:

$$\mathcal{M}(E,C,I,B)={\mathbf{b}}_{1}E\left(t\right)+{\mathbf{b}}_{2}C\left(t\right)+{\mathbf{b}}_{3}I\left(t\right)+{\mathbf{b}}_{4}B\left(t\right),$$

(10)

where ${\mathbf{b}}_1=1$, ${\mathbf{b}}_2=k_3(k_8{p}_c+p_i{p}_1{\gamma }_2)/[k_4{p}_i{q}_1{\gamma }_1+q{\gamma }_1(k_8{p}_c+p_i{p}_1{\gamma }_2)]$, and ${\mathbf{b}}_3=$$k_3{k}_4{p}_i/$$[k_4{p}_i{q}_1{\gamma }_1+q{\gamma }_1(k_8{p}_c+p_i{p}_1{\gamma }_2)]$ and ${\mathbf{b}}_4=k_3{k}_4{k}_8/[k_4{p}_i{q}_1{\gamma }_1+q{\gamma }_1(k_8{p}_c+p_i{p}_1{\gamma }_2)]$.

The fractional derivative of $\mathcal{M}$ is given by

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }\mathcal{M}(E,C,I,B)& \le {}_{t_0}^C{D}_t^{\eta }E{\mathbf{b}}_1{+}_{t_0}^C{D}_t^{\eta }C{\mathbf{b}}_2{+}_{t_0}^C{D}_t^{\eta }I{\mathbf{b}}_3{+}_{t_0}^C{D}_t^{\eta }B{\mathbf{b}}_4\hfill \\ & ={\mathbf{b}}_1\left(\nu B\left[S+\pi V\right]-k_{3}E\right)+{\mathbf{b}}_2\left(q{\gamma }_{1}E-k_{4}C\right)+{\mathbf{b}}_3\left(q_1{\gamma }_{1}E+p_1{\gamma }_{2}C-k_{8}I\right)\hfill \\ & +{\mathbf{b}}_4\left(p_{c}C+p_{i}I-{\mu }_{b}B\right)\hfill \\ & \le {\mathbf{b}}_1\left(\nu B\left[S^0+\pi V^0\right]-k_{3}E\right)+{\mathbf{b}}_2\left(q{\gamma }_{1}E-k_{4}C\right)+{\mathbf{b}}_3\left(q_1{\gamma }_{1}E+p_1{\gamma }_{2}C-k_{8}I\right)\hfill \\ & +{\mathbf{b}}_4\left(p_{c}C+p_{i}I-{\mu }_{b}B\right)\hfill \\ & ={\mathbf{b}}_1\nu B\left(S^0+\pi V^0\right)-{\mathbf{b}}_1{k}_{3}E+{\mathbf{b}}_{2}q{\gamma }_{1}E-{\mathbf{b}}_2{k}_{4}C+{\mathbf{b}}_3{q}_1{\gamma }_{1}E+{\mathbf{b}}_3{p}_1{\gamma }_{2}C\hfill \\ & -{\mathbf{b}}_3{k}_{8}I+{\mathbf{b}}_4{p}_{c}C+{\mathbf{b}}_4{p}_{i}I-{\mathbf{b}}_4{\mu }_{b}B\hfill \\ & ={\mathbf{b}}_1\nu B\left(S^0+\pi V^0\right)-{\mathbf{b}}_4{\mu }_{b}B+\left({\mathbf{b}}_3{q}_1{\gamma }_1+{\mathbf{b}}_{2}q{\gamma }_1-{\mathbf{b}}_1{k}_3\right)E\hfill \\ & +\left({\mathbf{b}}_4{p}_c+{\mathbf{b}}_3{p}_1{\gamma }_2-{\mathbf{b}}_2{k}_4\right)C+\left({\mathbf{b}}_4{p}_i-{\mathbf{b}}_3{k}_8\right)I\hfill \\ & ={\displaystyle \frac{{\mu }_b{k}_3{k}_4(k_5+\sigma )}{p_i{q}_1{\gamma }_1{k}_4+q{\gamma }_1(p_1{p}_i{\gamma }_2+p_c(k_5+\sigma ))}}\left({\mathcal{R}}_c^2-1\right)B.\hfill \end{array}$$

Thus, ${}_{t_0}^C{D}_t^{\eta }\mathcal{M}(E,C,I,B)<0$ whenever ${\mathcal{R}}_c<1$, and ${}_{t_0}^C{D}_t^{\eta }\mathcal{M}(E,C,I,B)=0$ if and only if ${\mathcal{R}}_c=1$ or $B\left(\zeta \right)=0$. Setting $B=0$ in (5), we obtain $S=S_0$, $V=V_0$, and $E=C=I=R=0$. Thus, $\underset{t\to \infty }{lim}{\left(S\left(t\right),V\left(t\right),E\left(t\right),C\left(t\right),I\left(t\right),R\left(t\right)\right)}^{\prime }\to {\left(S_0,V_0,0,0,0,0,0\right)}^{\prime }:={\mathcal{Q}}_0$. Consequently, by [31] (Theorem 2.5), it follows that if ${\mathcal{R}}_c<1$, then ${\mathcal{Q}}_0$ is uniformly asymptotically stable in $\mathcal{W}$. □

Existence and Uniqueness Analysis

Before describing the existence and uniqueness of solutions for the fractional model using the fixed point theorem, we define $\mathcal{T}$ as a Banach space of continuous functions defined on an interval $\mathcal{P}$ with the norm

$$\Vert \mathbf{X}\Vert =\sum _{i=1}^{i=7}\Vert {\mathbf{X}}_i\Vert ,$$

where $\mathbf{X}=\left(S,V,E,C,I,R,B\right)$, $\Vert {\mathbf{X}}_i\Vert =sup\{|{\mathbf{X}}_i\left(t\right)|:t\in \mathcal{P}\}$, and $\mathcal{T}=\mathcal{M}\left(\mathcal{P}\right)\times \mathcal{M}\left(\mathcal{P}\right)\times \mathcal{M}\left(\mathcal{P}\right)\times \mathcal{M}\left(\mathcal{P}\right)\times \mathcal{M}\left(\mathcal{P}\right)\times \mathcal{M}\left(\mathcal{P}\right)\times \mathcal{M}\left(\mathcal{P}\right)$.

Let us write system (5) as follows:

$$\begin{array}{cc}\hfill & {}^C{D}_t^{\eta }S\left(t\right)={\mathbf{H}}_1(t,S),\hfill \\ \hfill & {}^C{D}_t^{\eta }V\left(t\right)={\mathbf{H}}_2(t,V),\hfill \\ \hfill & {}^C{D}_t^{\eta }E\left(t\right)={\mathbf{H}}_3(t,E),\hfill \\ \hfill & {}^C{D}_t^{\eta }C\left(t\right)={\mathbf{H}}_4(t,C)\hfill \\ \hfill & {}^C{D}_t^{\eta }I\left(t\right)={\mathbf{H}}_5(t,I)\hfill \\ \hfill & {}^C{D}_t^{\eta }R\left(t\right)={\mathbf{H}}_6(t,R)\hfill \\ \hfill & {}^C{D}_t^{\eta }B\left(t\right)={\mathbf{H}}_7(t,B)\hfill \end{array}$$

(11)

Application of the Caputo fractional integral operator permits us to reduce (11) to the following system:

$$\begin{array}{cc}\hfill & -S\left(0\right)+S\left(t\right)=\left[{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_1(\varsigma ,S)d\varsigma \right]{\displaystyle \frac{1}{\Gamma \left(\eta \right)}},\hfill \\ \hfill & -V\left(0\right)+V\left(t\right)=\left[{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_2(\varsigma ,V)d\varsigma \right]{\displaystyle \frac{1}{\Gamma \left(\eta \right)}},\hfill \\ \hfill & -E\left(0\right)+E\left(t\right)=\left[{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_3(\varsigma ,E)d\varsigma \right]{\displaystyle \frac{1}{\Gamma \left(\eta \right)}},\hfill \\ \hfill & -C\left(0\right)+C\left(t\right)=\left[{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_4(\varsigma ,C)d\varsigma \right]{\displaystyle \frac{1}{\Gamma \left(\eta \right)}},\hfill \\ \hfill & -I\left(0\right)+I\left(t\right)=\left[{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_5(\varsigma ,I)d\varsigma \right]{\displaystyle \frac{1}{\Gamma \left(\eta \right)}},\hfill \\ \hfill & -R\left(0\right)+R\left(t\right)=\left[{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_6(\varsigma ,R)d\varsigma \right]{\displaystyle \frac{1}{\Gamma \left(\eta \right)}},\hfill \\ \hfill & -B\left(0\right)+B\left(t\right)=\left[{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_7(\varsigma ,R)d\varsigma \right]{\displaystyle \frac{1}{\Gamma \left(\eta \right)}},\hfill \end{array}$$

(12)

with $0<\eta <1$.

Now, we will provide the Lipschitz conditions fulfilled by ${\mathbf{H}}_i$, for $i=1,2,\dots ,7$, as well as the contraction conditions. In the following theorem, we only provide the condition for ${\mathbf{H}}_1$, the rest being similar.

Theorem 3.

The kernel ${\mathbf{H}}_1$ satisfies the Lipschitz and contraction conditions provided that $0\le \nu {\kappa }_7+k_1<1$.

Proof. 

For S, we proceed as below:

$$\begin{array}{cc}\hfill \Vert {\mathbf{H}}_1(t,S)-{\mathbf{H}}_1(t,S_1)\Vert & =\Vert -\nu B(S-S_1)-k_1(S-S_1)\Vert \hfill \\ & =\Vert \nu B+k_1\Vert \Vert (S\left(t\right)-S_1\left(t\right))\Vert \hfill \\ & \le \Vert \nu {\kappa }_7+k_1\Vert \Vert S\left(t\right)-S_1\left(t\right)\Vert \hfill \end{array}$$

where ${\kappa }_7$ is the upper bound of the function $B\left(t\right)$. Now, setting $W_1=\nu {\kappa }_7+k_1$, we finally obtain

$$\Vert {\mathbf{H}}_1(t,S)-{\mathbf{H}}_1(t,S_1)\Vert \le W_1\Vert S\left(t\right)-S\left(t_1\right)\Vert ,$$

(13)

which provide the Lipschitz condition. If, additionally, we can have $0<W_1=\nu {\kappa }_7+k_1<1$, then the contraction is also obtained.

As in the case of ${\mathbf{H}}_1$, it is easy to obtain the Lipschitz condition for the other kernels. Thus, we have

$$\begin{array}{cc}\hfill \Vert {\mathbf{H}}_2(t,C)-{\mathbf{H}}_2(t,C_1)\Vert & \le W_2\Vert V\left(t\right)-V\left(t_1\right)\Vert ,\hfill \\ \hfill \Vert {\mathbf{H}}_3(t,E)-{\mathbf{H}}_3(t,E_1)\Vert & \le W_3\Vert E\left(t\right)-E\left(t_1\right)\Vert ,\hfill \\ \hfill \Vert {\mathbf{H}}_4(t,C)-{\mathbf{H}}_4(t,C_1)\Vert & \le W_4\Vert C\left(t\right)-C\left(t_1\right)\Vert ,\hfill \\ \hfill \Vert {\mathbf{H}}_5(t,I)-{\mathbf{H}}_5(t,I_1)\Vert & \le W_5\Vert I\left(t\right)-I\left(t_1\right)\Vert ,\hfill \\ \hfill \Vert {\mathbf{H}}_6(t,R)-{\mathbf{H}}_6(t,R_1)\Vert & \le W_6\Vert R\left(t\right)-R\left(t_1\right)\Vert ,\hfill \\ \hfill \Vert {\mathbf{H}}_7(t,B)-{\mathbf{H}}_7(t,B_1)\Vert & \le W_7\Vert B\left(t\right)-B\left(t_1\right)\Vert .\hfill \end{array}$$

(14)

 □

Recursively, Equation (12) can be rewritten as follows:

$$\begin{array}{cc}\hfill S_n\left(t\right)-S\left(0\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_1(\varsigma ,S_{n-1})d\varsigma ,\hfill \\ \hfill V_n\left(t\right)-V\left(0\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_2(\varsigma ,V_{n-1})d\varsigma ,\hfill \\ \hfill E_n\left(t\right)-E\left(0\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_3(\varsigma ,E_{n-1})d\varsigma ,\hfill \\ \hfill C_n\left(t\right)-C\left(0\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_4(\varsigma ,C_{n-1})d\varsigma ,\hfill \\ \hfill I_n\left(t\right)-I\left(0\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_5(\varsigma ,I_{n-1})d\varsigma ,\hfill \\ \hfill R_n\left(t\right)-R\left(0\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_6(\varsigma ,R_{n-1})d\varsigma ,\hfill \\ \hfill B_n\left(t\right)-B\left(0\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}{\mathbf{H}}_7(\varsigma ,B_{n-1})d\varsigma .\hfill \end{array}$$

(15)

By determing, in a recursive manner, the difference between the successive terms of (11), we obtain

$$\begin{array}{cc}\hfill {\psi }_{1n}\left(t\right)=S_n\left(t\right)-S_{n-1}\left(t\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_1(\varsigma ,S_{n-1})-{\mathbf{H}}_1(\varsigma ,S_{n-2}))d\varsigma ,\hfill \\ \hfill {\psi }_{2n}\left(t\right)=V_n\left(t\right)-V_{n-1}\left(t\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_2(\varsigma ,V_{n-1})-{\mathbf{H}}_2(\varsigma ,V_{n-2}))d\varsigma ,\hfill \\ \hfill {\psi }_{3n}\left(t\right)=E_n\left(t\right)-E_{n-1}\left(t\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_3(\varsigma ,E_{n-1})-{\mathbf{H}}_3(\varsigma ,E_{n-2}))d\varsigma ,\hfill \\ \hfill {\psi }_{4n}\left(t\right)=C_n\left(t\right)-C_{n-1}\left(t\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_4(\varsigma ,C_{n-1})-{\mathbf{H}}_4(\varsigma ,C_{n-2}))d\varsigma ,\hfill \\ \hfill {\psi }_{5n}\left(t\right)=I_n\left(t\right)-I_{n-1}\left(t\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_5(\varsigma ,I_{n-1})-{\mathbf{H}}_5(\varsigma ,I_{n-2}))d\varsigma ,\hfill \\ \hfill {\psi }_{6n}\left(t\right)=R_n\left(t\right)-R_{n-1}\left(t\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_6(\varsigma ,R_{n-1})-{\mathbf{H}}_6(\varsigma ,R_{n-2}))d\varsigma ,\hfill \\ \hfill {\psi }_{7n}\left(t\right)=B_n\left(t\right)-B_{n-1}\left(t\right)& ={\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_7(\varsigma ,B_{n-1})-{\mathbf{H}}_7(\varsigma ,B_{n-2}))d\varsigma ,\hfill \end{array}$$

(16)

with $S_0\left(t\right)=S\left(0\right)$, $V_0\left(t\right)=V\left(0\right)$, $E_0\left(t\right)=E\left(0\right)$, $C_0\left(t\right)=C\left(0\right)$, $I_0\left(t\right)=I\left(0\right)$, $R_0\left(t\right)=R\left(0\right)$, and $B_0\left(t\right)=B\left(0\right)$.

The norm of ${\varphi }_{1n}\left(t\right)$ gives

$$\begin{array}{cc}\hfill \Vert {\psi }_{1n}\left(t\right)\Vert =\Vert S_n\left(t\right)-S_{n-1}\left(t\right)\Vert & =\Vert {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_1(\varsigma ,S_{n-1})-{\mathbf{H}}_1(\varsigma ,S_{n-2}))d\varsigma \Vert \hfill \\ \hfill & \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\Vert {\int }_0^t{(t-\varsigma )}^{\eta -1}({\mathbf{H}}_1(\varsigma ,S_{n-1})-{\mathbf{H}}_1(\varsigma ,S_{n-2}))d\varsigma \Vert .\hfill \end{array}$$

(17)

With the Lipschitz condition (13), we obtain

$$\begin{array}{c}\hfill \Vert {\psi }_{1n}\left(t\right)\Vert =\Vert S_n\left(t\right)-S_{n-1}\left(t\right)\Vert \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_1{\int }_0^t{(t-\varsigma )}^{\eta -1}\Vert S_{n-1}-S_{n-2}\Vert d\varsigma .\end{array}$$

(18)

Thus, we have

$$\Vert {\psi }_{1n}\left(t\right)\Vert \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_1{\int }_0^t{(t-\varsigma )}^{\eta -1}\Vert {\psi }_{1(n-1)}\left(\varsigma \right)\Vert d\varsigma .$$

(19)

By proceeding in a similar way, we obtain, for the other ${\varphi }_{in}\left(t\right)$, $i=2,\dots ,7$,

$$\begin{array}{c}\hfill \Vert {\psi }_{2n}\left(t\right)\Vert \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_2{\int }_0^t{(t-\varsigma )}^{\eta -1}\Vert {\psi }_{2(n-1)}\left(\varsigma \right)\Vert d\varsigma ,\\ \hfill \Vert {\psi }_{3n}\left(t\right)\Vert \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_3{\int }_0^t{(t-\varsigma )}^{\eta -1}\Vert {\psi }_{3(n-1)}\left(\varsigma \right)\Vert d\varsigma ,\\ \hfill \Vert {\psi }_{4n}\left(t\right)\Vert \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_4{\int }_0^t{(t-\varsigma )}^{\eta -1}\Vert {\psi }_{4(n-1)}\left(\varsigma \right)\Vert d\varsigma ,\\ \hfill \Vert {\psi }_{5n}\left(t\right)\Vert \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_5{\int }_0^t{(t-\varsigma )}^{\eta -1}\Vert {\psi }_{5(n-1)}\left(\varsigma \right)\Vert d\varsigma ,\\ \hfill \Vert {\psi }_{6n}\left(t\right)\Vert \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_6{\int }_0^t{(t-\varsigma )}^{\eta -1}\Vert {\psi }_{6(n-1)}\left(\varsigma \right)\Vert d\varsigma ,\\ \hfill \Vert {\psi }_{7n}\left(t\right)\Vert \le {\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_7{\int }_0^t{(t-\varsigma )}^{\eta -1}\Vert {\psi }_{7(n-1)}\left(\varsigma \right)\Vert d\varsigma .\end{array}$$

(20)

Each $n\mathrm{th}$ term of the state variables of (5) is given by

$$\left\{\begin{array}{c}{S}_n\left(t\right)={\displaystyle \sum _{i=1}^n}{\psi }_{1i}\left(t\right),V_n\left(t\right)={\displaystyle \sum _{i=1}^n}{\psi }_{2i}\left(t\right),E_n\left(t\right)={\displaystyle \sum _{i=1}^n}{\psi }_{3i}\left(t\right),\hfill \\ C_n\left(t\right)={\displaystyle \sum _{i=1}^n}{\psi }_{4i}\left(t\right),I_n\left(t\right)={\displaystyle \sum _{i=1}^n}{\psi }_{5i}\left(t\right),R_n\left(t\right)={\displaystyle \sum _{i=1}^n}{\psi }_{6i}\left(t\right),\hfill \\ B_n\left(t\right)={\displaystyle \sum _{i=1}^n}{\psi }_{7i}\left(t\right).\hfill \end{array}\right.$$

(21)

The following result guarantees that the solution of the fractional model (5) is unique.

Theorem 4.

If the following inequality holds,

$${\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\mathbf{x}}^{\eta }{W}_i<1,\mathrm{for}i=1,2,\dots ,7,$$

(22)

then the solution of the fractional model (5), for $t\in [0,T]$, is unique.

Proof. 

With Equation (13), inequalities (19) and (20), combined with a recursive technique, we obtain:

$$\begin{array}{cc}\hfill \Vert {\psi }_{1n}\left(t\right)\Vert \le \Vert S_0\left(t\right)\Vert {\left[{\displaystyle \frac{W_1}{\Gamma \left(\eta \right)}}{\mathbf{x}}^{\eta }\right]}^n,& \Vert {\psi }_{2n}\left(t\right)\Vert \le \Vert W_0\left(t\right)\Vert {\left[{\displaystyle \frac{W_2}{\Gamma \left(\eta \right)}}{\mathbf{x}}^{\eta }\right]}^n,\hfill \\ \hfill \Vert {\psi }_{3n}\left(t\right)\Vert \le \Vert E_0\left(t\right)\Vert {\left[{\displaystyle \frac{W_3}{\Gamma \left(\eta \right)}}{\mathbf{x}}^{\eta }\right]}^n,& \Vert {\psi }_{4n}\left(t\right)\Vert \le \Vert C_0\left(t\right)\Vert {\left[{\displaystyle \frac{W_4}{\Gamma \left(\eta \right)}}{\mathbf{x}}^{\eta }\right]}^n,\hfill \\ \hfill \Vert {\psi }_{5n}\left(t\right)\Vert \le \Vert I_0\left(t\right)\Vert {\left[{\displaystyle \frac{W_5}{\Gamma \left(\eta \right)}}{\mathbf{x}}^{\eta }\right]}^n,& \Vert {\psi }_{6n}\left(t\right)\Vert \le \Vert R_0\left(t\right)\Vert {\left[{\displaystyle \frac{W_6}{\Gamma \left(\eta \right)}}{\mathbf{x}}^{\eta }\right]}^n,\hfill \\ \hfill \Vert {\psi }_{7n}\left(t\right)\Vert \le \Vert B_0\left(t\right)\Vert {\left[{\displaystyle \frac{W_7}{\Gamma \left(\eta \right)}}{\mathbf{x}}^{\eta }\right]}^n& .\hfill \end{array}$$

(23)

Therefore, the above sequences satisfy $\underset{n\to \infty }{lim}\Vert {\psi }_{in}\left(t\right)\Vert \to 0$, $j=1,2,\dots ,7$. The triangle inequality applied to (23) permits us to obtain

$$\begin{array}{cc}\hfill & \Vert S_{k+n}\left(t\right)-S_n\left(t\right)\Vert \le \sum _{j=n+1}^{k+n}{\mathbf{Z}}_1^j={\displaystyle \frac{{\mathbf{Z}}_1^{n+1}-{\mathbf{Z}}_1^{k+n+1}}{1-{\mathbf{Z}}_1}},\hfill \\ \hfill & \Vert V_{k+n}\left(t\right)-V_n\left(t\right)\Vert \le \sum _{j=n+1}^{k+n}{\mathbf{Z}}_2^j={\displaystyle \frac{{\mathbf{Z}}_2^{n+1}-{\mathbf{Z}}_2^{k+n+1}}{1-{\mathbf{Z}}_2}},\hfill \\ \hfill & \Vert E_{k+n}\left(t\right)-E_n\left(t\right)\Vert \le \sum _{j=n+1}^{k+n}{\mathbf{Z}}_3^j={\displaystyle \frac{{\mathbf{Z}}_3^{n+1}-{\mathbf{Z}}_3^{k+n+1}}{1-{\mathbf{Z}}_3}},\hfill \\ \hfill & \Vert C_{k+n}\left(t\right)-C_n\left(t\right)\Vert \le \sum _{j=n+1}^{k+n}{\mathbf{Z}}_4^j={\displaystyle \frac{{\mathbf{Z}}_4^{n+1}-{\mathbf{Z}}_4^{k+n+1}}{1-{\mathbf{Z}}_4}},\hfill \\ \hfill & \Vert I_{k+n}\left(t\right)-I_n\left(t\right)\Vert \le \sum _{j=n+1}^{k+n}{\mathbf{Z}}_5^j={\displaystyle \frac{{\mathbf{Z}}_5^{n+1}-{\mathbf{Z}}_5^{k+n+1}}{1-{\mathbf{Z}}_5}},\hfill \\ \hfill & \Vert R_{k+n}\left(t\right)-R_n\left(t\right)\Vert \le \sum _{j=n+1}^{k+n}{\mathbf{Z}}_6^j={\displaystyle \frac{{\mathbf{Z}}_6^{n+1}-{\mathbf{Z}}_6^{k+n+1}}{1-{\mathbf{Z}}_6}},\hfill \\ \hfill & \Vert B_{k+n}\left(t\right)-B_n\left(t\right)\Vert \le \sum _{j=n+1}^{k+n}{\mathbf{Z}}_7^j={\displaystyle \frac{{\mathbf{Z}}_7^{n+1}-{\mathbf{Z}}_7^{n+k+1}}{1-{\mathbf{Z}}_7}},\hfill \end{array}$$

(24)

with ${\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{b}^{\eta }{W}_l<1$ and ${\mathbf{Z}}_l={\left({\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{W}_l{\mathbf{x}}^{\eta }\right)}^n$, $l=1,2,\dots ,7$.

Therefore, $S_n$, $V_n$, $E_n$, $C_n$, $I_n$, $R_n$, and $B_n$ are uniformly convergent Cauchy sequences (see [32]). With $n\to \infty$, it follows that the limit of these sequences represents the unique solution to model (5). □

Numerical Scheme of the Fractional Model and Its Stability Analysis

Several methods have been developed to construct numerical schemes for fractional models. One can cite, among others, the Implicit Quadrature method [24], the Approximate Mittag–Leffler method [33], the Predictor Corrector method [34], and the Adams–Bashforth–Moulton method [25]. The choice of the method depends on several factors, such as the amount of information treated [35] and the accuracy order [36]. The numerical scheme proposed in this work is constructed using the Adams–Bashforth–Moulton method.

Let us consider the following general form of a fractional differential equation [37]:

$$\left\{\begin{array}{ccc}{\mathbb{D}}_t^{\eta }\phi \left(t\right)\hfill & =h(t,\phi (t\left)\right),\hfill & 0\le t\le T,\hfill \\ {\phi }^{\left(l\right)}\left(0\right)\hfill & ={\phi }_0^l,\hfill & l=0,1,2,\dots ,n-1,wheren=\left[\eta \right],\hfill \end{array}\right.$$

(25)

which is equivalent to

$$\phi \left(t\right)=\sum _{l=0}^{n-1}{h}_0^l{\displaystyle \frac{t^l}{l!}}+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}{\int }_0^t{(t-\zeta )}^{\eta -1}h(\zeta ,\phi \left(\zeta \right))d\zeta .$$

(26)

For $\eta \in [0,1]$, $0\le t\le T$ and setting $\kappa =T/N$ and $t_m=m\kappa ,$ for $m=0,1,2,\dots ,N\in {\mathbb{Z}}^{+}$, the solution of the fractional model is

$$\begin{array}{cc}\hfill S_{1+m}& =S_0+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\left({\Lambda }_h+\eta R_{1+m}^p+\theta V_{1+m}^p-(\nu B_{1+m}^p+k_1)S_{1+m}^p\right)\hfill \\ \hfill & +{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\sum _{j=0}^m{a}_{j,1+m}\left({\Lambda }_h+\eta R_j+\theta V_j-(\nu B_j+k_1)S_j\right),\hfill \\ \hfill V_{1+m}& =V_0+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\left(\xi S_{1+m}^p-\left[(1-ϵ)\nu B_{1+m}^p+k_2\right]V_{1+m}^p\right)\hfill \\ \hfill & +{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\sum _{j=0}^m{a}_{j,1+m}\left(\xi S_j-\left[(1-ϵ)\nu B_j+k_2\right]V_j\right),\hfill \\ \hfill E_{1+m}& =E_0+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\left(\nu B_{1+m}^p\left[S_{1+m}^p+\pi V_{1+m}^p\right]-k_3{E}_{1+m}^p\right)\hfill \\ \hfill & +{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\sum _{j=0}^m{a}_{j,1+m}\left(\nu B_j\left[S_j+\pi V_j\right]-k_3{E}_j\right),\hfill \\ \hfill C_{1+m}& =C_0+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\left(q{\gamma }_1{E}_{1+m}^p-k_4{C}_{1+m}^p\right)+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\sum _{j=0}^m{a}_{j,1+m}\left(q{\gamma }_1{E}_j-k_4{C}_j\right),\hfill \\ \hfill I_{1+m}& =I_0+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\left(q_1{\gamma }_1{E}_{1+m}^p+p_1{\gamma }_2{C}_{1+m}^p-\left[k_5+\sigma \right]I_{1+m}^p\right)\hfill \\ \hfill & +{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\sum _{j=0}^m{a}_{j,1+m}\left(q_1{\gamma }_1{E}_j+p_1{\gamma }_2{C}_j-\left[k_5+\sigma \right]I_j\right),\hfill \\ \hfill R_{1+m}& =R_0+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\left(p{\gamma }_2{C}_{1+m}^p+\sigma I_{1+m}^p-k_6{R}_{1+m}^p\right)+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\sum _{j=0}^m{a}_{j,1+m}\left(p{\gamma }_2{C}_j+\sigma I_j-k_6{R}_j\right),\hfill \\ \hfill B_{1+m}& =B_0+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\left(p_c{C}_{1+m}^p+p_i{I}_{1+m}^p-{\mu }_b{B}_{1+m}^p\right)+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\sum _{j=0}^m{a}_{j,1+m}\left(p_c{C}_j+p_i{I}_j-{\mu }_b{B}_j\right),\hfill \end{array}$$

(27)

where

$$\begin{array}{cc}\hfill S_{1+m}^p& =S_0+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{j=0}^m{b}_{j,1+m}\left({\Lambda }_h+\eta R_j+\theta V_j-(\nu B_j+k_1)S_j\right),\hfill \\ \hfill V_{1+m}^p& =V_0+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{j=0}^m{b}_{j,1+m}\left(\xi S_j-\left[(1-ϵ)\nu B_j+k_2\right]V_j\right),\hfill \\ \hfill E_{1+m}^p& =E_0+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{j=0}^m{b}_{j,1+m}\left(\nu B_j\left[S_j+\pi V_j\right]-k_3{E}_j\right),\hfill \\ \hfill C_{1+m}^p& =C_0+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{j=0}^m{b}_{j,1+m}\left(q{\gamma }_1{E}_j-k_4{C}_j\right),\hfill \\ \hfill I_{1+m}^p& =I_0+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{j=0}^m{b}_{j,1+m}\left(=q_1{\gamma }_1{E}_j+p_1{\gamma }_2{C}_j-\left[k_5+\sigma \right]I_j\right),\hfill \\ \hfill R_{1+m}^p& =R_0+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{j=0}^m{b}_{j,1+m}\left(p{\gamma }_2{C}_j+\sigma I_j-k_6{R}_j\right),\hfill \\ \hfill B_{1+m}^p& =B_0+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{j=0}^m{b}_{j,1+m}\left(p_c{C}_j+p_i{I}_j-{\mu }_b{B}_j\right),\hfill \end{array}$$

(28)

and

$$\begin{array}{c}\hfill a_{j,1+m}=\left\{\begin{array}{c}{m}^{\eta +1}-(m+1)(-\eta +m),j=0,\hfill \\ {(2-j+m)}^{\eta +1}-2{(m-j+1)}^{1+\eta }+{(-j+m)}^{1+\eta }1\le j\le m,\hfill \\ 1,j=1+m,\hfill \end{array}\right.\end{array}$$

$$b_{j,1+m}={\displaystyle \frac{{\kappa }^{\eta }}{\eta }}\left({(m+1-j)}^{\eta }-{(m-j)}^{\eta }\right),0\le j\le m.$$

We then claim the following result.

Theorem 5.

Under some conditions, the above numerical scheme (see Equations (27) and (28)) is stable.

Proof. 

Let $S_0^{\star }$, $S_j^{\star }(j=0,\dots ,1+m)$ and $S_{1+m}^{\star p}(m=0,\dots ,N-1)$ be perturbations of $S_0$, $S_j$, and $S_{1+m}^p$, respectively. By using Equations (19) and (28), the following perturbation equations are obtained:

$$S_{1+m}^{\star p}=S_0^{\star }+{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{j=0}^m{b}_{j,1+m}({\mathcal{G}}_1(t_j,S_j+S_j^{\star })-{\mathcal{G}}_1(t_j,S_j)),$$

(29)

$$\begin{array}{cc}\hfill S_{1+m}^{\star }& =S_0^{\star }+{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}({\mathcal{G}}_1(t_{1+m},S_{1+m}^p+S_{1+m}^P)-{\mathcal{G}}_1(t_{1+m},S_{1+m}^p))\hfill \\ \hfill & +{\displaystyle \frac{{\kappa }^{\eta }}{\Gamma (\eta +2)}}\sum _{j=0}^m{a}_{j,1+m}({\mathcal{G}}_1(t_j,S_j+S_j^{\star })-{\mathcal{G}}_1(t_j,S_j)).\hfill \end{array}$$

(30)

The Lipschitz condition permits us to obtain

$$|S_{1+m}^{\star }|\le {\varphi }_0+{\displaystyle \frac{{\kappa }^{\eta }M}{\Gamma (\eta +2)}}\left(|S_{1+m}^{\star p}|+\sum _{j=1}^m{a}_{j,1+m}|S_j^{\star }|\right),$$

(31)

where ${\varphi }_0=\underset{0\le m\le N}{max}\left\{|S_0^{\star }|+{\displaystyle \frac{{\kappa }^{\eta }M{a}_{m,0}}{\Gamma (\eta +2)}}|S_0^{\star }|\right\}.$ From [32] (Equation (3.18)), it follows that

$$|S_{1+m}^{\star p}|\le {\Theta }_0+{\displaystyle \frac{M}{\Gamma \left(\eta \right)}}\sum _{j=1}^m{b}_{j,1+m}|S_j^{\star }|,$$

(32)

where ${\Theta }_0=\underset{0\le m\le N}{max}\left\{|S_0^{\star }|+{\displaystyle \frac{M{b}_{m,0}}{\Gamma \left(\eta \right)}}|S_0^{\star }|\right\}$. Substituting $|S_{1+m}^{\star p}|$ from Equation (32) into Equation (31) gives

$$\begin{array}{cc}\hfill |S_{1+m}^{\star }|& \le {\varrho }_0+{\displaystyle \frac{{\kappa }^{\eta }M}{\Gamma (\eta +2)}}\left({\displaystyle \frac{M}{\Gamma \left(\eta \right)}}\sum _{j=1}^m{b}_{j,1+m}|S_j^{\star }|+\sum _{j=1}^m{a}_{j,1+m}|S_j^{\star }|\right)\hfill \\ \hfill & \le {\varrho }_0+{\displaystyle \frac{{\kappa }^{\eta }M}{\Gamma (\eta +2)}}\sum _{j=1}^m\left({\displaystyle \frac{M}{\Gamma \left(\eta \right)}}{b}_{j,1+m}+a_{j,1+m}\right)|S_j^{\star }|\hfill \\ \hfill & \le {\varrho }_0+{\displaystyle \frac{{\kappa }^{\eta }M{\mathcal{C}}_{\eta ,2}}{\Gamma (\eta +2)}}\sum _{j=1}^m{(m+1-j)}^{\eta -1}|S_j^{\star }|,\hfill \end{array}$$

(33)

where ${\varrho }_0=max\{{\varphi }_0+{\displaystyle \frac{{\kappa }^{\eta }M{a}_{1+m,1+m}}{\Gamma (\eta +2)}}{\Theta }_0\}$.

Thanks to Lemma 2, we have that ${\mathcal{C}}_{\eta ,2}>0$ and depends only on $\eta$, and $\kappa$ is assumed to be small enough. A direct application of Lemma 1 implies $|S_{1+m}^{\star }|\le \mathcal{C}{\varrho }_0$. The proof for the other variables is obtained in the same way. This ends the proof. □

2.3. Model Dynamics with the Standard Incidence Law

In this section, we extend model (2) by replacing the mass action incidence law with the standard incidence law, and considering direct transmission (human to human). The new typhoid fever transmission dynamics model is thus presented as follows:

$$\begin{array}{cc}\hfill \dot{S}\left(t\right)& ={\Lambda }_h+\theta V\left(t\right)+\alpha R\left(t\right)-k_{1}S\left(t\right)-\beta {\displaystyle \frac{\left(I+C\right)}{N\left(t\right)}}S\left(t\right)-\nu {\displaystyle \frac{B\left(t\right)}{B\left(t\right)+K}}S\left(t\right),\hfill \end{array}$$

(34a)

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& =-\left[k_2+\pi \beta {\displaystyle \frac{\left(C+I\right)}{N\left(t\right)}}+\pi \nu {\displaystyle \frac{B\left(t\right)}{K+B\left(t\right)}}\right]V\left(t\right)+\xi S\left(t\right),\hfill \end{array}$$

(34b)

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)& =\left[\beta {\displaystyle \frac{\left(C+I\right)}{N\left(t\right)}}+\nu {\displaystyle \frac{B\left(t\right)}{B\left(t\right)+K}}\right]\left(\pi V\left(t\right)+S\left(t\right)\right)-k_{3}E\left(t\right),\hfill \end{array}$$

(34c)

$$\begin{array}{cc}\hfill \dot{C}\left(t\right)& =q{\gamma }_{1}E\left(t\right)-k_{4}C\left(t\right),\hfill \end{array}$$

(34d)

$$\begin{array}{cc}\hfill \dot{I}\left(t\right)& =q_1{\gamma }_{1}E\left(t\right)+p_1{\gamma }_{2}C\left(t\right)-k_{8}I\left(t\right),\hfill \end{array}$$

(34e)

$$\begin{array}{cc}\hfill \dot{R}\left(t\right)& =p{\gamma }_{2}C\left(t\right)+\sigma I\left(t\right)-k_{6}R\left(t\right),\hfill \end{array}$$

(34f)

$$\begin{array}{cc}\hfill \dot{B}\left(t\right)& =p_{c}C\left(t\right)+p_{i}I\left(t\right)-{\mu }_{b}B\left(t\right),\hfill \end{array}$$

(34g)

where $\beta$ is the direct transmission rate, and K represents the half-saturation constant.

The corresponding fractional model is given by

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }S\left(t\right)& ={\Lambda }_h+\theta V\left(t\right)+\alpha R\left(t\right)-k_{1}S\left(t\right)-\beta {\displaystyle \frac{\left(I+C\right)}{N\left(t\right)}}S\left(t\right)-\nu {\displaystyle \frac{B\left(t\right)}{K+B\left(t\right)}}S\left(t\right),\hfill \end{array}$$

(35a)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }V\left(t\right)& =-\left[k_2+\pi \beta {\displaystyle \frac{\left(I+C\right)}{N\left(t\right)}}+\pi \nu {\displaystyle \frac{B\left(t\right)}{K+B\left(t\right)}}\right]V\left(t\right)+\xi S\left(t\right),\hfill \end{array}$$

(35b)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }E\left(t\right)& =\left[\beta {\displaystyle \frac{\left(I+C\right)}{N\left(t\right)}}+\nu {\displaystyle \frac{B\left(t\right)}{K+B\left(t\right)}}\right]\left(\pi V\left(t\right)+S\left(t\right)\right)-k_{3}E\left(t\right),\hfill \end{array}$$

(35c)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }C\left(t\right)& =q{\gamma }_{1}E\left(t\right)-k_{4}C\left(t\right),\hfill \end{array}$$

(35d)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }I\left(t\right)& =q_1{\gamma }_{1}E\left(t\right)+p_1{\gamma }_{2}C\left(t\right)-k_{8}I\left(t\right),\hfill \end{array}$$

(35e)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }R\left(t\right)& =p{\gamma }_{2}C\left(t\right)+\sigma I\left(t\right)-k_{6}R\left(t\right),\hfill \end{array}$$

(35f)

$$\begin{array}{cc}\hfill {}_{t_0}^C{D}_t^{\eta }B\left(t\right)& =p_{c}C\left(t\right)+p_{i}I\left(t\right)-{\mu }_{b}B\left(t\right).\hfill \end{array}$$

(35g)

Without loss of generality, it is evident that the new model (34) (resp. (35)) is also defined in $\mathcal{W}$.

Model (34) has the same disease-free equilibrium as model system (2). Using the same approach developed in [29], we define the next-generation matrix of model system (34) as

$$NGM=\left(\begin{array}{cccc}{R}_1& \frac{H_0{p}_1{\gamma }_2\beta }{N_0{k}_4{k}_8}+\frac{H_0\beta }{N_0{k}_4}& \frac{H_0\beta }{N_0{k}_8}& R_4\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ R_5& \frac{p_1{\gamma }_2{p}_i}{k_4{k}_8}+\frac{p_c}{k_4}& \frac{p_i}{k_8}& 0\end{array}\right)$$

where $R_1={\displaystyle \frac{H_0\beta {\gamma }_1}{N_0{k}_3{k}_4}}\left[{\displaystyle \frac{\left(p_1{\gamma }_{2}q+q_1{k}_4\right)}{k_8}}+q\right]$, $R_4={\displaystyle \frac{H_0\nu }{K{\mu }_b}}$, $R_5={\displaystyle \frac{{\gamma }_1}{k_3{k}_4}}\left[{\displaystyle \frac{p_i\left(p_1{\gamma }_{2}q+q_1{k}_4\right)}{k_8}}+p_{c}q\right]$, and $H_0=S_0+\pi V_0$.

Thus, the control reproduction number of model (34), which is the spectral radius of NGM, is given by

$${\mathcal{R}}_{c\star }={\displaystyle \frac{R_1+\sqrt{R_1^2+4R_4{R}_5}}{2}}.$$

(36)

The following result is a direct consequence of Theorem 2 in [29] (see Appendix A for the proof).

Proposition 3.

For model (34) (resp. (35)), ${\mathcal{Q}}_0$ is locally asymptotically stable in $\mathcal{W}$ if ${\mathcal{R}}_{c\star }<1$ and unstable if ${\mathcal{R}}_{c\star }>1$.

Theorem 6.

For the new typhoid model (34) (resp. (35)), the disease-free equilibrium ${\mathcal{Q}}_0$ is globally asymptotically stable if ${\mathcal{R}}_{c\star }<1$ and unstable otherwise.

Proof. 

See Appendix B. □

3. Results

3.1. Numerical Results of the Fractional Model with Mass Action Incidence Law

We perform several simulations with the parameter values listed in Table 1.

Table 1. Parameter values of (2) taken from [5].

Parameter	Value	Parameter	Value	Parameter	Value
${\Lambda }_h$	1	${\mu }_b$	0.149990	$\nu$	$3.2618\times {10}^{-6}$
${\gamma }_1$	0.2145	$ϵ$	0.9495	$\delta$	0.1499
${\gamma }_2$	0.1498	$\xi$	0.3221	$\sigma$	0.49992
$\alpha$	0.0834	$\theta$	0.0833	${\mathcal{R}}_c$	2.4750

The step size is $\kappa ={10}^{-8}$, the initial time is T = 0, and the final time is $T>0$. We begin by showing the impact of fractional order on the dynamics of the disease. To this aim, the fractional-order parameter varies between $\eta =1$ and $\eta =0.5$.

Figure 1 displays the impact of the Caputo fractional operator on the model dynamics. For different values of the fractional-order parameter $\eta$, the infected state profiles are drawn. From Figure 1, it follows that when the fractional order $\eta$ decreases, the solutions of our fractional model (5) have different behaviors. Indeed, when the fractional order decreases, the number of infected humans in latent, carrier, and symptomatic states increases. This is the same for the compartment B. This phenomenon was also observed in a malaria fractional model studied by [38]. It is important to note that for $\eta =1$, the solutions of the fractional model converge to the solutions of the integer model.

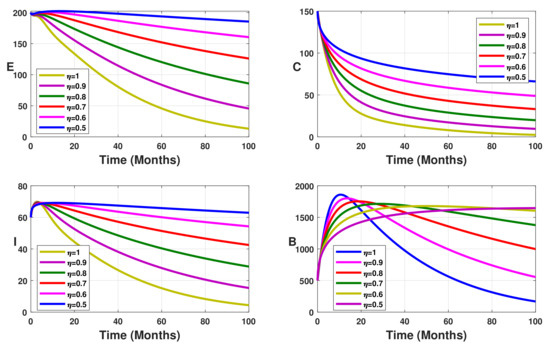
Figure 1. Simulation results showing the fractional dynamics on the infected state variable profiles for different values of the fractional-order parameter $\eta$.

To evaluate the impact of vaccination on typhoid fever transmission dynamics, we fix the vaccine efficacy at $ϵ=70\%$ while the vaccine coverage parameter varies between $\xi =0\%$ and $\xi =90\%$ ($\xi \in \{0.90,0.50,0.20,0\}$), with different values of the fractional-order $\eta$ ($\eta \in \{1,0.90,0.80,0.70,0.60,0.50\}$). The results are displayed in Figure 2, Figure 3, Figure 4 and Figure 5.

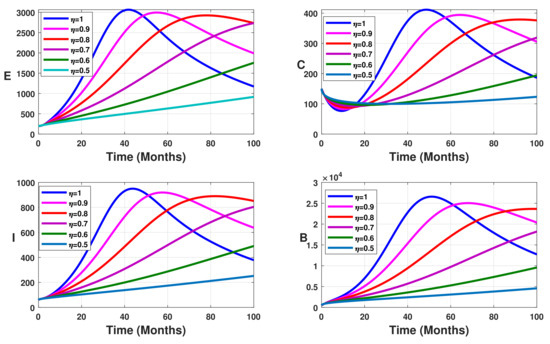
Figure 2. Simulation results showing the infected state variable profiles without vaccination ($\xi =0$).

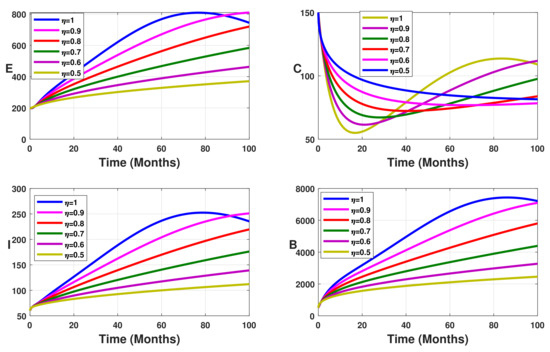
Figure 3. Simulation results showing the infected state variable profiles when the vaccination coverage $\xi =20\%$ with different values of the fractional order.

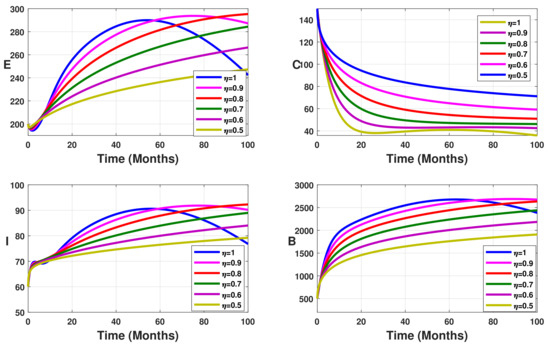
Figure 4. Simulation results showing the infected state variable profiles when the vaccination coverage $\xi =50\%$ with different values of the fractional order.

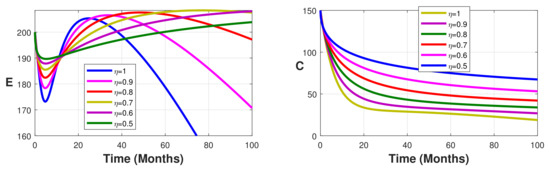
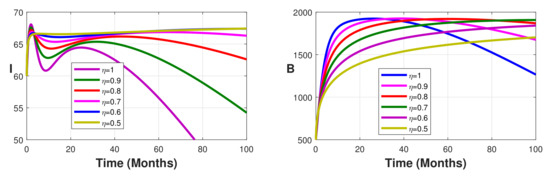
Figure 5. Simulation results showing the infected state variable profiles when the vaccination coverage $\xi =90\%$ with different values of the fractional order.

Without vaccination coverage $\xi =0$ (Figure 2), the peak delayed phenomenon is observable. Indeed, for $\eta =1$, the peak date corresponds to $T=45$ months, with approximately 3000 infected individuals in the latent stage, 400 asymptomatic individuals, 950 symptomatic individuals, and 26,000 free salmonella in the environment. This peak date is delayed when the fractional-order parameter $\eta$ decreases. Thus, the peak dates are beyond $T=45$ months. From Figure 3, Figure 4 and Figure 5 we note that this peak date is forward delayed beyond $T=45$ months whenever the fractional-order parameter $\eta$ decreases. Moreover, the number of infected individuals decreases with the decrease in the fractional-order parameter.

Now, in addition to vaccination, we consider environmental sanitation. To this aim, the bacterial decay rate ${\mu }_b$ is modified to ${\mu }_b:={\mu }_b+\omega$, where $\omega \in \{0,0.1,0.2.0.3,0.4\}$ represents the additional decay rate of free salmonella due to environmental sanitation [6]. The vaccination coverage is fixed at $\xi =32.21\%$ as reported in Table 1. From Figure 6, Figure 7, Figure 8 and Figure 9 it is evident that mass vaccination combined with environmental sanitation has a positive impact, reducing the disease burden.

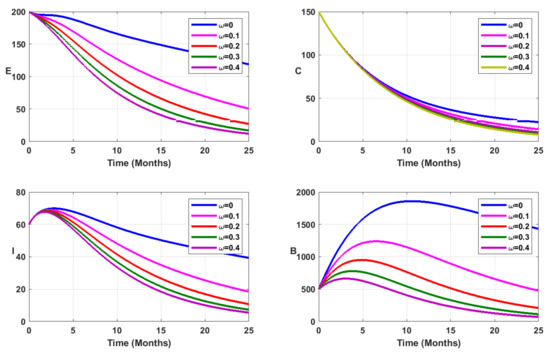
Figure 6. Simulation results showing the infected state variable profiles when vaccination is combined with environmental sanitation, for fractional order $\eta =1$.

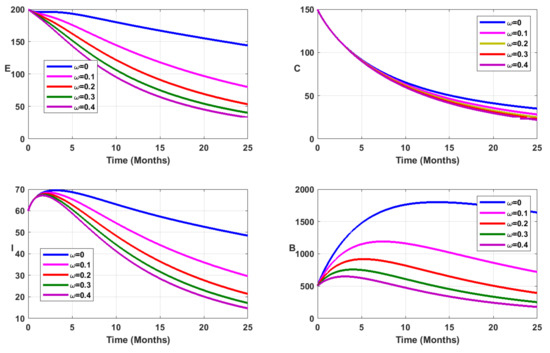
Figure 7. Simulation results showing the infected state variable profiles when vaccination is combined with environmental sanitation, for fractional order $\eta =0.90$.

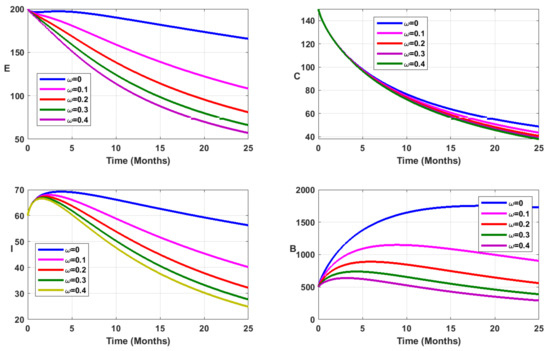
Figure 8. Simulation results showing the infected state variable profiles when vaccination is combined with environmental sanitation, for fractional order $\eta =0.80$.

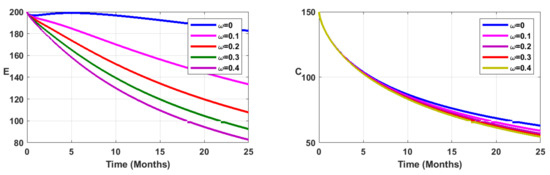
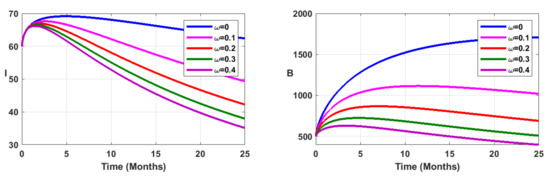
Figure 9. Simulation results showing the infected state variable profiles when vaccination is combined with environmental sanitation, for fractional order $\eta =0.70$.

3.2. Numerical Results of the Fractional Model with Standard Incidence Law

To simulate the new fractional model (35), we use the parameter values listed in Table 2. Note that the new typhoid model has been calibrated using real data from Mbandjock, Cameroon (see [5,6]). In Figure 10, panel (a) shows the cumulative typhoid cases versus fitted confirmed cases (infectious individuals tested positive), which is equal to $(1-q){\gamma }_{1}E\left(t\right)+(1-p){\gamma }_{2}C\left(t\right)$, while panel (b) presents the cumulative estimated cases for the next year. The following fractions are used as initial conditions $S\left(0\right)=$ 20,950/32,000, $V\left(0\right)=$ 20/32,000, $E\left(0\right)=$ 200/32,000, $C\left(0\right)=$ 150/32,000, $I\left(0\right)=$ 60/32,000, $R\left(0\right)=$ 1/32,000, and $B\left(0\right)=500/{10}^6$. The relative change is $r=1.83$×${10}^{-7}$ and the function tolerance is equal to ${10}^{-6}$.

Table 2. Estimated parameter values of the new typhoid model (35).

Parameter	Values	Source	Parameter	Values	Source
${\Lambda }_h$	3	Fitted	${\mu }_b$	0.0015	Fitted
${\gamma }_1$	0.1512	Fitted	$ϵ$	0.9497	Fitted
${\gamma }_2$	0.3039	Fitted	$\xi$	0.1538	Fitted
$\delta$	0.1382	Fitted	$\beta$	0.60	Fitted
$\nu$	0.00050	Fitted	K	995.7957	Fitted
$\sigma$	0.4992	Fitted	${\mathcal{R}}_{c\star }$	1.4348	Estimated

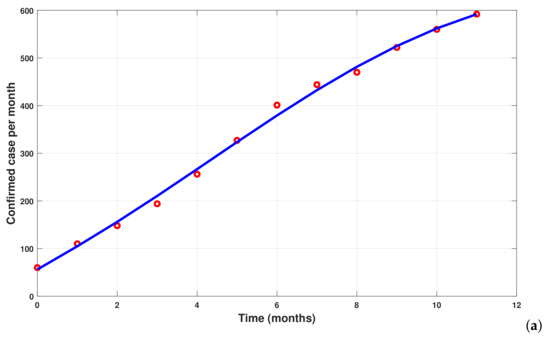
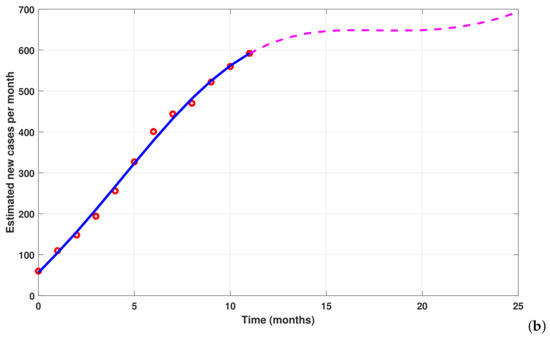
Figure 10. Parameter estimation and forecasting of cumulative new cases of typhoid fever in Mbandjock, Cameroon, from 1 July 2019 to 31 August 2020, for the new model (35). Red bullets denote real data (see [5,6]). The fitted model is represented with the blue line, and new forecasted cases are represented by the dotted line.

First, we observe the general dynamics of the new fractional model. The results are displayed in Figure 11. As for the case of the fractional model with mass incidence law (5), Figure 11 reveals that when the fractional order $\eta$ decreases, the solutions of our fractional model (35) have different behaviors. The number of typhoid cases decreases and the peak is delayed when the fractional order decreases.

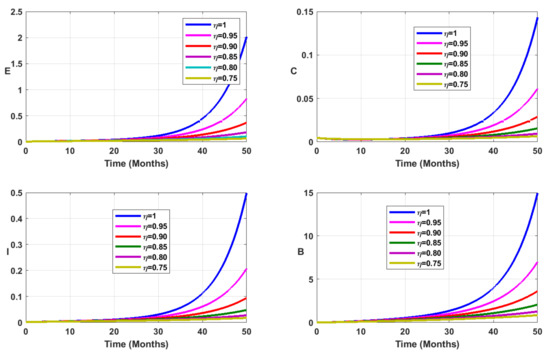
Figure 11. Simulation results showing the fractional dynamics on the infected state variable profiles for different values of the fractional-order parameter $\eta$.

Vaccination coverage impact is studied numerically. From Figure 12, Figure 13, Figure 14 and Figure 15, it follows that the more $\xi$ increases, the fewer individuals are infected. This shows that mass vaccination plays a important role in reducing the spread of the disease.

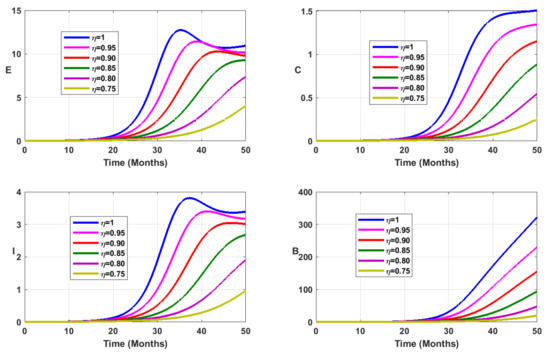
Figure 12. Simulation results showing the infected state variable profiles when the vaccination coverage $\xi =0\%$ with different values of the fractional order.

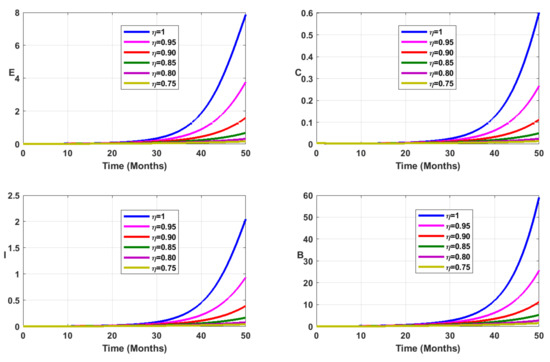
Figure 13. Simulation results showing the infected state variable profiles when the vaccination coverage $\xi =20\%$ with different values of the fractional order.

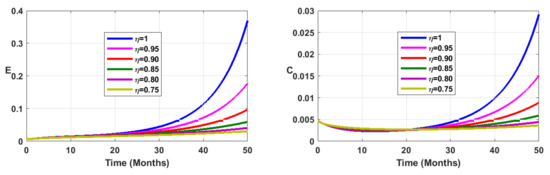
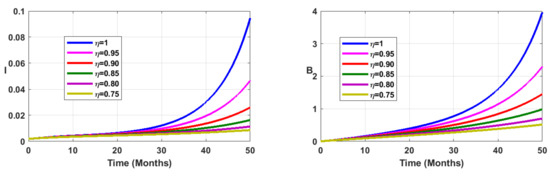
Figure 14. Simulation results showing the infected state variable profiles when the vaccination coverage $\xi =50\%$ with different values of the fractional order.

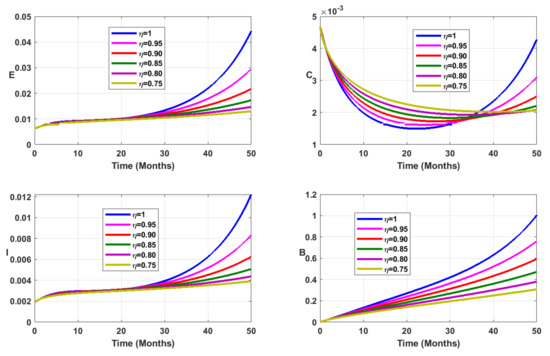
Figure 15. Simulation results showing the infected state variable profiles when the vaccination coverage $\xi =90\%$ with different values of the fractional order.

4. Discussion and Conclusions

In this work, we extended our previous $SVEIR$-B compartmental model [5] by replacing the integer derivative with fractional derivatives, to evaluate the memory effect on the transmission dynamics of typhoid fever. We began by recalling some previous results on the integer model (the control reproduction number ${\mathcal{R}}_c$, existence and stability of equilibrium points). In order to describe the non-local character as well as long-term memory effects in the typhoid fever transmission dynamics, we replaced the integer derivative with the fractional derivative in the Caputo sense and studied the asymptotic stability of the disease-free equilibrium. Using fixed point theory, we proved the existence as well as the uniqueness of the solutions of the fractional model. We used the Adams–Bashforth method to construct the numerical scheme of the proposed fractional model. We then established the stability of this proposed numerical scheme. We simulated our fractional model using the Adams–Bashforth–Moulton scheme implemented by [39]. Using parameter values for Mbandjock, a city in the central region of Cameroon, we simulates the model by varying the fractional-order parameter, the vaccination coverage, and the bacterial decay rate. Apart from the fact that the solutions of the fractional model converged to the solutions of the integer model when the fractional-order approached one ($\eta =1$), the simulation results showed that the expected date of the disease peak was forward delayed when the fractional-order parameter decreased. In addition, combining vaccination with environmental sanitation can permit a considerable reduction in the disease’s spread.

We then extended the previous models by replacing the mass action incidence law with the standard incidence. The analysis of the models showed that the disease-free equilibrium is also globally asymptotically stable whenever the corresponding reproduction number ${\mathcal{R}}_{c\star }$ is less than one. Due to the complexity of the newly proposed models, we could not prove the existence and uniqueness of the endemic equilibrium. However, numerical simulations showed that it is possible that the new typhoid fever models permit a unique endemic equilibrium that is globally stable whenever ${\mathcal{R}}_{c\star }>1$, and no equilibrium otherwise. We also found that, from a quantitative point of view, the disease burden was overestimated with the models the with mass incidence law compared to the one with the standard incidence law. Indeed, for the models with mass incidence, the control reproduction number was estimated at 2.4750, while the one with the standard incidence was estimated at 1.4348. This was in accordance with our previous work in which we considered the standard incidence law. In [6], the control reproduction number was estimated at 1.3722. As for the models with mass action incidences, we observed a delay in the disease peaks whenever the fractional-order derivative decreased.

It was observed that mass vaccination can overcome this disease. In fact, if the means are put in place to finance and implement vaccination campaigns in rural areas, it is possible to eradicate typhoid fever. Moreover, these vaccination campaigns must be accompanied by awareness campaigns among the population in order to combat this type of disease, as well as instructing citizens on ways to protect their environment against the proliferation of salmonella.

Our main contribution in this paper consisted in the formulation, using both integer and fractional derivatives, of new transmission dynamics typhoid fever models that incorporate the standard incidence rates and mass vaccination. The values of the control reproductive number differ from the model with mass action incidence and those with the standard incidences. Indeed, for the model with mass action incidences, ${\mathcal{R}}_c=2.4750$, while, for those with standard incidences, ${\mathcal{R}}_{c*}=1.4348$. This proves that mass action incidence overestimates the disease burden.