May the Piezoresistivity of GNP-Modified Cement Mortar Be Related to Its Fractal Structure?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Specimen Preparation
2.3. Experiments and Methods
2.3.1. Piezoresistive Test
2.3.2. MIP Test
2.3.3. SEM Test
2.3.4. Fractal Models
3. Results and Discussions
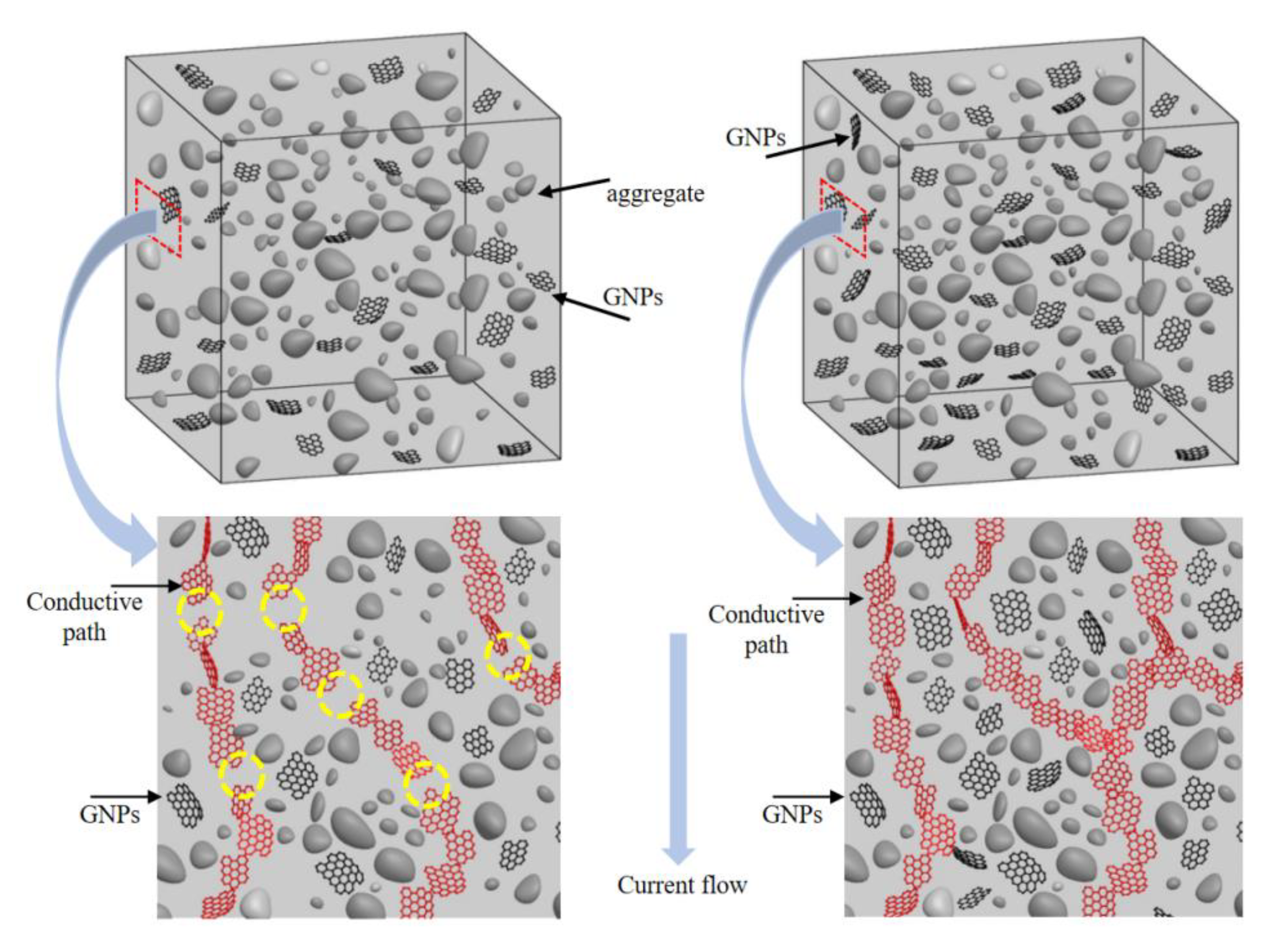
3.1. SEM Characteristics
3.2. Piezoresistive Behaviors
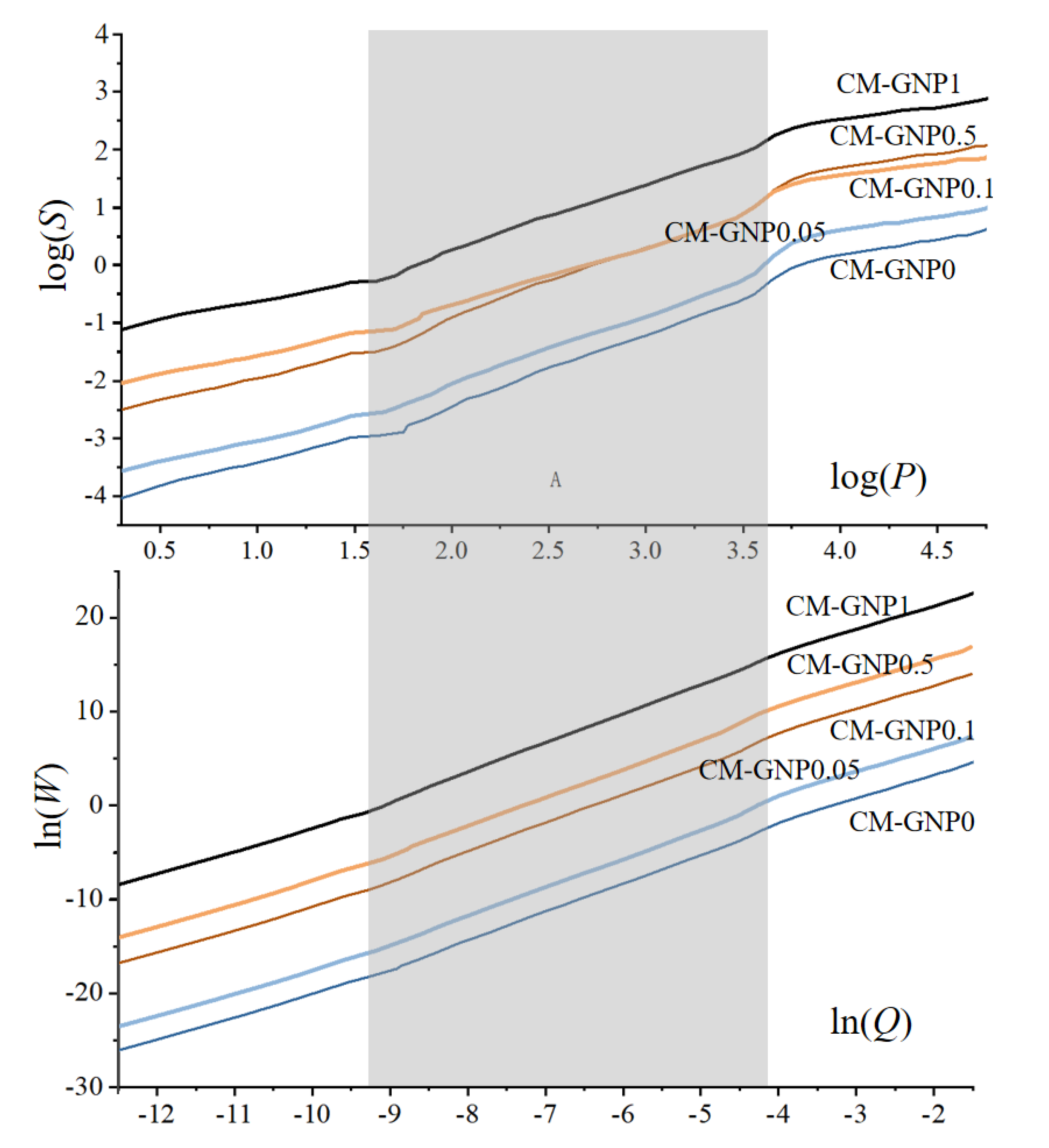
3.3. Fractal Dimensions and Fractal Regions
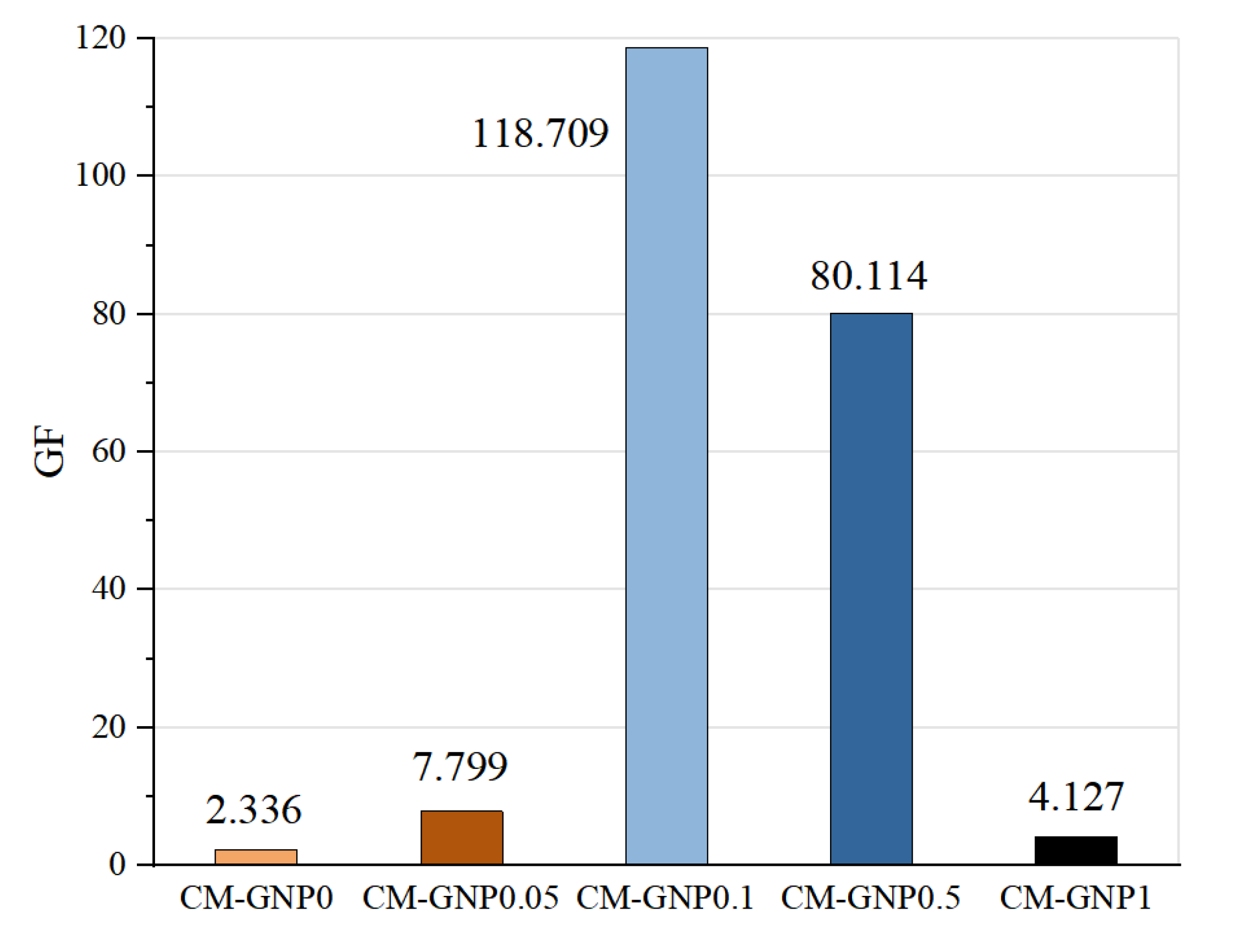
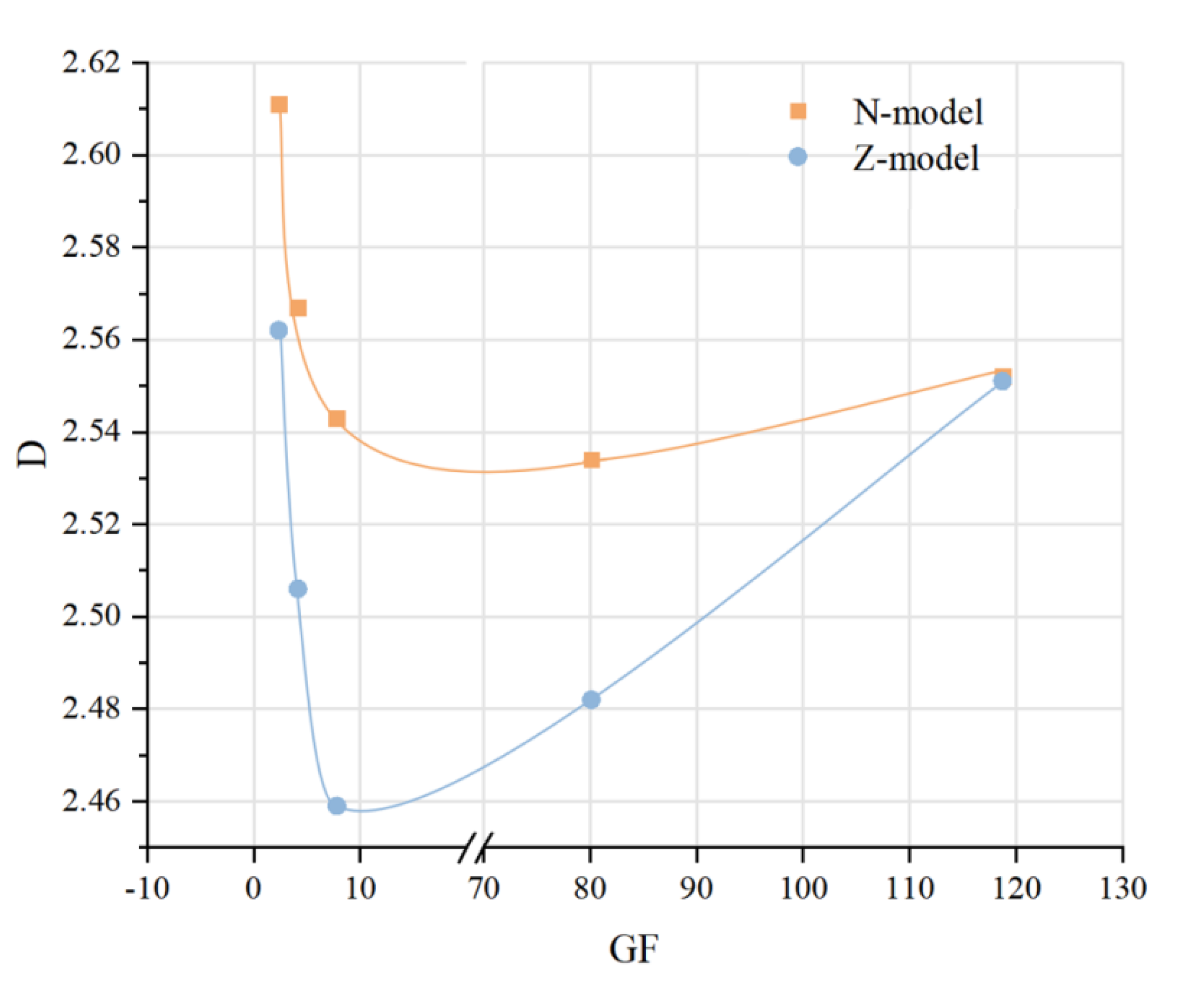
3.4. Relationship Between Gauge Factor and Fractal Dimensions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, W.K.; Guo, Y.P.; Sun, Z.H.; Tao, Z.; Li, W.G. Development of piezoresistive cement-based sensor using recycled waste glass cullets coated with carbon nanotubes. J. Clean. Prod. 2021, 314, 127968. [Google Scholar] [CrossRef]
- Xu, J.X.; Yin, T.J.; Wang, Y.; Liu, L. Anisotropic electrical and piezoresistive sensing properties of cement-based sensors with aligned carbon fibers. Cem. Concr. Compos. 2020, 116, 103873. [Google Scholar] [CrossRef]
- D’Antonella, A.; Matteo, T.; Andrea, M.; Filippo, U. Improved strain sensing properties of cement-based sensors through enhanced carbon nanotube dispersion. Cem. Concr. Compos. 2021, 115, 103842. [Google Scholar]
- Rouhi, S.; Moradi, H.; Hakimi, Y.; Nikpour, F. On the mechanical properties of the graphyne and graphdiyne with patterned hydrogenation and hole: A molecular dynamics investigation. Appl. Phys. A 2020, 126, 1–28. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, C.; Chen, Y.; Mortazavi, B.; Lu, Z.; Zhang, X.; Xu, K.; Zhang, H.; Liu, W.; Rabczuk, T.; et al. New group V graphyne: Two-dimensional direct semiconductors with remarkable carrier mobilities, thermoelectric performance, and thermal stability. Mater. Today Phys. 2020, 12, 100164. [Google Scholar] [CrossRef]
- Fazel, S.; Bohayra, M. Ultrahigh carrier mobility, Dirac cone and high stretchability in pyrenyl and pyrazinoquinoxaline graphdiyne/graphyne nanosheets confirmed by first-principles. Appl. Surf. Sci. 2021, 557, 149699. [Google Scholar]
- Li, X.Y.; Liu, Y.M.; Li, W.G.; Li, C.Y.; Sanjayan, J.G.; Duan, W.H.; Li, Z.J. Effects of graphene oxide agglomerates on workability, hydration, microstructure and compressive strength of cement paste. Constr. Build. Mater. 2017, 145, 402–410. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Que, L.X.; Cui, Z.Y.; Lambert, P. Physical Properties of Concrete Containing Graphene Oxide Nanosheets. Materials 2019, 10, 1707. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.; Ge, Y.P.; Cai, C.S.; Zhang, Y.X.; Liu, Z. Mechanical properties and microstructure of graphene oxide cement-based composites. Constr. Build. Mater. 2019, 194, 102–109. [Google Scholar] [CrossRef]
- Li, P.Q.; Liu, J.X.; Her, S.W.; Erfan, Z.N.; Seungmin, L.; Sungchul, B. Synthesis of Highly-Dispersed Graphene Oxide Nanoribbons-Functionalized Carbon Nanotubes-Graphene Oxide (GNFG) Complex and Its Application in Enhancing the Mechanical Properties of Cementitious Composites. Nanomaterials 2021, 11, 1669. [Google Scholar] [CrossRef]
- Wang, J.Y.; Tao, J.; Li, L.; Zhou, C.S.; Zeng, Q. Thinner fillers, coarser pores? A comparative study of the pore structure alterations of cement composites by graphene oxides and graphene nanoplatelets. Compos. Part A 2020, 130, 105750. [Google Scholar] [CrossRef]
- Zhu, X.H.; Kang, X.J.; Deng, J.X.; Yang, K.; Yu, L.W.; Yang, C.H. A comparative study on shrinkage characteristics of graphene oxide (GO) and graphene nanoplatelets (GNPs) modified alkali-activated slag cement composites. Mater. Struct. 2021, 54, 106. [Google Scholar] [CrossRef]
- Zhu, X.H.; Kang, X.J. Effect of graphene oxide(GO) on the hydration and dissolution of alite in a synthetic cement system. J. Mater. Sci. 2020, 55, 3419–3433. [Google Scholar] [CrossRef]
- Goracci, G.; Dolado, J.S. Elucidation of Conduction Mechanism in Graphene Nanoplatelets (GNPs)/Cement Composite Using Dielectric Spectroscopy. Materials 2020, 13, 275. [Google Scholar] [CrossRef] [Green Version]
- Ioanna, P.; Livia, R.S.; Chrysoula, L.; Abir, A.T. Investigation of the dispersion of multi-layer graphene nanoplatelets in cement composites using different superplasticiser treatments. Constr. Build. Mater. 2021, 293, 123543. [Google Scholar]
- Zhang, Q.; Sun, H.; Liu, W.G.; Zhou, Z.H.; Yuan, L.W.; Ren, Z.C.; Geng, D.J.; Wang, J.B.; Cheng, X. Effect of rGO on the mechanical strength, hydration and micromorphology of cement incorporated silica fume. Constr. Build. Mater. 2021, 300, 124325. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, L.; García-Sánchez, F.; García-Macías, E.; Buroni, F.C.; Sáez, A. Crack-induced electrical resistivity changes in cracked CNT-reinforced composites. Theor. Appl. Fract. Mech. 2020, 106, 102470. [Google Scholar] [CrossRef]
- Xu, J.M.; Zhang, D. Pressure-sensitive properties of emulsion modified graphene nanoplatelets/cement composites. Cem. Concr. Compos. 2017, 84, 74–82. [Google Scholar] [CrossRef]
- Wang, M.; Wang, R.; Yao, H. Study on the three dimensional mechanism modified cement. Construction and Building. Constr. Build. Mater. 2016, 126, 730–739. [Google Scholar]
- Li, C.Y.; Chen, S.J.; Li, W.G.; Li, X.Y.; Ruan, D.; Duan, W.H. Dynamic increased reinforcing effect of graphene oxide on cementitious nanocomposite. Constr. Build. Mater. 2019, 206, 694–702. [Google Scholar] [CrossRef]
- Gholampour, A.; Valizadeh, K.M.; Tran, D.N.H.; Ozbakkaloglu, T.; Losic, D. From graphene oxide: Impact on the physiochemical and mechanical properties of graphene-cement composites. ACS Appl. Mater. Interfaces 2017, 9, 43275–43286. [Google Scholar] [CrossRef]
- Buasiri, T.; Habermehl-Cwirzen, K.; Krzeminski, L.; Cwirzen, A. Piezoresistive Load Sensing and Percolation Phenomena in Portland Cement Composite Modified with In-Situ Synthesized Carbon Nanofibers. Nanomaterials 2019, 9, 594. [Google Scholar] [CrossRef] [Green Version]
- Jin, T.; Wang, X.H.; Wang, Z.D.; Zeng, Q. Graphene nanoplatelets as an effective additive to tune the microstructures and piezoresistive properties of cement-based composites. Constr. Build. Mater. 2019, 209, 665–678. [Google Scholar]
- Liu, C.J.; Huang, X.C.; Wu, Y.Y.; Deng, X.W.; Zheng, Z.L.; Xu, Z.; Hui, D. Advance on the dispersion treatment of graphene oxide and the graphene oxide modified cement-based materials. Nanotechnol. Rev. 2021, 10, 34–49. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K.F.; Fen-Chong, T. Surface fractal analysis of pore structure of high-volume fly-ash cement pastes. Appl. Surf. Sci. 2010, 257, 762–768. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Huang, M.; Yin, H.; Jiang, K.; Xiao, K.; Tang, S. Influence of Different Alkali Sulfates on the Shrinkage, Hydration, Pore Structure, Fractal Dimension and Microstructure of Low-Heat Portland Cement, Medium-Heat Portland Cement and Ordinary Portland Cement. Fractal Fract. 2021, 5, 79. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Y.; Geng, Z.C.; Xu, X.F.; Yu, W.Z.; A, H.; Chen, J.T. Structure, fractality, mechanics and durability of calcium silicate hydrates. Fractal Fract. 2021, 5, 47. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.X.; Lin, Y.Q.; Yang, H.M.; Tang, S.W. Comparison between the effects of phosphorous slag and fly ash on the C-S-H structure, long-term hydration heat and volume deformation of cement-based materials. Constr. Build. Mater. 2020, 250, 118807. [Google Scholar] [CrossRef]
- Wang, P.G.; Mo, R.; Li, S.; Xu, J.; Jin, Z.Q.; Zhao, T.J.; Wang, D.Z. A chemo-damage-transport model for chloride ions diffusion in cement-based materials: Combined effects of sulfate attack and temperature. Constr. Build. Mater. 2021, 288, 123121. [Google Scholar] [CrossRef]
- Wang, L.; Jin, M.; Zhou, S.; Tang, S.W.; Lu, X. Investigation of microstructure of C-S-H and micro-mechanics of cement pastes under NH4NO3 dissolution by 29Si MAS NMR and microhardness. Measurement 2021, 185, 110019. [Google Scholar] [CrossRef]
- Yaghoobi, K.R. A new approach to measure the fractal dimension of a trajectory in the high-dimensional phase space. Chaos Solitons Fractals 2021, 151, 111239. [Google Scholar]
- Tiina, V.; Gregor, R.; Anastasiia, L.; Basel, R.; Herje, S.; Liisa, P.; Mari, K.; Frank, L. Analysis of membrane fouling by Brunauer-Emmet-Teller nitrogen adsorption/desorption technique. Sci. Rep. 2020, 10, 3427. [Google Scholar]
- Chinh, N.D.; Hien, T.T.; Do, V.L.; Hieu, N.M.; Quang, N.D.; Lee, S.-M.; Kim, C.; Kim, D. Adsorption/desorption kinetics of nitric oxide on zinc oxide nano film sensor enhanced by light irradiation and gold-nanoparticles decoration. Sens. Actuators B Chem. 2019, 281, 262–272. [Google Scholar] [CrossRef]
- Muratov, D.S.; Gromov., S. Evaluating Hydrogen Uptake for Two Types of Multi-Wall Carbon Nanotubes from Nitrogen Adsorption/Desorption Data. Nano Hybrids Compos. 2017, 13, 341–347. [Google Scholar] [CrossRef]
- Yury, V.Z.; Natalia, A.; Philip, V.H.; Nele, D.B. Pore Size Distribution and Surface Multifractal Dimension by Multicycle Mercury Intrusion Porosimetry of GGBFS and Limestone Powder Blended Concrete. Appl. Sci. 2021, 11, 4851. [Google Scholar]
- Yang, Q.; Xue, J.; Li, W.; Du, X.; Ma, Q.; Zhan, K.; Chen, Z. Comprehensive evaluation and interpretation of mercury intrusion porosimetry data of coals based on fractal theory, Tait equation and matrix compressibility. Fuel 2021, 298, 120823. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, K.; Yuan, Q. Limited fractal behavior in cement paste upon mercury intrusion porosimetry test: Analysis and models. Constr. Build. Mater. 2021, 276, 122231. [Google Scholar] [CrossRef]
- Wang, X.L.; Pan, J.N.; Wang, K.; Ge, T.Y.; Wei, J.; Wu, W. Characterizing the shape, size, and distribution heterogeneity of pore-fractures in high rank coal based on X-ray CT image analysis and mercury intrusion porosimetry. Fuel 2020, 282, 118754. [Google Scholar] [CrossRef]
- Domenico, L.; Pietro, C.; Kiselev, M.A. Structural Characterization of Biomaterials by Means of Small Angle X-rays and Neutron Scattering (SAXS and SANS), and Light Scattering Experiments. Molecules 2020, 25, 5624. [Google Scholar]
- Yokaichiya, F.; Schmidt, C.; Storsberg, J.; Vollrath, M.K.; Araujo, D.R.; Kent, B.; Clemens, D.; Wingert, F.; Franco, M.K. Effects of doxorubicin on the structural and morphological characterization of solid lipid nanoparticles (SLN) using small angle neutron scattering (SANS) and small angle X-ray scattering (SAXS). Phys. B Phys. Condens. Matter 2018, 551, 191–196. [Google Scholar] [CrossRef]
- Razyq, N.; Luo, G.H.; Neil, R.; Fourie, A.; Johns, M.L.; Fridjonsson Einar, O. Understanding the microstructural evolution of hypersaline cemented paste backfill with low-field NMR relaxation. Cem. Concr. Res. 2021, 147, 106516. [Google Scholar]
- Wang, Y.; Diamand, S. A fractal study of the fracture surfaces of cement pastes and mortars using a stereoscopic SEM method. Cem. Concr. Res. 2001, 31, 1385–1392. [Google Scholar] [CrossRef]
- Niu, D.; Huang, D.; Zheng, H.; Su, L.; Fu, Q.; Luo, D. Experimental study on mechanical properties and fractal dimension of pore structure of basalt-polypropylene fiber-reinforced concrete. Appl. Sci. 2019, 9, 1602. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.C.; Zhou, J.K. Fractal characteristics of pore structure of hardened cement paste prepared by pressurized compact molding. Constr. Build. Mater. 2020, 259, 119856. [Google Scholar] [CrossRef]
- Calati, M.; Monte, E.D.; Mancin, S. Numerical Analysis of the Effects of the Structure Shape and Orientation of Kelvin Cell Porous Structures during Air Forced Convection. Appl. Sci. 2021, 11, 6189. [Google Scholar] [CrossRef]
- Kashchenko, S. Local Dynamics of Logistic Equation with Delay and Diffusion. Mathematics 2021, 9, 1566. [Google Scholar] [CrossRef]
- Pia, G.; Sanna, U. A geometrical fractal model for the porosity and thermal conductivity of insulting concrete. Constr. Build. Mater. 2013, 44, 551–556. [Google Scholar] [CrossRef]
- Tang, S.W.; He, Z.; Cai, X.H.; Cai, R.J.; Zhou, W.; Li, Z.J.; Shao, H.Y.; Wu, T.; Chen, E. Volume and surface fractal dimensions of pore structure by NAD and LT-DSC in calcium sulfoaluminate cement pastes. Constr. Build. Mater. 2017, 143, 395–418. [Google Scholar] [CrossRef]
- Dong, W.K.; Li, W.G.; Vessalas, K.; He, X.Z.; Sun, Z.H.; Sheng, D.C. Piezoresistivity deterioration of smart graphene nanoplate/cement-based sensors subjected to sulphuric acid attack. Compos. Commun. 2021, 23, 100563. [Google Scholar] [CrossRef]
- Szeląg, M. Mechano-Physical Properties and Microstructure of Carbon Nanotube Reinforced Cement Paste after Thermal Load. Nanomaterials 2017, 7, 269. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.Q.; Wei, J.; Dong, R.Z. Graphene-based piezoresistive composite and applicationin crack monitoring. J. ZheJiang Univ. 2020, 54, 233–240. [Google Scholar]
- Frac, M.; Waldemar, P. Piezoresistive properties of cement composites with expanded graphite. Compos. Commun. 2020, 19, 99–102. [Google Scholar] [CrossRef]
- Neimark, A.V. A new approach to the determination of the surface fractal dimension of porous solids. Phys. A 1992, 191, 258–262. [Google Scholar] [CrossRef]
- Rootare, H.M.; Prenzlow, C.F. Surface areas from mercury porosimeter measurements. J. Phys. Chem. 1967, 71, 2733–2736. [Google Scholar] [CrossRef]
- Pfeifer, P.; Avnir, D. Chemistry in noninteger dimensions between two and three I. Fractal theory of heterogeneous surface. J. Chem. Phys. 1983, 79, 3558–3565. [Google Scholar] [CrossRef]
- Zhang, B.; Li, S. Determination of the surface fractal dimension for porous media by mercury porosimetry. Ind. Eng. Chem. Res. 1995, 34, 1383–1386. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, W.; Liu, X. Scale-dependent nature of the surface fractal dimension for bi- and multi-disperse porous solids by mercury porosimetry. Appl. Surf. Sci. 2006, 253, 1349–1355. [Google Scholar] [CrossRef]
- Matalkah, F.; Soroushian, P. Graphene nanoplatelet for enhancement the mechanical properties and durability characteristics of alkali activated binder. Constr. Build. Mater. 2020, 249, 118773. [Google Scholar] [CrossRef]
- Du, H.; Gao, H.J.; Pang, S.D. Improvement in concrete resistance against water and chloride ingress by adding graphene nanoplatelet. Cem. Concr. Res. 2016, 83, 114–123. [Google Scholar] [CrossRef]
- Papanikolaou, I.; Arena, N.; Al-Tabbaa, A. Graphene nanoplatelet reinforced concrete for self-sensing structures—A lifecycle assessment perspective. J. Clean. Prod. 2019, 240, 118202. [Google Scholar] [CrossRef]
- Al-Dahawi, A.; Sarwary, M.H.; Öztürk, O.; Yıldırım, G.; Akın, A.; Sahmaran, M.; Lachemi, M. Electrical percolation threshold of cementitious composites possessing self-sensing functionality incorporating different carbon-based materials. Smart Mater. Struct. 2016, 25, 105005. [Google Scholar] [CrossRef]
- Jia, X.W.; Zhang, X.; Ma, D.; Yang, Z.F.; Shi, C.L.; Wang, Z. Conductive properties and influencing factors of electrically conductive concrete: A review. Mater. Rep. 2017, 31, 90–97. [Google Scholar]
- Belli, A.; Mobili, A.; Bellezze, T.; Tittarelli, F.; Cachim, P. Evaluating the Self-Sensing Ability of Cement Mortars Manufactured with Graphene Nanoplatelets, Virgin or Recycled Carbon Fibers through Piezoresistivity Tests. Sustainability 2018, 10, 4013. [Google Scholar] [CrossRef] [Green Version]
- Li, D.B.; Lei, P.B.; Zhang, H.C.; Liu, J.P.; Lu, W.; Majewski, P. Co-Effects of Graphene Oxide and Cement on Geotechnical Properties of Loess. Adv. Mater. Sci. Eng. 2021, 2021, 7429310. [Google Scholar]
- García-Macías, E.; Alessandro, A.D.; Castro-Triguero, R.; Pérez-Mira, D.; Bertini, F.U. Micromechanics modeling of the uniaxial strain-sensing propertyof carbon nanotube cement-matrix composites for SHM applications. Constr. Build. Mater. 2017, 163, 195–215. [Google Scholar]
- Li, H.; Xiao, H.; Ou, J. Effect of compressive strain on electrical resistivity ofcarbon black-filled cement-based composites. Constr. Build. Mater. 2006, 28, 824–828. [Google Scholar]
- Guo, R.X.; Suo, Y.X.; Xia, H.T.; Yang, Y.; Ma, Q.M.; Yan, F. Study of Piezoresistive Behavior of Smart Cement Filled with Graphene Oxide. Nanomaterials 2021, 11, 206. [Google Scholar] [CrossRef]
- Zeng, Q.; Luo, M.; Pang, X.; Li, K. Surface fractal dimension: An indicator to characterize the microstructure of blended cement-based materials. Appl. Surf. Sci. 2013, 282, 302–307. [Google Scholar] [CrossRef]
- Fan, J.C.; Zhang, B. Repair of ordinary Portland cement concrete using alkali activated slag/fly ash: Freeze-thaw resistance and pore size evolution of adhesive interface. Constr. Build. Mater. 2021, 300, 124334. [Google Scholar] [CrossRef]
- Lv, Q.; Qiu, Q.; Zheng, J.; Wang, J.; Zeng, Q. Fractal dimension of concrete incorporating silica fume and its correlations to pore structure, strength and permeability. Constr. Build. Mater. 2019, 228, 116986. [Google Scholar]
- Han, J.X.; Cai, J.M.; Pan, J.L.; Sun, Y.Q. Study on the conductivity of carbon fiber self-sensing high ductility cementitious composite. J. Build. Eng. 2021, 43, 103125. [Google Scholar] [CrossRef]

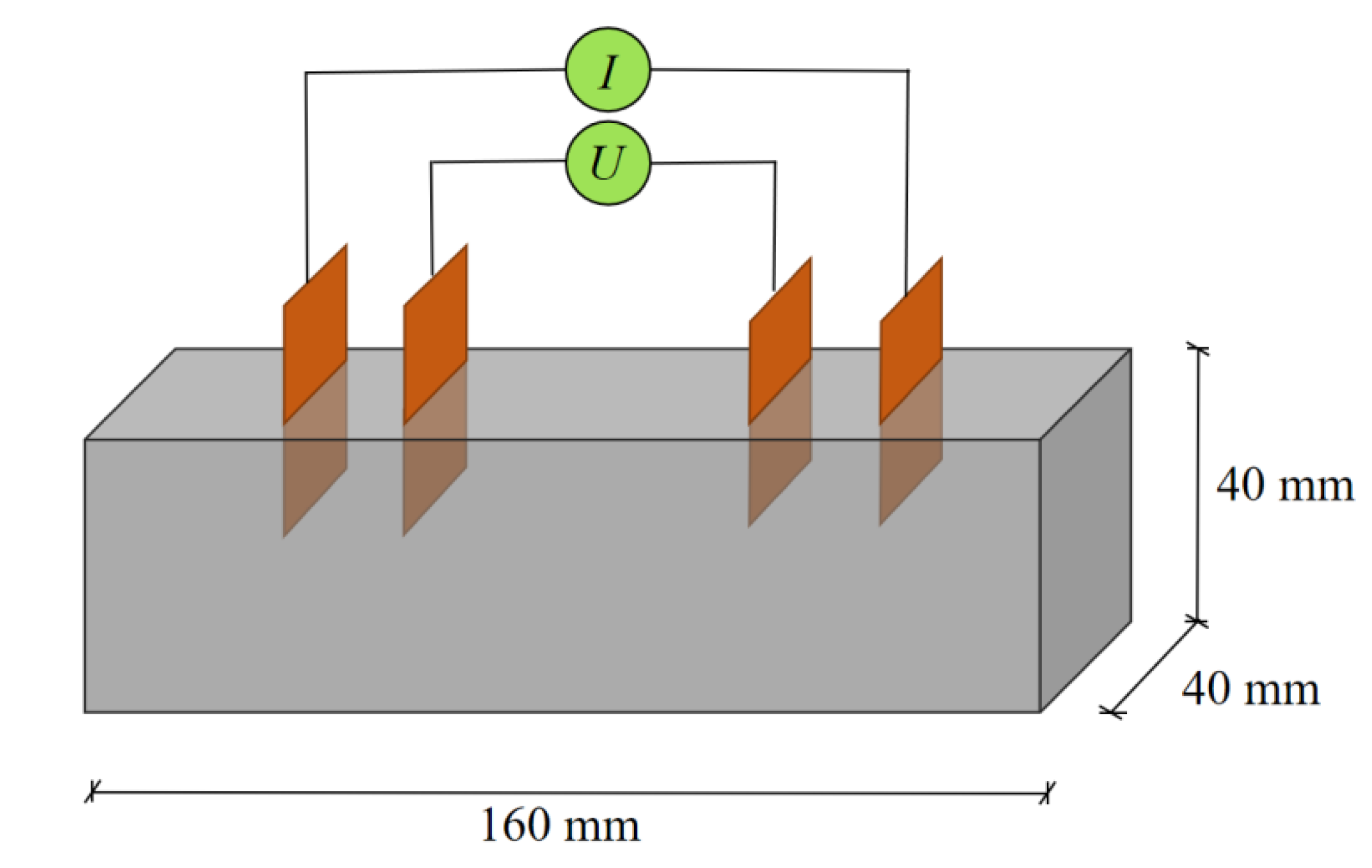

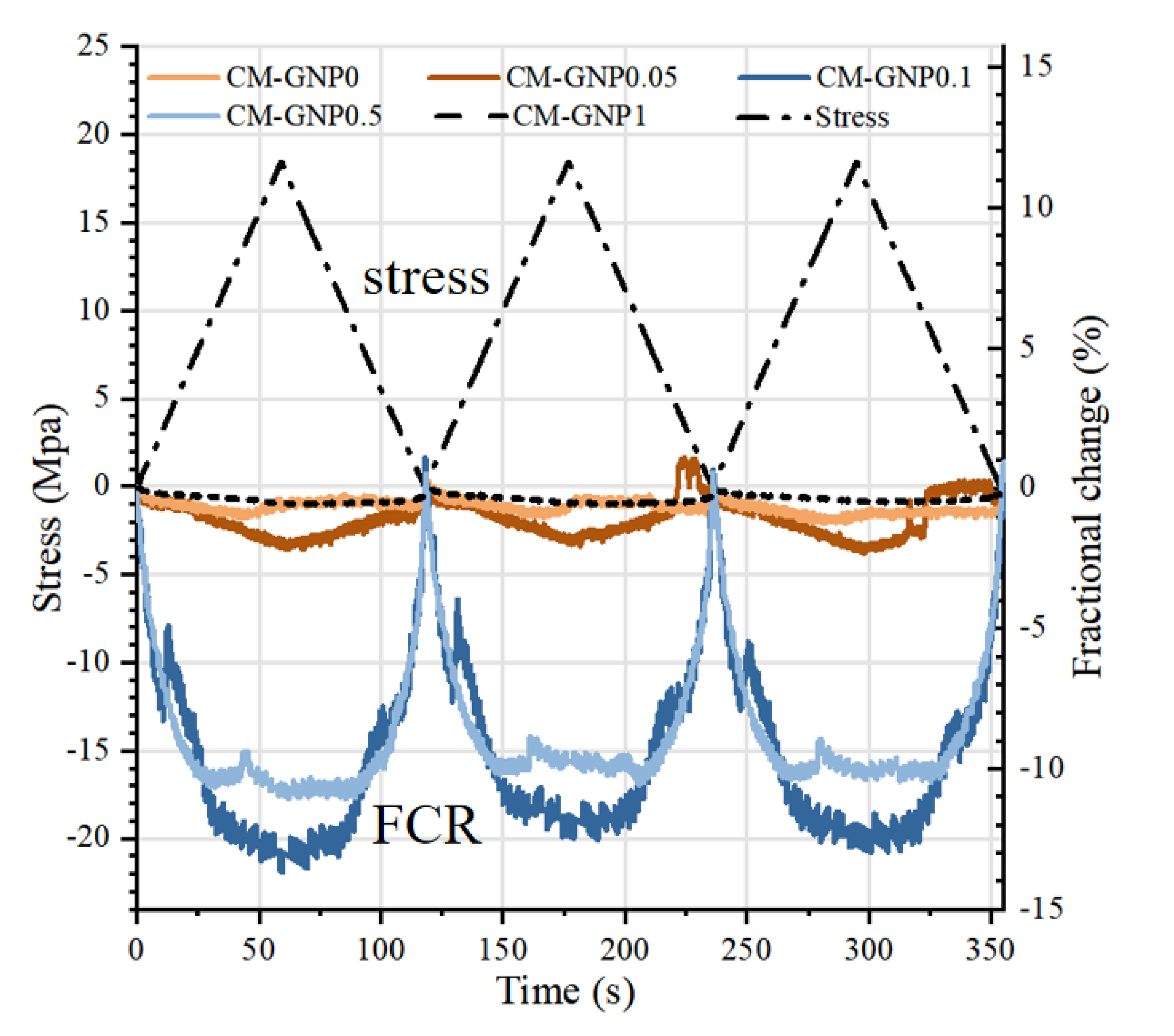
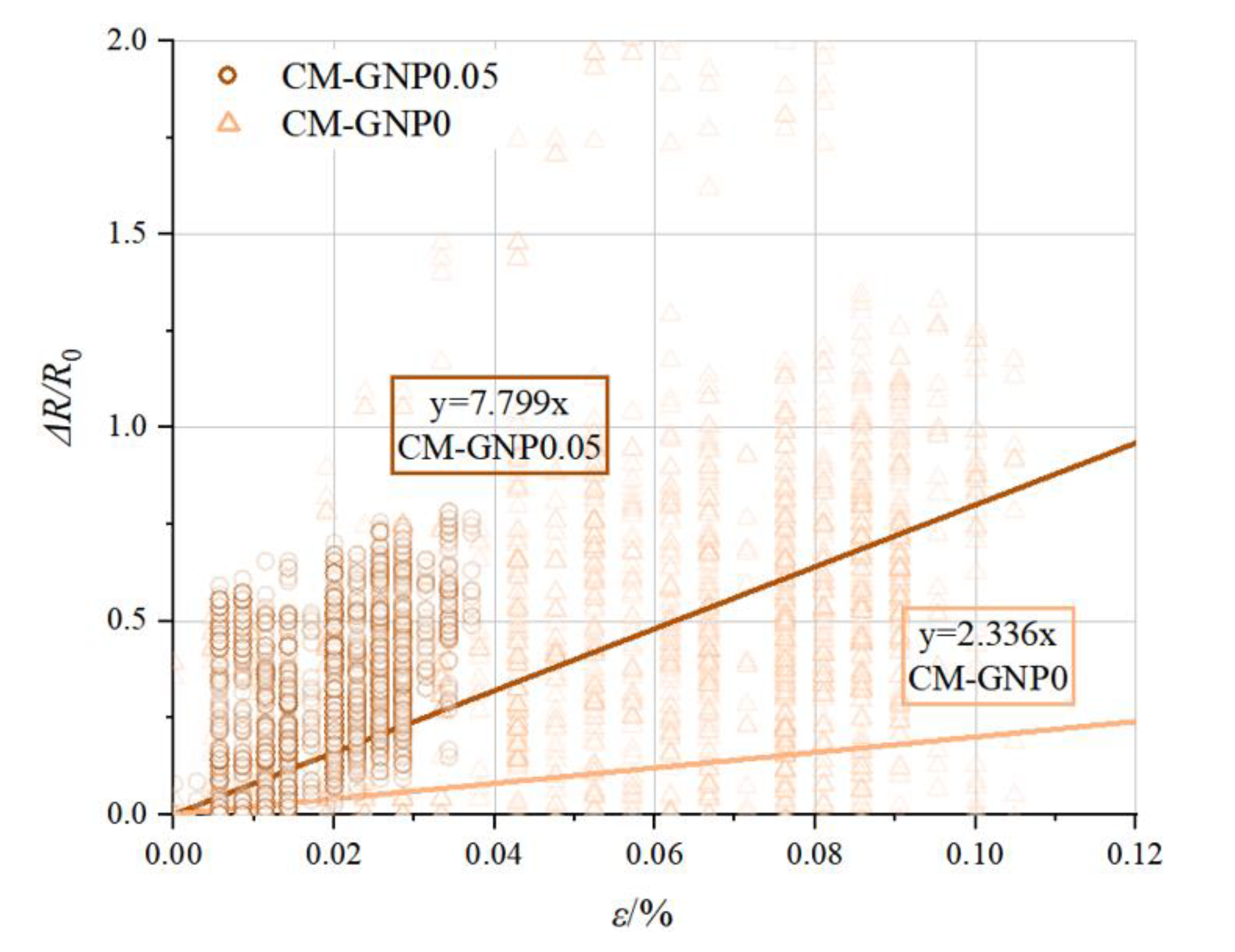
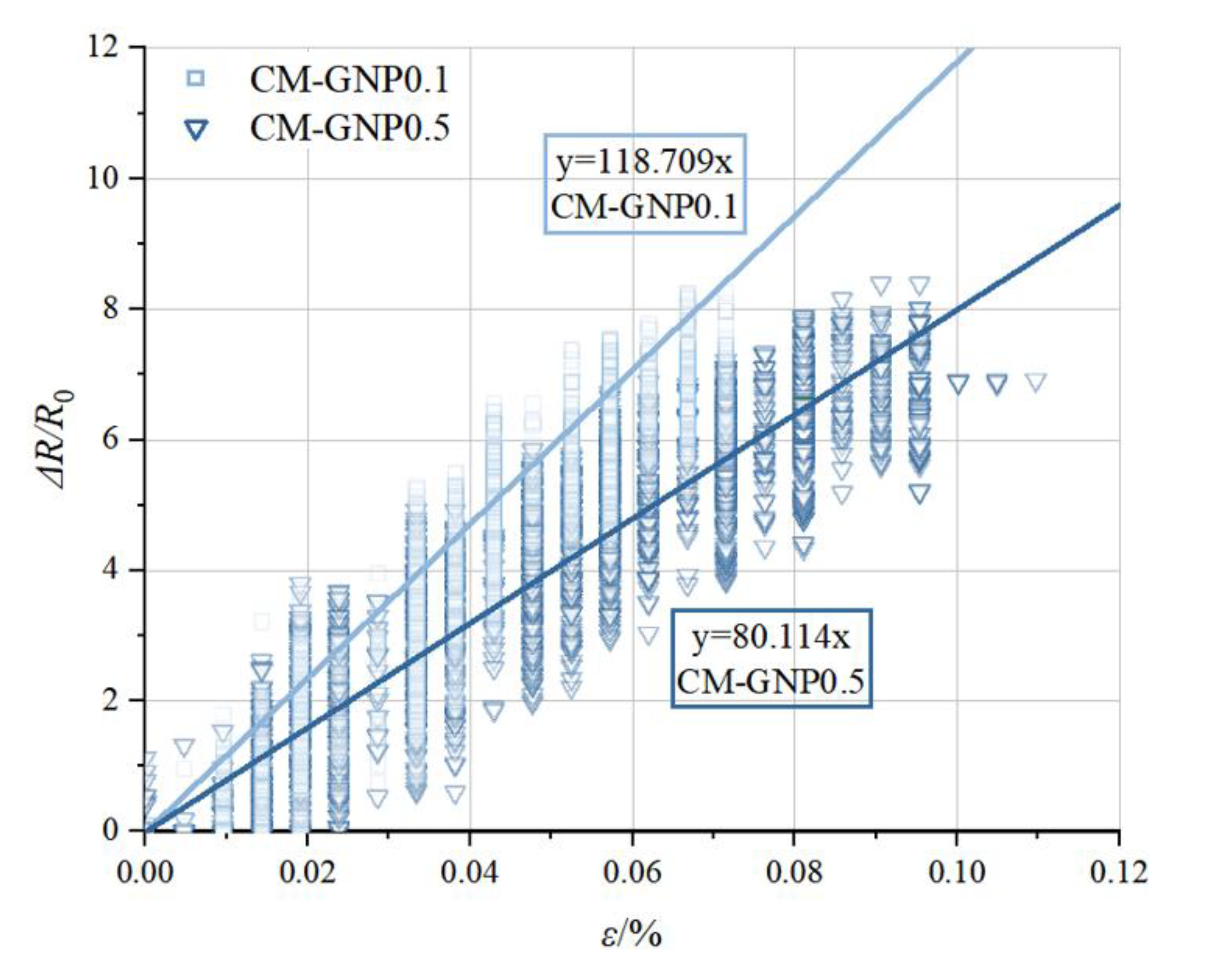


| Chemical Composition | Percentage | Mineral | Percentage |
|---|---|---|---|
| SiO2 | 22.15 | C3S | 56.54 |
| Al2O3 | 4.51 | C2S | 20.87 |
| Fe2O3 | 3.39 | C3A | 6.22 |
| CaO | 65.36 | C4AF | 10.31 |
| MgO | 2.31 | ||
| SO3 | 0.46 | ||
| NaOeq | 0.488 | ||
| f-CaO | 0.95 |
| Sample ID | GNP(%) | Cement (g) | Water (g) | Sand (g) | Dispersant (g) |
|---|---|---|---|---|---|
| CM-GNP0 | 0 | 900 | 330 | 2700 | 4.5 |
| CM-GNP0.05 | 0.05 | ||||
| CM-GNP0.1 | 0.1 | ||||
| CM-GNP0.5 | 0.5 | ||||
| CM-GNP1 | 1.0 |
| Specimen | CM-GNP0 | CM-GNP0.05 | CM-GNP0.1 | CM-GNP0.5 | CM-GNP1 | |
|---|---|---|---|---|---|---|
| GNP | 0 | 0.05% | 0.1% | 0.5% | 1% | |
| Region Ⅰ | DN | 2.877 | 2.784 | 2.814 | 2.843 | 2.776 |
| Pore diameter | >4322 nm | >4050 nm | >4526 nm | >4452 nm | >4520 nm | |
| Region Ⅱ | DN | - | - | - | - | - |
| Pore diameter | 32–4322 nm | 40–4050 nm | 40–4526 nm | 32–4452 nm | 32–4520 nm | |
| Region Ⅲ | DN | 2.611 | 2.543 | 2.552 | 2.534 | 2.567 |
| Pore diameter | <32 nm | <40 nm | <40 nm | <32 nm | <32 nm |
| Specimen | CM-GNP0 | CM-GNP0.05 | CM-GNP0.1 | CM-GNP0.5 | CM-GNP1 | |
|---|---|---|---|---|---|---|
| GNP | 0 | 0.05% | 0.1% | 0.5% | 1% | |
| RegionⅠ | DZ | 2.472 | 2.447 | 2.446 | 2.465 | 2.422 |
| Pore diameter | >2416 nm | >3011 nm | >3044 nm | >2681 nm | >3069 nm | |
| Region Ⅱ | DZ | - | - | - | - | - |
| Pore diameter | 50–2416 nm | 40–3011 nm | 50–3044 nm | 40–2681 nm | 50–3069 nm | |
| Region Ⅲ | DZ | 2.562 | 2.459 | 2.551 | 2.482 | 2.506 |
| Pore diameter | <50 nm | <40 nm | <50 nm | <40 nm | <50 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, N.; Tao, J.; Zeng, Q.; Zhao, W. May the Piezoresistivity of GNP-Modified Cement Mortar Be Related to Its Fractal Structure? Fractal Fract. 2021, 5, 148. https://doi.org/10.3390/fractalfract5040148
Dang N, Tao J, Zeng Q, Zhao W. May the Piezoresistivity of GNP-Modified Cement Mortar Be Related to Its Fractal Structure? Fractal and Fractional. 2021; 5(4):148. https://doi.org/10.3390/fractalfract5040148
Chicago/Turabian StyleDang, Nanxi, Jin Tao, Qiang Zeng, and Weijian Zhao. 2021. "May the Piezoresistivity of GNP-Modified Cement Mortar Be Related to Its Fractal Structure?" Fractal and Fractional 5, no. 4: 148. https://doi.org/10.3390/fractalfract5040148
APA StyleDang, N., Tao, J., Zeng, Q., & Zhao, W. (2021). May the Piezoresistivity of GNP-Modified Cement Mortar Be Related to Its Fractal Structure? Fractal and Fractional, 5(4), 148. https://doi.org/10.3390/fractalfract5040148







