Mittag–Leffler Function as an Approximant to the Concentrated Ferrofluid’s Magnetization Curve
Abstract
:1. Introduction
2. Experimental Data and Their Processing
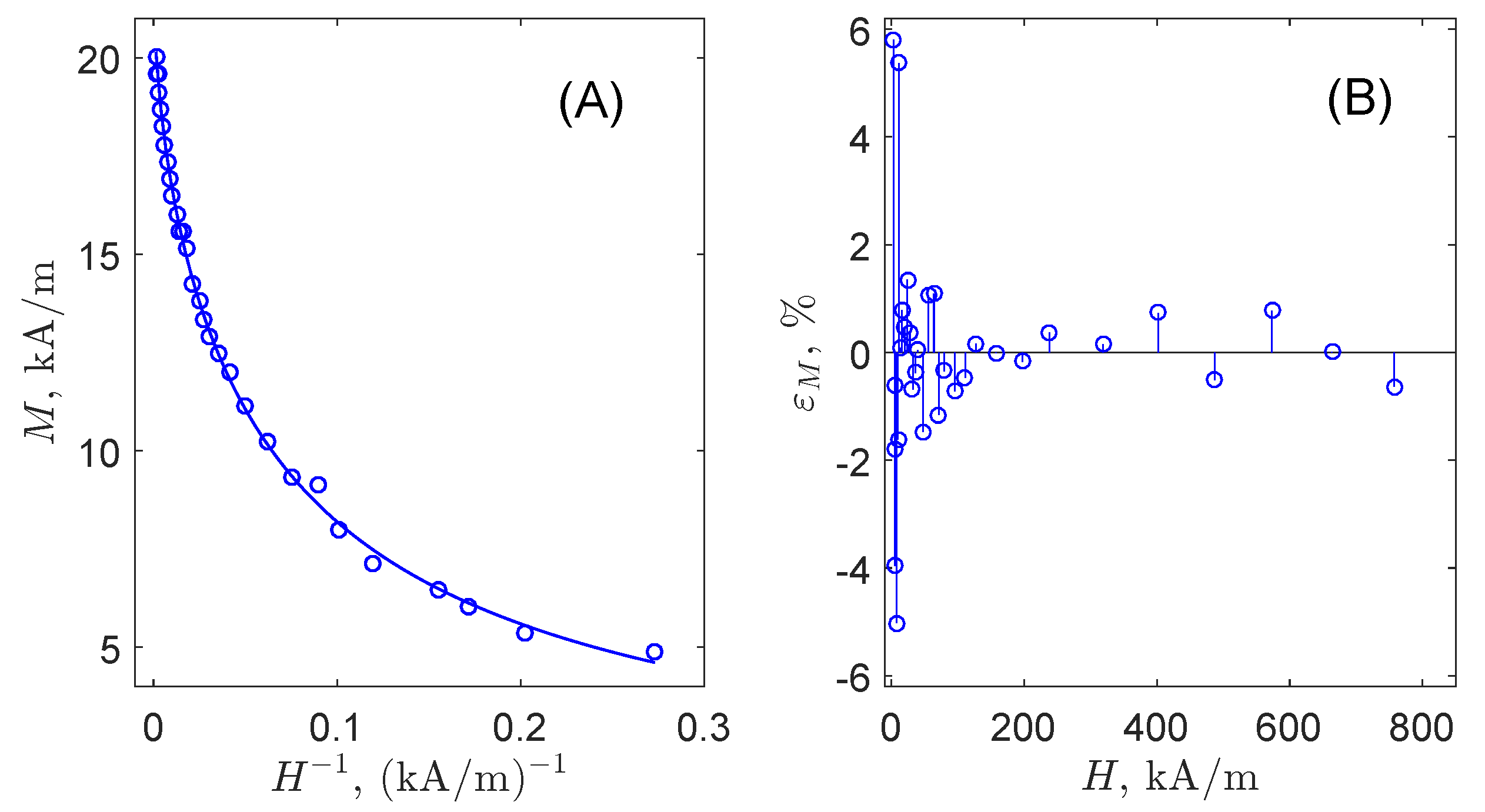
2.1. Measurements of Ferrofluid’s Magnetization
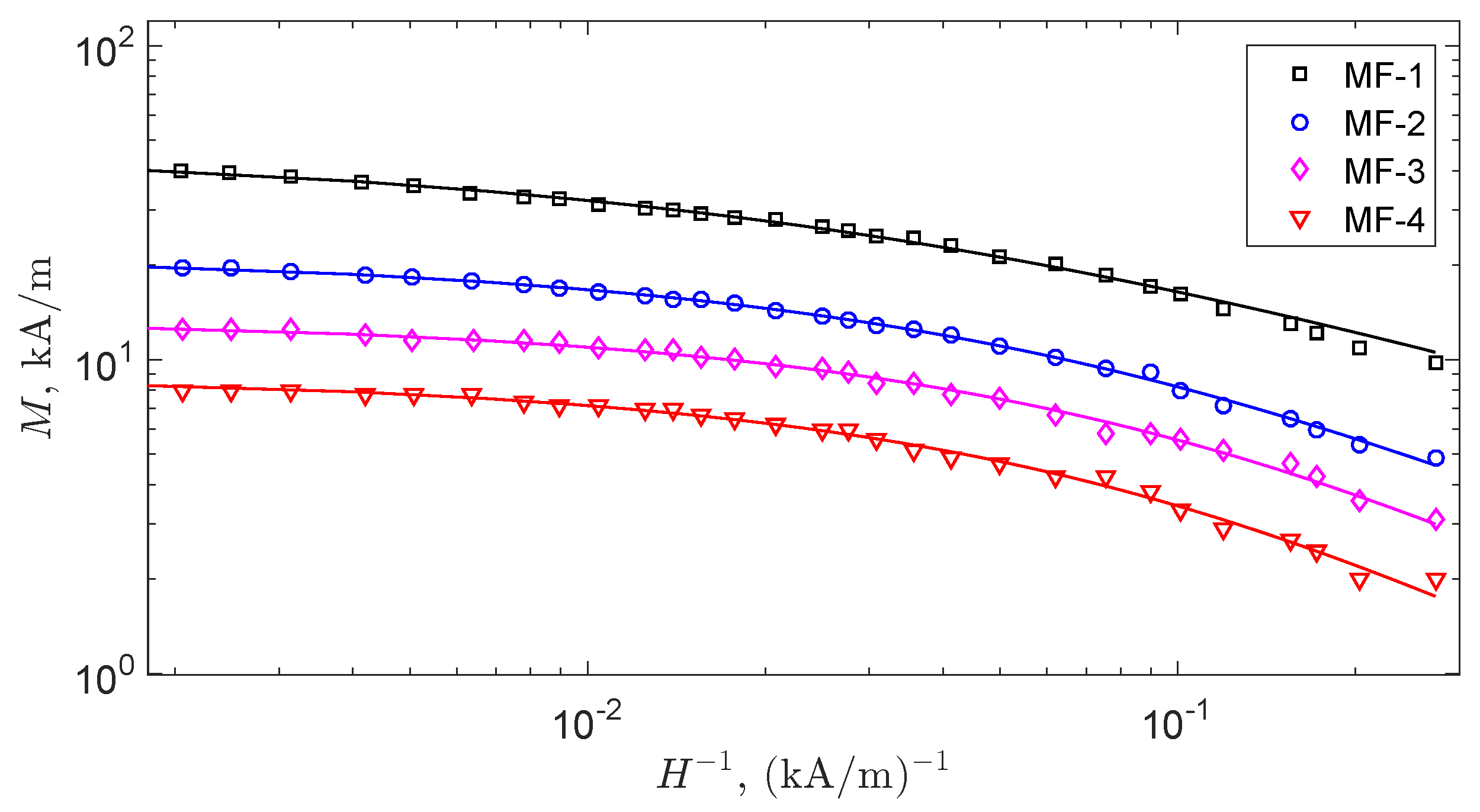
2.2. The Mittag–Leffler Function as an Approximant for the Static Magnetization Curve
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bedanta, S.; Kleemann, W. Supermagnetism. J. Phys. D Appl. Phys. 2008, 42, 013001. [Google Scholar] [CrossRef]
- Wu, K.; Tu, L.; Su, D.; Wang, J.P. Magnetic dynamics of ferrofluids: Mathematical models and experimental investigations. J. Phys. D Appl. Phys. 2017, 50, 085005. [Google Scholar] [CrossRef]
- Lebedev, A.V.; Stepanov, V.I.; Kuznetsov, A.A.; Ivanov, A.O.; Pshenichnikov, A.F. Dynamic susceptibility of a concentrated ferrofluid: The role of interparticle interactions. Phys. Rev. E 2019, 100, 032605. [Google Scholar] [CrossRef]
- Usov, N.A.; Serebryakova, O.N. Equilibrium properties of assembly of interacting superparamagnetic nanoparticles. Sci. Rep. 2020, 10, 13677. [Google Scholar] [CrossRef]
- Devi, E.C.; Singh, S.D. Tracing the Magnetization Curves: A Review on Their Importance, Strategy, and Outcomes. J. Supercond. Nov. Magn. 2020, 34, 15–25. [Google Scholar] [CrossRef]
- Dikansky, Y.I.; Ispiryan, A.G.; Arefyev, I.M.; Kunikin, S.A. Effective fields in magnetic colloids and features of their magnetization kinetics. Eur. Phys. J. E 2021, 44, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Rosensweig, R.E. Ferrohydrodynamics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Ivanov, A.O.; Kuznetsova, O.B. Magnetic properties of dense ferrofluids: An influence of interparticle correlations. Phys. Rev. E 2001, 64, 041405. [Google Scholar] [CrossRef] [PubMed]
- Solovyova, A.Y.; Elfimova, E.A.; Ivanov, A.O.; Camp, P.J. Modified mean-field theory of the magnetic properties of concentrated, high-susceptibility, polydisperse ferrofluids. Phys. Rev. E 2017, 96, 052609. [Google Scholar] [CrossRef] [Green Version]
- Rosensweig, R.E. Magnetic fluids. Annu. Rev. Fluid Mech. 1987, 19, 437–461. [Google Scholar] [CrossRef]
- Vékás, L. Ferrofluids and Magnetorheological Fluids. Adv. Sci. Technol. 2008, 54, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Cheng, R.; Miller, J.R.; Mao, L. Label-free microfluidic manipulation of particles and cells in magnetic liquids. Adv. Funct. Mater. 2016, 26, 3916–3932. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.S.; Pshenichnikov, A.F. Magnetophoresis and diffusion of colloidal particles in a thin layer of magnetic fluids. J. Magn. Magn. Mater. 2010, 322, 2575–2580. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J. Self-assembly of colloids based on microfluidics. Nanoscale 2019, 11, 16708–16722. [Google Scholar] [CrossRef]
- Gao, Q.H.; Zhang, W.M.; Zou, H.X.; Li, W.B.; Yan, H.; Peng, Z.K.; Meng, G. Label-free manipulation via the magneto-Archimedes effect: Fundamentals, methodology and applications. Mater. Horizons 2019, 6, 1359–1379. [Google Scholar] [CrossRef]
- Lee, J.H.; Nam, Y.J.; Yamane, R.; Park, M.K. Position feedback control of a nonmagnetic body levitated in magnetic fluid. J. Phys. Conf. Ser. 2009, 149, 012107. [Google Scholar] [CrossRef]
- Rehberg, I.; Richter, R.; Hartung, S.; Lucht, N.; Hankiewicz, B.; Friedrich, T. Measuring magnetic moments of polydisperse ferrofluids utilizing the inverse Langevin function. Phys. Rev. B 2019, 100, 134425. [Google Scholar] [CrossRef] [Green Version]
- Rehberg, I.; Richter, R.; Hartung, S. Graphical Magnetogranulometry of EMG909. J. Magn. Magn. Mater. 2020, 508, 166868. [Google Scholar] [CrossRef] [Green Version]
- Ryapolov, P.A.; Sokolov, E.A.; Bashtovoi, V.G.; Reks, A.G.; Postnikov, E.B. Equilibrium configurations in a magnetic fluid-based field mapping and gas pressure measuring system: Experiment and simulations. AIP Adv. 2021, 11, 015206. [Google Scholar] [CrossRef]
- Podlubny, I.; Petráš, I.; Škovránek, T. Fitting of experimental data using Mittag–Leffler function. In Proceedings of the IEEE 13th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 28–31 May 2012; pp. 578–581. [Google Scholar] [CrossRef]
- Fannin, P.C. On the use of dielectric formalism in the representation of ferrofluid data. J. Mol. Liq. 1996, 69, 39–51. [Google Scholar] [CrossRef]
- Kalmykov, Y.P. Fractional rotational Brownian motion in a uniform dc external field. Phys. Rev. E 2004, 70, 051106. [Google Scholar] [CrossRef]
- Ryapolov, P.A.; Polunin, V.M.; Postnikov, E.B.; Bashtovoi, V.G.; Reks, A.G.; Sokolov, E.A. The behaviour of gas inclusions in a magnetic fluid in a non-uniform magnetic field. J. Magn. Magn. Mater. 2020, 497, 165925. [Google Scholar] [CrossRef]
- Polunin, V.M. Acoustics of Nanodispersed Magnetic Fluids; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Mayer, A.; Vogt, E. Magnetische Messungen an Eisenamalgam zur Frage: Ferromagnetismus und Korngröße. Z. Naturforschung A 1952, 7, 334–340. [Google Scholar] [CrossRef]
- Bean, C.P.; Jacobs, I.S. Magnetic granulometry and super-paramagnetism. J. Appl. Phys. 1956, 27, 1448–1452. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Dractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Mainardi, F. Why the Mittag–Leffler function can be considered the Queen function of the Fractional Calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef]
- Podlubny, I. Fitting Data Using the Mittag–Leffler Function. Available online: https://www.mathworks.com/matlabcentral/fileexchange/32170-fitting-data-using-the-mittag-leffler-function (accessed on 30 September 2021).
- Podlubny, I. Mittag–Leffler Function. Available online: https://www.mathworks.com/matlabcentral/fileexchange/8738-mittag-leffler-function (accessed on 30 September 2021).
- Li, J.; Lin, Y.; Liu, X.; Lin, L.; Zhang, Q.; Fu, J.; Chen, L.; Li, D. The quasi-magnetic-hysteresis behavior of polydisperse ferrofluids with small coupling constant. Phys. B Condens. Matter 2012, 407, 4638–4642. [Google Scholar] [CrossRef]
- Lukashevich, M.V.; Naletova, V.A.; Turkov, V.A.; Nazarenko, A.V. A new method of measuring magnetization of a magnetic fluid not affecting its dispersive composition and calculation of volume distribution function. J. Magn. Magn. Mater. 1993, 122, 139–141. [Google Scholar] [CrossRef]
- Jin, D.; Kim, H. Magnetization of magnetite ferrofluid studied by using a magnetic balance. Bull. Korean Chem. Soc. 2013, 34, 1715–1721. [Google Scholar] [CrossRef] [Green Version]
- Sierociuk, D.; Podlubny, I.; Petras, I. Experimental evidence of variable-order behavior of ladders and nested ladders. IEEE Trans. Control Syst. Technol. 2012, 21, 459–466. [Google Scholar] [CrossRef] [Green Version]
- Myklatun, A.; Cappetta, M.; Winklhofer, M.; Ntziachristos, V.; Westmeyer, G.G. Microfluidic sorting of intrinsically magnetic cells under visual control. Sci. Rep. 2017, 7, 6942. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smolyaninov, I.I.; Smolyaninova, V.N. Fine tuning and MOND in a metamaterial “multiverse”. Sci. Rep. 2017, 7, 8023. [Google Scholar] [CrossRef] [Green Version]
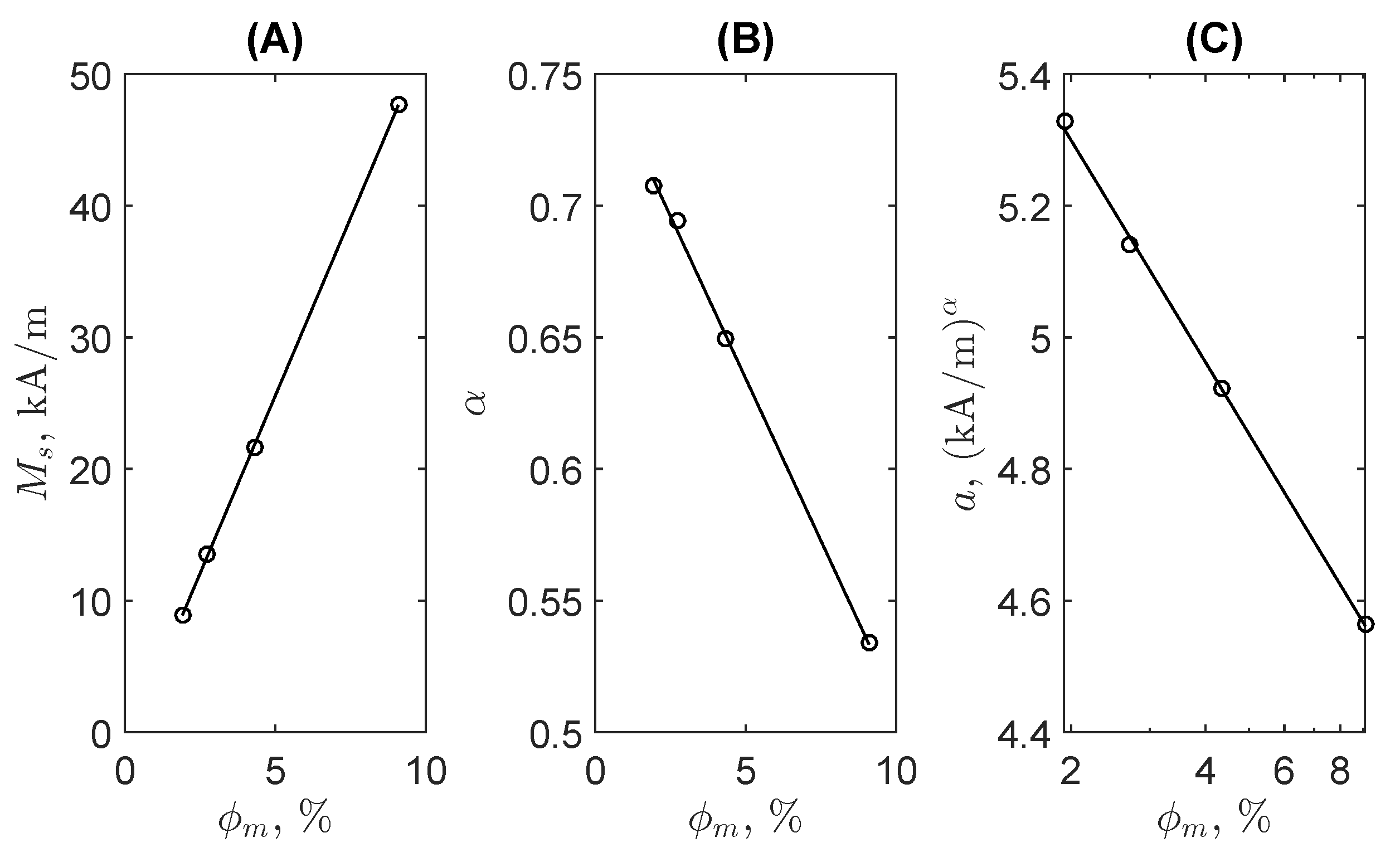
| MF-1 | MF-2 | MF-3 | MF-4 | |
|---|---|---|---|---|
| 1245 | 1058 | 952 | 870 | |
| 11.02 | 6.62 | 4.11 | 2.18 | |
| 9.08 | 4.34 | 2.70 | 1.93 | |
| 47.6 | 21.7 | 13.5 | 8.69 | |
| 4.56 | 4.92 | 4.77 | 5.33 | |
| 0.53 | 0.65 | 0.69 | 0.71 | |
| AAD, % | 2.1 | 1.2 | 2.0 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryapolov, P.A.; Postnikov, E.B. Mittag–Leffler Function as an Approximant to the Concentrated Ferrofluid’s Magnetization Curve. Fractal Fract. 2021, 5, 147. https://doi.org/10.3390/fractalfract5040147
Ryapolov PA, Postnikov EB. Mittag–Leffler Function as an Approximant to the Concentrated Ferrofluid’s Magnetization Curve. Fractal and Fractional. 2021; 5(4):147. https://doi.org/10.3390/fractalfract5040147
Chicago/Turabian StyleRyapolov, Petr A., and Eugene B. Postnikov. 2021. "Mittag–Leffler Function as an Approximant to the Concentrated Ferrofluid’s Magnetization Curve" Fractal and Fractional 5, no. 4: 147. https://doi.org/10.3390/fractalfract5040147
APA StyleRyapolov, P. A., & Postnikov, E. B. (2021). Mittag–Leffler Function as an Approximant to the Concentrated Ferrofluid’s Magnetization Curve. Fractal and Fractional, 5(4), 147. https://doi.org/10.3390/fractalfract5040147







