Reduced-Order Legendre–Galerkin Extrapolation Method with Scalar Auxiliary Variable for Time-Fractional Allen–Cahn Equation

Abstract

This paper presents a reduced-order Legendre–Galerkin extrapolation (ROLGE) method combined with the scalar auxiliary variable (SAV) approach (ROLGE-SAV) to numerically solve the time-fractional Allen–Cahn equation (tFAC). First, the nonlinear term is linearized via the SAV method, and the linearized system derived from this SAV-based linearization is time-discretized using the shifted fractional trapezoidal rule (SFTR), resulting in a semi-discrete unconditionally stable scheme (SFTR-SAV). The scheme is then fully discretized by incorporating Legendre–Galerkin (LG) spatial discretization. To enhance computational efficiency, a proper orthogonal decomposition (POD) basis is constructed from a small set of snapshots of the fully discrete solutions on an initial short time interval. A reduced-order LG extrapolation SFTR-SAV model (ROLGE-SFTR-SAV) is then implemented over a subsequent extended time interval, thereby avoiding redundant computations. Theoretical analysis establishes the stability of the reduced-order scheme and provides its error estimates. Numerical experiments validate the effectiveness of the proposed method and the correctness of the theoretical results.

1. Introduction

The Allen–Cahn (AC) equation stands as one of the core phase-field models for describing phenomena such as phase separation and interface evolution, and it finds extensive applications in fields such as materials science, fluid mechanics, and biological modeling. It is essentially a gradient flow driven by a double-well potential and nonlinear terms. In the AC equation, replacing the first-order time derivative with a fractional derivative (such as the Caputo or Riemann–Liouville derivative) leverages the memory (non-locality) and heredity properties inherent to fractional derivatives, which enable the description of physical processes characterized by anomalous diffusion, memory effects, and viscoelasticity, for example, in describing more complex phase separation dynamics and interface roughening in certain polymer materials [1,2], amorphous materials [3], and porous media [4,5], and in characterizing the viscoelastic interface behaviors in some non-Newtonian fluids [6,7]. In this work, we are interested in the tFAC equation [8]

$$\left\{\begin{array}{cc}{\partial }_t^{\alpha }u=\Delta u-f\left(u\right),& x\in \Omega ,0<t\le T,\\ u(x,0)=u_0,& x\in \Omega ,\end{array}\right.$$

(1)

where $\Omega =[-1,1],$ and the Caputo derivative ${\partial }_t^{\alpha }u\left(t\right)$ is defined by

$${\partial }_t^{\alpha }u\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_0^t{\displaystyle \frac{u^{\prime }\left(v\right)}{{(t-v)}^{\alpha }}}dv,$$

with $\Gamma (·)$ denoting the Gamma function. Here, the constant $\epsilon$ represents the interfacial thickness, $F\left(u\right)={\displaystyle \frac{1}{4{\epsilon }^2}}{(u^2-1)}^2,f\left(u\right)=F^{\prime }\left(u\right)={\displaystyle \frac{1}{{\epsilon }^2}}(u^3-u)$ represents the nonlinear bulk force. It is well-known that this problem satisfies the following energy law:

$${\partial }_t^{\alpha }u=-{\displaystyle \frac{\delta E}{\delta u}},\hspace{1em}x\in \Omega ,0<t\le T,$$

(2)

where

$$E\left(u\right)={\int }_{\Omega }({\displaystyle \frac{1}{2}}{|\nabla u|}^2+F\left(u\right))dx.$$

(3)

The tFAC equation has attracted extensive research in both theoretical and numerical fields, and numerous methods have been proposed for its numerical solution. The main concerns in designing numerical methods are computational complexity and stability. Currently, a great deal of research effort has been devoted to the development of stable, low-cost, and efficient time-stepping schemes. Broadly, the existing numerical techniques can be categorized into fully implicit methods [9,10], semi-implicit methods [11,12,13], stabilized linearly implicit methods [14], exponential time discretization methods [15], and SAV methods [16,17,18].

To linearize the nonlinear terms, Jie Shen proposed the SAV approach for gradient flows in [19]. In [8], by introducing some auxiliary constants and variables, the energy functional (3) is reformulated into the following form

$$E\left(u\right)={\int }_{\Omega }({\displaystyle \frac{1}{2}}{|\nabla u|}^2+{\displaystyle \frac{a}{2{\epsilon }^2}}{u}^2+{\displaystyle \frac{{(u^2-1-a)}^2}{4{\epsilon }^2}}-{\displaystyle \frac{a^2+2a}{4{\epsilon }^2}})dx,$$

(4)

where $a>0$ is a constant. The SAV method is a powerful tool for handling nonlinear terms in gradient flows and ensuring unconditional energy stability, which has achieved great success in integer-order equations. In recent years, the SAV framework has been systematically extended to the numerical solution of fractional differential equations. Ref. [16] proposes a high-order and efficient scheme for the time-fractional AC equation, which is based on the L1 discretization method for the time-fractional derivative and the SAV method. This scheme is more robust than existing methods, and its efficiency is not restricted by the specific form of the nonlinear potential. In [17], the authors consider a class of time-fractional phase-field models including the AC equation and the Cahn–Hilliard (CH) equation. Based on the exponential scalar auxiliary variable (ESAV) approach, two explicit time-stepping schemes are constructed, where the fractional derivatives are discretized via the $L1$ and $L1+$ formulas, respectively. Finally, the accuracy and efficiency of the proposed methods are verified through several numerical experiments. For the numerical solution of time-fractional phase-field models, a second-order numerical scheme is proposed in [18]. This scheme employs the fractional backward difference formula to approximate the time-fractional derivative and utilizes the extended SAV method to handle the nonlinear terms therein. The authors have proven that this numerical scheme possesses the energy dissipation property, and the relevant discussion covers the time-fractional AC equation, time-fractional CH equation, and time-fractional molecular beam epitaxy model. Similarly, we can linearize Equation (1) using the SAV method. It is straightforward to verify that the reformulated free energy (4) is mathematically equivalent to the original definition (3) for any constant a. The gradient flow corresponding to the free energy (4), along with the equation for the auxiliary function, is expressed as

$$\left\{\begin{array}{cc}{\partial }_t^{\alpha }u=\Delta u-{\displaystyle \frac{a}{{\epsilon }^2}}u-Q\left(u\right)s\left(t\right),& x\in \Omega , 0<t\le T,\\ s_t={\displaystyle \frac{1}{2}}(Q\left(u\right),u_t),& x\in \Omega , 0<t\le T,\end{array}\right.$$

(5)

with

$$E_1\left(u\right)={\int }_{\Omega }{\displaystyle \frac{{(u^2-1-a)}^2}{4{\epsilon }^2}}dx+1, s\left(t\right)=\sqrt{E_1\left(u\right)}, Q\left(u\right)={\displaystyle \frac{f\left(u\right)-\frac{a}{{\epsilon }^2}u}{\sqrt{E_1\left(u\right)}}},$$

and the initial conditions

$$\left\{\begin{array}{cc}u(x,0)=u_0,& x\in \Omega ,\\ s_0=\sqrt{E_1\left(u_0\right)},& x\in \Omega ,\\ u=0,& x\in \partial \Omega .\end{array}\right.$$

(6)

Thus, problem (5) constitutes a reformulation of (1) and is mathematically equivalent to it. We will work with this reformulated system (5) because it facilitates the derivation of an unconditionally energy-stable and computationally efficient scheme.

Although the SAV method successfully converts nonlinear terms into a linear system, the discretization of tFAC remains an independent and critical challenge, whose difficulty is not eliminated by the application of the SAV method. To discretize the resulting linearized system (5), we adopt the fractional trapezoidal rule with a special shift (SFTR $- {\displaystyle \frac{1}{2}}$) (i.e., SFTR with the shift parameter as ${\displaystyle \frac{1}{2}}$) scheme [20,21,22] in the temporal direction to handle the fractional derivative, thereby obtaining the SFTR-SAV formulation. This SFTR-SAV discretization scheme not only has unconditional stability but, more importantly, its mathematical structure facilitates the subsequent rigorous error analysis. Among them, SFTR $- {\displaystyle \frac{1}{2}}$ can effectively deal with the nonlocal historical dependence caused by the time-fractional derivative, while ensuring that the discrete scheme can preserve the energy decay law and maximum principle of the original problem during long-time integration. In [20], the authors propose a second-order accurate formula for the SFTR, reveal its unique characteristics that most other second-order formulas do not possess, and finally investigate high-order methods on uniform grids that can simultaneously preserve the two intrinsic properties of the tFAC equation, namely energy decay and the maximum principle. Spatially, the tFAC equation can become highly stiff due to the small interfacial parameter $\epsilon$ and the nonlinearity, leading to extremely high computational costs, particularly in high dimensions. To overcome this challenge and significantly enhance computational efficiency, the reduced-order method (ROM) can be adopted. Its goal is to reduce the total number of unknowns in the temporal-spatial discretization of the tFAC equation while ensuring theoretical accuracy. The motivation for this study stems from the success of ROMs as powerful tools for numerical simulation in modern engineering [23,24,25,26,27,28]. It is particularly worth noting that this method entails redundant computations, as it constructs a POD basis from classical approximate solutions across the entire time interval $[0,T]$ and subsequently performs iterative calculations to obtain reduced-order approximate solutions over the very same interval $[0,T]$. To reduce redundant computations and save storage space, thereby further improving computational efficiency, Luo and colleagues proposed the reduced-order extrapolation (ROE) method based on POD.

Since 2013, Luo and colleagues proposed a series of ROE methods based on POD numerical methods, including ROE finite element method, ROE finite difference method, ROE finite volume element method, and ROE natural boundary element method. These methods effectively reduce the computational load by eliminating redundancy while preserving the properties of the original solution space, and have been successfully applied to solve various partial differential equations such as parabolic equation [29], Stokes equation [30], heat equations [31], viscoelastic wave equations [32,33], hyperbolic equations [34,35], Sobolev equations [36], Boussinesq equations [37], and Navier–Stokes equations [38]. The core idea is to construct a POD basis using the classical solutions from a short initial time interval $[0,T_0]$ (with $T_0\ll T$), and then compute the ROE solution on the remaining interval $[T_0,T]$, thereby eliminating redundant computations.

The numerical solution of the tFAC equation poses multiple challenges: the inherent nonlocality of fractional derivatives leads to high storage and computational complexity; the nonlinear double-well potential term induces strong nonlinear coupling; the initial weak singularity of the solution impairs numerical accuracy; and the phase separation interface requires high spatial resolution. All these factors result in extremely high computational costs for simulating the full-order model. To the best of our knowledge, no prior study has investigated the application of the POD-based ROE method to the tFAC equation.

To address the aforementioned challenges, this work makes the following key contributions:

• We propose, for the first time, a ROLGE-SAV method for the tFAC equation. The framework integrates:

  –

  The SAV method for linearizing the nonlinear term and ensuring unconditional energy stability.

  –

  A LG spectral method for high-resolution spatial discretization.

• We develop a computationally efficient POD-based reduced-order algorithm that fundamentally avoids the redundancy common in conventional approaches. Instead of collecting snapshots over the entire time domain $[0,T]$, our algorithm constructs the POD basis using solutions from only a short initial interval $[0,T_0]$ (with $T_0\ll T$). The ROLGE-SFTR-SAV is then employed to extrapolate the solution efficiently over the extended interval $[T_0,T]$, leading to significant savings in both computation time and storage.
• We establish a complete theoretical foundation, including:

  –

  Proofs of unconditional energy stability for both SFTR-SAV and the LG-SFTR-SAV schemes.

  –

  Detailed error estimates for the SFTR-SAV, LG-SFTR-SAV, and ROLGE-SFTR-SAV models. These estimates provide practical guidance for selecting critical parameters such as the POD basis rank d and the snapshot interval length $T_0$.

• Extensive experiments are conducted to validate the theory and demonstrate efficiency.

  –

  The scheme achieves second-order temporal convergence and spectral spatial convergence.

  –

  The POD eigenvalues exhibit rapid exponential decay, justifying the low-dimensional approximation.

  –

  The ROLGE-SFTR-SAV scheme achieves a significant reduction in CPU time compared to the full-order model, while maintaining comparable numerical accuracy.

The structure of the remaining paper is as follows. In Section 2, we present the SFTR-SAV schemes for temporal discretization. For the reformulated tFAC equation, we also derive the property that the energy of the SAV scheme is monotonically non-increasing over time. In Section 3, we introduce the full discretization of the tFAC equation and establish the error estimates for the LG-SFTR-SAV scheme. In Section 4, we construct the reduced-order model, derive its stability properties, and perform the error analysis of the ROLGE-SFTR-SAV model. We present several numerical examples to validate the theoretical findings in Section 5. Finally, we summarize the key conclusions in Section 6.

We adopt the following notations throughout this paper. The standard Sobolev spaces and their norms are denoted by $H^m(\Omega )$ and ${\parallel ·\parallel }_m$ ($m=0,\pm 1,\dots$), respectively [39]. Specifically, for the space $L^2(\Omega )=H^0(\Omega )$, we use $\parallel ·\parallel$ for its norm and $(·,·)$ for its inner product. Additionally, the norm of the space $L^{\infty }(\Omega )$ is denoted by ${\parallel ·\parallel }_{\infty }$.

In the temporal direction, we will adopt the SFTR scheme to discretize Equation (5), resulting in the SFTR-SAV scheme. On this basis, we will further provide a rigorous proof for the energy non-increasing property and error estimation of this scheme.

2. SFTR-SAV Scheme and Error Estimate

2.1. Kernel Properties of the SFTR Formula

Consider a uniform temporal grid on $[0,T]$ with mesh size $\tau ={\displaystyle \frac{T}{M}}$, defined by nodal points $t_n=n\tau$ for $n=0,\dots ,M$. Let $u^n=u(x,t_n)$ denote the solution at time $t_n$. The SFTR $- {\displaystyle \frac{1}{2}}$ approximation to the Caputo fractional derivative ${\partial }_t^{\alpha }u$ at intermediate time $t_{n-{\displaystyle \frac{1}{2}}}$ takes the form [20,21,22]

$${\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}u={\tau }^{-\alpha }\sum _{m=0}^n{\varpi }_m(u^{n-m}-u^0),$$

(7)

where the coefficients ${\varpi }_m$ are defined via the generating function

$$\varpi \left(\zeta \right)=\sum _{m=0}^{\infty }{\varpi }_m{\zeta }^m={\left[{\displaystyle \frac{1-\zeta }{\frac{1}{2}(1+\zeta )+\frac{1}{2\alpha }(1-\zeta )}}\right]}^{\alpha },$$

or can be computed directly using the recurrence formula

$${\varpi }_0={\left({\displaystyle \frac{2\alpha }{\alpha +1}}\right)}^{\alpha },\hspace{1em}{\varpi }_1=-\alpha {\left({\displaystyle \frac{2\alpha }{\alpha +1}}\right)}^{\alpha +1},$$

$${\varpi }_m={\displaystyle \frac{2\alpha }{m(\alpha +1)}}\left\{[{\displaystyle \frac{1}{\alpha }}(m-1)-\alpha ]{\varpi }_{m-1}+{\displaystyle \frac{\alpha -1}{2\alpha }}(m-2){\varpi }_{m-2}\right\},m\ge 2.$$

Lemma 1

([20]). For weights ${\varpi }_m$ defined in (7), the following properties hold

(i) 

${\varpi }_0>0$ and ${\varpi }_m<0$ for all $m\ge 1$.

(ii) 

${\varpi }_m>{\varpi }_{m-1}$ for all $m\ge 2$.

(iii) 

${\displaystyle \sum _{m=0}^n}{\varpi }_m>0$ for any $n\ge 0$.

Discretizing the continuous-time system (5) using the SFTR $- {\displaystyle \frac{1}{2}}$ scheme (7) yields the following time-discrete system.

Problem 1.

For $n\ge 1$, find $U^n\in H^m(\Omega )$ satisfying the following equations

$$({\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}U,\upsilon )=(\Delta U^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{U}^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}},\upsilon ),$$

(8a)

$${\beta }_{\tau }{S}^n={\displaystyle \frac{1}{2}}(Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }{U}^n),$$

(8b)

$$U^n=0,\hspace{1em}\forall x\in \partial \Omega ,$$

(8c)

where $U^{n-{\displaystyle \frac{1}{2}}}={\displaystyle \frac{U^n+U^{n-1}}{2}},{\mathbb{U}}^{n-1}={\displaystyle \frac{3U^{n-1}-U^{n-2}}{2}},{\beta }_{\tau }{U}^n={\displaystyle \frac{U^n-U^{n-1}}{\tau }}.$

The following sequence plays a fundamental role in establishing the energy decay property and subsequent error estimates. In [20], the sequence ${\left\{{\theta }_m\right\}}_{m=0}^{\infty }$ is defined as

$$\sum _{m=0}^{\infty }{\theta }_m{\zeta }^m={\displaystyle \frac{1-\zeta }{\varpi \left(\zeta \right)}}=:\theta \left(\zeta \right),\hspace{1em}\mathit{for} \left|\zeta \right|<1.$$

(9)

Lemma 2

([20]). The sequence ${\left\{{\theta }_m\right\}}_{m=0}^{\infty }$, defined in (9), can be computed via the following recurrence relation

$${\theta }_m={\displaystyle \frac{2\alpha }{m(1+\alpha )}}\left\{\left[{\displaystyle \frac{1}{\alpha }}(m-1)-{\displaystyle \frac{1-\alpha }{2\alpha }}(2\alpha +1)\right]{\theta }_{m-1}+{\displaystyle \frac{1-\alpha }{2\alpha }}(3-m){\theta }_{m-2}\right\},m\ge 2,$$

(10)

initialized by

$${\theta }_0={\left({\displaystyle \frac{\alpha +1}{2\alpha }}\right)}^{\alpha },\hspace{1em}{\theta }_1={\displaystyle \frac{(\alpha -1)(2\alpha +1)}{\alpha +1}}{\theta }_0.$$

Lemma 3

([20]). For weights ${\theta }_m$ defined in (9), the following properties hold

(i) 

${\theta }_0>0$ and ${\theta }_m<0$ for all $m\ge 1$,

(ii) 

${\displaystyle \sum _{m=0}^n}{\theta }_m>0$ for any $n\ge 0$.

In [20], another sequence ${\left\{{\kappa }_m\right\}}_{m=0}^{\infty }$ is defined as,

$$\sum _{m=0}^{\infty }{\kappa }_m{\zeta }^m={\displaystyle \frac{\theta \left(\zeta \right)}{1-\zeta }}={\displaystyle \frac{1}{\varpi \left(\zeta \right)}}=:\kappa \left(\zeta \right), \mathrm{for} \left|\zeta \right|<1,$$

(11)

$${\kappa }_m=\sum _{i=0}^m{\theta }_i, {\kappa }_0>{\kappa }_1>{\kappa }_2>\dots >{\kappa }_n>\dots >0.$$

(12)

2.2. Discrete Energy Dissipation Law of the SFTR-SAV Scheme

Define $W^{n-{\displaystyle \frac{1}{2}}}=\Delta U^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{U}^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}}$.

Lemma 4.

The SFTR-SAV scheme (8) is unconditionally stable and satisfies the following discrete energy dissipation law

$$\mathbb{E}\left(U^n\right)-\mathbb{E}\left(U^{n-1}\right)\le 0,$$

(13)

where

$$\mathbb{E}\left(U^n\right)={\displaystyle \frac{1}{2}}\parallel \nabla U^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel U^n{\parallel }^2+|S^n{|}^2+{\displaystyle \frac{{\tau }^{\alpha }}{2}}\sum _{j=1}^n{\kappa }_{n-j}{\parallel W^{j-{\displaystyle \frac{1}{2}}}\parallel }^2.$$

Proof. 

Rewrite Equation (8a) as

$$({\tau }^{-\alpha }\sum _{m=0}^n{\varpi }_m(U^{n-m}-U^0),\upsilon )=(W^{n-{\displaystyle \frac{1}{2}}},\upsilon ).$$

(14)

Multiplying Equation (14) by ${\tau }^{\alpha -1}{\theta }_{n-j}$, summing over $j=1,\dots ,n$, and then applying an index transformation yields,

$${\tau }^{-1}\sum _{j=1}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_m(U^{j-m}-U^0)={\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{W}^{j-{\displaystyle \frac{1}{2}}}$$

(15)

$$\begin{array}{cc}\hfill {\tau }^{-1}\sum _{j=1}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_m(U^{j-m}-U^0)& ={\tau }^{-1}\sum _{j=0}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_{j-m}(U^m-U^0)\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(U^m-U^0)\sum _{j=m}^n{\varpi }_{j-m}{\theta }_{n-j}\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(U^m-U^0)\sum _{j=0}^{n-m}{\varpi }_j{\theta }_{n-j-m}\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(U^{n-m}-U^0){\mathbb{C}}_m,\hfill \end{array}$$

(16)

where ${\mathbb{C}}_m={\displaystyle \sum _{j=0}^m}{\varpi }_j{\theta }_{m-j},$ which corresponds to the m-th coefficient in the series expansion of the product $\varpi \left(\zeta \right)\theta \left(\zeta \right)$. From Equation (9), the convolution coefficients satisfy

$${\mathbb{C}}_m=\left\{\begin{array}{cc}1\hfill & m=0,\hfill \\ -1\hfill & m=1,\hfill \\ 0\hfill & m\ge 2.\hfill \end{array}\right.$$

We then have

$$({\displaystyle \frac{U^n-U^{n-1}}{\tau }},\upsilon )=({\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{W}^{j-{\displaystyle \frac{1}{2}}},\upsilon ).$$

(17)

Taking $\upsilon =W^{n-{\displaystyle \frac{1}{2}}}$ in (17), we obtain

$$\begin{array}{cc}\hfill & {\tau }^{-\alpha }\left[(\nabla (U^n-U^{n-1}),\nabla U^{n-{\displaystyle \frac{1}{2}}})+{\displaystyle \frac{a}{{\epsilon }^2}}(U^n-U^{n-1},U^{n-{\displaystyle \frac{1}{2}}})+(Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}},U^n-U^{n-1})\right]\hfill \\ & =-\left(\sum _{j=1}^n{\theta }_{n-j}{W}^{j-{\displaystyle \frac{1}{2}}},W^{n-{\displaystyle \frac{1}{2}}}\right).\hfill \end{array}$$

(18)

Multiplying both sides of (8b) by $2S^{n-{\displaystyle \frac{1}{2}}}$ yields,

$$|S^n{|}^2-{\left|S^{n-1}\right|}^2=(Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}},U^n-U^{n-1}).$$

(19)

Combining (18) and (19) gives,

$$\begin{array}{cc}\hfill & {\tau }^{-\alpha }\left[{\displaystyle \frac{1}{2}}(\parallel \nabla U^n{\parallel }^2-\parallel \nabla U^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel U^n{\parallel }^2-\parallel U^{n-1}{\parallel }^2)+|S^n{|}^2-{\left|S^{n-1}\right|}^2\right]\hfill \\ & =-\left(\sum _{j=1}^n{\theta }_{n-j}{W}^{j-{\displaystyle \frac{1}{2}}},W^{n-{\displaystyle \frac{1}{2}}}\right).\hfill \end{array}$$

(20)

From the relation ${\theta }_j={\kappa }_j-{\kappa }_{j-1}$ established in (12), where ${\theta }_j<0$ for $j\ge 1$ and ${\theta }_0={\kappa }_0>0$, it follows that

$$\left(\sum _{j=1}^n{\theta }_{n-j}{W}^{j-{\displaystyle \frac{1}{2}}},W^{n-{\displaystyle \frac{1}{2}}}\right)\ge {\displaystyle \frac{1}{2}}{\kappa }_{n-1}\parallel W^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\kappa }_{n-j}\parallel W^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-{\displaystyle \frac{1}{2}}\sum _{j=1}^{n-1}{\kappa }_{n-j-1}{\parallel W^{j-{\displaystyle \frac{1}{2}}}\parallel }^2.$$

(21)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel \nabla U^n{\parallel }^2-\parallel \nabla U^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel U^n{\parallel }^2-\parallel U^{n-1}{\parallel }^2)+|S^n{|}^2-{\left|S^{n-1}\right|}^2\hfill \\ & +{\displaystyle \frac{{\tau }^{\alpha }}{2}}\sum _{j=1}^n{\kappa }_{n-j}\parallel W^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-{\displaystyle \frac{{\tau }^{\alpha }}{2}}\sum _{j=1}^{n-1}{\kappa }_{n-j-1}{\parallel W^{j-{\displaystyle \frac{1}{2}}}\parallel }^2\le 0.\hfill \end{array}$$

(22)

□

Lemma 5.

For the solution $U^n$ of the discrete problem (8), there exists a positive constant C such that

$$\parallel {\beta }_{\tau }{U}^n\parallel \le C, 1\le n\le M.$$

Proof. 

The convolution quadrature theory [40] guarantees ${\tau }^{\alpha -1}{\displaystyle \sum _{j=1}^n}{\theta }_{n-j}{W}^{j-{\displaystyle \frac{1}{2}}}$ approximates ${\partial }_t^{\alpha }U(t_{n-{\displaystyle \frac{1}{2}}})$ with second-order accuracy under mild conditions. Let

$${\gamma }^{n-{\displaystyle \frac{1}{2}}}={\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{W}^{j-{\displaystyle \frac{1}{2}}}-{\partial }_t^{\alpha }U(t_{n-{\displaystyle \frac{1}{2}}}),$$

Equation (17) can be rewritten in the following form

$$({\beta }_{\tau }{U}^n,\upsilon )+(\nabla U^{n-{\displaystyle \frac{1}{2}}},\nabla \upsilon )+({\displaystyle \frac{a}{{\epsilon }^2}}{U}^{n-{\displaystyle \frac{1}{2}}},\upsilon )=(-Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}},\upsilon )+({\gamma }^{n-{\displaystyle \frac{1}{2}}},\upsilon ).$$

(23)

Taking the difference of (23) for n and $n-1$, we have

$$\begin{array}{cc}\hfill ({\beta }_{\tau }{U}^n-{\beta }_{\tau }{U}^{n-1},\upsilon )& +(\nabla U^{n-{\displaystyle \frac{1}{2}}}-\nabla U^{n-{\displaystyle \frac{3}{2}}},\nabla \upsilon )+{\displaystyle \frac{a}{{\epsilon }^2}}(U^{n-{\displaystyle \frac{1}{2}}}-U^{n-{\displaystyle \frac{3}{2}}},\upsilon )=\hfill \\ & (-Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}},\upsilon )+(Q\left({\mathbb{U}}^{n-2}\right)S^{n-{\displaystyle \frac{3}{2}}},\upsilon )+({\gamma }^{n-{\displaystyle \frac{1}{2}}},\upsilon )\hfill \\ & -({\gamma }^{n-{\displaystyle \frac{3}{2}}},\upsilon ).\hfill \end{array}$$

(24)

Similarly, it follows from (8b)

$$S^{n-{\displaystyle \frac{1}{2}}}-S^{n-{\displaystyle \frac{3}{2}}}={\displaystyle \frac{\tau }{4}}[(Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }{U}^n)+(Q\left({\mathbb{U}}^{n-2}\right),{\beta }_{\tau }{U}^{n-1})].$$

(25)

Taking $\upsilon ={\beta }_{\tau }{U}^n+{\beta }_{\tau }{U}^{n-1}$ in (24) and using (25), we obtain

$$\begin{array}{cc}\hfill & \parallel {\beta }_{\tau }{U}^n{\parallel }^2-\parallel {\beta }_{\tau }{U}^{n-1}{\parallel }^2+{\displaystyle \frac{\tau }{2}}\parallel {\beta }_{\tau }\nabla U^n+{\beta }_{\tau }\nabla U^{n-1}{\parallel }^2+{\displaystyle \frac{a\tau }{2{\epsilon }^2}}{\parallel {\beta }_{\tau }{U}^n+{\beta }_{\tau }{U}^{n-1}\parallel }^2\hfill \\ & =-(S^{n-{\displaystyle \frac{1}{2}}}-S^{n-{\displaystyle \frac{3}{2}}})(Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }{U}^n+{\beta }_{\tau }{U}^{n-1})\hfill \\ & -S^{n-{\displaystyle \frac{3}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}^{n-2}\right),{\beta }_{\tau }{U}^n+{\beta }_{\tau }{U}^{n-1})\hfill \\ & \le {\displaystyle \frac{\tau }{4}}[(Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }{U}^n)+(Q\left({\mathbb{U}}^{n-2}\right),{\beta }_{\tau }{U}^{n-1})](Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }{U}^n+{\beta }_{\tau }{U}^{n-1})\hfill \\ & +S^{n-{\displaystyle \frac{3}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}^{n-2}\right),{\beta }_{\tau }{U}^n+{\beta }_{\tau }{U}^{n-1})+({\gamma }^{n-{\displaystyle \frac{1}{2}}},{\beta }_{\tau }{U}^n+{\beta }_{\tau }{U}^{n-1})\hfill \\ & +({\gamma }^{n-{\displaystyle \frac{3}{2}}},{\beta }_{\tau }{U}^n+{\beta }_{\tau }{U}^{n-1}).\hfill \end{array}$$

(26)

Omitting the positive third and fourth terms on the left-hand side, we obtain

$$\parallel {\beta }_{\tau }{U}^n{\parallel }^2-\parallel {\beta }_{\tau }{U}^{n-1}{\parallel }^2\le C\tau \parallel {\beta }_{\tau }{U}^n{\parallel }^2+C\tau {\parallel {\beta }_{\tau }{U}^{n-1}\parallel }^2.$$

(27)

Summing (27) for $n=2,\dots ,M$ and applying the discrete Grönwall inequality yields the desired bound. □

2.3. Temporal Error Estimate

In this section, we define the error terms as $e^n=U^n-u^n,e_s^n=S^n-s^n.$

Rewrite Equation (5) in the following form

$$\begin{array}{cc}\hfill {\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}u=& \Delta u^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{u}^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathfrak{u}}^{n-1}\right)s^{n-{\displaystyle \frac{1}{2}}}-P_1+P_2+P_3+P_4,\hfill \end{array}$$

(28a)

$$\begin{array}{cc}\hfill {\beta }_{\tau }{s}^n& ={\displaystyle \frac{1}{2}}(Q\left({\mathfrak{u}}^{n-1}\right),{\beta }_{\tau }{u}^n)-K^n+{\displaystyle \frac{1}{2}}(Q\left({\mathfrak{u}}^{n-1}\right),{\sigma }^n)+{\displaystyle \frac{1}{2}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\sigma }^n)\hfill \\ & +{\displaystyle \frac{1}{2}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\beta }_{\tau }{u}^n),\hfill \end{array}$$

(28b)

where $P_1={\partial }_t^{\alpha }u-{\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}u,K^n=s_t-{\beta }_{\tau }{s}^n,{\sigma }^n=u_t-{\beta }_{\tau }{u}^n,{\mathfrak{u}}^{n-1}={\displaystyle \frac{3u^{n-1}-u^{n-2}}{2}},$$P_2=\Delta [u(t_{n-{\displaystyle \frac{1}{2}}})-u^{n-{\displaystyle \frac{1}{2}}}],$ $P_3={\displaystyle \frac{a}{{\epsilon }^2}}(u^{n-{\displaystyle \frac{1}{2}}}-u(t_{n-{\displaystyle \frac{1}{2}}})),P_4=-Q(u(t_{n-{\displaystyle \frac{1}{2}}}))s(t_{n-{\displaystyle \frac{1}{2}}})+Q({\mathfrak{u}}^{n-1})s^{n-{\displaystyle \frac{1}{2}}},$$u^{n-{\displaystyle \frac{1}{2}}}={\displaystyle \frac{u^n+u^{n-1}}{2}}.$

Taking the inner product of Equation (28), we obtain

$$\begin{array}{cc}\hfill ({\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}u,\upsilon )=& (\Delta u^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{u}^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathfrak{u}}^{n-1}\right)s^{n-{\displaystyle \frac{1}{2}}}-P_1,\upsilon )+(P_2+P_3+P_4,\upsilon ),\hfill \end{array}$$

(29a)

$$\begin{array}{cc}\hfill {\beta }_{\tau }{s}^n& ={\displaystyle \frac{1}{2}}(Q\left({\mathfrak{u}}^{n-1}\right),{\beta }_{\tau }{u}^n)-K^n+{\displaystyle \frac{1}{2}}(Q\left({\mathfrak{u}}^{n-1}\right),{\sigma }^n)+{\displaystyle \frac{1}{2}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\sigma }^n)\hfill \\ & +{\displaystyle \frac{1}{2}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\beta }_{\tau }{u}^n).\hfill \end{array}$$

(29b)

Subtracting (29) from (8), we have

$$({\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}e,\upsilon )=(\Delta e^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{e}^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}}+Q\left({\mathfrak{u}}^{n-1}\right)s^{n-{\displaystyle \frac{1}{2}}}+P_1-P_2-P_3-P_4,\upsilon ),$$

(30a)

$$\begin{array}{cc}\hfill {\beta }_{\tau }{e}_s^n& ={\displaystyle \frac{1}{2}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathfrak{u}}^{n-1}\right),{\beta }_{\tau }{U}^n)+{\displaystyle \frac{1}{2}}(Q\left({\mathfrak{u}}^{n-1}\right),{\beta }_{\tau }{e}^n)+K^n-{\displaystyle \frac{1}{2}}(Q\left({\mathfrak{u}}^{n-1}\right),{\sigma }^n)\hfill \\ & +{\displaystyle \frac{1}{2}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\sigma }^n)-{\displaystyle \frac{1}{2}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\beta }_{\tau }{u}^n).\hfill \end{array}$$

(30b)

Theorem 1.

For the solutions $U^n$ of (8) and $u\left(t^n\right)$ of (5), the following error estimate is valid

$${\displaystyle \frac{1}{2}}\parallel \nabla e^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel e^n{\parallel }^2+{\left|e_s^n\right|}^2\le C{\tau }^4.$$

(31)

Proof. 

Following [8], we note that, similar to other nonlinear equations, the boundedness of the numerical solution is vital for deriving the error estimate. Specifically, the boundedness of $\parallel U^n{\parallel }_{L^{\infty }}$ is a straightforward result of the stability inequality (13) and the norm equivalence in finite-dimensional spaces. Therefore, we denote

$$b:=\underset{1\le n\le M}{max}\{\parallel U^n{\parallel }_{L^{\infty }},\parallel u^n{\parallel }_{L^{\infty }}\}.$$

(32)

Define $V^{n-{\displaystyle \frac{1}{2}}}=\Delta e^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{e}^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}}+Q\left({\mathfrak{u}}^{n-1}\right)s^{n-{\displaystyle \frac{1}{2}}}+P_1-P_2-P_3-P_4$. Then, Equation (30a) can be written as

$$({\tau }^{-\alpha }\sum _{m=0}^n{\varpi }_m(e^{n-m}-e^0),\upsilon )=(V^{n-{\displaystyle \frac{1}{2}}},\upsilon ).$$

(33)

Multiplying Equation (33) by ${\tau }^{\alpha -1}{\theta }_{n-j}$, summing over $j=1,\dots ,n$, and applying an index substitution yields

$${\tau }^{-1}\sum _{j=1}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_m(e^{j-m}-e^0)={\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{V}^{j-{\displaystyle \frac{1}{2}}}.$$

(34)

Upon rearranging the terms in the left-hand side of (34), we have

$$\begin{array}{cc}\hfill {\tau }^{-1}\sum _{j=1}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_m(e^{j-m}-e^0)& ={\tau }^{-1}\sum _{j=0}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_{j-m}(e^m-e^0)\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(e^m-e^0)\sum _{j=m}^n{\varpi }_{j-m}{\theta }_{n-j}\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(e^m-e^0)\sum _{j=0}^{n-m}{\varpi }_j{\theta }_{n-j-m}\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(e^{n-m}-e^0){\mathbb{C}}_m.\hfill \end{array}$$

(35)

Since ${\mathbb{C}}_0=1,{\mathbb{C}}_1=-1$ and ${\mathbb{C}}_k=0$ for $k>1,$ we get

$$({\displaystyle \frac{e^n-e^{n-1}}{\tau }},\upsilon )=({\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{V}^{j-{\displaystyle \frac{1}{2}}},\upsilon ).$$

(36)

Setting $\upsilon =V^{n-{\displaystyle \frac{1}{2}}}$ in (36), we obtain

$$\begin{array}{cc}\hfill & (e^n-e^{n-1},\Delta e^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{e}^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)S^{n-{\displaystyle \frac{1}{2}}}+Q\left({\mathfrak{u}}^{n-1}\right)s^{n-{\displaystyle \frac{1}{2}}}+P_1-P_2-P_3-P_4)\hfill \\ & ={\tau }^{\alpha }(V^{n-{\displaystyle \frac{1}{2}}},\sum _{j=1}^n{\theta }_{n-j}{V}^{j-{\displaystyle \frac{1}{2}}}).\hfill \end{array}$$

(37)

Similarly to Equation (21), we deduce that

$$\left(\sum _{j=1}^n{\theta }_{n-j}{V}^{j-{\displaystyle \frac{1}{2}}},V^{n-{\displaystyle \frac{1}{2}}}\right)\ge {\displaystyle \frac{1}{2}}{\kappa }_{n-1}\parallel V^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\kappa }_{n-j}\parallel V^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-{\displaystyle \frac{1}{2}}\sum _{j=1}^{n-1}{\kappa }_{n-j-1}{\parallel V^{j-{\displaystyle \frac{1}{2}}}\parallel }^2.$$

(38)

Substituting Equation (38) into Equation (37) yields,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel \nabla e^n{\parallel }^2-\parallel \nabla e^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel e^n{\parallel }^2-\parallel e^{n-1}{\parallel }^2)+{\displaystyle \frac{{\tau }^{\alpha }}{2}}{\kappa }_{n-1}{\parallel V^{n-{\displaystyle \frac{1}{2}}}\parallel }^2\hfill \\ & +{\displaystyle \frac{{\tau }^{\alpha }}{2}}(\sum _{j=1}^n{\kappa }_{n-j}\parallel V^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-\sum _{j=1}^{n-1}{\kappa }_{n-j-1}\parallel V^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2)\hfill \\ & \le \tau ({\beta }_{\tau }{e}^n,-Q\left({\mathfrak{u}}^{n-1}\right)e_s^{n-{\displaystyle \frac{1}{2}}}+S^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathfrak{u}}^{n-1}\right)-Q\left({\mathbb{U}}^{n-1}\right)))+\tau ({\beta }_{\tau }{e}^n,P_1)\hfill \\ & -\tau (P_2+P_3+P_4,{\beta }_{\tau }{e}^n).\hfill \end{array}$$

(39)

Multiplying both sides of (30b) by $2e_s^{n-{\displaystyle \frac{1}{2}}}$, we get

$$\begin{array}{cc}\hfill \left(\right|e_s^n{|}^2-\left|e_s^{n-1}{|}^2\right)=& \tau e_s^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathfrak{u}}^{n-1}\right),{\beta }_{\tau }{U}^n)+\tau e_s^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathfrak{u}}^{n-1}\right),{\beta }_{\tau }{e}^n)\hfill \\ & +2\tau (K^n,e_s^{n-{\displaystyle \frac{1}{2}}})-\tau e_s^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathfrak{u}}^{n-1}\right),{\sigma }^n)\hfill \\ & -\tau e_s^{n-{\displaystyle \frac{1}{2}}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\sigma }^n)\hfill \\ & -\tau e_s^{n-{\displaystyle \frac{1}{2}}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\beta }_{\tau }{u}^n).\hfill \end{array}$$

(40)

Substituting (40) into (39), we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel \nabla e^n{\parallel }^2-\parallel \nabla e^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel e^n{\parallel }^2-\parallel e^{n-1}{\parallel }^2)+(|e_s^n{|}^2-|e_s^{n-1}{|}^2)+{\displaystyle \frac{{\tau }^{\alpha }}{2}}{\kappa }_{n-1}{\parallel V^{n-{\displaystyle \frac{1}{2}}}\parallel }^2\hfill \\ & +{\displaystyle \frac{{\tau }^{\alpha }}{2}}(\sum _{j=1}^n{\kappa }_{n-j}\parallel V^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-\sum _{j=1}^{n-1}{\kappa }_{n-j-1}\parallel V^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2)\le -\tau ({\beta }_{\tau }{u}^n,S^{n-{\displaystyle \frac{1}{2}}}\omega )-\tau ({\beta }_{\tau }{e}^n,P_4)\hfill \\ & +\tau s^{n-{\displaystyle \frac{1}{2}}}(\omega ,{\beta }_{\tau }{U}^n)+2\tau (K^n,e_s^{n-{\displaystyle \frac{1}{2}}})-\tau e_s^{n-{\displaystyle \frac{1}{2}}}(Q({\mathfrak{u}}^{n-1}),{\sigma }^n)+\tau (P_1-P_2-P_3,{\beta }_{\tau }{e}^n)\hfill \\ & -\tau e_s^{n-{\displaystyle \frac{1}{2}}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\sigma }^n)-\tau e_s^{n-{\displaystyle \frac{1}{2}}}(Q(u(t_{n-{\displaystyle \frac{1}{2}}}))-Q({\mathfrak{u}}^{n-1}),{\beta }_{\tau }{u}^n)=\sum _{i=1}^8{X}_i,\hfill \end{array}$$

(41)

where $\omega =Q({\mathfrak{u}}^{n-1})-Q({\mathbb{U}}^{n-1}).$

According to [8], we estimate $\omega$ as

$$\begin{array}{cc}\hfill \omega =& {\displaystyle \frac{Q\left({\mathfrak{u}}^{n-1}\right)-Q\left({\mathbb{U}}^{n-1}\right)-\frac{a}{{\epsilon }^2}({\mathfrak{u}}^{n-1}-{\mathbb{U}}^{n-1})}{\sqrt{E_1\left({\mathbb{U}}^{n-1}\right)}}}\hfill \\ & +{\displaystyle \frac{(Q\left({\mathfrak{u}}^{n-1}\right)-\frac{a}{{\epsilon }^2}{\mathfrak{u}}^{n-1})(E_1\left({\mathbb{U}}^{n-1}\right)-E_1\left({\mathfrak{u}}^{n-1}\right))}{\sqrt{E_1\left({\mathfrak{u}}^{n-1}\right)E_1\left({\mathbb{U}}^{n-1}\right)}(\sqrt{E_1\left({\mathfrak{u}}^{n-1}\right)}+\sqrt{E_1\left({\mathbb{U}}^{n-1}\right)})}}\hfill \\ & =A_1+A_2,\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill \parallel A_1\parallel & \le \parallel Q^{\prime }(\xi {\mathbb{U}}^{n-1}+(1-\xi ){\mathfrak{u}}^{n-1})\parallel \parallel {\mathbb{U}}^{n-1}-{\mathfrak{u}}^{n-1}\parallel +{\displaystyle \frac{a}{{\epsilon }^2}}\parallel {\mathbb{U}}^{n-1}-{\mathfrak{u}}^{n-1}\parallel \hfill \\ & \le {\displaystyle \frac{9b^2+3a+3}{{\epsilon }^2}}(\parallel e^{n-1}\parallel +\parallel e^{n-2}\parallel ),\hfill \end{array}$$

(43)

$$\parallel A_2\parallel \le {\displaystyle \frac{3b^2{(b^2+a+1)}^2|\Omega |}{2{\epsilon }^4}}(\parallel e^{n-1}\parallel +\parallel e^{n-2}\parallel ).$$

Therefore,

$$\parallel \omega \parallel \le A(\parallel e^{n-1}\parallel +\parallel e^{n-2}\parallel ),$$

where $A={\displaystyle \frac{2{\epsilon }^2(9b^2+3a+3)+3b^2{(b^2+a+1)}^2|\Omega |}{2{\epsilon }^4}}.$

In [41], the proof of $\nabla \omega$ has been introduced. Hence,

$$\parallel \nabla \omega \parallel \le C(\parallel e^{n-1}\parallel +\parallel e^{n-2}\parallel +\parallel \nabla e^{n-1}\parallel +\parallel \nabla e^{n-2}\parallel ).$$

(44)

By applying Lemma 5, we have

$$\begin{array}{cc}\hfill X_1\le \tau |S^{n-{\displaystyle \frac{1}{2}}}(\omega ,{\beta }_{\tau }{u}^n)|& \le {C\tau \parallel \omega \parallel }_1{\parallel {\beta }_{\tau }{u}^n\parallel }_{-1}\hfill \\ & \le C\tau (\parallel e^{n-1}{\parallel }^2+\parallel e^{n-2}{\parallel }^2+\parallel \nabla e^{n-1}{\parallel }^2+\parallel \nabla e^{n-2}{\parallel }^2).\hfill \end{array}$$

(45)

$$X_2\le \tau |(P_4,{\beta }_{\tau }{e}^n)|\le C\tau \parallel P_4{\parallel }^2\le C{\tau }^5.$$

(46)

$$\begin{array}{cc}\hfill X_3& \le \tau |s^{n-{\displaystyle \frac{1}{2}}}(\omega ,{\beta }_{\tau }{U}^n)|\le C\tau (\parallel e^{n-2}{\parallel }^2+\parallel e^{n-1}{\parallel }^2).\hfill \end{array}$$

(47)

Using Equation (44), Young inequality and Cauchy–Schwarz inequality, we derive

$$X_4\le \tau |2(K^n,e_s^{n-{\displaystyle \frac{1}{2}}})|\le C\tau (|e_s^n{|}^2+|e_s^{n-1}{|}^2)+\parallel K^n{\parallel }^2.$$

(48)

$$X_5\le \tau |(Q\left({\mathfrak{u}}^{n-1}\right)e_s^{n-{\displaystyle \frac{1}{2}}},{\sigma }^n)|\le \tau {\displaystyle \frac{{(b^3+(a+1)b)}^2}{4{\epsilon }^4}}|e_s^{n-{\displaystyle \frac{1}{2}}}{|}^2+\tau {\parallel {\sigma }^n\parallel }^2.$$

(49)

Given that $P_1,P_2,$ and $P_3$ all achieve second-order temporal accuracy, it can be concluded that

$$|X_6|\le C{\tau }^5.$$

(50)

Expanding the term $X_7,X_8$ through Equation (42) leads to the following estimate

$$|X_7|\le C\tau ({\tau }^4+\parallel {\sigma }^n{\parallel }^2+\parallel e_s^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2),$$

(51)

$$|X_8|\le C\tau ({\tau }^4+\parallel e_s^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2).$$

(52)

Incorporating the above inequalities into (41), we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel \nabla e^n{\parallel }^2-\parallel \nabla e^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel e^n{\parallel }^2-\parallel e^{n-1}{\parallel }^2)+(|e_s^n{|}^2-|e_s^{n-1}{|}^2)\le \tau (\parallel K^n{\parallel }^2+\parallel {\sigma }^n{\parallel }^2)\hfill \\ & +C{\tau }^5+C\tau (\parallel e^{n-1}\parallel +\parallel e^{n-2}\parallel +\parallel \nabla e^{n-1}\parallel +\parallel \nabla e^{n-2}\parallel +|e_s^n{|}^2+|e_s^{n-1}{|}^2).\hfill \end{array}$$

(53)

The summation for $n=1,2,3,\dots$ yields,

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}\parallel \nabla e^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel e^n{\parallel }^2+{\left|e_s^n\right|}^2 & \le \tau \sum _{i=1}^n(\parallel K^i{\parallel }^2+\parallel {\sigma }^i{\parallel }^2)+C{\tau }^5\hfill \\ & +C\tau \sum _{i=0}^n(\parallel e^i{\parallel }^2+\parallel \nabla e^i{\parallel }^2+|e_s^i{|}^2).\hfill \end{array}$$

(54)

Through the application of Taylor’s theorem, we can easily deduce that

$$(\sum _{n=1}^M\tau \parallel K^n{\parallel }^2{)}^{{\displaystyle \frac{1}{2}}}\le C{\tau }^2, (\sum _{n=1}^M\tau \parallel {\sigma }^n{{\parallel }^2)}^{{\displaystyle \frac{1}{2}}}\le C{\tau }^2.$$

(55)

Applying the above inequality, we obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}\parallel \nabla e^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel e^n{\parallel }^2+|e_s^n{|}^2\le C{\tau }^4+C\tau \sum _{i=0}^{n-1}(\parallel \nabla e^i{\parallel }^2+\parallel e^i{\parallel }^2+|e_s^i{|}^2).\end{array}$$

(56)

Applying Gronwall’s inequality, we deduce

$${\displaystyle \frac{1}{2}}\parallel \nabla e^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel e^n{\parallel }^2+{\left|e_s^n\right|}^2\le C{\tau }^4,$$

(57)

for sufficiently small $\tau$, which completes the proof of the theorem. □

By applying the LG method to spatially discretize the semi-discrete SFTR-SAV scheme (LG-SFTR-SAV), the following fully discrete LG-SFTR-SAV scheme is obtained.

3. The LG-SFTR-SAV Scheme

For spatial discretization, we employ Legendre–Gauss–Lobatto (LGL) interpolation points [42] as computational nodes. Specifically, we define discrete nodal sets ${\left\{x_j\right\}}_{j=0}^N$ along the x-axis. The exact solution $u\left(x\right)$ is approximated by its spectral projection $u_N\left(x\right)$, the space of polynomials of degree at most N, expressed as

$$u_N^n\left(x\right)=\sum _{i=0}^{N-2}{\widehat{u}}_i^n{\psi }_i\left(x\right),$$

(58)

where the basis functions ${\left\{{\psi }_i\left(x\right)\right\}}_{i=0}^{N-2}$ is defined as association of Legendre polynomials

$${\psi }_i\left(x\right)=L_i\left(x\right)-L_{i+2}\left(x\right),$$

(59)

constructed specifically to enforce homogeneous Dirichlet boundary conditions [42]. The approximation space is then defined as

$$Y_N=span\left\{{\psi }_i\left(x\right)\mid 0\le i\le N-2\right\}.$$

To ensure spectral accuracy, we introduce the orthogonal projection operator ${\Pi }_N:H^m(\Omega )\to Y_N$ characterized by the variational formulation

$$\left(\nabla (u^n-{\Pi }_N{u}^n),\nabla \upsilon \right)=0,\hspace{1em}\forall \upsilon \in Y_N,$$

(60)

which satisfies the following optimal approximation property.

Lemma 6

([42]). For any $u^n\in H^m(\Omega )$ with $m\ge 1$,

$$\parallel u^n-{\Pi }_N{u}^n{\parallel }_{H^{m_1}(\Omega )} \lesssim N^{m_1-m}{\parallel u^n\parallel }_{H^m(\Omega )}, 0\le l\le m,m_1=-1,0,1.$$

(61)

Problem 2.

Given $1\le n\le M$, find $U_N^n\in Y_N$ such that

$$({\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}{U}_N,{\upsilon }_N)=(\Delta U_N^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{U}_N^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}_N^{n-1}\right)S_N^{n-{\displaystyle \frac{1}{2}}},{\upsilon }_N),$$

(62a)

$${\beta }_{\tau }{S}_N^n={\displaystyle \frac{1}{2}}(Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{U}_N^n).$$

(62b)

We introduce the approximation errors

$$E_N^n=U^n-U_N^n={\xi }_N^n+{\rho }_N^n=U^n-{\Pi }_N{U}^n+{\Pi }_N{U}^n-U_N^n, E_S^n=S^n-S_N^n,$$

where $U^n$, $S^n$ denote semi-discrete solutions and $U_N^n$, $S_N^n$ represent their fully discrete solutions.

Error Analysis of LG-SFTR-SAV Solutions

Theorem 2.

Let $(\left\{U_N^n\right\},\left\{S_N^n\right\})$ be the solution of the (62). Then the following energy stability holds

$$\mathbb{E}\left(U_N^n\right)-\mathbb{E}\left(U_N^{n-1}\right)\le 0,$$

(63)

where

$$\mathbb{E}\left(U_N^n\right)={\displaystyle \frac{1}{2}}\parallel \nabla U_N^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel U_N^n{\parallel }^2+|S_N^n{|}^2+{\displaystyle \frac{{\tau }^{\alpha }}{2}}\sum _{j=1}^n{\kappa }_{n-j}{\parallel W_N^{j-{\displaystyle \frac{1}{2}}}\parallel }^2,$$

$$W_N^{n-{\displaystyle \frac{1}{2}}}=\Delta U_N^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{U}_N^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}_N^{n-1}\right)S_N^{n-{\displaystyle \frac{1}{2}}}.$$

For $0\le n\le M$, the following error estimate holds

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}\parallel \nabla ({\Pi }_N{U}^n-U_N^n){\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel {\Pi }_N{U}^n-U_N^n{\parallel }^2+{|S^n-S_N^n|}^2\le C{N}^{2-2m}.\hfill \end{array}$$

(64)

Proof. 

The approach developed in Lemma 4 extends directly to prove energy decay for the fully discrete system (63). By a method similar to that of Lemma 5, it can be proven that $\parallel {\beta }_{\tau }{U}_N^n\parallel$ is bounded. In [8], for any nonlinear equations, ensuring the boundedness of the numerical solution is crucial for establishing the error estimate. The boundedness of $\parallel U^n{\parallel }_{L^{\infty }},{\parallel U_N^n\parallel }_{L^{\infty }}$ is a direct consequence of the stability Lemma 4 and the equivalence of norms in finite-dimensional spaces. For the sake of notational simplicity, we define

$$b^{*}:=\underset{1\le n\le M}{max}\{\parallel U^n{\parallel }_{L^{\infty }},\parallel U_N^n{\parallel }_{L^{\infty }}\}.$$

(65)

By subtracting Equation (62) from Equation (8), we obtain

$$\begin{array}{cc}\hfill & ({\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}{E}_N,{\upsilon }_N)=(\Delta E_N^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{E}_N^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)(S^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})\hfill \\ & -S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right)),{\upsilon }_N),\hfill \end{array}$$

(66a)

$${\beta }_{\tau }{E}_S^n={\displaystyle \frac{1}{2}}(Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }(U^n-U_N^n))+{\displaystyle \frac{1}{2}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{U}_N^n).$$

(66b)

Set $V_N^{n-{\displaystyle \frac{1}{2}}}=\Delta E_N^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{E}_N^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)(S^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})-S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right))$,

$${\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}{E}_N=V_N^{n-{\displaystyle \frac{1}{2}}}.$$

(67)

Performing the index shift $n\mapsto j$ in Equation (67), we operate on (67) via multiplication by ${\tau }^{\alpha -1}{\theta }_{n-j}$ and execute the summation over $j=1$ to n to derive

$${\tau }^{-1}\sum _{j=1}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_m(E_N^{j-m}-E_N^0)={\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{V}_N^{j-{\displaystyle \frac{1}{2}}}.$$

(68)

Upon rearranging the terms in the left-hand side of (68), we have

$$\begin{array}{cc}\hfill {\tau }^{-1}\sum _{j=1}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_m(E_N^{j-m}-E_N^0)& ={\tau }^{-1}\sum _{j=0}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_{j-m}(E_N^m-E_N^0)\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(E_N^m-E_N^0)\sum _{j=m}^n{\varpi }_{j-m}{\theta }_{n-j}\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(E_N^m-E_N^0)\sum _{j=0}^{n-m}{\varpi }_j{\theta }_{n-j-m}\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(E_N^{n-m}-E_N^0){\mathbb{C}}_m.\hfill \end{array}$$

(69)

Equation (68) is rewritten as

$$({\displaystyle \frac{E_N^n-E_N^{n-1}}{\tau }},{\upsilon }_N)=({\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{V}_N^{j-{\displaystyle \frac{1}{2}}},{\upsilon }_N).$$

(70)

$$({\displaystyle \frac{{\rho }_N^n-{\rho }_N^{n-1}}{\tau }},{\upsilon }_N)=-({\displaystyle \frac{{\xi }_N^n-{\xi }_N^{n-1}}{\tau }},{\upsilon }_N)+({\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{V}_N^{j-{\displaystyle \frac{1}{2}}},{\upsilon }_N).$$

(71)

In (71), ${\upsilon }_N=V_N^{n-{\displaystyle \frac{1}{2}}}$, we have

$$\begin{array}{cc}\hfill & ({\displaystyle \frac{{\rho }_N^n-{\rho }_N^{n-1}}{\tau }},\Delta E_N^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{E}_N^{n-{\displaystyle \frac{1}{2}}}-Q({\mathbb{U}}^{n-1})(S^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})-S_N^{n-{\displaystyle \frac{1}{2}}}(Q({\mathbb{U}}^{n-1})-Q({\mathbb{U}}_N^{n-1}))\hfill \\ & =-({\displaystyle \frac{{\xi }_N^n-{\xi }_N^{n-1}}{\tau }},\Delta E_N^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{E}_N^{n-{\displaystyle \frac{1}{2}}}-Q({\mathbb{U}}^{n-1})(S^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})\hfill \\ & -S_N^{n-{\displaystyle \frac{1}{2}}}(Q({\mathbb{U}}^{n-1})-Q({\mathbb{U}}_N^{n-1}))+{\tau }^{\alpha -1}(V_N^{n-{\displaystyle \frac{1}{2}}},\sum _{j=1}^n{\theta }_{n-j}{V}_N^{j-{\displaystyle \frac{1}{2}}}).\hfill \end{array}$$

(72)

Multiply both sides of (66b) by $2E_S^{n-{\displaystyle \frac{1}{2}}}$, we get

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{\tau }}(|E_S^n{|}^2-|E_S^{n-1}{|}^2)& =E_S^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }{\xi }_N^n+{\beta }_{\tau }{\rho }_N^n)\hfill \\ & +E_S^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{U}_N^n).\hfill \end{array}$$

(73)

The left-hand side of Equation (72) is rearranged into the following form

$$\begin{array}{cc}\hfill & ({\displaystyle \frac{{\rho }_N^n-{\rho }_N^{n-1}}{\tau }},\Delta E_N^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{E}_N^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)(S^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})-S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right))\hfill \\ & =-{\displaystyle \frac{1}{2\tau }}(\parallel \nabla {\rho }_N^n{\parallel }^2-\parallel \nabla {\rho }_N^{n-1}{\parallel }^2)-{\displaystyle \frac{1}{2\tau }}(\nabla {\rho }_N^n-\nabla {\rho }_N^{n-1},\nabla {\xi }_N^n+\nabla {\xi }_N^{n-1})\hfill \\ & +E_S^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }{\xi }_N^n)-{\displaystyle \frac{a}{2\tau {\epsilon }^2}}(\parallel {\rho }_N^n{\parallel }^2-\parallel {\rho }_N^{n-1}{\parallel }^2)-{\displaystyle \frac{a}{2\tau {\epsilon }^2}}({\rho }_N^n-{\rho }_N^{n-1},{\xi }_N^n+{\xi }_N^{n-1})\hfill \\ & -{\displaystyle \frac{1}{\tau }}(|E_S^n{|}^2-|E_S^{n-1}{|}^2)+E_S^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{U}_N^n)\hfill \\ & -S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{\rho }_N^n).\hfill \end{array}$$

(74)

The first term on the right-hand side of (72) is rewritten as

$$\begin{array}{cc}\hfill & ({\displaystyle \frac{{\xi }_N^n-{\xi }_N^{n-1}}{\tau }},\Delta E_N^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{E}_N^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}^{n-1}\right)(S^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})-S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right))\hfill \\ & =-{\displaystyle \frac{1}{2\tau }}(\parallel \nabla {\xi }_N^n{\parallel }^2-\parallel \nabla {\xi }_N^{n-1}{\parallel }^2)-{\displaystyle \frac{1}{2\tau }}(\nabla {\xi }_N^n-\nabla {\xi }_N^{n-1},\nabla {\rho }_N^n+\nabla {\rho }_N^{n-1})\hfill \\ & -E_S^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right),{\beta }_{\tau }{\xi }_N^n)-{\displaystyle \frac{a}{2\tau {\epsilon }^2}}(\parallel {\xi }_N^n{\parallel }^2-\parallel {\xi }_N^{n-1}{\parallel }^2)-{\displaystyle \frac{a}{2\tau {\epsilon }^2}}({\xi }_N^n-{\xi }_N^{n-1},{\rho }_N^n+{\rho }_N^{n-1})\hfill \\ & -S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{\xi }_N^n).\hfill \end{array}$$

(75)

The second term on the right-hand side of (72) satisfies

$$\begin{array}{c}\hfill \left(\sum _{j=1}^n{\theta }_{n-j}{V}_N^{j-{\displaystyle \frac{1}{2}}},V_N^{n-{\displaystyle \frac{1}{2}}}\right)\ge {\displaystyle \frac{1}{2}}{\kappa }_{n-1}\parallel V_N^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\kappa }_{n-j}\parallel V_N^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-{\displaystyle \frac{1}{2}}\sum _{j=1}^{n-1}{\kappa }_{n-j-1}{\parallel V_N^{j-{\displaystyle \frac{1}{2}}}\parallel }^2.\end{array}$$

(76)

Upon substituting equations (73)–(76) into Equation (72), it follows that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel \nabla {\rho }_N^n{\parallel }^2-\parallel \nabla {\rho }_N^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel {\rho }_N^n{\parallel }^2-\parallel {\rho }_N^{n-1}{\parallel }^2)+(|E_S^n{|}^2-|E_S^{n-1}{|}^2)+\hfill \\ & {\tau }^{\alpha }\left[{\displaystyle \frac{1}{2}}{\kappa }_{n-1}\parallel V_N^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\kappa }_{n-j}\parallel V_N^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-{\displaystyle \frac{1}{2}}\sum _{j=1}^{n-1}{\kappa }_{n-j-1}{\parallel V_N^{j-{\displaystyle \frac{1}{2}}}\parallel }^2\right]\hfill \\ & \le -{\displaystyle \frac{1}{2}}(\parallel \nabla {\xi }_N^n{\parallel }^2-\parallel \nabla {\xi }_N^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{{\epsilon }^2}}({\rho }_N^{n-1},{\xi }_N^{n-1})-{\displaystyle \frac{a}{{\epsilon }^2}}({\rho }_N^n,{\xi }_N^n)\hfill \\ & -{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel {\xi }_N^n{\parallel }^2-\parallel {\xi }_N^{n-1}{\parallel }^2)-\tau S_N^{n-{\displaystyle \frac{1}{2}}}({\omega }_N,{\beta }_{\tau }{E}_N^n)+\tau E_S^{n-{\displaystyle \frac{1}{2}}}({\omega }_N,{\beta }_{\tau }{U}_N^n),\hfill \end{array}$$

(77)

where ${\omega }_N=Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right).$

We provide the following norm bounds for ${\omega }_N$,

$$\begin{array}{cc}\hfill {\omega }_N=& {\displaystyle \frac{Q\left({\mathbb{U}}^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right)-\frac{a}{{\epsilon }^2}({\mathbb{U}}^{n-1}-{\mathbb{U}}_N^{n-1})}{\sqrt{E_1\left({\mathbb{U}}_N^{n-1}\right)}}}\hfill \\ & +{\displaystyle \frac{(Q\left({\mathbb{U}}^{n-1}\right)-\frac{a}{{\epsilon }^2}{\mathbb{U}}^{n-1})(E_1\left({\mathbb{U}}^{n-1}\right)-E_1\left({\mathbb{U}}_N^{n-1}\right))}{\sqrt{E_1\left({\mathbb{U}}^{n-1}\right)E_1\left({\mathbb{U}}_N^{n-1}\right)}(\sqrt{E_1\left({\mathbb{U}}^{n-1}\right)}+\sqrt{E_1\left({\mathbb{U}}_N^{n-1}\right)})}}\hfill \\ & =B_1+B_2,\hfill \end{array}$$

(78)

$$\parallel B_1\parallel \le {\displaystyle \frac{9{b^{*}}^2+3a+3}{{\epsilon }^2}}(\parallel {\xi }_N^{n-1}\parallel +\parallel {\xi }_N^{n-2}\parallel +\parallel {\rho }_N^{n-1}\parallel +\parallel {\rho }_N^{n-2}\parallel ),$$

$$\parallel B_2\parallel \le {\displaystyle \frac{3{b^{*}}^2{({b^{*}}^2+a+1)}^2|\Omega |}{2{\epsilon }^4}}(\parallel {\xi }_N^{n-1}\parallel +\parallel {\xi }_N^{n-2}\parallel +\parallel {\rho }_N^{n-1}\parallel +\parallel {\rho }_N^{n-2}\parallel ),$$

$$\parallel {\omega }_N\parallel \le {\theta }_N(\parallel {\xi }_N^{n-1}\parallel +\parallel {\xi }_N^{n-2}\parallel +\parallel {\rho }_N^{n-1}\parallel +\parallel {\rho }_N^{n-2}\parallel ).$$

(79)

where ${\theta }_N={\displaystyle \frac{2{\epsilon }^2(9{b^{*}}^2+3a+3)+3{b^{*}}^2{({b^{*}}^2+a+1)}^2|\Omega |}{2{\epsilon }^4}}$.

Similarly, for $\nabla {\omega }_N$, we can derive

$$\begin{array}{cc}\hfill \parallel \nabla {\omega }_N\parallel & \le C(\parallel {\xi }_N^{n-1}\parallel +\parallel {\xi }_N^{n-2}\parallel +\parallel \nabla {\xi }_N^{n-1}\parallel +\parallel \nabla {\xi }_N^{n-2}\parallel +\parallel {\rho }_N^{n-1}\parallel +\parallel {\rho }_N^{n-2}\parallel \hfill \\ & +\parallel \nabla {\rho }_N^{n-1}\parallel +\parallel \nabla {\rho }_N^{n-2}\parallel ).\hfill \end{array}$$

(80)

A term-by-term analysis is conducted for the fifth, and sixth, terms of Equation (77),

$$\begin{array}{cc}& |E_S^{n-{\displaystyle \frac{1}{2}}}({\omega }_N,{\beta }_{\tau }{U}_N^n)|\le C|E_S^{n-{\displaystyle \frac{1}{2}}}|\parallel {\omega }_N\parallel \le C(\parallel {\omega }_N{\parallel }^2+|E_S^{n-{\displaystyle \frac{1}{2}}}{|}^2)\hfill \\ & \le C(\parallel {\xi }_N^{n-1}{\parallel }^2+\parallel {\xi }_N^{n-2}{\parallel }^2+\parallel {\rho }_N^{n-1}{\parallel }^2+\parallel {\rho }_N^{n-2}{\parallel }^2+|E_S^n{|}^2+\left|E_S^{n-1}{|}^2\right),\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill & |({\omega }_N,{\beta }_{\tau }{E}_N^n)|\le \parallel {\omega }_N{\parallel }_1\parallel {\beta }_{\tau }{E}_N^n{\parallel }_{-1}\le C{\parallel \nabla {\omega }_N\parallel }^2\hfill \\ & \le C(\parallel {\xi }_N^{n-1}\parallel +\parallel {\xi }_N^{n-2}\parallel +\parallel \nabla {\xi }_N^{n-1}\parallel +\parallel \nabla {\xi }_N^{n-2}\parallel +\parallel {\rho }_N^{n-1}\parallel +\parallel {\rho }_N^{n-2}\parallel +\parallel \nabla {\rho }_N^{n-1}\parallel \hfill \\ & +\parallel \nabla {\rho }_N^{n-2}\parallel ).\hfill \end{array}$$

(82)

Substituting the above expressions into Equation (77), $\tau =O\left(N^{-1}\right)$, and applying Lemma 6, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel \nabla {\rho }_N^n{\parallel }^2-\parallel \nabla {\rho }_N^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel {\rho }_N^n{\parallel }^2-\parallel {\rho }_N^{n-1}{\parallel }^2)+(|E_S^n{|}^2-|E_S^{n-1}{|}^2)\hfill \\ & \le C\tau \left(\right|E_S^n{|}^2+|E_S^{n-1}{|}^2+\parallel \nabla {\rho }_N^n{\parallel }^2+\parallel \nabla {\rho }_N^{n-1}{\parallel }^2+\parallel \nabla {\rho }_N^{n-2}{\parallel }^2+\parallel {\rho }_N^n{\parallel }^2+\parallel {\rho }_N^{n-1}{\parallel }^2\hfill \\ & +\parallel {\rho }_N^{n-2}{\parallel }^2)+C{N}^{2-2m}.\hfill \end{array}$$

(83)

Summing the above inequalities for $n=1,2,3,\dots$, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}\parallel \nabla {\rho }_N^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel {\rho }_N^n{\parallel }^2+|E_S^n{|}^2\le C\tau \sum _{i=0}^n\left(\right|E_S^i{|}^2+\parallel \nabla {\rho }_N^i{\parallel }^2+\parallel {\rho }_N^i{\parallel }^2)+C{N}^{2-2m}.\hfill \end{array}$$

(84)

By applying Gronwall’s lemma, we deduce that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}\parallel \nabla {\rho }_N^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel {\rho }_N^n{\parallel }^2+{\left|E_S^n\right|}^2\le C{N}^{2-2m}.\hfill \end{array}$$

(85)

□

Corollary 1.

For the solutions $u\left(t^n\right)$ of Equation (5) and $U_N^n$ to Equation (62), respectively, under the conditions of Theorem 2, the following error estimate holds

$$\parallel \nabla (u\left(t^n\right)-U_N^n)\parallel +{\displaystyle \frac{a}{{\epsilon }^2}}\parallel (u\left(t^n\right)-U_N^n)\parallel +2|s^n-S_N^n|\le C(N^{1-m}+{\tau }^2).$$

(86)

4. The ROLGE-SFTR-SAV Scheme

In this section, the concept introduced in [29,43] is adopted to construct a POD basis and develop the ROLGE-SFTR-SAV formulation for the tFAC equation.

4.1. Construct the POD Basis and Establish ROLGE-SFTR-SAV Formulation

Consider the snapshot solutions ${\left\{U_N^n\right\}}_{n=1}^L$ defined in Section 3. The space spanned by these snapshots is denoted as

$$\mathbf{V}=span\{U_N^1,U_N^2,\dots ,U_N^L\}.$$

The existence of at least one non-zero snapshot function is assumed. Let ${\left\{{\psi }_j\right\}}_{j=1}^l$ denote an orthonormal basis for $\mathbf{V}$, where $l=dim\mathbf{V}$. Consequently, any snapshot vector admits the expansion

$$U_N^i=\sum _{j=1}^l(\nabla U_N^i,\nabla {\psi }_j){\psi }_j, i=1,2,\dots ,L.$$

Definition 1

([29]). The POD method seeks a standard orthonormal basis ${\left\{{\psi }_j\right\}}_{j=1}^d$ that minimizes the projection error

$$\underset{{\left\{{\psi }_j\right\}}_{j=1}^d}{min}{\displaystyle \frac{1}{L}}\sum _{i=1}^L{∥\nabla \left(U_N^i-\sum _{j=1}^d(\nabla U_N^i,\nabla {\psi }_j){\psi }_j\right)∥}^2.$$

(87)

The basis ${\left\{{\psi }_j\right\}}_{j=1}^d$ of rank d optimally captures the dominant features of the snapshot ensemble while reducing dimensionality. A set of solutions ${\left\{{\psi }_j\right\}}_{j=1}^d$ of (87) is termed a POD basis of rank d.

We construct the $L\times L$ correlation matrix $\mathbf{B}$ with entries

$$B_{ij}={\displaystyle \frac{1}{L}}(\nabla U_N^i,\nabla U_N^j).$$

As $\mathbf{B}$ is positive semidefinite with rank l. This construction yields the following fundamental result.

Proposition 1

([31]). Let ${\left\{{\lambda }_j\right\}}_{j=1}^l$ with ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_l>0$ denote the positive eigenvalues of the correlation matrix B, and ${\left\{a^j\right\}}_{j=1}^l$ their corresponding orthonormal eigenvectors. A rank-d POD basis ($d\le l$) is then constructed as

$${\psi }_i={\displaystyle \frac{1}{\sqrt{L{\lambda }_i}}}\sum _{k=1}^L{a}_k^i{U}_N^k, 1\le i\le d,$$

(88)

where $a_k^i$ denotes the k-th component of eigenvector $a^i$. Moreover, the optimal approximation error satisfies

$${\displaystyle \frac{1}{L}}\sum _{i=1}^L{∥\nabla \left(U_N^i-\sum _{j=1}^d(\nabla U_N^i,\nabla {\psi }_j){\psi }_j\right)∥}^2=\sum _{j=d+1}^l{\lambda }_j.$$

(89)

Define the reduced-order subspace

$${\chi }_d=span\{{\psi }_1,{\psi }_2,\dots ,{\psi }_d\}.$$

For $U_N\in Y_N$, a Ritz operator ${\Pi }_d:Y_N\to {\chi }_d$ is denoted by

$$(\nabla {\Pi }_d{U}_N,\nabla {\upsilon }_d)=(\nabla U_N,\nabla {\upsilon }_d),\forall {\upsilon }_d\in {\chi }_d.$$

(90)

Then, by functional analysis, there exists an extension ${\Pi }_N:H^m(\Omega )\to Y_N$ of such that ${\Pi }_N{|}_{Y_N}={\Pi }_d:Y_N\to {\chi }_d$ and ${\Pi }_N:H^m(\Omega )\setminus Y_N\to Y_N\setminus {\chi }_d$. This projection is defined variationally by

$$(\nabla u,\nabla {\upsilon }_N)=(\nabla {\Pi }_{N}u,\nabla {\upsilon }_N), \forall {\upsilon }_N\in Y_N,$$

(91)

where $u\in H^m(\Omega )$. The variational formulation (91) ensures ${\Pi }_N$ is uniquely determined and satisfies the stability bound

$$\parallel \nabla \left({\Pi }_{d}u\right)\parallel \le \parallel \nabla u\parallel , \forall u\in H^m(\Omega ).$$

(92)

Lemma 7

([44]). For each integer d $(1\le d\le l)$, the projection operator ${\Pi }_d$ fulfills the inequality:

$${\displaystyle \frac{1}{L}}\sum _{i=1}^L{\parallel \nabla (U_N^i-{\Pi }_d{U}_N^i)\parallel }^2\le \sum _{j=d+1}^l{\lambda }_j,$$

(93)

$${\displaystyle \frac{1}{L}}\sum _{i=1}^L{\parallel U_N^i-{\Pi }_d{U}_N^i\parallel }^2\le C{N}^{-2}\sum _{j=d+1}^l{\lambda }_j.$$

(94)

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{L}}\sum _{i=1}^L{\parallel U_N^i-{\Pi }_d{U}_N^i\parallel }_{-1}^2 & \le {\displaystyle \frac{C{N}^{-2}}{L}}\sum _{i=1}^L{\parallel \nabla (U_N^i-{\Pi }_d{U}_N^i)\parallel }^2\hfill \\ & \le C{N}^{-2}\sum _{j=d+1}^l{\lambda }_j.\hfill \end{array}$$

(95)

Problem 3.

Find $U_d^n\in {\chi }_d(n=1,2,\dots ,M)$ such that

$$U_d^n={\Pi }_d{U}_N^n=\sum _{j=1}^d(\nabla U_N^n,\nabla {\psi }_j){\psi }_j, n=1,2,\dots ,L,$$

(96a)

$$({\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}{U}_d,{\upsilon }_d)=(\Delta U_d^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{U}_d^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}_d^{n-1}\right)S_d^{n-{\displaystyle \frac{1}{2}}},{\upsilon }_d), n=L+1,L+2,\dots ,M,$$

(96b)

$${\beta }_{\tau }{S}_d^n={\displaystyle \frac{1}{2}}(Q\left({\mathbb{U}}_d^{n-1}\right),{\beta }_{\tau }{U}_d^n), n=L+1,L+2,\dots ,M.$$

(96c)

Remark 1.

Problem 3 demonstrates the ROLGE-SFTR-SAV solutions for the tFAC equation. Specifically, the initial L ROLGE-SFTR-SAV solutions are constructed by projecting the first L classical LG solutions onto a POD basis, and subsequent $(M-L)$ solutions are generated through extrapolation and iterative solution of equations. This hybrid approach fundamentally differentiates Problem 3 from conventional POD-based reduced-order models [8,28], particularly in how it integrates projection with extrapolation and iteration steps.

We define the approximation errors

$$E_d^n=U_d^n-U_N^n={\rho }_d^n+{\xi }_d^n=U_d^n-{\Pi }_d{U}_N^n+{\Pi }_d{U}_N^n-U_N^n, E_{Sd}^n=S_d^n-S_N^n,$$

where $U_N^n,S_N^n$ denote the fully discrete solutions obtained from Problem 2 and $U_d^n,S_d^n$ represent the ROLGE solutions computed in Probelm 3. These error metrics will be analyzed in Section 4.

4.2. Error Estimates of the ROLGE-SFTR-SAV Solution for tFAC Equation

Theorem 3.

The solution $U_d^n(1\le n\le M)\in {\chi }^d$ to Problem 3 satisfies

$$\mathbb{E}(U_d^n,S_d^n)-\mathbb{E}(U_d^{n-1},S_d^{n-1})\le 0,$$

(97)

where

$$\begin{array}{c}\hfill \mathbb{E}(U_d^n,S_d^n)={\displaystyle \frac{1}{2}}\parallel \nabla U_d^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel U_d^n{\parallel }^2+|S_d^n{|}^2+{\displaystyle \frac{{\tau }^{\alpha }}{2}}\sum _{i=1}^n{\kappa }_{n-i}{\parallel W_d^{i-{\displaystyle \frac{1}{2}}}\parallel }^2,\end{array}$$

(98)

$$W_d^{n-{\displaystyle \frac{1}{2}}}=\Delta U_d^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{U}_d^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}_d^{n-1}\right)S_d^{n-{\displaystyle \frac{1}{2}}}.$$

When $\tau =O\left(N^{-1}\right)$, the following error estimate holds

$$\begin{array}{cc}\hfill \parallel \nabla (U_d^n-{\Pi }_d{U}_N^n)\parallel +{\displaystyle \frac{a}{{\epsilon }^2}}\parallel U_d^n-{\Pi }_d{U}_N^n\parallel +& 2|S_d^n-S_N^n|\le C{(L\sum _{j=d+1}^l{\lambda }_j)}^{{\displaystyle \frac{1}{2}}}\hfill \\ & +C\sigma \left(M\right)(N^{1-m}+{\tau }^2),\hfill \end{array}$$

(99)

where $U_N^i\in {\mathbf{Y}}_N(i=1,2,\dots ,M)$ is the solution of Problem 3, $\sigma \left(M\right)=0$$(1\le n\le L)$,$\sigma \left(M\right)=\sqrt{N^{-1}(M-L)}(L+1\le n\le M).$

Proof. 

The method established in Lemma 4 can be directly extended to establish the energy decay property of the ROLGE-SFTR-SAV scheme (97). Following an approach analogous to that employed in Lemma 5, one can show that $\parallel {\beta }_{\tau }{U}_d^n\parallel$ is bounded. As noted in [8], with respect to arbitrary nonlinear equations, guaranteeing the boundedness of the numerical solution plays a vital role in establishing the error estimate. The boundedness of $\parallel U_d^n{\parallel }_{L^{\infty }}$ and $\parallel U_N^n{\parallel }_{L^{\infty }}$ follows directly from the stability result presented in Equation (97) and the equivalence of norms in finite-dimensional spaces. For the sake of notational simplicity, we define

$$\overline{b}:=\underset{1\le n\le M}{max}\{\parallel U_d^n{\parallel }_{L^{\infty }},\parallel U_N^n{\parallel }_{L^{\infty }}\}.$$

(100)

By subtracting Equation (62) from Equation (96), we obtain

$$e_d^n=U_d^n-U_N^n=-U_N^n+{\Pi }_d{U}_N^n, n=1,\dots ,L,$$

(101)

$$\begin{array}{cc}\hfill & ({\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}{E}_d,{\upsilon }_d)=(\Delta E_d^{n-{\displaystyle \frac{1}{2}}}+{\displaystyle \frac{a}{{\epsilon }^2}}{E}_d^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}_d^{n-1}\right)(S_d^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})\hfill \\ & -S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right)),{\upsilon }_d), n=L+1,L+2,\dots ,M,\hfill \end{array}$$

(102a)

$$\begin{array}{cc}\hfill {\beta }_{\tau }{E}_{Sd}^n& ={\displaystyle \frac{1}{2}}(Q\left({\mathbb{U}}_d^{n-1}\right),{\beta }_{\tau }(U_d^n-U_N^n))+{\displaystyle \frac{1}{2}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{U}_N^n),\hfill \\ & n=L+1,L+2,\dots ,M.\hfill \end{array}$$

(102b)

For $n=1,\dots ,L$, by Lemma 7 and Equation (101), we have

$$\begin{array}{cc}\hfill & \parallel \nabla E_d^n\parallel =\parallel \nabla (U_N^n-U_d^n)\parallel =\parallel \nabla (U_N^n-{\Pi }_d{U}_N^n)\parallel \hfill \\ \hfill & \le {(L\sum _{j=d+1}^l{\lambda }_j)}^{{\displaystyle \frac{1}{2}}}.\hfill \end{array}$$

(103)

Set $V_d^{n-{\displaystyle \frac{1}{2}}}=\Delta E_d^{n-{\displaystyle \frac{1}{2}}}+{\displaystyle \frac{a}{{\epsilon }^2}}{E}_d^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}_d^{n-1}\right)(S_d^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})-S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right)),$

$$({\partial }_{\tau }^{\alpha ,n-{\displaystyle \frac{1}{2}}}{E}_d,{\upsilon }_d)=(V_d^{n-{\displaystyle \frac{1}{2}}},{\upsilon }_d).$$

(104)

Multiply both sides of (104) by ${\tau }^{\alpha -1}{\theta }_{n-j}$ after replacing n with j in, and sum the index j from 1 to n to obtain

$${\tau }^{-1}\sum _{j=1}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_m(E_d^{j-m}-E_d^0)={\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{V}_d^{j-{\displaystyle \frac{1}{2}}}.$$

(105)

Upon rearranging the terms in the left-hand side of (105), we obtain

$$\begin{array}{cc}\hfill {\tau }^{-1}\sum _{j=1}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_m(E_d^{j-m}-E_d^0)& ={\tau }^{-1}\sum _{j=0}^n{\theta }_{n-j}\sum _{m=0}^j{\varpi }_{j-m}(E_d^m-E_d^0)\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(E_d^m-E_d^0)\sum _{j=m}^n{\varpi }_{j-m}{\theta }_{n-j}\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(E_d^m-E_d^0)\sum _{j=0}^{n-m}{\varpi }_j{\theta }_{n-j-m}\hfill \\ & ={\tau }^{-1}\sum _{m=0}^n(E_d^{n-m}-E_d^0){\mathbb{C}}_m,\hfill \end{array}$$

(106)

where ${\mathbb{C}}_m={\displaystyle \sum _{j=0}^m}{\omega }_j{\theta }_{m-j}$ is the m-th coefficient of the series of the product $\omega \left(\zeta \right)\theta \left(\zeta \right),$ which by Lemma (3) yields ${\mathbb{C}}_0=1,{\mathbb{C}}_1=-1$ and ${\mathbb{C}}_k=0$ for $k>1.$ We then have

$$({\displaystyle \frac{E_d^n-E_d^{n-1}}{\tau }},{\upsilon }_d)=({\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{V}_d^{j-{\displaystyle \frac{1}{2}}},{\upsilon }_d),$$

(107)

$$({\displaystyle \frac{{\rho }_d^n-{\rho }_d^{n-1}}{\tau }},{\upsilon }_d)=-({\displaystyle \frac{{\xi }_d^n-{\xi }_d^{n-1}}{\tau }},{\upsilon }_d)+({\tau }^{\alpha -1}\sum _{j=1}^n{\theta }_{n-j}{V}_d^{j-{\displaystyle \frac{1}{2}}},{\upsilon }_d).$$

(108)

In (108), ${\upsilon }_d=V_d^{n-{\displaystyle \frac{1}{2}}}$, we have

$$\begin{array}{cc}\hfill & ({\displaystyle \frac{{\rho }_d^n-{\rho }_d^{n-1}}{\tau }},\Delta E_d^{n-{\displaystyle \frac{1}{2}}}+{\displaystyle \frac{a}{{\epsilon }^2}}{E}_d^{n-{\displaystyle \frac{1}{2}}}-Q({\mathbb{U}}_d^{n-1})(S_d^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})-S_N^{n-{\displaystyle \frac{1}{2}}}(Q({\mathbb{U}}_d^{n-1})-Q({\mathbb{U}}_N^{n-1}))\hfill \\ & =-({\displaystyle \frac{{\xi }_d^n-{\xi }_d^{n-1}}{\tau }},\Delta E_d^{n-{\displaystyle \frac{1}{2}}}+{\displaystyle \frac{a}{{\epsilon }^2}}{E}_d^{n-{\displaystyle \frac{1}{2}}}-Q({\mathbb{U}}_d^{n-1})(S_d^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})\hfill \\ & -S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right))+{\tau }^{\alpha -1}(V_d^{n-{\displaystyle \frac{1}{2}}},\sum _{j=1}^n{\theta }_{n-j}{V}_d^{j-{\displaystyle \frac{1}{2}}}).\hfill \end{array}$$

(109)

Multiply both sides of (102b) by $2E_{Sd}^{n-{\displaystyle \frac{1}{2}}}$, we get

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{\tau }}(|E_{Sd}^n{|}^2-|E_{Sd}^{n-1}{|}^2)=E_{Sd}^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right),{\beta }_{\tau }{\rho }_d^n+{\beta }_{\tau }{\xi }_d^n)+E_{Sd}^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{U}_N^n).\end{array}$$

(110)

The left-hand side of Equation (109) is rearranged into the following form

$$\begin{array}{cc}\hfill & ({\displaystyle \frac{{\rho }_d^n-{\rho }_d^{n-1}}{\tau }},\Delta E_d^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{E}_d^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}_d^{n-1}\right)(S_d^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})-S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right))\hfill \\ & =-{\displaystyle \frac{1}{2\tau }}(\parallel \nabla {\rho }_d^n{\parallel }^2-\parallel \nabla {\rho }_d^{n-1}{\parallel }^2)-{\displaystyle \frac{1}{2\tau }}(\nabla {\rho }_d^n-\nabla {\rho }_d^{n-1},\nabla {\xi }_d^n+\nabla {\xi }_d^{n-1})\hfill \\ & +E_{Sd}^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right),{\beta }_{\tau }{\xi }_d^n)-{\displaystyle \frac{a}{2\tau {\epsilon }^2}}(\parallel {\rho }_d^n{\parallel }^2-\parallel {\rho }_d^{n-1}{\parallel }^2)-{\displaystyle \frac{a}{2\tau {\epsilon }^2}}({\rho }_d^n-{\rho }_d^{n-1},{\xi }_d^n+{\xi }_d^{n-1})\hfill \\ & -{\displaystyle \frac{1}{\tau }}\left(\right|E_{Sd}^n{|}^2-|E_{Sd}^{n-1}{|}^2)+E_{Sd}^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{U}_N^n)\hfill \\ & -S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{\rho }_d^n).\hfill \end{array}$$

(111)

The first term on the right-hand side of (109) is rewritten as

$$\begin{array}{cc}\hfill & ({\displaystyle \frac{{\xi }_d^n-{\xi }_d^{n-1}}{\tau }},\Delta E_d^{n-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{a}{{\epsilon }^2}}{E}_d^{n-{\displaystyle \frac{1}{2}}}-Q\left({\mathbb{U}}_d^{n-1}\right)(S_d^{n-{\displaystyle \frac{1}{2}}}-S_N^{n-{\displaystyle \frac{1}{2}}})-S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right))\hfill \\ & =-{\displaystyle \frac{1}{2\tau }}(\parallel \nabla {\xi }_d^n{\parallel }^2-\parallel \nabla {\xi }_d^{n-1}{\parallel }^2)-{\displaystyle \frac{1}{2\tau }}(\nabla {\xi }_d^n-\nabla {\xi }_d^{n-1},\nabla {\rho }_d^n+\nabla {\rho }_d^{n-1})\hfill \\ & -E_{Sd}^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right),{\beta }_{\tau }{\xi }_d^n)-{\displaystyle \frac{a}{2\tau {\epsilon }^2}}(\parallel {\xi }_d^n{\parallel }^2-\parallel {\xi }_d^{n-1}{\parallel }^2)-{\displaystyle \frac{a}{2\tau {\epsilon }^2}}({\xi }_d^n-{\xi }_d^{n-1},{\rho }_d^n+{\rho }_d^{n-1})\hfill \\ & -S_N^{n-{\displaystyle \frac{1}{2}}}(Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right),{\beta }_{\tau }{\xi }_d^n).\hfill \end{array}$$

(112)

The second term on the right-hand side of (109) satisfies

$$\begin{array}{c}\hfill \left(\sum _{j=1}^n{\theta }_{n-j}{V}_d^{j-{\displaystyle \frac{1}{2}}},V_d^{n-{\displaystyle \frac{1}{2}}}\right)\ge {\displaystyle \frac{1}{2}}{\kappa }_{n-1}\parallel V_d^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\kappa }_{n-j}\parallel V_d^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-{\displaystyle \frac{1}{2}}\sum _{j=1}^{n-1}{\kappa }_{n-j-1}{\parallel V_d^{j-{\displaystyle \frac{1}{2}}}\parallel }^2.\end{array}$$

(113)

Upon substituting Equations (110)–(113) into Equation (109), it follows that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel \nabla {\rho }_d^n{\parallel }^2-\parallel \nabla {\rho }_d^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel {\rho }_d^n{\parallel }^2-\parallel {\rho }_d^{n-1}{\parallel }^2)+(|E_{Sd}^n{|}^2-|E_{Sd}^{n-1}{|}^2)\hfill \\ & +{\tau }^{\alpha }\left[{\displaystyle \frac{1}{2}}{\kappa }_{n-1}\parallel V_d^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\kappa }_{n-j}\parallel V_d^{j-{\displaystyle \frac{1}{2}}}{\parallel }^2-{\displaystyle \frac{1}{2}}\sum _{j=1}^{n-1}{\kappa }_{n-j-1}{\parallel V_d^{j-{\displaystyle \frac{1}{2}}}\parallel }^2\right]\hfill \\ & \le -{\displaystyle \frac{1}{2}}(\parallel \nabla {\xi }_d^n{\parallel }^2-\parallel \nabla {\xi }_d^{n-1}{\parallel }^2)-{\displaystyle \frac{a}{{\epsilon }^2}}({\rho }_d^n,{\xi }_d^n)+{\displaystyle \frac{a}{{\epsilon }^2}}({\rho }_d^{n-1},{\xi }_d^{n-1})\hfill \\ & +{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel {\xi }_d^n{\parallel }^2-\parallel {\xi }_d^{n-1}{\parallel }^2)-\tau S_N^{n-{\displaystyle \frac{1}{2}}}({\omega }_d,{\beta }_{\tau }{E}_d^n)+\tau E_{Sd}^{n-{\displaystyle \frac{1}{2}}}({\omega }_d,{\beta }_{\tau }{U}_N^n),\hfill \end{array}$$

(114)

where ${\omega }_d=Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right).$

We decompose ${\omega }_d$ into the following components

$$\begin{array}{cc}\hfill {\omega }_d=& {\displaystyle \frac{Q\left({\mathbb{U}}_d^{n-1}\right)-Q\left({\mathbb{U}}_N^{n-1}\right)-\frac{a}{{\epsilon }^2}({\mathbb{U}}_d^{n-1}-{\mathbb{U}}_N^{n-1})}{\sqrt{E_1\left({\mathbb{U}}_N^{n-1}\right)}}}\hfill \\ & +{\displaystyle \frac{(Q\left({\mathbb{U}}_d^{n-1}\right)-\frac{a}{{\epsilon }^2}{\mathbb{U}}_d^{n-1})(E_1\left({\mathbb{U}}_d^{n-1}\right)-E_1\left({\mathbb{U}}_N^{n-1}\right))}{\sqrt{E_1\left({\mathbb{U}}_d^{n-1}\right)E_1\left({\mathbb{U}}_N^{n-1}\right)}(\sqrt{E_1\left({\mathbb{U}}_d^{n-1}\right)}+\sqrt{E_1\left({\mathbb{U}}_N^{n-1}\right)})}}\hfill \\ & ={\overline{B}}_1+{\overline{B}}_2.\hfill \end{array}$$

(115)

The terms can be bounded separately by

$$\parallel {\overline{B}}_1\parallel \le {\displaystyle \frac{9{\overline{b}}^2+3a+3}{{\epsilon }^2}}(\parallel {\xi }_d^{n-1}\parallel +\parallel {\xi }_d^{n-2}\parallel +\parallel {\rho }_d^{n-1}\parallel +\parallel {\rho }_d^{n-2}\parallel ).$$

$$\parallel {\overline{B}}_2\parallel \le {\displaystyle \frac{3{\overline{b}}^2{({\overline{b}}^2+a+1)}^2|\Omega |}{2{\epsilon }^4}}(\parallel {\xi }_d^{n-1}\parallel +\parallel {\xi }_d^{n-2}\parallel +\parallel {\rho }_d^{n-1}\parallel +\parallel {\rho }_d^{n-2}\parallel ).$$

Let ${\theta }_d={\displaystyle \frac{2{\epsilon }^2(9{\overline{b}}^2+3a+3)+3{\overline{b}}^2{({\overline{b}}^2+a+1)}^2|\Omega |}{2{\epsilon }^4}}$, we have

$$\parallel {\omega }_d\parallel \le {\theta }_d(\parallel {\xi }_d^{n-1}\parallel +\parallel {\xi }_d^{n-2}\parallel +\parallel {\rho }_d^{n-1}\parallel +\parallel {\rho }_d^{n-2}\parallel ).$$

(116)

Similarly, for $\nabla {\omega }_d$, we can derive

$$\begin{array}{cc}\hfill \parallel \nabla {\omega }_d\parallel & \le C(\parallel {\xi }_d^{n-1}\parallel +\parallel {\xi }_d^{n-2}\parallel +\parallel \nabla {\xi }_d^{n-1}\parallel +\parallel \nabla {\xi }_d^{n-2}\parallel +\parallel {\rho }_d^{n-1}\parallel +\parallel {\rho }_d^{n-2}\parallel +\parallel \nabla {\rho }_d^{n-1}\parallel \hfill \\ & +\parallel \nabla {\rho }_d^{n-2}\parallel ).\hfill \end{array}$$

(117)

Using Equation (116) and Lemma 7, we have

$$\begin{array}{c}|E_{Sd}^{n-{\displaystyle \frac{1}{2}}}({\omega }_d,{\beta }_{\tau }{U}_N^n)|\le C|E_{Sd}^{n-{\displaystyle \frac{1}{2}}}|\parallel {\omega }_d\parallel \hfill \\ \le C(\parallel {\xi }_d^{n-1}{\parallel }^2+\parallel {\xi }_d^{n-2}{\parallel }^2+\parallel {\rho }_d^{n-1}{\parallel }^2+\parallel {\rho }_d^{n-2}{\parallel }^2+|E_{Sd}^n{|}^2+\left|E_{Sd}^{n-1}{|}^2\right).\hfill \end{array}$$

(118)

For $n=L+1,L+2,\dots ,M,$ using Lemma 6 and Theorem 1, we obtain

$$\begin{array}{cc}\hfill \parallel \nabla {\xi }_d^n\parallel & \le \parallel \nabla (U_N^n-U^n)\parallel +\parallel \nabla (U^n-{\Pi }_N{U}^n)\parallel +\parallel \nabla ({\Pi }_N{U}^n-{\Pi }_d{U}^n)\parallel \hfill \\ & +\parallel \nabla ({\Pi }_N{U}^n-{\Pi }_N{U}_N^n)\parallel \le C({\tau }^2+N^{1-m}).\hfill \end{array}$$

(119)

Using Equations (117) and (119), Lemma 6, we have

$$\begin{array}{cc}\hfill & |({\omega }_d,{\beta }_{\tau }{E}_d^n)|\le \parallel {\omega }_d{\parallel }_1{\parallel {\beta }_{\tau }{E}_d^n\parallel }_{-1}\hfill \\ & \le C(\parallel {\xi }_d^{n-1}\parallel +\parallel {\xi }_d^{n-2}\parallel +\parallel \nabla {\xi }_d^{n-1}\parallel +\parallel \nabla {\xi }_d^{n-2}\parallel +\parallel {\rho }_d^{n-1}\parallel +\parallel {\rho }_d^{n-2}\parallel \hfill \\ & +\parallel \nabla {\rho }_d^{n-1}\parallel +\parallel \nabla {\rho }_d^{n-2}\parallel )\hfill \\ & \le C({\tau }^4+N^{2-2m})+C(\parallel {\xi }_d^{n-1}\parallel +\parallel {\xi }_d^{n-2}\parallel +\parallel {\rho }_d^{n-1}\parallel +\parallel {\rho }_d^{n-2}\parallel +\parallel \nabla {\rho }_d^{n-1}\parallel +\parallel \nabla {\rho }_d^{n-2}\parallel ).\hfill \end{array}$$

(120)

If $\tau =O\left(N^{-1}\right)$, upon substituting Equations (118)–(120) into Equation (114), we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel \nabla {\rho }_d^n{\parallel }^2-\parallel \nabla {\rho }_d^{n-1}{\parallel }^2)+{\displaystyle \frac{a}{2{\epsilon }^2}}(\parallel {\rho }_d^n{\parallel }^2-\parallel {\rho }_d^{n-1}{\parallel }^2)+(|E_{Sd}^n{|}^2-|E_{Sd}^{n-1}{|}^2)\hfill \\ & \le C\tau (\parallel {\xi }_d^{n-1}{\parallel }^2+\parallel {\xi }_d^{n-2}{\parallel }^2+|E_{Sd}^n{|}^2+|E_{Sd}^{n-1}{|}^2+\parallel \nabla {\rho }_d^n{\parallel }^2+\parallel \nabla {\rho }_d^{n-1}{\parallel }^2\hfill \\ & +\parallel \nabla {\rho }_d^{n-2}{\parallel }^2+\parallel {\rho }_d^n{\parallel }^2+\parallel {\rho }_d^{n-1}{\parallel }^2+\parallel {\rho }_d^{n-2}{\parallel }^2)+C\tau ({\tau }^4+N^{2-2m}).\hfill \end{array}$$

(121)

By summing (121) for $n=L+1,\dots ,M$, using Lemma 7 and Equations (103) and (119), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}\parallel \nabla {\rho }_d^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel {\rho }_d^n{\parallel }^2+{\left|E_{Sd}^n\right|}^2\hfill \\ & \le C\tau \sum _{i=L+1}^n\left(\right|E_{Sd}^i{|}^2+\parallel \nabla {\rho }_d^i{\parallel }^2+\parallel {\rho }_d^i{\parallel }^2)+C\tau (M-L)({\tau }^4+N^{2-2m})\hfill \\ & +C{N}^{-1}L\sum _{j=d+1}^l{\lambda }_j.\hfill \end{array}$$

(122)

Employing the Gronwall lemma, we derive

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}\parallel \nabla {\rho }_d^n{\parallel }^2+{\displaystyle \frac{a}{2{\epsilon }^2}}\parallel {\rho }_d^n{\parallel }^2+{\left|E_{Sd}^n\right|}^2\le C\tau (M-L)({\tau }^4+N^{2-2m})+C{N}^{-1}L\sum _{j=d+1}^l{\lambda }_j.\hfill \end{array}$$

(123)

□

Corollary 2.

$(\left\{U_d^n\right\},\left\{S_d^n\right\})$ is the solution of the (96), we deduce the error estimate

$$\begin{array}{cc}\hfill & \parallel \nabla (u\left(t^n\right)-U_d^n)\parallel +{\displaystyle \frac{a}{{\epsilon }^2}}\parallel u\left(t^n\right)-U_d^n\parallel +2|S_d^{n+1}|\le C(\delta \left(M\right)+1)({\tau }^2+N^{1-m})\hfill \\ & +C{(N^{-1}L\sum _{j=d+1}^l{\lambda }_j)}^{{\displaystyle \frac{1}{2}}},\hfill \end{array}$$

(124)

where $\delta \left(M\right)=0$ for $1\le n\le L$, and $\delta \left(M\right)=\sqrt{N^{-1}(M-L)}$ for $L+1\le n\le M$.

Remark 2.

The error bounds derived in Theorem 3 and Corollary 2 inform the choice of the number of POD modes d. Specifically, d should satisfy

$$\begin{array}{c}\hfill N^{-1}L\sum _{j=d+1}^l{\lambda }_j=O(N^{2-2m},{\tau }^4),\end{array}$$

(125)

where ${\lambda }_j$ denotes the POD eigenvalues. The iterative error, quantified by $\sqrt{N^{-1}(M-L)}(N^{1-m}+{\tau }^2)$, dictates the need for POD basis updates during extrapolation. Specifically, a POD basis update is required when

$$\sqrt{N^{-1}(M-L)}(N^{1-m}+{\tau }^2)>1.$$

Remark 3.

We remark that while the numerical scheme and the accompanying analysis presented in this work are developed directly for the one-dimensional spatial case, they can be naturally extended to higher-dimensional settings. In fact, the efficiency gain of the reduced-order algorithm, when compared to its non-reduced counterpart, becomes even more pronounced in multi-dimensional problems. The one-dimensional framework is adopted primarily for clarity of exposition, as it allows for a more transparent illustration of the algorithmic construction and a streamlined theoretical analysis, without loss of generality.

5. Numerical Tests

In this section, we verify the convergence rates of the ROLGE-SFTR-SAV scheme and demonstrate its superior efficiency relative to the LG-SFTR-SAV scheme. The temporal convergence rate for the variable u is obtained by the formula

$$\mathrm{Rate}={log}_2{\displaystyle \frac{{max}_{0\le n\le M}\parallel u\left(t_n\right)-U_N^n\parallel }{{max}_{0\le n\le 2M}\parallel u\left(t_n\right)-U_N^n\parallel }},$$

by which the rates for $\nabla u$ and s can also be derived similarly. Since the explicit form of the solution of (1) is unknown, we assume the solution as $u(x,t)=(1-{\displaystyle \frac{1}{2}}{t}^3)sin(\mathsf{\ell }\pi x)$ where $\mathsf{\ell }\in {\mathbb{Z}}^{+}$ and rewrite (1) by adding the source term

$$g(x,t)=-{\displaystyle \frac{{(t^3-2)}^3}{8{\epsilon }^2}}sin{(\mathsf{\ell }\pi x)}^3+\left[\left({\displaystyle \frac{t^3}{2}}-1\right)({\epsilon }^{-2}-{\mathsf{\ell }}^2{\pi }^2)-{\displaystyle \frac{3t^{3-\alpha }}{\Gamma (4-\alpha )}}\right]sin(\mathsf{\ell }\pi x).$$

We illustrate the fast decay property of the eigenvalues ${\lambda }_j$ in Figure 1 (left) for different $\tau =2^{-8},2^{-9},2^{-10},2^{-11},$$2^{-12}$ with fixed $\alpha =0.5$ and in Figure 1 (right) for different $\alpha =0.1,0.3,0.5,0.7,0.9$ with fixed $\tau =2^{-10}$, under the setting $N=256,\mathsf{\ell }=20,L=20$. It is clear that only the first several ${\lambda }_j$ are sufficient to capture the essential properties. For the following test, we set $d=5$. While smaller values of d can yield acceptable results, the choice of $d=5$ provides a more robust solution.

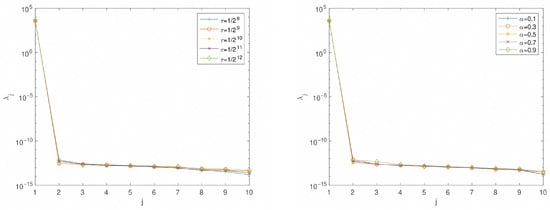
Figure 1. The fast decay of the eigenvalues ${\lambda }_j$ for different $\tau =2^{-8},2^{-9},2^{-10},2^{-11},2^{-12}$ with fixed $\alpha =0.5$ (left) and for different $\alpha =0.1,0.3,0.5,0.7,0.9$ with fixed $\tau =2^{-10}$ (right), under the setting $N=256,\mathsf{\ell }=20,L=20$.

In Table 1 and Table 2, we set $\epsilon =1,S=4,T=1,\mathsf{\ell }=40$ and fixing $N=512$. Both tables present the temporal convergence behavior and computational efficiency of the LG-SFTR-SAV and ROLGE-SFTR-SAV schemes, respectively, for varying values of the fractional order parameter $\alpha =0.1,0.5,0.9$. The time step $\tau$ is successively refined as $\tau =2^{-10},2^{-11},2^{-12}$, and the corresponding errors in the $L^2$-norm of the solution, its gradient, and the auxiliary variable s are reported, along with their convergence rates and CPU times.

Table 1. The temporal convergence rates and CPU time of the LG-SFTR-SAV scheme.

$\mathit{\alpha }$	$\mathit{\tau }$	${max}_{\mathit{n}}\parallel \mathit{u}\left({\mathit{t}}_{\mathit{n}}\right)-{\mathit{U}}_{\mathit{N}}^{\mathit{n}}\parallel$	Rates	${max}_{\mathit{n}}\parallel \mathit{\nabla }(\mathit{u}\left({\mathit{t}}_{\mathit{n}}\right)-{\mathit{U}}_{\mathit{N}}^{\mathit{n}})\parallel$	Rates	${max}_{\mathit{n}}|{\mathit{s}}^{\mathit{n}}-{\mathit{S}}_{\mathit{N}}^{\mathit{n}}|$	Rates	CPU(s)
0.1	$1/2^{10}$	6.766312 $\times {10}^{-10}$		8.502820$\times {10}^{-8}$		3.298273$\times {10}^{-7}$		4.298
	$1/2^{11}$	1.692652$\times {10}^{-10}$	2.00	2.127056$\times {10}^{-8}$	2.00	8.248303$\times {10}^{-8}$	2.00	9.831
	$1/2^{12}$	4.233224$\times {10}^{-11}$	2.00	5.319684$\times {10}^{-9}$	2.00	2.062403$\times {10}^{-8}$	2.00	25.719
0.5	$1/2^{10}$	4.839621$\times {10}^{-10}$		6.081676$\times {10}^{-8}$		3.298918$\times {10}^{-7}$		4.155
	$1/2^{11}$	1.210199$\times {10}^{-10}$	2.00	1.520789$\times {10}^{-8}$	2.00	8.249919$\times {10}^{-8}$	2.00	9.870
	$1/2^{12}$	3.026003$\times {10}^{-11}$	2.00	3.802590$\times {10}^{-9}$	2.00	2.062808$\times {10}^{-8}$	2.00	25.697
0.9	$1/2^{10}$	4.552962$\times {10}^{-10}$		5.721450$\times {10}^{-8}$		3.299014$\times {10}^{-7}$		4.418
	$1/2^{11}$	1.138514$\times {10}^{-10}$	2.00	1.430703$\times {10}^{-8}$	2.00	8.250160$\times {10}^{-8}$	2.00	9.916
	$1/2^{12}$	2.846870$\times {10}^{-11}$	2.00	3.577245$\times {10}^{-9}$	2.00	2.062867$\times {10}^{-8}$	2.00	25.365

Table 2. The temporal convergence rates and CPU time of the ROLGE-SFTR-SAV scheme.

$\mathit{\alpha }$	$\mathit{\tau }$	${max}_{\mathit{n}}\parallel \mathit{u}\left({\mathit{t}}_{\mathit{n}}\right)-{\mathit{U}}_{\mathit{d}}^{\mathit{n}}\parallel$	Rates	${max}_{\mathit{n}}\parallel \mathit{\nabla }(\mathit{u}\left({\mathit{t}}_{\mathit{n}}\right)-{\mathit{U}}_{\mathit{d}}^{\mathit{n}})\parallel$	Rates	${max}_{\mathit{n}}|{\mathit{s}}^{\mathit{n}}-{\mathit{S}}_{\mathit{d}}^{\mathit{n}}|$	Rates	CPU(s)
0.1	$1/2^{10}$	6.766247$\times {10}^{-10}$		8.502718$\times {10}^{-8}$		3.298266$\times {10}^{-7}$		2.496
	$1/2^{11}$	1.692561$\times {10}^{-10}$	2.00	2.126934$\times {10}^{-8}$	2.00	8.248300$\times {10}^{-8}$	2.00	5.645
	$1/2^{12}$	4.233295$\times {10}^{-11}$	2.00	5.319630$\times {10}^{-9}$	2.00	2.062403$\times {10}^{-8}$	2.00	15.517
0.5	$1/2^{10}$	4.839613$\times {10}^{-10}$		6.081639$\times {10}^{-8}$		3.298911$\times {10}^{-7}$		2.580
	$1/2^{11}$	1.210215$\times {10}^{-10}$	2.00	1.520801$\times {10}^{-8}$	2.00	8.249917$\times {10}^{-8}$	2.00	5.683
	$1/2^{12}$	3.025812$\times {10}^{-11}$	2.00	3.802332$\times {10}^{-9}$	2.00	2.062809$\times {10}^{-8}$	2.00	15.277
0.9	$1/2^{10}$	4.552957$\times {10}^{-10}$		5.721416$\times {10}^{-8}$		3.299007$\times {10}^{-7}$		2.594
	$1/2^{11}$	1.138505$\times {10}^{-10}$	2.00	1.430689$\times {10}^{-8}$	2.00	8.250157$\times {10}^{-8}$	2.00	5.654
	$1/2^{12}$	2.846576$\times {10}^{-11}$	2.00	3.577126$\times {10}^{-9}$	2.00	2.062868$\times {10}^{-8}$	2.00	15.303

Both schemes exhibit a clear second-order temporal convergence across all error measures, as indicated by the consistent rate value of 2.00. In terms of computational cost, the ROLGE-SFTR-SAV scheme shows a significant reduction in CPU time compared to the LG-SFTR-SAV scheme, while maintaining nearly identical accuracy and convergence rates. For instance, at $\tau =2^{-10}$, the CPU time for the ROLGE variant is approximately 2.5 s, compared to about 4.3 s for the LG variant—a reduction of over $40\%$. This efficiency gain is consistent across all time steps and values of $\alpha$, underscoring the advantage of the reduced-order approach.

In Figure 2 we investigate the spatial discretization errors under the setting $\mathsf{\ell }=10$, $M=2^{14},L=20,d=5$. Clearly, the errors for both LG-SFTR-SAV and ROLGE-SFTR-SAV schemes demonstrate spectral accuracy, as the errors decrease rapidly with increasing spatial resolution N. Both schemes exhibit nearly identical error levels and convergence rates, confirming that the reduced-order approach preserves the excellent spatial accuracy of the spectral method while maintaining computational efficiency.

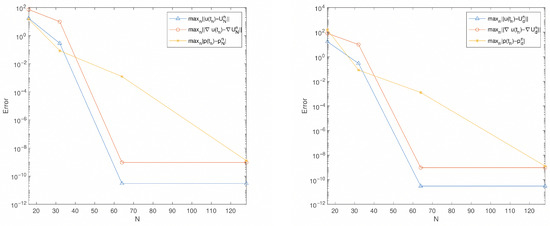
Figure 2. The spectral accuracy of the LG-SFTR-SAV scheme (left) and the ROLGE-SFTR-SAV scheme (right), under the setting $\mathsf{\ell }=10,M=2^{14},L=20,d=5$.

These results confirm that the ROLGE-SFTR-SAV scheme preserves the high-order accuracy of the original LG-SFTR-SAV method while offering enhanced computational efficiency, making it a preferable choice for long-time simulations or problems requiring repeated evaluations.

6. Conclusions

This study has presented a novel and efficient numerical framework for solving the tFAC equation. By combining the SAV method for linearization, the SFTR $- {\displaystyle \frac{1}{2}}$ for temporal discretization, and a LG spectral method in space, we developed a fully discrete scheme that is both energy-stable and computationally efficient. To further reduce the computational cost, a ROE model based on POD was introduced, effectively minimizing redundant computations while preserving numerical accuracy. Theoretical proofs of stability and error estimates were provided, confirming the reliability of the proposed approach. Numerical experiments demonstrated the validity of the method and aligned well with the theoretical predictions. This work offers a practical and theoretical foundation for simulating time-fractional phase-field models over long time intervals.