Fractional Bi-Susceptible Approach to COVID-19 Dynamics with Sensitivity and Optimal Control Analysis

Abstract

This study introduces a nonlinear fractional bi-susceptible model for COVID-19 using the Atangana–Baleanu derivative in Caputo sense (ABC). The fractional framework captures nonlocal effects and temporal decay, offering a realistic presentation of persistent infection cycles and delayed recovery. Within this setting, we investigate multiple transmission modes, determine the major risk factors, and analyze the long-term dynamics of the disease. Analytical results are obtained at equilibrium states, and fundamental properties of the model are validated. Numerical simulations based on the Toufik–Atangana method further endorse the theoretical results and emphasize the effectiveness of the ABC derivative. Bifurcation analysis illustrates that adjusting time-invariant treatment and awareness efforts can accelerate pandemic control. Sensitivity analysis identifies the most significant parameters, which are used to construct an optimal control problem to determine effective disease control strategies. The numerical results reveal that the proposed control interventions minimize both infection levels and associated costs. Overall, this research work demonstrates the modeling strength of the ABC derivative by integrating fractional calculus, bifurcation theory, and optimal control for efficient epidemic management.

1. Introduction

COVID-19, which results from infection with the Coronavirus SARS-CoV-2, is an exceptionally contagious disease that has resulted in millions of deaths globally. The pandemic has had a profound impact on personal lives and has caused major disruptions to economies and GDP even in the most advanced countries. The virus spreads primarily through direct or indirect physical contact between people [1]. Transmission usually happens when an individual breathes in or comes into contact with droplets of saliva or mucus from someone who is infected, particularly when they cough or sneeze. This mode of spread puts healthy people at considerable risk. Initially identified in December 2019 in Wuhan, China, the virus rapidly spread across China and eventually reached more than 223 countries across Europe, the Americas, Asia, and Australia [2]. The incubation period, which refers to the time between viral exposure and symptom onset, generally ranges from 2 to 14 days. During this phase, humans can transmit the virus even without showing symptoms. Most COVID-19 cases present mild to moderate symptoms, including fever, fatigue, muscle aches, cough, severe headaches, diarrhea, vomiting, insomnia, nasal congestion, and a sore throat. However, in some instances, the disease can progress to severe complications, such as difficulty breathing, confusion, chest pain, or loss of speech or movement, necessitating immediate medical intervention. Those experiencing severe symptoms should seek immediate emergency care [3]. The highest risk of severe disease is among individuals with preexisting health conditions like respiratory infections, compromised immune systems, hypertension, diabetes, and those over the age of 60. It is essential for these individuals to take additional precautions to safeguard themselves from infection [4].

Globally, between 20 November and 17 December 2023, there was a $52\%$ increase in new COVID-19 cases compared to the previous 28-day period, with more than 850,000 new infections recorded. In contrast, new deaths decreased by $8\%$, amounting to more than 3000 fatalities. By 17 December 2023, the global totals had reached over 772 million confirmed cases and nearly 7 million deaths. During the period from 13 November to 10 December 2023, there was a significant uptick in COVID-19 hospitalizations and ICU admissions, with increases of $23\%$ and $51\%$, respectively, among countries consistently reporting data [5]. This period saw over 118,000 new hospitalizations and more than 1600 new ICU admissions. As of 18 December 2023, the JN.1 sub-lineage of the BA.2.86 Omicron variant has been designated as a separate variant of interest (VOI) due to its rapid rise in prevalence [5,6]. JN.1, a descendant of the BA.2.86 lineage, has developed additional mutations that enhance its transmissibility while maintaining the immune evasion properties of its parent variant. Globally, the EG.5 variant remains the most commonly reported VOI and is closely related to the XBB variants observed in the U.S. over the past six months. Notably, EG.5 features a mutation that can partially evade immunity conferred by previous infections or vaccinations [7].

During the fall and winter months, respiratory viruses often see a significant increase in cases. With the emergence of COVID-19 in 2020, it joined the ranks of common respiratory viruses like the flu and RSV, which typically surge in colder weather. Although COVID-19 has evolved from a pandemic to an endemic status, it continues to exhibit a pattern of heightened activity twice a year. As of August 2024, COVID-19 continues to pose a significant challenge worldwide, with recent data indicating a resurgence in cases across multiple regions [7]. This summertime surge, observed in areas like Europe, the Americas, and the Western Pacific, has raised concerns among health experts and organizations like the World Health Organization (WHO). The increase in cases is attributed to several factors, including waning immunity, increased travel, and the emergence of new, more transmissible variants such as the FLiRT group, which are subvariants of the Omicron strain [8,9]. Interestingly, this resurgence is happening during the summer months, a period typically less associated with respiratory virus transmission. However, COVID-19’s ability to circulate year-round and its continuous mutation have made such atypical patterns more common. WHO reports have shown a rise in hospitalizations and ICU admissions, though these remain below the peak levels seen earlier in the pandemic. Nonetheless, the persistence of the virus and its potential to evolve into more severe variants have led to renewed calls for vigilance, especially in maintaining vaccination efforts among high-risk groups with new vaccines on the way [10]. The current situation underscores the need for ongoing public health measures and personal precautions. Although the overall severity of infections appears to be lower than in previous waves, the threat of long COVID remains, particularly for older and vulnerable populations. As we navigate this latest phase of the pandemic, it is clear that COVID-19 will continue to be a part of our lives for the foreseeable future [11].

Mathematical modeling is a vital tool in combating infectious diseases, helping to understand, predict, and manage their spread [12,13,14]. By integrating mathematical methods with epidemiological data, researchers can simulate scenarios and assess several precautionary measure, providing crucial insights for public health decisions. These models are essential for policymakers, enabling them to develop strategies that mitigate the impact of diseases and protect public health. During the COVID-19 pandemic, numerous models were created to study the virus’s transmission dynamics, evolution, and the effectiveness of various measures. Predictive models have been particularly valuable in forecasting infection rates and evaluating interventions like vaccination and social distancing [15]. They also help estimate outcomes such as case numbers, hospitalizations, and fatalities, while identifying vulnerable populations and potential hotspots. Further research has expanded these models to include factors like immunity waning and the effects of non-pharmaceutical interventions. These models provide insights into how such factors influence the pandemic’s course, offering powerful tools for designing and implementing control measures [16]. By developing these models, public health authorities are better equipped to make informed decisions and take proactive actions, improving our capacity to manage and address threats from infectious diseases.

Fractional-order derivatives extend classical differentiation to non-integer orders, allowing memory and hereditary effects to be embedded within dynamical systems [17,18]. This feature is particularly relevant for biological and epidemiological modeling, where standard integer-order models often struggle to represent time-dependent delays, immune memory, and cumulative exposure accurately [19,20]. By incorporating these effects, fractional derivatives improve both stability and biological realism, offering a more refined description of disease dynamics, as supported by several studies demonstrating their superiority over conventional integer-order models [21,22,23]. Additionally, fractional models can represent anomalous diffusion and complex transmission dynamics more accurately, reflecting real-world phenomena where individuals do not interact or move at constant rates [24].

Among the various fractional operators used in epidemic modeling, such as Riemann–Liouville (RL), Caputo, and Caputo–Fabrizio (CF), the ABC operator has emerged as a particularly powerful tool [25,26,27]. While the RL, Caputo, and RL operators have been used extensively, they each come with limitations that can hinder accurate modeling of real-world phenomena. The RL operator, for instance, often requires fractional initial conditions that are not always practical or well-defined in real-world scenarios. The Caputo derivative, although more practical with classical initial conditions, still has limitations in accurately modeling abrupt changes or complex memory effects [25]. The RL operator, despite its advantage of avoiding singularities, does not fully capture the diverse range of memory effects in systems with more complex behaviors. In contrast, the ABC operator offers superior modeling capabilities by addressing these limitations [28]. It uniquely combines non-local, non-singular properties with a more realistic representation of memory effects. This operator avoids the singularity issues present in the RL and CF derivatives and offers a more comprehensive framework for incorporating complex memory and hereditary effects without the restrictive assumptions required by the Caputo and RL operators [29,30]. This makes the ABC operator particularly effective for capturing the full spectrum of epidemic dynamics, leading to more accurate predictions and robust control strategies [31]. Therefore, although earlier models used RL, Caputo, and CF derivatives to improve our understanding, the ABC operator offers a more realistic and effective way to model and control epidemic outbreaks [32,33,34,35].

Optimal control analysis of epidemics involves designing strategies to mitigate the impact of infectious diseases on individuals while considering constraints and costs. This analysis typically uses mathematical models to simulate the spread of an epidemic and evaluates various control measures, such as quarantine, vaccination, and treatment strategies, to identify the most effective interventions [36,37]. The goal is to balance the cost of implementing these measures with their benefits, such as reducing infection rates and mitigating the burden on healthcare systems. Techniques from optimization theory, including dynamic programming and Pontryagin’s Maximum Principle, are often employed to derive control policies that optimize specific objectives, like minimizing the infected individuals or reducing the overall cost of interventions [38,39]. These models also account for factors like the variability in individual responses to treatments and the heterogeneity in population structure, providing a framework to assess how different control strategies can influence the trajectory of an epidemic. By incorporating real-time data and adapting to changing conditions, optimal control analysis can guide public health decision-making, enhance preparedness, and improve response strategies to better manage and eventually contain epidemic outbreaks [40].

In this research, we extend a recent COVID-19 model [41] with the inclusion of two susceptibility compartments, introducing the concept of awareness among susceptible individuals. We investigate the model’s global behavior, perform a sensitivity analysis, and examine the impact of constant treatment and awareness interventions. To formulate effective time-dependent disease control strategies, we establish an optimal control problem, apply Pontryagin’s Maximum Principle, and approximate it using the Toufik–Atangana method [42]. Numerical simulations demonstrate that our proposed approach accurately captures the dynamics of the model and effectively addresses the control problem.

The manuscript consists of seven sections. In Section 2, the compartmental model for COVID-19 is developed, including its dimensionless fractional representation. Section 3 addresses the aspects of existence, uniqueness, positivity, boundedness, equilibrium states, the threshold parameter, and stability analysis. Section 4 and Section 5 present numerical analyses using the Toufik–Atangana method, along with discussions, graphs, sensitivity analysis, bifurcation studies, and the impacts of constant treatment and awareness. Section 6 formulates an optimal control problem considering time-varying interventions and assesses the efficacy and cost-effectiveness of the optimal strategies. Finally, Section 7 summarizes the main findings and offers recommendations.

2. Coronavirus Disease Modeling

The spread of Coronavirus can be effectively modeled using SEIR-type compartmental frameworks and their variants [43,44]. In this study, we consider the model $S_1{S}_{2}ITR$ [41], which divides the population into two susceptible groups: $S_1$ (without underlying conditions) and $S_2$ (with underlying conditions). This distinction highlights varying susceptibility levels and informs targeted public health strategies for high-risk individuals. For example, individuals classified as $S_2$ might require different preventive measures and prioritized medical interventions. Their preexisting health issues can weaken their immune system, making it harder for their bodies to fight off infections. Identifying the biological differences between $S_1$ and $S_2$ is essential to accurately model disease progression and tailor interventions based on individual health profiles. This differentiation helps to develop precise treatments and vaccination approaches, boosting treatment effectiveness and increasing the reliability of transmission forecasts.

The suggested model $S_1{S}_{2}ITR$ incorporates the dynamics of the following human classes. The model categorizes the population into five groups: $S_1\left(t\right)$, representing healthy susceptible individuals without preexisting conditions; $S_2\left(t\right)$, which includes susceptible individuals who are older or have medical vulnerabilities; $I\left(t\right)$, the segment of the population that has tested positive for COVID-19; $T\left(t\right)$, referring to hospitalized patients with severe symptoms; and $R\left(t\right)$, which consists of individuals who have recovered and gained full immunity. For clarity and completeness, we summarize the following model assumptions and considerations:

• The susceptible population is categorized into two groups: individuals without underlying health conditions $\left(S_1\right)$ and individuals with underlying health conditions $\left(S_2\right)$. This distinction reflects different risk levels of infection and disease progression.
• Disease transmission occurs only through effective contact between susceptible individuals and infected individuals. We do not consider any environmental or indirect transmission pathways.
• Infectious individuals $\left(I\right)$ with severe symptoms are transferred to the treatment class $\left(T\right)$ at a constant rate $\mu$.
• Individuals in the treatment class $\left(T\right)$ either recover and move to the recovered class $\left(R\right)$ or leave the population due to natural death $\alpha$.
• Mild or asymptomatic infections are implicitly included in the infected class $\left(I\right)$ and are not modeled separately. This will maintain analytical tractability of the model.
• The population is supposed to be homogeneously mixed, meaning every human has an equal probability of contacting others.
• Recruitment into the susceptible classes $S_1$ and $S_2$ occurs at constant rates ${\Lambda }_1$ and ${\Lambda }_2$, and a constant natural death rate $\alpha$ is assumed across all compartments.
• Recovered individuals are assumed to get complete immunity for the duration of the study period, and hence, reinfection is not considered.
• Disease-induced mortality is not explicitly included in the model, as the focus is on treatment dynamics and awareness-related effects rather than fatal outcomes.
• This work offers a theoretical and strategic modeling platform rather than a predictive tool for a specific outbreak in a particular region.

In the latter part of the article, we refine the model by introducing a subgroup $S_2$ that participates in an awareness program based on their vulnerability. The model also includes $S_2$ people who may still experience a serious illness during awareness and may need treatment. This analysis provides valuable insights into controlling the spread of COVID-19.

The total population is given by

$$\begin{array}{c}\hfill N\left(t\right)=S_1\left(t\right)+S_2\left(t\right)+I\left(t\right)+T\left(t\right)+R\left(t\right).\end{array}$$

The mathematical form of the model $S_1{S}_{2}ITR$ is described by the following ODE system.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{d{S}_1}{dt}}& ={\Lambda }_1-\alpha S_1-{\beta }_1{S}_{1}I,\hfill \\ \hfill {\displaystyle \frac{d{S}_2}{dt}}& ={\Lambda }_2-\alpha S_2-{\beta }_2{S}_{2}I,\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\beta }_1{S}_{1}I+{\beta }_2{S}_{2}I-(\alpha +\mu )I,\hfill \\ \hfill {\displaystyle \frac{dT}{dt}}& =\mu I-(\alpha +\rho )T,\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& =\rho T-\alpha R,\hfill \end{array}\end{array}$$

(1)

with non-negative initial conditions,

$$\begin{array}{c}\hfill S_1\left(t_0\right)>0,S_2\left(t_0\right)>0,I\left(t_0\right)\ge 0,T\left(t_0\right)\ge 0,R\left(t_0\right)\ge 0\mathrm{and}{t}_0\ge 0.\end{array}$$

(2)

Model (1) considers different disease stages and their interactions among susceptible individuals. This model captures different phases of COVID-19 and the interactions among individuals within the population, helping to understand disease transmission and identify effective mitigation strategies. The state variables $S_1$, $S_2$, I, T, and R are real-valued functions that are continuously differentiable over interval $[0,+\infty )$. Table 1 reveals the physical relevance of the parameters used and their associations with specific phenomena. Moreover, Figure 1 schematically illustrates the impact of coronavirus disease on humans.

Table 1. Description of parameters and their values.

Parameter	Explanations	Numerical	Reference
		Value
${\Lambda }_1$	Entering rate of people to $S_1$.	$0.2$	[41,43]
${\Lambda }_2$	Entering rate of people to $S_2$.	$0.05$	[41,43]
${\beta }_1$	Infection acquiring rate of $S_1$ individuals.	0.2 (0.5)	[41,43]
${\beta }_2$	Infection acquiring rate of $S_2$ individuals.	0.4 (0.6)	[41,43]
$\mu$	Rate at which infected people move to treatment.	$0.1$	[41,43]
$\rho$	Rate at which treated people recover.	$0.3$	[41,43]
$\alpha$	Natural death rate.	$0.25$	[41,43]

Figure 1. Disease progression diagram through compartments.

Fractional Formulation

Conventional integer-order models often fail to capture the memory effects present in biological systems. To address this limitation in system (1), we replace the standard derivative of integer order $D_t$ with the fractional ABC operator ${}_0{}^{ABC}D_t^{\eta }$. This modification allows for a more accurate representation and analysis of memory effects in the COVID-19 dynamics.

Definition 1.

If a differentiable function $\Phi :[a,b]\to \mathbb{N}$ is defined on the interval $[a,b]$, where $\Phi \in H^1(a,b)$, $b>a$ and $\eta \in (0,1]$, then the AB fractional derivative of Φ in the Caputo sense is defined as

$$\begin{array}{c}\hfill {}_a{}^{ABC}D_t^{\eta }\Phi \left(t\right)={\displaystyle \frac{\mathfrak{B}\left(\eta \right)}{1-\eta }}{\int }_a^t{\Phi }^{\prime }\left(\xi \right)E_{\eta }\left[-\eta {\displaystyle \frac{{(t-\xi )}^{\eta }}{1-\eta }}\right]d\xi .\end{array}$$

Here, $E_{\eta }$ denotes a Mittag–Leffler function, whereas $\mathfrak{B}\left(\eta \right)>0$ is a normalization function satisfying $\mathfrak{B}\left(0\right)=\mathfrak{B}\left(1\right)=1$.

Theorem 1.

The fractional order differential equation

$$\begin{array}{c}\hfill {}_a{}^{ABC}D_t^{\eta }\Phi \left(t\right)=f\left(t\right),\end{array}$$

possesses the unique solution

$$\begin{array}{c}\hfill \Phi \left(t\right)=\Phi \left(a\right)+{\displaystyle \frac{1-\eta }{\mathfrak{B}\left(\eta \right)}}f\left(t\right)+{\displaystyle \frac{\eta }{\mathfrak{B}\left(\eta \right)\Gamma \left(\eta \right)}}{\int }_a^{t}f\left(\xi \right){(t-\xi )}^{\eta -1}d\xi .\end{array}$$

Conventional integer-order models are frequently unable to represent the memory phenomena inherent in biological systems. To address this limitation in system (1), we introduce a fractional order model that more accurately reflects the non-local dynamics and long-term dependencies associated with disease transmission. Therefore, for $t\ge 0$ and $\eta \in (0,1]$, the following formulation describes the proposed COVID-19 model, which integrates the Atangana-Baleanu fractional derivative in the Caputo sense:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{S}_1& ={\Lambda }_1-\alpha S_1-{\beta }_1{S}_{1}I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }{S}_2& ={\Lambda }_2-\alpha S_2-{\beta }_2{S}_{2}I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }I& ={\beta }_1{S}_{1}I+{\beta }_2{S}_{2}I-(\alpha +\mu )I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }T& =\mu I-(\alpha +\rho )T,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }R& =\rho T-\alpha R,\hfill \end{array}\end{array}$$

(3)

incorporating the initial conditions

$$\begin{array}{c}\hfill S_1\left(t_0\right)>0,S_2\left(t_0\right)>0,I\left(t_0\right)\ge 0,T\left(t_0\right)\ge 0,R\left(t_0\right)\ge 0\mathrm{where}{t}_0\ge 0.\end{array}$$

(4)

In model (3), the application of the fractional derivative ${}_0{}^{ABC}D_t^{\eta }$ leads to dimensional inconsistency when $\eta \ne 1$. Specifically, the left-hand side has dimensions of individuals·(time)^−η, while the right-hand side terms have dimensions of individuals·(time)⁻¹. These dimensions only align when $\eta =1$; otherwise, the model is not dimensionally consistent. The primary concern in model (3) stems from the use of the fractional derivative ${}_0{}^{ABC}D_t^{\eta }$, which results in dimensional inconsistency when $\eta \ne 1$.

The fractional derivative ${}_0{}^{ABC}D_t^{\eta }$ has dimensions of (time)^−η, whereas the rates $\alpha ,\mu ,\rho ,{\beta }_1,{\beta }_2$ have dimensions of (time)⁻¹, requiring adjustment for consistency. We introduce a characteristic time scale $\tau$ (time) to rescale the rate constants and align their dimensions with the fractional derivative. We define a time scale $\tau$ with dimensions of time. The rate constants are then rescaled as

$$\begin{array}{cc}\hfill & \overline{\alpha }=\alpha \ast {\tau }^{1-\eta },\overline{\mu }=\mu \ast {\tau }^{1-\eta },\overline{\rho }=\rho \ast {\tau }^{1-\eta },{\overline{\beta }}_1={\beta }_1\ast {\tau }^{1-\eta },\hfill \\ \hfill & {\overline{\beta }}_2={\beta }_2\ast {\tau }^{1-\eta },{\overline{\Lambda }}_1={\Lambda }_1\ast {\tau }^{1-\eta },{\overline{\Lambda }}_2={\Lambda }_2\ast {\tau }^{1-\eta }.\hfill \end{array}$$

The rescaled constants $\overline{\alpha }$, $\overline{\mu }$, ${\overline{\beta }}_1$, ${\overline{\beta }}_2$, ${\overline{\Lambda }}_1$, and ${\overline{\Lambda }}_2$ possess dimensions of individuals·(time)^−η, which aligns with the fractional derivative ${}_0{}^{ABC}D_t^{\eta }$. Substituting them into model (3), we obtain the following dimensionally consistent system:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{S}_1& ={\overline{\Lambda }}_1-\overline{\alpha }{S}_1-{\overline{\beta }}_1{S}_{1}I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }{S}_2& ={\overline{\Lambda }}_2-\overline{\alpha }{S}_2-{\overline{\beta }}_2{S}_{2}I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }I& ={\overline{\beta }}_1{S}_{1}I+{\overline{\beta }}_2{S}_{2}I-(\overline{\alpha }+\overline{\mu })I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }T& =\overline{\mu }I-(\overline{\alpha }+\overline{\rho })T,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }R& =\overline{\rho }T-\overline{\alpha }R,\hfill \end{array}\end{array}$$

(5)

with initial state values

$$\begin{array}{c}\hfill S_1\left(t_0\right)>0,S_2\left(t_0\right)>0,I\left(t_0\right)\ge 0,T\left(t_0\right)\ge 0,R\left(t_0\right)\ge 0\mathrm{and}{t}_0=0.\end{array}$$

(6)

For notational simplicity, we consider $\overline{\alpha }=\alpha$, ${\overline{\Lambda }}_1={\Lambda }_1$, ${\overline{\Lambda }}_2={\Lambda }_2$, $\overline{\mu }=\mu$, $\overline{\rho }=\rho$, ${\overline{\beta }}_1={\beta }_1$, and ${\overline{\beta }}_2={\beta }_2$. Thus, expressing system (5) in its simplified form gives

$$\begin{array}{c}\hfill {}_0{}^{ABC}D_t^{\eta }\upsilon \left(t\right)=F(t,\upsilon \left(t\right)),\upsilon \left(t_0\right)={\upsilon }_0,\mathrm{and}0<t_0<+\infty .\end{array}$$

(7)

where $\upsilon :[0,+\infty )\to {\mathbb{R}}^5$ and $F:[t_0,+\infty )\times \Delta \to {\mathbb{R}}^5$ are vector valued functions with

$$\begin{array}{c}\hfill \upsilon \left(t\right)=\left[\begin{array}{c}{S}_1\left(t\right)\\ S_2\left(t\right)\\ I\left(t\right)\\ T\left(t\right)\\ R\left(t\right)\end{array}\right],{\upsilon }_0=\left[\begin{array}{c}{S}_1\left(t_0\right)\\ S_2\left(t_0\right)\\ I\left(t_0\right)\\ T\left(t_0\right)\\ R\left(t_0\right)\end{array}\right],F(t,\upsilon \left(t\right))=\left[\begin{array}{c}{\Lambda }_1-\alpha S_1-{\beta }_1{S}_{1}I,\\ {\Lambda }_2-\alpha S_2-{\beta }_2{S}_{2}I,\\ {\beta }_1{S}_{1}I+{\beta }_2{S}_{2}I-(\alpha +\mu )I,\\ \mu I-(\alpha +\rho )T,\\ \rho T-\alpha R,\end{array}\right].\end{array}$$

By analyzing COVID-19 patterns with this model, we gain deeper insights into disease spread. This analysis is crucial for evaluating treatment and awareness strategies, acknowledging the practical challenges in achieving perfect outcomes. Our goal is to contribute to developing effective control strategies for managing and reducing the spread of coronavirus, balancing treatment rates and awareness measures.

3. Analytical Results with Discussions

This section presents theoretical results such as the existence and uniqueness of solutions, positivity and boundedness, the calculation of the reproductive number, and the evaluation of local and global stability at steady state points [45]. Each of these topics will be explored in the subsequent subsections.

3.1. Existence of a Unique Solution

Lemma 1 provides the conditions under which solutions to system (7) are unique and exist.

Lemma 1

([46]). For the fractional-order system (7) with $\eta \in (0,1]$, a unique solution exists on the interval $[t_0,+\infty )\times \Delta$ if the function $F(t,\upsilon )$ meets the Lipschitz condition with respect to the second argument.

Theorem 2.

For an initial point $X_{t_0}=(S_1\left(t_0\right),S_2\left(t_0\right),I\left(t_0\right),T\left(t_0\right),R\left(t_0\right))\in \Omega$, there exists a unique solution $X\left(t\right)=(S_1\left(t\right),S_2\left(t\right),I\left(t\right),T\left(t\right),R\left(t\right))\in \Omega$ satisfying system (7) $\forall t>t_0$.

Proof. 

Let $Y,Z\in \Omega$ where $Y=(S_1,S_2,I,T,R)$ and $Z=({\overline{S}}_1,{\overline{S}}_2,{\overline{I}}_1,{\overline{T}}_1,{\overline{R}}_1)$. Next, consider mapping $\psi :\Omega \to {\mathbb{R}}^5$ where $\psi \left(X\right)=({\psi }_1\left(X\right),{\psi }_2\left(X\right),{\psi }_3\left(X\right),{\psi }_4\left(X\right),{\psi }_5\left(X\right))$, with

$$\begin{array}{cc}\hfill {\psi }_1\left(X\right)& ={\Lambda }_1-\alpha S_1-{\beta }_1{S}_{1}I,\hfill \\ \hfill {\psi }_2\left(X\right)& ={\Lambda }_2-\alpha S_2-{\beta }_2{S}_{2}I,\hfill \\ \hfill {\psi }_3\left(X\right)& ={\beta }_1{S}_{1}I+{\beta }_2{S}_{2}I-(\alpha +\mu )I,\hfill \\ \hfill {\psi }_4\left(X\right)& =\mu I-(\alpha +\rho )T,\hfill \\ \hfill {\psi }_5\left(X\right)& =\rho T-\alpha R.\hfill \end{array}$$

For any Y, Z in $\Omega$, we have

$$\begin{array}{cc}\hfill \Vert \psi \left(Y\right)-\psi \left(Z\right)\Vert & =|{\Lambda }_1-\alpha S_1-{\beta }_1{S}_{1}I-{\Lambda }_1+\alpha {\overline{S}}_1+{\beta }_1{\overline{S}}_1\overline{I}|\hfill \\ & +|{\Lambda }_2-\alpha S_2-{\beta }_2{S}_{2}I-{\Lambda }_2+\alpha {\overline{S}}_2+{\beta }_2{\overline{S}}_2\overline{I}|\hfill \\ & +|{\beta }_1{S}_{1}I+{\beta }_2{S}_{2}I-(\alpha +\mu )I-{\beta }_1{\overline{S}}_1\overline{I}-{\beta }_2{\overline{S}}_2\overline{I}+(\alpha +\mu )\overline{I}|\hfill \\ & +|\mu I-(\alpha +\rho )T-\mu \overline{I}+(\alpha +\rho )\overline{T}|+|\rho T-\alpha R-\rho \overline{T}+\alpha \overline{R}|\hfill \\ \hfill & =|-\alpha (S_1-{\overline{S}}_1)-{\beta }_1(S_{1}I-{\overline{S}}_1\overline{I})|+|-\alpha (S_2-{\overline{S}}_2)-{\beta }_2(S_{2}I-{\overline{S}}_2\overline{I})|\hfill \\ & +|{\beta }_1(S_{1}I-{\overline{S}}_1\overline{I})+{\beta }_2(S_{2}I-{\overline{S}}_2\overline{I})-(\alpha +\mu )(I-\overline{I})|\hfill \\ & +|\mu (I-\overline{I})-(\alpha +\rho )(T-\overline{T})|+|\rho (T-\overline{T})-\alpha (R-\overline{R})|\hfill \\ \hfill & \le \alpha |S_1-{\overline{S}}_1|+\alpha |S_2-{\overline{S}}_2|+2{\beta }_1|S_{1}I-{\overline{S}}_1\overline{I}|+2{\beta }_2|S_{2}I-{\overline{S}}_2\overline{I}|\hfill \\ & +(\alpha +2\mu )|I-\overline{I}|+(\alpha +2\rho )|T-\overline{T}|+\alpha |R-\overline{R}|\hfill \\ \hfill & \le \alpha |S_1-{\overline{S}}_1|+\alpha |S_2-{\overline{S}}_2|+2{\beta }_1{\sigma }_2\left(\right|S_1-{\overline{S}}_1|+|I-\overline{I}\left|\right)+2{\beta }_2{\sigma }_2\left(\right|S_2-{\overline{S}}_2|+|I-\overline{I}\left|\right)\hfill \\ & +(\alpha +2\mu )|I-\overline{I}|+(\alpha +2\rho )|T-\overline{T}|+\alpha |R-\overline{R}|\hfill \\ \hfill & \le (\alpha +2{\beta }_1{\sigma }_2)|S_1-{\overline{S}}_1|+(\alpha +2{\beta }_2{\sigma }_2)|S_2-{\overline{S}}_2|+(\alpha +2\mu +2{\beta }_1{\sigma }_2+2{\beta }_2{\sigma }_2)|I-\overline{I}|\hfill \\ \hfill & +(\alpha +2\rho )|T-\overline{T}|+\alpha |R-\overline{R}|\hfill \\ \hfill & \le M_1\left[|S_1-{\overline{S}}_1|+|S_2-{\overline{S}}_2|+|I-\overline{I}|+|T-\overline{T}|+|R-\overline{R}|\right]=M_1\Vert Y-Z\Vert \hfill \end{array}$$

where $M_1=max\left\{\alpha +2{\beta }_1{\sigma }_2,\alpha +2{\beta }_2{\sigma }_2,\alpha +2\mu +2{\beta }_1{\sigma }_2+2{\beta }_2{\sigma }_2,\alpha +2\rho ,\alpha \right\}$. Therefore, the function $\psi \left(X\right)$ satisfies the Lipschitz condition. Consequently, the system (7) has a unique solution in $\Omega$. This completes the proof. □

3.2. Essential Model Characteristics

Now, we demonstrate the non-negativity and boundedness of the solution of system (7) for $t\ge 0$.

Theorem 3.

The system (7) has a positive and bounded solution provided that the initial conditions are non-negative $\forall t\ge 0$.

Proof. 

With $\Lambda ={\Lambda }_1+{\Lambda }_2$, the dynamics of the total population is given as

$$\begin{array}{c}\hfill {}_0{}^{ABC}D_t^{\eta }N\left(t\right)=\Lambda -\alpha N\left(t\right).\end{array}$$

(8)

After extensive computations, we conclude that

$$\begin{array}{c}\hfill N\left(t\right)=N\left(t_0\right)\times E_{\eta }(-\alpha t^{\eta })+{\displaystyle \frac{\Lambda }{\alpha }}\left[1-E_{\eta }(-\alpha t^{\eta })\right].\end{array}$$

Since $0<E_{\eta }(-\alpha t^{\eta })\le 1$ and $1-E_{\eta }(-\alpha t^{\eta })\le 1$, it follows that

$$\begin{array}{c}\hfill N\left(t\right)\le {\displaystyle \frac{\Lambda }{\alpha }}+N\left(t_0\right),\mathrm{where}N\left(t_0\right)\mathrm{denotes}\mathrm{the}\mathrm{initial}\mathrm{population}\mathrm{size}.\end{array}$$

Hence, $N\left(t\right)$ originating in ${\mathbb{R}}^5$ remains bounded for all $t\ge 0$. Thus, all other states of (7) also stay bounded over time [28].

To verify the non-negativity of solutions, we write the first equation of model (7) as follows:

$$\begin{array}{c}\hfill {}_0{}^{ABC}D_t^{\eta }{S}_1\left(t\right)\ge -(\alpha +{\beta }_{1}I\left(t\right))S_1\left(t\right).\end{array}$$

(9)

Since the solutions remain bounded, Equation (9) simplifies to

$$\begin{array}{c}\hfill {}_0{}^{ABC}D_t^{\eta }{S}_1\left(t\right)\ge -K{S}_1\left(t\right),\end{array}$$

(10)

where ${\displaystyle K=\underset{t\to \infty }{sup}\left\{\alpha +{\beta }_{1}I\left(t\right)\right\}}$ is defined as a constant.

Applying the Laplace transform to inequality (10) gives

$$\begin{array}{c}\hfill {\displaystyle \frac{B\left(\eta \right)s^{\eta }}{\eta +(1-\eta )s^{\eta }}}\mathcal{L}\left[S_1\left(t\right)\right]\left(s\right)\ge {\displaystyle \frac{B\left(\eta \right)s^{\eta -1}}{\eta +(1-\eta )s^{\eta }}}{S}_1\left(t_0\right)-K\mathcal{L}\left[S_1\left(t\right)\right]\left(s\right),\end{array}$$

After some manipulations, we obtain the following:

$$\begin{array}{c}\hfill \mathcal{L}\left[S_1\left(t\right)\right]\left(s\right)\ge {\displaystyle \frac{B\left(\eta \right)S_1\left(t_0\right)}{B\left(\eta \right)+K(1-\eta )}}\times {\displaystyle \frac{s^{\eta -1}}{s^{\eta }+\frac{K\eta }{B\left(\eta \right)+K(1-\eta )}}}.\end{array}$$

Using the inverse Laplace transform, the inequality becomes

$$\begin{array}{c}\hfill S_1\left(t\right)\ge {\displaystyle \frac{B\left(\eta \right)S_1\left(t_0\right)}{K(1-\eta )+B\left(\eta \right)}}\times E_{\eta ,1}\left(-{\displaystyle \frac{K\eta }{K(1-\eta )+B\left(\eta \right)}}{t}^{\eta }\right).\end{array}$$

(11)

The solution $S_1\left(t\right)$ is always positive for $t\ge 0$, because it exceeds the product of positive terms. Similarly, all other solutions remain positive for $t\ge 0$. Thus, any solution in ${\mathbb{R}}_{+}^5$ will asymptotically enter and stay within the feasible region provided initial conditions are non-negative.

$$\begin{array}{c}\hfill \Pi =\left\{(S_1,S_2,I,T,R)\in {\mathbb{R}}_{+}^5,0\le N\left(t\right)\le N\left(t_0\right)+{\displaystyle \frac{\Lambda }{\alpha }}\right\}.\end{array}$$

Hence, the region $\Pi$ is positively invariant under system (7). □

3.3. Equilibrium Points and Threshold Parameter

The disease-free equilibrium (DFE) signifies a state of the Corona model in which the disease is completely absent from the human community. Mathematically, this is the state where infectivity is zero. Therefore, the model (7) has a DFE point ${\mathcal{F}}^0=(S_1^0,S_2^0,I^0,T^0,R^0)\in \Pi$, with coordinates

$$\begin{array}{c}\hfill S_1^0={\displaystyle \frac{{\Lambda }_1}{\alpha }}>0,S_2^0={\displaystyle \frac{{\Lambda }_2}{\alpha }}>0,I^0=0,T^0=0,R^0=0.\end{array}$$

In infectious disease modeling, the reproductive number indicates whether an outbreak will cease or continue to spread. This is commonly denoted by ${\Re }_0$, representing the new infections induced by an infected human in a susceptible population. When ${\Re }_0>1$, each infected person spreads the disease to more than one other human, possibly causing an epidemic. Conversely, if ${\Re }_0<1$, each infected individual, on average, passes the disease to less than one individual, implying that the disease will vanish over time [43].

For model (7), we implement the next-generation matrix approach that focuses on the dynamics of compartments I and T, using sensitivity matrices for new infection and transition rates. These matrices are

$$\begin{array}{c}\hfill \mathcal{F}=\left[\begin{array}{c}({\beta }_1{S}_1+{\beta }_2{S}_2)I\\ 0\end{array}\right],\mathcal{G}=\left[\begin{array}{c}(\mu +\alpha )I\\ -\mu I+(\rho +\alpha )T\end{array}\right].\end{array}$$

The Jacobian of the matrices $\mathcal{F}$ and $\mathcal{G}$, evaluated at the point ${\mathcal{F}}^0$, are

$$\begin{array}{c}\hfill \overline{\mathcal{F}}=\left[\begin{array}{cc}{\beta }_1{S}_1^0+{\beta }_2{S}_2^0& 0\\ 0& 0\end{array}\right],\overline{\mathcal{G}}=\left[\begin{array}{cc}\mu +\alpha & 0\\ -\mu & \rho +\alpha \end{array}\right].\end{array}$$

Hence, the number

$$\begin{array}{c}\hfill {\Re }_0={\displaystyle \frac{{\beta }_1{\Lambda }_1+{\beta }_2{\Lambda }_2}{\alpha (\mu +\alpha )}},\end{array}$$

(12)

as the spectral radius of the matrix

$$\begin{array}{cc}\hfill \overline{\mathcal{F}}{\overline{\mathcal{V}}}^{-1}& ={\displaystyle \frac{1}{(\mu +\alpha )(\alpha +\rho )}}\left[\begin{array}{c}\begin{array}{cc}\left({\displaystyle \frac{{\beta }_1{\Lambda }_1}{\alpha }}+{\displaystyle \frac{{\beta }_2{\Lambda }_1}{\alpha }}\right)& 0\\ 0& 0\end{array}\end{array}\right].\left[\begin{array}{c}\begin{array}{cc}\alpha +\rho & 0\\ \mu & \mu +\alpha \end{array}\end{array}\right],\hfill \end{array}$$

specifies the threshold parameter value for the model (7).

The model (7) has a unique equilibrium for the disease-present case, occurring at ${\mathcal{F}}^{\ast }=(S_1^{\ast },S_2^{\ast },I^{\ast },T^{\ast },R^{\ast })\in \Pi$, where

$$\begin{array}{c}\hfill S_1^{\ast }={\displaystyle \frac{{\Lambda }_1}{\alpha +{\beta }_1{I}^{\ast }}},S_2^{\ast }={\displaystyle \frac{{\Lambda }_2}{\alpha +{\beta }_2{I}^{\ast }}},T^{\ast }={\displaystyle \frac{\mu I^{\ast }}{\rho +\alpha }},R^{\ast }={\displaystyle \frac{\rho \mu I^{\ast }}{\alpha (\rho +\alpha )}}.\end{array}$$

The third equation of the model (7) simplifies to

$$\begin{array}{c}\hfill ({\beta }_1{S}_1^{\ast }+{\beta }_2{S}_2^{\ast }-(\mu +\alpha ))I^{\ast }=0.\end{array}$$

At the Corona present state, where $I^{\ast }\ne 0$, it follows that

$$\begin{array}{c}\hfill {\beta }_1{S}_1^{\ast }+{\beta }_2{S}_2^{\ast }-(\mu +\alpha )=0.\end{array}$$

Plugging in $S_1^{\ast }$ and $S_2^{\ast }$ values in the above equation, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{{\beta }_1{\Lambda }_1}{\alpha +{\beta }_1{I}^{\ast }}}+{\displaystyle \frac{{\beta }_2{\Lambda }_2}{\alpha +{\beta }_2{I}^{\ast }}}-(\mu +\alpha )=0.\end{array}$$

(13)

After simplifying the left side of Equation (13), we have

$$\begin{array}{c}\hfill {\mathrm{a}}_1{\left(I^{\ast }\right)}^2+{\mathrm{a}}_2{I}^{\ast }+{\mathrm{a}}_3=0,\end{array}$$

(14)

where

$$\begin{array}{cc}\hfill {\mathrm{a}}_1& =(\mu +\alpha ){\beta }_1{\beta }_2>0,\hfill \\ \hfill {\mathrm{a}}_2& =\alpha (\mu +\alpha )({\beta }_1+{\beta }_2)-{\beta }_1{\beta }_2({\Lambda }_1+{\Lambda }_2)>0,\hfill \\ \hfill {\mathrm{a}}_3& ={\alpha }^2(\mu +\alpha )(1-{\Re }_0)<0,\mathrm{whenever}{\Re }_0>1.\hfill \end{array}$$

By Descartes’ rule of signs, polynomial (14) exhibits one sign change in its coefficients, given that $\mathrm{a}1,\mathrm{a}2>0$ and $\mathrm{a}3<0$ when $\Re 0>1$. Therefore, for $\Re 0>1$, it has precisely one positive real root, denoted as I, which justifies the existence of the equilibrium $\mathcal{F}$.

3.4. Stability Investigations

To prove that our problem is well posed, we investigate the stability of the model (7) at equilibrium points. To justify global stability, we implement the theory of Lyapunov functions [47] along with the LaSalle Invariance Principle (LIP) [48].

3.4.1. Analysis of Local Dynamics

Local stability is explored by linearizing the system at the equilibrium points and evaluating the eigenvalues of the Jacobian matrix. If the real parts of the eigenvalues are less than zero, the equilibrium points are stable.

Theorem 4.

Corona-free equilibrium ${\mathcal{F}}^0$ is locally asymptotically stable (LAS) when ${\Re }_0<1$. Conversely, if ${\Re }_0>1$, the equilibrium becomes unstable.

Proof. 

The Jacobian $J(S_1,S_2,I,T,R)$ for the system (3), when computed at ${\mathcal{F}}^0$, is given by

$$\begin{array}{c}\hfill J\left({\mathcal{F}}^0\right)=\left(\begin{array}{ccccc}-\alpha & 0& -{\beta }_1{S}_1^0& 0& 0\\ 0& -\alpha & -{\beta }_2{S}_2^0& 0& 0\\ 0& 0& {\beta }_1{S}_1^0+{\beta }_2{S}_2^0-(\mu +\alpha )& 0& 0\\ 0& 0& \mu & -(\rho +\alpha )& 0\\ 0& 0& 0& \rho & -\alpha \end{array}\right).\end{array}$$

Then $J\left({\mathcal{F}}^0\right)$ has the following eigenvalues:

$$\begin{array}{c}\hfill {\lambda }_1^0=-\alpha <0,{\lambda }_2^0=-\alpha <0,{\lambda }_3^0=-\alpha <0,{\lambda }_4^0=-(\rho +\alpha )<0,{\lambda }_5^0=(\mu +\alpha )({\Re }_0-1).\end{array}$$

The real parts of the eigenvalues ${\lambda }_i,i=1,\dots ,4$ are negative, while the real part of the eigenvalue ${\lambda }_5$ is negative provided ${\Re }_0<1$. This establishes the result that ${\mathcal{F}}^0$ is LAS if ${\Re }_0<1$. □

Theorem 5.

Corona-present equilibrium ${\mathcal{F}}^{\ast }$ is locally asymptotically stable (LAS) whenever ${\Re }_0>1$. Whenever ${\Re }_0<1$, the point ${\mathcal{F}}^{\ast }$ is unstable.

Proof. 

The Jacobian $J(S_1,S_2,I,T,R)$ for the system (7) at ${\mathcal{F}}^{\ast }$ can be expressed as

$$\begin{array}{c}\hfill J\left({\mathcal{F}}^{\ast }\right)=\left(\begin{array}{ccccc}-{\displaystyle \frac{{\Lambda }_1}{S_1^{\ast }}}& 0& -{\beta }_1{S}_1^{\ast }& 0& 0\\ 0& -{\displaystyle \frac{{\Lambda }_2}{S_2^{\ast }}}& -{\beta }_2{S}_2^{\ast }& 0& 0\\ {\beta }_1{I}^{\ast }& {\beta }_2{I}^{\ast }& 0& 0& 0\\ 0& 0& \mu & -(\rho +\alpha )& 0\\ 0& 0& 0& \rho & -\alpha \end{array}\right).\end{array}$$

To obtain eigenvalues of $J\left({\mathcal{F}}^{\ast }\right)$, we set $|J\left(C^{\ast }\right)-\lambda I^{\ast \ast }|=0$, which is

$$\begin{array}{c}\hfill \left|\begin{array}{c}\begin{array}{ccccc}-{\displaystyle \frac{{\Lambda }_1}{S_1^{\ast }}}-\lambda & 0& -{\beta }_1{S}_1^{\ast }& 0& 0\\ 0& -{\displaystyle \frac{{\Lambda }_2}{S_2^{\ast }}}-\lambda & -{\beta }_2{S}_2^{\ast }& 0& 0\\ {\beta }_1{I}^{\ast }& {\beta }_2{I}^{\ast }& 0-\lambda & 0& 0\\ 0& 0& \mu & -(\alpha +\rho )-\lambda & 0\\ 0& 0& 0& 0& -\alpha -\lambda \end{array}\end{array}\right|=0.\end{array}$$

$$\begin{array}{c}\hfill -(\alpha +\lambda )\left|\begin{array}{c}\begin{array}{cccc}-{\displaystyle \frac{{\Lambda }_1}{S_1^{\ast }}}-\lambda & 0& -{\beta }_1{S}_1^{\ast }& 0\\ 0& -{\displaystyle \frac{{\Lambda }_2}{S_2^{\ast }}}-\lambda & -{\beta }_2{S}_2^{\ast }& 0\\ {\beta }_1{I}^{\ast }& {\beta }_2{I}^{\ast }& -\lambda & 0\\ 0& 0& \mu & -(\alpha +\rho )-\lambda \end{array}\end{array}\right|=0.\end{array}$$

$$\begin{array}{c}\hfill (\alpha +\lambda )(\alpha +\rho +\lambda )\left|\begin{array}{c}\begin{array}{ccc}-{\displaystyle \frac{{\Lambda }_1}{S_1^{\ast }}}-\lambda & 0& -{\beta }_1{S}_1^{\ast }\\ 0& -{\displaystyle \frac{{\Lambda }_2}{S_2^{\ast }}}-\lambda & -{\beta }_2{S}_2^{\ast }\\ {\beta }_1{I}^{\ast }& {\beta }_2{I}^{\ast }& -\lambda \end{array}\end{array}\right|=0.\end{array}$$

Incorporation of $a={\displaystyle \frac{{\Lambda }_1}{S_1^{\ast }}}$, $b={\displaystyle \frac{{\Lambda }_2}{S_2^{\ast }}}$, $c={\beta }_1^2{S}_1^{\ast }$, and $d={\beta }_2^2{S}_2^{\ast }$ in above expression leads to

$$\begin{array}{c}\hfill (\alpha +\lambda )(\alpha +\rho +\lambda )\left|\begin{array}{c}\begin{array}{ccc}-a-\lambda & 0& -{\displaystyle \frac{c}{{\beta }_1}}\\ 0& -b-\lambda & -{\displaystyle \frac{d}{{\beta }_2}}\\ {\beta }_1{I}^{\ast }& {\beta }_2{I}^{\ast }& -\lambda \end{array}\end{array}\right|=0.\end{array}$$

This can also be written as

$$\begin{array}{cc}\hfill (\alpha +\lambda )(\alpha +\rho +\lambda )& \left[{\lambda }^3+(a+b){\lambda }^2+(ab+(c+d)I^{\ast })\lambda +(ad+bc)I^{\ast }\right]=0.\hfill \end{array}$$

Clearly, the first two eigenvalues of $J\left({\mathcal{F}}^{\ast }\right)$ are

$$\begin{array}{c}\hfill {\lambda }_1=-\alpha <0,{\lambda }_2=-(\alpha +\rho )<0.\end{array}$$

The remaining eigenvalues are obtained as the roots of the equation

$$\begin{array}{c}\hfill {\lambda }^3+(a+b){\lambda }^2+(ab+(c+d)I^{\ast })\lambda +(ad+bc)I^{\ast }=0.\end{array}$$

(15)

We apply the Routh–Hurwitz method. We need to prove that the polynomial (15) is a Hurwitz polynomial. For this, we have to show that $a_0$, $a_1$, and $a_2$ are positive and that $a_1{a}_2>a_0$. We verify these properties as follows. On comparison with (15), we have

$$\begin{array}{c}\hfill a_0=(ad+bc)I^{\ast }>0,a_1=ab+(c+d)I^{\ast }>0,a_2=a+b>0.\end{array}$$

Also,

$$\begin{array}{c}\hfill a_1{a}_2=(a+b)\left[ab+(c+d)I^{\ast }\right]=(a^{2}b+b^{2}a)+(ac+bd)I^{\ast }+(bc+ad)I^{\ast },\end{array}$$

which is clear greater than $a_0=(ad+bc)I^{\ast }$. Consequently, $a_1{a}_2>a_0$. This implies that the expression given in (15) is a Hurwitz polynomial. Hence, by Routh–Hurwitz criterion, the eigenvalues of the polynomial (15) are negative. Thus, the point ${\mathcal{F}}^{\ast }$ of system (7) is LAS, which completes the proof. Once the dynamical system (7) achieves stability at ${\mathcal{F}}^{\ast }$, the Coronavirus will remain in individuals, validating the claim. □

3.4.2. Analysis of Global Dynamics

Global stability is generally established using techniques such as Lyapunov functions to demonstrate that all trajectories converge to the equilibrium.

Theorem 6.

The equilibrium state ${\mathcal{F}}^0$ is globally asymptotically stable (GAS) when ${\Re }_0<1$.

Proof. 

Define a candidate Lyapunov function, given by the expression

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_0=L_0(S_1,S_2,I,T,R)=S_1-S_1^0-S_1^{0}ln{\displaystyle \frac{S_1}{S_1^0}}+S_2-S_2^0-S_2^{0}ln{\displaystyle \frac{S_2}{S_2^0}}+I.\end{array}\end{array}$$

(16)

Taking the fractional derivative of both sides with respect to time yields

$$\begin{array}{c}\hfill {}_0{}^{ABC}D_t^{\eta }{L}_0=\left(1-{\displaystyle \frac{S_1^0}{S_1}}\right){\displaystyle \frac{d{S}_1}{dt}}+\left(1-{\displaystyle \frac{S_2^0}{S_2}}\right){\displaystyle \frac{d{S}_2}{dt}}+{\displaystyle \frac{dI}{dt}}.\end{array}$$

Substitution of derivatives leads to

$$\begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{L}_0& =\left(1-{\displaystyle \frac{S_1^0}{S_1}}\right)({\Lambda }_1-\alpha S_1-{\beta }_1{S}_{1}I)\hfill \\ \hfill & +\left(1-{\displaystyle \frac{S_2^0}{S_2}}\right)({\Lambda }_2-\alpha S_2-{\beta }_2{S}_{2}I)+{\beta }_1{S}_{1}I+{\beta }_2{S}_{2}I-(\mu +\alpha )I.\hfill \end{array}$$

Performing some computations along with substitutions, we obtain the following expression:

$$\begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{L}_0& =-{\displaystyle \frac{\alpha }{S_1}}{(S_1-S_1^0)}^2-{\displaystyle \frac{\alpha }{S_2}}{(S_2-S_2^0)}^2+(\mu +\alpha )({\Re }_0-1)I.\hfill \end{array}$$

Clearly, ${}_0{}^{ABC}D_t^{\eta }{L}_0\le 0$, when ${\Re }_0<1$. Specifically, ${}_0{}^{ABC}D_t^{\eta }{L}_0=0$ if $S_1=S_1^0$, $S_2=S_2^0$, $I=I^0$. Thus, all trajectories originating from the initial condition ultimately reach a set where ${}_0{}^{ABC}D_t^{\eta }{L}_0=0$, which is

$$\begin{array}{c}\hfill N_0=\left\{(S_1,S_2,I,T,R)\in \Pi :{}_0{}^{ABC}D_t^{\eta }{L}_0=0\right\},\end{array}$$

where the largest invariant subset reduces to the equilibrium point ${\mathcal{F}}^0$. Thus, the point ${\mathcal{F}}^0$ is GAS. □

Theorem 7.

The steady-state point ${\mathcal{F}}^{\ast }$ is globally asymptotically stable (GAS) if ${\Re }_0>1$.

Proof. 

Assume a candidate Lyapunov function, defined by the expression

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_1=L_1(S_1,S_2,I,T,R)=S_1-S_1^{\ast }-S_1^{\ast }ln{\displaystyle \frac{S_1}{S_1^{\ast }}}+S_2-S_2^{\ast }-S_2^{\ast }ln{\displaystyle \frac{S_2}{S_2^{\ast }}}+I-I^{\ast }-I^{\ast }ln{\displaystyle \frac{I}{I^{\ast }}}.\end{array}\end{array}$$

(17)

Fractional differentiation of both sides gives

$$\begin{array}{c}\hfill {}_0{}^{ABC}D_t^{\eta }{L}_1=\left(1-{\displaystyle \frac{S_1^{\ast }}{S_1}}\right){\displaystyle \frac{d{S}_1}{dt}}+\left(1-{\displaystyle \frac{S_2^{\ast }}{S_2}}\right){\displaystyle \frac{d{S}_2}{dt}}+\left(1-{\displaystyle \frac{I^{\ast }}{I}}\right){\displaystyle \frac{dI}{dt}}.\end{array}$$

The inclusion of derivatives leads to

$$\begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{L}_1& =\left(1-{\displaystyle \frac{S_1^{\ast }}{S_1}}\right)({\Lambda }_1-\alpha S_1-{\beta }_1{S}_{1}I)\hfill \\ \hfill & +\left(1-{\displaystyle \frac{S_2^{\ast }}{S_2}}\right)({\Lambda }_2-\alpha S_2-{\beta }_2{S}_{2}I)+\left(1-{\displaystyle \frac{I^1}{I}}\right)\left[{\beta }_1{S}_{1}I+{\beta }_2{S}_{2}I-(\mu +\alpha )I\right].\hfill \end{array}$$

This can be written as

$$\begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{L}_1& =-{\displaystyle \frac{\alpha }{S_1}}{(S_1-S_1^{\ast })}^2-{\displaystyle \frac{\alpha }{S_2}}{(S_2-S_2^{\ast })}^2\hfill \\ \hfill & +{\beta }_1{S}_1^{\ast }{I}^{\ast }\left(2-{\displaystyle \frac{S_1^{\ast }}{S_1}}-{\displaystyle \frac{S_1}{S_1^{\ast }}}\right)+{\beta }_2{S}_2^{\ast }{I}^{\ast }\left(2-{\displaystyle \frac{S_2^{\ast }}{S_2}}-{\displaystyle \frac{S_2}{S_2^{\ast }}}\right).\hfill \end{array}$$

Applying the Arithmetic–Geometric Inequality, we verify that

$$\begin{array}{c}\hfill 2-{\displaystyle \frac{S_1^{\ast }}{S_1}}-{\displaystyle \frac{S_1}{S_1^{\ast }}}\le 0,2-{\displaystyle \frac{S_2^{\ast }}{S_2}}-{\displaystyle \frac{S_2}{S_2^{\ast }}}\le 0.\end{array}$$

Therefore, ${}_0{}^{ABC}D_t^{\eta }{L}_1<0$. In particular, ${}_0{}^{ABC}D_t^{\eta }{L}_1=0$ iff $S_1=S_1^{\ast }$ and $S_2=S_2^{\ast }$. Thus, all solution curves originating from non-negative ICs will eventually converge to a set where ${}_0{}^{ABC}D_t^{\eta }{L}_1=0$, i.e.:

$$\begin{array}{c}\hfill N_1=\left\{(S_1,S_2,I,T,R)\in \Pi :{}_0{}^{ABC}D_t^{\eta }{L}_1=0\right\}.\end{array}$$

Thus, the largest invariant set in $\Pi$ is the endemic equilibrium ${\mathcal{F}}^{\ast }$, indicating that ${\mathcal{F}}^{\ast }$ is GAS [48]. □

4. Computational Analysis-I

In this segment, we study the numerical stability of the model (7) using the Toufik–Atangana method [42]. This method transforms system (7) into its discrete form as follows:

At each time step $t_{n+1}$, the system variables $S_1,S_2,I,T,R$ are updated iteratively based on the initial conditions and a discrete summation process. The general update formula for each variable X (where X represents $S_1$, $S_2$, I, T, R) is given by

$$\begin{array}{c}\hfill X\left(t_{n+1}\right)=X\left(t_0\right)+{\displaystyle \frac{1-\eta }{\mathfrak{B}\left(\eta \right)}}{F}_X(t_n,\upsilon \left(t_n\right))+{\displaystyle \frac{\eta }{\mathfrak{B}\left(\eta \right)}}\sum _{j=0}^n{\mathcal{G}}_X(t_j,t_{j-1}),\end{array}$$

(18)

where the summation term ${\mathcal{G}}_X(t_j,t_{j-1})$ is defined as

$$\begin{array}{c}\hfill {\mathcal{G}}_X(t_j,t_{j-1})={\displaystyle \frac{h^n}{\Gamma (\eta +2)}}\left[F_X(t_j,\upsilon \left(t_j\right)){\mathcal{C}}_1(n,j)-F_X(t_{j-1},\upsilon \left(t_{j-1}\right)){\mathcal{C}}_2(n,j)\right].\end{array}$$

(19)

The coefficients ${\mathcal{C}}_1(n,j)$ and ${\mathcal{C}}_2(n,j)$ in (19) capture the influence of past states on the current state and are given by

$$\begin{array}{cc}\hfill {\mathcal{C}}_1(n,j)& =(n-j+2+\eta ){(n+1-j)}^{\eta }(n-j+2+2\eta ){(n-j)}^{\eta },\hfill \\ \hfill {\mathcal{C}}_2(n,j)& ={(n+1-j)}^{\eta +1}-(n-j+1+\eta ){(n-j)}^{\eta }.\hfill \end{array}$$

Specifically, $C_1(n,j)$ weights the contribution of the function $F_X(t_j,\upsilon \left(t_j\right))$, reflecting the influence of the state at the previous time level $t_j$ on the current update, while $C_2(n,j)$ accounts for the correction associated with the previous step $t_{j-1}$, ensuring numerical consistency and stability in the fractional scheme. These coefficients decay as $n-j$ increases, indicating that more recent states exert a stronger influence than older ones, but past states are never completely neglected.

Thus, each state variable follows the same iterative structure, with the function $F_X(t_n,\upsilon \left(t_n\right))$ determining the system (7) dynamics. Using the scheme (18), we evaluate the effect of a uniform treatment strategy at varying coverage levels. A detailed discretization of the Toufik–Atangana numerical scheme for the equation of type (7) is given in [42,49].

Impact of Time-Invariant Treatment

This study investigates how treatment coverage affects the population dynamics, as shown in Figure 2, Figure 3 and Figure 4. Higher treatment rates ($\mu$) and fractional orders ($\eta$) significantly reduce infections while increasing recovery. Greater treatment coverage also raises the susceptible populations $S_1$ and $S_2$. Notably, Figure 4 suggests that controlling COVID-19 is feasible if $32\%$ infected cases go through treatment as $\eta$ rises. Additionally, determining ${\Re }_0$ at varying treatment levels is essential for assessing COVID-19 control. Figure 5 shows that higher treatment rates reduce transmission, but the virus persists until at least $32\%$ of cases are treated. Below this threshold, ${\Re }_0>1$, indicating continued spread, while at $32\%$ or more, ${\Re }_0<1$, ensuring disease control. Therefore, Figure 4 and Figure 5 confirm that treating at least $32\%$ of infected individuals is essential for eradicating COVID-19.

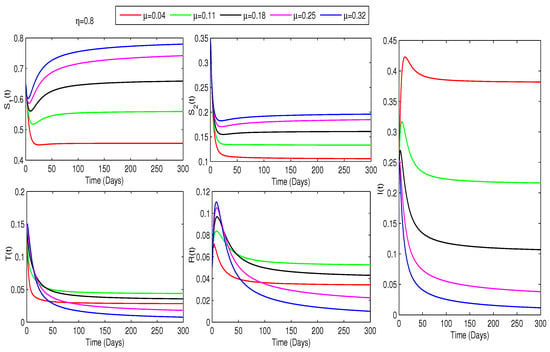
Figure 2. Impact of treatment on COVID-19 dynamics for $\eta =0.8$: Higher $\eta$ and $\mu$ increase $S_1$ and $S_2$ communities while reducing infections.

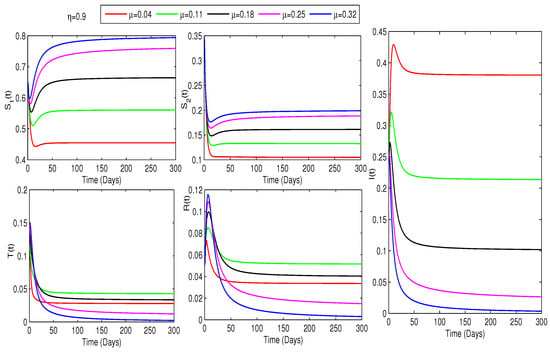
Figure 3. Effect of treatment on COVID-19 dynamics for $\eta =0.9$: An increase in $\eta$ and $\mu$ boosts $S_1$ and $S_2$ populations while lowering infections.

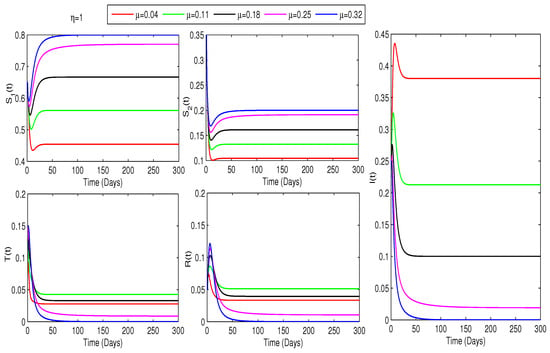
Figure 4. Impact of treatment on COVID-19 dynamics for $\eta =1.0$: Higher $\eta$ and $\mu$ increase $S_1$ and $S_2$ communities while reducing infections. Infectivity becomes zero when $\eta =1.0$ and $\mu =0.32$.

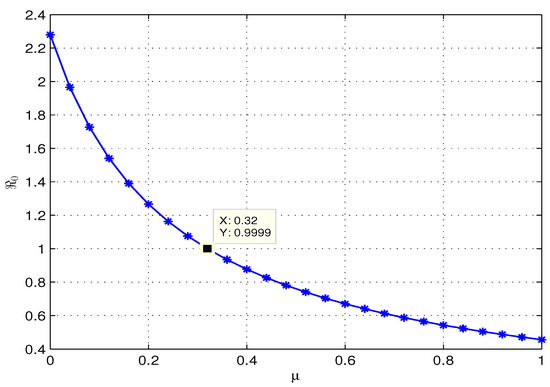
Figure 5. Effect of treatment on ${\Re }_0$. At a $32\%$ treatment level, ${\Re }_0$ falls below 1.

5. Refined Model for Disease Control

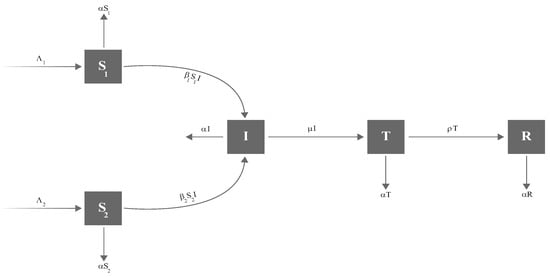
We now introduce a parameter $\xi$ in the model to capture the effect of awareness sessions in lowering the transmission rate from susceptible individuals ($S_2$) to infected individuals (I). These sessions address key topics such as hand hygiene, mask-wearing, social distancing, vaccination, symptom recognition, testing procedures, isolation, travel recommendations, protection of vulnerable groups, and managing mental health. These sessions can be organized through community gatherings, social media platforms, educational resources, or healthcare facilities. By increasing awareness, the parameter $\xi$ may help to slow the transition from $S_2$ to I, thereby restricting the virus spread. Considering these factors, the revised dynamics of the $S_1{S}_{2}ITR$ model, illustrated in Figure 6, is described as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{S}_1& ={\Lambda }_1-\alpha S_1-{\beta }_1{S}_{1}I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }{S}_2& ={\Lambda }_2-\alpha S_2-{\beta }_2(1-\xi )S_{2}I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }I& ={\beta }_1{S}_{1}I+{\beta }_2(1-\xi )S_{2}I-(\alpha +\mu )I,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }T& =\mu I-(\alpha +\rho )T,\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }R& =\rho T-\alpha R,\hfill \end{array}\end{array}$$

(20)

with the initial conditions (6). In the revised model (20), $S_1$ represents the susceptible who have not gone through any awareness sessions, whereas $S_2$ represents the susceptible who have attended awareness sessions.

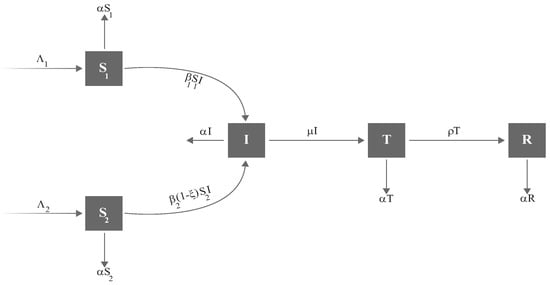
Figure 6. Updated Corona model with the addition of awareness rate $\xi$.

5.1. Analytical Results for Revised Model

The disease-free equilibrium ${\mathcal{F}}^{00}$ of the revised model (20) has the following coordinates:

$$\begin{array}{c}\hfill S_1^{00}={\displaystyle \frac{{\Lambda }_1}{\alpha }}>0,S_2^{00}={\displaystyle \frac{{\Lambda }_2}{\alpha }}>0,I^{00}=0,T^{00}=0,R^{00}=0.\end{array}$$

The reproduction number of the model (20) is computed to give the following number:

$$\begin{array}{c}\hfill {\Re }_{00}={\displaystyle \frac{{\beta }_1{\Lambda }_1+{\beta }_2(1-\xi ){\Lambda }_2}{\alpha (\mu +\alpha )}}.\end{array}$$

The Corona-present equilibrium ${\mathcal{F}}^{\ast \ast }$ of the model (20) has the following coordinates:

$$\begin{array}{c}\hfill S_1^{\ast \ast }={\displaystyle \frac{{\Lambda }_1}{\alpha +{\beta }_1{I}^{\ast \ast }}},S_2^{\ast \ast }={\displaystyle \frac{{\Lambda }_2}{\alpha +{\beta }_2(1-\xi )I^{\ast \ast }}},T^{\ast \ast }={\displaystyle \frac{\mu I^{\ast \ast }}{\rho +\alpha }},R^{\ast \ast }={\displaystyle \frac{\rho \mu I^{\ast \ast }}{\alpha (\rho +\alpha )}}.\end{array}$$

After simplifying the third Equation of model (20), we obtain the polynomial equation

$$\begin{array}{c}\hfill k_1{\left(I^{\ast \ast }\right)}^2+k_2{I}^{\ast \ast }+k_3=0,\end{array}$$

(21)

$$\begin{array}{cc}\hfill k_1& =(1-\xi )(\mu +\alpha ){\beta }_1{\beta }_2>0,\mathrm{provided}\mathrm{that}\xi <1,\hfill \\ \hfill k_2& =\alpha (\mu +\alpha )\left[{\beta }_1+{\beta }_2(1-\xi )\right]-{\beta }_1{\beta }_2(1-\xi )({\Lambda }_1+{\Lambda }_2)>0,\hfill \\ \hfill k_3& ={\alpha }^2(\mu +\alpha )(1-{\Re }_{00})<0,\mathrm{whenever}{\Re }_{00}>1.\hfill \end{array}$$

The polynomial (21) exhibits a single sign change in its coefficients, indicating the presence of one positive real root, denoted by $I^{\ast \ast }$. Hence, the equilibrium point ${\mathcal{F}}^{\ast \ast }$ exists when ${\Re }_{00}>1$.

5.2. Sensitivity of Parameters

Sensitivity analysis [50,51] evaluates the robustness of a model by identifying which parameters have the greatest impact on outcomes, particularly the threshold ${\Re }_{00}$ in system (20). The normalized forward sensitivity index [50] for a parameter p is defined as follows:

$$\begin{array}{c}\hfill {\mathcal{S}}_p^{{\Re }_{00}}={\displaystyle \frac{\partial {\Re }_{00}}{\partial p}}\ast {\displaystyle \frac{p}{{\Re }_{00}}},\end{array}$$

which shows how variations in p affect ${\Re }_{00}$. Parameters with the highest absolute sensitivity indices are the most significant, offering critical insights for accurate epidemic predictions.

The following are the computed sensitivity indices:

$$\begin{array}{cc}\hfill {\mathcal{H}}_{{\Lambda }_1}^{{\Re }_{00}}& ={\displaystyle \frac{{\beta }_1{\Lambda }_1}{{\beta }_1{\Lambda }_1+{\beta }_2(1-\xi ){\Lambda }_2}}>0,{\mathcal{H}}_{{\Lambda }_2}^{{\Re }_{00}}={\displaystyle \frac{{\beta }_2(1-\xi ){\Lambda }_2}{{\beta }_1{\Lambda }_1+{\beta }_2(1-\xi ){\Lambda }_2}}>0,\hfill \\ \hfill {\mathcal{H}}_{{\beta }_1}^{{\Re }_{00}}& ={\displaystyle \frac{{\beta }_1{\Lambda }_1}{{\beta }_1{\Lambda }_1+{\beta }_2(1-\xi ){\Lambda }_2}}>0,{\mathcal{H}}_{{\beta }_2}^{{\Re }_{00}}={\displaystyle \frac{{\beta }_2(1-\xi ){\Lambda }_2}{{\beta }_1{\Lambda }_1+{\beta }_2(1-\xi ){\Lambda }_2}}>0,\hfill \\ \hfill {\mathcal{H}}_{\xi }^{{\Re }_{00}}& ={\displaystyle \frac{-{\beta }_2{\Lambda }_2\xi }{{\beta }_1{\Lambda }_1+{\beta }_2(1-\xi ){\Lambda }_2}}<0,{\mathcal{H}}_{\mu }^{{\Re }_{00}}={\displaystyle \frac{-\mu }{\alpha +\mu }}<0,\hfill \\ \hfill {\mathcal{H}}_{\alpha }^{{\Re }_{00}}& ={\displaystyle \frac{-(\mu +2\alpha )\left[{\beta }_1{\Lambda }_1+{\beta }_2(1-\xi ){\Lambda }_2\right]}{{\alpha }^2{(\mu +\alpha )}^2}}<0.\hfill \end{array}$$

Table 2 shows that ${\Lambda }_1$, ${\Lambda }_2$, ${\beta }_1$, and ${\beta }_2$ increase ${\Re }_{00}$: a 10% increase in these model parameters leads to proportional changes of 8.584%, 1.416%, 8.584%, and 1.416%, respectively. In contrast, $\xi$, $\mu$, and $\alpha$ reduce ${\Re }_{00}$. A 10% increase in these parameters will decrease ${\Re }_{00}$ by 1.159%, 2.857%, and 91.298%, respectively (see Figure 7). Ignoring ${\Lambda }_1$ and ${\Lambda }_2$, ${\Re }_{00}$ is most sensitive to ${\beta }_1$, followed by $\mu$, then ${\beta }_2$, $\xi$, and $\alpha$. Given that the natural death rate $\alpha$ is difficult to manage, efforts should focus on decreasing ${\beta }_1$ through measures like mask-wearing, hygiene practices, and social distancing, followed by ${\beta }_2$.

Table 2. Computed sensitivities for ${\Re }_{00}$ when $\xi =0.45$.

Parameter	Sensitivity Index	Relationship
${\Lambda }_1$	$0.8584$	+ve
${\Lambda }_2$	$0.1416$	+ve
${\beta }_1$	$0.8584$	+ve
${\beta }_2$	$0.1416$	+ve
$\xi$	$-0.1159$	−ve
$\mu$	$-0.2857$	−ve
$\alpha$	$-9.1298$	−ve

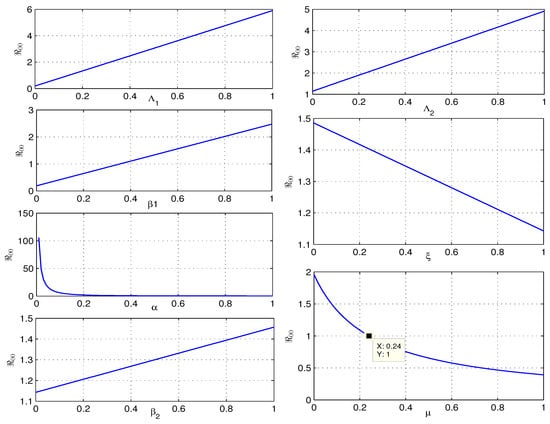
Figure 7. Graph of ${\Re }_{00}$ and the related sensitive parameters.

This analysis emphasizes the key parameters for controlling COVID-19, suggesting that preventive strategies such as wearing masks, maintaining social distancing, practicing good hygiene, and raising awareness are more effective than treatment procedures.

5.3. Forward Bifurcation

In this section, we examine the bifurcation behavior of system (20). We perform bifurcation analysis numerically by varying a key transmission parameter while keeping all other parameters constant. For each parameter value, the fractional-order system (20) was solved using the Toufik–Atangana numerical scheme. After eliminating transient dynamics, the asymptotic value of the infected population was recorded and plotted against the bifurcation parameter.

As shown in Figure 8, when ${\Re }_{00}<1$, there are no infected individuals, and the disease-free equilibrium ${\mathcal{F}}^{00}$ is stable, signifying the elimination of the disease. Conversely, when ${\Re }_{00}>1$, the system undergoes a forward transcritical bifurcation at $\beta =0.327$, resulting in a shift in stability from ${\mathcal{F}}^{00}$ to the endemic equilibrium ${\mathcal{F}}^{\ast \ast }$, where the disease remains present in the community. In this case, both equilibria coexist, as illustrated in Figure 8.

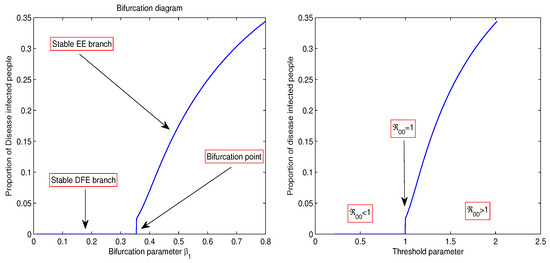
Figure 8. Bifurcation diagram showing the bifurcation point ${\beta }_1({\Re }_{00}=1)=0.354$ at which Corona model (20) experiences a transcritical bifurcation.

6. Optimal Control Setup and Analysis

The objective of analyzing treatment and awareness interventions is to formulate an optimal strategy for controlling COVID-19. This strategy is designed to minimize infections while increasing susceptible and recovered populations at minimal cost. Using Pontryagin’s Maximum Principle (PMP) [14], we establish the necessary conditions for optimal controls. Two control variables, $u_1\left(t\right)$ and $u_2\left(t\right)$, modulate treatment ($\mu \left(t\right)$) and awareness ($\xi \left(t\right)$) rates, enabling dynamic adjustments to effectively reduce infection while managing resources [37,51], thereby supporting well-informed public health decisions.

Therefore, the model adjusted with control variables $u_1$ and $u_2$ is described as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{S}_1\left(t\right)& ={\Lambda }_1-\alpha S_1\left(t\right)-{\beta }_1{S}_1\left(t\right)I\left(t\right),\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }{S}_2\left(t\right)& ={\Lambda }_2-\alpha S_2\left(t\right)-{\beta }_2(1-u_2\left(t\right))S_2\left(t\right)I\left(t\right),\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }I\left(t\right)& ={\beta }_1{S}_1\left(t\right)I\left(t\right)+{\beta }_2(1-u_2\left(t\right))S_2\left(t\right)I\left(t\right)-(\alpha +u_1\left(t\right))I\left(t\right),\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }T\left(t\right)& =u_1\left(t\right)I\left(t\right)-(\alpha +\rho )T\left(t\right),\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }R\left(t\right)& =\rho T\left(t\right)-\alpha R\left(t\right),\hfill \end{array}\end{array}$$

(22)

with the initial conditions given in (4).

We define the following cost functional:

$$\begin{array}{c}\hfill J(I,T,u_1,u_2)=\underset{0}{\overset{T_f}{\int }}\left[a_{1}I\left(t\right)+a_{2}T\left(t\right)+{\displaystyle \frac{1}{2}}{a}_3{u}_1^2\left(t\right)+{\displaystyle \frac{1}{2}}{a}_4{u}_2^2\left(t\right)\right]dt.\end{array}$$

(23)

The weights $a_i,i=1,\dots ,4$ are non-negative constants associated with states and controls. The space of controls is given by

$$\begin{array}{c}\hfill \mathcal{U}=\{u_i\left(t\right):i=1,2:\mathrm{each}{u}_i\left(t\right)\mathrm{is}\mathrm{Lebesgue}\mathrm{measurable}\mathrm{on}[0,1]\}.\end{array}$$

We seek the best controls $u_1^{\ast }$ and $u_2^{\ast }$ for treatment $\mu \left(t\right)$ and awareness $\xi \left(t\right)$ within the control set $\mathcal{U}$, to minimize the functional cost (23), i.e.,

$$\begin{array}{c}\hfill J^{\ast }(I,T,u_1^{\ast },u_2^{\ast })=\underset{u_1,u_2\in \mathcal{U}}{min}J(I,T,u_1,u_2),\mathrm{subject}\mathrm{to}\mathrm{the}\mathrm{model}(22).\end{array}$$

(24)

For optimality conditions, we construct the Hamiltonian as follows:

$$\begin{array}{cc}\hfill \mathbb{H}(\mathbf{v},u_1,u_2)& =a_{1}I\left(t\right)+a_{2}T\left(t\right)+{\displaystyle \frac{1}{2}}{a}_3{u}_1^2\left(t\right)+{\displaystyle \frac{1}{2}}{a}_4{u}_2^2\left(t\right)\hfill \\ \hfill & +{\Lambda }_{S_1}\left(t\right)\left[{\Lambda }_1-\alpha S_1\left(t\right)-{\beta }_1{S}_1\left(t\right)I\left(t\right)\right]\hfill \\ \hfill & +{\Lambda }_{S_2}\left(t\right)\left[{\Lambda }_2-\alpha S_2\left(t\right)-{\beta }_2(1-u_2\left(t\right))S_2\left(t\right)I\left(t\right)\right]\hfill \\ \hfill & +{\Lambda }_I\left(t\right)\left[{\beta }_1{S}_1\left(t\right)I\left(t\right)+{\beta }_2(1-u_2\left(t\right))S_2\left(t\right)I\left(t\right)-(\alpha +u_1\left(t\right))I\left(t\right)\right]\hfill \\ \hfill & +{\Lambda }_T\left(t\right)\left[u_1\left(t\right)I\left(t\right)-(\alpha +\rho )T\left(t\right)\right]\hfill \\ \hfill & +{\Lambda }_R\left(t\right)\left[\rho T\left(t\right)-\alpha R\left(t\right)\right],\hfill \end{array}$$

(25)

where $\mathbf{v}$ is a column vector of state variables, and ${\Lambda }_{S_1}$, ${\Lambda }_{S_2}$, ${\Lambda }_I$, ${\Lambda }_T$, and ${\Lambda }_R$ are the corresponding adjoint variables.

From (25), we derive the following system of adjoint equations:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{\Lambda }_{S_1}\left(t\right)& =-{\displaystyle \frac{\partial \mathbb{H}}{\partial S_1}}=\left[\alpha +{\beta }_{1}I\left(t\right)\right]{\Lambda }_{S_1}\left(t\right)-{\beta }_{1}I\left(t\right){\Lambda }_I\left(t\right),\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }{\Lambda }_{S_2}\left(t\right)& =-{\displaystyle \frac{\partial \mathbb{H}}{\partial S_2}}=\left[\alpha +{\beta }_2(1-u_2\left(t\right))I\left(t\right)\right]{\Lambda }_{S_2}\left(t\right)-{\beta }_2(1-u_2\left(t\right))I\left(t\right){\Lambda }_I\left(t\right),\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }{\Lambda }_I\left(t\right)& =-{\displaystyle \frac{\partial \mathbb{H}}{\partial I}}=-a_1+{\beta }_1{S}_1\left(t\right){\Lambda }_{S_1}\left(t\right)+{\beta }_2(1-u_2\left(t\right))S_2\left(t\right){\Lambda }_{S_2}\left(t\right)\hfill \\ \hfill & +(u_1\left(t\right)+\alpha ){\Lambda }_I\left(t\right)-u_1\left(t\right){\Lambda }_T\left(t\right)-\left[{\beta }_1{S}_1\left(t\right)+{\beta }_2(1-u_2\left(t\right))S_2\left(t\right)\right]{\Lambda }_I\left(t\right),\hfill \end{array}\end{array}$$

(26)

$$\begin{array}{cc}\hfill {}_0{}^{ABC}D_t^{\eta }{\Lambda }_T\left(t\right)& =-{\displaystyle \frac{\partial \mathbb{H}}{\partial H}}=-a_2+(\rho +\alpha ){\Lambda }_T\left(t\right)-\rho {\Lambda }_R\left(t\right),\hfill \\ \hfill {}_0{}^{ABC}D_t^{\eta }{\Lambda }_R\left(t\right)& =-{\displaystyle \frac{\partial \mathbb{H}}{\partial R}}=\alpha {\Lambda }_R\left(t\right),\hfill \end{array}$$

along with the transversality conditions

$${\Lambda }_{S_1}\left(T_s\right)={\Lambda }_{S_2}\left(T_s\right)={\Lambda }_I\left(T_s\right)={\Lambda }_T\left(T_s\right)={\Lambda }_R\left(T_s\right)=0.$$

(27)

State equations (22) are derived from the Hamiltonian by computing the following derivatives:

$$\begin{array}{c}\hfill {}_0{}^{ABC}D_t^{\eta }{\mathbf{v}}_k={\displaystyle \frac{\partial \mathbb{H}}{\partial {\Lambda }_{{\mathbf{v}}_k}}},k=1,\dots ,5.\end{array}$$

(28)

Equations ${\displaystyle \frac{\partial \mathbb{H}}{\partial u_1}}=0,{\displaystyle \frac{\partial \mathbb{H}}{\partial u_2}}=0,$ define optimal characterizations for the controls $u_1^{\ast }$ and $u_2^{\ast }$, stated as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill u_1^{\ast }\left(t\right)& =min\left\{1,max\left\{{\displaystyle \frac{{\Lambda }_I\left(t\right)-{\Lambda }_T\left(t\right)}{a_3}}I\left(t\right),0\right\}\right\},\hfill \\ \hfill u_2^{\ast }\left(t\right)& =min\left\{1,max\left\{{\displaystyle \frac{{\beta }_2}{a_4}}\left[{\Lambda }_I\left(t\right)-{\Lambda }_{S_2}\left(t\right)\right]S_2\left(t\right)I\left(t\right),0\right\}\right\}.\hfill \end{array}\end{array}$$

(29)

6.1. Simulations and Results

We provide the numerical results of the control problem (22) and provide a discussion of the corresponding results in this subsection. We implement the Toufik–Atangana scheme (18) in the forward direction with two controls to approximate the state equations (22), while the adjoint system (26) is solved backward in time. The control functions $u_i\left(t\right),i=1,2$ are iteratively updated in discrete time steps $t_n=n\Delta t$. The procedure for approximating the necessary optimality conditions is described as follows:

• Set the control $u_k\in \mathcal{U}$ for $k=0$.
• Approximate Equations (22) and (26) by implementing the scheme (18).
• Determine $u^{\ast }$ using Equation (29).
• Improve $u_k$ using $u_k={\displaystyle \frac{u^{\ast }+u_k}{2}}$.
• Terminate the iterations when $\delta \parallel {\theta }_k\parallel - \parallel {\theta }_k-{\theta }_{k-1}\parallel \ge 0$ for $k>0$; otherwise, increase index k by 1 and go to Step 2.

The tolerance level $\delta >0$ is set to achieve the desired precision.

We discuss the control problem (24) for the following three different cases:

• Implementation of the treatment strategy only.
• Implementation of the awareness strategy only.
• Implementation of treatment ($u_1$) and awareness ($u_2$) as a combined strategy.

6.1.1. Case-1: Implementation of Treatment Only Strategy

To determine the optimal treatment rate $u_1(=\mu \left(t\right))$ for problem (24), we analyze the cost functional (23) with $a_i\ne 0,i=1,2,3$ and $a_4=0$, while maintaining a constant awareness rate $u_2(=\xi )$. The non-zero weighting coefficients $a_i\ne 0,i=1,2,3$ reflect the relative importance of disease burden and treatment expenses, with a higher value of $a_1$ placing more emphasis on reducing the number of individuals in the I compartment. As illustrated in Figure 9, the optimizer $u_1$ and the cost functional vary across different fractional orders. The iteration counts for the optimal controls and the associated implementation costs are described in Table 3. The results suggest that during the initial stage of the pandemic, approximately 15–21% of infected individuals require treatment, after which the percentage gradually declines. The optimal treatment control $u_1$ minimizes the cost functional for each fractional order, achieving the lowest overall cost at $\eta =1.0$. Table 3 highlights that computations require more iterations as $\eta$ increases. This optimal treatment approach not only decreases the number of infections but also increases the susceptible population for all values of $\eta$ (as shown in Figure 10), signifying its effectiveness in controlling the spread of COVID-19. Additionally, as the number of infectious people declines, the number of people in the treatment class reaches its peak, leading to an increase in recoveries, as shown in Figure 10. Therefore, the strategy successfully decreases the rate of infection and boosts the number of people who recover.

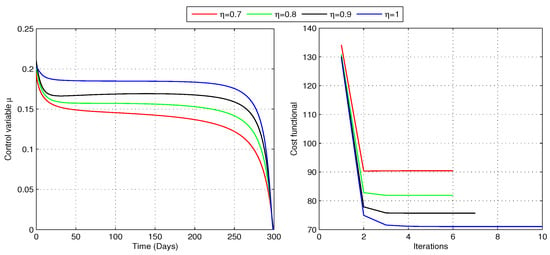
Figure 9. Optimal control $u_1$ for treatment of infectious individuals and the corresponding cost (Case-1).

Table 3. Number of iterations required to achieve the minimum cost in case 1 for different fractional-order values of $\eta$.

Implementation Cost Associated with Control $\mathit{\mu }$
Iterations	$\mathit{\eta }=\mathbf{0.7}$	$\mathit{\eta }=\mathbf{0.8}$	$\mathit{\eta }=\mathbf{0.9}$	$\mathit{\eta }=\mathbf{1.0}$
1	134.1363	130.8533	130.0788	129.6468
2	90.3452	82.8234	77.8782	74.9489
3	90.4006	81.8737	75.7589	71.5627
4	90.4274	81.8849	75.6836	71.1267
5	90.4303	81.8864	75.6814	71.0608
6	-	81.8861	75.6807	71.0497
7	-	-	75.6804	71.0475
8	-	-	-	71.0469
9	-	-	-	71.0467
10	-	-	-	71.0466

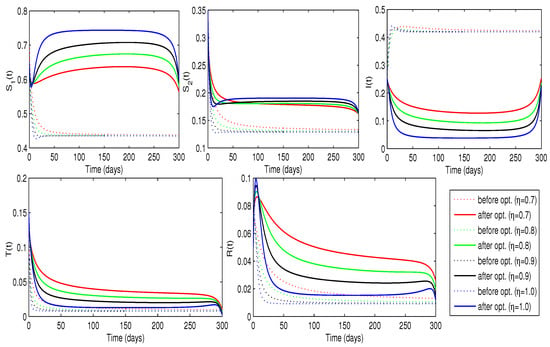
Figure 10. Trajectories of the disease model with and without optimized treatment rate $\mu$ for infected individuals (Case-1).

6.1.2. Case-2: COVID-19 Control Through the Awareness-Only Approach

In the second scenario, we address problem (24) to determine the optimal awareness rate $\xi$ while considering the treatment rate $\mu$ as a constant over time. Specifically, we evaluate the cost functional (23) with $a_1\ne 0$, $a_2\ne 0$, $a_3=0$, and $a_4\ne 0$. This configuration aims to minimize the number of infected individuals while keeping the cost associated with the control as low as possible. Figure 11 illustrates the solution trajectories for the best awareness rate $\xi$ and the related cost functional for different fractional-order values. We can conclude that raising awareness among nearly $88\%$ of the $S_2$ individuals is essential for achieving optimal disease control. Additionally, the vaccination rate may decrease just after 250 days. The lowest of all the minimum costs was observed when $\eta =1.0$. These results are further summarized in Table 4, which demonstrates that MATLAB R2024a requires between seven and nine iterations to attain the desired tolerance for the selected values of $\eta$. The optimal value of $\xi$ minimizes the cost functional, leading to a significant decline in the number of infected individuals and an increase in the number of susceptible individuals, as shown in Figure 12. Additionally, the decline in infected cases leads to a slight reduction in the number of individuals receiving treatment.

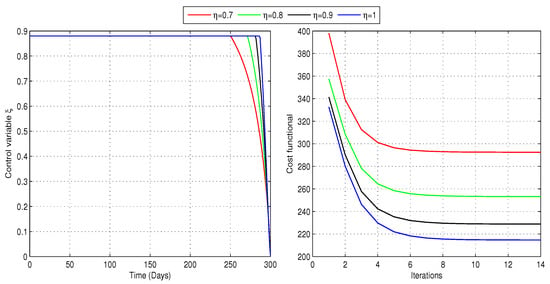
Figure 11. Optimal control $u_2$ for the awareness campaigns for $S_2$ people and the associated cost (Case-2). The study recommends maintaining an $88\%$ awareness rate for approximately 250 days, with possible adjustments thereafter.

Table 4. Number of iterations required to achieve the minimum cost in case-2 for different fractional-order values of $\eta$.

Implementation Cost Associated with Control $\mathit{\xi }$
No. of Iterations	$\mathit{\eta }=\mathbf{0.7}$	$\mathit{\eta }=\mathbf{0.8}$	$\mathit{\eta }=\mathbf{0.9}$	$\mathit{\eta }=\mathbf{1.0}$
1	398.0514	357.5174	341.4044	332.6591
2	339.1038	308.5018	290.2455	280.1609
3	312.5706	278.1348	257.7134	246.3437
4	301.1539	264.4600	242.3256	229.8219
5	296.4536	258.4596	235.2711	222.0205
6	294.3718	255.7349	231.9716	218.2973
7	293.4234	254.4486	230.3864	216.4887
8	292.9606	253.8241	229.6108	215.5987
9	292.7374	253.5169	229.2275	215.1573
10	292.6249	253.3645	229.0370	214.9374
11	292.5697	253.2886	228.9421	214.8276
12	292.5417	253.2507	228.8947	214.7728
13	292.5279	253.2318	228.8710	214.7454
14	292.5209	253.2224	228.8592	214.7316

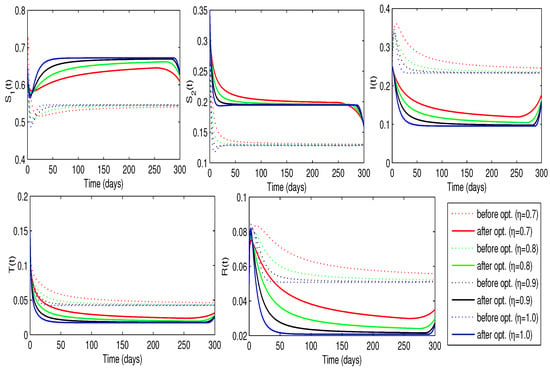
Figure 12. Trajectories of the disease model with and without optimized awareness rate $\xi$ for $S_2$ people (Case-2).

6.1.3. Case-3: Implementation of Treatment and Awareness as a Combined Strategy

Now, we approximate the optimal treatment rate, $\mu \left(t\right)$, and awareness rate, $\xi \left(t\right)$, that optimize the control problem. By assigning positive values to the weights $a_i,i=1,\dots ,4$, the objective is to minimize the number of infected individuals while keeping the overall implementation cost as low as possible. The results, shown in Figure 13, demonstrate that the combined implementation of controls significantly reduces the total cost. We observe a clear need for awareness sessions. Initially, around $30\%$ to $72\%$ of individuals in the $S_2$ group require education at the beginning, but this level of awareness may decline over time. At the same time, only $15\%$ to $18\%$ of the infected individuals require treatment, and this percentage gradually decreases over time. These profiles are illustrated in Table 5. As usual, the smallest minimum cost occurred when $\eta =1.0$. Moreover, implementing both controls simultaneously contributes to reducing the number of infected individuals while increasing the susceptible population, as illustrated in Figure 14.

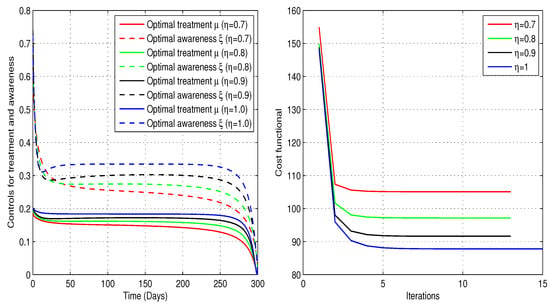
Figure 13. Fractional optimal controls for the treatment and awareness campaigns, respectively, for infected and $S_2$ individuals alongside corresponding costs (Case-3).

Table 5. Number of iterations required to achieve the minimum cost in case-3 for different fractional-order values of $\eta$.

Implementation Cost Associated with Controls $\mathit{\mu }$ and $\mathit{\xi }$
No. of Iterations	$\mathit{\eta }=\mathbf{0.7}$	$\mathit{\eta }=\mathbf{0.8}$	$\mathit{\eta }=\mathbf{0.9}$	$\mathit{\eta }=\mathbf{1.0}$
1	154.9364	149.8769	148.8031	148.2067
2	107.3266	101.6269	97.9859	95.9397
3	105.5942	98.0650	93.1941	90.2918
4	105.2374	97.4088	92.0843	88.6797
5	105.1329	97.2312	91.7685	88.1131
6	105.0933	97.1724	91.6683	87.9034
7	105.0807	97.1518	91.6345	87.8249
8	105.0757	97.1447	91.6229	87.7954
9	105.0743	97.1422	91.6188	87.7841
10	105.0739	97.1412	91.6173	87.7797
11	105.0737	97.1409	91.6167	87.7779
12	105.0735	97.1407	91.6164	87.7771
13	105.0732	97.1406	91.6163	87.7767
14	-	-	-	87.7765
15	-	-	-	87.7764

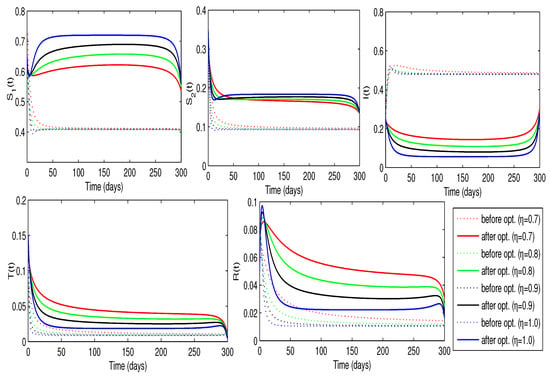
Figure 14. Trajectories of the disease model with and without optimized treatment and awareness rates (Case-3).

The comparative analysis of the three control strategies demonstrates that implementing early and combined interventions is more effective at suppressing peak infection rates and reducing long-term disease burden than using isolated measures. This finding reflects real-world COVID-19 outcomes, where layered interventions proved more effective than single-policy approaches.

6.1.4. Analysis of Cost Efficacy

To further enhance the analysis, we may include additional explanations and supportive remarks emphasizing the significance of the above findings, their implications, and the reasons behind the observed cost variations. The implementation of optimal treatment and awareness controls, $\mu \left(t\right)$ and $\xi \left(t\right)$, notably decreased infection levels and improved recovery outcomes at a lower overall cost in all cases. The iteration counts for the optimal controls and the associated implementation costs are described in Table 3, Table 4 and Table 5. For each fractional order $\eta$, Case-1 yields a lower minimum cost for employing the optimal treatment control compared to Case-2 and Case-3, and it also requires fewer optimization iterations, thereby reducing the overall computational cost. Moreover, the reduction in infected cases is greater in Case-1 and Case-3 than in Case-2 for every fractional order. The higher cost of the awareness-based intervention indicates that it requires greater resources to sustain, likely due to the ongoing need for public engagement and information dissemination efforts. Case-3, which combines treatment and awareness strategies, leverages the strengths of both approaches for more comprehensive infection control. In Case-3, the number of iterations required to achieve the combined optimal treatment and awareness controls is almost the same as in Case-2, but overall, it is smaller than in Case-1, indicating a reduced computational effort. Additionally, the implementation costs for different fractional-order values in Case-3 are slightly higher than in Case-1, but significantly lower than in Case-2.

For the proposed model, our findings suggest that using optimal awareness control alone results in an elevated cost compared to considering only treatment or combining both treatment and awareness controls. This higher cost of awareness-based strategy arises from the extensive efforts required to influence public behavior, in contrast to the more direct and immediate effects of treatment interventions. Thus, we conclude that better results can be achieved by using treatment alone or by combining optimal vaccination with treatment, leading to a significant decline in infections at a lower cost. This underscores the value of a multifaceted approach to public health, where integrating multiple strategies not only improves health outcomes but also maximizes cost-effectiveness.

7. Conclusions

In this work, we formulated a fractional-order $S_1{S}_{2}ITR$ COVID-19 model utilizing the Atangana-Baleanu derivative to capture complex disease dynamics. Analytical results demonstrated the model’s well-posedness, confirming the existence, uniqueness, positivity, and boundedness of solutions. Additionally, we derived a threshold parameter to describe the equilibrium behavior. We conducted a thorough stability analysis, establishing local and global stability by imposing suitable conditions on the threshold parameter.

Numerical simulations showed that increasing treatment rates and the fractional order $\eta$ significantly reduced infections, with full elimination achievable at $32\%$ treatment coverage for $\eta =1$. Incorporating awareness control further reduced infections and treatment needs, with just $24\%$ treatment coverage sufficient to eradicate the disease under high awareness levels. Sensitivity analysis identified contact rates between susceptible and infected individuals as the most influential factors, emphasizing the significance of public engagement, preventive measures, and vaccination promotion.

Optimal control analysis demonstrated that combining time-dependent treatment and awareness strategies is the most effective and cost-efficient strategy for reducing infections. Although awareness efforts alone contribute to controlling the disease, incorporating direct treatment interventions leads to improved health outcomes and more efficient use of resources. These findings underscore the importance of multifaceted intervention strategies in addressing COVID-19 threats and offer actionable insights for public health planning. Furthermore, the cost–efficacy analysis demonstrates that optimal allocation of limited resources can significantly impact outbreak outcomes, offering practical insights for public-health decision-making during pandemic scenarios. These findings emphasize that both timing and intensity of interventions are crucial in controlling COVID-19 transmission.

Although the study has its strengths, it also has certain limitations. The model assumes homogeneous mixing of the population and does not explicitly take into account spatial heterogeneity, demographic variations, or delays in behavior. In addition, the parameter values used in simulations were adopted from previously published studies, which may not fully reflect local or regional dynamics. Future research will address these limitations by extending the model to incorporate delays, stochastic effects, and data-driven parameterization to improve the robustness and applicability of the suggested control strategies.