Abstract
The optimisation of road construction planning and design prioritises safety, comfort, cost-effectiveness, and sustainability by aligning with sustainable development goals (SDGs) and integrating life cycle assessment (LCA)-based criteria. Asphalt mixture compaction is a critical construction-phase process that requires careful monitoring due to its significant impact on fuel consumption, CO2 emissions, and pavement performance. However, characterising the compaction process during the design stage is challenging due to the unavailability of primary data, such as the compaction energy applied by the roller on-site. This study addresses this gap by developing a methodology for deriving compaction-energy-related data at the laboratory stage. An algorithm is proposed to estimate key compaction parameters, specifically the locking point and compaction curves, based on aggregate grading. Equations to improve the design of bituminous mixtures based on compaction targets were derived. The findings support more sustainable planning, the optimised selection of construction equipment, and improved competitive equilibria between different pavement technologies by promoting low-carbon and energy-efficient strategies aligned with SDGS.
1. Introduction
In the road construction sector, the optimisation of planning and design criteria requires a systematic and comprehensive approach that prioritises safety, comfort, and cost-effectiveness while also aligning with sustainable development goals (SDGs). These factors play a crucial role in ensuring that road networks not only facilitate safe and efficient transportation but also contribute to creating healthy and more sustainable environments (SDG 11: Sustainable Cities and Communities). The need for infrastructures that reduce environmental impacts and mitigate the effects of their operations on the surroundings is part of the overall goal of improving the well-being of communities and the environment (SDG 3: Good Health and Well-Being). Based on the above, sustainability criteria should be integrated throughout the entire life cycle of road infrastructure, in particular during early project stages, such as planning and design. At these stages, a sustainability assessment that implements life cycle assessment (LCA)-based criteria becomes paramount [1,2]. One of the most common challenges in carrying out a sustainability assessment during the design phase is the availability of accurate data that allow for the realistic modelling of each life cycle process. The lack of specific data presents an obstacle to achieving the high level of detail of real-world conditions. Particularly when dealing with new pavement technologies, the unavailability of primary data concerning the most important life cycle processes, such as asphalt mixture manufacturing-related processes, i.e., in-plant operations and on-site construction-related processes, becomes a critical limitation. Indeed, the use of generic data cannot offer a proper realistic magnitude of the effects, in particular when comparing new materials and technologies at the design stage.
The negative impact is twofold. Indeed, not only does compaction affect environmental emissions (e.g., energy and carbon footprint), but it also governs the expected life, the latter being crucial in the life cycle assessment and the acceptance procedures.
In this study, the focus is on the construction phase, specifically on the compaction process. In fact, the ability to accurately assess the compaction process during the design phase is constrained by the lack of essential data, such as the actual compaction energy applied by the rollers in the field. In general, the on-site compaction energy density should align with the compaction energy density achieved in the laboratory [3]. Existing equations in the literature allow for estimating the on-site compaction energy density by considering specific roller-related variables. Zhao et al. [3], for example, carried out an experimental study and derived theoretical equations to quantify the compaction energy density provided by different types of rollers (e.g., pneumatic tire roller, vibratory roller, static steel wheel roller). These relationships take into account roller-related variables, such as the rolling speed and time, vibration period, and physical features (including the roller mass and the wheel width).
On-site construction processes could be less impactful compared to the production of input materials, asphalt mixture manufacturing, and transportation-related processes [4]. Some studies report that on-site activities account for approximately 10% of the CO2 emissions generated during cradle-to-gate processes, which include raw material production, transportation, and construction operations [5]. In the specific case of asphalt pavement construction, on-site construction-related impacts can primarily be attributed to the operations of different types of mechanical equipment, including pavers, rollers, milling machines, and trucks. Paving and rolling processes are often associated with significant fuel and electricity consumption, so they should be carefully monitored from a technical perspective to support low-carbon and energy-efficient construction practices. Furthermore, asphalt mixture compaction is one of the most important processes in the pavement construction phase. The relevance of on-site compaction-related activities is directly related to the final performance of the pavement layer, influencing its service life and its resulting mechanical properties [6].
When analysing the compaction of asphalt mixtures, several factors must be taken into account:
- On-site variables. Some variables, such as asphalt mixture properties, can be controlled during the design phase. Others, such as aspects of the construction process, are managed by contractors during the construction phase. The factors include the following: (1) The type and density of the underlying base course material (when on-site compaction is concerned). To this end, it is noted that the compaction energy depends on the type of underlayer material (e.g., subgrade soil, aggregate base course, cold mix asphalt layer, cracked friction course, new asphalt concrete layer, or a Portland cement concrete pavement layer). (2) The thickness of the asphalt layers. Indeed, thinner asphalt layers could cool faster than thicker layers. It is noted that for finer-density graded mixes (above the 0.45-power chart maximum density line), the minimum lift thickness should be three times the nominal maximum aggregate size. However, for a coarse-graded mix (below the maximum density line), the lift thickness should be at least four times the nominal maximum aggregate size. (3) The environmental conditions at the time of placement (see below). (4) The on-site procedures and machines, including the type of rollers, the number of rollers, and the rolling patterns used during the compaction process. (5) The mix temperature.
- Environmental conditions. Environmental conditions (e.g., ambient temperature, wind speed) also play a crucial role [7]. For the environmental conditions at the time of mix placement, note that air temperature, base temperature, wind velocity, and solar flux or cloud cover influence the compaction and the cooling rate of the mix.
- Bitumen. Asphalt binder percentage (lubricating effect) and type, where different methods of classifications are given (penetration-based, viscosity-graded, AC, and performance-graded, PG) and different strategies are followed, including polymer-modified binders (using either elastomeric- or plastomeric-type materials) and crumb rubber + binder blends (including asphalt rubber).
- Aggregate. Aggregate grading plays a pivotal role in determining the compaction behaviour of asphalt mixtures [8,9]. In more detail, aggregate type, grading, and characteristics, including angularity (cf., fine aggregate angularity, FAA, and coarse aggregate angularity, CAA) are important. There are many aggregate types, including sedimentary rocks (e.g., limestone), igneous rocks (e.g., basalt and granite), and their properties (e.g., absorption, soundness, angularity, surface texture, degree of flat and/or elongated particles, and percentage of crushed rocks) affect the compactability of the resulting mixture.
- Filler. The filler percentage and type affect compaction. Furthermore, the dust proportion (the filler to bitumen ratio) may also affect compaction.
- Type of mixture. The type of bituminous mixture, e.g., dense-graded mixes, DG, (fine-graded, coarse-graded, densely-graded mixes), gap-graded mixes, open-graded mixes, OG, (as a friction course or as a base layer), and stone matrix asphalt, SMA, mixes, influences the final result. Importantly, several factors may cause mixtures to be stiff or tender, including the following: (1) An excessive moisture content. (2) Excessive light ends in the asphalt cement. (3) An excess bitumen percentage. (4) Rounded aggregate particles (cf., FAA and CAA parameters). (5) An excess percentage of fine aggregate (0.3–0.6 mm). (6) An insufficient filler percentage (<0.075 mm). (7) Poor bonding to the underlayer pavement. (8) An excessive mix temperature. (9) Poor compaction techniques (quick stops and starts by a steel-wheeled roller, need for pneumatic tyre rollers). (10) Contamination with petroleum products.
Finally, it is noted that compaction results can be analysed in terms of Volumetric Properties, including the air void content, AV, voids in mineral aggregate, VMAs, and voids filled with asphalt, VFAs.
1.1. Compaction Energy in the Laboratory and On-Site: An Analysis of the Literature
As mentioned above, the compaction energy provided by the rollers during the rolling process should be consistent with the compaction energy density obtained in the laboratory according to a specific compaction procedure, such as the Superpave gyratory.
The significance of gyratory compaction and how it relates to on-site procedures was studied by many authors [10,11,12,13]. The parameters that provide information on the compaction of asphalt mixtures in the laboratory and the related main information are summarized below.
- Nini.
For the initial gyration (Nini), note that the values of gyrations in the range 1–8 are supposed to pertain to the compaction energy applied by the paver screed [14].
Based on AASHTO 2000 [12], the Nini ranges from six to nine (based on ESAL traffic, where lower values correspond to less than 0.3 million ESALs in 20 years, while higher values correspond to a 20-year traffic loading of more than 30 million ESALs). It represents a tenderness control, where the required density should be lower than 89–91.5%Gmm.
- Ndes.
For Ndes, it is noted that Ndes corresponds to the design density (and air void content (AV)), which is the same as that expected in the field after the indicated amount of traffic. Ndes corresponds to a content of 4% air voids for dense-graded friction courses. It is noted that Ndes may correspond to a content of about 20% air voids for porous asphalt concretes and to 10–14% for semi-dense (“grenu”) mixtures (cf., [15]).
- Compaction energy index (CEI).
The CEI refers to the area between the eighth gyration and 92%Gmm [11,16,17]. Previous studies have referred to the density prerequisite of 92%Gmm at the completion of construction works (before traffic opening) [10]. To achieve this density requirement, the CEI can be evaluated from the densification curve (%Gmm vs. the number of gyrations) obtained from the output of the gyratory compactor. As defined by [10], the CEI is the area under the densification curve between the eighth gyration and the number of gyrations corresponding to the specified target density of 92%Gmm. This area represents the construction effort required in laying operations. The first value in the range of gyrations (eighth gyration instead of the first gyration) simulates the pre-compaction effort provided by the paver action during the laydown of the mixture [10]. It is worth noting that a preliminary compaction effort should be considered prior to the first roller pass, taking into account the effort provided by the paver during laydown operations [11]. This compaction energy density could also be simulated by the compaction energy density applied during the first i-gyrations, where i-th is identified by the Nini (the first 10 gyrations according to Italian main specifications) [18,19]. It should be noted that a higher value of the CEI is associated with greater difficulty in compacting the mixture, whereas mixtures with lower CEI values demonstrate improved workability [10,20]. In study [16], the CEI is estimated to range from 333 to 613, with higher values recorded for open-graded mixtures. Also, the authors of [17] report values about two times higher for mixtures presenting high percentages of coarse aggregate compared to dense-graded mixtures.
- Locking Point (LP).
The Ndes and locking point concepts somehow overlap. The locking point is the number of gyrations where the sample being gyrated loses less than 0.1 mm in height between successive gyrations [21]. According to Mohammad and Shamsi [11], the locking point is reached when, for three consecutive gyrations, the height change rate stabilizes at or falls below 0.05 mm. This value represents the threshold beyond which further compaction may lead to aggregate damage [20,22]. Other methods to determine the LP are used by [16,22,23].
- Compaction densification index (CDI).
The CDI is the area under the densification curve from the first gyration to the LP. This parameter provides information about the compactability of the asphalt mixture [11]. In study [24], the CDI is estimated as the area under the compaction curve from N = 8 to 92%Gmm. Ref. [25] refers to the CDI as the area from the eighth gyration to 92%Gmm. The authors of [9] assess the CDI as the area from 88%Gmm to 92%Gmm.
- Traffic densification index (TDI).
The traffic densification index (TDI) represents the integral of the densification curve from the LP to the number of gyrations associated with 98%Gmm [10,26]. Ref. [11] defines this index as the area under the densification curve from the LP to N = 205, whereas other studies [9,27] refer to the area from 92%Gmm to 98%Gmm.
This index correlates with the stability of the mixtures under traffic-induced stress. Higher TDI values are associated with the greater stability of the mixture [11]. For this parameter, the values found in the literature are estimated to range from about 200 [26] to more than 5000 [20].
- Nmax.
Nmax refers to the laboratory density that should never be exceeded in the field (excessively low air voids and potential rutting). At Nmax, the AV should never be below 2%.
Table 1 reports the ranges for the abovementioned parameters and the ranking of in-lab compaction levels.

Table 1.
Approximate ranking of in-lab compaction levels.
- On-site versus in-laboratory compaction
In-lab compaction aims at simulating on-site compaction, and the reasonableness of this relationship was demonstrated (cf., [28]). Anyhow, many factors interpose between on-site and in-lab compaction and the pertaining energy density. The degree of compaction (%) is proportional (nonlinear proportionality) to the compaction energy density (kJ/kg) and the number of roller passes (cf., [3,15]). Methods to relate the number of passes of a given roller type to the energy and then to the obtained level of compaction were set up in [3,15]. Furthermore, the frequency response functions of the pavement structure emerge as a key factor of compaction and performance when dealing with different infrastructure types (e.g., roads, bridges, and tunnels, cf., [29,30,31]).
1.2. Objectives of the Study
Based on the above, the primary objective of this study is to develop a method to derive compaction energy-related data at the laboratory stage (cf., Figure 1). This approach addresses the lack of primary data that limits the accurate modelling of the compaction process and its related energy consumption during the design phase. To this end, a methodology is set up to estimate key compaction parameters, specifically the locking point and compaction curves, based on aggregate grading and related parameters, e.g., the percentages of dust and sand, the distance of the curve from the maximum density curve (dist), and the coarse aggregate percentage. The final scope includes balancing the need for adequate compaction against the risk of over-compaction (damaging the aggregate structure) or insufficient compaction (reducing life expectancy) and supporting the assessment of the sustainability of competing solutions (i.e., competitive equilibria in terms of Global Energy Requirement, GER). In simpler terms, the study seeks to translate laboratory data into more sustainable field practices (e.g., better equipment selection and improved planning of operations) by optimising the compaction process at the laboratory stage.
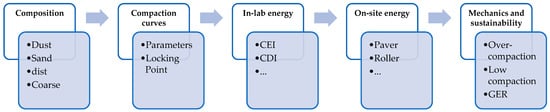
Figure 1.
Scopes and objectives.
2. Materials and Methods
2.1. Modelling
Figure 2 illustrates the rationale behind the method. As mentioned above, the method aims at setting up an algorithm to predict the LP based on aggregate gradation (G). Based on the relationship between the LP and Ndes, pieces of information about the compaction energy (E) and competitive equilibria (CE) are derived. This allows for the selection of the best pavement technology.
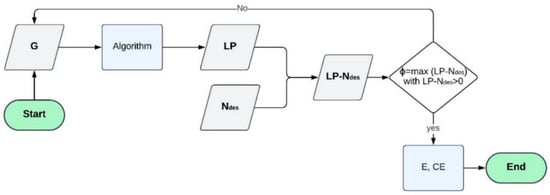
Figure 2.
The algorithm for the prediction of the compaction effort at the design stage. Symbols. G: aggregate gradation; LP: locking point; Ndes: design gyrations; ϕ: objective function; E: in-lab and on-site compaction energy; CE: competitive equilibrium.
By referring to the objective function, ϕ, the following can be noted:
- Reaching Ndes (i.e., the corresponding AV content, e.g., 4% for a dense mixture) is the main aim of the compaction effort. This implies that the LP should be higher than Ndes. On the contrary, the constraint at Nmax does not conflict with having the LP between Ndes and Nmax, nor with having the LP higher than Nmax.
- Having the LP in between Ndes and Nmax could allow reaching the required requirements through lower energy.
- The fact that the LP must be higher than Ndes implies that the function min abs (LP-Ndes) could not fulfil the rationale behind the compaction effort.
- On the other hand, having, as an objective, the function min (LP-Ndes) could be fallacious because of the need to have LP > Ndes.
- Based on the above, the objective function max (LP-Ndes), with LP-Ndes > 0 as a threshold value, is here tentatively set up (Equation (1)).
For the rationale behind Equation (1), it is noted that from an energy standpoint, the objective function above refers to the minimisation of the first derivative of AV as a function of the compaction energy, where if the energy increases, AV decreases.
This corresponds to the maximization of the Gmm%, where the latter is the ratio of Gmb and Gmm, with Gmb being the bulk-specific gravity and Gmm the theoretical maximum specific gravity.
As is well known, N > LP (where N is the number of gyrations and LP is the locking point) represents a quasi-zero condition of the first derivative of Gmm%, a condition in which the first derivative (speed) of the compaction process is negligible, and further compaction efforts are ineffective.
This implies that the physical and engineering rationale behind the max (LP-Ndes) function is to avoid this “ineffective” energy status, where, despite energy increases (i.e., gyrations), it would be very difficult to match the target air void content.
By referring to the derivation of the in-lab compaction energy from the LP, the following is noted:
- The in-lab compaction energy can be estimated by using key compaction parameters derived from the compaction curve, such as the CDI and the LP.
- The CDI is proportional to the compaction effort applied in the laboratory (and thus to the energy needed to achieve a given density). It is a useful measure for predicting on-site compaction efforts from laboratory data.
- The LP is a key indicator in this derivation as it translates into the optimisation of aggregate packing without the risk, for example, of over-compaction, which could lead to aggregate damage.
- By integrating the CDI and LP into the analysis, the in-lab compaction energy can be used to predict the energy required for on-site compaction. This prediction accounts for factors such as the mixture composition and design requirements, allowing for the optimisation of both the mixture and the pavement design.
By referring to the derivation of the on-site compaction energy from the in-lab compaction energy, the following is noted:
- The on-site compaction energy density (Joule/kg), which is provided by the rollers during the rolling process, should be consistent with the compaction energy density obtained in the laboratory (see [3]).
- On the one hand, the relationship between the energy density associated with compaction and the CDI is mixture-specific because of the many variables involved in both the production and construction processes; on the other hand, the on-site compaction energy can be derived by considering roller-specific parameters (i.e., type, weight) and the number of passes required to obtain the specific degree of compaction.
- Based on the above, the on-site compaction energy should be scaled from lab-derived values using mixture-specific coefficients and field parameters to ensure that the field compaction process meets the density and structural integrity requirements.
By referring to the derivation of the framework of competitive equilibria, note the following:
- Under the hypothesis of having different pavement technologies to compare, where the grading and the additives are different but comply with the contract specifications, the method set up herein could have the potential to allow the derivation of a further key performance indicator (KPI) useful for both energy estimation and sustainability assessment. Competitive equilibria among different technologies can be analysed by considering the environmental impact and expected life of each concurrent pavement technology (cf. [4]).
2.2. Derivation of the Parameters of the Model
The following main steps were implemented to develop the model:
- The selection of materials and data collection. Twenty-two asphalt mixtures were designed and tested. This dataset was increased using data from the literature to extend the range of the analysis.
- The compaction curve analysis. The Superpave Gyratory Compactor (SGC) was used to compact cylindrical specimens for each mixture. By analysing the resulting compaction curves, the LP was determined for each mixture.
- The correlation Analysis. Pearson correlation coefficients were analysed to assess the relationship between compaction-curve-related parameters and the aggregate grading and between the LP and the aggregate gradation parameters (e.g., passing percentages for different sieve sizes, fine content, and dust content).
- Regression modelling. A multivariable regression analysis was carried out to develop a predictive model for both the compaction curve parameters and the LP, based on aggregate-grading-related variables. The accuracy of the model was evaluated by comparing the predicted values against the observed data.
- The Ndes and LP analyses. For each mixture, the relationship between the LP (predicted values) and the Ndes (the values set up in the contract specifications as a part of the job mix formula) was analysed. The model set up above, where the proximity of the LP to Ndes from the right is an indicator of the energy efficiency of the mixture, was implemented and validated.
- Remaining steps. The remaining steps are as follows: (6.1) The estimation of the in-lab and on-site compaction energy. (6.2) The analysis of competitive equilibria and the derivation of the targets for the optimisation of the mixtures.
Concerning the aggregate-grading-related variables, the following were considered:
- The percentage passing (Pi) through the following sieves (i): 20, 16,12.5, 9.5, 4.75, 2.36, 1.18, 0.6, 0.3, 0.15, 0.075 mm.
- The squared distance from the maximum density line, dist (Equation (2)), defined as the square of the average distance between the maximum density curve and the actual gradation (considering the following sieves 31.5, 20, 16, 12.5, 8, 4, 2, 0.5, 0.25, and 0.075 mm).where Pi is the percentage passing through the sieve size i, Si is the sieve size i, and Smax is the maximum sieve size where the passing percentage is 100%.
- Sand or fine percentage, sand (the percentage passing through the 2.36 mm sieve and retained on the 0.075 mm sieve).
- Dust (or filler) percentage, dust (the percentage passing through the 0.075 mm sieve).
- Coarse aggregate, coarse (obtained as 100 − P2.36).
2.3. Materials
In order to derive the relationship between gradation and the locking point, 22 mixtures were produced and tested in the laboratory. The summary of the mixtures investigated in the study is reported in Table 2.

Table 2.
A summary of the mixtures produced and tested. Symbols. Mixture ID: mixture identifier. b: binder content expressed in %; a modified asphalt binder was used, type 50/70. NMAS: nominal maximum aggregate size. Tmix: mixing temperature. Ndes: design gyrations.
Furthermore, in order to improve the amount of data, the data from Pouranian and Haddock [16] were considered.
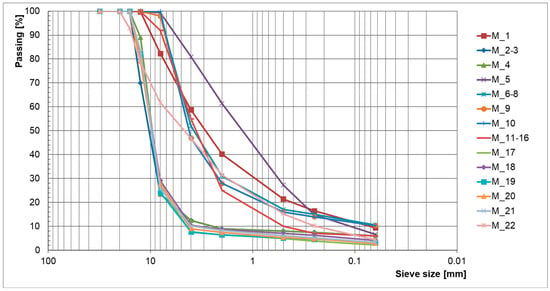
Figure 3.
Aggregate gradations of the mixtures produced and tested in this study.
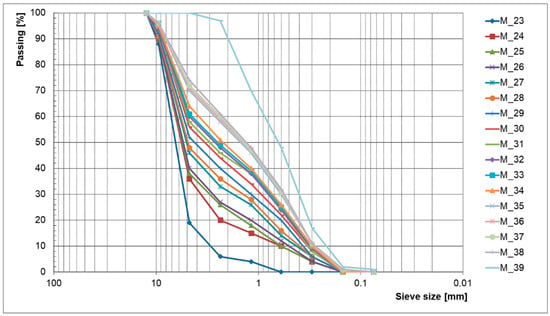
Figure 4.
Aggregate gradations of the mixtures collected from the literature [16].
The Superpave Gyratory Compactor was used to compact the material into 100 mm specimens. For each mixture, the height curve as a function of the number of gyrations was derived, and the locking point was assessed based on the definition by Mohammad and Shamsi [11]. According to these authors, the locking point is defined as the number of gyrations after which the change in height is equal to or less than 0.05 mm for three consecutive gyrations.
3. Results and Discussion
3.1. Compaction Curves
The following types of equations were used to fit the %Gmm curve:
- The power law (Equation (3)):
- The logarithm law (Equation (4)):
- The three-parameter quotient (Equation (5)):
- The Moutier model (Equation (6)):where N is the number of gyrations, and a, b…m, C0, C∞, β3, and β4 are the fitting parameters. Note that
- The first and second models are the ones commonly used.
- The three-parameter quotient is herein set up to properly account for %Gmm variability, where two theoretical requirements should be fulfilled: (1) Having a reasonable upper limit of %Gmm for an N that tends to infinity (i.e., l ≤ 100%). (2) Having a reasonable behaviour close to zero (e.g., h/m ≅ 55–90%).
- The Moutier model [32] has four parameters. It has an upper limit (when N tends to infinity) and a lower limit different from 0 (when N tends to 0). Unfortunately, the exponent is linked to the difference between the upper and lower levels, and this could cause issues when fitting real curves.
Table 3 illustrates the results obtained when applying the four models above to the mixtures considered (three cases are reported).

Table 3.
Parameters of the compaction curves.
Based on the results, the following is noted:
- The power law and the logarithm law fail to represent what happens at the beginning of the compaction procedure, where, as a result of gravity (as well as the normal pressure applied), the density has a given finite value, different from zero. Here, it is noted that not only do the two models fail to represent what happens (cf., “–” and “NA” in Table 3), but, at the same time, what happens in the laboratory could be quite different from what happens on-site. Indeed, the initial pressure (600 kPa) exerted by the head of the gyratory compactor does not seem to represent the action of gravity + paver bar well. Further studies will be needed. From a practical standpoint, this issue at N = 0 could have more theoretical than practical consequences, simply considering what happens at N = 1 or N = 8.
- The power law and the logarithm law fail to represent what happens for a high number of gyrations. Indeed, when N increases for sample heights, it should be hmin ≤ h(N) and for air voids, AV = 1 − Gmb/Gmm ≥ 0. Consequently, for %Gmm, it should be %Gmm = Gmb/Gmm = hmin/h(N) ≤ 100%. For the sake of comprehensiveness, slight deviations from the equations above could happen because of a change in Gsb due to aggregate pulverisation, but these inconsistencies of the two models above remain clear.
- For the Moutier model mentioned above, in contrast with the aim (i.e., having a reasonable upper limit when N tends to infinity), for actual curves, the boundary condition for %Gmm (i.e., C∞ ≤ 100%) is usually not fulfilled (cf., Table 3). Importantly, values higher than 100% for C∞ were also obtained by [33]. The theoretical problem was here solved by imposing C∞ ≤ 100% in the optimisation process, even if the values obtained at Ndes for M_3 are quite far from the reality.
Figure 5 illustrates the compaction curves obtained for the 22 mixtures designed and tested (M_1–M_22).
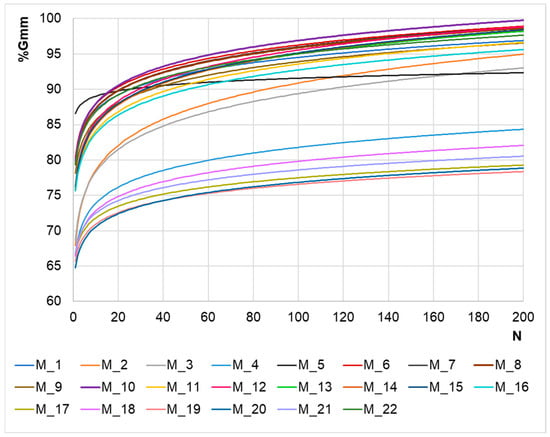
Figure 5.
Compaction curves.
By modelling the compaction curves using a power law (%Gmm = a·Nb), the values of “a” and “b” were obtained for the 22 mixtures. The values are reported in Table 4.

Table 4.
Parameters of the compaction curves (power law).
Based on K-means clustering, the curves in Table 4 essentially fall into four distinct groups: (1) M_20, M_19, M_18, M_17, M_4, M_21, M_2, M_3, where the centroid (a, b) is (66, 0.04). (2) M_11, M_16, M_14, M_15, M_13, M_12, where the centroid is (76, 0.05); (3) M_9, M_22, M_7, M_8, M_10, M_1, M_6, where the centroid is (80, 0.04). (4) M_5.
However, the following further observations should be taken into account (cf., Figure 5): (1) M_2 and M_3 have volumetric and compaction characteristics that differ from the remaining mixtures of the group 1 for a high number of gyrations. This would suggest splitting the first group into two different sets. (2) Even if groups 2 and 3 cluster differently, they are basically dense-grade mixtures, and this appears evident when N increases, and the compaction curves tend to AV values below 10%. This would suggest treating groups 2 and 3 above together.
Based on the above and considering the gradation of the mixture (dense or porous), the following four groups can be identified:
- The OG group (M_4, M_17, M_18, M_19, M_20, M_21), identified above as the main part of cluster 1.
- The intermediate group IN (M_2, M_3), identified above as a part of cluster 1.
- The DG group (M_1, M_6, M_7, M_8, M_9, M_10, M_11, M_12, M_13, M_14, M_15, M_16, M_22), assembling clusters 2 and 3 above.
- The one-datum cluster M5 (M_5, cluster 4 above).
This separation highlights the significant influence of aggregate gradation on compaction behaviour. In particular, the lower values of “a” and the slightly lower values of “b” recorded for open-graded mixtures can be associated with the following:
- A higher initial AV (air void content). Indeed, y (1) = a = Gmb (1)/Gmm = −AV(1) + 1; then, AV(1) = 1 − y(1) = 1 − a/100, resulting in about 34% for the OG cluster versus 22% for the DG cluster;
- A slower compaction “response”. In contrast, dense mixtures show higher values of the compaction parameters, reflecting a more rapid compaction process. Indeed, y′(50) = a⋅× b⋅× (50)^(b − 1) = a⋅× b/(50)^(1 − b), resulting in a slope of about 0.06 (OG) versus about 0.08 (DG).
The characterisation of the four groups is summarised in Table 5.

Table 5.
Average values for compaction curves.
These findings are in line with the results obtained by Leiva and West [17], who observed improved compactability behaviour in fine-graded mixtures. Their study concluded that gradation is one of the most influential factors affecting mix compaction in the laboratory.
Furthermore, as reported by [34], it should be noted that mixtures with the same NMAS but different gradation types require different levels of compaction effort to achieve the target density. A clear example is M_22, which has an NMAS of 14.5 mm, placing it within the range of the OG mixture cluster (these mixtures have an average NMAS of 14 mm). However, its compaction curve is included in the DG cluster behaviour, indicating that, despite similar NMAS values, gradation type significantly impacts the compaction behaviour.
Taken together, these considerations suggest how the gradation type plays a crucial role in characterising the compaction process of asphalt mixtures, directly influencing the degree of compaction required or achievable.
3.2. The Analysis of the Relationship Between the Aggregate Grading and a, b
As is well known, the compaction curve is affected by composition factors (including aggregate grading and properties), involved processes (including temperatures), and other minor effects (including sample heights), where the complexity increases when considering on-site versus in-lab production. In the pursuit of investigating the main variables that affect in-lab compaction curves, in order to improve the number of cases for the analysis of LP dependence on grading, three sets were used:
- The dataset of 22 mixtures produced and tested at UNIRC.
- The dataset of 17 mixtures studied by Pouranian and Haddock [16].
- The dataset of 39 mixtures, including both the sets above.
Table 6 provides the Pearson correlation coefficients for the three datasets (17 mixtures, 22 mixtures, and 17 + 22 mixtures). This analysis allows us to understand the relationships between the compaction curve parameters (where a is the constant and b is the exponent of the power law, herein denoted as a and b, respectively) and the aggregate-grading-related variables and, thus, how the latter affect the compaction behaviour. The grading-related variables are dist, sand, dust, and coarse, as defined in Section 2.2.

Table 6.
Pearson coefficients for compaction curve parameters (a and b) vs. grading-related variables. Average values for compaction curves. Note: correlations between parameters a and b and the “dust” variable for the 17-mixture dataset cannot be considered significant, as the mixtures in this dataset contain little to no filler.
These results confirm that aggregate gradation particularly affects the early stages of compaction, as also concluded by previous studies [35]. In fact, from Table 6, for parameter “a”, which represents the initial (N = 1) compaction level of the mixture, the following is noted:
- There is a strong negative correlation with the squared distance from the maximum density line “dist” (−0.95 for the 17-mixture dataset, −0.90 for the 22-mixture dataset, and −0.80 for all the data). This implies that when the gradation curve deviates more from the maximum density line (i.e., there is a higher squared distance), the initial compaction percentage decreases. This condition translates into a lower initial compaction for poorly graded mixtures. This result reflects the cluster separation (e.g., DG and OG clusters) noted in Section 3.1. Specifically, it is noted that the %Gmm@1 for the DG cluster is higher than that obtained for the OG cluster (77.88% vs. 66.16%).
- There is a positive correlation with the “sand” variable. The coefficients range from 0.63 to 0.93, indicating that as the sand percentage increases, the initial compaction increases as well. The sand content improves the density at early stages.
- For the “dust” variable, a strong positive correlation is recorded for the 22-mixture dataset, while for the entire database, a weak positive correlation is observed. The first value suggests that, for some mixtures, filler can facilitate quicker densification during the early compaction stages.
- As a consequence of the results discussed above, a strong negative correlation was obtained with the coarse aggregate content.
Given that lower “b” values indicate a slower response as the number of gyrations increases, for all the data taken together (17 + 22), it can be noted that the negative correlation of b (exponent) with the sand content (−0.76) indicates that higher sand contents reduce the rate of compaction with increased gyrations. This complies with the sphere packing model from [36], where the contact points in a sphere pack model (non-overlapping balls) in a given, ideal configuration are a given number depending only on the dimension of the Euclidean space (e.g., 12, cf., [37]).
The weak correlations with the other grading-related parameters suggest that these factors do not consistently affect compaction with increased gyrations, indicating that other factors could play a more significant role at higher gyration levels (e.g., particle shape and binder). This observation encourages further investigation into additional factors and multiple regression models (with more than one explanatory variable). Furthermore, a higher number of samples, including various types of mixtures, is needed to better investigate the compaction behaviour and improve the significance of the findings.
The regression models developed to predict a and b based on aggregate grading are expressed as follows:
where β1…β6 are the regression coefficients.
a = β1 ×⋅sand + β2⋅× dust + β3
b = β4⋅× sand + β5⋅× dust + β6
Table 7 reports the values of the regression coefficients. It is noted that these values were calibrated using the entire dataset (17 + 22) due to the limited variability in the values of parameter b. The latter appears to be basically governed by the known coefficient and is slightly affected by the sand percentage.

Table 7.
Regression coefficients for the prediction of a and b based on aggregate grading.
The following plots refer to the analysis of the abovementioned two-variable function. The Y-axis reports the predicted values, while the observed values are reported on the X-axis. Figure 6 refers to parameter a, while Figure 7 refers to parameter b. Dashed lines refer to the equality line, while dotted lines refer to the linear regression.
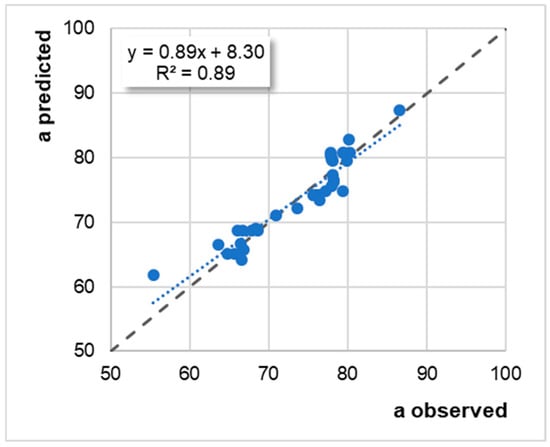
Figure 6.
The two-variable regression analysis for the observed vs. predicted values for parameter a.
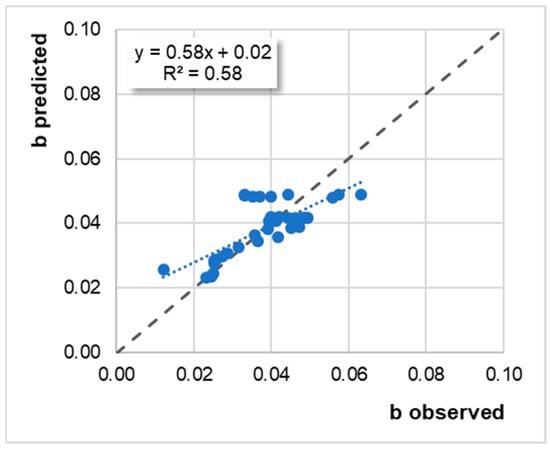
Figure 7.
The two-variable regression analysis for the observed vs. predicted values for parameter b.
As can be seen from these results, the multiple linear regression model provides a good fit to the experimental data, with determination coefficients of greater than 0.6 (R2 ranges from 0.58 to 0.89).
3.3. The Analysis of the Relationship Between the Aggregate Grading and the LP
Table 8 reports the Pearson coefficients that refer to the 39-mixture full dataset. Of the mixtures, 17 were derived from study [16], while the remaining 22 are from the present study. It is noted that the data from Pouranian have a quasi-null content of filler.

Table 8.
Pearson coefficients for LP vs. grading-related variables. Dataset: 17 + 22-mixture dataset.
In the analysis, the gradation-related variables defined in Section 3.2 were considered.
The data reported in Table 8 show that the most significant correlations with LP refer to sand, dust, and coarse percentages. In particular, the strong negative correlation between the LP and the fine aggregate content suggests that higher sand/fine percentages are strongly associated with a lower LP. This condition indicates that, during the compaction process, mixtures with a high fine aggregate content tend to reach the locking point more quickly. From a technical point of view, these mixtures can resist further compaction earlier in the process.
Strong positive correlations can be observed between the dust (filler) content and the LP, as well as between the coarse aggregate content and the LP (with Pearson coefficients of 0.69 and 0.72, respectively). This indicates that mixtures containing more particles of these sizes require more gyrations to reach the LP.
These results can be summarised as follows:
- Higher sand/fine percentages correspond to lower locking points. Specifically, the regression analysis indicated that sand percentages can explain about 52% of the variance of the LP.
- Higher dust/filler percentages correspond to higher locking points. Dust percentages can explain about 48% of the variance of the LP.
This behaviour is better detailed below (cf. Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, where dotted lines refer to linear regressions).
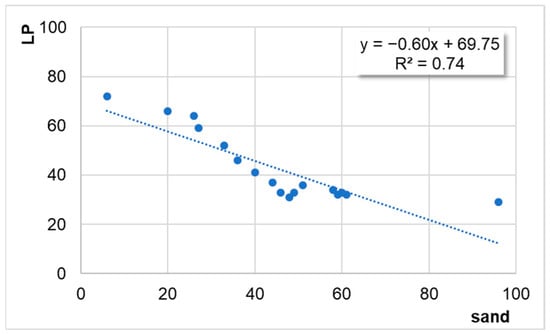
Figure 8.
Sand percentage (X-axis) vs. locking point (Y-axis). Note: the 17-mixture dataset [16].
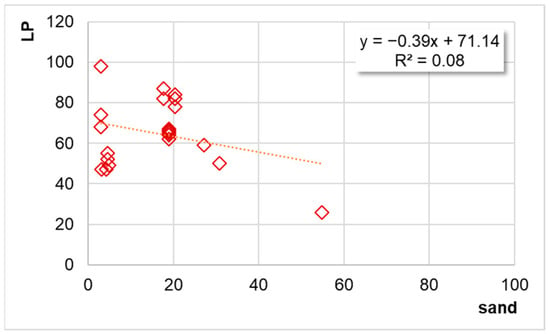
Figure 9.
Sand percentage (X-axis) vs. locking point (Y-axis). Note: the 22-mixture dataset (from the present study).
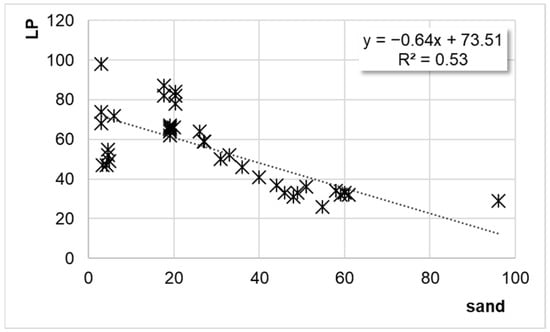
Figure 10.
Sand percentage (X-axis) vs. locking point (Y-axis). Note: the 39-mixture dataset (17 + 22).
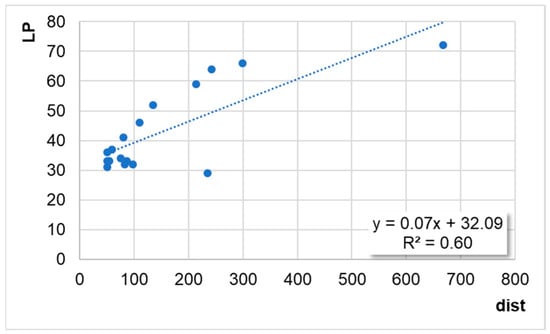
Figure 11.
Squared distance (X-axis) vs. locking point (Y-axis). Note: the 17-mixture dataset [16].
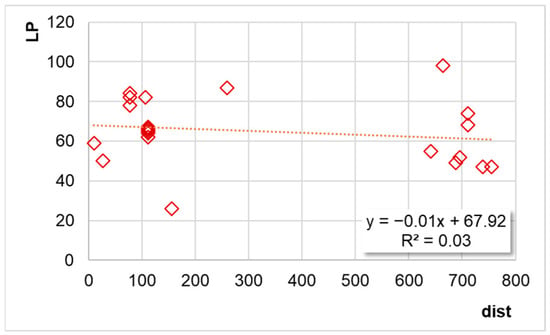
Figure 12.
Squared distance (X-axis) vs. locking point (Y-axis). Note: the 22-mixture dataset (from the present study).
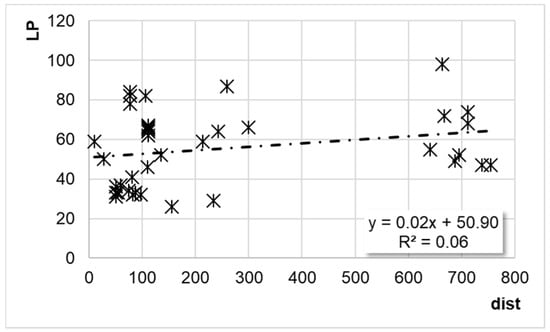
Figure 13.
Squared distance (X-axis) vs. locking point (Y-axis). Note: 39-mixture dataset (17 + 22).
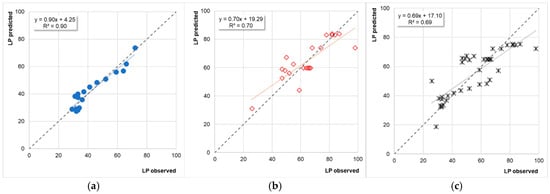
Figure 14.
Two-variable regression analysis for LP.
Case 1. When the data from [16] are considered, the following equation applies (see Figure 8):
where LP stands for locking point, and “sand” refers to the percentage passing through the 2.36 mm sieve and retained in the 0.075 mm sieve.
LP = −0.60·sand + 69.75
R2 = 0.74
R2 = 0.74
Case 2. When the results of the experiments carried out in the present study are considered, the negative correlation between the LP and sand is confirmed, even if lower determination coefficients are obtained (see Figure 9):
LP = −0.39·sand + 71.14
R2 = 0.08
R2 = 0.08
Case 3. When all the data are considered (17 + 22), the following results are obtained (see Figure 10):
LP = −0.64·sand + 73.51
R2 = 0.53
R2 = 0.53
In terms of distance (dist), the following applies (y = LP; x = dist):
Case 5. For the results obtained in the present study (the 22-mixture dataset) (see Figure 12),
LP = −0.01·dist + 67.92
R2 = 0.03
R2 = 0.03
Case 6. For the entire dataset (17 + 22-mixture dataset) (see Figure 13),
LP = 0.02·dist + 50.90
R2 = 0.06
R2 = 0.06
3.4. Regression Model Analysis for LP
The regression model developed to predict the LP based on aggregate grading is expressed as follows:
where A, B, and C are the regression coefficients.
LP = A·sand + B·dust + C
Table 9 reports the values of the regression coefficients for each dataset.

Table 9.
Regression coefficients for the prediction of LP based on aggregate grading.
It is noted that while the dataset containing 17 mixtures includes mixtures without filler (cf., Section 3.3), the remaining data refer to cases with a given percentage of filler. This could explain the variations of the coefficient B. This point calls for further investigations. The following plots (Figure 14) refer to the analysis of the abovementioned two-variable function. The Y-axis reports the predicted values, while the observed values are reported on the X-axis. The scatterplot (a) refers to the data from [16], plot (b) refers to the data herein derived, while plot (c) refers to the entire dataset.
3.5. Analysis of LP-Ndes Data
Figure 15 refers to the LP data (predicted) and Ndes data (as per contract specifications) for the 22-mixture dataset.
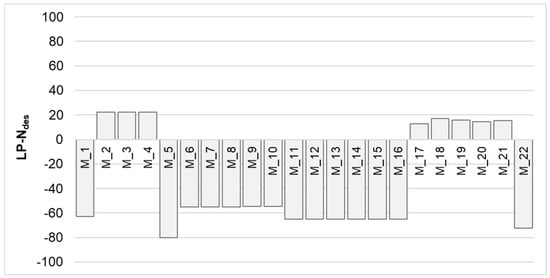
Figure 15.
LP-Ndes for the 22-mixture dataset.
For the 22-mixture dataset, the average observed LP is 65, the average predicted LP is 67, while the Ndes ranges from 50 to 130.
For the 17-mixture dataset, the average observed LP is 43, the average predicted LP is 40, while the Ndes cannot be assessed, being only research-related mixtures.
For the samples that refer to the experiments carried out, LP-Ndes has an average of −34, while for the set from Pouranian and Haddock [16], this value reaches a value of −57. This means that these mixtures are often not able to achieve the desired level of compaction.
The following analysis examines in more detail what happens in two selected scenarios.
For the mixture M_1 (basically a DGFC), LPobserved = 50 and %Gmm = 93%, LPpredicted = 67 and %Gmm = 94, Ndes = 130 and %Gmm@Ndes = 95%. This condition illustrates that even if the first derivative of %Gmm as a function of N is quite low, M_1 is able to achieve the target.
For the mixture M_4 (basically a PA), LPobserved = 98 and %Gmm = 82%, LPpredicted = 72 and %Gmm = 81%, Ndes = 50 and %Gmm@Ndes = 80%. This condition illustrates that M_4 is able to achieve the target at Ndes, well before tending to the less efficient dominion of gyrations (where the increase in %Gmm of 1% is obtained through about 30 supplementary gyrations). Even if more studies are needed, this confirms that having set it up as the objective function, ϕ = max (LP-Ndes) could fit the desirable condition.
4. Conclusions
The optimisation of road construction planning and design prioritises safety, comfort, cost-effectiveness, and sustainability by aligning with SDGs and integrating LCA criteria. The compaction of asphalt mixtures is a critical construction phase process. This process requires careful monitoring due to its significant impact on fuel consumption, CO2 emissions, and pavement performance. However, the characterisation of the compaction process at the design stage is limited by the unavailability of primary data, such as the compaction energy applied by the roller on-site. To this end, this study aims to develop a method to derive compaction-energy-related data at the laboratory stage.
To address this, the primary objective of this study was to set up an algorithm to predict the LP, based on aggregate gradation. To this end, the following objective function was set up and then validated: ϕ = max (LP-Ndes). This process involved the following steps:
- The laboratory production and testing of 22 mixtures. Furthermore, in order to improve the amount of data, 17 additional mixtures were collected from the literature.
- Define grading-related variables, such as the squared distance from the maximum density line, sand content, dust (or filler) percentage, and coarse aggregate.
- Analyse the relationships between compaction curve parameters and aggregate grading to observe how these factors affect compaction behaviour.
- Develop a regression model to predict the compaction curve parameters based on aggregate grading information.
- Analyse the relationship between aggregate grading and the LP.
- Develop a regression model to predict the LP based on the aggregate gradation.
- Validate the objective function by analysing the LP-Ndes data, where LP refers to the LP predicted and Ndes data refer to contract specifications.
- Derive information on the compaction energy at the laboratory stage by using the predicted compaction curve parameters and the LP (i.e., the assessment of the CDI for each mixture).
The conclusions drawn from the study include the following:
- Compaction curves can be modelled through a number of curves. A higher number of parameters allows for a better fit, but attention should also be focused on the intrinsic meaning of parameters and on what happens for very low and very high numbers of gyrations, where the constraints must be considered. The analyses carried out demonstrated that linking the theoretical maximum and the theoretical minimum with the exponents of the curve could lead to a bias between the supposed meaning of the parameter (e.g., maximum %Gmm) and its value as a result of a regression procedure (e.g., 102). The two-parameter and the three-parameter models used herein appeared quite consistent for the cases under analysis.
- Compaction curves can be modelled in terms of the power-law relationship expressed as %Gmm = a·Nb, where “a” represents the initial compaction of the mixture, and the exponent “b” is a measure of the rate of compaction as the number of gyrations increases. From the analyses and the study of the experimental mixtures designed and tested, it was observed that a higher value of the parameter “a” indicates a lower initial AV content, which was identified to be typical of dense-graded mixtures. Specifically, an average AV@1 of 22% was estimated for DG mixtures compared to 34% for OG mixtures. The slightly lower values of “b” recorded for OG mixtures can be associated with a slower compaction “response”, with slopes of approximately 0.06 for OG mixtures compared to 0.08 for DG mixtures.
- New relationships are herein derived to predict compaction curves through composition-related factors. The analysis of the relationship between the compaction curve parameters (a and b) and the aggregate-gradation-related parameters shows how the latter particularly affect the early stage of compaction (i.e., parameter “a”). The most significant correlations are identified between “a” and the squared distance from the maximum density line, indicating that when the gradation curve deviates more from the maximum density line, the initial compaction percentage decreases. This condition translates into a lower initial compaction for poorly graded mixtures. There is also a positive correlation between “a” and the sand content, indicating that as the sand percentage increases, the initial compaction increases as well. Obviously, this condition means that the sand content improves the density at early stages. In contrast, it was found that a higher sand content negatively affects the rate of compaction with increased gyrations. However, the weak correlations observed between “b” and other grading-related variables suggest that other factors, such as the particle shape and the binder, may play a more significant role in influencing compaction at higher gyration levels. For this reason, in future research, attention will be focused on including other mixture-related variables.
- New relationships are herein derived to predict the LP through composition-related factors. Pearson coefficients for the LP vs. grading-related variables show that the most significant correlations with the LP are the sand, filler, and coarse percentages. Higher sand/fine percentages correspond to lower locking points. Specifically, the regression analysis indicates that sand percentages can explain about 52% of the variance of the locking point. In contrast, higher dust/filler percentages correspond to higher locking points. Dust percentages can explain about 48% of the variance of the locking point. The regression model analysis demonstrated that the combined influence of the sand and dust contents explains a significant portion of the variance in the LP.
- On average, LP-Ndes= −34. The analysis of the trend LP-Ndes allows us to confirm the reasonability of the objective function set up herein.
Taken together, these findings suggest the following key aspects:
- Aggregate grading control is critical for optimising the compaction process.
- The prediction of the LP at the design stage, based on aggregate-grading-related parameters, allows for better planning and the optimisation of compaction practices.
- The characterisation of the compaction processes allows for the selection of the appropriate compaction equipment at the laboratory stage, which ensures that the compaction energy applied during the construction phase is effective.
- Low-carbon and low-energy strategies and practices can be implemented by optimising the compaction process at the laboratory stage. In fact, the study findings allow for translating lab data into more sustainable on-site compaction practices. It is noteworthy to observe that even with a negligible decrease in terms of the compaction energy, slight increases in the expected life due to the achievement of the correct compaction (e.g., 10%) yield appreciable savings in terms of the environmental impact per year.
- Algorithms allow for the better analysis of competitive equilibria, where competing technologies are compared at the laboratory stage.
The following limitations and opportunities for further study apply:
This is a prototypical study. Insights and correlations herein derived for the relationship between a mixture composition and its compaction- and energy-related behaviour and quantitative outputs should be considered as a foundation and not as a final output. To this end,
- The diversity among the mixtures that were considered (including dense-graded friction courses and open-graded friction courses) suggests that the conclusions above could have quite a wide applicability, and the replicability of the study could be quite high. Anyhow, a higher number of samples and a higher number of compaction-related variables would be needed in order to improve the significance of the findings. Indeed, the analysis should be extended to other mixture-related variables and additional factors to investigate the compaction behaviour of various mixtures better.
- This also applies to the objective function. Future research should explore more mixtures with different gradations and material types, considering the Akaike information criterion (AIC), the Bayesian Information Criterion (BIC), and Cross Validation (CV) for better selecting the best number of parameters.
- The objective function herein set up and the analyses carried out mainly refer to sustainability (energy-related) issues. A broader spectrum of instances should be involved, and the same definition of the objective function emerges as an opportunity for further refinement towards having an objective function that includes more equations.
- The validation of the clustering of mixtures into groups (e.g., OG, DG), the comparison of in-lab and on-site energy densities, and the editing of guidelines for practitioners are supplementary priorities for further research. This also includes finding a parametric way to deal with the issues deriving from the transition from laboratory conditions to on-site conditions (weather conditions, the actual temperatures of mixtures, and the layer thickness).
Author Contributions
Conceptualization, F.G.P.; data curation, F.G.P. and G.P.; investigation, F.G.P. and G.P.; methodology, F.G.P.; writing—original draft, F.G.P. and G.P.; writing—review and editing, F.G.P. and G.P.; supervision, F.G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that have been used are confidential.
Acknowledgments
The authors would like to thank all who sustained them with this research, especially the European Commission for the LIFE SILENT project “Sustainable Innovations for Long-life Environmental Noise Technologies”—LIFE22-ENV-IT-LIFE-SILENT/101114310|Acronym: LIFE22-ENV-IT-LIFE SILENT) and for the LIFE SNEAK Project “optimised Surfaces against NoisE And vibrations produced by tramway tracK and road traffic” (LIFE20 ENV/IT/000181|Acronym: LIFE SNEAK). The authors would also like to thank Vamsi K. Mypati for a software-based elaboration of one detail during revision.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SDGs | sustainable development goals |
| LCA | life cycle assessment |
| FAA | fine aggregate angularity |
| CAA | coarse aggregate angularity |
| AV | air void content |
| VMA | voids in mineral aggregate |
| VFA | voids filled with asphalt |
| DG | dense-graded mixes |
| OG | open-graded mixes |
| CEI | compaction energy index |
| LP | locking point |
| CDI | compaction densification index |
| TDI | traffic densification index |
| N | number of gyrations |
| Gmm | theoretical maximum density |
| GER | Global Energy Requirement |
| G | aggregate gradation |
| E | compaction energy |
| CE | competitive equilibrium |
| KPI | key performance indicator |
| SGC | Superpave Gyratory Compactor |
| NMAS | nominal maximum aggregate |
| DGFC | dense-graded friction course |
| PA | porous asphalt |
References
- Praticò, F.G.; Perri, G. A Study on Warm Mix Asphalt Sustainability. In Proceedings of the 10th International Conference on Maintenance and Rehabilitation of Pavements, Guimarães, Portugal, 24–26 July 2024; Pereira, P., Pais, J., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 284–292. [Google Scholar]
- Praticò, F.G.; Perri, G. Are Low-Temperature Asphalts a Good Choice? In Proceedings of the Pavement, Roadway, and Bridge Life Cycle Assessment 2024, Arlington, VA, USA, 6–8 June 2024; Flintsch, G.W., Amarh, E.A., Harvey, J., Al-Qadi, I.L., Ozer, H., Lo Presti, D., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 99–106. [Google Scholar]
- Zhao, Y.; Xie, S.; Gao, Y.; Zhang, Y.; Zhang, K. Prediction of the Number of Roller Passes and Degree of Compaction of Asphalt Layer Based on Compaction Energy. Constr. Build. Mater. 2021, 277, 122274. [Google Scholar] [CrossRef]
- Praticò, F.G.; Perri, G.; De Rose, M.; Vaiana, R. Comparing Bio-Binders, Rubberised Asphalts, and Traditional Pavement Technologies. Constr. Build. Mater. 2023, 400, 132813. [Google Scholar] [CrossRef]
- Wang, X.; Duan, Z.; Wu, L.; Yang, D. Estimation of Carbon Dioxide Emission in Highway Construction: A Case Study in Southwest Region of China. J. Clean. Prod. 2015, 103, 705–714. [Google Scholar] [CrossRef]
- Bijleveld, F.R.; Miller, S.R.; De Bondt, A.H.; Dorée, A.G. Aligning Laboratory and Field Compaction Practices for Asphalt—The Influence of Compaction Temperature on Mechanical Properties. Int. J. Pavement Eng. 2016, 17, 727–740. [Google Scholar] [CrossRef]
- Bertulienė, L.; Augutis, A. Experimental Study for Asphalt Laying Using Control of Pavement Compaction Technology on Roads. In Proceedings of the 10th International Conference Environmental Engineering, Vilnius, Lithuania, 27–28 April 2017. [Google Scholar] [CrossRef]
- Polaczyk, P.; Han, B.; Gong, H.; Ma, Y.; Xiao, R.; Hu, W.; Huang, B. Influence of Aggregate Gradation on the Compactability of Asphalt Mixtures Utilizing Locking Point. J. Mater. Civ. Eng. 2021, 33, 04021005. [Google Scholar] [CrossRef]
- Polaczyk, P.; Ma, Y.; Hu, W.; Xiao, R.; Jiang, X.; Huang, B. Effects of Mixture and Aggregate Type on Over-Compaction in Hot Mix Asphalt in Tennessee. Transp. Res. Rec. 2022, 2676, 448–460. [Google Scholar] [CrossRef]
- Mahmoud, A.F.F.; Bahia, H. Using Gyratory Compactor to Measure Mechanical Stability of Asphalt Mixtures; Wisconsin Highway Research Program: Portage, WI, USA, 2004. [Google Scholar]
- Mohammad, L.; Shamsi, K. A Look at the Bailey Method and Locking Point Concept in Superpave Mixture Design. Transp. Res. Circ. 2007, EC-124, 24–32. [Google Scholar]
- AASHTO. American Association of State Highway and Transportation Officials (AASHTO) AASHTO Provisional Standards, April 2001 Interim Edition; AASHTO: Washington, DC, USA, 2000. [Google Scholar]
- Airey, G.D.; Collop, A.C. Mechanical and Structural Assessment of Laboratory- and Field-Compacted Asphalt Mixtures. Int. J. Pavement Eng. 2016, 17, 50–63. [Google Scholar] [CrossRef]
- Bahia, H.U.; Friemel, T.P.; Peterson, P.A.; Russell, J.S.; Poehnelt, B. Optimization of Constructibility and Resistance to Traffic: A New Design Approach for HMA Using the Superpave Compactor. J. Assoc. Asph. Paving Technol. 1998, 67, 189–232. [Google Scholar]
- Mikhailenko, P.; Griffa, M.; Pieren, R.; Pachale, U.; Poulikakos, L.D. Pore Space of In-Situ Semi-Dense Asphalt: A Characterization by X-Ray Tomography. Constr. Build. Mater. 2024, 453, 139091. [Google Scholar] [CrossRef]
- Pouranian, M.R.; Haddock, J.E. A New Framework for Understanding Aggregate Structure in Asphalt Mixtures. Int. J. Pavement Eng. 2021, 22, 1090–1106. [Google Scholar] [CrossRef]
- Leiva, F.; West, R.C. Analysis of Hot-Mix Asphalt Lab Compactability Using Lab Compaction Parameters and Mix Characteristics. Transp. Res. Rec. 2008, 2057, 89–98. [Google Scholar] [CrossRef]
- ANAS S.p.A. Capitolato Speciale Di Appalto. In Norme Tecniche per l’esecuzione Del Contratto Parte 2. Pavimentazioni Stradali; ANAS S.p.A.: Rome, Italy, 2016. [Google Scholar]
- Ministero dei Lavori Pubblici CIRS. Centro Sperimentale Interuniversitario Di Ricerca Stradale. Capitolato Speciale d’appalto Tipo per Lavori Stradali; Ministero dei Lavori Pubblici: Rome, Italy, 2001.
- Caputo, P.; Calandra, P.; Vaiana, R.; Gallelli, V.; De Filpo, G.; Rossi, C.O. Preparation of Asphalt Concretes by Gyratory Compactor: A Case of Study with Rheological and Mechanical Aspects. Appl. Sci. 2020, 10, 8567. [Google Scholar] [CrossRef]
- Vavrik, W.R.; Carpenter, S.H. Calculating Air Voids at Specified Number of Gyrations in Superpave Gyratory Compactor. Transp. Res. Rec. 1998, 1630, 117–125. [Google Scholar] [CrossRef]
- Polaczyk, P.; Huang, B.; Shu, X.; Gong, H. Investigation into Locking Point of Asphalt Mixtures Utilizing Superpave and Marshall Compactors. J. Mater. Civ. Eng. 2019, 31, 04019188. [Google Scholar] [CrossRef]
- Cheng, Z.; Jia, X.; Jiang, H.; Hu, W.; Huang, B. Quantification of Impact Compaction Locking Point for Asphalt Mixture. Constr. Build. Mater. 2021, 302, 124410. [Google Scholar] [CrossRef]
- Poulikakos, L.D.; Pasquini, E.; Tusar, M.; Hernando, D.; Wang, D.; Mikhailenko, P.; Pasetto, M.; Baliello, A.; Cannone Falchetto, A.; Miljković, M.; et al. RILEM Interlaboratory Study on the Mechanical Properties of Asphalt Mixtures Modified with Polyethylene Waste. J. Clean. Prod. 2022, 375, 134124. [Google Scholar] [CrossRef]
- Mocelin, D.M.; Brito, L.A.T.; Johnston, M.G.; Alves, V.S.; Colpo, G.B.; Ceratti, J.A.P. Evaluation of Workability of Warm Mix Asphalt through Cdi Parameter and Air Voids. Transport Infrastructure and Systems. In Proceedings of the AIIT International Congress on Transport Infrastructure and Systems, TIS 2017, Rome, Italy, 10–12 April 2017; pp. 335–341. [Google Scholar] [CrossRef]
- Huang, J.; Kumar, G.S.; Sun, Y. Evaluation of Workability and Mechanical Properties of Asphalt Binder and Mixture Modified with Waste Toner. Constr. Build. Mater. 2021, 276, 122230. [Google Scholar] [CrossRef]
- Sanchez-Alonso, E.; Vega-Zamanillo, A.; Castro-Fresno, D.; Delrio-Prat, M. Evaluation of Compactability and Mechanical Properties of Bituminous Mixes with Warm Additives. Constr. Build. Mater. 2011, 25, 2304–2311. [Google Scholar] [CrossRef]
- Yu, S.; Shen, S.; Lu, M. Data Sensing and Compaction Condition Modeling for Asphalt Pavements. Autom. Constr. 2023, 154, 105021. [Google Scholar] [CrossRef]
- Dan, H.; Li, S.; Chen, J.; Li, W. Dynamic Response and Compaction Evaluation of Asphalt Pavement in Different Infrastructure Types through an Energy-Based Approach. Constr. Build. Mater. 2025, 479, 141501. [Google Scholar] [CrossRef]
- Shan, H.; Dan, H.-C.; Wang, S.; Zhang, Z.; Zhang, R.; Shan, H.; Dan, H.-C.; Wang, S.; Zhang, Z.; Zhang, R. Investigation on Dynamic Response and Compaction Degree Characterization of Multi-Layer Asphalt Pavement under Vibration Rolling. Electron. Res. Arch. 2023, 31, 2230–2251. [Google Scholar] [CrossRef]
- Praticò, F.G.; Fedele, R.; Pellicano, G. Pavement FRFs and Noise: A Theoretical and Experimental Investigation. Constr. Build. Mater. 2021, 294, 123487. [Google Scholar] [CrossRef]
- Moutier, F. Modelisation Des Resultats de La Pcg Reflexions a Propos Du Seuil Ultime de Compactage. In Proceedings of the Eurasphalt & Eurobitume Congress, Strasbourg, France, 7–10 May 1996; pp. 7–10. [Google Scholar]
- Margaritis, A.; Tanghe, T.; De Visscher, J.; Vansteenkiste, S.; Vanelstraete, A. The Use of Gyratory Compaction to Assess the Workability of Asphalt Mixtures. In Green and Intelligent Technologies for Sustainable and Smart Asphalt Pavements, Proceedings of the 5th International Symposium on Frontiers of Road and Airport Engineering IFRAE, Delft, The Netherlands, 12–14 July 2021; CRC Press: London, UK, 2022; pp. 91–97. [Google Scholar]
- Gao, Y.; Huang, X.; Yu, W. The Compaction Characteristics of Hot Mixed Asphalt Mixtures. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2014, 29, 956–959. [Google Scholar] [CrossRef]
- Stakston, A.D.; Bahia, H.U.; Bushek, J.J. Effect of Fine Aggregate Angularity on Compaction and Shearing Resistance of Asphalt Mixtures. Transp. Res. Rec. J. Transp. Res. Board 2002, 1789, 14–24. [Google Scholar] [CrossRef]
- Praticò, G.F.; Fedele, R. Road Pavement Macrotexture Estimation at the Design Stage. Constr. Build. Mater. 2023, 364, 129911. [Google Scholar] [CrossRef]
- Bezdek, K.; Khan, M.A. Contact Numbers for Sphere Packings. Bolyai Soc. Math. Stud. 2018, 27, 25–47. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).