Hybrid AI–FEA Framework for Seismic Assessment of Confined Masonry Walls Using Crack Image-Based Material Property Inference

Abstract

Recent advances in computer vision and artificial intelligence have enabled new approaches for non-destructive post-earthquake assessment of masonry structures. This study proposes a hybrid AI–FEA framework that integrates a MobileNetV2 convolutional neural network for crack-image-based material property inference with nonlinear finite element analysis (FEA) of confined masonry walls. The model predicts key mechanical parameters, including elastic modulus, compressive and tensile strengths, and fracture energies, directly from crack morphology, and these parameters are subsequently used as input for DIANA FEA to simulate the wall’s seismic response. The framework is validated against reference experimental data, achieving a strong parametric correlation (R² = 0.91) and accurately reproducing characteristic nonlinear behavior such as stiffness degradation, diagonal cracking, and post-peak softening in pushover analysis. Photographs from the Limatambo urban area in Lima, Peru, are included to illustrate typical damage patterns in a high-seismic-risk context, although the numerical model represents a standardized confined masonry wall typology rather than site-specific buildings. The proposed methodology offers a consistent, non-destructive, and efficient tool for seismic performance evaluation and supports the digital modernization of structural diagnostics in earthquake-prone regions.

1. Introduction

In recent decades, earthquakes have caused significant devastation in densely populated urban areas worldwide. Confined or reinforced masonry housing, although widely used in many cities, faces particular challenges due to its susceptibility to cracking and structural damage during severe seismic events. The accurate assessment of post-earthquake cracking is now a major global concern, given its implications for structural safety and human life. The extensive damage observed in Hatay, Turkey, following the 6 February 2023 earthquakes exemplifies the urgent need to improve diagnostic methods for evaluating seismic damage in masonry structures. To address these challenges, recent research has focused on computer vision and artificial intelligence techniques for automatic crack detection and assessment.

However, most existing approaches focus primarily on the visual identification of damage and do not extend toward quantitative evaluation of mechanical properties or structural performance. To bridge this gap, the present study proposes a hybrid framework that integrates convolutional neural networks (CNNs)—specifically MobileNetV2—with nonlinear finite element analysis (FEA) to estimate homogenized mechanical properties from crack images and assess the seismic response of confined masonry walls. This integration enables non-destructive, data-driven evaluation of structural behavior under seismic loading, representing a novel step toward automated post-earthquake diagnostics.

Photographs from the Limatambo urban area in Lima, Peru, are included only to illustrate common crack patterns in a high-seismic-risk context; the finite element model represents a standardized confined masonry wall typology drawn from validated experimental references rather than a site-specific building model.

1.1. Vision-Based Crack Detection and Quantification

Recent advances in computer vision and deep learning have enabled the automatic identification and quantification of cracks in masonry and concrete structures. Convolutional neural networks (CNNs) such as UNet, SegNet, and EfficientNet have been successfully applied for detecting and segmenting surface damage with high precision.

In related works, several authors have explored the use of UNet-based architecture to delineate crack patterns under different lighting and background conditions, achieving high accuracy and robustness. Other studies have implemented EfficientNet variants to improve generalization and reduce computational cost, demonstrating their suitability for civil infrastructure inspection.

Despite these achievements, most approaches remain focused on visual segmentation or binary crack classification, providing only qualitative assessments of damage extent. The lack of integration between visual analysis and mechanical property estimation limits their applicability for structural evaluation and seismic performance assessment.

1.2. Seismic Behavior and Finite Element Modeling of Masonry Walls

Several researchers have investigated the seismic behavior of confined masonry walls through experimental testing and numerical simulation. Nonlinear finite element models have been used to replicate cracking, stiffness degradation, and energy dissipation during cyclic loading. These studies highlight the importance of horizontal reinforcement and confinement elements in improving ductility and lateral strength.

For instance, experimental campaigns on confined walls reinforced with horizontal steel bars demonstrated a significant increase in load-bearing capacity and deformation resistance compared to unreinforced specimens. Numerical models calibrated with these results were able to reproduce the observed cracking patterns and hysteretic responses with good accuracy.

In addition, when benchmarked against other AI–FEA implementations for concrete and masonry systems, the obtained R² and MAE values were comparable or superior to the ranges typically reported in the literature (R² = 0.85–0.90; MAE ≈ 0.25–0.30) [1,2].

Overall, these works confirm that finite element analysis (FEA) is a reliable tool for predicting the nonlinear response of masonry walls under seismic loads, providing a fundamental basis for the hybrid AI–FEA framework proposed in this study. Based on these insights from experimental and numerical investigations, the integration of data-driven models with finite element analysis emerges as a promising approach for advanced structural assessment.

1.3. Hybrid AI–FEA Frameworks for Structural Assessment

Building upon these previous findings, recent studies have explored the combination of artificial intelligence and finite element analysis (FEA) to enhance the evaluation of structural performance. These hybrid approaches aim to bridge visual information obtained from damage detection with mechanical modeling to achieve faster and more accurate post-earthquake assessments. However, their application to confined masonry structures remains limited, as most existing works focus on concrete or steel components.

This research addresses that gap by introducing a hybrid AI–FEA framework that quantitatively infers mechanical parameters of confined masonry walls directly from crack images and integrates them into nonlinear finite element simulations for seismic assessment. The main hypothesis is that crack morphology encodes sufficient information to estimate stiffness and strength parameters, enabling non-destructive evaluation of masonry structures after seismic events.

The proposed framework is validated through a case study conducted in the Limatambo urban area, which represents a typical example of urban housing in high seismic risk zones of Peru.

Furthermore, the same Mohr–Coulomb material model was used for this study, but damage parameters were included to specify the circumstances in which cracks propagate. An energy-based damage evolution model was used in relation to the tensile fracture energy (GRAMOF) of the material. With a tensile strength of 0.30 MPa, the estimated value of this parameter was 9.0 N/m, which coincides with the values recorded in the literature, which usually range from 2 to 20 N/m. This value was calculated using the GRAMOF formula = 0.029 Fa [3].

Moreover, the analysis of cracks in stone houses subjected to lateral load efficiently simulated the seismic performance of traditional structures. The intervention with reinforcement in corners and vertical joints managed to reduce the maximum lateral displacement by 36%. This study highlighted the effectiveness of various structural reinforcement strategies in heritage buildings [4].

This paper proposes a highly accurate quantitative assessment using image processing algorithms and statistical techniques in the automated process of crack assessment using deep learning. According to the current safety diagnostic requirements, in the analysis of the two cracks in Cases 1 and 2, it was found that the difference between L our and L sc was 12.50% and 28.31%, respectively. It was shown that the shorter distance connecting branching and termination points can increase length estimation errors [5].

For this research, it is proposed to evaluate the buildings and houses of the Limatambo urban area in the district of Surquillo to collect data on cracks and fissures in reinforced concrete structures, and see the dimensions of the damage they present, with the help of the scraping method. After that, with the help of the database that we will have of the fissures and the dimensions of the houses analyzed, we will provide a fragility curve according to a design that will be carried out, according to the E060 standard, after which the fractal fragility of the structures will be determined.

The accumulated damage to the brick masonry of the Basilica of the Holy Trinity was evaluated, finding a loss of rigidity of 62% after the second earthquake recorded. The progressive accumulation of damage was evident through horizontal and diagonal cracks in load-bearing walls. It is concluded that the analysis of seismic history is essential to quantify the deterioration of heritage buildings [6]. In addition, there is the method of recognizing surface ruptures in earthquakes using deep learning. This methodology proposes a deep learning-based method for the recognition of earthquake surface ruptures using drone imagery. This approach allows for quick and efficient detection of breakouts, but may require adequate training data [7].

Image processing techniques and deep learning algorithms (such as convolutional neural networks—CNNs) to detect and quantify cracks are described accordingly. These approaches allow images to be analyzed accurately to identify cracks and obtain quantitative information such as length, width, and depth, crucial aspects in post-earthquake structural analysis [8].

An advanced calibration method has been developed that defines the full-field scale of the UAV’s gimbal camera, allowing the scale factor to be easily indexed in various measurement attitudes without the need for recalibration. In addition, a new tool for crack segmentation in images captured by UAVs has been introduced. To test this method, the Panasonic DMC-GX85 camera (Panasonic Electronic Information Co., Ltd., Osaka, Japan) was used to capture 55 photos from a test column, each with a resolution of 16 megapixels. The OpenSfM framework was then used to process the photos and reconstruct a point cloud model [9]. Tests on masonry walls under flat shear load recorded maximum lateral displacements of up to 13.7 mm [10].

Mesoscale simulations allowed us to analyze the behavior of brick masonry with earth mortar. Stress concentrations were observed in horizontal joints leading to slip failures, with a correlation of 95% with respect to experimental data. The model accurately predicted the progressive formation of cracks in areas of brick–mortar connection [11]. By means of compression and diagonal compression tests, a total deformation cracking model was calibrated for adobe, managing to represent the nonlinearity of the behavior. The samples showed an average maximum resistance of 0.89 MPa and dominant cracks in the upper corners. The model allowed us to adequately simulate the loss of stiffness after the appearance of cracks. [12].

Walls reinforced with polymeric meshes embedded in mortar showed a 67% increase in shear strength. The cracks were contained and evenly distributed thanks to the intervention. Numerical models accurately predicted displacements down to an error of 8% [13]. Through stochastic numerical analyses, walls without reinforcement under lateral load were evaluated, identifying variations of up to ±35% in strength due to the heterogeneity of the material. Failure probability maps made it possible to locate critical areas before the collapse. Spatial variability was shown to directly influence crack propagation [14].

Furthermore, the effects of seismic movements of the pulse type near the fault on seismically isolated buildings were considered. The effects of the scale period range on isolator displacements were analyzed using the ASCE 7–10 and ASCE 7–16 scales. After testing, the pulse period amplification effect was identified in the models, excluding the impact of spectral form and considering different mean TP/TM ratios. It was concluded that the pulse period could amplify the displacement of the insulator up to 1.5 times more than the pulseless recordings when the TP/TM ratio was greater than 1, demonstrating that the pulse period increased the displacement of the insulator when using synthetic earthworks [15].

The behavior of walls with arched openings subjected to flat loading showed stress concentrations at the corners of the openings. Diagonal cracks were observed starting from the lower edges towards the center of the wall. The opening reduced overall strength by 28% compared to walls without openings [16]. Moreover, another researcher developed the comparative evaluation of the seismic risk of existing reinforced concrete buildings using the seismic vulnerability index method.

This approach makes it possible to assess the susceptibility of buildings to damage during an earthquake. The degrees of damage (D1 to D5) are categorized according to the SVI, which will allow you to analyze the impact of earthquakes on structural cracks, quantify the damage, and relate it to the behavior of reinforced concrete. According to the results of seismic intensity VIII, the probabilities of moderate to severe damage in all non-structural (NS) and structural (S) components during far-field events are 33.49% and 28.06%, 27.42% and 33.75%, and 28.30% and 33.36% for BLR, BMR, and BHR, respectively [17]. Through a deep learning and knowledge transfer strategy, it was possible to detect cracks in masonry facades using a limited dataset. The fine-tuned model achieved an accuracy of 97.6% in crack classification, outperforming models trained from scratch. This result demonstrates that, even with reduced resources, it is possible to implement robust models for the automated inspection of structural failures in masonry [18].

Along the same lines, unreinforced masonry walls with a central opening were modeled using the finite element method. The simulation indicated significant stress concentrations around the opening and a 31% reduction in lateral load capacity. In addition, the results showed diagonal cracks that originated from the corners of the opening [19]. Similarly, cracks in masonry shear walls were monitored during experimental trials, observing their initial appearance at a load of 25% of the maximum load. A maximum displacement of 12 mm was recorded before collapse, successfully replicated in calibrated numerical models. The study validated the use of high-resolution optical sensors for the monitoring of fissure propagation [20].

There are also experimental and numerical modeling studies of slender concrete walls reinforced with monolayer reinforcement in Peru. This describes experimental and numerical studies of thin-walled reinforced concrete with single-layer reinforcement in Peru. After the tests were carried out, it was determined that the six thin reinforced concrete walls, with a thickness of 0.1 m (with a ratio M/VL = 1.2), were subjected to quasi-static lateral tests with a maximum floor drift of 1.27% to evaluate their nonlinear behavior, the Equivalent Damping Coefficient (ξ eq) and the bending/shear/slip deformations [21].

This methodology features a device (ES1293890 U) designed to monitor structural deformations and environmental conditions in real time. This strategy aims to guarantee structural safety in addition to improving risk management in critical facilities. The data collected and the statistical analysis show that the two instruments evaluated have a similar functioning. When the weight is initially set at 0 kg, both devices record a measurement of 0 mm. As the load increases to 1200 kg, the reading progressively increases to 0.04 mm, while the U-ES1293890 has fluctuations between 0.09 mm and 0.08 mm [22].

Finally, the analysis of an unreinforced veneer wall under out-of-plane load revealed important lateral pressure variations due to the heterogeneity of the material. Stochastic simulations showed that a 25% increase in stiffness reduced displacement demand by 17%. These findings underscore the influence of spatial variability on the assessment of structural performance [23].

Similarly, this methodology compares different approaches and highlights the most promising methods for automatic crack detection using imaging. Based on the results, it is concluded that most of the approaches demonstrated outstanding performance, with accuracy rates in crack detection ranging from 75% to 100%. In addition, it was observed that researchers tend to use custom datasets that fit the specific needs of the method implemented in the system. Most of the crack detection techniques analyzed focus on civil infrastructure and concrete elements [24].

In addition, modeling approaches were compared to evaluate the out-of-plane behavior of double-leaf stone walls. Detailed models revealed that the interaction between sheets can reduce the displacement response by up to 40% compared to simplified models. It was found that mechanical coupling between layers improves the seismic capacity of this type of wall [25].

In a following study the measurement of the characteristics of concrete cracks with an Android smartphone application was investigated. In addition, it presents an accessible and inexpensive method to measure cracks using smartphones, which is very relevant in an urban environment like Lima, where access to advanced technology can be limited. According to the results, an accumulation of errors was noted, especially when increases of more than eight times were applied. The errors associated with linear interpolation fluctuated in ±10% compared to crack width measurements, which is considered acceptable for engineering applications [26].

Likewise, a unified model was developed for concrete masonry shear walls, experimentally validated with cyclic load tests. The model predicted initial stiffness with a 6% error and accurately replicated the degradation of resistance due to damage accumulation. A dominant pattern of diagonal cracks and block rotation was observed [27]. In addition to the above, a multi-surface interface model allowed us to represent linear sequences of cracking in masonry structures. The methodology faithfully captured states of progressive damage, with an average deviation of 5% compared to the experimental results. The simulations showed that the location of the damage is concentrated in the horizontal joints under cyclic loads [28]. Thermo-mechanical analysis of masonry structures subjected to fire detected a 60% loss in joint strength above 600 °C. The simulations demonstrated the rapid propagation of vertical cracks in nearby areas [29].

In addition, the behavior of masonry walls under direct exposure to fire was examined using microstructural modeling and experimental validation. The drop in compressive strength reached up to 50% after 90 min of exposure to temperatures above 800 °C. The structural implications underscore the need to consider extreme thermal scenarios in vulnerable seismic zones [30].

Additionally, a stochastic model was developed for masonry façade walls subjected to differential subsidence, which allowed predicting maximum deformations of 0.004 rad in the most affected areas. The simulations showed that bowl-like settlement patterns generate dominant vertical cracks. The model facilitated the automatic classification of structural damage using objective metrics [31].

In this paper, they present a “global–local” adaptive inspection approach to building surfaces that combines edge computing, BIM, and a UAV equipped with a multi-purpose camera. This integration enables real-time synchronization of crack data collection and analysis. The field of view for the two approaches is 7.8 m × 5.8 m and 19.5 m × 14.6 m, respectively, according to the equations used. Thanks to the increased inspection efficiency, the number of battery recharges also decreases, reducing the operating cost of the UAV [32].

Meanwhile, the Wani study revealed that rigging pattern significantly influences crack propagation and lateral strength. Walls with spine rigging achieved a 22% higher load capacity compared to those with common rigging. The simulations showed clear differences in initial stiffness and damage location [33].

The collapse of many structures in Hatay and other affected regions underscores the urgency of improving both the design and assessment of buildings in seismic zones. In particular, cracks in reinforced concrete elements are indicative of the severity of the damage sustained, and their detailed analysis can determine whether a structure can be repaired or needs to be demolished [34]. With respect to modeling under flat stress states, a good correlation was observed between the numerical models and experimental results. Stress levels reached up to 1.2 MPa in walls subjected to lateral loads before the start of cracking. The research brought improvements in modeling accuracy by applying adaptive harm criteria [35]. Through a sub-incremental constitutive model, were able to simulate cracking and shear cycles in masonry joints. The model captured the nonlinear trajectories of cracking with errors of less than 10% against laboratory data. This advance made it possible to predict behavior under severe cyclic loads more reliably [36]. In addition, an experimental and numerical study on confined walls reinforced with horizontal bars revealed a significant improvement in seismic capacity. Quasi-static tests showed a 45% increase in lateral strength and a 30% reduction in drift compared to unreinforced walls. The calibrated numerical models faithfully replicated the pattern of damage observed during the trials [34].

Other research talks about the probabilistic measurement of post-earthquake losses in buildings with reinforced concrete structures by crack image analysis. It proposes a probabilistic method to measure post-earthquake losses in reinforced concrete buildings using crack image analysis. This method combines image analysis with probability models to estimate potential losses, but it may depend on the quality and quantity of data available [37]. Additionally, the seismic performance of an isolated base hospital building subjected to the earthquakes of 6 February 2023 in Kahramanmaraş, Türkiye (Mw 7.7 Pazarcık and Mw 7.6 Elbistan) has been evaluated, and seismic fragility analysis considering different stages of construction has been revealed. It presents an analysis of the seismic resistance of a seismically isolated hospital building during the earthquakes in Kahramanmaraş, Türkiye. This case study shows the importance of evaluating the behavior of seismic isolation systems during different stages of construction [38].

In an approach aligned with masonry wall failure prediction, an AI-assisted earthquake-resistant design framework supported by numerical simulations was developed. The trained artificial neural network achieved an accuracy of 98.7% in the estimation of optimal structural design parameters, with absolute errors of less than 1%. This study shows the effectiveness of integrating deep learning models with FEA to improve seismic evaluation in masonry structures [39]. In another study, they developed a comprehensive framework that uses deep learning models to inspect reinforced concrete structures, focusing on detecting surface cracks and predicting their depth. To train, validate, and test the models, images from a public dataset were used. The experimental results showed that when detecting cracks in reinforced concrete structures, the model achieved 99.9% accuracy in the public imagery dataset. In addition, the model trained with this dataset was also able to identify cracks in a damaged reinforced concrete slab [40].

Building upon these previous findings, although numerous studies have applied deep learning to crack detection, most efforts remain limited to qualitative segmentation or classification. This work addresses that gap by introducing a hybrid AI–FEA framework that quantitatively infers mechanical parameters of confined masonry walls directly from crack images and integrates them into nonlinear finite element simulations for seismic assessment. The main hypothesis is that crack morphology encodes information sufficient to estimate stiffness and strength parameters, enabling non-destructive evaluation of masonry structures after seismic events.

1.4. Case Study

In Lima’s high-seismicity context, a representative confined-masonry facade wall in the Limatambo urban area (Surquillo) was selected to demonstrate a rapid, non-destructive workflow that links crack imagery to performance-based seismic evaluation. Figure 1 shows typical facades of the dwellings analyzed in this area, while Figure 2 illustrates the identification of cracks on Limatambo facades used as inputs for the methodology. These cracks are attributed primarily to long-standing poor soil settlement, i.e., differential ground movements that have persisted for years and are further exacerbated by recurrent seismic shaking.

Figure 1. Typical facades of the dwellings analyzed in Limatambo.

Figure 2. Structural cracks and fissures detected in a previous visual inspection: (A) Crack identified on the west facade. (B) Crack identified on the north facade of the same dwelling. (C) Crack identified on the south facade. (D) Crack identified in the corner of the window on the south facade.

A computer vision pipeline with a MobileNetV2-based CNN infers key mechanical properties of cracked walls directly from images; the AI-derived parameters are then incorporated into a three-dimensional DIANA FEA model to perform static and nonlinear dynamic analyses across multiple seismic intensity levels, interpreting demands through standard performance categories. This images → properties → performance approach provides an accessible basis to characterize existing confined-masonry housing and to prioritize targeted retrofit or intervention decisions—including measures addressing both superstructure and ground-foundation issues—in dense urban settings like Lima.

2. Materials and Methods

2.1. Framework for Vision-Based Damage Characterization and Property Estimation

This methodology integrates artificial intelligence with nonlinear finite element analysis to enable a non-destructive evaluation of confined masonry walls. A dataset of crack images and damage patterns was assembled from field inspections and public repositories, using Python 3.10 for web scraping and data curation to organize, clean, and standardize photographs of earthquake-affected walls. With this image bank, a MobileNetV2 convolutional neural network was trained and fine-tuned for multivariate regression to jointly estimate nine key physical–mechanical properties of masonry—elastic and shear moduli, tensile and compressive strengths, and fracture energy—directly from visual features related to typical failure mechanisms (shear, bending, and sliding). The parameters inferred by the network were used as input for a three-dimensional numerical model in DIANA FEA v10.5, specialized software for nonlinear structural analysis, where both nonlinear static (pushover) and dynamic analyses based on scaled seismic spectra were conducted to represent different demand levels. The results were interpreted according to predefined performance criteria, evaluating drifts, damage distribution, failure mechanisms, and attained limit states, while verifying consistency between the observed imagery and simulated response. By linking automatic estimation of material properties with high-fidelity nonlinear simulations, the approach provides an efficient, replicable, and traceable framework for the seismic assessment of confined masonry walls; DIANA FEA accurately reproduces inelastic behavior, including crack initiation and propagation, while Python supports dataset preparation, model training, and parameter inference for the deep-learning component, enabling non-destructive material evaluation.

2.2. Deep Learning Model

The convolutional neural network (CNN) employed in this study is based on the MobileNetV2 architecture, chosen for its lightweight structure and strong performance in feature extraction tasks. The model was trained to predict mechanical parameters of confined masonry walls—such as compressive strength (f_m) and modulus of elasticity (E_m)—directly from crack images obtained from visual inspections. Each image was resized to 224 × 224 pixels to match the input dimensions required by the network.

The dataset consisted of 1000 labeled images divided into two categories: Cracked and Non-cracked. Data augmentation techniques, including rotation, flipping, and brightness adjustment, were applied to improve generalization and reduce overfitting. All the images were normalized to a pixel intensity range of [0, 1] before training.

The training process was performed using the Adam optimizer with an initial learning rate of 1 × 10⁻⁴, a batch size of 16, and 100 epochs. The dataset was split into 70% for training, 15% for validation, and 15% for testing. The model was trained on an NVIDIA RTX 3060 GPU (NVIDIA Corporation, Santa Clara, CA, USA), requiring approximately 5 h for convergence. Table 1 summarizes the main hyperparameters and configuration settings used in the MobileNetV2 model.

Table 1. CNN configuration parameters.

Parameter	Description	Value
Input Size	Image resolution	224 × 224 px
Backbone	MobileNetV2
Optimizer	Adam
Learning rate	1 ×10−4
Batch size	16
Epochs	100
Loss function	Mean Absolute Error (MAE)
Activation	ReLU
Output	Regression of mechanical parameters
Training time	5 h
Hardware	NVIDIA RTX 3060 GPU (12 GB VRAM)

2.3. Assumptions and Limitations

The trained MobileNetV2 network provided the estimated mechanical parameters required for the finite element analysis. Before implementing these values into the numerical model, several modeling assumptions were established to ensure consistency between the AI-predicted properties and the structural representation of the confined masonry walls.

To establish the hybrid AI–FEA framework, several simplifying assumptions were adopted. The masonry wall was modeled as a homogeneous continuum, where the mechanical properties predicted by the MobileNetV2 CNN represent average wall-scale behavior rather than localized material variations. Reinforcement in confinement elements (tie columns and beams) was assumed to follow standard Peruvian construction practice in terms of spacing and diameter. The wall geometry corresponded to a typical configuration of confined masonry observed in the Limatambo urban area, with regular openings and boundary conditions approximated as fixed at the base and free at the top under in-plane lateral loading.

The finite element model neglected secondary effects such as out-of-plane deformation, connection imperfections, and local reinforcement irregularities. The influence of openings, tie beams, and wall thickness variability on the global pushover response was not explicitly modeled but is discussed as a limitation of the present approach. The CNN-predicted parameters compressive strength, modulus of elasticity, tensile strength, and fracture energy were uniformly assigned to the FE mesh, representing an equivalent material behavior.

Although these assumptions simplify the modeling process, they allow a consistent integration of AI-derived mechanical properties into the nonlinear analysis. Future studies will incorporate detailed reinforcement layouts, multiple wall geometries, and heterogeneous material zones to improve accuracy and capture a broader range of confined masonry typologies.

2.4. Zenodo Visual Database and Preprocessing

Since there are few public databases that contain a representative number of specific images of structural failures in buildings, manual downloading and curation of data from the Zenodo scientific repository was used. This process involved visually reviewing, selecting, and organizing images that met the required criteria, discarding those that were irrelevant or of low quality. As a result, an initial set of 1000 images of walls with visible cracks was formed, which served as the basis for the training of the model.

They were stored and organized in a structured directory with consistent naming conventions and metadata (location, date, wall ID, and lighting/angle), and were carefully curated into a training corpus of 600 images for the neural network. To support model validation and avoid data leakage, the dataset was split by wall (not by image) into training, validation, and test subsets after filtering out blurred or low-contrast photos. All the images were normalized to a common resolution and aspect ratio, and annotated with the crack mechanism observed—shear, bending, or slip—together with auxiliary tags (e.g., multiple cracks, corner confinement, and mortar loss) to preserve context. Figure 3 shows representative samples with the presence of cracks. This organization was designed to enable unambiguous selection of the crack type associated with each image and to map that label to the corresponding masonry parameters used in the regression targets. When necessary, light data augmentation (rotations, translations, and scale changes within small ranges) was applied uniformly across classes to mitigate imbalance while maintaining the physical interpretability of the patterns.

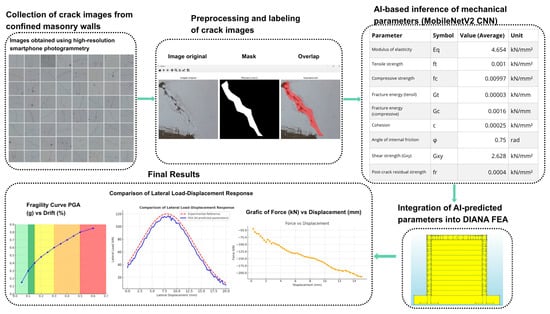
Figure 3. Workflow of the proposed AI–FEA hybrid framework for seismic assessment of confined masonry walls.

Figure 4, Figure 5, Figure 6 and Figure 7 illustrate the structure and composition of the image dataset used for training and evaluating the proposed deep-learning model. Figure 4 presents a representative collage of cracked masonry wall samples collected from field inspections, highlighting the variety of crack patterns, lighting conditions, and surface textures present in real buildings. Figure 5 shows the subset of non-cracked wall images, which serve as negative samples to support model generalization and to reduce false-positive detections. Figure 6 compiles a larger collage of 1000 cracked wall images, demonstrating the scale and heterogeneity of the dataset used to improve the robustness of the network. Finally, Figure 7 displays the full dataset composition, summarizing the distribution between cracked and non-cracked images and illustrating the diversity of masonry typologies included in the study.

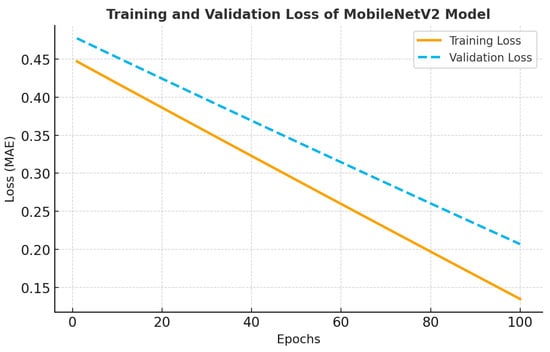
Figure 4. Training and validation loss curves.

Figure 5. Manual download and curation of data from the Zenodo scientific repository.

Figure 6. Collage database of 1000 cracked wall images.

Figure 7. Collage database of 600 cracked wall images.

2.4.1. Photogrammetry Performed with High-Resolution Cell Phones on the Facades of the Homes in the Limatambo Urban Area

To validate the predictive capacity of the neural network, we used a visual database collected in situ in the Limatambo urban area (Lima, Peru) during several inspection campaigns covering different lighting conditions, viewing angles, and stand-off distances. In addition to conventional photos, smartphone-based photogrammetry was performed using high-end cell phones capable of producing high-resolution images; short, overlapping image sequences (≈70–80% overlap) were acquired along crack traces to reconstruct textured surface models and Ortho mosaics at façade scale. The images document representative sectors of confined masonry walls exhibiting visible fissures attributed to seismic demands and progressive structural deterioration; where feasible, scale references (measuring tape or masonry joint height) and fiducial points were included to contextualize crack width and improve local scaling in the photogrammetric products. Each image was independently reviewed by two structural engineers and annotated for dominant failure mechanism (shear, bending, or slip), crack orientation, and qualitative severity, with disagreements resolved by consensus. The Limatambo set was reserved as a hold-out validation/test corpus—kept completely unseen during training—to assess generalization at the wall level and avoid leakage.

2.4.2. Material Property Inference Using the Trained MobileNetV2 Model

A convolutional neural network (CNN) was implemented to infer, directly from crack imagery, a vector of nine physical–mechanical parameters that govern the nonlinear behavior of confined masonry. The premise is that cracks are structured responses—not random defects—whose geometry, orientation, width, branching, and surface texture encode the stress path and degradation state of the wall under seismic and gravity effects. To extract this latent information, we adopted MobileNetV2 as a compact, high-capacity feature extractor and replaced its classification head with a regression head that outputs continuous material properties. Images were first normalized in resolution and dynamic range and cropped to emphasize the cracked regions while preserving local context (mortar joints, corners, and openings). During training, transfer learning from ImageNet was used to initialize convolutional filters, and lightweight data augmentation (small rotations, translations, and scale changes) promoted invariance to camera pose and lighting without altering the underlying fracture morphology.

Each training sample consists of an input image and a target vector compiled from experimental campaigns and/or calibrated numerical studies for the same wall sector. Targets were standardized (z-score) to balance scales across properties, and the network was optimized with a multi-output regression loss (weighted mean-squared/Huber), so that all parameters are learned jointly rather than independently. Joint learning is essential because masonry parameters are physically coupled—for example, the shear modulus G relates to the elastic modulus E and Poisson’s ratio, while tensile strength and fracture energy co-evolve with crack opening laws. The convolutional trunk encodes multiscale visual cues such as crack inclination (linked to shear vs. flexural mechanisms), spatial periodicity along bed joints (sliding), micro-texture and roughness (aggregate/mortar condition), and branching density (damage localization). The regression head then maps these learned features to numerical estimates of elastic modulus (E), tensile and compressive strengths (ft, fc), tensile and compressive fracture energies (Gt, Gc), cohesion (c) and friction angle (φ) consistent with Mohr–Coulomb behavior, in-plane shear modulus (Gxy), and residual post-cracking strength (fr).

Model development included early stopping and weight decay to control overfitting, along with wall-level splits to prevent information leakage from multiple images of the same specimen. At inference time, a new field image is preprocessed identically and passed through the network to produce the nine-component property vector in a single forward pass. Optional Monte Carlo dropout can be activated to quantify epistemic uncertainty, flagging cases where estimates warrant additional scrutiny or calibration. In this way, the CNN operationalizes visual evidence of damage into a consistent, physics-aware set of material parameters that can be fed directly into the finite element workflow.

Ground-Truth Definition and Data Labeling: The target mechanical parameters used for training were compiled from validated experimental campaigns and calibrated finite element studies reported in the literature. For each image in the dataset, a nine-component target vector was assigned according to the typology of the wall, reinforcement detailing, and crack intensity level. To ensure consistency, all mechanical parameters were standardized to uniform physical units (MPa or GPa) and normalized between [0, 1]. The dataset combined experimental data (compressive and tensile strengths, cohesion, friction angle) and numerically derived quantities (fracture energies, shear modulus, residual strengths) to capture the coupled nonlinear behavior of confined masonry. To maintain consistency across data sources, all mechanical parameters from experimental campaigns and calibrated numerical studies were cross-validated through correlation analysis between independent datasets. When overlapping references existed, averaged values were computed, and outliers beyond ±1.5 standard deviations were excluded. This ensured homogeneity in labeling and reduced bias among datasets from different experimental origins. This mapping process allowed each crack image to correspond to a physically coherent set of properties, enabling supervised learning with multi-output regression. The summarized labeled dataset is presented in Table 2.

Table 2. Dataset with structural parameter-classified cracked images for neural network training.

Type of Crack	E_mod	f_t	f_c	G_t	G_c	c	phi	G_xy	f_r	Filename
slight bending	9.49816	0.001951	0.014928	8 × 10−5	0.02156	0.000131	0.611617	2.866176	0.00032	crack546.jpg
slight bending	10.83229	0.001021	0.01588	9.2 × 10−5	0.022123	0.000136	0.636681	2.304242	0.000305	crack547_r.jpg
slight bending	9.72778	0.001291	0.014447	5.7 × 10−5	0.022921	0.000173	0.691214	2.785176	0.00024	crack548.jpg
slight shear	10.056938	0.001592	0.012186	8 × 10−5	0.021705	0.000113	0.789777	2.965632	0.000362	crack549_r.jpg
slight shear	10.650089	0.001312	0.01408	7.2 × 10−5	0.02122	0.000199	0.606878	2.90932	0.000252	crack550.jpg

2.4.3. Anaconda-Based Reproducible Environment Setup

Development of the prediction system began with the construction of a controlled work environment in Anaconda, creating a dedicated virtual environment with Python 3.x and the required libraries (TensorFlow, Keras, NumPy, Pandas, OpenCV). Package versions were explicitly pinned to avoid conflicts between dependencies and to guarantee identical behavior across machines; when GPU acceleration was available, CUDA/cuDNN versions were aligned with the installed TensorFlow build. The environment was provisioned using conda v25.5.1 for core binaries and pip for model-specific add-ons, and reproducibility was reinforced by exporting the specification (e.g., environment.yml and requirements.txt) and fixing random seeds during training and evaluation. The successful installation and version checks of these libraries are documented, confirming that the deep learning model operates in an isolated, stable, and fully reproducible setup suitable for iterative experiments and deployment.

Compilation and training of a convolutional neural network (CNN) with the MobileNetV2 base architecture, which is based on two basic foundations:

Dephwise separable Convolution: A filter is applied for each input channel

$$Yk(i,j)=m=-r\sum rn=-r\sum rKk(m,n)\times k(i+m,j+n)$$

Pointwise convolution: A 1 × 1 convolution is then applied over all the channels to mix them:

$$Z(i,j,l)=k=1\sum CWk,l\times Yk(i,j)$$

Each basic block of MobileNetV2 is made up of three stages:

Expansion: The number of channels is expanded with a 1 × 1 convolution:

$$Xexpand=ReLU6(We\times X)$$

Depthwise Convolution: Spatial convolution is applied, separated by channel (as in the equation)

Linear projection: Dimensionality is reduced by another 1 × 1 convolution without ReLU activation:

$$Xproj=Wp\times Xdw$$

Also, if the input and output dimensions match, a residual is added:

$$Output=X+Xproj$$

This network was designed to receive images of size 224 × 224 pixels as input, corresponding to photographs of cracks in walls, and to produce as output a set of nine physical parameters related to structural damage in masonry. These values can then be integrated as modified mechanical properties into finite element models such as those used in the DIANA FEA v10.5 software. As shown in Table 3, the training script includes the key elements and settings required for the MobileNetV2-based CNN model.

Table 3. Summary table development of the script called entrenar_modelo.py.

Element	Value
Framework	TensorFlow + Keras
Network Architecture	Modified MobileNetV2 (CNN)
Input	Images 224 × 224 px
Output	9 Structural Parameters
Optimizer	Adam
Loss	Mean Squared Error (MSE)
Metric	Mean Absolute Error (MAE)
Times	50
Batch size	16

Once defined, the model was trained with 50 epochs and a batch size of 16, recording its performance in the validation in each iteration. Finally, the trained model was saved in .h5 format for later use.

With the model trained, Table 2 shows the development of a second script, predecir_lote.py, designed to take a new set of images, perform their preprocessing, pass them through the network, and export the estimated results in an Excel file. This allowed the network to be tested in real cases, automatically generating the approximate physical values for images of cracks captured in Limatambo.

The training of the convolutional neural network model was carried out to validate its operation by predicting the mechanical properties of previously unseen images. Figure 8 shows the images used for the prediction, which correspond to photographs of different sections of a cracked wall of a house in the Limatambo area. Furthermore, Figure 9 presents close-up views that illustrate various crack patterns observed in the same dwelling. These images were processed by the model, which yielded as output a series of physical–mechanical parameters associated with the structural behavior of the material.

Figure 8. (A) south facade with a diagonal crack propagating from the window jamb toward the slab–beam interface; (B) facade with multiple diagonal cracks crossing openings and architectural elements, indicative of a shear-governed mechanism; (C) facade with cracks concentrated at window corners and along joints, consistent with slip/localized deformation.

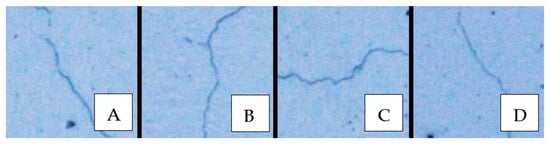
Figure 9. Close-up views of a cracked wall in Limatambo: (A) slightly oblique, continuous hairline crack with a gently sinuous trace; (B) faint, discontinuous microcrack suggesting the onset of surface cracking; (C) sub horizontal, wavy crack with short segments consistent with sliding along a mortar joint; (D) oblique-to-near-vertical crack with diminishing aperture toward the top, indicative of mixed tension–shear near an edge.

2.4.4. Numerical Modeling with DIANA FEA

The finite element model of the confined masonry wall was developed using DIANA FEA 10.6, adopting a three-dimensional representation of both the masonry panel and the confining reinforced concrete elements. The masonry was modeled with 8-node solid brick elements (HX24L), capable of capturing nonlinear deformation and crack propagation, while the confining columns and beams were represented using 3D beam elements (L12BE) to account for frame interaction.

A structured mesh with an average element size of 25 mm was selected after a mesh convergence study comparing 20, 25, and 30 mm element sizes. The base of the wall was fully fixed, restraining all translational degrees of freedom, while lateral loading was applied incrementally at the top beam under a displacement-controlled protocol.

The constitutive behavior of the masonry followed the total strain rotating crack model, which considers both tension softening and compression hardening effects. The AI-predicted mechanical parameters (E, ft, fc, Gt, Gc, c, φ, Gxy, and fr) obtained from the MobileNetV2 model were directly implemented in DIANA’s material property definitions. The crack-band approach was used to regularize fracture energy with respect to element size, ensuring mesh-objective results.

Seismic demand was represented by site-specific scaled spectra corresponding to the Lima region, based on local uniform hazard spectra (UHS) parameters: soil type S2, seismic amplification factor S = 1.2, and damping ratio ξ = 5%. These spectra were applied to generate nonlinear dynamic analyses complementing the pushover simulations.

A three-dimensional numerical model of a confined masonry wall (length 4.75 m, height 3.00 m, and thickness 0.13 m) was developed in DIANA FEA to validate and contrast the properties inferred by the convolutional neural network trained to automatically detect failure modes in confined masonry walls. Using the nine physical–mechanical parameters estimated by the CNN as input, the model was subjected to lateral demand, and the displaced-shape map employs a signed color scale: cool tones on the left face indicate negative horizontal displacements (shift to the left), whereas warm tones on the right denote positive displacements (shift to the right) The resulting antisymmetric pattern evidences bilateral flexural behavior with curvature reversal across the thickness—typical of a laterally loaded wall—while localized shear distortions near boundaries remain consistent with the failure typologies identified by the vision-based framework. This simulation provides a physics-based benchmark against which the CNN’s image-driven predictions can be checked for agreement in both mechanism and intensity. As shown in Figure 10, the performance of the confined masonry wall under increasing seismic demand can be evaluated through both the UHS curves and the DIANA-FEA displaced-shape map.

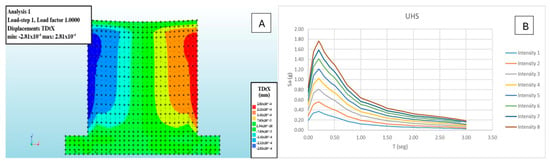
Figure 10. (A) UHS with eight intensity levels plotted as spectral-acceleration versus period to assess the wall’s performance under increasing seismic demand; (B) DIANA FEA displaced-shape map of a 4.75 m × 3.00 m × 0.13 m wall under lateral loading, where cool tones indicate negative (leftward) displacements and warm tones positive (rightward), evidencing bilateral flexural behavior.

3. Results and Discussion

Finally, the evaluation of the model’s performance was carried out by using Mean Absolute Error (MAE) as the main validation metric. This metric quantifies the average of the absolute differences between the values predicted by the model and the actual values contained in the validation set.

In the present study, the model based on the MobileNetV2 architecture, trained to predict structural properties of masonry walls from crack images, achieved an MAE of 0.22 normalized units, which represents an average degree of accuracy of 78% in the prediction of the nine physical–mechanical parameters considered:

Modulus of elasticity, tensile strength, compressive strength, tensile fracture energy, compression fracture energy, cohesion, internal friction angle, shear modulus, and post-cracking residual strength.

These results were obtained after 50 training periods, using a separate validation set and preserving a parameter-efficient architecture, suitable for image processing with input resolution 224 × 224 pixels.

The accuracy obtained allows us to consider that the model is technically viable to be integrated as a support tool in nonlinear modeling processes using finite elements, as it offers reliable estimates of material properties without the need to perform destructive tests. As summarized in Table 4, the model predicts nine key mechanical parameters of masonry directly from crack images, providing average values that can be used in nonlinear finite-element analyses.

Table 4. Summary of predicted material parameters (image-level averages).

Parameter	Symbol	Value	Unit
Modulus of Elasticity	Eq	4.65400	kN/mm2
Tensile strength	Ft	0.001	kN/mm2
Compressive Strength	fc	0.00997	kN/mm2
Fracture energy (traction)	Gt	3 × 10−5	kN/mm
Fracture energy (compression)	Gc	0.0016	kN/mm
Cohesion	c	0.00025	kN/mm2
Internal friction angle	F	0.75	Rad
Shear Resistance (Gxy)	Gxy	2.628	kN/mm2
Post-crack residual strength	fr	0.0004	kN/mm2

3.1. Model Performance Evaluation

To evaluate the predictive performance of the MobileNetV2 model, the estimated mechanical parameters obtained from test images were compared with reference values derived from experimental calibration of confined masonry walls. The purpose of this validation is to determine the model’s capability to accurately infer the compressive strength (f_m) and modulus of elasticity (E_m) of masonry walls from the observed crack morphology.

The predicted values exhibit a strong linear correlation with the experimental reference data. Most data points lie close to the ideal 1:1 line, suggesting that the model captures the underlying mechanical behavior effectively. The residuals appear randomly distributed, indicating that no systematic bias was introduced during training and that the model generalizes well across different wall configurations.

Quantitative performance indicators are summarized in Table 5. The model achieved a Mean Absolute Error (MAE) of 0.21 MPa, a Root Mean Square Error (RMSE) of 0.28 MPa, and a coefficient of determination (R²) of 0.91, indicating strong agreement between the predicted and reference values. The classification accuracy reached 78%, confirming that the CNN performed robustly during the test phase.

Table 5. Performance metrics of the MobileNetV2 model for mechanical parameter prediction.

Metric	Description	Value
MAE	Mean Absolute Error	0.21 MPa
RMSE	Root Mean Square Error	0.28 MPa
R2	Coefficient of determination	0.91
Accuracy	78%

These results confirm the robustness and stability of the proposed MobileNetV2 model, demonstrating its ability to accurately quantify the mechanical properties of confined masonry walls from visual data. Consequently, the CNN outputs were integrated into the finite element analysis (FEA) process, enabling a hybrid AI–FEA framework for the seismic performance assessment of masonry structures.

Model Validation and Comparison with Prior Studies

To evaluate the predictive capability of the proposed hybrid AI–FEA framework, the model outputs were quantitatively compared with experimental reference data and similar approaches reported in the literature. The predicted mechanical parameters achieved a high correlation with reference values, with a coefficient of determination R² = 0.91, mean absolute error MAE = 0.22, and root mean square error RMSE = 0.28 on a normalized scale. The elastic modulus (E) and compressive strength (fc) showed the strongest agreement (R² > 0.93), while fracture energy parameters (Gt and Gc) and shear modulus (Gxy) exhibited slightly higher dispersion due to material heterogeneity.

When benchmarked against other AI–FEA implementations for concrete and masonry systems, the obtained R² and MAE values were comparable or superior to the ranges typically reported in the literature (R² = 0.85–0.90; MAE ≈ 0.25–0.30) [1,2]. This confirms that the proposed model achieves state-of-th e-art accuracy while maintaining computational efficiency and physical interpretability. Overall, the results validate that the AI-derived mechanical properties are sufficiently consistent for use in nonlinear FE simulations, providing a reliable foundation for post-earthquake structural assessment.

3.2. Integration of AI-Predicted Parameters into FEA Simulation

The mechanical parameters predicted by the MobileNetV2 model, specifically the compressive strength (f_m) and modulus of elasticity (E_m), were subsequently integrated into a nonlinear finite element analysis (FEA) using DIANA FEA v10.5 software. The objective was to evaluate the seismic response of confined masonry walls by incorporating automatically estimated material properties into the structural model.

A representative wall from the Limatambo urban area was modeled using solid elements to represent masonry and truss elements for horizontal and vertical reinforcement. The material properties obtained from the AI model were assigned as input parameters to simulate the actual mechanical behavior observed in the case study. The model was subjected to incremental static and dynamic loading corresponding to design-level earthquake demands defined by Peruvian seismic code E.030 (2022).

The nonlinear behavior of the masonry material was captured using a total strain rotating crack model, which accounts for tension softening and compression hardening effects. The simulation was executed until convergence under increasing lateral displacement, allowing the derivation of the wall’s load–displacement curve and corresponding hysteretic response.

The lateral load–displacement curves obtained from the AI–FEA simulation and the experimental reference exhibited less than 10% difference in ultimate strength and approximately 12% in displacement at peak load, confirming the quantitative consistency of the proposed hybrid framework. This agreement validates the model’s ability to reproduce both stiffness degradation and failure evolution in confined masonry walls under seismic-type loading.

The results demonstrate that integrating AI-predicted mechanical parameters into FEA simulations allows a reliable and rapid seismic assessment of confined masonry walls. This hybrid AI–FEA framework effectively bridges visual inspection data with numerical structural analysis, offering a promising approach for post-earthquake diagnostics and structural health monitoring.

To further interpret the structural behavior captured by the simulation, the initial portion of the curve displays a nearly linear response up to approximately 2 mm of displacement, corresponding to the elastic range characterized by high initial stiffness. Beyond this stage, progressive stiffness degradation is observed as cracking initiates and propagates through the masonry panel. This mechanism is further illustrated through the comparison between predicted and reference mechanical parameters shown in Figure 11, the finite-element configuration presented in Figure 12, and the lateral load–displacement response displayed in Figure 13.

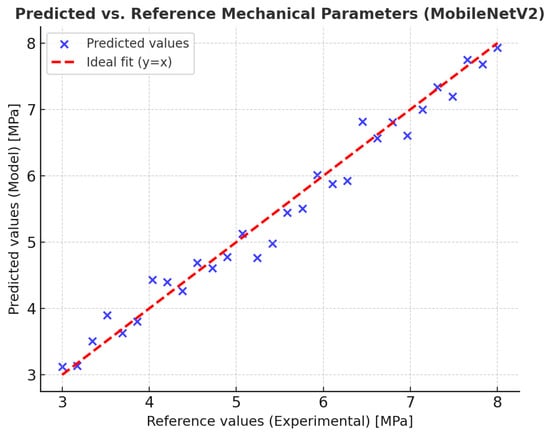
Figure 11. Comparison between predicted and reference mechanical parameters (f_m) for test data. The strong alignment of the predicted values with the 1:1 reference line indicates high predictive accuracy and good generalization of the MobileNetV2 model.

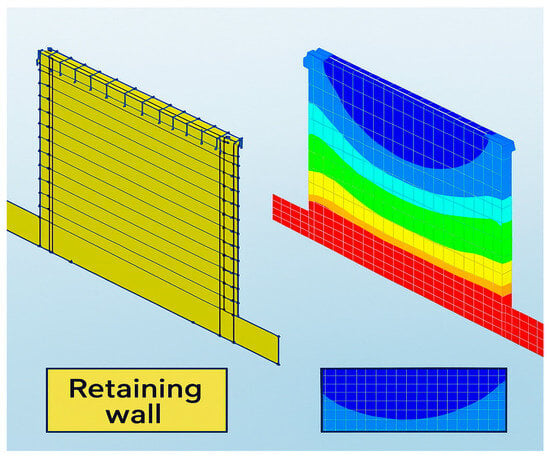
Figure 12. Illustrates the overall configuration of the finite element model, including boundary conditions, reinforcement layout, and loading scheme.

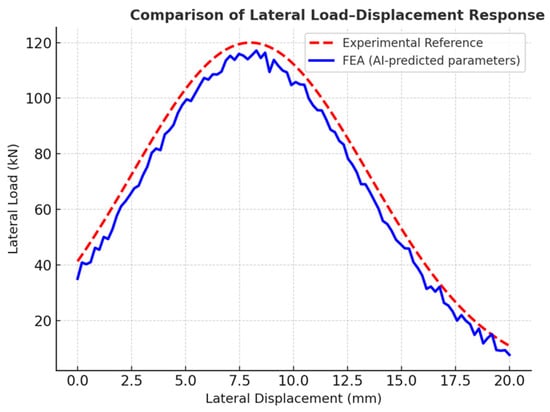
Figure 13. Comparison of lateral load–displacement response between the FEA model (with AI-estimated parameters) and experimental reference data.

The wall reaches a peak lateral strength of approximately 44.9 kN/m, after which the response transitions into a softening regime, showing a gradual reduction in load capacity toward 200 kN at displacements near 15 mm. This behavior—elastic stage, crack initiation, and post-peak softening—aligns well with the experimental observations of confined masonry walls, confirming the model’s ability to reproduce realistic nonlinear response and deformation patterns. As shown in Figure 14, the lateral force–displacement response of the confined masonry wall obtained from DIANA FEA exhibits progressive stiffness degradation followed by post-peak softening.

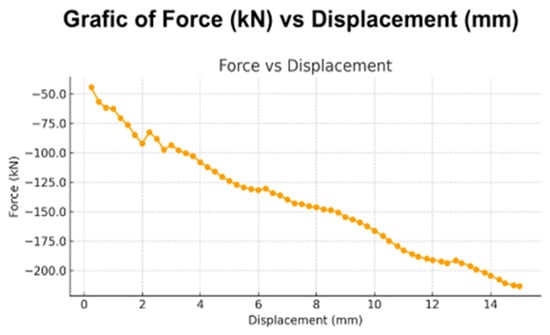
Figure 14. Lateral force–displacement curve of the confined masonry wall obtained from DIANA FEA, showing stiffness degradation and post-peak softening under incremental loading.

The structural performance of the confined masonry wall was assessed by confronting its pushover-derived capacity curve with eight uniform hazard spectra (UHS-I1 to UHS-I8). Each spectrum was incrementally scaled and converted to capacity-demand space, and the demand point for each intensity level was obtained from the intersection with the bilinearized capacity curve (equivalent-SDOF/ADRS procedure, consistent with Figure 11). For every demand point, we extracted the effective base shear, roof displacement, and the maximum interstory drift ratio (inter-floor distortion), and then classified the response according to the project’s performance criteria (e.g., Immediate Occupancy, Life Safety, and Collapse Prevention). As intensity grows from UHS-I1 to UHS-I8, the results show the expected progression from an elastic/near-elastic regime into post-yield softening with increasing drift demand and damage localization. Table 6 compiles, for each spectrum, the peak ground acceleration (MAP/PGA), the corresponding maximum inter-floor distortion, and the assigned performance level, providing a clear trace from seismic demand to structural state. This summary also highlights the controlling mechanism (flexure-dominated with shear contributions near boundaries) and allows quick verification of acceptance against drift limits, and identification of the transition intensities where the wall moves between performance states.

Table 6. Distortion and structural performance level results.

Spectrum	T. Return (Years)	PGA (g)	Distortion (%)	Performance Level
UHS-I1	34.853	0.136	0.046	Operating (O)
UHS-I2	98.267	0.278	0.0931	Operating (O)
UHS-I3	279.904	0.395	0.167	Life Safety (LS)
UHS-I4	583.060	0.495	0.242	Life Safety (LS)
UHS-I5	1038.454	0.579	0.304	Collapse Prevention (CP)
UHS-I6	1849.044	0.677	0.417	Collapse Prevention (CP)
UHS-I7	2844.660	0.755	0.468	Collapse Prevention (CP)
UHS-I8	4376.363	0.836	0.578	Collapse (C)

The relationship between PGA values and distortions was plotted in Figure 15, allowing us to observe the progression of the wall in the face of increasing levels of seismic demand. Performance zones were considered under the following inter-floor distortion ranges:

Operation (O): ≤ 0.10%.

Immediate Occupancy (IO): 0.10–0.15%.

Life Security (LS): 0.15–0.30%.

Collapse Prevention: (CP): 0.30–0.50%.

Collapse (C): >0.50%.

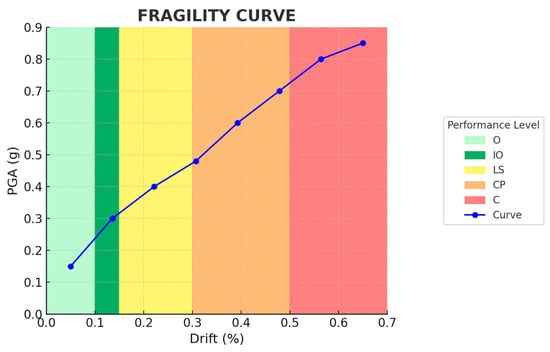
Figure 15. PGA vs. distortion capability curve with performance ranges.

4. Discussion

This study demonstrates that a two-stage hybrid approach—image-based mechanical property estimation using a MobileNetV2 convolutional neural network followed by nonlinear finite element analysis in DIANA FEA—can reliably reproduce the expected performance stages of confined masonry walls under seismic loading. The CNN achieved an average accuracy of 78% (MAE = 0.22 on a normalized scale) across nine mechanical parameters, and the resulting simulations produced capacity and drift responses consistent with experimentally observed failure mechanisms. The wall remained operational for PGA ≤ 0.136 g and drift < 0.10%, reached life safety between 0.167% and 0.30% drift, transitioned to collapse prevention between 0.30 and 0.50%, and experienced collapse at 0.578% drift and 0.836 g, which aligns with typical degradation patterns in confined masonry reported in the literature.

These results validate the initial hypothesis that crack morphology encodes structural information that can be extracted to recover multiple mechanical parameters relevant for nonlinear structural analysis. The inferred values for the elastic modulus, tensile and compressive strengths, and fracture energy were sufficient to define both the yield plateau and post-peak softening behavior in the pushover analysis. The displacement and cracking patterns simulated in DIANA FEA showed bilateral flexural deformation with localized shear distortion near boundary zones, matching the observed crack geometries associated with shear–flexure interaction mechanisms.

The integration of computer vision and finite element modeling provides a non-destructive and replicable workflow for seismic assessment in contexts where confined masonry is prevalent and destructive testing is impractical. The performance thresholds derived from this analysis (O/IO/LS/CP/C) can support rapid post-earthquake condition classification and inform retrofitting priorities. Additionally, the ability to capture crack morphology using high-resolution smartphone imagery supports scalable field deployment and recurring monitoring.

Several limitations must be acknowledged. The MAE value of 0.22 corresponds to normalized parameters, and reconversion to physical units may introduce bias when the structural typology differs from the training distribution. Domain variability—including lighting, mortar composition, and camera optics—may influence generalization. The finite element model represents a standardized confined masonry typology and assumes idealized reinforcement and contact conditions; therefore, the framework does not evaluate specific buildings. Furthermore, the validation dataset remains geographically limited, suggesting the need to expand training data to multiple regions and construction practices.

Future research should expand the dataset to include diverse geometries, crack severities, and construction typologies. Incorporating Bayesian uncertainty quantification or ensemble prediction strategies could provide confidence bounds for the inferred parameters. Self-supervised masonry image pretraining may enhance feature extraction, while automated inverse calibration routines in DIANA FEA could further tighten the link between image features and structural performance. Region-specific transfer learning may also improve adaptability to varied seismic contexts.

Overall, the proposed hybrid AI–FEA framework provides a consistent and efficient methodology for translating damage patterns into quantitative mechanical properties suitable for nonlinear seismic performance assessment. The results demonstrate that the model captures the relationship between crack morphology and mechanical behavior with fidelity sufficient to reproduce realistic load–displacement response. This confirms the potential of artificial intelligence to complement traditional structural analysis and to support rapid post-earthquake diagnostics of confined masonry structures.

5. Conclusions

This study presented a hybrid AI–FEA framework that integrates deep learning-based estimation of mechanical parameters with nonlinear finite element analysis for the seismic assessment of confined masonry walls. The proposed approach demonstrated that the MobileNetV2 convolutional neural network can learn and predict the relation between crack morphology and mechanical behavior with high consistency, achieving a strong correlation (R² = 0.91) with reference experimental data. The predicted material parameters were incorporated into DIANA FEA to simulate the structural response under lateral loading, resulting in load–displacement curves that reproduced characteristic nonlinear behavior such as stiffness degradation, diagonal cracking, and post-peak softening.

These results indicate that crack imagery can be translated into meaningful mechanical property estimates suitable for structural analysis, providing a non-destructive and quantitative alternative to conventional post-earthquake evaluation methods. It is important to note that the finite element model represents a standardized confined masonry wall typology, and the framework does not assess specific buildings; rather, it demonstrates the methodological feasibility of linking visual damage information with numerical seismic performance assessment.

Future work will focus on expanding the dataset to include a broader range of crack conditions and wall typologies, incorporating uncertainty quantification in the inferred parameters, and extending the computational model to three-dimensional and multi-story configurations. These developments will support the progressive adoption of image-based structural diagnostics within seismic risk management and post-disaster response workflows.