Machine Learning Approaches for Fatigue Life Prediction of Steel and Feature Importance Analyses

Abstract

Predicting fatigue behavior in steel components is highly challenging due to the nonlinear and uncertain nature of material degradation under cyclic loading. In this study, four hybrid machine learning models were developed—Histogram Gradient Boosting optimized with Prairie Dog Optimization (HGPD), Histogram Gradient Boosting optimized with Wild Geese Algorithm (HGGW), Categorical Gradient Boosting optimized with Prairie Dog Optimization (CAPD), and Categorical Gradient Boosting optimized with Wild Geese Algorithm (CAGW)—by coupling two advanced ensemble learning frameworks, Histogram Gradient Boosting (HGB) and Categorical Gradient Boosting (CAT), with two emerging metaheuristic optimization algorithms, Prairie Dog Optimization (PDO) and Wild Geese Algorithm (WGA). This integrated approach aims to enhance the accuracy, generalization, and robustness of predictive modeling for steel fatigue life assessment. Shapley Additive Explanations (SHAP) were employed to quantify feature importance and enhance interpretability. Results revealed that reduction ratio (RedRatio) and total heat treatment time (THT) exhibited the highest variability, with RedRatio emerging as the dominant factor due to its wide range and significant influence on model outcomes. The SHAP-driven analysis provided clear insights into complex interactions among processing parameters and fatigue behavior, enabling effective feature selection without loss of accuracy. Overall, integrating gradient boosting with novel optimization algorithms substantially improved predictive accuracy and robustness, advancing decision-making in materials science.

1. Introduction

Steel is among the most common engineering materials because it possesses a desirable combination of strength, plasticity, availability, and cost-effectiveness [1]. Steel is used in a wide array of structural and mechanical applications that consist of bridges, automobiles, pipelines, aircraft, and pressure vessels [2]. Steels with high static strength still experience gradual accumulation of damage over time under cyclic loading and eventually fail through fatigue [3]. Fatigue is a condition in which material under cyclic or fluctuating loading is broken at a loading level below its tensile strength [4]. The outcome is a sudden and catastrophic failure in most instances without noticeable prior deformation and warning signs, so it is an important engineering design and maintenance factor [5].

The fatigue response of steel in cyclic loading is affected by a broad variety of parameters, including chemistry, microstructure, loading conditions, shape, fabrication processes, and heat treatment parameters [6]. These parameters interact with each other in a complex manner to decide how cracks form and evolve. With so many influencing parameters, accurately predicting fatigue life is an ongoing challenge in engineering [7]. Historical empirical methods like load vs. cycle number (S-N curves) yield valuable but limited information, especially when complex material histories and processing conditions exist [8]. Developing more accurate predictions requires more subtle and data-driven methods to capture the interrelationships among various parameters that influence fatigue behavior [9].

One of the most influential factors affecting steel’s fatigue performance is its thermal and mechanical treatment history, specifically heat treatment processes and deformation processes such as rolling and forging [10]. Parameters including total heat treatment time (THT) and reduction ratio (RedRatio) play a very significant role in determining the final microstructure and grain and residual stress orientation in steel and hence affect how and when cracking develops during subsequent cyclic loading [11]. For instance, faulty heat treatment produces coarse grains and residual tensile stresses that reduce crack initiation life [12]. Similarly, the amount of plastic deformation induced during rolling or forging measured by the reduction ratio increases and shortens fatigue life based on its level and homogeneity [13].

Experimental research and industry observation have repeatedly indicated that changes in process conditions result in significant changes in fatigue life, even for similar material-grade specimens [14]. However, quantification of each input parameter’s relative influence on fatigue behavior is still challenging [15]. Multicollinearity in variables, noise in material property measurements, and complex interdependencies among them add to this challenge [16]. This emphasizes the need for statistically rigorous analysis approaches that can evaluate each causative factor’s relative importance in an interpretable and transparent manner [17].

The development of computational modeling over the past few years has made it possible to create more intricate fatigue life prediction models that utilize a larger variety of input variables and have more flexibility to incorporate practical data. While such forecasts could be very beneficial, the main defect that still exists is the limited visibility of the process from inputs to outputs [18]. That is, even if predictions about fatigue life are accurate, it is usually unknown which variables are causing them and to what degree [19]. Such a lack of interpretation could constrain usefulness for pragmatic decision-making applications such as finding optimal manufacturing settings or assessing quality in an industry setting [20,21].

In this case, an accurate measurement of input significance is no longer desirable but imperative [22]. Understanding the main factors that influence the fatigue behavior of materials allows engineers and scientists to focus on the improvement of those parameters, improving process control, and reducing the variability of performance [23]. Furthermore, with each parameter’s contributions being understood, irrelevant variables can be removed from the prediction model, simplifying calculations, minimizing computational load, and maximizing resistance to overfitting and noise [24]. These insights prove particularly valuable when testing and data gathering are restricted, and each input variable is an expenditure in measuring effort or equipment [25,26,27,28].

The purpose of this study is to explore the relative significances of variables that influence steel component fatigue life, specifically processing parameters. Through an investigation into attributes including RedRatio, THT, and others, this work is designed to identify variables that play the most significant roles in fatigue behavior and how their influence is quantified. The research depends on detailed data that is produced from experiments on steel under controlled conditions focusing on steel fatigue to thoroughly investigate the factors that govern the performance of the material under a repeating load.

To meet this goal, the research employs high-level analytical methodologies to determine the individual and collective implications of multiple input variables on fatigue performance. This includes measuring each variable’s variance and contribution, identifying leading factors, and evaluating how changes in major parameters affect the system response. By such feature-based understanding and quantification, the study makes a great deal of contributions to the very nature of fatigue behavior in steel and also to the provision of suggestions that make the performance improved and the process go better. Ultimately, it seeks to build a link between observation-based data and pragmatic engineering applications to guide further design and manufacture-based decisions for steel components with improved resistance to fatigue.

1.1. Related Work

Huang et al. [5] examine the fatigue properties of steel parts manufactured by Wire-Arc Directed Energy Deposition (DED), also referred to as Wire-Arc Additive Manufacturing (WAAM), a high-efficiency metal 3D printing technique commonly being evaluated for structural applications because of its cost-effectiveness and scalability. Although those benefits sound great, there is a lack of data on the structural properties of WAAM-manufactured parts, particularly their fatigue properties, which are crucial for ensuring long-term durability in practical engineering applications. To fill this gap, an extensive series of 75 uniaxial high-cycle fatigue tests on as-built (original roughness surface) and machined (smoothed surface) WAAM steel coupons was executed. Tests were conducted over various ranges of stresses and ratios of stresses (R = 0.1 to 0.4). Numerical modeling was also executed to explore the effect of as-built sample surface-induced stress concentrations. The examination utilized approaches based on S-N (stress life) and CLD (constant life diagram). The results indicated that as-built undulations significantly deteriorate fatigue performance by reducing endurance limit and fatigue life by about 35% and 60%, respectively, compared to machined specimens. Nevertheless, changes in stress ratio did not significantly affect fatigue strength. Characteristically, as-built WAAM specimens were found to behave like conventional steel welds, while machined WAAM specimens behaved similarly to structural steel S355. Last but not least, preliminary S-N curves for both local and nominal stresses were suggested and served as a baseline reference for future structural application design using WAAM steel.

Zhai et al. [29] concentrate on developing Structural Health Monitoring (SHM) in civil structures, specifically identifying fatigue cracks in steel-girder bridges. Visual inspections based on traditional approaches take considerable time and manual labor. Although computer vision and machine learning-based approaches offer an alternative solution with greater efficiency, they are hindered by the lack of high-quality image data from real damaged structures, particularly those suffering from fatigue and failing in service. As a solution to counter data paucity, researchers suggest that synthetic data augmentation be combined with real-world image databases. First, 3D graphical models with randomly generated textures representing simulated fatigue cracks are produced on steel surfaces. These are rendered as synthetic images under differing lighting and camera settings, closely similar to actual inspection conditions. An FCN is trained in both configurations—one with just real images and the other with real and synthetic data combined. The experiments exhibit that using synthetic images to enrich the dataset greatly enhances crack detection performance. In particular, Intersection over Union (IoU) increases from 35% to 40%, and accuracy increases from 49% to 62% through the inclusion of synthetic data. This is a clear demonstration that synthetic data can be an innovative application to solve the shortage of data in SHM (Structural Health Monitoring) applications and to facilitate the development of better and more scalable machine learning-based crack detection in steel infrastructure. Sousa et al. [30] study the fatigue of bonded single lap joints (SLJs) by combining the investigation of three main factors: joint morphology (adhesive thickness and overlap length), substrate material (GFRP, steel, and CFRP), and adhesive (epoxy and methacrylate). They opened the door to why each variable would affect the joint’s lifetime under cyclical loading by their controlled cyclic fatigue experiments. Although methacrylate had less strength at static rupture, it was the one that showed the longest fatigue life, up to 20 times under the same load ratio, even when the results were corrected to the ultimate static failure load. However, it was substrate flexibility that stole the show, taking GFRP to the limelight as the cause of a drastic drop in fatigue life (more than 10 times) in comparison with steel. What is really interesting is that the fatigue life of dissimilar material joints improved due to stress redistribution by the flexibility of the adhesive; finite element analysis confirmed this. In CFRP joints with an epoxy adhesive, the reduction of the fatigue performance due to interfacial failure was observed. The geometry discloses that the thicker the adhesives and the bigger the overlaps, the lower the fatigue life, which is contrary to the general assumption, as several parametric studies have been described. Almost all the aspects of the overlap length are changed due to the variation of the parameters, as is given in the parametric studies. The studies here are presented as a design and a materials selection guide for achieving an increase in the fatigue resistance of structural adhesive joints.

In contrast, the present study advances the field by combining ensemble gradient boosting (Histogram and Categorical Gradient Boosting) with novel metaheuristic optimizers (Prairie Dog Optimization and Wild Geese Algorithm) to enhance model accuracy and generalization. Furthermore, Shapley Additive Explanations (SHAP) are employed to quantify feature importance and improve model interpretability—addressing one of the major limitations of prior ML-based fatigue models. To the best of the authors’ knowledge, this is the first study integrating such hybrid optimization–boosting frameworks for fatigue life prediction of steel while providing an explainable analysis of influential factors such as reduction ratio and heat treatment time.

1.2. Study Objective and Novelty

This study presents a new approach to understanding steel fatigue through a change in paradigm from traditional surface-based or material-based evaluations to an examination based on process features. In contrast to previous research that largely dealt with surface conditions, types of bonds, or material interfaces, a focus is here developed on how all inputs to manufacture interact to affect fatigue performance and, more specifically, which inputs have the greatest bearing on endurance over time. What distinguishes this work is that it combines superior hybrid modeling approaches with a strong framework for interpretation. Histogram Gradient Boosting (HGB) and Categorical Gradient Boosting (CAT) models are combined with two nature-inspired optimization algorithms, Prairie Dog Optimization and Wild Geese Algorithm, to form four high-powered hybrid structures. These models are not just trained to forecast fatigue behavior with great accuracy but also to be able to explain and interpret the influence of each input parameter. This capability of bi-directional turns traditional black box modeling into an explanatory and insightful process. To find out on an objective basis which properties of input most significantly influence the fatigue life, the feature importance is computed via SHAP values. Using this methodology, it becomes achievable to assess input parameters arranged in order of their influence on model output. Rather than treating variables as the same or assigning them similar treatments, the method single out those attributes that require going into in-depth while designing and manufacturing and those that bring variation of the system and have the most significant impact on fatigue consequences. The core novelty in this work is its capability to merge modeling with a clear understanding. The findings improve prediction precision and further, the engineers as well as the decision-makers can see where efforts/work are required. This minimizes unnecessary experimentation, increases structural reliability, and results in more effective design approaches. In practice, it fills an essential gap between prediction based on data and engineering intuition. With it, manufacturers and scientists can go beyond trial and error by providing a transparent and interpretable route toward understanding steel’s fatigue behavior. By making the contributions of each input variable obvious, it paves the way for more intelligent and resilient part design within structural applications and ultimately enhances safety, lifespan, and performance in real-world structures.

2. Study Methodology

2.1. Data Collection

To build an interdisciplinary understanding of steel-fatigue properties, a data set from an open-source repository located at (https://www.kaggle.com/datasets/chaozhuang/steel-fatigue-strength-prediction (accessed on 9 September 2025)), Steel Fatigue Strength Prediction, was utilized [31]. This data set contains a broad set of metallurgical and processing variables applicable to the prediction of fatigue life. Each data point in the data set is a representative steel specimen processed using various thermal treatments and compositions with associated fatigue test data. The set is well-suited for fatigue and feature importance investigations due to the high diversity and depth of features. Table 1 shows the feature description.

Table 1. The description of the features.

Feature Name	Description
Sl. No	sample entry’s serial number.
NT	quantity of heat treatments used.
THT	Total heat treatment time, expressed in minutes or seconds.
THt	temperature at which heating is applied.
THQCr	temperature of quenching following chromium heat treatment.
CT1	cooling period in the initial phase.
Ct2	cooling period for the second phase.
DT1	length of the first tempering phase.
Dt2	Phase two tempering time.
QmT	medium temperature for quenching.
TT1	Stage 1 of tempering temperature.
Tt2	Stage two of tempering temperature.
TCr	processing input for total chromium temperature.
C	Steel’s carbon content (weight percentage).
Si	Content of silicon (weight percentage).
Mn	Content of manganese (weight percentage).
P	Weight percentage of phosphorus.
S	amount of sulfur (weight percentage).
Ni	The percentage of nickel by weight.
Cr	The weight percentage of chromium.
Cu	Weight percentage of copper content.
Mo	Weight percentage of molybdenum.
RedRatio	ratio of reduction while rolling or shaping.
d	Specimen diameter for the fatigue test.
dB	Diameter before formation.
dC	Diameter following formation.
Fatigue	The output variable, usually the number of cycles till failure, is the fatigue life value.

The data set in Table 2 consists of diverse variables measured over 437 samples, ranging from physical dimensions and mechanical properties to chemical compositions and fatigue life. The standard deviation and average values provide information on the extent of variation and central tendency in the dataset. Interestingly, variables like THT (Total Heat Treatment time) and RedRatio (Reduction Ratio) register extremely high values for standard deviations of 280.0 and 923.6, respectively, depicting high variability and potentially strong bearing on system behavior. Among all variables, RedRatio is particularly significant as an input because its maximum value is extremely high (5530), its range is wide, and its standard deviation is considerable. This indicates that it is an influential factor in defining the mechanical behavior of the system, especially its fatigue resistance. Knowledge about its distribution and role is crucial in material optimization and prediction in engineering applications.

Table 2. Statistical properties of the variables.

Variables	Indicators
	Min.	Max.	St. Dev.	Ave.
Sl. No.	1	437	219	126.3
NT	825	930	872.3	26.21
THT	30	865	737.6	280.0
THt	0	30	25.95	10.26
THQCr	0	24	10.654	7.841
CT1	30	930	128.9	281.7
Ct2	0	540	40.502	126.9
DT1	30	903.3	123.7	267.1
Dt2	0	70.2	4.844	15.70
QmT	30	140	35.49	19.4
TT1	30	680	536.8	164.1
Tt2	0	120	65.08	21.48
TCr	0	24	20.82	8.072
C	0.170	0.630	0.388	0.096
Si	0.160	2.050	0.300	0.246
Mn	0.370	1.600	0.823	0.279
P	0.002	0.031	0.016	0.005
S	0.003	0.030	0.015	0.006
Ni	0.010	2.780	0.517	0.853
Cr	0.010	1.170	0.570	0.412
Cu	0.010	0.260	0.068	0.049
Mo	0	0.240	0.070	0.088
RedRatio	240	5530	923.6	576.6
dA	0	0.130	0.047	0.031
dB	0	0.050	0.003	0.008
dC	0	0.058	0.008	0.010
Fatigue	225	1190	552.9	186.6

These multiple scatter plots with marginal histograms in Figure 1 demonstrate correlations among nine input variables and fatigue life: P, C, TT, NT, Mo, Cr, dA, RedRatio, and Ct. All variables exhibit high densities in the lower range (400–600), as seen from the horizontal histograms. More pronounced clustering or stratification is seen in Cr, TT, and Ct, indicating a strong or ordered relationship with fatigue life. In contrast, P, NT, and dA have broadly dispersed distributions and therefore weak or nonlinear relationships. Mo and C exhibit moderate trends and some concentration in their values and possible counter-effects. RedRatio is predominantly close to low values with little variation in fatigue and typically indicates little influence. These visualizations assist in interpreting variable behavior, outlier detection, and the choice of good features to use in modeling for predicting fatigue in materials and thus, are beneficial in machine learning pre-processing and feature selection applications.

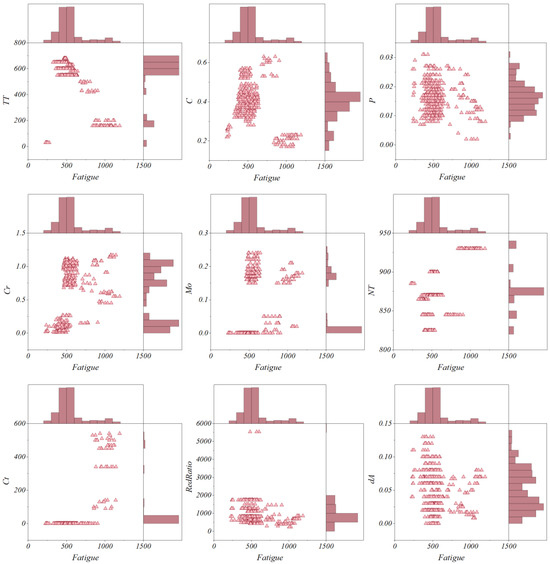
Figure 1. Multiple scatter plots with marginal histograms show the correlation between the 9 input variables and fatigue life.

2.1.1. Data Pre-Processing

Prior to model training, the raw dataset underwent several pre-processing steps to ensure data quality and consistency. The pre-processing workflow included three main stages: data cleaning, outlier treatment, and feature normalization.

The original dataset consisted of experimental fatigue life data of steel specimens subjected to different heat treatments, reduction ratios, and chemical compositions. Each record contained input variables such as reduction ratio (RedRatio), heat treatment temperature (HTT), total heat treatment time (THT), chemical composition (C, Mn, Si, Cr, etc.), and the corresponding fatigue life (Nf). Missing or incomplete entries (<5% of total records) were removed to maintain data integrity. Duplicated rows and inconsistent numerical entries (e.g., unit mismatches) were identified and corrected using Python’s pandas library.

Outliers were detected based on both statistical and physical considerations. Statistically, data points lying outside three standard deviations from the mean were flagged as potential outliers. Additionally, domain knowledge (e.g., physically unrealistic fatigue life values or processing parameters) was used to confirm or discard these anomalies. Identified outliers were removed only when they were confirmed as experimental errors; otherwise, they were retained to preserve the natural variability of fatigue data.

The pre-processed dataset was randomly divided into training and testing subsets using an 80:20 ratio to evaluate generalization performance. All pre-processing steps were applied consistently across both sets to avoid data leakage.

2.1.2. Normalization Process

To ensure consistency among input variables, all continuous features were scaled using Min–Max normalization, which maps the data to the range $[0,1]$ according to:

$$x’={\displaystyle \frac{x-x_{min}}{x_{max}-x_{min}}}$$

(1)

where $x’$ is the normalized value, $x_{min}$ and $x_{max}$ are the minimum and maximum feature values, respectively. This normalization method was chosen because it maintains the original feature distribution while ensuring that all features contribute equally during model training. Furthermore, Min–Max normalization improves the numerical stability and convergence speed of gradient boosting algorithms, which can be sensitive to differences in feature magnitudes.

2.2. Categorical Boosting (CATR)

The CATR algorithm, a type of ordered boosting tactic, aims to solve the overfitting problem of the boosting method, which is essentially the same issue faced by the boosting method [32]. Basically, ordered boosting is a method that takes a limited part of the data to build a model that calculates the residual error. The model is then used to perform calculations on the whole data set. Additionally, overfitting can be fended off by introducing a random permutation into the ordered boosting process. The boost method performs sample means calculations for variables that have undergone random permutation and belong to the same category, thereby pre-processing categorical variables. Besides that, ensemble methods such as random forest and gradient boosting require Grid Search or Randomized Search to identify the best hyperparameter, while CATR has its parameter set by default, so it does not have to go through such a process. CATR takes feature combinations, which not only speed up the training but also allow the data to be combined to represent similar information. Figure 2 shows the structure of the CATR model.

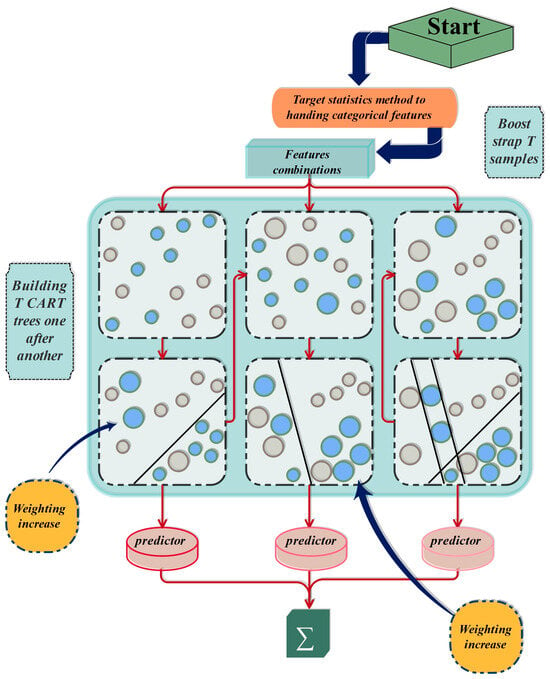
Figure 2. The structure of the CATR model.

2.3. Histogram Gradient Boosting Regression (HGBR)

One of the major recent accomplishments of the boosting methods is their effectiveness and ability to use Gradient Boosting of Histograms as the main method to achieve leading results. The training of the first model is done by using weighted data. Hence, some features are likely to be more common in the updated sets of the other models. After recognizing the samples that it has misclassified, the first model adjusts its parameters to increase the weights of the misclassified data samples. The second model is provided with these adjusted weights so that it can focus on them and correct the inaccurate predictions [32,33,34].

Gradient boosting is one of the decision-tree-based boosting methods that has been known to successfully solve classification and regression problems. Those who apply this newly developed method to several datasets get what is called “very good results”. Unfortunately, a major drawback of the gradient boosting method is its very long training time. Moreover, the problem is deeply connected with the nature of the decision tree, besides the huge number of attributes and samples. In fact, to build a decision tree, it is necessary to reclassify or break down all numerical values and numerical features. It takes an enormous amount of work and computation if there are hundreds of features and data samples. Performance also suffers as a result of this. HGB is designed to handle the issues of large data sets and efficiency.

Contrary to gradient boosting, this method enhances and accelerates the implementation of trees. The class Hist Gradient Boosting Classifier from the sklearn package is used to implement HGB in this version. Essentially, the technique reduces the distinct values of all features to a very small number of values, enabling a decision tree to focus on a small subset of features for the next split or partitioning of the tree. Figure 3 shows the structure of the HGBR model.

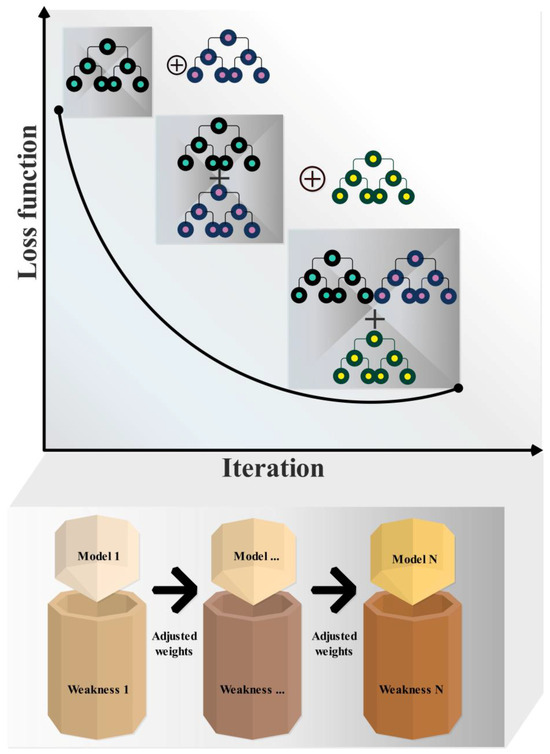
Figure 3. The structure of the HGBR model.

2.4. Wild Geese Algorithm (WGA)

The optimal location and power rating of Battery Energy Storage Systems (BESS) within a distribution system are calculated using the Wild Goose Algorithm (WGA) [35]. The algorithm starts with a random generation of an initial population in which each goose indicates a possible BESS configuration. The first variable in every solution determines the location of BESS, and the subsequent ones represent the percentage power rating. The fitness function takes into account objectives and constraint-related penalties, including voltage limits, line capacities, and state-of-charge deviations from required values. Violating solutions are assigned a higher fitness value based on penalties. New solutions are generated in step three through migration and food searching based on goose dynamics. At migration, each goose’s updated velocity and position are calculated using its own and its neighbors’ best-known positions. Geese tend to follow individuals ahead in food-seeking. On a probabilistic basis, a new position is selected from either the food-seeking or migration strategy. The new population is then assessed, and individual and global bests get updated accordingly. The fourth step is population reduction through the removal of weaker geese as the algorithm proceeds, step by step, minimizing the number of competitors. The size of the new population is computed by taking into account the number of evaluations so far and the maximum possible allowed.

To conclude, the process repeats itself iteratively through fitness evaluation, population updating, and reduction up to the maximum number of fitness evaluations. At that stage, the best solution is chosen as the optimal BESS installation design [36]. The approach integrates exploration and exploitation in a nature-inspired optimization technique to solve an intricate energy system planning problem.

2.5. Prairie Dog Optimization (PDO)

PDO, invented in 2022, is an algorithm based on nature and inspired by prairie dog’s activities, including foraging and burrowing habits [37]. It runs in three stages: initialization, exploration, and exploitation. In its initialization stage, a prairie dog colony is generated with a uniform distribution, and each prairie dog is assigned a position vector in n-dimensional space. The fitness is evaluated based on an objective function for which finding the solution with the minimum fitness is desired. During exploration, prairie dogs look for novel solutions through Levy flight-inspired mechanisms and digging capacity to support local and global searches. The exploitation stage imitates communication among prairie dogs so that they can improve their locations by exchanging information regarding food and predators. For better modification of the original PDO, an upgraded version (En-PDO) is proposed by incorporating two mechanisms, Random Learning (RL) and Logarithmic Spiral Search (LSS). RL mechanism promotes exploration by learning through differences among randomly chosen individuals with different fitness values. LSS mechanism enhances local search efficiency by making search directions spiral in nature about the best-known solution. These mechanisms are used selectively and randomly during optimization, so exploitation and exploration remain balanced. There is a selective replacement strategy in En-PDO as well. New solutions are accepted only if they provide an equivalent or superior fitness to existing ones, so that suboptimal solutions do not remain. Such continuous improvement allows more efficient convergence as time passes. The En-PDO example reveals how it initially performs the standard PDO process and then dynamically changes one of RL or LSS for better performance [38]. The new algorithm demonstrates improved efficiency and is more dependable especially for parameter extraction usage in solar cell (PV) models.

2.6. Performance Evaluation Metrics

Mean Absolute Error (MAE) is a metric that reflects the average absolute difference between the actual and the predicted values. The lower the MAE, the higher is the accuracy. Root Mean Square Error (RMSE) is a metric which represents the root of the average of the squared differences of the actual and predicted values. RMSE is a more severe penalty for a large error than MAE. The coefficient of Determination (R²) is a metric that signifies how much the variance in a dependent variable can be explained from the independent variables. Higher values closer to 1 indicate a better fit. Variance Accounted For (VAF) indicates the amount of variance in actual values explained by the model. Scatter Index (SI), a normalized version of RMSE, normalizes RMSE relative to the observed values’ mean. Symmetric Mean Absolute Percentage Error (SMAPE) estimates the average error between actual and forecasted values symmetric about zero. Uncertainty at 95% Confidence Interval (U95) estimates uncertainty bounds about forecasted values with 95% confidence. Often calculated using the prediction error standard deviation.

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(2)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(3)

$${\mathrm{R}}^2=1-{\displaystyle \frac{\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{\sum _{i=1}^n{(y_i-{\overline{y}}_i)}^2}}$$

(4)

$$VAF=\left(1-{\displaystyle \frac{Var\left(y-\widehat{y}\right)}{Var\left(y\right)}}\right)\times 100$$

(5)

$$SI={\displaystyle \frac{RMSE}{\overline{y}}}$$

(6)

$$SMAPE={\displaystyle \frac{100\%}{n}}\sum _{i=1}^n{\displaystyle \frac{\left|y_i-{\widehat{y}}_i\right|}{(\left|y_i\right|+\left|{\widehat{y}}_i\right|)/2}}$$

(7)

$$U95=1.96\times SD(y-\widehat{y})$$

(8)

• $y_i$ = actual value
• ${\widehat{y}}_i$ = predicted value
• $n$ = number of observations
• $\overline{y}$ = mean of actual values
• $SD$ = standard deviation of the residuals
• $1.96$ = corresponds to the 95% confidence level under a normal distribution

2.7. Justification of Model Selection and Optimization Strategy

The proposed hybrid models (HGPD, HGGW, CAPD, and CAGW) were not newly invented algorithms but rather strategically designed combinations of established learning frameworks and emerging optimization methods. The integration of Histogram Gradient Boosting (HGB) and Categorical Gradient Boosting (CAT) with Prairie Dog Optimization (PDO) and Wild Geese Algorithm (WGA) was motivated by the complementary capabilities of these algorithms in addressing the nonlinear and multivariate nature of fatigue life prediction.

(a)

Theoretical motivation

HGB and CAT are advanced boosting-based learners derived from decision tree ensembles. They can efficiently manage heterogeneous features—numerical and categorical—while minimizing overfitting through regularization and ordered boosting. Their prediction capability, however, depends strongly on appropriate selection of hyperparameters such as learning rate, maximum tree depth, and number of estimators. Manual or grid search-based tuning of these hyperparameters is computationally intensive and may not guarantee global optimality in highly nonlinear problems like fatigue modeling. Therefore, metaheuristic optimizers were introduced to automate this process.

(b)

Selection of PDO and WGA

PDO and WGA were selected after evaluating a range of popular metaheuristics such as Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Differential Evolution (DE). PDO offers strong local search ability via its Random Learning (RL) and Logarithmic Spiral Search (LSS) mechanisms, which enhance exploration and avoid premature convergence. WGA, on the other hand, maintains population diversity through its migration and food-seeking phases, ensuring global convergence and robust search over high-dimensional spaces. Both algorithms have recently demonstrated superior convergence speed and accuracy in solving complex engineering optimization problems. These properties make them well suited for tuning the hyperparameters of boosting models in this study.

(c)

Optimization objective

In all hybrid configurations, the metaheuristic algorithms were employed to minimize the Root Mean Square Error (RMSE) of the validation dataset by optimizing key hyperparameters of the HGB and CAT learners. Each candidate solution represented a hyperparameter vector, and its fitness was computed as the RMSE between predicted and measured fatigue life values. This coupling ensured that the optimization process directly targeted prediction accuracy and model generalization.

(d)

Comparison with conventional models

To evaluate the effectiveness of the proposed hybrid models, additional benchmarking was performed using conventional machine learning methods including Random Forest (RF), Support Vector Machine (SVM), and Extreme Gradient Boosting (XGBoost). The results indicated that the baseline HGB and CAT models achieved lower RMSE and higher R² values than RF, SVM, and XGBoost, confirming their suitability as foundational learners for fatigue prediction. Furthermore, when optimized with PDO and WGA, the hybrid models (particularly HGGW) provided substantial improvements in generalization and accuracy, demonstrating the synergistic benefit of coupling boosting and metaheuristic optimization.

(e)

Potential limitations

Although the hybrid framework significantly improved predictive accuracy, it also increased computational cost due to iterative optimization and multiple model evaluations during each metaheuristic iteration. Additionally, complex optimization may increase the risk of overfitting if early stopping or cross-validation strategies are not properly implemented. Future work may explore adaptive or lightweight optimization schemes to reduce computation time while maintaining accuracy.

3. Result and Discussion

In this research work, a thorough appraisal was made to forecast steel fatigue behavior based on a feature-rich data set involving parameters for thermal treatment, chemical constituents, and measurement properties. The features that were selected refer to the variables $NT,THT,THt,THQCr,CT1,Ct2,DT1,Dt2,QmT,TT1,Tt2$, and $TCr$, and also to the chemical constituents $C,Si,Mn,P,S,Ni,Cr,Cu,$ and $Mo$, and form parameters such as RedRatio and diameters $(d,dB,dC).$ The target variable was measured as the number of cycles to failure. Two innovative learning algorithms, HGB and CAT, were utilized to model the fatigue response. They were combined with two nature-inspired optimizations, namely PDO and WGA, and four hybrid prediction models were generated: HGPD, HGGW, CAPD, and CAGW. Each hybrid model sought to enhance learning accuracy and generalizability by parameter tuning with optimizations. The performance of these models was deeply inspected by a range of statistical measures including MAE, RMSE, R², VAF, SI, SMAPE, and U95. These metrics provided a fair and transparent evaluation of the model’s efficacy in predicting complex fatigue behavior.

Figure 4 illustrates the RMSE optimization trajectories for the four predictive models (CAPD, CAGW, HGPD, and HGGW) over 200 algorithmic iterations. Each curve represents a single deterministic optimization process rather than multiple independent runs. During each optimization, a population of 30 individuals was initialized, and the process converged after 200 iterations. To ensure stability, three independent optimization rounds were executed, and the trajectory with the best performance was selected for presentation. Among the models, the HGGW framework achieved the lowest RMSE (14.02), demonstrating superior convergence and predictive stability.

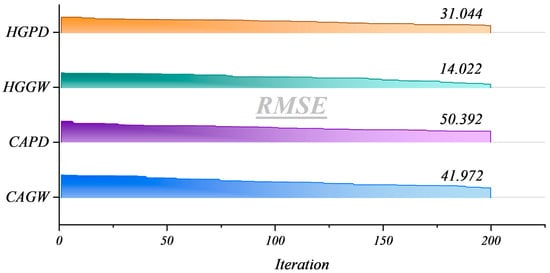
Figure 4. RMSE Optimization Trajectories of Four Predictive Models (Single Optimization with 200 Iterations). Each optimization round initializes 30 population individuals, converges after 200 iterations, and repeats 3 independent optimizations to select the optimal trajectory, ensuring result stability.

To ensure a fair and efficient optimization process, all hyperparameters were tuned using a random search strategy with 200 iterations. The following search spaces were employed for the hybrid models: epochs ∈ [10, 100], learning rate ∈ [0.0001, 0.01], number of membership functions (num_mf) ∈ [2, 10], alpha (regularization coefficient) ∈ [1 × 10⁻⁸, 0.1], and length scale ∈ [1, 50]. The selected parameter ranges were determined through preliminary experiments to balance computational efficiency and coverage of plausible values reported in previous studies. The optimal values obtained for each model are summarized in Table 3. Each optimization process was initialized with a population size of 30 and executed for a maximum of 200 iterations. The exploration–exploitation coefficient (β) was fixed at 0.6, and the cognitive/social coefficients (c₁, c₂) were set to 1.5 each to maintain balanced information sharing among candidate solutions. Random numbers were drawn from a uniform distribution [0, 1], and the stopping criterion was defined as a change in RMSE less than 10⁻⁶ across ten consecutive iterations. These settings ensured robust convergence while maintaining computational efficiency.

Table 3. Obtained values for the hyperparameters of the developed models.

Models	Hyperparameter
	Epochs	Learning_Rate		Num_mf
CAGW	30	0.001		5
CAPD	53	0.004		-
	alpha		length scale
HGGW	0.100001		6.0156
HGPD	5.44 × 10−8		31.045

Table 4 presents a detailed comparative assessment of six prediction models, CAT, CAGW, CAPD, HGB, HGGW, and HGPD, across training, validation, and test phases in steel fatigue prediction. The evaluation parameters are R² (a measure of determination), RMSE, MAE, VAF, SI, U95, and SMAPE, which collectively give a complete overview of each model’s accuracy, reliability, and generalizability. Among all models, RBGW performs better than the others throughout all phases. It obtains the best R² (validation 0.998 and test 0.997), minimum RMSE (validation 16.34 and test 15.41), and lowest MAE and SI, demonstrating the least prediction error and maximum robustness. These outcomes show that RBGW is most suited to providing predictions of steel’s fatigue behavior with maximum consistency and accuracy. On the other hand, the RBF is the worst performer among other models. It has poor results on both validation and test, as it gives the lowest values of R² (0.887 and 0.837) and the highest RMSE and U95, which indicate less stability and more uncertainty. The practical implications of these findings arise from achieving precise modeling of steel behavior under cyclic load conditions. By recognizing RBGW as the best model, engineers can now make better predictions of service life and design safer, more resilient steel structures. This is particularly important in aerospace, transportation, and civil engineering, where early onset fatigue failure causes dire consequences. Choosing a correct model, therefore, goes a direct step towards safety, economy, and material efficiency.

Table 4. A detailed comparative evaluation of six prediction models during training, validation, and testing phases in steel fatigue prediction.

	Model
	CAT	CAGW	CAPD	HGB	HGGW	HGPD
Training
R2	0.903	0.951	0.931	0.930	0.995	0.976
RMSE	60.44	41.97	50.39	50.67	14.02	31.04
MAE	49.45	34.38	41.25	29.17	12.49	17.38
VAF	90.25	95.09	93.04	90.72	99.45	96.75
SI	0.109	0.075	0.091	0.091	0.025	0.056
U95	167.3	116.1	139.4	140.3	38.51	86.00
SMAPE	0.0003	0.0002	0.0002	0.0002	0.0001	0.0001
Validation
R2	0.917	0.958	0.941	0.887	0.998	0.950
RMSE	62.47	43.48	52.10	77.94	16.34	53.92
MAE	51.23	35.69	42.82	46.99	14.97	30.60
VAF	91.68	95.75	94.04	73.82	99.60	89.64
SI	0.116	0.080	0.096	0.144	0.030	0.100
U95	172.3	119.9	143.7	215.8	40.03	149.5
SMAPE	0.002	0.002	0.002	0.002	0.0006	0.001
Testing
R2	0.909	0.933	0.952	0.837	0.997	0.948
RMSE	60.84	50.77	42.35	74.50	15.41	45.00
MAE	51.29	42.80	35.64	46.18	13.81	27.67
VAF	90.50	93.07	94.99	72.36	99.42	91.24
SI	0.114	0.095	0.079	0.139	0.029	0.0841
U95	168.6	140.7	117.4	205.9	39.28	124.5
SMAPE	0.002	0.002	0.002	0.0020	0.0006	0.001

Among all hybrid configurations, the HGGW model (Histogram Gradient Boosting optimized by the Wild Geese Algorithm) exhibited the highest predictive accuracy with an R² value of 0.998. This superior performance can be attributed to the effective interaction between the gradient boosting framework and the adaptive search dynamics of the WGA optimizer. The WGA employs a dynamic group-based search mechanism that balances global exploration and local exploitation more efficiently than PDO. This allows WGA to escape local minima and identify more optimal hyperparameter combinations for the HGB model, particularly for parameters such as learning rate, maximum depth, and number of leaf nodes. Moreover, the inherent regularization and histogram-based discretization in the HGB algorithm complement WGA’s adaptive convergence behavior, reducing overfitting and improving generalization on unseen fatigue data. The resulting synergy enhances the model’s robustness and stability across different random data splits. Overall, the HGGW model’s outstanding performance arises from the combination of WGA’s efficient parameter search and HGB’s structured ensemble learning, yielding a well-balanced model that captures nonlinear relationships while maintaining predictive smoothness and resistance to noise.

The six scatter plots in Figure 5 evaluate the prediction performance of six smart models on the correlation between measured and predicted values. Each model is measured using the R² and RMSE on training, testing, and validation datasets. Among all models, the HGGW model produces the most accurate and stable predictions with the highest R² values close to 0.998 and extremely low RMSE (e.g., 14.02 for training and 15.41 for testing), representative of high generalizability. CAGW performs strongly (up to R² = 0.958 and RMSE ≈ 42), with data points close together clustering around the line Y = X. CAPD and HGPD show moderate performance with near 0.94 values for R² and 45–52 for RMSE. However, HGB and CAT give an inferior performance with lower values for R² (as 0.837 and 0.903) and higher RMSE (up to 74.50 and 62.47), indicating more divergence from measured values. The region shaded out between Y = 0.8X and Y = 1.2X is an acceptable prediction zone. The performance indicates that HGGW is superior to others and is the most general and ideal model for performing the work.

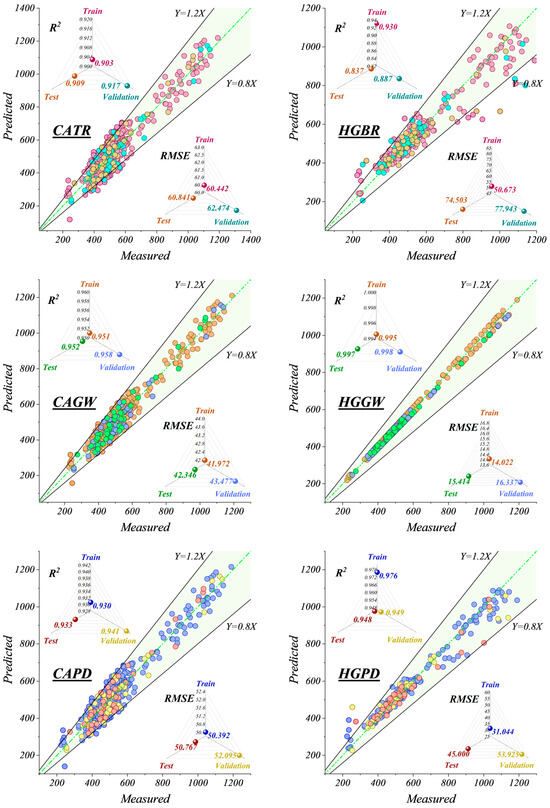
Figure 5. Evaluation of the prediction performance of six intelligent models on the relationship between measured values and predicted values using scatterplots.

Figure 6 clearly shows the distribution of error in six intelligent modeling approaches in predicting steel’s fatigue life during training, validation, and testing periods. The error in the HGB model is extremely volatile, with up to ±60%, presenting it with a lack of stability, high sensitivity to changes in inputs, and poor generalization to novel data points. The same is true for the CAT model, which exhibits high error variation during its training period, thereby exposing its shortcomings in modeling noise and nonlinear fatigue data. In contrast, HGGW, CAGW, and CAPD models exhibit superior stability and accuracy. HGGW is particularly good with errors confined to a small ±4% margin in all phases, indicating high prediction accuracy and strong generalizability. CAGW with errors below ±30% was found to have better stability and reliability of forecasts than the baselines. CAPD also demonstrates a similar performance with less fluctuation during the test phase, thus having more stability. Still, HGPD is on average limited and characterizes test errors that exceed 80%, which suggests the presence of overfitting or the incapability of adapting to new inputs. These outcomes disclose the potential of hybrid and adaptive modeling methods. The operations like HGGW, CAGW, and CAPD have a significant effect on performance and generalization of the solution of complex fatigue cases. Such upgrades become especially relevant in the real-world scenario where the safety margin is low and the failure risk is high; therefore, these models can be considered as reliable and trustworthy tools for monitoring metal structural fatigue life.

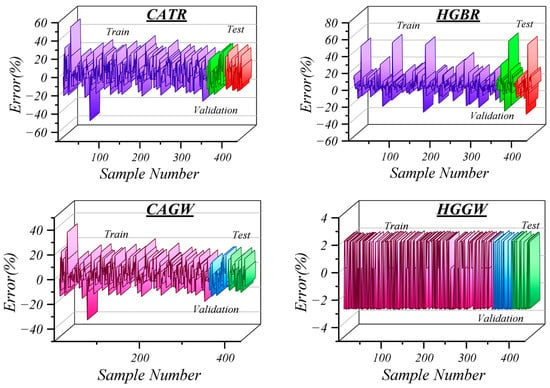
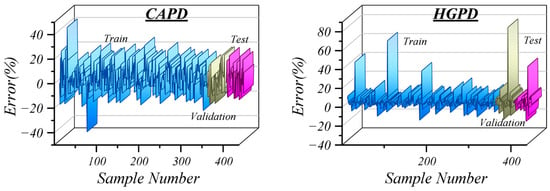
Figure 6. Error distribution across the six models during training, validation, and testing periods.

Figure 7 displays a comparison of different models by means of their Regression Error Characteristic (REC) curves. The REC curve is a graphical representation of prediction error distributions giving cues about model accuracy and reliability. The AUC, from which the lower the area under the curve the better a model is, is the main quantitative aspect of each curve. HGGW has the highest AUC value of 0.985, which is an indicator of its better capability to predict fatigue trends with less errors. The models are implemented with a mix of innovative fuzzy logic and neural network techniques to disclose the intricate and nonlinear nature of metal fatigue. In practice, precise prediction of fatigue is paramount in guaranteeing structural reliability and security in various industries, including aerospace, automobile, and civil engineering. Inaccurate predictions lead to disastrous failures and time-wasting downtime. For this reason, high AUC-rated models such as HGGW and HGPD provide valuable tools for preventive maintenance and lifespan maximization. The results demonstrate the real-life application utility of hybrid intelligent models in predictive maintenance approaches toward maximizing engineered system lifetime, safety, and cost-effectiveness.

Figure 7. Comparison between different models based on regression error characteristic (REC) curves.

Figure 8 presents the relative influence of individual input parameters on steel fatigue life as computed using the Cosine Amplitude Method (CAM). CAM quantifies the linear association between each input vector and the target variable by measuring their cosine similarity. This approach highlights global proportional trends between process variables and fatigue behavior. Among all inputs, the number of thermal cycles (NT) exhibits the highest CAM coefficient (0.503), signifying that repeated heat-treatment cycles exert the strongest linear correlation with fatigue performance. This finding agrees with metallurgical evidence that cyclic heating and cooling promote microstructural instability, leading to crack initiation and fatigue degradation. Secondary contributors include Chromium content (Cr, 0.233) and cooling time (Ct, 0.130), both of which influence grain refinement and residual stress formation during processing. In contrast, parameters such as reduction ratio (RedRatio) and Molybdenum content (Mo) show minimal direct linear correlation with fatigue life, indicating weaker overall trends in the dataset.

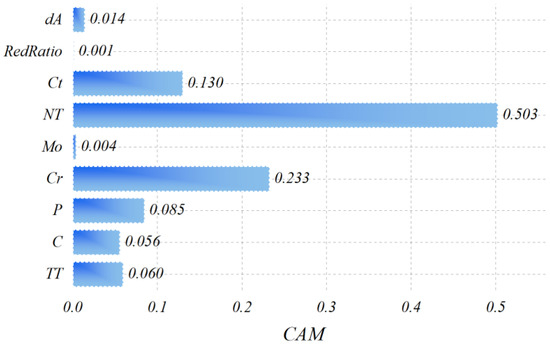
Figure 8. Presenting the relative contribution of various input parameters in steel fatigue prediction based on CAM.

From an engineering perspective, identifying such strongly correlated variables is essential for prioritizing process control. In industrial sectors where steel components endure repeated mechanical and thermal loading—such as aerospace landing gear, automotive shafts, and turbine blades—focusing on parameters like NT and Cr can significantly improve fatigue resistance, extend service life, and enhance operational safety.

Figure 9 illustrates feature importance derived from the Shapley Additive Explanations (SHAP) analysis, which provides a model-based interpretation of how each variable influences the predictions of the hybrid boosting models. Unlike CAM, SHAP evaluates each feature’s marginal contribution to the predicted fatigue life by averaging its effect across all possible combinations of features. This enables the capture of nonlinear interactions and synergistic effects among thermal, chemical, and geometric parameters. According to the SHAP analysis, Chromium (Cr) exhibits the highest mean absolute SHAP value, confirming it as the most influential variable in predicting fatigue performance. This aligns with Chromium’s known role in enhancing hardenability, corrosion resistance, and crack-growth retardation in steels. Nickel (Ni) and TT1 (first-stage tempering temperature) follow closely, reflecting their contribution to toughness and microstructural stability. Moderate importance is also observed for Carbon (C), Manganese (Mn), and Molybdenum (Mo), which jointly affect solid-solution strengthening. Conversely, NT, THT, and specimen-geometry variables (dB, dC) exhibit lower SHAP magnitudes, implying limited incremental predictive power once other interacting variables are accounted for.

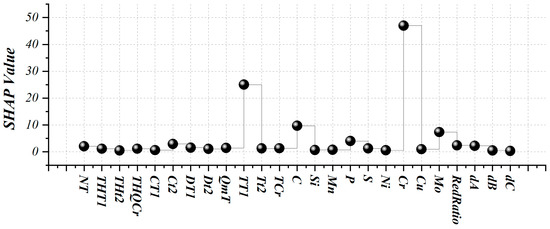
Figure 9. SHAP (Shapley Additive Explanations) values for various input variables.

The differences between CAM and SHAP rankings arise from their underlying principles: CAM measures global linear correlations, whereas SHAP quantifies nonlinear, model-learned contributions. Therefore, while NT appears most prominent in CAM due to its strong direct correlation with fatigue life, SHAP identifies Cr and Ni as dominant when nonlinear metallurgical interactions are considered. Together, these complementary analyses provide a comprehensive understanding of feature influence—from simple linear trends to complex coupled effects—guiding the optimization of processing parameters for improved fatigue durability.

SHAP was selected for this study because of its model-agnostic and additive properties, which make it especially suitable for tree-based ensemble learners such as HGB and CAT. Its ability to quantify each feature’s marginal contribution with exact additivity ensures consistent, physically interpretable explanations that bridge data-driven predictions with metallurgical understanding.

To further ensure reliability, potential multicollinearity among metallurgical variables (e.g., Ni, Cr, Mo) was analyzed during pre-processing, and redundant inputs were minimized through normalization and correlation screening. Consequently, the variations between CAM and SHAP rankings stem solely from methodological differences rather than dataset inconsistencies. While both approaches offer valuable insights, SHAP provides the more comprehensive interpretive framework for this study, as it captures nonlinear dependencies and feature interactions intrinsic to the hybrid boosting models. CAM serves as a complementary tool to visualize global linear trends and to cross-validate feature relevance.

To benchmark the performance of the proposed hybrid models, Table 5 compares the results of this study with several recently published fatigue life prediction models employing different machine learning frameworks. Zahran et al. [39] utilized a Gradient Boosting Regressor (GBR) and obtained an R² of 0.9332, while He et al. [40] implemented a Convolutional Neural Network (CNN) with R² = 0.972. Zhang et al. [41] applied a Deep Neural Network (DNN) model with relatively lower accuracy (R² = 0.893), and Guo et al. [42] adopted a Regression Tree (RT) yielding R² = 0.9484. Huang et al. [43] combined CNN and LSTM architectures, achieving R² = 0.9719. In contrast, the present HGGW model (Histogram Gradient Boosting + Wild Geese Algorithm) achieved an R² of 0.995, demonstrating higher predictive accuracy than the previously reported models. The improvement can be attributed to the synergistic optimization of hyperparameters via WGA and the strong nonlinear learning capability of Histogram Gradient Boosting, which together enhance generalization and convergence stability. This comparison highlights that the proposed hybrid optimization–boosting strategy represents a notable advancement in data-driven fatigue life prediction methods.

Table 5. Comparison between the presented published studies.

Study	Model	Evaluator
		R2	RMSE	MAE
Zahran et al. [39]	GBR	0.9332	4.334	-
He et al. [40]	CNN	0.972	-	27.1
Zhang et al. [41]	DNN	0.893	-	1168.9
Guo et al. [42]	RT	0.9484	28.01	18.22
Huang et al. [43]	CNN-LSTM	0.9719	0.1686	0.1122
Present study	HGGW	0.995	14.02	12.49

4. Discussion

This study employed a feature-based approach to enhance both the accuracy and interpretability of fatigue life prediction in steel. By combining advanced ensemble learners with nature-inspired optimization algorithms, the research successfully captured the nonlinear relationships among metallurgical, thermal, and geometric factors affecting fatigue behavior. Among the proposed hybrid models, the HGGW model demonstrated the highest performance with minimal error and superior generalization, validating the effectiveness of coupling gradient boosting with metaheuristic optimization. A key strength of this work lies not only in its predictive performance but also in its interpretability. The application of SHAP (Shapley Additive Explanations) analysis allowed a detailed evaluation of each feature’s contribution to fatigue life, revealing both expected and novel patterns. Results indicated that parameters such as Chromium (Cr), Nickel (Ni), and tempering temperature (TT1) exert the most significant influence, confirming their metallurgical roles in strengthening mechanisms, residual stress control, and microstructural refinement. At the same time, the Cosine Amplitude Method (CAM) analysis highlighted the number of heat-treatment cycles (NT) as the most linearly correlated factor. The integration of both SHAP and CAM therefore provided complementary insights—one capturing nonlinear model-driven interactions and the other linear global trends.

From an engineering perspective, these findings have practical implications for material design and process optimization. Understanding how variables such as heat-treatment cycles, alloy composition, and reduction ratio interact enables engineers to fine-tune manufacturing parameters to maximize fatigue resistance. Such data-driven interpretability transforms predictive models from “black boxes” into tools for informed decision-making in industrial applications such as aerospace, transportation, and civil infrastructure. This research also contributes methodologically by demonstrating how hybrid optimization techniques—specifically PDO and the WGA—can effectively tune model hyperparameters to achieve superior results without manual calibration. This approach strengthens model robustness and adaptability for complex materials problems where parameter interactions are highly nonlinear.

However, the study also has certain limitations. The dataset employed was sourced from an existing repository, meaning it may not fully capture temporal or environmental variations present in real-world conditions. Moreover, the computational cost associated with metaheuristic optimization increases with data complexity, which could limit scalability for larger industrial datasets. Future work should therefore explore real-time adaptive learning frameworks capable of integrating live sensor data from structural health monitoring systems and develop physically informed features that combine experimental metallurgy with machine learning insights. The present analysis focused on low-cycle fatigue (LCF) data with fatigue lives below approximately 10⁴ cycles. Although the proposed hybrid models exhibited strong predictive performance within this regime, high-cycle and very-high-cycle fatigue (HCF/VHCF) conditions often present greater variability and scatter. Future studies should extend the model framework to include broader fatigue life ranges and multiple loading regimes to fully assess its generalization capability and robustness.

While the current study focuses on steel fatigue under typical laboratory conditions, the proposed hybrid models can potentially be extended to more extreme scenarios, including ultra-high-cycle fatigue (UHCF) and corrosive environments, as well as to other engineering materials such as aluminum alloys or composites. Future research will explore transferring learning approaches to leverage pretrained models on steel datasets for rapid adaptation to new materials and fatigue regimes. This approach can facilitate model generalization and reduce the experimental effort required to develop reliable predictive models across diverse material systems.

5. Conclusions

This study presented a comprehensive, feature-driven investigation into the fatigue behavior of steel using advanced hybrid machine learning approaches. By integrating Histogram Gradient Boosting (HGB) and Categorical Gradient Boosting (CAT) frameworks with two recent metaheuristic optimizers—Prairie Dog Optimization (PDO) and the Wild Geese Algorithm (WGA)—four hybrid models (HGPD, HGGW, CAPD, and CAGW) were developed and systematically evaluated. The results demonstrated that coupling ensemble learners with adaptive optimization significantly enhances both predictive accuracy and generalization capacity in fatigue life estimation. Among the developed models, the HGGW model exhibited the most outstanding performance across all datasets, with superior R² and RMSE metrics, confirming its capability to model highly nonlinear metallurgical phenomena with stability and precision.

Beyond predictive success, this research makes a substantial contribution by advancing interpretability in data-driven materials modeling. Through the application of Shapley Additive Explanations (SHAP), the study quantitatively identified and ranked the influence of critical parameters such as Chromium (Cr), Nickel (Ni), and first-stage tempering temperature (TT1). These findings align with established metallurgical mechanisms that govern microstructural refinement, toughness, and fatigue crack resistance, thereby validating the model’s physical coherence. Together, these interpretive frameworks transformed the predictive model from a statistical tool into an explanatory system capable of revealing how process parameters shape fatigue behavior.

The implications of these findings extend well beyond numerical prediction. The proposed hybrid models provide a scientifically interpretable and practically applicable pathway for optimizing manufacturing processes, improving material design, and extending the operational lifespan of steel components. Such approaches are particularly relevant in industries where fatigue-induced failure poses critical risks, including aerospace, transportation, and civil infrastructure. The research thereby contributes to both the academic understanding and industrial practice of fatigue modeling by bridging data analytics with physical metallurgy. Nonetheless, certain limitations were acknowledged. The reliance on a pre-existing dataset introduces potential bias and limits temporal or environmental variability. Furthermore, the computational intensity of metaheuristic optimization may constrain scalability for larger real-world datasets. Future work should therefore focus on developing adaptive, real-time learning frameworks capable of continuous model updating using in-service data, as well as physically informed feature engineering to enhance model robustness and generalizability. Integrating these strategies with digital twin technologies and structural health monitoring systems would establish a more dynamic and intelligent framework for predicting and mitigating fatigue failure in steel infrastructures.