Abstract
We report the transmission spectra and electric field amplitudes of electromagnetic modes propagating in hybrid periodic/quasiperiodic multilayer photonic structures in one dimension (1D). We consider the case of the combination of biperiodic Bragg mirror and triperiodic Bragg mirrors with quasiregular (FB, Fibonacci) layered components. The corresponding hybrid structure (HB) is formed by concatenating BM(N)-FB(M)-BM(N), where N (M) means the number of periods (sequence order) used for the Bragg mirrors (FB) structure. A single defect layer (D) is considered in the middle of two HBs (HB-D-HB). Optimizing the parameters (the order of sequence, number of Bragg mirror layers, thickness, and the refractive index of D) allows us to obtain narrowband filters. The manipulation of these parameters fixes the number of photonic band gaps as well as the position of transmission peaks. The existence of the selectively localized behavior of some optical modes in the structures is discussed.
1. Introduction
Manipulating the properties of light transmission in artificially created systems has been made possible with the design and fabrication of photonic crystals (PCs). In the one-dimensional limit, they are usually built in the form of layered structures endowed with diverse features. One such property is the appearance of photonic band gaps (PBGs), which are wavelength intervals of forbidden light propagation. For many practical applications, a greater amplitude of this PBG as well as its persistence for sufficiently wide angles of incidence (the so-called omnidirectional reflectance) are sought. The typical configuration of Bragg mirror periodic dielectric multilayers does not always lead to a wide PBG. In consequence, different approaches have been put forward to enhance the angular range of the total reflectance. One of these proposals consists in the possibility of obtaining enlarged PBGs and wide-angular perfect reflection from the use of multiple and hybrid periodic/aperiodic dielectric structures in 1D. The first attempts in this sense can be traced back to the early years of the present century [1,2,3,4,5]. Several works have been devoted to introduce and explain the use of aperiodicity in designing these structures. It is described through different denominations such as quasiperiodic, quasiregular or, more specifically, photonic quasicrystals [6,7,8,9].
Deviations from periodicity may result in a number of new features. One such deviation comes from the use of quasiregular heterostructures, based on well-known mathematical aperiodic sequences, which are determined by a particular sequential algorithm [10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Among the more widely studied quasiperiodic sequences are the Fibonacci, Thue–Morse and Rudin–Shapiro ones. As mentioned, another kind of possible 1D photonic system arises from combining periodic and aperiodic layered structures. These are known as hybrid heterostructures [2,4,10,11,12,13,16,18,21]. Such a design was envisaged by Kanzari and Rezig (in the periodic/Cantor scheme) [2] and later used by one of us in the investigation of porous-silicon-based multilayers [10]. Viewed as a combination of dielectric arrays of different topological orders, these structures lead to complementary transmittance signals, resulting from the contributions of two kinds of subunits. In accordance, the photonic design becomes selective in the sense of a suitable tuning of the quasiregular sequence order involved as well as of the number BM periods. It has been found that a remarkable selective enhanced spatial confinement of electric field intensity can be achieved for some electromagnetic modes propagating in this kind of photonic structure [10,12]. In other words, amplitudes of such modes show a strong localization within either the periodic or quasiperiodic subunits of the multilayer. On the other hand, it is possible to speak about an improvement in the omnidirectionality of the reflectance response for the entire structure, as shown—even in a case of a not so high dielectric contrast—in a periodic/Fibonacci system simulated using porous silicon [12].
One-dimensional photonic heterostructures have also been considered to serve as sensors for diverse biomolecules and organisms [24,25,26,27,28,29,30,31,32,33,34,35]. In most cases, a significant improvement in the sensitivity, figure of merit (FoM), and Q-factor are reported. Defective layered structures are among those proposals [30,31,33]. In this work, we are precisely aiming at theoretically investigating the sensing performance of a photonic structure design consisting of a defective dielectric layer embedded in periodic/Fibonacci hybrid heterostructures. In particular, three-component periodic multilayers are assumed as the kind of BM-involved subunit. The materials considered for such a design are wide gap oxides chosen in such a way that absorption losses are avoided for the wavelength range considered.
2. Description of the System
Figure 1 schematically presents the 1D dielectric structures under investigation. A wider defect layer, labeled as D, was inserted between two multilayer sequences formed by a hybrid combination of biperiodic Bragg mirrors (BM), and triperiodic Bragg mirrors (TBM) with Fibonacci (FB) subunits. Layer D changed its refractive index when different analites were considered in the filter design. In the upper part of Figure 1a, a schematic diagram of the hybrid periodic/Fibonacci dielectric structure is presented. It utilized biperiodic Bragg mirrors (BM) in the configuration BM(4)FB(2)BM(4)-D-BM(4)FB(2)BM(4). Here, the BM represents the biperiodic Bragg mirror , and the label “4” indicates the number of repetitions of the mirror ; FB represents the Fibonacci sequence, and label “2” gives the order of this sequence. In general, we can denote the biperiodic hybrid structure as HFB(N,M), where HFB(N,M) represents BM(N)FB(M)BM(N), N is the number of mirrors, and M is the order of the Fibonacci sequence. The defective layer is represented by D; so in this notation, the mentioned structure can be represented as HFB(4,2)-D-HFB(4,2).

Figure 1.
(a) Schematic diagram of the hybrid periodic/Fibonacci dielectric structures enclosing the defect layer, D, in the filter. The upper plot corresponds to the case of HFB(4,2)-D-HFB(4,2) (see text for notation details), using 4-unit biperiodic Bragg mirrors (BMs) and the second-order Fibonacci sequence. The lower plot shows the case THFB(4,2)-D-THFB(4,2) in which the triperiodic Bragg mirrors (TBMs) with four units are use in the hybrid scheme, with the same Fibonacci FB(2) quasiperiodic part. (b) The variation in the refractive indices for constituent materials with respect to the signal wavelength () [36,37,38].
The lower plot in Figure 1a illustrates the case where triperiodic Bragg mirrors (TBM) were used in the hybrid scheme, specifically TBM(4)FB(2)TBM(4)-D-TBM(4)FB(2)TBM(4). Here, TBM represents the triperiodic Bragg mirror . Now, “4” represents the number of repetitions of the triperiodic mirror . In general, we can denote the triperiodic hybrid structure as THFB(N,M), where THFB(N,M) represents TBM(N)FB(M)TBM(N), N is the number of mirrors, and M is the order of the Fibonacci sequence. Including the defective layer, D, the system can be labeled as THFB(4,2)-D-THFB(4,2).
The wide energy gap () dielectric materials involved in the structure were TiO ( nm), SiO ( nm), and ZrO ( nm), corresponding to layers A, B, and C, respectively. As noticed, these materials are transparent in the visible and infrared range of radiation [36,37,38], which are precisely the frequency ranges of interest in our work. Therefore, we neglected the absorption losses due to the negligible extinction coefficients of the chosen materials. Additionally, the dielectric permittivity was assumed to be spatially homogeneous within each layer (see Figure 1b for details).
2.1. Theoretical Framework
Maxwell equations govern the propagation of electromagnetic waves in the PC. Electric and magnetic fields can be written as the linear combinations of the transverse electric (TE) and transverse magnetic (TM) components. Here, we restrict ourselves to dealing with the TM modes. Then, the sourceless Maxwell–Helmholtz equation for the magnetic field reads:
while the fields and wavevector, , are oriented according to the schematic representation of Figure 1. In addition, the time dependence of the fields is assumed to be of harmonic type:
2.2. Simulation Settings
The solution to the wave Equation (1) was accomplished numerically. In our case, we used the finite element method (FEM) as implemented in the COMSOL MULTIPHYSICS licensed software package 5.6 [39]. Details of this environment, such as the foundations of the FEM, mesh construction, discretization, optimization, and the convergence criteria, can be found in Refs. [40,41].
3. Results and Discussion
We are interested in analyzing the distribution of the electric field intensity along the entire structure for particular TM propagating modes identified from the transmission coefficient, T. Accordingly, Figure 2 shows the density plots for the relative amplitude, defined as the absolute ratio between this quantity at a given x-position and its value at the surface of light incidence, . Each density map is accompanied by the respective plot of . Here, hybrid heterostructures were built using BMs with four units, changing the order of the FB sequence from two to five (HFB(4,M)-D-HFB(4,M), with ). Using layers A and B, the condition , with μm was employed to define the optical thicknesses (, ) in the design: nm, and nm. For the defective layer, we used and a physical thickness nm.
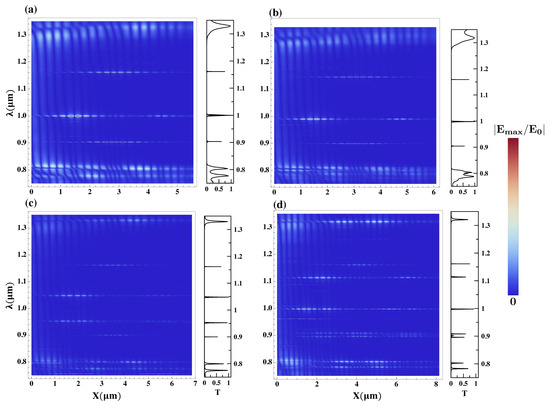
Figure 2.
Distribution of the normalized absolute field amplitude for different biperiodic/Fibonacci heterostructures with a defective layer HFB(4,M)-D-HFB(4,M) [see Figure 1a and the text for a detailed explanation]. Each plot corresponds to a different order of Fibonacci sequence: (a) FB(2)→ HFB(4,3)-D-HFB(4,3); (b) FB(3)→ HFB(4,3)-D-HFB(4,3); (c) FB(4)→ HFB(4,4)-D-HFB(4,4); (d) FB(5)→HFB(4,5)-D-HFB(4,5). The insets show the calculated optical transmission for each structure.
A detailed picture of the spatial field distribution in the cases of a stronger localization of signal amplitude, the hybrid sequences HFB(4,2)-D-HFB(4,2) and HFB(4,3)-D-HFB(4,3), [Figure 2a,b] is presented in Figure 3. There, the relative field amplitudes of the propagating modes located inside the forbidden regions (black in the density plots), are depicted as functions of the position along the structure, highlighting the central defect layer. A selective spatial localization of mode amplitude around the left-hand FB region was observed for the modes centered close to . Their amplitudes were very small within the defect region. However, the modes flanking the central transmission peak strongly localized within and around the defect region. Such modes exhibited higher values of the quality factor (where is the central transmission peak wavelength, and corresponds to its FWHM (full width at half maximum)), compared to that localized in the hybrid multilayer. These modes with centrally located main amplitudes also exhibited the largest values of . Something similar occurred for the propagating modes appearing in plots (c,d) of Figure 2. In the first case, one may again notice that the transmission peaks centered close to had very small amplitudes inside the defect region, and they mostly localized towards the left-hand hybrid sequence. Their Q values were small compared to those obtained for the modes located mainly within layer D, which had wavelengths above and below 1 μm. This resembled the two previously analyzed situations. However, for the second of the cases [Figure 2d], none of the peaks were centered close to , and their amplitudes were rather sparsely localized along the system, with much lower values of Q and for the cases where there was a significant accumulation of nomalized amplitude in D.

Figure 3.
The normalized electric field for propagating TM modes located within the photonic gap in the hybrid Bragg/Fibonacci -based heterostructures with a central defect layer D (see details in the text). (a–c) correspond to Figure 2a, whilst (d–f) correspond to Figure 2b, for the specific values of wavelength shown in the plot labels, together with their respective quality factors Q. In the upper inset of each graphics, the distribution of the normalized field amplitude appears as a density plot.
All of the above leads us to conclude that in the hybrid heterostructures consisting of biperiodic BM and FB layers, the latter also act as defect centers, somehow competing with layer D in what the mode localization has to do. This is precisely justified by the results appearing in Figure 4e–g. That is, with a higher FB sequence, there were more “defect-like” layers, associated with the aperiodicity. This made the field distribute its amplitude around those centers instead of the central one at nearly μm. Another interesting thing is the fact that for these HFB(4,2)-D-HFB(4,2), the non-central modes seem to be predominant over in localizing the field within the defect (cavity) layer D.
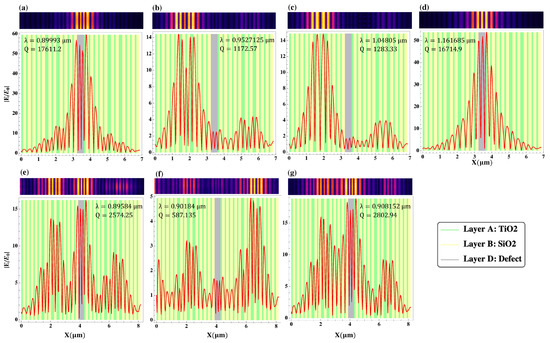
Figure 4.
The normalized electric field for propagating TM modes located within the photonic gap in the hybrid Bragg/Fibonacci -based heterostructures with a central defect layer D (see details in the text). (a–c) correspond to Figure 2c, whilst (d–g) correspond to Figure 2d, for the specific values of wavelength shown in the plot labels, together with their respective quality factors Q. In the upper inset of each graphics, the distribution of the normalized field amplitude appears as a density plot.
Now, we analyze the features of the normalized electric field amplitude in the situation in which the enclosing mirrors of hybrid heterostructures are triperiodic multilayers with an unit cell, THFB(N,M)-D-THFB(N,M), , with the enclosed defect layer. Figure 5 contains the corresponding density plots for cases with N = 4 and M = 2, 3, 4, 5. Here, the Bragg condition was set at and, again, μm. With the additional value (, see Figure 1b), this produced the optical thicknesses nm, nm, and nm. As in the previous case, we set and nm, and the respective plots of are shown as well. In all cases, the effect of using a triperiodic mirror seemed to be the isolation within the gap of a propagating mode slightly above μm. By observing Figure 6, Figure 7 and Figure 8, one realizes that such a mode appeared for all the different designs considered. In addition, it had the maximum normalized amplitude localized around and within the defective layer region, showing the largest values of Q and the highest values of , reaching two orders of magnitude in the case of M = 5, which means a relative field intensity four orders of magnitude greater than the incidence one within such a region. Thus, we can speak about a real defect mode, which can be used as the core of a sensing or filtering device based on our hybrid design. The remaining propagating modes that could be called edge-gap ones, have sparser amplitude distributions or, if localized within D, much smaller Q and relative field amplitudes. They could be attributed to the whole structure, with FB sequences acting, once more, as “defects”.

Figure 5.
Distribution of the normalized absolute TM field amplitude for different triperiodic Bragg/Fibonacci hybrid heterostructures with a defective layer (D) THFB(4,M)-D-THFB(4,M) with (see Figure 1). In all cases, four-period Bragg mirrors are used with Fibonacci sequences as follows: (a) FB(2)→THFB(4,2)-D-THFB(4,2); (b) FB(3)→THFB(4,3)-D-THFB(4,3); (c) FB(4)→ THFB(4,4)-D-THFB(4,4); (d) FB(5)→THFB(4,5)-D-THFB(4,5). The insets show the calculated optical transmission for each structure.
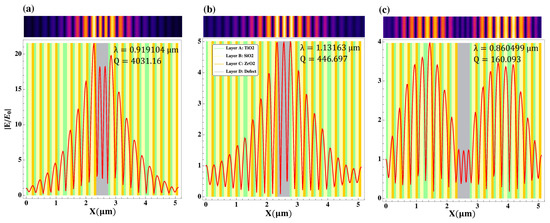
Figure 6.
The normalized electric field for propagating TM modes located within the photonic gap (black in the density plots) in the hybrid Bragg/Fibonacci -based heterostructures with a central defect layer D (see details in the text). (a–c) correspond to Figure 5a, for the specific values of wavelength shown in the plot labels, together with their respective quality factors Q. In the upper inset of each graphics, the distribution of normalized field amplitude appears as a density plot.
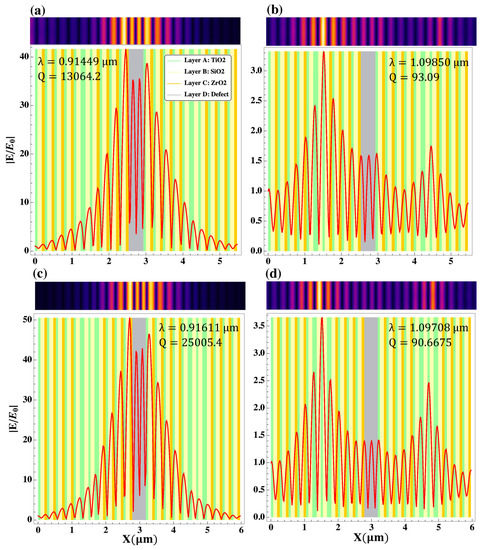
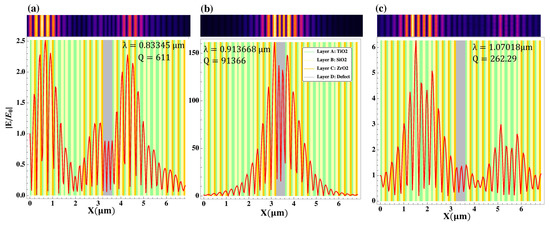
Figure 8.
The normalized electric field for propagating TM modes located within the photonic gap in the hybrid Bragg/Fibonacci -based heterostructures with a central defect layer D (see details in the text). (a–c) correspond to modes in Figure 5d.
The normalized electric field for propagating TM modes located within the photonic gap in the hybrid Bragg/Fibonacci -based heterostructures with a central defect layer D (see details in the text). (a,b) correspond to modes in Figure 5b, while (c,d) correspond to modes in Figure 5c.
It is noticed how the defects in the hybrid structures exhibited strong spatial and temporal confinement of light (high Q factor), enhancing the intensity of the interaction between the optical field and the material occupying the region with the defect. Specifically, the design with triperiodic Bragg mirrors in the hybrid heterostructures (THFB(N,M)-D-THFB(N,M)) produced desirable features such as mode fixation and field localization. This makes it suitable for fabricating selective filters for the identification of specific substances. For sensing applications, the enhanced interaction effect leads to an optical mode with a resonance frequency highly sensitive to variations in the surrounding medium (as demonstrated in the previous analysis), making the considered structures suitable for biosensing applications [39]. As is widely known, biosensors are devices with mechanisms for measuring changes in biological systems, such as creatinine concentration [42], glucose [43], and cholesterol [44]. In particular, optical biosensors utilize the property of resonant wavelength shift as a function of the refractive index of the defect. Accordingly, different biological substances, called analytes, are introduced into the defective layer. The refractive index of these analytes changes with the concentration of the substance, allowing the estimation of different concentrations through changes in the resonant wavelength [25,26].
This idea serves as the starting point for the proposal of the narrowband filter in this study. To conduct this analysis, we considered the case of the THFB(N,M)-D-THFB(N,M) structure since, according to the conducted analysis, it exhibited the best parameters in terms of the quality factor and resonant peak positions. In analyzing this filter, we used the refractive indices obtained by varying creatinine concentrations in the blood, as presented in [25] and shown in Table 1, as a reference. So, in our structure, creatinine was the analyte introduced into the defective layer.

Table 1.
Creatinine concentration (μmolL) with attributed refractive index.
Figure 9a presents an analysis of the THFB(6,5)-D-THFB(6,5) structure for different refractive indices of the analyte, as listed in Table 1. It can be observed that an increase in the refractive index of the defect induced a shift towards longer wavelengths of the resonant peak. This suggests that this filter can be used to detect changes in the refractive index associated with the material or substance filling the defective layer. From the obtained data, we calculated the sensitivity S, defined as the change in wavelength per refractive index unit (RIU) [45]. Based on this, the calculation is shown in Figure 9b. It displays the corresponding resonance wavelength for each analyte as a function of the refractive index. It can be observed that the data points exhibited a linear fit (), allowing us to conclude that the sensitivity was 119.4 nm/RIU. These results reveal that the proposed filter exhibits an efficient linear response.
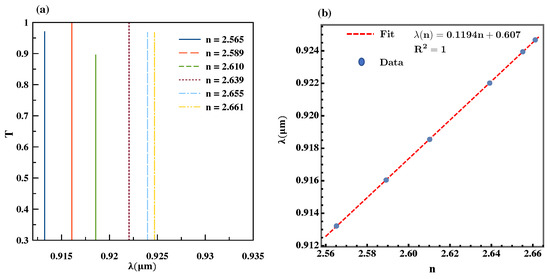
Figure 9.
(a) The change in the main transmission peak position for the filtering structure formed of hybrid triperiodic/Fibonacci multilayers enclosing a defect layer, as a result of the variation in refractive index of the substance inside it. (b) Linear fitting for the dependence of the peak wavelength with the refractive index.
Table 2 presents a comparison of the resonant wavelength values in μm, the quality factor, Q, of the proposed filter, and the figure of merit (, where is the resonant wavelength [46]), for different refractive index values of the analyte, n, shown in column 1. The proposed narrowband filter was tested using samples of creatinine with varying concentrations.

Table 2.
Comparison of the values of the resonant wavelength in μm, the quality factor of the proposed filter, and the function of merit (FOM) for the different values of the refractive index of analyte, n, shown in column 1.
On the other hand, Table 3 compares the numeric values of the sensitivity, FOM, and LOD (Limit of Detection [25]) of the proposed design with previously reported ones, evaluating the performance of the proposed narrowband filter. The same analyte was used in the defective layer as in the referenced works. The FOM provides a quantitative measure of sensor performance, where a higher FOM value implies a higher detection limit for sensing the refractive index. Comparatively, the biosensor proposed in this work achieved a theoretical FOM one order of magnitude higher than those reported in the referenced works. Additionally, the LOD value reported in our work was one order of magnitude lower than those reported in the mentioned works. This makes our narrowband filter capable of detecting small changes in the refractive index when analyzing different concentrations in creatinine samples.

Table 3.
Comparison of the numeric values for the sensitivity, FOM, and LOD of the proposed design with previous designs for evaluating the performance of the proposed narrowband filter.
Furthermore, the suitability of the narrowband filter for biosensing applications was verified by observing the profiles of field amplitude presented in Figure 10 for the cavity modes depicted in Figure 9a. In these figures, one can observe the strong localization of the field within the cavity region, with maximum values reaching 1200, and the presence of very high quality factors for all cases. These results confirm our conclusion regarding the feasibility of using the proposed hybrid design for filtering purposes.
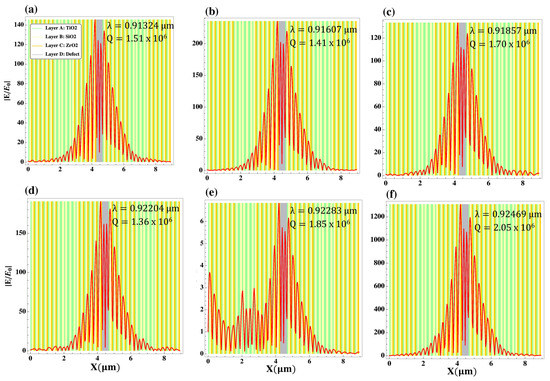
Figure 10.
Profiles of the normalized electric field amplitude for the transmission modes corresponding to the different values of refractive index in the data of Figure 9a. (a–f) conrresponding to refractive index , , , , and , respectively.
4. Conclusions
In this work, we investigated the properties of light propagation for the transverse magnetic modes traveling throughout a one-dimensional dielectric system composed of a defect layer enclosed by two identical hybrid periodic/Fibonacci heterostructures. The materials used for the simulation were TiO, SiO, and ZrO. The construction considered the periodic subunits to be Bragg mirrors with two (biperiodic) and three (triperiodic) layers in the unit cell. A detailed characterization of the transmission modes within the photonic gaps in terms of their electric field amplitude and spatial localization allowed identification of possible configurations for obtaining high-quality factor defect modes with some of them showing rather large amplitudes compared to the incident one. It was also shown that some “defect-like” modes were associated not with the cavity but to the very aperiodicity of the Fibonacci multilayers.
We can conclude that the design involving triperiodic Bragg mirrors in the configuration of the hybrid structures is the more convenient for achieving good filtering performance, as reported in the analysis of a system bearing Bragg mirrors of order 6 and Fibonacci subunits of order 5.
Author Contributions
The authors contributed by performing the indicated activities: Conceptualization, H.A.G.-U. and M.E.M.-R.; methodology, H.A.G.-U. and M.E.M.-R.; software, W.M.-G. and H.A.G.-U.; validation, W.M.-G. and H.A.G.-U.; formal analysis, H.A.G.-U. and M.E.M.-R.; writing—review and editing, H.A.G.-U., M.E.M.-R. and C.A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Mexican CONACYT grant number A1-S-8218 (M.E.M.R). C.A.D is grateful to the Colombian Agencies: CODI-Universidad de Antioquia (Estrategia de Sostenibilidad de la Universidad de Antioquia and projects “Propiedades magneto-ópticas y óptica no lineal en superredes de Grafeno”, “Estudio de propiedades ópticas en sistemas semiconductores de dimensiones nanoscópicas”, “Propiedades de transporte, espintrónicas y térmicas en el sistema molecular ZincPorfirina”, and “Complejos excitónicos y propiedades de transporte en sistemas nanométricos de semiconductores con simetría axial”) and Facultad de Ciencias Exactas y Naturales-Universidad de Antioquia (CAD exclusive dedication project 2022–2023).
Data Availability Statement
The data are partially available through direct contact with the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, C.; Qiao, F.; Wan, J. Enlargement of nontransmission frequency range in photonic crystals by using multiple heterostructures. J. Appl. Phys. 2000, 87, 3174. [Google Scholar] [CrossRef]
- Kanzari, M.; Rezig, B. Optical polychromatic filter by the combination of periodic and quasi-periodic one-dimensional, dielectric photonic bandgap structures. J. Opt. A Pure Appl. Opt. 2001, 3, S201. [Google Scholar] [CrossRef]
- Peng, R.W.; Huang, X.Q.; Qiu, F.; Wang, M.; Hu, A.; Jiang, S.S.; Mazzer, M. Symmetry-induced perfect transmission of light waves in quasiperiodic dielectric multilayers. Appl. Phys. Lett. 2002, 80, 3063. [Google Scholar] [CrossRef]
- Wen, D.J.; Peng, H.; Zhou, W.H. Broad Omnidirectional Reflection Band Forming using the Combination of Fibonacci Quasi-Periodic and Periodic One-Dimensional Photonic Crystals. Chin. Phys. Lett. 2003, 20, 1963. [Google Scholar] [CrossRef]
- Peng, R.W.; Liu, Y.M.; Huang, X.Q.; Qiu, F.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D.; Ouyang, L.Z.; Zou, J. Dimerlike positional correlation and resonant transmission of electromagnetic waves in aperiodic dielectric multilayers. Phys. Rev. B 2004, 69, 165109. [Google Scholar] [CrossRef]
- Maciá Barber, E. Aperiodic Structures in Condensed Matter. Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Maciá, E. Exploiting aperiodic designs in nanophotonic devices. Rep. Prog. Phys. 2012, 75, 036502. [Google Scholar] [CrossRef]
- Maciá, E. Exploiting quasiperiodic order in the design of optical devices. Phys. Rev. B 2001, 63, 205421. [Google Scholar] [CrossRef]
- Vardeny, Z.; Nahata, A.; Agrawal, A. Optics of photonic quasicrystals. Nat. Photon. 2013, 7, 177. [Google Scholar] [CrossRef]
- Escorcia-García, J.; Mora-Ramos, M.E. Study of optical propagation in hybrid periodic/quasiregular structures based on porous silicon. PIERS Online 2009, 5, 36. [Google Scholar] [CrossRef]
- Ben Ali, N.; Kanzari, M. Designing of omni-directional high reflectors by using one-dimensional modified hybrid Fibonacci/Cantor band-gap structures at optical telecommunication wavelength band. J. Mod. Opt. 2010, 57, 287. [Google Scholar] [CrossRef]
- Escorcia-García, J.; Duque, C.A.; Mora-Ramos, M.E. Optical properties of hybrid periodic/quasiregular dielectric multilayers. Superlattice Microstruct. 2011, 40, 203. [Google Scholar] [CrossRef]
- Ben Ali, N.; Kanzari, M. Designing of stop band filters using hybrid periodic/quasi-periodic one-dimensional photonic crystals in microwave domain. Phys. Status Solidi A 2011, 208, 161. [Google Scholar] [CrossRef]
- Zaghdoudi, J.; Maaloul, N.; Kanzari, M. Studies of optical properties of symmetrical quasi-periodic photonic crystals. Opt. Photon. J. 2012, 2, 270. [Google Scholar] [CrossRef]
- Bouazzi, Y.; Kanzari, M. Optical Fabry–Perot filter based on photonic band gap quasi-periodic one-dimensional multilayer according to the definite Rudin–Shapiro distribution. Opt. Commun. 2012, 285, 2774. [Google Scholar] [CrossRef]
- Escorcia-García, J.; Mora-Ramos, M.E. Propagation and confinement of electric field waves along one-dimensional porous silicon hybrid periodic/quasiperiodic structure. Opt. Photon. J. 2013, 3, 1. [Google Scholar] [CrossRef]
- Baraket, Z.; Zaghdoudi, J.; Kanzari, M. Study of optical responses in hybrid symmetrical quasi-periodic photonic crystals. Prog. Electromagn. Res. M 2016, 46, 29. [Google Scholar] [CrossRef]
- Asmi, R.; Ben Ali, N.; Kanzari, M. Enhancement of light localization in hybrid Thue–Morse/Periodic Photonic crystals. J. Mater. 2016, 2016, 9471312. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Bouazzi, Y.; Benali, N.; Kanzari, M. Narrow stop band optical filter using one-dimensional regular Fibonacci/Rudin Shapiro photonic quasicrystals. Opt. Quant. Electron. 2016, 48, 54. [Google Scholar] [CrossRef]
- Vyunishev, A.; Pankin, P.; Svyakhovskiy, S.; Timofeev, I.; Vetrov, S. Quasiperiodic one-dimensional photonic crystals with adjustable multiple photonic bandgaps. Opt. Lett. 2017, 42, 3602. [Google Scholar] [CrossRef]
- Elsayed, H.A.; Sharma, A.; Segovia-Chaves, F.; Sabra, W. Multi passbands filter for THz applications based on the one-dimensional photonic crystals heterostructure. Optik 2021, 248, 168056. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Belhadj, W.; Ben Ali, N.; Aly, A.H. Theoretical Study of Tunable Optical Resonators in Periodic and Quasiperiodic One-Dimensional Photonic Structures Incorporating a Nematic Liquid Crystal. Photonics 2021, 8, 150. [Google Scholar] [CrossRef]
- Segovia-Chaves, F.; Vinck-Posada, H. Tunability of multiple transmission channels in quasiperiodic one-dimensional photonic crystals. Rom. J. Phys. 2022, 67, 201. [Google Scholar]
- Sreekanth, K.V.; Zeng, S.; Yong, K.-T.; Yu, T. Sensitivity enhanced biosensor using graphene-based one-dimensional photonic crystal. Sens. Actuators B Chem. 2013, 182, 424. [Google Scholar] [CrossRef]
- Aly, A.H.; Mohamed, D.; Mohaseb, M.A.; Abd El-Gawaad, N.S.; Trabelsi, Y. Biophotonic sensor for the detection of creatinine concentration in blood serum based on 1D photonic crystal. RSC Adv. 2020, 10, 31765. [Google Scholar] [CrossRef] [PubMed]
- Nouman, W.M.; Abd El-Ghany, S.E.S.; Sallam, S.M.; Dawood, A.-F.B.; Aly, A.H. Biophotonic sensor for rapid detection of brain lesions using 1D photonic crystal. Opt. Quant. Electron. 2020, 52, 287. [Google Scholar] [CrossRef]
- Aly, A.H.; Zaky, Z.A.; Shalaby, A.S.; Ahmed, A.M.; Vigneswaran, D. Theoretical study of hybrid multifunctional one-dimensional photonic crystal as a flexible blood sugar sensor. Phys. Scr. 2020, 95, 035510. [Google Scholar] [CrossRef]
- Surdo, S.; Barillaro, G. Impact of Fabrication and Bioassay Surface Roughness on the Performance of Label-Free Resonant Biosensors Based on One-Dimensional Photonic Crystal Microcavities. ACS Sens. 2020, 5, 2894. [Google Scholar] [CrossRef]
- Panda, A.; Pukhrambam, P.D.; Ayyanar, N.; Nguyen, T.K. Investigation of transmission properties in defective one dimensional superconductive photonic crystal for ultralow level bioethanol detection. Optik 2021, 245, 167733. [Google Scholar] [CrossRef]
- Shalaby, A.S.; Alamri, S.; Mohamed, D.; Aly, A.H.; Awasthi, S.K.; Matar, Z.S.; Tammam, M.T. Theoretical study of one-dimensional defect photonic crystal as a high-performance sensor for water-borne bacteria. Opt. Quant. Electron. 2021, 53, 660. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Moustafa, B.; Aly, A.H. Plasma cell sensor using photonic crystal cavity. Opt. Quant. Electron. 2021, 53, 591. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Sharma, A.; Alamri, S.; Aly, A.H. Theoretical evaluation of the refractive index sensing capability using the coupling of Tamm–Fano resonance in one-dimensional photonic crystals. Appl. Nanosci. 2021, 11, 2261. [Google Scholar] [CrossRef]
- Malek, C.; Al-Dossari, M.; Awasthi, S.K.; Matar, Z.S.; Abd El-Gawaad, N.S.; Sabra, W.; Aly, A.H. Employing the Defective Photonic Crystal Composed of Nanocomposite Superconducting Material in Detection of Cancerous Brain Tumors Biosensor: Computational Study. Crystals 2022, 12, 540. [Google Scholar] [CrossRef]
- Matar, Z.S.; Al-Dossari, M.; Awasthi, S.K.; Mohamed, D.; Abd El-Gawaad, N.S.; Aly, A.H. Conventional Biophotonic Sensing Approach for Sensing and Detection of Normal and Infected Samples Containing Different Blood Components. Crystals 2022, 12, 650. [Google Scholar] [CrossRef]
- Taya, S.A.; Alhamss, D.N.; Colak, I.; Patel, S.K. Sensitivity enhancement of an optical sensor based on a binary photonic crystal for the detection of Escherichia coli by controlling the central wavelength and the angle of incidence. Opt. Quant. Electron. 2022, 54, 127. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- DeVore, J.R. Refractive Indices of Rutile and Sphalerite. J. Opt. Soc. Am. 1951, 41, 416–419. [Google Scholar] [CrossRef]
- Wood, D.L.; Nassau, K. Refractive index of cubic zirconia stabilized with yttria. Appl. Opt. 1982, 21, 2978–2981. [Google Scholar] [CrossRef]
- COMSOL Multiphysics, v. 5.6, COMSOL AB: Stockholm, Sweden, 2021.
- COMSOL Multiphysics Reference Guide; COMSOL AB: Stockholm, Sweden, 2012.
- COMSOL Multiphysics Users Guide; COMSOL AB: Stockholm, Sweden, 2012.
- Waikar, S.S.; Betensky, R.A.; Bonventre, J.V. Creatinine as the gold standard for kidney injury biomarker studies. Nephrol. Dial. Transplant. 2009, 24, 3263. [Google Scholar] [CrossRef]
- Parvesh, M.; Ohlsson, P.; BjOrkhem, I. Combined enzymic- Jaffe method for determination of creatinine in serum. Clin. Chem. 1981, 27, 8–21. [Google Scholar]
- Awad, M.A.; Aly, A.H. Experimental and theoretical studies of hybrid multifunctional TiO2/TiN/TiO2. Ceram. Int. 2015, 45, 19036–19043. [Google Scholar] [CrossRef]
- ElBeheiry, M.; Liu, V.; Fan, S.; Levi, O. Sensitivity enhancement in photonic crystal slab biosensors. Opt. Express 2010, 18, 22702–22714. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Li, C.; Wang, C.; Ji, Y.; Quan, Q. High figure of merit fano resonance in 2-D defect-free pillar array photonic crystal for refractive index sensing. IEEE Photonics J. 2016, 8, 4502414. [Google Scholar] [CrossRef]
- Gandhi, S.; Awasthi, S.K.; Aly, A.H. Biophotonic sensor design using a 1D defective annular photonic crystal for the detection of creatinine concentration in blood serum. RSC Adv. 2021, 11, 26655–26665. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).