Atomic Structure of Mn-Doped CoFe2O4 Nanoparticles for Metal–Air Battery Applications
Abstract
1. Introduction
2. Synthesis, Characterizations, and HE-XRD Experiments
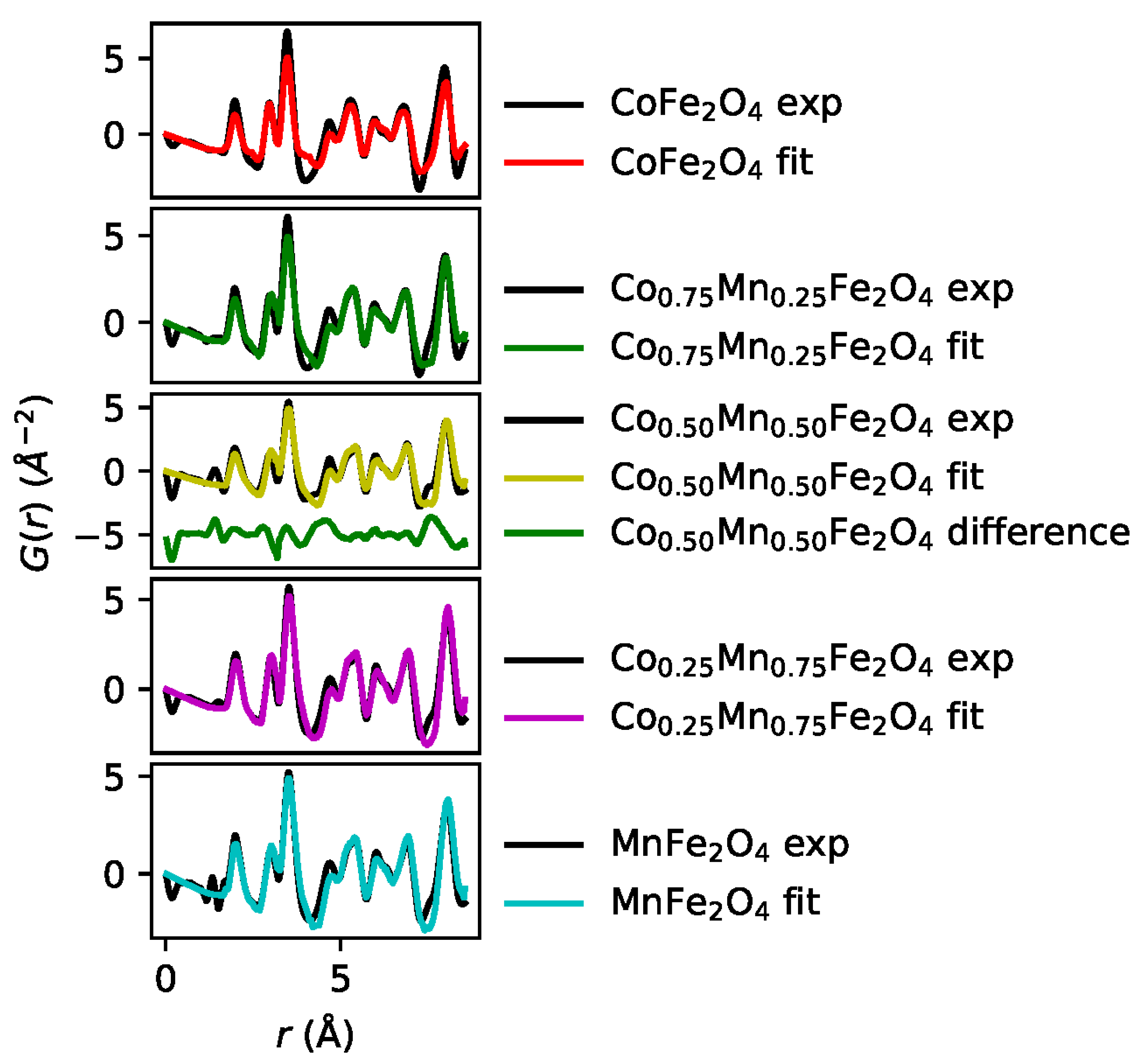
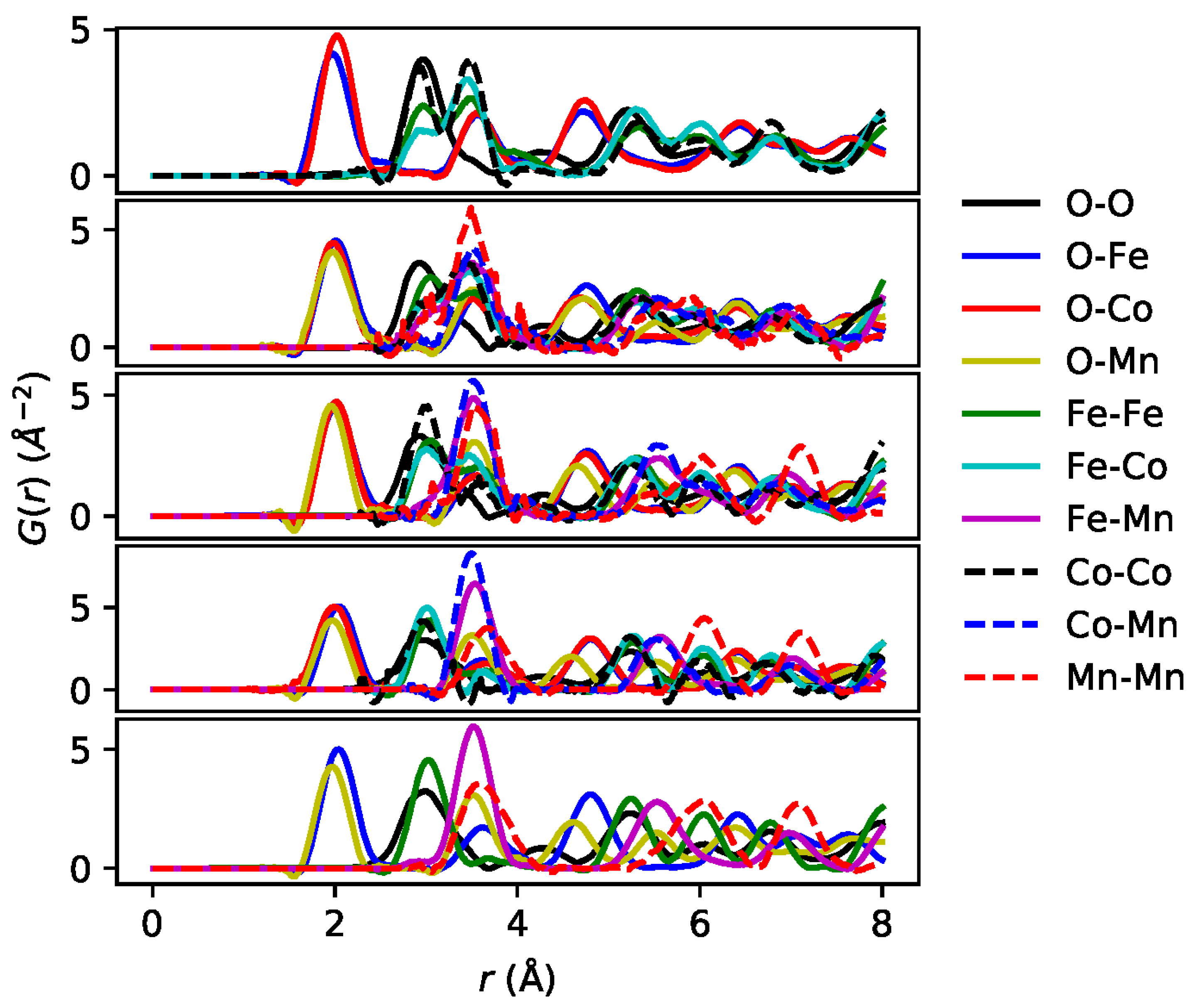
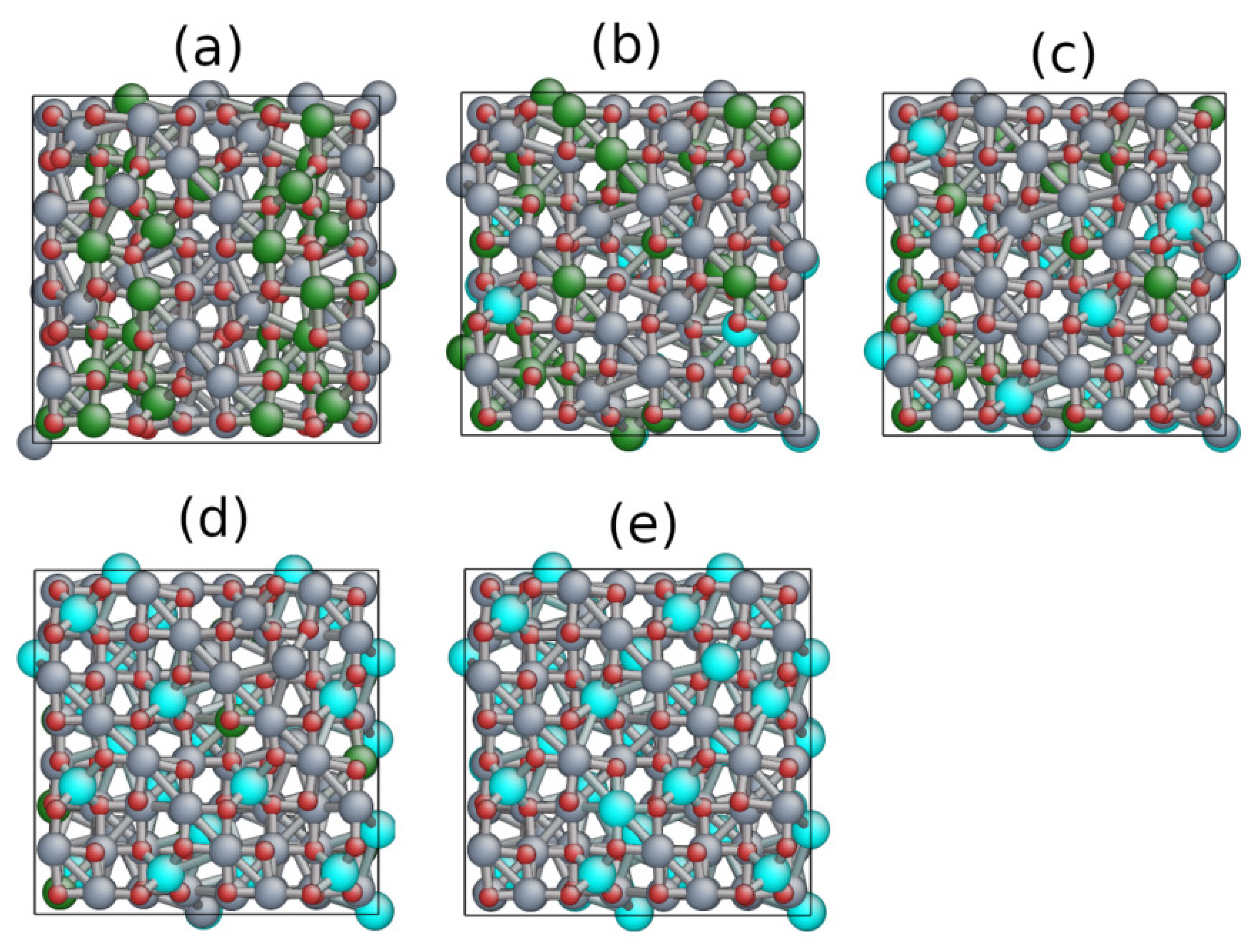
3. Reverse Monte Carlo Analysis and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yin, J.; Shen, L.; Li, Y.; Lu, M.; Sun, K.; Xi, P. CoFe2O4 nanoparticles as efficient bifunctional catalysts applied in Zn–air battery. J. Mater. Res. 2018, 33, 590–600. [Google Scholar] [CrossRef]
- Park, J.W.; Ju, Y.W. Evaluation of Bi-Functional Electrochemical Catalytic Activity of Co3O4-CoFe2O4 Composite Spinel Oxide. Energies 2023, 16, 173. [Google Scholar] [CrossRef]
- Jia, Q.; Ramaswamy, N.; Hafiz, H.; Tylus, U.; Strickland, K.; Wu, G.; Barbiellini, B.; Bansil, A.; Holby, E.F.; Zelenay, P.; et al. Experimental observation of redox-induced Fe–N switching behavior as a determinant role for oxygen reduction activity. ACS Nano 2015, 9, 12496–12505. [Google Scholar] [CrossRef]
- Nematollahi, P.; Barbiellini, B.; Bansil, A.; Lamoen, D.; Qingying, J.; Mukerjee, S.; Neyts, E.C. Identification of a Robust and Durable FeN4Cx Catalyst for ORR in PEM Fuel Cells and the Role of the Fifth Ligand. ACS Catal. 2022, 12, 7541–7549. [Google Scholar] [CrossRef]
- Hou, Y.; Yan, X.; Huang, Y.; Zheng, S.; Hou, S.; Ouyang, Y. Structural, electronic and magnetic properties of manganese substituted CoFe2O4: A first-principles study. J. Magn. Magn. Mater. 2020, 495, 165862. [Google Scholar] [CrossRef]
- Sharma, K.; Calmels, L.; Li, D.; Barbier, A.; Arras, R. Influence of the cation distribution, atomic substitution, and atomic vacancies on the physical properties of CoFe2O4 and NiFe2O4 spinel ferrites. Phys. Rev. Mater. 2022, 6, 124402. [Google Scholar] [CrossRef]
- Dileep, K.; Loukya, B.; Pachauri, N.; Gupta, A.; Datta, R. Probing optical band gaps at the nanoscale in NiFe2O4 and CoFe2O4 epitaxial films by high resolution electron energy loss spectroscopy. J. Appl. Phys. 2014, 116, 103505. [Google Scholar] [CrossRef]
- Kohara, S.; Itou, M.; Suzuya, K.; Inamura, Y.; Sakurai, Y.; Ohishi, Y.; Takata, M. Structural studies of disordered materials using high-energy x-ray diffraction from ambient to extreme conditions. J. Phys. Condens. Matter 2007, 19, 506101. [Google Scholar] [CrossRef]
- Ohara, K.; Onodera, Y.; Murakami, M.; Kohara, S. Structure of disordered materials under ambient to extreme conditions revealed by synchrotron X-ray diffraction techniques at SPring-8—Recent instrumentation and synergic collaboration with modelling and topological analyses. J. Phys. Condens. Matter 2021, 33, 383001. [Google Scholar] [CrossRef]
- FIJI. Available online: https://imagej.net/software/fiji/ (accessed on 17 March 2023).
- Billinge, S.J. The rise of the X-ray atomic pair distribution function method: A series of fortunate events. Philos. Trans. R. Soc. A 2019, 377, 20180413. [Google Scholar] [CrossRef]
- Faber, T.E.; Ziman, J.M. A theory of the electrical properties of liquid metals. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1965, 11, 153–173. [Google Scholar] [CrossRef]
- Harada, M.; Ikegami, R.; Kumara, L.S.R.; Kohara, S.; Sakata, O. Reverse Monte Carlo modeling for local structures of noble metal nanoparticles using high-energy XRD and EXAFS. RSC Adv. 2019, 9, 29511–29521. [Google Scholar] [CrossRef]
- Warren, B. X-ray Diffraction; Dover Publications, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Egami, T.; Billinge, S. Underneath the Bragg Peaks: Structural Analysis of Complex Materials; Pergamon Press: Oxford, UK, 2003. [Google Scholar]
- Billinge, S.J.L.; Levin, I. The problem with determining atomic structure at the nanoscale. Science 2007, 316, 561. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Deng, Z.T.; Tang, F.; Wang, C.; Ren, Y.; Moeck, P.; Petkov, V. Three-dimensional structure of Cd X (X = Se, Te) nanocrystals by total x-ray diffraction. J. Appl. Phys. 2007, 102, 044304. [Google Scholar] [CrossRef]
- Fernańdez-García, M.; Belver, C.; Hanson, J.C.; Wang, X.; Rodriguez, J.A. Anatase-TiO2 nanomaterials: Analysis of Key Parameters Controlling Crystallization. J. Am. Chem. Soc. 2007, 129, 13604–13612. [Google Scholar] [CrossRef]
- Petkov, V. Nanostructure by high-energy X-ray diffraction. Mater. Today 2008, 11, 28. [Google Scholar] [CrossRef]
- Bŏzin, E.S.; Malliakas, C.D.; Souvatzis, P.; Profferì, T.; Spaldin, N.A.; Kanatzidis, M.G.; Billinge, S.L. Entropically Stabilized Local Dipole Formation in Lead Chalcogenides. Science 2010, 330, 1660–1663. [Google Scholar] [CrossRef]
- Jensen, K.M.Ø.; Bŏzin, E.S.; Malliakas, C.D.; Stone, M.B.; Lumsden, M.D.; Kanatzidis, M.G.; Shapiro, S.M.; Billinge, S.J.L. Lattice Dynamics Reveals a Local Symmetry Breaking in the Emergent Dipole Phase of PbTe. Phys. Rev. 2012, B86, 085313. [Google Scholar] [CrossRef]
- Keen, D.A.; Goodwin, A.L. The crystallography of correlated disorder. Nature 2015, 521, 303. [Google Scholar] [CrossRef]
- Deepak, F.L.; Bañobre-López, M.; Carbó-Argibay, E.; Cerqueira, M.F.; Piñeiro-Redondo, Y.; Rivas, J.; Thompson, C.M.; Kamali, S.; Rodríguez-Abreu, C.; Kovnir, K.; et al. A systematic study of the structural and magnetic properties of Mn-, Co-, and Ni-doped colloidal magnetite nanoparticles. J. Phys. Chem. C 2015, 119, 11947–11957. [Google Scholar] [CrossRef]
- Mancini, A.; Malavasi, L. Recent advances in the application of total scattering methods to functional materials. Chem. Commun. 2015, 51, 16592. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.M.Ø.; Blichfeld, A.B.; Bauers, S.R.; Wood, S.R.; Dooryhee, E.; Johnson, D.C.; Iversen, B.B.; Billinge, S.J.L. Demonstration of thin film pair distribution function analysis (tfPDF) for the study of local structure in amorphous and crystalline thin films. IUCrJ 2015, 2, 481–489. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.M.; Juhas, P.; Tofanelli, M.A.; Heinecke, C.L.; Vaughan, G.; Ackerson, C.J.; Billinge, S.J. Polymorphism in magic-sized Au144 (SR) 60 clusters. Nat. Commun. 2016, 7, 11859. [Google Scholar] [CrossRef] [PubMed]
- Dippel, A.C.; Jensen, K.M.Ø.; Tyrsted, C.; Bremholm, M.; Bøjesen, E.D.; Saha, D.; Birgisson, S.; Christensen, M.; Billinge, S.J.L.; Iversen, B.B. Towards atomistic understanding of polymorphism in the solvothermal synthesis of ZrO2 nanoparticles. Acta Cryst. 2016, A72, 645–650. [Google Scholar]
- Dippel, A.C.; Roelsgaard, M.; Boettger, U.; Schneller, T.; Gutowski, O.; Ruett, U. Local atomic structure of thin and ultrathin films via rapid high-energy X-ray total scattering at grazing incidence. IUCrJ 2019, 6, 290–298. [Google Scholar] [CrossRef]
- Mathiesen, M.K.; Väli, R.; Härmas, M.; Lust, E.; Bulow, J.F.; Jensen, K.M.Ø.; Norby, P. Following the in-plane disorder of sodiated hard carbon through operando total scattering. J. Mater. Chem. A 2019, 7, 11709. [Google Scholar] [CrossRef]
- Christiansen, T.L.; Bøjesen, E.D.; Juelsholt, M.; Etheridge, J.; Jensen, K.M.Ø. Size induced structural changes in molybdenum oxide nanoparticles. ACS Nano 2019, 13, 8725–8735. [Google Scholar] [CrossRef]
- Banerjee, S.; Liu, C.H.; Jensen, K.M.Ø.; Juhas, P.; Lee, J.D.; Tofanelli, M.; Ackerson, C.J.; Murray, C.B.; Billinge, S.J.L. Cluster-mining: An approach for determining core structures of metallic nanoparticles from atomic pair distribution function data. Acta Cryst. 2020, A76, 24–31. [Google Scholar] [CrossRef]
- Christiansen, T.L.; Cooper, S.R.; Jensen, K.M.Ø. Thereś no place like real-space: Elucidating size-dependent atomic structure of nanomaterials using pair distribution function analysis. Nanoscale Adv. 2020, 2, 2234–2254. [Google Scholar] [CrossRef]
- Pussi, K.; Gallo, J.; Ohara, K.; Carb-Argibay, E.; Kolen’ko, Y.V.; Barbiellini, B.; Bansil, A.; Kamali, S. Structure of Manganese Oxide Nanoparticles Extracted via Pair Distribution Functions. Condens. Matter 2020, 5, 19. [Google Scholar] [CrossRef]
- Pussi, K.; Barbiellini, B.; Ohara, K.; Carbo-Argibay, E.; Kolen’ko, Y.V.; Bansil, A.; Kamali, S. Structural properties of PbTe quantum dots revealed by high-energy x-ray diffraction. J. Phys. Condens. Matter 2020, 32, 485401. [Google Scholar] [CrossRef] [PubMed]
- Tiano, A.L.; Papaefthymiou, G.C.; Lewis, C.S.; Han, J.; Zhang, C.; Li, Q.; Shi, C.; Abeykoon, A.M.; Billinge, S.J.; Stach, E.; et al. Correlating size and composition-dependent effects with magnetic, mossbauer, and pair distribution function measurements in a family of catalytically active ferrite nanoparticles. Chem. Mater. 2015, 27, 3572. [Google Scholar] [CrossRef]
- Michel, F.; Ehm, L.; Liu, G.; Han, W.; Antao, S.; Chupas, P.; Lee, P.; Knorr, K.; Eulert, H.; Kim, J.; et al. Similarities in 2-and 6-line ferrihydrite based on pair distribution function analysis of X-ray total scattering. Chem. Mater. 2007, 19, 1489–1496. [Google Scholar] [CrossRef]
- Mcgreevy, R. Reverse Monte Carlo modelling. J. Phys. Condens. Matter 2001, 13, R877. [Google Scholar] [CrossRef]
- Pussi, K.; Barbiellini, B.; Ohara, K.; Yamada, H.; Dwivedi, J.; Bansil, A.; Gupta, A.; Kamali, S. Atomic arrangements in an amorphous CoFeB ribbon extracted via an analysis of radial distribution functions. J. Phys. Condens. Matter 2021, 33, 395801. [Google Scholar] [CrossRef] [PubMed]
- Pussi, K.; Louzguine-Luzgin, D.; Nokelaineni, J.; Barbiellini, B.; Kothalawala, V.; Ohara, K.; Yamada, H.; Bansil, A.; Kamali, S. Atomic structure of an FeCrMoCBY metallic glass revealed by high energy x-ray diffraction. J. Phys. Condens. Matter 2022, 34, 285301. [Google Scholar] [CrossRef]
- Erba, A.; Baima, J.; Bush, I.; Orlando, R.; Dovesi, R. Large-Scale Condensed Matter DFT Simulations: Performance and Capabilities of the CRYSTAL Code. J. Chem. Theory Comput. 2017, 13, 5019–5027. [Google Scholar] [CrossRef]
- Tucker, M.G.; Keen, D.A.; Dove, M.T.; Goodwin, A.L.; Hui, Q. RMCProfile: Reverse Monte Carlo for polycrystalline materials. J. Phys. Condens. Matter 2007, 19, 335218. [Google Scholar] [CrossRef]
- Sanna Angotzi, M.; Mameli, V.; Zakutna, D.; Kubaniova, D.; Cara, C.; Cannas, C. Evolution of the Magnetic and Structural Properties with the Chemical Composition in Oleate-Capped Mn x Co1–x Fe2O4 Nanoparticles. J. Phys. Chem. C 2021, 125, 20626–20638. [Google Scholar] [CrossRef]
- Rushiti, A.; Hättig, C. Activation of Molecular O2 on CoFe2O4 (001) Surfaces: An Embedded Cluster Study. Chem. Eur. J. 2021, 27, 17115–17126. [Google Scholar] [CrossRef]
- Pussi, K.; Barbiellini, B.; Ohara, K.; Yamada, H.; Carbo-Argibay, E.; Sousa, V.; Kolen’ko, Y.V.; Bansil, A.; Kamali, S. Structural Properties of Nanometer-Sized Gold Nanoparticles on a Silicon Substrate. Phys. Status Solidi (B) 2022, 259, 2100572. [Google Scholar] [CrossRef]
- Dima, D.; Andrei, G. Interaction between ferrite particles and oxygen molecules within the polyester matrix of lightweight magnetic composites. Rom. J. Phys. 2004, 49, 795–806. [Google Scholar]
- Barbiellini, B.; Platzman, P. The healing mechanism for excited molecules near metallic surfaces. New J. Phys. 2006, 8, 20. [Google Scholar] [CrossRef]


| NPs | |||||
|---|---|---|---|---|---|
| Size (nm) | 32 ± 7 | 5.0 ± 0.7 | 5.1 ± 0.6 | 6.4 ± 1.0 | 6.0 ± 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pussi, K.; Ding, K.; Barbiellini, B.; Ohara, K.; Yamada, H.; Onuh, C.; McBride, J.; Bansil, A.; Chiang, R.K.; Kamali, S. Atomic Structure of Mn-Doped CoFe2O4 Nanoparticles for Metal–Air Battery Applications. Condens. Matter 2023, 8, 49. https://doi.org/10.3390/condmat8020049
Pussi K, Ding K, Barbiellini B, Ohara K, Yamada H, Onuh C, McBride J, Bansil A, Chiang RK, Kamali S. Atomic Structure of Mn-Doped CoFe2O4 Nanoparticles for Metal–Air Battery Applications. Condensed Matter. 2023; 8(2):49. https://doi.org/10.3390/condmat8020049
Chicago/Turabian StylePussi, Katariina, Keying Ding, Bernardo Barbiellini, Koji Ohara, Hiroki Yamada, Chuka Onuh, James McBride, Arun Bansil, Ray K. Chiang, and Saeed Kamali. 2023. "Atomic Structure of Mn-Doped CoFe2O4 Nanoparticles for Metal–Air Battery Applications" Condensed Matter 8, no. 2: 49. https://doi.org/10.3390/condmat8020049
APA StylePussi, K., Ding, K., Barbiellini, B., Ohara, K., Yamada, H., Onuh, C., McBride, J., Bansil, A., Chiang, R. K., & Kamali, S. (2023). Atomic Structure of Mn-Doped CoFe2O4 Nanoparticles for Metal–Air Battery Applications. Condensed Matter, 8(2), 49. https://doi.org/10.3390/condmat8020049








