Conceptualising Programming Language Semantics
Abstract
1. Introduction
“If, however, the user does not trust his intuition or does not understand what the short description on the lid implies in a particular case, he can open the machine to inspect the precise working. To his surprise, he finds there are actually two machines inside, named and . The working of the machines is explained in much more detail on the lids of the machines. The machine is a so-called preprocessor, which chews the offered text and produces another text in a more basic language which is evaluated by the processor, i.e., machine .”
“Knowing a language involves more than knowing its syntax; knowing a language involves knowing what the constructs of the language do, and this is semantic knowledge. In general, without such knowledge it would not be possible to construct or grasp such programs. But how is this semantic content given to us; how is it expressed? What constraints or principles must any adequate semantic account satisfy? What are the theoretical and practical roles of semantic theory? Is natural language an adequate medium for the expression of semantic accounts? These are some of the questions that any conceptual investigation of programming language semantics must address. [...] What are the relationships between [the] various approaches? Do they complement each other or are they competitors? Is one taken to be the most fundamental?”
2. Metaphor
3. Machines, Notations, and Languages
4. Texts and Machines
4.1. Background
“From the very beginning I have sensed the dual character of his unique personality: the large mind which has always extended beyond my horizon, and the sharp brain that can suddenly focus on the smallest detail, but will illustrate by it some general aspect; the “generalizer” who generalized even a general purpose programming language, and the “specializer” whose production of sentences and questions has often reminded me of a pencil sharpener.”
4.2. Processing and Preprocessing
“the definition of the language should be the description of an automatism, a set of axioms, A Machine or whateverone likes to call it that reads and interprets a text or program, any text for that matter, i.e., produces during the reading another Text, called the value of the text so far read.”
“We rather see the language as a machine which is fed with the program at one end and produces the value at the other end. The rules of the language, i.e., a rough description of the working of is printed on the lid of the machine”.
“If I look at the [ALGOL] Report, I say to myself, must I define all this by the processor—all these rules? This is far too much for me! So I say, let’s first take all the nonessential things out of ALGOL. Now, this is a task for the preprocessor—to look at this text and say, ‘I’ll translate this text into reduced ALGOL and then define only reduced ALGOL’.”
“if you do this trick I devised, then you will find that the actual execution of the program is equivalent to a set of statements; no procedure ever returns because it always calls for another one before it ends, and all of the ends of all the procedures will be at the end of the program: one million or two million ends. If one procedure gets to the end, that is the end of all; therefore, you can stop. That means you can make the procedure implementation so that it does not bother to enable the procedure to return. That is the whole difficulty with procedure implementation. That’s why this is so simple; it’s exactly the same as a goto, only called in other words.”
4.3. Discussion
DIJKSTRA
I just don’t understand. You have your text. You make another text that remains without procedure calls. Now, you say that somewhere or another you make the insertions; so that we do without procedure calls. Now we have only goto’s.
VAN WIJNGAARDEN
What! What? What? You have only statements—sequences of statements. You have no goto’s whatsoever! You have only sequences of statements, and these sequences of statements are exactly the same sequences of statements that would have been there in the other case. ([2], p. 21)
“Now, you say that numbers are not strings in that sense. Now, I know exactly what a number is; it is a string of digits. It may be preceded by a plus or minus sign, and it may be preceded by a decimal point. There is no other thing in ALGOL that is a metaconcept called ‘number’ of which this is the number. To me the number 13 is just the sequence of symbols 1, 3. I have never seen a ‘number’.”
“It is practically impossible to give such a mechanistic definition without being over-specific. The first time that I can remember having voiced these doubts in public was at the W.G.2.1 meeting in 1965 in Princeton, where van Wijngaarden was at that time advocating to define the sum of two numbers as the result of manipulating the two strings of decimal (!) digits. (I remember asking him whether he also cared to define the result of adding INSULT to INJURY; that is why I remember the whole episode.)”
5. Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Lakoff and Johnson [5] highlighted metaphors with small caps, and I use the same typography for illustrative devices. |
| 2 | |
| 3 | The encounter provided new epistemic tools and practices for the study of human languages as well [11]. |
| 4 | A useful overview of key concerns in the philosophy of computer science is given in [12]. |
| 5 | |
| 6 | Netz applies this criticism to all cognitive science, arguing that attempting to make universal statements about cognition is very hard (perhaps impossible), but cognitive history (study in a specific context) may be performed fruitfully [37]. |
| 7 | |
| 8 | The cited chapter presents a historico-philosophical study of other names—actually, illustrative devices in themselves—for programming entities (Algorithm, Code, and Program). |
| 9 | |
| 10 | Van Wijngaarden went on to lead the entire organisation in 1961 and remained there until his retirement twenty years later, just before its name change to Centrum Wiskunde & Informatica (Centre for Mathematics and Computer Science, CWI). |
| 11 | Eddy Alleda, Dineke Botterweg, Ria Debets, Marijke de Jong, Bertha Haanappel, Emmy Hagenaar, Truus Hurts, Loes Kaarsenmaker, Corrie Langereis, Reina Mulder, Diny Postema, and Trees Scheffer. Save for Eddy, who became a mathematics teacher, the rest left professional work for the family home. This is a sadly common pattern in the time period; for more on the ways women were forced out of computing work, see [76]. |
| 12 | |
| 13 | Further discussion is provided by Van den Hove, who observes that since the syntax of ALGOL is defined recursively, it would in fact require serious effort to make an ALGOL implementation which did not support recursive procedures [83]. |
| 14 | A fuller description of the conference and its effect on the field of programming language semantics is available in ([68], Ch. 4). |
| 15 | Backus–Naur Form, or Backus Normal Form—see [86]. |
| 16 | The ALGOL term given to named entities in a program, like variables and procedures. |
| 17 | This could be due to Van Wijngaarden’s familiarity by this point with the stored program concept: a computer program may be stored in the same memory as any other data and operated on by another program likewise. The idea is traceable to Turing, but it was Von Neumann who operationalised it in a computer [88]. |
| 18 | One might observe here some interesting similarity with Scott domains for semantics, which are partially ordered by information content [89]; of course at the time, Van Wijngaarden would not have known this. |
| 19 | Van Wijngaarden does not clarify whether and can each be opened to find two more machines; the implication from the rest of the paper is that it is only . |
| 20 | This is reminiscent of the Turing Machine, or perhaps Post’s machine [90], although Van Wijngaarden did not cite either author in his work. |
| 21 | Jones and I make a similar observation that “programming languages provide a repertoire of basic operators and, crucially, put in the hands of programmers ways to express functions that extend this repertoire.” ([91], p. 179). |
| 22 | The full program was a parameter to his semantic function, remaining such throughout interpretation; and this style went on to affect the subsequent “Vienna Definition Language”—see [56]. |
| 23 | Influential historian of mathematics and computing Mike Mahoney would not approve; he criticised this kind of reinterpretation of past work in terms of modern concepts, writing “Historically, a rose by another name may have a quite different smell.” [95]. |
| 24 | For more on this approach, historically interesting but lacking in much later influence, see ([56], §3). |
| 25 | By the time he wrote this in 1974, Dijkstra had moved from being interested in programming language definition to program correctness and was typically scornful of earlier work. |
| 26 | For more on this, see ([68], §7.1). |
| 27 | |
| 28 | SmallTalk has a long history, and rather than citing any one publication on the language I offer Kay’s own historical account [115]. |
References
- van Wijngaarden, A. Generalized ALGOL. In Proceedings of the Symposium on Symbolic Languages in Data Processing, sponsored and edited by the International Computation Centre, Rome, Italy, 26–31 March 1962; pp. 409–419. [Google Scholar]
- van Wijngaarden, A. Recursive definition of syntax and semantics. In Formal Language Description Languages for Computer Programming; North-Holland Publishing Company: Amsterdam, The Netherlands, 1966; pp. 13–24. [Google Scholar]
- Astarte, T.K. “Difficult things are difficult to describe”: The role of formal semantics in European computer science, 1960–1980. In Abstractions and Embodiments: New Histories of Computing and Society; Johns Hopkins University Press: Baltimore, MD, USA, 2022. [Google Scholar]
- Astarte, T.K. From Monitors to Monitors: An Early History of Concurrency Primitives. Minds Mach. 2023, 34, 51–71. [Google Scholar] [CrossRef]
- Lakoff, G.; Johnson, M. Conceptual Metaphor in Everyday Language. J. Philos. 1980, 77, 453–486. [Google Scholar] [CrossRef]
- Nofre, D.; Priestley, M.; Alberts, G. When Technology Became Language: The Origins of the Linguistic Conception of Computer Programming, 1950–1960. Technol. Cult. 2014, 55, 40–75. [Google Scholar] [CrossRef] [PubMed]
- Heurich, G.O. Coderspeak: The Language of Computer Programmers; UCL Press: London, UK, 2024. [Google Scholar]
- Nelson, S.L. Computers Can’t Get Wet: Queer Slippage and Play in the Rhetoric of Computational Structure. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2020. [Google Scholar]
- Berkeley, E.C. Giant Brains: Or Machines That Think; Wiley: New York, NY, USA, 1952. [Google Scholar]
- Priestley, M. A Science of Operations: Machines, Logic and the Invention of Programming; History of Computing; Springer: London, UK, 2011. [Google Scholar]
- Nofre, D. “Content Is Meaningless, and Structure Is All-Important”: Defining the Nature of Computer Science in the Age of High Modernism, c. 1950–c. 1965. IEEE Ann. Hist. Comput. 2023, 45, 29–42. [Google Scholar] [CrossRef]
- Angius, N.; Primiero, G.; Turner, R. The Philosophy of Computer Science. In The Stanford Encyclopedia of Philosophy, Summer 2024 ed.; Zalta, E.N., Nodelman, U., Eds.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2024. [Google Scholar]
- White, G. The philosophy of computer languages. In The Blackwell Guide to the Philosophy of Computing and Information; Floridi, L., Ed.; Blackwell Publishing: Hoboken, NJ, USA, 2004; pp. 237–247. [Google Scholar]
- Rapaport, W.J. Implementation is semantic interpretation. Monist 1999, 82, 109–130. [Google Scholar] [CrossRef]
- Rapaport, W.J. Implementation is semantic interpretation: Further thoughts. J. Exp. Theor. Artif. Intell. 2005, 17, 385–417. [Google Scholar] [CrossRef]
- Primiero, G. On the Foundations of Computing; Oxford University Press: Oxford, UK, 2019. [Google Scholar]
- Turner, R. Computational Artifacts: Towards a Philosophy of Computer Science; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Pérez-Escobar, J.A. Showing Mathematical Flies the Way Out of Foundational Bottles: The Later Wittgenstein as a Forerunner of Lakatos and the Philosophy of Mathematical Practice. KRITERION—J. Philos. 2022, 36, 157–178. [Google Scholar] [CrossRef]
- Sha, X.W. Differential Geometric Performance and the Technologies of Writing. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2001. [Google Scholar]
- Barany, M.J.; MacKenzie, D. Chalk: Materials and Concepts in Mathematics Research. In Representation in Scientific Practice Revisited; The MIT Press: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Maddy, P. Realism in Mathematics, Paperback ed.; Clarendon Press: Oxford, UK, 1992. [Google Scholar]
- Shapiro, S. Philosophy of Mathematics: Structure and Ontology; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Benacerraf, P. Mathematical truth. J. Philos. 1973, 70, 661–679. [Google Scholar] [CrossRef]
- MacKenzie, D. Mechanizing Proof: Computing, Risk, and Trust; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Jones, C.B. The Early Search for Tractable Ways of Reasoning about Programs. IEEE Ann. Hist. Comput. 2003, 25, 26–49. [Google Scholar] [CrossRef]
- Petricek, T. Miscomputation in software: Learning to live with errors. Art. Sci. Eng. Program. 2017, 1, 14-1–14-24. [Google Scholar] [CrossRef]
- Lakoff, G.; Johnson, M. Metaphors We Live By; University of Chicago Press: Chicago, IL, USA, 1980. [Google Scholar]
- Lakoff, G.; Johnson, M. Metaphors We Live By, 2nd ed.; University of Chicago Press: Chicago, IL, USA, 2003. [Google Scholar]
- Clark, K.M. Embodied Imagination: Lakoff and Johnson’s Experientialist View of Conceptual Understanding. Rev. Gen. Psychol. 2024, 28, 166–183. [Google Scholar] [CrossRef]
- Lakoff, G.; Núñez, R. Where Mathematics Comes From; Basic Books: New York, NY, USA, 2000. [Google Scholar]
- Johnson, M. Philosophy’s debt to metaphor. In The Cambridge Handbook of Metaphor and Thought; Cambridge University Press: Cambridge, UK, 2008; Chapter 2. [Google Scholar]
- Johnson, M. The Aesthetics of Meaning and Thought: The Bodily Roots of Philosophy, Science, Morality, and Art; University of Chicago Press: Chicago, IL, USA, 2018. [Google Scholar]
- Gibbs, R.W., Jr. (Ed.) The Cambridge Handbook of Metaphor and Thought; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Lakoff, G.; Johnson, M. Philosophy in the Flesh: The Embodied Mind and Its Challenge to Western Thought; Basic Books: New York, NY, USA, 1999. [Google Scholar]
- Tedre, M. The Science of Computing: Shaping a Discipline; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Jones, C.B. Understanding Programming Languages; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Netz, R. The Shaping of Deduction in Greek Mathematics: A Study in Cognitive History, 1st ed.; Number 51 in Ideas in Contex; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Friedman, M. On metaphors of mathematics: Between Blumenberg’s nonconceptuality and Grothendieck’s waves. Synthese 2024, 203, 149. [Google Scholar] [CrossRef]
- Lassègue, J. La genèse des concepts mathématiques: Entre sciences de la cognition et sciences de la culture. Rev. Synthèse 2003, 124, 223–236. [Google Scholar] [CrossRef]
- Barsalou, L.W. Perceptual symbol systems. Behav. Brain Sci. 1999, 22, 577–660. [Google Scholar] [CrossRef] [PubMed]
- Barsalou, L.W.; Santos, A.; Simmons, W.K.; Wilson, C.D. Language and simulation in conceptual processing. In Symbols and Embodiment: Debates on Meaning and Cognition; Oxford University Press: Oxford, UK, 2008. [Google Scholar] [CrossRef]
- Clark, A. Embodied, embedded, and extended cognition. In The Cambridge Handbook of Cognitive Science; Cambridge University Press: Cambridge, UK, 2012; p. 275. [Google Scholar]
- Latour, B.; Woolgar, S. Laboratory Life: The Social Construction of Scientific Facts; Sage: Thousand Oaks, CA, USA, 1979. [Google Scholar]
- Ricoeur, P. La Métaphore Vive; Seuil: Paris, France, 1975. [Google Scholar]
- Vincent, G. Paul Ricoeur’s “Living Metaphor”. Philos. Today 1977, 21, 412. [Google Scholar] [CrossRef]
- George, T. Hermeneutics. In The Stanford Encyclopedia of Philosophy, Winter 2021 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2021. [Google Scholar]
- McCarthy, J. A formal description of a subset of ALGOL. In Formal Language Description Languages for Computer Programming; North-Holland Publishing Company: Amsterdam, The Netherlands, 1966; pp. 1–12. [Google Scholar]
- Burke, K. Four master tropes. Kenyon Rev. 1941, 3, 421–438. [Google Scholar]
- Dijkstra, E.W. Hierarchical Ordering of Sequential Processes. Acta Inform. 1971, 1, 115–138. [Google Scholar] [CrossRef]
- Wexelblat, R.L. (Ed.) History of Programming Languages; Academic Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Bergin, T.J.; Gibson, R.G. (Eds.) History of Programming Languages—II; ACM Press: New York, NY, USA, 1996. [Google Scholar]
- Ryder, B.G.; Hailpern, B. (Eds.) HOPL III: Proceedings of the Third ACM SIGPLAN Conference on History of Programming Languages; Association for Computing Machinery: New York, NY, USA, 2007. [Google Scholar]
- Steele, G. History of Programming Languages IV [Special Issue]. Proc. ACM Program. Lang. 2020, 4. Available online: https://dl.acm.org/do/10.1145/event-12215/abs/ (accessed on 30 July 2025).
- Nofre, D. Unraveling Algol: US, Europe, and the Creation of a Programming Language. IEEE Ann. Hist. Comput. 2010, 32, 58–68. [Google Scholar] [CrossRef]
- Nofre, D. The Politics of Early Programming Languages: IBM and the Algol Project. Hist. Stud. Nat. Sci. 2021, 51, 379–413. [Google Scholar] [CrossRef]
- Astarte, T.K.; Jones, C.B. Formal Semantics of ALGOL 60: Four Descriptions in their Historical Context. In Reflections on Programming Systems—Historical and Philosophical Aspects; Philosophical Studies Series; De Mol, L., Primiero, G., Eds.; Springer: Cham, Switzerland, 2018; pp. 83–152. [Google Scholar] [CrossRef]
- Alberts, G. Algol Culture and Programming Styles [Guest editor’s introduction]. IEEE Ann. Hist. Comput. 2014, 36, 2–5. [Google Scholar] [CrossRef]
- Peláez Valdez, M.E. A Gift from Pandora’s Box: The Software Crisis. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 1988. [Google Scholar]
- Campbell-Kelly, M. Programming the EDSAC: Early programming activity at the University of Cambridge. Ann. Hist. Comput. 1980, 2, 7–36. [Google Scholar] [CrossRef]
- Hopper, G.M. Keynote address at ACM SIGPLAN History of Programming Languages conference, June C1–3 1978. In History of Programming Languages; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Knuth, D.E.; Trabb Pardo, L. The Early Development of Programming Languages; Technical Report STAN-CS-76-562; Stanford University: Stanford, CA, USA, 1976. [Google Scholar]
- Priestley, M. Synthetic machines and practical languages: Masking the computer in the 1950s. In Computing Cultures: Knowledges and Practices (1940–1990); Borrelli, A., Durnova, H., Eds.; Meson Press: Lüneburg, Germany, 2025. [Google Scholar]
- De Mol, L.; Bullynck, M. What’s in a name? Origins, transpositions and transformations of the triptych Algorithm—Code—Program. In Abstractions and Embodiments: New Histories of Computing and Society; Johns Hopkins University Press: Baltimore, MD, USA, 2022. [Google Scholar]
- Eco, U. The Search for the Perfect Language (Trans. James Fentress); John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Dick, S. Computer Science. In A Companion to the History of American Science; Montgomery, G.M., Largent, M.A., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 79–93. [Google Scholar]
- Strachey, C. Towards a Formal Semantics. In Formal Language Description Languages for Computer Programming; North-Holland Publishing Company: Amsterdam, The Netherlands, 1966; pp. 198–200. [Google Scholar]
- McCarthy, J. Towards a Mathematical Science of Computation. In Program Verification; Springer: Dordrecht, The Netherlands, 1962; Volume 62, pp. 21–28. [Google Scholar]
- Astarte, T.K. Formalising Meaning: A History of Programming Language Semantics. Ph.D. Thesis, Newcastle University, Newcastle upon Tyne, UK, 2019. [Google Scholar]
- Giacobazzi, R.; Ranzato, F. History of Abstract Interpretation. IEEE Ann. Hist. Comput. 2022, 44, 33–43. [Google Scholar] [CrossRef]
- Lindsey, C.H. A History of ALGOL 68. In Proceedings of the Second ACM SIGPLAN Conference on History of Programming Languages, HOPL-II, Cambridge, MA, USA, 20–23 April 1993; pp. 97–132. [Google Scholar] [CrossRef]
- Dijkstra, E.W.; Duncan, F.G.; Garwick, J.V.; Hoare, C.A.R.; Randell, B.; Seegmüller, G.; Turski, W.M.; Woodger, M. Minority Report. ALGOL Bull. 1970, 31, 7. [Google Scholar]
- Landin, P.J. WG 2.1 Minority Report of Subcomittee on Needs of ALGOL 60 Users. Circulated to IFIP TC-2. 1969. Available online: https://ershov.iis.nsk.su/en/node/805980 (accessed on 30 July 2025).
- Pérez, J.A. Report on CWI Lectures in Honor of Adriaan van Wijngaarden. ACM SIGLOG News 2017, 4, 40–41. [Google Scholar] [CrossRef]
- Alberts, G. International Informatics—On the Occasion of Aad van Wijngaarden’s 100th Birthday. ERCIM News 2016, 106, 6–7. [Google Scholar]
- Dijkstra, E.W. The Humble Programmer. Commun. ACM 1972, 15, 859–866. [Google Scholar] [CrossRef]
- Hicks, M. Programmed Inequality: How Britain Discarded Women Technologists and Lost Its Edge in Computing; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Belgraver Thissen, W.P.C.; Haffmans, W.J.; van den Heuvel, M.M.H.P.; Roeloffzen, M.J.M. Computing Girls. 2007. Available online: https://web.archive.org/web/20220120174546/http://www-set.win.tue.nl/UnsungHeroes/heroes/computing-girls.html (accessed on 20 January 2022).
- Perlis, A.J. The American Side of the Development of ALGOL. In History of Programming Languages; Wexelblat, R.L., Ed.; Academic Press: Cambridge, MA, USA, 1981; Chapter 3; pp. 75–91. [Google Scholar]
- Naur, P. The European side of the last phase of the development of ALGOL 60. In History of Programming Languages; Wexelblat, R.L., Ed.; Academic Press: Cambridge, MA, USA, 1981; Chapter 3; pp. 92–137. [Google Scholar]
- Backus, J.W.; Bauer, F.L.; Green, J.; Katz, C.; McCarthy, J.; Naur, P.; Perlis, A.J.; Rutishauser, H.; Samelson, K.; Vauquois, B.; et al. Report on the algorithmic language ALGOL 60. Numer. Math. 1960, 2, 106–136. [Google Scholar] [CrossRef]
- Backus, J.W.; Bauer, F.L.; Green, J.; Katz, C.; McCarthy, J.; Perlis, A.J.; Rutishauser, H.; Samelson, K.; Vauquois, B.; Wegstein, J.H.; et al. Revised Report on the Algorithm Language ALGOL 60. Commun. ACM 1963, 6, 1–17. [Google Scholar] [CrossRef]
- Alberts, G.; Daylight, E.G. Universality versus Locality: The Amsterdam Style of ALGOL Implementation. IEEE Ann. Hist. Comput. 2014, 36, 52–63. [Google Scholar] [CrossRef]
- van den Hove, G. On the Origin of Recursive Procedures. Comput. J. 2014, 58, 2892–2899. [Google Scholar] [CrossRef][Green Version]
- Zemanek, H. The Role of Professor A. van Wijngaarden in the History of IFIP. In Algorithmic Languages: Proceedings of the International Symposium on Algorithmic Languages; de Bakker, J.W., van Vliet, J.C., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Pohle, J. From a Global Informatics Order to Informatics for Development: The rise and fall of the Intergovernmental Bureau for Informatics. In Proceedings of the IAMCR Conference 2013, Dublin, Ireland, 25–29 June 2013. [Google Scholar]
- Knuth, D.E. Backus Normal Form vs. Backus Naur Form. Commun. ACM 1964, 7, 735–736. [Google Scholar] [CrossRef]
- Lucas, P. On the formalization of programming languages: Early history and main approaches. In The Vienna Development Method: The Meta-Language; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1978; Volume 61, pp. 1–23. [Google Scholar]
- Copeland, B.J. The Modern History of Computing. In The Stanford Encyclopedia of Philosophy, Winter 2020 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2020. [Google Scholar]
- Scott, D. Outline of a Mathematical Theory of Computation; Technical Report PRG-2; Oxford University Computing Laboratory, Programming Research Group: Oxford, UK, 1970. [Google Scholar]
- De Mol, L. Towards a diversified understanding of computability or why we should care more about our histories. In Proceedings of the Computability in Europe ’22, Swansea, UK, 11–15 July 2022. [Google Scholar]
- Jones, C.B.; Astarte, T.K. Challenges for semantic description: Comparing responses from the main approaches. In Engineering Trustworthy Software Systems; Lecture Notes in Computer Science; Bowen, J.P., Zhang, Z., Liu, Z., Eds.; Springer: Cham, Switzerland, 2018; Volume 11174, pp. 176–217. [Google Scholar] [CrossRef]
- IFIP. Working Conference Vienna 1964 Formal Language Description Languages. Program. Oxford, Bodleian Libraries. MS. Eng. misc. b. 287/E.39. 1964.
- Zemanek, H. Report on the Vienna conference, to IFIP TC2 Prague Meeting, 11 to 15 May 1964. Held in the Van Wijngaarden Collection, Universiteit van Amsterdam.
- Reynolds, J.C. The discoveries of continuations. Lisp Symb. Comput. 1993, 6, 233–247. [Google Scholar] [CrossRef]
- Mahoney, M.S. What Makes History? In History of Programming Languages—II; Bergin, T.J., Jr., Gibson, R.G., Jr., Eds.; ACM: New York, NY, USA, 1996; pp. 831–832. [Google Scholar] [CrossRef]
- Wirth, N. Comments on “Recursive definition of syntax and semantics” by A. van Wijngaarden. ALGOL Bull. 1965, 11–12. [Google Scholar]
- Landin, P.J. A formal description of ALGOL 60. In Formal Language Description Languages for Computer Programming; North-Holland Publishing Company: Amsterdam, The Netherlands, 1966; pp. 266–294. [Google Scholar]
- Landin, P.J. The mechanical evaluation of expressions. Comput. J. 1964, 6, 308–320. [Google Scholar] [CrossRef]
- Lucas, P.; Alber, K.; Bandat, K.; Bekič, H.; Oliva, P.; Walk, K.; Zeisel, G. Informal Introduction to the Abstract Syntax and Interpretation of PL/I; Technical Report 25.083; ULD Version II; IBM Laboratory Vienna: Vienna, Austria, 1968. [Google Scholar]
- Dijkstra, E.W. Some Meditations on Advanced Programming; Technical Report DR 30/62/R; Mathematisch Centrum: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Gorn, S. Summary Remarks (to a Working Conference on Mechanical Language Structures). Commun. ACM 1964, 7, 133–136. [Google Scholar] [CrossRef]
- Scott, D.S. Looking Backward; Looking Forward. In Proceedings of the Domains13 Workshop at Federated Logic Conference, Oxford, UK, 6–19 July 2018. [Google Scholar]
- Dijkstra, E.W. Letter to Hans Bekič. EWD 454. 1974. Available online: https://www.cs.utexas.edu/~EWD/ewd04xx/EWD454.PDF (accessed on 30 July 2025).
- van Wijngaarden, A.; Mailloux, B.J.; Peck, J.E.L.; Koster, C.H.A. Report on the Algorithmic Language ALGOL 68; Second printing, MR 101; Mathematisch Centrum: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Nofre, D. A Compelling Image: The Tower of Babel and the Proliferation of Programming Languages During the 1960s. IEEE Ann. Hist. Comput. 2025, 47, 22–35. [Google Scholar] [CrossRef]
- Friedman, M. On Blumenberg’s Mathematical Caves, or: How Did Blumenberg Read Wittgenstein’s Remarks on the Philosophy of Mathematics? In Hans Blumenberg’s History and Philosophy of Science; Fragio, A., Ros Velasco, J., Philippi, M., Borck, C., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 29–51. [Google Scholar] [CrossRef]
- Borghi, A.M. A Future of Words: Language and the Challenge of Abstract Concepts. J. Cogn. 2020, 3, 42. [Google Scholar] [CrossRef]
- Margulieux, L.E. Spatial Encoding Strategy Theory: The Relationship between Spatial Skill and STEM Achievement. In Proceedings of the 2019 ACM Conference on International Computing Education Research, Toronto, ON, Canada, 12–14 August 2019; pp. 81–90. [Google Scholar]
- Parkinson, J.; Margulieux, L. Improving CS Performance by Developing Spatial Skills. Commun. ACM 2025, 68, 68–75. [Google Scholar] [CrossRef]
- Low, G. Metaphor and education. In The Cambridge Handbook of Metaphor and Thought; Cambridge University Press: Cambridge, UK, 2008; Chapter 12. [Google Scholar]
- Eriksson, S.; Gericke, N.; Thörne, K. Analogy competence for science teachers. Stud. Sci. Educ. 2024, 1–29. [Google Scholar] [CrossRef]
- Sanford, J.P.; Tietz, A.; Farooq, S.; Guyer, S.; Shapiro, R.B. Metaphors we teach by. In Proceedings of the 45th ACM Technical Symposium on Computer Science Education, SIGCSE ’14, Atlanta, GA, USA, 5–8 March 2014; pp. 585–590. [Google Scholar] [CrossRef]
- Harper, C.; Mohammed, K.; Cooper, S. A Conceptual Metaphor Analysis of Recursion in a CS1 Course. In Proceedings of the 56th ACM Technical Symposium on Computer Science Education V. 1, SIGCSETS 2025, Pittsburgh, PA, USA, 26 February–1 March 2025; pp. 457–463. [Google Scholar] [CrossRef]
- Hewitt, C. Viewing control structures as patterns of passing messages. Artif. Intell. 1977, 8, 323–364. [Google Scholar] [CrossRef]
- Kay, A.C. The Early History of Smalltalk. SIGPLAN Not. 1993, 28, 69–95. [Google Scholar] [CrossRef]
- Simon, H.A.; Newell, A. Computer simulation of human thinking and problem solving. Monogr. Soc. Res. Child Dev. 1962, 27, 137–150. [Google Scholar] [CrossRef]
- Amarel, S. On representations of problems of reasoning about actions. In Machine Intelligence 3; Michie, D., Ed.; Edinburgh University Press: Edinburgh, UK, 1968; Volume 3. [Google Scholar]
- Eglash, R. Broken metaphor: The master-slave analogy in technical literature. Technol. Cult. 2007, 48, 360–369. [Google Scholar] [CrossRef]
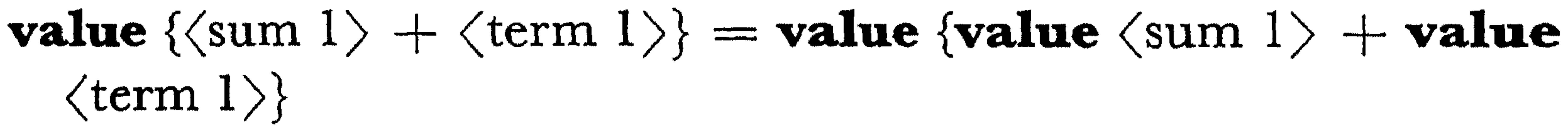
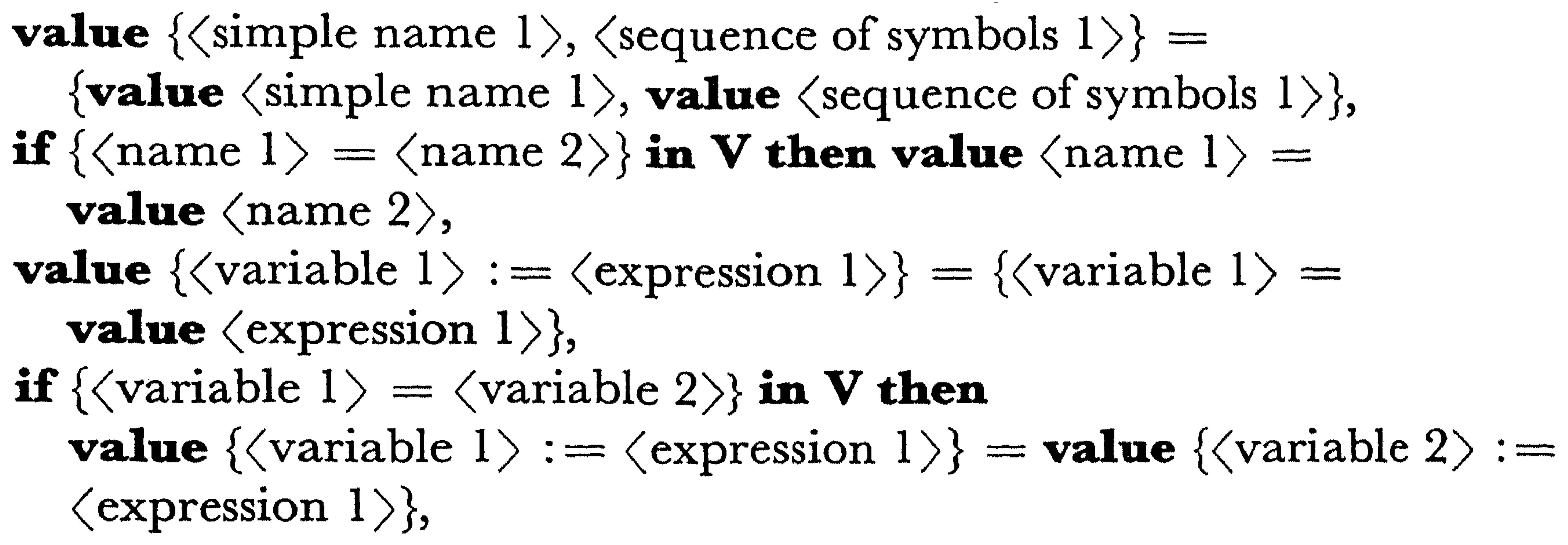
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Astarte, T.K. Conceptualising Programming Language Semantics. Philosophies 2025, 10, 90. https://doi.org/10.3390/philosophies10040090
Astarte TK. Conceptualising Programming Language Semantics. Philosophies. 2025; 10(4):90. https://doi.org/10.3390/philosophies10040090
Chicago/Turabian StyleAstarte, Troy Kaighin. 2025. "Conceptualising Programming Language Semantics" Philosophies 10, no. 4: 90. https://doi.org/10.3390/philosophies10040090
APA StyleAstarte, T. K. (2025). Conceptualising Programming Language Semantics. Philosophies, 10(4), 90. https://doi.org/10.3390/philosophies10040090





