Hydrodynamics of Butterfly-Mode Flapping Propulsion of Dolphin Pectoral Fins with Elliptical Trajectories
Abstract
1. Introduction
2. Materials and Methods
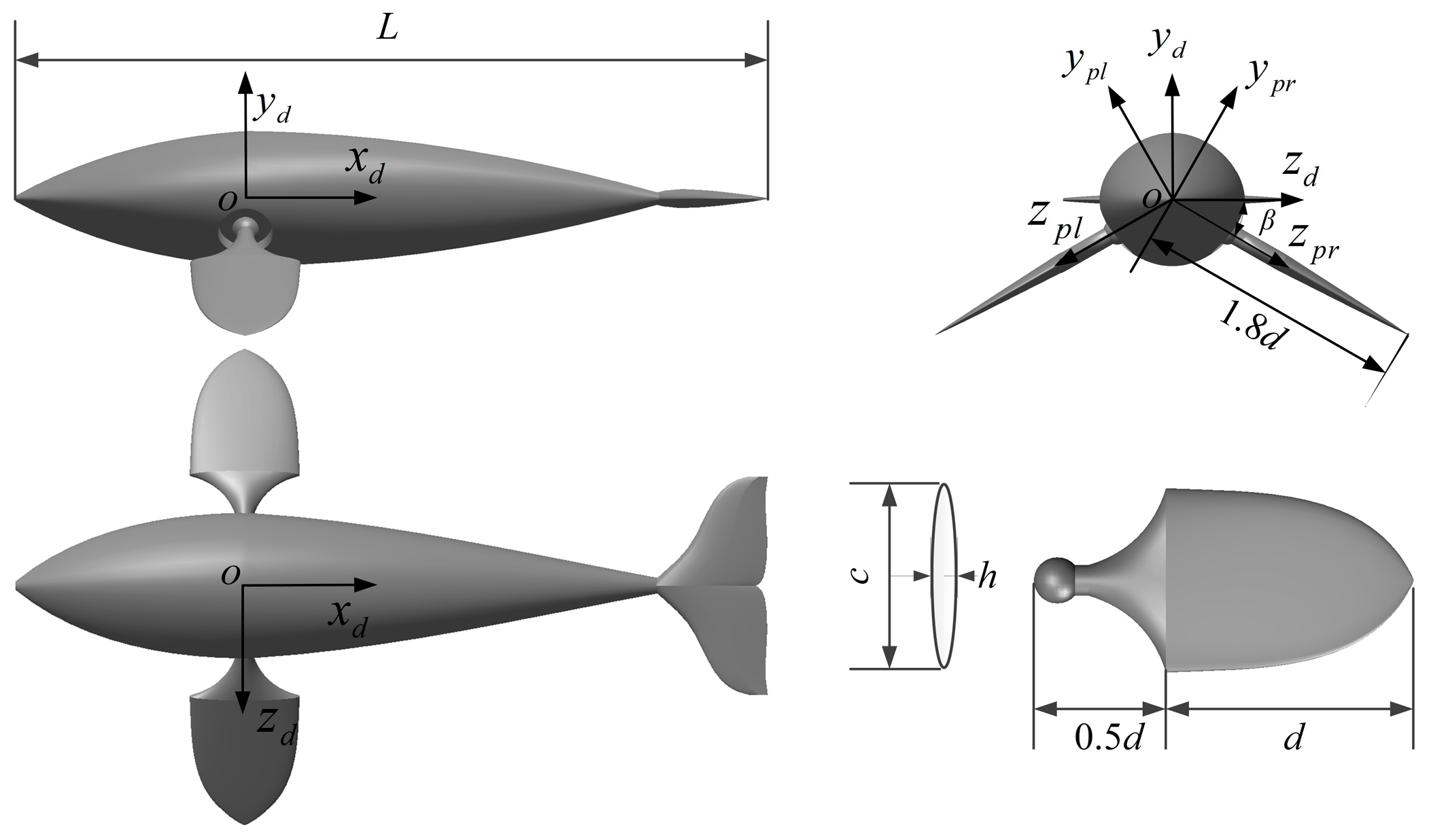
2.1. Computational Models and Grids
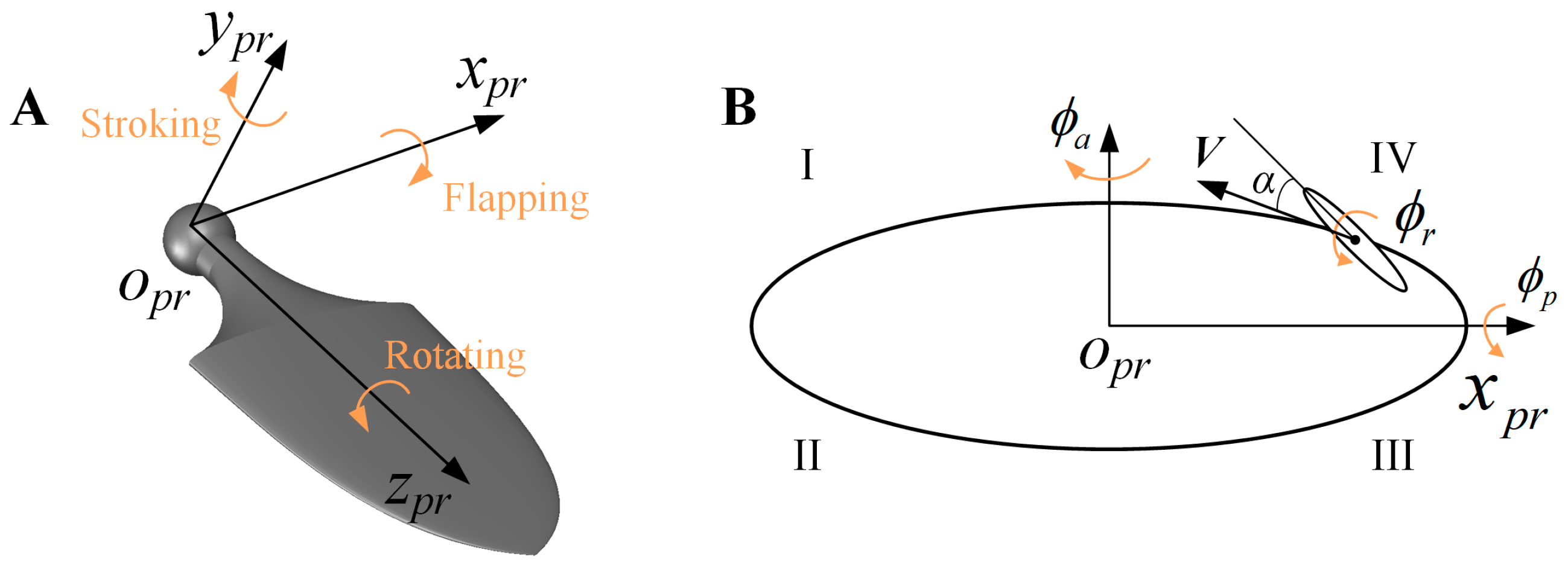
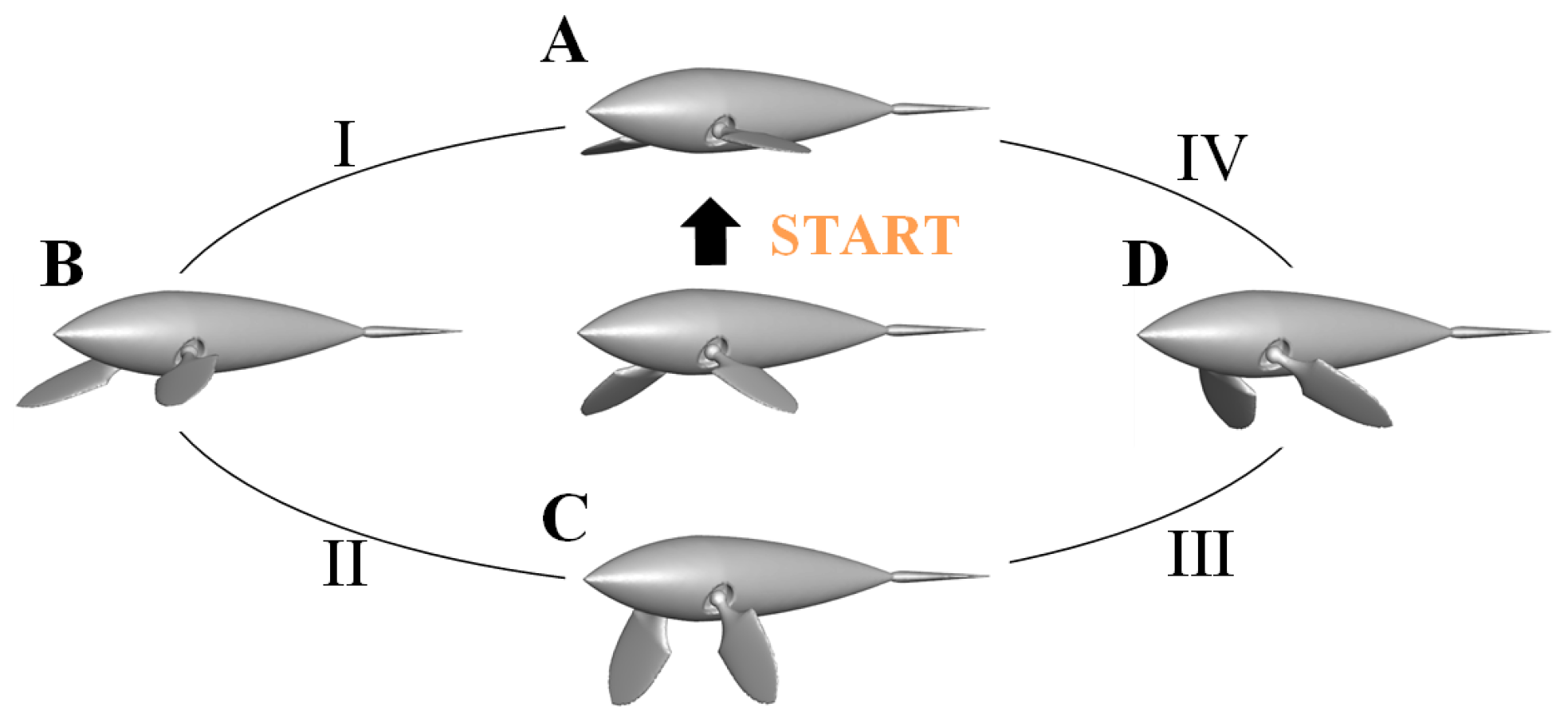
2.2. Kinematics of Pectoral Fins
2.3. The Governing Equations
2.4. Numerical Method and Validation Test
2.5. Calculation of Performance Parameters
3. Results and Discussion
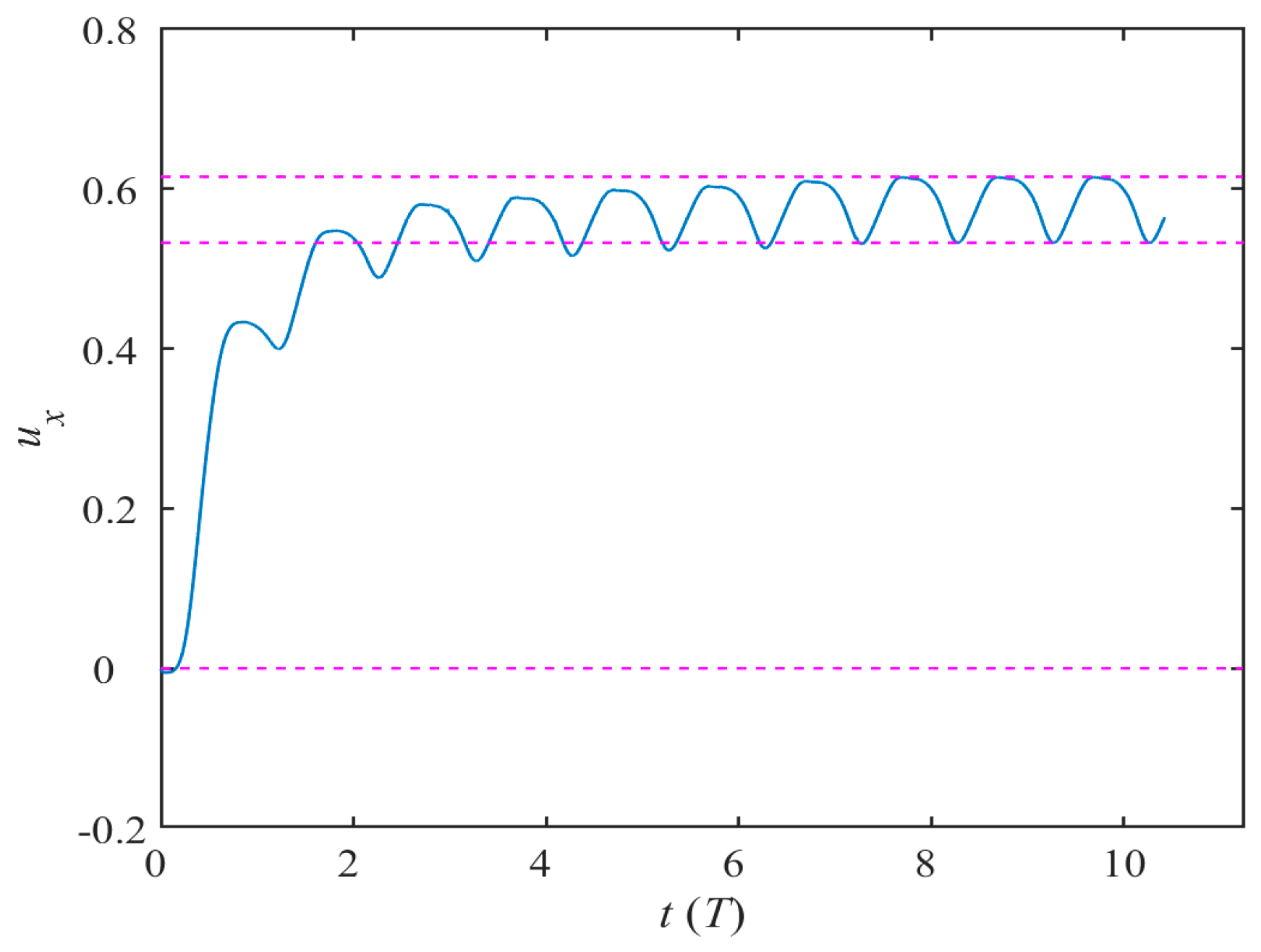
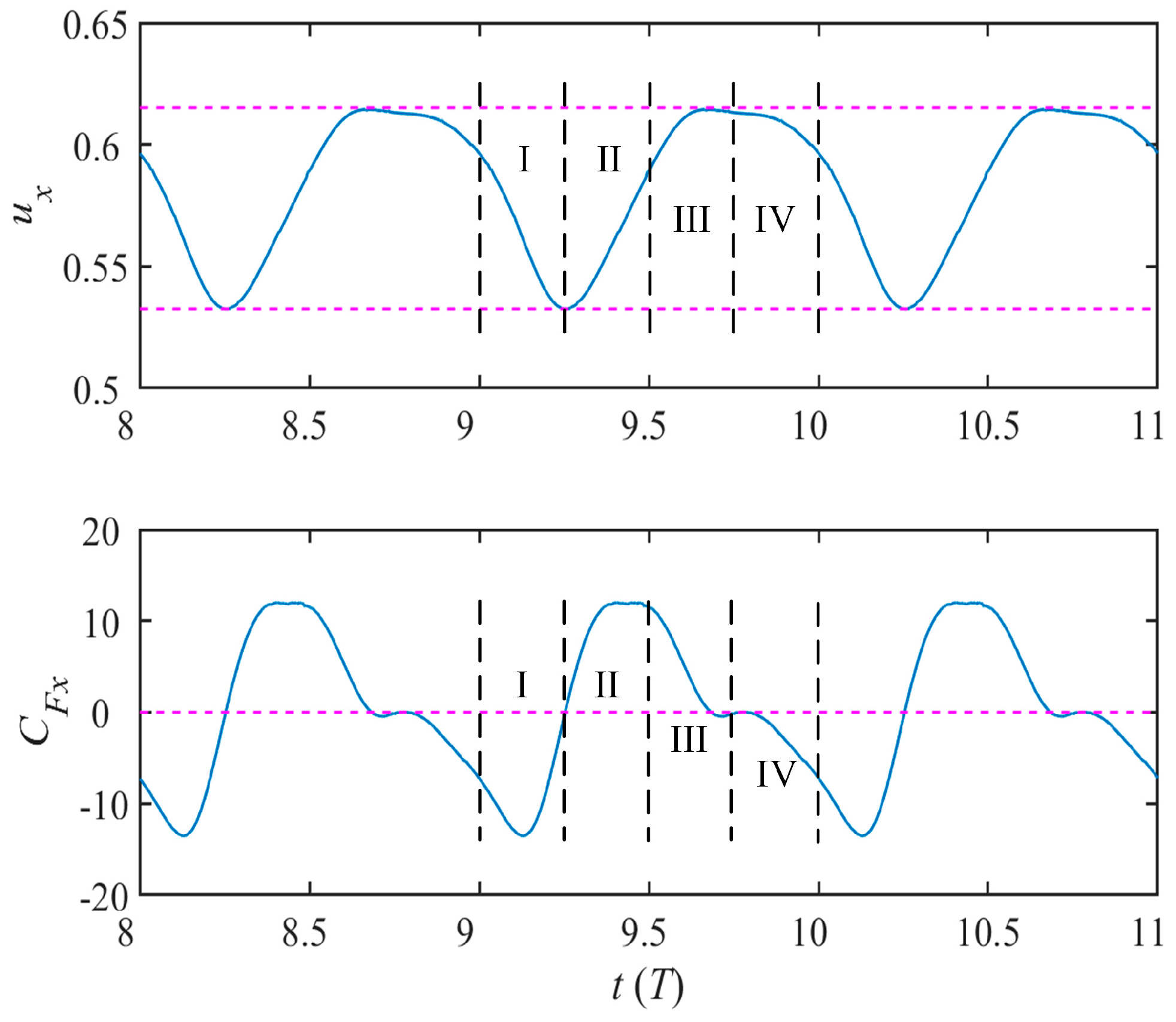
3.1. Time History Variations in Performance Parameters
3.2. Transient Variation in the Flow Field
3.3. Transient Pressure Evolution Process
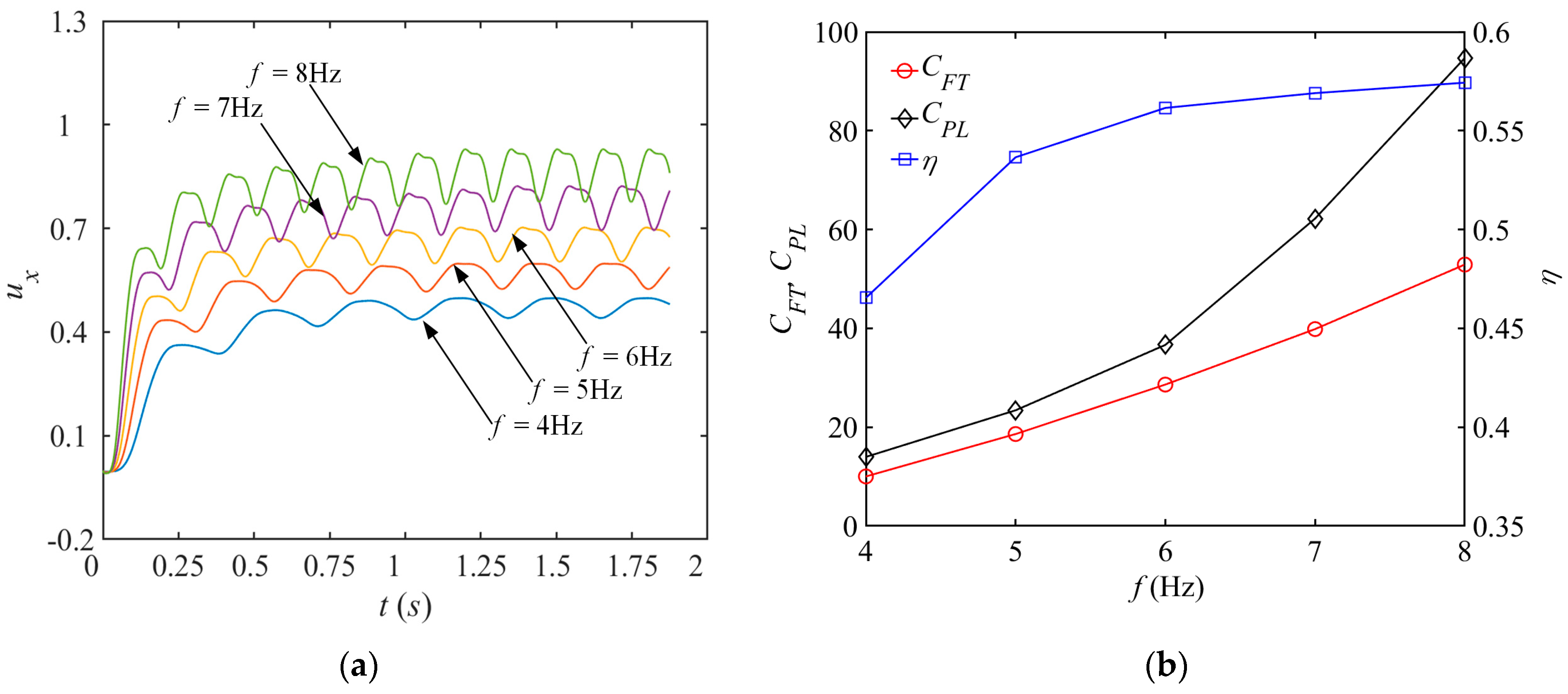
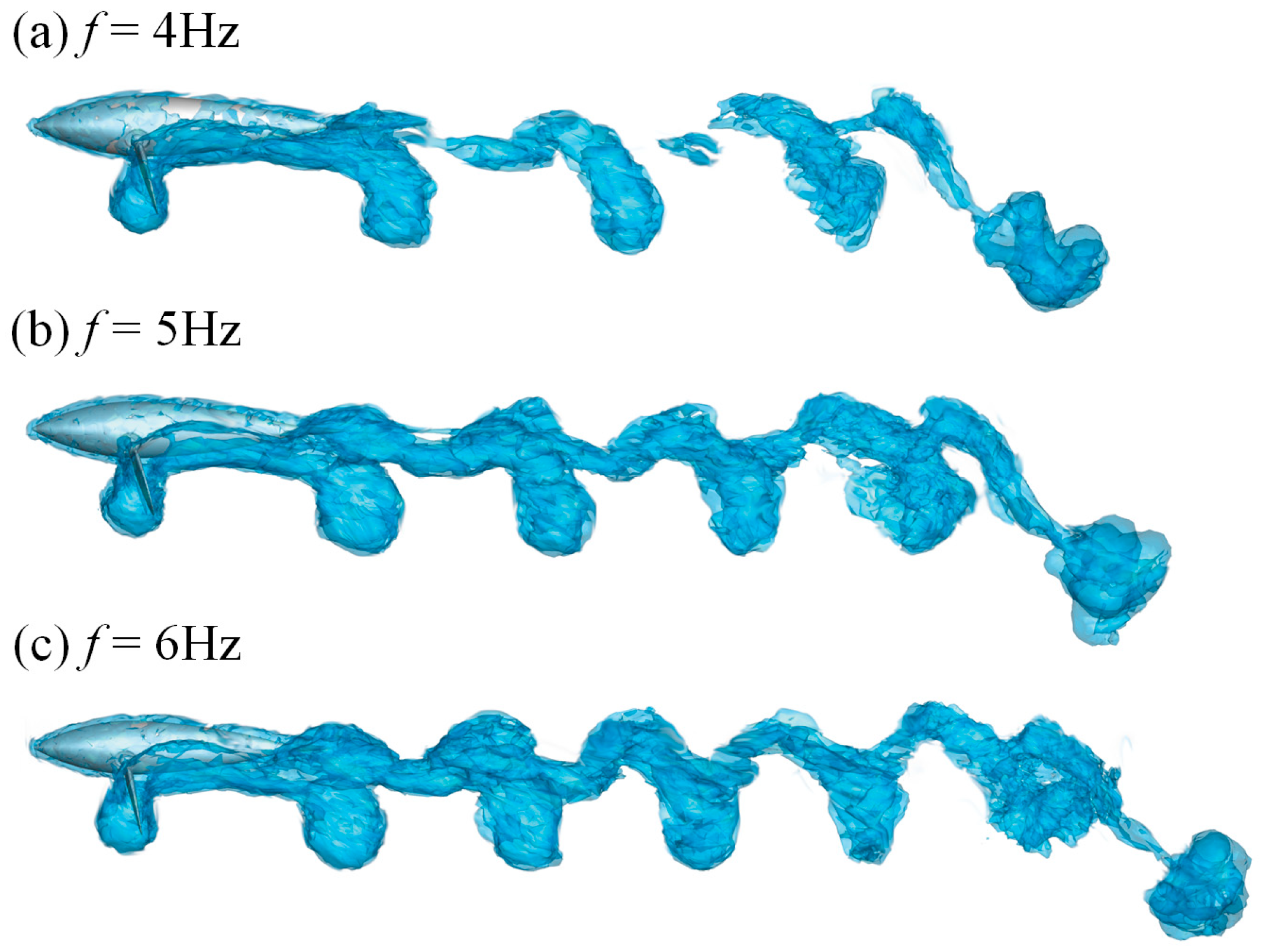
3.4. Effect of Water Striking Frequency on Butterfly Flapping Mode
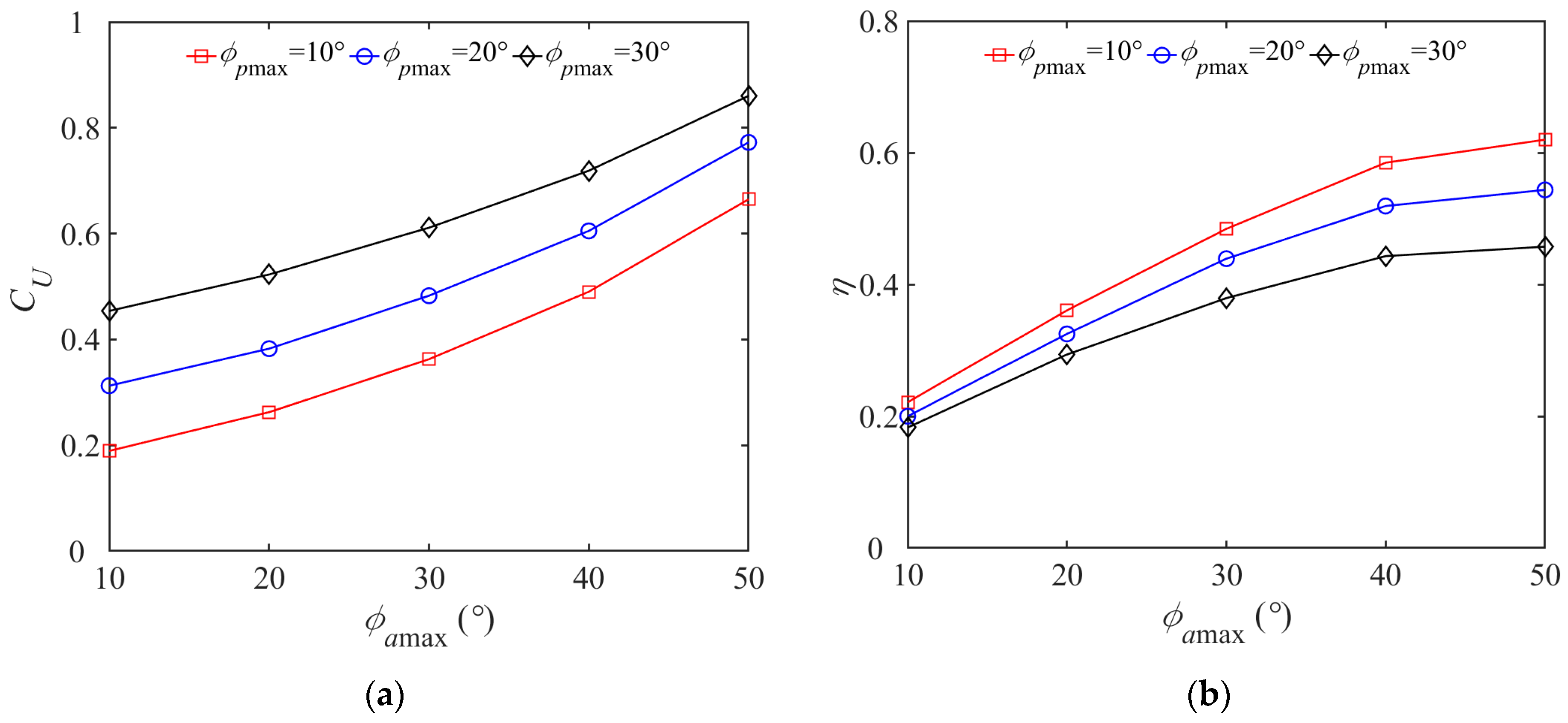
3.5. Effect of Offset Angle on Butterfly Flapping Mode
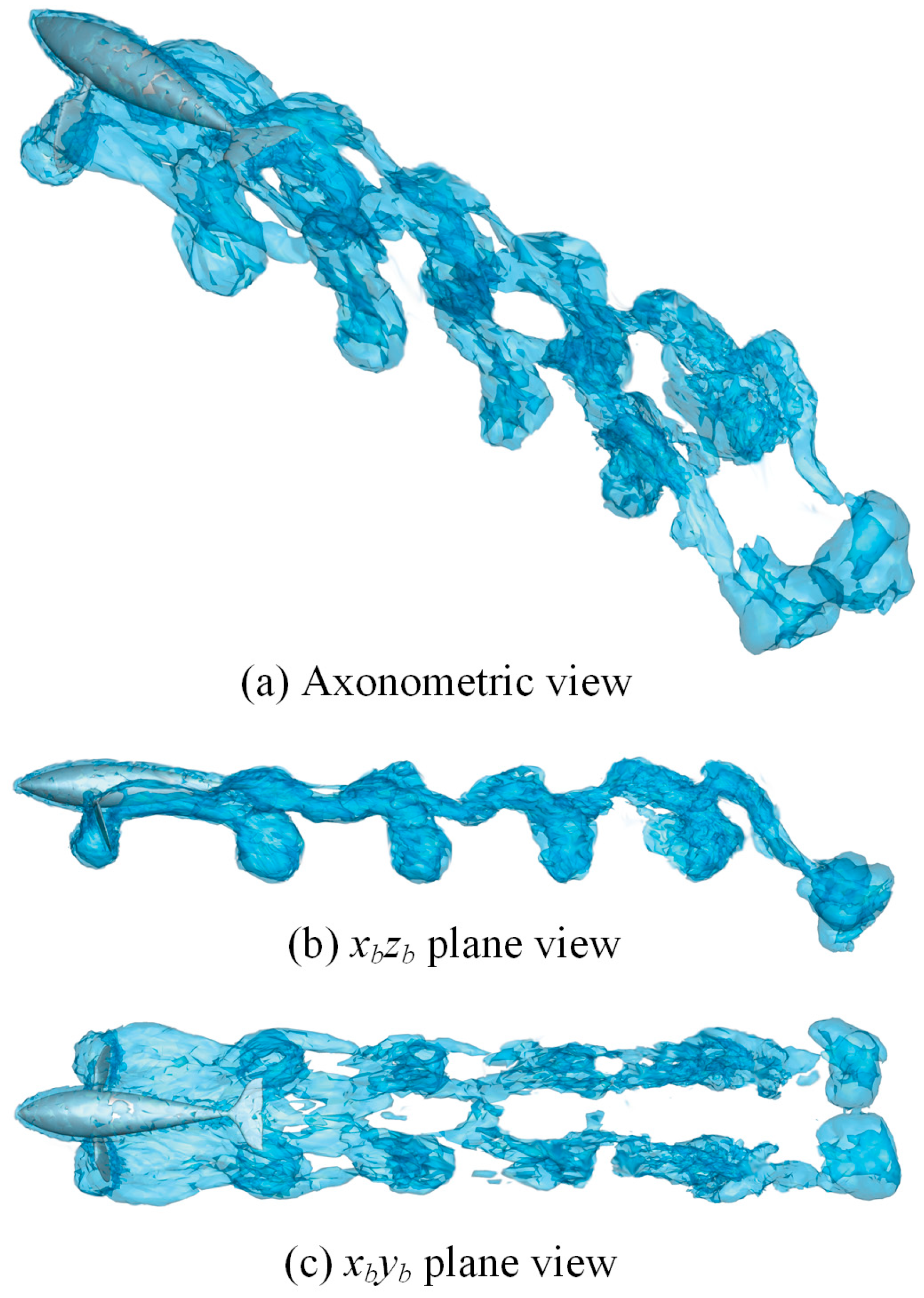
3.6. Three-Dimensional Flow Structure of Butterfly Stroke Mode
4. Conclusions
- (1)
- The advancing function of the butterfly mode is a transient process that gradually converges. The kinematics of pectoral fins can be described by an elliptical trajectory. In Phases II and III, the effective working area of the large backward water push is beneficial to quickly increase the propulsion speed, and the return of the pectoral fin is bound to bring resistance and energy loss.
- (2)
- Water striking frequency f and offset angle ϕ are two control parameters used to quantitatively describe the law of butterfly stroke. On one hand, increasing the frequency is indeed conducive to the realization of the butterfly motion effect. On the other hand, the monotonous increase in ϕpmax and ϕamax helps to improve the steady-state propulsion velocity coefficient CU of the dolphin. In terms of the propulsion efficiency, ϕamax plays a dominant role, while ϕpmax acts as an indispensable but adverse role. So within the range of parameters studied in this paper, the working condition (ϕpmax = 10°,ϕamax = 50°) is the best choice for effective propulsion. In addition, based on this working condition, if we increase the ϕpmax to 30°, the dolphin could maintain a faster propulsion speed but with slightly lower efficiency.
- (3)
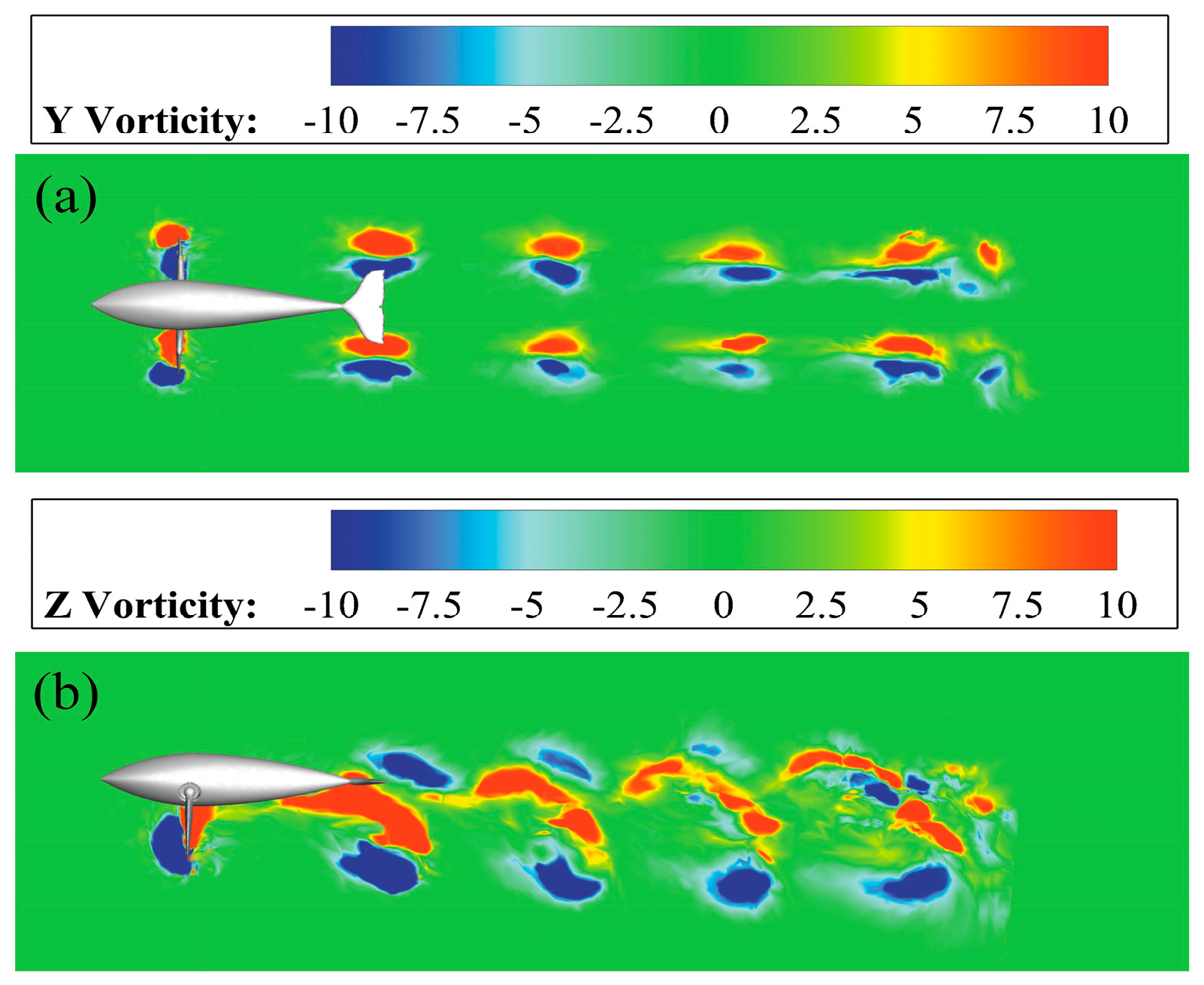
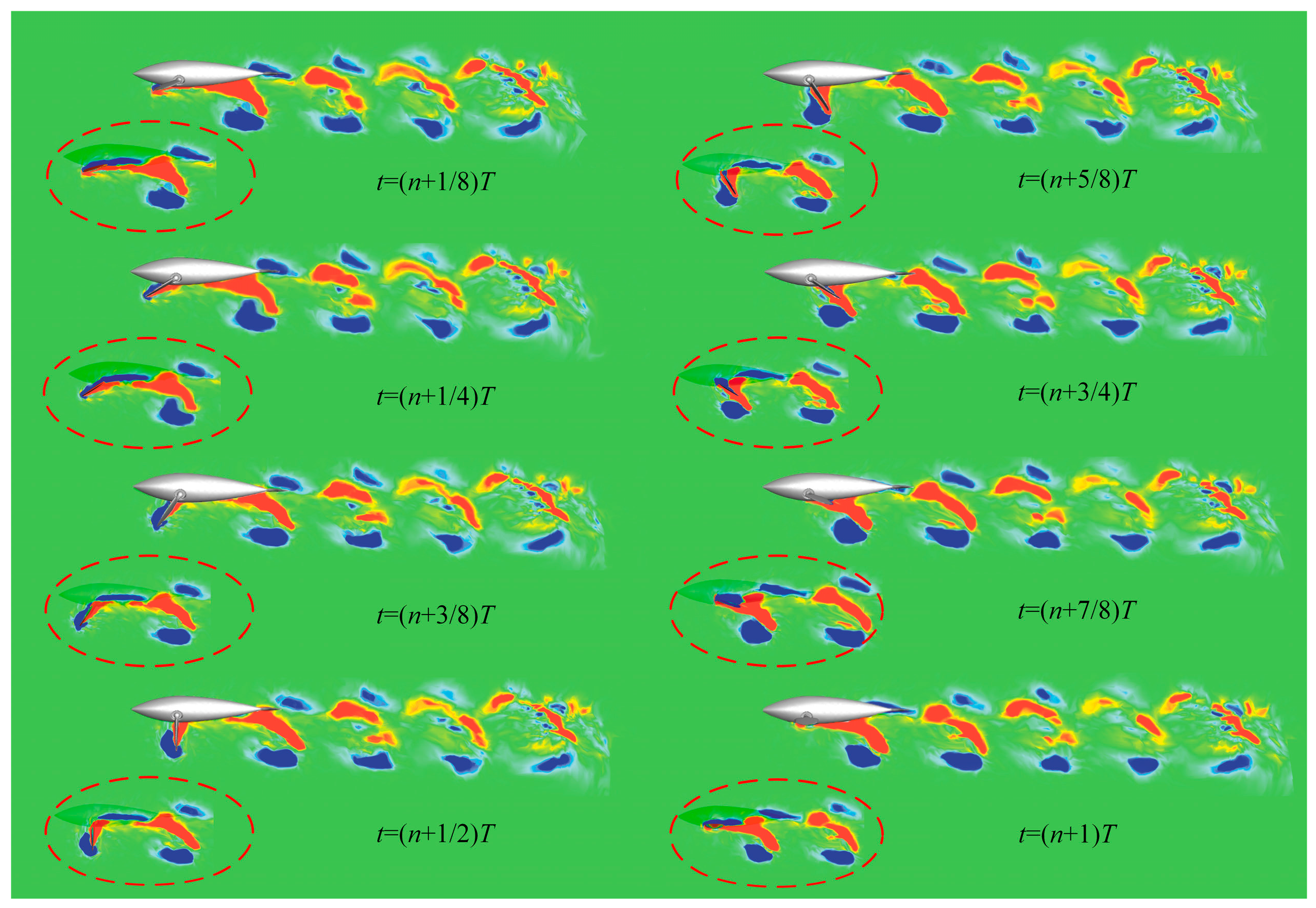
- The butterfly-mode propulsion can produce double rows of vortex streets downstream of the double pectoral fins. In addition, a “vortex dislocation” is formed between individual vortices, where the distance between each periodic vortex is determined by the water striking frequency f and offset angle ϕ. The entire shedding path follows the elliptical trajectory of the bionic pectoral fin, so the size of the sickle-shaped vortex depends on the size of the major and minor axis of the ellipse.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, J.; Sun, F.; Xu, D.; Tan, M. Embedded Vision-Guided 3-D Tracking Control for Robotic Fish. IEEE Trans. Ind. Electron. 2016, 63, 355–363. [Google Scholar] [CrossRef]
- Park, Y.J.; Huh, T.M.; Park, D.; Cho, K.J. Design of a Variable-Stiffness Flapping Mechanism for Maximizing the Thrust of a Bio-Inspired Underwater Robot. Bioinspir. Biomim. 2014, 9, 036002. [Google Scholar] [CrossRef] [PubMed]
- Lauder, G.V.; Drucker, E.G. Morphology and Experimental Hydrodynamics of Fish Fin Control Surfaces. IEEE J. Ocean. Eng. 2004, 29, 556–571. [Google Scholar] [CrossRef]
- Romano, D.; Wahi, A.; Miraglia, M.; Stefanini, C. Development of a Novel Underactuated Robotic Fish with Magnetic Transmission System. Machines 2022, 10, 755. [Google Scholar] [CrossRef]
- Park, Y.J.; Jeong, U.; Lee, J.; Kwon, S.R.; Kim, H.Y.; Cho, K.J. Kinematic Condition for Maximizing the Thrust of a Robotic Fish Using a Compliant Caudal Fin. IEEE Trans. Robot. 2012, 28, 1216–1227. [Google Scholar] [CrossRef]
- Gautreau, E.; Bonnet, X.; Sandoval, J.; Fosseries, G.; Herrel, A.; Arsicault, M.; Zeghloul, S.; Laribi, M.A. A Biomimetic Method to Replicate the Natural Fluid Movements of Swimming Snakes to Design Aquatic Robots. Biomimetics 2022, 7, 223. [Google Scholar] [CrossRef]
- Ng, T.J.K.; Chen, N.; Zhang, F. Snapp: An Agile Robotic Fish with 3-D Maneuverability for Open Water Swim. IEEE Robot. Autom. Lett. 2023, 8, 6499–6506. [Google Scholar] [CrossRef]
- Feilich, K.L.; Lauder, G.V. Passive Mechanical Models of Fish Caudal Fins: Effects of Shape and Stiffness on Self-Propulsion. Bioinspir. Biomim. 2015, 10, 036002. [Google Scholar] [CrossRef]
- Chung, H.; Cao, S.; Philen, M.; Beran, P.S.; Wang, K.G. CFD-CSD Coupled Analysis of Underwater Propulsion Using a Biomimetic Fin-and-Joint System. Comput. Fluids 2018, 172, 54–66. [Google Scholar] [CrossRef]
- Krishnadas, A.; Ravichandran, S.; Rajagopal, P. Analysis of Biomimetic Caudal Fin Shapes for Optimum Propulsive Efficiency. Ocean Eng. 2018, 153, 132–142. [Google Scholar] [CrossRef]
- Shi, G.; Xiao, Q.; Zhu, Q.; Liao, W. Fluid-Structure Interaction Modeling on a 3D Ray-Strengthened Caudal Fin. Bioinspir. Biomim. 2019, 14, 036012. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.; Chen, W.; Liu, J.; Wu, Z.; Cao, Y. The Three-Dimensional Hydrodynamics of Thunniform Swimming under Self-Propulsion. Ocean Eng. 2015, 110, 1–14. [Google Scholar] [CrossRef]
- Kato, N.; Liu, H. Optimization of Motion of a Mechanical Pectoral Fin. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2003, 46, 1356–1362. [Google Scholar] [CrossRef][Green Version]
- Behbahani, S.B.; Tan, X. Design and Modeling of Flexible Passive Rowing Joint for Robotic Fish Pectoral Fins. IEEE Trans. Robot. 2016, 32, 1119–1132. [Google Scholar] [CrossRef]
- Singh, N.; Gupta, A.; Mukherjee, S. A Dynamic Model for Underwater Robotic Fish with a Servo Actuated Pectoral Fin. SN Appl. Sci. 2019, 1, 659. [Google Scholar] [CrossRef]
- Di Santo, V.; Blevins, E.L.; Lauder, G.V. Batoid Locomotion: Effects of Speed on Pectoral Fin Deformation in the Little Skate, Leucoraja Erinacea. J. Exp. Biol. 2017, 220, 705–712. [Google Scholar] [CrossRef]
- Arastehfar, S.; Chew, C.M.; Jalalian, A.; Gunawan, G.; Yeo, K.S. A Relationship between Sweep Angle of Flapping Pectoral Fins and Thrust Generation. J. Mech. Robot. 2019, 11, 011014. [Google Scholar] [CrossRef]
- Chen, W.S.; Wu, Z.J.; Liu, J.K.; Shi, S.J.; Zhou, Y. Numerical Simulation of Batoid Locomotion. J. Hydrodyn. 2011, 23, 594–600. [Google Scholar] [CrossRef]
- Yu, C.L.; Ting, S.C.; Yeh, M.K.; Yang, J.T. Three-Dimensional Numerical Simulation of Hydrodynamic Interactions between Pectoral-Fin Vortices and Body Undulation in a Swimming Fish. Phys. Fluids 2011, 23, 091901. [Google Scholar] [CrossRef]
- Li, L.; Li, G.; Li, R.; Xiao, Q.; Liu, H. Multi-Fin Kinematics and Hydrodynamics in Pufferfish Steady Swimming. Ocean Eng. 2018, 158, 111–122. [Google Scholar] [CrossRef]
- Sampath, K.; Geder, J.D.; Ramamurti, R.; Pruessner, M.D.; Koehler, R. Hydrodynamics of Tandem Flapping Pectoral Fins with Varying Stroke Phase Offsets. Phys. Rev. Fluids 2020, 5, 094101. [Google Scholar] [CrossRef]
- Weng, J.; Zhu, Y.; Du, X.; Yang, G.; Hu, D. Theoretical and Numerical Studies on a Five-Ray Flexible Pectoral Fin during Labriform Swimming. Bioinspir. Biomim. 2020, 15, 016007. [Google Scholar] [CrossRef]
- Shoele, K.; Zhu, Q. Numerical Simulation of a Pectoral Fin during Labriform Swimming. J. Exp. Biol. 2010, 213, 2038–2047. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.G.; Wan, D.C. Numerical Simulation of Fish Swimming with Rigid Pectoral Fins. J. Hydrodyn. 2012, 24, 263–272. [Google Scholar] [CrossRef]
- Li, Z.; Xia, D.; Zhou, X.; Cao, J.; Chen, W.; Wang, X. The Hydrodynamics of Self-Rolling Locomotion Driven by the Flexible Pectoral Fins of 3-D Bionic Dolphin. J. Ocean Eng. Sci. 2022, 7, 29–40. [Google Scholar] [CrossRef]
- Li, Z.; Xia, D.; Cao, J.; Chen, W.; Wang, X. Hydrodynamics Study of Dolphin’s Self-Yaw Motion Realized by Spanwise Flexibility of Caudal Fin. J. Ocean Eng. Sci. 2022, 7, 213–224. [Google Scholar] [CrossRef]
- Xia, D.; Li, Z.; Lei, M.; Yan, H.; Zhou, Z. A Comparative and Collaborative Study of the Hydrodynamics of Two Swimming Modes Applicable to Dolphins. Biomimetics 2023, 8, 311. [Google Scholar] [CrossRef]
- Liu, H.; Wassersug, R.J.; Kawachi, K. A Computational Fluid Dynamics Study of Tadpole Swimming. J. Exp. Biol. 1996, 199, 1245–1260. [Google Scholar] [CrossRef]
- Ohashi, K.; Hino, T.; Kobayashi, H.; Onodera, N.; Sakamoto, N. Development of a Structured Overset Navier–Stokes Solver with a Moving Grid and Full Multigrid Method. J. Mar. Sci. Technol. 2019, 24, 884–901. [Google Scholar] [CrossRef]
- König, M.; Eisenlohr, H.; Eckelmann, H. The Fine Structure in the Strouhal-Reynolds Number Relationship of the Laminar Wake of a Circular Cylinder. Phys. Fluids A 1990, 2, 1607–1614. [Google Scholar] [CrossRef]

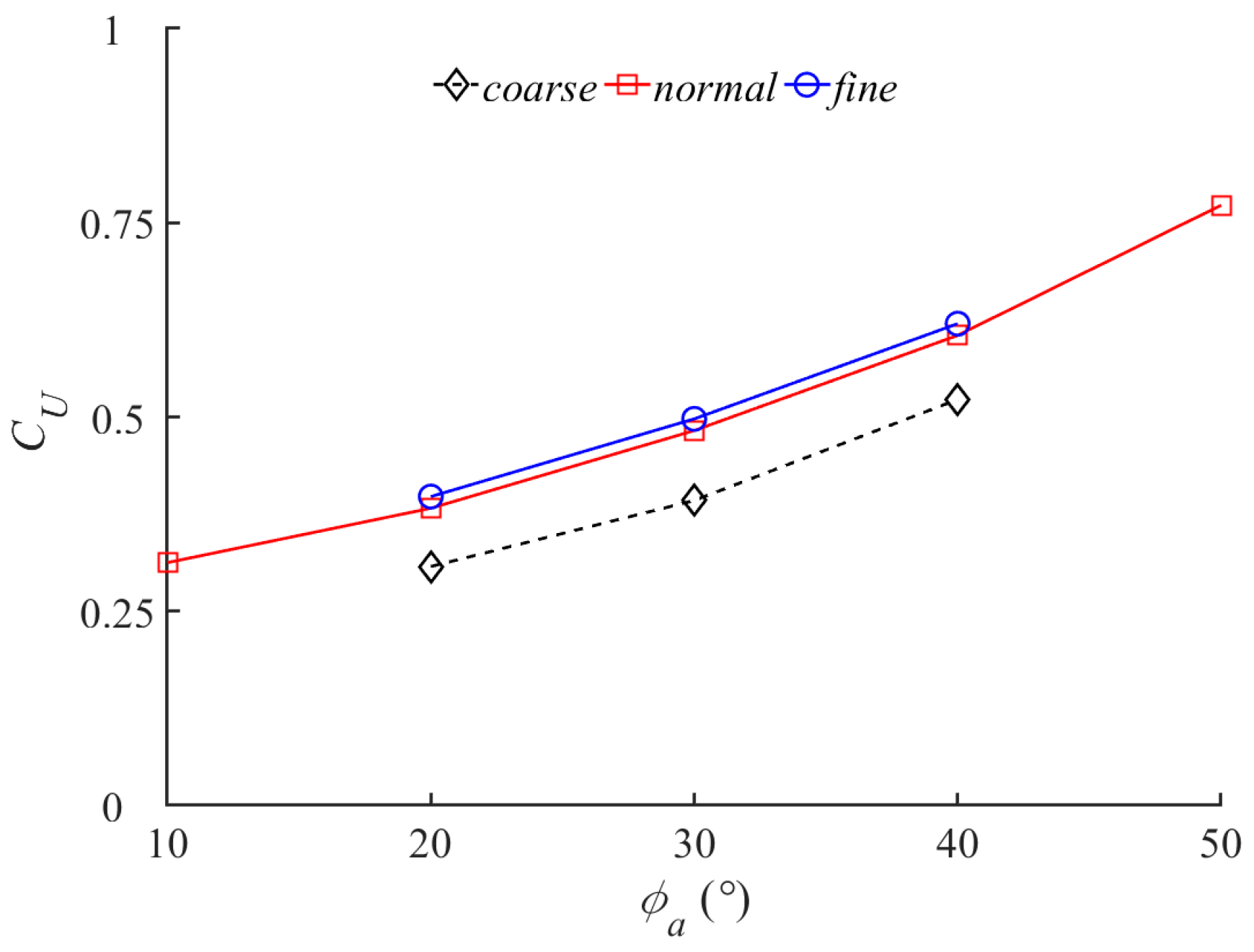


| ϕamax (°) | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| dt = 0.01 T | —— | 0.33 | 0.42 | 0.53 | —— |
| dt = 0.005 T | 0.31 | 0.38 | 0.48 | 0.60 | 0.77 |
| dt = 0.0025 T | —— | 0.39 | 0.50 | 0.62 | —— |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, D.; Li, Z.; Lei, M.; Shi, Y.; Luo, X. Hydrodynamics of Butterfly-Mode Flapping Propulsion of Dolphin Pectoral Fins with Elliptical Trajectories. Biomimetics 2023, 8, 522. https://doi.org/10.3390/biomimetics8070522
Xia D, Li Z, Lei M, Shi Y, Luo X. Hydrodynamics of Butterfly-Mode Flapping Propulsion of Dolphin Pectoral Fins with Elliptical Trajectories. Biomimetics. 2023; 8(7):522. https://doi.org/10.3390/biomimetics8070522
Chicago/Turabian StyleXia, Dan, Zhihan Li, Ming Lei, Yunde Shi, and Xiang Luo. 2023. "Hydrodynamics of Butterfly-Mode Flapping Propulsion of Dolphin Pectoral Fins with Elliptical Trajectories" Biomimetics 8, no. 7: 522. https://doi.org/10.3390/biomimetics8070522
APA StyleXia, D., Li, Z., Lei, M., Shi, Y., & Luo, X. (2023). Hydrodynamics of Butterfly-Mode Flapping Propulsion of Dolphin Pectoral Fins with Elliptical Trajectories. Biomimetics, 8(7), 522. https://doi.org/10.3390/biomimetics8070522





