Wind Dispersal of Natural and Biomimetic Maple Samaras
Abstract
1. Introduction
2. Development of Artificial Samaras
3. Experimental Methods
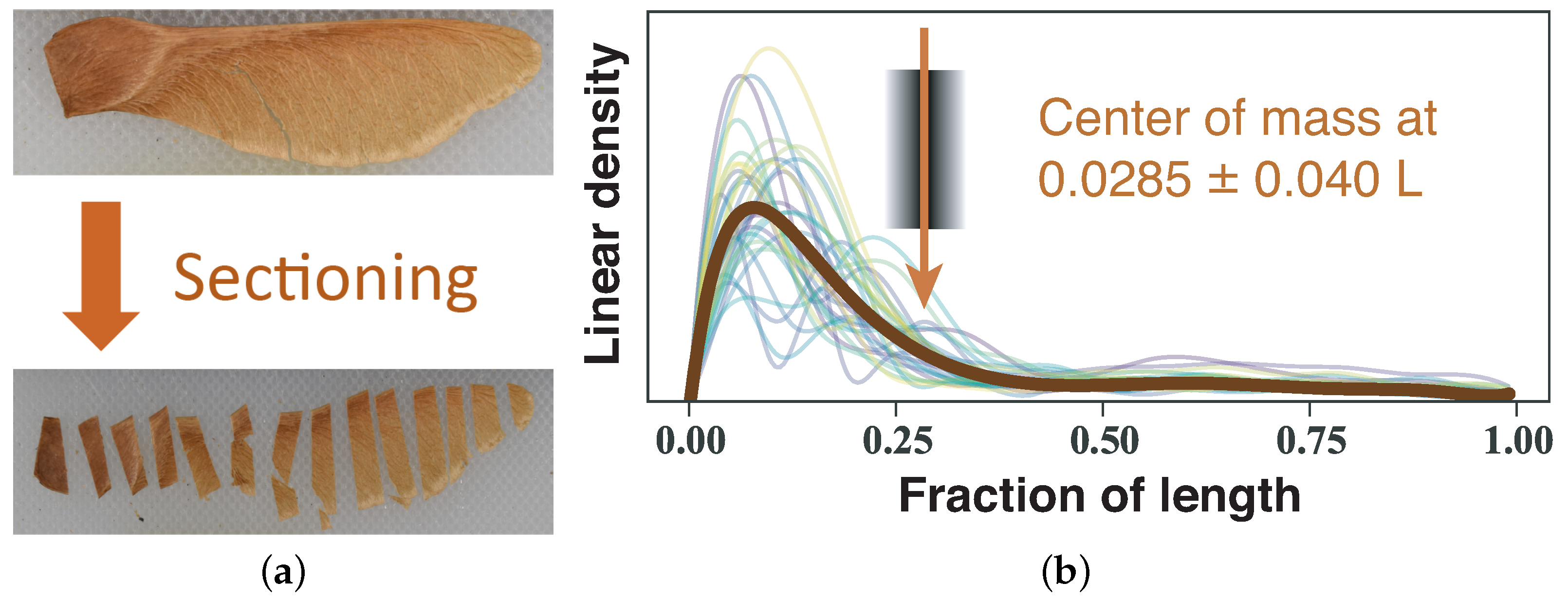
3.1. Samara Morphology
3.2. Still Air Experiments
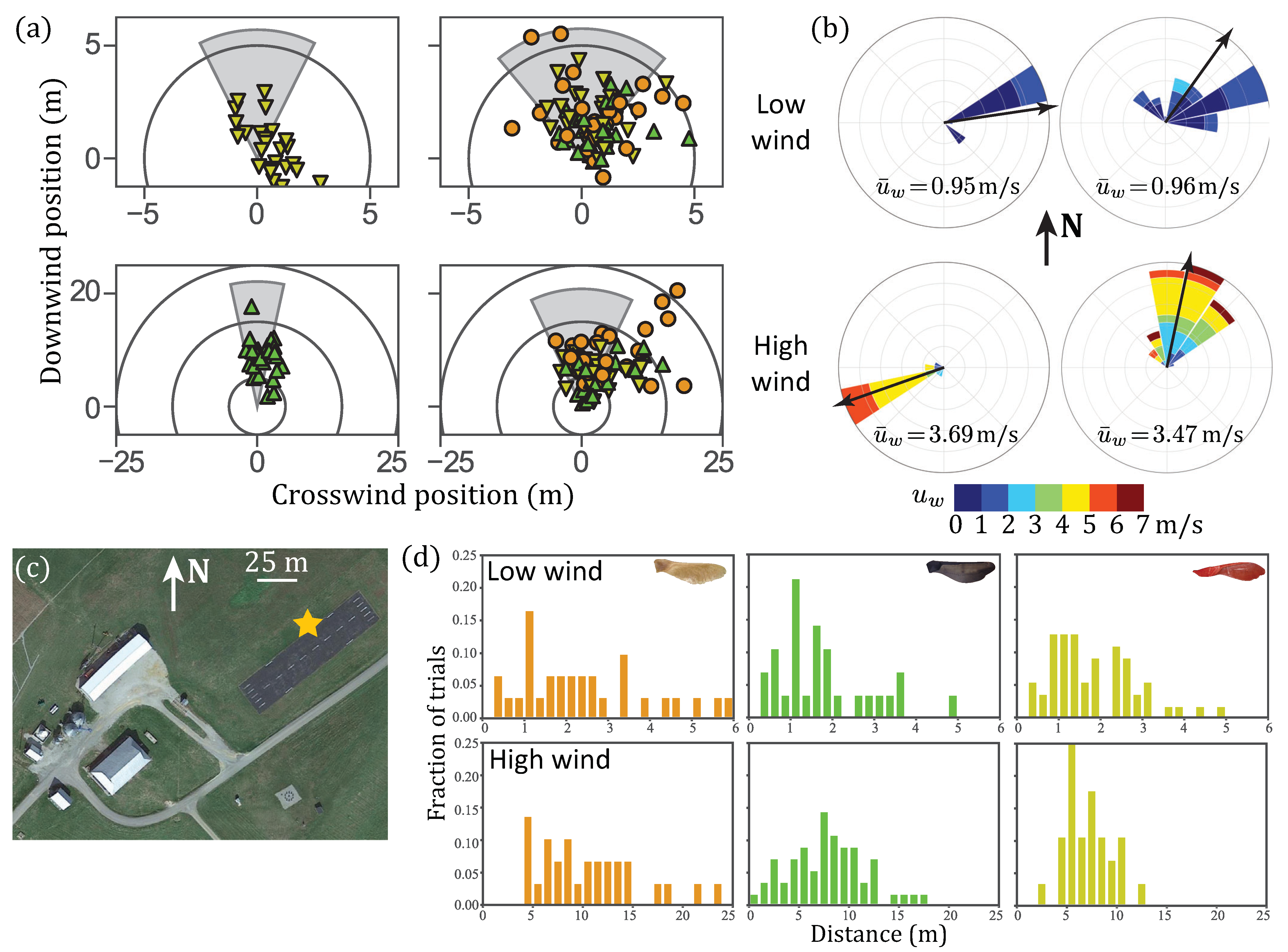
3.3. Field Experiments
3.4. Windage
4. Experimental Results
4.1. Samara Morphology
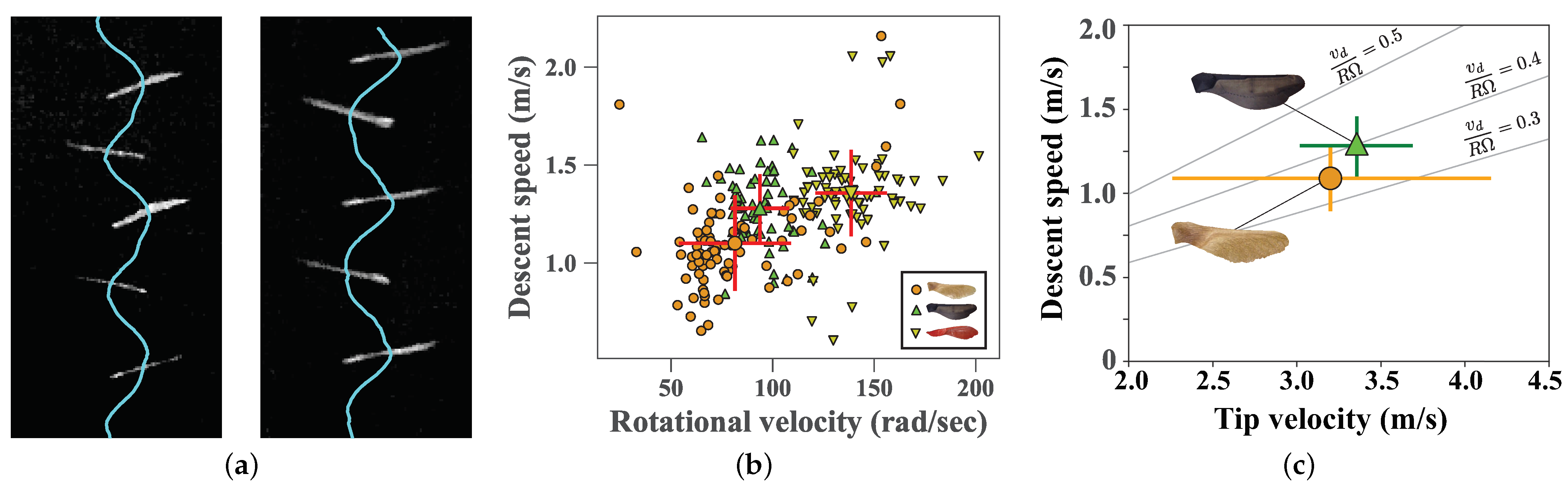
4.2. Still Air Experiments
4.3. Field Experiments
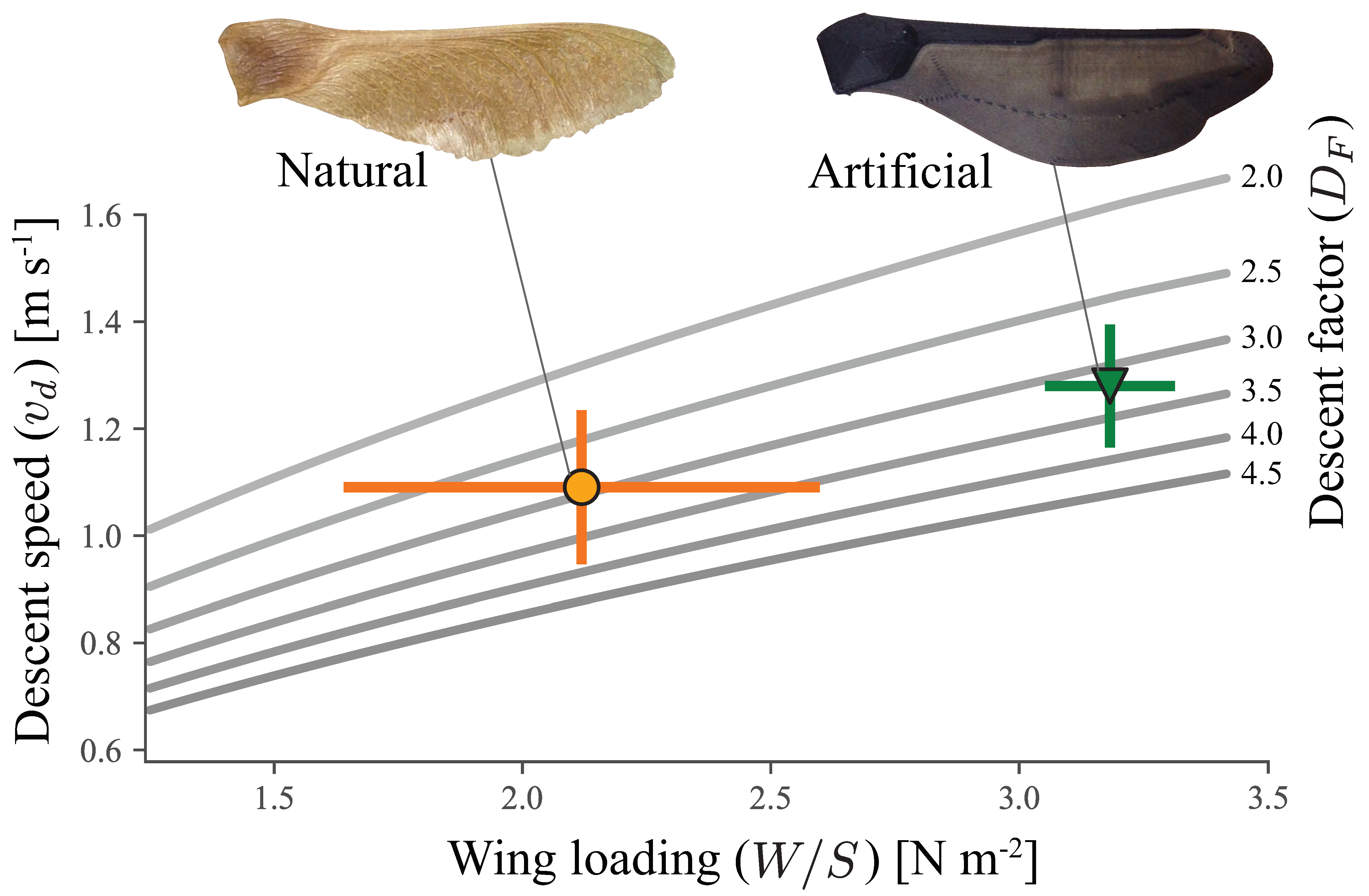
4.4. Morphology as Performance Indicator
5. Discussion
5.1. Biological Implications
5.2. Engineering Implications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Chilson, P.B.; Bell, T.M.; Brewster, K.A.; Britto Hupsel de Azevedo, G.; Carr, F.H.; Carson, K.; Doyle, W.; Fiebrich, C.A.; Greene, B.R.; Grimsley, J.L.; et al. Moving towards a Network of Autonomous UAS Atmospheric Profiling Stations for Observations in the Earth’s Lower Atmosphere: The 3D Mesonet Concept. Sensors 2019, 19, 2720. [Google Scholar] [CrossRef]
- Barbieri, L.K.; Kral, S.T.; Bailey, S.C.C.; Frazier, A.E.; Jacob, J.D.; Brus, P.B.C.; Crick, C.; Elston, J.; Foroutan, H.; González-Rocha, J.; et al. Intercomparison of small unmanned aircraft system (sUAS) measurements for atmospheric science during the LAPSE-RATE campaign. Sensors 2019, 19, 2179. [Google Scholar] [CrossRef]
- Lee, T.R.; Buban, M.; Dumas, E.; Baker, C.B. On the use of rotary-wing aircraft to sample near-surface thermodynamic fields: Results from recent field campaigns. Sensors 2019, 19, 10. [Google Scholar] [CrossRef]
- Rabinovich, S.; Curry, R.E.; Elkaim, G.H. Toward dynamic monitoring and suppressing uncertainty in wildfire by multiple unmanned air vehicle system. J. Robot. 2018, 2018, 6892153. [Google Scholar] [CrossRef]
- AL-Dhief, F.T.; Sabri, N.; Fouad, S.; Latiff, N.A.; Albader, M.A.A. A review of forest fire surveillance technologies: Mobile ad-hoc network routing protocols perspective. J. King Saud Univ. Comput. Inform. Sci. 2019, 31, 135–146. [Google Scholar] [CrossRef]
- Villa, T.F.; Gonzalez, F.; Miljievic, B.; Ristovski, Z.D.; Morawska, L. An overview of small unmanned aerial vehicles for air quality measurements: Present applications and future prospectives. Sensors 2016, 16, 1072. [Google Scholar] [CrossRef] [PubMed]
- Carranza, V.; Rafiq, T.; Frausto-Vicencio, I.; Hopkins, F.M.; Verhulst, K.R.; Rao, P.; Duren, R.M.; Miller, C.E. Vista-LA: Mapping methane-emitting infrastructure in the Los Angeles megacity. Earth Syst. Sci. Data 2018, 10, 653. [Google Scholar] [CrossRef]
- Schmale, D.G.; Ault, A.P.; Saad, W.; Scott, D.T.; Westrick, J.A. Perspectives on Harmful Algal Blooms (HABs) and the Cyberbiosecurity of Freshwater Systems. Front. Bioeng. Biotechnol. 2019, 7, 128. [Google Scholar] [CrossRef] [PubMed]
- Hart, J.K.; Martinez, K. Environmental sensor networks: A revolution in the earth system science? Earth Sci. Rev. 2006, 78, 177–191. [Google Scholar] [CrossRef]
- Barrientos, A.; Colorado, J.; Cerro, J.D.; Martinez, A.; Rossi, C.; Sanz, D.; Valente, J. Aerial remote sensing in agriculture: A practical approach to area coverage and path planning for fleets of mini aerial robots. J. Field Robot. 2011, 28, 667–689. [Google Scholar] [CrossRef]
- Pandolfi, C.; Izzo, D. Biomimetics on seed dispersal: Survey and insights for space exploration. Bioinspirat. Biomimet. 2013, 8, 025003. [Google Scholar] [CrossRef] [PubMed]
- Lohr, S. Smart Dust? Not Quite, but We’re Getting There. New York Times, 31 January 2010. [Google Scholar]
- Batista da Silva, L.C.; Bernardo, R.M.; de Oliveira, H.A.; Rosa, P.F.F. Unmanned aircraft system coordination for persistent surveillance with different priorities. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1153–1158. [Google Scholar]
- Prather, J.C.; Bolt, H.M.; Harrell, H.; Manobianco, J.; Adams, M.L. Antenna design for a massive multiple input environmental sensor network. Digit. Commun. Netw. 2016, 2, 256–259. [Google Scholar] [CrossRef]
- Horton, T.; Bolt, M.; Prather, C.; Manobianco, J.; Adams, M.L. Airborne Sensor Network for Atmospheric Profiling. Wirel. Sens. Netw. 2018, 10, 93–101. [Google Scholar] [CrossRef][Green Version]
- Bolt, M.; Prather, J.C.; Horton, T.; Adams, M. Massively Deployable, Low-Cost Airborne Sensor Motes for Atmospheric Characterization. Wirel. Sens. Netw. 2020, 12, 1–11. [Google Scholar] [CrossRef]
- Howe, H.F.; Smallwood, J. Ecology of seed dispersal. Ann. Rev. Ecol. Syst. 1982, 13, 201–228. [Google Scholar] [CrossRef]
- Hughes, L.; Dunlop, M.; French, K.; Leishman, M.R.; Rice, B.; Rodgerson, L.; Westoby, M. Predicting dispersal spectra: A minimal set of hypotheses based on plant attributes. J. Ecol. 1994, 82, 933–950. [Google Scholar] [CrossRef]
- Isard, S.; Gage, S.H. Flow of Life in the Atmosphere: An Airscape Approach to Understanding Invasive Organisms; Michigan State University Press: East Lansing, MI, USA, 2001. [Google Scholar]
- Schmale, D.G.; Ross, S.D. Highways in the Sky: Scales of Atmospheric Transport of Plant Pathogens. Ann. Rev. Phytopathol. 2015, 53, 591–611. [Google Scholar] [CrossRef]
- Lentink, D.; Dickson, W.B.; Van Leeuwen, J.L.; Dickinson, M.H. Leading-edge vortices elevate lift of autorotating plant seeds. Science 2009, 324, 1438–1440. [Google Scholar] [CrossRef]
- Lee, I.; Choi, H. Scaling law for the lift force of autorotating falling seeds at terminal velocity. J. Fluid Mech. 2018, 835, 406. [Google Scholar] [CrossRef]
- Fenner, M.W. Seed Ecology; Champan and Hall: New York, NY, USA, 1985. [Google Scholar]
- Harwell, M.C.; Orth, R.J. Long-distance dispersal potential in a marine macrophyte. Ecology 2002, 83, 3319–3330. [Google Scholar] [CrossRef]
- Ruiz-Montoya, L.; Lowe, R.J.; van Niel, K.P.; Kendrick, G.A. The role of hydrodynamics on seed dispersal in seagrasses. Limnol. Oceanograp. 2012, 57, 1257–1265. [Google Scholar] [CrossRef]
- Ruiz-Montoya, L.; Lowe, R.J.; Kendrick, G.A. Contemporary connectivity is sustained by wind-and current-driven seed dispersal among seagrass meadows. Mov. Ecol. 2015, 3, 9. [Google Scholar] [CrossRef]
- Augspurger, C.K.; Franson, S.E. Wind dispersal of artificial fruits varying in mass, area, and morphology. Ecology 1987, 68, 27–42. [Google Scholar] [CrossRef]
- Minami, S.; Azuma, A. Various flying modes of wind-dispersal seeds. J. Theor. Biol. 2003, 225, 1–14. [Google Scholar] [CrossRef]
- Nave, G.K., Jr.; Hall, N.; Somers, K.; Davis, B.; Collver, M.; Gruszewski, H.A.; Schmale, G.D., III; Ross, S. Wind dispersal of natural and biomimetic maple samaras—Supplemental design files. Figshare 2020. [Google Scholar] [CrossRef]
- Varshney, K.; Chang, S.; Wang, Z.J. The kinematics of falling maple seeds and the initial transition to a helical motion. Nonlinearity 2012, 25, C1. [Google Scholar] [CrossRef]
- Allshouse, M.R.; Ivey, G.N.; Lowe, R.J.; Jones, N.L.; Beegle-Krause, C.; Xu, J.; Peacock, T. Impact of windage on ocean surface Lagrangian coherent structures. Environ. Fluid Mech. 2017, 17, 473–483. [Google Scholar] [CrossRef]
- Breivik, Ø.; Allen, A.A.; Maisondieu, C.; Roth, J.C. Wind-induced drift of objects at sea: The leeway field method. Appl. Ocean Res. 2011, 33, 100–109. [Google Scholar] [CrossRef]
- Okubo, A.; Levin, S.A. A theoretical framework for data analysis of wind dispersal of seeds and pollen. Ecology 1989, 70, 329–338. [Google Scholar] [CrossRef]
- Murren, C.J.; Ellison, A.M. Seed dispersal characteristics of Brassavola nodosa (Orchidaceae). Am. J. Botan. 1998, 85, 675–680. [Google Scholar] [CrossRef]
- Cremer, K.W. Distance of seed dispersal in eucalyptus estimated from seed weights. Austral. Forest. Res. 1977, 7, 225–228. [Google Scholar]
- Greene, D.F.; Johnson, E.A. A model of wind dispersal of winged or plumed seeds. Ecology 1989, 70, 339–347. [Google Scholar] [CrossRef]
- Azuma, A.; Yasuda, K. Flight performance of rotary seeds. J. Theor. Biol. 1989, 138, 23–53. [Google Scholar] [CrossRef]
- Heisinger, L.; Newton, P.; Kanso, E. Coins falling in water. J. Fluid Mech. 2014, 742, 243–253. [Google Scholar] [CrossRef]
- Yasuda, K.; Azuma, A. The autorotation boundary in the flight of samaras. J. Theor. Biol. 1997, 185, 313–320. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, E.J.; Sohn, M.H. Mechanism of autorotation flight of maple samaras (Acer palmatum). Experiment. Fluids 2014, 55, 1718. [Google Scholar] [CrossRef]
- Rabinowitz, D.; Rapp, J.K. Dispersal abilities of seven sparse and common grasses from a Missouri prairie. Am. J. Botan. 1981, 68, 616–624. [Google Scholar] [CrossRef]
- Ern, P.; Risso, F.; Fabre, D.; Magnaudet, J. Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Ann. Rev. Fluid Mech. 2012, 44, 97–121. [Google Scholar] [CrossRef]
- Nave, G.K., Jr.; Ross, S.D. Global phase space structures in a model of passive descent. Commun. Nonlinear Sci. Numer. Simulat. 2019, 77, 54–80. [Google Scholar] [CrossRef]
- Archer, C.L.; Jacobson, M.Z. Evaluation of global wind power. J. Geophys. Res. Atmos. 2005, 110, D12220. [Google Scholar] [CrossRef]
- Gilman, E.F.; Watson, D.G. Acer Platanoides: Norway Maple; Fact Sheet ST-28, Adapted from a Series by the Environmental Horticulture Department; University of Florida for the United States Forest Service: Gainesville, FL, USA, 1993. [Google Scholar]
- Bullock, J.M.; Clarke, R.T. Long distance seed dispersal by wind: Measuring and modelling the tail of the curve. Oecologia 2000, 124, 506–521. [Google Scholar] [CrossRef] [PubMed]
- Rabault, J.; Fauli, R.A.; Carlson, A. Curving to fly: Synthetic adaptation unveils optimal flight performance of whirling fruits. Phys. Rev. Lett. 2019, 122, 024501. [Google Scholar] [CrossRef]
- Fauli, R.A.; Rabault, J.; Carlson, A. Effect of wing fold angles on the terminal descent velocity of double-winged autorotating seeds, fruits, and other diaspores. Phys. Rev. E 2019, 100, 013108. [Google Scholar] [CrossRef] [PubMed]
- Norberg, R.Å. Autorotation, self-stability, and structure of single-winged fruits and seeds (samaras) with comparative remarks on animal flight. Biol. Rev. 1973, 48, 561–596. [Google Scholar] [CrossRef]
- Field, S.B.; Klaus, M.; Moore, M.; Nori, F. Chaotic dynamics of falling disks. Nature 1997, 388, 252–254. [Google Scholar] [CrossRef]
- Andersen, A.; Pesavento, U.; Wang, Z.J. Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 2005, 541, 65–90. [Google Scholar] [CrossRef]


| Samara | Natural Norway Maple | Artificial Norway Maple | Artificial Silver Maple |
|---|---|---|---|
| Mass, m | mg | mg | — |
| Length, L | cm | cm | — |
| Center of mass | % L | % L | — |
| Wing loading, | N/m2 | N/m2 | — |
| Rotational velocity, | rad/s | rad/s | rad/s |
| Wing tip speed, | m/s | m/s | — |
| Lab descent speed, | m/s | m/s | m/s |
| Field descent speed, | m/s | m/s | m/s |
| Windage coefficient, |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nave, G.K., Jr.; Hall, N.; Somers, K.; Davis, B.; Gruszewski, H.; Powers, C.; Collver, M.; Schmale, D.G., III; Ross, S.D. Wind Dispersal of Natural and Biomimetic Maple Samaras. Biomimetics 2021, 6, 23. https://doi.org/10.3390/biomimetics6020023
Nave GK Jr., Hall N, Somers K, Davis B, Gruszewski H, Powers C, Collver M, Schmale DG III, Ross SD. Wind Dispersal of Natural and Biomimetic Maple Samaras. Biomimetics. 2021; 6(2):23. https://doi.org/10.3390/biomimetics6020023
Chicago/Turabian StyleNave, Gary K., Jr., Nathaniel Hall, Katrina Somers, Brock Davis, Hope Gruszewski, Craig Powers, Michael Collver, David G. Schmale, III, and Shane D. Ross. 2021. "Wind Dispersal of Natural and Biomimetic Maple Samaras" Biomimetics 6, no. 2: 23. https://doi.org/10.3390/biomimetics6020023
APA StyleNave, G. K., Jr., Hall, N., Somers, K., Davis, B., Gruszewski, H., Powers, C., Collver, M., Schmale, D. G., III, & Ross, S. D. (2021). Wind Dispersal of Natural and Biomimetic Maple Samaras. Biomimetics, 6(2), 23. https://doi.org/10.3390/biomimetics6020023







