An Enhanced Snow Geese Optimizer Integrating Multiple Strategies for Numerical Optimization
Abstract
1. Introduction
1.1. Research Background
1.2. Contribution of the Work
1.3. Section Arrangement
2. Literature Review
3. The Basic SGA
3.1. Inspiration Source
3.2. Initialization Phase
3.3. Exploration Phase
3.4. Exploitation Phase
4. The Proposed ESGA
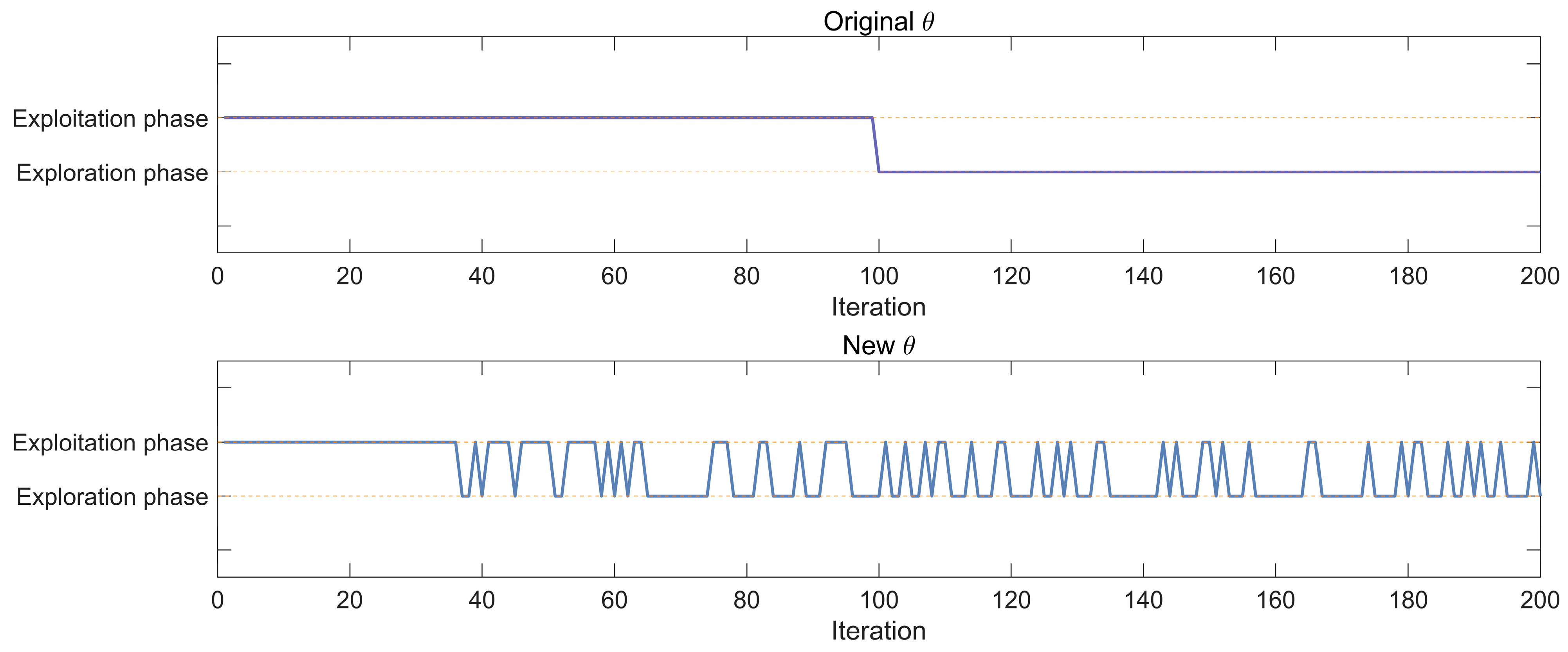
4.1. Adaptive Switching Strategy (ASS)
4.2. Dominant Group Guidance Strategy (DGS)
4.3. Dominant Stochastic Difference Search Strategy (DSS)
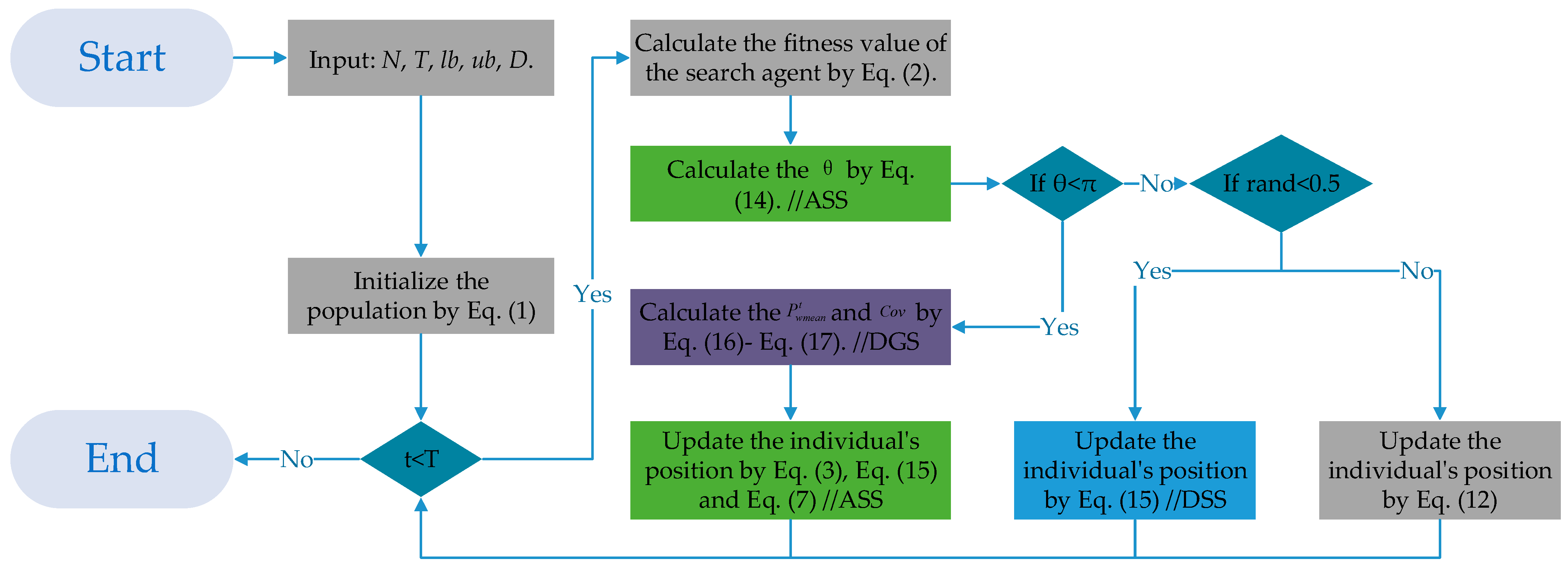
4.4. The Framework of the ESGA
| Algorithm 1: Pseudo-Code of ESGA |
| Input: N, T, lb, ub, D. Initialize the population using Equation (1). FOR t = 1: T Calculate the fitness value of the search agent using Equation (2). Calculate the θ using Equation (14). //ASS IF Calculate the and using Equations (16) and (17). //DGS Update the individual’s position using Equations (3), (7), and (15). ELSE IF rand < 0.5 Update the individual’s position using Equation (18). //DSS ELSE Update the individual’s position using Equation (12). END IF END IF END FOR Output: The best position and the best fitness. |
4.5. Complexity Analysis of the ESGA
5. Experimental Results and Analysis
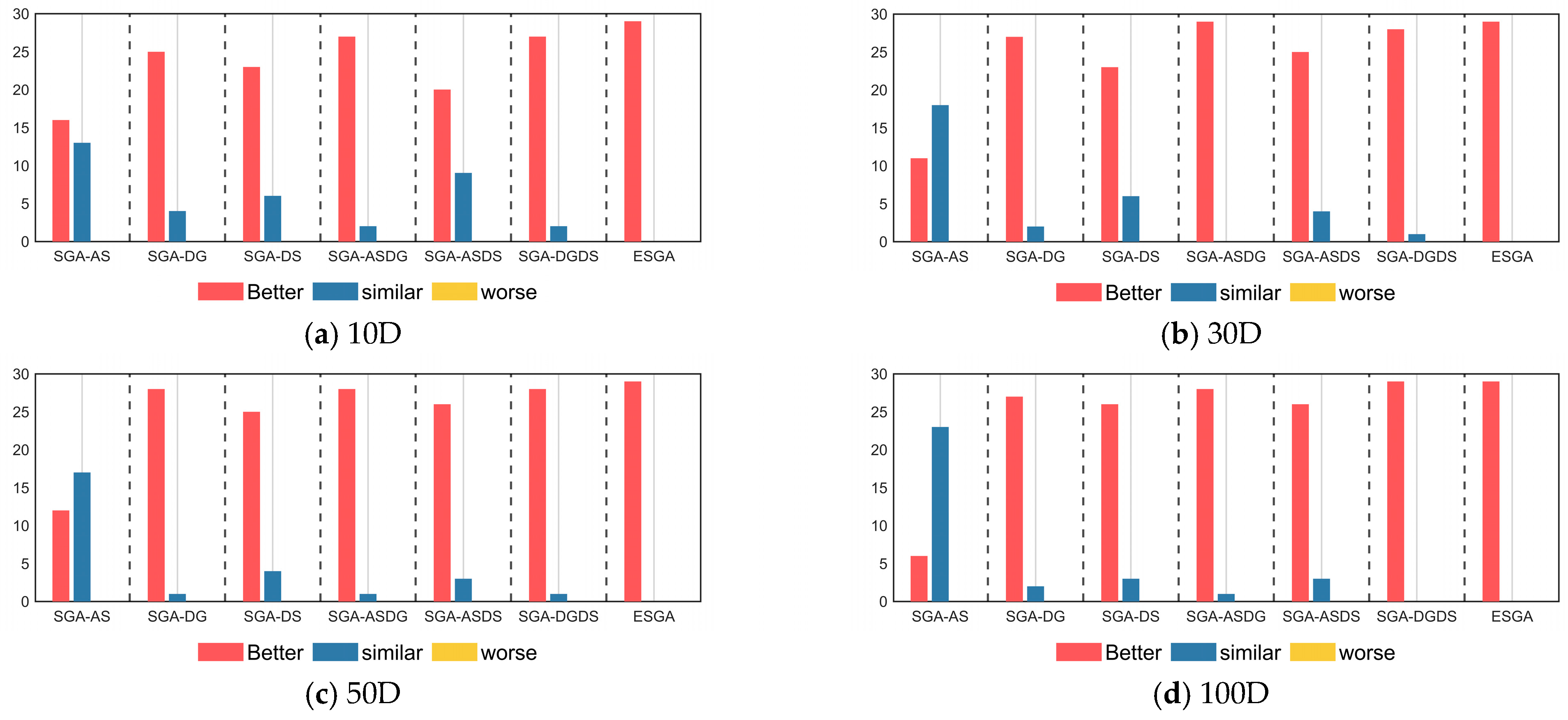
5.1. Ablation Experiments Using the CEC2017 Test Set
5.2. Comparison Test Using the CEC2022 Test Suite
5.3. Comparison Test Using Robot Path Planning
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Slowik, A.; Kwasnicka, H. Nature Inspired Methods and Their Industry Applications-Swarm Intelligence Algorithms. IEEE Trans. Ind. Inform. 2018, 14, 1004–1015. [Google Scholar] [CrossRef]
- Tang, A.D.; Han, T.; Zhou, H.; Xie, L. An Improved Equilibrium Optimizer with Application in Unmanned Aerial Vehicle Path Planning. Sensors 2021, 21, 1814. [Google Scholar] [CrossRef]
- Hu, G.; Huang, F.Y.; Shu, B.; Wei, G. MAHACO: Multi-Algorithm Hybrid Ant Colony Optimizer for 3D Path Planning of a Group of UAVs. Inf. Sci. 2025, 694, 121714. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Hu, G.; Shehadeh, H.A.; Wang, X.P.; Canatalay, P.J. V-Shaped and S-Shaped Binary Artificial Protozoa Optimizer (APO) Algorithm for Wrapper Feature Selection on Biological Data. Clust. Comput. J. Netw. Softw. Tools Appl. 2025, 28, 163. [Google Scholar] [CrossRef]
- Jia, H.; Sun, K.; Li, Y.; Cao, N. Improved Marine Predators Algorithm for Feature Selection and SVM Optimization. KSII Trans. Internet Inf. Syst. 2022, 16, 1128–1145. [Google Scholar] [CrossRef]
- Abualigah, L.; Habash, M.; Hanandeh, E.S.; Hussein, A.M.A.; Al Shinwan, M.; Zitar, R.A.; Jia, H. Improved Reptile Search Algorithm by Salp Swarm Algorithm for Medical Image Segmentation. J. Bionic Eng. 2023, 20, 1766–1790. [Google Scholar] [CrossRef]
- Hu, G.; Zheng, Y.X.; Houssein, E.H.; Wei, G. GSRPSO: A Multi-Strategy Integrated Particle Swarm Algorithm for Multi-Threshold Segmentation of Real Cervical Cancer Images. Swarm Evol. Comput. 2024, 91, 101766. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Huang, W.; Xu, J. Particle Swarm Optimization. In Springer Tracts in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.-R.; Han, B.; Tang, A. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.F.; Liu, D.; Chen, J.D.; He, L. Secretary Bird Optimization Algorithm: A New Metaheuristic for Solving Global Optimization Problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Spider Wasp Optimizer: A Novel Meta-Heuristic Optimization Algorithm. Artif. Intell. Rev. 2023, 56, 11675–11738. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf Mongoose Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Aribowo, W. A Novel Improved Sea-Horse Optimizer for Tuning Parameter Power System Stabilizer. J. Robot. Control 2023, 4, 12–22. [Google Scholar] [CrossRef]
- Jia, H.; Rao, H.; Wen, C.; Mirjalili, S. Crayfish Optimization Algorithm. Artif. Intell. Rev. 2023, 56, 1919–1979. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar Lights Optimizer: Algorithm and Applications in Image Segmentation and Feature Selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry Gas Solubility Optimization: A Novel Physics-Based Algorithm. Futur. Gener. Comput. Syst. Int. J. Escience 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Tian, A.Q.; Liu, F.F.; Lv, H.X. Snow Geese Algorithm: A Novel Migration-Inspired Meta-Heuristic Algorithm for Constrained Engineering Optimization Problems. Appl. Math. Model. 2024, 126, 327–347. [Google Scholar] [CrossRef]
- Wu, J.; Yang, Z.-J.; Du, Z.-G.; Tian, A.-Q. Surrogate-Assisted Multi-Objective Snow Goose Algorithm with Gaussian Process for Cold Chain Logistics. IEEE Access 2025, 13, 67350–67365. [Google Scholar] [CrossRef]
- Chandrashekhar, A.; Mallikarjuna, B.; Thiyagesan, M.; Umasankar, L.; Ezhil, G.; Devi, R. Dual-Stage Interleaved On-Board Charger for Electric Vehicle Using Snow Geese Algorithm. In Proceedings of the 2025 4th International Conference on Sentiment Analysis and Deep Learning (ICSADL), Birendranagar, Nepal, 18–20 February 2025; pp. 628–633. [Google Scholar]
- Bian, H.; Li, C.; Liu, Y.; Tong, Y.; Bing, S.; Chen, J.; Ren, Q.; Zhang, Z. Improved Snow Geese Algorithm for Engineering Applications and Clustering Optimization. Sci. Rep. 2025, 15, 4506. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Zhang, Z.; Wang, L. Manta Ray Foraging Optimization: An Effective Bio-Inspired Optimizer for Engineering Applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-Heuristic Algorithm for Global Optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A Physics-Based Optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Jia, H.; Lu, C. Guided Learning Strategy: A Novel Update Mechanism for Metaheuristic Algorithms Design and Improvement. Knowl.-Based Syst. 2024, 286, 111402. [Google Scholar] [CrossRef]
- Yin, S.; Luo, Q.; Zhou, Y. EOSMA: An Equilibrium Optimizer Slime Mould Algorithm for Engineering Design Problems. Arab. J. Sci. Eng. 2022, 47, 10115–10146. [Google Scholar] [CrossRef]
- Ozkaya, B.; Duman, S.; Kahraman, H.T.; Guvenc, U. Optimal Solution of the Combined Heat and Power Economic Dispatch Problem by Adaptive Fitness-Distance Balance Based Artificial Rabbits Optimization Algorithm. Expert Syst. Appl. 2024, 238, 122272. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the Search Performance of SHADE Using Linear Population Size Reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation, CEC 2014, Beijing, China, 6–11 July 2014. [Google Scholar]




| Algorithm | Parameter Settings |
|---|---|
| ESGA | No parameter |
| SGA | No parameter |
| MRFO | |
| DBO | |
| EO | |
| RIME | |
| GLS-MPA | |
| EOSMA | |
| AFDB-ARO | |
| LSHADE |
| Strategy | SGA | SGA-AS | SGA-DG | SGA-DS | SGA-ASDG | SGA-ASDS | SGA-DGDS | ESGA |
|---|---|---|---|---|---|---|---|---|
| ASS | N | Y | N | N | Y | Y | N | Y |
| DGS | N | N | Y | N | Y | N | Y | Y |
| DSS | N | N | N | Y | N | Y | Y | Y |
| Algorithm | SGA | SGA-AS | SGA-DG | SGA-DS | SGA-ASDG | SGA-ASDS | SGA-DGDS | ESGA | p-Value |
|---|---|---|---|---|---|---|---|---|---|
| 10D | 7.897 | 6.724 | 4.000 | 5.517 | 2.793 | 5.103 | 2.483 | 1.483 | 2.35 × 10−32 |
| 30D | 7.931 | 6.724 | 4.103 | 5.690 | 3.069 | 4.862 | 2.483 | 1.138 | 5.20 × 10−34 |
| 50D | 7.828 | 6.552 | 4.517 | 5.828 | 3.034 | 4.828 | 2.276 | 1.138 | 1.03 × 10−33 |
| 100D | 7.793 | 6.966 | 4.552 | 5.552 | 3.034 | 4.483 | 2.621 | 1.000 | 3.93 × 10−34 |
| Average ranking | 7.862 | 6.741 | 4.293 | 5.647 | 2.983 | 4.819 | 2.466 | 1.190 |
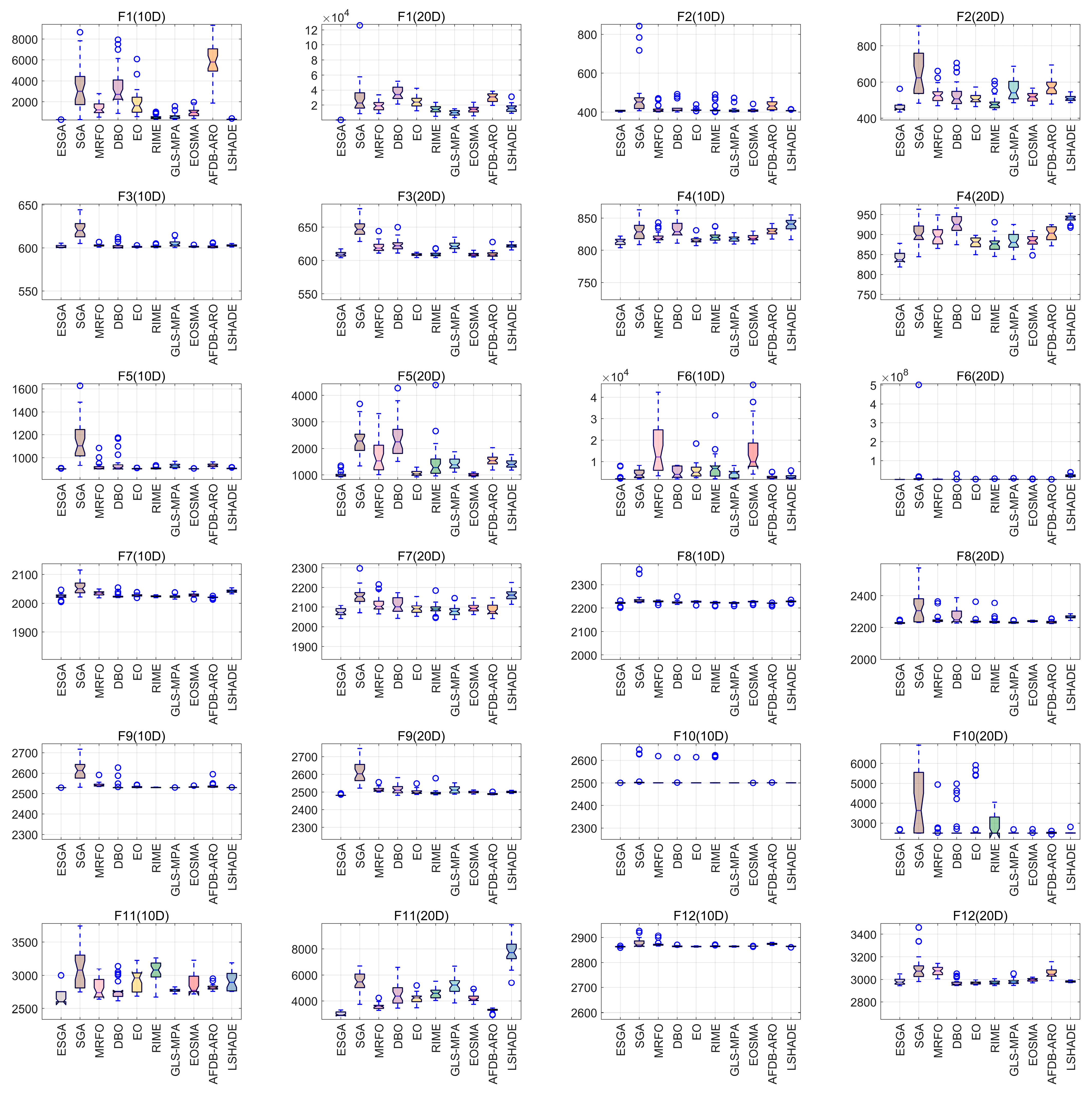
| Function No. | Indicators | ESGA | SGA | MRFO | DBO | EO | RIME | GLS-MPA | EOSMA | AFDB-ARO | LSHADE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Min | 3.000 × 102 | 3.070 × 102 | 5.305 × 102 | 8.887 × 102 | 5.782 × 102 | 3.451 × 102 | 3.200 × 102 | 4.084 × 102 | 1.871 × 103 | 3.082 × 102 |
| Avg | 3.000 × 102 | 3.392 × 103 | 1.386 × 103 | 3.389 × 103 | 1.911 × 103 | 5.214 × 102 | 6.268 × 102 | 1.006 × 103 | 5.840 × 103 | 3.375 × 102 | |
| Std | 7.029 × 10−4 | 2.138 × 103 | 6.118 × 102 | 1.749 × 103 | 1.204 × 103 | 1.705 × 102 | 2.678 × 102 | 3.938 × 102 | 1.664 × 103 | 2.625 × 101 | |
| F2 | Min | 4.000 × 102 | 4.071 × 102 | 4.007 × 102 | 4.006 × 102 | 4.049 × 102 | 4.006 × 102 | 4.005 × 102 | 4.012 × 102 | 4.071 × 102 | 4.055 × 102 |
| Avg | 4.063 × 102 | 4.776 × 102 | 4.167 × 102 | 4.192 × 102 | 4.106 × 102 | 4.179 × 102 | 4.105 × 102 | 4.091 × 102 | 4.344 × 102 | 4.075 × 102 | |
| Std | 3.074 | 1.074 × 102 | 2.188 × 101 | 2.443 × 101 | 5.795 | 2.443 × 101 | 1.498 × 101 | 7.239 | 2.319 × 101 | 1.850 | |
| F3 | Min | 6.002 × 102 | 6.052 × 102 | 6.009 × 102 | 6.000 × 102 | 6.005 × 102 | 6.003 × 102 | 6.004 × 102 | 6.006 × 102 | 6.001 × 102 | 6.012 × 102 |
| Avg | 6.017 × 102 | 6.223 × 102 | 6.030 × 102 | 6.022 × 102 | 6.014 × 102 | 6.018 × 102 | 6.047 × 102 | 6.015 × 102 | 6.018 × 102 | 6.030 × 102 | |
| Std | 1.559 | 1.118 × 101 | 1.133 | 3.149 | 6.195 × 10−1 | 1.180 | 3.299 | 5.912 × 10−1 | 1.643 | 1.012 | |
| F4 | Min | 8.040 × 102 | 8.087 × 102 | 8.119 × 102 | 8.110 × 102 | 8.071 × 102 | 8.112 × 102 | 8.096 × 102 | 8.101 × 102 | 8.173 × 102 | 8.164 × 102 |
| Avg | 8.133 × 102 | 8.286 × 102 | 8.204 × 102 | 8.325 × 102 | 8.151 × 102 | 8.211 × 102 | 8.176 × 102 | 8.191 × 102 | 8.298 × 102 | 8.392 × 102 | |
| Std | 4.648 | 1.318 × 101 | 7.453 | 1.266 × 101 | 4.274 | 7.373 | 4.921 | 5.345 | 6.382 | 8.848 | |
| F5 | Min | 9.000 × 102 | 9.321 × 102 | 9.004 × 102 | 9.001 × 102 | 9.002 × 102 | 9.004 × 102 | 9.031 × 102 | 9.003 × 102 | 9.053 × 102 | 9.017 × 102 |
| Avg | 9.014 × 102 | 1.150 × 103 | 9.192 × 102 | 9.411 × 102 | 9.026 × 102 | 9.065 × 102 | 9.289 × 102 | 9.017 × 102 | 9.332 × 102 | 9.052 × 102 | |
| Std | 1.963 | 1.836 × 102 | 3.745 × 101 | 7.505 × 101 | 2.545 | 7.311 | 1.850 × 101 | 1.296 | 1.561 × 101 | 3.665 | |
| F6 | Min | 1.823 × 103 | 1.918 × 103 | 3.286 × 103 | 1.854 × 103 | 2.467 × 103 | 1.961 × 103 | 1.927 × 103 | 4.052 × 103 | 1.938 × 103 | 1.967 × 103 |
| Avg | 2.310 × 103 | 4.313 × 103 | 1.625 × 104 | 4.727 × 103 | 5.655 × 103 | 6.930 × 103 | 4.112 × 103 | 1.415 × 104 | 2.723 × 103 | 2.780 × 103 | |
| Std | 1.523 × 103 | 2.136 × 103 | 1.116 × 104 | 2.430 × 103 | 3.213 × 103 | 5.722 × 103 | 1.823 × 103 | 1.026 × 104 | 7.638 × 102 | 8.892 × 102 | |
| F7 | Min | 2.005 × 103 | 2.022 × 103 | 2.019 × 103 | 2.020 × 103 | 2.019 × 103 | 2.020 × 103 | 2.015 × 103 | 2.014 × 103 | 2.013 × 103 | 2.033 × 103 |
| Avg | 2.024 × 103 | 2.053 × 103 | 2.035 × 103 | 2.025 × 103 | 2.028 × 103 | 2.025 × 103 | 2.024 × 103 | 2.029 × 103 | 2.021 × 103 | 2.042 × 103 | |
| Std | 8.270 | 2.089 × 101 | 7.063 | 6.855 | 4.085 | 2.417 | 4.570 | 5.459 | 2.260 | 4.909 | |
| F8 | Min | 2.201 × 103 | 2.223 × 103 | 2.213 × 103 | 2.217 × 103 | 2.211 × 103 | 2.208 × 103 | 2.208 × 103 | 2.213 × 103 | 2.208 × 103 | 2.219 × 103 |
| Avg | 2.221 × 103 | 2.240 × 103 | 2.229 × 103 | 2.226 × 103 | 2.227 × 103 | 2.223 × 103 | 2.222 × 103 | 2.227 × 103 | 2.221 × 103 | 2.229 × 103 | |
| Std | 7.912 | 3.216 × 101 | 3.878 | 6.005 | 4.715 | 4.884 | 4.170 | 4.311 | 3.269 | 3.454 | |
| F9 | Min | 2.529 × 103 | 2.531 × 103 | 2.535 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.529 × 103 | 2.530 × 103 | 2.531 × 103 | 2.529 × 103 |
| Avg | 2.529 × 103 | 2.609 × 103 | 2.543 × 103 | 2.536 × 103 | 2.533 × 103 | 2.530 × 103 | 2.530 × 103 | 2.532 × 103 | 2.537 × 103 | 2.530 × 103 | |
| Std | 4.266 × 10−6 | 4.869 × 101 | 1.075 × 101 | 2.070 × 101 | 3.982 | 7.675 × 10−1 | 2.613 × 10−1 | 1.723 | 1.206 × 101 | 3.058 × 10−1 | |
| F10 | Min | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.500 × 103 | 2.501 × 103 | 2.500 × 103 |
| Avg | 2.500 × 103 | 2.519 × 103 | 2.505 × 103 | 2.505 × 103 | 2.504 × 103 | 2.516 × 103 | 2.501 × 103 | 2.500 × 103 | 2.501 × 103 | 2.501 × 103 | |
| Std | 9.063 × 10−2 | 4.564 × 101 | 2.156 × 101 | 2.046 × 101 | 2.070 × 101 | 4.055 × 101 | 1.060 × 10−1 | 9.232 × 10−2 | 3.713 × 10−1 | 1.455 × 10−1 | |
| F11 | Min | 2.600 × 103 | 2.747 × 103 | 2.639 × 103 | 2.615 × 103 | 2.685 × 103 | 2.671 × 103 | 2.719 × 103 | 2.718 × 103 | 2.756 × 103 | 2.754 × 103 |
| Avg | 2.657 × 103 | 3.111 × 103 | 2.780 × 103 | 2.765 × 103 | 2.915 × 103 | 3.043 × 103 | 2.771 × 103 | 2.863 × 103 | 2.816 × 103 | 2.902 × 103 | |
| Std | 1.113 × 102 | 2.998 × 102 | 1.394 × 102 | 1.296 × 102 | 1.597 × 102 | 1.728 × 102 | 1.916 × 101 | 1.393 × 102 | 4.159 × 101 | 1.422 × 102 | |
| F12 | Min | 2.860 × 103 | 2.864 × 103 | 2.866 × 103 | 2.862 × 103 | 2.862 × 103 | 2.862 × 103 | 2.861 × 103 | 2.863 × 103 | 2.868 × 103 | 2.861 × 103 |
| Avg | 2.863 × 103 | 2.878 × 103 | 2.873 × 103 | 2.865 × 103 | 2.864 × 103 | 2.865 × 103 | 2.864 × 103 | 2.865 × 103 | 2.874 × 103 | 2.864 × 103 | |
| Std | 1.405 | 1.806 × 101 | 8.931 | 1.999 | 1.150 | 2.214 | 1.319 | 5.491 × 10−1 | 2.982 | 9.318 × 10−1 |
| Function No. | Indicators | ESGA | SGA | MRFO | DBO | EO | RIME | GLS-MPA | EOSMA | AFDB-ARO | LSHADE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Min | 3.000 × 102 | 8.507 × 103 | 8.784 × 103 | 2.124 × 104 | 1.236 × 104 | 4.966 × 103 | 3.331 × 103 | 5.645 × 103 | 1.956 × 104 | 9.058 × 103 |
| Avg | 3.018 × 102 | 2.848 × 104 | 1.980 × 104 | 3.545 × 104 | 2.471 × 104 | 1.426 × 104 | 9.735 × 103 | 1.433 × 104 | 2.959 × 104 | 1.615 × 104 | |
| Std | 3.173 | 2.217 × 104 | 7.099 × 103 | 8.568 × 103 | 8.166 × 103 | 5.125 × 103 | 3.136 × 103 | 4.159 × 103 | 5.669 × 103 | 5.017 × 103 | |
| F2 | Min | 4.339 × 102 | 4.827 × 102 | 4.688 × 102 | 4.503 × 102 | 4.639 × 102 | 4.472 × 102 | 4.857 × 102 | 4.702 × 102 | 4.779 × 102 | 4.858 × 102 |
| Avg | 4.591 × 102 | 6.565 × 102 | 5.324 × 102 | 5.256 × 102 | 5.092 × 102 | 4.847 × 102 | 5.525 × 102 | 5.175 × 102 | 5.681 × 102 | 5.090 × 102 | |
| Std | 2.314 × 101 | 1.281 × 102 | 4.543 × 101 | 6.388 × 101 | 2.756 × 101 | 3.958 × 101 | 5.234 × 101 | 2.601 × 101 | 5.195 × 101 | 1.481 × 101 | |
| F3 | Min | 6.043 × 102 | 6.283 × 102 | 6.110 × 102 | 6.111 × 102 | 6.044 × 102 | 6.045 × 102 | 6.120 × 102 | 6.053 × 102 | 6.014 × 102 | 6.157 × 102 |
| Avg | 6.097 × 102 | 6.477 × 102 | 6.201 × 102 | 6.231 × 102 | 6.088 × 102 | 6.095 × 102 | 6.221 × 102 | 6.092 × 102 | 6.092 × 102 | 6.216 × 102 | |
| Std | 3.426 | 1.186 × 101 | 6.920 | 8.136 | 1.845 | 3.255 | 5.900 | 2.558 | 4.739 | 2.532 | |
| F4 | Min | 8.189 × 102 | 8.445 × 102 | 8.650 × 102 | 8.743 × 102 | 8.497 × 102 | 8.453 × 102 | 8.379 × 102 | 8.479 × 102 | 8.715 × 102 | 9.178 × 102 |
| Avg | 8.415 × 102 | 9.023 × 102 | 8.961 × 102 | 9.244 × 102 | 8.801 × 102 | 8.759 × 102 | 8.827 × 102 | 8.844 × 102 | 9.027 × 102 | 9.402 × 102 | |
| Std | 1.471 × 101 | 2.520 × 101 | 2.191 × 101 | 2.625 × 101 | 1.227 × 101 | 1.900 × 101 | 2.326 × 101 | 1.394 × 101 | 1.714 × 101 | 9.359 | |
| F5 | Min | 9.276 × 102 | 1.339 × 103 | 1.010 × 103 | 1.517 × 103 | 9.275 × 102 | 9.626 × 102 | 1.104 × 103 | 9.278 × 102 | 1.184 × 103 | 1.182 × 103 |
| Avg | 1.009 × 103 | 2.314 × 103 | 1.722 × 103 | 2.340 × 103 | 1.060 × 103 | 1.466 × 103 | 1.431 × 103 | 1.009 × 103 | 1.559 × 103 | 1.409 × 103 | |
| Std | 9.871 × 101 | 5.110 × 102 | 6.378 × 102 | 6.309 × 102 | 9.279 × 101 | 6.769 × 102 | 2.206 × 102 | 4.949 × 101 | 1.928 × 102 | 1.356 × 102 | |
| F6 | Min | 2.030 × 103 | 4.193 × 103 | 1.590 × 105 | 2.311 × 103 | 2.177 × 104 | 1.950 × 104 | 3.438 × 103 | 6.569 × 104 | 2.128 × 104 | 1.145 × 107 |
| Avg | 8.505 × 103 | 1.870 × 107 | 7.970 × 105 | 1.136 × 106 | 3.418 × 105 | 8.791 × 105 | 9.867 × 105 | 5.427 × 105 | 8.254 × 104 | 1.998 × 107 | |
| Std | 6.488 × 103 | 9.124 × 107 | 4.826 × 105 | 5.347 × 106 | 4.088 × 105 | 8.182 × 105 | 1.484 × 106 | 5.766 × 105 | 5.492 × 104 | 7.041 × 106 | |
| F7 | Min | 2.042 × 103 | 2.071 × 103 | 2.066 × 103 | 2.043 × 103 | 2.053 × 103 | 2.046 × 103 | 2.037 × 103 | 2.062 × 103 | 2.042 × 103 | 2.115 × 103 |
| Avg | 2.075 × 103 | 2.155 × 103 | 2.115 × 103 | 2.107 × 103 | 2.092 × 103 | 2.091 × 103 | 2.081 × 103 | 2.098 × 103 | 2.088 × 103 | 2.163 × 103 | |
| Std | 1.853 × 101 | 4.455 × 101 | 3.639 × 101 | 3.628 × 101 | 2.231 × 101 | 2.633 × 101 | 2.515 × 101 | 2.221 × 101 | 3.155 × 101 | 2.599 × 101 | |
| F8 | Min | 2.222 × 103 | 2.231 × 103 | 2.232 × 103 | 2.228 × 103 | 2.229 × 103 | 2.227 × 103 | 2.226 × 103 | 2.233 × 103 | 2.224 × 103 | 2.244 × 103 |
| Avg | 2.230 × 103 | 2.326 × 103 | 2.250 × 103 | 2.273 × 103 | 2.241 × 103 | 2.240 × 103 | 2.231 × 103 | 2.240 × 103 | 2.235 × 103 | 2.264 × 103 | |
| Std | 6.356 | 1.016 × 102 | 2.997 × 101 | 5.373 × 101 | 2.324 × 101 | 2.338 × 101 | 4.586 | 3.342 | 7.858 | 1.002 × 101 | |
| F9 | Min | 2.481 × 103 | 2.522 × 103 | 2.500 × 103 | 2.481 × 103 | 2.486 × 103 | 2.484 × 103 | 2.487 × 103 | 2.488 × 103 | 2.484 × 103 | 2.491 × 103 |
| Avg | 2.482 × 103 | 2.611 × 103 | 2.514 × 103 | 2.512 × 103 | 2.501 × 103 | 2.496 × 103 | 2.513 × 103 | 2.500 × 103 | 2.489 × 103 | 2.501 × 103 | |
| Std | 3.217 | 5.949 × 101 | 1.131 × 101 | 2.430 × 101 | 1.250 × 101 | 1.672 × 101 | 1.944 × 101 | 6.073 | 4.283 | 5.025 | |
| F10 | Min | 2.500 × 103 | 2.501 × 103 | 2.501 × 103 | 2.501 × 103 | 2.501 × 103 | 2.501 × 103 | 2.501 × 103 | 2.501 × 103 | 2.436 × 103 | 2.501 × 103 |
| Avg | 2.519 × 103 | 4.043 × 103 | 2.616 × 103 | 2.798 × 103 | 2.927 × 103 | 2.883 × 103 | 2.510 × 103 | 2.508 × 103 | 2.514 × 103 | 2.518 × 103 | |
| Std | 5.475 × 101 | 1.588 × 103 | 4.473 × 102 | 7.239 × 102 | 1.071 × 103 | 5.248 × 102 | 3.359 × 101 | 3.610 × 101 | 3.864 × 101 | 5.612 × 101 | |
| F11 | Min | 2.902 × 103 | 3.740 × 103 | 3.279 × 103 | 3.447 × 103 | 3.474 × 103 | 4.036 × 103 | 3.847 × 103 | 3.740 × 103 | 2.949 × 103 | 5.395 × 103 |
| Avg | 3.010 × 103 | 5.386 × 103 | 3.587 × 103 | 4.556 × 103 | 4.226 × 103 | 4.570 × 103 | 5.130 × 103 | 4.213 × 103 | 3.299 × 103 | 7.868 × 103 | |
| Std | 1.406 × 102 | 8.346 × 102 | 1.952 × 102 | 9.359 × 102 | 3.311 × 102 | 3.443 × 102 | 6.091 × 102 | 2.878 × 102 | 1.082 × 102 | 1.017 × 103 | |
| F12 | Min | 2.943 × 103 | 2.980 × 103 | 3.006 × 103 | 2.944 × 103 | 2.950 × 103 | 2.944 × 103 | 2.945 × 103 | 2.968 × 103 | 2.988 × 103 | 2.970 × 103 |
| Avg | 2.983 × 103 | 3.102 × 103 | 3.076 × 103 | 2.969 × 103 | 2.967 × 103 | 2.971 × 103 | 2.979 × 103 | 2.996 × 103 | 3.056 × 103 | 2.981 × 103 | |
| Std | 3.126 × 101 | 1.109 × 102 | 3.611 × 101 | 2.934 × 101 | 1.156 × 101 | 1.660 × 101 | 2.264 × 101 | 1.516 × 101 | 4.014 × 101 | 7.135 |
| ESGA vs. +/=/− | SGA | MRFO | DBO | EO | RIME | GLS-MPA | EOSMA | AFDB-ARO | LSHADE |
|---|---|---|---|---|---|---|---|---|---|
| 10D | 12/0/0 | 11/1/0 | 9/3/0 | 9/3/0 | 10/2/0 | 9/3/0 | 11/1/0 | 10/1/1 | 11/1/0 |
| 20D | 12/0/0 | 12/0/0 | 10/2/0 | 10/2/0 | 10/2/0 | 9/2/1 | 9/2/1 | 9/2/1 | 10/1/1 |
| Total | 24/0/0 | 23/1/0 | 19/5/0 | 19/5/0 | 20/4/0 | 18/5/1 | 20/3/1 | 19/3/2 | 21/2/1 |
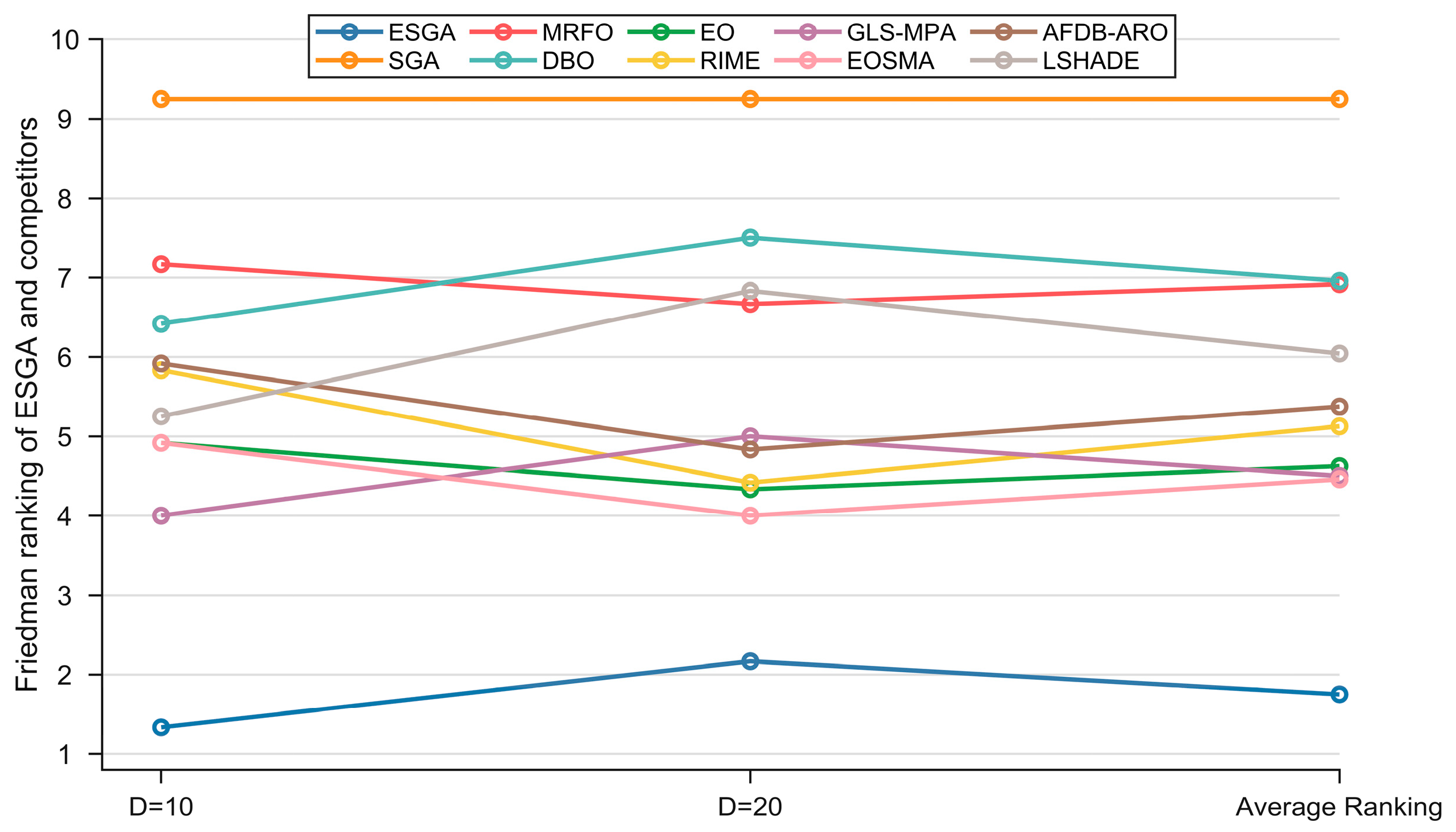
| Algorithm | 10D | 20D | Average Ranking |
|---|---|---|---|
| ESGA | 1.333 | 2.167 | 1.750 |
| SGA | 9.250 | 9.250 | 9.250 |
| MRFO | 7.167 | 6.667 | 6.917 |
| DBO | 6.417 | 7.500 | 6.958 |
| EO | 4.917 | 4.333 | 4.625 |
| RIME | 5.833 | 4.417 | 5.125 |
| GLS-MPA | 4.000 | 5.000 | 4.500 |
| EOSMA | 4.917 | 4.000 | 4.458 |
| AFDB-ARO | 5.917 | 4.833 | 5.375 |
| LSHADE | 5.250 | 6.833 | 6.042 |
| p-value | 1.00 × 10−7 | 1.35 × 10−7 |
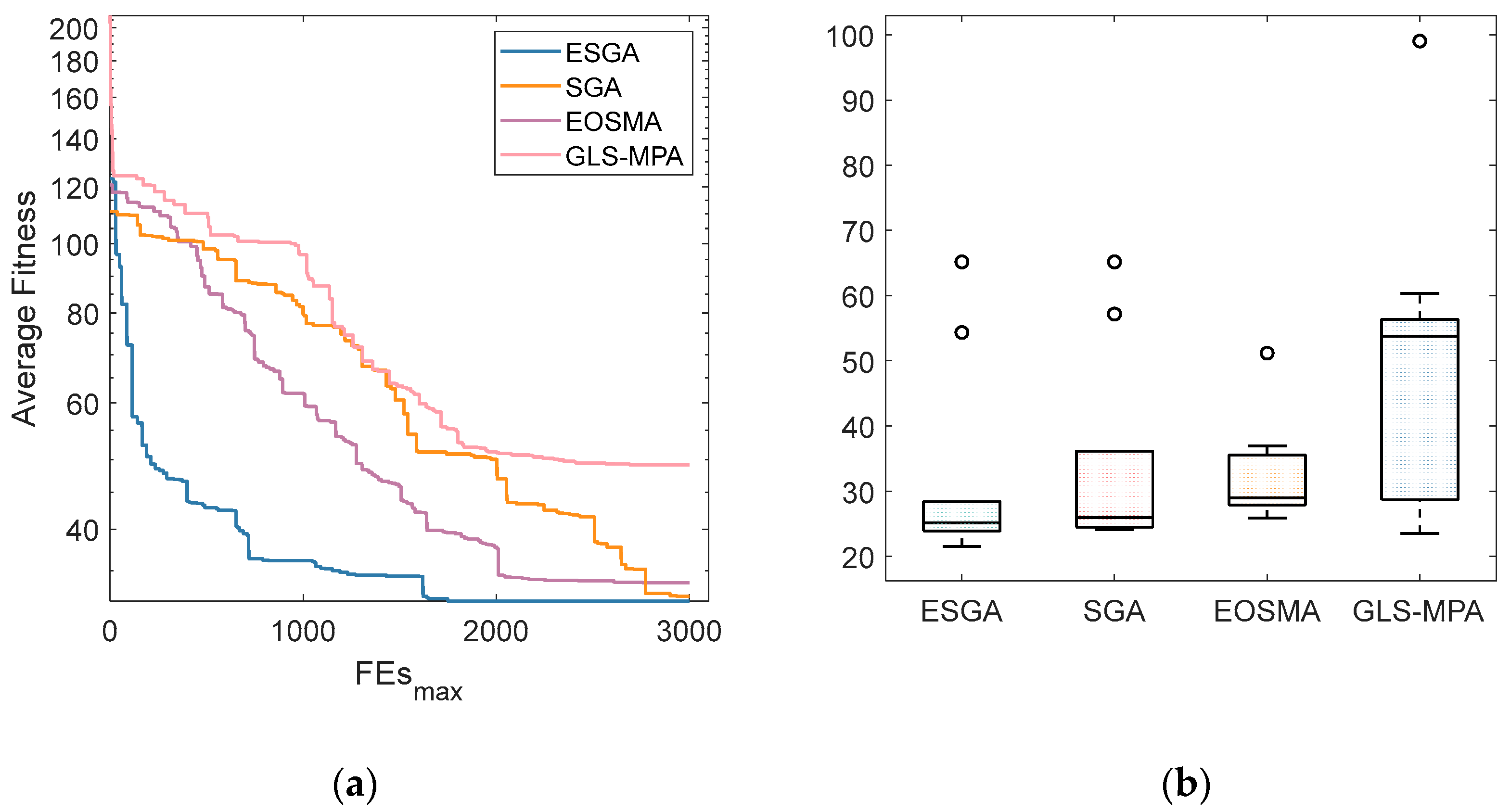
| Index | ESGA | SGA | EOSMA | GLS-MPA |
|---|---|---|---|---|
| Best | 21.56 | 25.90 | 24.14 | 23.56 |
| Avg | 31.78 | 32.26 | 33.70 | 49.18 |
| Std | 15.12 | 7.65 | 15.03 | 22.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Fang, Y.; Chen, T. An Enhanced Snow Geese Optimizer Integrating Multiple Strategies for Numerical Optimization. Biomimetics 2025, 10, 388. https://doi.org/10.3390/biomimetics10060388
Zhao B, Fang Y, Chen T. An Enhanced Snow Geese Optimizer Integrating Multiple Strategies for Numerical Optimization. Biomimetics. 2025; 10(6):388. https://doi.org/10.3390/biomimetics10060388
Chicago/Turabian StyleZhao, Baoqi, Yu Fang, and Tianyi Chen. 2025. "An Enhanced Snow Geese Optimizer Integrating Multiple Strategies for Numerical Optimization" Biomimetics 10, no. 6: 388. https://doi.org/10.3390/biomimetics10060388
APA StyleZhao, B., Fang, Y., & Chen, T. (2025). An Enhanced Snow Geese Optimizer Integrating Multiple Strategies for Numerical Optimization. Biomimetics, 10(6), 388. https://doi.org/10.3390/biomimetics10060388








