A Vector-Based Computational Model of Multimodal Insect Learning Walks
Abstract
1. Introduction
2. Methods
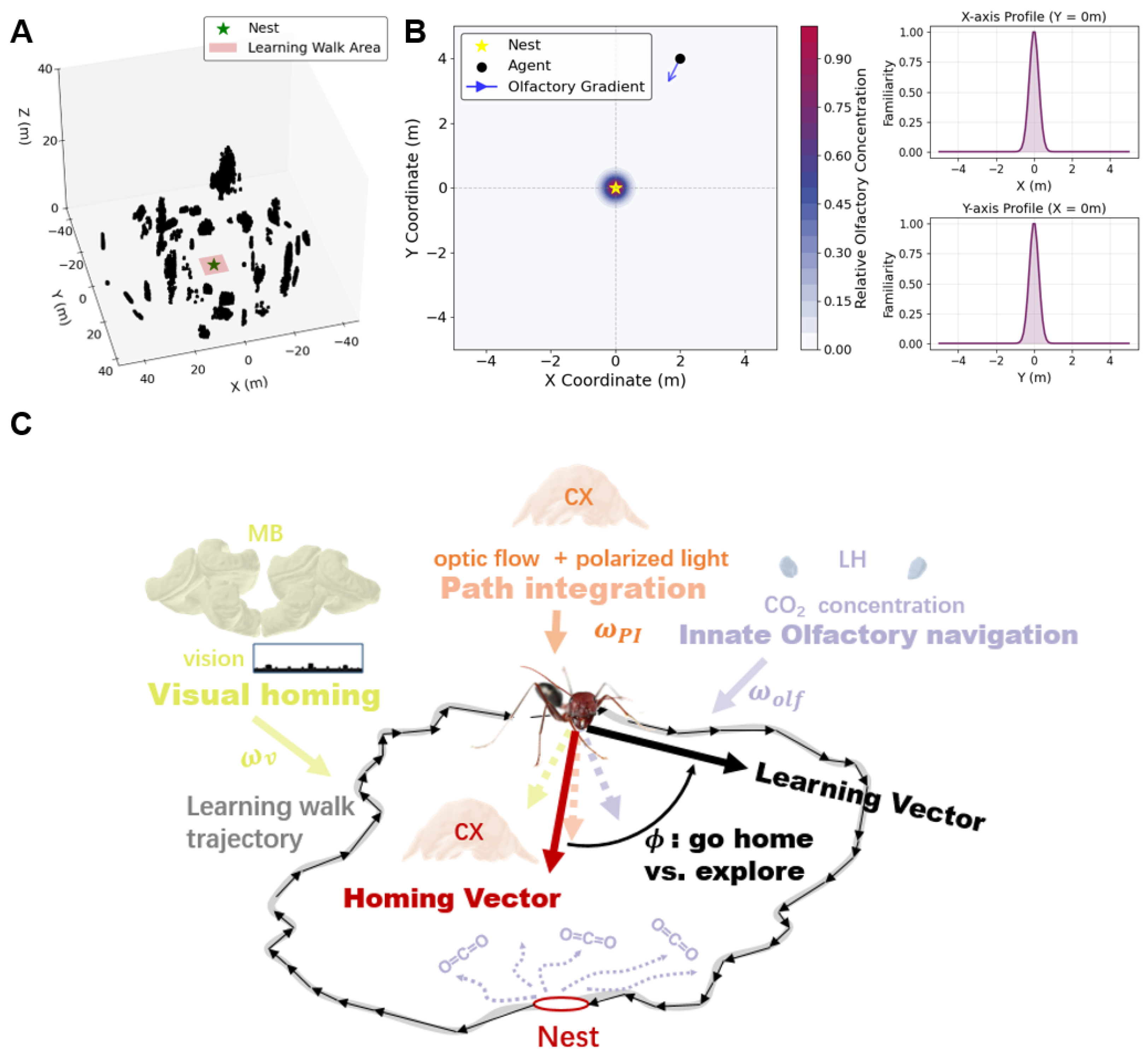
2.1. Environmental Simulation
2.1.1. Visual Environment
2.1.2. Olfactory Field
2.2. Navigation Models
2.2.1. Visual Learning
2.2.2. Olfactory Navigation
2.2.3. Path Integration
2.3. Leaning Vector
2.4. Simulation and Validation
2.4.1. Agent
2.4.2. Validation
2.4.3. Generalizability
3. Results
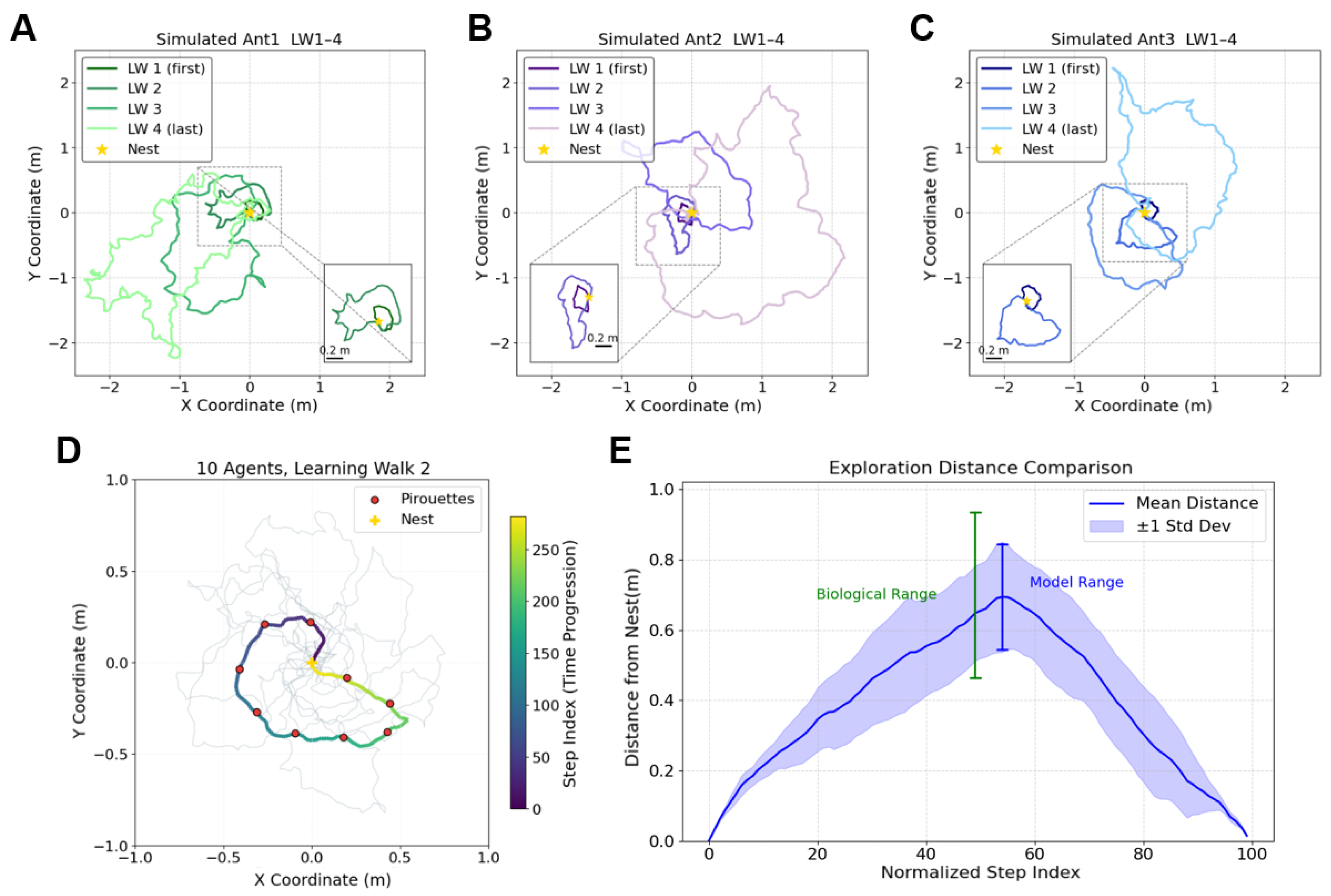
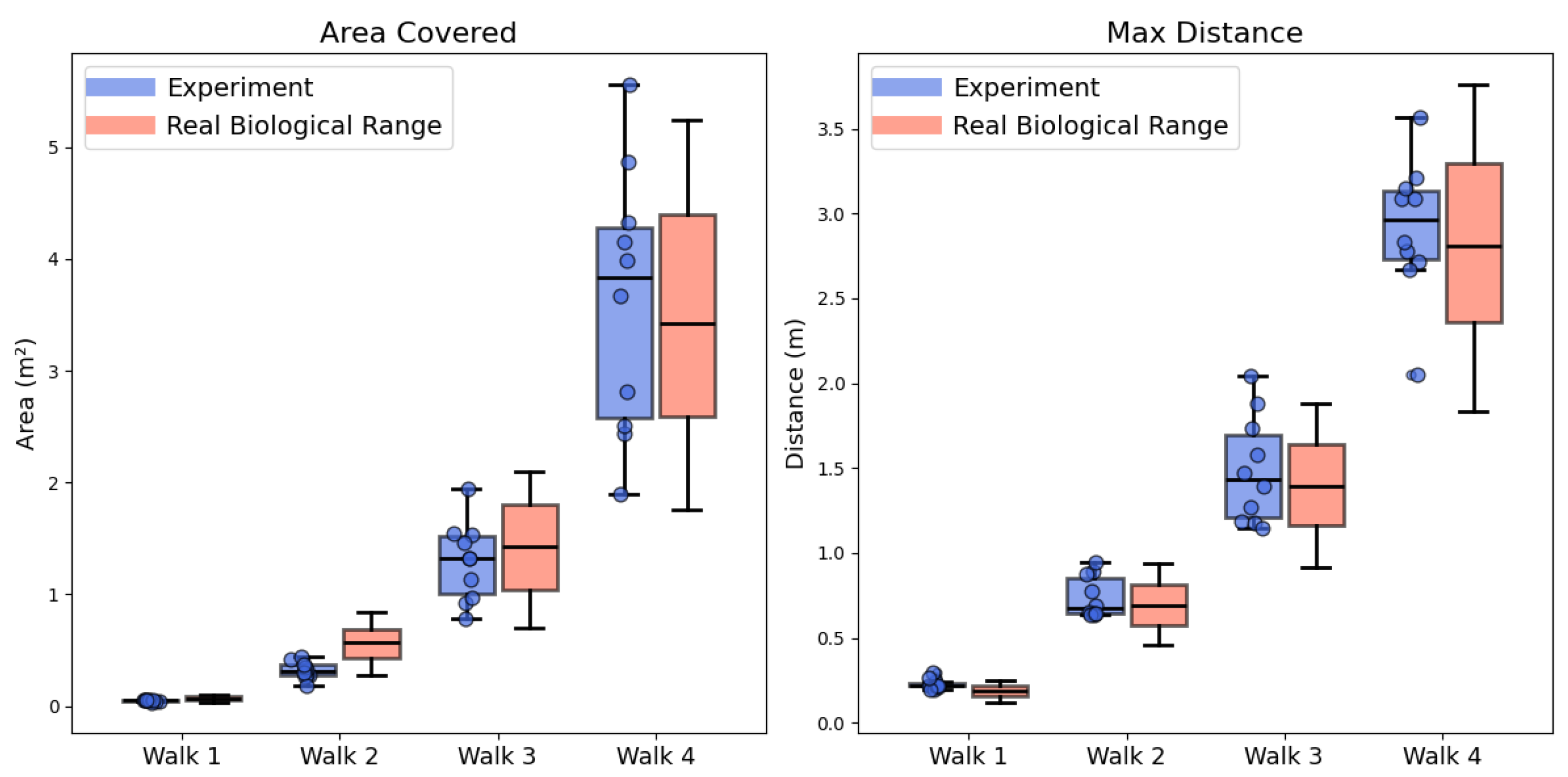
3.1. Replicate the Characteristics of Real Ant’s Learning Walk
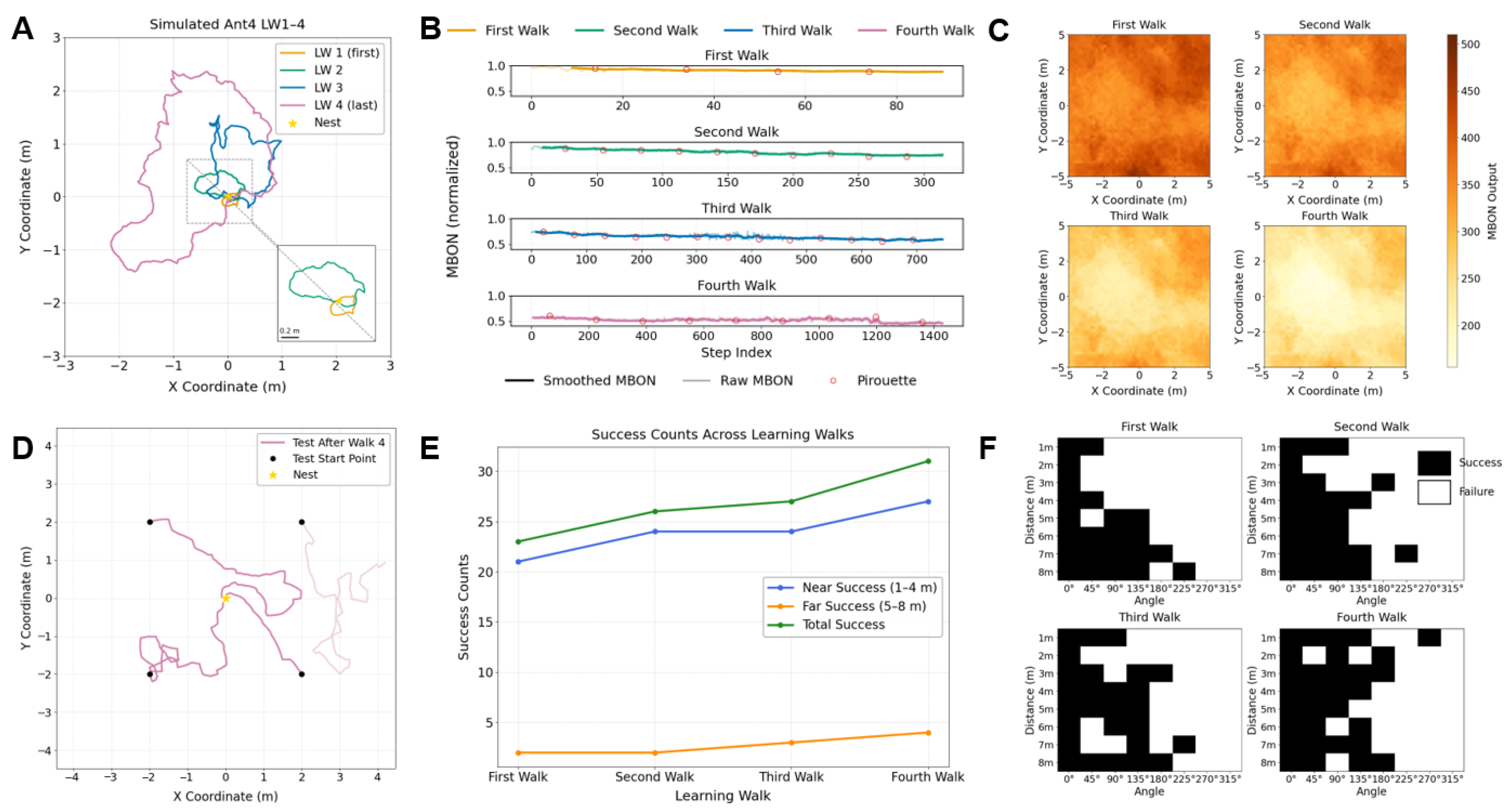
3.2. Evaluate Learning Performance by Visual Homing
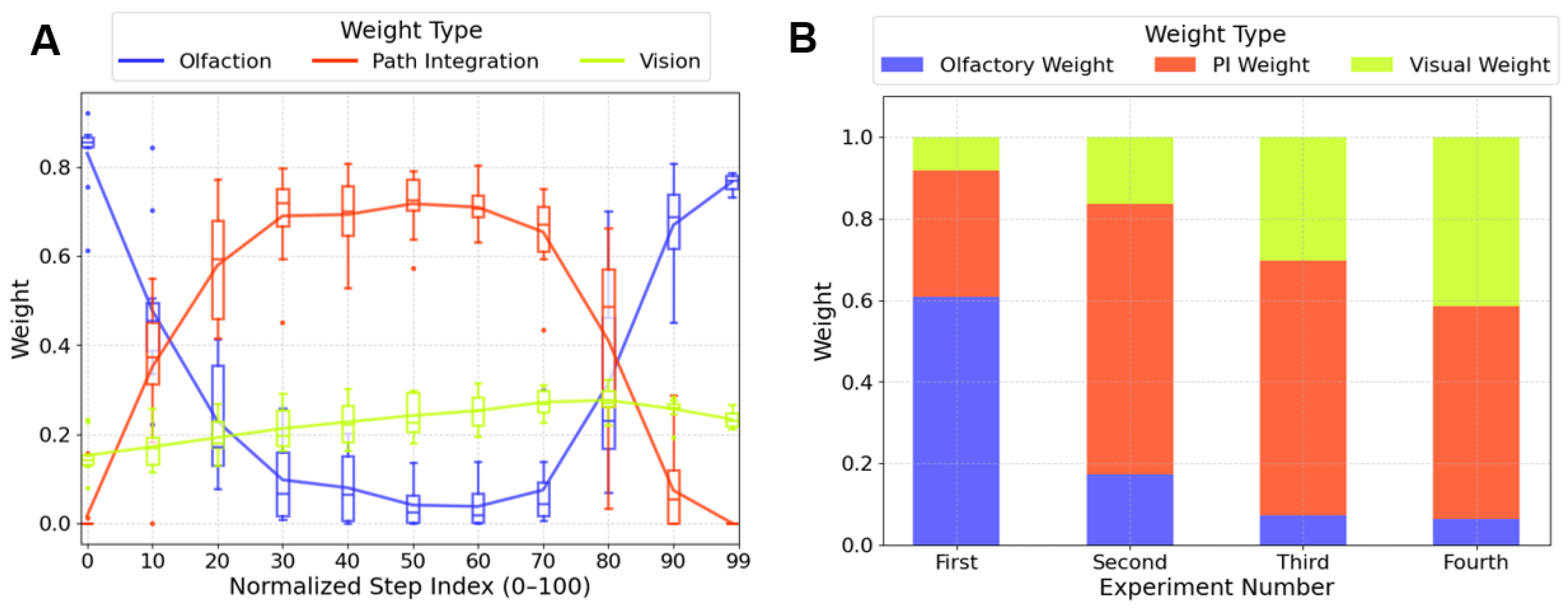
3.3. Adaptive Weighting Could Explain the Navigational Strategy Transition
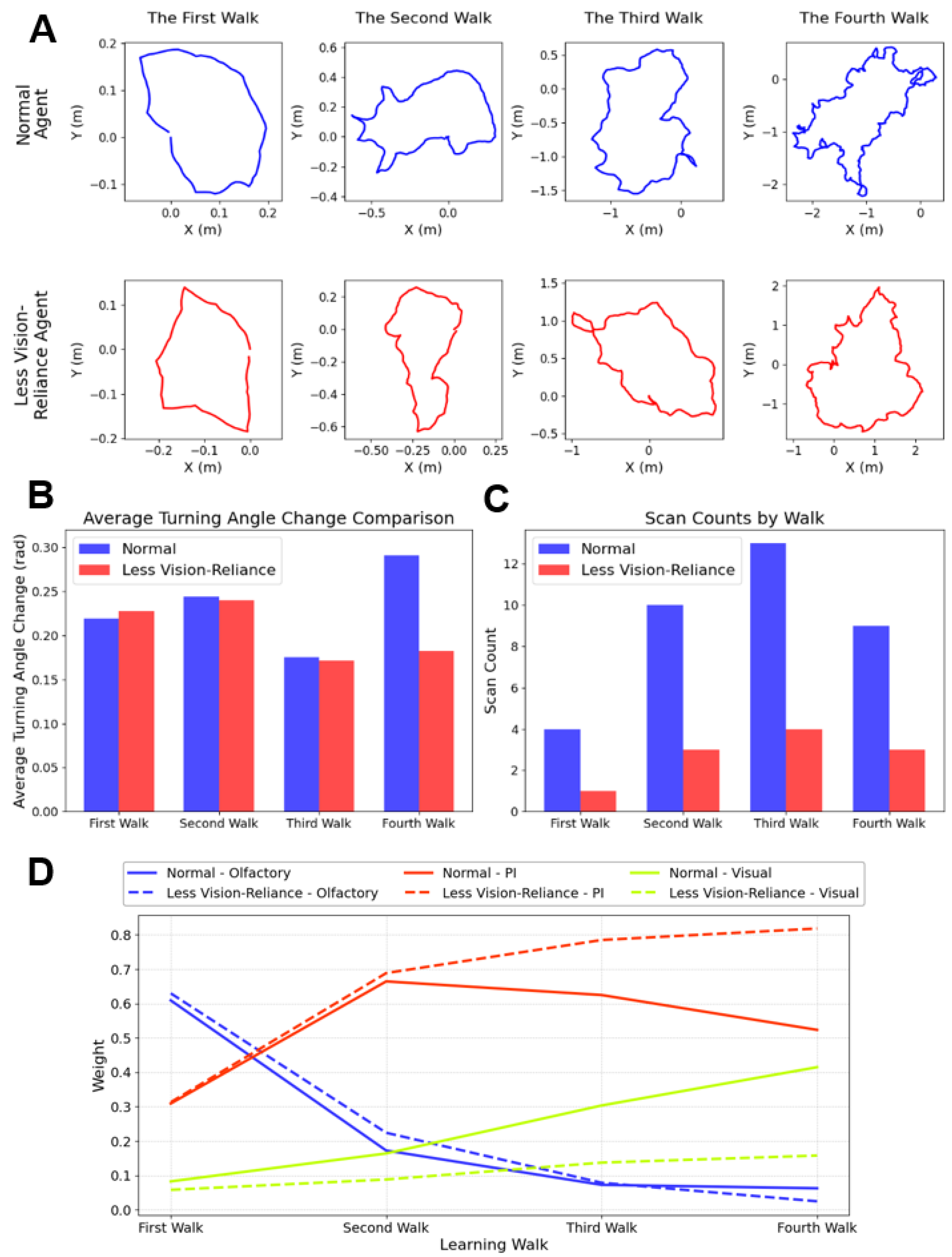
3.4. Account for Species-Specific Behaviour
4. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeffery, K.J. The mosaic structure of the mammalian cognitive map. Learn. Behav. 2024, 52, 19–34. [Google Scholar] [CrossRef] [PubMed]
- Wolf, H. Toward the vector map in insect navigation. Proc. Natl. Acad. Sci. USA 2024, 121, 2413202121. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, P.; Chatterjee, D.; Banerjee, A.; Das, S.S. Do magnetic murmurs guide birds? a directional statistical investigation for influence of earth’s magnetic field on bird navigation. PLoS ONE 2024, 19, e0304279. [Google Scholar] [CrossRef]
- Wehner, R. Large-scale navigation: The insect case. In Spatial Information Theory. Cognitive and Computational Foundations of Geographic Information Science; Freksa, C., Mark, D.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 1–20. [Google Scholar] [CrossRef]
- Wystrach, A.; Graham, P. What can we learn from studies of insect navigation? Anim. Behav. 2012, 84, 13–20. [Google Scholar] [CrossRef]
- Zeil, J.; Fleischmann, P.N. The learning walks of ants (hymenoptera: Formicidae). Myrmecol. News 2019, 29, 93–110. [Google Scholar] [CrossRef]
- Collett, T.S.; Zeil, J. Insect learning flights and walks. Curr. Biol. 2018, 28, R984–R988. [Google Scholar] [CrossRef]
- Fleischmann, P.N.; Christian, M.; Müller, V.L.; Rössler, W.; Wehner, R. Ontogeny of learning walks and the acquisition of land-mark information in desert ants, Cataglyphis fortis. J. Exp. Biol. 2016, 219, 3137–3145. [Google Scholar] [CrossRef]
- Bertrand, O.J.N.; Sonntag, A. The potential underlying mechanisms during learning flights. J. Comp. Physiol. A 2023, 209, 593–604. [Google Scholar] [CrossRef]
- Grah, G.; Ronacher, B. Three-dimensional orientation in desert ants: Context-independent memorisation and recall of sloped path segments. J. Comp. Physiol. A 2008, 194, 517–522. [Google Scholar] [CrossRef]
- Freas, C.A.; Schultheiss, P. How to navigate in different environments and situations: Lessons from ants. Front. Psychol. 2018, 9, 841. [Google Scholar] [CrossRef]
- Wehner, R.; Boyer, M.; Loertscher, F.; Sommer, S.; Menzi, U. Ant navigation: One-way routes rather than maps. Curr. Biol. 2006, 16, 75–79. [Google Scholar] [CrossRef]
- Cheng, K. How to navigate without maps: The power of taxon-like navigation in ants. Comp. Cogn. Behav. Rev. 2012, 7, 1–22. [Google Scholar] [CrossRef]
- Rössler, W.; Grob, R.; Fleischmann, P.N. The role of learning-walk related multisensory experience in rewiring visual circuits in the desert ant brain. J. Comp. Physiol. A 2023, 209, 605–623. [Google Scholar] [CrossRef]
- Müller, M.; Wehner, R. Path integration provides a scaffold for landmark learning in desert ants. Curr. Biol. 2010, 20, 1368–1371. [Google Scholar] [CrossRef] [PubMed]
- Jayatilaka, P.; Murray, T.; Narendra, A.; Zeil, J. The choreography of learning walks in the Australian jack jumper ant Myrmecia croslandi. J. Exp. Biol. 2018, 221, 185306. [Google Scholar] [CrossRef] [PubMed]
- Fleischmann, P.N.; Grob, R.; Wehner, R.; Rössler, W. Species-specific differences in the fine structure of learning walk elements in Cataglyphis ants. J. Exp. Biol. 2017, 220, 2426–2435. [Google Scholar] [CrossRef]
- Nicholson, D.J.; Judd, S.P.D.; Cartwright, B.A.; Collett, T.S. Learning walks and landmark guidance in wood ants (Formica rufa). J. Exp. Biol. 1999, 202, 1831–1838. [Google Scholar] [CrossRef]
- Wystrach, A.; Philippides, A.; Aurejac, A.; Cheng, K.; Graham, P. Visual scanning behaviours and their role in the navigation of the Australian desert ant Melophorus bagoti. J. Comp. Physiol. A 2014, 200, 615–626. [Google Scholar] [CrossRef]
- Grob, R.; Holland Cunz, O.; Grübel, K.; Pfeiffer, K.; Rössler, W.; Fleischmann, P.N. Rotation of skylight polarization during learning walks is necessary to trigger neuronal plasticity in Cataglyphis ants. Proc. R. Soc. B Biol. Sci. 2022, 289, 20212499. [Google Scholar] [CrossRef]
- Fleischmann, P.N.; Rössler, W.; Wehner, R. Early foraging life: Spatial and temporal aspects of landmark learning in the ant Cataglyphis noda. J. Comp. Physiol. A 2018, 204, 579–592. [Google Scholar] [CrossRef]
- Deeti, S.; Cheng, K. Learning walks in an Australian desert ant, Melophorus bagoti. J. Exp. Biol. 2021, 224, 242177. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Yue, S.; Mangan, M. A decentralised neural model explaining optimal integration of navigational strategies in insects. eLife 2020, 9, 54026. [Google Scholar] [CrossRef]
- Stone, T.; Mangan, M.; Wystrach, A.; Webb, B. Rotation invariant visual processing for spatial memory in insects. Interface Focus 2018, 8, 20180010. [Google Scholar] [CrossRef]
- Fleischmann, P.N.; Grob, R.; Müller, V.L.; Wehner, R.; Rössler, W. The geomagnetic field is a compass cue in Cataglyphis ant navigation. Curr. Biol. 2018, 28, 1440–14442. [Google Scholar] [CrossRef]
- Vega Vermehren, J.A.; Buehlmann, C.; Fernandes, A.S.D.; Graham, P. Multimodal influences on learning walks in desert ants (Cataglyphis fortis). J. Comp. Physiol. A 2020, 206, 701–709. [Google Scholar] [CrossRef]
- Stone, T.; Webb, B.; Adden, A.; Weddig, N.B.; Honkanen, A.; Templin, R.; Wcislo, W.; Scimeca, L.; Warrant, E.; Heinze, S. An anatomically constrained model for path integration in the bee brain. Curr. Biol. 2017, 27, 3069–308511. [Google Scholar] [CrossRef]
- Buehlmann, C.; Dell-Cronin, S.; Diyalagoda Pathirannahelage, A.; Goulard, R.; Webb, B.; Niven, J.E.; Graham, P. Impact of central complex lesions on innate and learnt visual navigation in ants. J. Comp. Physiol. A 2023, 209, 737–746. [Google Scholar] [CrossRef]
- Buehlmann, C.; Wozniak, B.; Goulard, R.; Webb, B.; Graham, P.; Niven, J.E. Mushroom bodies are required for learned visual navigation, but not for innate visual behavior, in ants. Curr. Biol. 2020, 30, 3438–34432. [Google Scholar] [CrossRef]
- Le Moël, F.; Stone, T.; Lihoreau, M.; Wystrach, A.; Webb, B. The central complex as a potential substrate for vector based naviga-tion. Front. Psychol. 2019, 10, 690. [Google Scholar] [CrossRef]
- Sun, X.; Yue, S.; Mangan, M. How the insect central complex could coordinate multimodal navigation. eLife 2021, 10, 73077. [Google Scholar] [CrossRef]
- Mussells Pires, P.; Zhang, L.; Parache, V.; Abbott, L.F.; Maimon, G. Converting an allocentric goal into an egocentric steering signal. Nature 2024, 626, 808–818. [Google Scholar] [CrossRef] [PubMed]
- Giurfa, M.; Capaldi, E.A. Vectors, routes and maps: New discoveries about navigation in insects. Trends Neurosci. 1999, 22, 237–242. [Google Scholar] [CrossRef] [PubMed]
- Turner-Evans, D.B.; Jayaraman, V. The insect central complex. Curr. Biol. 2016, 26, 453–457. [Google Scholar] [CrossRef]
- Arganda, S.; Pérez-Escudero, A.; Polavieja, G.G. A common rule for decision making in animal collectives across species. Proc. Natl. Acad. Sci. USA 2012, 109, 20508–20513. [Google Scholar] [CrossRef]
- Cheng, K.; Shettleworth, S.J.; Huttenlocher, J.; Rieser, J.J. Bayesian integration of spatial information. Psychol. Bull. 2007, 133, 625–637. [Google Scholar] [CrossRef]
- Le Möel, F.; Wystrach, A. Opponent processes in visual memories: A model of attraction and repulsion in navigating insects’ mushroom bodies. PLoS Comput. Biol. 2020, 16, e1007631. [Google Scholar] [CrossRef]
- Wystrach, A.; Le Moël, F.; Clement, L.; Schwarz, S. A lateralised design for the interaction of visual memories and heading representations in navigating ants. bioRxiv 2020. [Google Scholar] [CrossRef]
- Wystrach, A. Neurons from pre-motor areas to the mushroom bodies can orchestrate latent visual learning in navigating insects. bioRxiv 2023. [Google Scholar] [CrossRef]
- Goulard, R.; Buehlmann, C.; Niven, J.E.; Graham, P.; Webb, B. A unified mechanism for innate and learned visual landmark guidance in the insect central complex. PLoS Comput. Biol. 2021, 17, e1009383. [Google Scholar] [CrossRef]
- Gaudry, Q.; Hong, E.J.; Kain, J.; Bivort, B.L.; Wilson, R.I. Asymmetric neurotransmitter release enables rapid odour lateralization in drosophila. Nature 2013, 493, 424–428. [Google Scholar] [CrossRef]
- Webb, B. Robots with insect brains. Science 2020, 368, 244–245. [Google Scholar] [CrossRef] [PubMed]
- Manoonpong, P.; Patanè, L.; Xiong, X.; Brodoline, I.; Dupeyroux, J.; Viollet, S.; Arena, P.; Serres, J.R. Insect-inspired robots: Bridging biological and artificial systems. Sensors 2021, 21, 7609. [Google Scholar] [CrossRef]
- Sun, X.; Mangan, M.; Peng, J.; Yue, S. I2bot: An open-source tool for multi-modal and embodied simulation of insect navigation. J. R. Soc. Interface 2025, 22, 20240586. [Google Scholar] [CrossRef]
- Croon, G.C.H.E.; Dupeyroux, J.J.G.; Fuller, S.B.; Marshall, J.A.R. Insect-inspired ai for autonomous robots. Sci. Robot. 2022, 7, eabl6334. [Google Scholar] [CrossRef]
- Steck, K. Just follow your nose: Homing by olfactory cues in ants. Curr. Opin. Neurobiol. 2012, 22, 231–235. [Google Scholar] [CrossRef]
- Steck, K.; Hansson, B.S.; Knaden, M. Smells like home: Desert ants, Cataglyphis fortis, use olfactory landmarks to pinpoint the nest. Front. Zool. 2009, 6, 5. [Google Scholar] [CrossRef]
- Ardin, P.; Peng, F.; Mangan, M.; Lagogiannis, K.; Webb, B. Using an insect mushroom body circuit to encode route memory in complex natural environments. PLoS Comput. Biol. 2016, 12, e1004683. [Google Scholar] [CrossRef]
- Sun, X.; Mangan, M.; Yue, S. An analysis of a ring attractor model for cue integration. In Biomimetic and Biohybrid Systems, Proceedings of the 7th International Conference, Living Machines 2018, Paris, France, 17–20 July 2018; Vouloutsi, V., Halloy, J., Mura, A., Mangan, M., Lepora, N., Prescott, T.J., Verschure, P.F.M.J., Eds.; Springer: Cham, Switzerland, 2018; pp. 459–470. [Google Scholar] [CrossRef]
- Teague, M.R. Image analysis via the general theory of moments*. J. Opt. Soc. Am. 1980, 70, 920–930. [Google Scholar] [CrossRef]
- Khotanzad, A.; Hong, Y.H. Invariant image recognition by zernike moments. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 489–497. [Google Scholar] [CrossRef]
- Freas, C.A.; Cheng, K. Visual learning, route formation and the choreography of looking back in desert ants, Melophorus bagoti. Anim. Behav. 2025, 222, 123125. [Google Scholar] [CrossRef]
- Buehlmann, C.; Mangan, M.; Graham, P. Multimodal interactions in insect navigation. Anim. Cogn. 2020, 23, 1129–1141. [Google Scholar] [CrossRef] [PubMed]
- Zeil, J. Visual homing: An insect perspective. Curr. Opin. Neurobiol. 2012, 22, 285–293. [Google Scholar] [CrossRef] [PubMed]
- Fleischmann, P.N. Starting Foraging Life: Early Calibration and Daily Use of the Navigational System in Cataglyphis Ants. Ph.D. Thesis, Julius-Maximilians-Universität Würzburg, Würzburg, Germany, June 2018. [Google Scholar]
- Baddeley, B.; Graham, P.; Husbands, P.; Philippides, A. A model of ant route navigation driven by scene familiarity. PLoS Comput. Biol. 2012, 8, e1002336. [Google Scholar] [CrossRef]
- Collett, M.; Chittka, L.; Collett, T. Spatial memory in insect navigation. Curr. Biol. 2013, 23, 789–800. [Google Scholar] [CrossRef]
- Wystrach, A.; Buehlmann, C.; Schwarz, S.; Cheng, K.; Graham, P. Rapid aversive and memory trace learning during route navigation in desert ants. Curr. Biol. 2020, 30, 1927–19332. [Google Scholar] [CrossRef]
- Lionetti, V.A.G.; Deeti, S.; Murray, T.; Cheng, K. Resolving conflict between aversive and appetitive learning of views: How ants shift to a new route during navigation. Learn. Behav. 2023, 51, 446–457. [Google Scholar] [CrossRef]
- Bennett, J.E.M.; Philippides, A.; Nowotny, T. Learning with reinforcement prediction errors in a model of the drosophila mushroom body. Nat. Commun. 2021, 12, 2569. [Google Scholar] [CrossRef]
- Caron, S.J.C.; Ruta, V.; Abbott, L.F.; Axel, R. Random convergence of olfactory inputs in the drosophila mushroom body. Nature 2013, 497, 113–117. [Google Scholar] [CrossRef]
- Turner, G.C.; Bazhenov, M.; Laurent, G. Olfactory representations by drosophila mushroom body neurons. J. Neurophysiol. 2008, 99, 734–746. [Google Scholar] [CrossRef]
- Aso, Y.; Hattori, D.; Yu, Y.; Johnston, R.M.; Iyer, N.A.; Ngo, T.-T.; Dionne, H.; Abbott, L.; Axel, R.; Tanimoto, H.; et al. The neuronal architecture of the mushroom body provides a logic for associative learning. eLife 2014, 3, e04577. [Google Scholar] [CrossRef]
- Frechter, S.; Bates, A.S.; Tootoonian, S.; Dolan, M.-J.; Manton, J.; Jamasb, A.R.; Kohl, J.; Bock, D.; Jefferis, G. Functional and an-atomical specificity in a higher olfactory centre. eLife 2019, 8, 44590. [Google Scholar] [CrossRef] [PubMed]
- Hoinville, T.; Wehner, R. Optimal multiguidance integration in insect navigation. Proc. Natl. Acad. Sci. USA 2018, 115, 2824–2829. [Google Scholar] [CrossRef]
- Goulard, R.; Heinze, S.; Webb, B. Emergent spatial goals in an integrative model of the insect central complex. PLoS Comput. Biol. 2023, 19, e1011480. [Google Scholar] [CrossRef] [PubMed]
- Webb, B. The internal maps of insects. J. Exp. Biol. 2019, 222 (Suppl. S1), 188094. [Google Scholar] [CrossRef]
- Collett, M.; Collett, T.S. How does the insect central complex use mushroom body output for steering? Curr. Biol. 2018, 28, 733–734. [Google Scholar] [CrossRef]
- Wehner, R.; Hoinville, T.; Cruse, H.; Cheng, K. Steering intermediate courses: Desert ants combine information from various navigational routines. J. Comp. Physiol. A 2016, 202, 459–472. [Google Scholar] [CrossRef]
- Buehlmann, C.; Graham, P.; Hansson, B.S.; Knaden, M. Desert ants locate food by combining high sensitivity to food odors with extensive crosswind runs. Curr. Biol. 2014, 24, 960–964. [Google Scholar] [CrossRef]
- Fuentes-Pacheco, J.; Ruiz-Ascencio, J.; Rendón-Mancha, J.M. Visual simultaneous localization and mapping: A survey. Artif. Intell. Rev. 2015, 43, 55–81. [Google Scholar] [CrossRef]
- Zhu, J.; Rong, C.; Iida, F.; Rosendo, A. Bootstrapping virtual bipedal walkers with robotics scaffolded learning. Front. Robot. AI 2021, 8, 702599. [Google Scholar] [CrossRef]
- Niculescu, V.; Polonelli, T.; Magno, M.; Benini, L. Nanoslam: Enabling fully onboard slam for tiny robots. IEEE Internet Things J. 2024, 11, 13584–13607. [Google Scholar] [CrossRef]

| Parameter | Description | Value/Setting |
|---|---|---|
| Normalised olfactory concentration at the nest | 1 | |
| Spread of the Gaussian odour field | 0.15–0.25 | |
| U | Step size per simulation step | 0.01 m |
| Visual learning rate in MB network | 0.01–0.018 | |
| Kenyon Cell activation threshold | 0.04 | |
| Number of Visual Projection Neurons | 81 | |
| Number of Kenyon Cells | 4000 | |
| Path integration noise per step (Gaussian) | ||
| Familiarity-to-offset mapping functions | Piecewise linear | |
| Step limit per learning walk | Adaptive | |
| Visual scanning interval | Adaptive per walk | |
| r | Step scaling factor during learning walks | 2.0–2.5 |
| Random step probability | 0.2–0.8 | |
| von Mises concentration parameter | 5–50 |
| Comparison | Method | t | p | Adjusted p (Holm) |
|---|---|---|---|---|
| LW2 vs. LW1 | t-test | 3.783 | 0.00433 | 0.01299 |
| LW3 vs. LW2 | t-test | 1.121 | 0.29135 | 0.29135 |
| LW4 vs. LW3 | t-test | 4.147 | 0.00250 | 0.01000 |
| LW3 vs. LW1 | t-test | 5.352 | 0.00196 | 0.00980 |
| LW4 vs. LW2 | t-test | 4.045 | 0.00591 | 0.01299 |
| LW4 vs. LW1 | t-test | 7.740 | 0.00003 | 0.00018 |
| Comparison | Cohen’s d |
|---|---|
| LW2 vs. LW1 | 1.037 |
| LW3 vs. LW1 | 1.595 |
| LW4 vs. LW1 | 2.799 |
| LW3 vs. LW2 | 0.553 |
| LW4 vs. LW2 | 1.684 |
| LW4 vs. LW3 | 1.100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Z.; Sun, X.; Peng, J. A Vector-Based Computational Model of Multimodal Insect Learning Walks. Biomimetics 2025, 10, 736. https://doi.org/10.3390/biomimetics10110736
Xiang Z, Sun X, Peng J. A Vector-Based Computational Model of Multimodal Insect Learning Walks. Biomimetics. 2025; 10(11):736. https://doi.org/10.3390/biomimetics10110736
Chicago/Turabian StyleXiang, Zhehong, Xuelong Sun, and Jigen Peng. 2025. "A Vector-Based Computational Model of Multimodal Insect Learning Walks" Biomimetics 10, no. 11: 736. https://doi.org/10.3390/biomimetics10110736
APA StyleXiang, Z., Sun, X., & Peng, J. (2025). A Vector-Based Computational Model of Multimodal Insect Learning Walks. Biomimetics, 10(11), 736. https://doi.org/10.3390/biomimetics10110736






