An Economic Scheduling Management Method for Microgrids Using Multi-Strategy Improved Sand Cat Swarm Optimization
Abstract
1. Introduction
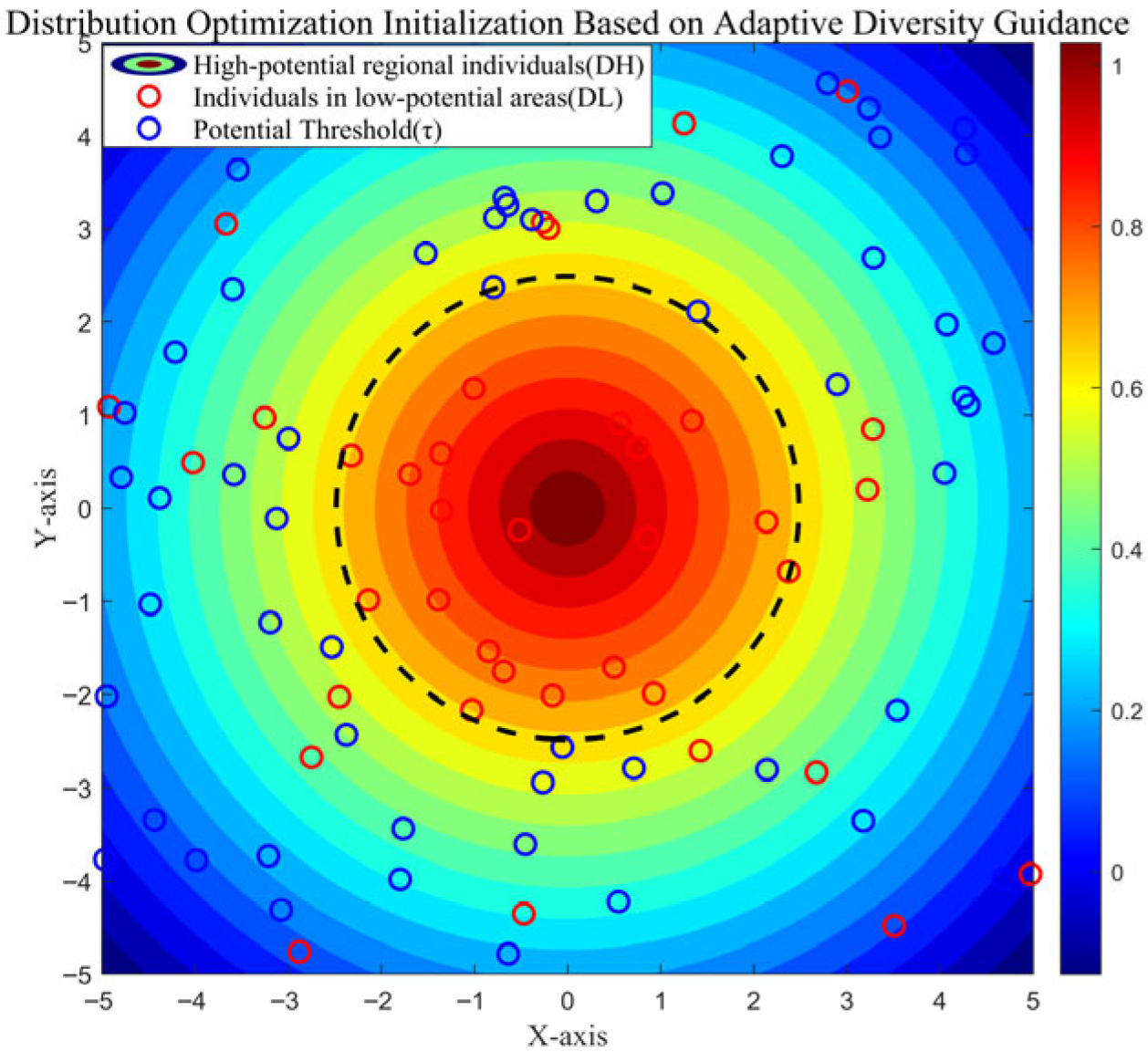
- To enhance the quality of the initial population, a distribution optimization initialization based on adaptive diversity guidance is proposed. This method enhances algorithm performance by generating individuals in high-potential regions to ensure initial solution quality, while also generating individuals in low-potential regions to maintain population diversity.
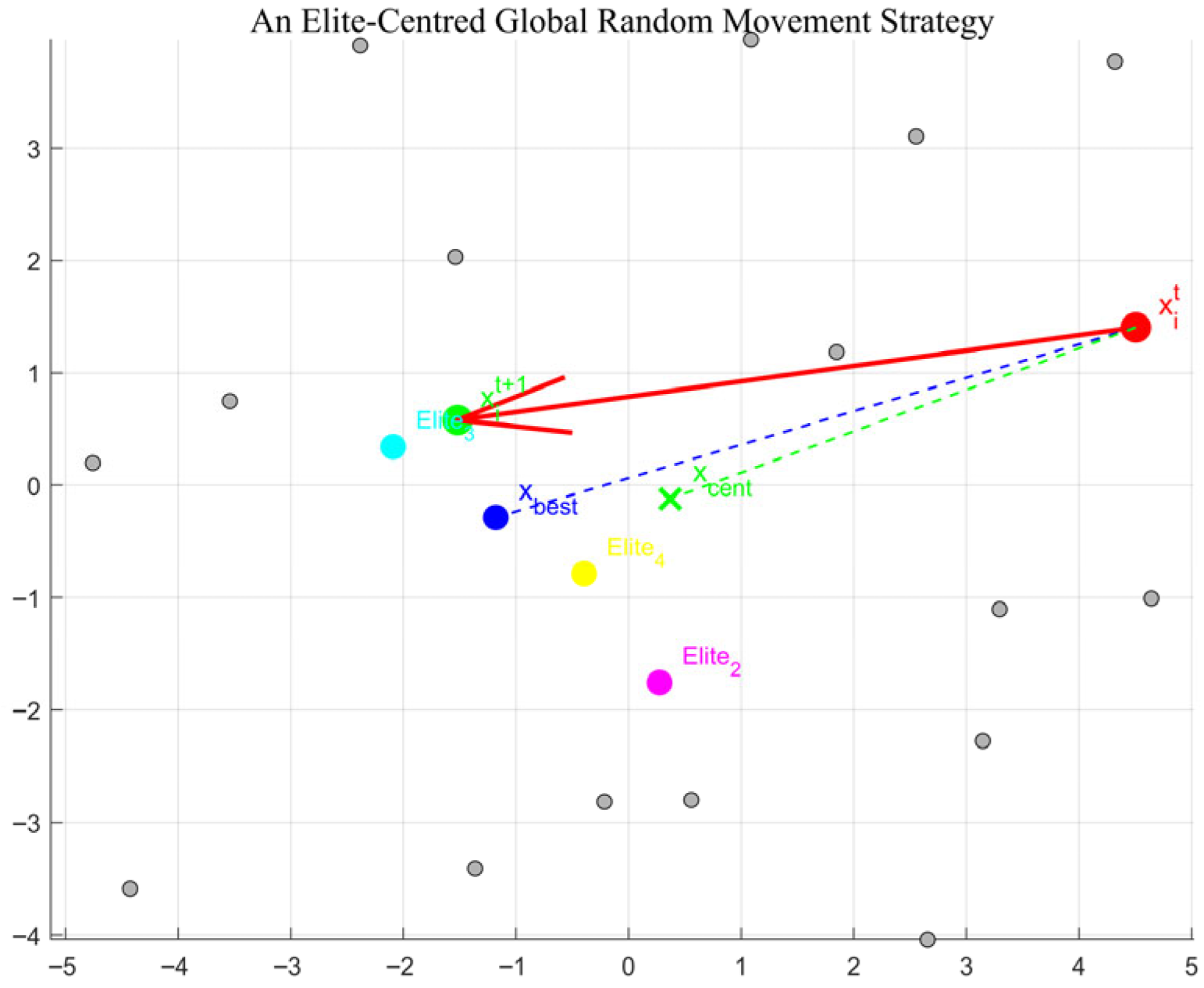
- We proposed an elite-centered global random movement strategy that balances elite guidance and global diversity, enhancing both the convergence speed and accuracy of the algorithm.
- We propose an adaptive elastic boundary mapping method to effectively handle out-of-bound individuals, balancing boundary constraints with enhanced global search capabilities to improve algorithm performance.
- The algorithms were qualitatively analyzed using 30 test functions from the IEEE CEC2017 test set and compared with 11 other algorithms to obtain competitive results. Most importantly, the algorithms were statistically analyzed to fully analyze the superior performance of MISCSO.
- The MISCSO is applied to the problem of economic dispatch in microgrids and compared with other comparative algorithms.
2. Sand Cat Swarm Optimization (SCSO)
2.1. Initial Population
2.2. Searching the Prey (Exploration)
2.3. Attacking on the Prey (Exploitation)
2.4. Exploration and Exploitation
| Algorithm 1: the pseudo-code of the SCSO |
| 1: Begin 2: Initialize: the relevant parameters and population initialization. 3: Calculate the fitness value for each individual and determine the optimal individual. 4: do 5: do 6: Randomly select an angle between 0 and 360 degrees. 7: 8: Attacking on the prey (exploitation): 8: Update the population by Equation (7) 9: else: 10: Searching the prey (exploration): 11: Update the population by Equation (6) 12: End If 16: 19: End for 20: 21: End while 22: return best solution 23: end |
3. Proposed MISCSO
3.1. Distribution Optimization Initialization Based on Adaptive Diversity Guidance
3.2. An Elite-Centered Global Random Movement Strategy
3.3. Adaptive Elastic Boundary Mapping Method
4. Experimental Results and Detailed Analyses on CEC2017
4.1. Benchmark Test Functions
4.2. Competitor Algorithms and Parameter Setting
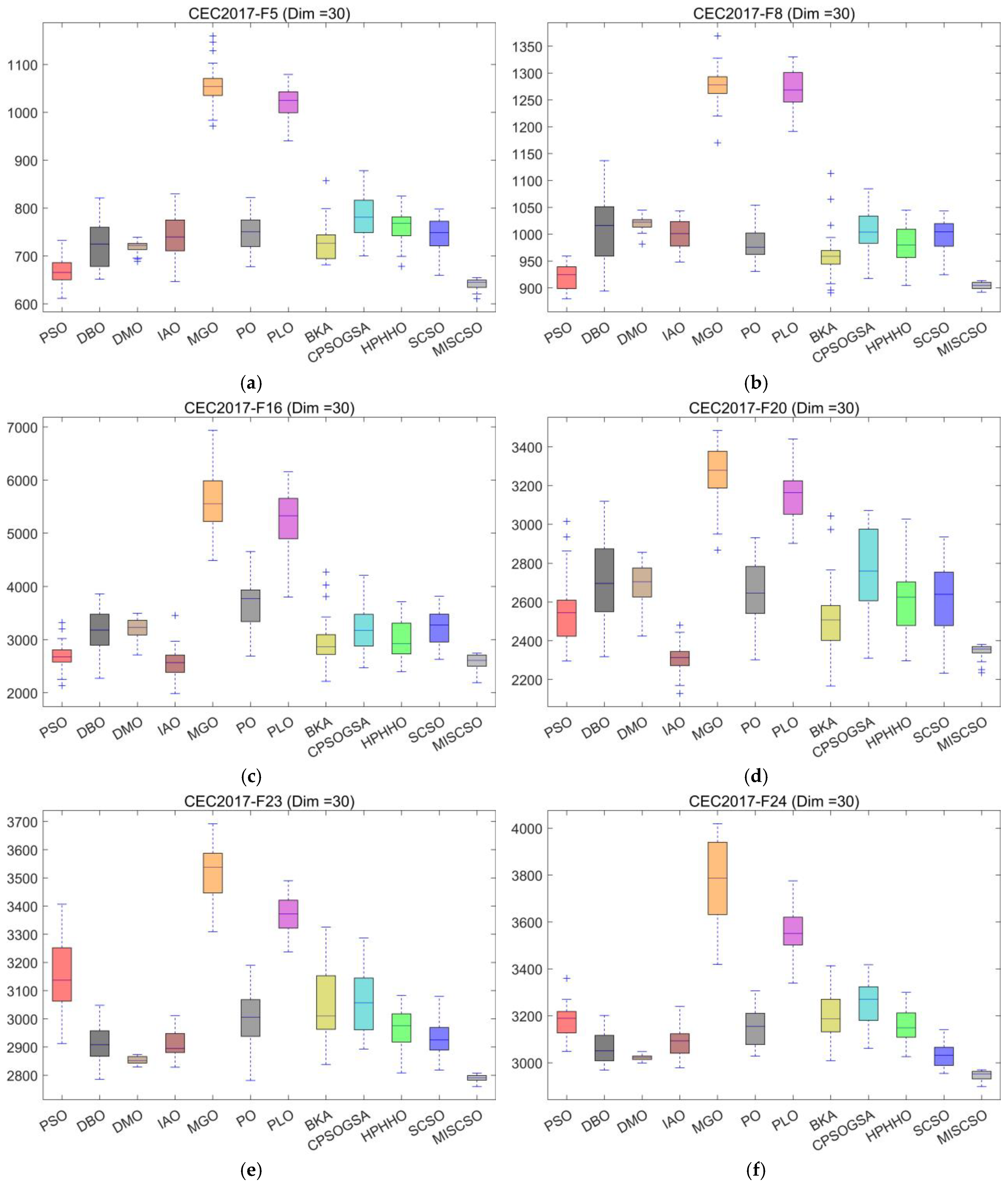
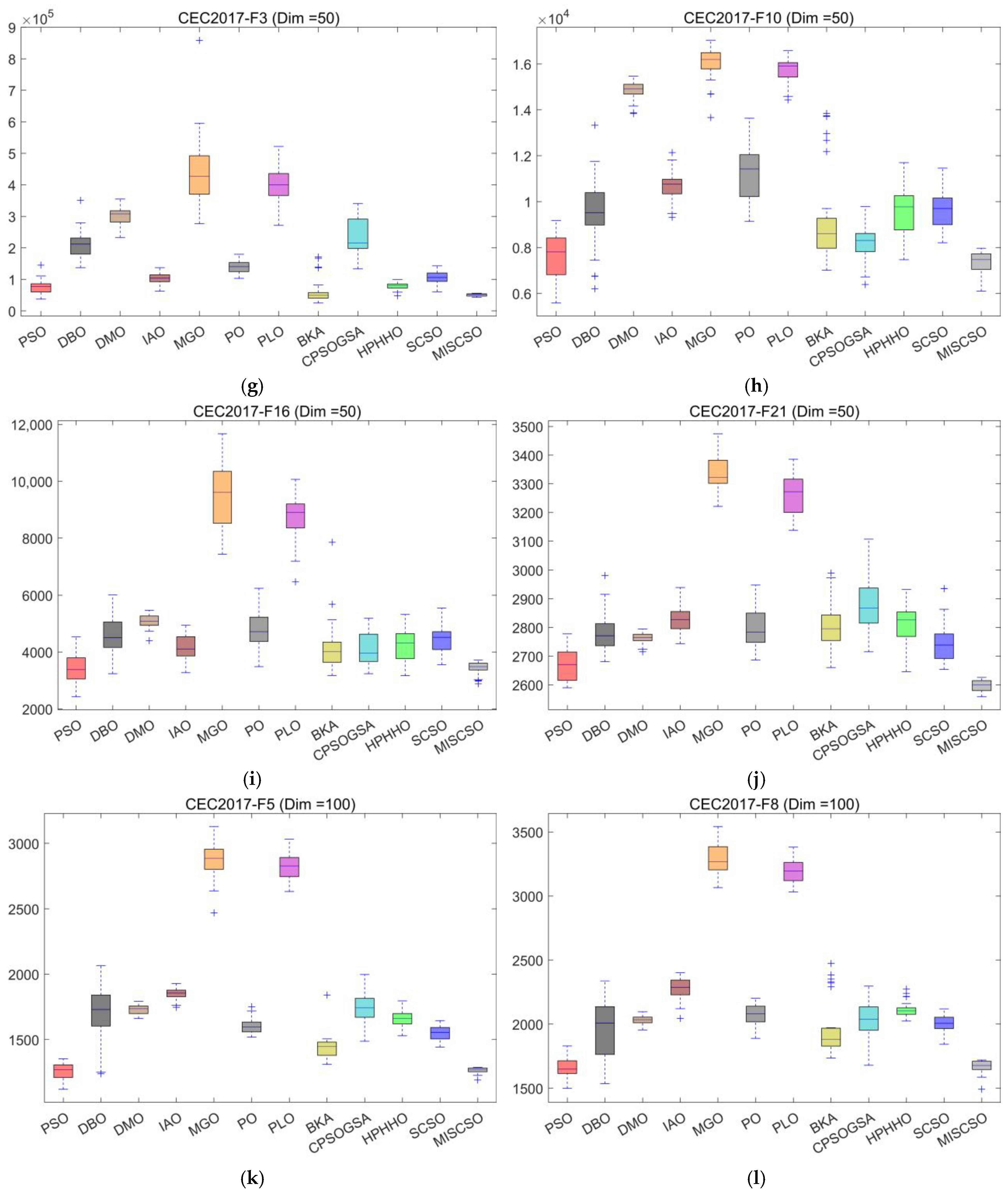
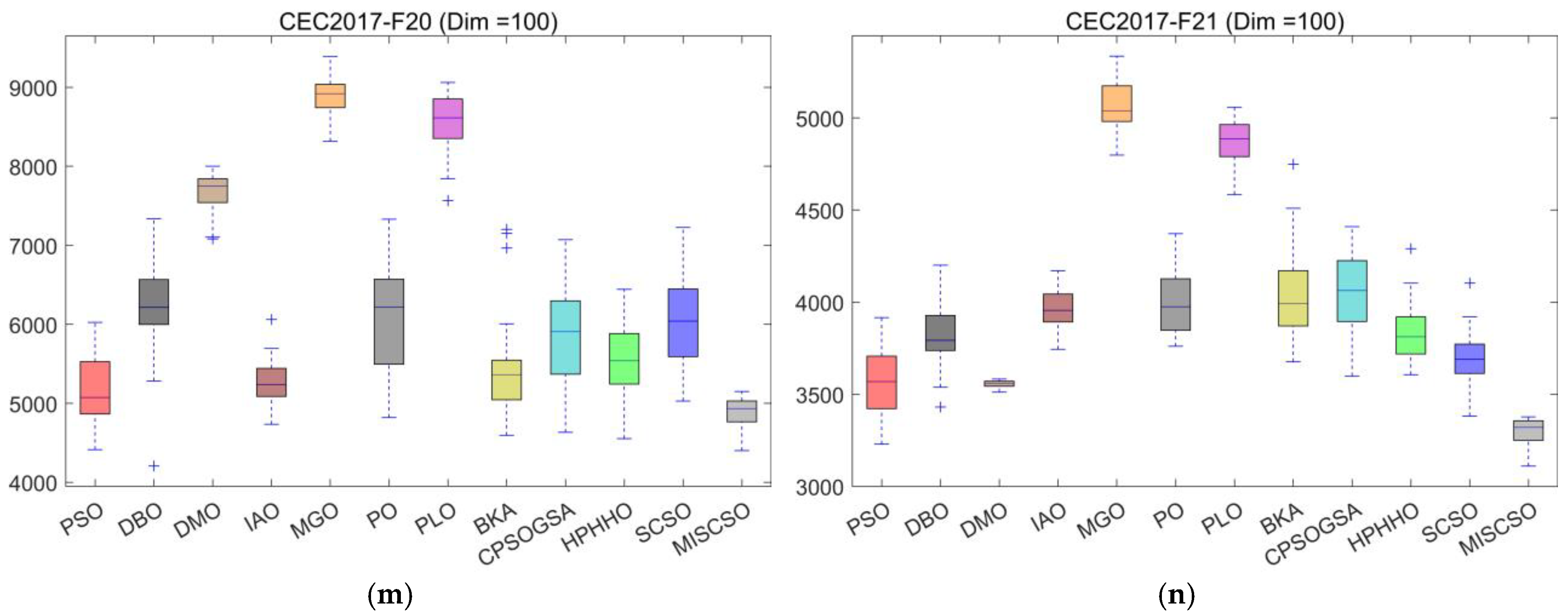
4.3. Compare Using CEC 2017 Test Functions
4.4. Statistical Analysis
4.4.1. Wilcoxon Rank Sum Test
4.4.2. Friedman Mean Rank Test
5. MISCSO for Economic Scheduling of Microgrids
5.1. Micro-Power Mathematical Model
5.1.1. Photovoltaic Power Generation Model
5.1.2. Wind Power Generation System Model
5.1.3. Energy Storage Device Model
5.1.4. Diesel Generator Model
5.2. Objective Function
5.2.1. Economic Cost
5.2.2. Environmental Costs
5.3. Constraints
5.4. Simulation Parameter Settings and Experimental Analysis
5.4.1. Simulation Parameters for the Case Study
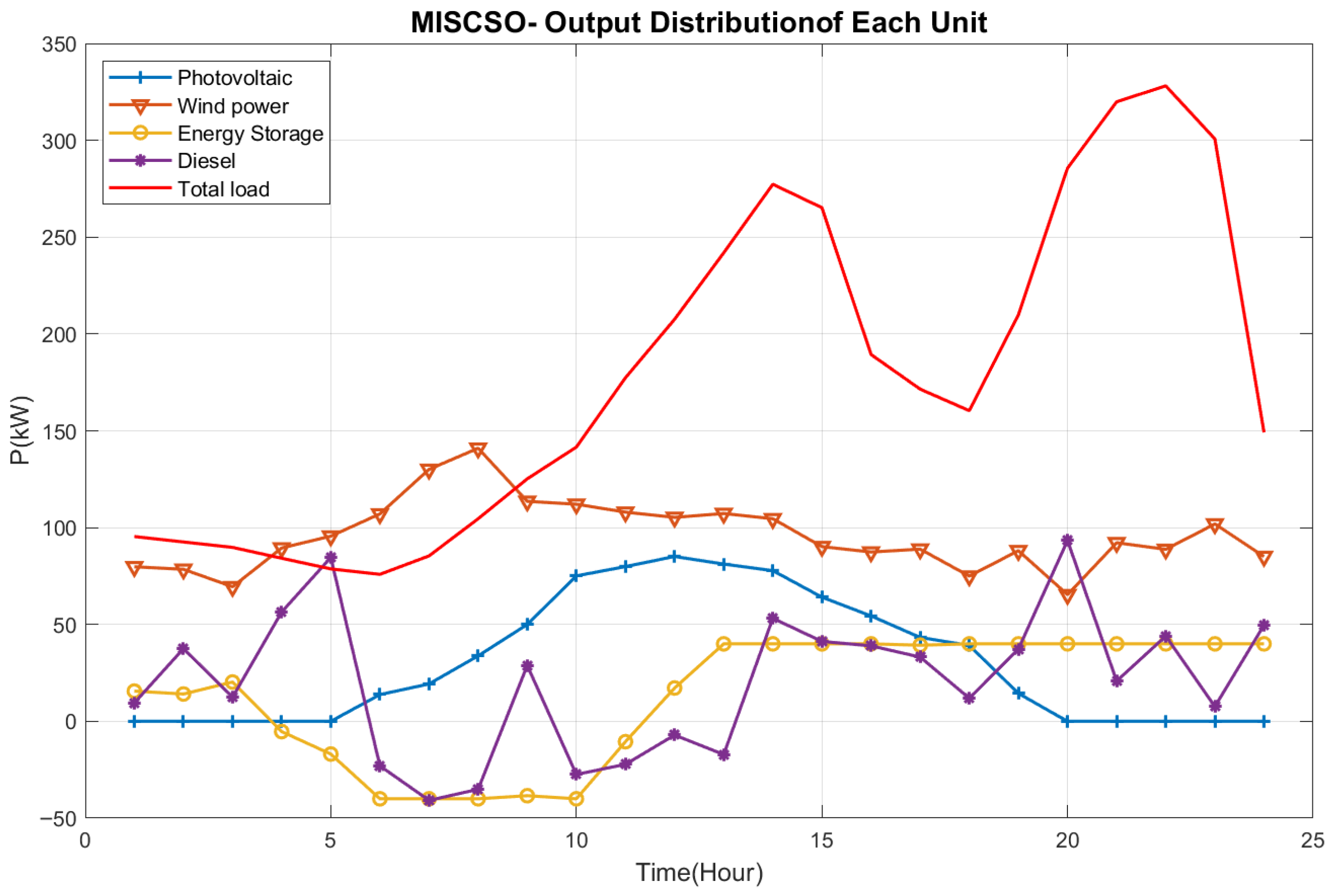
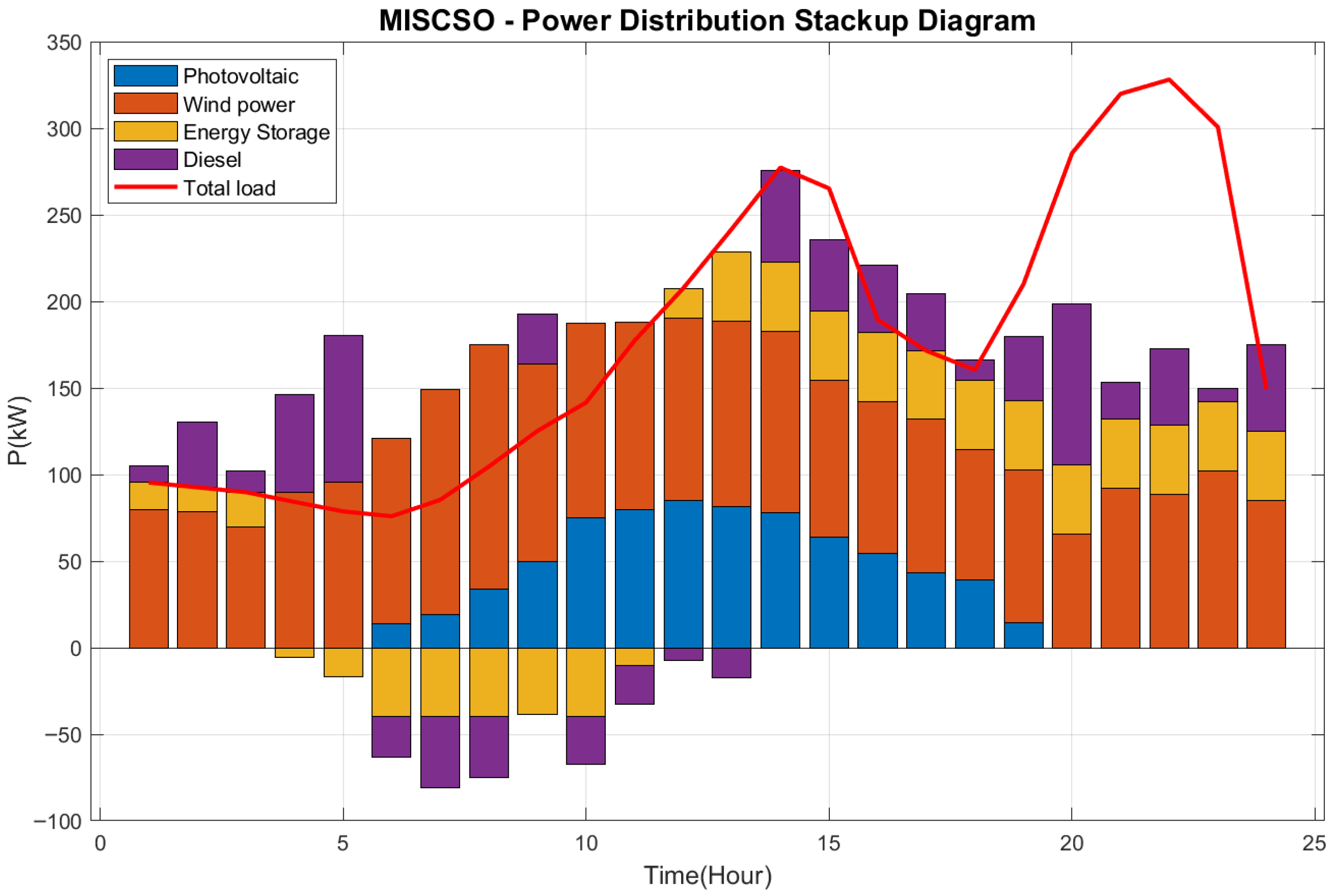
5.4.2. Analysis of Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nosratabadi, S.; Hooshmand, R.; Gholipour, E. A Comprehensive Review on Microgrid and Virtual Power Plant Concepts Employed for Distributed Energy Resources Scheduling in Power Systems. Renew. Sustain. Energy Rev. 2017, 67, 341–363. [Google Scholar] [CrossRef]
- Qing, K.; Du, Y.; Huang, Q.; Duan, C.; Hu, W. Energy Scheduling for Microgrids with Renewable Energy Sources Considering an Adjustable Convex Hull Based Uncertainty Set. Renew. Energy 2024, 220, 119611. [Google Scholar] [CrossRef]
- Baron, C.; Al-Sumaiti, A.; Rivera, S. Impact of Energy Storage Useful Life on Intelligent Microgrid Scheduling. Energy 2020, 13, 957. [Google Scholar] [CrossRef]
- Gamarra, C.; Guerrero, J. Computational Optimization Techniques Applied to Microgrids Planning: A Review. Renew. Sustain. Energy Rev. 2015, 48, 413–424. [Google Scholar] [CrossRef]
- Rezk, H.; Olabi, A.; Sayed, E.; Wilberforce, T. Role of Metaheuristics in Optimizing Microgrids Operating and Management Issues: A Comprehensive Review. Sustainability 2023, 15, 4982. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.; Zhang, C.; Liang, R.; Peng, T.; Yang, Y.; Wu, M.; Zhou, Y. Multi-Strategy Reference Vector Guided Evolutionary Algorithm and Its Application in Multi-Objective Optimal Scheduling of Microgrid Systems Containing Electric Vehicles. J. Energy Storage 2024, 95, 112500. [Google Scholar] [CrossRef]
- Selvaraj, G.; Rajangam, K.; Vishnuram, P.; Bajaj, M.; Zaitsev, I. Optimal Power Scheduling in Real-Time Distribution Systems Using Crow Search Algorithm for Enhanced Microgrid Performance. Sci. Rep. 2024, 14, 30982. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Ren, J.; Song, Z.; Zhang, S.; Feng, H. Optimizing Economic Dispatch for Microgrid Clusters Using Improved Grey Wolf Optimization. Electronics 2024, 13, 3139. [Google Scholar] [CrossRef]
- Xie, C.; Li, S.; Qin, X.; Fu, S.; Zhang, X. Multiple Elite Strategy Enhanced RIME Algorithm for 3D UAV Path Planning. Sci. Rep. 2024, 14, 21734. [Google Scholar] [CrossRef]
- Yue, X.; Zhang, H.; Yu, H. A Hybrid Grasshopper Optimization Algorithm with Invasive Weed for Global Optimization. IEEE Access 2020, 8, 5928–5960. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Zhang, Y. Novel WSN Coverage Optimization Strategy Via Monarch Butterfly Algorithm and Particle Swarm Optimization. Wirel. Pers. Commun. 2024, 135, 2255–2280. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat Swarm Optimization: A Nature-Inspired Algorithm to Solve Global Optimization Problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Yao, L.; Yang, J.; Yuan, P.; Li, G.; Lu, Y.; Zhang, T. Multi-Strategy Improved Sand Cat Swarm Optimization: Global Optimization and Feature Selection. Biomimetics 2023, 8, 492. [Google Scholar] [CrossRef]
- Zhan, Z.; Lai, D.; Huang, C.; Zhang, Z.; Deng, Y.; Yang, J. MSCSO: A Modified Sand Cat Swarm Algorithm for 3D UAV Path Planning in Complex Environments with Multiple Threats. Sensors 2025, 25, 2730. [Google Scholar] [CrossRef] [PubMed]
- Rauf, H.; Shoaib, U.; Lali, M.; Alhaisoni, M.; Irfan, M.; Khan, M. Particle Swarm Optimization with Probability Sequence for Global Optimization. IEEE Access 2020, 8, 110535–110549. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; pp. 372–379. [Google Scholar]
- Anantathanavit, M.; Munlin, M. IEEE Radius Particle Swarm Optimization. In Proceedings of the 2013 International Computer Science and Engineering Conference (ICSEC), Nakhonpathom, Thailand, 4–6 September 2013; pp. 126–130. [Google Scholar]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-Heuristic Algorithm for Global Optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Agushaka, J.; Ezugwu, A.; Abualigah, L. Dwarf Mongoose Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Wu, X.; Li, S.; Jiang, X.; Zhou, Y. Information Acquisition Optimizer: A New Efficient Algorithm for Solving Numerical and Constrained Engineering Optimization Problems. J. Supercomput. 2024, 80, 25736–25791. [Google Scholar] [CrossRef]
- Zheng, B.; Chen, Y.; Wang, C.; Heidari, A.; Liu, L.; Chen, H. The Moss Growth Optimization (MGO): Concepts and Performance. J. Comput. Des. Eng. 2024, 11, 184–221. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G.; Ma, L.; Zhu, T.; Wu, X.; Heidari, A.A.; Chen, Y.; Chen, H. Parrot Optimizer: Algorithm and Applications to Medical Problems. Comput. Biol. Med. 2024, 172, 108064. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar Lights Optimizer: Algorithm and Applications in Image Segmentation and Feature Selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H. Black-Winged Kite Algorithm: A Nature-Inspired Meta-Heuristic for Solving Benchmark Functions and Engineering Problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Dao, F.; Zou, Y.; Zeng, Y.; Qian, J.; Li, X. An Intelligent CPSOGSA-Based Mixed H2/H∞ Robust Controller for the Multi-Hydro-Turbine Governing System with Sharing Common Penstock. Renew. Energy 2023, 206, 481–497. [Google Scholar] [CrossRef]
- Su, Y.; Dai, Y.; Liu, Y. A Hybrid Parallel Harris Hawks Optimization Algorithm for Reusable Launch Vehicle Reentry Trajectory Optimization with No-Fly Zones. Soft Comput. 2021, 25, 14597–14617. [Google Scholar] [CrossRef]
- Dwivedi, A.; Mallawaarachchi, I.; Alvarado, L. Analysis of Small Sample Size Studies Using Nonparametric Bootstrap Test with Pooled Resampling Method. Stat. Med. 2017, 36, 2187–2205. [Google Scholar] [CrossRef]
- Fang, D.; Yan, J.; Zhou, Q. Channa Argus Optimizer for Solving Numerical Optimization and Engineering Problems. Sci. Rep. 2025, 15, 21502. [Google Scholar] [CrossRef] [PubMed]




| Algorithms | Parameter Name | Parameter Value | Reference |
|---|---|---|---|
| PSO | 6, 0.9, 0.6, 2, 2 | [17] | |
| DBO | 0.2 | [18] | |
| DMO | 2 | [19] | |
| IAO | 0.5 | [20] | |
| MGO | Rec, w, d1 | 1, 2, 0.2 | [21] |
| PO | 1.5 | [22] | |
| PLO | 1.5 | [23] | |
| BKA | 0.9 | [24] | |
| CPSOGSA | 2.05 | [25] | |
| HPHHO | 1 × 1020 | [26] | |
| SCSO | 2 | [12] |
| ID | Metric | PSO | DBO | DMO | IAO | MGO | PO | PLO | BKA | CPSOGSA | HPHHO | SCSO | MISCSO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 2.2091 × 105 | 1.8798 × 107 | 1.1622 × 106 | 2.2219 × 1010 | 8.3689 × 1010 | 5.1717 × 108 | 7.6459 × 1010 | 7.8964 × 109 | 2.8746 × 103 | 9.9424 × 108 | 4.2861 × 109 | 8.9823 × 105 |
| std | 1.2262 × 105 | 2.2615 × 107 | 1.4200 × 106 | 5.4481 × 109 | 1.3990 × 1010 | 5.2480 × 108 | 1.6098 × 1010 | 1.2665 × 1010 | 3.7008 × 103 | 5.7386 × 108 | 2.5945 × 109 | 2.0484 × 105 | |
| F2 | mean | 5.2899 × 109 | 4.2621 × 1028 | 4.8542 × 1031 | 4.9180 × 1029 | 3.0023 × 1046 | 1.6438 × 1031 | 8.8433 × 1044 | 5.0686 × 1039 | 7.8063 × 1027 | 1.0000 × 1020 | 1.2044 × 1033 | 6.6077 × 1013 |
| std | 1.2806 × 1010 | 1.6127 × 1029 | 1.6032 × 1032 | 1.3743 × 1030 | 9.9573 × 1046 | 7.1850 × 1031 | 3.1955 × 1045 | 2.7745 × 1040 | 4.0246 × 1028 | 0.0000 × 100 | 4.8686 × 1033 | 5.2354 × 1013 | |
| F3 | mean | 5.6855 × 103 | 6.7094 × 104 | 1.1122 × 105 | 3.7433 × 104 | 2.2896 × 105 | 4.1243 × 104 | 1.9017 × 105 | 1.1762 × 104 | 6.5738 × 104 | 3.3279 × 104 | 4.6717 × 104 | 8.6403 × 103 |
| std | 2.9498 × 103 | 1.3185 × 104 | 1.6079 × 104 | 1.1193 × 104 | 4.9962 × 104 | 7.5511 × 103 | 3.2697 × 104 | 8.0095 × 103 | 2.2409 × 104 | 9.2237 × 103 | 1.1329 × 104 | 1.1697 × 103 | |
| F4 | mean | 4.7371 × 102 | 5.8079 × 102 | 5.1558 × 102 | 3.8787 × 103 | 2.3917 × 104 | 5.7897 × 102 | 1.8050 × 104 | 1.2642 × 103 | 5.2289 × 102 | 6.0051 × 102 | 8.7244 × 102 | 4.8154 × 102 |
| std | 2.7466 × 101 | 9.2824 × 101 | 1.6464 × 101 | 1.7244 × 103 | 5.9704 × 103 | 4.3904 × 101 | 4.4268 × 103 | 2.2560 × 103 | 7.3596 × 101 | 4.9290 × 101 | 4.8649 × 102 | 7.4718 × 100 | |
| F5 | mean | 6.6823 × 102 | 7.2608 × 102 | 7.1876 × 102 | 7.4565 × 102 | 1.0537 × 103 | 7.4869 × 102 | 1.0185 × 103 | 7.2777 × 102 | 7.8766 × 102 | 7.5841 × 102 | 7.4342 × 102 | 6.4080 × 102 |
| std | 2.9983 × 101 | 4.8066 × 101 | 1.2375 × 101 | 4.6566 × 101 | 4.4448 × 101 | 3.8245 × 101 | 3.8090 × 101 | 3.8033 × 101 | 4.8540 × 101 | 3.4278 × 101 | 3.5956 × 101 | 1.1530 × 101 | |
| F6 | mean | 6.4100 × 102 | 6.3615 × 102 | 6.0054 × 102 | 6.5268 × 102 | 7.0926 × 102 | 6.5970 × 102 | 7.0524 × 102 | 6.5855 × 102 | 6.6671 × 102 | 6.5749 × 102 | 6.5761 × 102 | 6.3587 × 102 |
| std | 8.1053 × 100 | 1.1999 × 101 | 1.2669 × 10−1 | 1.1372 × 101 | 9.0599 × 100 | 8.3707 × 100 | 1.1216 × 101 | 6.0173 × 100 | 1.0812 × 101 | 7.4344 × 100 | 9.2870 × 100 | 3.7184 × 100 | |
| F7 | mean | 8.4572 × 102 | 9.4577 × 102 | 9.6538 × 102 | 1.1275 × 103 | 2.7866 × 103 | 1.1651 × 103 | 2.6477 × 103 | 1.1853 × 103 | 1.3761 × 103 | 1.1734 × 103 | 1.1047 × 103 | 9.1610 × 102 |
| std | 2.7599 × 101 | 8.5186 × 101 | 1.0709 × 101 | 8.1321 × 101 | 1.4542 × 102 | 7.8294 × 101 | 1.8454 × 102 | 7.2807 × 101 | 1.5558 × 102 | 9.8289 × 101 | 1.0274 × 102 | 2.8965 × 101 | |
| F8 | mean | 9.2037 × 102 | 1.0062 × 103 | 1.0198 × 103 | 9.9951 × 102 | 1.2775 × 103 | 9.8063 × 102 | 1.2681 × 103 | 9.6371 × 102 | 1.0062 × 103 | 9.8111 × 102 | 9.9628 × 102 | 9.0442 × 102 |
| std | 2.2809 × 101 | 6.1351 × 101 | 1.2538 × 101 | 2.7507 × 101 | 3.4889 × 101 | 3.0043 × 101 | 3.8253 × 101 | 4.3419 × 101 | 4.7866 × 101 | 3.3167 × 101 | 3.0428 × 101 | 6.3807 × 100 | |
| F9 | mean | 4.4760 × 103 | 5.5061 × 103 | 1.1026 × 103 | 4.8459 × 103 | 2.5527 × 104 | 5.9736 × 103 | 2.2294 × 104 | 4.7678 × 103 | 7.8899 × 103 | 5.7999 × 103 | 5.3273 × 103 | 3.1510 × 103 |
| std | 1.1760 × 103 | 2.0868 × 103 | 7.0045 × 101 | 9.2771 × 102 | 3.1517 × 103 | 1.3419 × 103 | 4.0851 × 103 | 8.0420 × 102 | 2.0837 × 103 | 4.6560 × 102 | 1.0388 × 103 | 3.0085 × 102 | |
| F10 | mean | 4.7975 × 103 | 5.3850 × 103 | 8.3255 × 103 | 5.6208 × 103 | 9.4978 × 103 | 6.2471 × 103 | 9.1113 × 103 | 5.0180 × 103 | 5.0336 × 103 | 5.1503 × 103 | 5.8335 × 103 | 4.3607 × 103 |
| std | 7.3037 × 102 | 7.6270 × 102 | 3.7251 × 102 | 3.9800 × 102 | 3.7859 × 102 | 9.1376 × 102 | 3.4878 × 102 | 8.6048 × 102 | 4.7119 × 102 | 5.7052 × 102 | 6.3513 × 102 | 3.3057 × 102 | |
| F11 | mean | 1.2146 × 103 | 1.5807 × 103 | 1.3076 × 103 | 1.6051 × 103 | 1.8695 × 104 | 1.6141 × 103 | 1.8857 × 104 | 1.3375 × 103 | 1.2660 × 103 | 1.4021 × 103 | 2.0465 × 103 | 1.2236 × 103 |
| std | 2.9453 × 101 | 3.0856 × 102 | 2.3674 × 101 | 2.1265 × 102 | 5.4881 × 103 | 1.9013 × 102 | 5.6987 × 103 | 2.5045 × 102 | 4.3000 × 101 | 4.2434 × 101 | 6.9747 × 102 | 2.4300 × 101 | |
| F12 | mean | 1.0111 × 106 | 2.5295 × 107 | 1.0060 × 107 | 2.8625 × 108 | 1.3365 × 1010 | 1.2902 × 108 | 1.1257 × 1010 | 4.3250 × 108 | 1.3944 × 106 | 7.6292 × 107 | 1.4023 × 108 | 4.3800 × 106 |
| std | 4.5521 × 105 | 3.5154 × 107 | 3.5443 × 106 | 3.6221 × 108 | 3.3381 × 109 | 1.2476 × 108 | 2.8103 × 109 | 1.0600 × 109 | 1.2581 × 106 | 5.5136 × 107 | 1.3252 × 108 | 1.6557 × 106 | |
| F13 | mean | 1.8993 × 104 | 1.6274 × 106 | 1.4709 × 104 | 2.9759 × 104 | 9.7732 × 109 | 4.6369 × 106 | 7.1522 × 109 | 5.5056 × 106 | 3.9751 × 104 | 1.0077 × 106 | 2.1756 × 107 | 4.1934 × 104 |
| std | 2.0013 × 104 | 1.9652 × 106 | 9.3708 × 103 | 2.2157 × 104 | 4.2451 × 109 | 1.3241 × 107 | 2.4771 × 109 | 2.1391 × 107 | 2.3361 × 104 | 1.7137 × 106 | 4.9355 × 107 | 1.2269 × 104 | |
| F14 | mean | 2.8124 × 104 | 1.3929 × 105 | 8.1612 × 104 | 1.5347 × 103 | 7.3854 × 106 | 4.3445 × 105 | 4.6119 × 106 | 2.4762 × 103 | 3.2515 × 104 | 1.0523 × 105 | 3.1896 × 105 | 9.2681 × 103 |
| std | 3.4144 × 104 | 1.6541 × 105 | 3.6973 × 104 | 3.4674 × 101 | 4.8434 × 106 | 4.1255 × 105 | 3.2202 × 106 | 1.3168 × 103 | 2.9287 × 104 | 6.9809 × 104 | 3.7534 × 105 | 3.1857 × 103 | |
| F15 | mean | 7.8991 × 103 | 8.5189 × 104 | 3.7989 × 103 | 3.0194 × 103 | 1.7927 × 109 | 1.5656 × 105 | 9.1793 × 108 | 3.0543 × 104 | 1.4028 × 104 | 4.7496 × 104 | 5.4897 × 105 | 1.1367 × 104 |
| std | 7.2737 × 103 | 9.4273 × 104 | 2.9766 × 103 | 1.0039 × 103 | 1.1773 × 109 | 2.4076 × 105 | 5.6871 × 108 | 3.7296 × 104 | 1.3247 × 104 | 3.9716 × 104 | 1.4112 × 106 | 3.1207 × 103 | |
| F16 | mean | 2.7016 × 103 | 3.1543 × 103 | 3.2198 × 103 | 2.5685 × 103 | 5.5876 × 103 | 3.6855 × 103 | 5.2419 × 103 | 2.9788 × 103 | 3.1881 × 103 | 2.9683 × 103 | 3.2435 × 103 | 2.5947 × 103 |
| std | 2.5256 × 102 | 4.4247 × 102 | 1.7290 × 102 | 2.9293 × 102 | 6.0550 × 102 | 4.7665 × 102 | 5.2355 × 102 | 4.4153 × 102 | 3.8850 × 102 | 3.6159 × 102 | 3.3138 × 102 | 1.2817 × 102 | |
| F17 | mean | 2.2794 × 103 | 2.5730 × 103 | 2.3092 × 103 | 1.9461 × 103 | 4.1238 × 103 | 2.4383 × 103 | 3.6327 × 103 | 2.2426 × 103 | 2.6080 × 103 | 2.3038 × 103 | 2.3449 × 103 | 1.9846 × 103 |
| std | 2.7717 × 102 | 2.5420 × 102 | 1.2729 × 102 | 1.0835 × 102 | 8.1611 × 102 | 2.2300 × 102 | 3.5718 × 102 | 1.7419 × 102 | 2.4774 × 102 | 2.3595 × 102 | 1.9392 × 102 | 8.0074 × 101 | |
| F18 | mean | 4.4829 × 105 | 1.1853 × 106 | 3.6019 × 106 | 4.7945 × 103 | 6.5949 × 107 | 2.2040 × 106 | 4.3159 × 107 | 1.6409 × 105 | 2.7332 × 105 | 1.5461 × 106 | 1.3844 × 106 | 1.5971 × 105 |
| std | 4.0547 × 105 | 1.2893 × 106 | 1.7371 × 106 | 5.1017 × 103 | 3.7026 × 107 | 1.6357 × 106 | 3.4046 × 107 | 4.8933 × 105 | 2.0796 × 105 | 1.4657 × 106 | 1.5346 × 106 | 4.9887 × 104 | |
| F19 | mean | 8.5089 × 103 | 4.9179 × 105 | 7.7215 × 103 | 2.4706 × 103 | 1.8294 × 109 | 3.8168 × 106 | 1.1551 × 109 | 2.9972 × 105 | 1.2667 × 104 | 6.8433 × 105 | 1.4214 × 106 | 1.0679 × 105 |
| std | 7.0987 × 103 | 9.8238 × 105 | 6.0219 × 103 | 1.0744 × 103 | 7.6056 × 108 | 2.5128 × 106 | 4.4618 × 108 | 6.6506 × 105 | 1.2903 × 104 | 9.0218 × 105 | 2.4026 × 106 | 7.3105 × 104 | |
| F20 | mean | 2.5483 × 103 | 2.7128 × 103 | 2.6962 × 103 | 2.3145 × 103 | 3.2669 × 103 | 2.6522 × 103 | 3.1480 × 103 | 2.5114 × 103 | 2.7583 × 103 | 2.6160 × 103 | 2.6266 × 103 | 2.3468 × 103 |
| std | 1.7608 × 102 | 2.1449 × 102 | 9.7777 × 101 | 7.1269 × 101 | 1.4208 × 102 | 1.6342 × 102 | 1.3700 × 102 | 1.8423 × 102 | 2.1798 × 102 | 1.8945 × 102 | 1.7636 × 102 | 3.6869 × 101 | |
| F21 | mean | 2.4721 × 103 | 2.5349 × 103 | 2.5125 × 103 | 2.4735 × 103 | 2.7991 × 103 | 2.5409 × 103 | 2.7590 × 103 | 2.5150 × 103 | 2.5705 × 103 | 2.5222 × 103 | 2.5184 × 103 | 2.4203 × 103 |
| std | 3.1714 × 101 | 3.7455 × 101 | 1.1836 × 101 | 6.5982 × 101 | 4.1707 × 101 | 4.2051 × 101 | 4.1855 × 101 | 5.5133 × 101 | 4.1515 × 101 | 3.9185 × 101 | 4.9359 × 101 | 1.1352 × 101 | |
| F22 | mean | 4.3993 × 103 | 5.4299 × 103 | 4.5365 × 103 | 4.8925 × 103 | 1.0689 × 104 | 3.7756 × 103 | 9.9037 × 103 | 5.7577 × 103 | 5.8230 × 103 | 4.5446 × 103 | 3.8712 × 103 | 2.3124 × 103 |
| std | 2.1899 × 103 | 2.0346 × 103 | 2.4460 × 103 | 8.0687 × 102 | 5.7949 × 102 | 2.1091 × 103 | 1.2695 × 103 | 2.0636 × 103 | 2.0755 × 103 | 2.5788 × 103 | 1.5267 × 103 | 1.3613 | |
| F23 | mean | 3.1413 × 103 | 2.9146 × 103 | 2.8537 × 103 | 2.9144 × 103 | 3.5201 × 103 | 2.9968 × 103 | 3.3742 × 103 | 3.0377 × 103 | 3.0621 × 103 | 2.9631 × 103 | 2.9316 × 103 | 2.7885 × 103 |
| std | 1.3554 × 102 | 6.4965 × 101 | 1.3865 × 101 | 4.7353 × 101 | 1.0623 × 102 | 9.2096 × 101 | 6.5209 × 101 | 1.1706 × 102 | 1.2011 × 102 | 6.8163 × 101 | 6.3598 × 101 | 1.3490 × 101 | |
| F24 | mean | 3.1804 × 103 | 3.0670 × 103 | 3.0217 × 103 | 3.0915 × 103 | 3.7703 × 103 | 3.1479 × 103 | 3.5671 × 103 | 3.1898 × 103 | 3.2614 × 103 | 3.1565 × 103 | 3.0356 × 103 | 2.9463 × 103 |
| std | 6.9984 × 101 | 7.0714 × 101 | 1.3135 × 101 | 7.0599 × 101 | 1.7933 × 102 | 7.9792 × 101 | 1.0491 × 102 | 1.0203 × 102 | 9.2964 × 101 | 6.6042 × 101 | 5.2799 × 101 | 1.8954 × 101 | |
| F25 | mean | 2.8868 × 103 | 2.9437 × 103 | 2.8892 × 103 | 3.5497 × 103 | 1.0953 × 104 | 2.9960 × 103 | 9.9811 × 103 | 3.0164 × 103 | 2.9273 × 103 | 3.0173 × 103 | 3.0673 × 103 | 2.8980 × 103 |
| std | 1.6211 × 101 | 3.7801 × 101 | 9.0494 × 10−1 | 2.8154 × 102 | 1.9415 × 103 | 3.2839 × 101 | 1.5360 × 103 | 2.6358 × 102 | 2.4654 × 101 | 5.0787 × 101 | 7.2889 × 101 | 7.4671 | |
| F26 | mean | 6.0316 × 103 | 6.2387 × 103 | 5.7669 × 103 | 7.0490 × 103 | 1.2366 × 104 | 6.7362 × 103 | 1.1209 × 104 | 7.3263 × 103 | 7.1320 × 103 | 6.2685 × 103 | 6.1536 × 103 | 2.8834 × 103 |
| std | 1.8462 × 103 | 1.0046 × 103 | 1.1892 × 102 | 1.2078 × 103 | 9.3537 × 102 | 1.4815 × 103 | 9.8286 × 102 | 1.3198 × 103 | 7.7884 × 102 | 1.6524 × 103 | 1.1082 × 103 | 6.1073 × 101 | |
| F27 | mean | 3.3207 × 103 | 3.2832 × 103 | 3.2265 × 103 | 3.3037 × 103 | 4.2525 × 103 | 3.3950 × 103 | 3.9930 × 103 | 3.3906 × 103 | 3.4781 × 103 | 3.3330 × 103 | 3.3631 × 103 | 3.2553 × 103 |
| std | 1.8663 × 102 | 4.2780 × 101 | 5.2334 × 100 | 8.2012 × 101 | 3.1731 × 102 | 8.0192 × 101 | 1.6880 × 102 | 1.1327 × 102 | 1.5062 × 102 | 7.9206 × 101 | 7.4251 × 101 | 1.0003 × 101 | |
| F28 | mean | 3.2273 × 103 | 3.4576 × 103 | 3.2813 × 103 | 4.5518 × 103 | 9.2000 × 103 | 3.3852 × 103 | 8.5148 × 103 | 3.5787 × 103 | 3.2535 × 103 | 3.3838 × 103 | 3.4963 × 103 | 3.2263 × 103 |
| std | 2.5873 × 101 | 4.1676 × 102 | 1.7738 × 101 | 5.4461 × 102 | 1.1052 × 103 | 5.8650 × 101 | 7.6068 × 102 | 7.5970 × 102 | 2.1426 × 101 | 5.8545 × 101 | 9.7327 × 101 | 9.1916 | |
| F29 | mean | 4.1318 × 103 | 4.1407 × 103 | 4.2951 × 103 | 4.0358 × 103 | 7.4570 × 103 | 4.8503 × 103 | 6.5519 × 103 | 4.4184 × 103 | 4.3611 × 103 | 4.2380 × 103 | 4.6267 × 103 | 4.0188 × 103 |
| std | 2.3381 × 102 | 3.0088 × 102 | 1.6788 × 102 | 2.1658 × 102 | 1.5567 × 103 | 4.4456 × 102 | 6.6381 × 102 | 3.4373 × 102 | 2.8790 × 102 | 3.0932 × 102 | 3.7478 × 102 | 9.3907 × 101 | |
| F30 | mean | 4.6429 × 104 | 1.7286 × 106 | 1.7652 × 105 | 9.8724 × 104 | 1.1312 × 109 | 2.8170 × 107 | 8.8037 × 108 | 1.9250 × 106 | 1.1450 × 105 | 6.7548 × 106 | 1.2843 × 107 | 1.5369 × 106 |
| std | 2.9880 × 104 | 2.6549 × 106 | 1.1343 × 105 | 1.5524 × 105 | 6.3220 × 108 | 4.0626 × 107 | 4.9386 × 108 | 3.1153 × 106 | 8.5736 × 104 | 5.7149 × 106 | 1.1160 × 107 | 5.4004 × 105 |
| ID | Metric | PSO | DBO | DMO | IAO | MGO | PO | PLO | BKA | CPSOGSA | HPHHO | SCSO | MISCSO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 8.9897 × 106 | 3.8830 × 108 | 6.8241 × 108 | 7.2852 × 1010 | 2.0034 × 1011 | 3.0362 × 109 | 1.8587 × 1011 | 1.3892 × 1010 | 8.0228 × 107 | 1.2151 × 1010 | 1.6462 × 1010 | 1.7401 × 107 |
| std | 3.0397 × 106 | 2.0759 × 108 | 1.6897 × 108 | 1.1916 × 1010 | 1.7560 × 1010 | 1.6281 × 109 | 1.7736 × 1010 | 1.3333 × 1010 | 3.1379 × 108 | 2.9029 × 109 | 4.5194 × 109 | 3.1662 × 106 | |
| F2 | mean | 1.7366 × 1023 | 4.9106 × 1059 | 2.5265 × 1065 | 2.5978 × 1067 | 4.5250 × 1085 | 6.3464 × 1055 | 1.6571 × 1081 | 1.1868 × 1070 | 7.5540 × 1057 | 1.0000 × 1020 | 1.7256 × 1061 | 1.5470 × 1035 |
| std | 6.0879 × 1023 | 1.7983 × 1060 | 7.1325 × 1065 | 1.4213 × 1068 | 2.0008 × 1086 | 3.0826 × 1056 | 4.7047 × 1081 | 6.5005 × 1070 | 4.0307 × 1058 | 0.0000 × 100 | 9.4203 × 1061 | 2.0672 × 1035 | |
| F3 | mean | 7.6456 × 104 | 2.1162 × 105 | 3.0074 × 105 | 1.0315 × 105 | 4.4547 × 105 | 1.3993 × 105 | 3.9858 × 105 | 6.1453 × 104 | 2.3049 × 105 | 7.8358 × 104 | 1.0695 × 105 | 5.0798 × 104 |
| std | 2.2408 × 104 | 4.5391 × 104 | 2.8965 × 104 | 1.8764 × 104 | 1.1217 × 105 | 1.9049 × 104 | 5.1826 × 104 | 3.8998 × 104 | 5.8799 × 104 | 1.0846 × 104 | 1.8706 × 104 | 4.2001 × 103 | |
| F4 | mean | 5.3716 × 102 | 8.0239 × 102 | 8.7736 × 102 | 1.8250 × 104 | 7.0239 × 104 | 1.0449 × 103 | 5.5375 × 104 | 3.1949 × 103 | 6.4201 × 102 | 1.9547 × 103 | 2.4143 × 103 | 5.6831 × 102 |
| std | 5.0765 × 101 | 1.2802 × 102 | 5.5883 × 101 | 5.6579 × 103 | 1.2618 × 104 | 2.1039 × 102 | 1.2311 × 104 | 5.6780 × 103 | 5.7264 × 101 | 6.7531 × 102 | 1.1714 × 103 | 3.3318 × 101 | |
| F5 | mean | 7.6352 × 102 | 9.4542 × 102 | 9.7494 × 102 | 9.9920 × 102 | 1.5085 × 103 | 9.1577 × 102 | 1.4719 × 103 | 8.7416 × 102 | 9.7727 × 102 | 9.3596 × 102 | 9.1821 × 102 | 7.6681 × 102 |
| std | 3.2423 × 101 | 8.4692 × 101 | 1.7387 × 101 | 3.6338 × 101 | 6.1268 × 101 | 4.3380 × 101 | 5.6923 × 101 | 6.6440 × 101 | 7.5410 × 101 | 3.3968 × 101 | 3.8691 × 101 | 1.2256 × 101 | |
| F6 | mean | 6.5033 × 102 | 6.5599 × 102 | 6.1348 × 102 | 6.6854 × 102 | 7.2929 × 102 | 6.7630 × 102 | 7.2743 × 102 | 6.6713 × 102 | 6.7526 × 102 | 6.7319 × 102 | 6.7171 × 102 | 6.5399 × 102 |
| std | 5.6599 × 100 | 1.1148 × 101 | 1.7602 × 100 | 8.5585 × 100 | 1.0039 × 101 | 6.9614 × 100 | 7.6965 × 100 | 6.3200 × 100 | 9.1079 × 100 | 6.6246 × 100 | 6.7441 × 100 | 3.2413 × 100 | |
| F7 | mean | 1.0948 × 103 | 1.2719 × 103 | 1.2956 × 103 | 1.6689 × 103 | 5.0273 × 103 | 1.6449 × 103 | 5.0203 × 103 | 1.6836 × 103 | 2.3661 × 103 | 1.6965 × 103 | 1.6117 × 103 | 1.2508 × 103 |
| std | 8.8706 × 101 | 1.7884 × 102 | 2.8861 × 101 | 1.1367 × 102 | 3.0848 × 102 | 1.0492 × 102 | 3.9740 × 102 | 8.4073 × 101 | 2.7540 × 102 | 1.2634 × 102 | 1.2786 × 102 | 5.6057 × 101 | |
| F8 | mean | 1.0851 × 103 | 1.2816 × 103 | 1.2715 × 103 | 1.3117 × 103 | 1.8246 × 103 | 1.2461 × 103 | 1.7768 × 103 | 1.2152 × 103 | 1.2208 × 103 | 1.2429 × 103 | 1.2261 × 103 | 1.0789 × 103 |
| std | 3.3980 × 101 | 8.4717 × 101 | 1.8896 × 101 | 3.9585 × 101 | 8.4306 × 101 | 4.0751 × 101 | 5.2736 × 101 | 8.0004 × 101 | 6.1311 × 101 | 3.4434 × 101 | 4.4748 × 101 | 1.9967 × 101 | |
| F9 | mean | 2.2091 × 104 | 1.6831 × 104 | 6.8065 × 103 | 2.0580 × 104 | 7.5428 × 104 | 2.2588 × 104 | 6.8868 × 104 | 1.5273 × 104 | 1.9327 × 104 | 1.9931 × 104 | 1.9139 × 104 | 1.1559 × 104 |
| std | 4.4515 × 103 | 6.8780 × 103 | 1.4345 × 103 | 2.6027 × 103 | 8.0130 × 103 | 2.6779 × 103 | 8.1827 × 103 | 3.7172 × 103 | 3.9444 × 103 | 3.0756 × 103 | 2.9953 × 103 | 1.4641 × 103 | |
| F10 | mean | 7.5691 × 103 | 9.4782 × 103 | 1.4822 × 104 | 1.0629 × 104 | 1.6027 × 104 | 1.1254 × 104 | 1.5770 × 104 | 9.3151 × 103 | 8.2329 × 103 | 9.5573 × 103 | 9.7088 × 103 | 7.3454 × 103 |
| std | 1.0257 × 103 | 1.6171 × 103 | 3.8813 × 102 | 6.7649 × 102 | 7.1636 × 102 | 1.1608 × 103 | 4.8646 × 102 | 2.0822 × 103 | 7.2495 × 102 | 1.0361 × 103 | 8.8439 × 102 | 5.1975 × 102 | |
| F11 | mean | 1.3084 × 103 | 2.8057 × 103 | 3.4290 × 103 | 8.4334 × 103 | 5.0425 × 104 | 3.4656 × 103 | 5.0020 × 104 | 2.1447 × 103 | 1.6932 × 103 | 2.0302 × 103 | 5.3820 × 103 | 1.4838 × 103 |
| std | 4.4726 × 101 | 3.1472 × 103 | 6.6895 × 102 | 2.5305 × 103 | 9.6248 × 103 | 8.4350 × 102 | 8.9463 × 103 | 8.1748 × 102 | 2.1881 × 102 | 2.1977 × 102 | 2.2845 × 103 | 4.1901 × 101 | |
| F12 | mean | 1.2636 × 107 | 4.4924 × 108 | 4.0077 × 108 | 1.9878 × 1010 | 8.3546 × 1010 | 6.4397 × 108 | 7.2780 × 1010 | 5.2672 × 109 | 2.8980 × 107 | 7.4617 × 108 | 2.3667 × 109 | 4.3955 × 107 |
| std | 6.8351 × 106 | 4.3211 × 108 | 9.2467 × 107 | 8.4191 × 109 | 1.8339 × 1010 | 3.2408 × 108 | 1.2532 × 1010 | 1.1417 × 1010 | 1.6236 × 107 | 5.5954 × 108 | 1.7902 × 109 | 1.5910 × 107 | |
| F13 | mean | 3.1687 × 104 | 1.3667 × 107 | 6.6872 × 103 | 4.7262 × 108 | 4.1161 × 1010 | 6.6942 × 107 | 3.5808 × 1010 | 1.4816 × 109 | 6.6906 × 104 | 2.3602 × 107 | 1.7187 × 108 | 1.3468 × 105 |
| std | 1.6727 × 104 | 1.6969 × 107 | 4.1016 × 103 | 6.3704 × 108 | 1.2017 × 1010 | 9.7544 × 107 | 9.5093 × 109 | 3.9241 × 109 | 4.7047 × 104 | 2.7145 × 107 | 2.3588 × 108 | 2.6952 × 104 | |
| F14 | mean | 1.3470 × 105 | 2.1477 × 106 | 1.5048 × 106 | 2.0190 × 103 | 7.4678 × 107 | 3.0796 × 106 | 4.4965 × 107 | 1.0076 × 105 | 2.3467 × 105 | 1.1184 × 106 | 1.3126 × 106 | 1.8089 × 105 |
| std | 9.3046 × 104 | 2.1338 × 106 | 5.8449 × 105 | 4.5436 × 102 | 6.0237 × 107 | 1.6255 × 106 | 2.8857 × 107 | 1.7383 × 105 | 1.6995 × 105 | 7.7343 × 105 | 1.6067 × 106 | 6.1229 × 104 | |
| F15 | mean | 9.4583 × 103 | 4.1022 × 107 | 1.0580 × 104 | 2.4265 × 104 | 1.4440 × 1010 | 3.7018 × 106 | 1.0244 × 1010 | 1.3835 × 108 | 3.3724 × 104 | 2.2098 × 106 | 3.5576 × 107 | 2.5660 × 104 |
| std | 7.4309 × 103 | 1.6150 × 108 | 4.1280 × 103 | 1.4673 × 104 | 5.0160 × 109 | 5.7302 × 106 | 3.2543 × 109 | 3.5153 × 108 | 1.6147 × 104 | 3.2240 × 106 | 1.1387 × 108 | 4.2022 × 103 | |
| F16 | mean | 3.3922 × 103 | 4.5915 × 103 | 5.0723 × 103 | 4.1689 × 103 | 9.4577 × 103 | 4.7916 × 103 | 8.6668 × 103 | 4.1650 × 103 | 4.0791 × 103 | 4.2674 × 103 | 4.4603 × 103 | 3.4372 × 103 |
| std | 4.9670 × 102 | 5.9073 × 102 | 2.3257 × 102 | 4.4128 × 102 | 1.0670 × 103 | 7.3801 × 102 | 8.1791 × 102 | 9.4155 × 102 | 5.4438 × 102 | 5.6211 × 102 | 5.2932 × 102 | 2.3198 × 102 | |
| F17 | mean | 3.1624 × 103 | 4.0404 × 103 | 3.9932 × 103 | 3.1527 × 103 | 6.2401 × 104 | 3.9160 × 103 | 3.4947 × 104 | 3.4769 × 103 | 3.8316 × 103 | 3.5956 × 103 | 3.7673 × 103 | 3.0168 × 103 |
| std | 3.5573 × 102 | 4.9686 × 102 | 1.5217 × 102 | 2.3741 × 102 | 6.6416 × 104 | 3.9606 × 102 | 4.0201 × 104 | 4.6386 × 102 | 4.9900 × 102 | 3.3314 × 102 | 4.1176 × 102 | 1.5959 × 102 | |
| F18 | mean | 1.4819 × 106 | 6.1166 × 106 | 1.6441 × 107 | 8.8023 × 104 | 2.5618 × 108 | 1.2051 × 107 | 1.7325 × 108 | 3.1260 × 106 | 1.2420 × 106 | 5.8020 × 106 | 1.1772 × 107 | 8.2573 × 105 |
| std | 1.0028 × 106 | 6.3179 × 106 | 6.0826 × 106 | 3.8600 × 104 | 1.3547 × 108 | 1.0071 × 107 | 6.4040 × 107 | 9.7107 × 106 | 1.1660 × 106 | 4.8214 × 106 | 1.5287 × 107 | 2.4819 × 105 | |
| F19 | mean | 1.5635 × 104 | 4.4341 × 106 | 1.6262 × 104 | 3.3861 × 105 | 5.5993 × 109 | 7.8509 × 106 | 4.2829 × 109 | 5.0375 × 107 | 2.6380 × 104 | 7.0202 × 105 | 8.4308 × 106 | 3.5103 × 105 |
| std | 1.0625 × 104 | 6.9827 × 106 | 6.8507 × 103 | 5.0725 × 105 | 1.5878 × 109 | 6.7613 × 106 | 1.2356 × 109 | 1.5638 × 108 | 1.6900 × 104 | 7.7571 × 105 | 1.1979 × 107 | 2.1807 × 105 | |
| F20 | mean | 3.1615 × 103 | 3.5236 × 103 | 4.0469 × 103 | 2.8847 × 103 | 4.7552 × 103 | 3.5465 × 103 | 4.7079 × 103 | 3.2162 × 103 | 3.4197 × 103 | 3.1248 × 103 | 3.3806 × 103 | 2.9304 × 103 |
| std | 3.4935 × 102 | 3.6323 × 102 | 2.1201 × 102 | 1.5020 × 102 | 2.7404 × 102 | 3.2637 × 102 | 2.8110 × 102 | 2.5417 × 102 | 3.1547 × 102 | 2.8352 × 102 | 2.6095 × 102 | 1.0680 × 102 | |
| F21 | mean | 2.6717 × 103 | 2.7804 × 103 | 2.7634 × 103 | 2.8274 × 103 | 3.3412 × 103 | 2.7984 × 103 | 3.2658 × 103 | 2.7986 × 103 | 2.8834 × 103 | 2.8095 × 103 | 2.7442 × 103 | 2.5964 × 103 |
| std | 5.9562 × 101 | 7.0692 × 101 | 1.8472 × 101 | 4.9625 × 101 | 6.4493 × 101 | 7.3872 × 101 | 6.7888 × 101 | 8.3227 × 101 | 9.5616 × 101 | 6.9845 × 101 | 6.6961 × 101 | 2.1165 × 101 | |
| F22 | mean | 9.2216 × 103 | 1.1527 × 104 | 1.6071 × 104 | 1.2242 × 104 | 1.7902 × 104 | 1.2663 × 104 | 1.7281 × 104 | 9.9427 × 103 | 1.0028 × 104 | 1.2031 × 104 | 1.1786 × 104 | 8.4733 × 103 |
| std | 9.5078 × 102 | 1.3529 × 103 | 1.0737 × 103 | 1.2702 × 103 | 4.7019 × 102 | 1.2700 × 103 | 5.6768 × 102 | 8.9377 × 102 | 9.3330 × 102 | 9.1668 × 102 | 1.1439 × 103 | 2.1008 × 103 | |
| F23 | mean | 3.5916 × 103 | 3.3896 × 103 | 3.1828 × 103 | 3.4926 × 103 | 4.4736 × 103 | 3.5000 × 103 | 4.2168 × 103 | 3.7011 × 103 | 3.5119 × 103 | 3.4746 × 103 | 3.2987 × 103 | 3.1267 × 103 |
| std | 2.2505 × 102 | 1.1927 × 102 | 1.7076 × 101 | 1.3328 × 102 | 2.4277 × 102 | 1.2086 × 102 | 1.4020 × 102 | 1.8246 × 102 | 1.1937 × 102 | 1.5604 × 102 | 8.8678 × 101 | 2.1117 × 101 | |
| F24 | mean | 3.5469 × 103 | 3.4724 × 103 | 3.3312 × 103 | 3.5904 × 103 | 4.9357 × 103 | 3.6792 × 103 | 4.5729 × 103 | 3.7385 × 103 | 3.9314 × 103 | 3.6763 × 103 | 3.4205 × 103 | 3.2304 × 103 |
| std | 1.2528 × 102 | 1.0877 × 102 | 1.2478 × 101 | 9.1181 × 101 | 2.4920 × 102 | 1.4087 × 102 | 1.5763 × 102 | 1.2822 × 102 | 1.6048 × 102 | 1.3779 × 102 | 9.0690 × 101 | 2.7000 × 101 | |
| F25 | mean | 2.9835 × 103 | 3.2277 × 103 | 3.3276 × 103 | 1.0425 × 104 | 3.9095 × 104 | 3.5450 × 103 | 3.5369 × 104 | 4.5997 × 103 | 3.1239 × 103 | 3.9349 × 103 | 4.3439 × 103 | 3.1040 × 103 |
| std | 4.3010 × 101 | 8.7647 × 101 | 6.4777 × 101 | 1.3513 × 103 | 5.6212 × 103 | 1.7605 × 102 | 5.3989 × 103 | 2.4586 × 103 | 3.2608 × 101 | 3.0082 × 102 | 5.1200 × 102 | 2.1872 × 101 | |
| F26 | mean | 8.4219 × 103 | 1.0059 × 104 | 8.3198 × 103 | 1.3926 × 104 | 2.3770 × 104 | 9.5870 × 103 | 2.0979 × 104 | 1.1074 × 104 | 1.1839 × 104 | 1.1393 × 104 | 1.0844 × 104 | 3.7741 × 103 |
| std | 3.4611 × 103 | 1.0294 × 103 | 2.0570 × 102 | 1.0432 × 103 | 2.2506 × 103 | 2.5757 × 103 | 1.8586 × 103 | 2.2617 × 103 | 1.3737 × 103 | 1.3204 × 103 | 2.2053 × 103 | 3.7862 × 102 | |
| F27 | mean | 3.8664 × 103 | 3.7775 × 103 | 3.5385 × 103 | 3.8716 × 103 | 6.6507 × 103 | 4.0439 × 103 | 5.9407 × 103 | 4.1983 × 103 | 4.6542 × 103 | 3.9183 × 103 | 4.1476 × 103 | 3.6785 × 103 |
| std | 6.8506 × 102 | 1.9470 × 102 | 3.7385 × 101 | 1.1793 × 102 | 4.7349 × 102 | 3.0257 × 102 | 3.5751 × 102 | 3.9154 × 102 | 3.2811 × 102 | 2.4541 × 102 | 2.2826 × 102 | 5.6679 × 101 | |
| F28 | mean | 3.2911 × 103 | 5.3736 × 103 | 3.7746 × 103 | 8.5576 × 103 | 1.8003 × 104 | 4.1462 × 103 | 1.6527 × 104 | 4.6413 × 103 | 3.4260 × 103 | 4.6468 × 103 | 5.0102 × 103 | 3.3727 × 103 |
| std | 3.1086 × 101 | 2.2895 × 103 | 1.3090 × 102 | 8.5361 × 102 | 1.8625 × 103 | 2.2770 × 102 | 1.3132 × 103 | 1.2330 × 103 | 1.1099 × 102 | 3.4522 × 102 | 4.9098 × 102 | 1.7543 × 101 | |
| F29 | mean | 5.1661 × 103 | 5.7056 × 103 | 5.6765 × 103 | 6.5253 × 103 | 7.6935 × 104 | 7.2752 × 103 | 4.5461 × 104 | 6.1550 × 103 | 6.3027 × 103 | 6.4383 × 103 | 6.4535 × 103 | 5.3625 × 103 |
| std | 3.5375 × 102 | 8.6028 × 102 | 2.6418 × 102 | 1.0053 × 103 | 6.7638 × 104 | 9.4449 × 102 | 2.5702 × 104 | 1.2094 × 103 | 5.5447 × 102 | 7.1051 × 102 | 8.0067 × 102 | 2.1798 × 102 | |
| F30 | mean | 4.5567 × 106 | 2.9449 × 107 | 1.6845 × 107 | 6.0409 × 107 | 7.9246 × 109 | 2.0830 × 108 | 6.7389 × 109 | 1.0056 × 108 | 4.1553 × 107 | 1.4806 × 108 | 1.6542 × 108 | 6.7228 × 107 |
| std | 1.5213 × 106 | 2.3182 × 107 | 7.0009 × 106 | 3.1111 × 107 | 2.9827 × 109 | 8.3280 × 107 | 2.9003 × 109 | 3.0905 × 108 | 1.6847 × 107 | 5.7281 × 107 | 1.2992 × 108 | 1.0398 × 107 |
| ID | Metric | PSO | DBO | DMO | IAO | MGO | PO | PLO | BKA | CPSOGSA | HPHHO | SCSO | MISCSO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 1.3417 × 108 | 7.5275 × 1010 | 5.3144 × 1010 | 2.1959 × 1011 | 5.2807 × 1011 | 2.4302 × 1010 | 5.1969 × 1011 | 9.9858 × 1010 | 2.6018 × 109 | 6.8836 × 1010 | 7.1122 × 1010 | 5.9830 × 108 |
| std | 3.0715 × 107 | 7.1062 × 1010 | 4.5607 × 109 | 1.9282 × 1010 | 3.1059 × 1010 | 5.1713 × 109 | 3.9216 × 1010 | 3.7310 × 1010 | 1.4501 × 109 | 1.3717 × 1010 | 1.5200 × 1010 | 8.6889 × 107 | |
| F2 | mean | 3.4896 × 1070 | 7.6065 × 10149 | 1.0263 × 10154 | 4.6125 × 10153 | 1.5353 × 10184 | 2.0033 × 10147 | 7.7085 × 10180 | 8.5159 × 10159 | 1.0393 × 10144 | 1.0000 × 1020 | 3.1511 × 10147 | 3.9429 × 10106 |
| std | 1.8584 × 1071 | 4.1657 × 10150 | 6.5535 × 104 | 6.5535 × 104 | 6.5535 × 104 | 1.0931 × 10148 | 6.5535 × 104 | 6.5535 × 104 | 4.1438 × 10144 | 0.0000 × 100 | 1.2700 × 10148 | 6.4596 × 10106 | |
| F3 | mean | 3.8388 × 105 | 5.1027 × 105 | 7.9320 × 105 | 2.7192 × 105 | 7.1314 × 106 | 3.2742 × 105 | 9.6133 × 105 | 2.1070 × 105 | 7.1606 × 105 | 2.6138 × 105 | 2.7788 × 105 | 2.4673 × 105 |
| std | 6.5156 × 104 | 1.9002 × 105 | 5.5838 × 104 | 2.2068 × 104 | 3.2253 × 107 | 1.7737 × 104 | 1.1674 × 105 | 4.7311 × 104 | 1.0491 × 105 | 2.3532 × 104 | 1.9801 × 104 | 9.3426 × 103 | |
| F4 | mean | 7.2547 × 102 | 7.3972 × 103 | 6.8730 × 103 | 6.6603 × 104 | 2.2101 × 105 | 3.7932 × 103 | 1.9902 × 105 | 1.8181 × 104 | 1.7090 × 103 | 9.1244 × 103 | 8.5617 × 103 | 1.0729 × 103 |
| std | 7.8092 × 101 | 7.3116 × 103 | 9.7090 × 102 | 1.2471 × 104 | 2.7481 × 104 | 8.6808 × 102 | 2.5537 × 104 | 2.1043 × 104 | 4.1576 × 102 | 2.1043 × 103 | 2.2072 × 103 | 4.6174 × 101 | |
| F5 | mean | 1.2616 × 103 | 1.6985 × 103 | 1.7317 × 103 | 1.8512 × 103 | 2.8740 × 103 | 1.6066 × 103 | 2.8265 × 103 | 1.4397 × 103 | 1.7515 × 103 | 1.6633 × 103 | 1.5491 × 103 | 1.2647 × 103 |
| std | 6.3621 × 101 | 2.1028 × 102 | 3.4889 × 101 | 4.4516 × 101 | 1.2735 × 102 | 5.9595 × 101 | 9.7750 × 101 | 9.4815 × 101 | 1.1151 × 102 | 6.3565 × 101 | 6.1464 × 101 | 2.2101 × 101 | |
| F6 | mean | 6.6425 × 102 | 6.7480 × 102 | 6.5356 × 102 | 6.8974 × 102 | 7.4996 × 102 | 6.8707 × 102 | 7.4546 × 102 | 6.7519 × 102 | 6.7767 × 102 | 6.8418 × 102 | 6.8075 × 102 | 6.6850 × 102 |
| std | 4.0104 × 100 | 1.0430 × 101 | 2.9298 × 100 | 3.5934 × 100 | 7.2824 × 100 | 4.8998 × 100 | 6.5568 × 100 | 7.4819 × 100 | 5.0511 × 100 | 3.6326 × 100 | 5.2711 × 100 | 1.4058 × 100 | |
| F7 | mean | 1.9310 × 103 | 2.4859 × 103 | 3.6656 × 103 | 3.5548 × 103 | 1.2055 × 104 | 3.4556 × 103 | 1.2102 × 104 | 3.3425 × 103 | 5.6263 × 103 | 3.4906 × 103 | 3.2834 × 103 | 2.6046 × 103 |
| std | 1.9336 × 102 | 3.5410 × 102 | 1.8671 × 102 | 1.3194 × 102 | 6.7245 × 102 | 1.4942 × 102 | 4.9136 × 102 | 2.3969 × 102 | 3.9818 × 102 | 1.5693 × 102 | 1.9165 × 102 | 8.1318 × 101 | |
| F8 | mean | 1.6581 × 103 | 1.9770 × 103 | 2.0341 × 103 | 2.2749 × 103 | 3.3048 × 103 | 2.0662 × 103 | 3.1968 × 103 | 1.9594 × 103 | 2.0318 × 103 | 2.1104 × 103 | 2.0049 × 103 | 1.6702 × 103 |
| std | 7.7515 × 101 | 2.1795 × 102 | 3.0489 × 101 | 8.7933 × 101 | 1.2395 × 102 | 8.4005 × 101 | 9.9289 × 101 | 2.1150 × 102 | 1.4369 × 102 | 5.9972 × 101 | 6.5791 × 101 | 4.9479 × 101 | |
| F9 | mean | 6.0135 × 104 | 5.3976 × 104 | 5.7983 × 104 | 5.1146 × 104 | 1.8895 × 105 | 5.2315 × 104 | 1.8141 × 105 | 3.1862 × 104 | 4.2118 × 104 | 4.5908 × 104 | 3.6853 × 104 | 3.0554 × 104 |
| std | 5.6835 × 103 | 1.9578 × 104 | 5.5381 × 103 | 3.4822 × 103 | 1.3739 × 104 | 7.0990 × 103 | 1.3169 × 104 | 7.9575 × 103 | 4.3950 × 103 | 5.4467 × 103 | 3.8356 × 103 | 1.8353 × 103 | |
| F10 | mean | 1.6112 × 104 | 2.0124 × 104 | 3.2166 × 104 | 2.5587 × 104 | 3.4078 × 104 | 2.4590 × 104 | 3.3289 × 104 | 1.9880 × 104 | 1.5535 × 104 | 2.3895 × 104 | 2.0994 × 104 | 1.6721 × 104 |
| std | 1.3922 × 103 | 4.1579 × 103 | 4.7389 × 102 | 9.3680 × 102 | 7.2730 × 102 | 1.8571 × 103 | 8.0971 × 102 | 3.8254 × 103 | 1.6013 × 103 | 2.2183 × 103 | 1.7852 × 103 | 6.8311 × 102 | |
| F11 | mean | 5.5082 × 103 | 1.2994 × 105 | 2.0793 × 105 | 1.0047 × 105 | 4.5115 × 105 | 1.0318 × 105 | 4.1373 × 105 | 2.8720 × 104 | 8.0193 × 104 | 4.7338 × 104 | 6.5927 × 104 | 1.2607 × 104 |
| std | 7.8387 × 102 | 3.9820 × 104 | 3.2477 × 104 | 2.0703 × 104 | 7.4983 × 104 | 2.0204 × 104 | 5.8962 × 104 | 1.6852 × 104 | 2.8207 × 104 | 8.0111 × 103 | 1.4250 × 104 | 1.4629 × 103 | |
| F12 | mean | 1.9315 × 108 | 2.1943 × 109 | 6.4257 × 109 | 1.1456 × 1011 | 2.7801 × 1011 | 5.1881 × 109 | 2.5099 × 1011 | 3.2564 × 1010 | 7.3962 × 108 | 1.1653 × 1010 | 2.0530 × 1010 | 4.5209 × 108 |
| std | 6.4261 × 107 | 8.1147 × 108 | 7.6621 × 108 | 2.4020 × 1010 | 2.9384 × 1010 | 1.5215 × 109 | 2.5618 × 1010 | 4.4735 × 1010 | 2.8725 × 108 | 3.7579 × 109 | 9.5426 × 109 | 7.3371 × 107 | |
| F13 | mean | 2.1439 × 105 | 1.0409 × 108 | 2.5152 × 104 | 2.1896 × 1010 | 6.3415 × 1010 | 1.8314 × 108 | 5.9511 × 1010 | 2.5207 × 109 | 5.9130 × 104 | 5.6564 × 108 | 2.7126 × 109 | 5.3201 × 105 |
| std | 9.1403 × 104 | 1.2228 × 108 | 5.1916 × 103 | 6.4544 × 109 | 1.0951 × 1010 | 1.3609 × 108 | 1.0263 × 1010 | 6.7668 × 109 | 2.0832 × 104 | 3.6837 × 108 | 2.1081 × 109 | 9.1890 × 104 | |
| F14 | mean | 1.6929 × 106 | 1.0114 × 107 | 4.3416 × 107 | 1.2523 × 106 | 2.8907 × 108 | 1.0307 × 107 | 2.0241 × 108 | 2.9805 × 106 | 1.2923 × 106 | 5.6790 × 106 | 9.0924 × 106 | 1.9009 × 106 |
| std | 7.3655 × 105 | 8.9530 × 106 | 1.0916 × 107 | 7.5832 × 105 | 1.0941 × 108 | 3.3532 × 106 | 6.6580 × 107 | 5.1294 × 106 | 5.9305 × 105 | 2.3965 × 106 | 5.3195 × 106 | 3.1197 × 105 | |
| F15 | mean | 3.8409 × 104 | 2.5386 × 107 | 4.3138 × 103 | 4.7115 × 109 | 2.9896 × 1010 | 2.9369 × 107 | 2.4322 × 1010 | 1.5839 × 109 | 9.9209 × 107 | 1.6142 × 107 | 4.1581 × 108 | 9.8767 × 104 |
| std | 1.5797 × 104 | 4.2384 × 107 | 1.2470 × 103 | 2.1347 × 109 | 6.5440 × 109 | 2.7073 × 107 | 4.3845 × 109 | 3.6645 × 109 | 5.4314 × 108 | 1.3577 × 107 | 6.5657 × 108 | 1.2761 × 104 | |
| F16 | mean | 5.9023 × 103 | 8.6327 × 103 | 1.1152 × 104 | 1.3122 × 104 | 2.7906 × 104 | 1.1317 × 104 | 2.4361 × 104 | 9.0805 × 103 | 7.1024 × 103 | 1.1695 × 104 | 9.9139 × 103 | 7.2233 × 103 |
| std | 7.4294 × 102 | 1.2257 × 103 | 2.7198 × 102 | 2.3579 × 103 | 3.8252 × 103 | 1.3929 × 103 | 3.1986 × 103 | 2.4697 × 103 | 8.4138 × 102 | 1.3186 × 103 | 1.3788 × 103 | 4.5936 × 102 | |
| F17 | mean | 5.2135 × 103 | 8.2577 × 103 | 7.8288 × 103 | 2.8828 × 104 | 1.3481 × 107 | 8.0902 × 103 | 9.5828 × 106 | 2.7447 × 104 | 6.2810 × 103 | 7.4052 × 103 | 1.2082 × 104 | 5.3440 × 103 |
| std | 4.8549 × 102 | 1.2441 × 103 | 1.9766 × 102 | 4.9208 × 104 | 1.0991 × 107 | 1.3704 × 103 | 7.4423 × 106 | 7.7080 × 104 | 6.5333 × 102 | 1.2525 × 103 | 1.1775 × 104 | 2.4747 × 102 | |
| F18 | mean | 2.9703 × 106 | 1.7444 × 107 | 7.4587 × 107 | 2.7474 × 106 | 5.4712 × 108 | 1.0270 × 107 | 3.3874 × 108 | 3.0589 × 106 | 2.1624 × 106 | 8.4424 × 106 | 7.6992 × 106 | 2.1353 × 106 |
| std | 1.6847 × 106 | 1.1891 × 107 | 2.0434 × 107 | 2.1554 × 106 | 2.1677 × 108 | 3.7278 × 106 | 1.1721 × 108 | 9.6891 × 106 | 1.2873 × 106 | 5.2353 × 106 | 4.5529 × 106 | 4.0130 × 105 | |
| F19 | mean | 1.3983 × 105 | 3.2923 × 107 | 7.3914 × 103 | 6.0907 × 109 | 3.1967 × 1010 | 5.6972 × 107 | 2.4464 × 1010 | 1.1938 × 109 | 3.0443 × 105 | 3.4562 × 107 | 2.7124 × 108 | 2.7859 × 106 |
| std | 1.0726 × 105 | 2.3692 × 107 | 5.2099 × 103 | 3.6484 × 109 | 7.0427 × 109 | 3.0206 × 107 | 6.0497 × 109 | 3.9181 × 109 | 2.4613 × 105 | 3.1005 × 107 | 4.1897 × 108 | 1.2052 × 106 | |
| F20 | mean | 5.2029 × 103 | 6.2214 × 103 | 7.6732 × 103 | 5.2612 × 103 | 8.8850 × 103 | 6.0953 × 103 | 8.5595 × 103 | 5.4585 × 103 | 5.8445 × 103 | 5.5406 × 103 | 6.0480 × 103 | 4.8782 × 103 |
| std | 4.2759 × 102 | 6.3022 × 102 | 2.4911 × 102 | 2.7328 × 102 | 2.4668 × 102 | 6.8116 × 102 | 3.6335 × 102 | 6.4669 × 102 | 6.3348 × 102 | 4.7647 × 102 | 5.8050 × 102 | 2.0478 × 102 | |
| F21 | mean | 3.5566 × 103 | 3.8161 × 103 | 3.5552 × 103 | 3.9587 × 103 | 5.0584 × 103 | 3.9986 × 103 | 4.8757 × 103 | 4.0417 × 103 | 4.0718 × 103 | 3.8261 × 103 | 3.6868 × 103 | 3.3045 × 103 |
| std | 1.6298 × 102 | 1.5814 × 102 | 1.9908 × 101 | 1.1317 × 102 | 1.3765 × 102 | 1.7688 × 102 | 1.2379 × 102 | 2.4963 × 102 | 2.1573 × 102 | 1.5736 × 102 | 1.5412 × 102 | 6.5374 × 101 | |
| F22 | mean | 1.9438 × 104 | 2.3606 × 104 | 3.4357 × 104 | 2.9350 × 104 | 3.6714 × 104 | 2.7450 × 104 | 3.5858 × 104 | 2.3450 × 104 | 1.9149 × 104 | 2.7190 × 104 | 2.4304 × 104 | 2.0667 × 104 |
| std | 1.4741 × 103 | 4.5183 × 103 | 5.9876 × 102 | 7.5912 × 102 | 6.7439 × 102 | 1.6484 × 103 | 6.0757 × 102 | 4.3770 × 103 | 1.7701 × 103 | 1.2764 × 103 | 1.6426 × 103 | 7.0815 × 102 | |
| F23 | mean | 4.8375 × 103 | 4.4524 × 103 | 3.9615 × 103 | 4.6464 × 103 | 6.8251 × 103 | 4.8022 × 103 | 6.1770 × 103 | 4.9967 × 103 | 4.8377 × 103 | 4.6312 × 103 | 4.3476 × 103 | 3.9001 × 103 |
| std | 3.4874 × 102 | 1.7784 × 102 | 2.8351 × 101 | 1.7691 × 102 | 3.4460 × 102 | 2.0527 × 102 | 2.1078 × 102 | 3.0879 × 102 | 1.9663 × 102 | 2.2894 × 102 | 1.7691 × 102 | 7.6276 × 101 | |
| F24 | mean | 5.4915 × 103 | 5.5158 × 103 | 4.4254 × 103 | 6.0469 × 103 | 1.1242 × 104 | 6.0808 × 103 | 9.6470 × 103 | 6.5956 × 103 | 6.4250 × 103 | 5.5311 × 103 | 5.4512 × 103 | 4.6226 × 103 |
| std | 4.7362 × 102 | 2.8658 × 102 | 2.7806 × 101 | 2.8678 × 102 | 7.9258 × 102 | 3.4380 × 102 | 6.6463 × 102 | 6.5386 × 102 | 3.7405 × 102 | 3.5290 × 102 | 3.7562 × 102 | 6.4913 × 101 | |
| F25 | mean | 3.3535 × 103 | 8.8468 × 103 | 1.3265 × 104 | 2.2048 × 104 | 1.0759 × 105 | 5.6565 × 103 | 9.9680 × 104 | 9.9253 × 103 | 3.9953 × 103 | 7.4599 × 103 | 8.1929 × 103 | 3.7610 × 103 |
| std | 4.7772 × 101 | 5.2477 × 103 | 8.7086 × 102 | 2.0174 × 103 | 1.3457 × 104 | 4.0243 × 102 | 1.4290 × 104 | 5.5418 × 103 | 2.6511 × 102 | 6.6584 × 102 | 1.4645 × 103 | 3.5168 × 101 | |
| F26 | mean | 1.7600 × 104 | 2.4786 × 104 | 1.7903 × 104 | 4.2072 × 104 | 7.1745 × 104 | 2.9723 × 104 | 6.3946 × 104 | 3.2939 × 104 | 3.1013 × 104 | 2.8991 × 104 | 3.0282 × 104 | 1.3552 × 104 |
| std | 7.5967 × 103 | 3.1601 × 103 | 4.3060 × 102 | 2.9494 × 103 | 7.6872 × 103 | 4.7466 × 103 | 5.0715 × 103 | 6.2733 × 103 | 2.5840 × 103 | 3.4741 × 103 | 2.0934 × 103 | 5.1113 × 103 | |
| F27 | mean | 3.4709 × 103 | 4.2447 × 103 | 4.5080 × 103 | 5.6710 × 103 | 1.3122 × 104 | 4.6439 × 103 | 1.1341 × 104 | 5.5933 × 103 | 5.5228 × 103 | 4.8841 × 103 | 5.2115 × 103 | 4.1508 × 103 |
| std | 2.0127 × 102 | 2.8770 × 102 | 1.0691 × 102 | 4.3914 × 102 | 1.2431 × 103 | 2.9640 × 102 | 1.3540 × 103 | 1.0501 × 103 | 5.4416 × 102 | 3.7166 × 102 | 4.9903 × 102 | 1.1908 × 102 | |
| F28 | mean | 3.4068 × 103 | 1.8846 × 104 | 1.5219 × 104 | 2.5772 × 104 | 6.0657 × 104 | 7.0005 × 103 | 5.5754 × 104 | 1.5308 × 104 | 4.1726 × 103 | 9.3222 × 103 | 1.0817 × 104 | 3.8440 × 103 |
| std | 5.9616 × 101 | 6.5191 × 103 | 8.9659 × 102 | 2.4713 × 103 | 4.8545 × 103 | 8.0981 × 102 | 4.6421 × 103 | 8.7921 × 103 | 4.2315 × 102 | 1.1253 × 103 | 1.7695 × 103 | 3.9568 × 101 | |
| F29 | mean | 8.3723 × 103 | 1.0313 × 104 | 1.0708 × 104 | 2.5008 × 104 | 2.4034 × 106 | 1.4682 × 104 | 1.3342 × 106 | 1.5583 × 104 | 1.0435 × 104 | 1.3225 × 104 | 1.2871 × 104 | 9.5424 × 103 |
| std | 6.1003 × 102 | 1.6888 × 103 | 3.7774 × 102 | 1.4571 × 104 | 2.3469 × 106 | 1.8804 × 103 | 9.0266 × 105 | 1.1953 × 104 | 1.1081 × 103 | 1.3959 × 103 | 1.5185 × 103 | 4.2615 × 102 | |
| F30 | mean | 6.3701 × 106 | 9.7467 × 107 | 1.0439 × 107 | 1.4970 × 1010 | 5.0011 × 1010 | 7.4598 × 108 | 4.1053 × 1010 | 2.4285 × 109 | 1.1978 × 107 | 8.2198 × 108 | 1.4441 × 109 | 9.0562 × 107 |
| std | 3.2492 × 106 | 6.1779 × 107 | 4.1847 × 106 | 7.4639 × 109 | 9.7578 × 109 | 3.4036 × 108 | 7.5905 × 109 | 5.5095 × 109 | 5.9905 × 106 | 3.2161 × 108 | 1.1092 × 109 | 1.5677 × 107 |
| Item | PSO | DBO | DMO | IAO | MGO | PO | PLO | BKA | CPSOGSA | HPHHO | SCSO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.3384 × 10−11 | 2.7548 × 10−3 | 1.2967 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.6132 × 10−10 | 3.0199 × 10−11 | 1.2118 × 10−12 | 3.0199 × 10−11 |
| F3 | 2.1959 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.1199 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F4 | 2.7719 × 10−1 | 6.1210 × 10−10 | 4.5043 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.5726 × 10−9 | 4.4272 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F5 | 8.8829 × 10−6 | 5.4941 × 10−11 | 3.0199 × 10−11 | 8.9934 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F6 | 9.0307 × 10−4 | 3.3285 × 10−1 | 3.0199 × 10−11 | 7.0881 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.3715 × 10−10 | 1.4643 × 10−10 |
| F7 | 1.8567 × 10−9 | 2.9047 × 10−1 | 1.0937 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F8 | 6.3772 × 10−3 | 2.9215 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.2023 × 10−8 | 3.0199 × 10−11 | 1.4643 × 10−10 | 3.0199 × 10−11 |
| F9 | 9.5139 × 10−6 | 2.1959 × 10−7 | 3.0199 × 10−11 | 1.0105 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.4941 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F10 | 1.1711 × 10−2 | 1.3853 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.5727 × 10−10 | 3.0199 × 10−11 | 1.5292 × 10−5 | 2.1959 × 10−7 | 1.1077 × 10−6 | 1.6947 × 10−9 |
| F11 | 9.3341 × 10−2 | 3.0199 × 10−11 | 4.5043 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.3768 × 10−7 | 4.2175 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F12 | 2.2273 × 10−9 | 1.0407 × 10−4 | 7.3803 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.2640 × 10−4 | 6.5277 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F13 | 2.3168 × 10−6 | 1.7294 × 10−7 | 1.0702 × 10−9 | 7.2884 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.0338 × 10−9 | 4.1191 × 10−1 | 3.0199 × 10−11 | 2.7829 × 10−7 |
| F14 | 6.5671 × 10−2 | 2.4386 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.3715 × 10−10 | 2.6243 × 10−3 | 5.0723 × 10−10 | 8.4848 × 10−9 |
| F15 | 4.9818 × 10−4 | 1.0105 × 10−8 | 3.1967 × 10−9 | 6.0658 × 10−11 | 3.0199 × 10−11 | 4.5043 × 10−11 | 3.0199 × 10−11 | 7.5991 × 10−7 | 2.3985 × 10−1 | 3.4742 × 10−10 | 3.0199 × 10−11 |
| F16 | 4.8413 × 10−2 | 4.7445 × 10−6 | 6.0658 × 10−11 | 4.4642 × 10−1 | 3.0199 × 10−11 | 8.1527 × 10−11 | 3.0199 × 10−11 | 1.4918 × 10−6 | 9.2603 × 10−9 | 1.3367 × 10−5 | 3.1589 × 10−10 |
| F17 | 2.1540 × 10−6 | 5.4941 × 10−11 | 5.5727 × 10−10 | 1.0547 × 10−1 | 3.0199 × 10−11 | 2.3715 × 10−10 | 3.0199 × 10−11 | 9.2603 × 10−9 | 3.0199 × 10−11 | 1.7294 × 10−7 | 8.1014 × 10−10 |
| F18 | 1.5178 × 10−3 | 3.2555 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.1544 × 10−10 | 3.0199 × 10−11 | 5.1857 × 10−7 | 8.5000 × 10−2 | 2.9215 × 10−9 | 1.1567 × 10−7 |
| F19 | 2.4386 × 10−9 | 7.0617 × 10−1 | 1.8567 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.0937 × 10−10 | 3.0199 × 10−11 | 9.9410 × 10−1 | 2.0152 × 10−8 | 2.0523 × 10−3 | 3.4742 × 10−10 |
| F20 | 3.5708 × 10−6 | 2.9215 × 10−9 | 3.0199 × 10−11 | 5.8282 × 10−3 | 3.0199 × 10−11 | 4.1997 × 10−10 | 3.0199 × 10−11 | 7.2208 × 10−6 | 1.2870 × 10−9 | 1.5964 × 10−7 | 1.2023 × 10−8 |
| F21 | 3.6459 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 | 9.5332 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.6695 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.7769 × 10−10 |
| F22 | 1.0000 × 100 | 7.3803 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.9881 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F23 | 3.0199 × 10−11 | 1.9568 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.4742 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F24 | 3.0199 × 10−11 | 4.5043 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.1589 × 10−10 |
| F25 | 5.0912 × 10−6 | 6.0459 × 10−7 | 6.5261 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.6099 × 10−10 | 4.3531 × 10−5 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F26 | 4.1178 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F27 | 9.9410 × 10−1 | 5.7460 × 10−2 | 6.6955 × 10−11 | 1.2362 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 8.8910 × 10−10 | 3.4742 × 10−10 | 4.1127 × 10−7 | 1.0702 × 10−9 |
| F28 | 6.2040 × 10−1 | 3.6897 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.7769 × 10−10 | 6.7362 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F29 | 2.8129 × 10−2 | 3.6439 × 10−2 | 2.8314 × 10−8 | 9.2344 × 10−1 | 3.0199 × 10−11 | 8.1527 × 10−11 | 3.0199 × 10−11 | 1.5964 × 10−7 | 6.5261 × 10−7 | 1.2362 × 10−3 | 9.2603 × 10−9 |
| F30 | 3.0199 × 10−11 | 2.2360 × 10−2 | 7.3891 × 10−11 | 4.9752 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.1702 × 10−1 | 4.0772 × 10−11 | 1.6947 × 10−9 | 3.0199 × 10−11 |
| Item | PSO | DBO | DMO | IAO | MGO | PO | PLO | BKA | CPSOGSA | HPHHO | SCSO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.2870 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 9.3519 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.2118 × 10−12 | 3.0199 × 10−11 |
| F3 | 3.0103 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 6.5204 × 10−1 | 3.0199 × 10−11 | 2.1544 × 10−10 | 3.0199 × 10−11 |
| F4 | 9.0688 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.1937 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F5 | 2.2823 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F6 | 5.5699 × 10−3 | 3.5547 × 10−1 | 3.0199 × 10−11 | 5.9673 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.6159 × 10−10 | 6.0658 × 10−11 | 3.0199 × 10−11 | 3.6897 × 10−11 |
| F7 | 6.5277 × 10−8 | 3.7904 × 10−1 | 2.6806 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F8 | 6.3088 × 10−1 | 3.1589 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F9 | 3.0199 × 10−11 | 3.3386 × 10−3 | 3.4742 × 10−10 | 1.0937 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 6.1210 × 10−10 | 6.0658 × 10−11 | 3.0199 × 10−11 | 2.6099 × 10−10 |
| F10 | 1.1882 × 10−1 | 7.5991 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.0666 × 10−7 | 1.7290 × 10−6 | 4.1997 × 10−10 | 3.0199 × 10−11 |
| F11 | 3.6897 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.3111 × 10−8 | 1.0277 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F12 | 2.8716 × 10−10 | 6.6955 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.0912 × 10−6 | 1.0035 × 10−3 | 3.0199 × 10−11 | 3.1589 × 10−10 |
| F13 | 3.0199 × 10−11 | 2.0283 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 7.1186 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F14 | 4.2259 × 10−3 | 7.7387 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.4913 × 10−6 | 5.6922 × 10−1 | 2.2273 × 10−9 | 2.0152 × 10−8 |
| F15 | 9.7555 × 10−10 | 5.5727 × 10−10 | 4.9752 × 10−11 | 1.2597 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.0152 × 10−8 | 6.5671 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F16 | 9.1171 × 10−1 | 3.1589 × 10−10 | 3.0199 × 10−11 | 5.9673 × 10−9 | 3.0199 × 10−11 | 6.1210 × 10−10 | 3.0199 × 10−11 | 1.6351 × 10−5 | 1.7290 × 10−6 | 3.0811 × 10−8 | 1.3289 × 10−10 |
| F17 | 7.7272 × 10−2 | 5.0723 × 10−10 | 3.0199 × 10−11 | 3.5137 × 10−2 | 3.0199 × 10−11 | 4.0772 × 10−11 | 3.0199 × 10−11 | 2.8790 × 10−6 | 1.6132 × 10−10 | 8.4848 × 10−9 | 3.8249 × 10−9 |
| F18 | 3.0339 × 10−3 | 1.4733 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 9.4683 × 10−3 | 5.2978 × 10−1 | 4.6159 × 10−10 | 5.4617 × 10−9 |
| F19 | 3.3384 × 10−11 | 4.0595 × 10−2 | 3.0199 × 10−11 | 1.8368 × 10−2 | 3.0199 × 10−11 | 3.4742 × 10−10 | 3.0199 × 10−11 | 9.0688 × 10−3 | 3.6897 × 10−11 | 1.1536 × 10−1 | 1.1737 × 10−9 |
| F20 | 7.6171 × 10−3 | 4.5726 × 10−9 | 3.0199 × 10−11 | 1.2967 × 10−1 | 3.0199 × 10−11 | 4.1997 × 10−10 | 3.0199 × 10−11 | 6.7362 × 10−6 | 7.1186 × 10−9 | 7.2951 × 10−4 | 2.6695 × 10−9 |
| F21 | 1.1937 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F22 | 4.3764 × 10−1 | 8.1527 × 10−11 | 3.0199 × 10−11 | 8.8910 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.5292 × 10−5 | 8.2919 × 10−6 | 3.0199 × 10−11 | 2.8716 × 10−10 |
| F23 | 2.1544 × 10−10 | 6.6955 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.6159 × 10−10 |
| F24 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.4941 × 10−11 |
| F25 | 7.3891 × 10−11 | 2.6099 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.9428 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F26 | 1.9527 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F27 | 9.7052 × 10−1 | 3.3874 × 10−2 | 2.8716 × 10−10 | 1.8567 × 10−9 | 3.0199 × 10−11 | 4.6856 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.0666 × 10−7 | 8.1527 × 10−11 |
| F28 | 2.2273 × 10−9 | 7.3803 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.5923 × 10−5 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F29 | 7.9590 × 10−3 | 1.2597 × 10−1 | 1.8731 × 10−7 | 8.8411 × 10−7 | 3.0199 × 10−11 | 4.0772 × 10−11 | 3.0199 × 10−11 | 1.0277 × 10−6 | 2.3715 × 10−10 | 1.4110 × 10−9 | 1.1567 × 10−7 |
| F30 | 3.0199 × 10−11 | 9.8329 × 10−8 | 3.0199 × 10−11 | 4.6756 × 10−2 | 3.0199 × 10−11 | 8.1527 × 10−11 | 3.0199 × 10−11 | 3.6459 × 10−8 | 1.1567 × 10−7 | 7.3803 × 10−10 | 4.5726 × 10−9 |
| Item | PSO | DBO | DMO | IAO | MGO | PO | PLO | BKA | CPSOGSA | HPHHO | SCSO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.6947 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.2118 × 10−12 | 3.0199 × 10−11 |
| F3 | 1.9568 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.1857 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.4918 × 10−6 | 3.0199 × 10−11 | 1.3703 × 10−3 | 3.6459 × 10−8 |
| F4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F5 | 5.9969 × 10−1 | 3.4971 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F6 | 1.5292 × 10−5 | 2.0523 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 8.8411 × 10−7 | 1.6980 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F7 | 3.3384 × 10−11 | 1.4412 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F8 | 2.5805 × 10−1 | 3.8249 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.2057 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F9 | 3.0199 × 10−11 | 1.3367 × 10−5 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.8945 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.9673 × 10−9 |
| F10 | 6.5671 × 10−2 | 3.0103 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.9215 × 10−9 | 1.5969 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F12 | 4.9752 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 6.7362 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F13 | 8.9934 × 10−11 | 4.0772 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F14 | 1.3832 × 10−2 | 2.5721 × 10−7 | 3.0199 × 10−11 | 7.1988 × 10−5 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.7836 × 10−4 | 6.7362 × 10−6 | 4.5043 × 10−11 | 4.6159 × 10−10 |
| F15 | 3.6897 × 10−11 | 1.2057 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.5465 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F16 | 1.1023 × 10−8 | 4.6856 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.1857 × 10−7 | 5.9428 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F17 | 1.5798 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.8202 × 10−10 | 3.2555 × 10−7 | 5.0723 × 10−10 | 5.5727 × 10−10 |
| F18 | 1.4128 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 7.7312 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.0188 × 10−5 | 2.7071 × 10−1 | 3.0199 × 10−11 | 2.9215 × 10−9 |
| F19 | 3.0199 × 10−11 | 2.6695 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 7.7725 × 10−9 | 5.4941 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F20 | 7.9590 × 10−3 | 5.5727 × 10−10 | 3.0199 × 10−11 | 3.8053 × 10−7 | 3.0199 × 10−11 | 3.1589 × 10−10 | 3.0199 × 10−11 | 2.0023 × 10−6 | 3.9648 × 10−8 | 1.1567 × 10−7 | 6.6955 × 10−11 |
| F21 | 7.7725 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F22 | 1.7836 × 10−4 | 1.1711 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.7836 × 10−4 | 1.3017 × 10−3 | 3.0199 × 10−11 | 2.6099 × 10−10 |
| F23 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.3679 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F24 | 1.3289 × 10−10 | 3.0199 × 10−11 | 1.7769 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F25 | 3.0199 × 10−11 | 4.1825 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 6.5261 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F26 | 8.1200 × 10−4 | 8.9934 × 10−11 | 3.2651 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.0937 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F27 | 9.9186 × 10−11 | 4.1191 × 10−1 | 5.4941 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 8.1014 × 10−10 | 3.0199 × 10−11 | 8.1527 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F28 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.1573 × 10−5 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F29 | 1.4294 × 10−8 | 1.2235 × 10−1 | 3.1589 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.2057 × 10−10 | 8.6634 × 10−5 | 6.0658 × 10−11 | 6.0658 × 10−11 |
| F30 | 3.0199 × 10−11 | 8.7663 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.7666 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.6159 × 10−10 |
| Suites | CEC2017 | |||||
|---|---|---|---|---|---|---|
| Dimensions | 10 | 30 | 50 | |||
| Algorithms | ||||||
| PSO | 3.03 | 2 | 2.57 | 2 | 2.50 | 2 |
| DBO | 5.83 | 6 | 5.60 | 5 | 5.60 | 4 |
| DMO | 4.73 | 3 | 5.53 | 4 | 6.10 | 6 |
| IAO | 5.13 | 4 | 6.90 | 8 | 8.37 | 10 |
| MGO | 12.00 | 12 | 11.93 | 12 | 11.93 | 12 |
| PO | 7.93 | 10 | 7.63 | 10 | 6.87 | 9 |
| PLO | 11.00 | 11 | 11.07 | 11 | 11.07 | 11 |
| BKA | 5.57 | 5 | 5.27 | 3 | 5.67 | 5 |
| CPSOGSA | 6.53 | 7 | 5.67 | 6 | 5.07 | 3 |
| HPHHO | 6.57 | 8 | 6.60 | 7 | 6.20 | 7 |
| SCSO | 7.33 | 9 | 6.90 | 9 | 6.23 | 8 |
| MISCSO | 2.33 | 1 | 2.33 | 1 | 2.40 | 1 |
| Type | Minimum Power/kW | Maximum Power/kW | ||
|---|---|---|---|---|
| Photovoltaic Power (PV) | 0 | 150 | 0.0450 | 0 |
| Wind Power (WT) | 0 | 100 | 0.0096 | 0 |
| Energy Storage Device (BSS) | −60 | 60 | 0.0550 | 0 |
| Diesel Generator (DE) | 0 | 150 | 0.0780 | 0.21 |
| Pollutant Type | ||
|---|---|---|
| 4.33 | 0.028 | |
| 0.46 | 5.950 | |
| 2.32 | 8.510 |
| Time Slot | ||||||
|---|---|---|---|---|---|---|
| Peak Hours | Off-Peak Hours | Regular Hours | ||||
| 10:00–14:00 | 18:00–20:00 | 07:00–09:00 | 15:00–17:00 | 00:00–06:00 | 23:00–24:00 | |
| Purchase electricity | 0.69 | 0.46 | 0.31 | |||
| Electricity Sales | 0.64 | 0.38 | 0.23 | |||
| Algorithm | Max | Min | Mean | Std | CPU Time | Rank |
|---|---|---|---|---|---|---|
| PSO | 9053.31 | 5026.37 | 6571.94 | 679.16 | 213.96 | 2 |
| DBO | 9314.99 | 6153.18 | 6765.53 | 537.96 | 228.13 | 3 |
| DMO | 9922.43 | 6541.88 | 8371.58 | 598.43 | 235.05 | 8 |
| IAO | 13,126.44 | 10,707.35 | 11,052.59 | 412.19 | 246.11 | 12 |
| MGO | 9563.78 | 6098.10 | 7239.33 | 596.69 | 253.06 | 4 |
| PO | 8635.95 | 7569.52 | 8094.38 | 185.62 | 259.56 | 6 |
| PLO | 9862.89 | 7635.81 | 8639.25 | 394.87 | 265.03 | 10 |
| BKA | 9948.46 | 7991.50 | 8742.36 | 347.86 | 270.03 | 11 |
| CPSOGSA | 9849.87 | 6213.96 | 8234.95 | 623.58 | 288.50 | 7 |
| HPHHO | 9767.54 | 7036.79 | 8524.15 | 171.69 | 276.23 | 9 |
| SCSO | 9122.86 | 6584.94 | 7974.97 | 2097.3 | 208.54 | 5 |
| MISCSO | 6258.32 | 4986.87 | 5495.67 | 242.91 | 210.08 | 1 |
| Abbreviation | Full Name |
|---|---|
| BKA | black-winged kite algorithm |
| CPSOGSA | hybridization of constriction coefficient based on particle swarm optimization and gravitational search algorithm |
| DBO | dung beetle optimizer |
| DMO | dwarf mongoose optimization algorithm |
| GOA | Grasshopper Optimization Algorithm |
| GWO | gray wolf optimizer |
| HPHHO | hybrid parallel Harris hawks optimization algorithm |
| IAO | information acquisition optimizer |
| IWO | Invasive Weed Optimization algorithm |
| MGO | moss growth optimization |
| MISCSO | Multi-Strategy Improved Sand Cat Swarm Optimization |
| PSO | particle swarm optimization |
| PO | parrot optimizer |
| PLO | polar lights optimizer |
| RVEA | real-valued evolutionary algorithm |
| RIME | Rime optimization algorithm |
| SCSO | sand cat optimization algorithm |
| Symbol | Meaning |
|---|---|
| Problem Dimensions | |
| Population size | |
| Interactive Power Between Microgrids and the Main Grid | |
| Photovoltaic power generation capacity | |
| Wind power generation capacity | |
| Diesel Generator Power | |
| Maximum number of iterations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Song, Z.; Wang, H. An Economic Scheduling Management Method for Microgrids Using Multi-Strategy Improved Sand Cat Swarm Optimization. Biomimetics 2025, 10, 735. https://doi.org/10.3390/biomimetics10110735
Liu B, Song Z, Wang H. An Economic Scheduling Management Method for Microgrids Using Multi-Strategy Improved Sand Cat Swarm Optimization. Biomimetics. 2025; 10(11):735. https://doi.org/10.3390/biomimetics10110735
Chicago/Turabian StyleLiu, Bingnan, Zhiyi Song, and Huiji Wang. 2025. "An Economic Scheduling Management Method for Microgrids Using Multi-Strategy Improved Sand Cat Swarm Optimization" Biomimetics 10, no. 11: 735. https://doi.org/10.3390/biomimetics10110735
APA StyleLiu, B., Song, Z., & Wang, H. (2025). An Economic Scheduling Management Method for Microgrids Using Multi-Strategy Improved Sand Cat Swarm Optimization. Biomimetics, 10(11), 735. https://doi.org/10.3390/biomimetics10110735







