1. Introduction
Digital Breast Tomosynthesis (DBT) is a 3D X-ray cone-beam Computed Tomography (CT) technique for the early detection of breast tumors [
1,
2].
While the traditional digital mammography provides a unique 2D breast image, DBT reconstructs the breast as a stack of 2D images by using a comparable radiation dose. Hence, DBT is also used in screening programs, because the volumetric reconstruction reduces the tissue overlaps allowing for a better visibility of malignant structures. DBT is characterized by a limited-angle geometry: since the object is scanned only from a narrow angular range, the DBT projection data are incomplete if compared to classical CT cases.
The reconstruction algorithm plays an important role, influencing the accuracy of the recovered breast images. It is well known that traditional fast analytic reconstruction methods, such as Feldkamp [
3], produce poor noisy images in limited-angle tomography, hence they have been left in favor of Iterative Reconstruction (IR) algorithms [
4,
5,
6]. IR solvers provide a sequence of solutions, by computing an improved reconstructed volume at each iteration. Iterative approaches have been introduced since the first years of CT, but they have not been used for a long time due to their high computational time request. Recently, IR methods got a renewed interest in scientific communities and among the major vendors, due to the advent of more performing processors [
7]. As a consequence, a wide amount of IR methods has been proposed to reconstruct tomographic images and an exhaustive analysis can be found in [
8], whereas an overview of IR methods for CT image reconstruction is presented in
Section 1.1.
In this work we consider three IR algorithms as solvers of three slightly different model-based formulations. They all solve optimization problems where the objective function both describes the CT process (by modeling the physics of the system and including the presence of noise on the projection data) and introduces some image priors. Such a mathematical approach is quite uncommon in 3D tomographic imaging, where a constrained formulation is preferred [
9,
10,
11,
12]. In particular, we mainly consider the objective function as the sum of the Least Squares (LS) data-fitting term and the Total Variation (TV) regularization function. The TV regularizer is chosen by many authors because of its excellent shape recovering and denoising properties, even if it is known that TV can produce staircasing effects when the regularization parameter is too high [
8,
9,
10,
11,
12,
13]: the choice of the regularization parameter plays a fundamental role in the considered framework.
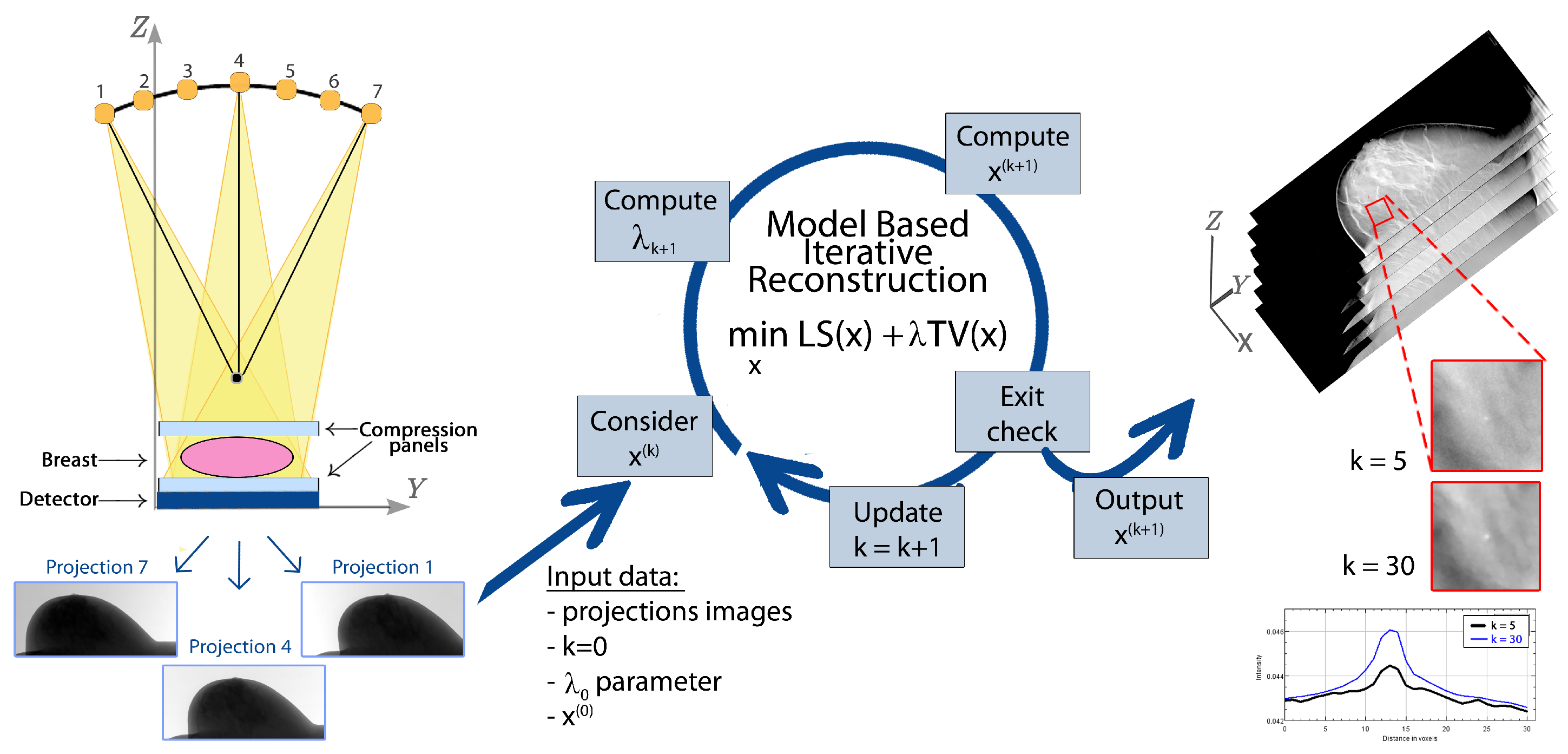
Figure 1 shows the model-based approach workflow, from the numerical modeling of the projection step during the breast scanning, to the reconstructed volume inspection searching for breast cancer objects, via the implementation of an iterative solver for the minimization problem.
1.1. A Short Review on Iterative Methods for CT
The worldwide increasing interest in Compressive Sensing (CS) [
14] has promoted the novel model-based iterative approach (which uses an optimization framework to exploit CS theory). Among the wide class of model-based IR procedures, the so called Sparsity-Exploiting Image Reconstruction (SEIR) methods have produced significant improvement to the image quality in all the low-dose CT applications (see [
8,
13] and references therein). In particular, many authors have introduced the TV regularization function to take advantage of the sparsity in the image gradient domain for edge detection [
4,
5,
15,
16,
17,
18,
19,
20,
21,
22]. This property turns into practice as a noise smoothing effect and as a reliable detection of shape and size of anatomical objects.
It is possible to distinguish two main categories of algorithms in the class of SEIR methods: the approximate solvers and the accurate solvers. The first one contains algorithms using, at each step, an algebraic approach (such as SART and SIRT) and then decreasing the TV of the just calculated solution. Examples are the well-known POCS algorithm and its developments [
16,
23,
24]. They provide reliable reconstructions in few iterations, but the quality of the recovered images strongly depends on the tuning of many inner parameters and the algorithm convergence is not guaranteed. On the other hand, the accurate solvers are optimization methods minimizing an objective function, which is defined as a sum of a data-fitting term and a regularization function. The two quantities are typically weighted by a regularization parameter. This class is represented by classical optimization methods adapted to the huge size 3D tomographic reconstruction problems. Their solution is proved to converge to the exact solution of the minimization problem.
Nowadays, only preliminary investigations on simulations or phantoms have been performed to analyze the results of accurate solvers for few-views CT applications [
25,
26,
27].
Concerning existing rules for the regularization parameter choice in tomography, in [
28] the authors propose a strategy based on multiresolution and apply it to 2D reconstructions. The proposed rule is very promising, but it is quite expensive for a very large size 3D application, such as DBT image reconstruction. An exhaustive list of existing rules for the selection of the regularization parameter is reported in [
28].
1.2. Aim and Contribution of the Paper
The aim of this paper was to propose a new TV-based optimization framework for the reconstruction of DBT images. The framework, described in a rigorous numerical setting, includes both constrained and unconstrained models, thus it is a flexible tool easily enabling the use of different data-fitting or regularization terms as well as the addition of further box constraints, to reconstruct reliable volumes from subsampled noisy data.We are also interested in finding an automatic strategy to set the regularization parameter, which strongly affects the quality of the reconstructions, in order to avoid its manually tuning (which is infeasible in a clinical setting).
The contribution of this work can be summarized as follows.
We remark that in clinical routine almost real time reconstructions are required. However, we underline the importance of improving the image quality with ongoing iterations in longer execution times, for two main reasons: first, having more reliable images can be crucial in difficult diagnosable cases to avoid false interpretations; second, the fast evolution of multiprocessor boards, such as GPUs, is drastically reducing the time per iteration of the methods, hence we can suppose that more iterations could be performed in clinical reconstructions in a next future.
The paper is organized as follows. In
Section 2, we state the optimization framework for the image reconstruction, thus we illustrate the three proposed model-based approach and IR solvers in
Section 3.
Section 4 and
Section 5 present the data sets and the experimental results, respectively. Finally,
Section 6 contains some conclusions.
2. The Optimization Framework in a Model-Based Formulation
Mathematically, tomographic image reconstruction is an ill-posed inverse problem whose solution can be obtained by minimizing a suitable objective function related to the physical process. To define the model describing image reconstruction, a deep understanding of the acquisition steps characterizing the DBT technique is therefore crucial. A schematic example of a DBT system is shown in the left of
Figure 1. In DBT routine, the breast is first compressed along the
Z-axis, over the flat detector plane. The source moves along an arc trajectory and emits low-dose radiations from a discrete number of angles. Once the X-ray cone-beam has passed through the body, the detector records its attenuation: the set of the resulting projection images constitutes the raw tomographic data set. The breast volume to be recovered is composed by a stack of high resolution images, parallel to the detector plane along the
Z vertical direction.
In order to define the numerical model of tomographic image formation, we recall the physical law underlying the acquisition process. Supposing the 2D detector panel is made of
recording units, for each fixed projection angle
and
ith recording unit, the Lambert–Beer law relates the projection
, along a ray
, to the attenuation coefficient function
of a point
w [
29] as:
where
represents the intensity of the energy emitted by the X-ray source. By discretizing the 3D object into
voxels and by considering all the
scanning angles, the integral in (
1) yields the following linear system:
In Equation (
2), we denote with
x the
dimensional vector stacking the attenuation coefficients of all the voxels, while
b is the vector of size
storing all the projections (i.e., the right hand sides of (
1)) and
M is the matrix of size
, built according to the DBT device geometry and representing the projection process onto the detector.
Some issues arise when solving the linear system (
2) as an inverse problem, such as the existence of infinite solutions (since
) and the presence of high noise in the reconstructed images (due to the ill-posedness of the problem). The model-based approach is introduced to overcome these numerical controversies, by adding some a priori information. The resulting formulation can be stated as an unconstrained or constrained minimization problem [
8], involving a data-fitting function
and a prior operator
(acting here as a regularizer).
In particular, we settle
as the Least Squares (LS) function
and
as the Total Variation (TV) operator defined as [
30]:
The TV operator is not differentiable in the origin, thus we consider the smoothed TV version:
where
is a small positive parameter [
30], when a solver requires the objective function differentiability.
We remark that both the TV and the
quantities can be computed with forward differences with boundary periodic conditions on the volumes. In addition, if we reshape the vector
x of length
as a 3-dimensional object
of size
, we can introduce the notation
to indicate the indices of the
jth voxel with respect to the three Cartesian axes (
and
). Hence, for all
the
elements in Equations (
4) and (
5) can be read as
and thus expressed as:
Since the model-based problem statement is a flexible framework, in this work we consider three different LS-TV like formulations, i.e.,:
where
is a regularization parameter and
is an estimate of a noise measure. The introduction of the box constraint
reflects the non-negativity property of the linear attenuation coefficient
in (
1), hence it is coherent to the DBT numerical formulation.
We remark that exploiting the linearity of the objective function
in (
7) and (
8), the objective function gradient
can be evaluated by separately computing
as:
and
through finite forward differences (see [
27] for its detailed derivation).
3. Iterative Optimization Methods
For each considered model formulation (
7)–(
9), we propose an accurate solver whose convergence to the global minimum is demonstrated. We thus apply and compare the Scaled Gradient Projection (SGP), the Fixed Point (FP) and the Chambolle–Pock (CP) methods to solve the optimization problems (
7), (
8) and (
9), respectively.
Among the wide class of optimization methods they have been chosen since they satisfy the requirements necessary to be usable on DBT devices:
a fast error decreasing in the initial algorithm execution, in order to obtain a good image in few iterations;
a low computational cost per iteration (which is mainly determined by the number of matrix-vector products), to efficiently run the solver in short time;
a limited request of memory, to solve real-size problems on commercially affordable hardware.
A challenging issue (common to the implementation of the three algorithms) is the computation of the projection matrix M; since it can not be stored due to its huge dimensions, it must be recalculated at each call. Thus, this section ends with a focus on the algorithm we use to generate M.
3.1. Scaled Gradient Projection Algorithm
The SGP algorithm is a first order accelerated method. We apply it to solve the non-negative constrained and differentiable optimization problem (
7). Algorithm 1 reports the main steps of the SGP algorithm.
At each
kth iteration, the new solution is computed by moving along a descent direction
of a quantity
, as:
The direction
is obtained through a projection
onto the non-negative orthant of the scaled gradient direction
:
where
is the step length and
is the scaling matrix (step 7 in Algorithm 1).
Essentially, the method follows a Gradient Projection approach accelerated by choosing the
step length with Barzilai–Borwein techniques as proposed in [
27] and by introducing a suitable scaling matrix improving the matrix conditioning. In particular, the scaling matrix
is a diagonal matrix with entries in a limited interval. To update
(line 5 of Algorithm 1), we compute a splitting of the objective function gradient into its positive and negative parts, as:
where
and
. The diagonal elements
of
are updated, for
as:
where
is a decreasing bounded positive sequence, ensuring the procedure convergence [
31]. We finally denote by
the set of diagonal matrices with entries in the interval
.
Regarding the convergence, it is proved in [
32] that the SGP algorithm converges without any further restriction on the step length
and on the scaling matrix
to the unique minimum of (
7). In [
31], the authors proved that the theoretical convergence rate of the SGP method is
(1/k).
| Algorithm 1 Scaled Gradient Projection algorithm (SGP) |
Input:- 1:
Initialize: - 2:
k = 0 - 3:
while not convergence do - 4:
Compute - 5:
Compute as in ( 14) - 6:
Define with alternate BB rules - 7:
- 8:
- 9:
while do - 10:
- 11:
- 12:
k = k+1
Output: |
3.2. The Fixed Point Algorithm
The FP algorithm solves the unconstrained problem (
8) and it has been proposed for image deblurring in [
33]. Starting from this approach, we derived the lagged diffusivity FP Algorithm 2 for 3D tomographic image reconstruction.
| Algorithm 2 Lagged diffusivity Fixed Point algorithm (FP) |
Input:- 1:
Initialize: - 2:
for to do - 3:
Compute - 4:
Solve the linear system , where , with the Conjugate Gradient method. - 5:
Output: |
At each
kth iteration, the FP algorithm updates the solution with the following rule:
where the descent direction
is computed by solving a linear system
(line 4 of Algorithm 2). The matrix
in line 4 approximates the Hessian matrix. It contains the seven diagonals banded matrix
which is the discretization matrix of the diffusion operator
so that
[
30]. We solve the linear system with very few iterations of a Conjugate Gradient (CG) algorithm [
34]. We stop it far before convergence, both to limit the computational time and to prevent noise from affecting the solution. We remark that each CG iteration requires a matrix-vector product involving
and that, to save memory space, we perform it without storing the matrix
. We only store
and re-compute
M and
at run time. At the end, we project the last computed solution onto the non-negative orthant. For more details on the FP method applied to tomographic image reconstruction and its convergence, see [
26] and [
35], respectively.
3.3. The Chambolle–Pock Algorithm
The CP algorithm (originally proposed in [
36]) solves the constrained minimization problem stated as in (
9), by considering an equivalent unconstrained formulation:
where
and the
ball is the set
and its indicator function
is defined as
In addition, we set:
as the indicator function
of the convex set
to embed the non-negativity constraint in the unconstrained formulation. Equation (
17) allows to fully exploit the linearity of the
K transform, combining here both the X-ray projector M and the discrete gradient operator, if we build
K as the following four-blocks matrix:
where
and
are the forward difference operators acting along the
and
Z axes, respectively.
Considering the convex conjugate
of
F, defined as
, and the proximal mappings of
and
G, i.e.,
the
kth CP iteration can be summarized in the following three steps:
compute as ;
compute as ;
define with an extrapolation step: and .
We denote as
a matrix of size
and we use Matlab-like notation to indicate element by element matrix multiplication and division. In particular, the proximal mapping
can be computed as the sum of two independent blocks, as in lines 5–6 and 7–9 of the Algorithm 3; its detailed derivation can be found in [
37] for 2D imaging applications. We have here extended the method to 3D imaging. For the sake of clarity, we remark that the weights
,
and
in lines 7–9 are stored in
-dimensional variables
where
for
, whereas
is a vector of size
with components
| Algorithm 3 Chambolle–Pock algorithm (CP) |
Input:: - 1:
Compute: as an approximation of - 2:
Initialize:, - 3:
Initialize:, and to zeros-vectors - 4:
for to do - 5:
- 6:
- 7:
- 8:
- 9:
- 10:
- 11:
- 12:
Output: |
The proximal mapping of
G is defined as:
hence, it is exactly the projection
of
x onto the feasible set
(line 11 of Algorithm 3). The updated iterate
is computed with an extrapolation strategy as in line 12 of Algorithm 3. The algorithm convergence is demonstrated in [
36].
We finally observe that the algorithm needs to compute the value
(line 1 of Algorithm 3): to estimate the matrix 2-norm as
(where
is the spectral radius of a matrix), we perform two iterations of the power method for computation of the maximum eigenvalue in module [
38].
3.4. User-Independent Choice of the Regularization Parameter
In model-based optimization approaches, the choice of the regularization parameter
plays a key role for the quality of the reconstruction and it represents a crucial challenge in a clinical setting, where the trial-and-error approach is not doable for each reconstruction. Moreover, experimental results show that Hence, we propose to reduce the regularization weight along the iterations, by choosing the
values with a decreasing updating rule. Interestingly, state-of-art studies have already proposed semi-automatic rules for the selection of a decreasing sequence
of regularization parameters defining a sequence of minimization problems, whose solutions converge to a good reconstructed image. See [
39] for more details and the convergence proof.
We propose the following fully-automatic strategy to compute a decreasing sequence . At the beginning of our algorithm, we leave out the regularization by setting the first parameter : we are in fact interested in a very good data fitting, to recover as many image features as possible. Next, the starting value is set to balance the residual norm and the amount of TV of the first iterate. Afterward, we propose to decrease of a constant factor at each kth iteration, since we need a very simple and computationally cheap rule, reducing the regularization weight slightly. The resulting strategy is summarized in the following scheme and it can be introduced in each of the previously considered algorithms.
3.5. The Projection Matrix Algorithm
In addition to the choice of the model parameter and the solver, in optimization approach a key point consists in numerical modeling the geometric projection process, schematically displayed from a frontal view in
Figure 1, through a matrix.
The coefficient matrix
M of the linear system (
2) is commonly called
projection operator in tomography, since it represents the action of the tomographic system in projecting an object onto the detector, whereas the matrix modeling the backprojection of the tomographic data onto a volume is called
backprojection operator. In the proposed optimization algorithms, the backprojection coincides with the transpose matrix
.
Different algorithms have been proposed in literature for the computation of the matrix
M. We have adopted the Distance Driven (DD), which accurately models the discretization of the Lambert–Beer’s law (
1) for cone-beam projections [
40]. In DD,
M of size
is constituted by
submatrices
of size
. Each element
represents the contribution of the
jth voxel (for
) to the projection onto the
i-th detector pixel (for
), for a projection angle
. Images in
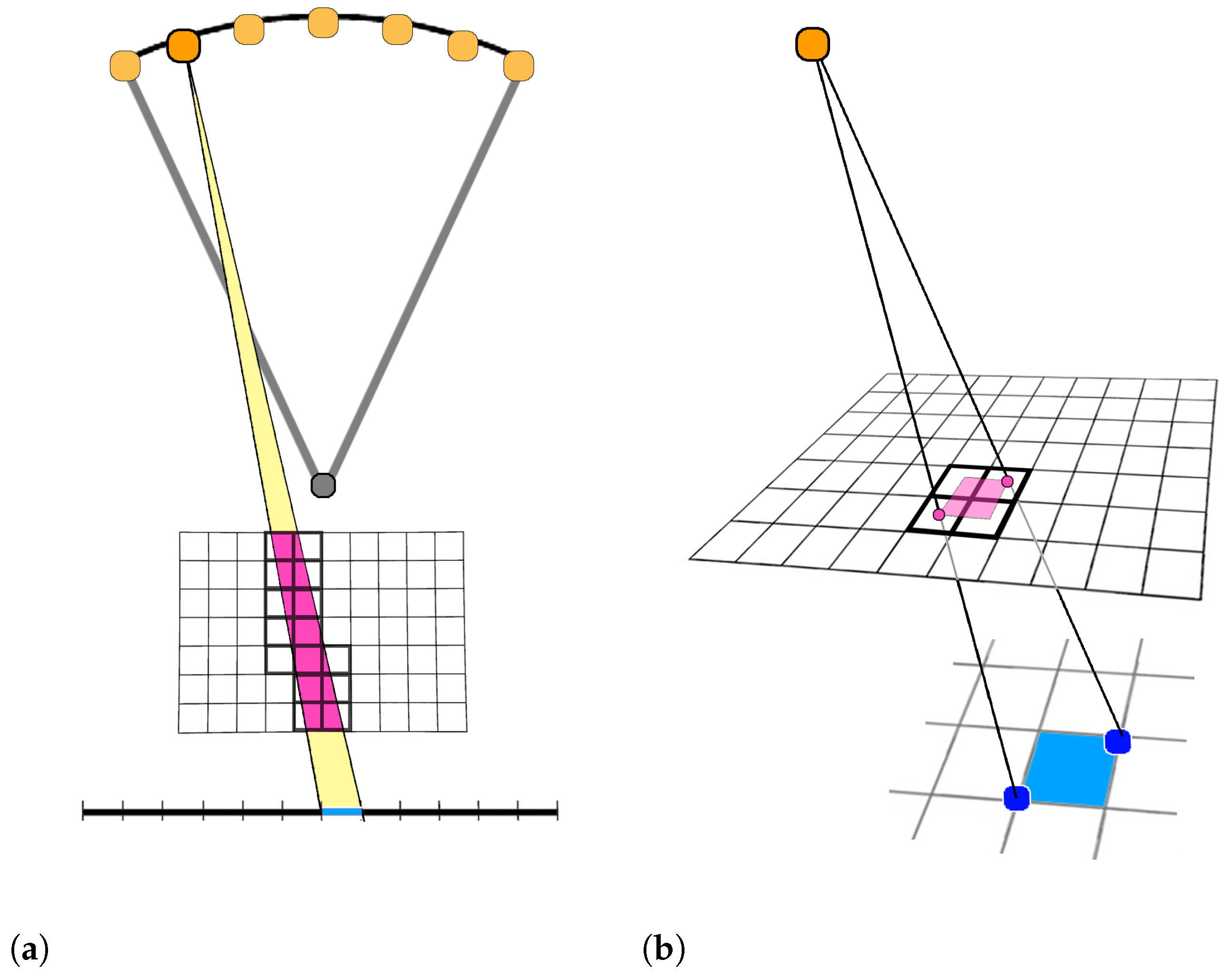
Figure 2 help in understanding the DD procedure. In
Figure 2a, for a scanning angle, we consider the X-ray cone-beam projecting onto the
ith blue pixel and intersecting the voxels with bold contours (in the magenta colored area). Only these voxels contribute to the value of the projection in the considered pixel. In
Figure 2b, we highlight the
ith cell of the detector (the blue area) and its backward footprint on a plane parallel to the detector (the magenta area). The ratio between the magenta area inside the
jth voxel and the whole magenta extension is proportional to the value
of the matrix. For all the voxels
j not contributing to the
ith projection, the corresponding matrix element
; hence,
M is extremely sparse. However, despite the huge number of nonzero elements, for its very large size, in real applications
M cannot be stored and it must be recomputed whenever a matrix-vector product is needed.
We finally remark that we have modified the general approach presented in [
40] by efficiently exploiting the characteristics of our specific mammographic setting. Really, since the DBT detector is a stationary flat panel and it is parallel to the compression plane of the breast, the footprints can be directly projected onto the detector plane, thus avoiding the use of an intermediate projection plane and further computational costs.
5. Numerical Results and Discussion
In this section we present the results obtained with the proposed optimization approach and the accurate solvers described in
Section 3. At first we compare the BR3D phantom reconstructions produced by the SGP, FP and CP solvers in a similar computational time. Then, in order to analyze the best achievable image quality, we have run the SGP up to convergence both on the phantom and on the clinical data set. At last, we test the automatic rule proposed in
Section 3.4 to decrease the
values along the iterations.
When setting a constant value for
is required, we fixed it by trial and error. The sequence
for the SGP scheme has been defined as:
as suggested in [
31].
5.1. Methods Comparison for Early Reconstructions
The aim of this paragraph is to show the behavior of the proposed solvers at different stages of their executions. We fixed 5 and 15 iterations: the workload of 5 iterations is compatible with the execution of a reconstruction on a commercial hardware in a clinical setting, whereas in 15 iterations we get fairly accurate results with all the three methods, reflecting that they are sufficiently close to the computed convergence solution. From a computational perspective, the SGP and the CP iterations are almost equally expensive, hence we stopped them exactly at 5 or 15 iterations. In the special case of FP solver, the number of allowed iterations corresponds to the sum of the external and CG iterations: since we always perform 4 CG iterations, the FP execution is stopped after one or three outer iterations (loop k in Algorithm 2), respectively.
The value of
in (
5) has been fixed as
. Since the three considered algorithms solve different optimization problems, the three
parameters have been chosen independently for each method to achieve the best reconstruction in 5 iterations: we have set
for both SGP and CP methods and
for the FP algorithm.
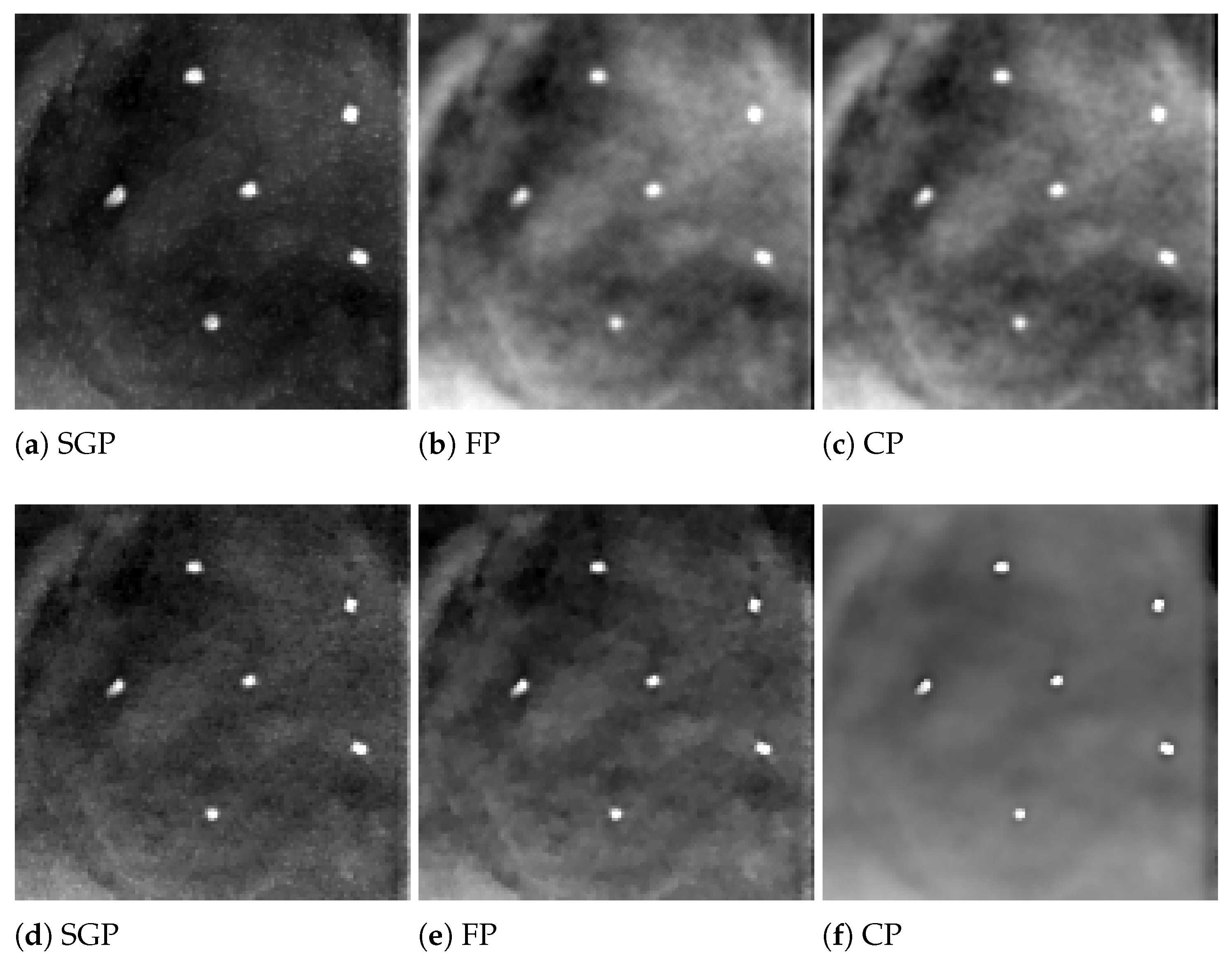
In the following analysis, we focus on the reconstruction of MC cluster number 3 in the BR3D phantom. For each solver,
Figure 3 reports a
pixels crop taken from the fifth slice of the reconstructions in 5 and 15 iterations. The images are represented by automatically enhancing the gray level contrast computed on the same considered region. In
Figure 4 we compare the PP and ASF curves taken on one MC.
Looking at
Figure 3, we observe that the detection of the MC cluster is comparable at equal iterations, whereas the background appears slightly different for the three methods. For example, in the case of CP reconstruction in 15 iterations it looks smoother and more blurred. Focusing on the objects of interest, we notice that in 5 iterations the MCs are perfectly visible; moreover, in 15 iterations the MC edges are sharper as confirmed by the plots (a) and (c) in
Figure 4. From plots (b) and (d) of
Figure 4, we observe that in all the three reconstructions the object is placed in the correct slice and it is not diffused in the adjacent layers. Hence, we can conclude that the proposed model-based optimization framework yields good quality images in early reconstructions, regardless the considered model formulation.
We highlight that the above results have been computed by a C-language-based scalar implementation of each solver, where it is not possible to reconstruct the whole volume of the phantom because of the too high memory demand. Working on one node HPE ProLiant DL560 Gen10 with 4 Intel(R) Xeon(R) Gold 6140 CPU @ 2.30 GHz and 512 Gb RAM, we considered cropped projections (corresponding to measurement data approximately) and we recovered a partial volume ( voxels). The execution time of the SGP, FP and CP functions resulted to be 262, 272 and 241 s, respectively, to perform 15 iterations. We remark that the reported time for the CP solver does not include the execution of step 1 since the approximation of has been computed externally. As already mentioned, a parallel implementation is required to reconstruct a whole phantom volume or a real breast. The results reported in the following, have been achieved by a CUDA-based SGP software, exploiting one Nvidia Tesla V100 GPU board.
5.2. SGP Algorithm Insights
In the following, we raise the SGP as the representative solver in the proposed optimization framework. We explore the performance of the model-based approach on many different objects of the BR3D phantom (such as microcalcifications of very small diameter and masses with a low contrast with the background tissue) and we analyze the quality of the reconstructions also after 15 iterations, i.e., approaching convergence.
In particular, we run the SGP solver on the BR3D phantom until the stopping condition:
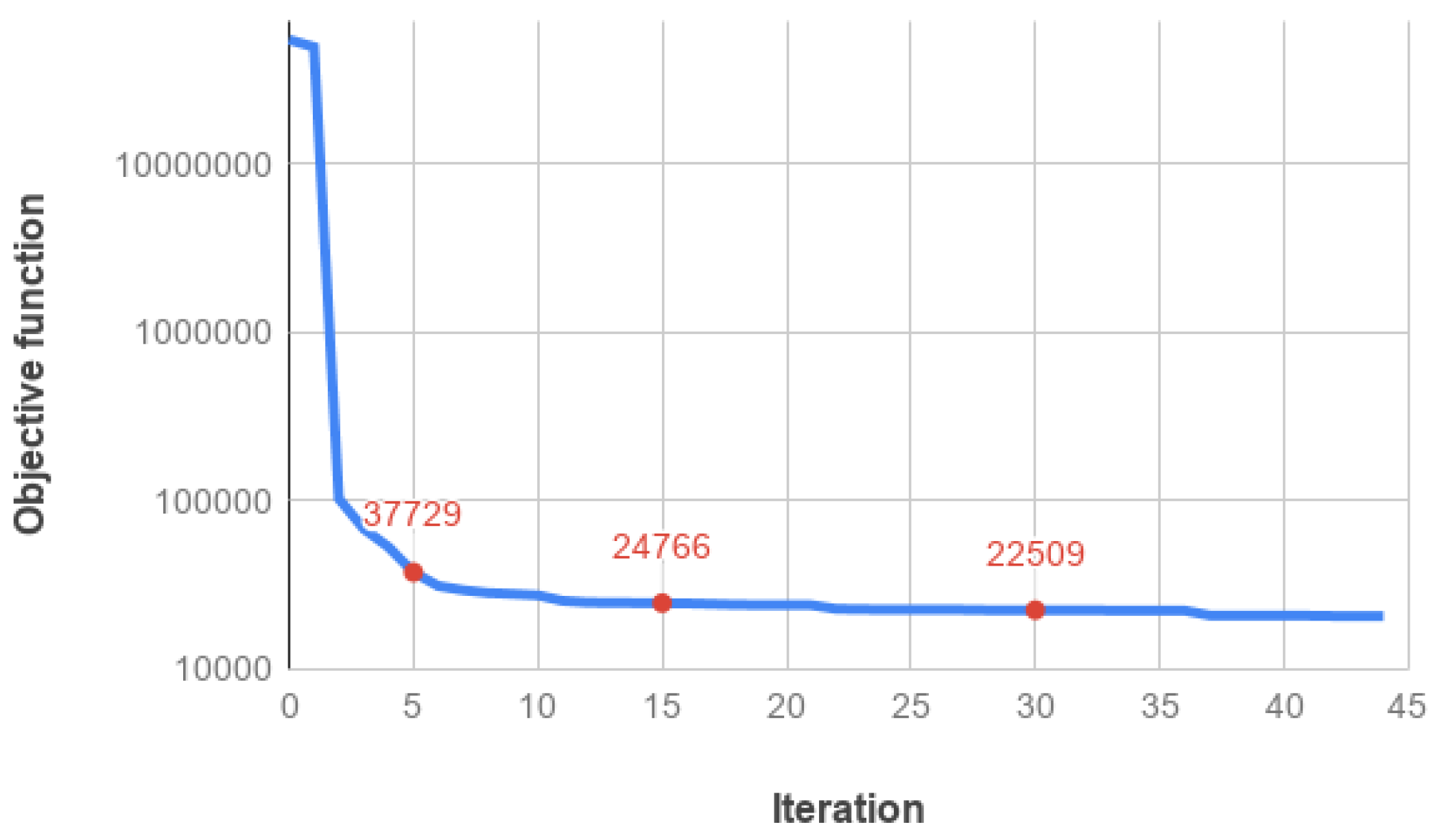
is satisfied. It occurs after 44 iterations. In
Figure 5, we plot the objective function values vs. the number of iterations: we observe that the objective function fast decreases in the first 5 iterations, whereas it exhibits a very flat trend from 10 iterations on, as it is confirmed by the red labeled values. We have seen, in fact, that the reconstructed images are visually almost indistinguishable after 30 iterations.
In
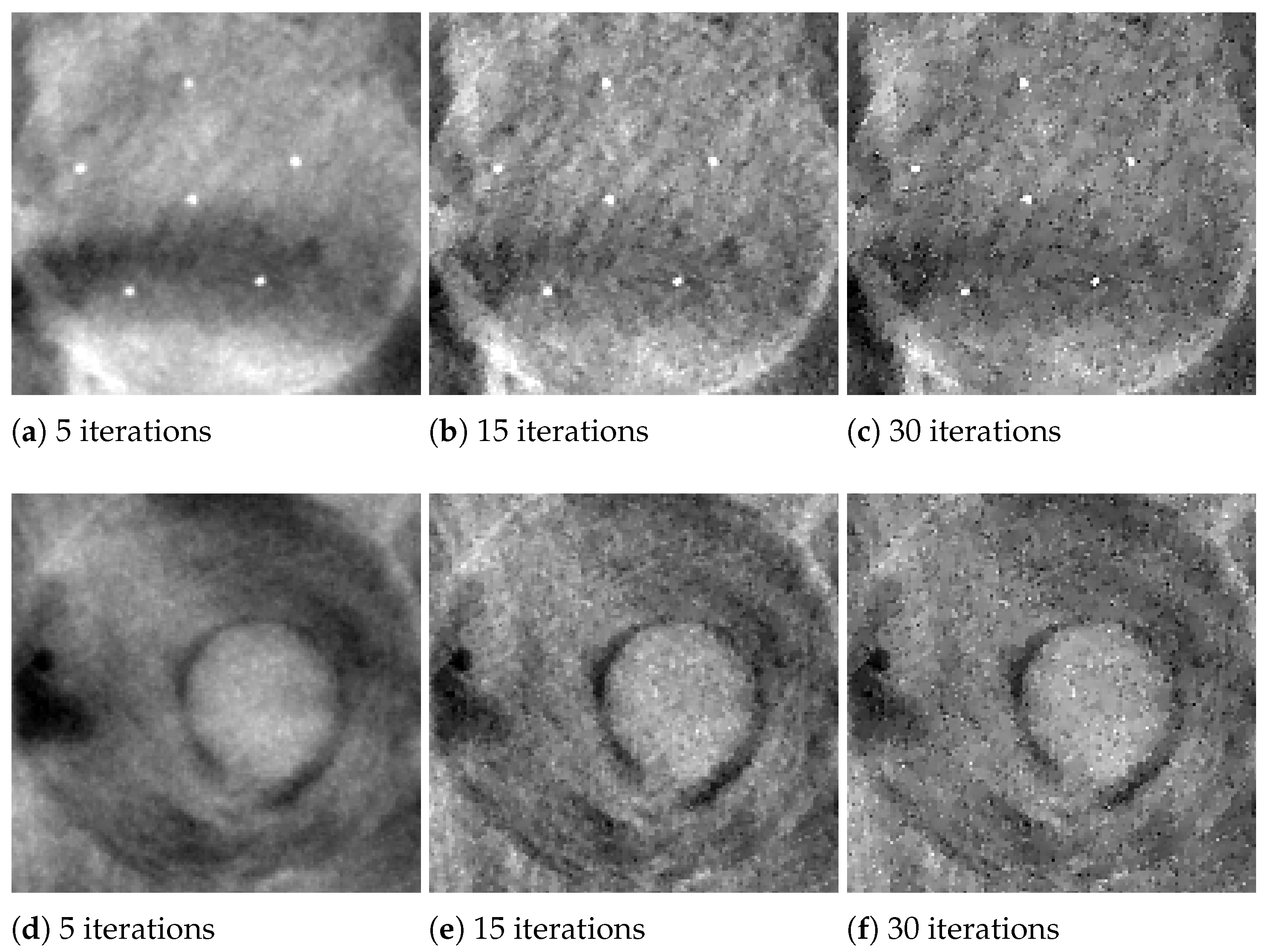
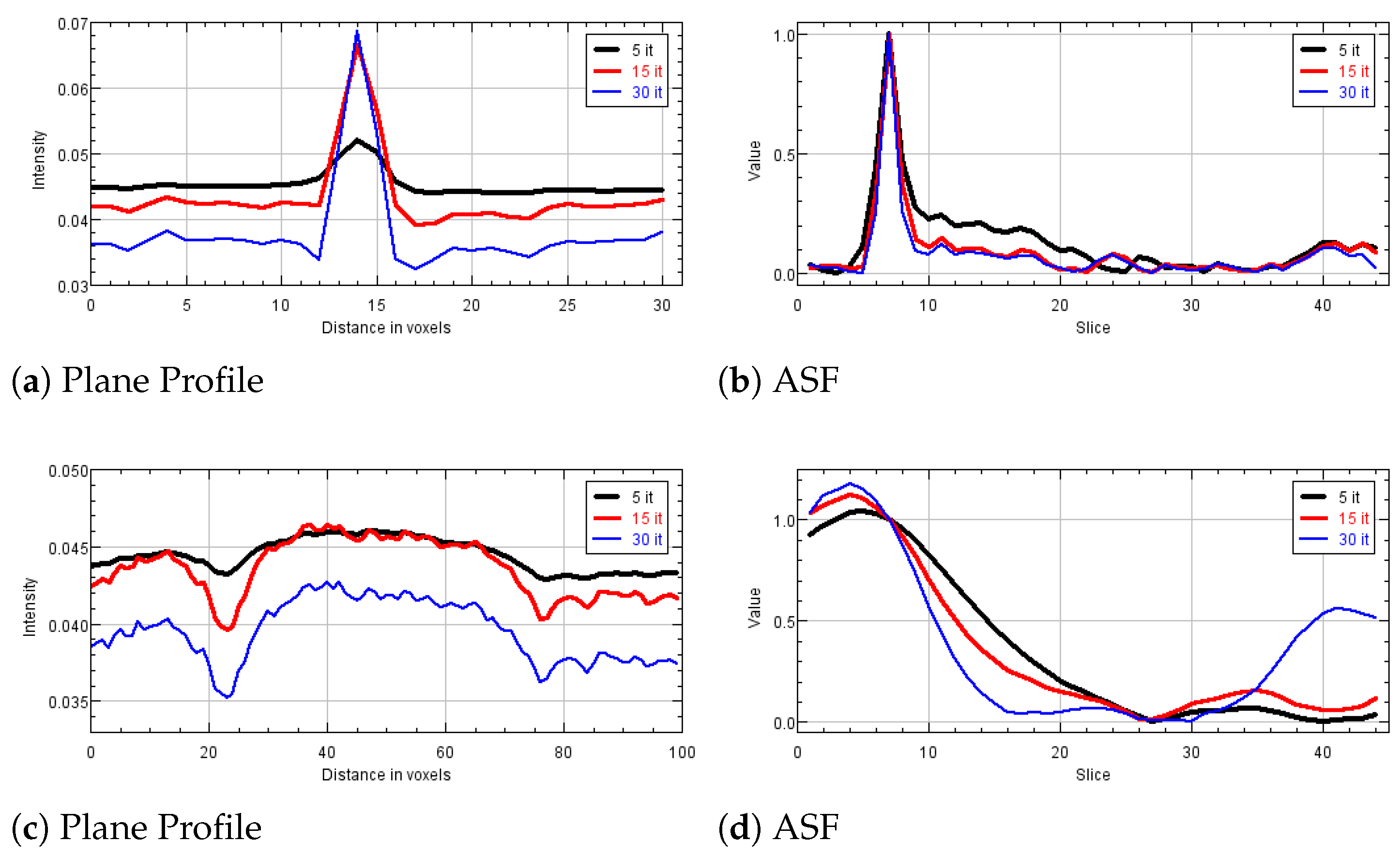
Figure 6, we exhibit the reconstructions of the 165 μm MCs of cluster 5, and the 4.7 mm mass (MS 2), obtained by the SGP algorithm after 5, 15 and 30 iterations. In
Figure 7 we report the corresponding PP and ASF plots.
Figure 6a shows that the MC of cluster 5 can be clearly visible after only 5 iterations and the PP plots of
Figure 7a confirms that it gets more and more enhanced from the background. The ASF plot in
Figure 7b shows an improvement in the object detection along the
Z direction. As visible in
Figure 6 and from the PP plot of
Figure 7c, MS 2 is out of focus at 5 iterations but its contours become more and more defined when the algorithm approaches to convergence. The previous plots confirm that the proposed model with TV regularization is more effective in recovering high contrast objects such as microcalcifications than low absorbing structures such as masses.
In
Table 2, we report the values of the CNR parameter on the examined reconstructed microcalcifications and masses. In particular, recalling the CNR definition (
24) for the masses, the background area is a circle with diameter of 80 voxels, whereas we have considered circles of diameter 40 and 25 voxels inside the masses 2 and 4, respectively. When evaluating the CNR index on a MC with Equation (
25), we regard as background area a circle of 20 voxels diameter and we compute
on a small circle of diameter 5 voxels containing the microcalcification.
Table 3 shows the values of the FWHM index defined in (
26) and computed on one of the reconstructed microcalcification in each cluster. The corresponding MCs widths
w, computed in micrometers as in (
27), are reported for a comparison with the values of the actual diameters, shown in
Table 1. Both tables demonstrate that we can get improved and more accurate reconstructions as the SGP approaches to the convergence: the increasing CNR indexes exhibit good denoising effects whereas the object enhancement is confirmed by the FWHM decreasing values. We remark that the MCs of cluster 6 are not discernible from the background in only 5 iterations (the FWHM is not measurable on the sixth MC cluster), because they are 130 μm width and they should approximately fill inside only two voxels. However, they can be well recovered in more iterations with a good approximation of their real size.
5.3. Experiments on a Human Data Set
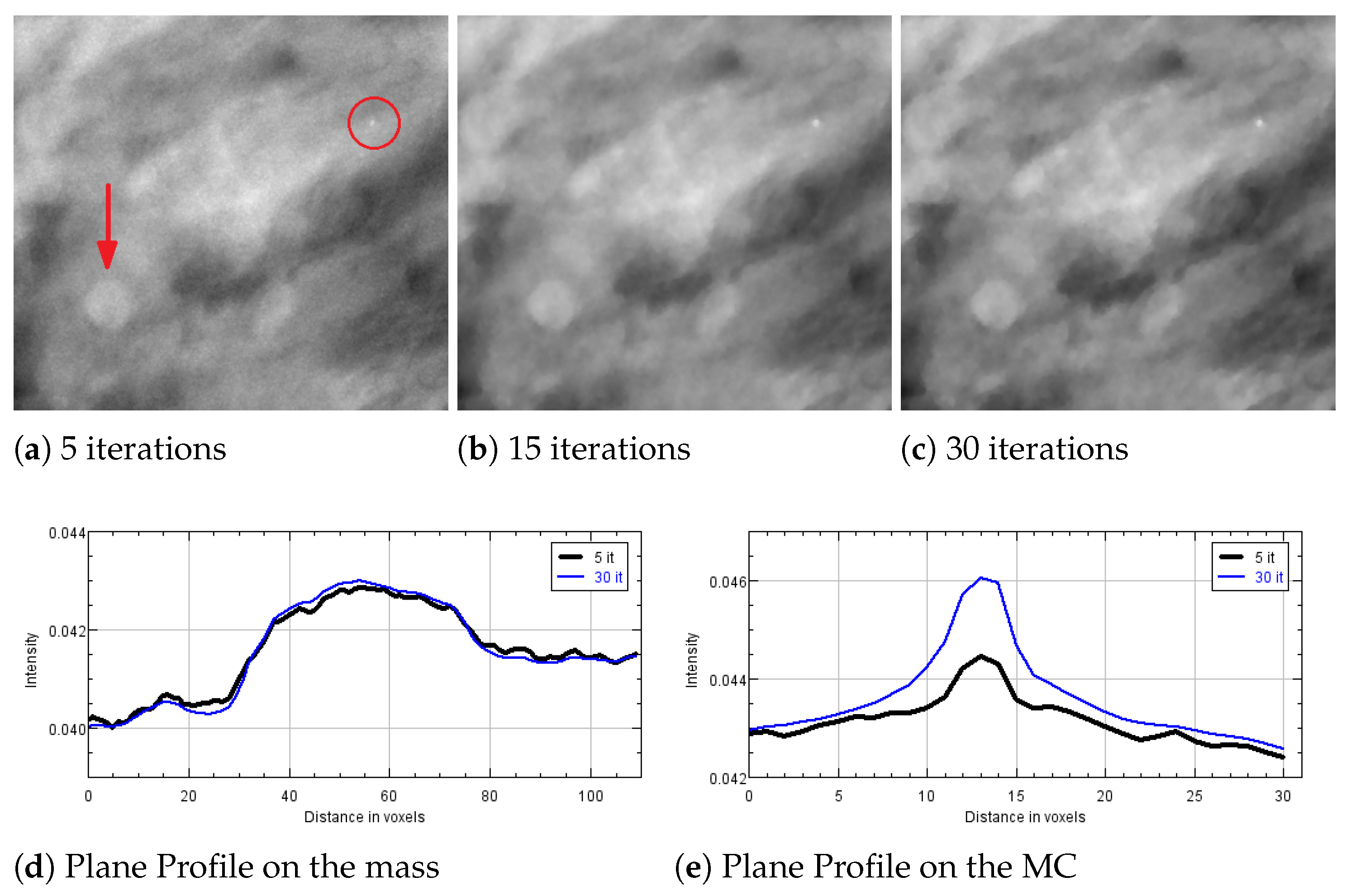
We now illustrate the results obtained by reconstructing a real breast volume with the SGP solver at different iterative stages. In
Figure 8a–c, we report a crop of a reconstructed slice, where we can distinguish objects of interest, i.e., a spherical mass and a small microcalcification. The plots in
Figure 8d,e represent the PP calculated on the mass and the microcalcification, respectively. The mass is well distinguishable since the earliest reconstruction and its shape and gray level intensity do not change remarkably; however the regular blue and thin profile in
Figure 8d points out the denoising effects of the TV function in the last iterations. In addition, the microcalcification is detected in few iterations, even if a more time-consuming SGP execution enhances the contrast of the object with respect to the background.
Table 4, reporting CNR and FWHM values computed on the objects in
Figure 8, gives more insight on the quality of the reconstructions. In particular, it confirms that the noise progressively decreases and the microcalcification gets more and more defined, from 5 to 30 iterations.
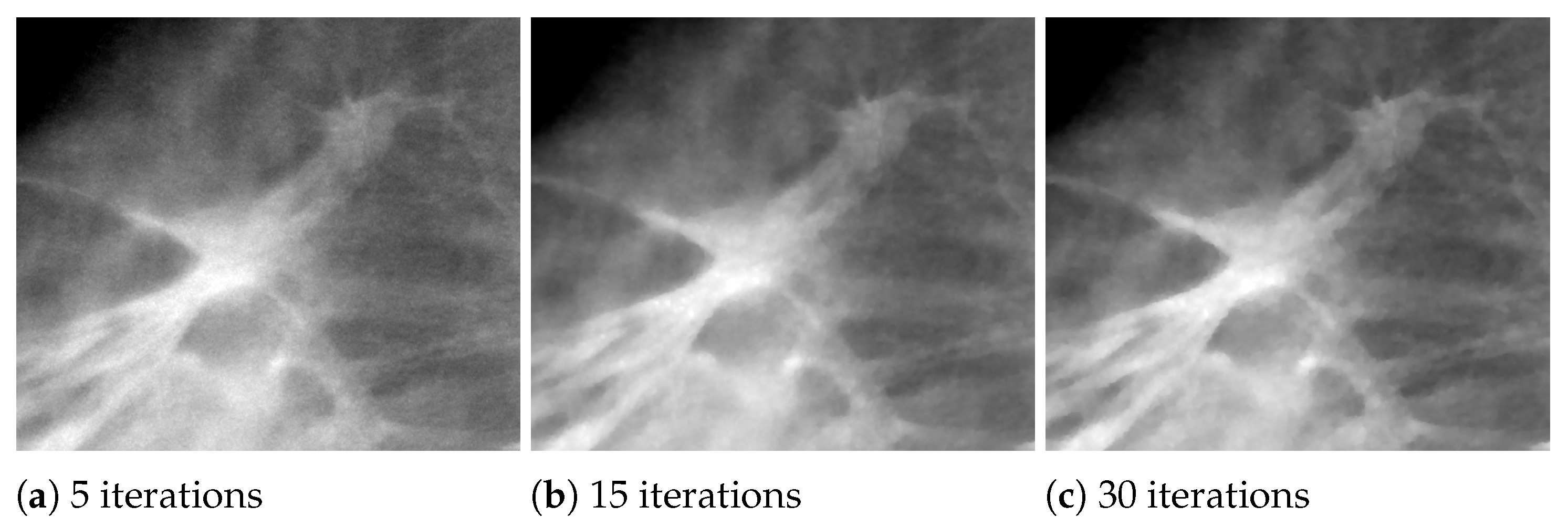
In
Figure 9, we report the reconstruction of two speculated masses, which can occur in clinical cases. For such breast objects, the previous measures of merits are not applicable. However, we can observe that they both are well recognizable in the earliest reconstruction and the edges become sharper with increasing iterations.
5.4. Experiments with a Variable Regularization Parameter
In all the above experiments, we have set a constant value of the regularization parameter along the iterations, to let the solvers perform at their best on the prefixed model derived by the settled
. In this paragraph, we show the results achieved with the automatic rule (
23) for the choice of a decreasing sequence
applied to the SGP solver, to reconstruct the BR3D phantom.
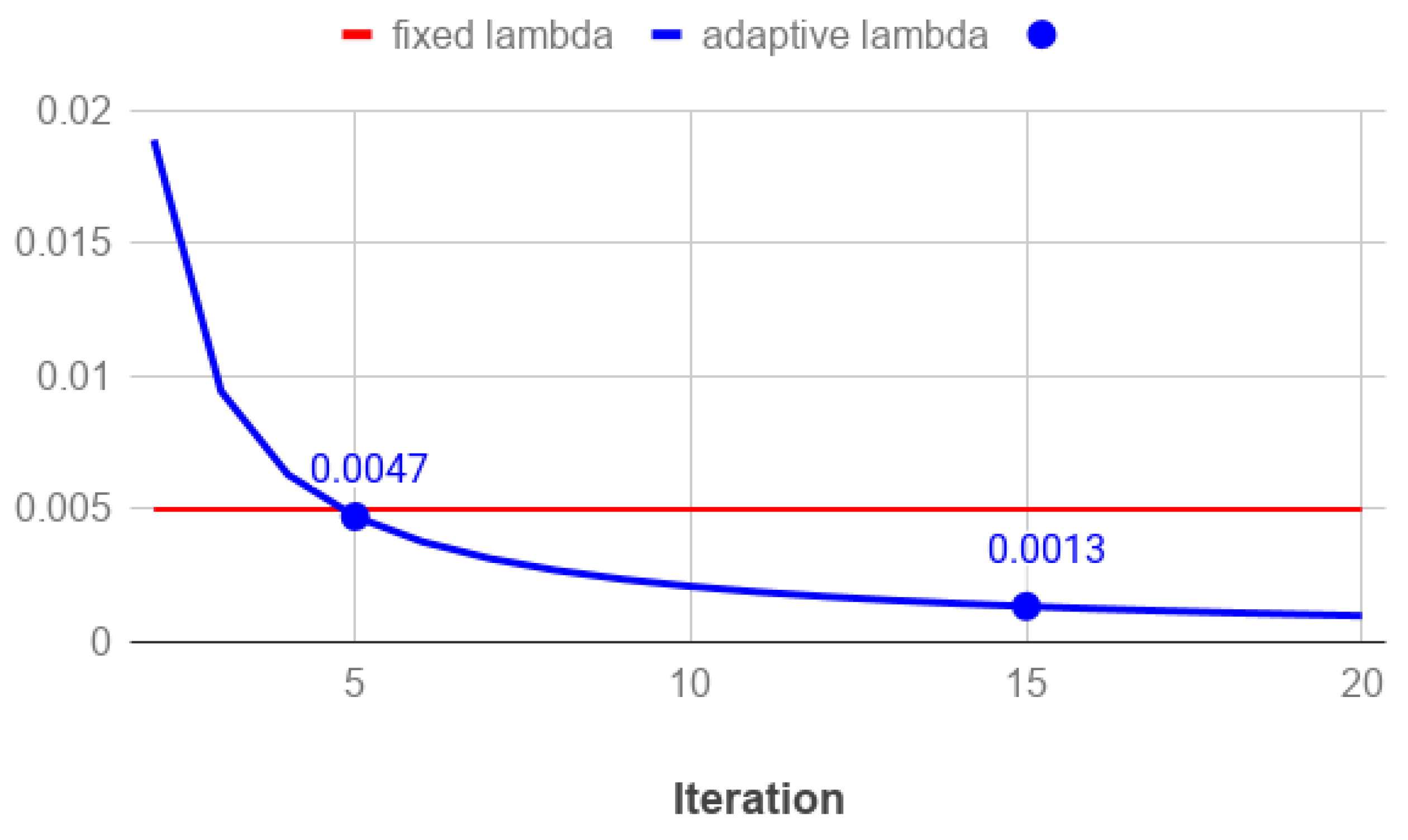
Figure 10 plots the sequence
with the blue line, while the red line represents the constant
value used in the SGP implementation in the previous experiments. We observe that the proposed strategy computes values greater than the heuristically fixed one
until the fifth iteration. In
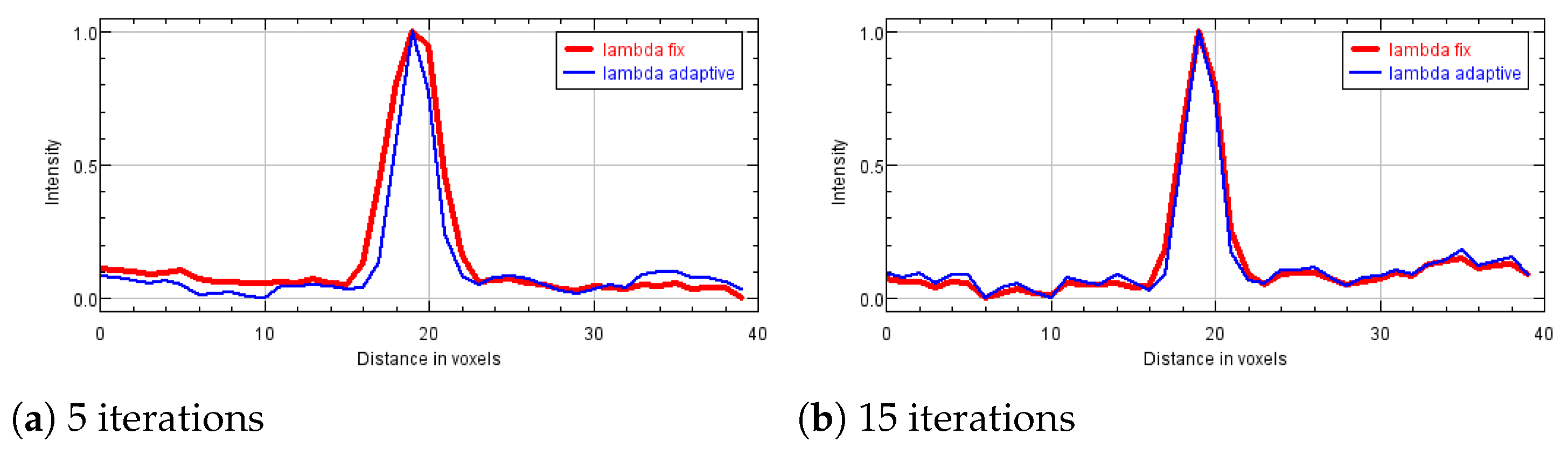
Figure 11 we compare the PP of one microcalcification from cluster 3, reconstructed at 5 and 15 iterations using both a fixed value and the proposed strategy for the regularization parameter. We can infer from
Figure 11a that the resulting larger TV weights in the first iterations produce more accurate results. However, on advanced reconstructions the differences are negligible. We can conclude that the proposed automatic strategy results very efficient.
6. Conclusions
In this paper, we have presented three model-based problem statements under a unique optimization framework for DBT image reconstruction. Each minimization problem has been solved by a convergent and efficient algorithm, for very large-size image reconstruction. We have also proposed a user-independent rule for selecting suitable values of the regularization parameter.
The results obtained with three solvers are encouraging. In early reconstructions, objects of interest of size greater than 150 μm are visible and correctly located in the volume, whereas the object detection quality improves and the noise drastically reduces if more iterations are allowed. When extending the computation from 5 to 30 algorithm iterations, the increasing rate of the CNR value lies in a range to . At last, we have shown that varying the regularization parameter along the iterations produces better results, especially in the early stage of the algorithm execution, when compared to the use of a fixed value heuristically chosen.
Since the three considered solvers produce comparable high quality reconstructions, we can conclude that the proposed model-based approach can be successfully used to detect the most interesting objects in an early diagnosis of breast tumor.