Active Learning with Bayesian UNet for Efficient Semantic Image Segmentation
Abstract
1. Introduction
1.1. Problem Statement and Suggested Solution—The AB-UNet Algorithm
- Pixel-wise segmentation of the image—no need for manual labelling of the training set.
- Efficient and fast active training via informative scoring, achieving good generalization. Also, ensure faster training after each interaction between model and the oracle.
- Translation, rotation and scale invariance to improve generalisation.
1.2. Structure of the Paper
1.3. Notation and Assumptions
2. Active Learning for Image Segmentation
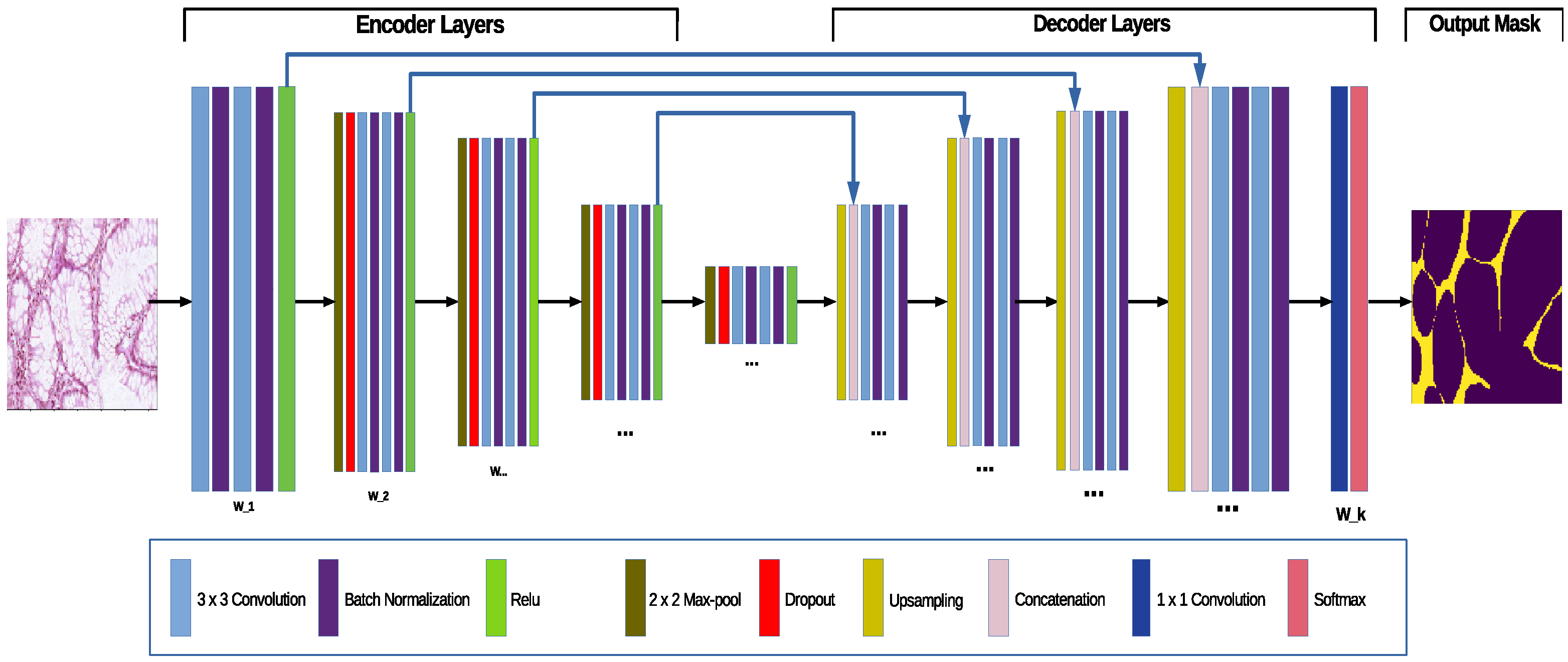
3. The Extended UNet Architecture—The AB-UNet
3.1. Standard UNet Convolutional Network
3.2. Bayesian Neural Networks
- 1
- Batch Normalization [19] is a procedure to speed up network training by reducing the internal covariate shift (this describes the changes in the distributions of activation units due to changes in parameters [19]) done by normalizing the hidden layers activations using an estimated and from each mini-batch. Teye et al. [18] found that batch normalization helps improving convergence.
- 2
- Dropout [16] is a regularization technique, also viewed as an approximate Bayesian method: the algorithm randomly removes parts of the network, making the weights stochastic quantities: , where , are the initial weights of the network, and ⊗ is the direct product with the random binary vector.
3.3. The Probabilistic Extension, the AB-UNet Architecture
3.3.1. Model Performance and Uncertainty Quantification AB-UNet
3.3.2. Dice Coefficient
3.3.3. The Results of Model Uncertainty Quantification
- Cell membrane segmentation dataset [32] from the EM segmentation challenge. It contains a full stack of EM slices images used to train machine learning models for automatic segmentation of neural structures. These images contain noise and small image alignment errors. For our experiments we discretized each pixels as binary values.
- DIC-C2DH-HeLa (The dataset is provided by Dr. Gert van Cappellen, from the Erasmus Medical Center, Rotterdam, The Netherlands.) cell tracking dataset of images recorded by differential interference contrast (DIC) microscopy. We discretized each pixel in this dataset into 20 classes.
- PhC-C2DH-U373 dataset:The data is provided by Dr. Sanjay Kumar. Department of Bio-engineering University of California at Berkeley. Berkeley CA (USA). on Glioblastoma-astrocytoma U373 cells on a polyacrylimide substrate recorded by phase contrast microscopy. For our segmentation experiments we used 14 classes.
- Warwick gland segmentation in colon histology images dataset [33]. This dataset consists of images of Hematoxylin and Eosin (H&E) stained slides, consisting of a variety of histologic grades (Figure 2). The dataset is provided together with ground truth annotations by expert pathologists and the task is to build an algorithm that segments the glands within the image. For our experiment we discretized each pixel into 50 classes.
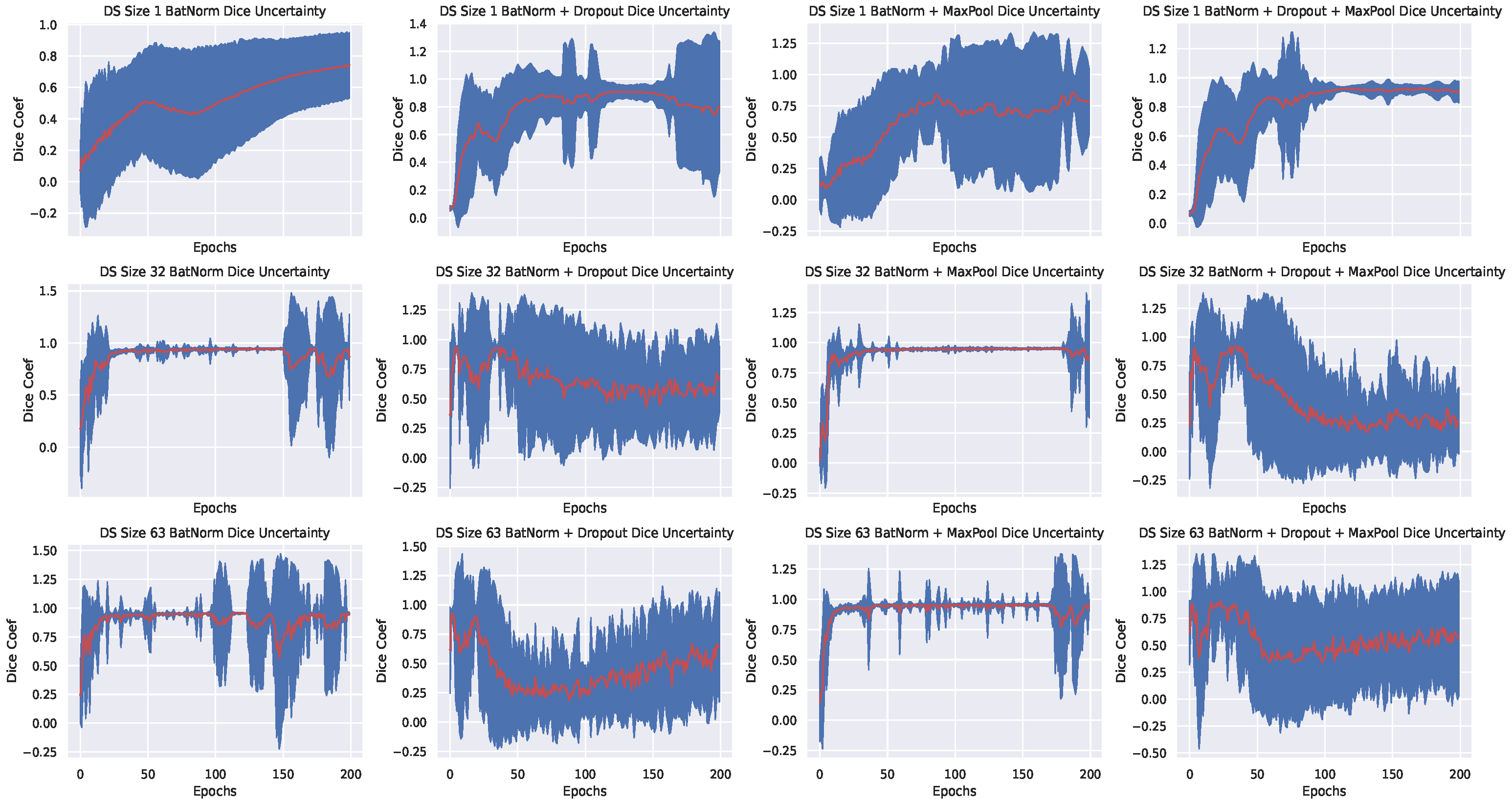
- By using batch normalization and max-pool dropout, we achieved better generalization and uncertainty quantification on all datasets; in contrast to batch normalization + standard dropout only, or batch normalization + standard dropout + max-pool dropout. Using only Batch normalization, exhibited similar model confidence when compared with batch normalization and max-pool dropout but it resulted to a slightly lower dice coefficient values across various sizes of training dataset.
- Better uncertainty (We define better uncertainty as the confidence of the model when it has seen more data) with more data: this is observed via the low variance in the plots shown in Figure 3—for the PhC-C2DH-U373 dataset, but the training behaviour for other datasets is similar. We see that our Bayesian model trained with either batch normalization + max-pool dropout or batch normalization only exhibit better confidence as the size of the training set increases—a clear contrast with the other setups. In particular, model confidence is better exhibited when using batch normalization and max-pool dropout.
- Average generalization begins below 60 epochs-An observation that we later exploited in active learning retraining (see Section 4.4). We believe that the fast generalization is a result of the batch normalization of input features. This is because batch normalization has been shown to reduce internal covariant shift, resulting to faster training and convergence [19].
4. Active Learning—A More Data-Efficient Method
4.1. Acquisition Functions for Active Learning
- Entropy based techniques compute the informativeness of an image as the sum of pixel entropies within the image. We define the following cases:
- (a)
- Maximum entropy [35]: measures the informativeness of pixel predictions within the image. The entropy of a pixel is . Therefore,
- (b)
- BALD (Bayesian Active learning by disagreement) [27]: chooses the image that maximizes the mutual information between the standard prediction and posterior prediction of each pixel. The BALD of a pixel is thus defined as . Therefore,
- Divergence based techniques: Computes the divergence between standard model prediction and MCMC prediction, therefore taking into account the disagreements of predictions in weight space while also considering noise in data space. We consider the following variants:
- (a)
- Committee posterior KL-divergence: computes the divergence between standard predictions and posterior predictions: given , the prediction from our AB-UNet model, and our MCMC prediction, we define the as the information gained if we approximate with our MCMC prediction . Using this acquisition function, we select samples with the highest KL divergence.
- (b)
- Committee posterior Jensen divergence is similar to the KL divergence, but here we quantize the symmetric bi-directional divergence between the standard prediction and the MCMC predictions. The Jensen divergence is defined as where , –MCMC prediction.
4.2. The AB-UNet Algorithm
| Algorithm 1: The Active Convolutional Network Segmentation (Bayesian UNet) Algorithm | ||
| 1: | procedureTraining() | |
| 2: | Select ; | ▹ Set of images from unlabelled set |
| 3: | ▹ acquire label from Oracle | |
| 4: | ||
| 5: | ||
| 6: | ▹ initial training | |
| 7: | repeat | |
| 8: | ||
| 9: | ▹ Computing score of | |
| 10: | ▹ acquisition function from Section 4.1 | |
| 11: | ▹ request labels | |
| 12: | ||
| 13: | ||
| 14: | ▹ re-train until early stopping | |
| 15: | ||
| 16: | until | |
| 17: | return trainedModel | |
| 18: | end procedure | |
4.3. Active Bayesian UNet Experiments
4.4. AB-UNet Algorithm Results
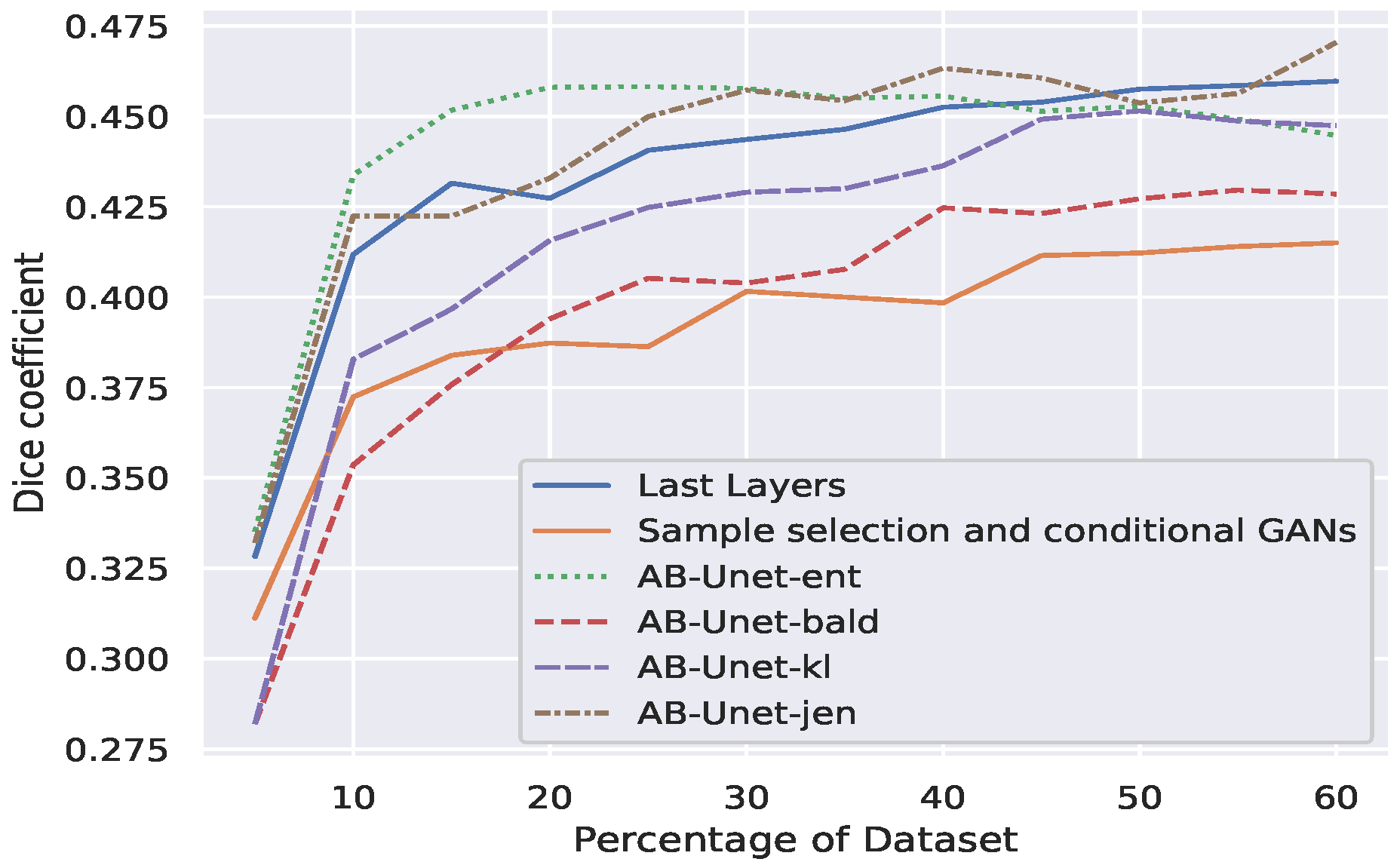
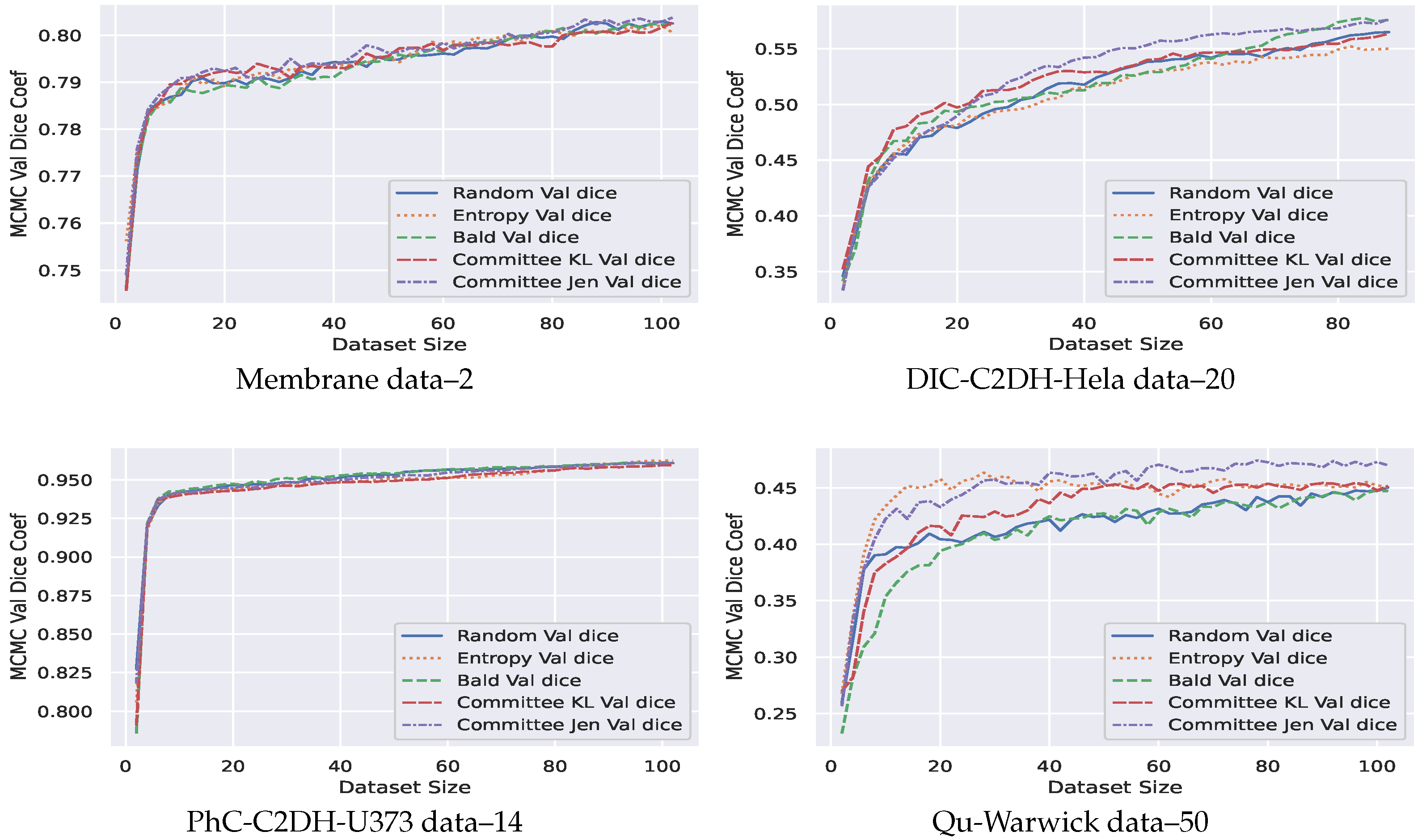
- Our AB-Net shows significant early peak using entropy. However, a robust performance in terms of dice coefficient is observed for Jensen divergence acquisition function—a divergence based approach (Figure 5).
- Our technique is more effective for problems involving higher number of pixel classes. This is clearly seen in Figure 5: the Qu-warwick datasets has 50 classes, DIC C2DH Hela dataset has 20, PhC-C2DH-U373 dataset has 14 and Membrane dataset is binary. Comparing the performance of all datasets, we observe that the sample complexity for models trained using active learning is a function of the dimension of the classes.
- Finally we compared our AB-UNet technique with other related techniques in literature (see Section 2), using Qu-warwick dataset and the result is presented Figure 6. Observe that our AB-UNet outperforms these other techniques by a good margin and the committee-Jensen acquisition is comparatively better than entropy and KL divergence, as more labels are acquired. In general our technique performed better due to the following;
- The max-pool dropout and batch normalization act as regularizers in our model compared to the work by Mahapatra et al. [23].
- Our AB-UNet algorithm-with committee Jensen, better models differences in predictive distributions induced by weight-space as well as noisy data. This is in contrast to standard entropy used in [23], hence the stability of our method.
- The averaging term in the Jensen divergence, makes the resulting measure smooth, more robust and well defined, implying that its range is well quantized and suitable when used to quantify the informativeness of an image among other images.
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer: Berlin, Germany, 2010. [Google Scholar]
- Hu, Z.; Zou, Q.; Li, Q. Watershed superpixel. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 349–353. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N.; Getoor, L.; Taskar, B. Graphical Models in a Nutshell. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.146.2935 (accessed on 3 October 2019).
- Vezhnevets, A.; Ferrari, V.; Buhmann, J. Weakly Supervised Semantic Segmentation with Multi Image Model. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 643–650. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, Y.; Xia, Y.; Lu, K.; Shen, J.; Ji, R. Representative discovery of structure cues for weakly-supervised image segmentation. IEEE Trans. Multimed. 2014, 16, 470–479. [Google Scholar] [CrossRef]
- Konyushkova, K.; Sznitman, R.; Fua, P. Introducing geometry in active learning for image segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; Volume 2015, pp. 2974–2982. [Google Scholar]
- Lafferty, J.; McCallum, A.; Pereira, F.C.N. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. Proc. ICML 2001, 8, 282–289. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the NIPS’12: 25th International Conference on Neural Information Processing Systems-Volume 1; Curran Associates Inc.: New York, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Ciresan, D.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: New York, NY, USA, 2012; pp. 2843–2851. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2015; pp. 91–99. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R.B. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9351. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- Lecun, Y.; Bengio, Y. Convolutional Networks for Images, Speech and Time Series. In The Handbook of Brain Theory and Neural Networks; Arbib, M.A., Ed.; The MIT Press: Cambridge, MA, USA, 1995; pp. 255–258. [Google Scholar]
- Gal, Y. Uncertainty in Deep Learning. Ph.D. Thesis, University of Cambridge, Cambridge, MA, USA, 2016. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd ICML, New York, NY, USA, 20–22 June 2016. [Google Scholar]
- Teye, M.; Azizpour, H.; Smith, K. Bayesian Uncertainty Estimation for Batch Normalized Deep Networks. In Proceedings of the 35th ICML, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2015; Volume 37 (ICML’15), pp. 448–456. [Google Scholar]
- Vezhnevets, A.; Buhmann, J.M.; Ferrari, V. Active learning for semantic segmentation with expected change. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3162–3169. [Google Scholar] [CrossRef]
- Fathi, A.; Balcan, M.F.; Ren, X.; Rehg, J.M. Combining Self Training and Active Learning for Video Segmentation. In Proceedings of the British Machine Vision Conference, Dundee, UK, 29 August–2 September 2011; pp. 78.1–78.11. [Google Scholar]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 5574–5584. [Google Scholar]
- Mahapatra, D.; Bozorgtabar, B.; Thiran, J.; Reyes, M. Efficient Active Learning for Image Classification and Segmentation using a Sample Selection and Conditional Generative Adversarial Network. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switherland, 2018. [Google Scholar]
- Gorriz, M.; Carlier, A.; Faure, E.; Giró i Nieto, X. Cost-Effective Active Learning for Melanoma Segmentation. Available online: https://ui.adsabs.harvard.edu/abs/2017arXiv171109168G (accessed on 1 February 2021).
- Saidu, C.I.; Csató, L. Medical Image Analysis with Semantic Segmentation and Active Learning. Stud. Univ. Babes-Bolyai Inform. 2019, 64. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Houlsby, N.; Huszár, F.; Ghahramani, Z.; Lengyel, M. Bayesian Active Learning for Classification and Preference Learning. arXiv 2011, arXiv:1112.5745. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. Available online: http://arxiv.org/abs/1412.6980 (accessed on 1 February 2021).
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Sørensen, T. A Method of Establishing Groups of Equal Amplitude in Plant Sociology Based on Similarity of Species Content and Its Application to Analyses of the Vegetation on Danish Commons. Biol. Skar. 1948, 5, 1–34. [Google Scholar]
- Arganda-Carreras, I.; Turaga, S.C.; Berger, D.R.; Ciresan, D.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J.; Laptev, D.; Dwivedi, S.; Buhmann, J.M.; et al. Crowdsourcing the creation of image segmentation algorithms for connectomics. Front. Neuroanat. 2015, 9, 142. [Google Scholar] [CrossRef] [PubMed]
- Sirinukunwattana, K.; Pluim, J.P.W.; Chen, H.; Qi, X.; Heng, P.; Guo, Y.B.; Wang, L.Y.; Matuszewski, B.J.; Bruni, E.; Sanchez, U.; et al. Gland Segmentation in Colon Histology Images: The GlaS Challenge Contest. Medical Image Analysis. 2016, 35, 489–502. [Google Scholar] [CrossRef] [PubMed]
- Settles, B. Active Learning Literature Survey. Mach. Learn. 2010, 15, 201–221. [Google Scholar]
- MacKay, D.J.C. Information Theory, Inference & Learning Algorithms; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saidu, I.C.; Csató, L. Active Learning with Bayesian UNet for Efficient Semantic Image Segmentation. J. Imaging 2021, 7, 37. https://doi.org/10.3390/jimaging7020037
Saidu IC, Csató L. Active Learning with Bayesian UNet for Efficient Semantic Image Segmentation. Journal of Imaging. 2021; 7(2):37. https://doi.org/10.3390/jimaging7020037
Chicago/Turabian StyleSaidu, Isah Charles, and Lehel Csató. 2021. "Active Learning with Bayesian UNet for Efficient Semantic Image Segmentation" Journal of Imaging 7, no. 2: 37. https://doi.org/10.3390/jimaging7020037
APA StyleSaidu, I. C., & Csató, L. (2021). Active Learning with Bayesian UNet for Efficient Semantic Image Segmentation. Journal of Imaging, 7(2), 37. https://doi.org/10.3390/jimaging7020037