Reducing Manual Annotation Costs for Cell Segmentation by Upgrading Low-Quality Annotations †
Abstract
1. Introduction
- Providing a formal introduction of the perturbations used throughout the experiments together with illustrative examples;
- Adding extensive experiments to further evaluate (i) the training requirements of the upgrade network, (ii) the effect of inconsistencies in the annotations of the high-quality data set, (iii) the trade-off between annotation cost and segmentation performance when upgrading the low-quality annotations, (iv) the performance of segmentation networks based on the annotation quality;
- Adding comparisons with related solutions;
- Adding experiments on complex RGB cell segmentation data sets;
- Expanding the discussion by elaborating on the potential consequences of our observations and scenarios under which our framework can contribute the most.
2. Materials and Methods
2.1. Data Sets
2.1.1. Synthetic Data
2.1.2. Real Data
2.2. Method
2.2.1. Background
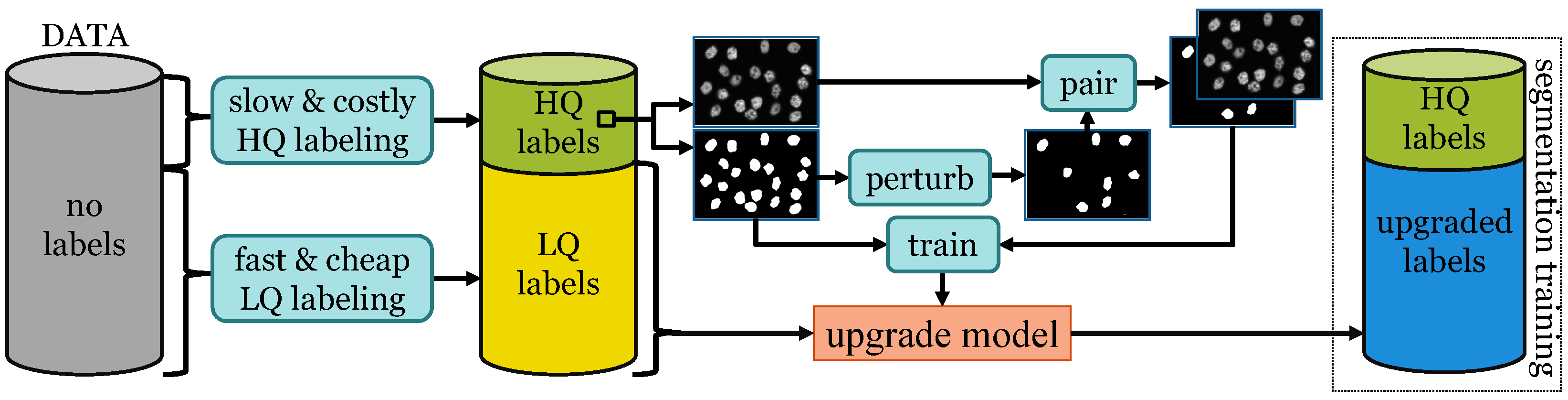
2.2.2. Perturbation-Removal Framework
| Algorithm 1 Upgrade Framework |
| Require: return (1) Train the upgrade network : for do Perturb y: Predict upgraded label: Compute loss: end for Estimate according to Equation (6) (2) Upgrade low-quality set and expand segmentation training data: for do Upgrade low-quality label: end for Estimate according to Equation (7) |
2.2.3. Producing Low-Quality Annotations
- Omission Perturbation. We randomly select a subset of of cell instance labels , whose size is chosen such that it satisfies the omission rate . Our perturbation function, therefore, becomes
- Inclusion Perturbation. Given an image x and , a set of instance labels of other objects belonging to x (), we perform inclusion by randomly selecting a subset of the objects, whose size satisfies the inclusion rate . Hence, we apply the perturbation as
- Bias Perturbation. We model the inconsistency in border delineation by performing morphological operations [35] on the cell labels. We employ dilation operations, D, to enlarge the cell area and erosion operations, E, to shrink the cell area. The operation is randomly chosen and the impact of the operation is controlled by factor q that controls the number of iterations, with a all-ones matrix as the fixed structural element, for which we perform the chosen operation. This bias severity constant, randomly picked between 1 and , indicates the largest allowed number of iterations. As a result, the perturbation is formed either aswhere and denote q iterations of erosion and dilation, respectively.
2.3. Experimental Setup
3. Results
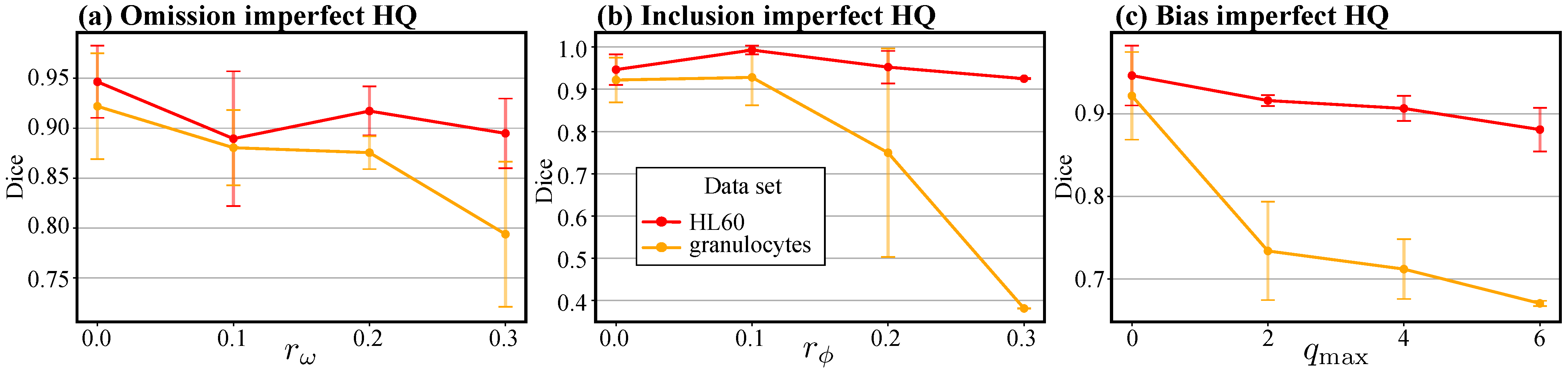
3.1. Analysis of the Upgrade Network
3.2. Segmentation Improvements
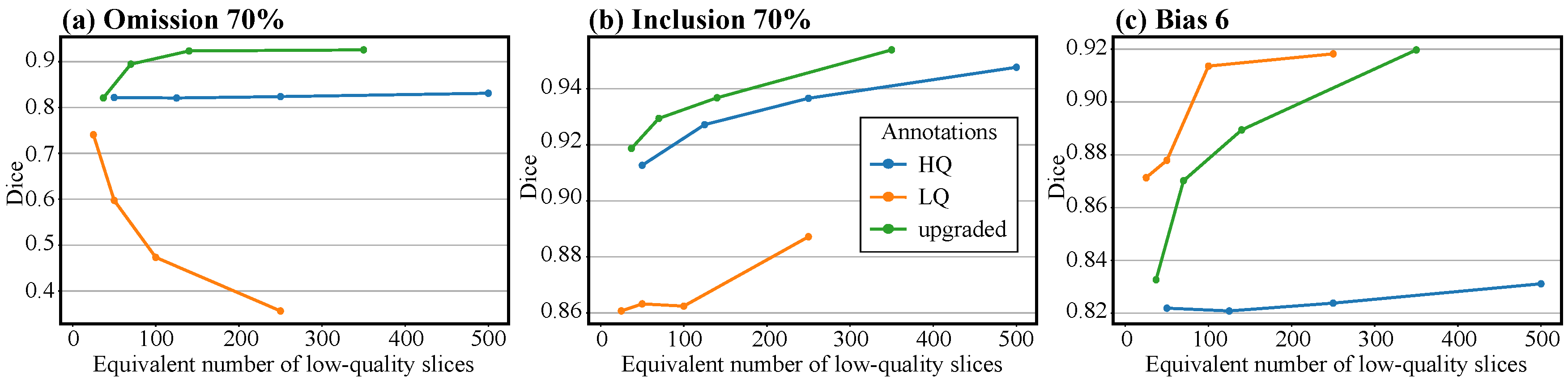
3.3. Enhancing Manual Annotations
3.4. Case Study: Upgrading Low-Quality Predictions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kamath, U.; Liu, J.; Whitaker, J. Deep Learning for NLP and Speech Recognition; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.D.; Protopapadakis, E. Deep Learning for Computer Vision: A Brief Review. Comput. Intell. Neurosci. 2018, 2018, 7068349:1–7068349:13. [Google Scholar] [CrossRef] [PubMed]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3523–3542. [Google Scholar] [CrossRef] [PubMed]
- Greenwald, N.F.; Miller, G.; Moen, E.; Kong, A.; Kagel, A.; Dougherty, T.; Fullaway, C.C.; McIntosh, B.J.; Leow, K.X.; Schwartz, M.S.; et al. Whole-cell segmentation of tissue images with human-level performance using large-scale data annotation and deep learning. Nat. Biotechnol. 2022, 40, 555–565. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Tanno, R.; Xu, M.C.; Jin, C.; Jacob, J.; Cicarrelli, O.; Barkhof, F.; Alexander, D. Disentangling human error from ground truth in segmentation of medical images. Adv. Neural Inf. Process. Syst. 2020, 33, 15750–15762. [Google Scholar]
- Vădineanu, S.; Pelt, D.M.; Dzyubachyk, O.; Batenburg, K.J. An Analysis of the Impact of Annotation Errors on the Accuracy of Deep Learning for Cell Segmentation. In Proceedings of the 5th International Conference on Medical Imaging with Deep Learning, Zurich, Switzerland, 6–8 July 2022; Volume 172, pp. 1251–1267. [Google Scholar]
- Rajchl, M.; Lee, M.C.H.; Oktay, O.; Kamnitsas, K.; Passerat-Palmbach, J.; Bai, W.; Damodaram, M.; Rutherford, M.A.; Hajnal, J.V.; Kainz, B.; et al. DeepCut: Object Segmentation From Bounding Box Annotations Using Convolutional Neural Networks. IEEE Trans. Med. Imaging 2017, 36, 674–683. [Google Scholar] [CrossRef] [PubMed]
- Can, Y.B.; Chaitanya, K.; Mustafa, B.; Koch, L.M.; Konukoglu, E.; Baumgartner, C.F. Learning to segment medical images with scribble-supervision alone. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Cham, Switzerland, 2018; pp. 236–244. [Google Scholar]
- Matuszewski, D.J.; Sintorn, I.M. Minimal annotation training for segmentation of microscopy images. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging, Washington, DC, USA, 4–7 April 2018; pp. 387–390. [Google Scholar]
- Peng, L.; Lin, L.; Hu, H.; Zhang, Y.; Li, H.; Iwamoto, Y.; Han, X.; Chen, Y. Semi-Supervised Learning for Semantic Segmentation of Emphysema with Partial Annotations. IEEE J. Biomed. Health Inform. 2020, 24, 2327–2336. [Google Scholar] [CrossRef] [PubMed]
- Min, S.; Chen, X.; Zha, Z.J.; Wu, F.; Zhang, Y. A two-stream mutual attention network for semi-supervised biomedical segmentation with noisy labels. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4578–4585. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Zhang, M.; Gao, J.; Lyu, Z.; Zhao, W.; Wang, Q.; Ding, W.; Wang, S.; Li, Z.; Cui, S. Characterizing Label Errors: Confident Learning for Noisy-Labeled Image Segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI, Lima, Peru, 4–8 October 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 721–730. [Google Scholar]
- Nie, D.; Gao, Y.; Wang, L.; Shen, D. ASDNet: Attention Based Semi-supervised Deep Networks for Medical Image Segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI, Granada, Spain, 16–20 September 2018; Frangi, A.F., Schnabel, J.A., Davatzikos, C., Alberola-López, C., Fichtinger, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 370–378. [Google Scholar]
- Dai, W.; Dong, N.; Wang, Z.; Liang, X.; Zhang, H.; Xing, E.P. SCAN: Structure Correcting Adversarial Network for Organ Segmentation in Chest X-rays; Springer: Cham, Switzerland, 2018; Volume 11045, pp. 263–273. [Google Scholar]
- Araújo, R.J.; Cardoso, J.S.; Oliveira, H.P. A Deep Learning Design for Improving Topology Coherence in Blood Vessel Segmentation; Springer: Cham, Switzerland, 2019; Volume 11764, pp. 93–101. [Google Scholar]
- Chen, S.; Juarez, A.G.; Su, J.; van Tulder, G.; Wolff, L.; van Walsum, T.; de Bruijne, M. Label Refinement Network from Synthetic Error Augmentation for Medical Image Segmentation. arXiv 2022, arXiv:2209.06353. [Google Scholar]
- Wang, S.; Li, C.; Wang, R.; Liu, Z.; Wang, M.; Tan, H.; Wu, Y.; Liu, X.; Sun, H.; Yang, R.; et al. Annotation-efficient deep learning for automatic medical image segmentation. Nat. Commun. 2021, 12, 5915. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Liu, J.; Cheng, K.T.; Yang, X. Label refinement with an iterative generative adversarial network for boosting retinal vessel segmentation. arXiv 2019, arXiv:1912.02589. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Feyjie, A.R.; Azad, R.; Pedersoli, M.; Kauffman, C.; Ayed, I.B.; Dolz, J. Semi-supervised few-shot learning for medical image segmentation. arXiv 2020, arXiv:2003.08462. [Google Scholar]
- Feng, R.; Zheng, X.; Gao, T.; Chen, J.; Wang, W.; Chen, D.Z.; Wu, J. Interactive few-shot learning: Limited supervision, better medical image segmentation. IEEE Trans. Med. Imaging 2021, 40, 2575–2588. [Google Scholar] [CrossRef] [PubMed]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 4015–4026. [Google Scholar]
- Stringer, C.; Wang, T.; Michaelos, M.; Pachitariu, M. Cellpose: A generalist algorithm for cellular segmentation. Nat. Methods 2021, 18, 100–106. [Google Scholar] [CrossRef]
- Ma, J.; He, Y.; Li, F.; Han, L.; You, C.; Wang, B. Segment anything in medical images. Nat. Commun. 2024, 15, 654. [Google Scholar] [CrossRef] [PubMed]
- Akram, S.U.; Kannala, J.; Eklund, L.; Heikkilä, J. Cell segmentation proposal network for microscopy image analysis. In Proceedings of the Deep Learning and Data Labeling for Medical Applications: First International Workshop, LABELS 2016, and Second International Workshop, DLMIA 2016, Conjunction with MICCAI 2016, Athens, Greece, 21 October 2016; Proceedings 1. Springer: Cham, Switzerland, 2016; pp. 21–29. [Google Scholar]
- Vădineanu, Ş.; Pelt, D.M.; Dzyubachyk, O.; Batenburg, K.J. Reducing Manual Annotation Costs for Cell Segmentation by Upgrading Low-Quality Annotations. In Proceedings of the Workshop on Medical Image Learning with Limited and Noisy Data, Vancouver, BC, Canada, 13 October 2023; Springer: Cham, Switzerland, 2023; pp. 3–13. [Google Scholar]
- Svoboda, D.; Kozubek, M.; Stejskal, S. Generation of digital phantoms of cell nuclei and simulation of image formation in 3D image cytometry. Cytom. Part A 2009, 75A, 494–509. [Google Scholar] [CrossRef]
- Wiesner, D.; Svoboda, D.; Maska, M.; Kozubek, M. CytoPacq: A web-interface for simulating multi-dimensional cell imaging. Bioinformatics 2019, 35, 4531–4533. [Google Scholar] [CrossRef]
- Lucchi, A.; Smith, K.; Achanta, R.; Knott, G.; Fua, P. Supervoxel-Based Segmentation of Mitochondria in EM Image Stacks with Learned Shape Features. IEEE Trans. Med. Imaging 2012, 31, 474–486. [Google Scholar] [CrossRef]
- Graham, S.; Jahanifar, M.; Azam, A.; Nimir, M.; Tsang, Y.W.; Dodd, K.; Hero, E.; Sahota, H.; Tank, A.; Benes, K.; et al. Lizard: A Large-Scale Dataset for Colonic Nuclear Instance Segmentation and Classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 684–693. [Google Scholar]
- Knott, A.B.; Perkins, G.; Schwarzenbacher, R.; Bossy-Wetzel, E. Mitochondrial fragmentation in neurodegeneration. Nat. Rev. Neurosci. 2008, 9, 505–518. [Google Scholar] [CrossRef]
- Bensch, R.; Ronneberger, O. Cell Segmentation and Tracking in Phase Contrast Images Using Graph Cut with Asymmetric Boundary Costs. In Proceedings of the IEEE 12th International Symposium on Biomedical Imaging, ISBI 2015, Brooklyn, NY, USA, 16–19 April 2015; pp. 1220–1223. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-level Histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- Serra, J.P.F. Image Analysis and Mathematical Morphology; Academic Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Paszke, A. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 8024–8035. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015—18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III. Navab, N., Hornegger, J.W.M.W., III, Frangi, A.F., Eds.; Springer: Cham, Switzerland, 2015. Lecture Notes in Computer Science. Volume 9351, pp. 234–241. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Rey, D.; Neuhäuser, M. Wilcoxon-Signed-Rank Test. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Cham, Switzerland, 2011; pp. 1658–1659. [Google Scholar]
- Benchoufi, M.; Matzner-Løber, E.; Molinari, N.; Jannot, A.; Soyer, P. Interobserver agreement issues in radiology. Diagn. Interv. Imaging 2020, 101, 639–641. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.G.; Han, E.; Petersen, J.; Olsen, N.A.F.; Giese, C.; Athmann, M.; Dresbøll, D.B.; Thorup-Kristensen, K. RootPainter: Deep learning segmentation of biological images with corrective annotation. New Phytol. 2022, 236, 774–791. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Xian, Y.; He, Y.; Akata, Z.; Schiele, B. Urban Scene Semantic Segmentation with Low-Cost Coarse Annotation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–7 January 2023; pp. 5978–5987. [Google Scholar]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Efficient graph-based image segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]





| Training Setup for Upgrade Network | Quality of Training Annotations | Quality of Segmentation Network | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Training Data | ||||||||||
| Perturbation | Data | Vols. | Slices | LQ | Upg. | HQ | HQ + upg. | HQ + LQ | LQ only | Thrs. |
| 70% omission | HL60 | 10 | 10 | 0.462 | 0.939 | 0.823 | 0.929 | 0.311 | 0.311 | 0.887 |
| gran. | 10 | 80 | 0.495 | 0.92 | 0.892 | 0.894 | 0.41 | 0.414 | 0.732 | |
| 70% inclusion | HL60 * | 10 | 10 | 0.925 | 0.992 | 0.913 | 0.962 | 0.891 | 0.89 | 0.892 |
| gran. * | 10 | 10 | 0.381 | 0.98 | 0.856 | 0.898 | 0.364 | 0.353 | 0.214 | |
| bias 6 | HL60 | 10 | 10 | 0.857 | 0.909 | 0.823 | 0.923 | 0.931 | 0.933 | 0.887 |
| gran. | 10 | 40 | 0.675 | 0.865 | 0.868 | 0.877 | 0.827 | 0.81 | 0.732 | |
| 30% om. 30% inc. bias 4 | HL60 * | 10 | 10 | 0.71 | 0.929 | 0.913 | 0.934 | 0.739 | 0.745 | 0.892 |
| gran. * | 10 | 10 | 0.54 | 0.86 | 0.856 | 0.854 | 0.505 | 0.5 | 0.214 | |
| Training Perturbation for Upgrade Network | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Omission | Inclusion | Bias | |||||||
| 20% | 30% | 50% | 20% | 30% | 50% | 2 | 4 | 6 | |
| HL60 | 0.955 | 0.972 | 0.952 | 0.973 | 0.972 | 0.986 | 0.915 | 0.918 | 0.926 |
| gran. | 0.838 | 0.86 | 0.93 | 0.984 | 0.98 | 0.981 | 0.821 | 0.837 | 0.884 |
| Perturbation | |||
|---|---|---|---|
| Method | 70% Omission | 70% Inclusion | Bias 6 |
| Partial Labeling [10] | 0.906 | 0.859 | 0.803 |
| Confident Learning [13] | 0.381 | 0.888 | 0.947 |
| Ours | 0.923 | 0.962 | 0.916 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vădineanu, S.; Pelt, D.M.; Dzyubachyk, O.; Batenburg, K.J. Reducing Manual Annotation Costs for Cell Segmentation by Upgrading Low-Quality Annotations. J. Imaging 2024, 10, 172. https://doi.org/10.3390/jimaging10070172
Vădineanu S, Pelt DM, Dzyubachyk O, Batenburg KJ. Reducing Manual Annotation Costs for Cell Segmentation by Upgrading Low-Quality Annotations. Journal of Imaging. 2024; 10(7):172. https://doi.org/10.3390/jimaging10070172
Chicago/Turabian StyleVădineanu, Serban, Daniël M. Pelt, Oleh Dzyubachyk, and Kees Joost Batenburg. 2024. "Reducing Manual Annotation Costs for Cell Segmentation by Upgrading Low-Quality Annotations" Journal of Imaging 10, no. 7: 172. https://doi.org/10.3390/jimaging10070172
APA StyleVădineanu, S., Pelt, D. M., Dzyubachyk, O., & Batenburg, K. J. (2024). Reducing Manual Annotation Costs for Cell Segmentation by Upgrading Low-Quality Annotations. Journal of Imaging, 10(7), 172. https://doi.org/10.3390/jimaging10070172








