Abstract
The effects of sulfuric acid concentration in VO2+ solutions were investigated via electrochemical methods and electron paramagnetic resonance. The viscosity of solutions containing 0.01 M VOSO4 in 0.1–7.0 M H2SO4 was measured. Diffusion coefficients were independently measured via electrochemical methods and electron paramagnetic resonance (EPR), with excellent agreement between the techniques employed and literature values. Analysis of cyclic voltammograms suggest the oxidation of VO2+ to VO2+ is quasi-reversible at high H2SO4 concentrations (>5 mol/L), and approaching irreversible at lower H2SO4 concentrations. Further analysis reveals a likely electrochemical/chemical (EC) mechanism where the H2SO4 facilitates the electrochemical step but hinders the chemical step. Fundamental insights of VO2+/H2SO4 solutions can lead to a more comprehensive understanding of the concentration effects in electrolyte solutions.
1. Introduction
Flow batteries, including the all-vanadium redox flow battery (VRFB), have recently received considerable attention as a possible solution to large grid energy storage needs [1]. Numerous experimental [2] and modeling studies [3] have been conducted to understand and improve flow battery technology. A detailed understanding of the electrolyte dynamics and how they change with parameters like temperature and concentration is an important fundamental step in flow battery research [4,5,6]. For instance, many modeling studies rely on physical parameters, such as viscosity, diffusion coefficient, permeability, mobility, activation energy, and others. However, these values are often not known for the specific conditions at which models are evaluated; thus, modelers often rely on the available parameters of nearest relevance, potentially leading to incorrect models.
The vanadium electrolyte in VRFBs frequently begins as a solution of vanadyl sulfate and sulfuric acid, which is charged to the necessary oxidation states to form the anolyte and catholyte solutions for the uncharged battery [7]. Concentrations ranging from 0.1–2 M VOSO4 and 1–5 M H2SO4 have been reported in characterization studies [6]. Significant interest has been given to the diffusion and uptake of vanadium in the ion exchange membranes that separate the negative and positive electrodes. Vanadium crossover through the membrane leads to self-discharge of the battery. The composition of the electrolyte has been shown to play an important role in this process [8,9,10,11]. Vanadium crossover could potentially lead to concentration mismatches, which, in severe cases could require complete electrolyte remixing which could result in downtime. Thus, a complete understanding of these dynamics will assist in further development of VRFBs and enhance their performance and marketability.
Some limitations of current battery technology include the kinetics of the reactions and the solubility of the reactants at varying temperatures and pH values. A number of organic additives, including L-Glutamic acid [12] and inositol and phytic acid [13], have been investigated to improve the energy density of the battery. A variety of sulfates and phosphates have also been investigated to inhibit vanadium precipitation [14]. A foundation of fundamental information to understand the effects of sulfate, acid, and other components of the electrolyte systems can aide in the pursuit of improved electrolytes for battery operation by using a knowledge-based approach.
Diffusion coefficients for translational diffusion can be measured in a variety of ways. Electrochemically, it is possible to measure the diffusion coefficient with cyclic voltammetry using the Randles–Sevcik equation, through chronoamperometry using the Cottrell equation, and through rotating disc electrode methods (cyclic or linear sweep voltammetry) using the Koutecky–Levich equation. Furthermore, these methods can provide complementary information, as long as they are carefully executed under the conditions for which the equations have been developed. In many cases, the validity of these equations depends on boundary conditions that are not relevant to actual battery operation. For instance, activities are often replaced by concentrations for convenience, as the assumption is acceptable for dilute solutions. However, as concentrations increase appreciably (i.e., values relevant to VRFBs) so does the deviation from activity, thus rendering the equations inaccurate. For this reason, we employ ideal-dilute battery electrolytes for this initial study. It is worth noting that as H2SO4 concentrations increase, so does viscosity which will cause a decrease in diffusion coefficients. This is also the case for VOSO4 concentrations [4,15] but the focus of this paper is on the effect of the acid concentration on the system, so low concentrations of VOSO4 minimize the effect of the later, which will be addressed in future studies.
Rotational diffusion can be determined using electron paramagnetic resonance (EPR). EPR is a technique that can be used to observe species with unpaired electrons, which the V(IV) in VO2+ has. EPR is sensitive to the motions of detectible species, which makes it a useful tool for energy research where species mobility is important [16,17,18,19,20]. Rotational diffusion and translational diffusion can be related via the Stokes–Einstein and the Stokes–Einstein–Debye equations. In this approach, the translational diffusion can be determined separately by different methods and compared to ensure accuracy.
The concept of electrochemical reversibility/irreversibility, which is kinetically driven, is another important consideration, and should not be confused with chemical reversibility/irreversibility, which is thermodynamically driven. Electrochemical reversibility can be measured using cyclic voltammetry by inspecting the difference in peak potentials, ΔEp, which is related to the reaction rate k0 [21,22]. This is a powerful electroanalytical method applicable to any redox process, including VRFB reactions. Previous investigations [23] have indicated that VO2+ oxidation exhibits higher reversibility with increasing H2SO4 concentration, though the voltammograms are highly asymmetric at 2 M VO2+. Here, we fully investigate the reversibility of VO2+ oxidation and interpret the data to make conclusions about the effects of H2SO4 on the electrochemical rate.
In order to more fully understand the dynamics in these electrolyte solutions, we begin with a study looking at the effects of H2SO4 concentration on the diffusion, hydrodynamic or Stokes radius and oxidation of the vanadyl (VO2+) ion in dilute solutions of VOSO4. The effects of H2SO4 on these physical and electrochemical properties can be used to guide further electrolyte and battery developments and provide insight into the kinetics of VO2+ oxidation. In addition to gaining understanding of the effects of H2SO4 concentration, these physical characteristics, we develop some insight into the electrochemical redox mechanism for the oxidation of VO2+ and subsequent reduction of VO2+, which cannot be achieved by standard VRFB cycling studies. It is worth noting that these fundamental studies have been carried out on smooth, polished glassy carbon electrodes. The kinetics of VO2+/VO2+ are sensitive to the electrode surface structure and area as described previously [24,25].
2. Results and Discussion
The influence of 0.01 M VOSO4 has a negligible effect on the viscosity of the H2SO4 electrolyte. Figure 1 plots the Arrhenius-type plots for viscous flow for solutions with and without VO2+:
where Ea is the activation energy for viscous flow, is the viscosity at infinite temperature, R is the gas constant, and T is temperature. The viscosity data and extracted Arrhenius parameters are made available in Table A2 and Table A3 in Appendix A, respectively. As with the viscosity, the presence of this low concentration of VO2+ has little to no effect on the activation energy (Ea) or the intercept (). The systematic increase in solution viscosity with H2SO4 concentration is expected, as pure H2SO4 has a high viscosity (~26 cP at 20 °C); thus, the viscosity is expected to generally increase with the increasing mole fraction of H2SO4. These viscosity data were collected and used in the analyses of the electrochemistry and EPR experiments discussed below.
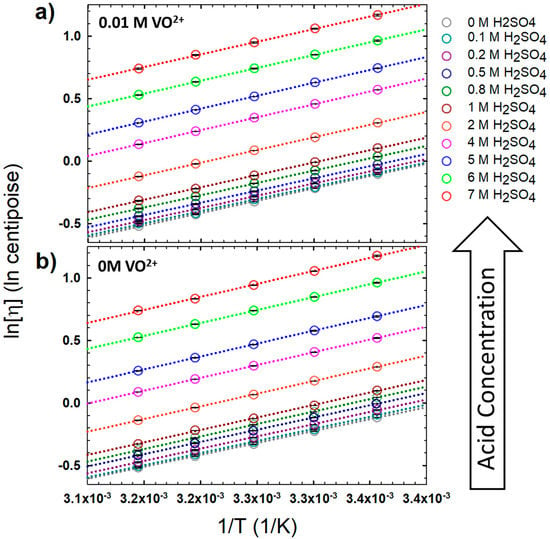
Figure 2a,b shows sample EPR spectra of the VO2+ ion in 0.1 M and 7 M H2SO4 at 25 °C and −180 °C, respectively. In Figure 2b, the lower H2SO4 concentration spectra show broadening due to unresolved hyperfine interactions, most likely a result of solute aggregation in the frozen solutions. Broadening in frozen solutions has been observed to dissipate with the addition of glycerin to the solution to deter nucleation, probably by slowing mobility with increased viscosity [26]. This broadening decreases with increasing H2SO4 concentration, which also increases the viscosity and lowers the VO2+ mobility (Figure 2b, inset). However, a steep drop in spectral broadening is observed with only small increases in H2SO4 concentration, where the viscosity does not significantly increase. For the lowest H2SO4 concentration measured, 0.1 M, the pH should be <1, and the VO2+ structure should be stable as an aquo-cation ligated by five water molecules [27]. The increased presence of additional ions in the solution must also play a role in deterring aggregation upon freezing, possibly by adding competition to ion redistribution observed in freezing liquids [28].
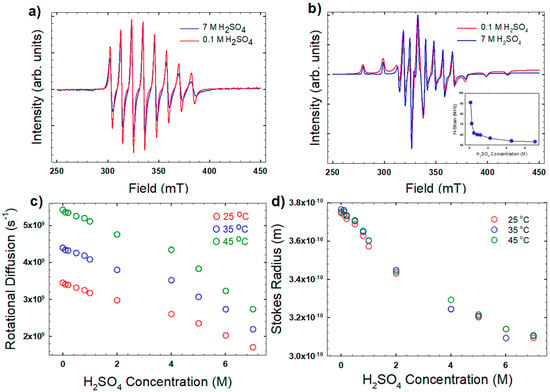
Figure 2.
(a) Representative electron paramagnetic resonance (EPR) spectra at 25 °C for the highest and lowest H2SO4 concentrations investigated; (b) EPR spectra collected at −180 °C (inset shows unrefined hyperfine coupling); (c) extracted rotational diffusion coefficients using Equation (2); and (d) the Stokes radius of the vanadyl ion using Equation (2). EPR fitting parameters were = 542.6 MHz; = 203.3 MHz; = 1.943; and = 1.989.
The initial parameters for fitting the higher temperature spectra were determined by fits to the frozen spectra at −180 °C. The value of , determined from the rigid limit spectra, is consistent with values reported in the literature [29], and is as expected for a complex with four equatorial water ligands [30]. EPR fitting parameters that were unaffected by the H2SO4 concentration are listed in the Figure 2 caption. The fitting parameter most affected by the H2SO4 concentration was the rotational diffusion, which decreased as H2SO4 concentration and viscosity increased (Figure 2c).
The stokes radius of the VO(H2O)52+ complex is related to the rotational diffusion through the Stokes–Einstein–Debye (SED) equation:
Figure 2d shows the results of this calculation. The radius decreases from 3.7 A to 3.1 Å with increasing H2SO4 concentration. These values are in good agreement with values reported elsewhere [29,31,32]. The trend with H2SO4 concentration, however, is different than what was observed by Oriji et al. [23] in solutions with significantly higher VO2+ concentration (~2 M), where considerably lower Stokes radii (2 Å) were reported. The decreasing trend in the Stokes radius observed here is likely due to the higher H2SO4 concentrations disrupting the outermost hydration layer, possibly to hydrate the H2SO4.
The rotational diffusion and Stokes radius can be related to the translational diffusion through the Stokes–Einstein (SE) equation relating translational diffusion and viscosity:
In addition, by combining Equations (2) and (3):
The translational diffusion of VO2+ in the H2SO4 solutions as determined by EPR is shown in Figure 3, and will be discussed in greater detail in comparison to results obtained via electrochemistry below.
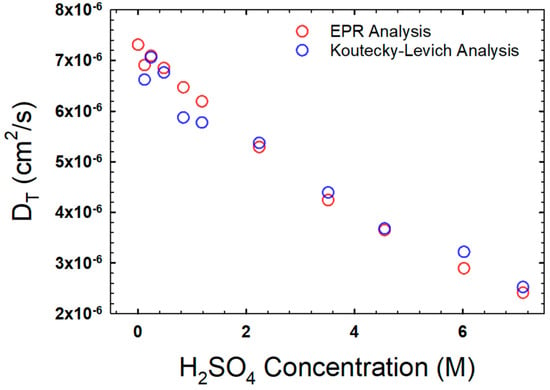
Figure 3.
Translational diffusion coefficients as a function of H2SO4 concentration, as obtained via EPR (red circles) and rotating disc electrode analyses (blue circles). Both datasets are measured at 25 °C.
The oxidation of the VO2+ ion to VO2+ proceeds via the following reaction:
At a pH < 1 and low vanadium concentration, the V(V) is expected to exist as a VO2+ ion with a bent geometry, though there is some discussion as to whether it is more likely to be ligated by four or three water molecules [33].
Linear sweep voltammetry at a rotating disc electrode was analyzed by plotting the inverse of the square root of the rotation rate versus 1/i in Figure 4. The linear results fit with the Koutecky–Levich (K-L) equation:
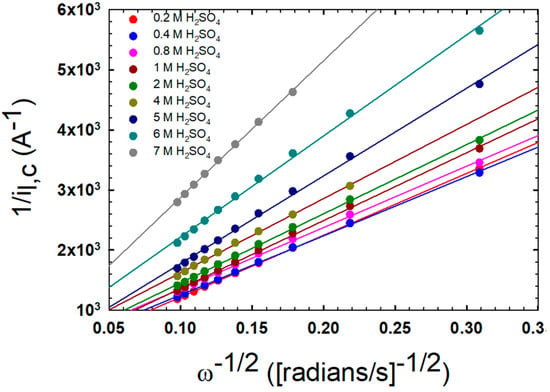
Figure 4.
Results of the Koutecky–Levich (K–L) analysis of linear sweep voltammetry data measured for 0.01 M VO2+ in the indicated H2SO4 solutions at 25 °C.
Using this method, the translational diffusion, DT, can be calculated from the slope of the line. The results from this method are compared to the results from the EPR in Figure 3, and they correlate well.
Figure 5 shows sample cyclic voltammograms for VOSO4/H2SO4 solutions. Figure 5a shows the CVs as a function of the scan rate for the 7 M H2SO4 solution, while Figure 5b plots the peak separation (ΔEp) for the same. These data reveal that even for this highest acid concentration, the redox process is quasi-reversible at best, as fully reversible redox couples would exhibit ΔEp ~ 59 mV. Here we observe a minimal peak separation of 86 mV when the scan rate is 1 mV/s. Additionally, the values of ΔEp increase with the scan rate, which suggests that the reaction kinetics become in competition with mass transport for the faster scan rates, where the diffusion layer is thinner than for the slower rates [20]. Figure 5c shows the cyclic voltammogram (CV) as a function of H2SO4concentration at a fixed scan rate of 15 mV/s. These CVs are qualitatively similar to those reported elsewhere [22]. Between 1–1.2 V vs. Ag/AgCl, the anodic part of the scan shows a peak associated with the oxidation of V(IV) to V(V). Ranging from 0.2–1 V of the cathodic part of the scan, there is a peak associated with the subsequent reduction of V(V) back to V(IV). This peak drifts to lower potentials with lower H2SO4 concentrations, and is more dependent on H2SO4 concentration than the anodic peak. Overall, as H2SO4 concentration decreases, the shape of the CV becomes more stretched out as ΔEp increases and the peak currents decrease, which is characteristic of a shift from quasi-reversible to irreversible.
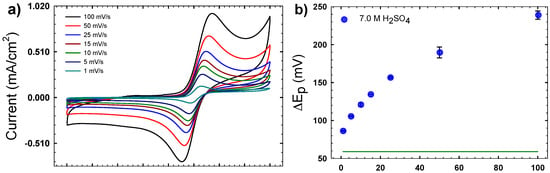
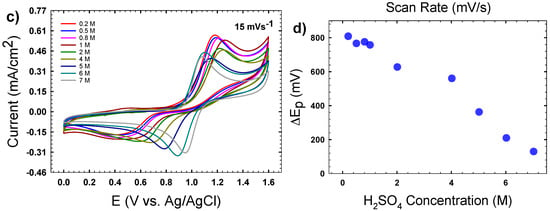
Figure 5.
(a) Cyclic voltammograms (CVs) of 0.01 M VO2+ in 7 M H2SO4 at the indicated scan rates measured at 25 °C; (b) plot of peak separation (ΔEp) from the CVs in (a); (c) a representative set of CVs of 0.01 M VO2+ as a function of H2SO4 concentration at 25 °C, with a scan rate of 15 mV/s; (d) average ΔEp for CVs measured at varying H2SO4 concentrations.
Further analyses of the CVs reveal interesting kinetic information on the oxidation of VO2+. The shape of the CVs, particularly at lower H2SO4 concentrations where ip,a > ip,c, suggests an EC (electrochemical [first reaction]/chemical [second reaction]) mechanism:
which is consistent with the EC mechanism proposed by Gattrell et al. [34]. The effect of the chemical step on the shape of the CV is then expected to truncate the cathodic peak and should be more pronounced in conditions where: (a) the chemical step has more time to occur before the cathodic scan begins (i.e., lower scan rate) and (b) the chemical reaction is able to occur very quickly before the cathodic scan begins (i.e., faster rate of the chemical step). The effect of scan rate can be probed qualitatively by observing the ratio of the peak heights (ip,c/ip,a), In Figure 6a the calculated results are shown using the approximation by Nicholson [35]:
where is the position of the cathodic peak and is the current at the switching potential, which here is taken as the minima between the anodic peak associated with the VO2+ oxidation and the switching potential. As the scan rates increase, the peak height ratio approaches 1. At higher H2SO4 concentrations, the peak ratios also approach 1, suggesting that the presence of H+ in the solution (a product of the chemical step of the mechanism) alters the rate of the chemical step. Modeling works [36] have shown that an EC mechanism mostly effects the cathodic peak, leaving the anodic peak available for traditional analysis.
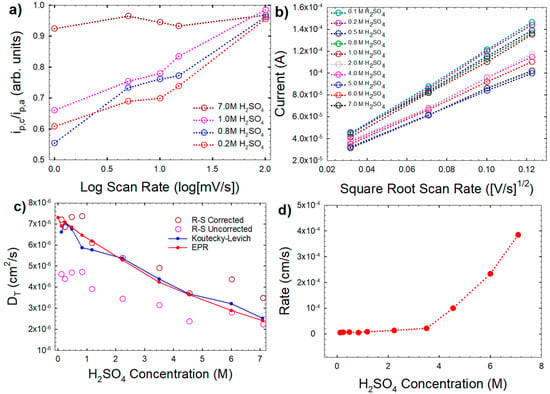
Figure 6.
(a) Peak current ratios for the CVs of 0.01 M VO2+ in the indicated H2SO4 solutions as a function of scan rate (shown here as log of scan rate for clarity); (b) Randles–Sevcik (R–S) analysis of the CVs (four slowest scan rates) using Equation (8); (c) translational diffusion coefficient (DT) calculated from R–S analysis for corrected (red circles) and uncorrected (dark red hollow circles) peak currents in comparison to values obtained via K–L and EPR analyses (the latter from Figure 3). The peak current correction applied was +20% added to the anodic peak. (d) Heterogeneous rate constant (k0) at varying H2SO4 concentrations, as calculated using Equation (10).
It can be observed from Figure 5 that as the CVs deviate from reversibility the peak heights decrease. The Randles-Sevcik equation for irreversible redox reactions accounts for this by adding the term:
where n’ is the number of electrons transferred before the rate determining step. The relationship of ip,a with the square root of scan rate is shown in Figure 6b. If = 0.5, the peak of the irreversible process is expected to be 80% of a theoretical reversible process with identical parameters [37].
Figure 6c demonstrates the use of the Randles–Sevcik equation for a reversible process to calculate the diffusion coefficient (DT) based on the actual anodic peak currents and anodic peak currents with an added 20% of height. Only the lowest scan rates were used to determine DT using this method. Low scan rates have been shown to deviate the least from peak values predicted by the Randles–Sevcik equation, in the case where pure Butler–Volmer kinetics are not predicted [38], which is suggested in publications reporting Tafel slopes for this system [34,39]. The average DT values determined from EPR and rotating disc electrodes (RDE) are plotted for comparison. At higher H2SO4 concentrations, the results calculating the diffusion from uncorrected peak heights compare well with those measured by other means, but the diffusion for lower H2SO4 concentrations trends low. The results of the calculation of the DT using the corrected peak currents, also plotted in Figure 6c, show that lower H2SO4 concentrations compare well with the other methods, but also that higher H2SO4 concentrations trend high. This suggests that as the H2SO4 concentration decreases, and the redox processes deviate from reversibility, the 80% relationship becomes viable with an α value of 0.5. Assuming an α value of 0.5 and diffusion coefficients determined by EPR and RDE, the potential peak separation, ΔEp, can be used to determine the standard heterogenous rate constant, ko, using the relationship of Klingler and Kochi [22,40]:
This method is similar to the commonly used method of Nicholson and Shane [41], but is more appropriate for the larger values of ΔEp (and therefore lower values of ko), which are observed here for the lower H2SO4 concentrations. As Figure 6d illustrates, the rate of the electrochemical step on glassy carbon increases dramatically as H2SO4 concentration is increased (e.g., 72 times larger at 7 M versus 0.1 M H2SO4).
3. Materials and Methods
3.1. Preparation of Electrolyte Solutions
Electrolyte solutions were made to consist of 0.01 M VOSO4·xH2O (x = 4.2 via the certificate of analysis; Alfa Aesar, Ward Hill, MA, USA) and sulfuric acid (Sigma Aldrich, Burlington, MA, USA) at approximate target concentrations of 0 M, 0.1 M, 0.2 M, 0.5 M, 0.8 M, 1.0 M, 2.0 M, 4.0 M, 5.0 M, 6.0 M, and 7.0 M. All acid stock solution concentrations were verified via titration with standardized NaOH prior to the addition of VOSO4. The actual titrated concentrations of H2SO4 were as follows: 0.1180 M, 0.2390 M, 0.4761 M, 0.8334 M, 1.176 M, 2.231 M, 3.502 M, 4.539 M, 6.012 M, and 7.086 M.
3.2. Viscosity Measurements
Measurements of dynamic viscosity were performed on each H2SO4 stock solutions, as well as the VOSO4 electrolyte solutions using a Cannon–Fenske routine viscometer (Fungilab, sizes 25, 50, 75, and 100, Hauppauge, NY, USA). Cleaned (piranha solution) and dried viscometers were filled with approximately 7 mL of solution and immersed in a thermostatic water bath (PolyScience, Niles, IL, USA) equipped with digital temperature control. Viscosity measurements were collected for each H2SO4 stock and electrolyte solutions at 25 °C, 30 °C, 35 °C, 40 °C, and 45 °C. To obtain the dynamic viscosity from the kinematic viscosity, the kinematic viscosity was divided by the density, ρ, for each solution, which was measured using calibrated micropipettes and an analytical balance accurate to five decimal places (Mettler Toledo XS105, Columbus, OH, USA).
Viscosity was calculated using the following relationship:
where the subscript s refers to the solution investigated and subscript w refers to water, while η is viscosity (cP), ρ is density (g/cm3), and t is time (s). Values for ηw were adopted from known sources [42]. Errors were propagated using standard methods for error analysis in multi-measurement systems [43].
3.3. Electron Paramagnetic Resonance (EPR) Measurements
The H2SO4 and VOSO4 solutions were deoxygenated by bubbling with hydrated nitrogen for 1 h. Samples were sealed in a capillary. Measurements were collected on an x-band EPR (Magnettech 5000 miniscope, Berlin, Germany) at 25–45 °C and at −180 °C. The spectra were fitted using Easyspin [44,45].
3.4. Electrochemical Measurements
All electrochemical measurements were carried out in a 50 mL glass jacketed beaker electrochemical cell maintained at 25 °C and fitted with a machined Teflon lid. The working electrode was a glassy carbon rotating disc electrode (Pine Instruments, Grove City, PA, USA) with a 5.0 mm diameter attached to a Pine Instruments model MSR rotator. A Pt mesh spot welded to Pt wire was employed as the counter electrode, and the reference electrode was an Ag/AgCl (saturated NaCl, BASi, West Lafayette, IN, USA) reference electrode. All characterization was carried out using a Bio Logic SP-300 potentiostat equipped with two channel boards. Electrode pre-treatment included polishing with 1 μm and 0.05 μm alumina slurry (Electron Microscopy Sciences, Hatfield PA, USA) and sonicating in MilliQ 18.2 MΩ·cm deionized water (Millipore Sigma, Burlington MA, USA) for 5 min.
3.4.1. Rotating Disc Electrode (RDE) Experiments
All RDE experiments were conducted on a Pine Instruments MSR rotator at rotation rates of 100, 200, 300, 400, 500, 600, 700, 800, 900, and 1000 RPMs sequentially. Five linear sweep voltammograms were collected for each rotation rate with potential limits of 0.1–1.6 V versus Ag/AgCl. In all cases, the electrolyte solutions were previously degassed by sparging with pre-hydrated Ar (ultra-high purity; Airgas, Radnor, PA, USA).
3.4.2. Cyclic Voltammograms
Cyclic voltammograms were collected for each of the 0.01 M VOSO4 electrolyte solutions using potential limits of 0.0–1.6 V versus Ag/AgCl and scan rates of 100, 50, 25, 15, 10, 5, and 1 mVs−1 for all H2SO4 concentrations.
4. Conclusions
In this initial investigation into the relationship between the VO2+ ion and H2SO4 concentration in bulk solution, diffusion of the VO2+ ion has been measured with similar results by different methods, and is in agreement with published reports. Of the three methods investigated, results from EPR and Koutecky–Levich were very consistent. The Stokes radius of VO2+ was observed to decrease with increasing acid concentration, likely as a result of the disruption of the second hydration layer by the higher H2SO4 concentrations. Qualitative mechanistic and rate information was observed from the electrochemistry of the solutions. These data suggest that the oxidation of VO2+ to VO2+ proceeds by an EC mechanism, with the electrochemical step being faster with higher acid concentrations at the expense of the rate of the chemical step, as H+ is a reaction product. Analysis of the cyclic voltammetry revealed that the redox process was electrochemically irreversible at H2SO4 concentrations of <5 M, and quasi-reversible from 5–7 M, but approaching reversible with ΔEp = 75 mV at 1 mV/s and 7 M H2SO4. The methods developed here can be applied to the other VRFB-relevant reactions to gain a more detailed understanding of electrolyte solutions for redox flow batteries. This includes observations of more concentrated solutions and different electrode surfaces.
Author Contributions
J.S.L. and T.M.A. conceived the project and designed the experiments. S.M.T. collected all the electrochemistry data and a portion of the viscosity measurements and titrations. D.J.D. and S.P.F. measured the viscosity and performed the acid-base titrations. J.S.L. and T.M.A. collected the EPR data; J.S.L. analyzed and interpreted the EPR data. J.S.L. and T.M.A. analyzed the electrochemistry data and wrote the manuscript. All authors reviewed the manuscript.
Funding
This research was funded by in part by a Student Collaborative and Integrated Grant for Research (SCIG) from Salve Regina University, grant number [558112].
Acknowledgments
Sophia M. Tiano, Daniel J. Donnelly and Sean P. Flanagan acknowledge the NASA Rhode Island Space Grant Consortium (NASA) for summer undergraduate research scholarships (NNX15AI06H).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
List of terms and symbols.
Table A1.
List of terms and symbols.
| Term/Symbol | Definition |
|---|---|
| Hyperfine splitting tensor, MHz | |
| A | Electrode area, cm2 |
| Co | Concentration, mol m−3 |
| DR | Rotational diffusion, s−1 |
| DT | Translational diffusion, m2 s−1 |
| Anodic peak potential, V | |
| Cathodic peak potential, V | |
| Ea | Activation energy, kJ mol−1 |
| F | Faraday’s constant, C mol−1 |
| g-tensor | |
| i | Current, Amperes |
| iK | Kinetic current, Amperes |
| ip,a | Anodic peak current, Amperes |
| ip,c | Cathodic peak current, Amperes |
| (ip,c)o | Cathodic peak current position, Amperes |
| isp | Switching potential current, Amperes |
| kB | Boltzmann Constant, m2 kg s−2 K−1 |
| ko | Rate constant cm s−1 |
| n | Moles |
| ɳ | Viscosity, cP |
| ɳ∞ | Arrhenius preexponential factor cP |
| r | Hydrodynamic radius, m |
| R | Gas constant, J mol−1 K−1 |
| T | Temperature, K |
| α | Electron transfer constant |
| ΔEp | Difference in peak potentials, V |
| ν | Scan rate, V s−1 |
| ω | Rotation rate, rad s−1 |

Table A2.
Dynamic viscosity of sulfuric acid/sulfuric acid VO2+ electrolytes at the indicated temperatures, in units of centipoise (cP).
Table A2.
Dynamic viscosity of sulfuric acid/sulfuric acid VO2+ electrolytes at the indicated temperatures, in units of centipoise (cP).
| No VO2+ | Temperature (K) | ||||
| Sulfuric Acid Conc. (mol L−1) | 298 | 303 | 308 | 313 | 318 |
| 0 | 0.890 | 0.797 | 0.719 | 0.653 | 0.596 |
| 0.1 | 0.909 | 0.809 | 0.730 | 0.663 | 0.603 |
| 0.2 | 0.945 | 0.840 | 0.758 | 0.686 | 0.623 |
| 0.5 | 0.993 | 0.890 | 0.801 | 0.724 | 0.658 |
| 0.8 | 1.046 | 0.929 | 0.839 | 0.756 | 0.685 |
| 1.0 | 1.102 | 0.979 | 0.882 | 0.802 | 0.719 |
| 2.0 | 1.333 | 1.192 | 1.067 | 0.962 | 0.870 |
| 4.0 | 1.679 | 1.499 | 1.344 | 1.208 | 1.090 |
| 5.0 | 1.999 | 1.781 | 1.595 | 1.433 | 1.291 |
| 6.0 | 2.613 | 2.330 | 2.089 | 1.875 | 1.685 |
| 7.0 | 3.242 | 2.869 | 2.562 | 2.296 | 2.092 |
| 0.01 mol L−1 VO2+ | Temperature (K) | ||||
| Sulfuric Acid Conc. (mol L−1) | 298 | 303 | 308 | 313 | 318 |
| 0 | 0.901 | 0.804 | 0.723 | 0.652 | 0.595 |
| 0.1 | 0.913 | 0.812 | 0.736 | 0.658 | 0.607 |
| 0.2 | 0.935 | 0.836 | 0.754 | 0.681 | 0.619 |
| 0.5 | 0.973 | 0.874 | 0.785 | 0.710 | 0.644 |
| 0.8 | 1.037 | 0.927 | 0.836 | 0.753 | 0.684 |
| 1.0 | 1.108 | 0.991 | 0.890 | 0.801 | 0.729 |
| 2.0 | 1.358 | 1.209 | 1.089 | 0.979 | 0.884 |
| 4.0 | 1.768 | 1.579 | 1.414 | 1.268 | 1.144 |
| 5.0 | 2.103 | 1.875 | 1.675 | 1.507 | 1.359 |
| 6.0 | 2.622 | 2.342 | 2.098 | 1.885 | 1.698 |
| 7.0 | 3.215 | 2.887 | 2.583 | 2.339 | 2.095 |

Table A3.
Arrhenius parameters extracted from data in Figure 1.
Table A3.
Arrhenius parameters extracted from data in Figure 1.
| H2SO4 Concentration (M) No VO2+ | Ea (kJ/mol) | η∞ (cP) |
| 0 | 16.41 | 1.19 × 10−3 |
| 0.1 | 16.19 | 1.32 × 10−3 |
| 0.2 | 16.25 | 1.32 × 10−3 |
| 0.5 | 16.27 | 1.37 × 10−3 |
| 0.8 | 16.37 | 1.40 × 10−3 |
| 1.0 | 16.56 | 1.39 × 10−3 |
| 2.0 | 16.88 | 1.42 × 10−3 |
| 4.0 | 17.18 | 1.72 × 10−3 |
| 5.0 | 17.22 | 2.02 × 10−3 |
| 6.0 | 17.12 | 2.62 × 10−3 |
| 7.0 | 16.81 | 3.63 × 10−3 |
| H2SO4 Concentration (M) With 0.01 M VO2+ | Ea (kJ/mol) | η∞ (cP) |
| 0.1 | 16.08 | 1.37 × 10−3 |
| 0.2 | 16.32 | 1.30 × 10−3 |
| 0.5 | 16.23 | 1.42 × 10−3 |
| 0.8 | 16.58 | 1.29 × 10−3 |
| 1.0 | 16.58 | 1.36 × 10−3 |
| 2.0 | 16.84 | 1.49 × 10−3 |
| 4.0 | 17.01 | 1.75 × 10−3 |
| 5.0 | 17.17 | 1.96 × 10−3 |
| 6.0 | 17.24 | 2.49 × 10−3 |
| 7.0 | 17.33 | 2.97 × 10−3 |
References
- Skyllas-Kazacas, M.; Rychcik, M.; Robins, R.G.; Fane, A.G.; Green, M.A. New All-Vanadium Redox Flow Cell. J. Electrochem. Soc. 1986, 133, 1057–1058. [Google Scholar] [CrossRef]
- Elgammal, R.A.; Tang, Z.; Sun, C.-N.; Lawton, J.; Zawodzinski, T.A. Species Uptake and Mass Transport in Membranes for Vanadium Redox Flow Batteries. Electrochim. Acta 2017, 237, 1–11. [Google Scholar] [CrossRef]
- Gandomi, Y.A.; Aaron, D.S.; Zawodzinski, T.A.; Mench, M.M. In Situ Potential Distribution Measurement and Validated Model for All-Vanadium Redox Flow Battery. J. Electrochem. Soc. 2016, 163, A5188–A5201. [Google Scholar] [CrossRef]
- Lawton, J.S.; Jones, A.; Zawodzinski, T. Concentration dependence of VO2+ crossover of nafion for vanadium redox flow batteries. J. Electrochem. Soc. 2013, 160, A697–A702. [Google Scholar] [CrossRef]
- Lawton, J.S.; Jones, A.M.; Tang, Z.; Lindsey, M.; Zawodzinski, T. Ion effects on vanadium transport in Nafion membranes for vanadium redox flow batteries. J. Electrochem. Soc. 2017, 164, A2987–A2991. [Google Scholar] [CrossRef]
- Gandomi, Y.A.; Aaron, D.S.; Houser, J.R.; Daugherty, M.C.; Clement, J.T.; Pezeshki, A.M.; Ertugrul, T.Y.; Moseley, D.P.; Mench, M.M. Critical Review—Experimental Diagnostics and Material Characterization Techniques Used on Redox Flow Batteries. J. Electrochem. Soc. 2018, 165, A970–A1010. [Google Scholar] [CrossRef]
- Knehr, K.W.; Kumbur, E.C. Open circuit voltage of vanadium redox flow batteries: Discrepancy between models and experiments. Electrochem. Commun. 2011, 13, 342–345. [Google Scholar] [CrossRef]
- Lawton, J.S.; Jones, A.M.; Tang, Z.; Lindsey, M.; Fujimoto, C.; Zawodzinski, T.A. Characterization of Vanadium Ion Uptake in Sulfonated Diels Alder Poly(phenylene) Membranes. J. Electrochem. Soc. 2016, 163, A5229–A5235. [Google Scholar] [CrossRef]
- Lawton, J.S.; Aaron, D.S.; Tang, Z.; Zawodzinski, T.A. Qualitative behavior of vanadium ions in Nafion membranes using electron spin resonance. J. Membr. Sci. 2013, 428, 38–45. [Google Scholar] [CrossRef]
- Kim, S.; Yan, J.; Schwenzer, B.; Zhang, J.; Li, L.; Liu, J.; Yang, Z.; Hickner, M.A. Cycling performance and efficiency of sulfonated poly(sulfone) membranes in vanadium redox flow batteries. Electrochem. Commun. 2010, 12, 1650–1653. [Google Scholar] [CrossRef]
- Schwenzer, B.; Kim, S.; Vijayakumar, M.; Yang, Z.; Liu, J. Correlation of structural differences between Nafion/polyaniline and Nafion/polypyrrole composite membranes and observed transport properties. J. Membr. Sci. 2011, 372, 11–19. [Google Scholar] [CrossRef]
- Liang, X.; Peng, S.; Lei, Y.; Gao, C.; Wang, N.; Liu, S.; Fang, D. Effect of L-glutamic acid on the positive electrolyte for all-vanadium redox flow battery. Electrochim. Acta 2013, 95, 80–86. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, N.; Peng, S.; He, Z. Influence of organic additives on electrochemical properties of the positive electrolyte for all vanadium redox flow battery. Electrochim. Acta 2012, 78, 475–482. [Google Scholar] [CrossRef]
- Roe, S.; Menictas, C.; Skyllas-Kazacos, M. A High Energy Density Vanadium Redox Flow Battery with 3 M Vanadium Electrolyte. J. Electrochem. Soc. 2016, 163, A5023–A5028. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Cao, L.; Kazacos, M.; Kausar, N.; Mousa, A. Vanadium Electrolyte Studies for the Vanadium Redox Battery—A Review. ChemSusChem 2016, 9. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Schlick, S. Effect of solvents on phase separation in perfluorinated ionomers, from electron spin resonance of VO2+ in swollen membranes, and solutions. Polymer 1995, 36, 1141–1146. [Google Scholar] [CrossRef]
- Szajdzinska-pietek, E.; Pilar, J.; Schlick, S. Structure and Dynamics of Perfluorinated Ionomers in Aqueous Solutions and Swollen Membranes Based on Simulations of ESR Spectra From Spin Propes. J. Phys. Chem. 1995, 99, 313–319. [Google Scholar] [CrossRef]
- Alonso-Amigo, M.G.; Schlick, S. Determination of the Distance between Paramagnetic Centers from Electron Spin Resonance Spectra at L, S, and X Bands. Copper(2+) in Nafion Ionomers. Macromolecules 1989, 22, 2628–2634. [Google Scholar] [CrossRef]
- Lawton, J.S.; Smotkin, E.S.; Budil, D.E. Electron spin resonance investigation of microscopic viscosity, ordering, and polarity in nafion membranes containing methanol-water mixtures. J. Phys. Chem. B 2008, 112, 8549–8557. [Google Scholar] [CrossRef] [PubMed]
- Lawton, J.S.; Budil, D.E. Electron spin resonance investigaion of the effects of methanol on microscopic viscosity, ordering, and polarity in different phases of ionomer membranes with sulfonated polyarylene backbones. J. Membr. Sci. 2010, 357, 47–53. [Google Scholar] [CrossRef]
- Aristov, N.; Habekost, A. Cyclic Voltammetry—A Versatile Electrochemical Method Investigating Electron Transfer Processes. World J. Chem. Educ. 2015, 3, 115–119. [Google Scholar]
- Brownson, D.A.C.; Banks, C.E. The Handbook of Graphene Electrochemistry, 1st ed.; Springer: London, UK, 2014. [Google Scholar]
- Oriji, G.; Katayama, Y.; Miura, T. Investigation on V(IV)/V(V) species in a vanadium redox flow battery. Electrochim. Acta 2004, 49, 3091–3095. [Google Scholar] [CrossRef]
- Aaron, D.; Sun, C.-N.; Bright, M.; Papandrew, A.B.; Mench, M.M.; Zawodzinski, T.A. In Situ Kinetics Studies in All-Vanadium Redox Flow Batteries. ECS Electrochem. Lett. 2013, 2, A29–A31. [Google Scholar] [CrossRef]
- Bourke, A.; Miller, M.A.; Lynch, R.P.; Wainright, J.S.; Savinell, R.F.; Buckley, D.N. Electrode Kinetics in All-Vanadium Flow Batteries: Effects of Electrochemical Treatment. ECS Trans. 2015, 66, 181–211. [Google Scholar] [CrossRef]
- Albanese, N.F.; Chasteen, N.D. Origin of the electron paramagnetic resonance line widths in frozen solution of the oxovanadium(IV) ion. J. Phys. Chem. 1978, 82, 910–914. [Google Scholar] [CrossRef]
- Selbin, J. The Chemistry of Oxovanadium(IV). Chem. Rev. 1965, 65, 153–175. [Google Scholar] [CrossRef]
- Shafique, U.; Anwar, J.; Ali Munawar, M.; Zaman, W.U.; Rehman, R.; Dar, A.; Salman, M.; Saleem, M.; Shahid, N.; Akram, M.; et al. Chemistry of ice: Migration of ions and gases by directional freezing of water. Arab. J. Chem. 2016, 9, S47–S53. [Google Scholar] [CrossRef]
- Barklie, R.C.; Girard, O.; Braddell, O. EPR of vanadyl (2+) in a Nafion membrane. J. Phys. Chem. 1988, 92, 1371–1377. [Google Scholar] [CrossRef]
- Smith, T.S.; LoBrutto, R.; Pecoraro, V.L. Paramagnetic spectroscopy of vanadyl complexes and its applications to biological systems. Coord. Chem. Rev. 2002, 228, 1–18. [Google Scholar] [CrossRef]
- Reuben, J.; Fiat, D. Proton and Deuteron Relaxation in Aqueous Solutions of Vanadyl(IV). Effects of Electron Spin Relaxation and Chemical Exchange. J. Am. Chem. Soc. 1969, 1611, 4652–4656. [Google Scholar] [CrossRef]
- Chasteen, D.; Hanna, M. Resonance Line Widths of vanadyl(IV) hydroxycarboxylates. J. Phys. Chem. 1972, 76, 3951–3959. [Google Scholar] [CrossRef]
- Vijayakumar, M.; Li, L.; Graff, G.; Liu, J.; Zhang, H.; Yang, Z.; Zhi, J. Towards understanding the poor thermal stability of V5+ electrolyte solution in Vanadium Redox Flow Batteries. J. Power Sources 2011, 196, 3669–3672. [Google Scholar] [CrossRef]
- Gattrell, M.; Park, J.; MacDougall, B.; Apte, J.; McCarthy, S.; Wu, C.W. Study of the Mechanism of the Vanadium 4+/5+ Redox Reaction in Acidic Solutions. J. Electrochem. Soc. 2004, 151, A123–A130. [Google Scholar] [CrossRef]
- Nicholson, R.S. Theory and Application of Cyclic Voltammetry for Measurement of Electrode Reaction Kinetics. Anal. Chem. 1965, 37, 1351–1355. [Google Scholar] [CrossRef]
- Elgrishi, N.; Rountree, K.J.; McCarthy, B.D.; Rountree, E.S.; Eisenhart, T.T.; Dempsey, J.L. A Practical Beginner’s Guide to Cyclic Voltammetry. J. Chem. Educ. 2018, 95, 197–206. [Google Scholar] [CrossRef]
- Batchelor-Mcauley, C.; Kätelhön, E.; Barnes, E.O.; Compton, R.G.; Laborda, E.; Molina, A. Recent Advances in Voltammetry. ChemistryOpen 2015, 4, 224–260. [Google Scholar] [CrossRef] [PubMed]
- Henstridge, M.C.; Laborda, E.; Dickinson, E.J.F.; Compton, R.G. Redox systems obeying Marcus-Hush-Chidsey electrode kinetics do not obey the Randles-Ševčík equation for linear sweep voltammetry. J. Electroanal. Chem. 2012, 664, 73–79. [Google Scholar] [CrossRef]
- Zhong, S.; Skyllas-Kazacos, M. Electrochemical behaviour of vanadium(V)/vanadium(IV) redox couple at graphite electrodes. J. Power Sources 1992, 39, 1–9. [Google Scholar] [CrossRef]
- Klingler, R.J.; Kochi, J.K. Electron-transfer kinetics from cyclic voltammetry. Quantitative description of electrochemical reversibility. J. Phys. Chem. 1981, 85, 1731–1741. [Google Scholar] [CrossRef]
- Nicholson, R.S.; Shain, I. Theory of Stationary Electrode Polarography: Single Scan and Cyclic Methods Applied to Reversible, Irreversible, and Kinetic Systems. Anal. Chem. 1964, 36, 706–723. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press LLC: New York, NY, USA, 2003. [Google Scholar]
- Shoemaker, D.P.G.; Carl, W.; Nibler, J.W. Experiments in Physical Chemistry, 6th ed.; McGraw Hill: Boston, MA, USA, 1996. [Google Scholar]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Stoll, S.; Schweiger, A. EasySpin: Simulating cw ESR spectra. Biol. Magn. Reson. 2007, 27, 299–321. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).