Aging Estimation and Clustering of Used EV Batteries for Second-Life Applications

Abstract

This study presents an integrated machine learning framework to evaluate the aging states of lithium-ion batteries and to classify them according to their second-life application potential. The methodology combines two key components: a set of regression models to estimate critical health indicators, such as capacity and internal resistance, and a classification stage to group batteries based on these parameters. The proposed models were trained and validated using the NASA Battery Aging Datasets. Through an in-depth analysis of environmental conditions, the study identifies their influence on aging metrics, reinforcing the relevance of the input features selected. Furthermore, a clustering-based approach was employed to validate the classification performance and to reveal the link between a battery’s operation and its aging in the Euclidean space. The results show accurate predictions without signs of overfitting or underfitting, and the classification framework proved robust across the evaluated cases. This suggests that the proposed method can serve as a scalable and adaptable tool to guide battery repurposing strategies. Overall, the findings contribute to bridging the gap between battery diagnostics and real-world energy storage applications, offering practical insights to optimize second-life deployment.

1. Introduction

1.1. State of Art

The increasing global awareness of environmental concerns, particularly related to greenhouse gas emissions, has led to the implementation of policies aimed at promoting electric mobility as a sustainable alternative in the transportation sector [1]. This transition, while crucial in mitigating climate change [2], presents significant challenges to the industry, particularly in terms of production, resource management, and long-term sustainability [3].

One of the components with the greatest reuse potential is the electric vehicle’s (EV) battery pack. Lithium-ion battery technology is dominant due to their high energy density, making them ideal for efficient storage and easy transportation while minimizing the overall system size. This article seeks to extend the EV battery’s lifespan by exploring its potential for second-life stationary applications [4]. An EV battery’s lifespan in mobility applications ends when its capacity drops below 80%. This threshold is determined by the performance requirements of electric vehicles; however, it raises the question of whether a reduction in capacity necessarily limits the battery’s overall functionality or if it could still serve other purposes in different applications [4].

In recent years, the evaluation of lithium-ion battery health has emerged as a critical area of research, particularly related to second-life applications. This growing body of work reflects a broader shift toward data-driven strategies, where machine learning techniques are employed to estimate key aging metrics such as capacity, internal resistance, and state of health (SoH). Kim et al. [5] investigated the impact of the training set size and variability on the accuracy of capacity estimation models, highlighting the significance of the composition of the training data in the predictive outcomes. In a complementary effort, Wang et al. [6] proposed a dual LSTM-based framework capable of concurrently estimating the SoH and internal resistances, eliminating the need for electrochemical impedance spectroscopy and thus enhancing the real-world applicability. Xu et al. [7] further demonstrated the utility of machine learning by applying random forest and decision tree algorithms to features extracted from voltage, current, and temperature signals obtained from the NASA Battery Aging Datasets, achieving high classification performance. Other authors, such as as Qaadan et al. [8], combine k-means clustering with GRU models to capture degradation patterns and enhance predictive tasks. These studies collectively illustrate the potential of artificial intelligence in advancing battery aging diagnostics. From a physics-based modeling standpoint, recent work has continued to improve the understanding of electrothermal and aging dynamics in lithium-ion batteries. For example, Min et al. [9] proposed a comprehensive methodology to model and validate the coupled electrical, thermal, and aging behaviors of lithium-ion cells under various operating conditions. Such developments underscore the value of integrating physically interpretable features with machine learning approaches to enhance the accuracy and reliability of battery health assessments.

Building upon advances in battery state estimation, other studies have focused on assessing the technical feasibility of repurposing aged batteries for grid-related applications, where accurate health diagnostics are essential in ensuring reliable performance. These applications include voltage regulation, ancillary services, and the integration of renewable energy sources. Lacey et al. [10] examined the use of second-life electric vehicle batteries to support low-voltage distribution networks, demonstrating their potential to mitigate peak demands and delay costly infrastructure upgrades. For example, a study published in 2023 investigated the optimal capacity of second-life batteries by analyzing the relationship between ramp rate requirements and the initial battery capacity, providing valuable insights into battery degradation and performance. These contributions highlight the effectiveness of integrating physically interpretable features with machine learning models to enhance the accuracy and robustness of battery health assessments [11]. More recent studies [12] have analyzed the influence of first-life aging on second-life performance, showing that batteries retired at earlier degradation stages exhibit superior long-term viability in secondary applications.

Unlike other approaches that rely on historical cycling data for each battery, the methodology proposed here does not require access to first-life usage records. Instead, it uses a representative set of reference cells tested under controlled conditions to train the models and generate classification maps, making it directly applicable in industrial scenarios, where operational histories are often unavailable.

To ensure robustness and generalization, the methodology also includes validation experiments in which entire batteries are excluded from the training phase. This approach simulates the practical situation of evaluating a cell with no prior data in the training set, verifying the model’s ability to accurately predict its health indicators under unseen operating conditions.

This paper proposes an integrated machine learning framework that connects both battery diagnostics and second-life applications using the NASA Battery Aging Datasets. Indeed, prior efforts have focused on only one of the two approaches—either aging estimation or second-life applications. Specifically, this paper presents a model for the estimation of critical health indicators, namely capacity and internal resistance, and a subsequent model that classifies batteries into second-life application categories. The proposed combined approach of aging estimation and the classification of second-life applications not only enables a more detailed understanding of battery aging but also facilitates data-driven decision-making for second-life deployment.

1.2. NASA Database

The datasets used in this study are the publicly available Li-ion Battery Aging Datasets, provided by NASA and accessible through its open data portal. NASA recorded a total of 7575 battery tests, where each test consisted of charge–discharge cycles and the characterization of internal resistance parameters [13]. To create diverse testing scenarios, nine different discharge conditions were applied to 31 batteries, with varying current and temperature settings.

This dataset was chosen due to the large amount of information that it provides and its extensive use in previous scientific articles. It has been widely employed to analyze predictive models or to validate key variables such as capacity, state of charge (SoC), and the remaining useful life (RUL) of batteries [7,14,15,16].

As previously mentioned, the first stage of the machine learning model focuses on estimating battery aging, which requires a strong correlation with the dataset. Consequently, the model’s performance heavily depends on the available information, making it essential to carefully filter the data. This filtering process was also applied to the batteries, discarding discharge profiles that significantly deviated from the norm to prevent the models from being trained on atypical behaviors.

Consequently, the batteries used in this study were 5, 6, 7, 29, 30, 31, 32, 33, 34, 36, 53, 54, 55, and 56. These batteries underwent discharge cycles at temperatures of 24 °C, 4 °C, and 43 °C, with currents ranging between 2 and 4 A. NASA tested each battery under specific and consistent temperature and current conditions throughout its discharge cycles.

Table 1. NASA dataset test protocol for the batteries used in this study.

Battery ID	Temperature [°C]	Discharge Current [A]	Final Voltage [V]	DoD [%]
B0005	24	2	2.7	70
B0006	24	2	2.5	80
B0007	24	2	2.2	90
B0029	43	4	2.0	100
B0030	43	4	2.2	90
B0031	43	4	2.5	80
B0032	43	4	2.7	70
B0033	24	4	2.0	100
B0034	24	4	2.2	90
B0036	24	2	2.7	70
B0053	4	2	2.0	100
B0054	4	2	2.2	90
B0055	4	2	2.5	80
B0056	4	2	2.7	70

summarizes the test protocols for each battery included in this study, showing the ambient temperature, discharge current, final discharge voltage, and depth of discharge (DoD) applied during cycling. This overview clarifies the experimental conditions from which the features were extracted for model training and classification.

Each battery was cycled according to the specified test conditions until reaching its end-of-life criterion, defined as approximately 80% of the initial nominal capacity. In some cases (B0005, B0006, B0007, B0036, B0053, B0054, B0055, and B0056), cycling was extended past this threshold in order to monitor further degradation trends beyond the typical second-life cutoff. This extended cycling did not affect the model’s creation and it is taken into account in subsequent analyses.

As shown in Figure 1, the capacity and internal resistance do not follow a simple or direct relationship with the test conditions, beyond the general trend of decreasing capacity and increasing internal resistance as the number of cycles increases.

However, occasional deviations from this trend can be observed at specific points in the cycling process, where values may appear higher or lower than expected for a given stage of aging. These variations can arise from reversible effects associated with changes in temperature or current or from measurement dispersion in individual cycles. For instance, an increase in discharge current can also lead to a temporary drop in internal resistance due to ionic stabilization within the electrolyte and electrodes, which improves charge transport and reduces polarization effects [17]. On the other hand, small inconsistencies in the measurement process can introduce point-to-point variability in the recorded data.

In practice, as detailed in Section 3.3.1, this variability is addressed by performing more than one controlled charge–discharge cycle to extract the features required by the model.

2. Aging Estimation

2.1. Deep Learning Algorithm for Capacity and Resistance Estimation

To estimate the aging-related parameters of lithium-ion batteries, a deep learning model was developed using TensorFlow and Keras. These frameworks were selected for their flexibility, scalability, and high performance in managing non-linear regression tasks, particularly in scenarios involving high-dimensional and time-series data such as battery cycling profiles [18]. Although recurrent neural network (RNN) architectures, such as long short-term memory (LSTM) or gated recurrent units (GRU), are frequently used for battery degradation modeling due to their ability to capture temporal dependencies [19], the approach in this study is based on feature extraction from complete charge–discharge cycles. By condensing the voltage, current, and temperature time series into physically meaningful features, the model leverages patterns that are stable across cycles, without requiring the sequential processing of entire time series. This design choice reduces the computational cost and data requirements compared to LSTM-based methods, which typically need large-scale datasets containing a wide variety of usage profiles in order to generalize effectively. In contrast, the proposed method only requires charge and discharge cycles that are sufficiently deep to capture the relevant electrochemical behavior, making it directly applicable in industrial scenarios where complete historical time-series data are unavailable. Furthermore, since the NASA dataset contains complete charge–discharge cycles under fixed operating conditions, a time-series model trained on these sequences would be biased toward this specific cycling profile and less transferable to applications where batteries undergo partial or irregular cycling. Similar feature-driven approaches using feedforward neural networks have been successfully applied in recent studies for state-of-health and resistance prediction, achieving high accuracy with reduced complexity [20,21].

The model was implemented as a feedforward neural network with a fully customizable architecture. Key hyperparameters, including the number of hidden layers, number of neurons per layer, activation functions, batch size, and learning rates, were carefully tuned to improve the model performance, as shown in the next subsection. This level of configurability provides a significant advantage over traditional machine learning algorithms by offering greater control over the learning process and reducing the risks of underfitting or overfitting [22].

The core of the model’s functionality lies in the self-adjustment of the parameters associated with each neuron, following the general formulation in Equation (1) [23]. Each neuron contains a set of weights and a bias term that are updated iteratively during training to minimize the prediction error. Neurons are organized into layers, with each layer potentially incorporating a non-inear activation function to allow the model to capture complex patterns in the input–output mapping [23].

$$\mathit{a}=(\sum _{i=1}^n{x}_i{w}_i+b)g$$

(1)

Compared to conventional regression techniques such as random forest or support vector regression, deep learning models have demonstrated superior performance in modeling the non-linear dependencies between input features and target outputs, such as capacity and internal resistance [24]. Training and evaluation were conducted using the NASA Battery Aging Datasets, which provide a broad and heterogeneous representation of battery degradation behavior.

Model accuracy was evaluated using two standard regression metrics, the root mean squared error (RMSE) and mean absolute error (MAE), defined by Equations (2) and (3), respectively. The RMSE places greater emphasis on larger errors, offering insight into the model’s sensitivity to outliers, while the MAE provides a more general measure of the average predictive accuracy [25]. Together, these metrics offer a comprehensive perspective on model performance.

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{(y_i-{\widehat{y}}_i)}^2}$$

(2)

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(3)

In addition to the MAE and RMSE, model uncertainty was quantified through a prediction interval (PI) analysis. For each leave-one-battery-out (LOBO) validation, an ensemble of $N=10$ models was trained using different random seeds but identical hyperparameters. Let ${\widehat{y}}_i^{\left(r\right)}$ denote the prediction of run $r\in \{1,\dots ,10\}$ for sample i. The ensemble mean is defined as

$${\mu }_i={\displaystyle \frac{1}{N}}\sum _{r=1}^N{\widehat{y}}_i^{\left(r\right)},$$

and the sample standard deviation as $s_i$. Assuming approximate normality of ensemble predictions, the 95% prediction interval for each sample is given by

$$\left[{\mu }_i-1.96s_i,{\mu }_i+1.96s_i\right].$$

Two complementary metrics were computed: coverage (95% PI), defined as the fraction of ground-truth values falling inside the PI, and PI Width, the mean width of the PI across all samples. The point-estimate accuracy was determined using the MAE and RMSE calculated with respect to ${\mu }_i$. In the figures, shaded bands correspond to the 95% PI of the ensemble.

2.2. Feature Extraction

Features are a fundamental concept in machine learning, representing the measurable parameters that describe a given phenomenon. These features serve as input variables, which are fed into a model for training and validation. Recent studies, such as that of Sosa-Cabrera et al. [26], have explored the intercooperation among features, emphasizing the importance of understanding feature interactions to improve model performance.

If an excessively high number of features is included in the model, the computational costs can increase significantly, requiring longer processing times and more expensive hardware. Handling such a large volume of data demands greater memory and computational power, making model training inefficient and resource-intensive. Moreover, an overabundance of features can lead to overfitting, where the algorithm becomes too specialized in recognizing patterns from the training data but struggles to generalize effectively to new, unseen data [27].

Conversely, including too few features can hinder the algorithm’s ability to discern meaningful patterns, resulting in a suboptimal model. Insufficient data representation deprives the model of critical information needed for accurate predictions, thereby diminishing its effectiveness and overall performance. Recent studies, such as the comprehensive review by Büyükkececi and Okur, underscore the delicate balance required in feature selection to optimize model accuracy and stability [28].

To extract the relevant features from the dataset, an evaluation was conducted to analyze how the current and voltage values varied throughout the charge and discharge cycles. Additionally, the durations of the constant-current (CC) and constant-voltage (CV) phases during charging were examined. This feature extraction process was inspired by previous studies and further expanded by incorporating variables related to battery aging, such as the temperature, current, and depth of discharge.

Some of the selected features are illustrated in Figure 2, where the trends and varying importance of each parameter under different testing conditions can be observed. The graphs correspond to (a) the voltage at 1000 s after the start of charging—this voltage tends to increase as the battery ages; (b) the current at 4000 s after the start of the constant-voltage (CV) charging phase—this current tends to decrease as the battery ages, as it requires smaller currents to be fully charged at a smaller capacity; (c) the duration of the constant-current (CC) charging phase—this trend is also downward, as the time that the battery requires to charge is smaller as the capacity is reduced; (d) the duration of the constant-voltage (CV) charging phase—this trend is opposite to the CC time duration, so it tends to increase as the CV phase is reached earlier as the battery ages. In all cases, the slope of the variation changes depending on the testing conditions for each battery.

2.3. Capacity Estimation

Capacity is a key parameter that defines the total amount of electrical charge that a battery can store and discharge, measured in ampere-hours (Ah) and specified by the manufacturer. Over time, the degradation of the battery’s internal components leads to a progressive decline in its total capacity, which in turn reduces its state of health (SoH), a critical indicator of the battery’s overall condition and remaining useful life. Understanding these parameters is essential in assessing battery degradation and determining its potential second-life applications, where the importance may vary depending on the specific use case. Recent studies, such as the comprehensive review by Pradhan and Chakraborty [29], provide insights into battery management strategies and SoH monitoring techniques.

To estimate the battery capacity using machine learning, the selected features included the voltage at 1000 s after charging begins, the current at 4000 s, the constant-current (CC) charging time, and the constant-voltage (CV) charging time, along with the temperature, discharge current, and depth of discharge, which are specific to each battery. This feature selection was based on the existing literature [30] and key differentiating characteristics among the batteries in the dataset, ensuring a robust and well-informed model. For different datasets, the sample selection at specific times may be different, depending on how the voltage and current dynamically evolve during aging.

Hyperparameter selection followed the configuration shown in

Table 2. Hyperparameters for the capacity estimation model.

Hyperparameter	Value
Number of layers	4 (Dense)
Neurons per layer	[128, 64, 32, 1]
Activation function	[ReLU, ReLU, ReLU, Linear]
Regularization	L2 = 1 × 10−4; dropout = 0.15
Normalization	BatchNorm (after first two layers)
Initializer	He normal
Optimizer	Adam (clipnorm = 1.0)
Learning rate	0.001
Batch size	64
Epochs (max.)	200
Loss function	MSE

, consisting of a neural network with four fully connected layers and a total of 225 neurons, with 128 neurons in the first hidden layer, 64 neurons in the second, and 32 neurons in the third, followed by a single neuron in the output layer. Batch normalization was applied after the first two layers, with ReLU activation functions in all hidden layers and a linear activation function in the output layer. The model was regularized using the L2 penalty and dropout and trained with the Adam optimizer and a learning rate scheduler. The model underwent an overfitting and underfitting analysis, showing no signs of either. The good performance observed in the validation results, shown in Table 2, may be attributed to the appropriate selection of input features.

To visually illustrate the model’s effectiveness, three different models were trained, each time excluding the data from one battery (B0005, B0054, and B0030) and using the remaining batteries for training. Each model was trained 10 times to obtain a 95% confidence interval for the predictions. Figure 3 presents a comparison between the actual and predicted capacity values in the three models, and

Table 3. Validation metrics for the capacity estimation models.

ID	Metric	Value
B0005	MAE	0.0253
	RMSE	0.1230
	Coverage (95% CI)	99.4%
	PI Width (95% CI)	0.1009
B0054	MAE	0.0308
	RMSE	0.0493
	Coverage (95% CI)	66.7%
	PI Width (95% CI)	0.0797
B0030	MAE	0.0143
	RMSE	0.016
	Coverage (95% CI)	100%
	PI Width (95% CI)	0.0663

show the metrics in each one.

The validation metrics obtained for the three leave-one-battery-out experiments (B0005, B0054, and B0030), in Table 3, demonstrate the robustness of the proposed capacity estimation approach. Despite not having been trained with data from the excluded batteries, or with any battery sharing the same combination of current profile, depth of discharge, or operating temperature, the models achieved low MAE and RMSE values, along with high coverage rates, in two out of the three cases. These results highlight the effectiveness of both the feature selection process and the chosen hyperparameter configuration, enabling the model to generalize well to unseen operating conditions and accurately capture the underlying capacity degradation trends. It is worth noting that the lower number of available cycles for B0030 could have influenced its results, while the greater variability typically observed in low-temperature batteries, such as B0054, may explain the comparatively lower coverage obtained for this case.

2.4. Resistance Estimation

Resistance is a key parameter in battery performance and is composed of four main elements, as reported by NASA and shown in Figure 4: the double-layer capacitance (Cdl), which arises from electrochemical charge accumulation at the interface between the electrode and the electrolyte; the charge transfer resistance (Rct), which represents the opposition to the flow of charge between the electrodes and the electrolyte, directly influencing battery efficiency; the Warburg impedance (Rw), a frequency-dependent resistance observed during electrochemical impedance spectroscopy (EIS) and related to ion diffusion within the cell; and, finally, the electrolyte resistance (Re), which stems from the electrolyte itself and affects the overall battery behavior. Each of these components can be seen in the equivalent circuit diagram shown in the following image. Internal resistance is one of the most influential factors in battery aging. Its increase can result from a combination of various mechanisms, including the growth of the solid electrolyte interphase (SEI), lithium loss, electrolyte drying, and the degradation of internal materials, among others. These factors contribute to reduced battery performance and lifespan over time [6,17].

The internal resistance values provided in the NASA dataset correspond to charge transfer resistance (Rct) and electrolyte resistance (Re), both measured using electrochemical impedance spectroscopy (EIS). These parameters play a crucial role in assessing battery health and aging.

In the NASA dataset, EIS measurements were performed repeatedly throughout cycling, using a frequency sweep from 0.1 Hz to 5 kHz. The tests were conducted at a state of charge close to 100%, as they were performed immediately after completing the charging process [21,31]. The ambient temperature during the EIS measurements was the same as the cycling temperature assigned to each battery in the corresponding test [21,31]. The Nyquist plots obtained were fitted using a Randles-type equivalent circuit, similar to Figure 4: the high-frequency intercept with the real axis was taken as the ohmic resistance, while the diameter of the semicircular arc was interpreted as the charge transfer resistance. This standardized procedure ensured the consistency and comparability of the resistance values across different operating conditions.

In order to estimate the equivalent total resistance as accurately as possible, based on the available data, the total resistance was calculated as the addition of the charge transfer resistance (Rct) and the electrolyte resistance (Re) for each discharge cycle.

Furthermore, the resistance values were interpolated across successive discharge cycles for each battery to obtain an approximate resistance value at any given moment, providing a more continuous and accurate estimation of its evolution over time.

To estimate the equivalent battery resistance in a machine learning-based model and its fundamental characteristics, a review of the literature was conducted. In particular, Chi Nguyen Van proposed an iterative model in which the battery capacity is first estimated using a long short-term memory (LSTM) machine learning algorithm. Then, leveraging both the features used to predict the capacity and the obtained capacity values, a second model is trained to estimate the battery’s internal resistance [17].

The methodology adopted in this work targets the joint estimation of the capacity and internal resistance through machine learning. However, it differs from the literature in both the algorithm used and the feature selection strategy. Specifically, for internal resistance estimation, a deep neural network was implemented with six fully connected layers and a total of 737 neurons, preceded by Gaussian noise injection in the input layer to improve the robustness. The architecture included two initial hidden layers of 256 neurons each, followed by layers of 128, 64, and 32 neurons and a single neuron in the output layer. Batch normalization was applied after the first four layers, with ReLU activation functions in all hidden layers and a linear activation function in the output layer. The model was regularized through the L2 penalty and progressively reduced dropout rates, and it was trained with the Adam optimizer using gradient clipping, a learning rate scheduler, and early stopping. The loss function used was the Huber loss, which combines the advantages of the MSE and MAE for improved robustness against outliers. In this approach, the model predicts the variation in resistance relative to an initial reference value ($R_0$), which must be known to reconstruct the absolute resistance estimation over time. This architecture proved to be effective in capturing the complex relationships between the selected features and the battery’s internal resistance.

This model required a more complex neural network architecture compared to the one used for capacity estimation, as shown in

Table 4. Hyperparameters for the internal resistance estimation model.

Hyperparameter	Value
Number of layers	6 (Dense) + Gaussian Noise
Neurons per layer	[256, 256, 128, 64, 32, 1]
Activation function	[ReLU, ReLU, ReLU, ReLU, ReLU, Linear]
Regularization	L2 = 5 × 10−4; dropout = [0.30, 0.30, 0.20, 0.15]
Normalization	BatchNorm (after first four layers)
Noise injection	Gaussian noise ($\sigma$ = 0.01) in input
Initializer	He normal
Optimizer	Adam (clipnorm = 1.0)
Learning rate	0.001
Batch size	64
Epochs (max.)	250
Early stopping patience	15
Loss function	Huber loss ($\delta$ = 1.0)

. This may be attributed either to the limited informativeness of the selected input features or to the fact that the internal resistance is more sensitive to varying operating conditions, making it inherently more difficult to predict. Nonetheless, the error metrics reported in

Table 5. Validation metrics for the internal resistance estimation models.

ID	Metric	Value
B0005	MAE	0.00366
	RMSE	0.00496
	Coverage (95% CI)	68.8%
	PI Width (95% CI)	0.00904
B0054	MAE	0.00988
	RMSE	0.01292
	Coverage (95% CI)	84.3%
	PI Width (95% CI)	0.03333
B0030	MAE	0.00138
	RMSE	0.00154
	Coverage (95% CI)	72.5%
	PI Width (95% CI)	0.00422

indicate satisfactory performance, with no evidence of overfitting or underfitting based on the analysis conducted. As with the capacity, three different models were trained, each time excluding the data from one battery (B0005, B0054, and B0030) and using the remaining batteries for training. Each model was run 10 times to obtain a 95% confidence interval for the predictions. Figure 5 presents a comparison between the actual and predicted resistance values in the three models.

The validation metrics obtained for the three leave-one-battery-out experiments (B0005, B0054, and B0030), shown in Table 5, demonstrate the robustness of the proposed internal resistance estimation approach. Despite not having been trained with data from the excluded batteries, or with any battery sharing the same combination of current profile, depth of discharge, or operating temperature, the models achieved low MAE and RMSE values across all cases. Although the confidence intervals may appear wide in the figures, they in fact correspond to deviations of only a few tens of milliohms, which is small in practical terms. As in the case of capacity estimation, the limited number of available cycles for high-temperature batteries, such as B0030, could have influenced its results, while the greater variability typically observed in low-temperature batteries, such as B0054, may explain part of the difference in coverage obtained for these cases.

3. Machine Learning Clustering Algorithm for Second-Life Applications

Once the battery capacity and internal resistance have been obtained, along with a model capable of determining these key variables to assess battery health, the next step is to integrate this information into a classification system using a machine learning clustering algorithm.

In this approach, operational data from real-world usage, including current, voltage, and temperature data, are converted into complex variables that offer a deeper understanding of the battery’s condition. This transformation improves the accuracy of battery state assessments and helps to determine its most suitable applications [32].

3.1. Power and Energy Applications

Firstly, the classification of batteries will be based on their suitability for either energy applications, which focus on long-term energy storage, or power applications, which involve providing support in systems experiencing voltage drops, requiring high currents over short periods of time.

For energy applications, it is necessary to deliver power continuously over extended periods of time, prioritizing both capacity and stability. This is essential for load leveling services, which help to balance the energy supply over several hours, as well as for integration with renewable energy sources and distributed generation systems [33].

In energy applications, discharges typically occur at a moderate rate. As a result, except for cases where heating or battery safety are a concern, a battery’s higher internal resistance does not significantly impact its efficiency [34]. Ultimately, capacity is a critical parameter in these stationary backup applications, as they demand a steady and substantial energy supply over time. Therefore, for this type of application, it is essential to prioritize batteries that retain a higher capacity, ensuring reliable long-term energy storage and delivery [12].

On the other hand, in power applications requiring high-current discharges over short periods, batteries play a crucial role in stabilizing the grid during critical moments and providing support in transient conditions. Recent studies, such as the comprehensive review by Faisal et al. [35], highlight the significance of energy storage systems in microgrids, emphasizing their role in enhancing power quality and grid stability.

In this context, internal resistance is a key factor. Higher internal resistance creates greater opposition to current flow, reducing the C-rate and limiting the battery’s ability to deliver peak currents [34]. In contrast, capacity is not a critical parameter for power applications, as multiple batteries with low internal resistance can be connected in series to increase the overall capacity. Additionally, since discharges occur within seconds, the individual battery’s capacity is less relevant compared to its ability to deliver high power efficiently [12].

Given this, and considering that multiple batteries can be connected to increase the capacity in stationary applications, the internal resistance was established as the most limiting factor in the classification process. Batteries with lower internal resistance, even if suitable for energy applications, were prioritized as more optimal for power applications, where low resistance is essential in efficiently delivering high currents in short bursts.

3.2. K-Means Algorithm for Battery Second-Life Classification

The K-means algorithm first creates a Euclidean space with n dimensions, where n corresponds to the number of input parameters—in this case, capacity and internal resistance [36].

It then initializes k cluster centers, where k represents the number of desired groups. The algorithm places the data points within the generated space and assigns them to the nearest cluster center. Next, it recalculates the cluster centers by determining the mean position of all points within each group.

This process is repeated iteratively, repositioning data points, reassigning them to the closest cluster, and updating the cluster centers. The iterations continue until the cluster centers stabilize, meaning that they no longer change position, and the points within each group remain consistent [36,37].

Since the features used to estimate the capacity and internal resistance do not account for the number of charge and discharge cycles performed by the batteries, each cycle can be treated as an independent battery with its own distinct characteristics. This approach effectively increases the number of batteries per group, enhancing the dataset and improving the robustness of the classification process [37].

It is important to note that the classification performed by the algorithm is entirely based on the information provided by the batteries, defining the classification space according to the capacity and resistance values of the studied dataset. This limits the model to categorizing batteries strictly based on the given data, which may affect the direct applicability of the classification model in real-world scenarios.

This limitation could be addressed by cycling batteries under different discharge currents and varying discharge durations, allowing the model to generalize better across different operating conditions. However, this study primarily focuses on analyzing the synergy between both machine learning models, establishing a general framework that enables classification based on any type of battery under study.

After characterizing the algorithm’s behavior, the model was applied to segment the dataset into six distinct clusters. This number of clusters was selected to achieve a balance between granularity and interpretability, allowing for the clear differentiation of batteries based on their estimated capacity and internal resistance. As illustrated in the corresponding Figure 6, each cluster is visually represented with a distinct color in a two-dimensional space defined by these two variables. The centroid of each cluster, computed during the unsupervised learning process, is marked with an ‘X’, indicating the representative center of each group. This visualization provides an intuitive overview of how the algorithm groups batteries with similar health profiles, serving as the foundation for the subsequent analysis of their suitability for second-life applications.

Using a very low number of clusters could result in overgeneralization, where batteries with significantly different properties are grouped together under the same category. This would make it difficult to determine whether batteries located near the boundaries of the clusters are suitable for one application or another [31,38].

Conversely, having too many clusters would complicate the classification process and make it more difficult to distinguish between groups associated with different applications. In such cases, a more efficient approach would be to analyze each battery’s characteristics individually, rather than relying on an overly granular clustering system.

In this way, considering the limitations of each application and the assumptions previously explained, the following table can be obtained. It presents the different battery classes and their corresponding applications, providing a clear overview of how each group aligns with specific usage requirements.

According to the classification presented in

Table 6. Clusters according to application.

Class	Capacity	Resistance	Application
A	Medium	Medium	Energy
B	High	Low	Power
C	Low	High	Void
D	Low	High	Void
E	Low	Low	Power
F	High	Low	Power

, Classes B, E, and F include batteries with low internal resistance, making them suitable for power applications, where capacity is less critical.

Class A consists of batteries that have experienced less capacity degradation and are potentially suitable for energy applications, as internal resistance is not a decisive factor in this case.

Finally, Classes C and D include batteries with low capacity and high resistance, which do not fit well into either power or energy applications. Instead of being repurposed for reuse, a more suitable approach for these batteries could be recycling, ensuring their proper disposal and material recovery.

3.3. Discussion

3.3.1. Practical Application

The procedure proposed in this study can be integrated into the industrial workflow for the evaluation and reallocation of batteries for second-life applications. In a practical scenario, the company responsible for this process would first conduct controlled capacity and internal resistance tests on a representative set of batteries sourced from different electric vehicle models. These tests would be carried out at various temperatures and under full charge–discharge profiles, with the objective of training and validating the predictive models for capacity and internal resistance. Including data from different operating temperatures, currents, and depths of discharge (DoDs) allows the model to account for the influence of a battery’s typical operating environment on its degradation profile. In fact, for precise classification, it is necessary to know at least the average operating temperature, current, and DoD of the battery during its first life so that these can be incorporated as input features for capacity and resistance estimation. If these values are highly variable over the first life, then a more detailed characterization would be required, ideally including full charge–discharge curves under representative conditions, to enable a more accurate aging assessment.

This initial phase also involves applying the K-means algorithm to the test cell dataset in order to define the cluster structure in the capacity–resistance plane, thus establishing reference groupings for subsequent classification.

Once the clusters have been defined and the predictive models validated for each cell type (brand, model, and chemistry), the classification of an individual user battery involves performing a limited number of or standardized charge–discharge cycles under controlled temperature and current conditions, to minimize additional aging. From the recorded voltage, current, and temperature signals, the required features would be extracted and fed into the corresponding deep neural network (DNN) model to estimate the current capacity and internal resistance. These values would then be used to position the battery within the pre-established K-means clustering space, assigning it to the group that best represents its health profile.

To verify the robustness of the classification, at least one additional standardized cycle should be performed, confirming that the cell remains within the same cluster despite minor variations in the test procedure. The resulting classification would enable the preliminary allocation of the battery to power-oriented or energy-oriented applications or, alternatively, to recycling if its parameters fail to meet the minimum thresholds. Prior to integration into a new battery pack, an additional quality control stage would be required, including performance testing under real operating conditions, the verification of homogeneity between cells, and safety parameter checks. These measures would ensure the electrical and thermal compatibility of the assembled pack and mitigate the risk of accelerated degradation or premature failure during its second-life operation.

This methodology does not require access to the historical data or cycling records of a battery throughout its first life, and it is scalable and transferable to different battery models. It only requires the cycling of a representative set of test cells, the building of the predictive model, and the generation of the classification maps. In cases where the specific battery or vehicle model is not available, an approximation could be made by leveraging data from multiple battery types that share similar cell chemistries, electrode materials, or design characteristics. Such flexibility broadens the applicability of the proposed framework to a wide range of electric vehicle batteries, supporting second-life decision-making even in the absence of model-specific datasets.

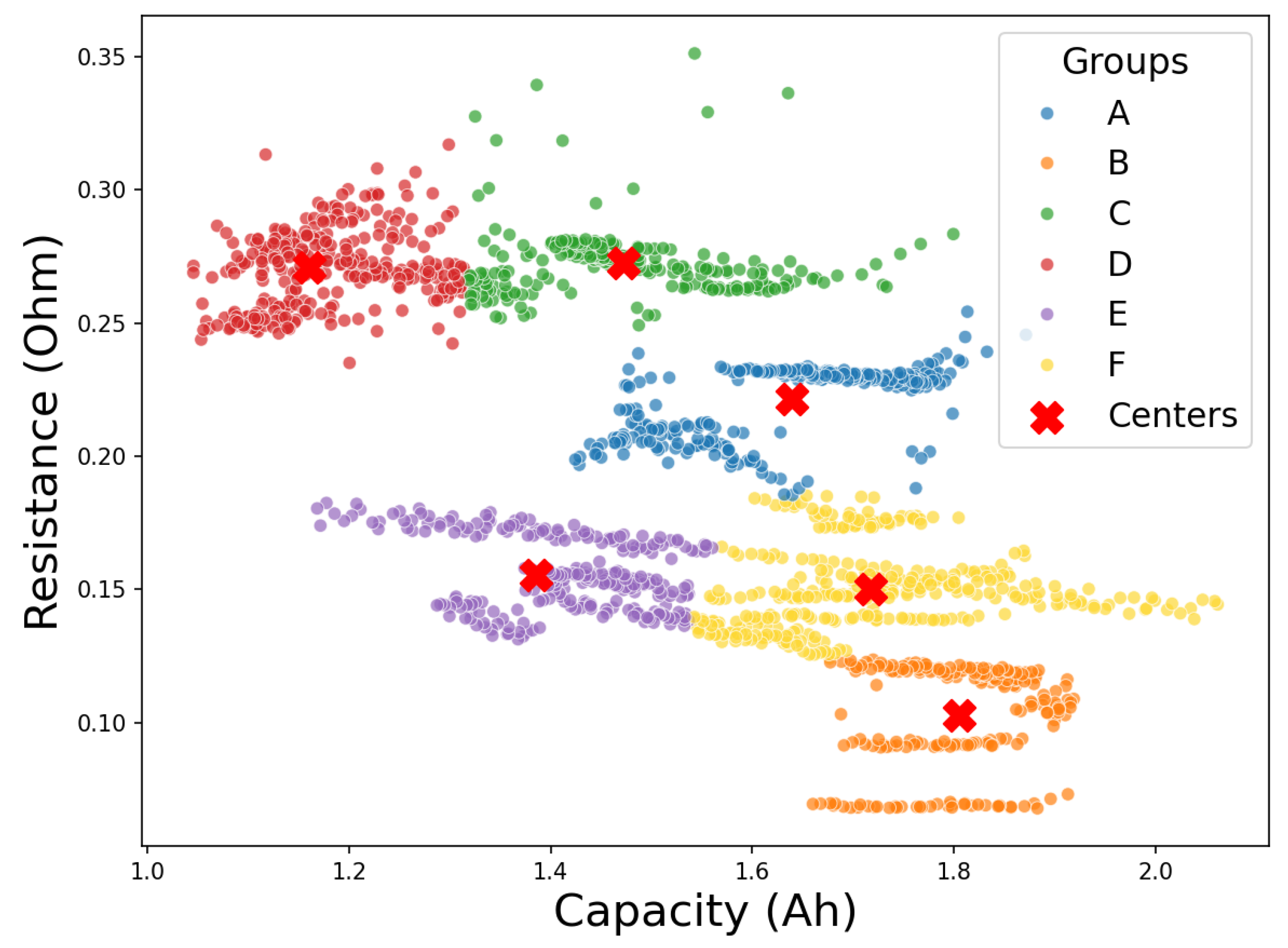
In this study, the classification maps were generated from multiple charge–discharge cycles performed under different operating conditions on a common battery type, as used in the NASA experiments. These maps define the reference structure in the capacity–resistance plane shown in Figure 6. Consequently, if a battery with an unknown operational background becomes available, its aging characteristics can be determined by measuring a set of key parameters and performing a small number of complete charge–discharge tests. The resulting capacity and internal resistance values would allow its direct positioning within the classification map, thus enabling the identification of the most suitable second-life application for this battery.

3.3.2. Influence of Operating Conditions on Battery Health

Following the execution of the clustering algorithm, it is essential to carry out a detailed interpretation of the resulting groupings and their physical relevance, with a particular emphasis on the variables that influence battery aging. Analyzing the structure and composition of the clusters is key to determining whether all critical features have been appropriately captured in the classification process and whether these groupings provide meaningful insights into the second-life potential of each battery.

This section focuses on the temperature, discharge current, and depth of discharge (DoD), which are also included as input features in the proposed model. These parameters are widely recognized as the primary external drivers of lithium-ion battery degradation, owing to their direct impacts on ion transport, interfacial reaction rates, and mechanical stresses within the electrode structure [17,34,39]. By examining their effects on both the capacity and internal resistance, the observed cluster trajectories can be physically interpreted in terms of the dominant aging mechanisms activated under different operating regimes.

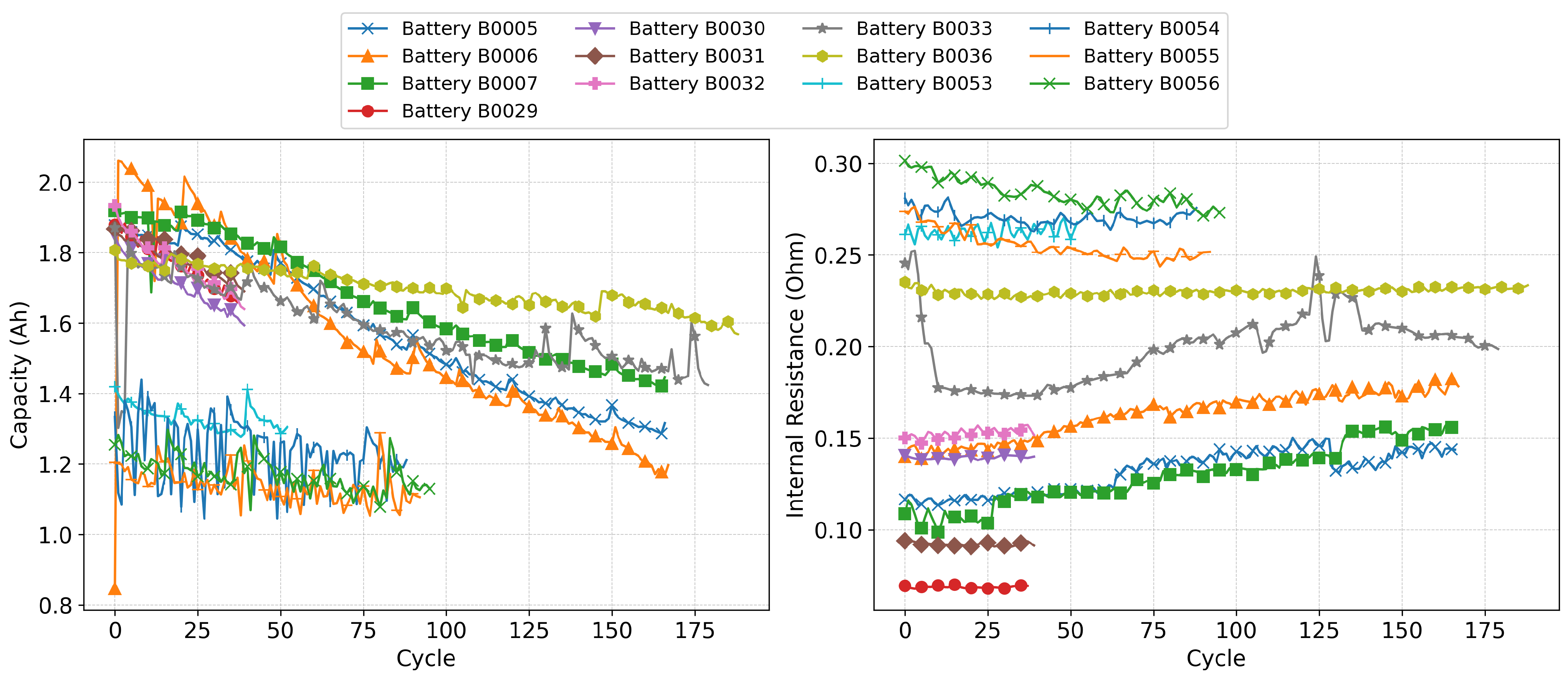
The NASA Battery Aging Datasets offer valuable context for this analysis. Specifically, the batteries numbered 5, 6, 7, 53, 54, 55, and 56 underwent charge–discharge cycling until their capacities dropped below 30% of the initial values recorded during the first cycle. This extended testing period may explain why these batteries appear with a higher number of data points. In contrast, batteries 29 to 34 and battery 36 were only tested until a 20% capacity drop was observed, which could account for their lower representation in the dataset.

To explore the underlying patterns in the dataset, a clustering analysis was performed using estimated health parameters, including the capacity and internal resistance. When the batteries are visualized according to the environmental and operational conditions that were initially considered as classification features—specifically, the temperature, discharge current, and depth of discharge—distinct patterns emerge. As shown in Figure 7, certain clusters align with specific ranges of these variables, suggesting that external stress factors play a significant role in determining the trajectory of battery degradation. In all three subfigures, a color gradient is used to represent battery cycling progression: lighter tones correspond to early cycles, while darker, more intense tones indicate later cycles. Across the plots, a subtle shift is noticeable toward the upper-left quadrant, reflecting a general trend of increasing internal resistance and decreasing capacity as the number of cycles grows. This allows one to trace the evolution of the capacity and resistance depending on different variables. This plot is particularly interesting as, typically, only the capacity or resistance evolution is plotted. However, the combined plot provides additional insight into the battery life and its degradation.

Figure 7a displays the temperatures at which the charge–discharge cycles were performed, as indicated in the legend. A noticeable pattern can be observed: the internal resistance increases and the capacity decreases at lower operating temperatures [17]. This phenomenon can be attributed to the reduction in ionic conductivity and the increase in electrolyte viscosity at low temperatures, which hinder lithium-ion transport and elevate the overpotential. Such conditions promote lithium plating during charging and accelerate impedance growth, leading to the combined loss of usable capacity and increased resistance [17,40].

Figure 7b uses a similar color scheme, where blue corresponds to a lower discharge current of 2 A and black to a higher current of 4 A. At first glance, one might infer a significant reduction in capacity at lower current levels; however, a more detailed analysis is required, especially considering the number of cycles performed for each battery.Higher discharge currents increase the cell polarization and overpotential, intensifying side reactions such as SEI growth and, under low-temperature conditions, lithium plating. At moderate temperatures, high C-rates tend to accelerate the mechanical degradation of electrodes and loss of active material, often causing capacity fade without a proportional resistance rise [17,39].

Figure 7c illustrates the final discharge voltage for each battery, represented through a color-coded scale. Contrary to the trends observed in Figure 7a,b, this parameter does not reveal any evident pattern in terms of correlating with either capacity degradation or an internal resistance increase. This observation aligns with prior findings that indicate that the discharge voltage alone is not always a reliable indicator of battery aging, especially when considered independently of other parameters, such as resistance or impedance evolution [39].

To better understand how batteries are affected by the depth of discharge—particularly through a more in-depth examination of Figure 7—the batteries were grouped according to the discharge current and temperature conditions applied during cycling. A similar methodological approach has been applied in prior research to analyze the impact of varying thermal and electrical profiles on degradation behavior, allowing for the identification of distinct aging pathways across groups [12]. These groupings are consistent with the dataset’s own classification under the term ‘Experiments’, as detailed in

Table 7. Experiments based on current and temperature.

Experiment	Current [A]	Temperature [°C]
1	2	4
2	2	24
3	4	24
4	4	43

. As a result, Figure 6 is subdivided as in Figure 8, which displays these experiments along with their corresponding current and temperature values.

Figure 8 illustrates how the battery distributions vary depending on their depth of discharge under experimental conditions with a fixed current and temperature. In Experiment 4, where both the current and temperature were high, there was a clear trend showing that batteries subjected to lower depths of discharge exhibit reduced internal resistance. This observation aligns with previous studies, which have shown that lower depths of discharge can mitigate internal resistance growth when the current and thermal conditions are kept constant [39]. A similar pattern could be observed in Experiment 3. Notably, although battery 6 displayed the highest depth of discharge and occupied an intermediate position in terms of internal resistance, it is still grouped under this experiment in the dataset. This intermediate behavior could potentially be explained by the lower discharge current used during its cycling, despite its classification alongside batteries tested under more demanding conditions.

In contrast, Experiments 1 and 2 did not exhibit any clearly recognizable pattern in the variation in internal resistance with respect to the depth of discharge. This observation suggests that the depth of discharge may be a secondary factor in determining the internal resistance, particularly under discharge currents exceeding 1C, where the resistance tends to increase as the depth of discharge decreases.The depth of discharge affects both the fraction of active material utilized and the magnitude of volumetric strain experienced during cycling. A high DoD increases SEI turnover and the mechanical stress on electrodes, accelerating particle cracking and contact loss. Conversely, a moderate DoD under stable thermal and current conditions can mitigate impedance growth, which is consistent with the clustering trends observed in this study [9,34].

Beyond the previously discussed findings, and based on the graphical information and the known characterization process of each battery, several insights can be drawn regarding the classifications produced by the algorithm. Firstly, batteries grouped into Classes B, E, and F correspond primarily to cells cycled under Experiment 1 and Experiment 4. Although the batteries in Experiment 4 experienced severe capacity degradation within just 40 cycles, they maintained remarkably low internal resistance. This trait makes them promising candidates for power-oriented applications—an aspect that could be overlooked if the classification was based solely on the capacity. This distinction between capacity and resistance is consistent with recent findings that emphasize the importance of using both parameters to accurately evaluate the suitability of aged batteries for second-life applications [34].

Batteries categorized as ’Void’, corresponding to Classes C and D, belong largely to subsets of Experiment 1 and to Experiment 3. The latter involved very low-temperature conditions. While the rate of capacity fade was slower than in batteries tested at higher temperatures, factors such as electrolyte freezing may have caused a significant loss of capacity—up to 30% of the expected nominal value—starting from the very first cycle. This behavior is consistent with studies indicating that low temperatures can trigger immediate and substantial capacity loss due to phenomena like lithium plating and electrolyte solidification, even in the early stages of cycling [12,17].

Most batteries from Experiment 3 were associated with energy-oriented applications. Despite being subjected to high discharge currents, the ambient temperature remained stable at 24 °C. This moderate thermal environment played a key role in reducing the rate of capacity degradation, as temperatures close to room temperature are known to mitigate stress-induced side reactions within the cell, even under elevated C-rates. Recent studies, such as the work by Waldmann et al. [41], have demonstrated that the aging rate of lithium-ion batteries is minimal at temperatures around 25 °C, highlighting the importance of maintaining optimal thermal conditions during operation. As a result, it was possible to collect a substantial number of valid samples during the experimental campaign.

Standard operating conditions, as represented in Experiment 1, suggest that elevated temperatures accelerate electrochemical reactions within the battery, resulting in lower internal resistance. This is consistent with previous findings showing that higher temperatures enhance ionic mobility and interfacial kinetics, leading to reduced impedance during operation [42]. However, when these thermal conditions are combined with high discharge currents, the cumulative stress accelerates capacity fade due to side reactions such as SEI growth or the loss of active material, without a proportional increase in internal resistance. In contrast, lower temperatures lead to faster equilibrium stabilization, which mitigates aging effects but increases the internal resistance and reduces the usable capacity—likely due to hindered lithium-ion transport and increased electrolyte viscosity [40].

Finally, batteries exposed to high currents under standard temperatures exhibited mixed behaviors. These cells degraded more slowly than those tested under elevated temperatures, while also maintaining intermediate values in terms of both capacity and resistance. This hybrid behavior reinforces the complex interplay between thermal and electrical stress factors in shaping battery aging trajectories. This observation is supported by recent findings that emphasize how battery degradation is governed by a coupled mechanism involving both electrochemical and thermal factors, rather than by either variable in isolation [32].

To deepen the interpretation of the battery degradation dynamics, a vector field analysis was introduced to track the average direction and intensity of aging progression in the SoH-R plane. These flow fields were computed by aggregating intercycle transitions among the SoH and R and segmented according to key operational variables.

Figure 9 illustrates the vector field resulting from ambient temperature conditions. Notably, it shows a clear trend: at low temperatures (4 °C), the aging vectors point sharply toward higher internal resistance, with relatively modest SoH loss, indicating impedance-dominated degradation. At moderate temperatures (24 °C), the transitions are more evenly balanced, while, at high temperatures (43 °C), the capacity degrades rapidly, with a minimal increase in R, confirming that elevated thermal conditions favor the kinetic acceleration of side reactions without significantly worsening the internal resistance. These graphical observations align strongly with the previous conclusions regarding Experiments 2 and 4 and reinforce the role of the temperature as a primary aging determinant.

4. Conclusions

In conclusion, this study successfully integrated both algorithms, effectively identifying essential characteristics needed to assess battery health. These extracted features were then utilized to classify batteries based on their potential second-life applications, ensuring a structured and data-driven approach to battery reuse and optimization.

From the analysis of both capacity and internal resistance, relationships were identified between environmental conditions, such as the temperature, current, and depth of discharge, and the evolution of aging parameters. This also supports the clustering algorithm’s results, as certain patterns were found between the groupings in the Euclidean space and the operational conditions under which the batteries were tested. In this way, the clustering-based evaluation of the batteries provides a roadmap of how different conditions affect their characteristics.

The primary objective of this work was to take a further step toward the initial, industrially viable classification of batteries based solely on measurable features and the known operating conditions of the cell, without relying on historical cycling records. By focusing on parameters that can be obtained through short, controlled tests, the proposed method offers a practical route for sorting batteries at the end of their first life into the most suitable second-life categories.

To ensure robustness, the methodology includes validation experiments in which complete batteries are excluded from the training dataset. This approach confirms the model’s capacity to generalize to cells operating under conditions not represented in the training phase, a scenario that is common in real-world repurposing workflows.

A key advantage of this approach is its scalability and transferability to different battery chemistries and models. By relying solely on reference cell testing to build the predictive models and classification maps, the framework can be applied even when the operational history of the target battery is unknown, enabling robust second-life decision-making across diverse electric vehicle platforms.

Finally, the model is capable of extracting aging metrics and associating them with specific classes, enabling the design of new battery sets tailored to grid applications.