Electro-Thermal Modeling and Parameter Identification of an EV Battery Pack Using Drive Cycle Data
Abstract
1. Introduction
2. Vehicle Test Data
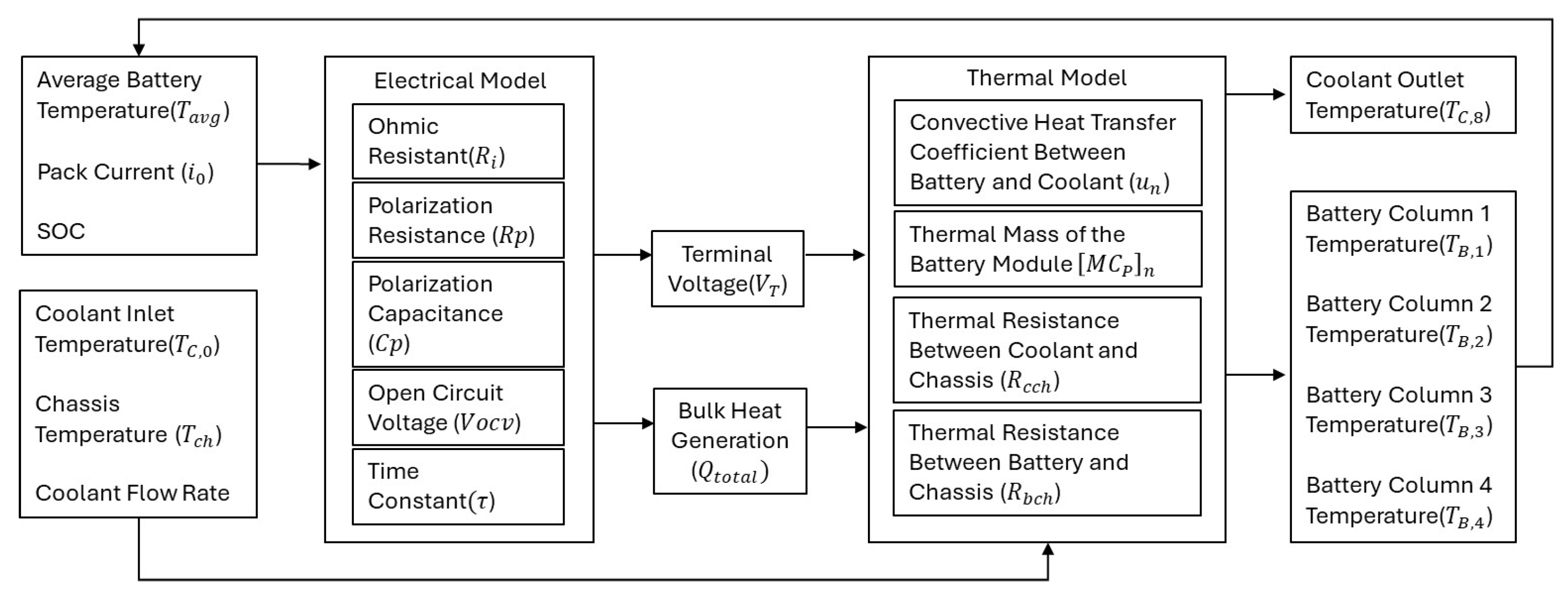
3. Configuration of the Electro-Thermal Model
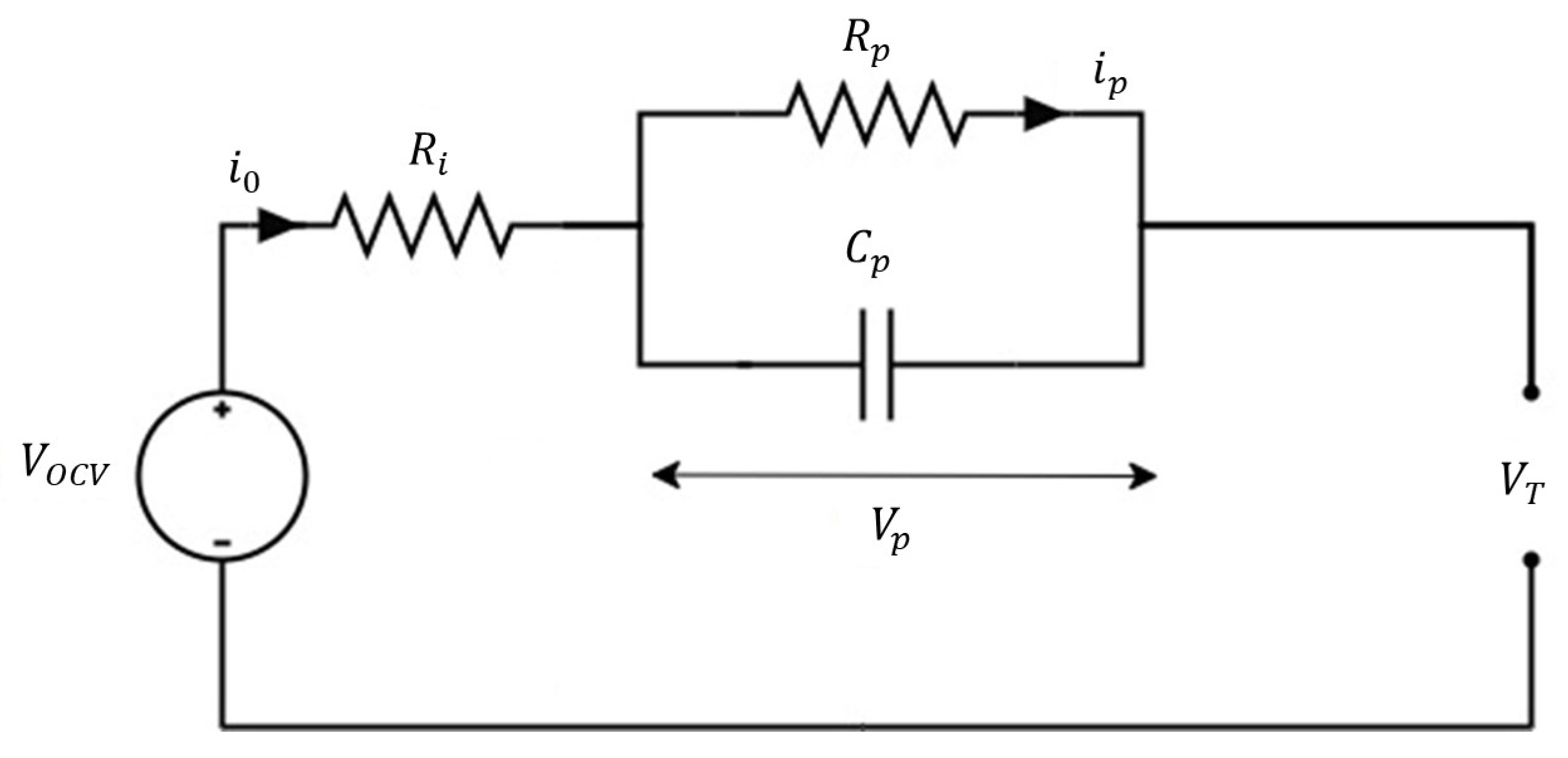
3.1. Electrical Model
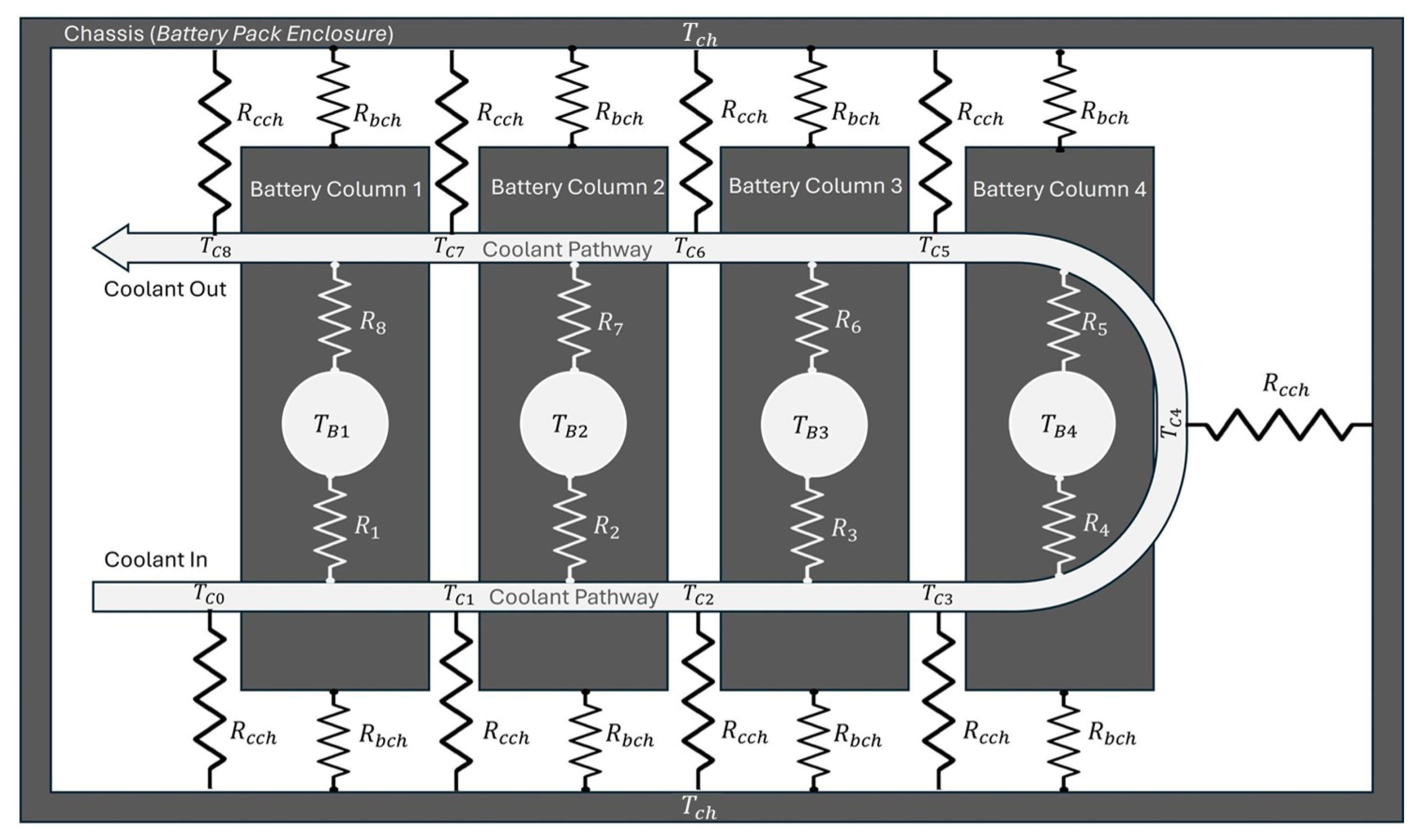
3.2. Thermal Model
4. Parameter Identification
4.1. Electrical Parameter Identification
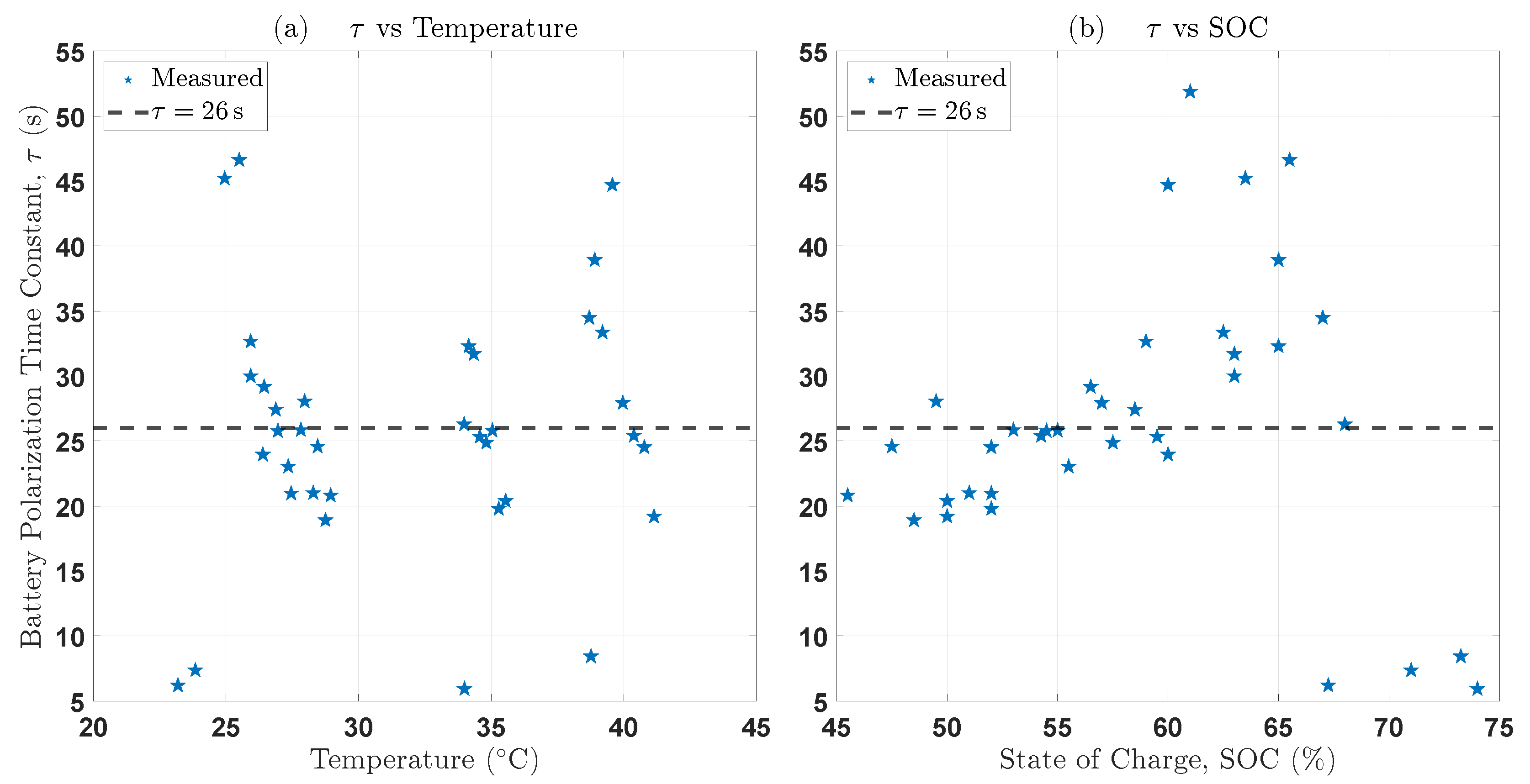
4.1.1. Polarization Time Constant
4.1.2. Internal Resistance
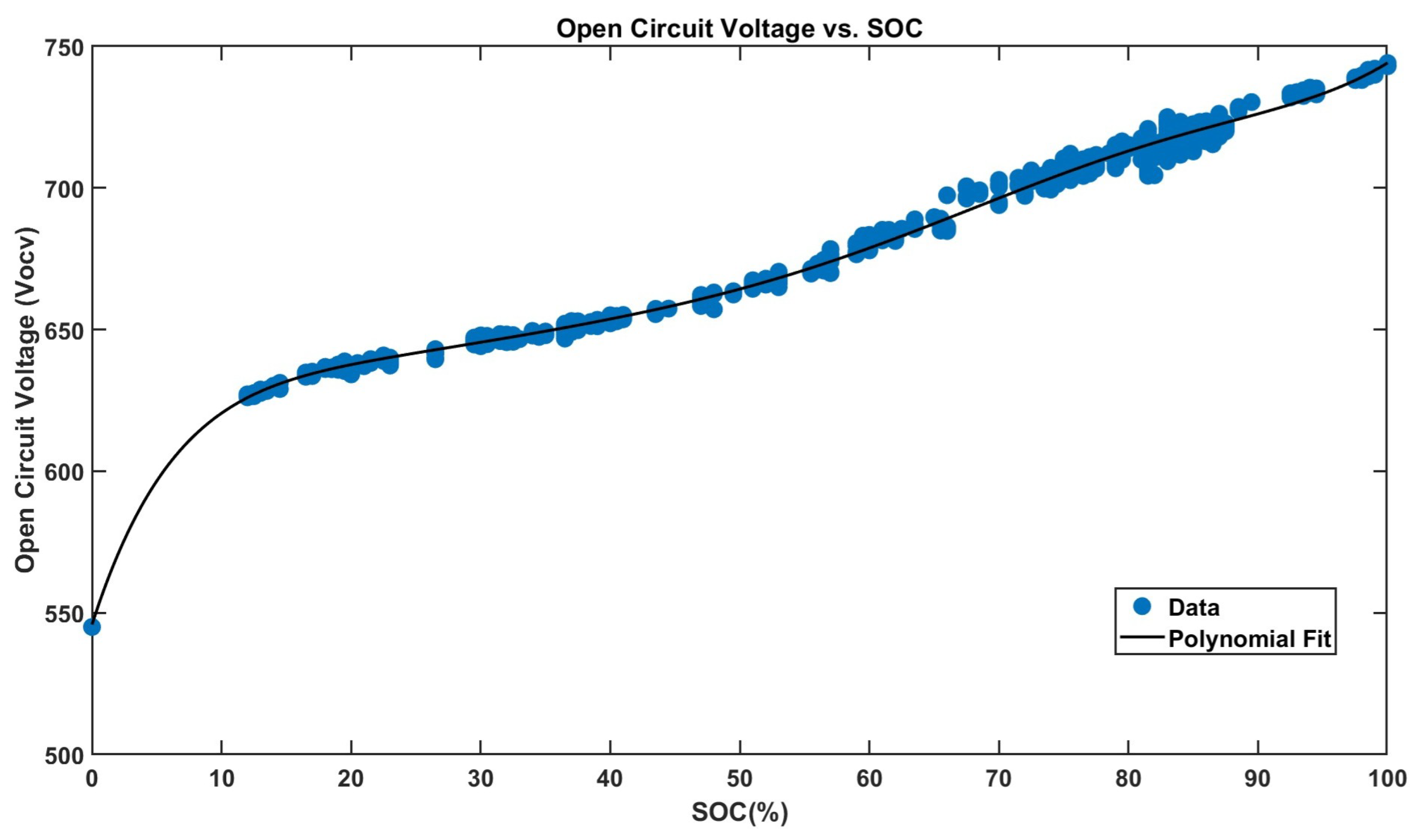
4.1.3. Open-Circuit Voltage
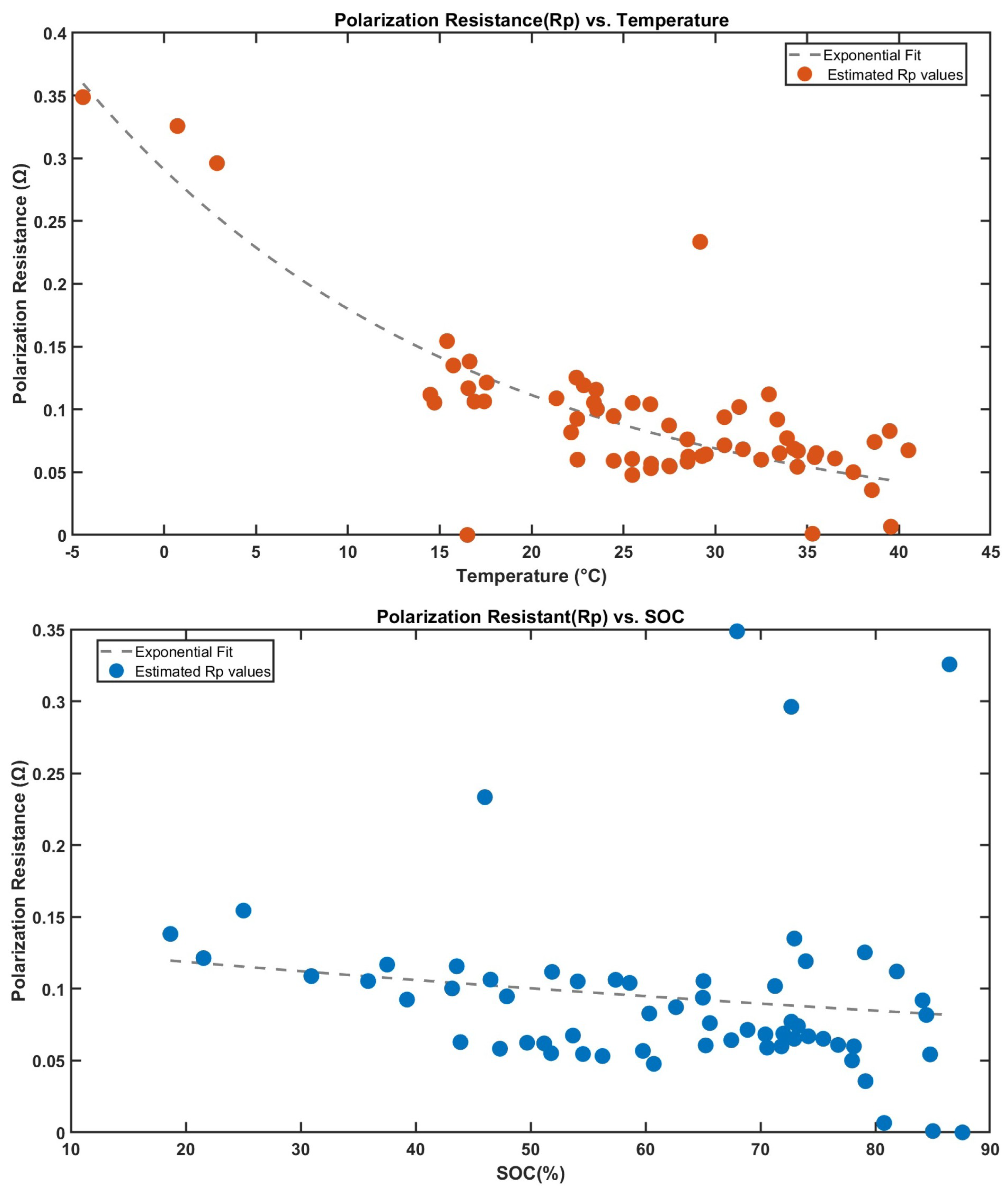
4.1.4. Polarization Resistance and Capacitance
4.2. Thermal Parameter Identification
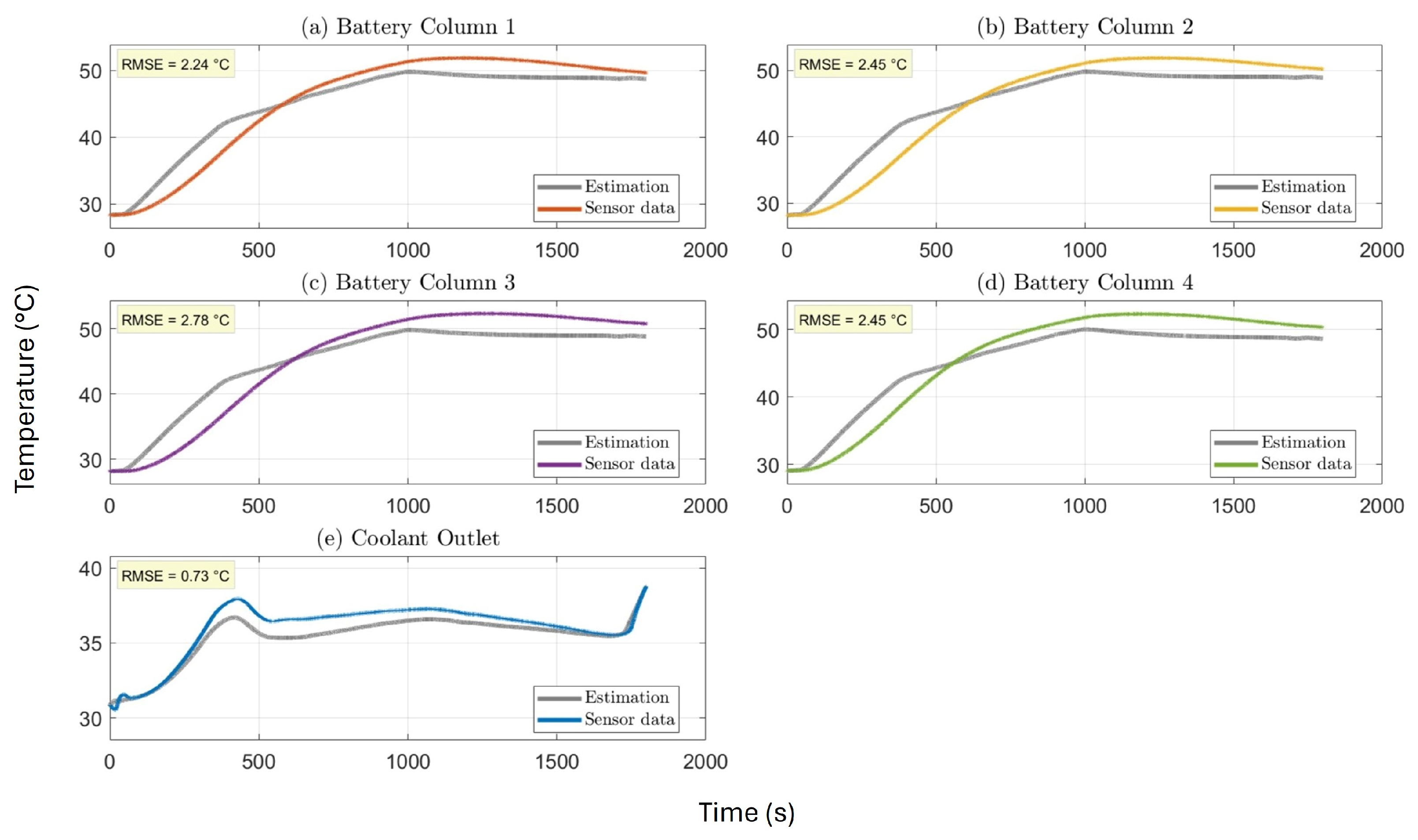
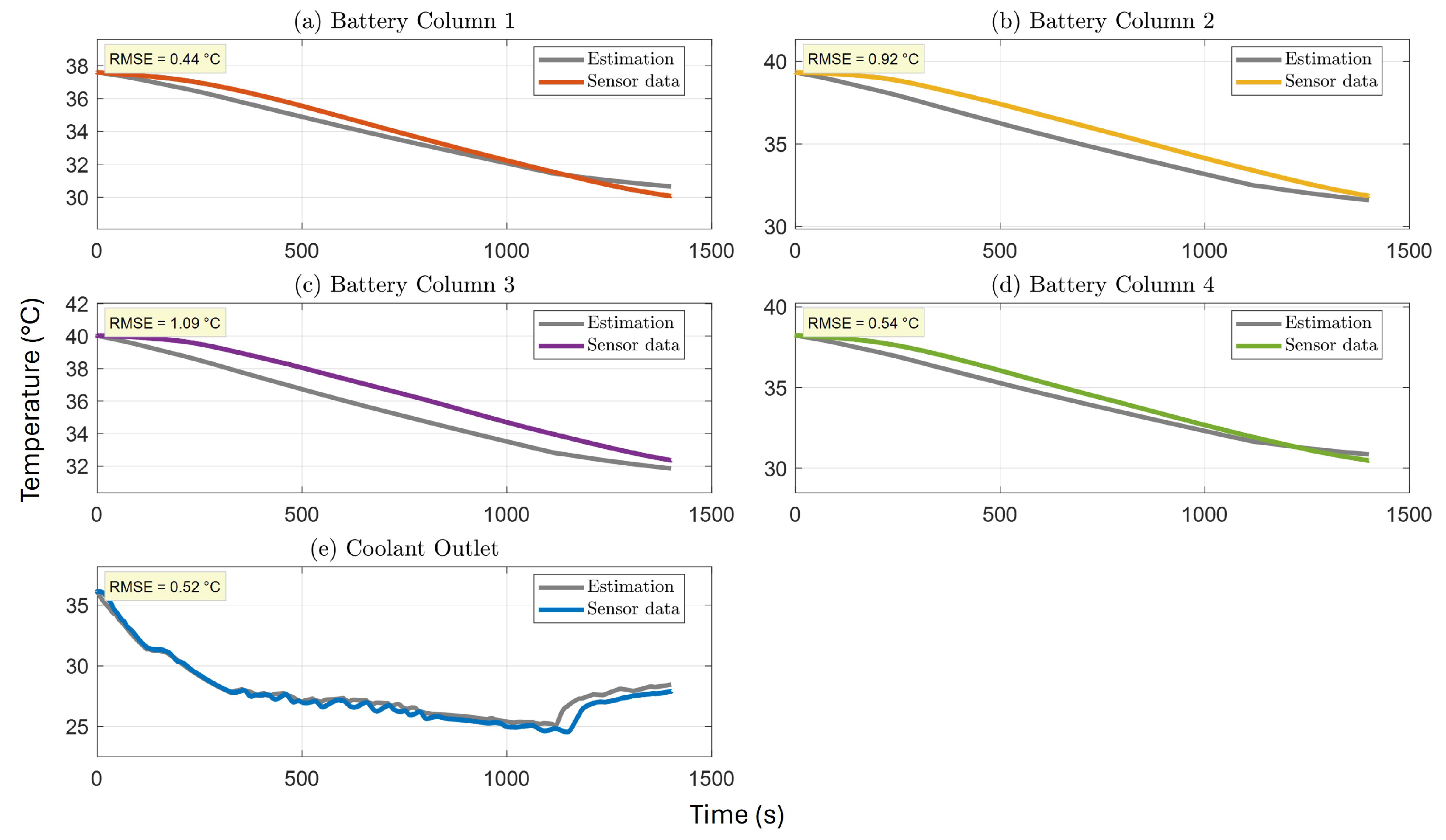
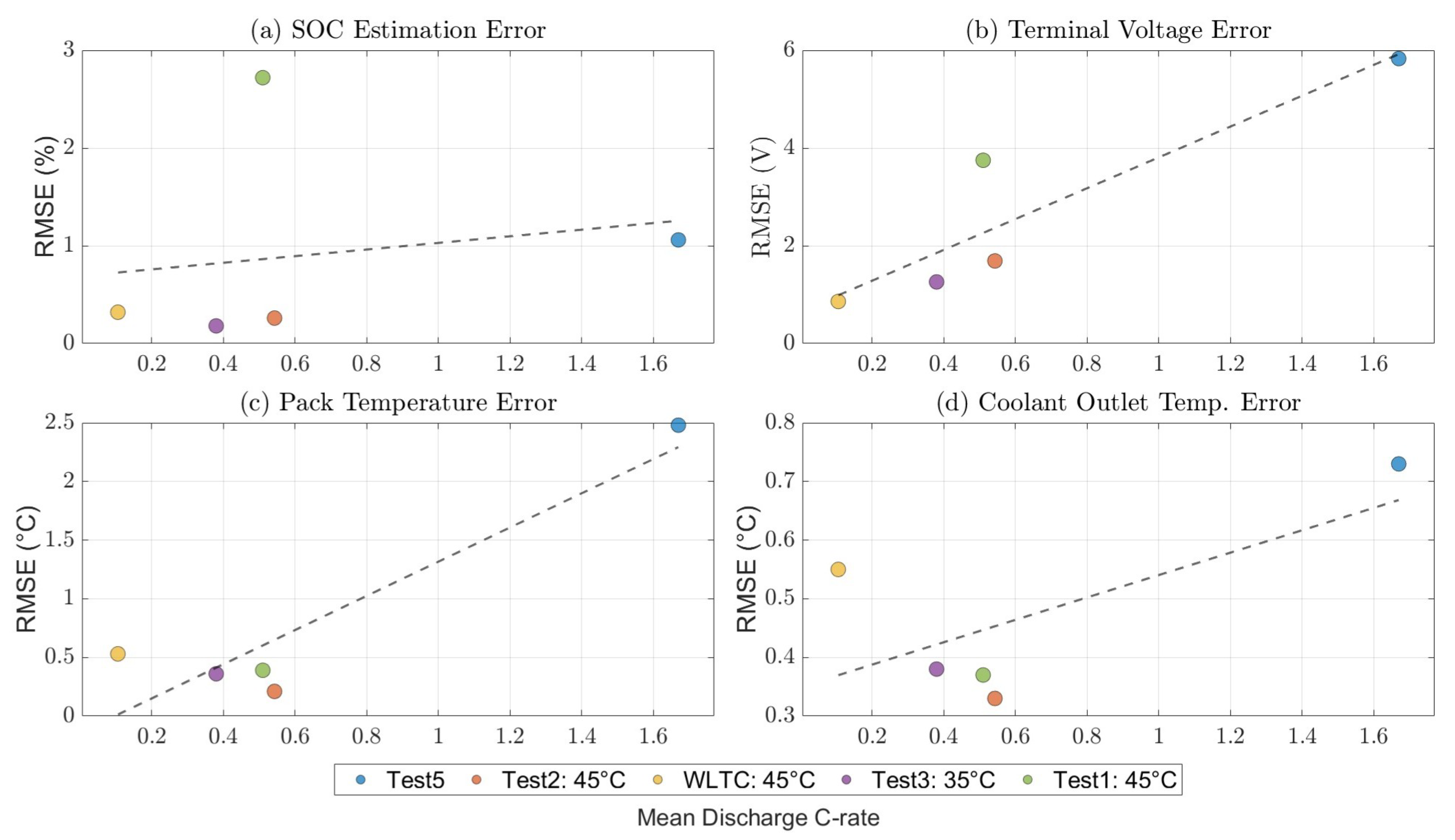
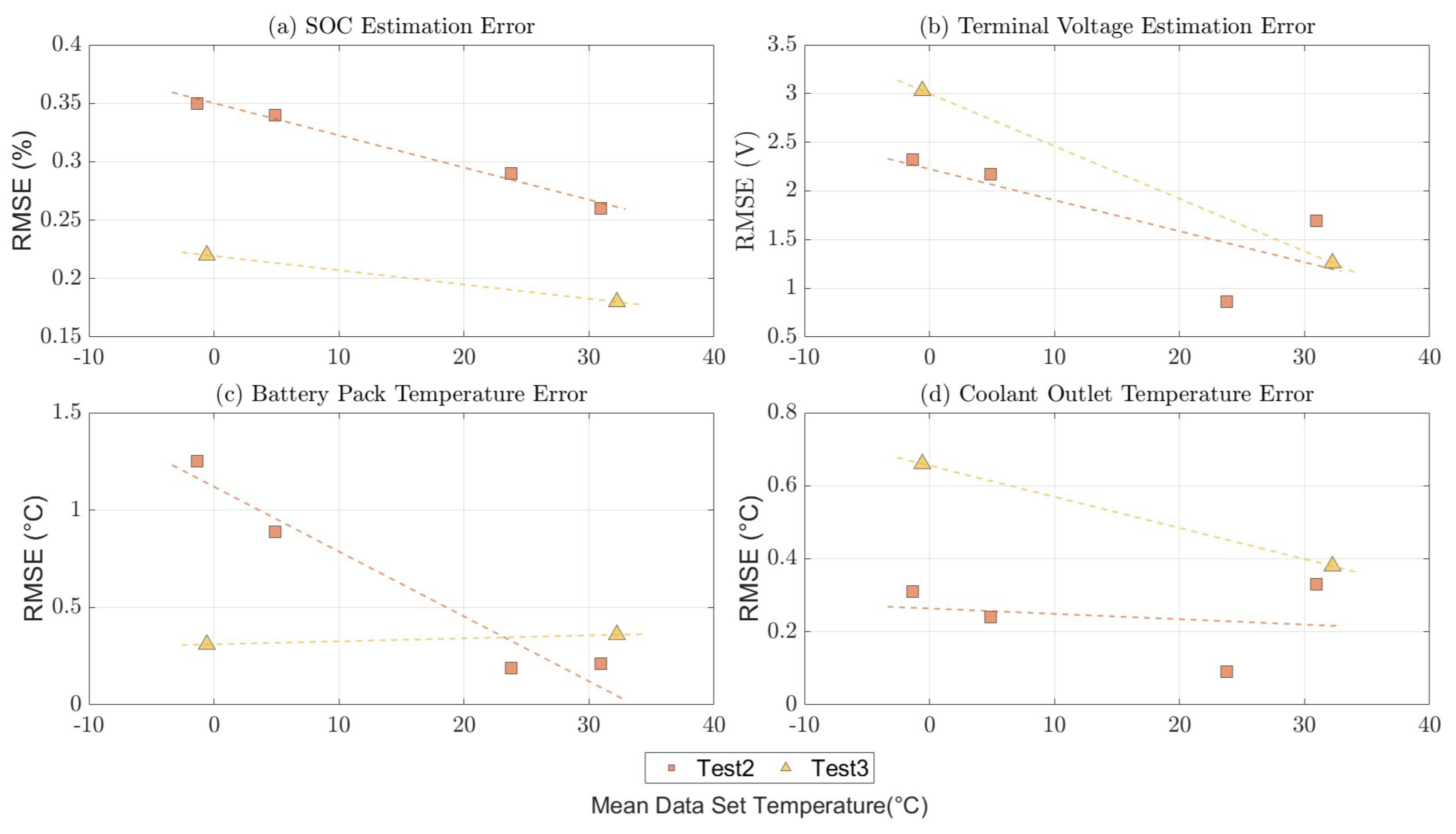
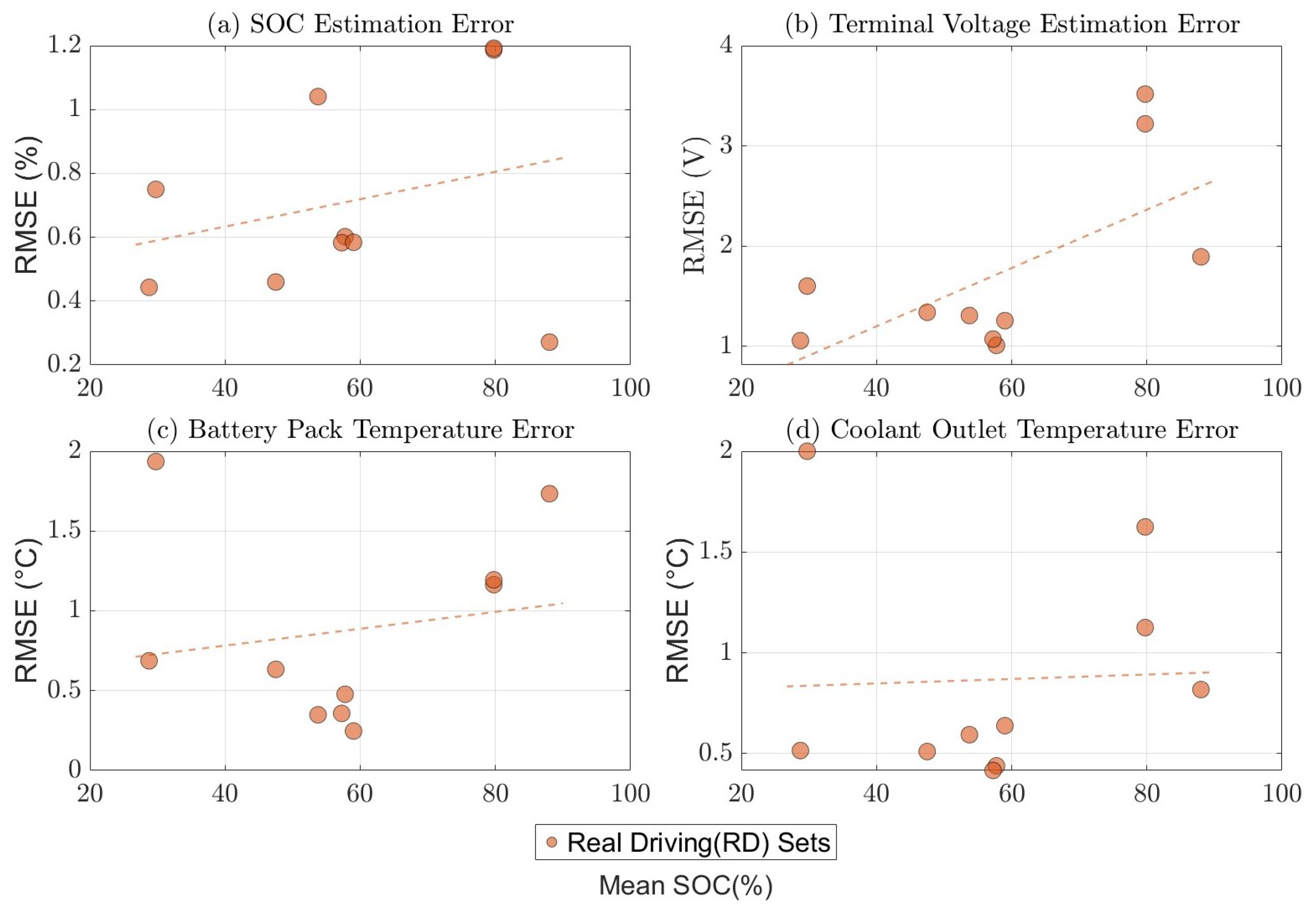
5. Model Validation and Discussion
5.1. Electro-Thermal Model Validation
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Terminal Voltage (V) | |
| Open Circuit Voltage (V) | |
| Internal Resistance () | |
| Battery Pack Current (A) | |
| Polarization Voltage (V) | |
| Polarization Current (A) | |
| Polarization Resistance () | |
| Polarization Capacitance (F) | |
| State of Charge (%) | |
| Equivalent Circuit Model | |
| Polarization Time Constant (s) | |
| Electric Vehicle | |
| Control Area Network | |
| Nickel Manganese Cobalt | |
| Real Driving | |
| Thermal Mass of n Battery Column (J ) | |
| Thermal Mass of the Battery Pack (J ) | |
| Worldwide Harmonized Light vehicle Test Cycles | |
| Federal Test Procedure | |
| Battery Pack Capacity (Ah) | |
| Chassis/Battery Enclosure Temperature (°C) | |
| Thermal Resistance Between the Chassis and Coolant (K/W) | |
| Thermal Resistance Between the Battery and Chassis (K/W) | |
| Thermal Resistance Between the Battery Module and Coolant (K/W) | |
| Coolant Temperature at Location k (°C) | |
| Battery Column n Temperature (°C) | |
| Bulk Heat Generation in Battery Column n (Watt) | |
| Bulk Heat Generation in Battery Pack (Watt) | |
| Irreversible Heat Generation in the Battery Pack (Watt) | |
| Reversible Heat Generation in the Battery Pack (Watt) | |
| Convective Heat Transfer Coefficient () | |
| Contact Surface Area of Battery Column n and Coolant Plate (m2) | |
| Coolant Flow Capacity () | |
| Open Circuit Voltage (V) | |
| Base Voltage at Zero Output Current (V) | |
| Equivalent Impedance () | |
| Frequency of Current (Hz) | |
| Particle Swarm Optimization | |
| Nusselt Number | |
| Reynolds Number | |
| Mass Flow Rate () | |
| T | Battery Pack Surface Temperature (°C) |
| Average Battery Pack Surface Temperature (°C) | |
| Specific Heat Capacity () |
References
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Hoke, A.; Brissette, A.; Smith, K.; Pratt, A.; Maksimovic, D. Accounting for Lithium-Ion Battery Degradation in Electric Vehicle Charging Optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 691–700. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; McLoone, S.; Yang, Z. Battery modelling methods for electric vehicles—A review. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 2673–2678. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model with Electrolyte Dynamics. IEEE Trans. Control Syst. Technol. 2017, 25, 453–468. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L.; Deng, H.; Cai, Y.; Li, D. Polynomial approximation pseudo-two-dimensional battery model for online application in embedded battery management system. Energy 2018, 142, 838–850. [Google Scholar] [CrossRef]
- Oyewole, I.; Kwak, K.H.; Kim, Y.; Lin, X. Optimal Discretization Approach to the Enhanced Single-Particle Model for Li-Ion Batteries. IEEE Trans. Transp. Electrif. 2021, 7, 369–381. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Madani, S.S.; Ziebert, C.; Marzband, M. Thermal Behavior Modeling of Lithium-Ion Batteries: A Comprehensive Review. Symmetry 2023, 15, 1597. [Google Scholar] [CrossRef]
- Tekin, M.; Karamangil, M.İ. Comparative analysis of equivalent circuit battery models for electric vehicle battery management systems. J. Energy Storage 2024, 86, 111327. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, C.; Zong, Y.; Zuo, Q.; Guo, H.; Song, S.; Jiang, L. Effect of Sample Interval on the Parameter Identification Results of RC Equivalent Circuit Models of Li-ion Battery: An Investigation Based on HPPC Test Data. Batteries 2023, 9, 1. [Google Scholar] [CrossRef]
- Kim, N.; Rousseau, A.; Rask, E. Parameter Estimation for a Lithium-Ion Battery from Chassis Dynamometer Tests. IEEE Trans. Veh. Technol. 2016, 65, 4393–4400. [Google Scholar] [CrossRef]
- Shin, J.; Kim, W.; Yoo, K.; Kim, H.; Han, M. Vehicular level battery modeling and its application to battery electric vehicle simulation. J. Power Sources 2023, 556, 232531. [Google Scholar] [CrossRef]
- Lin, X.; Fu, H.; Perez, H.E.; Siege, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. Parameterization and Observability Analysis of Scalable Battery Clusters for Onboard Thermal Management. Oil Gas Sci. Technol.-Rev. IFP Energies Nouv. 2013, 68, 165–178. [Google Scholar] [CrossRef]
- Samad, N.A.; Wang, B.; Siegel, J.B.; Stefanopoulou, A.G. Parameterization of Battery Electrothermal Models Coupled with Finite Element Flow Models for Cooling. J. Dyn. Syst. Meas. Control 2017, 139, 071003. [Google Scholar] [CrossRef]
- Park, S.; Jung, D. Battery cell arrangement and heat transfer fluid effects on the parasitic power consumption and the cell temperature distribution in a hybrid electric vehicle. J. Power Sources 2013, 227, 191–198. [Google Scholar] [CrossRef]
- Chiang, Y.-H.; Sean, W.-Y.; Ke, J.-C. Online estimation of internal resistance and open-circuit voltage of lithium-ion batteries in electric vehicles. J. Power Sources 2011, 196, 3921–3932. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. From Li-ion single cell model to battery pack simulation. In Proceedings of the 2008 IEEE International Conference on Control Applications, San Antonio, TX, USA, 3–5 September 2008; pp. 708–713. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Nagasubramanian, G.; Jungst, R.G.; Doughty, D.H. Modeling of lithium ion cells—A simple equivalent-circuit model approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar] [CrossRef]
- Lucero, J.N.E.; Sujan, V.A.; Onori, S. An Experimentally Validated Electro-Thermal EV Battery Pack Model Incorporating Cycle-Life Aging and Cell-to-Cell Variations. IEEE Trans. Transp. Electrif. 2024, 10, 8122–8136. [Google Scholar] [CrossRef]
- Geng, Z.; Groot, J.; Thiringer, T. A Time- and Cost-Effective Method for Entropic Coefficient Determination of a Large Commercial Battery Cell. IEEE Trans. Transp. Electrif. 2020, 6, 257–266. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5. [Google Scholar] [CrossRef]
- Han, U.; Choi, H.; Lee, H.; Lee, H. Inverse Heat Transfer Analysis Method to Determine the Entropic Coefficient of Reversible Heat in Lithium-Ion Battery. Int. J. Energy Res. 2023, 2023, 9929496. [Google Scholar] [CrossRef]
- Lempert, J.; Kollmeyer, P.; Malysz, P.; Gross, O.; Cotton, J.; Emadi, A. Battery Entropic Heating Coefficient Testing and Use in Cell-Level Loss Modeling for Extreme Fast Charging. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 2, 2712–2720. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 347–534. ISBN 978-0-471-45728-2. [Google Scholar]
- Bryden, T.S.; Dimitrov, B.; Hilton, G.; Ponce de León, C.; Bugryniec, P.; Brown, S.; Cumming, D.; Cruden, A. Methodology to determine the heat capacity of lithium-ion cells. J. Power Sources 2018, 395, 369–378. [Google Scholar] [CrossRef]
- Auch, M.; Kuthada, T.; Wagner, A. Simple experimental method to determine the specific heat capacity of cylindrical Lithium-Ion-Battery cells. Appl. Therm. Eng. 2023, 234, 121212. [Google Scholar] [CrossRef]




| Type | Name | Ambient Temp. C] | SOC Range | # Sets | Note |
|---|---|---|---|---|---|
| Chassis Dynamometer Test | WLTC | −10–45 | 80–90% | 6 | Harmonized light-vehicle cycle |
| FTP-75 | 22 | 80–85% | 1 | Urban driving with stops & starts | |
| US06 | 22 | 65–75% | 1 | Aggressive driving | |
| Test1 | −10–45 | 40–80% | 4 | Inclines from % to % | |
| Test2 | −10–45 | 45–75% | 4 | Speed steps of 20 km | |
| Test3 | −10–35 | 45–75% | 2 | Constant 120 km | |
| On-road Test | RealDriving | 0–20 | 15–100% | 10 | General on-road test |
| Test4 | 15–30 | 25–85% | 1 | Steady cruising on highway | |
| Test5 | 35–45 | 0–85% | 1 | Acceleration to 130 km | |
| Test6 | 5–15 | 80–100% | 1 | Congested traffic |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Total heat transfer coefficient | coefficient (a) | 1.68 | – |
| exponent (b) | 0 | – | |
| constant (C) | 31.01 | W/m2K | |
| Thermal mass of the battery column | 100,262 | J/K | |
| Thermal resistance (chassis–coolant) | 0.080 | K/W | |
| Thermal resistance (battery–chassis) | 0.076 | K/W |
| Dataset Name | RMSE–Temperature (°C) | Terminal Voltage (V) | SOC (%) | ||||
|---|---|---|---|---|---|---|---|
| Battery Column 1 | Battery Column 2 | Battery Column 3 | Battery Column 4 |
Coolant Outlet | |||
| Test5 | 2.24 | 2.45 | 2.78 | 2.45 | 0.73 | 5.83 | 1.06 |
| Test4 | 0.59 | 0.48 | 0.42 | 0.37 | 0.20 | 6.67 | 3.70 |
| Test2:45C | 0.10 | 0.31 | 0.27 | 0.17 | 0.33 | 1.69 | 0.26 |
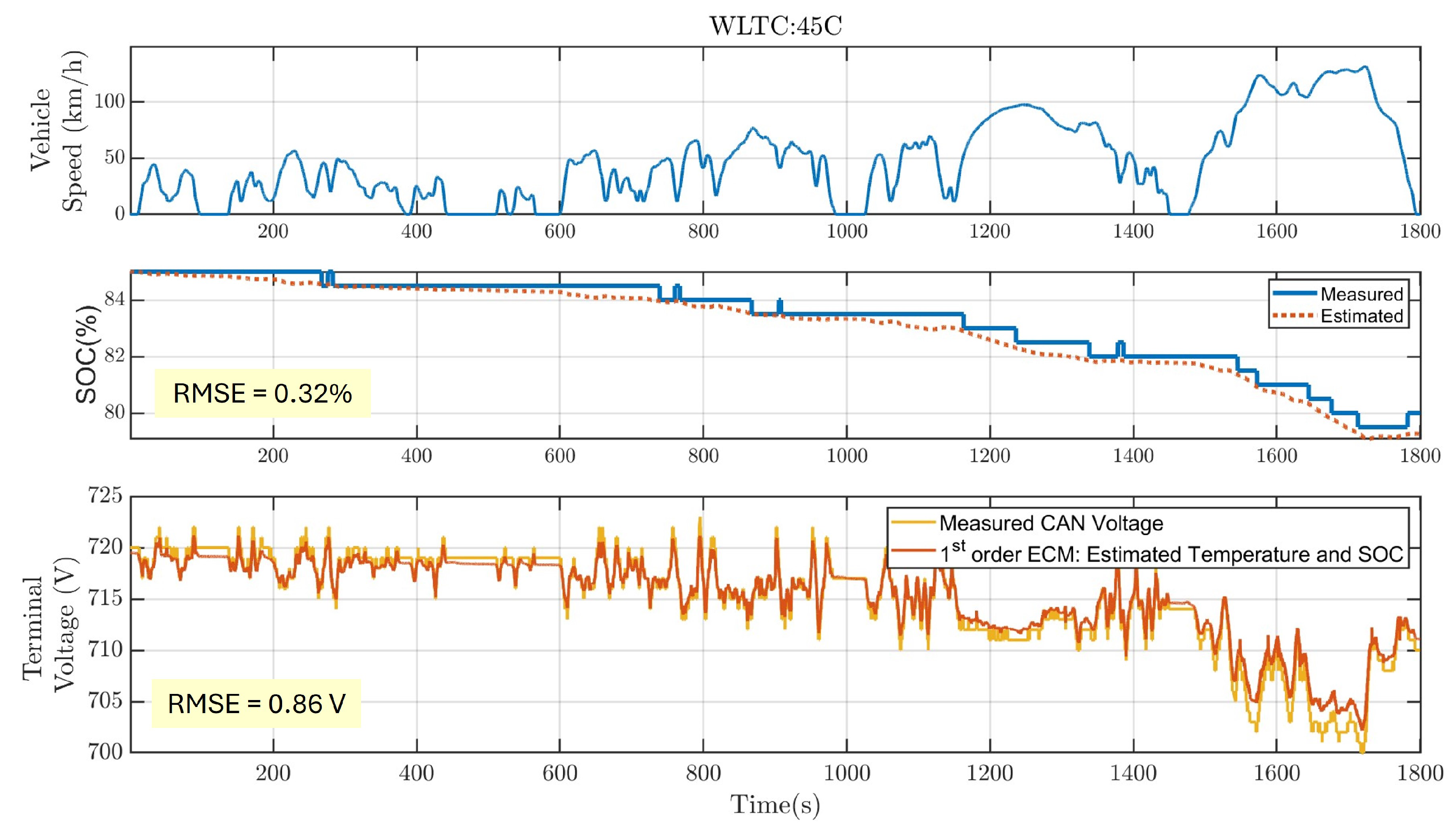
| WLTC:45C | 0.54 | 0.47 | 0.55 | 0.57 | 0.55 | 0.86 | 0.32 |
| Test3:35C | 0.42 | 0.37 | 0.37 | 0.28 | 0.38 | 1.26 | 0.18 |
| WLTC:35C | 0.16 | 0.15 | 0.39 | 0.19 | 0.33 | 4.44 | 0.61 |
| Test1:45C | 0.28 | 0.38 | 0.47 | 0.42 | 0.37 | 3.75 | 2.72 |
| Test1:22C | 0.22 | 0.24 | 0.39 | 0.22 | 0.16 | 2.70 | 1.20 |
| Test1:0C | 0.22 | 0.26 | 0.34 | 0.23 | 1.04 | 6.36 | 0.59 |
| Test1:-10C | 0.21 | 0.24 | 0.24 | 0.21 | 1.25 | 4.58 | 0.49 |
| FTP75:20C | 0.44 | 0.92 | 1.09 | 0.54 | 0.52 | 5.25 | 0.43 |
| RD1 | 1.29 | 0.85 | 0.91 | 1.60 | 1.63 | 3.52 | 1.19 |
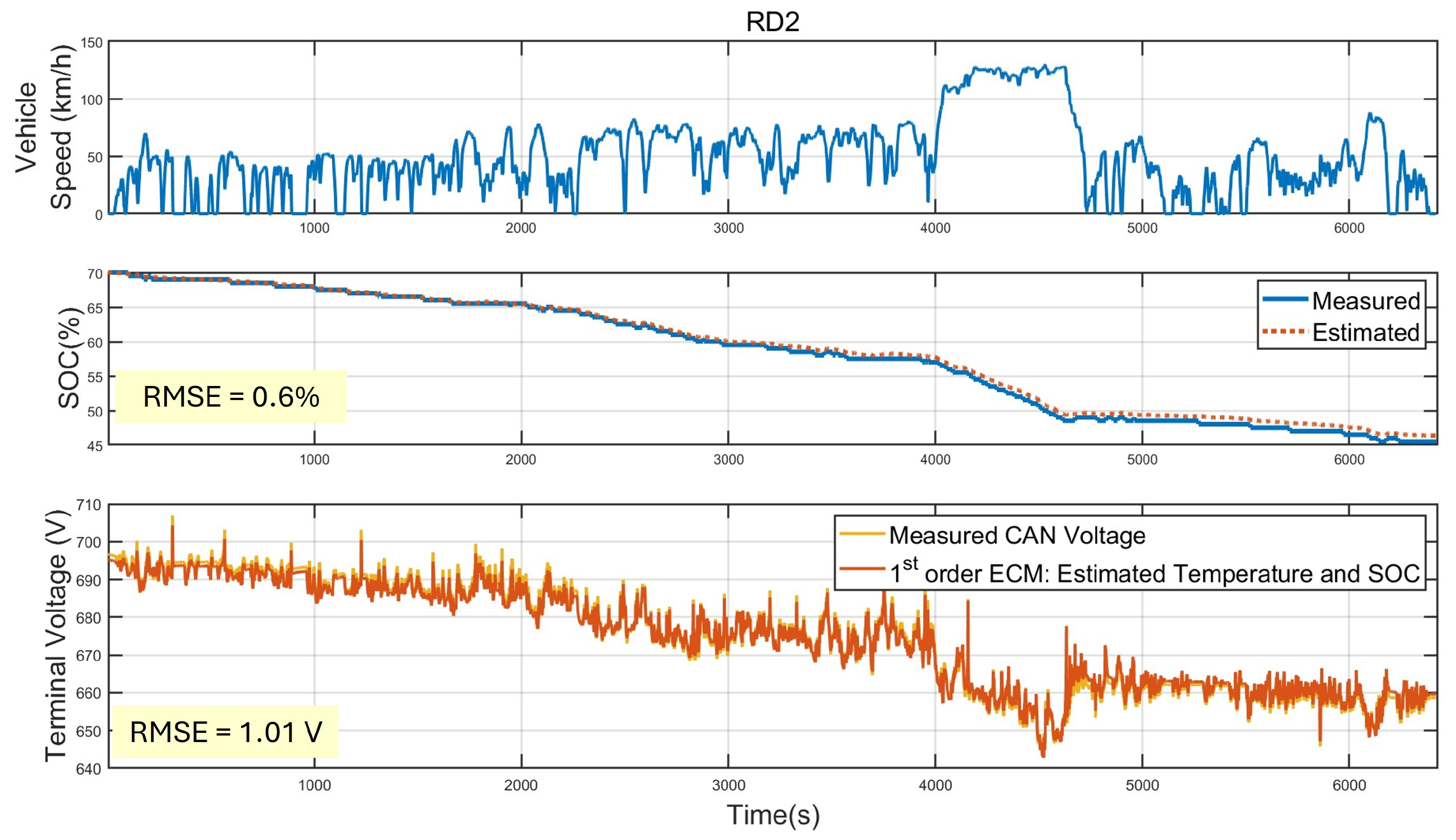
| RD2 | 0.50 | 0.69 | 0.50 | 0.21 | 0.44 | 1.01 | 0.60 |
| RD3 | 1.31 | 0.86 | 0.94 | 1.67 | 1.13 | 3.22 | 1.19 |
| RD4 | 0.62 | 0.75 | 0.70 | 0.68 | 0.51 | 1.06 | 0.44 |
| RD5 | 0.34 | 0.60 | 0.37 | 0.12 | 0.42 | 1.07 | 0.58 |
| RD6 | 1.54 | 1.64 | 1.76 | 2.00 | 0.82 | 1.89 | 0.27 |
| RD7 | 0.18 | 0.42 | 0.40 | 0.40 | 0.59 | 1.31 | 1.04 |
| RD8 | 0.66 | 0.45 | 0.51 | 0.90 | 0.51 | 1.34 | 0.46 |
| RD9 | 0.30 | 0.35 | 0.22 | 0.12 | 0.64 | 1.26 | 0.58 |
| RD10 | 2.07 | 1.33 | 1.62 | 2.71 | 2.00 | 1.60 | 0.75 |
| Test6 | 0.82 | 0.27 | 0.51 | 1.53 | 0.89 | 2.81 | 0.75 |
| WLTC:-7C | 0.33 | 0.43 | 0.08 | 0.08 | 0.52 | 3.41 | 0.63 |
| Test3:-7C | 0.32 | 0.24 | 0.29 | 0.40 | 0.66 | 3.03 | 0.22 |
| Test2:-10C | 1.11 | 1.63 | 1.29 | 0.97 | 0.31 | 2.32 | 0.35 |
| Test2:0C | 0.83 | 1.06 | 0.92 | 0.76 | 0.24 | 2.17 | 0.34 |
| Test2:22C | 0.15 | 0.22 | 0.23 | 0.17 | 0.09 | 0.86 | 0.29 |
| US06:22C | 0.10 | 0.18 | 0.14 | 0.12 | 0.20 | 4.19 | 0.44 |
| WLTC:-10C | 0.12 | 0.14 | 0.15 | 0.12 | 0.27 | 3.91 | 0.34 |
| WLTC:0C | 0.08 | 0.12 | 0.11 | 0.09 | 0.21 | 2.07 | 0.33 |
| WLTC:22C | 0.06 | 0.06 | 0.06 | 0.07 | 0.22 | 1.55 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mannapperuma, V.; Gaddala, L.C.; Zheng, R.; Kim, D.; Kim, Y.; Ullal, A.; Zhu, S.; Ha, K.P. Electro-Thermal Modeling and Parameter Identification of an EV Battery Pack Using Drive Cycle Data. Batteries 2025, 11, 319. https://doi.org/10.3390/batteries11090319
Mannapperuma V, Gaddala LC, Zheng R, Kim D, Kim Y, Ullal A, Zhu S, Ha KP. Electro-Thermal Modeling and Parameter Identification of an EV Battery Pack Using Drive Cycle Data. Batteries. 2025; 11(9):319. https://doi.org/10.3390/batteries11090319
Chicago/Turabian StyleMannapperuma, Vinura, Lalith Chandra Gaddala, Ruixin Zheng, Doohyun Kim, Youngki Kim, Ankith Ullal, Shengrong Zhu, and Kyoung Pyo Ha. 2025. "Electro-Thermal Modeling and Parameter Identification of an EV Battery Pack Using Drive Cycle Data" Batteries 11, no. 9: 319. https://doi.org/10.3390/batteries11090319
APA StyleMannapperuma, V., Gaddala, L. C., Zheng, R., Kim, D., Kim, Y., Ullal, A., Zhu, S., & Ha, K. P. (2025). Electro-Thermal Modeling and Parameter Identification of an EV Battery Pack Using Drive Cycle Data. Batteries, 11(9), 319. https://doi.org/10.3390/batteries11090319







