Abstract
Battery management systems (BMSs) play a critical role in electric vehicles (EVs), relying heavily on two essential factors: the state of charge (SOC) and state of health (SOH). However, accurately estimating the SOC and SOH in lithium-ion (Li-ion) batteries remains a challenge. To address this, many researchers have turned to machine learning (ML) techniques. This study provides a comprehensive overview of both BMSs and ML, reviewing the latest research on popular ML methods for estimating the SOC and SOH. Additionally, it highlights the challenges involved. Beyond traditional models like equivalent circuit models (ECMs) and electrochemical battery models, this review emphasizes the prevalence of a support vector machine (SVM), fuzzy logic (FL), k-nearest neighbors (KNN) algorithm, genetic algorithm (GA), and transfer learning in SOC and SOH estimation.
1. Introduction
The transportation sector significantly impacts carbon emissions and must seek to reduce its environmental footprint. Governments worldwide have established CO2 emission reduction targets for transportation [1]. Many major automobile-producing nations have also committed to reducing CO2 emissions. Over the past decade, fossil fuel usage has declined as renewable energy sources like wind, solar, and hydroelectric power have expanded rapidly. This shift has made lithium-ion (Li-ion) batteries popular due to their high power and energy density, energy efficiency, and extended life cycle. These features make Li-ion batteries suitable for various applications, including portable electronic devices [2], electric vehicles [3], and energy storage systems. However, Li-ion battery performance degrades over time [4], necessitating an understanding of the battery’s state of health (SOH) and state of charge (SOC) [5]. To estimate these states accurately, battery management system (BMS) software has been developed to manage SOC and SOH while addressing potential risks like overheating and overvoltage [6]. Given concerns about battery system safety and performance, a well-designed BMS is essential to prevent battery failure [7]. With enhanced battery protection, SOC and SOH estimation, cell balancing, and thermal management [8], batteries can operate more safely and efficiently, with SOC and SOH estimation being crucial components. The SOC represents the battery’s current capacity to its full charge, and the SOH signifies the battery’s capacity compared to its original nominal capacity when brand new. A Li-ion battery is considered to reach its end of life (EOL) when its capacity decreases.
The research and development of battery state estimation methods have been significantly improved with the recent advancements in artificial intelligence (AI) and machine learning (ML) [9]. Estimating the states of batteries has gained some interest, and this is primarily attributed to the widespread adoption of data-driven approaches, particularly those based on ML. This popularity is driven by the greater availability of battery data and advancements in computing power capabilities.
During operation, the complex chemical processes within a battery pose a significant challenge for parameter measurement and prediction. Long-term degradation prediction is especially challenging. While physics-based (PB) models can capture electrochemical cycling behavior [10,11] and have incorporated specific capacity degradation mechanisms, many degradation modes remain poorly understood, and existing models suffer from poor identifiability of physical mechanisms [12].
Contrary to traditional model-based approaches, ML models identify high-dimensional patterns in data, independent of underlying physical processes. This makes their study unaffected by hard-to-study factors, making ML less favorable for battery state estimation [13]. However, ML model-based methods encounter certain challenges. ML models may have more parameters than physics-based models, necessitating extensive training data. They can also face issues when generalizing to unseen scenarios. Learning from available data may require dimensionality reduction and problem-specific feature engineering [14]. It is argued that, without considering physical processes, ML is unlikely to yield highly accurate health forecasting for situations far beyond available data. Combining ML models with other models like PB can yield improved results. This paper aims to comprehensively review recent machine learning applications in estimating the SOC and SOH for batteries. It is a valuable resource for researchers seeking to employ machine learning techniques to address battery-related challenges.
The subsequent sections of this paper are organized as follows. Section 2 covers relevant aspects of Li-ion batteries for EVs, including the BMS, SOC, and SOH. While this may not directly pertain to machine learning applications, it offers essential background for researchers new to the field. Section 3 provides a separate review of ML methods and their applications in SOC and SOH estimation. This includes a general introduction to ML, its historical development, five main categories, common approaches, and their applications. Section 4 outlines future challenges and developments based on current research. Finally, Section 5 concludes the paper.
2. Li-Ion Battery for Electric Vehicles
Numerous battery types have been utilized, with the lithium-ion battery (LIB) [15,16] gaining attention from both research communities and the automotive industries due to its exceptional attributes, including its high energy density, low self-discharge rate, elevated voltage, extensive lifespan, remarkable reliability, and rapid recharging capabilities. To maintain safe operating conditions, a battery management system (BMS) is employed, responsible for determining optimal charging and discharging times. Figure 1 illustrates the typical structure and functions of the BMS, which involve collecting operational data from the battery pack, processing this information to estimate the battery’s current state, and subsequently regulating the battery in alignment with the estimated parameters.
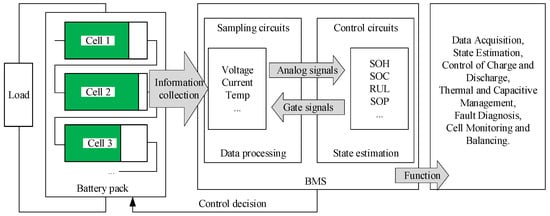
Figure 1.
Structure and functions of a BMS.
A BMS must stay robust over its life cycle. But, predicting battery states in modern EVs is tough due to lithium-ion batteries’ nonlinear behavior. These rechargeable batteries react swiftly to temperature, charge, discharge, and DoD changes. Aging induces significant nonlinear shifts in battery traits. A battery pack comprises cells, whose performance degrades over time, affecting overall pack performance. Regular monitoring is essential for functionality. Techniques for assessing Li-ion battery states include the SOC, SOH, RUL, capacity, impedance, and available power. Estimating SOC and SOH is more intricate than other parameters [17,18,19,20].
2.1. State of Charge (SOC)
A battery management system extends a battery lifespan by monitoring overcharging and over-discharging. Accurate assessment of battery cell capacity ensures timely replacement. Cell health is evaluated by comparing initial and current capacity. The SOC is crucial for the SOH calculation, cell balancing, and power management. It resembles a fuel gauge but is not directly measurable. While Equation (1) is the standard, some studies use modified versions. Coulomb efficiency measures the ratio of discharging to charging capacity. The SOC dynamics equation, based on Coulomb counting, is as follows [21].
where SOC(t) is the SOC at time t, SOC(t0) is the SOC at time t0, I(t) is the discharge current from t0 to t, η is the Coulomb efficiency, and Qfull is the capacity of the battery.
2.2. State of Health (SOH)
The state of health (SOH) refers to a battery’s capacity when fully charged in its current cycle compared to when new. Over time, the battery’s capacity diminishes, a process called degradation. Research shows that lithium-ion batteries degrade gradually at first, then rapidly later, with the point of rapid degradation defined as the Knee-point (Figure 2) [22]. Accurate SOH prediction helps anticipate the Knee-point and mitigate premature battery failures. The main objective of SOH estimation is to track Li-ion battery aging over time, with multiple approaches providing valuable insights.
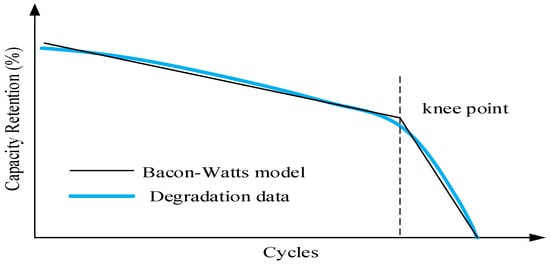
Figure 2.
Capacity degradation and knee-point obtained using the Bacon-Watts model.
Battery capacity directly indicates performance. The term “health” can be unclear, leading to alternative definitions in some studies [23]. For example, instead of measuring capacity, which can be challenging, some research defines health based on the easier measurement of electric charge or discharge power.
where is the electric quantity of charge or discharge of the battery in its current state, and is the nominal electric quantity of charge or discharge of the battery when it is first installed. The SOH can, to some extent, reflect battery aging, with the primary cause being an increase in internal resistance. Therefore, it can be defined based on internal resistance.
where is the internal resistance of the battery at its end of life (EOL), is the internal resistance of the battery in its current state, and is the internal resistance of the battery when it was first installed. However, it is challenging to measure precisely as the internal resistance is easily influenced by the temperature and SOC.
Estimating the remaining useful life (RUL) of a battery is equally crucial as determining its SOH. The RUL represents the cumulative charge and discharge cycles a battery undergoes before reaching its current capacity decay and failure threshold [24]. The RUL is closely linked to the SOH and can be defined as follows.
where is the cycle numbers in the entire life of the battery, and is its current number of charge and discharge cycles. Although there are some studies on the RUL separately, most studies combine the RUL and SOH [25]. The SOH is predicted first, followed by the RUL, based on the SOH, where the RUL is typically referred to as the quantity of charge or discharge cycles until the battery’s SOH is at 0%.
Various metrics, like capacity and resistance, indicate a battery’s health index (HI) for SOH assessment. Data-driven methods are vital for estimating a battery’s SOH and RUL. The choice of the HI impacts prediction accuracy, crucial for SOH and RUL estimation. HIs serve as training data for SOC estimation, either directly (e.g., capacity, resistance) or indirectly (e.g., voltage, current). Fusion models enhance accuracy by combining multiple HIs. Recent research has analyzed HI selection, comparing benefits and drawbacks for SOH and RUL calculation. The literature includes a comprehensive comparison, as summarized in Table 1. Although not the primary focus of this article, the selection of appropriate HIs from the table can facilitate the estimation of the state of charge (SOC) or SOH, including the RUL.

Table 1.
Comparison of advantages and disadvantages of various health indicators (HIs).
3. Estimation Methods for the SOC and SOH
Different classifications are employed to categorize techniques for estimating the SOC and SOH. Some researchers consolidate these methods into distinct categories that share notable similarities. Figure 3 illustrates that the upcoming section will look into methods associated with machine learning.
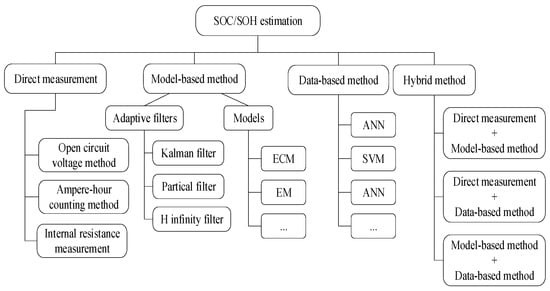
Figure 3.
Classification of SOC estimation methods.
The direct measurement method is sometimes called the experimental estimation method. The approach mainly depends on experimental data for measurement. It involves using techniques and algorithms with observable battery metrics like voltage, current, and temperature to deduce a battery’s state. There are two prevalent techniques for estimating both the SOC and SOH.
The ampere-hour counting method or Coulomb counting method estimates the battery status by cumulatively measuring the charged and discharged current. The estimation of the SOH can be calculated by the following equation:
where represents the total amount of power charged or discharged (the SOC from 0% to 100% or 100% to 0%) in the current cycle, and is the rated charge of the battery.
This approach offers advantages like minimal processing power demands and easy integration. Nevertheless, it does not account for alterations in a battery’s internal state. When current measurement becomes inaccurate due to calibration and measurement issues, it leads to errors in the SOC.
On the other hand, open circuit voltage (OCV) estimates the SOC based on the open circuit voltage for an extended period. Relaxation is a somewhat constant function of the SOC. In this method, the open circuit voltage can be defined as follows.
where is the OCV, U is the terminal voltage, I is the battery current, and R is the battery’s internal voltage.
The process is simple and feasible but unsuitable for real-world usage due to the lengthy resting period required during testing. While the open circuit voltage remains consistent, the battery’s actual state of charge (SOC) and state of health (SOH) differ when it operates at varying temperatures [26]. Nevertheless, internal resistance is a variable feature of a battery’s internal chemistry, which depends on the battery capacity. Generally, as the SOC and SOH decrease, the internal resistance tends to rise. Hence, precise SOC and SOH estimation can be grounded in a reliable measurement of internal resistance [26]. Ohm’s law can be employed to estimate a battery’s internal resistance based on changes in the voltage curve.
where ∆U and ∆I are the step changes in voltage and current, respectively. The current internal resistance value can be obtained by measuring the voltage and current in different current pulse methodologies.
The ohmic internal resistance is typically low and exhibits minimal variation during charge and discharge cycles. However, it is sensitive to external influences, making precise measurement challenging. Furthermore, certain studies have highlighted the temperature’s substantial influence on internal resistance growth [27]. Apart from the previously discussed methods, the direct measurement approach encompasses additional techniques such as electrochemical impedance spectroscopy (EIS), destructive testing, and ultrasonic measurements. Nonetheless, many of these techniques are primarily suitable for laboratory use and offer limited practical utility in real-world scenarios.
The model-based method has been widely used in the literature to model measured battery parameters. The model-based approach usually involves two elements: filtering and modeling. This approach estimates the battery state by identifying model parameters. Estimation accuracy is primarily influenced by two factors: the model’s accuracy and the chosen filtering method [28].
The Kalman filter (KF) is utilized for estimating the state of charge (SOC) in power batteries. It employs the concept of Kalman filtering to determine the current “optimal value” based on the “measured value” from the present instrument and the “predicted amount” from the previous hour. The prediction and measurement errors are often referred to as noise. The Kalman filter can be divided into three segments: (1) prediction of the current state based on the estimated state from the previous moment, encompassing state prediction and prediction of the random state distribution; (2) computation of the Kalman gain; and (3) updating of the current predicted state and predicted state distribution using the measured value and Kalman gain [29]. Initially applied to linear systems, the Kalman filter has seen modifications such as the extended Kalman filter (EKF) [30], dual extended Kalman filter (DEKF) [31], unscented Kalman filter (UKF) [32], and others in the various literature for SOC and SOH estimation. The advantages of the Kalman filter method include real-time computer data processing, applicability to nonlinear systems, and positive effects on predicting the charge state of electric vehicles during operation. Its primary limitation is its reliance on the accuracy of the battery model, necessitating the development of a reliable battery model to enhance precision. The KF is a valuable tool for handling state estimation problems with Gaussian noise. However, it has limitations when dealing with non-Gaussian state and measurement noise in battery operation.
Particle filters (PFs) and their variations are a more suitable choice for nonlinear systems. A PF [33], based on the Monte Carlo method, employs particle sets to represent probabilities and is applicable to various state-space models. It sequentially samples random state particles from posterior probabilities, involving four steps: prediction, weight update, resampling, and output. Advancements in PFs have yielded positive results in state of charge (SOC) and state of health (SOH) estimation. Its strength lies in handling nonlinear, non-Gaussian systems. However, challenges remain. One major concern is the need for a substantial number of samples to accurately approximate the system’s posterior probability density. Additionally, the resampling stage can lead to a loss of sample diversity, resulting in sample depletion issues.
An H-infinity filter (HIF) addresses sensitivity to model errors and the assumption of noise statistics in KF-based algorithms. By introducing the H-infinity norm [34] and boundary condition, an HIF mitigates these issues. An HIF establishes a sub-filter to limit uncertainty and model perturbation effects, reducing estimation errors even in worst-case scenarios without specifying disturbances or model uncertainties. Performance depends on design specifications. Research suggests that an HIF is a straightforward and highly reliable solution for time-variant systems, e.g., SOC and SOH estimation in LIBs [35]. Compared to the Kalman filter, the HIF offers robustness improvements, making it a robust Kalman filter variant. In SOC estimation, the HIF outperforms [36]. Furthermore, models play a vital role in model-based estimation. The equivalent circuit model (ECM) and electrochemical model (EM) are two key models. Here is a brief overview of these essential elements.
The equivalent circuit model (ECM) is also be referred to as the electrical battery model or electrical equivalent circuit model (EECM) [37]. Since ECMs are commonly used, they become quite popular for machine learning methods. Figure 4 provides a brief explanation of several typical ECMs. Each ECM uses the same basic components: an ideal voltage source, a series resistance, and one or more groups of resistor–capacitors (RCs) that are wired in series with the resistance. UL and RL are used to represent the voltage and resistance of the external load circuit.

Figure 4.
Three typical ECMs of a Li-ion battery.
- The battery’s internal resistance equivalent model is simple to use. The open circuit voltage of the battery (OCV, denoted as UOC), which is represented by the ideal voltage source, is a crucial input parameter used in a variety of estimation techniques. When using a constant charge or discharge current I(t), the battery’s internal resistance, also known as the series or ohmic resistance (abbreviated as R0), increases.
- Rp–Cp pairs (known as RCs), in which the resistance is always connected in parallel with the capacitance, are used for modeling the battery behavior under dynamic operating conditions. Sometimes, multiple sets of RCs are connected in series to improve accuracy. For example, when there are two RCs in series, the model is called a second-order RC ECM.
- The resistance of the battery differs during charging and discharging, and if the effect of this factor is considered, a resistor and diode in series will be used. In this way, only one resistor will work in the ECM during charging and discharging. For example, the commonly used RC model can be expressed as the following:
In many cases, enhancing simulation accuracy with more intricate models comes at the cost of complicating parameter identification. Generally, many studies deem a first-order RC model or a second-order RC model adequate [38,39].
Electrochemical models (EMs) depict the underlying processes within a battery’s operation, striving to replicate the chemical reactions occurring in a Li-ion battery during charging, discharging, and resting periods. An EM, with its ability to capture electrochemical kinetics, material properties, and ion transport within the cell, sometimes surpasses an ECM in providing a more comprehensive view of the cell’s internal state. EM models fall into four primary categories [40]: the pseudo-two-dimensional (P2D) model [41], single particle (SP) model [42], enhanced single particle (ESP) model [43], and multiphysics coupling (MC) model [44].
The EM model, compared to ECM, accurately tracks battery changes across diverse conditions and enables continuous monitoring throughout its lifespan. However, its complexity stems from intricate partial differential equations describing ion motion and chemical reactions, including solid-phase and electrolyte-phase electric potential, electrochemical kinetics, and electrolyte ionic diffusivity [45]. Various models exist, such as CC-CV charge, OCV mathematical, exponential, polynomial, and ensemble models. Life cycle models offer an alternative for state of health (SOH) prediction, based on extensive offline tests, distinct from real-time parameter-based methods [46,47,48].
3.1. SOC and SOH Estimation Using Machine Learning
Machine learning methods like Coulomb counting estimate the SOC by tracking current flow in/out of the battery and are prone to errors and reliant on the initial SOC. The OCV method correlates battery voltage with the SOC using OCV-SOC curves. But the mapping accuracy is crucial and susceptible to temperature changes. Kalman filters blend measurements with system dynamics, adapting to conditions, but require a battery model and intensive computation. ML models, including neural networks and regression, learn SOC patterns from data and are versatile but require labeled training data and face complexity/overfitting challenges. For the SOH, the capacity fade rate monitors the capacity decline but may miss early degradation and be affected by cycle counting inaccuracies. Impedance spectroscopy offers insights into internal changes but requires specialized equipment and interpretation. Voltage relaxation measures recovery after load removal and is sensitive to aging but needs precise voltage measurements and is specific to certain degradation modes. Combining methods yields better results by adapting to the battery type, data availability, and application needs. Advancements in computer technology enable the utilization of AI, ML, RL, and DL for SOC and SOH estimation [49]. This section introduces machine learning for non-experts, highlighting its learning capability from data [50]. As seen in Figure 5, the machine learning encompasses supervised, unsupervised, and reinforcement learning [50].
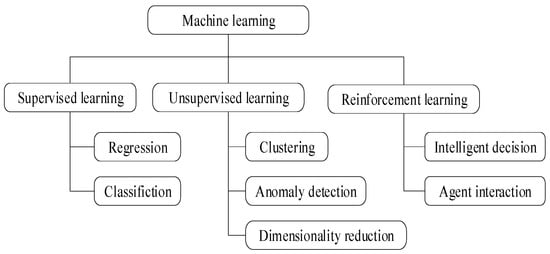
Figure 5.
Categories and roles of machine learning.
Supervised learning relies on labeled examples for training. It necessitates correct labels for given inputs, enabling the algorithm to make accurate predictions. This can be categorized into regression, predicting a number from an infinite set, and classification, predicting from a discrete set of outputs. Unsupervised learning, on the other hand, operates without predefined output labels. It identifies patterns or structures within the data autonomously. This can include clustering, grouping data without labels, anomaly detection for identifying unusual events, and dimensionality reduction for compressing large datasets while retaining essential information.
Reinforcement learning, inspired by behaviorist psychology, emphasizes online learning and maintains a balance between exploration and exploitation. It does not require prior data but learns from environmental feedback on actions. It is employed to solve problems where an entity learns strategies to maximize rewards or achieve specific goals through interaction.
Consequently, supervised learning methods for regression are paramount. It is noteworthy that classification models derive from regression models, discretizing their output. Therefore, algorithms initially designed for classification, like support vector machines and k-nearest neighbors algorithms, find extensive application in battery state prediction. Pedro Domingos’ taxonomy categorizes these algorithms into five tribes, symbolists, connectionists, evolutionaries, Bayesians, and analogizers, each offering distinct approaches applicable across domains and providing foundational theories for other algorithms within their respective tribes, as illustrated in Table 2.

Table 2.
Five tribes of machine learning.
Several significant methods for estimating the SOC and SOH have been introduced. Traditional direct measurement techniques are simple but vulnerable to aging, temperature, sensor drift, and external disturbances. Model-based estimation methods yield precise results but exhibit limited robustness and complexity. Machine learning-based SOC and SOH estimation methods show the best results among all evaluated methods, offering high accuracy under aging and temperature conditions. While these methods may demand substantial computational time, advancements in computing technology have mitigated this issue. The abundance of data enables ML techniques to enhance BMS performance, especially during the offline training phase, without considering chemical reactions and battery models.
Estimating the SOC and SOH remains challenging due to battery behavior variations and complex EV battery architecture. ML’s ability to improve using existing data and established algorithms, rather than building accurate theoretical models, has driven its increased adoption. The availability of more battery data and improved computing power further supports data-driven ML applications.
Joint estimation of SOH and SOC is crucial, with capacity-based and resistance-based SOH estimation processes playing a significant role in updating SOC estimation. Researchers categorize ML algorithms for battery state estimation into non-probabilistic and probabilistic methods, with studies emphasizing non-probabilistic algorithms, including neural networks, support vector machines, fuzzy logic, and their derivatives. This section provides a comprehensive overview of ML techniques for SOC and SOH estimation, offering comparisons. The overall workflow can be seen in Figure 6.
Figure 6.
ML-based battery state estimation workflow.
When employing machine learning to estimate the SOC and SOH of batteries, various crucial aspects come into play. These aspects, as shown, help to capture pertinent details regarding the battery’s behavior and condition.
- Battery voltage serves as a foundational indicator for estimating both the SOC and SOH. It mirrors the stored energy in the battery and fluctuates with SOC changes, which can be directly measured or inferred from other sensor data.
- Battery current, whether charging or discharging, offers insights into the battery’s activity. Integrating current over time assists in SOC estimation, while irregular patterns may signify degradation or anomalies, affecting the SOH.
- Battery temperature significantly affects its performance and longevity. Elevated temperatures expedite degradation, impacting the SOH. Temperature sensors offer valuable inputs for SOC and SOH models.
- SOC estimation often hinges on capacity measurements, which can be derived through methods like Coulomb counting or impedance spectroscopy. Precision in capacity estimation bolsters SOC accuracy.
- Internal resistance influences voltage drop during current flow and changes therein can indicate aging or damage. Factoring internal resistance as a feature enhances SOH estimation.
- The number of charge–discharge cycles influences battery health, with more cycles leading to capacity fading and a diminished SOH. Therefore, the cycle count as a feature, aids in SOH prediction.
- Coulomb efficiency reflects how efficiently a battery stores and releases charge, deviations from which affect SOC estimation. Monitoring Coulomb efficiency assists in SOH assessment.
- Features tied to aging, such as the capacity fade rate or impedance alterations, are crucial. Machine learning models can discern patterns associated with aging, thereby refining SOH estimation.
- The SOC and SOH undergo changes over time, making time-related features (e.g., aging rates, calendar aging effects) invaluable for predictions. Long-term trends impact both the SOC and SOH.
- Integrating multiple sensor inputs like voltage, current, and temperature enhances accuracy. Sensor fusion techniques, such as Kalman filters, bolster SOC and SOH estimation.
Machine learning necessitates a substantial volume of curated data, particularly for estimating SOC and SOH through experimentation. Leveraging these datasets for methodological investigations without requiring new experiments is a valuable approach. Examples of assessable datasets can be obtained from the following websites.
- Center for Advanced Life Cycle Engineering (CALCE) [65]: The CALCE at the University of Maryland provides battery data for research purposes, covering battery state estimation, remaining useful life prediction, accelerated battery degradation modeling, and reliability analysis.
- NASA datasets [66]: The Prognostic Center of Excellence (PCoE) at NASA Ames maintains the Prognostic Data Repository, which contains various battery datasets. Among these are the PCoE Battery Dataset, featuring cycling data for 3,418,650 cells with a 2 Ah capacity cycled to 70% or 80% of initial capacity at different temperatures using a custom-built battery tester. Additionally, there is the Randomized Battery Usage Dataset, providing cycling data for commercial cells, and the HIRF Battery Dataset, which includes data from testing battery packs for a small aircraft. Also, the Small Satellite Power Simulation Dataset includes data from testing battery packs for a small satellite.
- BatteryArchive.org [67]: It is an open-access battery dataset repository built on open-source software. Its goal is to standardize battery testing and reporting by offering a user-friendly interface for comparing battery datasets.
- An article published by Springer stresses the importance of standardizing battery testing and reporting through open databases [68] to enhance overall field research and advance toward more efficient and reliable battery systems. However, the reliability of these datasets varies depending on the specific research context and use case. Hence, it is crucial to carefully assess datasets based on their requirements and objectives.
- Carnegie Mellon University Kilthub Dataset [69]: A dataset of lithium-ion battery discharge data including voltage, temperature, and current from electric vertical take-off and landing (eVTOL) duty cycles (https://kilthub.cmu.edu/articles/dataset/eVTOL_Battery_Dataset/14226830 (accessed on 21 May 2024)).
3.1.1. Neural Network (NN)
Neural network, also known as artificial neural network (ANN), methods are categorized into three main groups as described in reference [70]. The first category is the feedforward neural network (FFNN) method, which includes variations like the backpropagation neural network (BPNN), Elman neural network (ENN), radial basis function neural network (RBF-NN), and time delay neural network (TDNN). The second category is deep learning (DL), encompassing deep belief networks (DBNs), convolutional neural networks (CNNs), and recurrent neural networks (RNNs). The last category is the hybrid method, combining two or three approaches. Other methods, such as the extreme learning machine (ELM), can also be considered part of the FFNN category. While the classification in [70] is logical, we will focus on widely used NN methods.
We can observe the basic structure of a feedforward neural network (FFNN), which was the original neural network developed for artificial intelligence. All neural network methods have evolved from the FFNN, making it a popular method for SOC estimation in lithium-ion batteries due to its simplicity, ease of training, and good generalization [71,72].
A neural network comprises interconnected neurons organized into three primary layers. The input layer, with four inputs for example, can represent parameters like voltage, current, temperature, and time in battery state estimation. The output layer has three outputs, typically SOC, SOH, and SOP, in battery state estimation. Hidden layers can create complex nonlinear functions by integrating input data. The number of hidden layers can make it a deep neural network (DNN) if there are more than three hidden layers. Each neuron has an input and an output, with inputs from the previous layer and outputs to the next layer in the middle–hidden layer. The input and output of the input and output layers are the data. In each neuron, it is calculated as the following:
where y is the output of this neuron, f is the activation function, and usually a sigmoid function is used, is the weight coefficient of the input , while is the input of this neuron, and b is the bias term. and b are determined based on training on a known dataset by using a perceptron. The value of is updated according to the following equation until it converges.
where α is the learning rate, which is used to control the step size, y is the true output of the training data, and is the predicted output. This perceptron is obtained based on the gradient descent method. The same idea can be used for complex neural networks to update the parameters based on the chain rule of derivation.
Employing a neural network to generate output from an input is called feedforward. Conversely, the process of adjusting the parameters in a neural network based on the disparity between the output and actual results is known as backpropagation. The well-trained model exhibits a notable likelihood of providing accurate outputs for data with both known inputs and unknown outputs, denoted as its generalization ability. Several enhanced approaches rooted in neural networks have emerged for diverse SOC and SOH prediction challenges. This includes the introduction of fundamental principles for a selection of frequently utilized techniques.
3.1.2. Feedforward Neural Network (FFNN)
A FFNN, also known as an FNN in some of the literature, is distinct from a fuzzy neural network (FNN), which is also abbreviated as an FNN. To prevent confusion, this article refers to the feedforward neural network as FFNN. An NN can handle extensive data in complex nonlinear systems independently of a battery’s electrochemical processes, making it a widely used tool for battery state estimation. An FFNN’s effectiveness in estimating a battery’s SOH has been confirmed using calendar aging data under different degradation conditions [73] and one year of real-time data from a BMS [74]. The BPNN [75] was effective at various temperatures.
An NN model [76] estimated battery capacity degradation, while the SOC [77] for both lithium phosphate batteries (LPBs) and lithium-ion batteries was estimated using a two-layer neural network with a tensing activation function, consistently achieving an MSE under 10%. The SOC and SOH were estimated using data-driven FFNNs [73] of a multilayer perceptron (MLP) developed with a charge and discharge dataset collected over ten months. The SOC and SOH were predicted based on the cell voltage, current, storage temperature, aging period, and storage state. One study [78] reduced the input dimension for the FFNN, simplifying the network. Another approach [79] used the sample entropy of discharge voltage as the input for the FFNN to predict the battery’s SOH intervals accurately. An FFNN can also be combined with models like the ECM and KF for SOC and SOH estimation.
An RBF-NN, a type of FFNN, employs the radial basis function as an activation function. It can prevent training from converging to local minima [80] and reduce reliance on dataset quality [81], often achieving higher estimation accuracy. An improved RBF-NN in [82] estimated the SOC with a generalization error of less than half of other methods. An improved radial basis function neural network (IRBFNN) [83] was proposed to improve SOH estimation. An RBF can be combined with other models, as seen in a battery model [84,85] used to derive state-space equations for an EKF. The works in [86,87] were similar, with H-infinity and UKF used separately.
3.1.3. Deep Neural Network (DNN)
To enhance neural network predictions, deep neural networks (DNNs) can be employed. For instance, the estimation of the SOC utilized a deep feedforward neural network (DFNN) [88]. This model exhibited excellent estimation performance under constant ambient temperature conditions, outperforming models using complex differential equations like the EKF in computational efficiency. To estimate a battery’s SOH across different SOC and current conditions [89], a paper employed the SOC to adjust the kernel function within the DNN, making it adaptable to real-world scenarios. A comparison between a DNN, linear regression, SVM, k-NN, and ANN for SOH estimation revealed the DNN’s superior performance. However, it is important to note that DNN-based approaches require more computation time and resources. This issue can be alleviated by reducing neural connections [90] and downsizing the dataset [91].
3.1.4. Extreme Learning Machine (ELM)
The FFNN algorithm, which relies on gradient descent, may exhibit slow performance and demand extensive computational resources. The extreme learning machine (ELM) was introduced to address this issue. The ELM is built upon feedforward neural networks [92] and can encompass single or multiple layers of hidden nodes. These nodes serve various purposes such as classification, regression, clustering, sparse approximation, compression, and feature learning. In an ELM, the parameters of these hidden nodes can be configured. These hidden nodes can either be randomly selected and remain unaltered or be passed down without modifications. Typically, the output weights of the hidden nodes are trained in a single step, akin to learning a linear model. As shown in Figure 7, w and b are randomly given and will never be changed; only β is learned in a single step, while these parameters need to be solved and consume a lot of computational resources. Obviously, this greatly improves the solution efficiency of the neural network.
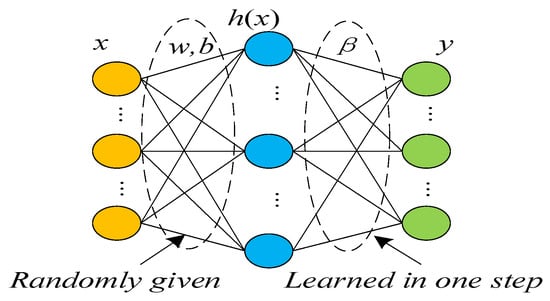
Figure 7.
Basic principles of an ELM.
However, the ELM has been found to be effective enough in many applications including in the SOC and SOH estimation of batteries [93,94]. However, compared to traditional learning methods, estimating the weights of an ELM is much faster and requires less computation. It is still important to admit that the ELM approach will always be less accurate than an FFNN because it has fewer trainable weights.
As mentioned previously, the ELM effectively reduces computational effort with a minor trade-off in accuracy, which is crucial for SOC/SOH estimation in engineering applications. In a study by researchers [95], they combined ELM and Thevenin models to achieve online identification of internal resistance for battery SOH estimation. The ELM, trained offline using a collected dataset, exhibited faster learning than a traditional FFNN. This method is suitable for online implementation. In another study by researchers [96], an online sequential ELM approach was proposed to efficiently utilize old and new data. Initially, a subset of samples determined the output weight of the ELM, and this weight was updated with new samples. This approach offers quick learning, strong generalization, and high accuracy. It was noted that the ELM, compared to an RBF, demonstrated a lower computational load and improved estimation error.
3.1.5. Recurrent Neural Network (RNN)
Long short-term memory (LSTM) is a recurrent neural network (RNN) technique frequently found in research and stands out for its ability to consider time dynamics. This characteristic contributes to its popularity in tasks like speech recognition and SOC/SOH estimation, which are inherently time-dependent [97,98,99,100]. Figure 8 illustrates the fundamental concepts of an RNN and LSTM in a way that differs slightly.
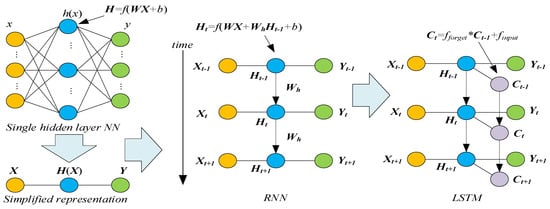
Figure 8.
Basic principles of an RNN and LSTM.
Figure 8 shows a simplified vector representation of a single hidden layer neural network. The hidden layer in the recurrent neural network (RNN) considers time, and its activation function is incorporated, representing the hidden layer’s connection weight. During training, the hidden layer adjusts based on the previous instant, primarily associated with short-term memory. However, for long-term memory, LSTM is recommended. To work with the data in the hidden layer, C is introduced to the LSTM, combining the functions of the forgetting gate, input gate, and output gate. This enables long-term memory retention and adjustments during training. LSTM is particularly effective for scenarios where a battery’s state is influenced by its usage history.
The characteristics of common neural network (NN) methods can be summarized concisely. Neural networks use activation functions to introduce nonlinearity, making them universal function approximators and allowing them to learn battery degradation patterns. Deep neural networks (DNNs) are effective at modeling complex data with many inputs and can achieve high accuracy, especially with extensive aging data. However, DNNs require significant computational power and large datasets.
- Extreme learning machines (ELMs) simplify the solution process by generating layer parameters with minimal iterations. Although they may slightly reduce accuracy, ELMs are advantageous for handling large datasets.
- Recurrent neural networks (RNNs) can process time-series data of varying lengths and remember historical information, making them suitable for state of health (SOH) estimation under dynamic conditions. However, they may face gradient vanishing or exploding issues during backpropagation in long sequences.
- Elman neural networks (ENNs) are akin to RNNs and have global feedforward and local recurrent properties. They can be used for SOC and SOH predictions with good accuracy.
- Long short-term memory (LSTM) variants of RNNs are effective for modeling long-term dependencies in battery degradation. They outperform other methods and offer the advantage of recognizing and correcting lengthy relationships.
- Improved LSTM methods like the active state-tracking-LSTM neural network (AST-LSTM NN) and LSTM with an attention procedure combined with particle swarm optimization offer more accuracy in RUL prognosis and SOH observation.
- A deep learning approach using LSTM quickly estimates the remaining useful life (RUL) of Li-ion batteries without offline training data.
- Other RNN-based methods, including the gated recurrent unit (GRU)-RNN and clockwise recurrent neural network (CWRNN), are proposed to address the issue of lengthy dependencies in battery models and achieve high accuracy.
3.1.6. Convolution Neural Network (CNN)
Convolutional neural networks (CNNs) are commonly employed for image recognition tasks. However, their utility extends to battery state estimation as well. Their architecture, featuring convolutional and pooling layers, excels at automatically discerning key features from raw data. A CNN was initially applied for state of health (SOH) estimation using voltage, current, and charging capacity data from a partial charging cycle. The CNN proved to be a practical choice for online SOH estimation, offering high accuracy, quick testing, and minimal memory usage. Another CNN model [101] was introduced for estimating remaining useful life (RUL), complete capacity, and internal resistance based on a single cycle’s input data. This model incorporates two closely connected layers for convolutional feature extraction, utilizing voltage, SOC, and current data. CNNs, with their advantageous traits, are frequently used with other methods for battery state estimation. For instance, to harness the strengths of both a CNN’s feature extraction and recurrent neural networks’ time-series prediction, researchers [102,103,104] combined a CNN and an RNN by adding a convolutional layer to the LSTM. This optimized network structure fully leverages a CNN’s automatic feature extraction while reducing the computational load.
3.1.7. Other NN Variants
While neural networks (NNs) exhibit strong performance in estimating battery life at the beginning, their effectiveness diminishes toward the end of a battery’s life cycle. As a result, researchers have strived to enhance NNs and introduce novel approaches. These include the adaptive neural network (ADNN) [105], confidence prediction neural network (CPNN) [106], and adaptive recurrent neural network (ARNN) [107], which is RNN-based. Furthermore, the authors in [108] optimized the recurrent nonlinear autoregressive with exogenous inputs (RNARX) method, a well-known RNN subclass. They combined it with the lightning search algorithm (LSA), an intelligent optimization technique that simplifies SOC estimation under various temperatures and drive cycles. Another model [109] showcased SOC forecasting over 54 real driving cycles using the nonlinear autoregressive with an external input (NARX) technique based on NNs. This model took inputs such as battery pack temperatures, current, and voltage and output the SOC, achieving a low MSE of 9.2727 × 10−7.
An NN’s versatility extends beyond its state determination; it aids in modeling and complements other methods. For instance, NN models measure battery electrochemical properties using activation functions, enabling SOH calculation based on voltage–capacity slopes with fuzzy logic (FL). Other researchers [110] employed a structured NN with sub-NNs to estimate voltage, RC parameters, and SOH. Additionally, artificial neural networks (ANNs) [111] were combined with an extended Kalman filter (EKF) for SOC estimation at room temperature with an RMSE of 2%. It is important to acknowledge that NNs are computationally intensive. Table 3 summarizes the pros and cons of current NN techniques. It is worth noting that the Adaptive Neuro-Fuzzy Inference System (ANFIS) is another significant NN method, which incorporates fuzzy logic (FL) principles into its design.

Table 3.
Comparison of NN-based SOC and SOH estimation methods.
3.1.8. Support Vector Machine (SVM) and Support Vector Regression (SVR)
As neural networks regained attention and became increasingly popular in various research fields, support vector machines (SVMs) [112] emerged as one of the most widely adopted machine learning techniques. The conventional SVM primarily addresses classification problems. To handle regression problems, the support vector regression (SVR) concept was introduced as an extension of SVMs. The fundamental principles are illustrated in a simple two-dimensional linear case that can be seen in Figure 9.
Figure 9.
Geometric representations of an SVM and SVR.
An SVM endeavors to establish hyperplanes in high-dimensional space to differentiate data from different classes. It achieves an optimal separation boundary when maximizing the distance between the hyperplane and the closest data point of any class. The hyperplane simplifies to a straight line in this two-dimensional linear scenario. Notably, option “a” outperforms option “b” by offering a broader range of tolerances. It effectively separates white circles and squares, which may exist outside the sample data, while “b” does not. The support vector, representing the distance between the nearest sample point and the hyperplane, plays a pivotal role in constructing the hyperplane. It is named a “support vector” because it supports the tolerance space from positive and negative directions, enhancing generalization ability. This concept is the basis for support vector machines in machine learning. An SVR shares the core idea with an SVM but differs in the solution direction. An SVM aims to maximize the “distance” to the nearest sample point from the hyperplane, while an SVR strives to minimize the “distance” to the farthest sample point from the hyperplane.
An SVM employs kernel functions to transform sample points into a higher-dimensional space for tackling multidimensional or nonlinear complex problems. Take the two-dimensional XOR problem depicted in Figure 10. In two dimensions, it is impossible to distinguish between positive and negative signs using a linear line. However, this separation becomes achievable by mapping it to a three-dimensional space with a linear plane.
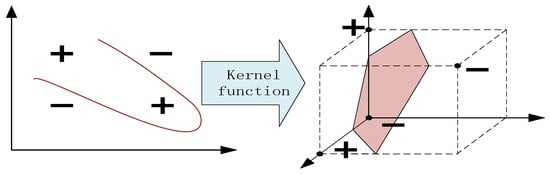
Figure 10.
Kernel function role.
An SVM uses a regularization parameter, mitigates overfitting, and demonstrates robust generalization abilities. It adeptly handles nonlinear data, even in high dimensions, thanks to kernel functions. However, selecting the appropriate kernel function is not a straightforward task. Additionally, an SVM may not be suitable for large datasets due to the need to store support vectors in memory, resulting in increased training time and computational demands. In contrast, neural networks (NNs) are better suited for large volumes of data, while SVMs may outperform when the dataset is relatively small.
An SVM overcomes an NN’s drawbacks like a local extremum, complex network structures, extensive sample training, and high computational costs. It excels with finite small sample datasets and enhances algorithm generalization. Therefore, an SVM, including support vector regression (SVR), finds widespread use in SOC/SOH estimation [113]. In an SVM, diagnosis relies on functions defined in the input space, while learning involves parameter calculation. For SOH estimation, a two-layer structure SVM [114] was employed. The introduced cost function constitutes the core of this method. Other researchers [115] developed a two-level SVM for RUL estimation, initially providing a rough estimate using classification, then refining it through regression. Researchers are actively exploring improved algorithms and fusion with other methods to enhance SVM applicability. Four primary avenues of research to enhance SVM estimating performance include the following.
An initial estimation of battery internal resistance [116] and terminal voltage using an SVM can be used to comprehend battery aging under different conditions. These variables exhibit a linear relationship with battery capacity. Hence, effective features derived directly from partial constant current charging or discharging voltage curves [117,118] are employed as SVM model inputs or features.
The most common approach involves modifying the kernel function to enhance model performance. For example, the Gaussian kernel’s double deviation parameter significantly influences an output curve’s properties. This enhanced kernel function can adapt to curve shapes with various curvatures, preventing over- and underfitting. Other approaches [119] decompose the kernel function into two terms, representing overall degradation trends and small SOH fluctuations separately, thereby improving estimation accuracy.
Combining SVM with other methods as an auxiliary approach is third method. For instance, a robust and real-time SOC and SOH estimation method was developed. It utilized SVM estimation as the initial capacity of a Kalman filter (KF) and updated the current capacity. An SVR model [120] combined with possibilistic clustering classification (PCC) was proposed to predict the RUL under different operating states. Researchers [121] estimated the SOC based on a method that combined an optimized SVR and a double search optimization process, which was found to be both more accurate and easier to use than an artificial neural network (ANN).
The least squares support vector machine (LS-SVM), a significant SVM variant, is considered the fourth improvement method. A traditional SVM requires extensive computation to solve quadratic programming problems with large datasets, making it challenging for real-world applications. However, the LS-SVM faces non-sparseness issues, leading to a complex model with poor generalization. A fixed-size LS-SVM algorithm [122] was proposed to address this, showing substantial improvement in calculation speed over the traditional SVM. For regression problems, the least squares support vector regression (LS-SVR) algorithm was employed to estimate the SOH.
Using an SVM, the estimation error is comparable to the unscented Kalman filter (UKF). An SVM [123] was applied to data gathered using electrochemical impedance spectroscopy (EIS), which considers capacity fading and internal resistance. The error of the SVM was similar, approximately 2%. Like other machine learning methods, the SVM requires many calculations during training, can only perform offline prediction, and has limited practical applicability. To address this, several improvements have been proposed. By dynamically updating the vectors in an SVM, it can make online predictions. Application to NASA data demonstrated that the average absolute estimation error for the SOH was 2% to 3%. In [124], an alternative improvement was adopted. First, offline training was performed, and the obtained model was used in the initial estimation stages. Then, SVMs were updated based on the current online data. This reduced the absolute error to 1%.
Previous studies indicate that SVM-based methods generally offer high estimation precision. However, achieving this precision comes at the cost of high computational complexity. For instance, other researchers [125] compared support vector regression (SVR) and the recent gradient boost algorithm extreme gradient boosting (XGBoost) for SOC estimation. They pointed out that to obtain precise predictions from SVR, the appropriate kernel function must be configured with workable parameter settings. Even with two SVR parameters tuned, the root mean square error (RMSE) is still significant when compared to XGBoost. Consequently, SVR tends to be time- and energy-intensive, resulting in a low level of practical applications.
3.1.9. Fuzzy Logic Method (FL)
Fuzzy logic (FL) can be employed in conjunction with various machine learning techniques to enhance their applicability, such as the sigmoid function in neural networks like the adaptive neuro-fuzzy inference system (ANFIS) method. As a result, FL holds significant importance and is often discussed independently. Fuzzification, the fuzzy rule base, the inference engine, and defuzzification are integral components of the FL interface system structure [126]. FFL was initially applied for battery state estimation using EIS data from an electrochemical model. It estimated both the SOC and SOH by combining an ARMA, NN, and FL. Researchers [127] used measured data from a life cycle test on 95 Li-ion batteries for SOH estimation, with errors ranging from 1.4% to 9.2% [128].
Fuzzy identification divided the SOH into four states, healthy, acceptable, weak, and bad, with an estimation error of less than 5%. FL models nonlinear systems without needing mathematical models or ECMs. It considers input variables like ambient temperature, current, and a battery’s terminal voltage for accurate state estimation.
FL’s flexibility allows for specifying output membership functions for the SOH, like healthy, acceptable, and unhealthy. An online SOH prediction method [129] calculates crucial parameters under specific conditions and predicts the SOH. FL, in combination with other methods like ANFIS, can be very useful.
ANFIS, a neuro-fuzzy model, has five layers and minimal error in SOC estimation [130]. It is particularly accurate in vehicle simulators, making inferences under uncertainty. Combining FL and SVM enhances SOC estimation accuracy, while fusing fuzzy adaptive factors and Kalman filters improves robustness and accuracy [131]. FL’s computational complexity is relatively high but supports both data processing and offline parameter calculations. On average, FL’s reported estimation errors range from 1.4% to 10% [132].
3.1.10. Genetic Algorithm (GA) and Particle Swarm Optimization (PSO)
Evolutionary algorithms, including the genetic algorithm (GA) and particle swarm optimization (PSO), play a crucial role in machine learning, particularly in SOC/SOH estimation. The GA is widely applied in engineering optimization. It leverages natural selection and genetic mechanisms to find optimal solutions. It offers advantages like direct manipulation of structural objects, inherent parallelism, global search capabilities, probabilistic search methods, and adaptive search direction adjustment.
The essential workflow of a GA can be seen in Figure 11. Initially, the population to be optimized is encoded into genetic chromosome genes, forming the first generation, with each chromosome string representing an individual. These chromosomes can undergo crossover and mutation, creating new individuals. The best of these new individuals forms the second generation, and this process continues until the population stabilizes, leading to the best possible outcome.
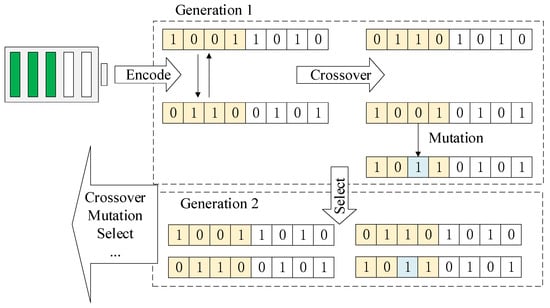
Figure 11.
Basic workflow of a GA.
PSO, inspired by bird behavior, enables birds to find food collectively. They communicate their distances to food and help each other locate the ideal solution, successfully applied in engineering problems. Another paper [133] demonstrated the use of genetic algorithms (GAs) in identifying battery model parameters in state of charge (SOC) estimation. A novel SOC estimation method employing a GA and gray model (GM) was developed for improved repeatability and accuracy [134]. PSO has been used for model parameter identification in battery state estimation [135,136] and often combined with machine learning (ML) techniques. PSO-LSTM optimized LSTM hyperparameters, reducing the error to 0.5%. PSO is also combined with support vector regression (SVR) [137], outperforming SVM in SOC estimation. PSO-SVR is robust, even with noisy training data [138]. In SOC/SOH estimation, GA and PSO are commonly used for parameter optimization in ML methods like neural networks (NNs) and support vector machines (SVMs).
3.1.11. K-Nearest Neighbor (KNN)
The KNN is a simple classification method [139] and assigns new sample points to the same class as their closest training samples in a feature space. It is a lazy learning approach, meaning it relies heavily on training cases without involving abstraction steps. In regression, a KNN follows a similar principle. It identifies the K closest points (x1, x2, …, xk) to the new point based on distance and calculates their weighted average, with closer points having greater influence. This average becomes the value for the new point. The geometric representation of this fundamental principle can be seen in Figure 12.
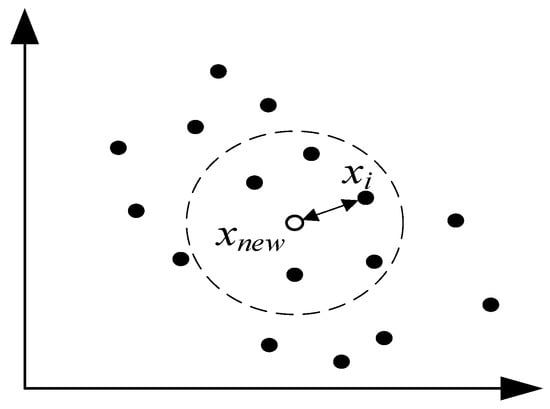
Figure 12.
Geometric representation of a KNN.
KNN regression, a simple and practical method, was utilized for battery state estimation. For example, five key parameters from constant charge curves were used, which included the initial charge voltage, CC charge capacity, CV charge capacity, final charge voltage, and final charge current. These parameters served as inputs for the KNN regression model. A model for estimating the remaining useful life (RUL) [140] was also developed using a KNN. It calculated the RUL by taking a weighted average of similar cells’ useful lives with comparable degradation rates.
While a KNN is straightforward, efficient, and provides reasonably accurate results, it has not received as much attention as neural networks (NNs) and support vector machines (SVMs). This can be attributed to the requirement of understanding battery degradation across its entire range because a KNN model cannot extrapolate beyond observed data. Additionally, a KNN may not be resource-efficient, particularly with large datasets or high-dimensional features, as it needs to store all data and locate neighbor nodes.
3.1.12. Transfer Learning
Transfer learning is regarded as a powerful way to enhance conventional machine learning methods. One paper discussed the data-driven solutions, particularly transfer learning [141], to making more accurate predictions about battery parameters, such as the state of charge (SOC), state of health (SOH), and remaining useful life (RUL). Transfer learning for battery parameter estimation has its drawbacks. For example, pre-trained models might not directly apply to battery parameter estimation due to differences in their target domain, potentially leading to less accurate results. Pre-trained models are often complex, requiring significant computational resources and memory, making them less practical for resource-constrained battery applications. Furthermore, learning models can be less interpretable, making it challenging to understand the reasons behind their predictions, which is crucial in battery-related applications. Finetuning large pre-trained models can be time-consuming, especially when dealing with limited data, delaying the deployment of battery parameter estimation systems. Thus, there is a need for careful consideration and domain-specific adaptations when applying transfer learning to battery parameter estimation tasks.
Another study introduced a Gaussian mixture model [142] for lifetime clustering to assess the effectiveness of proposed health indicators. Additionally, an automatic reference battery selection method was suggested to identify the most relevant candidates for model training. A long short-term memory network with probabilistic regression was then employed, providing mean values and confidence intervals through Bayesian inference, showing relative reductions of 43.7% and 45.3% compared to conventional methods.
A semi-supervised self-learning method [143] was proposed to handle the uncertainty for probabilistic predictions. The results achieved a mean prediction error of below 4.1% for long lifespan batteries and 5.21% for short lifespan batteries, providing possible solutions for some real-world scenarios. Another paper [144] presents a method for accurate battery pack health prognosis using universal health indicators and model fusion. These indicators are adaptable to various battery types, cell numbers, and aging statuses that were further extended to dynamic working conditions using deep learning frameworks. The model’s performance improved through migration and fusion, making it suitable for different battery packs and working conditions with high accuracy and reliability of mean absolute errors of less than 2.5% and root mean square errors less than 3.1% in various applications.
Lastly, researchers [145,146] introduced a novel method for predicting remaining useful life involving optimizing health indicators and applying online model correction with transfer learning. The process uses Gaussian regression to optimize health indicator thresholds for end-of-life determination. The combination of transfer learning and gated recurrent neural networks was designed to predict remaining useful life based on the optimized health indicators, enabling online applications. A self-correction strategy was used to improve prediction performance during operating cycles, showing the method’s accuracy and predicting remaining useful life with an error of less than five cycles.
3.1.13. Hybrid Method (HM)
Hybrid methods combine multiple techniques for better accuracy and robust results, mainly focusing on integrating various ML methods. These methods, known as model-level ensemble learning (EL), merge outputs from different base learners. They often use a weighted average of these base learners to produce the final output. For example, in [147], logic and Gaussian process regression models were combined using the mean method for SOH estimation. In [148], base learners like the ANN, SVM, gray model, and ARIMA were combined with a time-varying weight assignment approach. Probabilistic integration [149] is used to enhance base learners, making the output based on their probability distribution. For example, eight CNN models [76] were pre-trained with aging data from battery cells, using transfer learning and ensemble methods. EL compensates for base learner performance flaws, eliminating the need for precise parameter optimization. Instead, it allows for random initialization of model parameters and enhances accuracy.
4. Comparison of Several Types of Machine Learning
Several ML-based methods for SOC and SOH (including the RUL) estimation are compared in Table 4. Numerous relevant studies exist, but the presented sections offer insight into the current research status. Notably, variations in these methods show significant differences in practice. We consolidated key information and ultimate accuracy. These studies used different batteries, datasets, and assessment criteria. Therefore, precise comparative conclusions were challenging due to different dataset, battery, testing conditions, and criteria used. It was evident that the RBF exhibited the highest error, whereas the FFNN and RNN were presently the most promising techniques for estimating both the SOC and SOH. The ELM, SVM, and transfer learning also showed promise but warranted additional investigation through more iterations.

Table 4.
Comparison of various ML methods for the SOC and SOH (including RUL) estimation.
5. Challenges and Future Works
The existing literature reveals numerous studies on SOC and SOH estimation, each with merits and drawbacks. Therefore, thoroughly analyzing these methods is essential to determining suitable applications. ML-based approaches have become popular despite minimal knowledge of a battery’s internal workings and reliance on abundant data and powerful processors for SOC estimation. However, imbalanced data can lead to overfitting and underfitting issues. Data quality and quantity significantly impact the ML method’s accuracy and performance. Precision in data acquisition, reading, transmission, and analysis is crucial, as errors can lead to poor data quality. Effective techniques must be developed to eliminate inaccurate or biased data. Small sample problems can affect model generalizability and performance. Clustering algorithms, reasoning models, crowdsourcing database technology, and transfer learning may address these issues.
Current estimation methods grapple with robustness concerns, particularly considering complex battery cell behavior. Prognostics are essential as many battery cell parameters are not directly measurable, influenced by environmental factors. Online and offline estimation challenges are intertwined. Online algorithms work with new data during system operation, while offline methods require all data and model parameters before training. Most ML-based methods lean toward offline estimation, potentially leading to challenges in real-time settings.
Spontaneous combustion of EV batteries is a reported issue. Inconsistencies in battery pack design, overcharging, and thermal runaway contribute to this problem. The weakest cell governs pack performance, and low-capacity cells face overcharging and over-discharging, reducing battery life and raising combustion risks. Complexities in EV battery packs pose challenges for BMSs in accurate SOC/SOH estimation.
Some ML algorithms lack model interpretability. Improved interpretability is crucial, as it provides explicit physical meaning to estimation models. Hyperparameter selection through trial and error can lead to computation complexities and unsatisfactory SOC and SOH results. Early-cycle accurate battery life prediction can enhance cell development and effectiveness given initial cycle anomalies and subtle deterioration. One significant disadvantage of transfer learning is the potential for overfitting, where a pre-trained model is finetuned on a new task with limited data. It could become too specialized and perform poorly on unseen data, reducing generalization and accuracy. In addition, domain shifts can occur due to variations in data distribution, which can be challenging to address as new batteries emerge from the market.
6. Conclusions
The paper discussed the state of charge (SOC) and state of health (SOH) estimation methods, including direct measurement and model-based approaches. Machine learning (ML) techniques, such as neural networks and deep learning, were introduced as effective tools for SOC and SOH prediction, leveraging data to enhance accuracy. Various ML algorithms were discussed for battery state estimation, offering promise for improving BMS performance in EV batteries. The paper also highlighted ongoing research involving ML applications for SOC and SOH prediction, shedding light on current challenges and prospective developments.
Our literature review showed that data-driven strategies are preferable when substantial data are available, surpassing model-based approaches. Neural networks (NNs) have gained significant attention in recent years, followed by support vector machines (SVMs), fuzzy logic (FL), the k-nearest neighbors (k-NN) algorithm, and genetic algorithms (GAs). Studies suggest that NN methods outperform SVMs in specific conditions, while optimized support vector regression (SVR) excels in SOC estimation accuracy. However, NNs exhibit lower mean absolute error (MSE) and handle nonlinear data effectively. An SVM proves practical with smaller datasets but poses challenges in human intervention, learning progress delays, and scalability limitations.
Overall, ML-based methods for SOC and SOH estimation remain a primary research focus for BMSs, with NNs and SVMs being the primary techniques. Conventional methods like the equivalent circuit model (ECM), electrochemical model (EM), and FL continue to validate findings. The challenge lies in translating research outcomes into practical applications. Further real-time estimation research will require different system-level configurations, battery physics-informed learning, intelligent thermal management, and geographically sensitive learning. Furthermore, sometimes human-in-the-loop can be helpful to increase the robustness of a battery management system. Explainable artificial intelligence (XAI) is making waves in battery technology. XAI can explain its decisions or outputs in a way that humans can understand.
Author Contributions
All the authors made substantial contributions to this manuscript. C.S., C.S.C., V.M. and C.Z. participated in drafting the manuscript. C.S., C.S.C., V.M. and C.Z. wrote the main manuscript. All authors discussed the results and implications of the manuscript at all stages. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the China Scholarship Council [202105290005].
Data Availability Statement
No new data were created from this work.
Acknowledgments
The authors would like to thank Newcastle University in Singapore.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jing, Q.-L.; Liu, H.-Z.; Yu, W.-Q.; He, X. The Impact of Public Transportation on Carbon Emissions—From the Perspective of Energy Consumption. Sustainability 2022, 14, 6248. [Google Scholar] [CrossRef]
- Rouholamini, M.; Wang, C.; Nehrir, H.; Hu, X.; Hu, Z.; Aki, H.; Zhao, B.; Miao, Z.; Strunz, K. A Review of Modeling, Management, and Applications of Grid-Connected Li-Ion Battery Storage Systems. IEEE Trans. Smart Grid 2022, 13, 4505–4524. [Google Scholar] [CrossRef]
- Kumar, R.R.; Bharatiraja, C.; Udhayakumar, K.; Devakirubakaran, S.; Sekar, K.S.; Mihet-Popa, L. Advances in Batteries, Battery Modeling, Battery Management System, Battery Thermal Management, SOC, SOH, and Charge/Discharge Characteristics in EV Applications. IEEE Access 2023, 11, 105761–105809. [Google Scholar] [CrossRef]
- Xu, X.; Yu, C.; Tang, S.; Sun, X.; Si, X.; Wu, L. Remaining useful life prediction of lithium-ion batteries based on Wiener processes with considering the relaxation effect. Energies 2019, 12, 1685. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.D.M.; Hussain, A.; Yusof, Y.; Ker, A.P.J. State-of-the-Art and Energy Management System of Lithium-Ion Batteries in Electric Vehicle Applications: Issues and Recommendations. IEEE Access 2018, 6, 19362–19378. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Alvi, M.J.; Kim, H.-J. Towards a Smarter Battery Management System for Electric Vehicle Applications: A Critical Review of Lithium-Ion Battery State of Charge Estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Krishna, G.; Singh, R.; Gehlot, A.; Akram, S.V.; Priyadarshi, N.; Twala, B. Digital Technology Implementation in Battery-Management Systems for Sustainable Energy Storage: Review, Challenges, and Recommendations. Electronics 2022, 11, 2695. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine Learning Applied to Electrified Vehicle Battery State of Charge and State of Health Estimation: State-of-the-Art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Horstmann, B.; Single, F.; Latz, A. Review on multi-scale models of solid-electrolyte interphase formation. Curr. Opin. Electrochem. 2018, 13, 61–69. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Elfouly, T.; Alouani, A.; Massoud, A.M. A Comprehensive Review of Lithium-Ion Batteries Modeling, and State of Health and Remaining Useful Lifetime Prediction. IEEE Access 2022, 10, 119040–119070. [Google Scholar] [CrossRef]
- Timilsina, L.; Badr, P.R.; Hoang, P.H.; Ozkan, G.; Papari, B.; Edrington, C.S. Battery Degradation in Electric and Hybrid Electric Vehicles: A Survey Study. IEEE Access 2023, 11, 42431–42462. [Google Scholar] [CrossRef]
- Ng, M.-F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Aykol, M.; Gopal, C.B.; Anapolsky, A.; Herring, P.K.; van Vlijmen, B.; Berliner, M.D.; Bazant, M.Z.; Braatz, R.D.; Chueh, W.C.; Storey, B.D. Perspective—Combining physics and machine learning to predict battery lifetime. J. Electrochem. Soc. 2021, 168, 030525. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Iqbal, A.; Sibtain, D.; Khalid, M. An Innovative Converterless Solar PV Control Strategy for a Grid Connected Hybrid PV/Wind/Fuel-Cell System Coupled with Battery Energy Storage. IEEE Access 2023, 11, 23245–23259. [Google Scholar] [CrossRef]
- Jayasinghe, A.E.; Fernando, N.; Kumarawadu, S.; Wang, L. Review on Li-ion Battery Parameter Extraction Methods. IEEE Access 2023, 11, 73180–73197. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Qu, C.; Ma, F.; Xu, X.; Yang, J.; Zhang, J.; Zhou, Y.; Shan, T.; Hou, Y. Fault Prognosis and Isolation of Lithium-Ion Batteries in Electric Vehicles Considering Real-Scenario Thermal Runaway Risks. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 88–99. [Google Scholar] [CrossRef]
- Che, Y.; Hu, X.; Lin, X.; Guo, J.; Teodorescu, R. Health prognostics for lithium-ion batteries: Mechanisms, methods, and prospects. Energy Environ. Sci. 2023, 16, 338–371. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Chen, X.; Hong, M.; Hu, C. A deep learning method for online capacity estimation of lithium-ion batteries. J. Energy Storage 2019, 25, 100817. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, G.; Zhen, D.; Gu, F.; Ball, A. A review on online state of charge and state of health estimation for lithium-ion batteries in electric vehicles. Energy Rep. 2021, 7, 5141–5161. [Google Scholar] [CrossRef]
- He, L.; Guo, D. An Improved Coulomb Counting Approach Based on Numerical Iteration for SOC Estimation with Real-Time Error Correction Ability. IEEE Access 2019, 7, 74274–74282. [Google Scholar] [CrossRef]
- You, H.; Zhu, J.; Wang, X.; Jiang, B.; Sun, H.; Wei, X.; Han, G.; Dai, H. The Lithium-ion Battery Nonlinear Aging Knee-Point Prediction Based on Sliding Window with Stacked Long Short-Term Memory Neural Network. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; pp. 206–211. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C.; Jiang, J.; Zhang, W.; Zhang, L.; Wang, Y. Review on state-of-health of lithium-ion batteries: Characterizations, estimations and applications. J. Clean. Prod. 2021, 314, 128015. [Google Scholar] [CrossRef]
- Qiu, X.; Wu, W.; Wang, S. Remaining useful life prediction of lithium-ion battery based on improved cuckoo search particle filter and a novel state of charge estimation method. J. Power Sources 2020, 450, 227700. [Google Scholar] [CrossRef]
- Zhou, W.; Lu, Q.; Zheng, Y. Review on the selection of health indicator for lithium ion batteries. Machines 2022, 10, 512. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; Groenewald, J.; McGordon, A.; Widanage, W.D.; Marco, J. Accelerated internal resistance measurements of lithium-ion cells to support future end-of-life strategies for electric vehicles. Batteries 2018, 4, 49. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Yang, G.; Geng, H. An internal resistance estimation method of lithium-ion batteries with constant current tests considering thermal effect. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7629–7634. [Google Scholar] [CrossRef]
- Shah, A.; Shah, K.; Shah, C.; Shah, M. State of charge, remaining useful life and knee point estimation based on artificial intelligence and Machine learning in lithium-ion EV batteries: A comprehensive review. Renew. Energy Focus 2022, 42, 146–164. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; Shen, W. On-board diagnosis of soft short circuit fault in lithium-ion battery packs for electric vehicles using an extended Kalman filter. CSEE J. Power Energy Syst. 2020, 8, 258–270. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, J.; Fan, Y. Cascade Storage Power Station Lithium Battery SOC Estimation Based on PID-EKF Algorithm. In Proceedings of the 2023 5th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 23–26 March 2023; pp. 1552–1557. [Google Scholar] [CrossRef]
- Jin, S.; Yang, X.; Wang, C.; Wang, S.; Store, D.-I. A novel robust back propagation neural network-dual extended Kalman filter model for state-of-charge and state-of-health co-estimation of lithium ion batteries. In Proceedings of the 2023 IEEE PES Conference on Innovative Smart Grid Technologies—Middle East (ISGT Middle East), Abu Dhabi, United Arab Emirates, 12–15 March 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Wankhede, Y.E.; Rana, S.; Kazi, F. SoC Estimation of Battery in FCHEVs Using Reformulated Constrained Unscented Kalman Filter. In Proceedings of the 2022 1st International Conference on Sustainable Technology for Power and Energy Systems (STPES), Srinagar, India, 4–6 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Hou, Z.; Qu, Q.; Yang, T.; Su, H.; Zheng, Y. Remaining Useful Life Prediction of Lithium-ion Battery based on Dual Particle Filter. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 5374–5379. [Google Scholar] [CrossRef]
- Da, Y.; Wan, Y.; He, W. An Adaptive Central Difference H-infinity Filter Based SOC Estimation for Lithium-ion Batteries with Measurement Noise. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 1402–1407. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zhang, F.; Liu, G.; Fang, L.; Wang, H. Estimation of battery state of charge with H∞ observer: Applied to a robot for inspecting power transmission lines. IEEE Trans. Ind. Electron. 2011, 59, 1086–1095. [Google Scholar] [CrossRef]
- Vedel, P.; Hubka, L. Linear Regression Model of Li-Ion Battery Capacity Losing Rate Based on Equivalent Circuit Model Parameters and Operation Modes. In Proceedings of the 2022 International Conference on Smart Systems and Technologies (SST), Osijek, Croatia, 19–21 October 2022; pp. 243–248. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Stroe, D.-I.; Zou, C.; Fernandez, C.; Yu, C. An accurate time constant parameter determination method for the varying condition equivalent circuit model of lithium batteries. Energies 2020, 13, 2057. [Google Scholar] [CrossRef]
- Saleem, K.; Mehran, K.; Ali, Z. Online reduced complexity parameter estimation technique for equivalent circuit model of lithium-ion battery. Electr. Power Syst. Res. 2020, 185, 106356. [Google Scholar] [CrossRef]
- Wu, L.; Pang, H.; Jin, J.; Geng, Y.; Liu, K. A review of SOC estimation methods for Lithium-Ion batteries based on electro-chemical model. Trans. China Electrotech. Soc. 2022, 37, 1703–1725. [Google Scholar] [CrossRef]
- Han, S.; Tang, Y.; Rahimian, S.K. A numerically efficient method of solving the full-order pseudo-2-dimensional (P2D) Li-ion cell model. J. Power Sources 2021, 490, 229571. [Google Scholar] [CrossRef]
- Guo, M.; Sikha, G.; White, R.E. Single-particle model for a lithium-ion cell: Thermal behavior. J. Electrochem. Soc. 2011, 158, A122–A132. [Google Scholar] [CrossRef]
- Schmidt, A.P.; Bitzer, M.; Imre, W.; Guzzella, L. Experiment-driven electrochemical modeling and systematic parameterization for a lithium-ion battery cell. J. Power Sources 2010, 195, 5071–5080. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Deng, L.; Cui, Z.; Lyu, C.; Wang, L.; Pecht, M. Aging modes analysis and physical parameter identification based on a simplified electrochemical model for lithium-ion batteries. J. Energy Storage 2020, 31, 101538. [Google Scholar] [CrossRef]
- Liu, G.; Lu, L.; Fu, H.; Hua, J.; Li, J.; Ouyang, M.; Wang, Y.; Xue, S.; Chen, P. A comparative study of equivalent circuit models and enhanced equivalent circuit models of lithium-ion batteries with different model structures. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; Van Den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Xing, Y.; Miao, Q.; Tsui, K.-L.; Pecht, M. Prognostics and health monitoring for lithium-ion battery. In Proceedings of the Proceedings of 2011 IEEE International Conference on Intelligence and Security Informatics, Beijing, China, 10–12 July 2011; pp. 242–247. [Google Scholar] [CrossRef]
- Penna, J.A.M.; Nascimento, C.L.; Rodrigues, L.R. Health monitoring and remaining useful life estimation of lithium-ion aeronautical batteries. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–12. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Samuel, A.L. Programming computers to play games. Adv. Comput. 1960, 1, 165–192. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997; Volume 1. [Google Scholar]
- Muggleton, S.; de Raedt, L. Inductive Logic Programming: Theory and methods. J. Log. Program. 1994, 19, 629–679. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar] [CrossRef]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Amos, B. Tutorial on Amortized Optimization. Found. Trends® Mach. Learn. 2023, 16, 592–732. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar] [CrossRef]
- Lipson, H.; Pollack, J.B. Automatic design and manufacture of robotic lifeforms. Nature 2000, 406, 974–978. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Hofstadter, D.R. Analogy as the core of cognition. In The Analogical Mind: Perspectives from Cognitive Science; MIT Press: Cambridge, MA, USA, 2001; pp. 499–538. [Google Scholar] [CrossRef]
- CALCE Battery Group. Available online: https://web.calce.umd.edu/batteries/data.htm (accessed on 27 April 2024).
- Dawn Mcintosh, Li-Ion Battery Aging Datasets. Available online: https://c3.ndc.nasa.gov/dashlink/resources/133/ (accessed on 27 April 2024).
- Battery Archive. Available online: https://www.batteryarchive.org/study_summaries.html (accessed on 27 April 2024).
- Kim, E.; Kim, M.; Kim, J.; Kim, J.; Park, J.-H.; Kim, K.-T.; Park, J.-H.; Kim, T.; Min, K. Data-Driven Methods for Predicting the State of Health, State of Charge, and Remaining Useful Life of Li-Ion Batteries: A Comprehensive Review. Int. J. Precis. Eng. Manuf. 2023, 24, 1281–1304. [Google Scholar] [CrossRef]
- Bills, A.; Viswanathan, V.; Sripad, S.; Frank, E.; Charles, D.; Fredericks, W.L. Carnegie Mellon University Kilthub Dataset. Available online: https://kilthub.cmu.edu/articles/dataset/eVTOL_Battery_Dataset/14226830 (accessed on 27 April 2024).
- Cui, Z.; Wang, L.; Li, Q.; Wang, K. A comprehensive review on the state of charge estimation for lithium-ion battery based on neural network. Int. J. Energy Res. 2021, 46, 5423–5440. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Yang, R.; Shen, W.; Sun, F. State-of-charge estimation of lithium-ion battery using an improved neural network model and extended Kalman filter. J. Clean. Prod. 2019, 234, 1153–1164. [Google Scholar] [CrossRef]
- Bu, C.; Li, F.; Yin, K.; Pang, J.; Wang, L.; Wang, K. Research progress and prospect of triboelectric nanogenerators as self-powered human body sensors. ACS Appl. Electron. Mater. 2020, 2, 863–878. [Google Scholar] [CrossRef]
- Kashkooli, A.G.; Fathiannasab, H.; Mao, Z.; Chen, Z. Application of artificial intelligence to state-of-charge and state-of-health estimation of calendar-aged lithium-ion pouch cells. J. Electrochem. Soc. 2019, 166, A605–A615. [Google Scholar] [CrossRef]
- You, G.-W.; Park, S.; Oh, D. Real-time state-of-health estimation for electric vehicle batteries: A data-driven approach. Appl. Energy 2016, 176, 92–103. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Li, M.; Wang, Z.; Hu, C. Deep convolutional neural networks with ensemble learning and transfer learning for capacity estimation of lithium-ion batteries. Appl. Energy 2020, 260, 114296. [Google Scholar] [CrossRef]
- Affanni, A.; Bellini, A.; Concari, C.; Franceschini, G.; Lorenzani, E.; Tassoni, C. EV battery state of charge: Neural network based estimation. In Proceedings of the IEEE International Electric Machines and Drives Conference, 2003, IEMDC’03, Madison, WI, USA, 1–4 June 2003; Volume 2, pp. 684–688. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.; Chen, Z. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks. Appl. Energy 2016, 173, 134–140. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, T.; Yu, B.; Liu, Y. A method for interval prediction of satellite battery state of health based on sample entropy. IEEE Access 2019, 7, 141549–141561. [Google Scholar] [CrossRef]
- Li, G.; Shi, J. On comparing three artificial neural networks for wind speed forecasting. Appl. Energy 2010, 87, 2313–2320. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, Z. A method for state-of-charge estimation of Li-ion batteries based on multi-model switching strategy. Appl. Energy 2015, 137, 427–434. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, M.; Du, D.; Li, Y.; Fei, M.; Guo, Y.; Li, K. State-of-charge estimation of lithium-ion battery pack based on improved RBF neural networks. Complexity 2020, 2020, 8840240. [Google Scholar] [CrossRef]
- Wu, J.; Fang, L.; Dong, G.; Lin, M. State of health estimation of lithium-ion battery with improved radial basis function neural network. Energy 2023, 262, 125380. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF. Int. J. Electr. Power Energy Syst. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Shahriari, M.; Farrokhi, M. Online state-of-health estimation of VRLA batteries using state of charge. IEEE Trans. Ind. Electron. 2012, 60, 191–202. [Google Scholar] [CrossRef]
- Alfi, A.; Charkhgard, M.; Zarif, M.H. Hybrid state of charge estimation for lithium-ion batteries: Design and implementation. IET Power Electron. 2014, 7, 2758–2764. [Google Scholar] [CrossRef]
- Charkhgard, M.; Gholizade-Narm, H. Lithium-ion battery state of charge estimation based on square-root unscented Kalman filter. IET Power Electron. 2013, 6, 1833–1841. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Park, M.; Seo, M.; Song, Y.; Kim, S.W. Capacity estimation of Li-ion batteries using constant current charging voltage with multilayer perceptron. IEEE Access 2020, 8, 180762–180772. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.; Zhang, X.; Chen, Z. A novel state of health estimation method of Li-ion battery using group method of data handling. J. Power Sources 2016, 327, 457–464. [Google Scholar] [CrossRef]
- Song, L.; Zhang, K.; Liang, T.; Han, X.; Zhang, Y. Intelligent state of health estimation for lithium-ion battery pack based on big data analysis. J. Energy Storage 2020, 32, 101836. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D.; Yang, Y.; Liu, F. More intelligent and robust estimation of battery state-of-charge with an improved regularized extreme learning machine. Eng. Appl. Artif. Intell. 2021, 104, 104407. [Google Scholar] [CrossRef]
- Chen, L.; Wang, H.; Liu, B.; Wang, Y.; Ding, Y.; Pan, H. Battery state-of-health estimation based on a metabolic extreme learning machine combining degradation state model and error compensation. Energy 2020, 215, 119078. [Google Scholar] [CrossRef]
- Pan, H.; Lu, Z.; Wang, H.; Wei, H.; Chen, L. Novel battery state-of-health online estimation method using multiple health indicators and an extreme learning machine. Energy 2018, 160, 466–477. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, F.; Kang, J.; Du, C. State of health estimation based on OS-ELM for lithium-ion batteries. Int. J. Electrochem. Sci. 2017, 12, 6895–6907. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-charge estimation of lithium-ion batteries using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Ren, X.; Liu, S.; Yu, X.; Dong, X. A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 2021, 234, 121236. [Google Scholar] [CrossRef]
- Ma, Y.; Shan, C.; Gao, J.; Chen, H. A novel method for state of health estimation of lithium-ion batteries based on improved LSTM and health indicators extraction. Energy 2022, 251, 123973. [Google Scholar] [CrossRef]
- Tan, Y.; Zhao, G. Transfer learning with long short-term memory network for state-of-health prediction of lithium-ion batteries. IEEE Trans. Ind. Electron. 2019, 67, 8723–8731. [Google Scholar] [CrossRef]
- Strange, C.; dos Reis, G. Prediction of future capacity and internal resistance of Li-ion cells from one cycle of input data. Energy AI 2021, 5, 100097. [Google Scholar] [CrossRef]
- Crocioni, G.; Pau, D.; Delorme, J.-M.; Gruosso, G. Li-ion batteries parameter estimation with tiny neural networks embedded on intelligent iot microcontrollers. IEEE Access 2020, 8, 122135–122146. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, Y.; Cheng, C.; Zhou, B.; Hu, P.; Yuan, Y. Remaining useful life prediction of lithium-ion batteries based on false nearest neighbors and a hybrid neural network. Appl. Energy 2019, 253, 113626. [Google Scholar] [CrossRef]
- Fan, Y.; Xiao, F.; Li, C.; Yang, G.; Tang, X. A novel deep learning framework for state of health estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101741. [Google Scholar] [CrossRef]
- Rezvani, M.; AbuAli, M.; Lee, S.; Lee, J.; Ni, J. A comparative analysis of techniques for electric vehicle battery prognostics and health management (PHM). In Proceedings of the Commercial Vehicle Engineering Congress, Rosemont, IL, USA, 13–14 September 2011; SAE Technical Paper. Volume 191, pp. 1–9. [Google Scholar] [CrossRef]
- Rufus, F.; Lee, S.; Thakker, A. Health monitoring algorithms for space application batteries. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, J.; Saxena, A.; Goebel, K.; Saha, B.; Wang, W. An adaptive recurrent neural network for remaining useful life prediction of lithium-ion batteries. In Proceedings of the Annual Conference of the PHM Society 2010, Portland, OR, USA, 10–16 October 2010. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Ker, P.J.; Mahlia, T.M.I.; Mansor, M.; Ayob, A.; Saad, M.H.; Dong, Z.Y. Toward enhanced state of charge estimation of lithium-ion batteries using optimized machine learning techniques. Sci. Rep. 2020, 10, 4687. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Bermejo, D.; Fraile-Ardanuy, J.; Castaño-Solis, S.; Merino, J.; Álvaro-Hermana, R. Using dynamic neural networks for battery state of charge estimation in electric vehicles. Procedia Comput. Sci. 2018, 130, 533–540. [Google Scholar] [CrossRef]
- Andre, D.; Nuhic, A.; Soczka-Guth, T.; Sauer, D. Comparative study of a structured neural network and an extended Kalman filter for state of health determination of lithium-ion batteries in hybrid electric vehicles. Eng. Appl. Artif. Intell. 2013, 26, 951–961. [Google Scholar] [CrossRef]
- Rupanwong, K.; Kittiratsatcha, S.; Polmai, S. Comparison of Extended Kalman Filter and Long Short-Term Memory Neural Network for State of Charge Estimation of Lithium-Ion Battery. In Proceedings of the 2023 9th International Conference on Engineering, Applied Sciences, and Technology (ICEAST), Vientiane, Laos, 1–4 June 2023; pp. 55–58. [Google Scholar] [CrossRef]
- Sun, S.; Lin, Q.; Li, H.; Zhan, Y.; Dai, Y. Simultaneous Estimation of SOH and SOC of Batteries Based on SVM. In Proceedings of the 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 9–12 December 2022; pp. 1934–1938. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, Y.; Lu, S.; Wang, J.; Zhang, X. Remaining Useful Life Prediction of Lithium-Ion Batteries Using Support Vector Regression Optimized by Artificial Bee Colony. IEEE Trans. Veh. Technol. 2019, 68, 9543–9553. [Google Scholar] [CrossRef]
- Meng, J.; Cai, L.; Luo, G.; Stroe, D.-I.; Teodorescu, R. Lithium-ion battery state of health estimation with short-term current pulse test and support vector machine. Microelectron. Reliab. 2018, 88, 1216–1220. [Google Scholar] [CrossRef]
- Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Doo, S. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Tan, X.; Tan, Y.; Zhan, D.; Yu, Z.; Fan, Y.; Qiu, J.; Li, J. Real-time state-of-health estimation of lithium-ion batteries based on the equivalent internal resistance. IEEE Access 2020, 8, 56811–56822. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W. State-of-health estimation based on differential temperature for lithium ion batteries. IEEE Trans. Power Electron. 2020, 35, 10363–10373. [Google Scholar] [CrossRef]
- Cai, L.; Meng, J.; Stroe, D.-I.; Peng, J.; Luo, G.; Teodorescu, R. Multiobjective optimization of data-driven model for lithium-ion battery SOH estimation with short-term feature. IEEE Trans. Power Electron. 2020, 35, 11855–11864. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, J.; Wang, H.; Yang, C. A new lithium-ion battery SOH estimation method based on an indirect enhanced health indicator and support vector regression in PHMs. Energies 2020, 13, 830. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W. A support vector regression-based prognostic method for li-ion batteries working in variable operating states. In Proceedings of the 2016 Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Hu, J.; Lin, H.; Li, X.; Jiang, C.; Qiu, X.; Li, W. State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Sources 2014, 269, 682–693. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, X.; Sun, M.; Shen, J.; Xiao, R. State of health estimation of lithium-ion batteries based on fixed size LS-SVM. In Proceedings of the 2018 IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 27–30 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Pattipati, B.; Sankavaram, C.; Pattipati, K. System identification and estimation framework for pivotal automotive battery management system characteristics. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2011, 41, 869–884. [Google Scholar] [CrossRef]
- Weng, C.; Cui, Y.; Sun, J.; Peng, H. On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression. J. Power Sources 2013, 235, 36–44. [Google Scholar] [CrossRef]
- Ipek, E.; Eren, M.K.; Yilmaz, M. State-of-charge estimation of li-ion battery cell using support vector regression and gradient boosting techniques. In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Turkey, 27–29 August 2019; pp. 604–609. [Google Scholar] [CrossRef]
- Li, R.; Liu, P.; Li, K.; Zhang, X. Research on Retired Battery Equalization System Based on Multi-Objective Adaptive Fuzzy Control Algorithm. IEEE Access 2023, 11, 89535–89549. [Google Scholar] [CrossRef]
- Lin, H.-T.; Liang, T.-J.; Chen, S.-M. The state-of-health diagnosis of Li-Co batteries with fuzzy identification. In Proceedings of the 2012 7th International Power Electronics and Motion Control Conference (IPEMC 2012), Harbin, China, 2–5 June 2012; Volume 4, pp. 2678–2682. [Google Scholar] [CrossRef]
- Kozlowski, J. Electrochemical cell prognostics using online impedance measurements and model-based data fusion techniques. In Proceedings of the 2003 IEEE Aerospace (Cat. No.03TH8652), Big Sky, MT, USA, 8–15 March 2003; Volume 7, pp. 3257–3270. [Google Scholar] [CrossRef]
- Kim, J.; Nikitenkov, D. Fuzzy logic-controlled online state-of-health (SOH) prediction in large format LiMn2O4 cell for energy storage system (ESS) applications. In Proceedings of the 2014 IEEE International Conference on Industrial Technology (IICIT), Busan, Republic of Korea, 26 February–1 March 2014; pp. 474–479. [Google Scholar]
- Zahid, T.; Xu, K.; Li, W.; Li, C.; Li, H. State of charge estimation for electric vehicle power battery using advanced machine learning algorithm under diversified drive cycles. Energy 2018, 162, 871–882. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Gong, J. A combination Kalman filter approach for State of Charge estimation of lithium-ion battery con-sidering model uncertainty. Energy 2016, 109, 933–946. [Google Scholar] [CrossRef]
- Ungurean, L.; Cârstoiu, G.; Micea, M.V.; Groza, V. Battery state of health estimation: A structured review of models, methods and commercial devices. Int. J. Energy Res. 2016, 41, 151–181. [Google Scholar] [CrossRef]
- Ting, T.O.; Man, K.L.; Lim, E.G.; Leach, M. Tuning of Kalman filter parameters via genetic algorithm for state-of-charge estimation in battery management system. Sci. World J. 2014, 2014, 176052. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wang, Z.; Lu, Z.; Li, J.; Ji, B.; Wei, H.; Pan, H. A novel state-of-charge estimation method of lithium-ion batteries combining the grey model and genetic algo-rithms. IEEE Trans. Power Electron. 2017, 33, 8797–8807. [Google Scholar] [CrossRef]
- Lai, X.; Yi, W.; Zheng, Y.; Zhou, L. An all-region state-of-charge estimator based on global particle swarm optimization and improved extended Kalman filter for lithium-ion batteries. Electronics 2018, 7, 321. [Google Scholar] [CrossRef]
- Bian, X.; Wei, Z.; He, J.; Yan, F.; Liu, L. A two-step parameter optimization method for low-order model-based state-of-charge estimation. IEEE Trans. Transp. Electrif. 2020, 7, 399–409. [Google Scholar] [CrossRef]
- Li, R.; Xu, S.; Li, S.; Zhou, Y.; Zhou, K.; Liu, X.; Yao, J. State of charge prediction algorithm of lithium-ion battery based on PSO-SVR cross validation. IEEE Access 2020, 8, 10234–10242. [Google Scholar] [CrossRef]
- Qin, T.; Zeng, S.; Guo, J. Robust prognostics for state of health estimation of lithium-ion batteries based on an improved PSO–SVR model. Microelectron. Reliab. 2015, 55, 1280–1284. [Google Scholar] [CrossRef]
- Allirani, S.; Pooja, K.; Soundarya, E.; Nair, S.S. Li-ion Battery Life Estimation using K-Nearest Neighbor Algorithm. In Proceedings of the 2023 2nd International Conference on Edge Computing and Applications (ICECAA), Namakkal, India, 19–21 July 2023; pp. 1606–1610. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M.; Pecht, M. Remaining useful life estimation of lithium-ion cells based on k-nearest neighbor regression with differential evolution optimization. J. Clean. Prod. 2020, 249, 119409. [Google Scholar] [CrossRef]
- Liu, K.; Peng, Q.; Che, Y.; Zheng, Y.; Li, K.; Teodorescu, R.; Widanage, D.; Barai, A. Transfer learning for battery smarter state estimation and ageing prognostics: Recent progress, challenges, and prospects. Adv. Appl. Energy 2023, 9, 100117. [Google Scholar] [CrossRef]
- Che, Y.; Zheng, Y.; Wu, Y.; Sui, X.; Bharadwaj, P.; Stroe, D.-I.; Yang, Y.; Hu, X.; Teodorescu, R. Data efficient health prognostic for batteries based on sequential information-driven probabilistic neural network. Appl. Energy 2022, 323, 119663. [Google Scholar] [CrossRef]
- Che, Y.; Stroe, D.-I.; Hu, X.; Teodorescu, R. Semi-Supervised Self-Learning-Based Lifetime Prediction for Batteries. IEEE Trans. Ind. Inform. 2022, 19, 6471–6481. [Google Scholar] [CrossRef]
- Che, Y.; Deng, Z.; Li, P.; Tang, X.; Khosravinia, K.; Lin, X.; Hu, X. State of health prognostics for series battery packs: A universal deep learning method. Energy 2021, 238, 121857. [Google Scholar] [CrossRef]
- Che, Y.; Deng, Z.; Lin, X.; Hu, L.; Hu, X. Predictive Battery Health Management with Transfer Learning and Online Model Correction. IEEE Trans. Veh. Technol. 2021, 70, 1269–1277. [Google Scholar] [CrossRef]
- Yu, J. State of health prediction of lithium-ion batteries: Multiscale logic regression and Gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Cheng, Y.; Son, D.; Wang, Z.; Lu, C.; Zerhouni, N. An ensemble prognostic method for lithium-ion battery capacity estimation based on time-varying weight allocation. Appl. Energy 2020, 266, 114817. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Feng, X. An ensemble learning-based data-driven method for online state-of-health estimation of lithium-ion batteries. IEEE Trans. Transp. Electrif. 2020, 7, 422–436. [Google Scholar] [CrossRef]
- Meng, J.; Cai, L.; Stroe, D.-I.; Ma, J.; Luo, G.; Teodorescu, R. An optimized ensemble learning framework for lithium-ion battery state of health estimation in energy storage system. Energy 2020, 206, 118140. [Google Scholar] [CrossRef]
- Lin, H.-T.; Liang, T.-J.; Chen, S.-M. Estimation of battery state of health using probabilistic neural network. IEEE Trans. Ind. Inform. 2012, 9, 679–685. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Xiong, Q.; Ding, B.; Hou, J.; Luo, D.; Rong, Y.; Li, S. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network. J. Power Sources 2020, 459, 228069. [Google Scholar] [CrossRef]
- Zhang, S.; Zhai, B.; Guo, X.; Wang, K.; Peng, N.; Zhang, X. Synchronous estimation of state of health and remaining useful lifetime for lithium-ion battery using the incremental capacity and artificial neural networks. J. Energy Storage 2019, 26, 100951. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Landi, M.; Gross, G. Measurement techniques for online battery state of health estimation in vehicle-to-grid applications. IEEE Trans. Instrum. Meas. 2014, 63, 1224–1234. [Google Scholar] [CrossRef]
- Tsang, K.; Chan, W. State of health detection for Lithium ion batteries in photovoltaic system. Energy Convers. Manag. 2013, 65, 7–12. [Google Scholar] [CrossRef]
- Andre, D.; Appel, C.; Soczka-Guth, T.; Sauer, D.U. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries. J. Power Sources 2013, 224, 20–27. [Google Scholar] [CrossRef]
- Wang, X.; Hao, Z.; Chen, Z.; Zhang, J. Joint Prediction of Li-ion Battery State of Charge and State of Health Based on the DRSN-CW-LSTM Model. IEEE Access 2023, 11, 70263–70273. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, D.; Peng, Y.; Peng, X. Dynamic battery remaining useful life estimation: An on-line data-driven approach. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Graz, Austria, 13–16 May 2012; pp. 2196–2199. [Google Scholar] [CrossRef]
- Berecibar, M.; Devriendt, F.; Dubarry, M.; Villarreal, I.; Omar, N.; Verbeke, W.; Van Mierlo, J. Online state of health estimation on NMC cells based on predictive analytics. J. Power Sources 2016, 320, 239–250. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, M.; Shu, X.; Xiao, R.; Shen, J. Online state of health estimation for lithium-ion batteries based on support vector machine. Appl. Sci. 2018, 8, 925. [Google Scholar] [CrossRef]
- Wang, F.-K.; Mamo, T. A hybrid model based on support vector regression and differential evolution for remaining useful lifetime prediction of lithium-ion batteries. J. Power Sources 2018, 401, 49–54. [Google Scholar] [CrossRef]
- Xing, L.; Liu, X.; Luo, W.; Wu, L. State of Health Estimation for Lithium-Ion Batteries Using IAO–SVR. World Electr. Veh. J. 2023, 14, 122. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Sources 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Li, J.; Liu, M. State-of-charge estimation of lithium-ion batteries using composite multi-dimensional features and a neural network. IET Power Electron. 2019, 12, 1470–1478. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Saad, M.H.M.; Ayob, A.; Blaabjerg, F. State of charge estimation for lithium-ion battery using recurrent NARX neural network model based lighting search algorithm. IEEE Access 2018, 6, 28150–28161. [Google Scholar] [CrossRef]
- Ghosh, N.; Garg, A.; Panigrahi, B.; Kim, J. An Evolving Quantum Fuzzy Neural Network for online State-of-Health estimation of Li-ion cell. Appl. Soft Comput. 2023, 143, 110263. [Google Scholar] [CrossRef]
- Deng, Z.; Lin, X.; Cai, J.; Hu, X. Battery health estimation with degradation pattern recognition and transfer learning. J. Power Sources 2022, 525, 231027. [Google Scholar] [CrossRef]
- Ye, Z.; Yu, J.; Mao, L. Multisource Domain Adaption for Health Degradation Monitoring of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2021, 7, 2279–2292. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).