Abstract
A nanonet consisting of ultrathin Ni nanowires (diameter <4 nm) and Ni nanoballs (diameter <20 nm) has been grown through laser ablation of a Ni target in superfluid helium. At a low Ni concentration, the nanonet consists mainly of nanowires and manifests a rectangular magnetic hysteresis loop, while an increase in the Ni concentration results in an increase in both the concentration and diameter of the nanoballs. A decrease in hysteresis loop rectangularity is observed as the concentration of the nanoball increases. We show that the composition of the system can be determined from the changes in the magnetic hysteresis loop and the temperature dependence of magnetization. The significance of the work consists of the observation of evolution of magnetic properties of the ferromagnetic nanonet, while its composition varies from nanowires to a combined nanowires–nanoballs system.
1. Introduction
Magnetic nanowires and nanoballs [1,2] are widely applied in medicine [3,4] spintronics [5,6] and data storage [7]. Ni nanowires show very attractive properties in many applications. Recently, stretchable strain sensors based on Ni nanowires embedded in soft elastomeric materials were proposed [8]. A flexible strain sensor based on a sandwich-structured Ni-polymer nanocomposite detects tensile strain since the resistance of the conductive Ni network increases when the device is stretched. A Ni nano network can be used in smart sensors for next generation robotics as well as for human–machine interfacing applications including the magnetic sensor industry [8,9,10].
Ferromagnetic Ni nanowires attract growing attention in medical applications [9,10] due to the anisotropy of their physical properties. An increased surface-to-volume ratio is necessary for drug delivery or immunoassays because the small diameter of nanowires provides their penetration through narrow capillaries. The high remnant magnetization of Ni provides effective magnetic manipulations in the absence of external magnetic field. This provides deeper penetration of magnetic drug targets inside living bodies. Cell guidance and cell magnetic separation become possible in the presence of Ni nanowires. The magnetic anisotropy of Ni nanowires is mainly controlled by shape factor.
For this reason, the application of torque in a relatively weak external magnetic field can be used in cell therapy and the field controlling spatial organization of cells. Though, most of papers are devoted to nanowires of a 10–100-nanometer diameter [8,9,10], we report nanonetwork, consisting of nanowires of extremely low diameter, ~5 nm.
We use laser ablation in superfluid helium (He II) [11]. This method is based on nanowire growth in He II quantum vortices (Figure 1), which are known as one-dimensional excitations appearing in liquid helium. When metal particles and clusters are attracted into the core of the vortex, their motion becomes limited by Bernoulli force [12]. The axial direction along the axis of the vortex becomes favorable, providing nanowire growth. The resulting diameter of transition metal nanowires, ~2–5 nm, is defined by the thermophysical parameters of the material [13,14]. These parameters are similar for many alloys and metals conventional for the creation of nanowires in liquid He II and provide the universality of the method. Laser ablation in He II results in the formation of nanoballs, the amount and size of which increase with ablation time and Ni concentration (Figure 2). The origin of the nanowires’ and nanoballs’ coexistence and their development with ablation time are unknown.
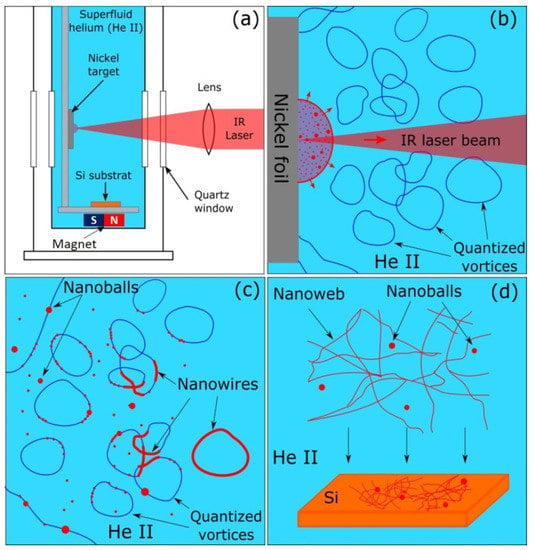
Figure 1.
(a) Cryostat equipped with laser focusing system, quartz window, Ni target, permanent magnet and Si substrate covered with TEM grid; (b) Laser induced evaporation of the Ni accompanied by creation of quantum vortices in He II; (c) Ni atoms and clusters captured by vortices; (d) Elongated nanowire segments cross and result in net, containing nanoballs. All products attracted by permanent magnet are deposited on the Si substrate.
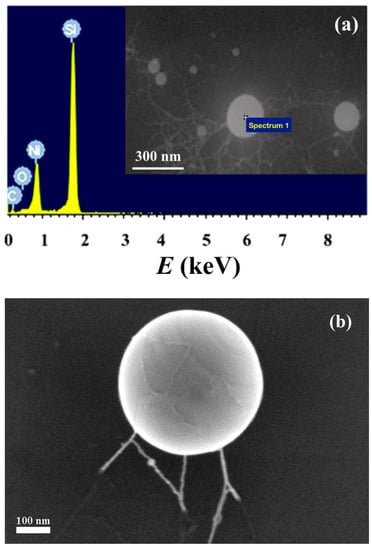
Figure 2.
(a) EDX spectrum of a separated nanoball. SEM image is shown in the right inset; (b) morphology of the large ball formed by microwires.
The importance of the analysis of ferromagnetic nanonets corresponds to the modern trend in magnetic logic devices, where great attention of specialists is focused on objects simulating neurophysical systems [15,16]. The galvanic and magnetic responses of the artificial metallic net can be used for the development of a new kind of calculation systems, which satisfy the requirements of artificial intelligence. A series of modern investigations of magnetic nanonets are presented in [17,18,19]. An artificial nanonet is applied for capturing rare living cells from mixtures [20]. An artificial neuron and synapse realized in antiferromagnet/ferromagnet heterostructures are reported in [21]. A ferromagnetic nanonet is an artificial simulation of new solutions of differential equations in mathematics, where stationary configurations of the magnetic moment in a network of ferromagnetic nanowires were found [22].
Our work is aimed at visualizing the gradual transformation of the morphology of the Ni nanonet and analyzing the simultaneous changes in the network magnetic properties with an increasing duration of laser ablation.
2. Results
An SEM image of the large ball selected for the demonstration of fine details of its surface relief at a later stage of ablation (1 h) is shown in Figure 2b. The share of such large particles is very small, and their contribution to size histogram is negligible. Similar relief on the ball surface can be distinguished in nanoballs of smaller diameters. Figure 2b allows one to conclude that nanoballs and nanowires are not independently grown particles. The wrapping of the round Ni nuclei in curling nanowires is a possible mechanism of the growth of the balls.
A TEM image of the Ni networks without balls at the early stage of 10 min ablation (Figure 3a) and an SEM image of continuous nanowires network containing balls at the later stage of 20–60 min ablation (Figure 3b–d) allow one to judge on the evolution of the system as the laser irradiation time and corresponding amount of Ni increase. Figure 3c,d corresponds to the selected areas electron diffraction (SAED) of the parts of the networks corresponding to nanowires and nanoballs. No point reflexes can be found in SAED patterns of the nanowire (Figure 3c), while clear patterns appear when the SAED of the nanoballs is recorded (Figure 3d). Thus, the polycrystalline structure of the nanoballs and the highly disordered amorphous or nanocrystalline structure of nanowires are identified. According to multiple TEM images of different parts of the net, 2260 free nanowire segments and 70 balls have been treated statistically. The corresponding distribution of lengths of free Ni nanowires segments (Figure 3e) and the distribution of nanoballs diameters (Figure 3f) have been plotted. Statistical analysis of the nanowires and the nanoballs shows that both distributions follow the lognormal function (solid lines in Figure 3e,f). The distributions indicate a wide enough scattering of geometrical sizes correspondingly to the chaotic process of the Ni distribution between He vortexes. Crystalline structure in the balls (Figure 3d) suggests that they cannot consist of amorphous nanowires (Figure 3c). Therefore, there are the following two mechanisms for increasing the size of the balls: (1) the growth of polycrystalline balls nucleated during ablation due to the absorption of nickel; (2) the winding of amorphous nanowires onto the nanoballs generated by ablation. It is reasonable to suppose that amorphous nanowires are formed at a very high cooling rate in He vortexes, while polycrystalline nanoballs are grown at a lower cooling rate in the He bulk. The series of net images used for statistical calculations are presented in Supplementary Materials, Figure S1.
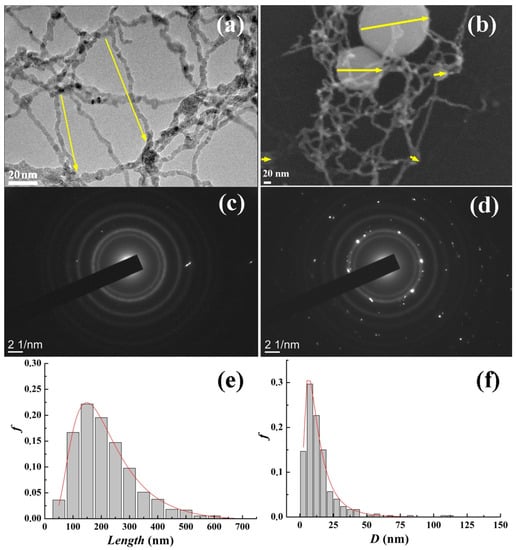
Figure 3.
(a) TEM image of Ni nanowires at early stage of ablation (free segments of nanowires are shown by arrows); (b) SEM image of the net consisting of nanowires and balls at later stage of ablation. Nanoball diameters are marked by arrows; (c) electron diffraction patterns of the sample at early stage of ablation; (d) electron diffraction patterns of the net at later stage of ablation; (e) distribution of lengths of free nanowire segments normalized to their total number at later stage of ablation; (f) distribution of ball diameters normalized to the total number of balls in sample. Solid lines are approximations by lognormal functions.
Images of the network at subsequent stages of laser ablation are presented in Figure 4. Increase in size and number of nanoballs with ablation time can be distinguished.

Figure 4.
TEM images of the network at different stages of ablation: (a,b) Early stage (10 min), (c,d) intermediate stage (30 min), (e,f) later stage (60 min).
Figure 5 presents a series of the hysteresis loops corresponding to the samples obtained at different ablation stages. The amount of Ni grows with ablation time. Field dependences were recorded at 300 K in the in-plane orientation of the magnetic field relative to the flat silicon substrate. The magnetic signal in the out-of-plane orientation is negligibly small. At the “in plane” orientation, there are fragments of nanowires perpendicular and parallel to the field, while at the “out-of-plane” orientation all the nanowires are perpendicular to the magnetic field. Since, in the out-of-plane orientation, the magnetic moment of the sample is lower than in the “in-plane” orientation, one can conclude that the easy magnetization axis of the nanowires is directed along their axis. One can conclude that the magnetic anisotropy of the nanowires is controlled by the shape anisotropy [23].
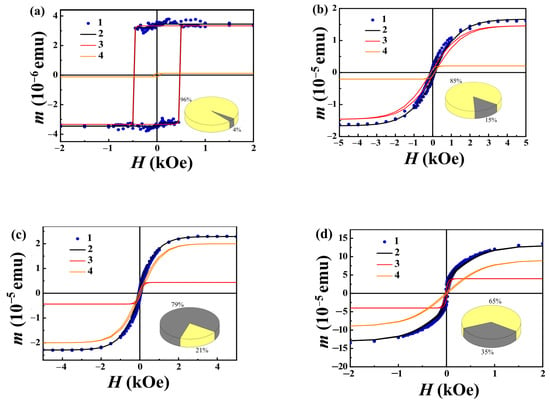
Figure 5.
Magnetic hysteresis at 300 K: (a) in the sample with low Ni concentration (after short (10 min) laser exposure), (b) lower-intermediate Ni concentration (after 20 min laser exposure); (c) upper-intermediate concentration (30 min laser exposure); (d) high Ni concentration after laser ablation for 1 h. Symbols are experimental data, and solid lines are approximation by the two-hysteresis model described in the text. Separate magnetic contributions of the nanowires and nanoballs are shown by thin red solid lines. Relative volume concentrations of the nanowires (yellow) and nanoballs (grey) are shown in the circle diagrams in the bottom insets to the correspondent hysteresis.
Separation of the nanowires’ and nanoballs’ contributions can be reached by analysis of blocking temperatures on the temperature dependences of the magnetic moment recorded for the sample extracted at the later stage of ablation (60 min). At this stage, nanoballs give a valuable contribution, and the volume ratio of nanoballs to nanowires is 85:15, respectively (Figure 5). The sample was cooled from 350 down to 2 K in an applied magnetic field of 1 T (FC mode). After cooling, the temperature dependence of the sample magnetic moment was recorded during heating in a weak magnetic field of 300 Oe (full symbols in Figure 6). If the sample is cooled in a zero magnetic field (ZFC mode), the M(T) curve lies below the FC curve (empty symbols in Figure 6).
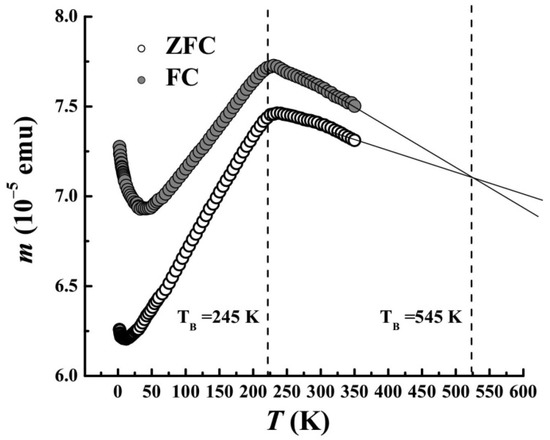
Figure 6.
Temperature dependences of magnetic moment m of the sample cooled in zero magnetic field (ZFC mode is shown by empty symbols) and in magnetic field of 1 T (FC mode is shown by full symbols). Measurement field was 300 Oe in FC and ZFC modes, both. Possible blocking temperatures, which are 245 K for nanowires and 545 K for nanoballs, are shown by vertical dashed lines.
The magnetic moment μ of an individual nanoball was determined using Magnetic Force Microscopy [24]. The measured magnetic force was proportional to the second derivative of the magnetic field near the nanoball surface. The microscope response was directly proportional to the phase shift of the vibrating ferromagnetic Co cantilever scanning in the tapping-lift mode. Distribution of the local stray field of a single nanoball was scanned at different lift h (the distance between the surface and cantilever tip). Images of the nanoball in Atomic Force Microscopy (AFM) and Magnetic Force Microscopy (MFM) modes were recorded (Supplementary Materials, Figure S2a,b, correspondently). In AFM mode, the cantilever height above the surface was scanned, while in MFM mode, the phase shift was recorded as a function of the coordinate (Supplementary Materials, Figure S2c,d, correspondently). The stray field of a single Ni nanoball with saturation magnetization Ms equals the stray field of a point dipole positioned in its center. The lift value h and the proportionality coefficient c−1(h) were measured to calculate the phase shift Δφ of the vibrating cantilever [24] as follows:
Δφ = Ms·π·d3/6·c(h)
We used the calibration algorithm proposed in [24] to measure the calibration coefficient c(h). At h = 50 nm, constant value c = 0.04 A·nm2 was obtained from the dependences of phase shift Δφ on diameter d of nanoballs (Supplementary Materials, Figure S3). Thus, the corresponding magnetic moment of a single nanoball of a 75-nanometer diameter is μ = 4.5 × 10−19 A·m2, which coincides well with the theoretically estimated value μ = Msπd3/6 = 4.2 × 10−19 A·m2 calculated for a single domain nanoball of a 75-nanometer diameter. In addition, we have measured the field dependence of the magnetic moment (Supplementary Materials, Figure S4). Though the approximation of the m(H) dependence and saturation magnetization Ms = 510 emu/cm3 are more or less convenient, the moments of the nanowires or nanoballs cannot be determined separately from the integrated magnetic moment, including contributions of objects of both types.
3. Discussion
Nickel nanowires and nanoparticles are widely reported in the literature. In particular, it is known that amorphous nano- and microwires have a rectangular magnetic hysteresis loop when they have a single-domain magnetic structure [25,26]. This property is called magnetic bistability, meaning that magnetization abruptly changes its direction when the polarity of the applied external field changes [26], while a perpendicular magnetic field results in a sloping hysteresis loop. In a nano-network, where there are segments equiprobably directed in respect to the magnetic field, a change in the sign of the magnetic field can lead to an abrupt switching of the magnetization of those segments, whose direction is parallel to the field.
On the other hand, the resulting network can be presented as a non-continuous thin film, in which the easy magnetization axis lies in the plane of the film, as it is often observed for transition metal films. It is obvious that the above cases (a system of independent chaotically distributed nanowires and a thin discontinuous film) are limiting cases for our system. The real properties of the network lie between these two extreme cases.
When the ablation time and Ni amount increase, the saturation magnetic moment ms also increases, while the coercive field HC decreases (Figure 5). We decomposed the recorded hysteresis loops into two contributions from nanowires and from nanoballs in accordance with the following expression [25]:
where indexes i = 1 and i = 2 correspond to nanowires and balls, respectively; signs «+» and «−» correspond to the descending and ascending parts of the hysteresis loops; ms is the magnetic moment at saturation; H is the external magnetic field; and are the respective coercive fields of nanowires and nanoballs. The adjustment of coefficients pi to reach a true hysteresis loop shape (Figure 5) allowed us to determine the parameters characterizing the rectangularity of the hysteresis loops, p1 = 0.95 for nanowires and p2 = 0.45 for nanoballs. One can see the following two components: a rectangular component belonging to the nanowires and a sloped component corresponding to the nanoballs. We took into account the demagnetizing factors (2/3 for ball and 2π for cylinder) and calculated the relative volume shares of the Ni nanowires and nanoballs at different stages of ablation. In the insets to each hysteresis loop (Figure 5), one can find a circle diagram indicating the relative volume fractions of the nanowires and nanoballs. Simple regularity follows from the comparison of the hysteresis shapes and volume fraction of the nanoballs. The rectangularity of the hysteresis loop decreases as the number of nanoballs grows.
Figure 7 shows the increasing dependence of the saturation magnetic moment mS of the sample for the entire amount of nickel on the ablation time (curve one). Since the saturation magnetization of nickel Ms = 58.6 emu/g (522 emu/cm3) is well known [27], and there is no reason to think that the magnetic moment in saturation can change due to variations in ms, the increase in the Ni amount on the substrate is the only reason for the increasing m. It is impossible to determine the mass of nickel deposited on the substrate in another way since it is very small as compared to the mass of the substrate. We can estimate the order of value of Ni yield using an increase in the absolute value of the magnetic moment of the Si substrate Δm ~ 10−6–10−5 emu caused by network formation. Using the known in advance saturation magnetization Ms = 58.6 emu/g of Ni, we can determine the network mass Δm/Ms ~ 10−8–10−7 g.
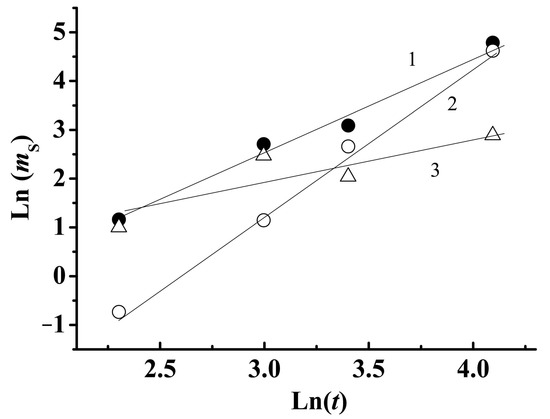
Figure 7.
Dependence of saturation magnetic moment ms of sample on ablation duration (1), dependence of magnetic moment of nanoballs on ablation duration (2), dependence of magnetic moment of nanowires on ablation duration (3).
Since we know the percentage ratio for the volume of nanowires and the volume of nanospheres at each stage of the formation of a nanowire (Figure 5), we have plotted the dependences of the magnetic moment of nanoballs and nanowires on ablation time separately (Figure 7, curves two and three, respectively). It is seen that at the later stage of ablation, the main additional contribution to the magnetic moment m is provided by nanoballs, the number and size of which increase with the ablation time. The straightening of curves 1–3 in ln(m)–ln(t) coordinates (Figure 7) corresponds to the power law of the m(t) dependence m ~ tn, n = 1.36 > 1. If one assumes that the nickel mass increases linearly with the ablation time, the power law corresponds to a situation when the magnetic properties of the system depend on its size. In our experiments, the gradually changing ratio of the number of nanowires to that of nanoballs as well as the formation of a network are possible reasons for a superlinear m(t) dependence.
The magnetic anisotropy of the bulk Ni crystal is Kbulk = −5.12 × 104 erg/cm3 [23,28], and its value diminishes due to spin disorder in the surface layer of a 1–2-nanometer depth. Since shape anisotropy is one order of magnitude higher than crystalline anisotropy constant Ksh = 7.4 × 104 J m−3 = 7.4 × 105 erg/cm−3 and has the opposite sign, an effective anisotropy field is only due to the shape anisotropy in the nickel nanowire. Neglecting crystalline anisotropy, one can obtain an effective anisotropy field of a single segment of nanowire as Heff = 2πMs = 243 kA m−1 = 3042 Oe. This value is quite high in comparison with Hc = 500 Oe obtained in pure nanowires at the early ablation stage (Figure 5a). A similar value of coercive field HC can be obtained from the Neel–Brawn formula allowing one to calculate the coercive field of a single domain particle HC = 2Ksh/Ms = 2874 Oe.
The typical domain wall width in Ni is lw = 2(A/Ksh)1/2 = 30 nm, where A is the exchange stiffness of Ni and thereby the multidomain structure within a single wire is likely to form if the nanowire diameter exceeds 30 nm. In fact, single domain nanowires are usually obtained in wire with a diameter narrowing or of the same order as lw~30 nm and showing coercivity of about 1000 Oe [25,26]. We have obtained coercivity 500 Oe for samples at the early ablation stage, where nanowires 1–2 nm in diameter are presented in the absence of nanoballs. Thus, one should conclude that domain motion should be excluded to explain the decreased Hc value of 500 Oe in the frames of the independent nanowires model. The diminished value of an experimentally determined switching field in the system under study may differ from that predicted theoretically for independent nanowires because non-coherent switching modes, such as curling and fanning, can contribute to magnetization reversal. We should take into account that the wires are connected to each other in our samples. This affects both the demagnetization field and shape factor, and the estimation of the single domain limit. The presence of junctions of nanowires can facilitate propagation of the domain walls or nucleation of the magnetic reversal phase at 500 Oe, i.e., properties of the magnetic network are different from properties of single nanowires.
A simple expression connecting magnetic anisotropy and blocking temperature is valid for nanoballs. We used the formula applicable for the determination of blocking temperature TB in a SQUID magnetometer [29], which is as follows:
Keff·V = 25·kB·TB
This formula allows one to estimate the blocking temperatures TB by substituting effective anisotropy constant Keff and particle volume V into Equation (3). If we substitute the shape anisotropy of nanoballs that decreased due to form factor KA = 2/3πMs = 0.74 · 105 erg/cm3 instead of Keff, and Vball ≈ 4.2 · 10−18 nm3 corresponding to the average diameter of the balls of 5 nm at the later stage of ablation (see histogram in Figure 3f) into Equation (3), we can obtain TB = 548 K. This value coincides well with that found by the extrapolation of the FC and ZFC dependences to their intersection (Figure 6). According to the Neel–Brown theory, in the system of non-interacting separated nanoparticles, the temperature corresponding to the maximum of the M(T) curve is exactly equal to the blocking temperature Tb [30]. The crossing point of the FC and ZFC curves is very close to the blocking temperature, and we assume an approximate equality of these temperatures Tc ≈ Tb neglecting the interparticle interaction.
Thus, 548 K is an average blocking temperature for the nanoballs, while maximum on the ZFC curve near 235 K is obviously blocking temperature for the nanowire network. The blocking temperatures of nanoballs and nanowires are both below the Curie temperature of 631 K for the bulk Ni sample.
4. Materials and Methods
Low-temperature synthesis of the nanowires was carried out in an optical helium cryostat (Supplementary Materials, Figure S5a). Bottom part of the cryostat was equipped with quartz windows. Ni target was placed inside the cryostat in front of the window. The cryostat was filled with liquid helium at 4.2 K, and the temperature decrease down to 1.5 K was attained by pumping. Then, helium was transferred to the superfluid phase. Laser ablation of the Ni target was carried out using an LSB diode-pumped Nd laser with pulse duration of 0.4 ns, pulse repetition of 4 kHz, pulse energy of 0.1 mJ and wavelength of 1.062 μm (Supplementary Materials, Figure S5b). Laser irradiation was focused on the target Ni surface. Duration of laser ablation was varied depending on desirable Ni concentration in helium. We placed a permanent magnet inside the cryostat to attract ferromagnetic products to the Si substrate to obtain larger amount of the products.
In general, the process of growth was the following. Laser-induced evaporation of the Ni target was accompanied by generation of quantum vortices (Figure 1b). At the first stage of ablation, series of isolated individual nanowires were observed at a low concentration of Ni. At the second stage when concentration of the nanowires increased, one observed the formation of a net (Figure 1c). At the third stage at high concentrations of Ni, nanowires reeled to the balls. Ablation products formed a net deposited on silicon substrate of 1 × 1 × 4 mm3 size, which was covered by TEM grid and placed at the bottom of the cryostat (Figure 1d).
Microstructure, morphology and local elemental analyses were carried out using a JEM-2100 transmission electron microscope (TEM) (JEOL, Benelux, Welwyn Garden, England) and a Zeiss Supra 25 scanning electron microscope (SEM) (Carl Zeiss AG, Oberkochen, Germany) with energy dispersive microanalysis (EDX). EDX analysis indicated 99% Ni and 1% O contained in a single Ni ball (Figure 2a). TEM picture of a separate nanoball clearly indicated multiple nanowires reeled on a ball (Figure 2b).
Magnetic properties of the net deposited on Si wafer were recorded using a MPMX 5XL (Quantum Design SQUID magnetometer, Berlin, Germany) at different stages of the structure formation. Magnetic moment of the individual nanoball was recorded using an Integra-Aura (NT MDT, Moscow, Russia) atomic and magnetic force microscope. Two-pass tapping-lift algorithm of MFM scanning provided high accuracy of measurements. We used a standard silicon based MFM LM cantilever covered by thin CoCr film.
5. Conclusions
- (a)
- The laser ablation of Ni in He II supplies Ni to vortexes, where amorphous or nanocrystalline nanowires grow. Crossing nanowires form a continuous ferromagnetic net. In addition to nanowires, the net consists of polycrystalline Ni nanoballs incorporated into the net. The increased ablation time provides an increase in the corresponding Ni concentration in superfluid He and in the resulting number and diameter of nanoballs. Nanowires wrapped around a nanoball have been observed. A possible origin of the nanoball growth with an increase in ablation time is the nucleation of invisible small Ni nuclei and a following increase in their diameters due to the adsorption of Ni nanowires and adatoms from superfluid He.
- (b)
- Analysis of the time dependence of hysteresis shape and comparison with the morphology of the network at each ablation stage allows the contributions of nanowires and nanoballs to the magnetic moment of the network to be distinguished. The nanowire gives perfect rectangular hysteresis, while the hysteresis loop of the nanoballs has a sloped gradual shape at 300 K. The nanowires and nanoballs have different blocking temperatures equal to 235 and 545 K, respectively.
- (c)
- The magneto-crystalline anisotropies of Ni in the nanowires and nanoballs, both, are close to the magnetic anisotropy of the bulk magnetic Ni known in the literature. We have observed a diminished value of coercive field in the nanonet in comparison with a theoretically predicted value for the system of isolated non interacting microwires at the early stage of ablation when nanowires are mainly present. A possible explanation of this deviation is the facilitated nucleation of the magnetic reversal phase at junctions of nanowires.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/magnetochemistry7100139/s1, Figure S1. TEM images of the network used to statistical analysis. Figure S2. Images of separated Ni nanoball recorded in AFM mode (a) and in MFM mode (b). Profiles of the AFM (c) and MFM phase contrasts (d). Figure S3. Dependences of the phase shift Δφ on diameter of nanoballs d with same lift value (h = 50 nm). Figure S4. Field dependence of magnetic moment of nanonet at late stage of ablation, when 85% of Ni volume belong to nanoballs. Solid line is approximation by Langevin function. – Figure S5. (a) Homemade setup for synthesis nanowire network in superfluid He; (b) Solid state LSB diode-pumped Nd laser with 0.4 ns pulse duration, 4 kHz pulse repetition, pulse energy of 0.1 mJ, and wavelength λ = 1.062 μm.
Author Contributions
Conceptualization, O.K.; methodology, O.K.; software, M.S.; validation, M.S., A.K. and V.M.; formal analysis, R.M.; investigation, E.D.; resources, R.M.; data curation, E.D.; writing—original draft preparation, O.K.; writing—review and editing, O.K.; visualization, E.D.; supervision, R.M.; project administration, O.K.; funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Program of the Institute of Problems of Chemical Physics RAS AAAA-A19-119111390022-2 and grant of President of the Russian Federation 2644.2020.2.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in writing the manuscript, or in the decision to publish the results.
References
- Stoner, E.C.; Wohlfarth, E.P. A Mechanism of Magnetic Hysteresis in Heterogeneous Alloys. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 240, 599–642. [Google Scholar]
- Nepijko, S.A.; Wiesendanger, R. Size dependence of magnetic characteristics measured on separate nickel particles. Semicond. Phys. Quantum Electron. Optoelectron. 1999, 2, 5–9. [Google Scholar] [CrossRef]
- Akbarzadeh, A.; Samiei, M.; Davaran, S. Magnetic nanoparticles: Preparation, physical properties, and applications in biomedicine. Nanoscale Res. Lett. 2012, 7, 144. [Google Scholar] [CrossRef] [Green Version]
- Murthy, S.K. Nanoparticles in modern medicine: State of the art and future challenges. Int. J. Nanomed. 2007, 2, 129–141. [Google Scholar]
- Gubin, S.P.; Spichkin, Y.I.; Yurkov, G.Y.; Tishin, A.M. Nanomaterial for high-density magnetic data storage. Russ. J. Inorg. Chem. 2002, 47, 32–67. [Google Scholar]
- Malik, P.; Pandya, S.; Katyal, V. Synthesis and application of magnetic nanomaterials for memory storage devices. Int. J. Adv. Res. 2013, 1, 1. [Google Scholar]
- Karmakar, S.; Kumar, S.; Rinaldi, R.; Maruccio, G. Nano-electronics and spintronics with nanoparticles. J. Phys. Conf. Ser. 2011, 292, 012002. [Google Scholar] [CrossRef]
- Wang, S.; Chen, K.; Wang, M.; Li, H.; Chen, G.; Liu, J.; Xu, L.; Jian, Y.; Meng, C.; Zheng, X.; et al. Controllable synthesis of nickel nanowires and its application in high sensitivity, stretchable strain sensor for body motion sensing. J. Mater. Chem. C 2018, 6, 4737–4745. [Google Scholar] [CrossRef]
- Pondman, K.M.; Wouter Maijenburg, A.; Celikkol, F.B.; Pathan, A.A.; Kishore, U.; ten Hakena, B.; ten Elshof, J.E. Au coated Ni nanowires with tuneable dimensions for biomedical applications. J. Mater. Chem. B 2013, 1, 6129–6136. [Google Scholar] [CrossRef] [Green Version]
- Remadevi, A.; Sreedeviamma, D.K.; Surendran, K.P. Printable Hierarchical Nickel Nanowires for Soft Magnetic Applications. ACS Omega 2018, 3, 14245–14257. [Google Scholar] [CrossRef]
- Gordon, E.B.; Nishida, R.; Nomura, R.; Okuda, Y. Filament formation by impurities embedding into superfluid helium. JETP Lett. 2007, 85, 581–584. [Google Scholar] [CrossRef]
- Mateo, D.; Eloranta, J.; Williams, G.A. Interaction of ions, atoms, and small molecules with quantized vortex lines in superfluid 4 He. J. Chem. Phys. 2015, 142, 064510. [Google Scholar] [CrossRef] [PubMed]
- Gordon, E.B.; Karabulin, A.V.; Matyushenko, V.I.; Sizov, V.D.; Khodos, I.I. Structure of metallic nanowires and nanoclusters formed in superfluid helium. J. Exp. Theor. Phys. 2011, 112, 1061–1070. [Google Scholar] [CrossRef]
- Gordon, E.B.; Stepanov, M.E.; Kulish, M.I.; Karabulin, A.V.; Matyushenko, V.I.; Khodos, I.I. The nanowires growth by laser ablation of metals inside rotating superfluid helium. Laser Phys. Lett. 2019, 16, 026002. [Google Scholar] [CrossRef]
- Kittel, C. Theory of the Structure of Ferromagnetic Domains in Films and Small Particles. Phys. Rev. 1946, 70, 965–971. [Google Scholar] [CrossRef]
- Vajda, F.; Torre, E.D. Characteristics of the complete moving hysteresis mode. J. Appl. Phys. 1993, 73, 5833–5835. [Google Scholar] [CrossRef]
- Bürger, D.; Zhou, S.; Höwler, M.; Ou, X.; Kovacs, G.J.; Reuther, H.; Mücklich, A.; Skorupa, W.; Schmidt, H. Nanonet formation by constitutional supercooling of pulsed laser annealed, Mn-implanted Germanium. In Subsecond Annealing of Advanced Materials; Skorupa, W., Schmidt, H., Eds.; Springer: Cham, Switzerland, 2014; Volume 192, pp. 15–33. [Google Scholar]
- Lin, Y.; Zhou, S.; Sheehan, S.W.; Wang, D. Nanonet-based hematite heteronanostructures for efficient solar water splitting. J. Am. Chem. Soc. 2011, 133, 2398–2401. [Google Scholar] [CrossRef] [PubMed]
- Saitoh, E.; Tanaka, M.; Miyajima, H.; Yamaoka, T. Domain-wall trapping in a ferromagnetic nanowire network. J. Appl. Phys. 2003, 93, 7444–7446. [Google Scholar] [CrossRef]
- Lai, C.; Tsai, W.; Yang, M.; Chou, T.; Chang, Y. Two-dimensional immunomagnetic nano-net for the efficient isolation of circulating tumor cells in whole blood. Nanoscale 2019, 11, 21119–21127. [Google Scholar] [CrossRef]
- Kurenkov, A.; DuttaGupta, S.; Zhang, C.; Fukami, S.; Horio, Y.; Ohno, H. Artificial neuron and synapse realized in an antiferromagnet/ferromagnet heterostructure using dynamics of spin–orbit torque switching. Adv. Mater. 2019, 31, 1900636. [Google Scholar] [CrossRef]
- Labbé, S.; Privat, Y.; Trélat, E. Stability properties of steady-states for a network of ferromagnetic nanowires. J. Differ. Equ. 2012, 253, 1709–1728. [Google Scholar] [CrossRef]
- Vega, V.; Prida, V.M.; García, J.A.; Vazquez, M. Torque magnetometry analysis of magnetic anisotropy distribution in Ni nanowire arrays. Phys. Status Solidi A 2011, 208, 553–558. [Google Scholar] [CrossRef]
- Sievers, S.; Braun, K.-F.; Eberbeck, D.; Gustafsson, S.; Olsson, E.; Werner Schumacher, H.; Siegner, U. Quantitative measurement of the magnetic moment of individual magnetic nanoparticles by magnetic force microscopy. Small 2012, 8, 2675–2679. [Google Scholar] [CrossRef] [Green Version]
- Tian, F.; Huang, Z.P.; Whitmore, L. Fabrication and magnetic properties of Ni nanowire arrays with ultrahigh axial squareness. Phys. Chem. Chem. Phys. 2012, 14, 8537. [Google Scholar] [CrossRef]
- Razeeb, K.M.; Rhen, F.M.F.; Roy, S. Magnetic properties of nickel nanowires: Effect of deposition temperature. J. Appl. Phys. 2009, 105, 083922. [Google Scholar] [CrossRef]
- Danan, H.; Herr, A.; Meyer, A.J.P. New Determinations of the saturation magnetization of nickel and iron. J. Appl. Phys. 1968, 39, 669–670. [Google Scholar] [CrossRef]
- Fedosyuk, V.M.; Danishevskii, A.M.; Kurdyukov, D.A.; Shuman, V.B.; Gordeev, S.K. Magnetic properties of nickel clusters in nanoporous carbon. Phys. Solid State 2003, 45, 1750–1753. [Google Scholar] [CrossRef]
- Dormann, J.L.; Fiorani, D.; Tronc, E. Magnetic relaxation in fine-particle systems. Adv. Chem. Phys. 1997, 98, 283–494. [Google Scholar]
- Madsen, D.E.; Hansen, M.F.; Mørup, S. The correlation between superparamagnetic blocking temperatures and peak temperatures obtained from ac magnetization measurements. J. Phys. Cond. Mat. 2008, 20, 345209. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).