Abstract
We design a one-dimensional magnetoelastic phononic crystal slab composed of the smart magnetostrictive material Terfenol-D and pure tungsten. Band inversion and topological phase transitions are achieved by modifying the geometric parameters of the non-magnetic medium within the unit cell. The emergence of topological interface states within overlapping bandgaps, exhibiting distinct topological properties, along with their robustness against interfacial structural defects, is confirmed. The coupling effects between adjacent topological interface states in a sandwich-like supercell configuration are investigated, and their tunability under external magnetic fields is demonstrated. A Su-Schrieffer-Heeger (SSH) phononic crystal slab system under gradient magnetic fields is proposed. Critically, and in stark contrast to previous static or structurally graded designs, we achieve reconfigurable rainbow trapping of topological interface states solely by reprogramming the gradient magnetic field, leaving the physical structure entirely unchanged. This highly localized, compact, and broadband-tunable topological rainbow trapping system design holds significant promise for applications in elastic energy harvesting, wave filtering, and multi-frequency signal processing.
1. Introduction
With the development of periodic structures and metamaterials, the concept of “rainbow trapping” [1,2,3,4,5], proposed to overcome the limitations between high optical delays and broad bandwidth in optics, has been extensively studied in photonic [6,7,8,9,10] and phononic [11,12,13,14,15,16,17,18] crystal systems. Traditional optical or acoustic rainbow trapping devices [19] are typically based on gradually varying periodic structures, such as introducing graded defects [20,21,22,23,24,25,26] or constructing highly graded harmonic oscillators [27,28]. These devices manipulate and isolate different frequency components by slowing down the group velocity of waves, allowing them to encounter effective local band gaps at different spatial positions to capture energy [29,30].
In recent years, the concept of topological states, originating from condensed matter physics, has become a research hotspot in optical, acoustic, and elastic wave systems due to their unique interface states and topological robustness against structural defects and perturbations. For example, Zhao et al. [31] investigated the existence conditions for multiple topological interface states of Shear Horizontal (SH) waves in one-dimensional quasi-periodic Fibonacci sequence phononic crystal slab. Similarly, Huang et al. [32] studied the existence of topological interface states of SH waves in one-dimensional phononic crystal slab where both localized resonance and Bragg scattering mechanisms coexist. Owing to the local field enhancement characteristics of topological interface states [33], combining them with the concept of rainbow trapping makes one-dimensional topological rainbow systems a promising solution for the localization and collection of elastic energy. To date, topological rainbow phenomena have been separately realized in one-dimensional topological optical and elastic systems. For instance, Sayed Elshahat et al. [34] achieved unidirectional and bidirectional topological rainbow trapping of optical waves in a sandwich structure composed of two topological photonic crystals and a one-dimensional dielectric photonic crystal by modulating the thickness of the dielectric layer. This approach can separate and capture topological photonic states of different frequencies at different positions. Chaplain et al. [35] demonstrated the topological rainbow effect of elastic waves in a super-wedge structure of a one-dimensional graded SSH model and proved its potential superiority over traditional wedge structures in energy harvesting scenarios. However, current methods for achieving topological rainbow effects are limited and constrained by their dependence on structural dimensions. This dependence permanently fixes the operational frequency in practical applications, limiting tunability. For instance, the pioneering works by Elshahat et al. [34] and Chaplain et al. [35] demonstrate remarkable topological rainbow effects; however, their operational bandwidth and frequency are permanently encoded into the physical geometry during fabrication—e.g., through graded thickness or wedge-shaped structures. This inherent lack of post-fabrication tunability severely limits their adaptability to changing operational requirements or environments. In contrast, tunable topological rainbow systems provide a fundamentally higher degree of flexibility and adaptability compared to inflexible, fixed structures. Such systems enable dynamic adjustments in real time to accommodate varying operational conditions and application needs, thereby significantly enhancing performance in elastic energy localization and signal processing. Recently, externally field-tunable functional devices based on magnetostrictive materials such as Terfenol-D have garnered significant attention. These designs offer a novel paradigm for non-contact, real-time acoustic wave manipulation. For instance, Omrani, E. M. et al. [36] reported a magnetically tunable 4 × 2 encoder that modulates the Young’s modulus of Terfenol-D ring resonators by varying the magnetic field strength, achieving an encoding function at approximately 1.74 MHz with an average contrast ratio of 10.16 dB [36], they also demonstrated magnetically adjustable AND/XOR logic gates [37] and a magnetically tunable acoustic add-drop filter [38], both operating on a similar principle. Furthermore, Ranjbar, S. et al. [39] designed a magnetically controlled bidirectional 2 × 2 elastic switch based on a Mach-Zehnder interferometer (MZI), which achieves high-performance waveguide switching through phase-difference control, exhibiting an average extinction ratio of up to 15.14 dB and an insertion loss of only 0.26 dB. Collectively, these works demonstrate the potential of embedding Terfenol-D into phononic crystal structures to achieve powerful magnetically tunable functionalities. However, integrating such dynamic tunability with topologically protected states—particularly to achieve reconfigurable topological rainbow effects—remains a challenging and underexplored area.
To overcome the limitations of static geometric approaches, we introduce a paradigm shift from structural grading to field-driven tuning. In this work, we design a one-dimensional magnetoelastic phononic crystal slab composed of the smart magnetostrictive material Terfenol-D and pure tungsten. By modulating the geometric parameters of the non-magnetic medium within a unit cell, we achieve band inversion and topological phase transitions of Lamb waves. Subsequently, the eigenfrequency spectrum and corresponding transmission spectrum of the supercell structure demonstrate the existence of topological interface states within the second overlapping band gaps with different topological characteristics in the phononic crystal. Furthermore, numerical simulation results confirm the robustness of the topological interface states against interface defects and the highly localized modes generated by the coupling of adjacent topological interface states under intelligent modulation by an external magnetic field. Finally, we propose an SSH-lattice phononic crystal under a gradient magnetic field, achieving tunable topological rainbow trapping of Lamb waves topological interface states without altering the system structure by reconstructing the gradient magnetic field. The designed topological rainbow trapping system can be applied to the design of new types of acoustic isolators, sensors, and modulators, capable of addressing various dynamic scenarios.
2. Models and Methods
As shown in Figure 1a, the one-dimensional magnetoelastic phononic crystal slab under discussion consists of a stepped thin-plate structure formed by alternately combining magnetic Terfenol-D medium (dark blue) and non-magnetic pure tungsten medium (gray) with a horizontal thickness of d = 2 mm along the x-axis. Terfenol-D, as a smart material, exhibits magnetoresponsive characteristics, allowing its effective elastic modulus and other physical properties to be modulated by an external static magnetic field [40]. The model is designed with an infinite periodic arrangement along the x-direction within the x-y plane, while maintaining a finite height in the y-direction. The external static magnetic field H is applied along the y-axis. Since the z-axis of the system is non-periodic, it is assumed to be infinite by default. Figure 1b,c show two different unit cells with the same lattice constant . For the consideration of inversion symmetry in the unit cell, the media at different positions are labeled as A, B, and C. For the S1 unit cell, the heights are , and . For the S1’ unit cell, the heights are , .
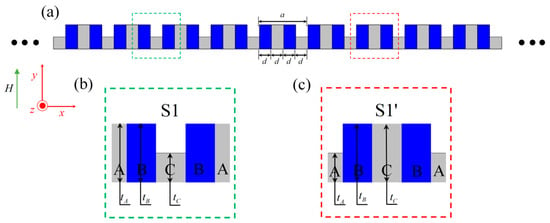
Figure 1.
(a) Schematic of the 1D phononic crystal structure. (b) Schematic of the concave unit cell S1 outlined by green dashed lines. (c) Schematic of the convex unit cell S1’ outlined by red dashed lines.
In this paper, the studied phononic crystal slab includes the magnetostrictive material Terfenol-D. When elastic waves propagate through this medium, an external magnetic field couples with its displacement field. Therefore, it is inappropriate to use only the constitutive equations for elastic wave propagation in an isotropic solid medium. Instead, piezomagnetic constitutive equations that account for the magneto-elastic coupling effect are employed [41]:
where the indices i (or j, k, l, n) represent the Cartesian coordinates x, y, or z; ρ, ui, xi, bi, σij, Cijkl, μil, φn, and Qij denote the density, particle displacement along the i-axis, Eulerian coordinates, magnetic induction component, stress tensor elements, elastic constants, magnetic permeability matrix, n-th component of the magnetic potential, and piezomagnetic tensor elements, respectively. Note that Equations (1)–(4) apply to both magnetoelastic and non-magnetic materials. For non-magnetic materials (tungsten), the piezomagnetic coefficients Qij are set to zero, and the magnetic permeability μil is set to the permeability of free space (vacuum) μ0. This yields results identical to solving the elastic wave equation. For computational consistency, the piezomagnetic constitutive equations are applied to both media in our model. Under uniform magnetization, the equivalent piezomagnetic material model describes the phononic crystal slab with an external magnetic field along the y-axis [41]. The equivalent material parameters of Terfenol-D, controlled by the magnetic field amplitude, are as follows [42]:
where the equivalent piezomagnetic tensor Qlij and the equivalent elastic constants Cijkl are expressed using Voigt notation. B1 (or B2), K1, Ms, and μ0 denote the magnetoelastic coupling coefficient, the magnetic anisotropy constant, the saturation magnetization, and the permeability of vacuum, respectively. The internal magnetic field strength H0 is defined as the sum of the externally applied static magnetic field H and the demagnetizing field Hd induced by magnetization. Here, an external magnetic field H is uniformly applied along the positive y-axis of the entire model, as shown in Figure 1a. Consequently, the resulting internal field H0 is also oriented predominantly along the y-axis, with its precise magnitude and direction within each magnetic domain being adjusted by the local demagnetizing field Hd. Mathematically, the demagnetizing field Hd can be expressed as:
where N is the demagnetizing factor. It is important to note that Equation (8) and the demagnetizing factor N describe the relationship along the direction of the applied magnetic field, which is the y-axis in our model. The demagnetizing factor in the Terfenol-D medium depends not only on its geometric structure and size but also on the demagnetizing fields produced in other adjacent magnetoelastic layers within the periodic arrangement. To fully account for the interaction of the demagnetizing fields between adjacent magnetic layers in a one-dimensional array, the x-direction component of the demagnetizing factor Nx can be expressed as [43]:
where represents the aspect ratio of the rectangular cross-section, is the pitch-to-width ratio of the array, and is the number of magnetic layers in the array. Additionally, and the function are expanded as follows:
Although Equations (9)–(11) are expressed using dimensionless ratios, these ratios are directly derived from the physical dimensions of the periodic array, thereby inherently capturing the interaction between adjacent layers.
Equation (10) represents the demagnetizing factor in the x-direction considering only a single rectangular section of magnetic material with infinite dimensions. For the demagnetizing factor in the y-direction, Ny, according to , and assuming the phononic crystal slab has an infinite size in the z-axis direction (), it follows that:
It is important to note that, to avoid the influence of magnetic spin reorientation and ensure the validity of the equations, the strength of the external static magnetic field H must always exceed the critical magnetic field strength Hlim at which magnetic spin reorientation occurs. The corresponding expression can be written as [44]:
where K1 is the magnetic anisotropy constant and MS is the saturation magnetization. From Equation (13), it can be seen that if an external static magnetic field is applied along the y-axis of the phononic crystal slab, the critical magnetic field strength Hlim for the occurrence of magnetic spin reorientation is 3.39 kOe. Therefore, throughout this study, the external static magnetic field H is maintained above 3.39 kOe to ensure the accuracy of the simulation results based on the equivalent piezomagnetic material model.
In this paper, COMSOL Multiphysics 6.2 software is employed to solve the equivalent piezomagnetic constitutive equations. First, the field-dependent equivalent parameters within the equations, specifically the elastic constants, piezomagnetic constants, and magnetic permeability, are resolved. Then, the finite element method is used to solve the equations, thereby obtaining the dispersion relations and eigenspectra of Lamb waves in the one-dimensional magnetoelastic phononic crystal slab. When solving for the band structure of Lamb waves, Bloch–Floquet boundary conditions are applied to the periodic end faces along the y-axis in both the S1 and S1’ unit cell models, mechanical free boundary conditions are applied to all upper and lower surfaces, and magnetic open-circuit boundary conditions are set on the surfaces of the magnetic medium to assume the entire system is in a vacuum environment. Finally, by sweeping the wave vector k along the boundary (0, π/a) of the irreducible Brillouin zone in the momentum space, the dispersion relation diagram w(k) of Lamb waves in the ideal model of the one-dimensional magnetoelastic phononic crystal slab shown in Figure 1 can be obtained. The material parameters studied in this paper are as follows: For tungsten, the density , elastic constants , , ; for the Terfenol-D, , , , ; the magnetic anisotropy constant , the saturation magnetization , and the magnetoelastic constants and .
3. Numerical Simulation
3.1. Unit Cell Band Structure and Topological Phase Transition
To explore the topological properties of the one-dimensional magnetoelastic phononic crystal slab, based on the SSH model in electronic systems, we investigate the band structures of two unit cells, S1 and S1’, with different inversion centers in the phononic crystal slab. To clearly explain this band inversion process, we define a structural symmetry parameter and discuss . As depicted in Figure 2a,b, the band structure diagrams for both unit cells exhibit three complete band gaps. This phenomenon can be attributed to the asymmetric structure of the plate in the thickness direction [19], which leads to the coupling of the A0 and S0 modes, as well as the A1 and S0 modes. However, there are differences in the characteristics of the second band gap in the band structures of the two unit cells. Figure 2c shows the x-component of the displacement field at the boundary of the Brillouin zone k = π/a, corresponding to the two unit cells (labeled as B1, B2, B1’, and B2’). Note that the distribution of these modes exhibits even symmetry (indicated by red dots) or odd symmetry (indicated by green dots). For the S1 unit cell, the frequencies of the modes exhibiting even symmetry on either side of the second complete band gap are higher than those of the modes with odd symmetry. For the S1’ unit cell, the situation is reversed for the edge modes on either side of the second complete band gap. Clearly, a mode inversion occurs at the boundary k = π/a for the third and fourth bands.
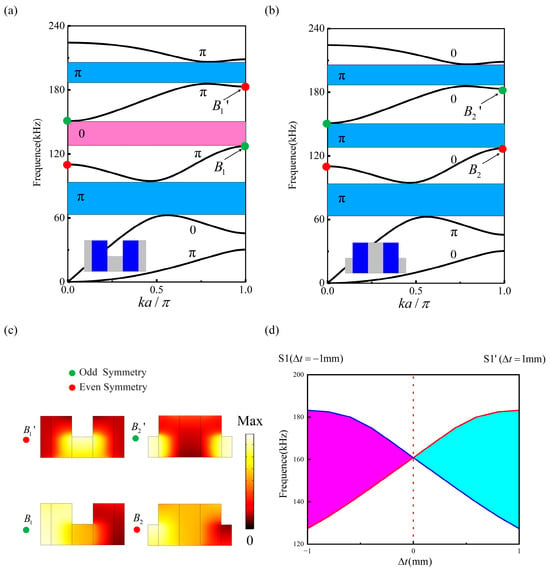
Figure 2.
(a,b) Band structure of the S1 and S1’ unit cell. (c) Symmetry of the edge states at the band edges of the third and fourth bands k = π/a at the four points B1, B2, B1’, B2’. The red and green dots represent even and odd symmetry, respectively. (d) The correlation between the edge frequencies of the third and fourth energy bands at the Brillouin zone boundary k = π/a and their variations is shown. The red and blue lines represent even and odd symmetries, respectively.
Figure 2d illustrates the evolution of the edge state frequencies of the second complete band gap in the unit cell of the magnetoelastic phononic crystal slab at k = π/a under different structural parameters . The blue curve corresponds to the even symmetry mode, while the red curve corresponds to the odd symmetry mode. It can be clearly seen that as increases from −1 mm to 1 mm, the band gap width between the two modes gradually narrows to zero and then widens again with further increase in . Therefore, the second band gap arises due to the introduction of structural perturbation in the system, which breaks the degeneracy of the third and fourth bands at the Brillouin zone boundary k = π/a. More importantly, during this “opening-closing-opening” process of the second complete band gap, the edge states of the two different symmetry modes undergo a band inversion at the topological transition point , indicating that a topological phase transition has occurred in this one-dimensional phononic crystal slab system. Thus, the second overlapping complete band gap of the S1 and S1’ unit cells exhibits different topological properties.
Next, to further explore the topological properties of the complete band gaps in the S1 and S1’ unit cells, we use the Zak phase [45,46] to describe the n-th band of Lamb waves in a 1D periodic system. The Zak phase, a type of Berry phase, is calculated as the integral of the Berry connection across the first Brillouin zone, and its expression is as follows [45,47,48]:
Here, is the normalized cell-periodic part of the Bloch wavefunction corresponding to the eigenstate of the n-th energy band at point k in momentum space, satisfying the relation .
Based on the connection between the Zak phase and Wannier charge centers [49], the Zak phase in this phononic crystal system is either 0 (trivial) or π (non-trivial) due to the mirror symmetry of the S1 and S1’ unit cells [33]. The Zak phase of the n-th band can be deduced from the symmetry of its edge states at k = 0 and k = π/a [33]. For instance, the third band of S1 has a π Zak phase due to differing edge state symmetries, while S1’ has a 0 Zak phase due to identical symmetries. Performing numerical solutions for Equation (15) in the discretized Brillouin zone [50], the numerical calculation results are consistent with the band degeneracy results. Summing the Zak phases of all bands below the target gap characterizes their topology. For S1, the Zak phases are π, 0, π for the first three gaps, and π, π, π for S1’. The second gap in S1 is trivial (magenta), and in S1’ it is non-trivial (blue), indicating different topological properties. This explains the topological phase transition induced by structural perturbations, which is essential for creating topological interface states in one-dimensional magnetoelastic phononic crystal slabs.
3.2. Topological Interface States in One-Dimensional Magnetoelastic Phononic Crystal Slabs
Analogous to electronic systems, for the elastic wave system formed by connecting the phononic crystal slabs S1 and S1’, which have different topological properties within their overlapping band gaps, an additional interface state emerges [33]. This interface state manifests as a high degree of localization and energy enhancement of elastic waves at the interface. To verify the existence of topological interface states within the Lamb waves system, mechanical free boundary conditions were applied to all upper and lower surfaces of the phononic crystal slab, and magnetic open boundary conditions were set on the surfaces of the magnetic medium. as shown in Figure 3a, we assemble a supercell by linking two one-dimensional magnetoelastic phononic crystal slabs, with each plate consisting of 10 S1’ and S1 unit cells. Figure 3b presents the eigenfrequency spectrum of the S1’ + S1 supercell under an external magnetic field of , clearly showing an additional eigenstate, indicated by a red dot, within the overlapping band gap of the second bands of S1 and S1’. Additionally, Figure 3c illustrates the eigendisplacement field distribution corresponding to this extra eigenstate at a frequency of within the S1’ + S1 supercell structure. It is evident that the displacement field peaks are predominantly localized at the interface marked by the green dashed line and decay rapidly towards both ends of the supercell. Thus, this additional eigenstate indeed exhibits the characteristics of a typical topological interface state in a one-dimensional periodic system.
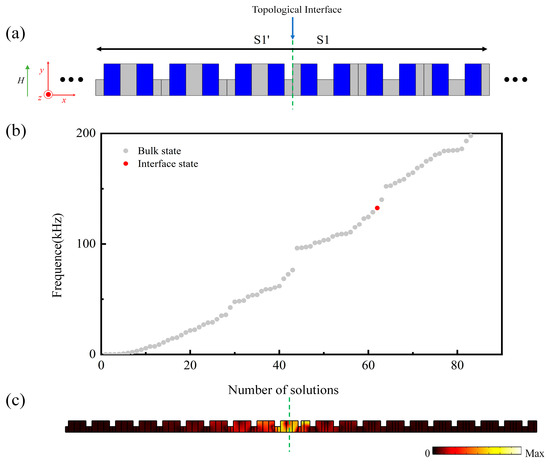
Figure 3.
(a) Schematic of the S1 + S1’ phononic crystal slabs. (b) At , the eigenfrequency spectrum of the S1’ + S1 supercell structure. (c) At the frequency , the eigen displacement field of the S1’ + S1 supercell structure.
Subsequently, to further verify the above interface states, frequency response studies are conducted using the finite element method to calculate the transmission spectra of three types of supercell structures (composed of 22 unit cells) under an external magnetic field : S1 + S1, S1’ + S1, and S1 + S1’. Figure 4a provides a schematic illustration of the transmission characteristics of Lamb waves in one-dimensional phononic crystal slab supercells, with the supercell located in the middle of the structure and the matrix on both sides, where the excitation and reception points are set accordingly. Additionally, during the transmission simulation of the entire structure, low-reflection boundary conditions are applied to the outermost boundaries of the left and right matrices to minimize the impact of reflected elastic waves on the calculated frequency spectra. Figure 4b presents the frequency response spectra obtained from numerical simulations of the S1 + S1, S1’ + S1, and S1 + S1’ supercell structures using the finite element method. In the transmission spectra of the S1’ + S1 and S1 + S1’ supercell structures with two different topological properties, a sharp transmission peak (indicated by a black arrow) can be observed at the same position corresponding to the frequency range of the second overlapping band gap. However, such a transmission peak does not exist in the transmission spectrum of the supercell structure composed entirely of S1 unit cells.
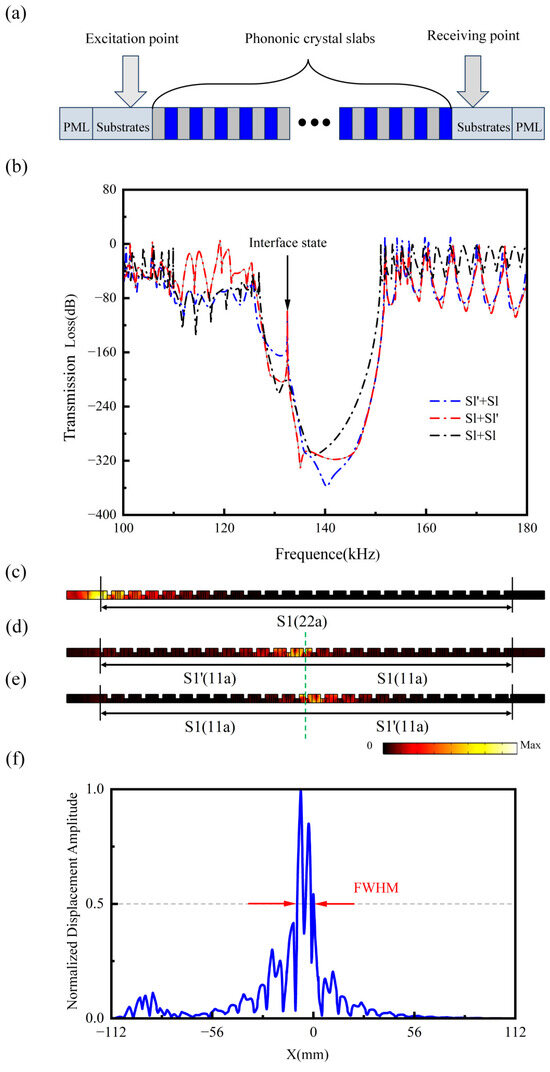
Figure 4.
(a) Schematic of the phononic crystal slabs transmission model. (b) The transmission spectra corresponding to the phononic crystal structures of S1 + S1, S1 + S1’, and S1’ + S1. (c–e) Displacement fields corresponding to the supercells S1 + S1, S1’ + S1, and S1 + S1’, respectively. (f) The normalized spatial distribution of the displacement field amplitude along the central crossline (white dashed line in d) obtained from eigenfrequency analysis using COMSOL’s cross-section extraction tool, representing the interface state mode profile.
Through frequency domain analysis, we examined the displacement field distribution patterns in these three supercell structures at the interface state frequency . Figure 4c shows that no vibrational mode excited by the left excitation is produced in the S1 + S1 supercell structure. Instead, in the displacement fields of the S1’ + S1 and S1 + S1’ supercell structures shown in Figure 4d,e, the elastic energy in the system is clearly concentrated near the topological interface within the supercell structure. Due to the impedance mismatch at the interface, the energy concentration region is more biased towards the S1’ unit cell side. It is worth noting that further analysis of the energy concentration behavior of the topological interface state reveals that in Figure 4f, the normalized spatial distribution of the displacement amplitude along the central crossline (white dashed line) of the S1’ + S1 supercell structure is plotted. It can be seen that the full width at half maximum (FWHM) of the displacement field distribution corresponding to the topological interface state in the system is approximately 1.17a, further confirming the highly localized nature of the topological interface state.
The strong topological robustness against interface structural defects has led to widespread attention on topological interface states in phononic crystal systems. To verify that the interface states of the elastic wave system composed of S1 and S1’ unit cells possess this remarkable characteristic, the influence of two types of interface defects on the system is considered here: the interface size defect and the slab defect, as shown in Figure 5a,b. These two types of defects are introduced into the topological interface of the S1’ + S1 supercell structure, respectively. Figure 5c–f present the corresponding eigenfrequency spectra of the supercell structures with the introduced interface defects and the eigendisplacement field distributions of the topological interface states, respectively. It is evident that although the interface defects are deliberately introduced into the interface of the S1’ + S1 supercell structure, thereby disrupting the original ideal structure, the topological interface states still exist within the overlapped bandgap of the ideal structure for both defect structures, thanks to topological protection, although their frequencies are slightly shifted. As can be intuitively seen from Figure 5e,f, the introduction of the two types of interface defects does not significantly affect the highly localized elastic energy characteristic of the previous topological interface states. Only because the slab defect causes greater structural damage to the topological boundary does the elastic energy attenuate further into the phononic crystal slab on both sides, nearly four lattice units. In summary, these results not only demonstrate that the interface states in the aforementioned system are topologically robust against interface structural defects but also confirm that the interface states discussed above are not trivial defect states [51].
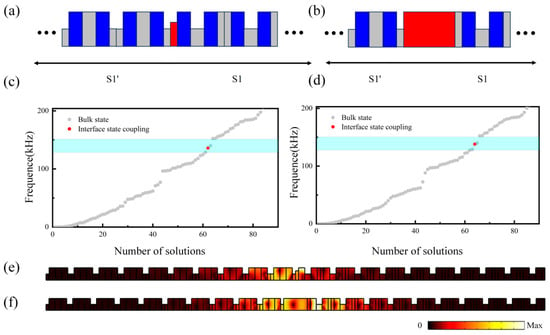
Figure 5.
(a,b) A schematic diagram of introducing interface size defects and slab defects at the interface. (c,d) The eigenfrequency spectrum of the S1’ + S1 supercell structure after introducing interface size and slab defects. (e,f) The distribution of eigendisplacement fields for topological interface states under interface size and slab size defects.
3.3. Tunable Topological Rainbow Trapping with Gradient Magnetic Field
Leveraging the phenomenon of energy concentration at the topological interface due to interfacial impedance mismatch, one can exploit the coupling between adjacent modes of topological edge states to achieve a topological rainbow effect in one-dimensional magnetoelastic phononic crystal slabs. To quantitatively address the mechanism of energy concentration, the acoustic impedance mismatch at the topological interface was calculated. The acoustic impedance is given by , where the shear wave velocity Ct is defined as , G is the shear modulus. For the non-magnetic tungsten medium, the shear modulus , resulting in an impedance of . For the calculation of Terfenol-D impedance, its elastic constant C44 varies with the applied magnetic field. For example, under an external magnetic field of , the equivalent shear modulus of the magnetostrictive Terfenol-D medium is , yielding a significantly lower impedance of . This results in a substantial impedance ratio of approximately 6.27. Such a pronounced mismatch strongly promotes wave reflection and energy confinement at the interface, fundamentally explaining the highly localized nature of the topological interface states observed in Figure 4 and Figure 5. As depicted in Figure 6a,b, the study examines two one-dimensional phononic crystal slab supercells constructed from 20 unit cells each, specifically the S1 + S1’ + S1 supercell and the S1’ + S1 + S1’ supercell. These supercells are arranged in a sandwich structure, with each containing a pair of topological interfaces (marked by red dashed lines). Figure 6c,d present the eigenfrequency spectra and corresponding eigenfield distributions of the S1 + S1’ + S1 and S1’ + S1 + S1’ supercell structures under an external magnetic field , from which it can be observed that both sandwich structures exhibit eigenstates (red dots) indicative of interface state coupling effects. In Figure 6e, it is clear that the eigendisplacement fields of the coupled interface states in both sandwich structures are highly concentrated between the corresponding pair of topological interfaces [34]. Subsequently, we further explore the non-contact tunability of the aforementioned interface coupling states in the S1 + S1’ + S1 and S1’ + S1 + S1’ supercell structures under an external magnetic field. Figure 7 illustrates the evolution of the interface coupling states with the external magnetic field H. It is clear that throughout the entire evolution process of the interface coupling states, the two curves remain distinct without intersecting, which lays the groundwork for multi-frequency energy localization. This change is due to the increase in the external magnetic field, which increases the effective stiffness of the magnetostrictive material Terfenol-D within the structure [52].
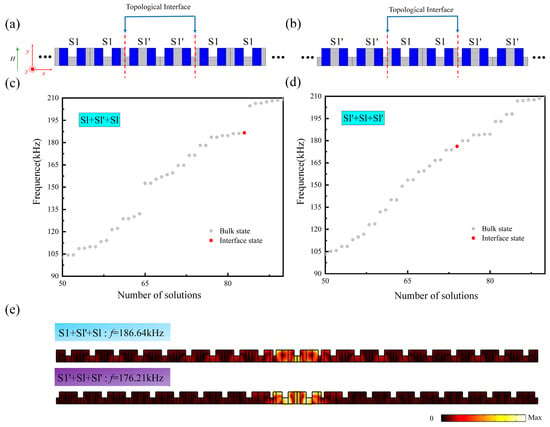
Figure 6.
(a,b) Schematic diagram of the phononic crystal structures S1 + S1’ + S1 and S1’ + S1 + S1’. (c,d) Corresponding eigenfrequency spectra of the supercell structures S1 + S1’ + S1 and S1’ + S1 + S1’; (e) Interface coupling modes in the S1 + S1’ + S1 and S1’ + S1 + S1’ supercell structures.
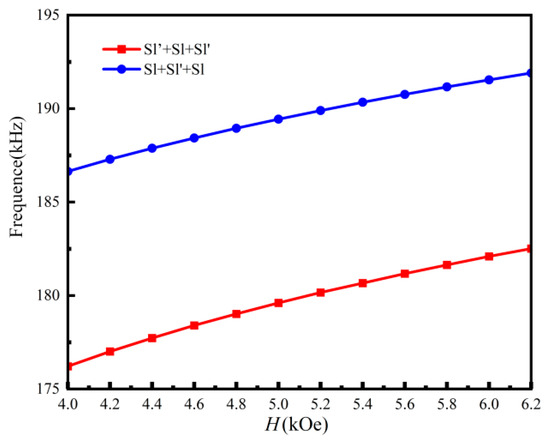
Figure 7.
Interface coupling states in the S1 + S1’ + S1 and S1’ + S1 + S1’ supercell structures under different external magnetic fields.
The resonant frequency f of the topological interface states exhibits a distinct dependence on the applied magnetic field H, which is governed by the field-induced variation in the elastic modulus in the Terfenol-D medium. Based on the equivalent piezomagnetic model (Equations (5)–(7)), the resonant frequency scales with the field-dependent elastic modulus, denoted as C44,H, according to the following relation:
where is the density of Terfenol-D. Substituting the expression for from Equation (5) yields the explicit relationship:
Here, f0 is the reference frequency at magnetic saturation ().
Having established the existence of a single topological interface state, we proceed to investigate the interaction between two such interfaces. The coupling between topological states is the fundamental mechanism underpinning advanced phenomena such as rainbow trapping.
We construct superlattices featuring two parallel interfaces separated by a buffer region consisting of n (n = 1, 2, or 3) unit cells of a topologically distinct crystal. As shown in Figure 8a,b, the configuration with a large separation of three unit cells (e.g., S1 + three S1’ unit cells + S1 and S1’ + three S1 unit cell + S1’) exhibits negligible overlap and coupling between the interfaces due to the exponential decay of their evanescent field profiles. Consequently, the spectra in Figure 8c and Figure 8d each exhibit a single sharp resonance at 169.68 kHz and 165.64 kHz, respectively, confirming the near-degeneracy of these two independent states.
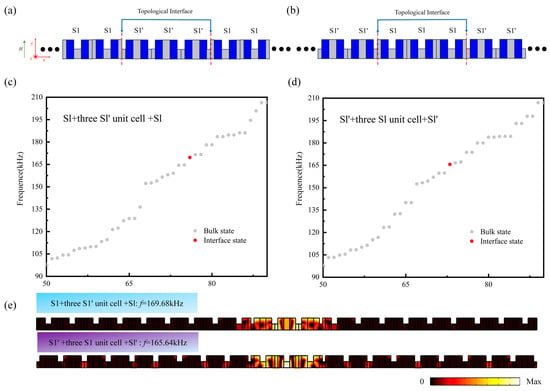
Figure 8.
(a,b) Schematic diagram of the phononic crystal structures S1 + three S1’ unit cell + S1 and S1’ + three S1 unit cell + S1’. (c,d) Corresponding eigenfrequency spectra of the supercell structures S1 + three S1’ unit cell + S1 and S1’ + three S1 unit cell + S1’. (e) Interface coupling modes in the S1 + three S1’ unit cell + S1 and S1’ + three S1 unit cell + S1’ supercell structures.
When the separation is reduced to two unit cells (as in the S1 + two S1’ unit cell + S1 and S1’ + two S1 unit cell + S1’ configurations, shown in Figure 6a,b), the inter-cell coupling is significantly enhanced due to substantial overlap between the interfacial wavefunctions. This intermediate coupling strength lifts the degeneracy of the system and induces the formation of new, localized interface states within the bandgap. The emergence of two distinct, sharp resonance peaks at 176.21 kHz and 186.64 kHz in the eigenfrequency spectra (Figure 6c,d) unambiguously confirms this behavior. The corresponding displacement field profiles confirm that these states are highly localized at the two topological boundaries, exhibiting characteristics of symmetric and antisymmetric supermodes resulting from interfacial hybridization.
When the separation is further reduced to a single unit cell (as in the S1 + one S1’ unit cell + S1 and S1’ + one S1 unit cell + S1’, shown in Figure 9a,b) the coupling strength is maximized. The strong overlap leads to pronounced hybridization, significantly shifting the resonant frequencies of the interface modes. A single, prominent hybridized supermode is observed deep within the bandgap at 156.51 kHz and 149.35 kHz, respectively (Figure 9c and Figure 9d), while its counterpart may shift outside the gap or merge with the bulk spectrum. The field distribution of this state remains highly localized, indicating that topological protection persists even under strong coupling conditions.
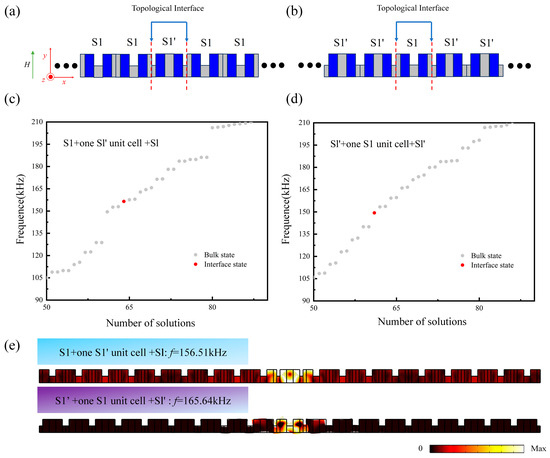
Figure 9.
(a,b) Schematic diagram of the phononic crystal structures S1+ one S1’ unit cell + S1 and S1’ + one S1 unit cell + S1’. (c,d) Corresponding eigenfrequency spectra of the supercell structures S1 + one S1’ unit cell + S1 and S1’ + one S1 unit cell + S1’. (e) Interface coupling modes in the S1 + one S1’ unit cell + S1 and S1’+ one S1 unit cell + S1’ supercell structures.
This systematic evolution—from uncoupled bulk-like states at large separation, to the coupling-induced generation of split interface modes, and finally to a strongly shifted hybridized state—clearly demonstrates that the spectral position and very existence of topological interface states are governed by the coupling strength between adjacent boundaries. The ability to manipulate modal properties through a geometric parameter underscores the tunability of topological phenomena in this system.
In topological systems, the highly localized nature of topological edge states can provide new solutions for the localization and harvesting of energy in elastic systems. As shown in Figure 10a, similar to gradient elastic metasurfaces, a one-dimensional phononic crystal slab is constructed using S1 and S1’ cells to form an alternating SSH structure with periodic unit cells of S1-S1’-S1’-S1 [29]. An external magnetic field Hg, perpendicular to the thickness direction of the slab, is applied along the x-axis. Here, the magnetic field strength experienced by the N-th structural unit is denoted as . For the supercell structure of the above-mentioned phononic crystal slab with N = 4, it contains a total of eight topological interfaces. Due to the coupling that can occur between adjacent topological interface states, the supercell structure theoretically contains seven spatially separated localized interface coupling modes with enhanced energy, that is, seven topological rainbow states [34].
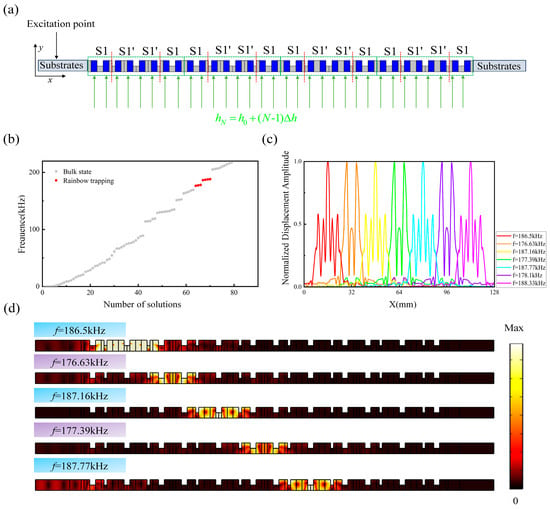
Figure 10.
(a) One-dimensional magnetoelastic phononic crystal slab rainbow trapping structure. (b) When N = 4, the eigenfrequency spectrum of the supercell structure. (c) The normalized amplitude spatial distribution of the displacement field for the rainbow states. These data are obtained from the eigenfrequency study. (d) The steady-state displacement field distribution of topological rainbow states under a gradient magnetic field of 4~4.8 kOe.
To verify that the supercell structure possesses seven topological rainbow states, a study of the eigenfrequencies of the phononic crystal slab supercell structure for N = 4 is conducted in COMSOL Multiphysics software. The initial components of the gradient magnetic field Hg are set to and . Figure 10b shows the calculated eigenfrequency spectrum of the aforementioned structure, where the seven rainbow states marked by red dots are clearly visible. Figure 10c depicts the normalized distribution of the corresponding eigendisplacement field amplitudes along the x-axis. It can be clearly seen that rainbow states of different frequencies are highly localized at different spatial positions in the phononic crystal slab, with a full width at half maximum (FWHM) of approximately 2a, and there is almost no overlap between the rainbow states. Subsequently, further full-wave simulations were performed to validate the N = 4 supercell structure, with low-reflective boundary conditions applied at the outermost boundaries to absorb the elastic waves reflected from the ends. Figure 10d shows the steady-state displacement field distribution of the phononic crystal slab supercell structure for excitation frequencies of 176.63 kHz, 177.39 kHz, 186.5 kHz, 187.16 kHz, and 187.77 kHz. It can be seen that the simulation results are consistent with the corresponding eigenfield distributions mentioned above. Specifically, incident elastic waves of different frequency components are almost completely separated and captured between the different topological interfaces of the alternating SSH structure phononic crystal slab along the x-axis, with the corresponding displacement fields being highly localized. Here, the mechanism for the generation of the localized rainbow states in the phononic crystal slab system of the rainbow supercell can be explained based on the modal coupling between adjacent topological interface states discussed in the aforementioned S1-S1’-S1 and S1’-S1-S1’ supercell structures.
To demonstrate the tunability of our system, we subsequently reconstruct the gradient external magnetic field Hg to regulate the frequencies of the aforementioned rainbow states within the structure, while keeping the initial components and unchanged. Figure 11a,b present the spatial distribution of the normalized amplitude values after reconstruction, as well as the steady-state displacement fields of the associated rainbow states. It is evident that through contactless tuning of the external magnetic field, the captured rainbow states remain highly localized, but their operating frequencies can be modulated. The frequencies of the five new rainbow states are 181.43 kHz, 181.89 kHz, 190.7 kHz, 191.08 kHz, and 191.47 kHz, respectively. Therefore, compared to traditional gradient metamaterials [19,27,28,29], the one-dimensional topological rainbow system we propose exhibits significant features of high localization, compact structure, and wide frequency tunability, holding great potential in the design of compact energy harvesters in elastic wave systems.
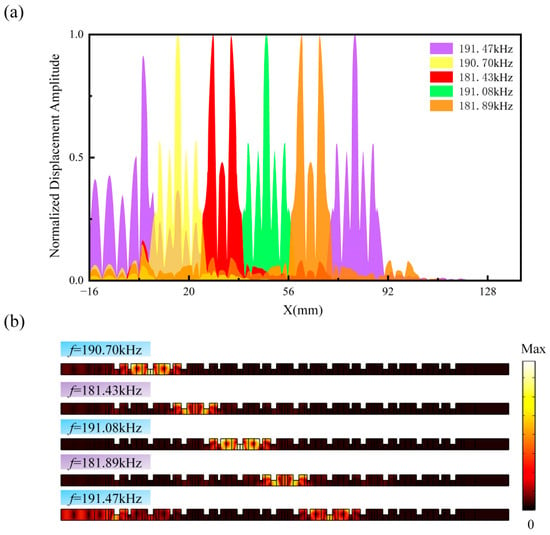
Figure 11.
(a) The normalized spatial distribution of the eigenmode displacement amplitude for the new rainbow states under a reconstructed gradient magnetic field of 5.8 to 6.2 kOe, obtained from the eigenfrequency study. (b) The steady-state displacement field distribution of the new rainbow states under a gradient magnetic field of 5.8 to 6.2 kOe.
To further validate the system’s tunability and address practical implementation, we simulate a structure with a larger number of unit cells (N = 32, a graded magnetic field is applied to each Terfenol-D rod.) under a linearly graded magnetic field , as opposed to the discrete jumps in the previous SSH configuration, the initial components of the gradient magnetic field Hg are set to and . Figure 12b shows the calculated eigenfrequency spectrum of the aforementioned structure, where the seven rainbow states marked by red dots are clearly visible. Figure 12c depicts the normalized distribution of the corresponding eigendisplacement field amplitudes along the x-axis. Subsequently, further full-wave simulations were performed to validate the N = 32 supercell structure, with low-reflective boundary conditions applied at the outermost boundaries to absorb the elastic waves reflected from the ends. Figure 12d shows the steady-state displacement field distribution of the phononic crystal slab supercell structure for excitation frequencies of 188.58 kHz, 180.93 kHz, 191.58 kHz, 184.28 kHz, and 194.57 kHz. It can be seen that the simulation results are consistent with the corresponding eigenfield distributions mentioned above. The result, presented in Figure 12, demonstrates a clear rainbow trapping effect, where seven distinct frequency components are separated and localized at different spatial positions. This outcome confirms that a continuous field gradient is sufficient to achieve robust rainbow trapping, as the local resonant frequency of the topological interface state at any position is dictated by the local field strength H. The monotonic gradient establishes a continuous spatial-frequency mapping, causing incident waves to be adiabatically slowed and trapped at their respective matching locations. The spectrum of trapped states under continuous grading resembles a quasi-continuum, differing from the discrete eigenstates of the SSH supercell but equally effective for frequency sorting.
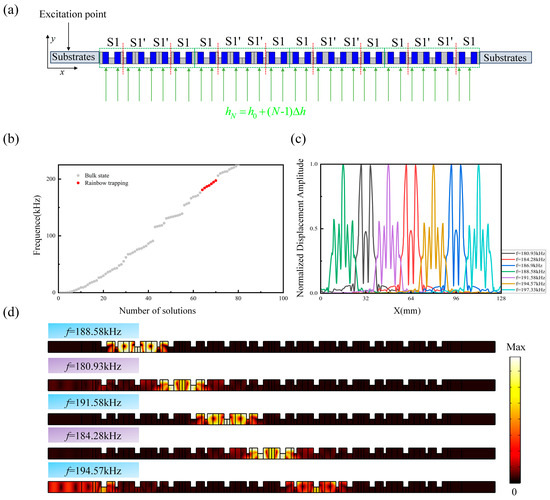
Figure 12.
(a) One-dimensional magnetoelastic phononic crystal slab rainbow trapping structure. (b) When N = 32, the eigenfrequency spectrum of the supercell structure. (c) The normalized amplitude spatial distribution of the displacement field for the rainbow states. These data are obtained from the eigenfrequency study. (d) The steady-state displacement field distribution of topological rainbow states under a gradient magnetic field of 4~10.2 kOe.
4. Discussion and Future Perspectives
While the numerical simulations presented in this work robustly demonstrate the principle of magnetically tunable topological rainbow trapping, the practical implementation and experimental validation of such a system entail several considerations that warrant further discussion.
4.1. Model Limitations and Experimental Challenges
The accuracy of our equivalent piezomagnetic material model is highly dependent on the precise description of the internal demagnetizing field distribution. In a practical periodic array of magnetoelastic materials, the demagnetizing fields from adjacent magnetic layers superimpose, leading to a complex internal field landscape that our model, based on established theoretical formulations [43,44], approximates but may not fully capture. Furthermore, the assumption of infinite extent in the z-direction simplifies the analysis but neglects finite-width edge effects that could perturb the guided wave modes in a real sample.
Experimental verification poses significant challenges. The fabrication of a high-quality, alternating Terfenol-D/tungsten superlattice requires precision techniques such as wire-cutting and diffusion bonding. Most critically, the application of a stable and precisely controlled gradient magnetic field Hg would necessitate a customized array of electromagnetic coils with independent current control, introducing complexities in system integration, power consumption, and thermal management. Measuring the highly localized rainbow states would further require advanced techniques like laser Doppler vibrometry to spatially map the displacement field.
4.2. Practical Limitations and Future Perspectives
It is important to note that the bandgaps and topological effects in this design originate from Bragg scattering mechanisms, which typically operate at high frequencies (hundreds of kHz as shown). This limits the direct application of the current structure for controlling low-frequency vibrations, which is a paramount concern in many engineering fields like vehicle dynamics and structural vibration. Therefore, future work will focus on two main directions: Firstly, on overcoming the experimental hurdles to validate the proposed concept, which includes developing a more sophisticated model that accounts for inter-layer demagnetizing effects and finite sample dimensions. Secondly, and more importantly, on transcending the current design paradigm by exploring locally resonant (LR) phononic crystals incorporating smart materials. The LR mechanism is well-known for generating low-frequency bandgaps. Coupling this with topological physics and magnetic tunability could unlock a new generation of intelligent metamaterials for low-frequency vibration control and energy harvesting, effectively bridging the gap between theoretical concepts and practical engineering applications.
5. Conclusions
In this paper, we design a one-dimensional magnetoelastic phononic crystal slab composed of the smart magnetostrictive material Terfenol-D and pure tungsten. By adjusting the geometric parameters of the non-magnetic medium within a unit cell, we achieve band inversion and topological phase transitions of Lamb waves. Subsequently, the eigenfrequency spectrum and corresponding transmission spectrum of the phononic crystal slab supercell structure demonstrate the existence of topological interface states within the second overlapping band gaps with different topological characteristics in the phononic crystal. Moreover, numerical simulation results confirm that the topological interface states in the system exhibit good robustness against interface defects and are intelligently tunable by an external magnetic field, resulting in highly localized modes arising from the coupling between adjacent topological interface states. Finally, by calculating eigenfrequencies and steady-state displacement field distributions of the phononic crystal slab supercell structure under a gradient magnetic field of alternating SSH configuration, we realize tunable topological rainbow trapping of Lamb waves interface states without altering the system geometric structure by reconstructing the gradient magnetic field.
However, this study has certain limitations. Our theoretical model incorporates simplifications, including the assumption of an infinite z-direction and the use of an equivalent medium for the complex demagnetizing fields. The practical realization of the proposed system faces challenges, such as the fabrication of the material superlattice and the generation of a precisely controlled gradient magnetic field. Most notably, the operating frequencies of these Bragg-type bandgaps remain high, limiting their immediate applicability to low-frequency vibration control scenarios. Despite these limitations, this work establishes a foundational principle for non-contact, active control of topological states. The proposed system holds significant potential for applications in reconfigurable wave filtering, signal processing, and energy harvesting in elastic wave systems. Looking forward, our future efforts will be directed towards the experimental validation of this concept and the exploration of locally resonant phononic crystals integrated with smart materials, aiming to achieve magnetically tunable topological effects at lower frequencies for broader engineering applications.
Author Contributions
W.X. carried out methodology, supervision, writing the review and editing. F.S. conducted investigation and writing the review and editing. J.C. conducted methodology, formal analysis, investigation, and project administration. H.H. and T.L. conducted methodology and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge financial support from Nature Science Foundation of Hunan under Grant No. 2025JJ50040 and No. 2023JJ41030, National Science Foundation of China under Grant No. 12074114 and Excellent Youth Project of Hunan Provincial Department of Education under Grant No. 23B0259.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hess, O.; Tsakmakidis, K.L. ‘Trapped rainbow’ storage of light in metamaterials. Adv. Sci. Technol.-Res. J. 2010, 75, 256–265. [Google Scholar]
- Gan, Q.; Gao, Y.; Wagner, K.; Vezenov, D.; Ding, Y.J.; Bartoli, F.J. Experimental verification of the rainbow trapping effect in adiabatic plasmonic gratings. Proc. Natl. Acad. Sci. USA 2011, 108, 5169–5173. [Google Scholar] [CrossRef]
- Hu, H.; Ji, D.; Zeng, X.; Liu, K.; Gan, Q. Rainbow Trapping in Hyperbolic Metamaterial Waveguide. Sci. Rep. 2013, 3, 1249. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Chen, Y.; Zhu, X.; Garcia-Vidal, F.J.; Yin, X.; Zhang, W.; Zhang, X. Acoustic rainbow trapping. Sci. Rep. 2013, 3, 1728. [Google Scholar] [CrossRef]
- Jang, M.S.; Atwater, H. Plasmonic Rainbow Trapping Structures for Light Localization and Spectrum Splitting. Phys. Rev. Lett. 2011, 107, 207401. [Google Scholar] [CrossRef]
- Haldane, F.D.M.; Raghu, S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Hafezi, M.; Mittal, S.; Fan, J.; Migdall, A.L.; Taylor, J.M. Imaging topological edge states in silicon photonics. Nat. Photonics 2013, 7, 1001–1005. [Google Scholar] [CrossRef]
- Moiseev, S.; Glukhov, I. Tuning and total resonant suppression of reflection in the photonic bandgap range of Bragg reflector by two-dimensional nanoparticle array. J. Appl. Phys. 2024, 135, 083106. [Google Scholar] [CrossRef]
- Wu, L.H.; Hu, X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Page, J.H.; Liu, Z.; Cowan, M.L.; Chan, C.T.; Sheng, P. Focusing of Sound in a 3D Phononic Crystal. Phys. Rev. Lett. 2004, 93, 024301. [Google Scholar] [CrossRef]
- Wu, T.T.; Huang, Z.G.; Lin, S. Surface and bulk acoustic waves in two-dimensional phononic crystal consisting of materials with general anisotropy. Phys. Rev. B 2004, 69, 94301. [Google Scholar] [CrossRef]
- Khelif, A.; Aoubiza, B.; Mohammadi, S.; Adibi, A.; Laude, V. Complete band gaps in two-dimensional phononic crystal slabs. Phys. Rev. E 2006, 74, 046610. [Google Scholar] [CrossRef] [PubMed]
- Vasseur, J.; Deymier, P.; Djafari-Rouhani, B.; Pennec, Y.; Hladky-Hennion, A.C. Absolute forbidden bands and waveguiding in two-dimensional phononic crystal plates. Phys. Rev. B-Condens. Matter. 2009, 20, 439–446. [Google Scholar] [CrossRef]
- Khelif, A.; Choujaa, A.; Benchabane, S.; Djafari-Rouhani, B.; Laude, V. Guiding and bending of acoustic waves in highly confined phononic crystal waveguides. Appl. Phys. Lett. 2004, 84, 4400–4402. [Google Scholar] [CrossRef]
- Vasseur, J.O.; Deymier, P.A.; Khelif, A.; Lambin, P.; Djafari-Rouhani, B.; Akjouj, A.; Dobrzynski, L.; Fettouhi, N.; Zemmouri, J. Phononic crystal with low filling fraction and absolute acoustic band gap in the audible frequency range: A theoretical and experimental study. Phys. Rev. E 2002, 65, 056608. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Sun, T.; Zhang, Z.; Wang, Z. Thermally tunable topological transmission of elastic waves in solid phononic crystals. Appl. Phys. A-Mater. Sci. Process. 2025, 131, 259. [Google Scholar] [CrossRef]
- Swift, S.H.; El-Kady, I.F.; Kellogg, R.A.; Cillessen, D.E.; Denison, M.H. Cyclically symmetric radially self-similar phononic pseudocrystal isolator for broadband, ultrasonic vibration bandstop filtering. Appl. Phys. Lett. 2025, 126, 082201. [Google Scholar] [CrossRef]
- Tian, Z.; Yu, L. Rainbow trapping of ultrasonic guided waves in chirped phononic crystal plates. Sci. Rep. 2017, 7, 40004. [Google Scholar] [CrossRef]
- Gan, Q.; Ding, Y.J.; Bartoli, F.J. ‘rainbow’ Trapping and Releasing at Telecommunication Wavelengths. Phys. Rev. Lett. 2009, 102, 199–202. [Google Scholar] [CrossRef]
- Khelif, A.; Mohammadi, S.; Eftekhar, A.A.; Adibi, A.; Aoubiza, B. Acoustic confinement and waveguiding with a line-defect structure in phononic crystal slabs. J. Appl. Phys. 2010, 108, 084515. [Google Scholar] [CrossRef]
- Bessière, A.; Lecointre, A.; Priolkar, K.R.; Gourier, D. Role of crystal defects in red long-lasting phosphorescence of CaMgSi2O6: Mn diopsides. J. Mater. Chem. 2012, 22, 19039–19046. [Google Scholar] [CrossRef]
- Sainidou, R.; Stefanou, N.; Modinos, A. Linear chain of weakly coupled defects in a three-dimensional phononic crystal: A model acoustic waveguide. Phys. Rev. B 2006, 74, 172302. [Google Scholar] [CrossRef]
- Min, Z.; Yun-Tuan, F.; Ting-Gen, S. Study on One Dimension Phononic Crystal with Defects. J. Synth. Cryst. 2005, 34, 536–541. [Google Scholar]
- Khelif, A.; Achaoui, Y.; Aoubiza, B. In-plane confinement and waveguiding of surface acoustic waves through line defects in pillars-based phononic crystal. AIP Adv. 2011, 1, 141. [Google Scholar] [CrossRef]
- Wang, N.; Hsiao, F.L.; Palaniapan, M.; Lee, C. Silicon two-dimensional phononic crystal resonators using alternate defects. Appl. Phys. Lett. 2011, 99, 765. [Google Scholar] [CrossRef]
- Romero-Garcia, V.; Pico, R.; Cebrecos, A.; Sanchez-Morcillo, V.J.; Staliunas, K. Enhancement of sound in chirped sonic crystals. Appl. Phys. Lett. 2013, 102, 2022-R. [Google Scholar] [CrossRef]
- Ryosuke, N. Equivalence Between Non-Commutative Harmonic Oscillators and Two-Photon Quantum Rabi Models. Int. Math. Res. Notices 2025, 7, rnaf066. [Google Scholar]
- Zhou, Y.; Kong, F.; Liu, H.; Jin, Y.; Chen, H.; Sun, C. Numerical study on hydrodynamic characteristics of deep sea microfluidic eel energy capture device. Renew. Energy 2024, 225, 120325. [Google Scholar] [CrossRef]
- Masha, E.; Barbieri, L.; Skowronski, J.; Aliotta, M.; Ananna, C.; Barile, F.; Bemmerer, D.; Best, A.; Boeltzig, A.; Broggini, C. First measurement of the low-energy direct capture in 20Ne(p, γ)21Na and improved energy and strength of the Ec.m.=368 keV resonance. Phys. Rev. C 2023, 108, L052801. [Google Scholar] [CrossRef]
- Zhao, J.M.; Huo, S.Y.; Huang, H.; Chen, J. Topological Interface States of Shear Horizontal Guided Wave in One-Dimensional Phononic Quasicrystal Slabs. Phys. Status Solidi-Rapid Res. Lett. 2018, 12, 1800322. [Google Scholar] [CrossRef]
- Huang, H.B.; Chen, J.; Huo, S. Simultaneous topological Bragg and locally resonant edge modes of shear horizontal guided wave in one-dimensional structure. J. Phys. D-Appl. Phys. 2017, 50, 275102. [Google Scholar] [CrossRef]
- Ge, Z.; Sang, T.; Luo, C.; Zhang, X.; Pian, C. Configurable dual-topological-interface-states induced reflection in hybrid multilayers consisting of a Ge2Sb2Te5 film. Opt. Express 2024, 32, 16351–16361. [Google Scholar] [CrossRef]
- Elshahat, S.; Lu, C. Bidirectional rainbow trapping in 1-D chirped topological photonic crystal. Front. Phys. 2022, 10, 831203. [Google Scholar] [CrossRef]
- Chaplain, G.J.; Ponti, J.M.D.; Colombi, A.; Fuentes-Dominguez, R.; Craster, R.V. Tailored elastic surface to body wave Umklapp conversion. Nat. Commun. 2020, 11, 3267. [Google Scholar] [CrossRef] [PubMed]
- Omrani, E.M.; Nazari, F. Magnetically tunable 4 × 2 encoder utilizing Terfenol-D-embedded phononic crystal ring resonators. J. Sci. Adv. Mater. Devices 2025, 10, 100861. [Google Scholar] [CrossRef]
- Omrani, E.M.; Nazari, F. Magnetically adjustable AND/XOR logic gates using Terfenol-D in phononic crystal. Sci. Rep. 2025, 15, 12169. [Google Scholar] [CrossRef] [PubMed]
- Omrani, E.M.; Nazari, F. Magnetically tunable acoustic add-drop filter via Terfenol-D. Phys. Scr. 2024, 99, 105924. [Google Scholar] [CrossRef]
- Ranjbar, S.; Nazari, F.; Hajizadeh, R. Magnetically Controlled Bidirectional 2 × 2 Elastic Switch Using Terfenol-D in a Phononic Crystal-Based Mach-Zehnder Interferometer. J. Sci. Adv. Mater. Devices 2025, 10, 100926. [Google Scholar] [CrossRef]
- Ansari, M.H.; Attarzadeh, M.A.; Nouh, M.; Karami, A. Application of magnetoelastic materials in spatiotemporally modulated phononic crystals for nonreciprocal wave propagation. Smart Mater. Struct. 2018, 27, 015030. [Google Scholar] [CrossRef]
- Vasseur, J.O.; Matar, O.B.; Robillard, J.F.; Hladky-Hennion, A.C.; Deymier, P.A. Band structures tunability of bulk 2D phononic crystals made of magneto-elastic materials. AIP Adv. 2011, 1, 041904. [Google Scholar] [CrossRef]
- Matar, O.B.; Robillard, J.F.; Vasseur, J.O.; Hladky-Hennion, A.C.; Deymier, P.A.; Pernod, P.; Preobrazhensky, V. Band gap tunability of magneto-elastic phononic crystal. J. Appl. Phys. 2012, 111, 141. [Google Scholar] [CrossRef]
- Tartakovskaya, E.V.; Vovk, A.; Golub, V. Dipolar interaction in ordered superlattices of ferromagnetic nanoparticles. Phys. Status Solidi B-Basic. Res. 2010, 205, 1787–1789. [Google Scholar] [CrossRef]
- Turov, E.A.; Shavrov, V.G. Broken symmetry and magnetoacoustic effects in ferroand antiferromagnetics. Sov. Phys. Usp. 1983, 26, 593–611. [Google Scholar] [CrossRef]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef] [PubMed]
- Delplace, P.; Ullmo, D.; Montambaux, G. The Zak phase and the existence of edge states in graphene. Phys. Rev. B-Condens. Matter. 2011, 84, 5324–5326. [Google Scholar] [CrossRef]
- Kim, I.; Iwamoto, S.; Arakawa, Y. Topologically protected elastic waves in one-dimensional phononic crystals of continuous media. Appl. Phys. Express 2018, 11, 017201. [Google Scholar] [CrossRef]
- Feng, L.; Huang, K.; Chen, J.; Luo, J.C.; Huo, S. Magnetically tunable topological interface states for Lamb waves in one-dimensional magnetoelastic phononic crystal slabs. AIP Adv. 2019, 9, 115201. [Google Scholar] [CrossRef]
- Kivelson, S. Wannier functions in one-dimensional disordered systems: Application to fractionally charged solitons. Phys. Rev. B 2008, 26, 4269–4277. [Google Scholar] [CrossRef]
- Wang, H.X.; Guo, G.Y.; Jiang, J.H. Band topology in classical waves: Wilson-loop approach to topological numbers and fragile topology. New J. Phys. 2019, 2, 093029. [Google Scholar] [CrossRef]
- Blanco-Redondo, A.; Andonegui, I.; Collins, M.J.; Harari, G.; Segev, M. Topological Optical Waveguiding in Silicon and the Transition between Topological and Trivial Defect States. Phys. Rev. Lett. 2016, 117, 129901. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Sai, Y.; Chen, J. Tunable Lamb wave band gaps in two-dimensional magnetoelastic phononic crystal slabs by an applied external magnetostatic field. Ultrasonics 2016, 71, 69–74. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).