Abstract
The contributions of magnetohydrodynamic (MHD) vortexes to chiral electrodeposition in a vertical magnetic field were theoretically examined based on the three-generation model of the 2D nucleus, 3D nucleus, and screw dislocation; for the vortexes to rotate in the second and third-generation, the kinematic viscosity must be at least 10−18 and 10−30 times lower than the ordinary value in the first generation, i.e., almost equal to zero. This implies that the ionic vacancy created on the electrode surface works as an atomic-scale lubricant. At the same time, the vortexes played three roles: promotion and suppression of nucleation, and transport of the chirality from the upper generation to the lower generation through precessional motion. Then, the rule of the chirality transfer was established, and finally, the relationship between the chiral activity and magnetic field was clarified in the presence and absence of chloride ions.
1. Introduction
In an electrode reaction under a vertical magnetic field, a tornado-like macroscopic rotation called vertical magnetohydrodynamic (MHD) flow (VMHDF) appears on a disk electrode (vertical MHD electrode (VMHDE)). On the electrode surface under a VMHDF, numerous microscopic vortexes called micro- and nano-MHD flows are formed, accompanied by the rotations of microbubble clusters originating from ionic vacancies produced by electrode reactions [1,2,3].
Ionic vacancies are created for conserving the linear momentum and electricity in the electron transfer of an electrode reaction, and initial naked vacancies, i.e., embryo vacancies, are formed in a free space [4,5]. Charged particles such as embryo vacancies are energetically unstable in a solvent, so they are quickly solvated by emitting solvation energy and enveloped by ionic clouds. Using the energy, ionic vacancies make their cores become enlarged, so the solvation energy is stored in them without entropy production. As shown in Figure 1, a vacancy core of about 0.1 nm is composed of a free space surrounded by polarized solvent molecules. An ionic vacancy migrates among solvent molecules by repeating shrinking and expanding reversibly without entropy production. This means that an ionic vacancy does not interact with surrounding solvent molecules, working as an atomic-scale lubricant. In other words, there is no energy dispersion in this diffusional motion. This is experimentally validated because the natural lifetime of an ionic vacancy is about 1 s [6,7], which is extraordinarily long compared with the collision frequency of solvent molecules of 10−10 s. Therefore, a vacancy layer formed under a VMHDF is expected to have superfluidity similar to that of liquid helium.
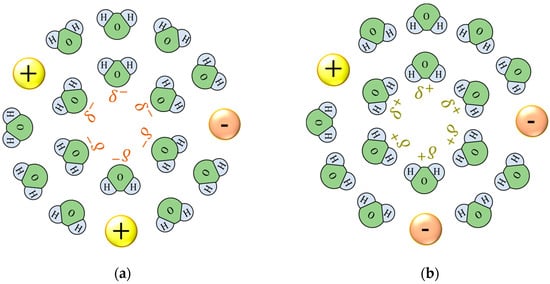
Figure 1.
Solvated ionic vacancies. (a) Negative vacancy. (b) Positive vacancy. H: proton; O: oxygen atom; and : partial polarized charges of water molecules surrounding the free spaces; ⊕: cation;  : anion.
: anion.
Copper electrodeposition under a vertical magnetic field gives rise to chiral screw dislocations with remarkable chiral activity caused by a VMHDF [1]. However, for the formation of chiral screw dislocations of the order of 0.1 nm from a VMHDF with a diameter of 1 cm, size control over eight figures was directly required, which seemed impossible. To solve such a difficulty, the three-generation model of chiral screw dislocation was proposed in Part 1 [1]; chiral two-dimensional (2D) nuclei arise from chiral vortexes of micro-MHD flows (~0.1 mm) as the first generation, then chiral three-dimensional (3D) nuclei are formed by chiral vortexes of nano-MHD flows (~0.1 μm) as the second generation, and finally, chiral screw dislocations are created by chiral ultra-micro vortexes (~0.1 nm) as the third generation. As shown in Figure 2, all three steps constitute a nesting box structure. The validity of this model was proven by the fact that a measure of the chiral activity, i.e., the enantiomeric excess (ee) ratio, cannot exceed a limiting value of 0.125 [1].
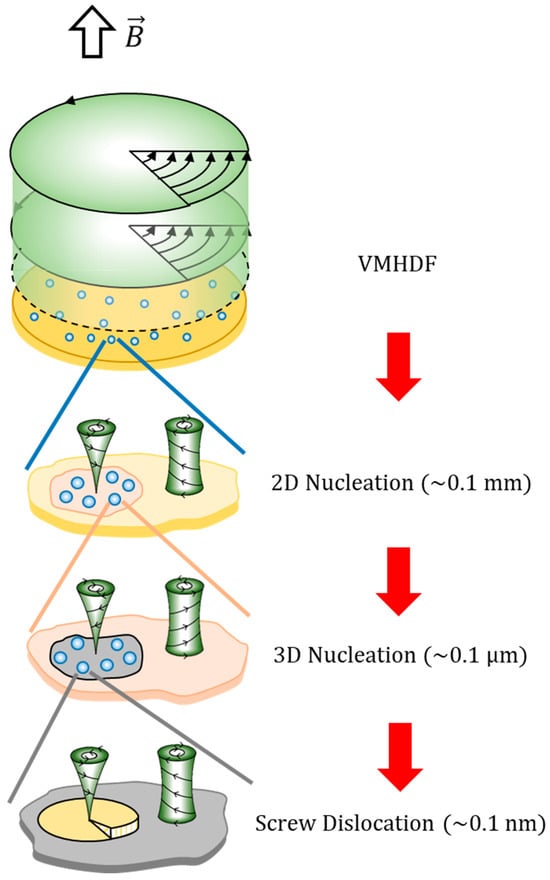
Figure 2.
The three-generation model of chiral screw dislocation in a nesting box structure [1]. , magnetic flux density.
Chiral vortexes in each generation are, as shown in Figure 3a, produced by a two-layer system; the upper layer rotates around a vertical axis, driven by the bottom of a vortex on a rigid-surface nucleus of the upper generation, which, in the present second generation, corresponds to the bottom of the micro-MHD vortex on a rigid-surface of the 2D nucleus. In contrast, the lower layer is kept stationary by the pinning effect of the frictions of the rigid-surface vortexes, i.e., nano-MHD vortexes on the rigid-surface 3D nuclei. The lower-layer vortexes are reproduced with the same rotations as the upper-layer vortexes through the boundary between the two layers. Some upper-layer vortexes revolve with the upper layer, receiving precession from the upper-layer rotation. Such precessional motion transfers back to the vortexes in the lower layer. As a whole, they form a positive feedback cycle between the two layers.
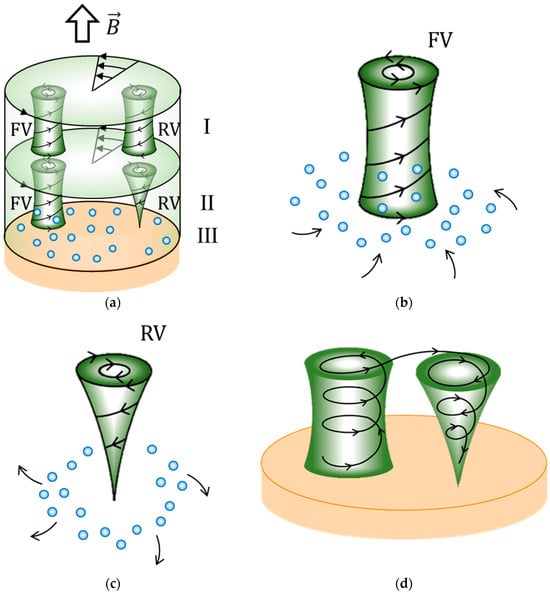
Figure 3.
The two-layer system for chirality transfer and two kinds of nano-MHD vortexes formed on the electrode surface. (a) Chiral transfer from the upper-layer vortex of the upper generation to the lower-layer vortexes of the lower generation. An unstable case in an upward magnetic field. (b) An upward free-surface vortex (FV). (c) A downward rigid-surface vortex (RV). (d) Pair formation of upward anticlockwise (ACW) and downward clockwise (CW) vortexes. I: rotating upper layer; II: stationary lower layer; III: electrode; light-blue sphere: ionic vacancy.
Here, the vortexes in the lower layer are composed of a pair of vortexes with rigid and free surfaces, which, due to local linear momentum conservation, correspond to downward and upward flows, respectively. As shown in Figure 3b,c, an upward flow gathers ionic vacancies produced at the electrode, making a free surface covered with ionic vacancies without friction, whereas a downward flow blows off the ionic vacancies, exposing a bare surface with friction. At the same time, due to the continuity of vortexes, i.e., the local conservation of angular momentum, they have anticlockwise (ACW) and clockwise (CW) rotations, and vice versa. Figure 3d represents the case of upward (free-surface) ACW and downward (rigid-surface) CW vortexes.
Which vortexes, ACW or CW, receive the precession depends on whether they are unstable or not; if they are unstable, the vortex without friction on the free surface develops faster than the vortex with friction on the rigid surface, so the free-surface vortex (FV) will receive the precession. The rigid-surface vortex (RV) subordinately rotates in the opposite direction. On the contrary, when they are stable, though the vortex without friction on the free surface quickly disappears, due to friction, the vortex on the rigid surface dwindles more slowly. This time, the rigid surface vortex will gain the precessional motion. The chirality transfer of the vortexes between the two layers shown in Figure 3a represents the unstable case under an upward magnetic field, i.e., the ACW rotation of the upper-layer provided by a rigid-surface micro-MHD vortex transfers to a free-surface nano-MHD vortex in the lower layer, so a rigid-surface nano-MHD vortex obtains a CW rotation, forming a CW 3D nucleus of the second generation.
As discussed above, chiral nuclei of the lower generation are created by the rigid-surface vortexes of the same generation under a rigid-surface vortex of the upper generation. Namely, chirality transfers from the upper generation to the lower generation through rigid-surface vortexes. Under the free-surface vortexes, the nucleation proceeds with the revolution of the vacancy layer on the electrode surface, so that no chiral nuclei emerge due to the lack of relative rotation. In the unstable case, the chiral rotations of the rigid-surface vortexes of the upper generation are transferred to the free-surface vortexes of the lower generation. However, the chirality of the lower-generation nucleus is determined by the rigid-surface vortex of the same generation, so the chirality is changed. On the contrary, in the stable case, the chirality of the rigid-surface vortexes of the upper generation directly transfers to the rigid-surface ones of the lower generation, i.e., the chirality is preserved.
In chiral deposition, vortexes in various scales play important roles. Here, we come up against a serious problem; the smaller the vortex is, the more difficult it is to rotate. In short, much smaller vortexes cannot exist due to increasing effective viscosity. However, fortunately, since ionic vacancies work as atomic-scale lubricants and form a vacancy layer with a thickness of around 1 μm, 3D nuclei with a size of about 0.1 μm are prepared by rigid-surface nano-MHD vortexes in a liquid with extremely low viscosity. As will be discussed later, theoretical calculation allows us to expect that the vortexes over 3D nuclei can rotate in a liquid with a kinematic viscosity less than 10−18 m2 s−1, which is 10−12 times smaller than the ordinary one (~10−6 m2 s−1). This means that the ultra-micro vortexes for chiral screw dislocations require almost zero viscosity.
Chiral magnetoelectrodeposition was first found by Mogi [8]; he and his coworkers have been experimentally clarifying the various aspects of the chirality evolution under magnetic fields [9,10,11,12,13,14,15,16,17,18,19,20,21], e.g., the dependence on magnetic field intensity, the effect on the presence and absence of chloride ions, and even the application in rotating systems. Based on these experimental results, in this paper, we theoretically examine the mechanism through which chiral activity arises from the various microscopic vortexes under a vertical magnetic field. As for magneto-electrochemistry, for about five decades, many researchers have been making great efforts to establish its foundations; electrode reactions under magnetic fields inevitably induce Lorentz forces, leading to many characteristic applications. For example, in calorimetry experiments, it is critically important to keep an experimental system iso-thermal. In this point, magneto-electrochemistry has a great advantage because the Lorentz force induces an MHD flow, in which mixing motion easily accomplishes a uniform distribution of temperature. Recently, using an electrode with a rectangular channel for an MHD flow called an MHD electrode, we succeeded in measuring the excess heat arising from the pair annihilation of ionic vacancies with opposite charges created at the cathode and anode [22,23,24]. The measured heat amounts were in good agreement with the theoretical calculation. In those cases, the Lorentz force not only mixes the ionic vacancies but also guides them to collision.
Several useful tools have been also developed for reaction analyses in magnetic fields [25,26,27,28,29,30,31,32]. Fahidy commented that an MHD flow decreases the thickness of a diffusion layer, enhancing mass transfer in an electrode reaction [29,30,31]. Olivier theoretically examined the MHD effect on microelectrodes [32,33,34,35] and conducted electrochemical impedance spectroscopy in a magnetic field [36,37]. White studied the MHD flow of ultra-micro-disk-electrodes in non-aqueous systems containing organic reactants [38,39,40]. Using flow visualization techniques in a magnetic field, Mutschke and co-workers examined electrodeposition in cuboid cells under magnetic fields accompanied by 3D convections affected by a gravitational field, which were compared with numerical simulations [41,42]. The contributions of the MHD flow to the phase compositions of composite metals have been investigated by many researchers (Oliver, Alemany, Daltin, Chopart, Hinds, Coey, and Zabiński) [43,44,45,46,47,48,49,50,51]. As a remarkable magneto-electrochemical effect, we can cite the magneto-convection by the gradient field force under a heterogeneous magnetic field, which promotes the mass transfer process in an electrode reaction [52,53,54]. Tschulik, Uhlemann, and Mutshchke, as well as Dunne and Coey, clarified that a superimposed Lorentz force donates more complicated effects to deposit patterns and compositions [55,56,57,58,59]. As mentioned above, effective MHD flows under parallel magnetic fields are provided by the MHD electrode (MHDE) [60,61,62]. The velocity and concentration distributions of the electrode are expressed by simple equations of velocity and the limiting diffusion current. As Fahidy said, the agreement between the theory and the experimental result is excellent [29].
In recent days, various studies on the transport of microscopic materials in solutions by using MHD forces have been reported. Kuhn et al. proposed an efficient alternative mechanism with which to power self-electrophoretic Mg/Pt Janus swimmers based on the Lorentz force and designed a self-propelled bimetallic Janus rotor and a wireless magnetoelectrochemical rotor [63,64,65]. Celzard et al. proposed self-propelled particles based on the MHD acceleration of the surrounding fluid [66]. Fritsch et al. designed analysis systems with microfluidics based on the redox MHD concept and proposed a method for combining dark-field microscopy with self-contained redox MHD microfluidics to facilitate single-particle analysis in mixtures of dispersion single-nanoparticle populations [67,68].
In the present paper, we first examine the similarity of the various MHD vortexes in the three generations, and derive the relationship between the representative length and the kinematic viscosity, determining the effective values of viscosity in each generation. Then, we establish the instability equations of 3D nucleation under nano-MHD vortexes in the second generation. Finally, using the equations, we present a general method to determine the chirality under a VMHDF in the absence and presence of chloride ions.
2. Theory
Briefly, 3D nuclei grow on a 2D nucleus formed in an electric double layer, developing the diffusion layer outside the electric double layer [69,70,71]. As the reaction proceeds, the physical quantities concerned change, approximately expressed by symmetrical fluctuations, i.e., changes around their average values [71].
For example, the concentration fluctuation of the metallic ion is defined by the following:
where superscript “s” implies a symmetrical fluctuation. and are the molar concentration and its average value, respectively. The sign “” means the average over the electrode surface. As shown in Figure 4a, at the equilibrium potential, , the concentration itself and the concentration gradient fluctuate toward the positive and negative sides of their equilibrium values. However, when the electrode potential deviates to a cathodic direction, , as shown in Figure 4b, the electrodeposition proceeds on 3D nuclei and they one-sidedly fluctuate. Only negative and positive components of the fluctuations survive. This means that in a non-equilibrium state, either side of the amplitude of the equilibrium fluctuation is cut off, which depends on whether the cathodic or anodic phase cutting of symmetrical fluctuations occurs. The phase cutting is, as will be shown later in computer graphics, important for creating a cut surface on the 3D nucleus without roughening via diffusion.
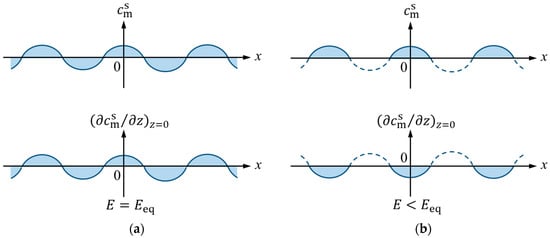
Figure 4.
Schematics of symmetrical concentration fluctuation and its gradient fluctuation of deposit metal ion. (a) Both-sided fluctuations at the equilibrium potential, . (b) One-sided fluctuations at a cathodic overpotential, . : symmetrical concentration fluctuation at the electrode surface; : symmetrical concentration gradient fluctuation at the electrode surface.
As for vortexes, as exhibited in Figure 3, vortexes having downward and upward flows correspond to rigid- and free-surface vortexes, respectively. That is, the signs of the z-components of the velocities of the rigid- and free-surface vortexes are fixed as and , respectively, where the subscripts “r” and “f” indicate rigid- and free-surfaces. Figure 3d indicates that to conserve the local angular momentum, a pair of vortexes with upward and downward flows rotate in opposite directions to each other, which means that the z-components of the vorticities of a vortex pair must have different signs, and or and . Adopting a right-handed system with an upward magnetic field, we can define the negative and positive z-components of the vorticities as CW and ACW rotations. As a result, as shown in Figure 5, the vortexes in the lower layer are simply classified into two sets, where the phase-cutting quantities in the x-direction are schematically exhibited.
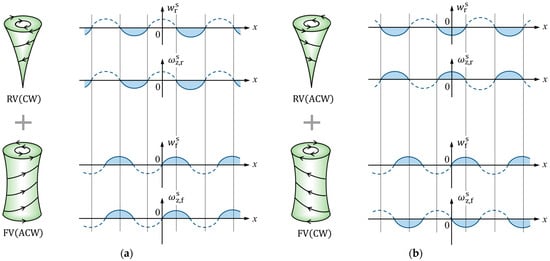
Figure 5.
Two sets of the nano-MHD vortex pairs formed on the rigid and free surfaces. (a) Clockwise (CW)–anticlockwise (ACW) vortex pair. (b) ACW–CW vortex pair. : rigid-surface vortex, : free-surface vortex. : z-velocity component of the RV, : z-vorticity component of the RV, : z-velocity component of the FV, : z-vorticity component of the FV.
2.1. Similarity of the MHD Vortexes in the Three Generations
2.1.1. Vorticity Coefficient Functions (VCF)
The motion of MHD vortexes under a VMHDF is described by the vorticity coefficient function (VCF) established in Part 1 [1], which works as the characteristic function of the lower generation vortexes, controlling vortex instability. Using the functions, we can examine the similarity of each generation of vortexes. From now on, for similarity, we use the nondimensional wavenumber as “a” without superscript a and s, implying asymmetrical and symmetrical fluctuations in the first and second generations.
For rigid-surface vortexes, we have the three-generation functions:
The function is expressed by the ratio of the torque component from the Lorentz force to the total torque of the vortexes. Here, the coefficients , , and are defined by the following:
and
where for 1st, denotes the ordinary kinematic viscosity of the electrolyte solution (, and for 2nd and 3rd, denotes the effective kinematic viscosity of a vacancy layer formed on the electrode. As has been discussed in the introduction, due to atomic-scale lubricants, for ionic vacancies, the value greatly decreases down to zero. is the representative angular velocity of the rigid-surface vortexes of the upper generation, i.e., non, a and s indicate VMHDF, micro-MHD vortexes, and nano-MHD vortexes, respectively. is the external magnetic flux density, is the concentration gradient, and is the diffusion coefficient of metallic ions. is the electric conductivity, is the solution density, and is the representative length of the i-generation.
Then, from Part 1 [1], , and are given by the following:
where is the charge number of the deposit ion, and F is the Faraday constant.
For free-surface vortexes, we obtain the following:
where , and are given by the following:
The vortex rotations are controlled by the second terms of the denominators of Equations (2) and (5) arising from the precession by an upper-generation rigid-surface vortex, and the similarity of the vortexes of the three generations depends on the representative length, , and the kinematic viscosity, .
In the following, to examine chiral similarity, we extract and from Equations (2) and (5). For simplicity, except for the sign, the angular velocity of the upper-generation rigid-surface vortex, , is equalized to that of a VMHDF, . Then, the following parameters are rewritten as follows:
where is defined by
and the parameters , and are defined by
Therefore, we obtain the relationship:
For rigid-surface vortexes, the function controlling vortex rotations is expressed by the following:
The function corresponds to the torque component of the rigid-surface MHD vortexes activated by the applied magnetic field, whereas is the torque component of the precession from the upper-generation rigid-surface MHD vortexes.
and
As a result, the function in Equation (2) is rewritten as follows:
Namely, the similarity of vortex rotations between the three generations is concentrated to which determines the lower-generation vortex motion, expressed by the following:
As decreases with lower generations, Equation (13) reveals that the contribution from the magnetic activation of the vortexes also decreases. To maintain a similar vortex motion though decreasing , in Equation (12) must therefore be kept in the same function form, i.e., the value of must be almost the same in any generation.
For free-surface vortexes, the function of the vortex rotation, , in Equation (6c) is expressed as follows:
The function is the magnetic field component of the free-surface vortex torque, and is the precession component. Namely, we have the following:
and
As a result, the function in Equation (5) is rewritten as follows:
In the same way as Equation (13), the similarity is concentrated to , i.e.,
For free-surface vortexes to keep the similarity, the term must be almost the same in all generations. The characteristic functions, VCFs of the MHD vortexes in Equations (12) and (16), indicate the ratio of the Lorentz force–torque component to the total torque. The total torques of the denominators in Equations (12) and (16) are composed of Lorentz force torque and induced vortex torques. Concerning the vortex torques, as shown in Equations (13) and (17), the MHD vortexes are induced via magnetic activation and the precession by the rotation of the upper-generation rigid-surface MHD vortex.
The induced vortex-torque component on the rigid surface with friction is larger than that on the free surface without friction. Namely, we have the following relationship:
This relationship leads to the difference between the rigid- and free-surface vortex motion.
2.1.2. Occurrence of Chiral Symmetry
The induced vortex torques change the sign depending on the rotational direction of the upper-generation rigid-surface vortex, , which is more generally expressed by for a right-handed system and for a left-handed system. Namely, because the term is proportional to , the functions in Equations (12) and (16) are continuous for wavenumber for the right-handed system, , whereas they have singular points of for the left-handed system,
However, considering the case where the induced vortex torques are dominant over the Lorentz force torque, we can make the singular point disappear. Equations (12) and (16) are therefore expressed as follows:
and
Therefore, for the right-handed system, we obtain
and for the left-handed system, we obtain
From Equation (18), the following relationship is satisfied:
2.1.3. Conservation of Chiral Vortex Motion in the Three Generations
The representative length, , decreases with each generation. Under a constant kinematic viscosity, , in Equations (13) and (17), the induced vortex torque components and converge to zero with decreasing . This is because the effective viscosity increases with decreasing representative length. Actually, in Equations (12) and (16), under a constant , as approaches zero, we have
and
These results indicate that at the lower limit of , as will be shown later, the induced vortexes vanish.
In Equations (13) and (17), the induced vortex torque components are further separated by the magnetic activation and precession components, which decrease with and , respectively. For the induced vortexes to survive though decreasing , the kinematic viscosity, , must also decrease in proportion to
In the case of the first-generation , for m, an ordinary value for kinematic viscosity, m2 s−1 is assumed, so we have the following:
According to this situation, in the second-generation of m, assuming m2 s−1, we obtain m2 s. In the third generation of m, with m2 s−1, we derive the same value of m2 s. As shown here, the actual high chiral activity obtained via copper deposition strongly requires a non-viscous vacancy layer to be formed on the electrode. In Figure 6, the VCFs in the three generations are plotted against the nondimensional wavenumber, . As discussed in Equations (21a) and (21b), for the right-handed system, the VCFs take positive values, whereas the VCFs of the left-handed system become negative. Then, as pointed out in Equation (21c), the absolute value of the VCF on the free surface is larger than that of the VCF on the rigid surface. Under the present condition of Equation (23), the VCFs of the second and third generations are consistent with each other.
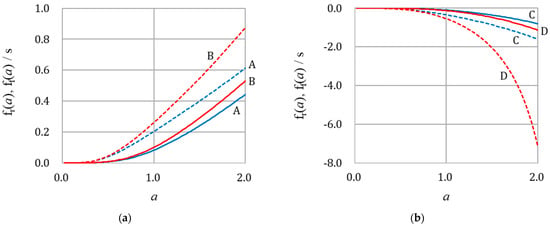
Figure 6.
Vorticity coefficient functions (VCFs) in the three generations under condition m2 s. (a) For the right-handed system. A: the 1st generation. Blue solid line: ; blue break line: . B: the 2nd and 3rd generations. Red solid line: ; red break line: . (b) For the left-handed system. C: the 1st generation. Blue solid line: ; blue break line: . D: the 2nd and 3rd generations. Red solid line: ; red break line: . Here, and in the 3rd generation are consistent with and in the 2nd generation. Calculation data: for the 1st generation, = 10−4 m and = 10−6 m2 s−1; for the 2nd generation, = 10−7 m and = 10−18 m2 s−1; and for the 3rd generation, = 10−10 m and = 10−30 m2 s−1. Other data: = 5 T, = 6.28 s−1, = 3.6 × 10−4 m, = 2, = 6.0 × 10−10 m2 s−1, = 50.0 mol m−3, = 96,485 C mol−1, = 0.8312 J K−1 mol−1, = 300 K, = 1.073 × 103 kg m−3, and = 10.0 Ω−1 m−1.
2.2. Characteristic Equations of 3D Nucleation under Nano-MHD Vortexes
In the second generation, the characteristic equations of 3D nucleation under nano-MHD vortexes control the instability of the 3D nucleation and nano-MHD vortexes, which are, as will be mentioned later, described by the characteristic equation of 3D nucleation in a stationary solution multiplied by the VCFs of the rigid-surface and free-surface nano-MHD vortexes. Therefore, we first examine the 3D nucleation in a stationary solution.
2.2.1. Surface Height Equation in 3D Nucleation
In Figure 7, the 3D nucleation process on the surface of a 2D nucleus in a stationary solution is exhibited. Assuming that the mass transfer is rate-determining, we will treat the electron transfer process in a quasi-equilibrium state. The mass balance between the adatoms and the metallic ions comes from the mass flux density, , of the metallic ion from the solution phase to the electrode surface, the mass flux density of the adatom, , by the surface diffusion and the mass flux density, , of the adatom by the incorporation into the crystal lattice [72,73,74,75].
where denotes the symmetrical fluctuation of the adatom concentration, is the unit normal vector of the electrode surface, and is defined by .
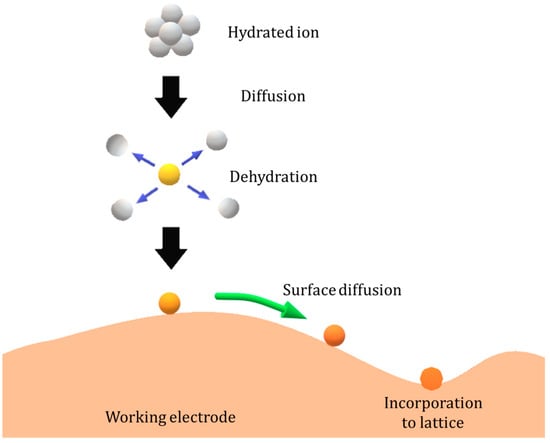
Figure 7.
The 3D nucleation process on the surface of the 2D nucleus in a stationary solution [71].
Using the surface diffusion coefficient, , and the equilibrium surface concentration of the adatom, , we can write the mass flux density of the adatom along the surface as follows:
where R and T are the universal gas constant and absolute temperature, respectively. expresses the fluctuation of the chemical potential of the adatoms by the change in surface height, i.e.,
where , is the molar volume of the depositing metal, is the isotropic surface free energy, and is the surface height fluctuation of the deposit surface. The flux density of the metallic ion at the interface is given as follows:
where indicates . The sign of the flux density is defined as a plus sign in the case of deposition.
Finally, the surface deformation rate is determined by the deposition rate and mass flux density of the adatom as follows:
The substitution of Equations (25) to (28) into Equation (24) leads to the surface–height equation.
where represents .
2.2.2. Electrochemical Boundary Conditions
As has been discussed above, the electron transfer is assumed to be in quasi-equilibrium.
where and are the adatom and the metallic ion at the inner Helmholtz plane (IHP), respectively. is a free electron in the electrode, and is the charge number of the metallic ion.
According to Equation (30), their chemical and electrochemical potentials are related to the following:
where is the chemical potential of the adatoms, is the electrochemical potential of the metallic ions, and is the electrochemical potential of the electrons. denotes , i.e., the surface height fluctuation via 3D nucleation.
Here, if a minute projection by the electrodeposition accidentally happens in the diffusion layer, the concentration of the metallic ions fluctuates around it, as expressed by Equation (1). The fluctuation of the free electrons in the metal phase is neglected due to their large mobility in light speed, so the fluctuation of the chemical potential of the adatoms is expressed by the fluctuation of the electrochemical potential of the metallic ions.
At the top of the projection, the chemical potential of the adatoms also fluctuates according to Equation (26):
On the other hand, the fluctuation of the electrochemical potential of the metallic ions induces the fluctuation of the concentration overpotential arising from the projection.
where F is the Faraday constant, and denotes the fluctuation of the concentration overpotential, expressed by the following Nernst-type equation:
where is the bulk concentration.
The fluctuation is explicitly written as follows:
where represents the average surface concentration equal to , where the asterisk means electrostatic equilibrium. To derive Equation (36), we assumed the condition The concentration fluctuation at the top of the projection is expanded in the first order for .
where represents the average concentration gradient in the diffusion layer.
where is the concentration difference between the bulk and surface, i.e.,
and is the average diffusion layer thickness.
Substituting Equations (26) and (33) into Equation (32), and inserting Equations (34), (36), and (37a) into the resulting equation, we obtain the electrochemical boundary condition for the symmetrical fluctuations.
2.2.3. Characteristic Equations of the Nano-MHD Vortexes and 3D Nuclei
Equations (29) and (38) are transformed via Fourier transformation concerning x- and y-coordinates into the following amplitude equations:
and
where and denote the amplitudes of and on the rigid surface (j = r) and the free surface (j = f), respectively, and indicates . k denotes the wavenumber defined by and and are the x- and y-components of the wavenumber, respectively.
Substituting from Equation (39b) into Equation (39a), we obtain the amplitude equation of the concentration fluctuation:
Here, using the representative length, , of 3D nucleation in the second generation, we introduce the nondimensional wavenumber, , as well as the nondimensional coordinates x, y, and z. Equation (40a) is therefore revised as follows:
where the nondimensional parameters are defined by , and . In the following, introducing the vorticity coefficient functions, VCFs, of the rigid- and free-surface nano-MHD vortexes, we obtain the characteristic equations of rigid- and free-surface nucleation with nano-MHD vortexes in the second generation.
As was shown initially, since a symmetrical fluctuation is essentially one among the asymmetrical fluctuations, from the general amplitude equation of the asymmetrical concentration fluctuation based on the two-layer system formulated in Part 1 [1], we can derive the amplitude equation of the symmetrical concentration fluctuation on the rigid and free surfaces as follows:
where is the vorticity coefficient of the rigid-surface (i = 1) and free-surface (i = 0) vortexes, and is the vorticity coefficient function, VCF, of the rigid-surface (j = r) and free-surface (j = f) nano-MHD vortexes. In Part 1 [1], they were generally used in the equations of the amplitudes, , of the z-components of the vorticity fluctuations, , i.e., and . From Part 1, the gradient of the amplitude of the symmetrical concentration fluctuation is also obtained via the following:
Substituting Equations (41a) and (41b) into Equation (40b), we have the characteristic equation of the vorticity coefficient, :
Here, as shown in Equations (22a) and (22b), the VCFs converge to with decreasing representative length, . This result indicates that the activated MHD vortexes vanish as decreases with the lower generation.
When the average surface concentration is regarded as constant, i.e., under a potentiostatic condition, Equation (42a) is solved as follows:
where denotes the amplitude factor of the rigid- and free-surface vortexes. As will be shown later, if the amplitude factor, , is positive for some of the wavenumber , the vortex coefficient, , increasing with time gives rise to unstably growing nano-MHD vortexes. However, when is kept negative for all values, all of the values decreasing with time lead to stably dwindling vortexes. The instability of the nano-MHD vortexes depends on the sign of the amplitude factor,
A similar relationship to that in Equation (42a) concerning the surface height fluctuation is also obtained; from Equations (41a) and (41b), we have the following:
Substituting Equation (43) into Equations (39a) and (39b), and adding the resulting equations together, we obtain the amplitude equation of the surface height fluctuation:
Equation (44a) is similar to Equation (42a), so we also obtain the following equation:
Namely, the surface height fluctuation is also controlled by the same amplitude factor, , which is defined by the following:
Under limiting diffusion, i.e., , Equation (45a) is simplified via the following:
The first term on the right-hand side of Equation (45b) is the main part of the amplitude factor, and the second term is the additional one expressing the suppression by surface diffusion [76]. Therefore, the sign of is mainly determined by the first term. As mentioned above, inserting the stationary-solution condition, , in Equations (22a) and (22b) into Equations (45a) and (45b), we can make the amplitude factor exist in a stationary solution [69,70,71]. In the case of cathodic deposition, the concentration gradient, , is positive and considered to consist of the main part, so becomes positive for a certain wavenumber range. Namely, 3D nucleation in a stationary solution is always unstable. On the other hand, the vorticity coefficient function, VCF, , indicates the contribution of the nano-MHD vortexes to 3D nucleation. As shown in Figure 6, it takes positive and negative values for right- and left-handed systems of the upper generation, respectively, so the MHD vortexes sometimes promote and sometimes suppress the instability. This behavior of MHD vortexes is different from the behavior under a parallel magnetic field; the MHD vortexes under a parallel magnetic field only give rise to suppression [72].
Therefore, in general, the instability of the nucleation under MHD vortexes is determined by the sign of the product of the main part of the amplitude factor in a stationary solution of the VCF, i.e., positive and negative correspond to unstable and stable for the MHD vortexes and nucleation in each generation. This process is simply expressed in a schematic form:
where NI denotes nucleation instability, MHDV represents the MHD vortex, and S.S. represents a stationary solution. “[ ]” expresses the sign of each term. It should be noted that Equation (46) also expresses the instability of the MHD vortexes themselves.
3. Results and Discussion
As was shown in Part 1 [1], in the first generation, the micro-MHD vortexes unstably develop with 2D nuclei under a VMHDF. Since the rotation of the VMHDF forms a right-handed system with the external magnetic field, , as shown in Equation (21a), the VCFs of the micro-MHD vortexes are defined as positive functions, for j = r and f. In the absence of chloride ions, 2D nucleation is unstable in a stationary solution [65], so the main part of the amplitude factor in a stationary solution is positive. BY Equation (46), the instability of 2D nucleation under micro-MHD vortexes is therefore defined by the sign of the product of the stationary-solution main part of the VCF, i.e., due to the derived positive values, the micro-MHD vortexes unstably develop together with 2D nuclei. Namely, the instability of 2D nucleation in a stationary solution is promoted by the micro-MHD vortexes.
Since the value, as well as the sign of the amplitude factor under MHD vortexes is approximately determined by the same product, the difference in the instability strength between the rigid-surface and free-surface vortexes results from the values of the corresponding VCFs. As has been discussed in Equation (21c), they generally have the relationship in every generation “i”, i.e., the absolute value of the free-surface VCF is larger than that of the rigid-surface VCF. This means that in the unstable case, the positive free-surface amplitude factor is larger than the positive rigid-surface amplitude factor. Namely, the free-surface micro-MHD vortexes grow faster than the rigid-surface ones, so the free-surface ones preferentially receive the precession from the upper generation vortex, VMHDF, rotating in the same direction.
As mentioned initially, chiral nucleation occurs only on the rigid surfaces because the free surfaces rotating with the vortexes yield no chirality. Then, to conserve a local angular momentum, as shown in Figure 3d, a pair of rigid- and free-surface vortexes rotate oppositely. Therefore, following the precessional rotation of the free-surface micro-MHD vortexes, the rigid-surface micro-MHD vortexes rotate in the opposite direction, forming a left-handed system, , with the external magnetic field. As a result, the first-generation 2D nuclei under the rigid-surface micro-vortexes are created with opposite chirality to that of the VMHDF.
At the same time, the left-handed system of a rigid-surface micro-MHD vortex leads to negative VCFs of the nano-MHD vortexes in the second generation, i.e., < 0 for j = r and f in Equation (21b). As discussed above, 3D nucleation in a stationary solution is always unstable, i.e., the main part of the amplitude factor, the concentration gradient in Equation (45b), is kept positive so that the products of the main part of the VCFs, i.e., the main parts of the amplitude factors under nano-MHD vortexes, become negative, < 0. This time, the unstable 3D nucleation in a stationary solution is stabilized by the nano-MHD vortexes. From Equation (21c), the relationship is derived, so concerning the main parts of the nano-MHD vortexes under the rigid-surface micro-MHD vortexes, the relationship, is derived. According to Equations (42b) and (45b), the rigid-surface nano-MHD vortexes dwindle more slowly than the free-surface ones. Therefore, the precession from the rigid-surface micro-MHD vortex directly transfers to the rigid-surface nano-MHD vortexes, forming a left-handed system again in the third generation. From these discussions, it is concluded that in stable nucleation, lower-generation rigid-surface vortexes obtain the same chirality as upper-generation rigid-surface vortexes, whereas they receive the opposite chirality in the unstable case. Figure 8 exhibits the amplitude factors of 3D nucleation in a stationary solution and the amplitude factors under nano-MHD vortexes in the right-handed and left-handed systems. Though the left-handed system is derived from the case without chloride ions, as will be discussed later, the right-handed system corresponds to the case with chloride ions. As shown in Figure 8b,c, the former and latter lead to stable and unstable 3D nucleation, changing chirality.
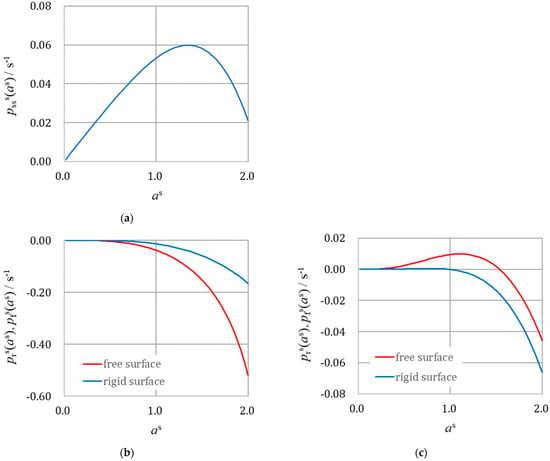
Figure 8.
The amplitude factors of the 3D nuclei in a stationary solution and under nano-MHD vortexes in the absence and presence of chloride ions in the 2nd generation. (a) The case of a stationary solution. of 3D nuclei in a stationary solution. (b) The case of a right-handed system (corresponding to the absence of chloride ions). Blue line: of 3D nuclei under rigid-surface vortexes. Red line: of 3D nuclei under free-surface vortexes. (c) The case of a left-handed system (corresponding to the presence of chloride ions). Blue line: of 3D nuclei under rigid-surface vortexes. Red line: of 3D nuclei under free-surface vortexes. Calculation data: for the 2nd generation, = 10−7 m and = 10−18 m2 s−1. Other data: = 5 T, = 6.28 s−1, = 3.6 × 10−4 m, = 2, = 6.0 × 10−10 m2 s−1, = 50.0 mol m−3, = 96,485 C mol−1, = 0.8312 J K−1 mol−1, = 300 K, = 1.073 × 103 kg m−3, = 10.0 Ω−1 m−1. = 0.3 J m−2, = 1.0 10−10 m s−1, = 1.0 10−6 mol m−2, and = −0.4 V.
In the third generation, though the detailed mechanism has been not yet established, screw dislocations were created by some instability based on the mass transfer and electrode reaction, which we could discuss in the same way: In the absence of chloride ions, because the screw dislocation process in a stationary solution is unstable [77], the main part of its amplitude factor must be positive. However, due to the left-handed system of the rigid-surface nano-MHD vortex, the VCFs of the ultra-micro-MHD vortexes forming the screw dislocations become negative functions. As a result, the main part of the amplitude factors of the screw dislocations under the ultra-micro-MHD vortexes are determined as negative, i.e., they are stable, so the rigid-surface ultra-micro-MHD vortexes show the same chirality of the left-handed system as that of the rigid-surface nano-MHD vortexes. This result represents that, as shown in the experimental results obtained by Mogi and coworkers [8,9,10,11,12,13,14,15,16,17,18,19,20,21], the CW activity (D-activity) and ACW activity (L-activity) of the deposit surface appear under antiparallel (upward) and parallel (downward) magnetic fields, respectively.
On the contrary, in the presence of chloride ions, as has been shown in Part 1 [1], due to the specific adsorption of chloride ions in the electric double layer, the micro-MHD vortexes and 2D nucleation turn stable, so the rigid-surface micro-MHD vortexes in the first generation directly progress toward the chirality of the VMHDF, i.e., the rotation of the right-handed system of the VMHDF with the external magnetic field is inherited in the first generation. The VCFs of the micro-MHD vortexes therefore become positive functions in the second generation. However, as mentioned above, whether chloride ions are present or not, 3D nucleation in a stationary solution is always unstable, so the main part of the amplitude factor in a stationary solution is kept positive. This time, due to the positive products of the positive main part of the positive VCFs, the nano-MHD vortexes and 3D nucleation become unstable, so the rigid-surface nano-MHD vortexes of the second generation obtain the opposite chirality to that of the rigid-surface micro-MHD vortexes of the first generation, i.e., the left-handed-system’s chirality. Therefore, the VCFs of the ultra-micro vortexes of the third generation become negative functions. Here, as for screw dislocation, chloride ions are well-known leveling reagents for copper deposition, which make copper screw dislocations vanish and become stabilized in a stationary solution [77]. This implies that the main part of the amplitude factor of screw dislocation in a stationary solution takes a negative value. The positive products of the negative main part of the negative VCFs lead to the instability of screw dislocation and ultra-micro MHD vortexes. At the same time, this instability gives rise to the change in chirality from the left-handed system to that of the right-handed system; the chiral activity of screw dislocations is reversed via the addition of chloride ions.
In the three-generation model without chloride ions, the chiral activity of screw dislocations in the third generation is therefore consistent with that of the rigid-surface 2D nucleus shown in the first generation: For a positive magnetic field, , i.e., for an upward antiparallel magnetic field, ACW (VMHDF) CW (2D nucleus) CW (3D nucleus) CW (screw dislocation). For a negative magnetic field, i.e., for a downward parallel magnetic field, , CW (VMHDF)CW (2D nucleus) ACW (3D nucleus) ACW (screw dislocation). Namely, under an upward (anti-parallel) magnetic field , D-activity emerges, whereas under a downward (parallel) magnetic field , screw dislocations with L-activity are produced. In the presence of chloride ions, the chiral activity of screw dislocations in the third generation is changed to reverse one: For an upward antiparallel (positive) magnetic field, , ACW (VMHDF) ACW (2D nucleus) CW (3D nucleus) ACW (screw dislocation). For a downward parallel (negative) magnetic field, , CW (VMHDF) CW (2D nucleus) ACW (3D nucleus) CW (screw dislocation). In the presence of chloride ions, due to specific adsorption on the electric double layer, we can expect that inversed chirality appears, depending on the direction of the magnetic field, i.e., for and , L-activity and D-activity arise, respectively.
The above discussions are summarized as follows:
- (1)
- The rigid-surface vortex rotation, , of the upper generation, “i” and the external magnetic field, forms a right-handed system, , 0 or a left-handed system, 0. The vorticity coefficient function, , of the lower generation, “i+1”, is defined as a positive function, 0, for 0 and a negative function, , for 0.
- (2)
- The main part (MP) of the amplitude factor in a stationary solution (S.S.) in the lower generation, , is defined as positive, or negative, , depending on whether the nucleation in a stationary solution is “unstable” or “stable”.
- (3)
- The nucleation under the rigid-surface vortexes is determined to be unstable for and stable for .
- (4)
- For the unstable case, , the chirality of the lower generation, ‘i+1”, is changed from that of the upper generation, “i”, and for the stable case, , the chirality of the present lower generation, “i + 1”, preserves that of the upper generation, “i”. In Figure 9, we exhibit the flow chart for MHD vortexes to obtain chirality in the three generations and the actual chirality obtained in each generation in the absence and presence of chloride ions.
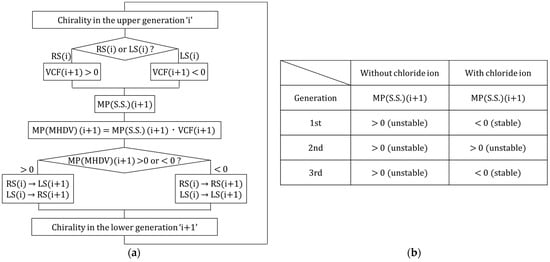
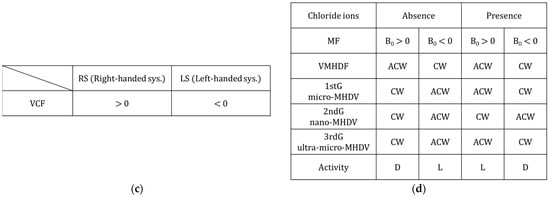 Figure 9. Flow chart for MHD vortexes to obtain chirality in the three generations. (a) Flow chart of how to determine the chirality in the three generations. (b) Signs of the main parts of the amplitude factors in a stationary solution, (MP(S.S.)(i + 1)), in the three generations. (c) Sign of the vorticity coefficient function (VCF) in the right-handed system (RS) and the left-handed system (LS). (d) Chirality obtained in each generation in the absence and presence of chloride ions. RS: right-handed system, LS: left-handed system. MP(S.S.): the main part of the amplitude factor in a stationary solution; MP(MHDV): the main part of the amplitude factor under MHD vortexes. MF: magnetic field; VMHDF: vertical MHD flow; MHDV: MHD vortex. 1stG: 1st generation; 2ndG: 2nd generation; 3rdG: 3rd generation. D: D-activity; L: L-activity. “i” and “i + 1” indicate the quantities in the upper and lower generations.
Figure 9. Flow chart for MHD vortexes to obtain chirality in the three generations. (a) Flow chart of how to determine the chirality in the three generations. (b) Signs of the main parts of the amplitude factors in a stationary solution, (MP(S.S.)(i + 1)), in the three generations. (c) Sign of the vorticity coefficient function (VCF) in the right-handed system (RS) and the left-handed system (LS). (d) Chirality obtained in each generation in the absence and presence of chloride ions. RS: right-handed system, LS: left-handed system. MP(S.S.): the main part of the amplitude factor in a stationary solution; MP(MHDV): the main part of the amplitude factor under MHD vortexes. MF: magnetic field; VMHDF: vertical MHD flow; MHDV: MHD vortex. 1stG: 1st generation; 2ndG: 2nd generation; 3rdG: 3rd generation. D: D-activity; L: L-activity. “i” and “i + 1” indicate the quantities in the upper and lower generations.
The experimental result of copper deposition onto a copper electrode with a larger diameter of 3 mm in a copper sulfate solution from a study by Mogi and coworkers told us that the reversal of chirality by adding chloride ions is partial, i.e., only in the upward magnetic field does D-activity change to L-activity, whereas L-activity in the downward magnetic field keeps the same chirality [14,20,21]. This result strongly suggests disturbance from magneto-convection by a gradient field force, which is induced from the magnetic field gradient applied to a paramagnetic material, being dependent on the magnetic field direction. A copper sulfate solution is paramagnetic, and it is well known that the characteristic magneto-convection arises through a vertical magnetic field gradient [54].
Finally, following Appendix A, the surface morphology of 3D nuclei in the second generation was calculated. Figure 10a shows a calculated 3D nucleus formed on a rigid electrode surface under an antiparallel upward magnetic field . Under a stable CW nano-MHD vortex, though not the third generation, a screw dislocation-like 3D nucleus with chirality is formed. The clear-cut surfaces without obscurity due to diffusion come from the phase cutting of the symmetrical fluctuation shown in Figure 4. This result suggests that the chiral screw dislocations of the third generation also evolve from the formation process, similar to the chiral 3D nuclei of the second generation. At this time, a question is brought about: how should we determine the chirality of it? Namely, when climbing up the slope shown in Figure 10a, we turn anticlockwise. However, we must turn clockwise to go down it. The nucleus grows under a rigid-surface nano-MHD vortex, which has, as shown in Figure 3c, a downward flow. An enantiomeric reagent also approaches downwards, so the chirality should be defined as a system with a downward direction, i.e., for the present case, CW chirality and D-activity are derived. Figure 10b is a deposit surface of the second generation after 100 rounds of nucleation. In every nucleation, chiral 3D nuclei are formed at fixed points on the rigid surfaces, whereas on the free surfaces covered with ionic vacancies, due to rotation with the micro-MHD vortexes, nuclei without chirality are developed.

Figure 10.
Three-dimensional nuclei calculated via complex Fourier transform in the absence of chloride ions. (a) A screw dislocation-like 3D nucleus under a CW rigid-surface nano-MHD vortex under an antiparallel upward magnetic field. The down arrow indicates a downward direction. The rotating arrow indicates a CW rigid-surface nano-MHD vortex. (b) A 3D-nuclei deposit surface under rigid- and free-surface nano-MHD vortexes after 100 rounds of nucleation. The calculation data are as follows: = 5 T, = 6.28 s−1, = 2, = 6.0 × 10−10 m2 s−1, = 3.74 × 10−4 m, and = 50 mol m−3. Supporting electrolyte, 500 mol m−3; applied overpotential, −0.4 V; nucleation period, 1.0 s.
4. Conclusions
In the three-generation model, chirality transfers from the upper generation the to lower generation via the instability or stability difference between the rigid- and free-surface MHD vortexes rotating in opposite directions. Since the effective viscosity increases with lowering generations, for the vortexes to rotate in the second and third generations, the kinematic viscosity must decrease to a zero level. Ionic vacancies therefore work as atomic-scale lubricants, lowering the viscosity of the vacancy layer on the electrode to almost zero. At the same time, the vortexes promote or suppress 3D nucleation, depending on whether the system is right-handed or left-handed.
The addition of chloride ions reverses the chiral activity of the electrode. However, in the case of copper deposition, due to magneto-convection from the gradient force to the paramagnetic copper sulfate solution, such reversal becomes partial, leading to a breakdown in chiral symmetry.
Author Contributions
Conceptualization, R.A.; methodology, A.S., M.M. (Makoto Miura), Y.O. and R.A.; software, R.M., M.M. (Miki Miura) and R.A.; validation, A.S., M.M. (Makoto Miura), Y.O. and R.A.; formal analysis, R.M., A.S., M.M. (Makoto Miura), Y.O. and R.A.; investigation, R.M., A.S., M.M. (Makoto Miura) and Y.O.; resources, Y.O., I.M. and R.A.; data curation, R.M., and R.A.; writing—original draft preparation, R.A.; writing—review and editing, R.M., A.S., M.M. (Makoto Miura) and Y.O.; visualization, R.M., A.S., M.M. (Makoto Miura) and Y.O.; supervision, Y.Y. and R.A.; project administration, Y.O. and R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the JSPS KAKENHI Grant-in-Aid for Scientific Research (C), no. 19K05230.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This work was performed in part at the Queensland node of the Australian National Fabrication Facility, a company established under the National Collaborative Research Infrastructure Strategy, to provide nano- and micro-fabrication facilities for Australia’s researchers. The authors thank the staff members of High Field Laboratory for Superconducting Materials of IMR, Tohoku University, for the use of the cryocooled superconducting magnet, and the Tsukuba Magnet Laboratory, National Institute for Materials Science (NIMS), for the use of superconducting magnets.
Conflicts of Interest
Author Atsushi Sugiyama was employed by the company Yoshino Denka Kogyo, Inc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
List of Symbols
| x-coordinate (m), or nondimensional x-coordinate defined by . | |
| y-coordinate (m), or nondimensional y-coordinate defined by | |
| z-coordinate (m), or nondimensional z-coordinate defined by | |
| X | nondimensional x-length of the electrode. |
| Y | nondimensional y-length of the electrode. |
| representative length of 3D nucleation in the 2nd generation. | |
| representative length of the i generation (i = 1st, 2nd and 3rd) (m). | |
| average diffusion layer thickness (m). | |
| symmetrical concentration fluctuation of the metallic ion (mol m−3). | |
| molar concentration of the metallic ion (mol m−3). | |
| average surface concentration (mol m−3). | |
| bulk concentration (mol m−3). | |
| average value of (mol m−3). | |
| average value of equal to (mol m−3). | |
| concentration difference between the bulk and surface defined by in Equation (37c) (mol m−3). | |
| H | concentration overpotential (V). |
| H | symmetrical fluctuation of concentration overpotential (V). |
| average concentration overpotential (V). | |
| amplitude of on the rigid surface (j = r) and the free surface (j = f). | |
| electrode potential (V). | |
| equilibrium potential (V). | |
| z-components of the velocity of a rigid-surface vortex (m s−1). | |
| z-components of the velocity of a free-surface vortex (m s−1). | |
| z-component of the vorticity of a rigid-surface vortex (s−1). | |
| z-component of the vorticity of a free-surface vortex (s−1). | |
| the vorticity coefficient function (VCF) of the rigid-surface vortexes defined by Equation (2) (i = 1st, 2nd, and 3rd). | |
| the vorticity coefficient function (VCF) of the free-surface vortexes defined by Equation (5) (i = 1st, 2nd, and 3rd). | |
| function of defined by Equation (6a). | |
| function of defined by Equation (6b). | |
| function of defined by Equation (6c). | |
| function of defined by Equation (4a). | |
| function of defined by Equation (4b). | |
| function of defined by Equation (4c). | |
| magneto-viscosity coefficient in the i generation defined by Equation (3a) (i = 1st, 2nd and 3rd) (m2 A−1 s−1). | |
| rotation coefficient in the i generation defined by Equation (3b) (i = 1st, 2nd, and 3rd) (m−1). | |
| magneto-induction coefficient in the i generation defined by Equation (3c) (i = 1st, 2nd and 3rd). | |
| mass transfer coefficient in the ith generation defined by Equation (3d) (i = 1st, 2nd, and 3rd) (mol m−4 s). | |
| coefficient of defined by Equation (8a) (m3 A−1 s−2). | |
| coefficient of defined by Equation (8b) (m2 s−1). | |
| coefficient of defined by Equation (8c) (s−1). | |
| coefficient of defined by Equation (8d) (mol m−6 s). | |
| representative kinematic viscosity of the i generation (i = 1st, 2nd and 3rd) (m2 s−1). | |
| i | parameter defined by (m−1 s). |
| external magnetic flux density (T). | |
| solution density (kg m−3). | |
| angular velocity of a VMHDF (s−1). | |
| angular velocity of the upper-generation rigid-surface vortex ( non, a and s) (s−1). | |
| electric conductivity (−1m−1). | |
| concentration gradient, defined by Equation (37b) in the 2nd generation (mol m−4). | |
| diffusion coefficient of the metallic ion (m2 s−1). | |
| concentration difference between the bulk and surface defined by Equation (37c) (mol m−3). | |
| average diffusion layer thickness (m). | |
| function of the torque component of the rigid-surface MHD vortexes activated by the applied magnetic field defined by Equation (11a). | |
| function of the torque component of the precession from the upper-generation rigid-surface vortexes defined by Equation (11b). | |
| rewritten form of in the generation defined by Equation (13). | |
| function of the torque component of the free-surface MHD vortexes activated by the applied magnetic field defined by Equation (15a). | |
| function of the torque component of the precession from the upper-generation free-surface vortexes defined by Equation (15b). | |
| rewritten form of in the generation defined by Equation (17). | |
| the mass flux density of the metallic ion from the solution phase to the electrode surface (mol m−3 s−1). | |
| the mass flux density of the adatom due to surface diffusion (mol m−2 s−1). | |
| the mass flux density of the adatom due to the incorporation of the crystal lattice (mol m−3 s−1). | |
| symmetrical fluctuation of the adatom concentration (mol m−3). | |
| surface diffusion coefficient of the adatom (m2 s−1). | |
| equilibrium surface concentration of the adatom (mol m−2). | |
| universal gas constant, 8.31 (J K−1 mol−1). | |
| absolute temperature (K). | |
| F | Faraday constant (96,485 C mol−1). |
| symmetrical fluctuation of the chemical potential of the adatoms by the change of surface form (J mol−1). | |
| molar volume of the depositing metal (m3 mol−1). | |
| isotropic surface free energy (J m−2). | |
| surface height fluctuation of the deposit surface of 3D nuclei (m). | |
| abbreviation of (m). | |
| rigid-surface component of (m). | |
| free-surface component of (m). | |
| mean square (ms) value of at the initial steady state (m2). | |
| amplitudes of on the rigid surface (j = r) and the free surface (j = f). | |
| amplitude of the rigid-surface component of the initial surface height fluctuation . | |
| amplitude of the free-surface component of the initial surface height fluctuation . | |
| diffusion current fluctuation on 3D nuclei (A m−2). | |
| rigid-surface component of (A m−2). | |
| free-surface component of (A m−2). | |
| the chemical potential of the adatoms. | |
| symmetrical fluctuation of | |
| the electrochemical potential of the metallic ions. | |
| symmetrical fluctuation of | |
| the electrochemical potential of the electrons. | |
| concentration overpotential (V). | |
| fluctuation of the concentration overpotential (V). | |
| k | wavenumber defined by (m−1). |
| x-component of the wavenumber (m−1). | |
| y-component of the wavenumber (m−1). | |
| nondimensional wavenumber common in every generation. | |
| nondimensional wavenumber of the 2nd generation defined by . | |
| x-component of the nondimensional wavenumber | |
| y-component of the nondimensional wavenumber | |
| the upper limit of the wavenumber . | |
| autocorrelation distance of the symmetrical fluctuation. | |
| vorticity coefficient of the rigid-surface vortexes. | |
| vorticity coefficient of the free-surface vortexes. | |
| amplitude factor under the rigid-surface vortexes (s−1). | |
| amplitude factor under the free-surface vortexes (s−1). | |
| amplitude factor in a stationary solution (s−1). | |
| the nondimensional spatial spectrum of the surface height fluctuation. | |
| the ratio of the rigid-surface component, . | |
| the ratio of the free-surface component, | |
| vorticity coefficient of rigid-surface MHD vortexes. | |
| vorticity coefficient of free-surface MHD vortexes. | |
| vorticity coefficient constant of rigid-surface nano-MHD vortexes defined by Equation (A6b). | |
| vorticity coefficient constant of free-surface nano-MHD vortexes defined by Equation (A8b). | |
| vorticity coefficient function of rigid-surface nano-MHD vortexes defined by Equations (A6c) and (A11a). | |
| vorticity coefficient function of free-surface nano-MHD vortexes defined by Equations (A8c) and (A11b). | |
| unit random complex number defined by Equation (A9). | |
| normal random number between 0 and . | |
| a general function of and . | |
| even component concerning and of the function . | |
| odd component concerning and of the function . | |
| a | superscript of the asymmetrical fluctuation in the 1st generation. |
| s | superscript of the symmetrical fluctuation in the 2nd generation. |
| average over the electrode surface. | |
| [ ] | sign of physical quantity. |
| operator defined by | |
| operator defined by | |
| operator defined by . | |
| operator defined by . | |
| operator defined by or nondimensional operator defined by | |
| operator describing a complex function. | |
| Re | sign expressing the real part of a complex number or function. |
| Im | sign expressing the imaginary part of a complex number or function. |
| unit imaginary number. | |
| even | sign expressing the even function. |
| odd | sign expressing the odd function. |
| NI | nucleation and MHD vortex instability. |
| MHDV | MHD vortex. |
| S.S. | stationary solution. |
| rigid-surface vortex angular velocity of the upper generation, ‘i’. | |
| vorticity coefficient function of the lower generation, ‘i + 1′. | |
| the main part (MP) of the amplitude factor in a stationary solution (S.S.) in the lower generation, ‘i + 1′. | |
| right-handed system in the upper generation, ‘i’. | |
| right-handed system in the lower generation, ‘i + 1′. | |
| left-handed system in the upper generation, ‘i’. | |
| left-handed system in the lower generation, ‘i + 1′. | |
| magnetic field | |
| adatom of the deposit metal. | |
| metallic ion at the inner Helmholtz plane (IHP). | |
| charge number of the metallic ion. | |
| free electron in the electrode. |
Appendix A. Calculation of 3D Nucleus Morphology
Appendix A.1. Initial Spectrum of Symmetrical Fluctuation
Different from asymmetrical fluctuations arising from 2D nucleation in an electric double layer, symmetrical fluctuations are controlled by the surface process of 3D nucleation in a diffusion layer. A non-dimensional spatial spectrum of the surface height fluctuation in a steady state should be defined as follows [73]:
where and are the x- and y-components of the nondimensional wavenumber , and X and Y are the nondimensional x- and y-lengths of the electrode, respectively. is the mean square (ms) value of the surface height of 3D nuclei at the initial steady state. is the amplitude of the initial surface height fluctuation. Assuming isotropic white noise with normalization, we have the actual form of the power spectrum:
where is the upper limit of the wavenumber .
Using the representative length, , of the symmetrical fluctuation in the 2nd generation, the nondimensional wavenumber is defined as follows:
Assuming that is defined by the upper limit of the wavenumber , i.e., as the lower limit of the wavelength, we obtain the following:
Here, is equalized to the autocorrelation distance of the symmetrical fluctuation The upper limit of is therefore written as follows:
The power spectrum Equation (A1b) is simply expressed by the following:
Then, substituting from Equation (A2d) into Equation (A1a), we obtain the following:
Since the total surface height amplitude, , is composed of the rigid- and free-surface components, and , introducing the ratios of the rigid-surface and free-surface components, and , each surface-height amplitude is expressed as follows:
Here, the following relationship is satisfied:
For a stationary VMHDE without mechanical rotation, ACW and CW vortexes are equally induced, i.e., .
Following Part 1, introducing an operator, , describing a complex function, we can treat both amplitude components at once as the real and imaginary parts of the complex function.
where “i” is the unit imaginary number, and “Re” and “Im” denote the real and imaginary parts of a complex number. Subscripts ‘even’ and ‘odd’ represent even and odd functions of the wavenumber, respectively. As an example of a pair of cosine and sine functions, the even and odd functions, and , are orthogonal, so they are independent of each other. Namely, we can determine the formation processes of rigid-surface and free-surface 3D nuclei at once via the complex surface-height amplitude, .
Appendix A.2. Formation Process of 3D Nuclei
The amplitudes of the symmetrical surface height fluctuations are solved as Equation (44b), where is the initial value of defined by Equation (A3b), and is the amplitude factor expressed by Equation (45a).
To calculate the concentration gradients in Equation (41b), the explicit expressions of the vorticity coefficients and are required. Substituting from Equation (41a) into Equation (39b), we have the following:
The substitution of Equations (44b) and (A3b) into Equation (A5) leads to
where
and
Then, in the same way as Equation (A5), we obtain
The substitution of Equations (44b) and (A3b) into Equation (A7) leads to
where
and
The calculation of this system is performed as follows: First, the solution phase including the electrode surface is virtually divided by 3D grids. Each grid point is defined at intervals of the autocorrelation distance. Then, to simultaneously deal with two components on the rigid and free surfaces, it is necessary to assign a single random complex number to the amplitudes of both components. Because of the stochastic process in multiple nucleation, the following unit random complex number is introduced to each grid point of the 3D wavenumber plane.
where is a normal random number between 0 and , which is renewed over all grid points whenever nucleation is restarted.
Substituting for and from Equations (A6a) and (A8a) in Equation (41b), respectively, we obtain
and
We also have Equations (A6a) and (A8a) represented as follows:
and
Since 3D nuclei grow independently on rigid and free surfaces, and must distribute independently over the electrode surface without any contradiction, which mathematically implies that they are orthogonally normally packed. To calculate their self-organization processes self-consistently, a complex Fourier transform is utilized, e.g., the rigid- and free-surface components that are embedded as the real and imaginary parts in the forms of odd and even functions are normal to each other, the symmetries of which are preserved in the transformations.
In the same way as the initial amplitude of the surface height fluctuation in Equation (A4) is introduced, the operator, , is introduced, which embeds odd and even components of a function into a complex space.
or
where is generally decomposed into the even and odd functions, and , about and , i.e.,
The signs and denote the real and imaginary parts. Even and odd functions such as cosine and sine functions are orthogonal to each other, so they are embedded as the real and imaginary parts, and vice versa.
Through the operator the amplitudes of the concentration gradient fluctuations on rigid and free surfaces are assigned to real and imaginary parts of a complex amplitude, e.g.,
where the rigid- and free-surface components are defined as even and odd functions concerning and , respectively. As shown in Equation (A9), due to the introduction of a unit random complex number, , the discrimination between even and odd functions is finally canceled.
The complex function is transformed into the complex concentration gradient via complex Fourier inversion, i.e.,
where and are the x and y components of the nondimensional wavenumber , i.e., +.
Under Equations (A12a) or (A12b), the complex concentration gradient fluctuation is expressed as follows:
where and are the rigid- and free-surface components of the symmetrical concentration fluctuation , respectively. As mentioned above, due to complex random numbers initially introduced, the natures of even and odd functions disappear in the fluctuations on the x–y plane.
Finally, the symmetrical fluctuation of the concentration gradient is obtained via the linear combination of both components. Here, the concentration gradient fluctuations are also asymmetrical, so by Figure 3, their minus parts are cut off (phase cutting).
The diffusion current fluctuation on 3D nuclei is also expressed by the rigid- and free-surface components.
where and are rigid- and free-surface components, respectively. Using the concentration gradient fluctuations in Equation (A14b), we obtain
and
Due to phase cutting, the diffusion current fluctuations are defined as negative. As a result, the surface morphology of the 3D nuclei is effectively calculated via the symmetrical surface height fluctuation, so with the diffusion current fluctuations, we derive the following equations:
and
Negative current fluctuations lead to positive height fluctuations. The total surface morphology is the linear combination of both components.
The introduction of the complex Fourier transform allows us to separately calculate the self-organization of 3D nuclei on the rigid and free surfaces.
References
- Morimoto, R.; Miura, M.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Mogi, I.; Yamauchi, Y.; Takagi, S.; Aogaki, R. Theory of Chiral Electrodeposition by Chiral Micro-Nano-Vortices under a Vertical Magnetic Field -1: 2D Nucleation by Micro-Vortices. Magnetochemistry 2022, 8, 71. [Google Scholar] [CrossRef]
- Takagi, S.; Asada, T.; Oshikiri, Y.; Miura, M.; Morimoto, R.; Sugiyama, A.; Mogi, I.; Aogaki, R. Nanobubble formation from ionic vacancies in an electrode reaction on a fringed electrode under a uniform vertical magnetic field -1. Formation process in a vertical magnetohydrodynamic (MHD) flow. J. Electroanal. Chem. 2022, 914, 116291. [Google Scholar] [CrossRef]
- Takagi, S.; Asada, T.; Oshikiri, Y.; Miura, M.; Morimoto, R.; Sugiyama, A.; Mogi, I.; Aogaki, R. Nanobubble formation from ionic vacancies in an electrode reaction on a fringed electrode under a uniform vertical magnetic field -2. Measurement of the angular velocity of a vertical magnetohydrodynamic (MHD) flow by the microbubbles originating from ionic vacancies. J. Electroanal. Chem. 2022, 916, 116375. [Google Scholar] [CrossRef]
- Aogaki, R. Theory of stable formation of ionic vacancy in a liquid solution. Electrochemistry 2008, 76, 458–465. [Google Scholar] [CrossRef][Green Version]
- Aogaki, R.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Miura, M.; Morimoto, R.; Takagi, S.; Mogi, I.; Yamauchi, Y. Origin of nanobubbles electrochemically formed in a magnetic field: Ionic vacancy production in electrode reaction. Sci. Rep. 2016, 6, 28297. [Google Scholar] [CrossRef] [PubMed]
- Aogaki, R.; Motomura, K.; Sugiyama, A.; Morimoto, R.; Mogi, I.; Miura, M.; Asanuma, M.; Oshikiri, Y. Measurement of the lifetime of ionic vacancy by the cyclotron-MHD electrode. Magnetohydrodynamics 2012, 48, 289–297. [Google Scholar] [CrossRef]
- Sugiyama, A.; Morimoto, R.; Osaka, T.; Mogi, I.; Asanuma, M.; Miura, M.; Oshikiri, Y.; Yamauchi, Y.; Aogaki, R. Lifetime of ionic vacancy created in redox electrode reaction measured by cyclotron MHD electrode. Sci. Rep. 2016, 6, 19795. [Google Scholar] [CrossRef] [PubMed]
- Mogi, I.; Watanabe, K. Chiral recognition of amino acids magnetoelectrodeposited Cu film electrodes. Int. J. Electrochem. 2011, 2011, 239637. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Watanabe, K. Surface chirality induced by rotational electrodeposition in magnetic fields. Sci. Rep. 2013, 3, 2574. [Google Scholar] [CrossRef]
- Mogi, I.; Aogaki, R.; Watanabe, K. Chiral surface formation of copper films by magnetoelectrochemical etching. Magnetohydrodynamics 2015, 51, 361–368. [Google Scholar] [CrossRef]
- Mogi, I.; Aogaki, R.; Watanabe, K. Tailoring of surface chirality by micro-vortices and specific adsorption in magnetoelectrodeposition. Bull. Chem. Soc. Jpn. 2015, 88, 1479–1485. [Google Scholar] [CrossRef]
- Mogi, I.; Aogaki, R.; Takahashi, K. Chiral surface formation in magnetoelectrolysis on micro-electrodes. Magnetohydrodynamics 2017, 53, 321–328. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R. Surface chirality effects induced by magnetic fields. Curr. Opin. Electrochem. 2018, 7, 1–6. [Google Scholar] [CrossRef]
- Mogi, I.; Aogaki, R.; Takahashi, K. Chiral symmetry breaking in magnetoelectrochemical etching with chloride additives. Molecules 2018, 23, 19. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Takahashi, K. Effects of vertical magnetohydrodynamic flows on chiral surface formation in magnetoelectrolysis. Magnetochemistry 2018, 4, 40. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Takahashi, K. Effects of vertical MHD flows and cell rotation on surface chirality in magnetoelectrodeposition. IOP Conf. Ser. Mater. Sci. Eng. 2018, 424, 012024. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Takahashi, K. Surface chirality in rotational magnetoelectrodeposition of copper films. Magnetochemistry 2019, 5, 53. [Google Scholar] [CrossRef]
- Mogi, I.; Iwasaka, M.; Aogaki, R.; Takahashi, K. Visualization of magnetohydrodynamic micro-vortices with guanine micro-crystals. J. Electrochem. Soc. 2017, 164, H584–H586. [Google Scholar] [CrossRef]
- Mogi, I.; Aogaki, R.; Takahashi, K. Fluctuation effects of magnetohydrodynamic micro-vortices on odd chirality in magnetoelectrolysis. Magnetochemistry 2020, 6, 43. [Google Scholar] [CrossRef]
- Mogi, I.; Aogaki, R.; Takahashi, K. Breaking of Odd Chirality in Magnetoelectrodeposition of copper film on micro-electrode. Magnetochemistry 2021, 7, 142. [Google Scholar] [CrossRef]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Takahashi, K. Breaking of Odd Chirality in Magnetoelectrodeposition. Magnetochemistry 2022, 8, 67. [Google Scholar] [CrossRef]
- Miura, M.; Sugiyama, A.; Oshikiri, Y.; Morimoto, R.; Mogi, I.; Miura, M.; Takagi, S.; Kim, J.; Yamauchi, Y.; Aogaki, R. Excess heat production by the pair annihilation of ionic vacancies in copper redox reactions. Sci. Rep. 2019, 9, 13695. [Google Scholar] [CrossRef]
- Sugiyama, A.; Miura, M.; Oshikiri, Y.; Kim, Y.; Morimoto, R.; Miura, M.; Osaka, T.; Mogi, I.; Yamauchi, Y.; Aogaki, R. Excess heat production in the redox couple reaction of ferricyanide and ferrocyanide. Sci. Rep. 2020, 10, 20072. [Google Scholar] [CrossRef]
- Miura, M.; Sugiyama, A.; Oshikiri, Y.; Morimoto, R.; Mogi, I.; Miura, M.; Yamauchi, Y.; Aogaki, R. Excess heat production of the pair annihilation of ionic vacancies in a copper redox reaction using a double bipolar MHD electrode. Sci. Rep. 2024, 14, 1424. [Google Scholar] [CrossRef] [PubMed]
- Fahidy, T.Z. The effect of magnetic fields on electrochemical processes. In Modern Aspects of Electrochemistry No. 32; Conway, B.E., Bockris, J.O.M., White, R.E., Eds.; Springer: Boston, MA, USA, 2002; pp. 333–354. [Google Scholar] [CrossRef]
- Alemany, A.; Chopart, J.P. An Outline of Magnetoelectrochemistry. In Magnetohydrodynamics—Historical Evolution and Trends; Molokov, S., Moreau, R., Moffatt, K., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 391–407. [Google Scholar] [CrossRef]
- Aogaki, R.; Morimoto, R. Nonequilibrium fluctuation in micro-MHD effects on electrodeposition. In Heat and Mass Transfer—Modelling and Simulation; Hossain, M., Ed.; Intech: Rijeka, Croatia, 2011; pp. 189–216. [Google Scholar] [CrossRef]
- Monzon, L.M.A.; Coey, J.M.D. Magnetic field in electrochemistry: The Lorentz force. A mini-review. Electrochem. Commun. 2014, 42, 38–41. [Google Scholar] [CrossRef]
- Fahidy, T.Z. Wave phenomena in magnetoelectrolytic systems. Electrochim. Acta 1976, 21, 21–24. [Google Scholar] [CrossRef]
- Mohanta, S.; Fahidy, T.Z. The hydrodynamics of a magnetoelectrolytic cell. J. Appl. Electrochem. 1976, 6, 211–220. [Google Scholar] [CrossRef]
- Fahidy, T.Z. Magnetoelectrolysis. J. Appl. Electrochem. 1983, 13, 553–563. [Google Scholar] [CrossRef]
- Olivier, A.; Merienne, E.; Chopart, J.P.; Aaboubi, O. Thermoelectrochemical impedances—I. A new experimental device to measure thermoelectrical transfer functions. Electrochim. Acta 1992, 37, 1945–1950. [Google Scholar] [CrossRef]
- Aaboubi, O.; Chopart, J.P.; Douglade, J.; Olivier, A.; Gabrielli, C.; Tribollet, B. Magnetic field effects on mass transport. J. Electrochem. Soc. 1990, 137, 1796–1804. [Google Scholar] [CrossRef]
- Devos, O.; Aaboubi, O.; Chopart, J.P.; Merienne, E.; Olivier, A.R. Magnetic impedance method: The MHD transfer function. Electrochemistry 1999, 67, 180–187. [Google Scholar] [CrossRef][Green Version]
- Aaboubi, O.; Amblard, J.; Chopart, J.P.; Olivier, A. Magnetohydrodynamic analysis of silver electrocrystallization from a nitric and tartaric solution. J. Electrochem. Soc. 2004, 151, C112–C118. [Google Scholar] [CrossRef]
- Aaboubi, O.; Lòs, P.; Amblard, J.; Chopart, J.P.; Olivier, A. Electrochemical investigations of the magnetic field influence on mass transport toward an ultramicrodisk. J. Electrochem. Soc. 2003, 150, E125–E130. [Google Scholar] [CrossRef]
- Devos, O.; Aaboubi, O.; Chopart, J.P.; Merienne, E.; Olivier, A.; Gabrielli, C.; Tribollet, B. A new experimental device for magnetoelectrochemical (M.E.C.) transfer function measurements. Polish J. Chem. 1997, 71, 1160–1170. [Google Scholar]
- Ragsdale, S.R.; Lee, J.; Gao, X.; White, H.S. Magnetic field effects in electrochemistry. Voltammetric reduction of acetophenone at microdisk electrodes. J. Phys. Chem. 1996, 100, 5913–5922. [Google Scholar] [CrossRef]
- Ragsdale, S.R.; Lee, J.; White, H.S. Analysis of the magnetic force generated at a hemispherical microelectrode. Anal. Chem. 1997, 69, 2070–2076. [Google Scholar] [CrossRef] [PubMed]
- Ragsdale, S.R.; Grant, K.M.; White, H.S. Electrochemically generated magnetic forces. Enhanced transport of a paramagnetic redox species in large, nonuniform magnetic fields. J. Am. Chem. Soc. 1998, 120, 13461–13468. [Google Scholar] [CrossRef]
- Mutschke, G.; Bund, A. On the 3D character of the magnetohydrodynamic effect during metal electrodeposition in cuboid cells. Electrochem. Commun. 2008, 10, 597–601. [Google Scholar] [CrossRef]
- Mühlenhoff, S.; Mutschke, G.; Koschichow, D.; Yang, X.; Bund, A.; Fröhlich, J.; Odenbach, S.; Eckert, K. Lorentz-force-driven convection during copper magnetoelectrolysis in the presence of a supporting buoyancy force. Electrochim. Acta 2012, 69, 209–219. [Google Scholar] [CrossRef]
- Devos, O.; Olivier, A.; Chopart, J.P.; Aaboubi, O.; Maurin, G. Magnetic field effects on nickel electrodeposition. J. Electrochem. Soc. 1998, 145, 401–405. [Google Scholar] [CrossRef]
- Olivas, P.; Alemany, A.; Bark, F.H. Electromagnetic control of electroplating of a cylinder in forced convection. J. Appl. Electrochem. 2004, 34, 19–30. [Google Scholar] [CrossRef]
- Daltin, A.L.; Bohr, F.; Chopart, J.P. Kinetics of Cu2O electrocrystallization under magnetic fields. Electrochim. Acta 2009, 54, 5813–5817. [Google Scholar] [CrossRef]
- Fernández, D.; Coey, J.M.D. Inhomogeneous electrodeposition of copper in a magnetic field. Electrochem. Commun. 2009, 11, 379–382. [Google Scholar] [CrossRef]
- Msellak, K.; Chopart, J.P.; Jbara, O.; Aaboubi, O.; Amblard, J. Magnetic field effect on Ni-Fe alloys codeposition. J. Magn. Magn. Mater. 2004, 281, 295–304. [Google Scholar] [CrossRef]
- Żabiński, P.R.; Mech, K.; Kowalik, R. Co-Mo and Co-Mo-C alloys deposited in a magnetic field of high intensity and their electrocatalytic properties. Arch. Metall. Mater. 2012, 57, 127–133. [Google Scholar] [CrossRef]
- Żabiński, P.R.; Franczak, K.; Kowalik, R. Electrocatalytically active Ni-Re binary alloys electrodeposited with superimposed magnetic field. Arch. Metall. Mater. 2012, 57, 495–501. [Google Scholar] [CrossRef]
- Żabiński, P.R.; Mech, K.; Kowalik, R. Electrocalalytically active Co-W and Co-W-C alloys electrodeposited in a magnetic field. Electrochim. Acta 2013, 104, 542–548. [Google Scholar] [CrossRef]
- Chouchane, S.; Levesque, A.; Żabiński, P.R.; Rehamnia, R.; Chopart, J.P. Electrochemical corrosion behavior in NaCl medium of zinc-nickel alloys electrodeposited under applied magnetic field. J. Alloys Compd. 2010, 506, 575–580. [Google Scholar] [CrossRef]
- Kishioka, S.; Yamada, A.; Aogaki, R. Analysis of gas dissolution rate into liquid phase under magnetic field gradient. Phys. Chem. Chem. Phys. 2000, 2, 4179–4183. [Google Scholar] [CrossRef]
- Devos, O.; Aogaki, R. Transport of paramagnetic liquids under nonuniform high magnetic field. Anal. Chem. 2000, 72, 2835–2840. [Google Scholar] [CrossRef]
- Sugiyama, A.; Morisaki, S.; Aogaki, R. Mass transfer process by magneto-convection at a solid-liquid interface in a heterogeneous vertical magnetic field. Jpn. J. Appl. Phys. 2003, 42, 5322–5329. [Google Scholar] [CrossRef]
- Tschulik, K.; Koza, J.A.; Uhlemann, M.; Gebert, A.; Schultz, L. Effects of well-defined magnetic field gradients on the electrodeposition of copper and bismuth. Electrochem. Commun. 2009, 11, 2241–2244. [Google Scholar] [CrossRef]
- Dunne, P.; Mazza, L.; Coey, J.M.D. Magnetic structuring of electrodeposits. Phys. Rev. Lett. 2011, 107, 024501. [Google Scholar] [CrossRef] [PubMed]
- Tschulik, K.; Yang, X.; Mutschke, G.; Uhlemann, M.; Eckert, K.; Sueptitz, R.; Schultz, L.; Gebert, A. How to obtain structural deposits from diamagnetic ions in magnetic gradient fields? Electrochem. Commun. 2011, 13, 946–950. [Google Scholar] [CrossRef]
- Tschulik, K.; Sueptitz, R.; Koza, J.; Uhlemann, M.; Mutschke, G.; Weier, T.; Gebert, A.; Schultz, L. Studies on the patterning effect of copper deposits in magnetic gradient fields. Electrochim. Acta 2010, 56, 297–304. [Google Scholar] [CrossRef]
- Tschulik, K.; Cierpka, C.; Muschke, G.; Gebert, A.; Schultz, L.; Uhlemann, M. Clarifying the mechanism of reverse structuring during electrodeposition in magnetic gradient fields. Anal. Chem. 2012, 84, 2328–2334. [Google Scholar] [CrossRef] [PubMed]
- Aogaki, R.; Fueki, K.; Mukaibo, T. Application of magnetohydrodynamic effect to the analysis of electrochemical reactions—1. MHD flow of an electrolyte solution in an electrode-cell with a short rectangular channel. Denki Kagaku (Present. Electrochem.) 1975, 43, 504–508. [Google Scholar] [CrossRef]
- Aogaki, R.; Fueki, K.; Mukaibo, T. Application of magnetohydrodynamic effect to the analysis of electrochemical reactions—2. Diffusion process in MHD forced flow of electrolyte solutions. Denki Kagaku (Present. Electrochem.) 1975, 43, 509–514. [Google Scholar] [CrossRef]
- Aogaki, R.; Fueki, K.; Mukaibo, T. Diffusion process in viscous-flow of electrolyte solution in magnetohydrodynamic pump electrodes. Denki Kagaku (Present. Electrochem.) 1976, 44, 89–94. [Google Scholar] [CrossRef]
- Salinas, G.; Tieriekhov, K.; Garrigue, P.; Sojic, N.; Bouffier, L.; Kuhn, A. Lorentz Force-Driven Autonomous Janus Swimmers. J. Am. Chem. Soc. 2021, 143, 12708–12714. [Google Scholar] [CrossRef]
- Salinas, G.; Kuhn, A.; Arnaboldi, S. Self-Sustained Rotation of Lorentz Force-Driven Janus Systems. J. Phys. Chem. C 2023, 127, 14704–14710. [Google Scholar] [CrossRef]
- Tieriekhov, K.; Sojic, N.; Bouffier, L.; Salinas, G.; Kuhn, A. Wireless Magnetoelectrochemical Induction of Rotational Motion. Adv. Sci. 2024, 11, 2306635. [Google Scholar] [CrossRef] [PubMed]
- Zharov, A.; Fierro, V.; Celzard, A. Magnetohydrodynamic self-propulsion of active matter agents. Appl. Phys. Lett. 2020, 117, 104101. [Google Scholar] [CrossRef]
- Anderson, E.C.; Weston, M.C.; Fritsch, I. Investigations of Redox Magnetohydrodynamic Fluid Flow at Microelectrode Arrays Using Microbeads. Anal. Chem. 2010, 82, 2643–2651. [Google Scholar] [CrossRef] [PubMed]
- Sikes, J.C.; Wonner, K.; Nicholson, A.; Cignoni, P.; Fritsch, I.; Tschulik, K. Characterization of Nanoparticles in Diverse Mixtures Using Localized Surface Plasmon Resonance and Nanoparticle Tracking by Dark-Field Microscopy with Redox Magnetohydrodynamics Microfluidics. ACS Phys. Chem. Au 2022, 2, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Aogaki, R.; Kitazawa, K.; Kose, Y.; Fueki, K. Theory of powdered crystal formation in electrocrystallization-Occurrence of morphological instability at the electrode surface. Electrochim. Acta 1980, 25, 965–972. [Google Scholar] [CrossRef]
- Aogaki, R.; Makino, T. Theory of powdered metal formation in electrochemistry-Morphological instability in galvanostatic crystal growth under diffusion control. Electrochim. Acta 1981, 26, 1509–1517. [Google Scholar] [CrossRef]
- Aogaki, R. Instability of nonequilibrium fluctuation in electrochemical nucleation. 1. Occurrence of instability. J. Chem. Phys. 1995, 103, 8602–8615. [Google Scholar] [CrossRef]
- Morimoto, R.; Miura, M.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Mogi, I.; Takagi, S.; Yamauchi, Y.; Aogaki, R. Theory of microscopic electrodeposition under a uniform parallel magnetic field-1. Nonequilibrium fluctuations of magnetohydrodynamic (MHD) flow. J. Electroanal. Chem. 2019, 848, 113254. [Google Scholar] [CrossRef]
- Morimoto, R.; Miura, M.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Mogi, I.; Takagi, S.; Yamauchi, Y.; Aogaki, R. Theory of microscopic electrodeposition under a uniform parallel magnetic field-2. Suppression of 3D nucleation by micro-MHD flow. J. Electroanal. Chem. 2019, 847, 113255. [Google Scholar] [CrossRef]
- Morimoto, R.; Miura, M.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Kim, Y.; Mogi, I.; Takagi, S.; Yamauchi, Y.; Aogaki, R. Long-term Electrodeposition under a uniform parallel magnetic field. 1. Instability of two-dimensional nucleation in an electric double layer. J. Phys. Chem. B 2020, 124, 11854–11869. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, R.; Miura, M.; Sugiyama, A.; Miura, M.; Oshikiri, Y.; Kim, Y.; Mogi, I.; Takagi, S.; Yamauchi, Y.; Aogaki, R. Long-term Electrodeposition under a uniform parallel magnetic field. 2. Flow-mode transition from laminar flow to convection cells with two-dimensional (2D) nucleation. J. Phys. Chem. B 2020, 124, 11870–11881. [Google Scholar] [CrossRef] [PubMed]
- Aogaki, R.; Makino, T. Morphological instability in nonsteady galvanostatic electrodeposition 1. Effect of surface diffusion of adatoms. J. Electrochem. Soc. 1984, 131, 40–46. [Google Scholar] [CrossRef]
- Yanson, Y.I.; Rost, M.J. Structural accelerating effect of chloride on copper electrodeposition. Angew. Chem. Int. Ed. 2013, 52, 2454–2458. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).