Abstract
Large-scale, ordered magnetic fields in several astrophysical sources are supposed to be originated, and maintained against dissipation, by the combined amplifying action of rotation and small-scale turbulence. For instance, in the solar interior, the so-called mean-field dynamo is known to be responsible for the observed 22-years magnetic cycle. Similar mechanisms could operate in more extreme environments, like proto neutron stars and accretion disks around black holes, for which the physical modelling needs to be translated from the regime of magnetohydrodynamics (MHD) and Newtonian gravity to that of a plasma in a general relativistic curved spacetime (GRMHD). Here we review the theory behind the mean field dynamo in GRMHD, the strategies for the implementation of the relevant equations in numerical conservative schemes, and we show the most important applications to the mentioned astrophysical compact objects obtained by our group in Florence. We also present novel results, such as three-dimensional GRMHD simulations of accretion disks with dynamo and the application of our dynamo model to a super massive neutron star, remnant of a binary neutron star merger as obtained from full numerical relativity simulations.
1. Introduction
The baryonic matter in the universe is mainly found in the form of ionized gas, mostly protons and electrons forming an electrically conducting fluid capable of interacting with magnetic fields, either external or self-generated by the currents of the streaming particles. This state is that of a plasma, and the physical modeling on the large, fluid scales is named magnetohydrodynamics (MHD), the simplest but usually still a perfectly adequate one when dealing with astrophysical sources. When the conditions of the plasma are extreme, like bulk, kinetic, or Alfvén velocities close to the speed of light, and when dealing with compact objects where the Newtonian gravity must be replaced by Einstein’s theory, the appropriate regime is rather that of general relativistic magnetohydrodynamics (GRMHD).
A long-standing problem in astrophysics has always been the origin of large-scale ordered magnetic fields, as required to explain for instance jet launching from young stellar objects (YSOs), microquasars, active galactic nuclei (AGNs), or the large coronal flares from the Sun, stars, and even magnetars (where G). Given that the origin of initial seed fields cannot be explained within the MHD regime, kinetic effects have been proposed for primordial cosmic fields, in particular battery-like mechanisms where separation of charges induce the presence of electric fields produced by spatial derivatives of the electron pressure in the generalized Ohm’s law [1], or plasma instabilities driven by anisotropies in velocity space or differentially streaming species [2,3]. Once a seed magnetic field is created, MHD-like mechanisms are needed to amplify the field up to the high values often observed, even to equipartition or more, and to sustain the field in time against dissipation. These mechanisms are known as dynamo [4,5]. The first application to astrophysics was the prediction of the presence of oscillatory magnetic modes in the Sun (resembling the solar cycle) induced by differential rotation and small-scale cyclonic motions [6], following previous results about Earth’s magnetism in the liquid core [7]. This approach overcomes the difficulties posed by the so-called Cowling’s anti-dynamo theorem [8], according to which an MHD dynamo cannot operate in axisymmetric plasma configurations.
The breakthrough in dynamo theory occurred in the 1960s, when the mean-field dynamo statistical approach was proposed [9,10,11], based on the decomposition of MHD quantities into large-scale mean values and stochastic turbulent fluctuations, given that turbulence is ubiquitously present in the astrophysical plasmas, characterized by extremely high Reynolds numbers [12]. The key assumption in turbulent dynamo theory is that the mean of the quadratic term of velocity and magnetic field fluctuations in the generalized Ohm’s law, which is essentially an electromotive force, is proportional to the mean magnetic field (and to its derivatives ), thus reaching a mean-field closure of the MHD equations. In its simplest form, the electric field measured in the fluid’s rest frame, or comoving frame, can be written as
where the and terms depend on the turbulent properties (namely fluid helicity, energy, and correlation time) and comprises both Ohmic and turbulent resistivity coefficients. Assuming uniform resistivity, the induction equation for the magnetic field thus becomes
In the simplest case of a static plasma and uniform dynamo coefficient, a magnetic field can grow exponentially provided , where k is the typical spatial wave number (the so-called -effect). In non-static axisymmetric configurations, the mutual excitation of toroidal and poloidal modes may occur in differentially rotating systems like stellar interiors or accretion disks. This is the dynamo mechanism, a cycle in which a toroidal mean flow creates a toroidal magnetic field out of a poloidal one (the -effect), and small-scale helical motions convert a toroidal field back into a poloidal one (the -effect), as first suggested by Parker [6]. For static configurations or uniform rotators, dynamos are also possible. The main problem of mean-field dynamo theory is how to close the system, that is how to derive the coefficients and in terms of the turbulent properties [13], and how to generate turbulence itself.
A promising (ideal MHD) mechanism to amplify directly the magnetic field and to induce the turbulence required for the mean-field dynamo to operate, hence amplifying the field even further, is the magneto-rotational instability (MRI) [14,15,16], also invoked to explain outward angular momentum transport in accretion disks [17]. Dynamo effects based on MRI-driven turbulence have been studied intensively by means of both local and global direct 3D MHD simulations, without the need to resort to a mean-field closure. This has been done mainly in the context of accretion disks, for which it is shown that indeed the shearing due to differential rotation induces a turbulent dynamo capable of amplifying and sustaining magnetic fields against dissipation [18,19,20,21,22,23,24]. However, direct 3D simulations are computationally expensive and there is no hope to adequately resolve both large scales (the whole disk) and the turbulent cascade down to realistic dissipation scales. This is why the mean-field dynamo approach, working even in 2D axisymmetric configurations, is often preferred, especially for global simulations in classical MHD, but is also more computationally demanding in the relativistic case.
Mean-field dynamo models for relativistic plasmas in strong gravity fields, where GRMHD applies, have been proposed to explain the origin of large-scale magnetic fields in accretion thick disks around black holes [25,26,27,28], see also [29,30] for the contribution of dynamo action to jet launching in thin disks systems, and in (proto) neutron stars, where dynamo could explain the formation of magnetar-like magnetic fields [31]. The theoretical framework is based on the extension of the classical mean-field assumption in Ohm’s law, now written in four-dimensional covariant form and in the comoving frame of the plasma, namely [32,33]
Here , , and are the electric field, magnetic field, and electric conduction current density as measured in the comoving frame, and the two coefficients and are again assumed to be scalars and not tensors for simplicity, as in the classical case. The ideal MHD limit is obtained for a vanishing resistivity or infinite electric conductivity, correctly implying in the comoving frame and extending the classical condition . Thanks to the above closure, to be rewritten in terms of the fields in the laboratory frame, the system of resistive-dynamo GRMHD equations is complete and can be solved (numerically) either in its fully nonlinear version or in the so-called kinematic approximation in which the fluid configuration is fixed, and only the (linear) Maxwell equations for the electromagnetic fields are evolved in time.
In the present paper, we illustrate the general framework for the numerical implementation of the full set of resistive-dynamo GRMHD equations in the formalism, needed for evolution with conservative schemes, and we discuss the latest developments of applications of mean-field dynamo to the amplification of initial seed magnetic fields in accretion disks around black holes and proto neutron stars. As far as notation is concerned, we let (and in the Maxwell equations), we use Greek indices for 4-vectors, and Latin indices, or boldface notation, for spatial 3D vectors.
2. Resistive-Dynamo GRMHD Equations in Form
The evolution of the hyperbolic set of GRMHD equations in time, invariably achieved by means of numerical methods, requires replacing the covariant form by the so-called splitting of space and time coordinates [34,35,36]. The metric of a generic spacetime curved by gravity is usually expressed in terms of a scalar lapse function , a spatial vector shift vector , and the three-metric , that is
where spatial 3-D vectors and tensors are those measured by the so-called Eulerian observer, with unit time-like vector and , with and for a flat Minkowski’s spacetime. For the description of the Eulerian formalism for ideal GRMHD, numerical implementation, and validation in Minkowski, Schwarzschild, and Kerr metrics, the reader is referred to the paper describing the Eulerian Conservative High-Order (ECHO) code [37], and to its extended version (X-ECHO) [38] where the spacetime metric terms are also evolved in time by solving Einstein equations (under the extended conformally flat condition).
Using the above splitting for the metric, the resistive-dynamo GRMHD equations in form for the evolution of the fluid and electromagnetic fields are
The above GRMHD set is then a system of 11 evolution equations for the 11 conservative variables , as measured by the Eulerian observer. The term is the 3D Levi-Civita alternating symbol. Here is the mass density ( is the Lorentz factor of the fluid velocity ), the total momentum density, is the total energy density and is the electromagnetic energy density, and are the electric and magnetic fields, is the total stress tensor. Moreover, , , and p are the proper mass density, energy density, and pressure, respectively, for which an equation of state (EoS) of the form must hold, for instance the ideal gas law , with the adiabatic index. The term with the extrinsic curvature can be rewritten as
with for a stationary spacetime, or directly provided by the solution of Einstein equations. Notice that the first three hydrodynamics equations contain fluxes in the standard divergence form, while Maxwell equations are in curl form. This fact is related to the presence of the two non-evolutionary constraints
and while the solenoidal constraint for is analytically (but not numerically, especially for shock-capturing schemes) preserved during evolution, the first relation (Gauss’s law) is used to define the charge density q in the equation for . For an infinitely conducting fluid with , the relation holds in the relativistic case also, so that the evolution equation for is redundant. For a non-vanishing resistivity coefficient, the system is closed by the version of the generalized Ohm’s law Equation (3), providing the spatial current density in the form
Notice that the resistivity is usually a very small (positive) number, requiring a special numerical treatment because it leads to a stiff source term [39], whereas the coefficient responsible for the dynamo -effect may have both signs (recall that we have defined , in order to avoid confusion with the lapse function, where we have also swapped the sign). For the implementation of the resistive-dynamo GRMHD equations within the numerical code ECHO, see [26,33].
3. Dynamo in Thick Disks around Kerr Black Holes
The most promising mechanism for powering the luminosity of AGNs and launching the associated powerful kiloparsec-scale jets often observed in radio is probably the Blandford–Znajek model [40,41], requiring a substantial magnetic field continuously accreted by the surrounding disk and twisted by the ergosphere of the central rotating supermassive black hole. See [42] for a recent review on MHD modeling of AGN accretion from the disk and jet launching. The recent radio interferometric imaging of the magnetized plasma around the black hole of M87 by the Event Horizon Telescope (EHT) and of the polarization properties of the emission [43,44] seem to confirm the scenario arising from theoretical models and GRMHD simulations of accretion from thick disks in Kerr metric, either in the so-called SANE (Standard And Normal Evolution) or MAD (Magnetically Arrested Disk) accretion regimes [45,46]. In these models, an initial field made of poloidal loops with a magnetization of and pressure perturbations are able to trigger MRI and thus to induce accretion onto the rotating black hole. This typically occurs from the inner cusp of the disk. At the same time, a conical region of evacuated plasma is realized in the polar regions, where magnetically dominated outflows are present, likely to drive jets further out.
However, we can think to a more agnostic situation in which the disk is initially threaded by a negligible magnetic field with a simpler morphology, even purely toroidal, and no perturbations. In the presence of (unresolved) small-scale turbulence and differential rotation, the mechanism of mean-field dynamo could operate and create the necessary level of magnetization in the disk in order to trigger MRI and accretion. An important aspect is also that the mean-field mechanism operates even in axisymmetric configurations, so there is no need to resort to expensive 3D GRMHD simulations in order to produce a turbulent dynamo action that amplifies the field further. For instance, global simulations have been recently performed by [47] with an extremely high resolution in order to capture MRI and the turbulent dynamo actions, though the initial magnetization is still assumed rather high. On the contrary, our mean-field approach requires modest computational resources and allows an initialization of the disk with extremely low magnetization levels.
This kind of model has been first applied to thick disks in the kinematic regime (that is by evolving in time only the electromagnetic field, maintaining the background fluid structure of the initial equilibrium) by Bugli et al. [25], where it is shown that depending on the combination of the and parameters, axisymmetric simulations show an exponential growth of both the toroidal and magnetic field components, with magnetic islands that grow periodically and migrate towards the pole or the equator, similarly to the solar case, according to the sign of the -dynamo parameter .
The fully nonlinear case has been investigated by Tomei et al. [26,27], in particular in the latter paper where the same disk setup and diagnostic tools employed for EHT-like simulations [45] are used, with a Kerr spin parameter of the black hole of and the same structure of the disk (that appropriate for a SANE-type evolution), the main difference being that the initial magnetic field is not a substantial poloidal field as in the simulations for EHT but rather a simpler toroidal seed field with . In spite of this, the dynamo term is able to grow all field components exponentially inside the disk and to trigger accretion onto the black hole, basically mimicking or even replacing the role of MRI.
The creation of a poloidal component within the disk begins from the earliest times, as shown in Figure 1, where the temporal evolution of the disk-averaged radial magnetic field (that measured in the frame comoving with the fluid) is plotted. Notice a saturation effect for M (time in geometrized units, adopting the Kerr–Schild horizon-penetrating coordinates for the spacetime metric). When the field is too high, MRI drives the accretion very efficiently and the process of dynamo apparently is quenched, while for lower values the dynamo operates for a longer time and drives a smoother accretion.
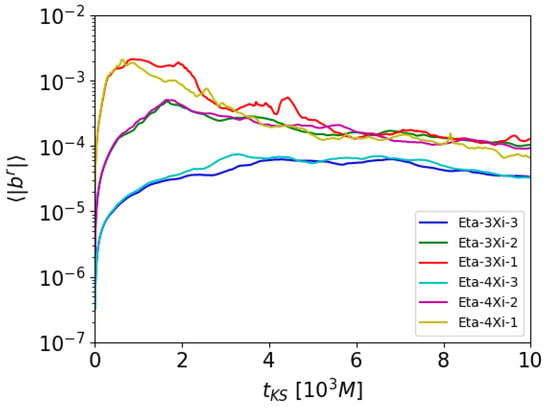
Figure 1.
Time evolution of disk-averaged for each model. The maximum values of resistivity and dynamo term are indicated in the label (reprinted from [27]).
While all quantities show a turbulent behavior in the disk, to better appreciate the spatial dependance we plot in Figure 2 time averages in the interval , when an almost steady state is achieved for the lower resistivity case (stronger and especially dynamo action). Notice the denser and less magnetized disk equatorial region with accretion from a cusp, the low-density Poynting-dominated plasma in the polar funnel, and the the jet sheath separating these regions where the material outflow is more important. The same color scales used in the EHT code-comparison project [45] are adopted for ease of comparison. Notice that basically our axisymmetric simulations with dynamo action are able to reproduce most of the physics of the 3D runs starting with a much higher magnetic field. A nearly equipartition field is found in both cases, also providing a comparable synchrotron emission from the disk (further details in [27]).
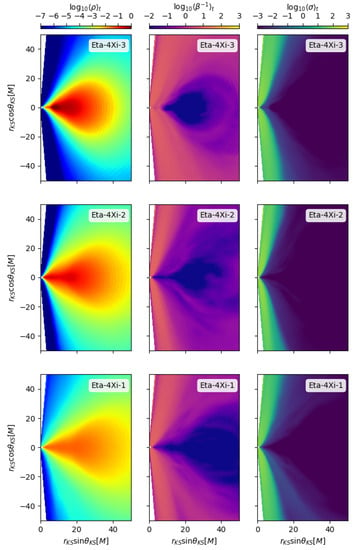
Figure 2.
Time-averaged data for rest-mass density, inverse plasma , and magnetization for the three runs with maximum resistivity of (reprinted from [27]).
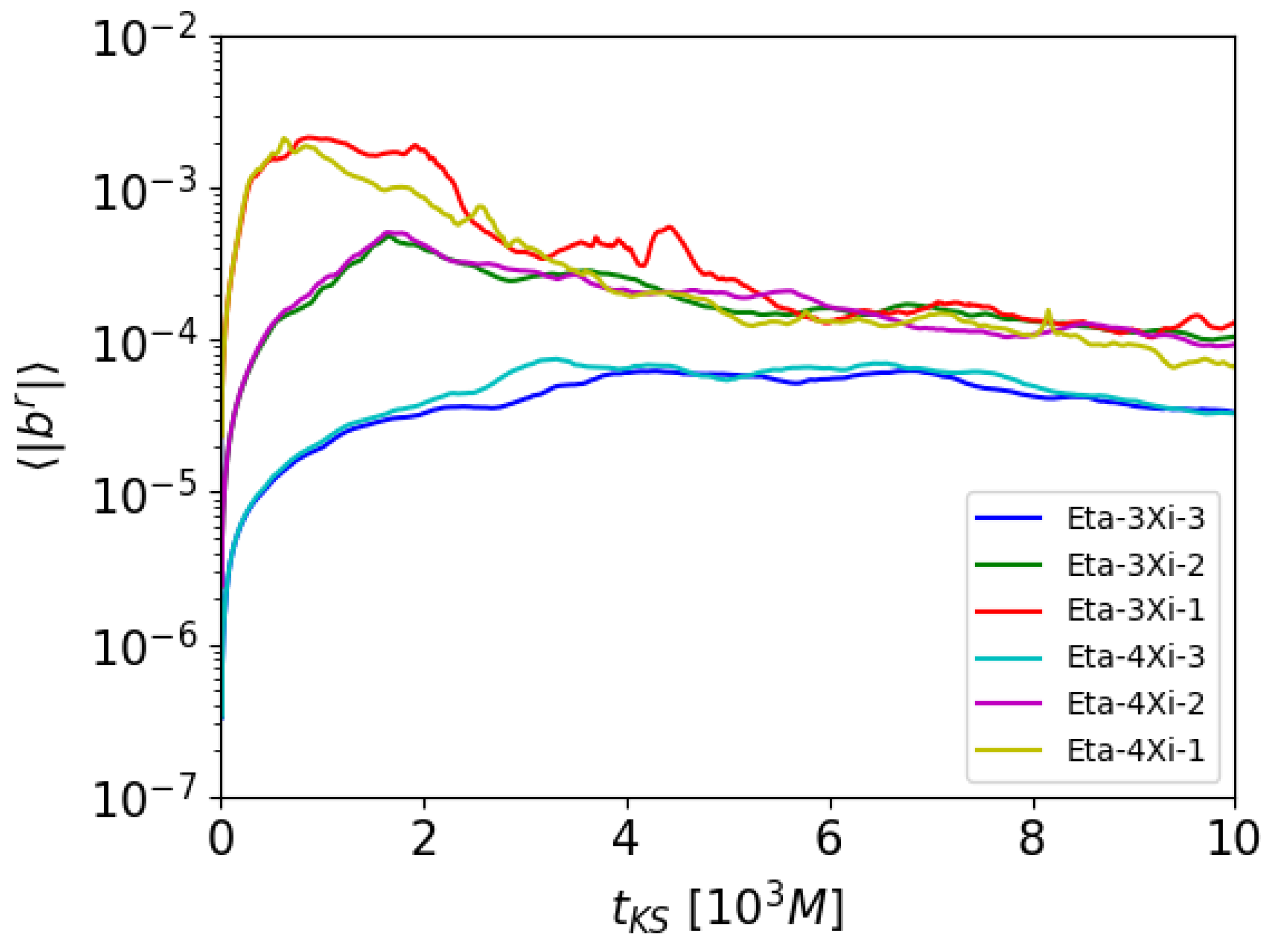
In spite of the promising axisymmetric results concerning the dynamo action, it is known that 3D simulations are able to capture additional physics like azimuthally-dependent fluid instabilities [48]. A novel set of 3D runs with a similar setup has been recently performed, and here we report some preliminary results. Differently from [27] where , leading to a migration of the dynamo-created magnetic fields towards the poles (we name this as the outgoing case), we also test here the opposite case (incoming, ), with an expected solar-like behavior of migration towards the equator. Moreover, studies of 3D MHD turbulence in stratified shearing-box models [49] indicate that the turbulent resistivity coefficient may be higher at the disk’s boundaries rather than at the center, where density peaks at , of a factor of a few, so here we test the two possible dependences . For all the four simulations we chose to have a maximum value of the dynamo of (in absolute value) and of for the resistivity.
In Figure 3, the quantity averaged on the disk is plotted for the four possible combinations of the parameters as discussed above. The outgoing cases are very similar, while the incoming case towards the equatorial region where the resistivity is higher (the green curve) provides a very low field, basically even preventing the development of MRI and accretion itself. Notice that the combination providing the strongest field is rather that of an incoming -dynamo towards the equator, where the resistivity is at its minimum (the cyan curve). The corresponding precise prescription is
with and , where a threshold value of is applied at the disk’s boundary and in the atmosphere. Given that the power of the dynamo action is mainly determined by the non-dimensional numbers defined in [25,27], both proportional to , it is clear why this combination is the best one in terms of amplifying the dynamo against dissipation. As far as resolution is concerned, the number of grid points is 100 for the three coordinates of KS metric r, , and , and radial logarithmic stretching is enforced to better resolve the inner region, as is also done in the axisymmetric simulations discussed above.
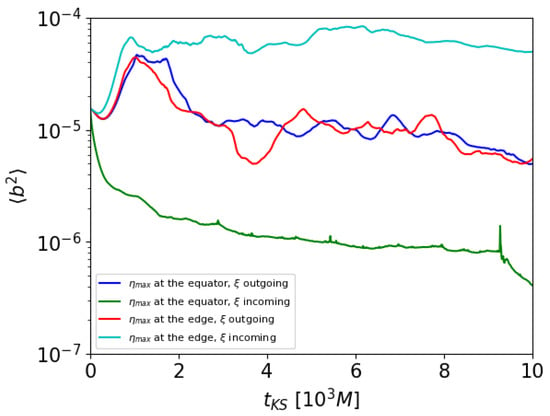
Figure 3.
Time evolution of the disk-averaged quantity for the new 3D simulations with four different combinations of and .
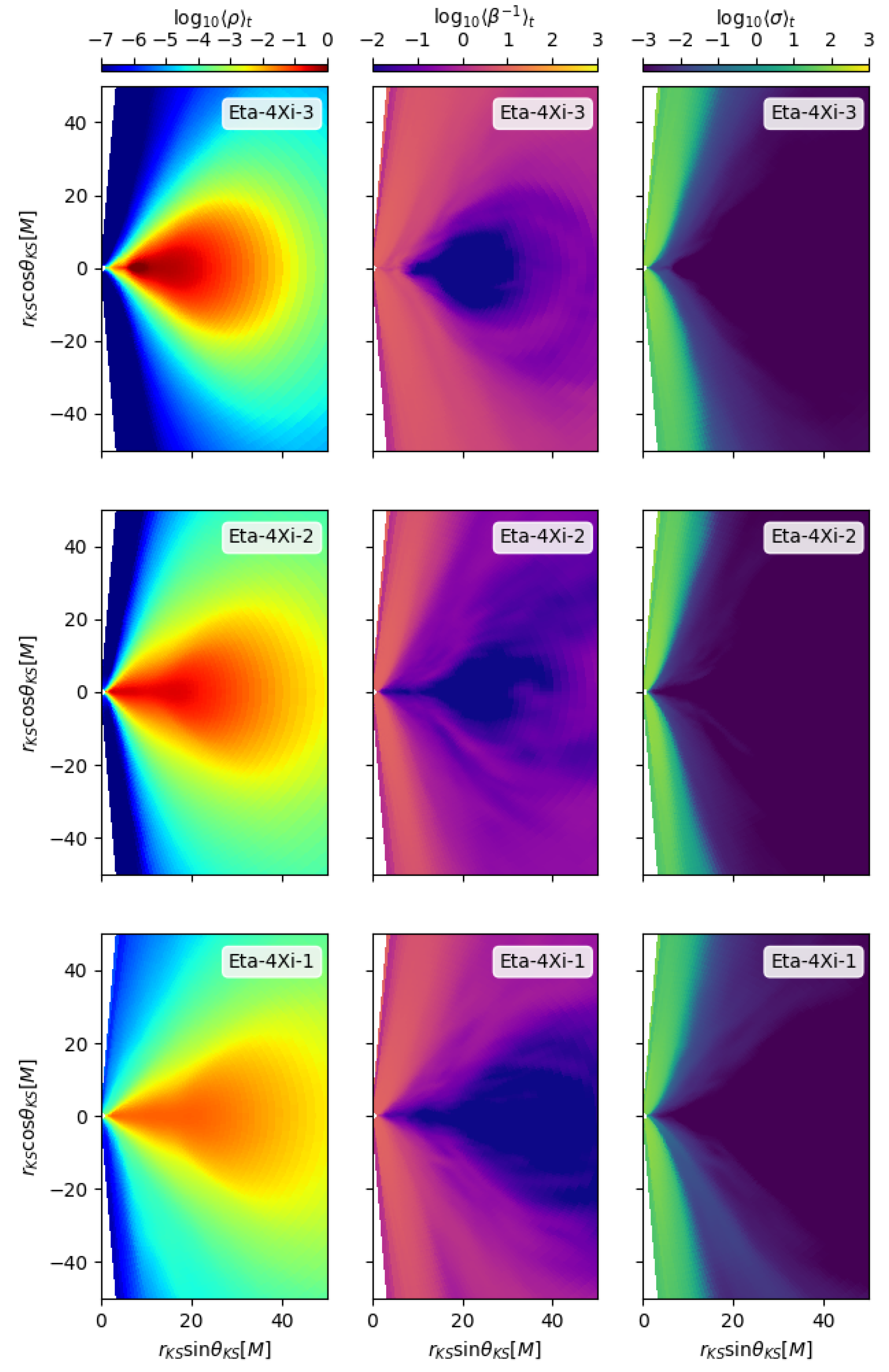
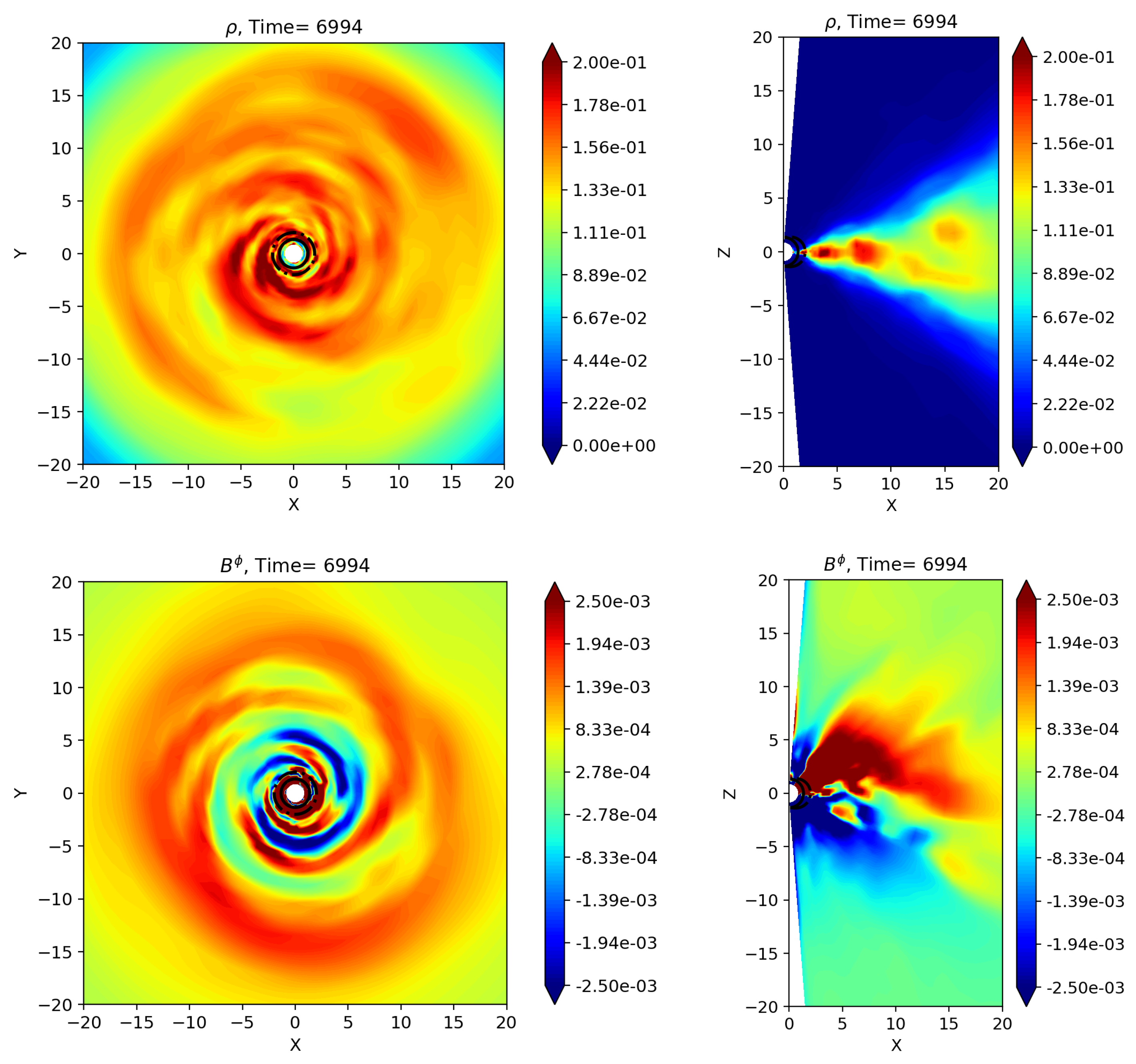
With reference to the simulation with the best parameters as discussed above, in Figure 4 we show the equatorial and meridional cuts of the rest mass density and of the toroidal magnetic field for . Notice the presence in the disk of a sort of spiral arms, anti-correlated for the two quantities, that is the field is stronger where density and pressure are lower. These are clearly dynamo waves, as can be deduced by the change of sign of the toroidal field of nearby arms. As it happens for sunsposts during the solar cycle, magnetic islands are periodically created at high latitudes and then migrate towards the equator where they appear with different polarity for each cycle (the butterfly diagram). Very similar patterns are alsoobserved and attributed to the mean field dynamo in the disks of nearby galaxies [12,50,51], hence our findings have a solid background even if for a different scenario.
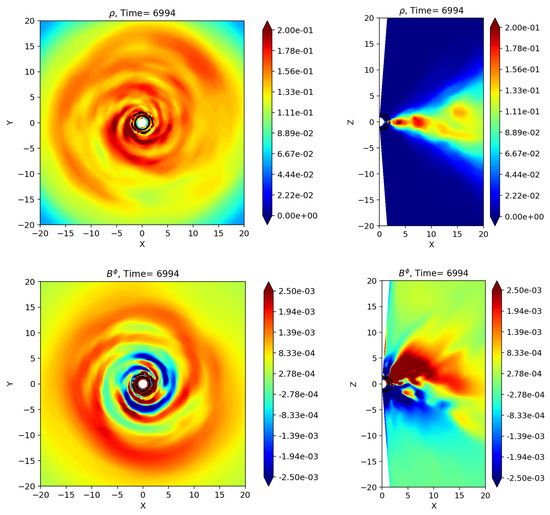
Figure 4.
Equatorial and meridional cuts for our new 3D reference run for , showing the rest mass density (above panels) and toroidal field component (lower panels).
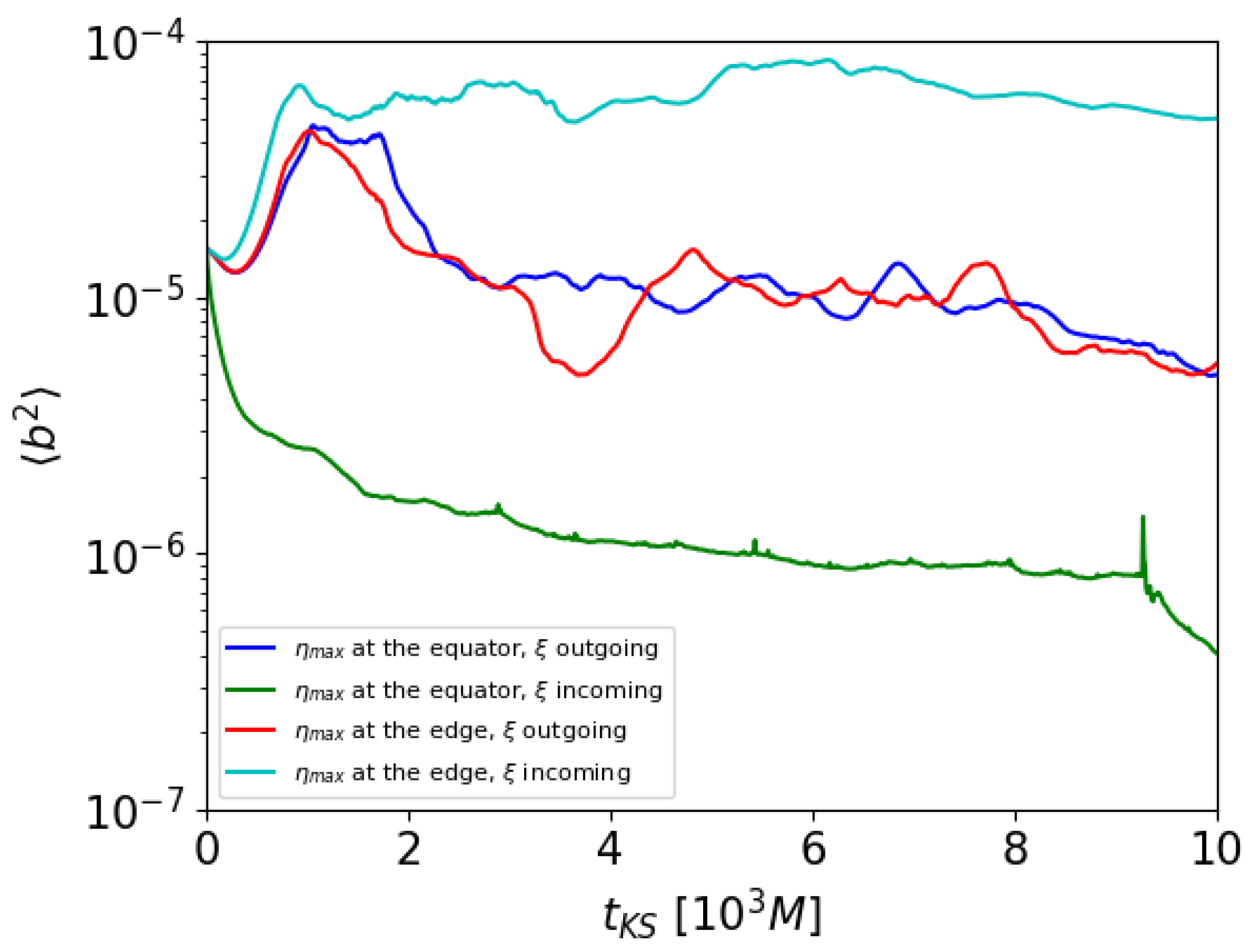
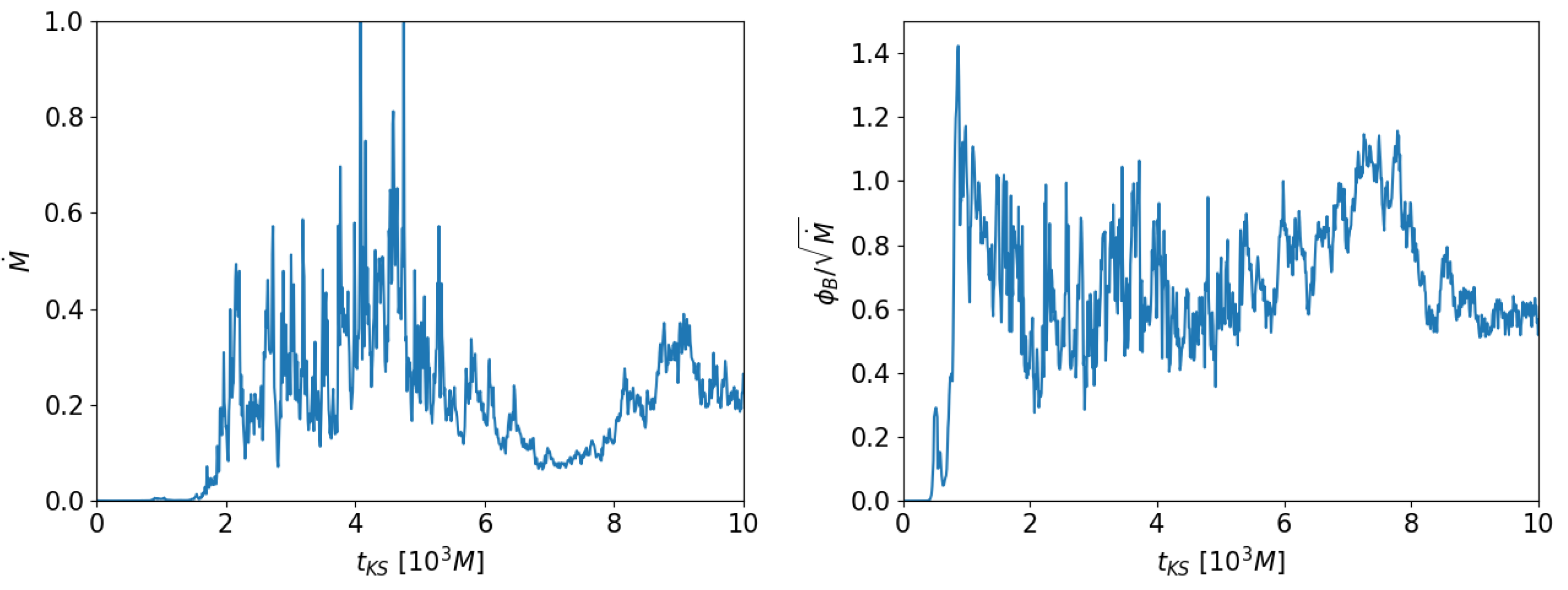
It is interesting to measure the mass accretion rate onto the central black hole and the parameter , where is the advected magnetic flux, as defined in [27,45], for our 3D reference run. In Figure 5, the two quantities are plotted as a function of time. The behavior is typical of the SANE regime (we recall that the MAD regime is defined when reaches values around 15), so we believe that in order to reach such a regime the choice of the initial fluid structure of the disk may be important (even dimensions are very different), and we leave the investigation of this aspect to future work.
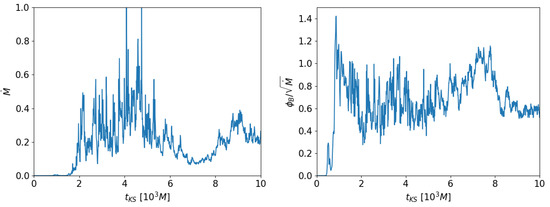
Figure 5.
Time evolution of the disk-averaged and for our new 3D reference run.
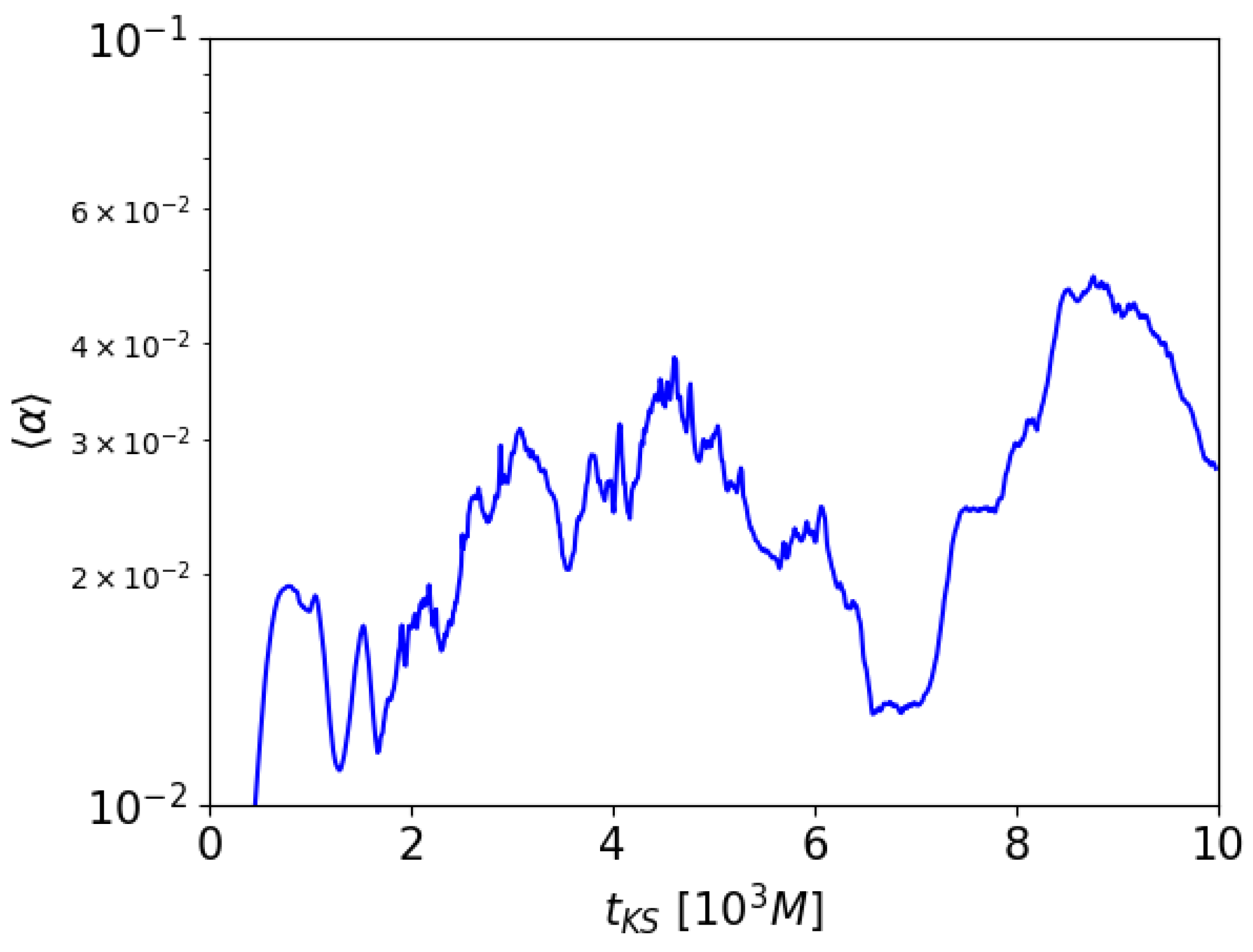
In [26], the Shakura–Sunyaev -disk parameter, due to fluid and magnetic fluctuations, was calculated by averaging over the whole disk, obtaining reasonable values between 0.01 and 0.1, which is the desired number often invoked to reproduce turbulence in accretion disks. Such simulations were axisymmetric. Here we repeat the calculation in 3D and the results are reported in Figure 6 as a function of time. Again, in spite of a rather low resolution, results are encouraging, meaning that the full 3D dynamo behaves similarly to the axisymmetric one, at least for this aspect.
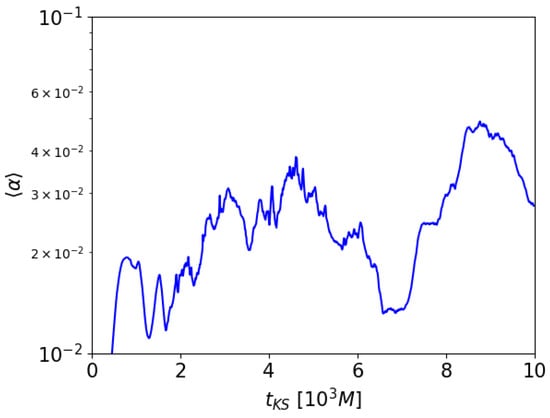
Figure 6.
Time evolution of the disk-averaged -disk coefficient for our new 3D reference run.
The presence of spiral dynamo waves, characteristic of the 3D run presented here, may have an impact on other crucial aspects such as the accretion regime, as discussed above, and on the emission of Poynting-flux dominated jets in the funnel, but we leave the investigation of these important aspects to future work.
4. Dynamo in Proto Neutron Stars and Proto Magnetars
The release of spin-down energy by a fast-rotating magnetar or by dissipation of its huge coronal fields may explain several classes of transient high-energy events, like gamma ray bursts (GRBs) [52] and soft gamma repeaters (SGRs) [53,54]. However, the magnetic fields involved are so large that they must be created by some sort of internal dynamo [55,56] in order to go beyond the standard pulsar values and to reach the required values of at least G.
The (kinematic) version of our model for the mean-field dynamo was recently applied by Franceschetti et al. [31] on top of a (proto) NS equilibrium model, which is an axisymmetric GRMHD configuration with differential rotation and polytropic equation of state built with the XNS code. This is a freely downloadable numerical tool for magnetized relativistic stars in a general relativistic metric under the conformally flat condition, including mixed field components, uniform or differential rotation, analytical (polytropic), and more realistic (tabulated) equations of state, and even extended theories of gravity, namely scalar tensor theories [38,57,58,59]. The official website is at www.arcetri.inaf.it/science/ahead/XNS (accessed on 15 February 2022).
The initial magnetic field is purely toroidal with a maximum value of G, appropriate for a standard NS, to be amplified by the dynamo action up to magnetar values, say G. While the kinematic dynamo is expected to work without upper bounds, we prefer to limit the growth of the magnetic field to a threshold well below equipartition, when back reaction of the fluid should be included (say G). In order to achieve this and to safely remain in the kinematic regime, a local quenching in the dynamo coefficient that basically limits the field to values G is applied. In order to enhance the effect of rotation, a fast spinning star with maximum ms is chosen to mimic a newly born millisecond period proto-magnetar, known to be a possible central engine for long-duration GRBs [52]. Obviously we are far from the rotation periods of standard magnetars, which are known to be much longer, of a few seconds, as measured by observations of the pulsating tail of giant flares from SGRs [60]).
Moreover, we limit the presence of dynamo in the region , if R is the radius of the NS, since the turbulence responsible for the mean-field action may be enhanced there due to the development of the neutron finger instability [61,62], but also convection [63] or MRI [64]. For further details, the reader is referred to [31]. Even higher magnetic fields could be reached in the stellar core if different prescriptions for the dynamo coefficient were used. In that case, consistent equations of state dependent on the magnetic field should be employed [65,66].
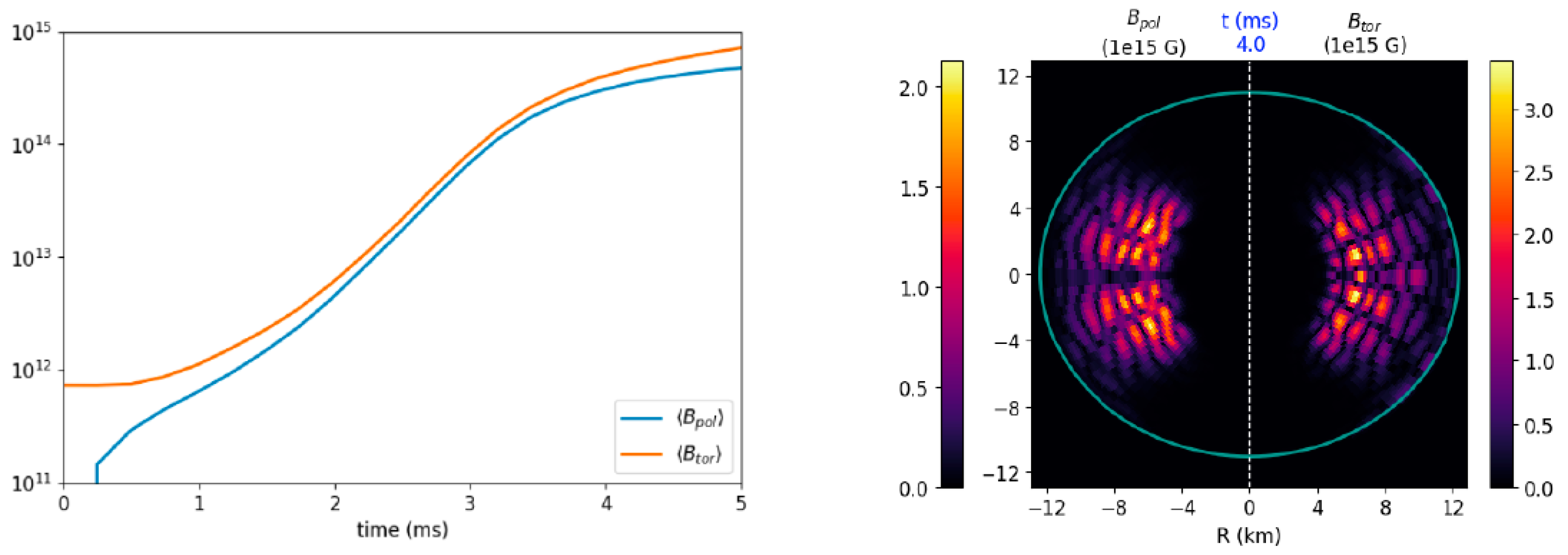
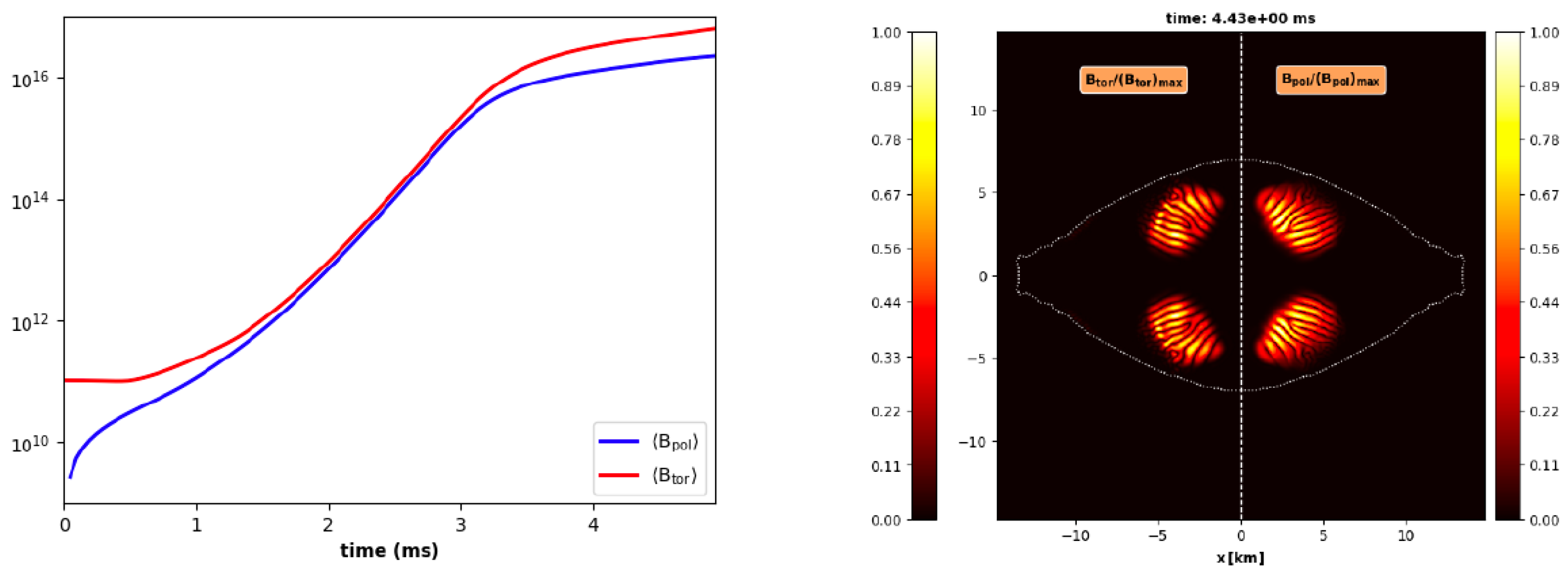
In Figure 7, the growth in time of the two magnetic field components (averaged values) is shown in the left panel. Notice that the poloidal one is created from an initial vanishing value and that in a few milliseconds the quenching values are reached, as expected. In the plot on the right, the magnetic fields components for ms are shown, where we can notice a sort of wavy structure and a growth limited to the regions where the dynamo action is stronger.
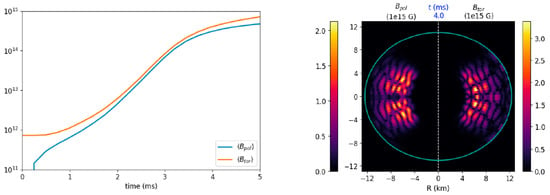
Figure 7.
GRMHD dynamo amplification of poloidal and toroidal field components in a differentially rotating, polytropic neutron star (reprinted from [31]).
The type of model described above is relevant for isolated (proto) neutron stars and magnetars, formed by core-collapse during supernova explosions and maybe long-duration GRBs, as discussed above.
However, more interesting situations can be investigated. The first multimessenger observation of a binary neutron star (BNS) merger in 2017 [67] has confirmed that these systems can power both short GRBs [68,69] and kilonova emission. The 2017 event most likely resulted in the formation of a meta-stable NS remnant that eventually collapsed into a BH, and numerous groups are currently investigating whether such a meta-stable object could have launched the short GRB jet or whether its mass ejection could have powered at least the early part of the observed kilonova signal [70,71,72,73,74,75,76].
The lifetime of these objects may be short, but a meta-stable and approximately axisymmetric configuration is often observed in numerical simulations of BNS mergers, supported against direct collapse to a black hole by strong (differential) rotation and thermal gradients, for at least 10 ms. The rotation profile of such remnants can be very different from that of a standard neutron star [77,78,79], showing a shallow behavior with near the center, a rapid increase towards , and then a Keplerian-like decay for larger radii. Two families of analytical solutions [80] with the desired properties have been recently implemented in our XNS code [81].
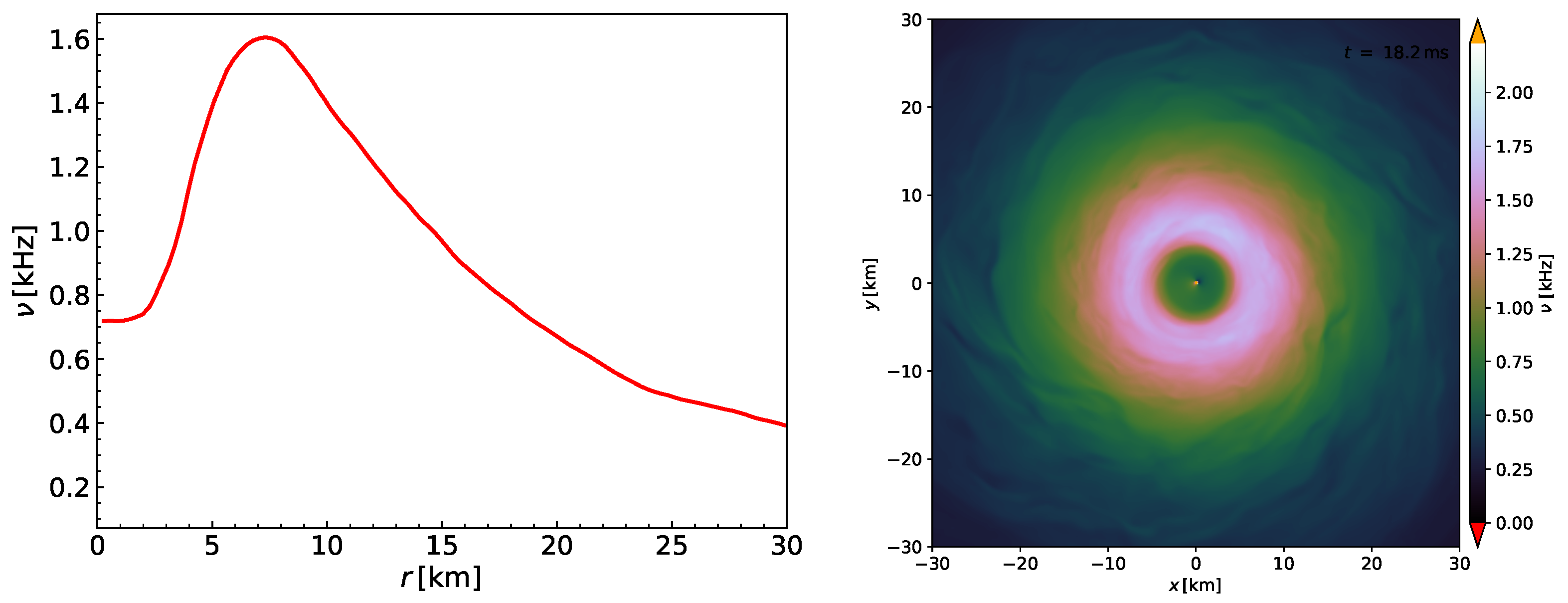
Here we use hydrodynamical data from a BNS 3D simulation (with evolving spacetimes) by R. Ciolfi and J. Kalinani, of the type described in [78], where a meta-stable super-massive neutron star (SMNS) remnant of has formed, with a central rotation rate of kHz and a maximum rotation rate of kHz, at a distance from the center of about km. In Figure 8, the rotation frequency is plotted as a function of the radius (left panel, after averaging in the azimuthal direction) and in the orbital plane, notice the particular shape of , typical of this scenario.
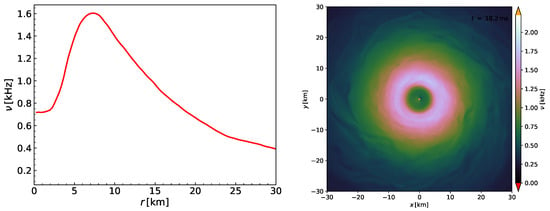
Figure 8.
Rotation frequency of the SMNS remnant obtained from BNS merger simulations.
After performing an azimuthal average of all 3-D quantities and mapping to spherical-like coordinates, including the metric terms, an initial configuration for the GRMHD ECHO code is found. In order to see whether the (kinematic) dynamo can also develop in this SMNS configuration, a seed toroidal field is added and the following prescription for the dynamo and resistivity coefficients is used
with central values and , where is the central density. The dependence on the polar angle has been chosen in order to have a vanishing -dynamo near the polar axis and near the equator, where the sign changes. As usual, in a few rotational periods the magnetic field grows exponentially from the typical values of a standard NS before merging (our initial toroidal field, dynamically negligible) up to magnetar values, with an upper threshold artificially set by a quenching term. The time averaged field components and the corresponding meridional maps at a time near the maximum can be seen in Figure 9.
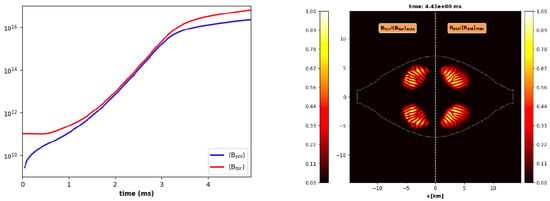
Figure 9.
GRMHD dynamo amplification of poloidal and toroidal field components in a differentially rotating SMNS remnant obtained from a simulation of a BNS merger.
Again, even higher fields could be reached by simply changing the quenching threshold, but we prefer to remain safely in the appropriate kinematic regime. Fields beyond G are expected for millisecond rotators if the dynamo can operate for tens of milliseconds [55], and even less would be necessary for the parameters chosen in our models. Moreover, notice that the toroidal and poloidal field components grow together with similar values, in both types of runs considered here. In stable equilibrium GRMHD models of magnetars with mixed polarities (the so-called twisted torus configurations), the poloidal component is instead expected to be dominant [82], though particular cases with similar maximum values seem to be actually possible [83]. However, enhanced rotation in the core could easily lead to a stronger winding ( effect) of the toroidal component, which may even become the dominant one. This is expected to have a strong influence in similar contexts, like that of core-collapse supernovae [84] (see also [85,86] for recent simulations with complex magnetic structures).
The growth rates obviously depend on the characteristic dynamo numbers [25,31], and in any case these are related to the properties of the (unresolved) turbulence, like the correlation time, and not on the period of rotation. Depending on the choice of the parameters, the magnetic field growth can be the usual one due to both rotation and dynamo effect (the case), or just due to the nonlinear effect. The case shown here is at the threshold of the two mentioned regimes.
5. Summary and Conclusions
In the present paper we have reviewed the work by the group in Florence on GRMHD dynamos. First, the appropriate formalism is discussed, from the covariant form of Ohm’s law proposed by Bucciantini and Del Zanna [32] to the full numerical implementation in shock capturing schemes detailed in [26,33], and in the ECHO code in particular [37].
The application of the mean-field GRMHD dynamo to thick accretion disks around rotating black holes in the context of EHT observations is then discussed, showing the main results in axisymmetry by [27], here extended for the first time to 3D. We see that when the term is chosen such to lead to magnetic field migration converging towards the disk’s equator, and resistivity is lower there, magnetized spiral arms of alternating polarity are continuously created and advected, creating a situation resembling what was observed in nearby galaxies. The regime found is that typical of the so-called SANE accretion. As in the previous axisymmetric case, we leave the implementation of our dynamo model to the fluid disk’s structure, typically leading to MAD accretion (when threaded by substantial poloidal fields) for future investigation.
A mean-field dynamo model in GRMHD has been also invoked to enhance a standard pulsar-type magnetic field up to magnetar values in proto neutron stars [31]. Here we report the main results of axisymmetric kinematic simulations of the growth of the toroidal and poloidal magnetic field components due to the (unresolved) turbulent motions in the outer regions of a proto neutron star, modeled using a fluid equilibrium found with our XNS code [38,57,81]. Moreover, we show here for the first time results of the application of the dynamo action to a realistic super-massive neutron star obtained from a full numerical relativity simulation of a binary neutron star merger event, kindly provided by R. Ciolfi and J. Kalinani. The growth of the field occurs in a few millisecond in the regions where the gradients of the differential rotation is stronger, as expected. We leave the investigation of both a deeper parameter study and above all of the fully dynamical scenario, in which dynamo action may interact with fluid an MHD instabilities, to future works.
Obviously, the coefficients providing dissipation and amplification of magnetic fields, namely and ( in our notation), and all other tensorial components when the hypothesis of isotropic response is relaxed, should be computed on top of extremely high resolution 3D simulations where MHD turbulence can fully develop. These are impossible to achieve in global setups, while there are several studies in shearing box (stratified) MHD models, e.g., [49]. Typical expected values are of the order of , where H is the pressure scale-height and the mean rotation rate (for a Keplerian rotation law). Such scaling should be approximately valid in GRMHD also, in both cases of thick accretion disks and proton neutron stars (especially in the external layers where rotation is Keplerian-like, even for BNS remnants).
Concluding, we believe that the GRMHD mean field dynamo is an essential ingredient that should be considered whenever rotating configurations and turbulent plasmas are present. The growth of the magnetic field may be efficient against dissipation, with rates depending on (unresolved) turbulent properties rather than on rotation itself, and this result may help to explain many unresolved important issues in high-energy astrophysics.
Author Contributions
Conceptualization, L.D.Z., N.T., K.F., M.B. and N.B.; Data curation, N.T. and K.F.; Supervision, L.D.Z.; Writing—original draft, L.D.Z.; Writing—review and editing, M.B. and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
Matteo Bugli acknowledges support from the European Research Council (ERC starting grant no. 715368—MagBURST).
Acknowledgments
The authors thank R. Ciolfi and J. Kalinani for providing the data of the remnant obtained from their numerical relativity simulations of a binary neutron star merger. Numerical calculations have been made possible through a CINECA-INFN agreement, providing access to resources on MARCONI at CINECA.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Biermann, L. Kometenschweife und solare Korpuskularstrahlung. Z. Astrophys. 1951, 29, 274. [Google Scholar]
- Weibel, E.S. Spontaneously Growing Transverse Waves in a Plasma Due to an Anisotropic Velocity Distribution. Phys. Rev. Lett. 1959, 2, 83–84. [Google Scholar] [CrossRef]
- Fried, B.D. Mechanism for Instability of Transverse Plasma Waves. Phys. Fluids 1959, 2, 337. [Google Scholar] [CrossRef]
- Rincon, F. Dynamo theories. J. Plasma Phys. 2019, 85, 205850401. [Google Scholar] [CrossRef]
- Tobias, S.M. The turbulent dynamo. J. Fluid Mech. 2021, 912, P1. [Google Scholar] [CrossRef] [PubMed]
- Parker, E.N. Hydromagnetic Dynamo Models. Astrophys. J. 1955, 122, 293. [Google Scholar] [CrossRef]
- Elsasser, W.M. Induction Effects in Terrestrial Magnetism Part I. Theory. Phys. Rev. 1946, 69, 106–116. [Google Scholar] [CrossRef]
- Cowling, T.G. The magnetic field of sunspots. Mon. Not. R. Astron. Soc. 1933, 94, 39–48. [Google Scholar] [CrossRef]
- Moffatt, H.K. Magnetic Field Generation in Electrically Conducting Fluids; Cambridge Univ. Press: Cambridge, UK, 1978. [Google Scholar]
- Parker, E.N. Cosmical Magnetic Fields. Their Origin and Their Activity; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Krause, F.; Raedler, K.H. Mean-Field Magnetohydrodynamics and Dynamo Theory; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2005, 417, 1–209. [Google Scholar] [CrossRef]
- Blackman, E.G.; Field, G.B. New Dynamical Mean-Field Dynamo Theory and Closure Approach. Phys. Rev. Lett. 2002, 89, 265007. [Google Scholar] [CrossRef]
- Velikhov, E. Stability of an ideally conducting liquid flowing between cylinders rotating in a magnetic field. Sov. Phys. JETP 1959, 36, 1398–1404. [Google Scholar]
- Chandrasekhar, S. The Stability of Non-Dissipative Couette Flow in Hydromagnetics. Proc. Natl. Acad. Sci. USA 1960, 46, 253–257. [Google Scholar] [CrossRef] [PubMed]
- Balbus, S.A.; Hawley, J.F. A Powerful Local Shear Instability in Weakly Magnetized Disks. I. Linear Analysis. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- Balbus, S.A. Enhanced Angular Momentum Transport in Accretion Disks. Annu. Rev. Astron. Astrophys. 2003, 41, 555–597. [Google Scholar] [CrossRef]
- Brandenburg, A.; Nordlund, A.; Stein, R.F.; Torkelsson, U. Dynamo-generated Turbulence and Large-Scale Magnetic Fields in a Keplerian Shear Flow. Astrophys. J. 1995, 446, 741. [Google Scholar] [CrossRef]
- Hawley, J.F.; Gammie, C.F.; Balbus, S.A. Local Three-dimensional Magnetohydrodynamic Simulations of Accretion Disks. Astrophys. J. 1995, 440, 742. [Google Scholar] [CrossRef]
- Bodo, G.; Mignone, A.; Cattaneo, F.; Rossi, P.; Ferrari, A. Aspect ratio dependence in magnetorotational instability shearing box simulations. Astron. Astrophys. 2008, 487, 1–5. [Google Scholar] [CrossRef]
- Davis, S.W.; Stone, J.M.; Pessah, M.E. Sustained Magnetorotational Turbulence in Local Simulations of Stratified Disks with Zero Net Magnetic Flux. Astrophys. J. 2010, 713, 52–65. [Google Scholar] [CrossRef]
- Flock, M.; Dzyurkevich, N.; Klahr, H.; Turner, N.; Henning, T. Large-scale Azimuthal Structures of Turbulence in Accretion Disks: Dynamo Triggered Variability of Accretion. Astrophys. J. 2012, 744, 144. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Stone, J.M.; Davis, S.W. A Global Three-dimensional Radiation Magneto-hydrodynamic Simulation of Super-Eddington Accretion Disks. Astrophys. J. 2014, 796, 106. [Google Scholar] [CrossRef]
- Hogg, J.D.; Reynolds, C.S. The Influence of Accretion Disk Thickness on the Large-scale Magnetic Dynamo. Astrophys. J. 2018, 861, 24. [Google Scholar] [CrossRef]
- Bugli, M.; Del Zanna, L.; Bucciantini, N. Dynamo action in thick discs around Kerr black holes: High-order resistive GRMHD simulations. Mon. Not. R. Astron. Soc. 2014, 440, L41–L45. [Google Scholar] [CrossRef]
- Tomei, N.; Del Zanna, L.; Bugli, M.; Bucciantini, N. General relativistic magnetohydrodynamic dynamo in thick accretion discs: Fully non-linear simulations. Mon. Not. R. Astron. Soc. 2020, 491, 2346–2359. [Google Scholar] [CrossRef]
- Tomei, N.; Del Zanna, L.; Bugli, M.; Bucciantini, N. Are GRMHD Mean-Field Dynamo Models of Thick Accretion Disks SANE? Universe 2021, 7, 259. [Google Scholar] [CrossRef]
- Vourellis, C.; Fendt, C. Relativistic Outflows from a GRMHD Mean-field Disk Dynamo. Astrophys. J. 2021, 911, 85. [Google Scholar] [CrossRef]
- Mattia, G.; Fendt, C. Magnetohydrodynamic Accretion-Ejection: Jets Launched by a Nonisotropic Accretion-disk Dynamo. I. Validation and Application of Selected Dynamo Tensorial Components. Astrophys. J. 2020, 900, 59. [Google Scholar] [CrossRef]
- Mattia, G.; Fendt, C. Magnetohydrodynamic Accretion-Ejection: Jets Launched by a Nonisotropic Accretion-disk Dynamo. II. A Dynamo Tensor Defined by the Disk Coriolis Number. Astrophys. J. 2020, 900, 60. [Google Scholar] [CrossRef]
- Franceschetti, K.; Del Zanna, L. General Relativistic Mean-Field Dynamo Model for Proto-Neutron Stars. Universe 2020, 6, 83. [Google Scholar] [CrossRef]
- Bucciantini, N.; Del Zanna, L. A fully covariant mean-field dynamo closure for numerical 3 + 1 resistive GRMHD. Mon. Not. R. Astron. Soc. 2013, 428, 71–85. [Google Scholar] [CrossRef]
- Del Zanna, L.; Bucciantini, N. Covariant and 3 + 1 equations for dynamo-chiral general relativistic magnetohydrodynamics. Mon. Not. R. Astron. Soc. 2018, 479, 657–666. [Google Scholar] [CrossRef]
- Alcubierre, M. Introduction to 3+1 Numerical Relativity; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Gourgoulhon, E. 3+1 Formalism in General Relativity; Lecture Notes in Physics 846; Springer: Berlin, Germany, 2012. [Google Scholar]
- Rezzolla, L.; Zanotti, O. Relativistic Hydrodynamics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Del Zanna, L.; Zanotti, O.; Bucciantini, N.; Londrillo, P. ECHO: A Eulerian conservative high-order scheme for general relativistic magnetohydrodynamics and magnetodynamics. Astron. Astrophys. 2007, 473, 11–30. [Google Scholar] [CrossRef]
- Bucciantini, N.; Del Zanna, L. General relativistic magnetohydrodynamics in axisymmetric dynamical spacetimes: The X-ECHO code. Astron. Astrophys. 2011, 528, A101. [Google Scholar] [CrossRef]
- Palenzuela, C.; Lehner, L.; Reula, O.; Rezzolla, L. Beyond ideal MHD: Towards a more realistic modelling of relativistic astrophysical plasmas. Mon. Not. R. Astron. Soc. 2009, 394, 1727–1740. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Komissarov, S.S. Electrodynamics of black hole magnetospheres. Mon. Not. R. Astron. Soc. 2004, 350, 427–448. [Google Scholar] [CrossRef]
- Davis, S.W.; Tchekhovskoy, A. Magnetohydrodynamics Simulations of Active Galactic Nucleus Disks and Jets. Annu. Rev. Astron. Astrophys. 2020, 58, 407–439. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Rao, R.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. Lett. 2019, 875, L5. [Google Scholar] [CrossRef]
- Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.-K.; Nadolski, A. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Porth, O.; Chatterjee, K.; Narayan, R.; Gammie, C.F.; Mizuno, Y.; Anninos, P.; Baker, J.G.; Bugli, M.; Chan, C.k.; Neri, R.; et al. The Event Horizon General Relativistic Magnetohydrodynamic Code Comparison Project. Astrophys. J. Suppl. Ser. 2019, 243, 26. [Google Scholar] [CrossRef]
- Cruz-Osorio, A.; Fromm, C.M.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Davelaar, J.; Falcke, H.; Kramer, M.; Rezzolla, L. State-of-the-art energetic and morphological modelling of the launching site of the M87 jet. Nat. Astron. 2022, 6, 103–108. [Google Scholar] [CrossRef]
- Liska, M.; Tchekhovskoy, A.; Quataert, E. Large-scale poloidal magnetic field dynamo leads to powerful jets in GRMHD simulations of black hole accretion with toroidal field. Mon. Not. R. Astron. Soc. 2020, 494, 3656–3662. [Google Scholar] [CrossRef]
- Bugli, M.; Guilet, J.; Müller, E.; Del Zanna, L.; Bucciantini, N.; Montero, P.J. Papaloizou-Pringle instability suppression by the magnetorotational instability in relativistic accretion discs. Mon. Not. R. Astron. Soc. 2018, 475, 108–120. [Google Scholar] [CrossRef]
- Gressel, O.; Pessah, M.E. Characterizing the Mean-field Dynamo in Turbulent Accretion Disks. Astrophys. J. 2015, 810, 59. [Google Scholar] [CrossRef]
- Beck, R.; Brandenburg, A.; Moss, D.; Shukurov, A.; Sokoloff, D. Galactic Magnetism: Recent Developments and Perspectives. Annu. Rev. Astron. Astrophys. 1996, 34, 155–206. [Google Scholar] [CrossRef]
- Kulsrud, R.M. A Critical Review of Galactic Dynamos. Annu. Rev. Astron. Astrophys. 1999, 37, 37–64. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 413, 2031–2056. [Google Scholar] [CrossRef]
- Lyutikov, M. Explosive reconnection in magnetars. Mon. Not. R. Astron. Soc. 2003, 346, 540–554. [Google Scholar] [CrossRef]
- Del Zanna, L.; Papini, E.; Landi, S.; Bugli, M.; Bucciantini, N. Fast reconnection in relativistic plasmas: The magnetohydrodynamics tearing instability revisited. Mon. Not. R. Astron. Soc. 2016, 460, 3753–3765. [Google Scholar] [CrossRef]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-Ray Bursts. Astrophys. J. Lett. 1992, 392, L9. [Google Scholar] [CrossRef]
- Mösta, P.; Ott, C.D.; Radice, D.; Roberts, L.F.; Schnetter, E.; Haas, R. A large-scale dynamo and magnetoturbulence in rapidly rotating core-collapse supernovae. Nature 2015, 528, 376–379. [Google Scholar] [CrossRef]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. Axisymmetric equilibrium models for magnetized neutron stars in General Relativity under the Conformally Flat Condition. Mon. Not. R. Astron. Soc. 2014, 439, 3541–3563. [Google Scholar] [CrossRef]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. General relativistic models for rotating magnetized neutron stars in conformally flat space-time. Mon. Not. R. Astron. Soc. 2017, 470, 2469–2493. [Google Scholar] [CrossRef]
- Soldateschi, J.; Bucciantini, N.; Del Zanna, L. Quasi-universality of the magnetic deformation of neutron stars in general relativity and beyond. Astron. Astrophys. 2021, 654, A162. [Google Scholar] [CrossRef]
- Mereghetti, S. The strongest cosmic magnets: Soft gamma-ray repeaters and anomalous X-ray pulsars. Astron. Astrophys. Rev. 2008, 15, 225–287. [Google Scholar] [CrossRef]
- Bonanno, A.; Rezzolla, L.; Urpin, V. Mean-field dynamo action in protoneutron stars. Astron. Astrophys. 2003, 410, L33–L36. [Google Scholar] [CrossRef]
- Naso, L.; Rezzolla, L.; Bonanno, A.; Paternò, L. Magnetic field amplification in proto-neutron stars. The role of the neutron-finger instability for dynamo excitation. Astron. Astrophys. 2008, 479, 167–176. [Google Scholar] [CrossRef]
- Raynaud, R.; Guilet, J.; Janka, H.T.; Gastine, T. Magnetar formation through a convective dynamo in protoneutron stars. Sci. Adv. 2020, 6, eaay2732. [Google Scholar] [CrossRef]
- Reboul-Salze, A.; Guilet, J.; Raynaud, R.; Bugli, M. A global model of the magnetorotational instability in protoneutron stars. Astron. Astrophys. 2021, 645, A109. [Google Scholar] [CrossRef]
- Broderick, A.E.; Prakash, M.; Lattimer, J.M. Effects of strong magnetic fields in strange baryonic matter. Phys. Lett. B 2002, 531, 167–174. [Google Scholar] [CrossRef][Green Version]
- Chatterjee, D.; Elghozi, T.; Novak, J.; Oertel, M. Consistent neutron star models with magnetic-field-dependent equations of state. Mon. Not. R. Astron. Soc. 2015, 447, 3785–3796. [Google Scholar] [CrossRef]
- Abbott, B.P.; Bloemen, S.; Canizares, P.; Falcke, H.; Fender, R.P.; Ghosh, S.; Arnaud, N.; Arun, K.G.; Ascenzi, S.; Williamson, A.R.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Rezzolla, L.; Giacomazzo, B.; Baiotti, L.; Granot, J.; Kouveliotou, C.; Aloy, M.A. The Missing Link: Merging Neutron Stars Naturally Produce Jet-like Structures and Can Power Short Gamma-ray Bursts. Astrophys. J. Lett. 2011, 732, L6. [Google Scholar] [CrossRef]
- Giacomazzo, B.; Zrake, J.; Duffell, P.C.; MacFadyen, A.I.; Perna, R. Producing Magnetar Magnetic Fields in the Merger of Binary Neutron Stars. Astrophys. J. 2015, 809, 39. [Google Scholar] [CrossRef]
- Metzger, B.D. Kilonovae. Living Rev. Relativ. 2019, 23, 1. [Google Scholar] [CrossRef]
- Bucciantini, N.; Metzger, B.D.; Thompson, T.A.; Quataert, E. Short gamma-ray bursts with extended emission from magnetar birth: Jet formation and collimation. Mon. Not. R. Astron. Soc. 2012, 419, 1537–1545. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kastaun, W.; Giacomazzo, B.; Endrizzi, A.; Siegel, D.M.; Perna, R. General relativistic magnetohydrodynamic simulations of binary neutron star mergers forming a long-lived neutron star. Phys. Rev. D 2017, 95, 063016. [Google Scholar] [CrossRef]
- Ciolfi, R. Collimated outflows from long-lived binary neutron star merger remnants. Mon. Not. R. Astron. Soc. 2020, 495, L66–L70. [Google Scholar] [CrossRef]
- Metzger, B.D.; Thompson, T.A.; Quataert, E. A Magnetar Origin for the Kilonova Ejecta in GW170817. Astrophys. J. 2018, 856, 101. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kalinani, J.V. Magnetically Driven Baryon Winds from Binary Neutron Star Merger Remnants and the Blue Kilonova of 2017 August. Astrophys. J. Lett. 2020, 900, L35. [Google Scholar] [CrossRef]
- Mösta, P.; Radice, D.; Haas, R.; Schnetter, E.; Bernuzzi, S. A Magnetar Engine for Short GRBs and Kilonovae. Astrophys. J. Lett. 2020, 901, L37. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Ujevic, M.; Brügmann, B. Numerical relativity simulations of neutron star merger remnants using conservative mesh refinement. Phys. Rev. D 2015, 91, 124041. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kastaun, W.; Kalinani, J.V.; Giacomazzo, B. First 100 ms of a long-lived magnetized neutron star formed in a binary neutron star merger. Phys. Rev. D 2019, 100, 023005. [Google Scholar] [CrossRef]
- De Pietri, R.; Feo, A.; Font, J.A.; Löffler, F.; Pasquali, M.; Stergioulas, N. Numerical-relativity simulations of long-lived remnants of binary neutron star mergers. Phys. Rev. D 2020, 101, 064052. [Google Scholar] [CrossRef]
- Uryū, K.; Tsokaros, A.; Baiotti, L.; Galeazzi, F.; Taniguchi, K.; Yoshida, S. Modeling differential rotations of compact stars in equilibriums. Phys. Rev. D 2017, 96, 103011. [Google Scholar] [CrossRef]
- Franceschetti, K.; Del Zanna, L.; Soldateschi, J.; Bucciantini, N. Numerical equilibrium configurations and quadrupole moments of post-merger differentially rotating relativistic stars. Universe 2022. submitted. [Google Scholar]
- Bucciantini, N.; Pili, A.G.; Del Zanna, L. The role of currents distribution in general relativistic equilibria of magnetized neutron stars. Mon. Not. R. Astron. Soc. 2015, 447, 3278–3290. [Google Scholar] [CrossRef]
- Uryū, K.; Yoshida, S.; Gourgoulhon, E.; Markakis, C.; Fujisawa, K.; Tsokaros, A.; Taniguchi, K.; Eriguchi, Y. New code for equilibriums and quasiequilibrium initial data of compact objects. IV. Rotating relativistic stars with mixed poloidal and toroidal magnetic fields. Phys. Rev. D 2019, 100, 123019. [Google Scholar] [CrossRef]
- Kotake, K.; Sato, K.; Takahashi, K. Explosion mechanism, neutrino burst and gravitational wave in core-collapse supernovae. Rep. Prog. Phys. 2006, 69, 971–1143. [Google Scholar] [CrossRef]
- Bugli, M.; Guilet, J.; Obergaulinger, M.; Cerdá-Durán, P.; Aloy, M.A. The impact of non-dipolar magnetic fields in core-collapse supernovae. Mon. Not. R. Astron. Soc. 2020, 492, 58–71. [Google Scholar] [CrossRef]
- Bugli, M.; Guilet, J.; Obergaulinger, M. Three-dimensional core-collapse supernovae with complex magnetic structures—I. Explosion dynamics. Mon. Not. R. Astron. Soc. 2021, 507, 443–454. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).