On the Computational Modeling of Inclined Brine Discharges
Abstract
:1. Introduction
2. Analysis
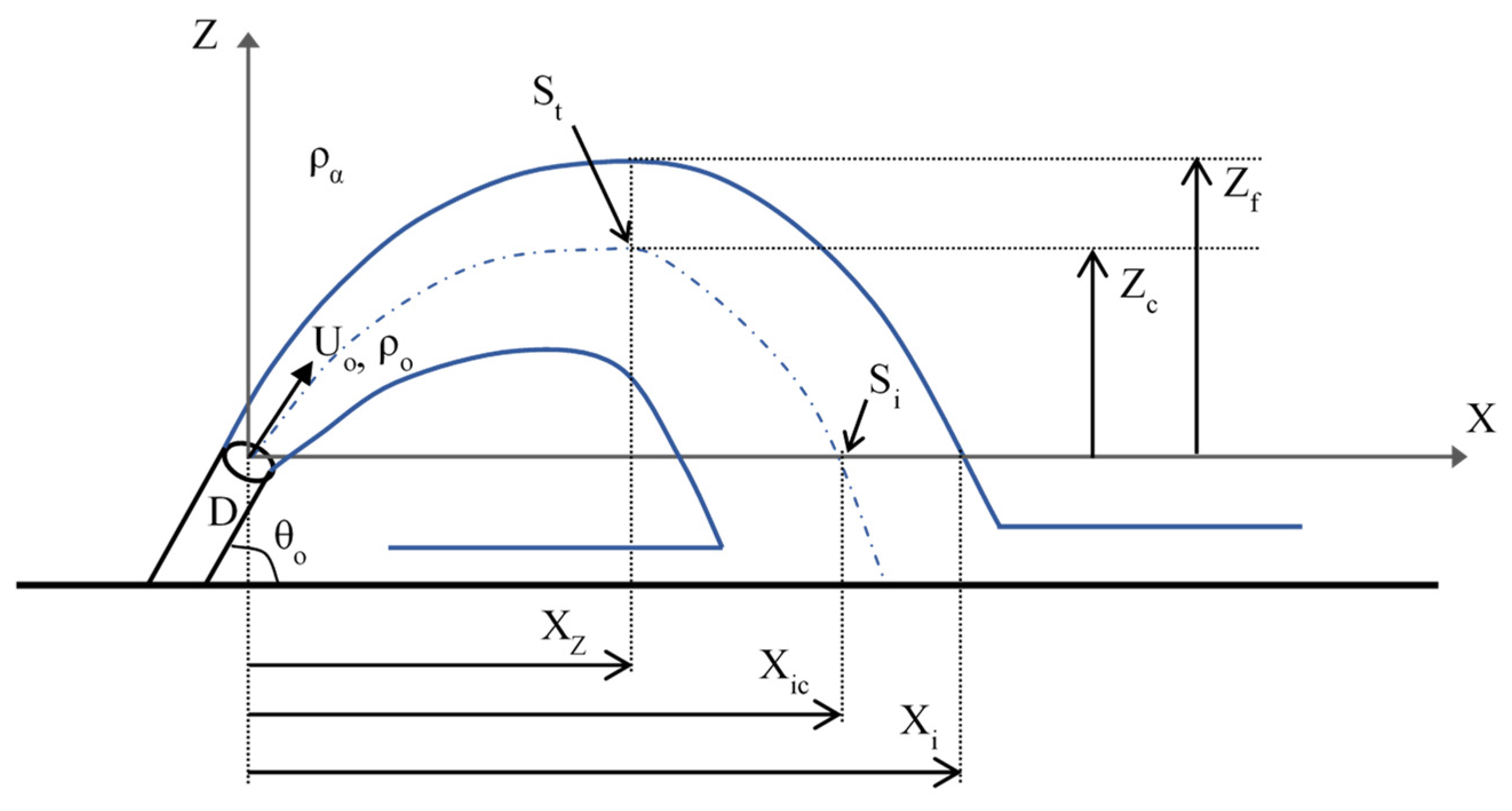
2.1. The Problem Considered and Dimensional Arguments
2.2. The Computational Models
3. Results and Discussion
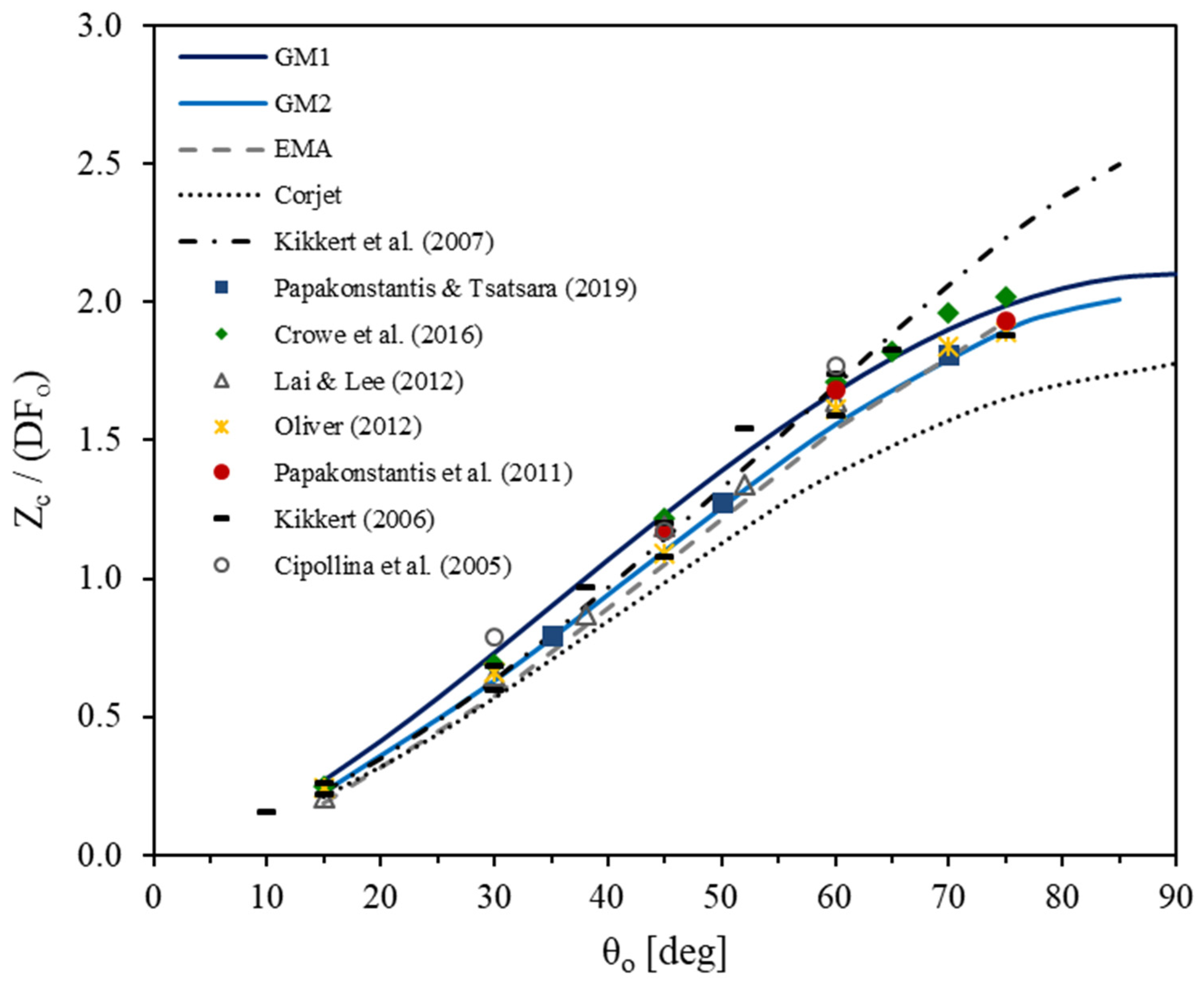
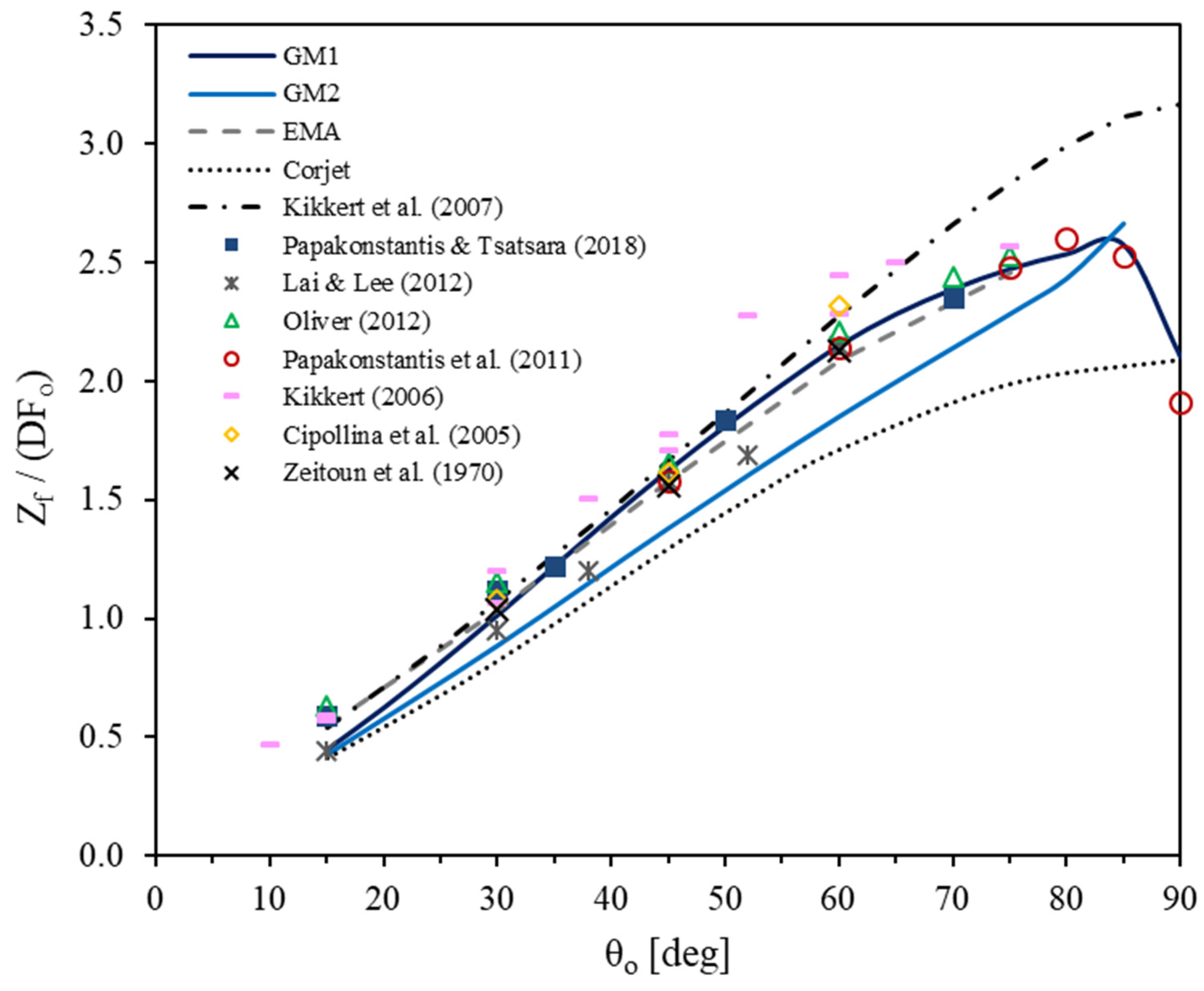
3.1. Vertical Distances
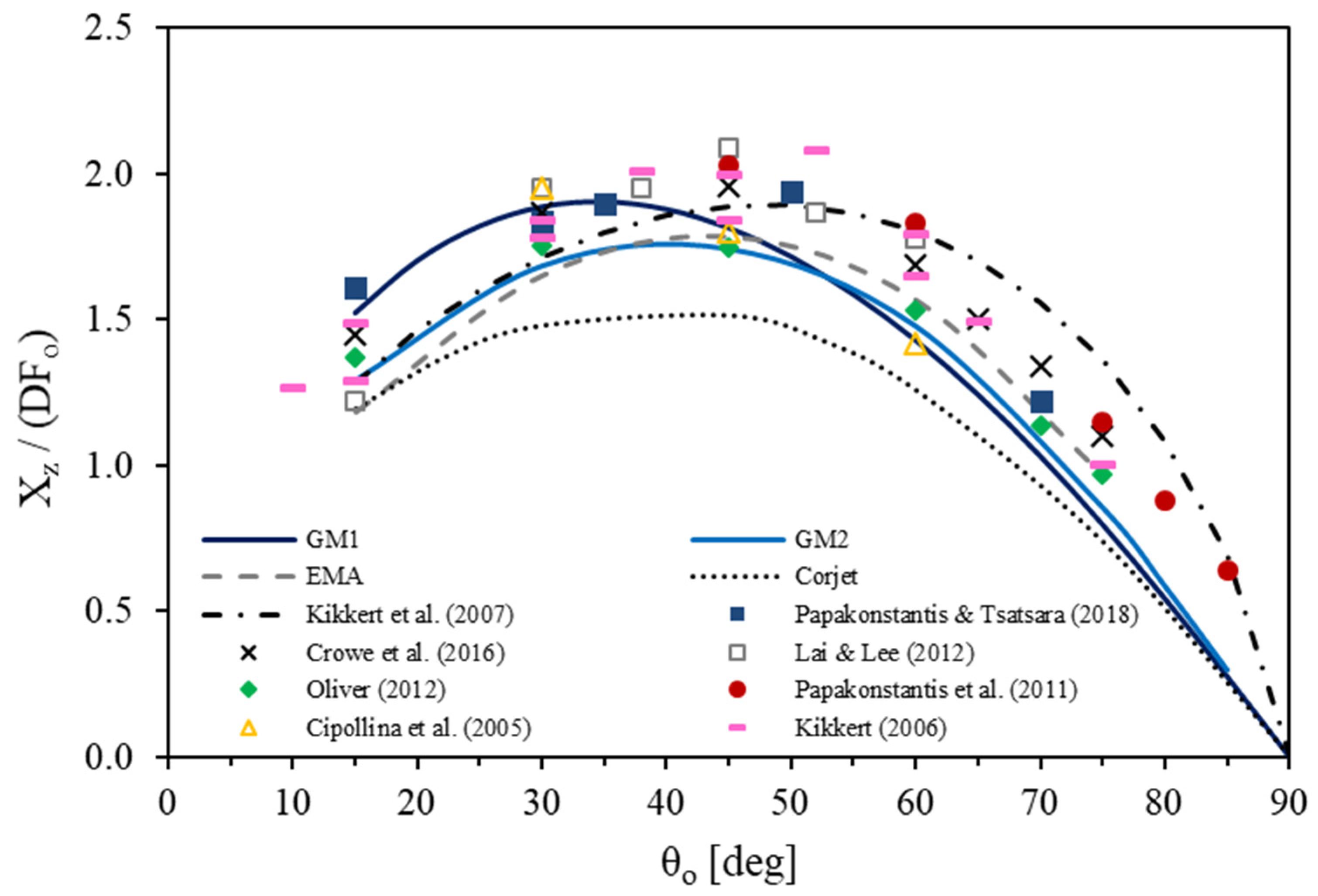
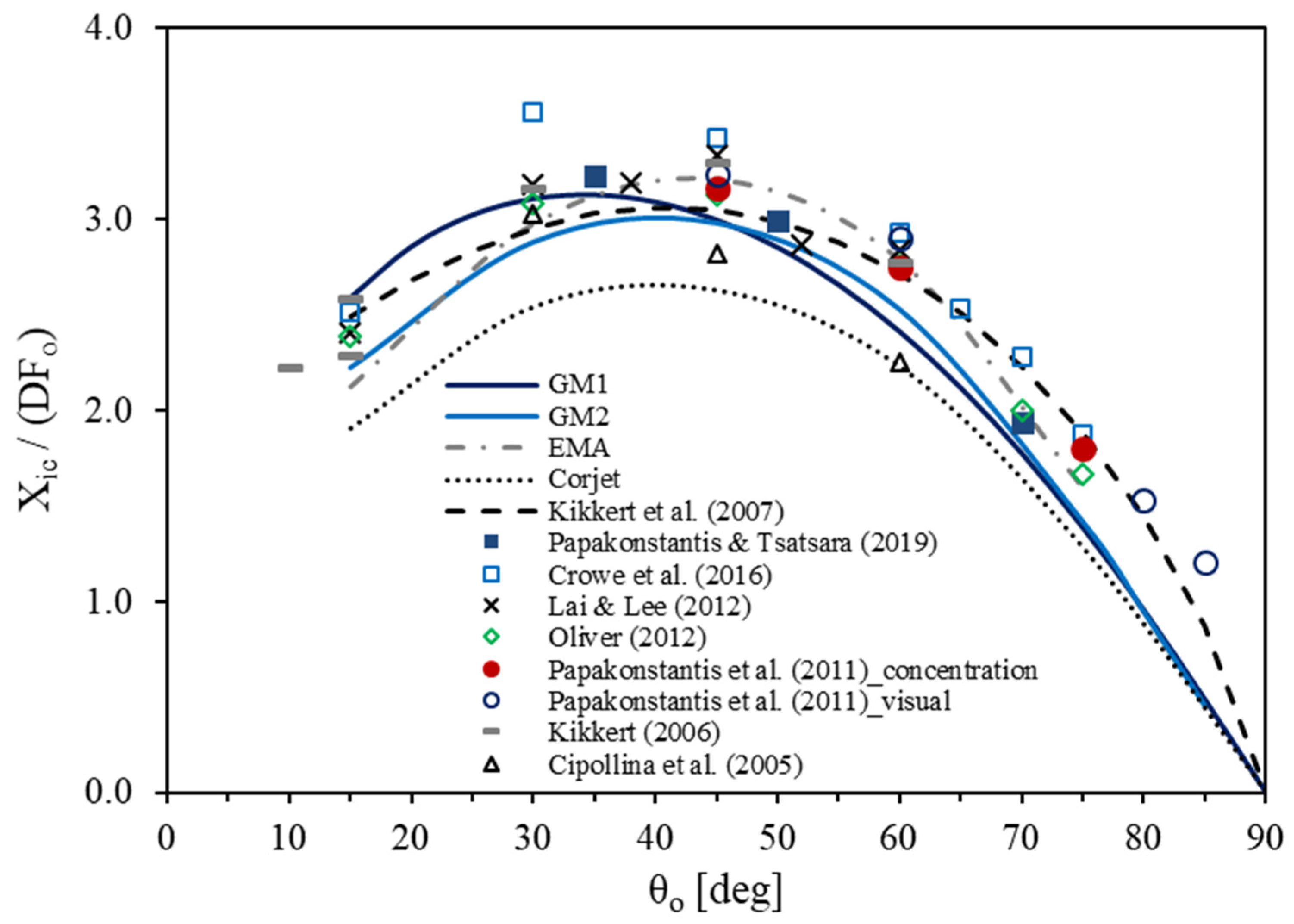
3.2. Horizontal Distances
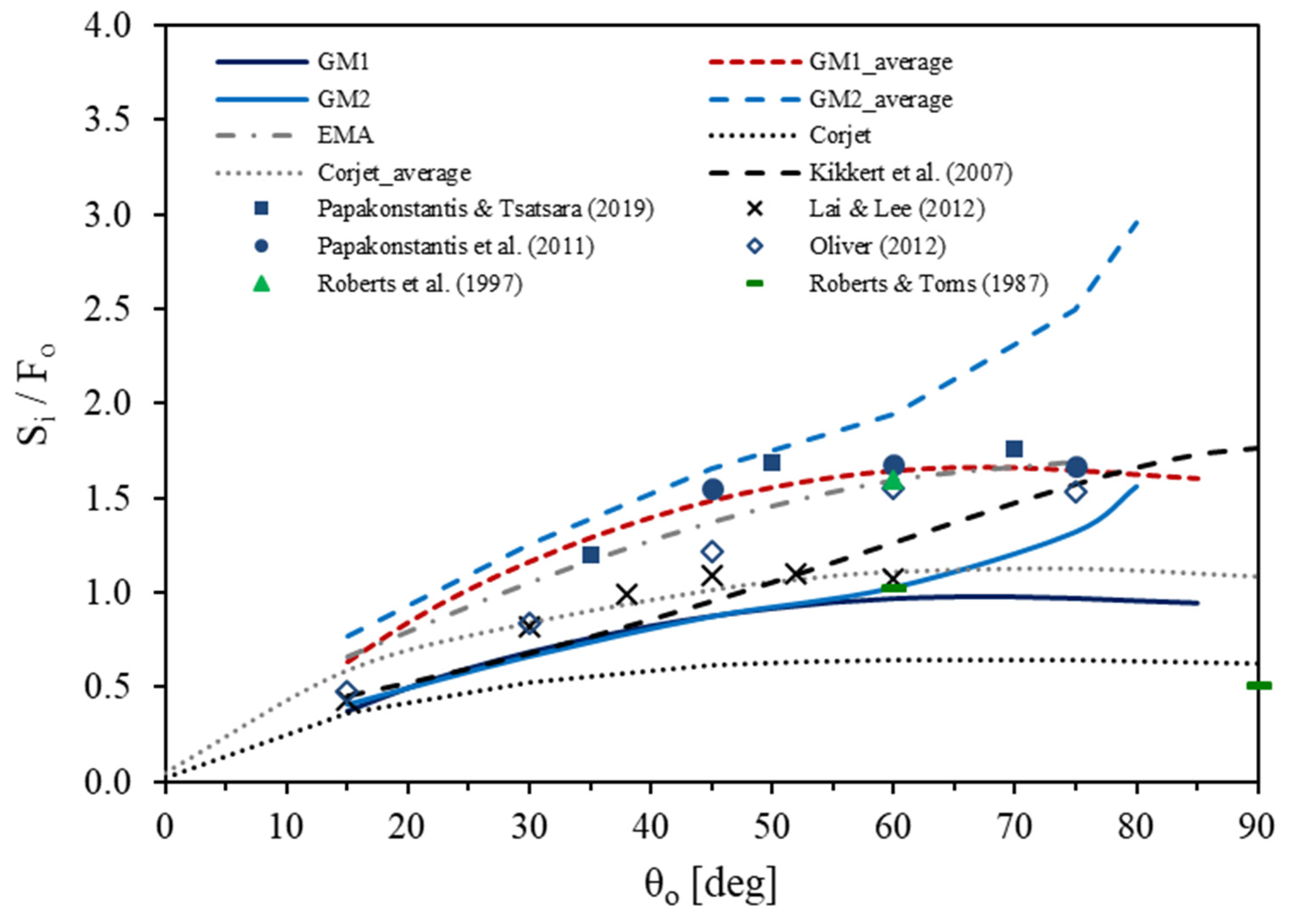
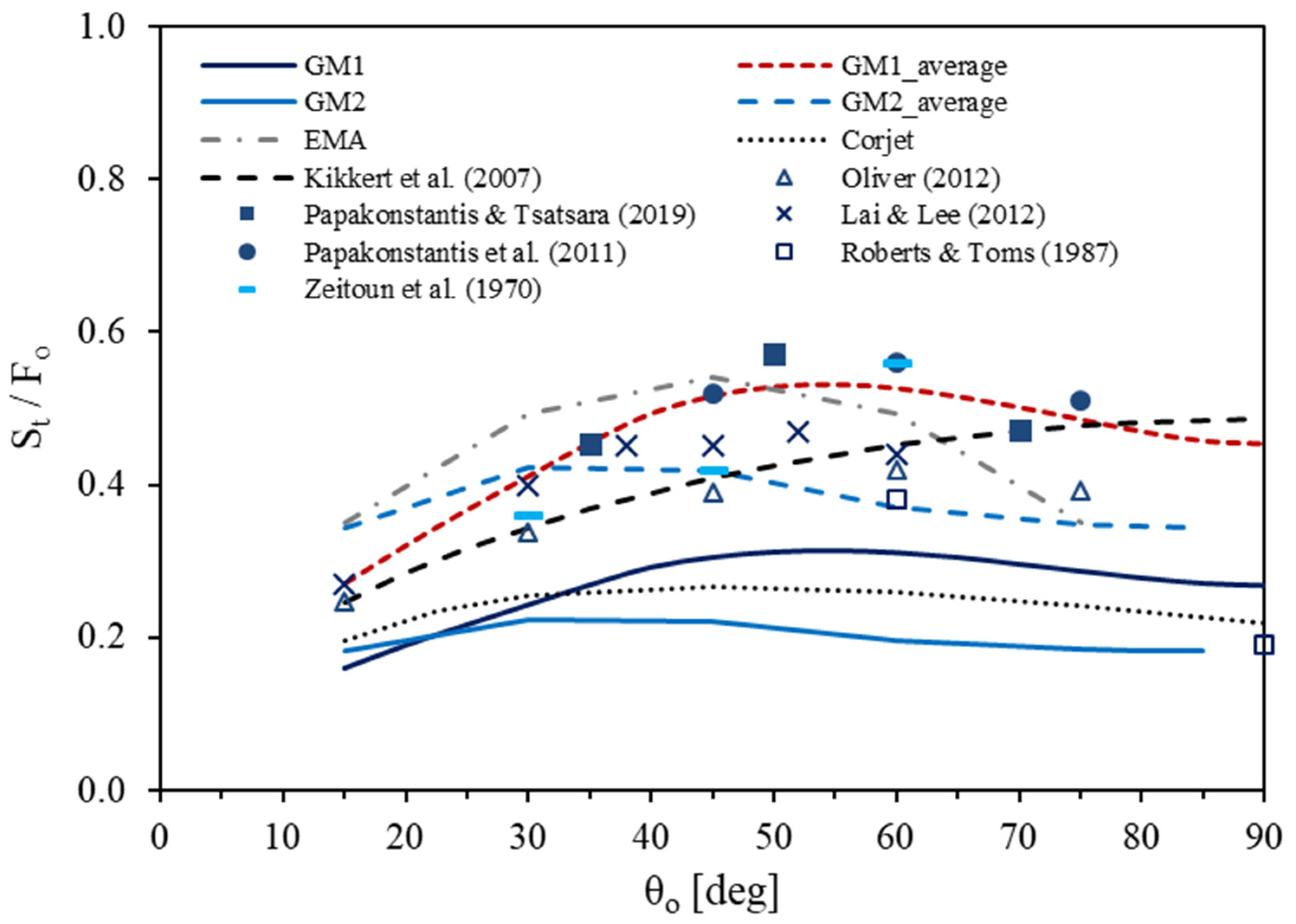
3.3. Minimum Dilution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Entrainment Coefficient Function in Round Buoyant Jets
References
- Lattemann, S.; Höpner, T. Environmental impact and impact assessment of seawater desalination. Desalination 2008, 220, 1–15. [Google Scholar] [CrossRef]
- Ahmad, N.; Baddour, R.E. A review of sources, effects, disposal methods, and regulations of brine into marine environments. Ocean. Coast. Manag. 2014, 87, 1–7. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C. Spreading of round dense jets impinging on a horizontal bottom. J. Hydro-Environ. Res. 2010, 4, 289–300. [Google Scholar] [CrossRef]
- Zeitoun, M.A.; McIlhenny, W.F.; Reid, R.O. Conceptual Designs of Outfall Systems for Desalting Plants; Res. and Devel. Progress Report No 550; Office of Saline Water, US Dept of Interior: Washington, DC, USA, 1970.
- Roberts, P.J.W.; Toms, G. Inclined dense jets in flowing current. J. Hydraul. Eng. 1987, 113, 323–341. [Google Scholar] [CrossRef]
- Roberts, P.J.W.; Ferrier, A.; Daviero, G. Mixing in inclined dense jets. J. Hydraul. Eng. 1997, 123, 693–699. [Google Scholar] [CrossRef]
- Cipollina, A.; Brucato, A.; Grisafi, F.; Nicosia, S. Bench-scale investigation of inclined dense jets. J. Hydraul. Eng. 2005, 131, 1017–1022. [Google Scholar] [CrossRef]
- Kikkert, G.A. Buoyant jets with two and three-dimensional trajectories. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2006. [Google Scholar]
- Kikkert, G.A.; Davidson, M.J.; Nokes, R.I. Inclined negatively buoyant discharges. J. Hydraul. Eng. 2007, 133, 545–554. [Google Scholar] [CrossRef]
- Shao, D.; Law, A.W.K. Mixing and boundary interactions of 30° and 45° inclined dense jets. Environ. Fluid Mech. 2010, 10, 521–553. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 1: Geometrical characteristics. J. Hydraul. Res. 2011, 49, 3–12. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 2: Concentration measurements. J. Hydraul. Res. 2011, 49, 13–22. [Google Scholar] [CrossRef]
- Lai, C.C.K.; Lee, J.H.W. Mixing of inclined dense jets in stationary ambient. J. Hydro-Environ. Res. 2012, 6, 9–28. [Google Scholar] [CrossRef]
- Oliver, C.J. Near field mixing of negatively buoyant jets. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2012. [Google Scholar]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. Removing the boundary influence on negatively buoyant jets. Environ. Fluid Mech. 2013, 13, 625–648. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.W. Effect of nozzle orientation on dense jets in stagnant environments. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Crowe, A.T.; Davidson, M.J.; Nokes, R.I. Velocity measurements in inclined negatively buoyant jets. Environ. Fluid Mech. 2016, 16, 503–520. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Tsatsara, E.I. Trajectory Characteristics of Inclined Turbulent Dense Jets. Environ. Process. 2018, 5, 539–554. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Tsatsara, E.I. Mixing Characteristics of Inclined Turbulent Dense Jets. Environ. Process. 2019, 6, 525–541. [Google Scholar] [CrossRef]
- Vafeiadou, P.; Papakonstantis, I.; Christodoulou, G. Numerical simulation of inclined negatively buoyant jets. In Proceedings of the 9th International Conference on Environmental Science and Technology, Rhodes, Greece, 1–3 September 2005; pp. A1537–A1542. [Google Scholar]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. k-ε Predictions of the initial mixing of desalination discharges. Environ. Fluid Mech. 2008, 8, 617–625. [Google Scholar] [CrossRef]
- Kheirkhah Gildeh, H.; Mohammadian, A.; Nistor, I.; Qiblawey, H. Numerical modeling of 30∘ and 45∘ inclined dense turbulent jets in stationary ambient. Environ. Fluid Mech. 2015, 15, 537–562. [Google Scholar] [CrossRef]
- Kheirkhah Gildeh, H.; Mohammadian, A.; Nistor, I.; Qiblawey, H.; Yan, X. CFD modeling and analysis of the behavior of 30° and 45° inclined dense jets-New numerical insights. J. Appl. Water Eng. Res. 2016, 4, 112–127. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, B.; Law, A.W.K.; Zhao, B. Large eddy simulations of 45° inclined dense jets. Environ. Fluid Mech. 2016, 16, 101–121. [Google Scholar] [CrossRef]
- Zhang, S.; Law, A.W.K.; Jiang, M. Large eddy simulations of 45° and 60° inclined dense jets with bottom impact. J. Hydro-Environ. Res. 2017, 15, 54–66. [Google Scholar] [CrossRef]
- Christodoulou, G.C.; Papakonstantis, I.G. Simplified estimates of trajectory of inclined negatively buoyant jets. In Proceedings of the Environmental Hydraulics-Proceedings of the 6th International Symposium on Environmental Hydraulics, Athens, Greece, 23–25 June 2010; Christodoulou, G.C., Stamou, A.I., Eds.; Taylor & Francis Group: London, UK; Volume 1, pp. 165–170. [Google Scholar]
- Papakonstantis, I.G.; Christodoulou, G.C. Simplified modelling of inclined turbulent dense jets. Fluids 2020, 5, 204. [Google Scholar] [CrossRef]
- Angelidis, P.B. A numerical model for the mixing of an inclined submerged heated plane water jet in calm fluid. Int. J. Heat Mass Transf. 2002, 45, 2567–2575. [Google Scholar] [CrossRef]
- Yannopoulos, P.C. An improved integral model for plane and round turbulent buoyant jets. J. Fluid Mech. 2006, 547, 267–296. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; Papakonstantis, I.G.; Christodoulou, G.C. On the entrainment coefficient in negatively buoyant jets. J. Fluid Mech. 2008, 614, 447–470. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Yannopoulos, P.C.; Bloutsos, A.A. Escaping mass approach for inclined plane and round buoyant jets. J. Fluid Mech. 2012, 695, 81–111. [Google Scholar] [CrossRef]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. Predicting the near-field mixing of desalination discharges in a stationary environment. Desalination 2013, 309, 148–155. [Google Scholar] [CrossRef]
- Christodoulou, G.C.; Yannopoulos, P.C.; Papakonstantis, I.G.; Bloutsos, A.A. A Comparison of Integral Models for Negatively Buoyant Jets. In Proceedings of the 7th International Symposium on Environmental Hydraulics, Singapore, 7–9 January 2014. [Google Scholar]
- Bloutsos, A.A.; Yannopoulos, P.C. Revisiting mean flow and mixing properties of negatively round buoyant jets using the escaping mass approach (EMA). Fluids 2020, 5, 131. [Google Scholar] [CrossRef]
- Palomar, P.; Lara, J.L.; Losada, I.J. Near field brine discharge modeling part 2: Validation of commercial tools. Desalination 2012, 290, 28–42. [Google Scholar] [CrossRef]
- Papakonstantis, I.G. Turbulent round negatively buoyant jets at an angle in a calm homogeneous ambient. Doctoral Thesis, School of Civil Engineering, National Technical University of Athens, Athens, Greece, 2009. (In Greek). [Google Scholar]
- Jirka, G.H. Integral Model for Turbulent Buoyant Jets in Unbounded Stratified Flows. Part I: Single Round Jet. Environ. Fluid Mech. 2004, 4, 1–56. [Google Scholar] [CrossRef]
- Jirka, G.H. Improved Discharge Configurations for Brine Effluents from Desalination Plants. J. Hydraul. Eng. 2008, 134, 116–120. [Google Scholar] [CrossRef] [Green Version]
- Papanicolaou, P.; List, E.J. Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 1988, 195, 341–391. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; Stamoulis, G.C. Vertical round buoyant jets and fountains in a linearly, density-stratified fluid. Fluids 2020, 5, 232. [Google Scholar] [CrossRef]
- List, E.J.; Imberger, J. Turbulent Entrainment in Buoyant Jets and Plumes. J. Hydraul. Div. 1973, 99, 1461–1474. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papakonstantis, I.G.; Papanicolaou, P.N. On the Computational Modeling of Inclined Brine Discharges. Fluids 2022, 7, 86. https://doi.org/10.3390/fluids7020086
Papakonstantis IG, Papanicolaou PN. On the Computational Modeling of Inclined Brine Discharges. Fluids. 2022; 7(2):86. https://doi.org/10.3390/fluids7020086
Chicago/Turabian StylePapakonstantis, Ilias G., and Panos N. Papanicolaou. 2022. "On the Computational Modeling of Inclined Brine Discharges" Fluids 7, no. 2: 86. https://doi.org/10.3390/fluids7020086
APA StylePapakonstantis, I. G., & Papanicolaou, P. N. (2022). On the Computational Modeling of Inclined Brine Discharges. Fluids, 7(2), 86. https://doi.org/10.3390/fluids7020086