Abstract
This paper reviews existing studies relating to the assessment of sediment concentration profiles within various flow conditions due to their importance in representing pollutant propagation. The effects of sediment particle size, flow depth, and velocity were considered, as well as the eddy viscosity and Rouse number influence on the drag of the particle. It is also widely considered that there is a minimum threshold velocity required to increase sediment concentration within a flow above the washload. The bursting effect has also been investigated within this review, in which it presents the mechanism for sediment to be entrained within the flow at low average velocities. A review of the existing state-of-the-art literature has shown there are many variables to consider, i.e., particle density, flow velocity, and turbulence, when assessing the suspended sediment characteristics within flow; this outcome further evidences the complexity of suspended sediment transport modelling.
1. Introduction
Sediment suspension describes the solid particles that have been lifted into the water column from the channel bed. It is beneficial to have a thorough understanding of sediment transport and thus two-phase flow to allow for its effective mathematical modelling, since it is a regular occurrence within large water bodies in the natural environment. This study looks to review a range of existing literature and compare proven evidence to provide a sound understanding of solid-fluid interactions within two-phase flow conditions.
When there is sufficient lift force for sediment particles to overcome the friction between them, the turbulent upward flux will generate sediment suspension. Generally, it is accepted that the mean concentration decreases with height above the bed, as shown in Figure 1 and described by [1].
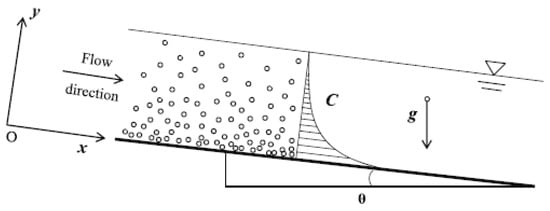
Figure 1.
Sediment Concentration Profile. Reprinted with permission from [1]. 2021 Hanmaiahgari, P.R.
Two-phase flow is the combination of two states of matter flowing together; in this case, solid and liquid. During two-phase sediment transport flow, there are complex interactions between the solid and fluid phases. This complexity has been presented in various studies, such as on natural channel flow [2,3], flow with natural bedform [4,5], and sediment transport modelling [6,7]. These interactions can be difficult to model mathematically due to the large number of variables present within open channel flow and the chaotic nature of fluid dynamics. Early methods of modelling sediment concentration [8,9,10,11,12] resolved some of these difficulties by ignoring forces acting on the sediment particle. However, applying these assumptions limits the model accuracy to certain sediment transport conditions, e.g., light particle transport. To create a more holistic formula, recent research has incorporated other forces acting on the particle phase [13,14,15]. This has resulted in some diverse formulations for predicting the sediment profile.
A popular consensus when assessing two-phase flow is to consider a two-dimensional (2D) observation, i.e., look at how concentration varies with depth and along the streamwise space. The considered parameters to assess such flow often include fluid velocity, particle diameter, Rouse number, and mean concentration [16,17,18,19]. Other research has incorporated the velocity fluctuations due to drift-flux and vortices considering eddy viscosity [19,20,21].
Most research into sedimentology has associated suspension with a time-averaged shear stress at the bed, whereas further studies have shown that sediment suspension can occur due to instantaneous velocity fluctuations in the vertical direction at the channel bed [22,23,24]. A concept to describe this is that the sediment near the bed experiences the highest concentration gradient and thus a high-pressure gradient, which forces the particle into suspension. This corresponds to the concentration profile shown in Figure 1. However, recent observations have also further revealed alternative sediment concentration profiles where concentration peaks at a height above the channel bed region. This has been shown to be largely dependent on the various concentration of sediment entrained within a flow from dilute to dense conditions [18].
2. Literature Review
Several methods can be used to model sediment concentration, which the diffusion and kinetic theories are among the most common. Diffusion theory, which is recognized as one of the simplest methods for modelling sediment concentration, has been used by many scientists to describe the solid phase with reasonable accuracy [11,21]. On the other hand, the kinetic theory is widely regarded as the best approach for concentration distribution modelling as it includes the response of both the solid and liquid phases as well as the two-phase interactions [13]. Extensive research has been undertaken to understand and model these two-phase interactions and their effects on the sediment profile [9,15,19,25,26], where they will be explored in the coming sub-sections.
2.1. Reynolds Number Approach
Drag is a mechanical force that arises due to the interaction between a body moving. through a fluid and the induced resultant opposing frictional forces, where it can be represented by the following equation:
where denotes drag force, is the drag coefficient, is the density of fluid, and is the relative velocity of the particle. Of the parameters contained within Equation (1), is the most ambiguous and requires careful consideration. can be defined as a constant [27]:
In multiple studies, constant is shown to be inconsistent with reality. Therefore, a more robust approach was developed. Following further research [28,29,30], it is generally considered that is proportional to Reynolds number (), and extensive studies have been performed to confirm this relationship.
It has been stated that for a perfectly smooth spherical particle, the drag coefficient shares an asymptotic relationship with Reynolds number for both laminar and turbulent flows [28]. Further study concluded that for rough particles, the relationship varies and is dependent on the flow regime. This is due to stresses and frictional forces arising from the boundary conditions. For example, Cheng [30] studied the settling velocity and effects of drag on experimental spherical particles. Within that study, a new equation for was formed and compared with laboratory data. Figure 2 shows Equations (3)–(6) fitted against experimental data. The curve plotted in Figure 2 is subdivided into three sections. For laminar flow (), can be defined as:
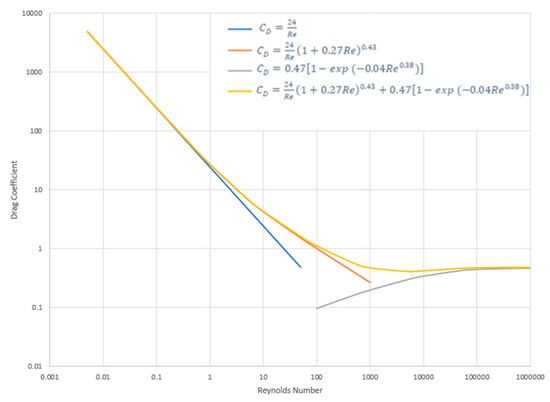
Figure 2.
Coefficient of Drag and Reynolds Number Correlation (Adapted from Cheng [30]).
The flow becomes transitional at , where is defined as:
Finally, when the flow becomes turbulent (), can be represented by:
Equations (3)–(5) can then be combined to produce one explicit function for , defined as [30]:
Alternatively, Equation (6) can be rewritten as:
where is a function of , in which is the particulate Reynolds number. The first term on the right-hand side of Equation (7) relates to laminar flow. The second term represents the drag force due to turbulence [13].
2.2. Velocity Lag Approach
The effects of drag force can also be assessed in terms of the velocity lag, which is the time differential for the momentum to transfer from the fluid phase to the solid phase [13,20,26]. Utilizing the fluid viscosity, Stokes’ law studies the resistance to motion when an object is dropped in a fluid. When falling due to gravity, the object is acted upon by an equal and opposite reaction, as stated by Newton’s third law. Therefore, when a particle is falling in laminar flow with no turbulent flux, the exerting forces are only those which arise due to fluid inertia from the falling velocity and its associated acceleration. Due to that, the drag force must be equal to the submerged weight of the particle, and any lift forces are caused by turbulence.
When assessing a two-phase flow, it is necessary to assess separate timeframes, i.e., the particle and integral turbulence timeframes . As shown by Equation (8), can be separated into two factors for laminar and turbulent flows [20]:
where is the mean concentration, is the fall velocity of sediment, and is the velocity flux difference between the two phases and is considered proportional to . Particle crowding can have a significant impact on the particle timeframe. Research has shown that particle flocculation is a function of Reynolds number; however, it has also been defined as a constant in some studies [14]. Nonetheless, for dilute flows, the gravitational particle timeframe can be defined as [20]:
where and are the sediment and fluid densities, respectively. is often associated with Stokes’ drag. Stokes’ number, , describes the relationship between the relative particle velocity and the particulate timeframe. When a particle moves within turbulent flow, the fluid velocity fluctuation and formation of vortices exert a force on the particle and causes longer , where this timeframe can be determined by [13,14,20,31]:
For light sediment, i.e., sediment moves in equilibrium with the fluid, the flow can effectively be treated as a uniform medium. In this case, Stokes’ number will be very small. When a particle experiences considerable inertial forces, will be close to one. Therefore, substituting Equations (9) and (10) into Equation (8) yields:
The first term on the right-hand side of Equation (11) refers to the laminar drag force, and the second term refers to the turbulent drag force.
2.3. Lift Force
Conventionally lift is considered to act upwards from the horizontal plane opposing gravity. However, it is practical to consider lift acting perpendicular to the streamwise direction [32,33]. Besides lift, the cohesive force between particles can also cause the drag between them to create a change in suspended sediment transport. However, the cohesive force is more effective within bedload and not suspended load. This is due to the fact that the distance between particles in bedload is much shorter than that in suspended load, which is usually very scattered. Due to this, the cohesive force between suspended particles is not a determinant factor of its behavior as compared to bedload [34].
Commonly, lift force is considered to be composed of two parts: hydrodynamic lift and turbulent diffusion. One of the limits of original Rouse suspended sediment model is that it suggests an infinite concentration at the bed and zero concentration at the surface. It has been shown that a lower concentration corresponds to a higher horizontal velocity, where this is represented in Figure 3. The importance of this factor is not fully understood; however, it is known that hydrodynamic lift is the result of the concentration variation and thus velocity differential across the sediment particle from the lower to upper suspension region (Figure 3 presents the pattern of velocity differential across a particle in non-laminar flow). Additionally, the displacement of fluid around the body causes a pressure distribution across the particle, which consequently causes a velocity gradient. Therefore, a lift force is acted on the particle to equalize the pressure gradient [35].

Figure 3.
Uplift due to shear stresses on a particles surface. Reprinted with permission from [36]. 2021 Hanmaiahgari, P.R.
Turbulence diffusion is the mixing due to the turbulent velocity fluctuation and vortices. Many studies have been conducted to understand the causes and effects of turbulence. It has been assessed statistically as an overlaying function of the time-averaged velocity [20,21,22]. The wake of a sediment particle (shown in Figure 3) is often considered to cause turbulent mixing due to the velocity fluctuations. Generally, this turbulent mixing is associated with large vortices as small eddies relative to the sediment size do not contain sufficient energy to lift the sediment particle. By this consideration, turbulence can be correlated with shear velocity [23]. Additionally, turbulent diffusion primarily occurs away from near-bed flow region. This is due to the lower horizontal velocities apparent at the region, as sediment concentration is generally higher.
Within the research of sediment-laden flow, Zhong et al. [37] concluded that near the bed, there is no sufficient space for vortices to form within the fluid. Additionally, it is also found that a lower eddy viscosity is correlated with a lower bed slope, and thus, density stratification is more prevalent [21,33,38]. This supports the notion that higher velocities produce more turbulence. Furthermore, Figure 4 shows that the strongest eddy viscosity occur within the center of the flow column whereas the highest velocity occurs at the surface of the flow [39].
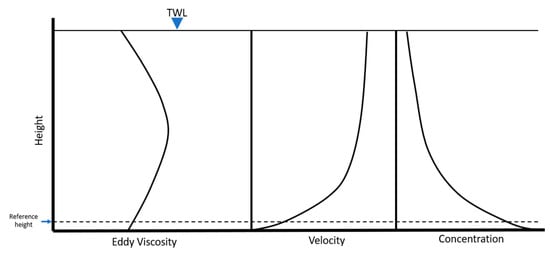
Figure 4.
Eddy viscosity, velocity, and concentration distribution profile (Adapted from Liu and Nayamatullah [39]).
Upward turbulent velocities are countered by gravity and downward turbulent bursting mechanism, i.e., sweep. Huang et al. [9] suggest that settling velocity is composed of these two components in the form of
where is the sediment fluctuation, is the settling flux due to gravity, and is the turbulent diffusive flux. The settling flux due to gravity is well understood, where it is influenced by the downward gravitional acceleration. However, as stated previously, the diffusive flux is more chaotic and random in nature and is thus more difficult to model. Previous studies have described this by analyzing a vertical unit sectional area and describing the turbulent velocity dependent on the concentration differential at the top and bottom of the sectional area of flow channel [9,24]. In an alternative and simpler way of interpreting this, the relative velocity of a particle is described by the difference between the fluid and particle velocity take in account any drift velocity [13,14,25]:
where is the relative velocity, is the fluid velocity, is the solid velocity, and is the drift velocity. The difficulty then lies in determining . As stated previously, it is known that drift velocity is a result of vortices and fluid turbulence. The drift velocity can be further defined as [14]:
where is the diffusion tensor and is considered to be dependent on the Reynolds stress, which, in turn, is related to the vortex viscosity [25]:
where is the Reynolds stress and it can be calculated by:
where is the eddy viscosity, is the kinetic energy, and is the Kronecker delta.
Furthermore, research inspecting the velocity lag of a particle within flow arising from the drag force shows that the relationship for the lag velocity in dilute flow is defined as [40]:
where is the shear velocity, and is the kinematic viscosity. It is worth noting that Equation (17) is only valid when assessing dilute flow. For alternative cases, i.e., concentrated flow, the constants and exponents will be varying [18]. As is considered the difference between and , it can be assumed that:
Therefore, inputting Equations (10), (14), (15) and (17) into Equation (18) gives a conclusive definition of the dimensionless relative velocity:
For a single particle, its effective lift force can be defined as [37,41]:
Alternatively, the lift force per unit of mass is described by [8]:
Thus, the total lift force exerted on the solid phase can be calculated by:
Inputting Equation (19) into Equation (20) determines the lift force acting upon a single particle due to the turbulent diffusion as:
Theodore von Karman determined that hydraulic flow within close proximity to the wall follow a velocity distribution proportional to the logarithm of the distance from the wall [42]:
where is the von Karman constant, and is the log-law constant. However, this is generally only for boundaries close to the bed, and it loses its accuracy within the upper flow region, especially when suspended sediment is detected. The effect of a boundary causes shear on the particles, which results in secondary currents within the flow. Considerable research has been undertaken to study the effect of secondary vortices and wake within the near bed region [16,21]. In Equation (24), when the law of wake has been considered, the constant can be defined as [16]:
where is Cole’s wake parameter. Therefore, inputting Equation (23) into Equation (22) produces:
Substituting Equation (23) into Equation (21) and then inserting into Equation (22) with the inclusion of Equation (26) defines the total lift force, which occurs on the sediment phase from the turbulent velocity and secondary currents:
where and are constants defined as
and
2.4. Turbulent Bursting
When mathematically modelled, a time-averaged mean velocity is often employed to represent the suspended solid phase. However, more recently, studies have shown that instantaneous turbulent velocities at the near bed region can have significant impact on the overall sediment concentration distribution in flow [22,43]. These instantaneous flow properties are also responsible for solid particles to be entrained into the suspended region from the bed-load, which can be analyzed as turbulent bursting. Additionally, the sediment particles at the bed experience higher velocity gradients, thus generating larger lift acts on the particle. In some instances, this can cause scouring of the sea-bed, as well as unexpected deposition, resulting in risk to marine infrastructure as well as aquatic life [44,45,46].
Turbulence is hard to consider in modelling terms. Due to the nature of fluid, a vortex will impose a force on the surrounding fluid producing smaller vortices until the vortex’s kinetic energy is insufficient to overcome the viscosity of the fluid. Turbulence can be broken down in to three main stages: production, transfer, and dissipation, otherwise known as integral scale, inertial scale, and Kolmogorov scale, respectively, as shown in Figure 5.
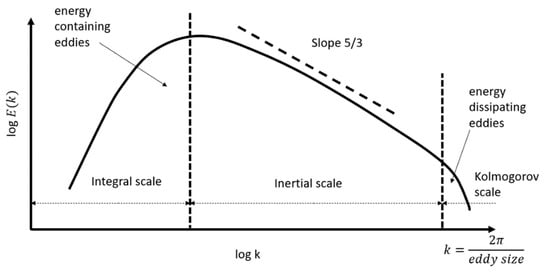
Figure 5.
Turbulence eddy scaling. Reprinted with permission from [41]. 2021 Hanmaiahgari, P.R.
A vortex can be defined by its diameter, velocity, and timeframe. Andrey Kolmogorov discovered that within the transfer region (i.e., the inertial scale), the kinetic energy is proportional to the diameter of the eddy, where it can be described as [47]
where is the Kolmogorov constant, is the dissipation rate, and is the wave number in a function of the eddy size. The eddy scale is defined by varying characteristics dependent upon the stage of turbulence, i.e., the integral scale is a function of kinetic energy and dissipation, the inertial scale is a function of dissipation and length, and the Kolmogorov scale is a function of dissipation and viscosity.
It is understood that a critical velocity value criterion is required to meet for sediment suspension to occur, and sediment entrained within the fluid phase below the critical velocity is considered as wash-load [24,48,49]. Salim et al. [22] studied the sediment suspension at the near-bed level in the Australian ocean for locations with current and wave velocities lower than the critical value. They found that despite the relatively low recorded flow velocity, sediment suspension still took place due to turbulent bursting. Similarly, Tsai and Huang [43] investigated the advection-diffusion method of modelling sediment concentration and concluded the instantaneous velocity fluctuations are mainly due to turbulent ejection.
Figure 6 shows a comparison of field data at the seabed for study by Salim et al. [22]. From Figure 6, it is possible to see that a higher mean velocity value commonly corresponds to higher backscatter and TKE shear stress. Timeframes (i), (ii), and (iii) in the figure all represent sediment suspension occurrences. This was considered sensible, as the velocity was at or above the critical value for their study where sediment suspension occurred. However, conversely at timeframes TS-1 and TS-2, it was observed that there was a high value for the TKE shear stress and backscatter, whereas there was a low value for the streamwise velocity, i.e., below the critical velocity value. This increase in the TKE shear stress suggests the formation of vortices, which could lift the sediment into the suspension zone, and it is supported by the high backscatter reading, proving sediment suspension due to bursting’s sweep events.
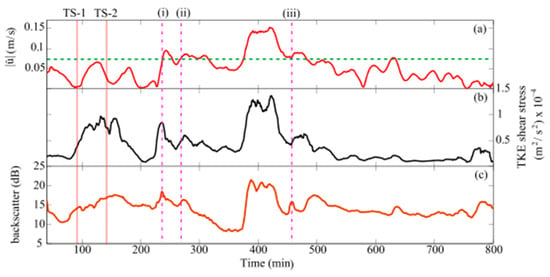
Figure 6.
Time series showing: (a) 1 min averaged velocity streamwise velocity, (b) turbulent kinetic energy (TKE) shear stress, and (c) backscatter. The horizontal line shown in (a) represents the critical velocity value for suspension. Reprinted with permission from [22]. 2021 Hanmaiahgari, P.R.
In recent experimental advances, particle-imaging velocimetry (PIV) has been used for suspended particle investigation in various wave-induced and turbulent flow conditions [50,51]. It has been evidenced that PIV is a good method to capture the suspended sediment dynamics as long as relatively good resolution of camera has been deployed. By this finding, one can project that the suspended sediment transport behavior can be accurately captured in real-world events in the future.
2.5. Continuity Equations and Modelling Studies
Within common solid-liquid flow modelling, the mass conservation system is usually assumed, while its acceleration can be variable. The coordinate system of a single particle is represented in Figure 7.
Figure 7.
Polar coordinate system.
Within a fluid flow convection, acceleration can be considered by continuity rule over time, as defined by [52]:
Equation (31) can be decomposed into constituent directions, which include each spatial plane. Thus, the vertical flow acceleration can be expressed by expanding Equation (31) to give:
However, within a two-phase turbulent flow, there are other resulting forces acting on the particle, which cause velocity fluctuations. Stokes and Navier individually derived the Navier-Stokes equations stemming from Equation (17) to incorporate the additional flow effects within viscous flow regimes.
In general, suspended load transport is derived from the continuity equations and a balancing of forces acting on the solid phase [8,15,20,53,54,55]. A closed channel model assumes no particle enters or exits the flow. In a mathematical model, the respective interactions and boundaries are then considered to give an overall expression for the sediment profile.
The mass conservation equation is derived from the Navier-Stokes equations in accordance with the closed system assumption and can be expressed as:
where is the mean concentration of the solid phase. Similarly, the conservation of momentum equation is given as:
where is the fluid flow pressure, is the tensor stress arising from particle interactions, and is the vertical forces arising due to phase interactions. Considering a 2D flow, where the flow across channel width is considered having ignorable change, the term can be removed from Equation (34). Furthermore, within steady-uniform flow assumption, one can obtain:
Therefore, the only varying values are given in the streamwise-vertical plane. Additionally, for dilute flow conditions, the particle-particle interactions are negligible:
Thus, if Equations (35)–(37) are inserted into Equation (34), the vertical momentum for the solid phase can be defined as:
Within turbulent flow, Reynolds decomposition is a mathematical method used to isolate the velocity fluctuation values from the averaged value (as presented by Figure 8), given by [56]:
where is the time-averaged velocity, and is the velocity flux.
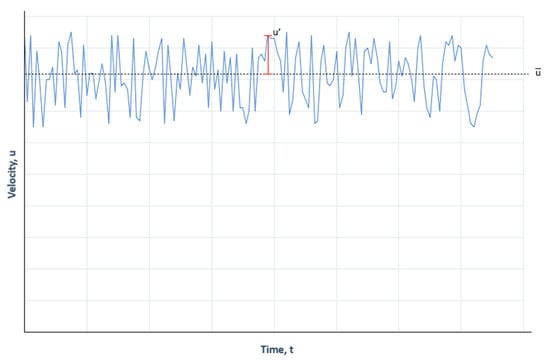
Figure 8.
Depiction of turbulent velocity fluctuation.
Applying Reynolds decomposition to the solid phase by inputting Equation (39) into Equation (38) yields:
Expanding and simplifying Equation (40) gives:
Additionally, applying the assumptions of Equations (35) and (40) to Equation (33) gives:
Equation (42) can be solved through integration to obtain:
The first term on the left-hand side of Equation (40) is usually considered negligible, and thus, rewriting and multiplying by , Equation (40) becomes:
The first term accounts for the pressure variation due to increasing depth.
The hydrostatic pressure is a result of the weight of the fluid and can be defined as:
Two main interactions that have been discussed within this report are drag and lift. These forces can be combined by adding Equations (11) and (29) together to produce:
Therefore, inputting Equations (43) and (44) into Equation (42) produces:
Rearranging for sediment concentration finally gives:
Equation (48) is a comprehensive and inclusive approach to mathematically represent the sediment concentration distribution profile. It accounts for the velocity lag due to particle inertia associated with the drag force as well as the velocity fluctuations arising due to the turbulent flow and formation of vortices. Recently, the non-local theory through the fractional advection–diffusion equation (fADE) has also been proven to represent suspension sediment concentration well [57]. In terms of numerical modelling, various lattice Boltzmann (LB) [58,59] and smoothed particle hydrodynamics (SPH) models [60,61] have also been investigated for their representation toward flow with suspended and bed loads, and great success has been achieved in terms of accuracy in reproducing the experimental and field data.
The above-mentioned final equation (Equation (48)) can also be simplified. If small particles are measured, then it is justifiable to assume that the solid phase moves in equilibrium with main flow, and there is no velocity lag. Therefore, can be taken as zero. Additionally, for fine smooth particles, there would be very little shear stress on the surface of the particle to give rise to lift forces. Finally, if the formation of eddies due to turbulence is ignored, these assumptions in Equation (48) can give rise to the following:
Inputting Equation (9) into Equation (49) gives:
This equates to Fick’s Law, which defines diffusion theory and states that diffusion from an area of high concentration to an area of low concentration should be balanced by settling velocity term.
3. Conclusions
A wide range of research has been reviewed to provide a holistic understanding of sediment concentration profiles, suspension, and transport for practical use when modelling hydrodynamic flows. Drag on the sediment particle has been assessed using the Reynolds number approach. It has been highlighted that the turbulent flow condition plays a significant role on the drag force experienced by the particle. This is dependent upon the shear forces between the solid and fluid phase. A study of velocity lag has also been considered by utilizing the Stokes number, which is a relationship between the particle velocity and particle transport timeframe. Research has supported the notion that drag force is significantly affected by the turbulent flow condition.
The idea of velocity fluctuations and vortex mixing has been studied. Velocity fluctuations in the upward direction give lift to the sediment particle. A general approach of the time-averaged velocity fluctuations has been considered. The effects of turbulent bursting in the upward motion close to the bed has also been reviewed. Within low flow conditions, where there are no sufficient velocities for suspension action, a time-averaged velocity method is not sufficient to describe particle suspension. In this case, research has found that upward eddies can alternatively lift particles into the flow column. The continuity equations have been investigated to assess the variance of acceleration with positional displacement over time. This has been expanded by researchers to incorporate other forces that act upon the sediment particle such as the fluid-induced lift and drag forces, forces arising from turbulence, particle inertia, and pressure gradient.
Conclusively, as found from this review study, there are a wide range of flow parameters that affect the suspended sediment transport. Due to this, reasonable assumptions and simplifications have been proposed to ease the mathematical modelling burden. In-depth suspended sediment transport study can benefit flow modelling under marine and water infrastructure influences. For bridge-pier or abutment-induced flow, the flow turbulence will be significant. This will impact the characteristic of scour and suspended sediment transport. Thus, in future studies, a more inclusive research strategy will be needed to accurately model the suspended solid behavior within flow to foresee any environmental problem that could be caused in man-made or natural channels.
Author Contributions
J.T.W.: writing—original draft preparation, review and editing, funding; J.H.P.: writing—original draft preparation, review and editing; S.K.: writing—review and editing; P.R.H.: writing—review and editing; M.P.: writing—review and editing; A.S.: writing—review and editing; M.A.K.: writing—review and editing; and A.W.: writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The author, Jaan H. Pu, acknowledges a travel grant from the Faculty of Engineering and Informatics, University of Bradford, to explore potential research collaboration opportunity.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kundu, S.; Ghoshal, K. Effects of Secondary Current and Stratification on Suspension Concentration in an Open Channel Flow. Environ. Fluid Mech. 2014, 14, 1357–1380. [Google Scholar] [CrossRef]
- Pu, J.H. Turbulent rectangular compound open channel flow study using multi-zonal approach. Environ. Fluid Mech. 2018, 19, 785–800. [Google Scholar] [CrossRef] [Green Version]
- Pu, J.H.; Pandey, M.; Hanmaiahgari, P.R. Analytical modelling of sidewall turbulence effect on streamwise velocity profile using 2D approach: A comparison of rectangular and trapezoidal open channel flows. J. Hydro-Environ. Res. 2020, 32, 17–25. [Google Scholar] [CrossRef]
- Pu, J.H. Velocity profile and turbulence structure measurement corrections for sediment transport-induced water-worked bed. Fluids 2021, 6, 86. [Google Scholar] [CrossRef]
- Pu, J.H.; Wei, J.; Huang, Y. Velocity distribution and 3D turbulence characteristic analysis for flow over water-worked rough bed. Water 2017, 9, 668. [Google Scholar] [CrossRef] [Green Version]
- Hanmaiahgari, P.R.; Gompa, N.R.; Pal, D.; Pu, J.H. Numerical modeling of the sakuma dam reservoir sedimentation. Nat. Hazards 2018, 91, 1075–1096. [Google Scholar] [CrossRef] [Green Version]
- Pu, J.H.; Huang, Y.; Shao, S.; Hussain, K. Three-gorges dam fine sediment pollutant transport: Turbulence SPH model simulation of multi-fluid flows. J. Appl. Fluid Mech. 2016, 9, 1–10. [Google Scholar] [CrossRef]
- Zhong, D.; Wang, G.; Sun, Q. Transport Equation for Suspended Sediment Based on Two Fluid Model of Solid/Liquid Two-Phase Flows. J. Hydraul. Eng. 2011, 137, 530–542. [Google Scholar] [CrossRef]
- Huang, S.H.; Sun, Z.L.; Xu, D.; Xia, S.S. Vertical Distribution of Sediment Concentration. J. Zhejiang Univ. Sci. 2003, 9, 1560–1566. [Google Scholar] [CrossRef]
- Hsu, T.J.; Jenkins, J.T.; Liu, P.L.F. On Two-Phase Sediment Transport: Dilute Flow. J. Geophys. Res. 2003, 108, 2–14. [Google Scholar] [CrossRef]
- Rouse, H. Modern Conceptions of the Mechanics of Fluid Turbulence; American Society of Civil Engineers: Reston, VI, USA, 1936; Volume 62, pp. 21–64. [Google Scholar]
- Fick, A. On Liquid Diffusion. J. Membr. Sci. 1995, 100, 33–38. [Google Scholar] [CrossRef]
- Kundu, S.; Ghoshal, K. A mathematical model for type II profile of concentration distribution in turbulent flows. Environ. Fluid Mech. 2017, 17, 449–472. [Google Scholar] [CrossRef]
- Greimann, B.P.; Holly, F.M., Jr. Two-phase flow analysis of concentration profiles. Hydraul. Eng. 2001, 127, 753–762. [Google Scholar] [CrossRef]
- Jha, S.K.; Bombardelli, F.A. Two-Phase Modelling of Turbulence in Dilute Sediment Laden Open-Channel Flow. Environ. Fluid Mech. 2009, 9, 237. [Google Scholar] [CrossRef] [Green Version]
- Kundu, S.; Ghoshal, K. Explicit formulation for suspended concentration distribution with near-bed particle deficiency. Powder Technol. 2013, 253, 429–437. [Google Scholar] [CrossRef]
- Jha, S.K.; Bombardelli, F.A. Toward two-phase flow modelling of nondilute sediment transport in open channels. J. Geophys. Res. 2010, 115, F3. [Google Scholar]
- Pu, J.H.; Wallwork, J.T.; Khan, M.A.; Pandey, M.; Pourhahbaz, H.; Satyanaga, A.; Hanmaiahgari, P.R.; Gough, T. Flood suspended sediment transport: Combined modelling from dilute to hyper-concentrated flow. Water 2021, 13, 379. [Google Scholar]
- Goree, J.C.; Keetels, G.H.; Munts, E.A.; Bugdayci, H.H.; Rhee, C.V. Concentration and velocit profiles of sediment-water mixtures using the drift flux model. Can. J. Chem. Eng. 2016, 94, 1048–1058. [Google Scholar]
- Toorman, E.A. Vertical Mixing in the Fully Developed Layer of Sediment-Laden Open-Channel Flow. J. Hydraul. Eng. 2008, 134, 1225–1235. [Google Scholar] [CrossRef]
- Moodie, A.J.; Nittrouer, J.A.; Ma, H.; Carlson, B.N.; Wang, Y.; Lamb, M.P.; Parker, G. Suspended-sediment induced stratification inferred from concentration and velocity profile measurements in the Yellow River, China. Water Resour. Res. 2019, e2020WR027192. [Google Scholar] [CrossRef]
- Salim, S.; Pattiaratchi, C.; Tinoco, R.O.; Jayaratne, R. Sediment resuspension due to near-bed turbulent effects: A deep sea case study on the northwest continental slope of Western Australia. J. Geophys. Res. Ocean. 2018, 123, 7102–7119. [Google Scholar] [CrossRef]
- Einstein, H.A. The Bed-Load Function for Sediment Transport in Open Channel Flows; Departmetn of Agriculture: Washington, DC, USA, 1950. [Google Scholar]
- Drew, D.A. Mathematical modelling of two-phase flow. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Ni, J.R.; Wang, G.Q.; Borthwick, A.G.L. Kinetic Theory for Particles in Dilute and Dense Solid-Liquid Flows. J. Hydraul. Eng. 2000, 126, 893–903. [Google Scholar] [CrossRef]
- Sun, Z.; Zheng, H.; Xu, D.; Hu, C.; Zhang, C. Verticle Concentration Profile of Nonuniform Sediment. Int. J. Sediment Res. 2021, 36, 120–126. [Google Scholar] [CrossRef]
- Soo, S.L. Fluid Dynamics of Multiphase Systems; Blaisdell Publishing Company: Waltham, MA, USA, 1967. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles Drops and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Van Nierop, E.A.; Luther, S.; Bluemink, J.J.; Magnaudet, J.; Prosperetti, A.; Lohse, D. Drag and Lift Force on Bubbles in a Rotating Flow. J. Fluid Mech. 2007, 571, 439–454. [Google Scholar] [CrossRef]
- Cheng, N.S. Comparison of formulas for drag coefficient and settling velocity of spherical particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Pal, D.; Ghoshal, K. Hydrodynamic Interaction in Suspended Sediment Distribution of Open Chanel Turbulent Flow. Appl. Math. Model. 2017, 49, 630–646. [Google Scholar] [CrossRef]
- Liu, D.Y. Fluid Dynamics of Two-Phase Systems; Chinese Higher Education Press: Beijing, China, 1993. [Google Scholar]
- Hamil, L. Understanding Hydraulics; Palgrave MacMillan: London, UK, 2001. [Google Scholar]
- Jain, R.K.; Kothyari, U.C. Cohesion influences on erosion and bed load transport. Water Resour. Res. 2009, 45, 6. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Open Channel Flow; Hodder Headline Group: London, UK, 1999. [Google Scholar]
- Kurose, R.; Komori, S. Drag and Lift Force on a Rotating Sphere in Linear Shear Flow. J. Fluid Mech. 1999, 384, 183–206. [Google Scholar] [CrossRef]
- Zhong, D.; Zhang, L.; Wu, B.; Wang, Y. Velocity Profile of Turbulent Sediment-Laden Flows in Open-Channels. Int. J. Sediment Res. 2015, 30, 285–296. [Google Scholar] [CrossRef]
- Wright, S.; Parker, G. Density Stratification Effects in Sand-Bed Rivers. J. Hydraul. Eng. 2004, 130, 783–795. [Google Scholar] [CrossRef]
- Liu, X.; Nayamatullah, M. Semianalytical solutions for one-dimensional unsteady nonequilibrium suspended transport in channels with arbitrary eddy viscosity distribution and realistic boundary conditions. J. Hydraul. Enigneering 2014, 5, 1–10. [Google Scholar] [CrossRef]
- Cheng, N.S. Analysis of velocity lag in sediment-laden open channel flows. J. Hydraul. Eng. 2004, 130, 657–666. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Niu, X.; Li, M.; Chen, D.; Yu, X. A general two-phase turbulent flow model applied to the study of sediment transport in open channels. Int. J. Multiph. Flow 2011, 37, 1099–1108. [Google Scholar] [CrossRef] [Green Version]
- Bradshaw, P.; Huang, G.P. The law of the wall in turbulent flow. Math. Phys. Sci. 1995, 451, 165–188. [Google Scholar]
- Tsai, C.W.; Huang, S.H. Modeling suspended sediment transport under influence of turbulence ejection and sweep events. Water Resour. Res. 2019, 55, 5379–5393. [Google Scholar] [CrossRef]
- Leckie, S.H.F.; Mohr, H.; Draper, S.; McLean, D.L.; White, D.J.; Cheng, L. Sedimentation-induced Burial os Subsea Pipelines: Observation from Field Data and Laboratory Experiments. Coast. Eng. 2016, 114, 137–158. [Google Scholar] [CrossRef]
- Isadinia, E.; Heidarpour, M.; Schleiss, A.J. Investigation of turbulence flow and sediment entrainment around bridge peir. Stoch. Environ. Res. Risk Assess. 2013, 27, 1303–1314. [Google Scholar] [CrossRef] [Green Version]
- Sinha, N. Towards RANS Parameterized of Vertical Mixing by Langmuir Turbulence in Shallow Coastal Shelves; University of South Florida Scholar Commons: Sarasota, FL, USA, 2013. [Google Scholar]
- Kolmogorov, A.N. The Local Structure of Turbulence in Incomressible Viscious Fluids at Very Large Reynolds Numbers. Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar]
- Baumert, H.Z.; Simpson, J.; Sundermann, J. Marine Turbulence: Theories, Observations and Models; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Wang, Y.Y.; He, Q.; Liu, H. Variations of Near-Bed Suspended Sediment Concentration in South Passage of the Changjiang Estuary. J. Sediment Res. 2009, 6, 6–13. [Google Scholar]
- Stachurska, B.; Staroszczyk, R. Loboratory study of suspended sediment dynamics Over a mildly sloping sandy bed. Oceanologia 2019, 61, 350–367. [Google Scholar] [CrossRef]
- Li, G.; Gao, Z.; Li, Z.; Wang, J.; Derksen, J.J. Particle-Resolved PIV Experiments of Solid-Liquid Mixing in a Turbulent Stirred Tank. Am. Inst. Chem. Eng. J. 2017, 64, 389–402. [Google Scholar] [CrossRef] [Green Version]
- Batchelor, G. An Introduction to Fluid Mechanics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Gavrilov, A.A.; Finnikov, K.A.; Ignatenko, Y.S.; Bocharov, O.B.; May, R. Drag and lift forces acting on a sphere in shear flow of power-law fluid. J. Eng. Thermophys. 2018, 27, 474–488. [Google Scholar] [CrossRef]
- Ali, S.Z.; Dey, S. Mechanics of Advection of Suspended Particles in Turbulent Flow; The Royal Society Publishing: Kharagpur, India, 2016. [Google Scholar]
- Cui, H.; Singh, V.P. Suspended sediment concentration in open channel using tsallis entropy. J. Hydraul. Eng. 2014, 19, 966–977. [Google Scholar] [CrossRef]
- Bose, S.K.; Dey, S. Curvilinear Flow Profiles Based on Reynolds Averaging. J. Hydraul. Eng. 2007, 133, 1074–1079. [Google Scholar] [CrossRef]
- Kundu, S. Suspension concentration distribution in turbulent flows: An analytical study using fractional advection-diffusion equation. Phys. A Stat. Mech. Its Appl. 2017, 506, 135–155. [Google Scholar] [CrossRef]
- Marcou, O.; Chopard, B.; Yacoubi, S.E.; Hamroun, B.; Lefevre, L.; Mendes, E. A Lattice Boltzmann Model to Study Sedimentation Phenomena in Irrigation Chanals. Commun. Comput. Phys. 2013, 13, 880–899. [Google Scholar] [CrossRef]
- Dolanský, J.; Chára, Z.; Vlasák, P.; Kysela, B. Lattice Boltzmann Method used to Simulate Particle Motion in a Conduit. J. Hydrol. Hydromech. 2017, 65, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Shi, H.; Si, P.; Dong, P.; Yu, X. A Two-Phase SPH Model for Massive Sediment Motion in Free Surface Flows. Adv. Water Resour. 2019, 129, 80–98. [Google Scholar] [CrossRef]
- Fourtakas, G.; Rogers, B.D. Modelling Multi-Phase Liquid-Sediment Scour and Resuspension Induced by Rapid Flows Using Smoothed Particle Hydrodynamics (SPH). Accel. Graph. Process. Unit (GPU) Adv. Water Resour. 2016, 92, 186–199. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).