Analysis of Carleman Linearization of Lattice Boltzmann
Abstract
1. Introduction
1.1. Early Attempts for Quantum Simulation of Fluids
1.2. Carleman Linearization
2. Lattice Boltzmann
Nonlinearity Ratio
3. Carleman Linearization for Lattice Boltzmann
3.1. Number of Variables
3.2. Carleman Linearization of Collision Step
3.3. Carleman Linearization of Streaming Step
3.4. Error Bound
4. Numerical Results
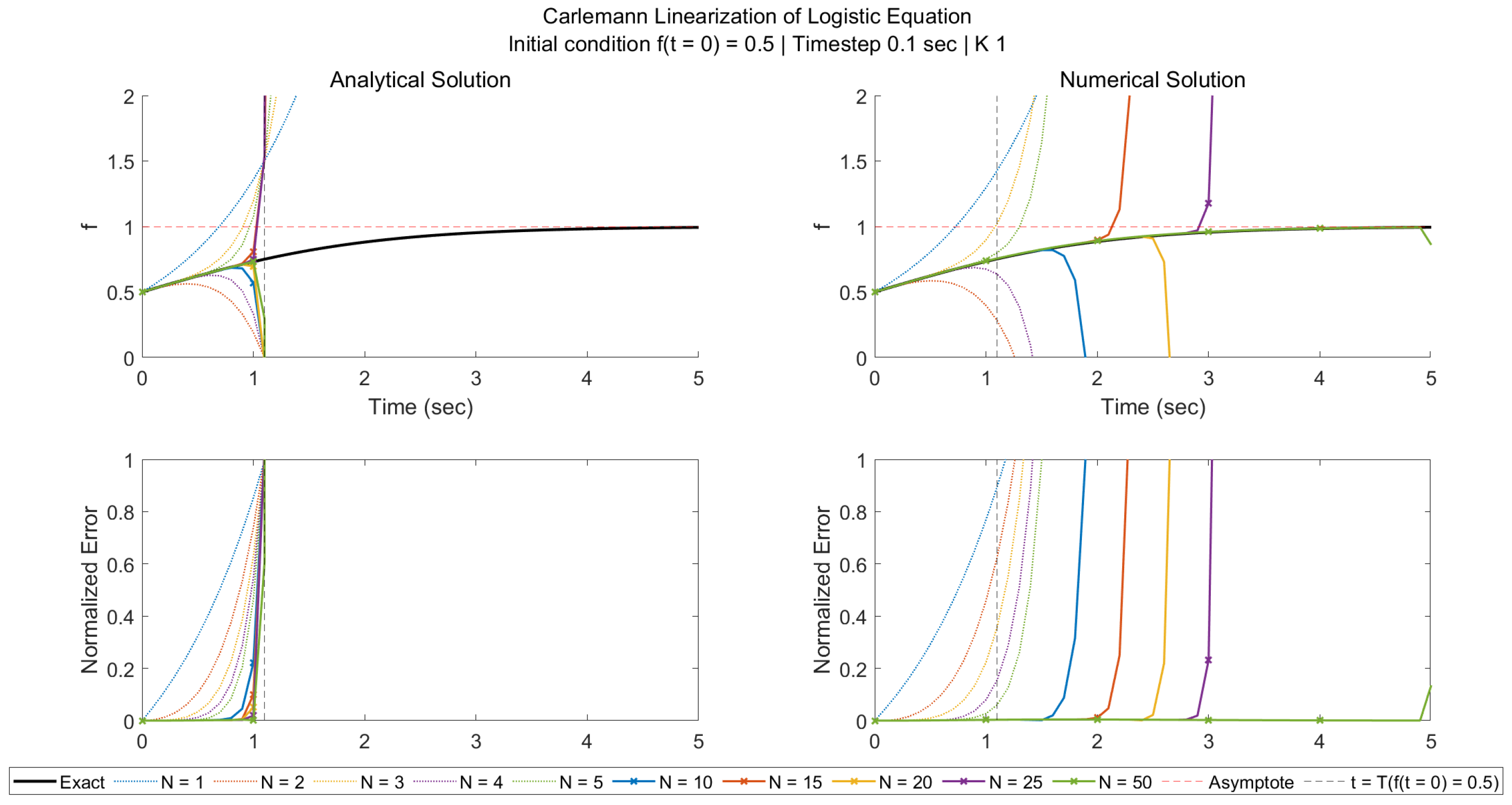
4.1. Logistic Equation
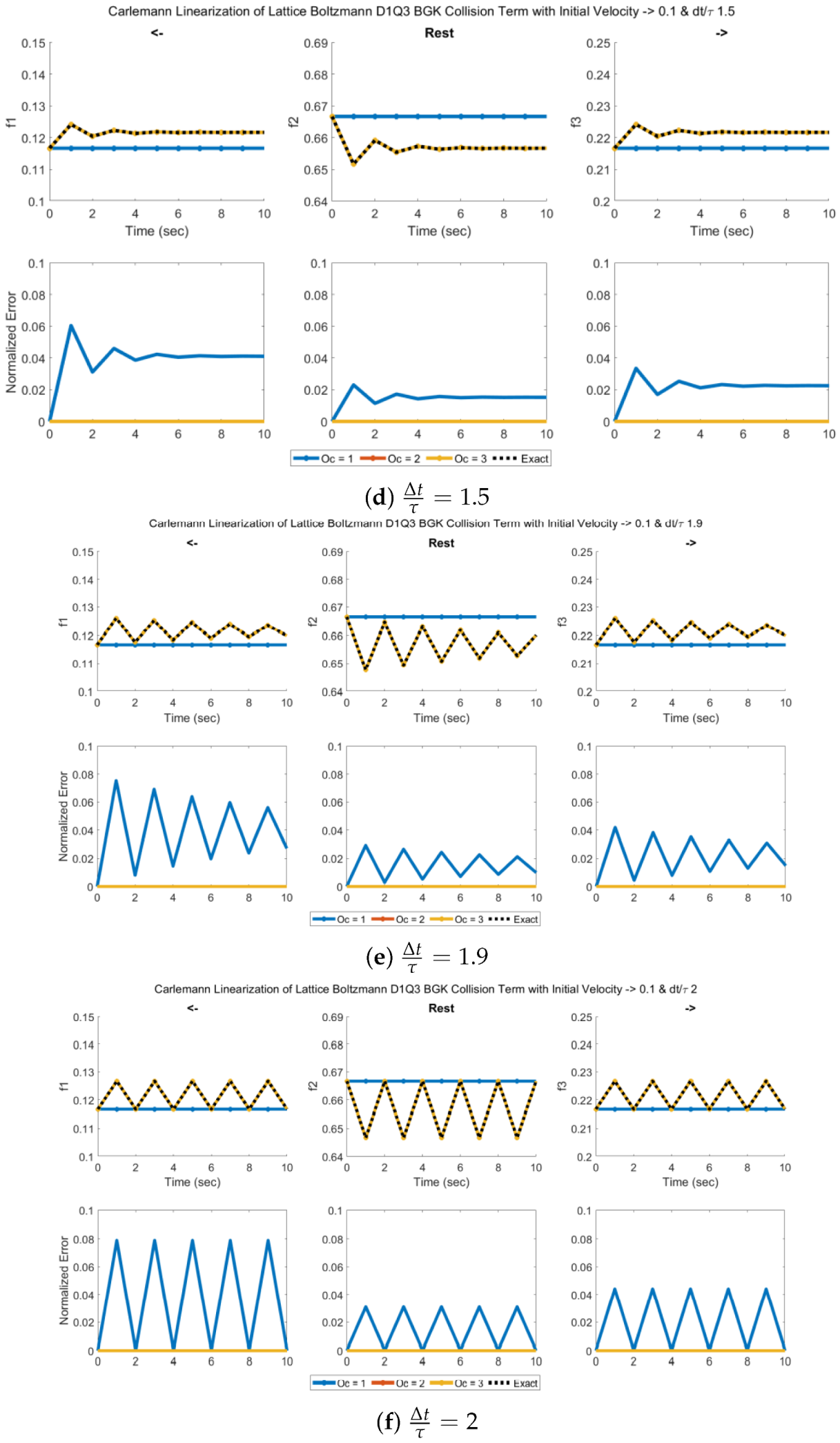
4.2. D1Q3
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Continuum particle velocity | |
| Discrete velocity in the ith direction | |
| Q | Number of discrete velocities number of modes at each lattice site, indexed by i |
| D | Number of dimensions of the lattice |
| x | Dimensions of the lattice, indexed by d, independent position vector variable |
| N | Number of Carleman variables |
| Number of sites across the dth dimension of the lattice | |
| G | Volume of the lattice in the units obtained by the product of the number of sites in each dimension |
| Discrete density distribution weight | |
| Collision operator defined by | |
| Weight of the ith discrete density | |
| Truncation order in Carleman linearization | |
| R | Ratio providing measure of nonlinearity parametrizing the error bound of the Carleman technique |
| Coefficient vector of zero-order terms in a quadratic ODE | |
| Coefficient matrix of first-order terms in a quadratic ODE | |
| Coefficient matrix of second-order terms in a quadratic ODE | |
| t | Independent time variable |
| Flow velocity | |
| Local fluid density in lattice units | |
| c | Lattice speed |
| C | Carleman linearization matrix |
| Norm of the solution error | |
| Approximated solution of the system | |
| Discrete timestep | |
| V | Vector of Carleman variables |
| Lattice vectors | |
| Mach number | |
| K | Scaling factor of the logistic equation |
| T | Total integration time |
| p | Order of the polynomial describing the driving function |
| a vector of polynomial functions of kth order in Carlemann variables | |
| Reynold’s number | |
| L | Characteristic length scale defined in units of |
| U | Characteristic velocity in lattice units |
| Kinematic viscosity in lattice units | |
| Speed of sound in lattice units |
References
- Nitzberg, B. Weather Forecasting Gets Real, Thanks to High-Performance Computing. 2017. Available online: https://www.altair.com/c2r/ws2017/weather-forecasting-gets-real-thanks-high-performance-computing (accessed on 25 November 2021).
- Moss, S. China May Already Have Two Exascale Supercomputers. 2021. Available online: https://www.datacenterdynamics.com/en/news/china-may-already-have-two-exascale-supercomputers/ (accessed on 25 November 2021).
- Benzi, R.; Succi, S.; Vergassola, M. The lattice Boltzmann equation: Theory and applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Succi, S.; Benzi, R. Lattice Boltzmann equation for quantum mechanics. Phys. D Nonlinear Phenom. 1993, 69, 327–332. [Google Scholar] [CrossRef]
- Yepez, J. Quantum Computation of Fluid Dynamics. In Quantum Computing and Quantum Communications; Williams, C.P., Goos, G., Hartmanis, J., van Leeuwen, J., Eds.; Series Title: Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1509, pp. 34–60. [Google Scholar] [CrossRef]
- Vahala, G.; Yepez, J.; Vahala, L. Quantum Lattice Gas Algorithm for Quantum Turbulence and Vortex Reconnection in the Gross-Pitaevskii Equation. In Proceedings of the 2008 SPIE Quantum Information and Computation VI, Orlando, FL, USA, 23 April 2008; Volume 6976. [Google Scholar] [CrossRef]
- Yepez, J. Lattice-Gas Quantum Computation. Int. J. Mod. Phys. C 1998, 9, 1587–1596. [Google Scholar] [CrossRef]
- Yepez, J. An efficient quantum algorithm for the one-dimensional Burgers equation. arXiv 2002, arXiv:0210092. [Google Scholar]
- Yepez, J. Open quantum system model of the one-dimensional Burgers equation with tunable shear viscosity. Phys. Rev. A 2006, 74, 042322. [Google Scholar] [CrossRef]
- Boghosian, B.M.; Yepez, J.; Coveney, P.V.; Wager, A. Entropic lattice Boltzmann methods. Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 2001, 457, 717–766. [Google Scholar] [CrossRef]
- Boghosian, B.M.; Taylor, W. Simulating quantum mechanics on a quantum computer. Phys. D Nonlinear Phenom. 1998, 120, 30–42. [Google Scholar] [CrossRef]
- Steijl, R. Quantum Algorithms for Fluid Simulations. In Advances in Quantum Communication and Information; Bulnes, F.N., Stavrou, V., Morozov, O.V., Bourdine, A., Eds.; IntechOpen: Rijeka, Licko-Senjska, Croatia, 2020. [Google Scholar] [CrossRef]
- Mezzacapo, A.; Sanz, M.; Lamata, L.; Egusquiza, I.L.; Succi, S.; Solano, E. Quantum Simulator for Transport Phenomena in Fluid Flows. Sci. Rep. 2015, 5, 13153. [Google Scholar] [CrossRef] [PubMed]
- Budinski, L. Quantum algorithm for the advection—Diffusion equation simulated with the lattice Boltzmann method. Quantum Inf. Process. 2021, 20, 57. [Google Scholar] [CrossRef]
- Lloyd, S.; De Palma, G.; Gokler, C.; Kiani, B.; Liu, Z.W.; Marvian, M.; Tennie, F.; Palmer, T. Quantum algorithm for nonlinear differential equations. arXiv 2020, arXiv:2011.06571. [Google Scholar]
- Succi, S. Lattice Boltzmann 2038. EPL Europhys. Lett. 2015, 109, 50001. [Google Scholar] [CrossRef]
- Steeb, W.H. Linearization Procedure and Nonlinear Systems of Differential and Difference Equations. In Nonlinear Phenomena in Chemical Dynamics; Vidal, C., Pacault, A., Eds.; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 1981; p. 275. [Google Scholar] [CrossRef]
- Forets, M.; Pouly, A. Explicit Error Bounds for Carleman Linearization. arXiv 2017, arXiv:1711.02552. [Google Scholar]
- Steeb, W.H. Linearization Procedure and Nonlinear Systems of DitJerential and DitJerence Equations. In Nonlinear Phenomena in Chemical Dynamics: Proceedings of an International Conference, Bordeaux, France, 7–11 September 1981; Vidal, C., Pacault, A., Haken, H., Eds.; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 1981; Volume 12. [Google Scholar] [CrossRef]
- Liu, J.P.; Kolden, H.O.; Krovi, H.K.; Loureiro, N.F.; Trivisa, K.; Childs, A.M. Efficient quantum algorithm for dissipative nonlinear differential equations. arXiv 2020, arXiv:2011.03185. [Google Scholar] [CrossRef] [PubMed]
- Succi, S. The Lattice Boltzmann Equation: For Complex States of Flowing Matter, 1st ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Bill, Y.; Meskas, J. Lattice Boltzmann Method for Fluid Simulations. 1997. Available online: https://www.researchgate.net/publication/265077140_Lattice_Boltzmann_Method_for_Fluid_Simulations/ (accessed on 25 November 2021).
- Randles, A.P.; Kale, V.; Hammond, J.; Gropp, W.; Kaxiras, E. Performance Analysis of the Lattice Boltzmann Model Beyond Navier-Stokes. In Proceedings of the 2013 IEEE 27th International Symposium on Parallel and Distributed Processing, Boston, MA, USA, 20–24 May 2013; IEEE: Cambridge, MA, USA, 2013; pp. 1063–1074. [Google Scholar] [CrossRef]
- He, X.; Luo, L.S. Lattice Boltzmann Model for the Incompressible Navier—Stokes Equation. J. Stat. Phys. 1997, 88, 927–944. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.S.; Krafczyk, M.; Yong, W.A. The lattice Boltzmann method for nearly incompressible flows. J. Comput. Phys. 2021, 431, 109713. [Google Scholar] [CrossRef]
- Itani, W.; Mezzacapo, A.; Succi, S. Quantum Carlemann Algorithm for Lattice Boltzmann Fluid Simulation. 2021; In preparation. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice, 1st ed.; Graduate Texts in Physics; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]






| Carleman Variables | Lattice Variables |
|---|---|
| 1 | |
| T | |
|---|---|
| 0 | ∞ |
| 0.1 | 2.40 |
| 0.2 | 1.79 |
| 0.3 | 1.47 |
| 0.4 | 1.25 |
| 0.5 | 1.10 |
| 0.6 | 0.98 |
| 0.7 | 0.89 |
| 0.8 | 0.81 |
| 0.9 | 0.75 |
| 1 | 0.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Itani, W.; Succi, S. Analysis of Carleman Linearization of Lattice Boltzmann. Fluids 2022, 7, 24. https://doi.org/10.3390/fluids7010024
Itani W, Succi S. Analysis of Carleman Linearization of Lattice Boltzmann. Fluids. 2022; 7(1):24. https://doi.org/10.3390/fluids7010024
Chicago/Turabian StyleItani, Wael, and Sauro Succi. 2022. "Analysis of Carleman Linearization of Lattice Boltzmann" Fluids 7, no. 1: 24. https://doi.org/10.3390/fluids7010024
APA StyleItani, W., & Succi, S. (2022). Analysis of Carleman Linearization of Lattice Boltzmann. Fluids, 7(1), 24. https://doi.org/10.3390/fluids7010024






