Abstract
In this study, a new set of direct numerical simulations is generated and used to examine the influence of mixture composition heterogeneities on the propagation of a premixed iso-octane/air spherical turbulent flame, with a representative chemical description. The dynamic effects of both turbulence and combustion heterogeneities are considered, and their competition is assessed. The results of the turbulent homogeneous case are compared with those of heterogeneous cases which are characterized by multiple stratification length scales and segregation rates in the regime of a wrinkled flame. The comparison reveals that stratification does not alter turbulent flame behaviors such as the preferential alignment of the convex flame front with the direction of the compression. However, we find that the overall flame front propagation is slower in the presence of heterogeneities because of the differential on speed propagation. Furthermore, analysis of different displacement speed components is performed by taking multi-species formalism into account. This analysis shows that the global flame propagation front slows down due to the heterogeneities caused by the reaction mechanism and the differential diffusion accompanied by flame surface density variations. Quantification of the effects of each of these mechanisms shows that their intensity increases with the increase in stratification’s length scale and segregation rate.
The aviation sector is a constantly changing industry that is heavily regulated and employs highly skilled individuals. Nowadays, it generates several million jobs world-wide and several hundred billion euros in revenue. However, it is also one of the fastest-growing sources of greenhouse gas emissions. Direct emissions from aviation account for 2–3% of the global emissions and about 12% of all carbon dioxide CO2 and nitrogen oxide NOx emissions of the transportation sector [1]. In 2020, the global annual international aviation emissions are already around 70% higher than in 2005. The International Civil Aviation Organization (ICAO) forecasts that, in the absence of additional measures, they could grow by over further 300% by 2050 [2]. Unfortunately, the current aeronautics propulsion systems have almost reached their technological limits and do not offer too many opportunities for a drastic reduction in greenhouse gas emissions. Thus, new propulsion concepts based on technological breakthroughs must be sought to improve the efficiency of the energy systems and meet the necessary emission targets, such as stabilizing CO2 emissions at 2020 levels by requiring airlines to offset the increase of their emissions after 2020.
One of the possible co-solutions to achieve carbon offsetting and reduction for international aviation is to change the combustion mode of current thrusters using the Brayton thermodynamic cycle and a constant pressure combustion (CPC), to a constant volume combustion (CVC) mode characterized by the Humphrey thermodynamic cycle [3]. It has been shown that in a Humphrey thermodynamic cycle engine, a possible procedure of achieving clean combustion is lean burning in a stratified charge [4]. The stratified combustion approach has also been shown to generate higher average effective pressure and better thermal efficiency, with lower flammability limits than in the homogeneous case with the same average equivalence ratio. As a corollary, reductions in fuel consumption and polluting emissions (greenhouse gases, nitrogen oxides and soot) have been achieved.
Among the first detailed examinations of stratified combustion, we note the work of Zhao et al. [4] and Cho and Santavicca [5], who specifically examined the effect of the heterogeneity of the reactants (the amplitude of the spatial and temporal fluctuations of the composition of the mixture) on the properties of the flame. They concluded that the degree and amplitude of the homogeneities affect the overall combustion properties and modify the characteristics of the local flames when neighboring pockets of different concentrations of reactants interact. This last observation has significant implications. It suggests that, contrary to the widely accepted theory of flames (see, for instance, [6]), on which many numerical models are based, the expected behavior of local flames, or flammelets, cannot be predicted solely from the local properties of the reactive medium and the characteristics of the turbulent flow.
Despite the importance of the partial premix for practical combustion devices, as well as the potential optimization that it offers, little fundamental work undertaken to quantify the effects of stratification on the local properties of the turbulent flames. From an experimental point of view, the difficulty lies in the implementation of an experiment capable of precisely reproducing the partial premix and coupling it with the diagnostics necessary for evaluating these complex flames. From a numerical point of view, many difficulties related to the models have been reported, and corrections have been proposed for stratified combustion, but they suffer from a lack of generality. For instance, using direct numerical simulation (DNS) and for mixture cases close to the previous experimentation of Cho and Santavicca [5], and Hélie and Trouvé [7] have shown that the combustion rate could decrease by up to 20%; however, no influence of heterogeneities on wrinkling has been observed. Other studies have investigated lower equivalence ratio ranges. Zhou et al. [8] reproduced the same turbulent conditions experimentally and identified an optimum level of heterogeneity that offers more efficient combustion (in terms of propagation) than the equivalent homogeneous flame. This has been emphasized for mean equivalent ratio different from unity. In the same way, the DNS of Jiménez et al. [9] has shown that, for lean mean conditions, heterogeneity increases the flame surface. The local concentrations and temperature are clearly affected and the combustion efficiency can be greatly improved, up to 60%. The DNSs of Haworth et al. [10] and Hélie and Trouvé [7] predict a different behavior, whereby the heterogeneous mixture results in less efficient combustion (in terms of heat release) or an essentially similar efficiency. There seems to be no real agreement between these authors, since the results strongly depend on the initial conditions. However, but with a few exceptions [11,12], most previous analyses were conducted under single-step chemistry simplification. Our work thus aims to complement some of these investigations, which were focused on the smallest-scale features in such inhomogeneous conditions, through the analysis of a new two-dimensional DNS dataset, that relies on a representative chemical scheme with 29 chemical species and 48 elementary reaction steps. Two-dimensional turbulence suffers from a lack of precision because of the non-consideration of the critical three-dimensional vortex stretching mechanism. However, in the present work the authors have not focused on the transfer of kinetic energy and its spectrum which are distinct in a 3D configuration, nor suggested an analysis based on the turbulent eddies’ distribution or temporal evolution. Although the two-dimensional nature of the flow-field considered in the DNS database is not the ideal situation to study the turbulent kinetic energy statistics, it has been shown, in the past, that it bears physical relevance thanks to its ability to capture the corrugating of the flame structure elements which are exposed to the turbulent motions. For instance, thermal heterogeneities and turbulent velocity fluctuations were studied by Pal et al. [13] using Two-dimensional DNS of auto-ignition in a lean syngas/air. Thanks to this study, Pal et al. [13] proposed regime diagrams linking different modes of combustion to velocity and temperature fluctuations characteristics. Moreover, Karimkashi et al. [14] recently used two-dimensional DNS to elaborate on the role of convective mixing and turbulence effects on combustion modes in locally stratified dual-fuel mixtures. Luong et al. [15] based their study of the role of temperature and composition fluctuations on dimethyl-ether/air mixtures ignition on a two-dimensional DNS database.
The rest of this paper is organized as follows. In Section 1, we briefly introduce the reactive compressible Navier–Stokes equations and provide an overview of the methods and algorithms that we use to solve them numerically. The DNS database description and characteristics are given in Section 2. The results are presented and discussed in Section 4 and a summary of the findings is provided in Section 5.
1. Governing Equations and Numerical Methods
In this work, the low Mach number (LMN) approximation of the fully compressible Navier–Stokes equations (NSE) is considered. Thanks to the LMN approximation, the compressible NSE can be simplified such that the thermochemical state of the flow is decoupled from the momentum equation [16]. In this framework, the mass conservation equation is expressed as
where and are respectively the mixture density and the velocity vector. The pressure is split in two components: (i) a space-uniform thermodynamic pressure, , and a hydrodynamic pressure, , linked to the fluid motion. Hence, the momentum conservation equation reads
with the viscous stress tensor, which takes the following form for a Newtonian fluid
where and are the mixture dynamic viscosity and the identity tensor, respectively. In addition to momentum and density, the primary transported variables are the species mass fractions, , and the sensible enthalpy, , expressed as
where denotes the sensible enthalpy of the kth species. For each species k the transport equation of is written
where is the molecular diffusion coefficient of species k and is the production/destruction rate of chemical species k. The energy equation requires the greatest attention because multiple form exists. The equation involving sensible enthalpy is preferred [17] and it reads
In the above equation, is the ratio of the specific heats, is the thermal conductivity and is the resulting heat release rate. This rate is expressed in terms of the species production rates, , and the standard enthalpies of formation as
The quantity is the corrected molecular diffusion velocity given by
The system of Equations (1)–(6) is completed by the perfect gas equation of state , where the mixture molecular weight W is given by , with being the molecular weight of the species k and R the universal gas constant.
The species viscosities and conductivities are evaluated according to the standard kinetic gases theory [18]. The diffusion coefficients are obtained following Hirschfelder et al. [18]. Mixture’s viscosity and thermal conductivity are computed using Wilke [19] and Mathur et al. [20] formulas, respectively. The species sensible enthalpies and specific heat coefficients are obtained using the polynomials provided by Gordon and McBride [21].
The system of Equations (1)–(6) is solved numerically using the low Mach DNS solver, which has been used to perform the numerical simulation of many canonical flowfields in simple geometries [11,22]. An exhaustive presentation of the computational methodology has been already made by Réveillon and Demoulin [23] and only its salient features are recalled in this paper. The sixth-order Padé scheme from Lele [24] is used to compute the spatial derivatives on a regular mesh. The time integration is carried out with a third-order accurate explicit Runge–Kutta scheme with a minimal data storage method [25]. The reaction rates in species transport equations are integrated using the stiff CVODE solver [26]. The variable-coefficient Poisson equation for pressure differences are solved using the multigrid method provided by the HYPRE library [27].
2. Flow Configuration
To truly simulate a turbulent reacting flow, it is necessary to consider the three dimensionality of the flow field together with a detailed description of the chemistry and the molecular transport. However, prohibitive computational cost limits the simulation either to take into account detailed chemistry at the expense of one spatial dimension or three dimensionality at the expense of detailed chemistry. In this work, the detailed chemistry description of the turbulent velocity field takes precedence over the three-dimensionality of the flow. This approximation is generally not suitable for non-reactive flows. For premixed combustion, however, the DNS of Cant et al. [28] showed that the probability of finding locally cylindrical two-dimensional flame topologies is higher than that of finding spheroidal three-dimensional flame surfaces. Therefore, two-dimensional flames seem more likely even if the flow field in front of them is in fact three-dimensional. In addition, Veynante et al. [29] compared two- and three-dimensional simulations. They found no significant differences in terms of turbulent transport, and the proposed criterion for delineating the “gradient” and “counter-gradient” regimes was in excellent agreement in both DNS databases.
With this in mind, the configuration of our study will be two-dimensional and corresponds to a statistically circular iso-octane/air flame propagating in a square domain of dimensions mm with periodic boundary conditions in both directions, in the presence of velocity fluctuations, and/or compositional heterogeneities.
The initial field of velocity fluctuations is generated by prescribing an energy spectrum using Rogallo’s procedure [30] and the theoretical spectrum of Passot and Pouquet [31],
where and are the root mean square of the velocity fluctuations and the most energetic wave-number, respectively. We have to emphasize that (i) the Passot–Pouquet spectrum concentrates the energy in the largest scales and (ii) the evolution of the turbulent velocity fields associated to those scales produces smaller and smaller scales of fluctuations without adding any significant dissipation. Similarly, the spectral method based on a probability density function (PDF) described by Réveillon [32] allows to generate a scalar field bounded between 0 and 1 by prescribing the mean value, the variance and a characteristic length scale associated to the PDF. In the current study, the composition PDF is approximated by the following -distribution
where
Thus, the computed scalar is rescaled to represent the equivalence ratio field . Here, the heterogeneous equivalence ratio scalar field is characterized by its (i) characteristic length scale, and (ii) segregation rate, . The latter is defined from the mean value, , and the fluctuations variance, , by
The chemistry of the iso-octane is described using the mechanism developed by Hasse et al. [33], which comprises 29 chemical species and 48 elementary reactions. This mechanism has been largely validated with experimental data [34,35]. The flame kernel is initialized in the center of the domain by interpolating a one-dimensional profiles obtained from a one-dimensional laminar premixed flame computed using CANTERA [36].
3. DNS Database
The DNS database is generated using a mean value of the equivalence ratio field equal to . To avoid bias in the identification of trends, the fluctuations of the heterogeneous field are considered identical on both sides of the mean value with a variation of . An example of such a situation is the case of a lean average equivalence ratio with asymmetrical heterogeneities and excursions deeper than the average to a richer (leaner) region. For this example, local propagation speed higher (respectively lower) than the propagation speed corresponding to the mean value is more likely to find slower (respectively faster) zones. As a result, on average, heterogeneities tend to accelerate (respectively slow down) the flame front.
The segregation rate, , can be considered as an indicator of the degree of heterogeneity; and is the signature of the amplitude of the gradients in the fuel mass fraction. To study the influence of this parameter on the dynamics of flame propagation, two values were considered for the the segregation rate. The first value, , corresponds to strong segregation of the reactive mixture, while the second, set at , corresponds to a moderate segregation.
The amount of flame front wrinkling produced by the heterogeneities depends on their size. In this database, characteristic length scales are applied following a criterion based on the flame thickness, . A priori, it is expected that pockets larger than the flame thickness will introduce more noticeable deformations of the flame front than pockets characterized by smaller length scales [37]. The flame thicknesses obtained for the mean equivalence ratio, , is m. The efficiency criterion is, a priori, valid in this case if the characteristic lengths are greater than or in the order of m. However, it is important to remember that as molecular diffusion and mixing in fresh gases tend to homogenize the mixture, the turbulent mixing of the fresh gas and the “effective” length scales are smaller than those initially applied. Thus, two values were chosen for the characteristic length heterogeneities: m and m. To characterize the propagation of the flame front subjected to the competition between the strengths of the turbulent structures and the fresh mixture composition heterogeneities, the DNS database was designed so that the dynamic effects of turbulence and the chemical effects relating to combustion heterogeneities are initially comparable. An illustration of the conditions selected is given on the diagram of the turbulent combustion regimes (see Figure 1).
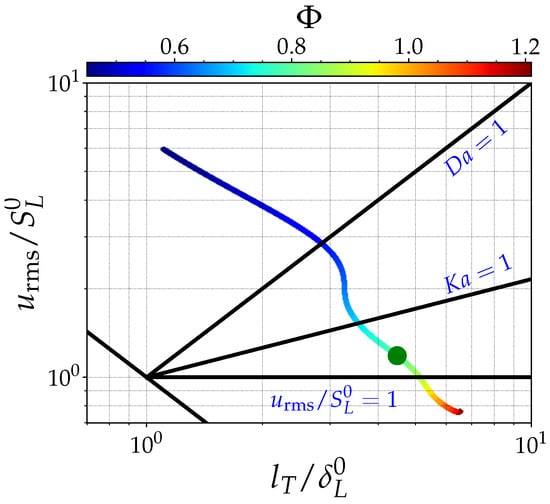
Figure 1.
Turbulent combustion diagram in presence of heterogeneities within moderate characteristic length and segregation rate. The green dot corresponds to the average equivalence ratio.
In terms of turbulence intensity, the flow considered is characterized by turbulent speed fluctuations m/s and the autocorrelation integral length scale m. A second advantage associated with these low turbulence levels lies in their similarities to the laminar cases. In fact, within these values, the mean flame regime falls between the wrinkled and corrugated flames regimes.
To obtain converging statistics and to ensure that the trends observed are representative of physical phenomena, four draws of the turbulent field are considered for each case. These were obtained by dividing the initial field into four quadrants which are symmetrically swapped with respect to both domain axis [11]. Moreover, for each equivalence ratio distribution two draws were considered by using two complementary draws with respect to the set mean value (see Figure 2). This was done in order to ensure that the mean of the two fields at initialization was strictly the scalar mean corresponding to the homogeneous configurations at each grid point, and therefore avoiding that the observed trends were biased by the spatial distribution (see Figure 3). As a result, each case in the DNS database counts 8 computations.
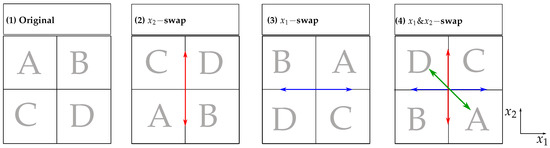
Figure 2.
Diagram of the process of quadrants swapping to represent the deposit of the flame kernel at different places in a turbulent field.

Figure 3.
Illustration of the process of swapping the quadrants of a speed field. Superposition of the contours of the vorticity fields and the generated speed fields.
The complementarity of the distributions is combined with the four interversions of the velocity field, which leads to eight calculations per configuration. These calculations are indexed by an index ranging from 1 to 8. Calculations indexed by a value between 1 and 4 are carried out with the first distribution of the scalar, while those corresponding to a value between 5 and 8 are carried out on the basis of the complementary scalar distribution. The latter indexing is illustrated in Figure 4.
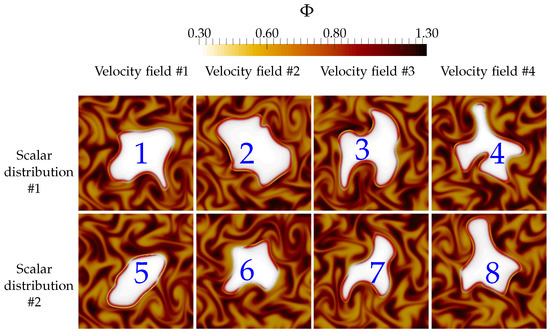
Figure 4.
Indexing of heterogeneous turbulent calculations. Fields of heat release superimposed on the local equivalence ratio fields for the eight computations corresponding to the case BH at .
For all the cases, the domain is discretized into a mesh of grid points. Table 1 summarizes the turbulence characteristics i.e., the integral length scale, , the turbulent velocity fluctuation, , the turbulent Reynolds number, and the Kolmogorov time scale, (of the corresponding initial turbulent flowfields), and the thermo-chemical characteristics (i.e., the laminar flame speed, , the laminar flame thickness, , the chemical time scales, , the Damköhler number, and the Karlovitz number, . The characteristics of the considered heterogeneities distributions for the simulations of the current DNS database are recapitulated in Table 2.

Table 1.
Characteristics of the direct numerical simulation (DNS) database simulations. Turbulence parameters and dimensionless numbers (Da, Ka and Re) are given for the initial fields.

Table 2.
Characteristics of the distributions of the heterogeneities considered in the DNS database simulations. Each configuration is designated by an identifier in the form , where X is associated to the characteristic size of heterogeneous pockets (N for the homogeneous case, M for moderate size and B for relatively high size), while Y represents the distribution segregation rate (N for absence of heterogeneities, M for moderate segregation rate, and H for high segregation rate).
Description of the Mixture Fraction and the Reaction Progress Variable
For a DNS using one-step chemistry, the mixture fraction is defined as
where and are the mass fraction of fuel and oxidizer, respectively, and is the stoichiometric fuel-to-air mass ratio, and is the nitrogen-oxygen mass ratio. In simulations using a detailed description of chemical kinetics, Equation (13) is modified to include the radicals. The elementary mixture fraction is obtained from [10]
where refers to the elements (C, H and O), is the atomic mass of the element , and is the number of atoms of the element in the species . In this context, the mixture fraction is defined as
where and are the fractions of the elementary mixture of carbon and hydrogen, respectively. Given Equation (15), the local equivalence ratio is defined as by [10]:
where the index “” indicates a value associated with a stoichiometric mixture. The value of is obtained by adding to . In particular, for an hydrocarbon CnHm, the local equivalence ratio is expressed as follows
In the case of a heterogeneous mixture, the local equivalence ratio, , and the elementary mixture fractions, , are functions of the independent variables space and time. The transport equation of the mixture fraction is written as
where is the diffusion coefficient of the mixture fraction and and are the diffusion coefficients for the elementary mixture fractions of carbon and hydrogen.
In the present study, the progress variable based on the mass fractions of the species and the mixture fraction is preferred to that based on the temperature. Here, we generate the DNS database by using a multi-species mechanism, which allows to evaluate the elementary mixture fractions. Thus, the progress variable, c, is defined using the mass fractions of certain species present in the burnt products, , and their equilibrium values in the form
where is the set of species chosen to define the progress variable, c, and is the mass fraction of the species k at equilibrium conditions. In addition, in the case where the conditions are lean, it is possible to consider a progress variable based on the mass fraction of the fuel and the mixture fraction, :
Figure 5 shows the density field obtained for a single run (one of the 8 simulations) from the BH case, while in Figure 6 we report the contours of the iso-values of c obtained by considering four definitions of the progress variables, i.e., combustible, the couple H2/H2O, the triplet CO/CO2/H2O and the couple CO/CO2.
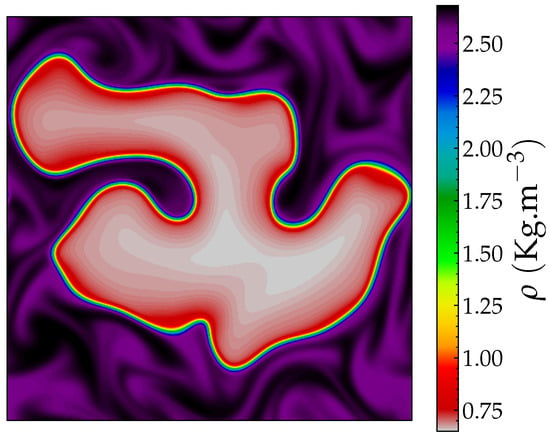
Figure 5.
Density field for the BH case at .
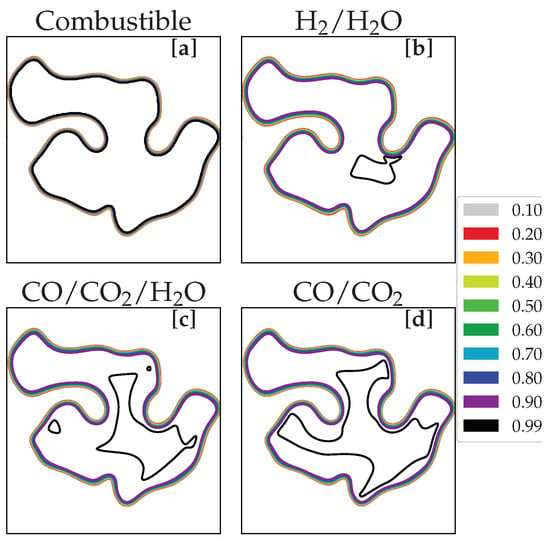
Figure 6.
Isocontours of the progress variable for the BH at computed with definitions based on (a) fuel consumption Equation (20), (b) the couple H2/H2O, (c) the triplet CO/CO2/H2O and (d) the couple CO/CO2.
The progress variable definition to be considered, should respect three constraints. These are: (i) monotonic evolution along the chemical trajectories from fresh gas state to the burnt gas, (ii) variation on a sufficient number of grid points, so that the gradients of c are finite and can be calculated with, relatively good precision and (iii) since the flames considered belong to the wrinkled/corrugated flame regime, i.e., small Karlovitz number, no turbulence flame front distortion occurs. Hence, the isocontours of c remain parallel to each other. Thanks to the general definition given by Equation (19), constraint (i) is respected by all four definitions. However, by adopting the definition of c based on the mixture fraction and on the mass fraction of the fuel (Equation (20)), we obtain isocontours very close to each other. This is because the fuel is the first species to react and decomposes very quickly. Thus, the variation of the values of the progress variable is conducted on a small number of points of the computational grid leading to a violation of constraint (ii). For this reason, this definition is not retained. The definitions involving hydrogen (H2/H2O) and (CO/CO2/H2O) respect criteria (iii) for all the isocontours except those in the vicinity of (on the side of the burnt gases), in this case , which is relatively distant from the rest of the isocontours and not parallel to them. Indeed, the intermediate species and the radicals containing hydrogen continue to react in the burnt gases. Thus, these two definitions are also rejected. Finally, the introduction of the definition based on the couple CO/CO2, the isocontour approaches the others and the criterion of “parallelism” is respected. In addition, it combines a good discretization on the mesh with a monotony between 0 and 1. This definition could therefore be considered, since it respects the three constraints mentioned earlier. The transport equation of c can be written as (see Appendix A for a detailed development of this equation)
with
and is the diffusion coefficient, defined so that it satisfies the condition
and and are respectively the scalar dissipation terms for the mixture fraction and the cross scalar dissipation term for the progress variable and the mixture fraction, they read
The role of these scalar dissipation terms as sink or source terms depends on the partial derivatives of the mass fractions of the species with respect to the mixture fraction.
4. Results and Discussion
4.1. Preferential Propagation
Previous studies have shown that the fluctuations in the local equivalence ratio result in a additional wrinkling mechanism of the flame [38,39,40,41]. Moreover, it has been suggested that the magnitude of this mechanism is mainly determined by the spatial distribution of the local stratification field. Indeed, the flame front preferential propagation, especially on the leading edge of the flame rush, depends on the local mixture fraction that it encounters and which in turn is the result of the competition between the strengths of the turbulent structures and the heterogeneities present in the flow field. Motivated by these observations, our study aims to complete the understanding of previous works through the quantification of the influence of the spatial distribution of the stratified equivalence ratio field on the flame wrinkling mechanism. A first investigation of this effect can be conducted by studying the evolution of the local mixture fraction field, as it directly influences the local propagation speed.
First, we observe regardless of the initial conditions, the mixing effect induced by the turbulence leads to the homogenization of the local mixture fraction, . Therefore, the PDF of evolves towards a mostly Gaussian distribution as shown in Figure 7. In these plots, despite a global skewness toward smaller mixture fraction values, the PDFs are centered around values close to the homogeneous reference mixture fraction, that is, . The influence of the initial equivalence ratio distribution is also highlighted in Figure 7 by plotting the temporal evolution of mixture PDFs computed on the flame front. On the one hand, we observe that for the same segregation rate level, the mixture fraction distribution becomes broader as the stratification length scale increases. This is because the mixing effect of the turbulent structures is less efficient in the presence of large scale heterogeneities. On the other hand, we notice a similar effect of mixture fraction PDF broadening when the segregation rate is increased, at iso-. The explanation for this lies in the fact that the characteristic time needed by the turbulent scales to homogenize a scalar field characterized by high variance/gradient is longer than the characteristic time needed to homogenize a scalar field which presents smaller gradients (see Figure 8). Therefore, when the flame front reaches such zones it encounters a wide range of mixture fraction values.
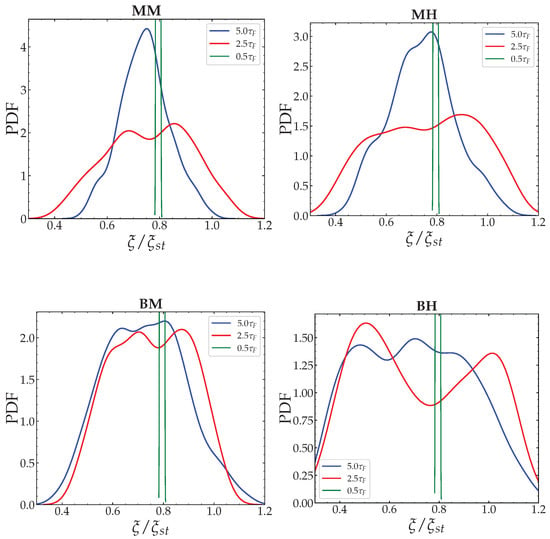
Figure 7.
Probability density function (PDF) of the mixture fraction on the side of fresh side, which corresponds to the isocontour , at three instants , and .
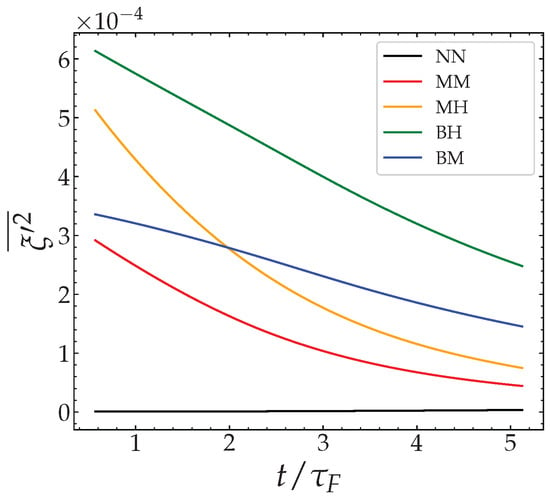
Figure 8.
Temporal evolution of the variance of the mixture fraction.
As shown by the skewness of the mixture fraction PDF, the distribution of the mixture fractions on the stratified flame fronts evolve, on average, towards a leaner condition than the homogeneous case. This is a direct consequence of the preferential propagation of the flame front in the direction of the richer zones. In other words, the richer regions encountered by the flame front in the fresh gases are consumed more rapidly than the leaner zones, resulting in an accumulation of the latter in the vicinity of the flame front. In particular, these richer regions are close to the stoichiometry value in which the maximum of the laminar flame speed is reached. This phenomenon is more pronounced as and increase. An illustration of this effect can be obtained by considering the alignment between the gradients of the mixture fraction and the progress variable.
With this in mind, we define the angle between the normals of the iso-surfaces of the progress variable, c, and the mixture fraction, , as
The normal to the flame front is oriented in the opposite direction to the gradient of the progress variable, i.e., . Thus, indicates that the flame propagates in a richer mixture along the gradient of the mixture fraction. Conversely, indicates that the flame propagates in a locally leaner mixture along the gradient of the mixture fraction.
The PDFs of the cosine of the angle between the gradients of the progress variable and the mixture fraction on the flame front exhibit much greater likelihood of negative values than positive values as shown in Figure 9. This is equivalent to a preferential alignment of the direction of the flame propagation with the direction of the increase in the mixture fraction. In this case, the probability of observing a value of close to increases by increasing the characteristic pocket size and the rate of segregation. However, in regions where the stratification is small-scaled and characterized by a low turbulent intensity, i.e., the MM case, no clear alignment is apparent between and . Nevertheless, in these conditions, an angle is more likely probable because the stratified flame is close to a homogeneous flame.
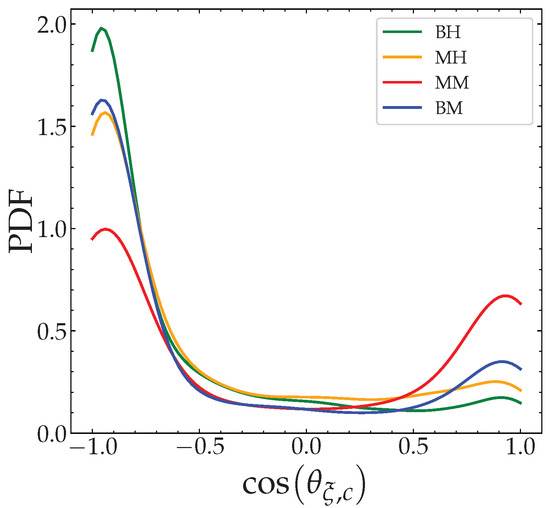
Figure 9.
PDF of the alignment angle between the gradients of the progress variable and the mixture fraction on the flame front.
4.1.1. Influence on Flame Surface Generation Mechanisms
In an analogous context, where the flame in propagation in a turbulent flow undergoes similar wrinkling, the instantaneous rate of change of the flame surface, A, can be calculated according to Pope [42] and Candel and Poinsot [43] from the rate of stretching in the the tangent plane, , the local mean curvature, and the speed of displacement, , as follows
The rate of stretching in the tangent plane, , reads , while The local mean curvature, , is defined as
The displacement speed, , can be decomposed as
where
The definitions of , and are given in Equation (A19). The terms , , and represent the components of arising from normal diffusion, curvature, reaction, differential diffusion, respectively. The terms and represent an additional diffusion related to the flamelet structure and the cross-scalar dissipation term, respectively.
According to Equation (25), a change in the flame area may be caused by two different terms. The first term on the right-hand side, , represents the rate of change of the flame surface due to hydrodynamic strain. Indeed, stretching in the direction of extension tends to increase the surface unlike stretching in the direction of compression. The second term, , corresponds to the potential surface changes of a curved flame front during its propagation; the surface decreases in the case of a propagation towards the center of curvature and increases in the case of a propagation in the opposite direction, i.e., the outward direction. Thus, by means of Equation (25) we can express the fundamental dependence of the rate of change of the flame surface into this two decoupled contributions. Specifically, for the transport equation for the flame surface density function, Pope [42] and Candel and Poinsot [43] distinguished three effects governing the evolution of the elements of the flame surface: (i) stretching, (ii) the propagation and (iii) the hydrodynamic effects resulting from the combination of the effects of the propagation and the curvature induced by the flow structures. In the following, we study the influence of the heterogeneities of the composition on each of these three contributions.
The flame front curvature PDFs (normalized by the laminar flame thickness ) are presented in Figure 10.
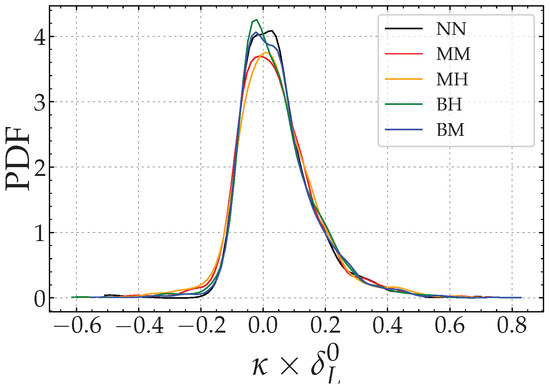
Figure 10.
PDF of normalized curvature evaluated at the flame front at normalized instant .
The values taken by the distribution of the curvature suggest that the elements of the flame fronts tend to be rather convex in the directions of the fresh reactants (positive curvatures). However, except for the case MH, we note that the peak of the PDFs of the stratified flames appears for slightly negative values which correspond to convex zones unlike the homogeneous case where the most probable value of the curvature is positive.
In addition, the PDFs of curvature of the flame front are wider than their homogeneous counterpart. However, these results show that the curvature of the flame front is weakly influenced by the stratification. The similarities observed on the PDFs associated with homogeneous and stratified flames suggest that the additional wrinkling induced by the composition heterogeneities remains moderate compared to that induced by the turbulence.
On the other hand, the PDFs of the tangential stretch rate (normalized by the characteristic time of propagation of the laminar flame) are presented in Figure 11.
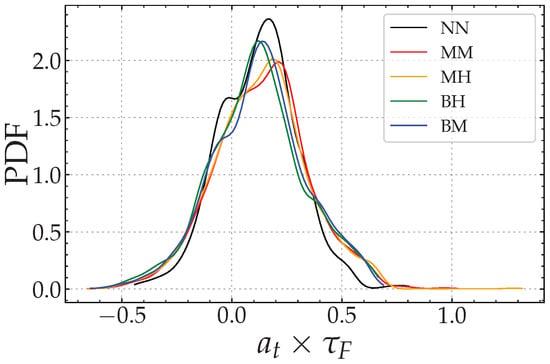
Figure 11.
PDF of the tangential stretching rate on the flame front at .
They are characterized by an almost symmetrical shape, with more excursions on the side of positive values (extension). The relative positions of the PDF peaks are slightly modified with the presence of heterogeneities. For a local equivalence ratio distribution characterized by small , the most likely value of the tangential stretch rate increases, while it decreases in the presence of large-scale heterogeneities. In addition, as with curvature, the PDF of broadens by stratification.
A typical behavior observed in turbulent homogeneous premixed flames and highlighted by Haworth and Poinsot [44], consists in a strong correlation between the tangential stretching rate and the curvature of the flame front.
The convex elements of the flame front (with respect to fresh reactants, and concave with respect to burnt products), i.e., of positive curvatures, are aligned with the direction of compression characterized by negative values of the in-planar strain rate , while the concave zones are aligned with the direction of extension whose signature is positive values. In Figure 12, we gather the joint PDFs of the curvature and the tangential strain rate of the flame front at the instant for the stratified and homogeneous conditions. In the homogeneous case we can find the alignment effect, which results in a fairly high negative correlation coefficient (The correlation coefficients used here correspond to the Pearson definition, in which a correlation coefficient is between −1 and 1. A coefficient which approaches 1 in absolute value is synonymous with a strong correlation between the variables considered, the sign of this coefficient, meanwhile, represents the sign of the correlation). The presence of heterogeneities decreases, relatively, this correlation following the modification of the distributions of and . Furthermore, this effect’s intensity increases with the increase in the intensity of the heterogeneities and their characteristic size. On the other hand, from a global perspective, the stratifications do not alter the correlation of the positive (negative) curvatures with the direction of the compression (extension). The joint PDFs of and portrayed in Figure 12 show a trend (which can also be assessed in Figure 11) characterized by the dominance of positive values in the distribution of the tangential strain rate. This could be a sign of a preferential alignment of the flame with the direction of the extension. Indeed, in the homogeneous case, we can observe a positive correlation between the displacement speed of the flame front and (see Figure 13), which means that displacement speed of the flame front increases with the increasing stretch in the direction of the extension. As previously mentioned, the introduction of composition heterogeneities induces a broadening of the PDF, especially on the side of positive values. This results in an intensification of the alignment between the flame and the direction of the extension, which is manifested by an increase in the correlation between and , especially for high segregation rate values (see Figure 13).
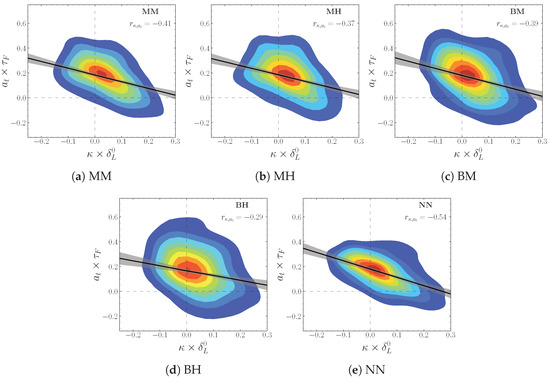
Figure 12.
Joint PDF of the curvature and the tangential stretch rate at .
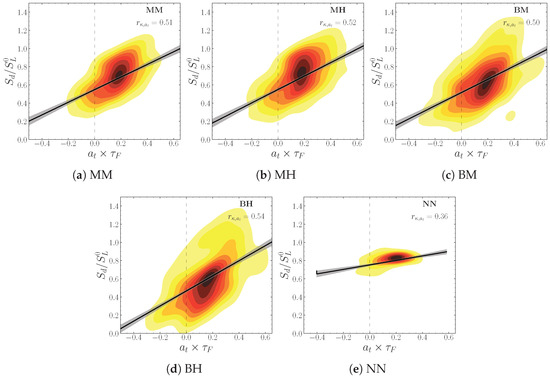
Figure 13.
Joint PDF of the displacement speed and the rate of tangential stretching on the flame front at .
Thus, due to the correlation of the negative curvature zones with the extensive direction, it is expected that these regions correspond to a faster flame front propagation. This is particularly illustrated by the distribution of the curvature and the displacement speed shown in Figure 14. Indeed, it appears that these two quantities strongly correlate in the homogeneous case (correlation factor ). However, this correlation becomes less intense as composition heterogeneities are introduced, especially for larger and stronger .
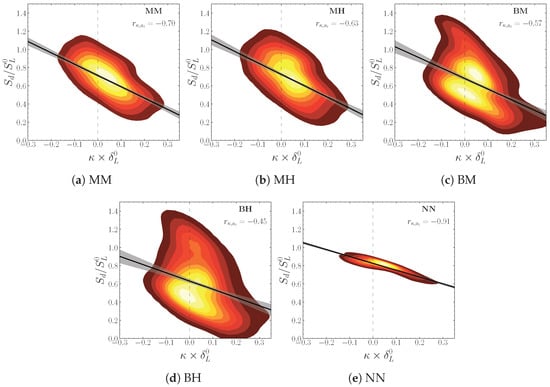
Figure 14.
Joint PDF of displacement speed and the curvature on the flame front at .
4.1.2. Flame Surface Density Budget
We have analyzed the behavior of the strain and curvature mechanisms of the flame front. However, it has not yet been a question of quantifying their respective contributions to the variation of the flame surface. Furthermore, in addition to these two quantities, we have mentioned the effect of propagation in the modification of the surface of the flame front. Since the relative influence of this effect has not been addressed yet, it is suggested herein to assess the contribution of each of the mechanisms governing the flame surface evolution. Therefore, the budget of the flame surface density function (SDF) will be considered for this analysis. Unlike the previous analysis, performed only on the flame front defined by a progress variable iso-surface (), the budget analysis will be performed on the entire flame brush. The transport equation of the SDF is expressed as follows
where . In Equation (29), the first term on the RHS is referred to as the SDF strain rate term. The second term on the right-hand side of Equation (29) is called the SDF curvature term, while the third and last term is referred to as the SDF propagation term. It is sometimes convenient for the second and third terms to be taken together as the combined SDF curvature and propagation terms [45]. We illustrate in Figure 15 the dispersion of the individual source terms of the SDF transport equation with respect to the variable of progress c, for the homogeneous case at . We depict also the average profile of each source term of the Equation (29) conditioned by the variable of progress in Figure 15b. From these, we note that the term combining the unsteady and convection effects (LHS in Figure 15) acts as a production term on the side of fresh gases (), but as a sink term for products (). Indeed, with the unsteady propagation of the flame front, the surface is generated at the level of the flame front and it is destroyed in the burnt products, which is consistent with previous modeling and DNS results of Trouvé and Poinsot [46]. The profile of the SDF propagation term is similar (with opposite signs) to that of the term combining unsteady and convection effects, their amplitude is comparable. This shows that the contribution of the terms of strain and curvature is minimal for the homogeneous case.
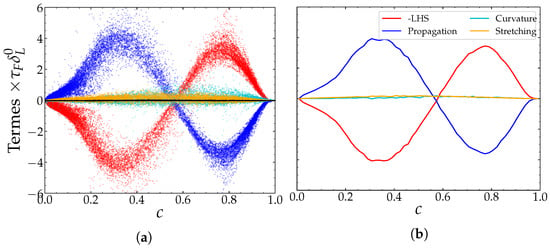
Figure 15.
Terms of the transport equation of the flame surface density function as a function of the progress variable for the homogeneous case at . The difference between the right and left hand side of the Equation (29) is given by black points. (a): scattering of the point cloud, (b): averages conditioned by c.
The latter behavior is not altered by the presence of equivalence ration stratification. Indeed, in the area of fresh gases and that of burnt gases, the order of magnitude of the conditioned means of the terms of strain and curvature of the stratified flames is comparable to that associated with the homogeneous case, and it is negligible compared to propagation (see Figure 16). On the other hand, in the transition zone between the two states, , the contributions of and reach their maximum value which therefore become comparable to the propagation effect. In this zone and along the entire flame thickness, the terms of curvature and strain in the Equation (29) have positive values, and therefore contribute to the generation of the flame surface per volume unit. In summary, the heterogeneities of composition slightly modify the amplitude of the terms associated with curvature and strain. However, the fact that the contribution of the latter two remains moderate, in comparison with that of propagation, implies that the zone generated by the heterogeneities of composition, is not due, in the first order, to the modification of the behavior of these two mechanisms, but rather, the mechanism of propagation via the displacement speed. For this reason, the impact of heterogeneities on the displacement speed will be quantified in the next section.
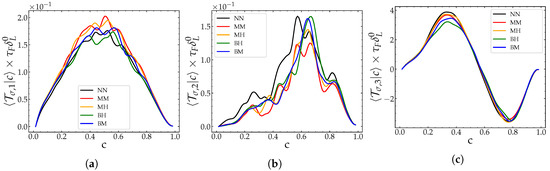
Figure 16.
Conditioned averages of the terms (a), (b) and (c) of the flame surface density function budget as a function of the progress variable at .
4.2. Effect of Stratification on Displacement Flame Speed
In the previous section, it has been shown that the distribution of the mixture fraction on the unburnt gases side of the flame front becomes wider with the increase of and . Furthermore, we demonstrated that the PDF of evolves to a Gaussian-like distribution skewed toward leaner values. As a result, we expect that the flame front displacement speed distribution will feature a wide range of values when large characteristic scales and more segregated stratifications are considered. Indeed, as illustrated in Figure 17a, the distribution of the displacement speed on the fresh gases side, represented here by the 0.1 iso-c level, is broader for the stratified cases in comparison to the homogeneous case. In particular, as the distribution of the mixture fraction, the PDF of is skewed toward smaller values compared to the mean of the homogeneous case displacement speed. Hence, it is expected that, as the flame front propagates, the accumulation of lean zones and regions with slow displacement will slower down the flame front in the stratified cases. The temporal evolution of the average of the displacement speed on the fresh gases side, depicted in Figure 17, essentially leads to this conclusion.
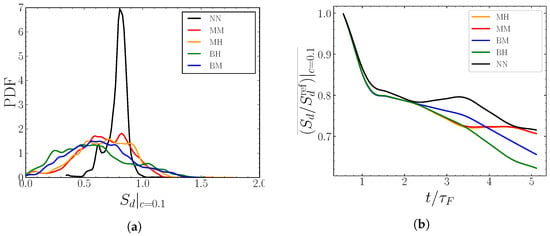
Figure 17.
Impact of composition heterogeneities on the displacement speed of the flame front (iso-c = 0.1). Left (a): PDF at , right (b): temporal evolution.
Moreover, the trends shown by these evolutions confirm the behaviors observed earlier for the mixture fraction. Specifically, as the stratification characteristic length scale increases, a larger spectrum of flame displacement speed is observed. However, it can be noticed that the influence of the segregation rate is smaller than that of the characteristic length scale, . Since the flame elements are propagating at different speeds, the flame front presents more wrinkling, and thus more surface with respect to the homogeneous reference case. Herein, we propose to study the influence of composition heterogeneities on the evolution of the displacement speed. For this purpose, the different components of are analyzed. Since these components are based on the terms of the progress variable budget, it is first necessary to examine the behavior of the latter, that is, the weights of those terms in the c transport equation.
An example of such a budget is shown in Figure 18a for the configuration BH. The closing of this equation is an indicator of the respect of the required level of accuracy in the simulation and post-processing procedure. Figure 18c shows the residual error resulting from subtracting the right- and left-hand sides of the Equation (21). The numerical error in the computations under consideration is significantly smaller (by about three orders of magnitude) than the smallest term involved in the equation. The predominance of the reaction term is shown in Figure 18a,b. In order of weight, the diffusion term, , comes after the latter, and acts as a production term on the fresh gases side up to . The diffusion appears as a destruction term with intensity comparable to that of . The role of the mechanisms associated with the mixture fraction dissipation and the cross-dissipation remains moderate compared to the other contributions. It is noteworthy, however, that the amplitude of is significant in a relatively small range of the progress variable . This is attributed to the fact that the sum of the equilibrium mass fractions of the species involved in the definition of c, , corresponds to an almost linear function of under the considered conditions. In other words, , where and are constant coefficients. Figure 19 illustrates this effect which was also discussed by [47]. Finally, it is important to note that the term expressing the effects resulting from the species differential diffusion have a non-negligible contribution with a magnitude comparable in some zones comparable to that of the diffusive and reactive terms. The effect associated with differential diffusion, , is often negligible in previous studies, which often adopted the hypothesis of a unitary Lewis number, assuming not only that the effects of molecular and thermal diffusion are equal, but also that all species diffuse at the molecular scale in the same manner. As a result, the term vanishes in the Equation (21) under this assumption. In our study, the consideration of the differential diffusion effect was motivated by the fact that the considered values of the Lewis number of the fuel, and the species which the progress variable is constructed, are very different from the unity (see Figure 20). Therefore, this hypothesis cannot be adopted, given that the closure of the Equation (21) balance cannot be obtained with such an approximation.
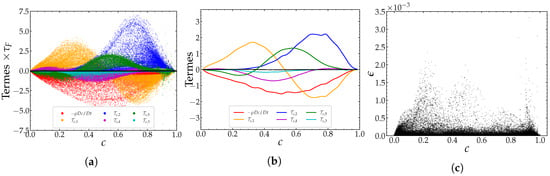
Figure 18.
Terms of the progress variable c budget obtained for the case BH at . Left (a): scatterplot, middle (b): averages conditioned by c, right (c): residual.
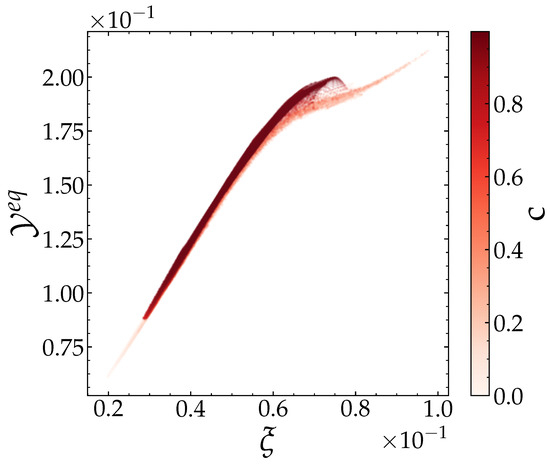
Figure 19.
Sum of the mass fractions of CO and CO2 at equilibrium as a function of the mixing fraction for the case BH at .
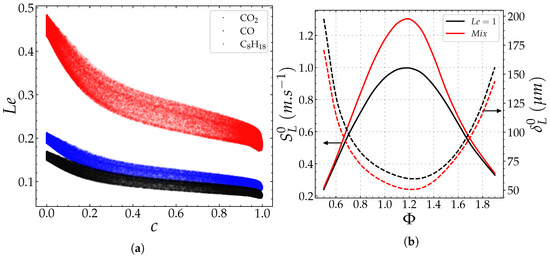
Figure 20.
Influence of the unitary Lewis number hypothesis. Left (a): Evolution of the Lewis number
of the fuel, of CO and of CO2 as a function of the progress variable for the case BH at , right (b): profiles of the laminar flame velocity and thickness in the considered ranges of variations.
Moreover, on the basis of the computations of mono-dimensional laminar flames, a rather pronounced difference in the laminar flame velocity was observed by comparing the values obtained by the multi-species approach [18] and those calculated by adopting the formalism of a unitary Lewis number. In addition, this difference is more pronounced in the range of equivalent ratios considered in the configurations of our study (see Figure 20b). A direct consequence of omitting the effects of differential diffusion would be an underestimation of the difference in local propagation speeds and consequently a decrease in the additional wrinkling effect introduced by the heterogeneities.
From the previous analysis of the progress variable budget, it is clear that the terms and are smaller in magnitude than the reactive term , the differential diffusion term and the sum of the diffusive terms and . The latter, which is linked to the curvature, has been addressed above, and it has been shown that its effect is relatively negligible in comparison to the other mechanisms. Thus, the components , and are expected to be dominant in behavior. An illustration of this trend is given by Figure 21, which groups the evolutions of each of these components in function of the progress variable for the case BH.
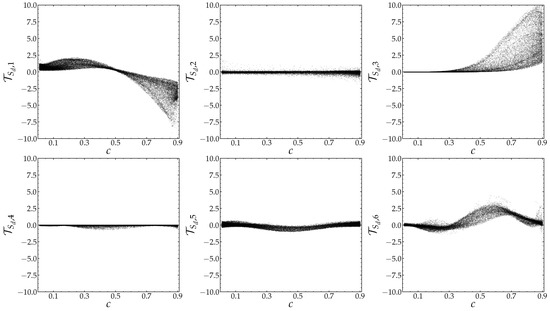
Figure 21.
Evolution of the components of the displacement speed as a function of the progress variable for the case BH at .
The study of the influence of the heterogeneities on will be limited in the following to the three dominant terms. To do so, we will compare the evolution of each component at iso-c level representative of the three zones of the flame, i.e., the preheating zone, the reaction zone, and the burnt gases zone. The PDF of the normal component of in these three zones at is reported in Figure 22. The values of the progress variables, c, in the preheating, the reaction and the burnt gases zones are , and , respectively. On the fresh gas side, the distribution of the normal component of is wider than the one corresponding to the homogeneous case. We observe again that the width of the PDF increases more with the increase than with . In addition, as for the distribution of in this zone (see Figure 17a), the PDF of is skewed toward smaller values than their homogeneous counterpart. At this stage, the effect of the segregation rate on this decrease of remains weak. However, an opposite behavior is observed for higher values of c, i.e, and , for which changes sign from positive to negative. In addition, the heterogeneities tend to increase the value of this speed component. This effect is intensified by the increase in and slightly impacted by the increase in the intensity of the heterogeneities. It should be noted that the normal flame front velocity, , is also decomposed into three contributions representing the effects of variations in (i) the diffusion coefficient, (ii) the density and (iii) the flame surface density. The latter is expressed as follows:
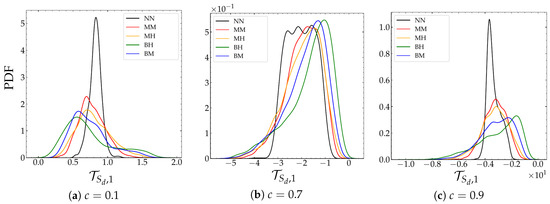
Figure 22.
Evolution of the PDF of the normal component of for three levels of the progress variable at .
A typical evolution of the , and contributions is shown in Figure 23a. Over the entire range of the flame brush, the amplitudes of the and contributions are comparable and of opposite signs. Thus, the effect of the term related to variations in surface density, , is the dominant contribution in the normal displacement speed. These features are also noticeable in the PDF of (see Figure 23b at iso-c level of ) which is similar to the PDF showed in Figure 22a. This result indicates also the predominance of flame surface density variation effects in the normal propagation of the flame.
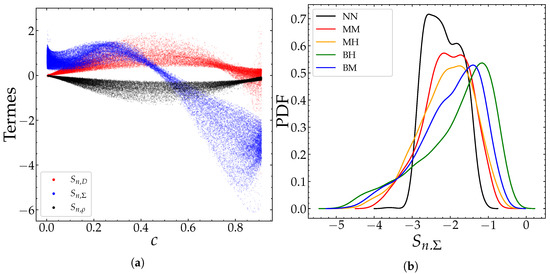
Figure 23.
(a) Illustration of the contributions relative to the variations in surface, density and diffusion,
in the normal displacement speed, for the case BH at . (b) PDF of the contribution related to the
variation of the flame surface density in the normal displacement speed on the isocontour c = 0.7.
In addition, a shift in the distribution of the mixture fraction towards lower values has been shown earlier (see Figure 7). The latter leads to a decrease in the propagation speed by reducing the reaction rates, particularly those of CO and CO2. Therefore, the presence of heterogeneities induces a decrease in the reactive component of the speed of displacement . We reiterate that this effect is more pronounced in large as can be seen from the results depicted in the Figure 24.
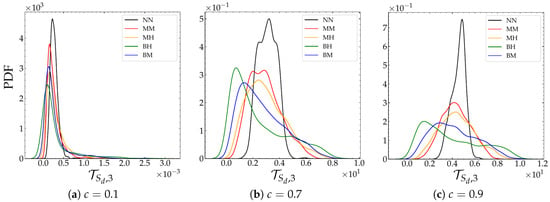
Figure 24.
Evolution of the PDF of the reactive component of the displacement speed for three levels of
the progress variable at .
Finally, in both the preheating and the burnt gases zones, the differential diffusion component has larger PDFs in the stratified flames than in the homogeneous case as shown in Figure 25. In addition, averaged values of tend to increase with the introduction of compositional heterogeneities, especially when their characteristic length scale is relatively large (see Figure 25). This trend, however, is not noticeable in the reaction zone, i.e., for .
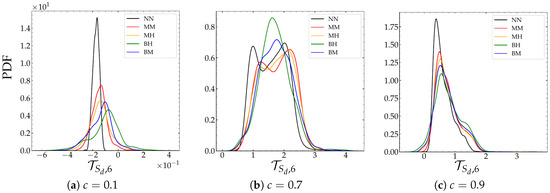
Figure 25.
Evolution of the PDF of the differential diffusion component of the displacement speed for
three levels of the progress variable at .
In summary, the analysis of the components of the displacement speed reveals that the impact of the heterogeneities is not only due to the reactive term, which in turn, is directly influenced by the composition distribution, but also through the differential diffusion and the flame surface density variations mechanisms. Moreover, we observe that (i) this influence becomes more intense as the characteristic length scale becomes larger and (ii) the characteristic length effect is more pronounced than the effect due to the segregation rate. Indeed, the measurement of the average deviations of these quantities from the homogeneous case along the entire flame brush quantifies this trend (see Figure 26).
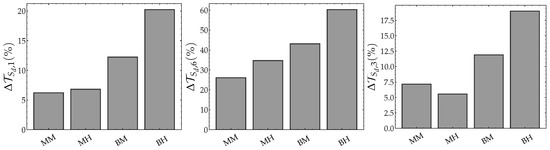
Figure 26.
Average relative deviations of the normal (left), reactive (right) and differential diffusion (middle) components from their homogeneous counterparts at .
5. Conclusions
In this work, a computational study of the effects of composition heterogeneities on the development and propagation of a premixed flame kernel was performed. A new two-dimensional DNS database considering homogeneous and heterogeneous flames in turbulent iso-octane/air flow was generated taking into account a representative chemical description with 29 species and 48 elementary reactions. To obtain converging statistics and consequently trends representative of the physical phenomena, a multiplication of DNS realizations was performed for each configuration. Moreover, this DNS database was designed in such a way that the dynamic effects of turbulence and the chemical effects related to combustion heterogeneities would initially be comparable. The motivation behind this choice was to characterize the propagation of the flame front subjected to the competition between the strengths of the turbulent structures and the fresh mixture composition heterogeneities. The DNS database analysis revealed that the mixture fraction distribution becomes globally skewed toward leaner mixture (with respect to the homogeneous case) when stratification is introduced. Indeed, the preferential propagation induced by the presence of heterogeneities leads to an accumulation of the lean zones in the vicinity of the flame front. Moreover, this distribution becomes broader as the characteristic length scale and the segregation rate increase. This effect is attributed to the fact that the mixing effect of the turbulent structures is less efficient in the presence of large-scale/high-gradient heterogeneities.
Since the preferential propagation leads to additional flame wrinkling and flame surface generation, the mechanisms governing the variations of the flame surface were also studied. The analysis showed that the composition heterogeneities broaden the curvature and strain distributions. However, this broadening effect does not alter the classical turbulent flame behaviors. For instance, the flame front elements (characterized by a positive curvature) tend to be rather convex in the directions of the fresh reactants. The property of the alignment of the convex (concave) flame front elements with the direction of the compression (expansion) was also found to be valid in the stratified cases although some slight changes in the intensity of this alignment were observed. These findings suggest that the additional surface generated by the composition heterogeneities operates, in the first order, through the propagation mechanism via the displacement speed.
Examination of the displacement speed showed that the distribution of on the flame front is more skewed towards smaller values compared to the homogeneous case. As a result, the introduction of heterogeneities leads to a slower overall flame propagation, and the deceleration becomes more intense at high . In particular, the width of the distribution of becomes greater as increases.
To assess the influence of the mixture stratification effects on the displacement speed, an analysis of the components of the latter was performed. It was found that the major contributions are (i) the diffusive, (ii) the normal propagation and (iii) the preferential diffusion terms. In fact, consideration of multi-species formalism without unitary Lewis hypothesis showed that the preferential diffusion term is not negligible and should, thus, be taken into account. One of the manifestations of the importance of this term is the fact that the budget equation of cannot be closed with such an approximation in the studied cases. Moreover, the presence of stratifications has a non-trivial influence on the preferential diffusion, showing that this term should be taken into account when modeling turbulent flame propagation in such mixtures. On the other hand, the reactive component of , which is its major component, is also skewed towards smaller values. This explains the fact that the stratified flames propagate more slowly than the homogeneous flame.
Finally, analysis of the components of the displacement speed revealed that the impact of the heterogeneities is not only due to the reactive term, which is, in turn, directly influenced by the composition distribution, but also due to the differential diffusion and flame surface density variation mechanisms.
Author Contributions
A.E.-r. and R.B., methodology, software, data curation, writing—original draft preparation; M.P., writing—original draft preparation, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Derivation of the Transport Equation from the Progress Variable
Assuming that the progress variables, c, are defined using the mass fractions of certain species present in the mixture, , and the mixture fraction, , yields
where is the set of species chosen to construct the progress variable, c, and is the mass fraction of the kth species at equilibrium. From this point onward, we adopt the following notation
From the term-to-term summation of the transport equation for the species contained in , we obtain
It is possible to express the transport equation of as
where
According to Equation (A1), the mass fraction can be considered as a function of c and , , which allows to express its total derivative as
By reorganizing this equation, the transport equation of c is expressed as follows:
Using Equation (A4), we can therefore write
The spatial derivatives of can also be decomposed into partial derivatives with respect to c and , i.e.,
so that we can rewrite the diffusive term of as follows,
where
Furthermore, the partial derivatives of with respect to c and can be expressed as
Therefore,
Thus, Equation (A8) can be re-written as
which we can also be reformulate with compact notation as
where
Thus, we have
and the transport equation of the progress variable can be written as
References
- Hall, D.; Pavlenko, N.; Lutsey, N. Beyond Road Vehicles: Survey of Zero-Emission Technology Options Across the Transport Sector; International Council on Clean Transportation: Washington, DC, USA, 2018; Volume 11, 22p. [Google Scholar]
- Macintosh, A.; Wallace, L. International aviation emissions to 2025: Can emissions be stabilised without restricting demand? Energy Policy 2009, 37, 264–273. [Google Scholar] [CrossRef]
- Heiser, W.H.; Pratt, D.T. Thermodynamic cycle analysis of pulse detonation engines. J. Propuls. Power 2002, 18, 68–76. [Google Scholar] [CrossRef]
- Zhao, F.; Lai, M.C.; Harrington, D.L. Automotive spark-ignited direct-injection gasoline engines. Prog. Energy Combust. Sci. 1999, 25, 437–562. [Google Scholar] [CrossRef]
- Cho, Y.S.; Santavicca, D.A. The Effect of Incomplete Fuel-Air Mixing on Spark-Ignited Flame Kernel Growth; Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 1993. [Google Scholar]
- Zeldovich, I.A.; Barenblatt, G.I.; Librovich, V.B.; Makhviladze, G.M. Mathematical Theory of Combustion and Explosions; Consultants Bureau: New York, NY, USA, 1985. [Google Scholar]
- Hélie, J.; Trouvé, A. Turbulent flame propagation in partially premixed combustion. In Proceedings of the Symposium (International) on Combustion, Monterey, CA, USA, 1–4 March 1998; Volume 27, pp. 891–898. [Google Scholar]
- Zhou, J.; Nishida, K.; Yoshizaki, T.; Hiroyasu, H. Flame Propagation Characteristics in a Heterogeneous Concentration Distribution of a Fuel-Air Mixture; Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 1998. [Google Scholar]
- Jiménez, C.; Cuenot, B.; Poinsot, T.; Haworth, D. Numerical simulation and modeling for lean stratified Propane-air flames. Combust. Flame 2002, 128, 1–21. [Google Scholar] [CrossRef]
- Haworth, D.; Blint, R.J.; Cuenot, B.; Poinsot, T. Numerical simulation of turbulent Propane-air combustion with nonhomogeneous reactants. Combust. Flame 2000, 121, 395–417. [Google Scholar] [CrossRef]
- Pera, C.; Chevillard, S.; Réveillon, J. Effects of residual burnt gas heterogeneity on early flame propagation and on cyclic variability in spark-ignited engines. Combust. Flame 2013, 160, 1020–1032. [Google Scholar] [CrossRef]
- Chevillard, S.; Michel, J.B.; Pera, C.; Réveillon, J. Evaluation of different turbulent combustion models based on tabulated chemistry using DNS of heterogeneous mixtures. Combust. Theory Model. 2017, 21, 440–465. [Google Scholar] [CrossRef]
- Pal, P.; Valorani, M.; Arias, P.G.; Im, H.G.; Wooldridge, M.S.; Ciottoli, P.P.; Galassi, R.M. Computational characterization of ignition regimes in a syngas/air mixture with temperature fluctuations. Proc. Combust. Inst. 2017, 36, 3705–3716. [Google Scholar] [CrossRef]
- Karimkashi, S.; Kahila, H.; Kaario, O.; Larmi, M.; Vuorinen, V. A numerical study on combustion mode characterization for locally stratified dual-fuel mixtures. Combust. Flame 2020, 214, 121–135. [Google Scholar] [CrossRef]
- Luong, M.B.; Hernandez Perez, F.E.; Sow, A.; Im, H.G. Prediction of ignition regimes in DME/air mixtures with temperature and concentration fluctuations. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 2241. [Google Scholar]
- Paolucci, S. Filtering of Sound from the Navier-Stokes Equations; Sandia National Laboratories: Livermore, CA, USA, 1982.
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion; R.T. Edwards Inc.: Morningside, Australia, 2005. [Google Scholar]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B.; Mayer, M.G. Molecular Theory of Gases and Liquids; Wiley: New York, NY, USA, 1954; Volume 26. [Google Scholar]
- Wilke, C.R. A viscosity equation for gas mixtures. J. Chem. Phys. 1950, 18, 517–519. [Google Scholar] [CrossRef]
- Mathur, S.; Tondon, P.K.; Saxena, S.C. Thermal conductivity of binary, ternary and quaternary mixtures of rare gases. Mol. Phys. 1967, 12, 569–579. [Google Scholar] [CrossRef]
- Gordon, S.; McBride, B.J. Computer Program for Calculation of Complex Chemical Equilibrium Compositions, Rocket Performance, Incident and Reflected Shocks, and Chapman-Jouguet Detonations; Technical Report SP-273; NASA Lewis Research Center: Cleveland, OH, USA, 1971.
- Réveillon, J.; Péra, C.; Bouali, Z. Examples of the potential of DNS for the understanding of reactive multiphase flows. Int. J. Spray Combust. Dyn. 2011, 3, 63–92. [Google Scholar] [CrossRef]
- Réveillon, J.; Demoulin, F.X. Effects of the preferential segregation of droplets on evaporation and turbulent mixing. J. Fluid Mech. 2007, 583, 273–302. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Wray, A.A. Minimal Storage Time Advancement Schemes for Spectral Methods; Technical Report; NASA Ames Research Center: Cleveland, OH, USA, 1990.
- Cohen, S.D.; Hindmarsh, A.C.; Dubois, P.F. CVODE, a stiff/nonstiff ODE solver in C. Comput. Phys. 1996, 10, 138–143. [Google Scholar] [CrossRef]
- Falgout, R.D.; Yang, U.M. HYPRE: A library of high performance preconditioners. In Proceedings of the International Conference on Computational Science, Amsterdam, The Netherlands, 21–24 April 2002; pp. 632–641. [Google Scholar]
- Cant, R.S.; Rutland, C.J.; Trouvé, A. Statistics for laminar flamelet modeling. In Proceedings of the Summer Program; Center for Turbulence Research: Stanford, CA, USA, 1990; pp. 271–279. [Google Scholar]
- Veynante, D.; Trouvé, A.; Bray, K.N.C.; Mantel, T. Gradient and counter-gradient scalar transport in turbulent premixed flames. J. Fluid Mech. 1997, 332, 263–293. [Google Scholar] [CrossRef]
- Rogallo, R.S. Numerical Experiments in Homogeneous Turbulence; Technical Report; NASA Lewis Research Center: Cleveland, OH, USA, 1981.
- Passot, T.; Pouquet, A. Numerical simulation of compressible homogeneous flows in the turbulent regime. J. Fluid Mech. 1987, 181, 441–466. [Google Scholar] [CrossRef]
- Réveillon, J. Numerical procedures to generate and to visualize flow fields from analytical or experimental statistics: Turbulent velocity, fluctuating scalars, and variable density sprays. J. Flow Vis. Image Process. 2005, 12, 251–269. [Google Scholar] [CrossRef]
- Hasse, C.; Bollig, M.; Peters, N.; Dwyer, H.A. Quenching of laminar iso-Octane flames at cold walls. Combust. Flame 2000, 122, 117–129. [Google Scholar] [CrossRef]
- Halter, F.; Foucher, F.; Landry, L.; Mounaïm-Rousselle, C. Effect of dilution by Nitrogen and/or Carbon dioxide on Methane and iso-Octane air flames. Combust. Sci. Technol. 2009, 181, 813–827. [Google Scholar] [CrossRef]
- Marshall, S.P.; Taylor, S.; Stone, C.R.; Davies, T.J.; Cracknell, R.F. Laminar burning velocity measurements of liquid fuels at elevated pressures and temperatures with combustion residuals. Combust. Flame 2011, 158, 1920–1932. [Google Scholar] [CrossRef]
- Goodwin, D.G.; Moffat, H.K.; Speth, R.L. CANTERA: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes; Version 2.2.1; Caltech: Pasadena, CA, USA, 2016. [Google Scholar]
- Lipatnikov, A.N. Stratified turbulent flames: Recent advances in understanding the influence of mixture inhomogeneities on premixed combustion and modeling challenges. Prog. Energy Combust. Sci. 2017, 62, 87–132. [Google Scholar] [CrossRef]
- Pasquier, N.; Lecordier, B.; Trinite, M.; Cessou, A. An experimental investigation of flame propagation through a turbulent stratified mixture. Proc. Combust. Inst. 2007, 31, 1567–1574. [Google Scholar] [CrossRef]
- Robin, V.; Mura, A.; Champion, M.; Degardin, O.; Renou, B.; Boukhalfa, M. Experimental and numerical analysis of stratified turbulent V-shaped flames. Combust. Flame 2008, 153, 288–315. [Google Scholar] [CrossRef]
- Anselmo-Filho, P.; Hochgreb, S.; Barlow, R.S.; Cant, R.S. Experimental measurements of geometric properties of turbulent stratified flames. Proc. Combust. Inst. 2009, 32, 1763–1770. [Google Scholar] [CrossRef]
- Sweeney, M.S.; Hochgreb, S.; Dunn, M.J.; Barlow, R.S. The structure of turbulent stratified and premixed methane/air flames I: Non-swirling flows. Combust. Flame 2012, 159, 2896–2911. [Google Scholar] [CrossRef]
- Pope, S.B. The evolution of surfaces in turbulence. Int. J. Eng. Sci. 1988, 26, 445–469. [Google Scholar] [CrossRef]
- Candel, S.M.; Poinsot, T.J. Flame stretch and the balance equation for the flame area. Combust. Sci. Technol. 1990, 70, 1–15. [Google Scholar] [CrossRef]
- Haworth, D.C.; Poinsot, T.J. Numerical simulations of Lewis number effects in turbulent premixed flames. J. Fluid Mech. 1992, 244, 405–436. [Google Scholar] [CrossRef]
- Hawkes, E.R.; Cant, R.S. Implications of a flame surface density approach to large eddy simulation of premixed turbulent combustion. Combust. Flame 2001, 126, 1617–1629. [Google Scholar] [CrossRef]
- Trouvé, A.; Poinsot, T. The evolution equation for the flame surface density in turbulent premixed combustion. J. Fluid Mech. 1994, 278, 1–31. [Google Scholar] [CrossRef]
- Bray, K.; Domingo, P.; Vervisch, L. Role of the progress variable in models for partially premixed turbulent combustion. Combust. Flame 2005, 141, 431–437. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).