Abstract
The region where the vascular lumen meets the surrounding endothelium cell layer, hence the interface region between haemodynamics and cell tissue, is of primary importance in the physiological functions of the cardiovascular system. The functions include mass transport to/from the blood and tissue, and signalling via mechanotransduction, which are primary functions of the cardiovascular system and abnormalities in these functions are known to affect disease formation and vascular remodelling. This region is denoted by the near-wall region in the present work, and we outline simple yet effective numerical recipes to analyse the near-wall flow field. Computational haemodynamics solutions are presented for six patient specific cerebral aneurysms, at three instances in the cardiac cycle: peak systole, end systole (taken as dicrotic notch) and end diastole. A sensitivity study, based on Newtonian and non-Newtonian rheological models, and different flow rate profiles, is effected for a selection of aneurysm cases. The near-wall flow field is described by the wall shear stress (WSS) and the divergence of wall shear stress (WSSdiv), as descriptors of tangential and normal velocity components, respectively, as well as the wall shear stress critical points. Relations between near-wall and free-stream flow fields are discussed.
1. Introduction
Biological systems are complex, often involving a multitude of coupled processes occurring at different scales, both spatially and temporally. When events such as diseases form, it is a challenging and daunting task to deconstruct the processes involved in identifying succinctly a relation and cause. The cardiovascular system is responsible for transport and signalling, thus linking cells throughout the body, and acting as a conduit. Cardiovascular diseases have benefited from intense research and the resulting important breakthroughs; however, they remain prevalent and a leading causes of mortality. A pathophysiology which has been the focus of much research is that of aneurysms, especially cerebral and abdominal. Aneurysms are largely asymptomatic, until they rupture, at which stage the risks of mortality or morbidity are very high. The task of unravelling the cause of aneurysm initiation, growth and rupture has developed immensely over recent decades, and while there are still many open questions it is widely accepted that the fluid mechanics plays an important role in all aneurysm stages.
The consensus is that the haemodynamics plays a determining role in cardiovascular diseases in large arteries [1,2,3,4], and both the mechanical and transport properties have been scrutinised. Simply put, an abnormal flow field, usually described as complex and disturbed (not necessarily turbulent flow), is often related to diseased states. The greatest attention has involved principally the fluid mechanics in the near-wall region, hence the flow field at or near the lumen boundary since it is in this region that the haemodynamics in effect interfaces with the body’s tissues. Measures such as wall shear stress (WSS) and spatial WSS gradients [5,6,7,8,9,10,11,12,13,14,15,16,17], aneurysm formation index (AFI) [18], oscillatory shear index (OSI) [19], gradient oscillatory number (GON) [20], transverse wall shear stress [21], viscous dissipation and kinetic energy [11], energy loss [22,23], helicity and vortical flow [24,25,26], among others [4,27], have all been used as correlators to diseases. There have also been efforts in characterising the vessel’s shape, since this is the no-slip boundary condition, together with the resulting fluid mechanics [22,28,29,30,31,32,33]. Means of recovering the no-slip boundary from flow data have also been proposed [34,35]. The fluid-structure interactions and constitutive models of the cerebral tissues have also been investigated [36,37], but even with the simpler rigid wall boundary condition one can also show that the spatial gradients of all shear stress would be expected to generate inter-cellular tension and shearing forces in the vessel tissue [38].
As a result of the many studies, often with limited cohort sizes, overall mean trends have emerged and have spurred various formulations for fluid mechanics correlators to disease [27]. However, when considering patient-specific studies with personalised results and conclusions, there is evident conflicting information and confusion as to how to post-process and extract meaningful information from the haemodynamic observables [4,39]. It is evident that one cannot singularly look at the haemodynamics as a indication of disease, and the mass transport [40,41], inflammation process [42,43], auto-regulation [44] and genetic factors [3], among others, must be ultimately incorporated in any analysis. While the problem is indeed multi-scale and multi-physics, the consensus that the haemodynamics plays a determining role in cardiovascular diseases in large arteries still remains.
In recent years, a novel analysis of the flow field at or near the lumen boundary was undertaken, based on observation from the wall shear stress field, its spatial gradients and temporal evolution. It was shown in [15] that the flow field at a small distance inside the free-stream domain can be recovered from the wall shear stress and its gradients, leading to further promising developments and interest in the field [16,45,46]. The methodology in effect revolves around a perturbation analysis (which has been previously explored in [47]) together with the realisation that: (i) the wall shear stress, which is the tangential component of the viscous traction exerted by the flow on the wall, can also be seen as the tangential component of the fluid velocity in the limit of the wall; (ii) the divergence of wall shear stress on the other hand is related to the normal component of the fluid velocity in the limit of the wall [15]. These works were further extended by considering Lagrangian Coherent Structures (LSC) [48] of the wall shear stress, and the time evolved partitioning of the flow, as well as investigating the effects of transport and diffusion in the near-wall region [45,46,49].
This is then the setting for the present paper. We do not aim to provide insight into the coupled and complex problem of cardiovascular diseases. Rather, since it is widely accepted that the haemodynamics does play an important role, we focus on providing an accessible means to better understand the fluid mechanics. From this, we can also develop a better appreciation of the lumen-endothelial interface, denoted by the near-wall region in the present work. In this region, mass transport to/from the blood and tissue, and signalling via mechanotransduction occurs. We will use the analysis proposed in [15] based on a Taylor expansion of the flow field, together with wall shear stress critical points, which are locations where the wall shear stress is zero, to recover dividing surface shear lines, which provide information about the flow partitioning at an instance in time [16,17]. The physical appreciation, as well as the numerical tools developed, are certainly valuable in studying cardiovascular and physiological flows in general, where the near-wall flow field is a defining factor. Additionally, we hope that the greater physical appreciation of the fluid mechanics will avoid the unfortunate disarray of metrics used to correlate fluids measures to disease [4,27,39]. In the present investigation, we apply the methodology to investigate the near-wall haemodynamics in cerebral aneurysms of six patient cases under pulsatile flow conditions.
While the patient cohort is limited, to investigate variability and sensitivity to flow conditions and modelling assumptions, we make use of different cardiac flow rate profiles, as well as both Newtonian and non-Newtonian rheological models. These results are tabulated in the Appendix A.
2. Materials and Methods
2.1. Patient Anatomies
In this work, the cohort size consists of six patient specific cases. The details of the cases are provided in Table 1. The datasets were presented as three-dimensional greyscale CTA images. The segmentation was performed in a semi-automatic manner, using first in-house tools for an automatic segmentation [50,51], and subsequently by manual correction using ITK-SNAP 3.6.0. The final segmentation and was verified against the medical images in a similar fashion as reported in [52], and by an experienced clinician.

Table 1.
Patient specific case information.
2.2. Simulation Setup
The domains were artificially truncated to exclude an extensive computational domain of cerebral vasculature. Effects to geometry truncation and pruning, as well as outflow boundary condition models, we investigated in previous work [53,54]. All sections were then extruded in the coaxial direction as a straight pipe, using Blender 2.79b, to ensure the flow is developed when reaching the aneurysm and is not sensitive to the artificial domain truncation. The extensions also allow for the flow to be coaxial, hence enter or leave the computational domain perpendicular to the boundary sections. The extruded lengths are 20 times the inlet diameter [55,56,57,58] and approximately 6 times the outlet diameter, at respective sections. The mesh at the no-slip boundary consists of eight prism layers, and within the aneurysm the average total thickness is 0.1 mm, and the height of the first prism layer was set to 0.005 mm. Polyhedral elements were used to generate the volume mesh in the free-slip region. The mesh is locally refined in the aneurysm region. This local mesh refinement resulted in a three-fold finer mesh within the aneurysm compared to the inlet/outlet sections, resulting in a average cell volume of mm. An example cross-section of the mesh for Case 1 is shown Figure 1. Due to varying volumes of the computational domain, the number of mesh elements varied between cases, ranging between ∼2.3–4 M elements, with an average of 3 M elements. Mesh convergence studies were performed based on the wall shear stress values, ensuring differences were below 5%.

Figure 1.
Cross-section through aneurysm of Case 1, showing details of the prism layers and polyhedral mesh.
Cerebral aneurysms are located inside the cranium, as a result of which there are typically small displacements in arterial lumen diameter during the cardiac cycle. Consequently, fluid-structure interaction effects are small, and in this work we have assumed the aneurysm wall to be rigid. A Standard boundary condition choice was adopted: no-slip boundary condition at the walls, zero pressure at outflows and a velocity profile was prescribed at inflow. The velocity profile was based on the work of [59], in which several cardiac flow rates for different patients are reported. Of these, the cardiac profile of Patient 5 was chosen for our simulations because of its close similarity with patient dataset we have used. To provide a sensitivity study, hence providing generality to our results and ensure better translation to the wider research community, the other cardiac profiles reported in [59] were also investigated for a selection of cases, and these results are reported in the Appendix A. The flow rate profiles are shown in Figure 2, and have approximately a 0.8 s duration. In order to adjust the shape of the curve to each aneurysms, the flow rate was scaled using Reynolds number of , based on the time average velocity and the inflow diameter. This Reynolds number was chosen as it presents a representative value for cerebral aneurysms, and is close to the ‘Patient 5’ dataset in [59]. Since the Reynolds number is fixed for all cases, which allows for direct comparison of the simulations, it however means that the flow rates are not the same for the cases. Each of the the profiles in Figure 2 is marked by three points, indicating approximately peak systole, end systole (in fact the dicrotic notch) and end diastole.
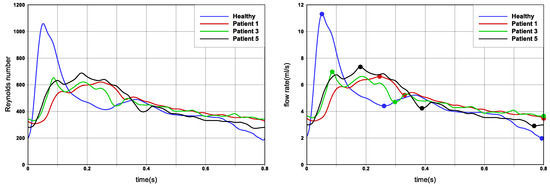
Figure 2.
Inflow profiles obtained from [59], based on four subject datasets. The profiles from [59] were scaled to have mean Reynolds number of 450, as shown in the left plot. The right plot shows the flow rate profile for Case 6. Please note that the flow rate profiles for each Case will differ, due to geometric differences, however the Reynolds number profiles are the same for all Cases. The cardiac time period is approximately 0.8 s for each profile. The flow rate profile is marked with time instances, which approximately relate to peak systole ( s), end systole (dicrotic notch) ( s) and end diastole ( s). Times in brackets are related to the waveform for Patient 5. Results of the numerical simulations are presented for these times.
STAR-CCM+13.04.010-r8 (Siemens) was used for both the mesh generation and the numerical simulations as a finite volume solver. The flow was assumed to be incompressible and unsteady. The SIMPLE algorithm, with inner iterations which results in an unsteady implicit scheme, was used for computing pressure and velocity fields in a segregated manner. The temporal and spatial schemes were second order accurate. The convergence criteria for the residual was set to be 10. The time step size was set to 0.001 s, therefore approximately 800 time steps per cardiac cycle. A total of ten heartbeats were simulated to avoid sensitivity to initial conditions, and only the last period was used in the presentation and analysis of the results.
2.3. Newtonian and Generalised Newtonian Model for Blood Rheology
In this work we consider blood as a continuum medium, and adopt both a Newtonian and a non-Newtonian rheology model for the viscous stresses. The density of blood was considered to be 1030 kg m. For the non-Newtonian model, we have chosen the Carreau generalised Newtonian fluid model. In this model, the stress tensor is given by , hence only a function of which is the shear rate and is calculated from the second invariant of the rate of strain tensor as , where is the rate of strain tensor. The viscosity is defined as
The coefficients adopted are taken from [60,61] and are based on experimental results and comparisons with other non-Newtonian models. These are Poi, Poi, s, . Constants were obtained by nonlinear least squares fit from viscosity data with Ht = 40% and T = 23 C, and extrapolated to T = 37 C.
In order to define an equivalent constant viscosity for a Newtonian model, we have followed [60] and computed the average experimental viscosity in the range s. Consequently for the Newtonian model, we have considered a kinematic viscosity of m s, hence a dynamics viscosity Poi.
Numerical simulations with the Carreau generalised Newtonian fluid model were run for Case 2, Case 3 and Case 6 for comparison purposes.
2.4. Methods for Analysing the Flow Field in the Near-Wall Region
We can write the wall shear stress in terms of the wall traction , where is the stress tensor and is the unit normal vector to the surface
Since wall shear stress acts tangentially to the wall, the stress tensor can be either the full stress tensor , or solely the extra stress tensor since pressure only acts normal to the surface.
The near-wall convective transport can be derived by Taylor expansion of a fluid element’s trajectory (in a moving reference frame) in the limit of wall [15]. In the limit of the wall, the tangential transport (in the plane of the wall) is given by the wall shear stress , while the normal transport is given by the divergence of the wall shear stress . Consequently, the fluid velocity at a small distance normal to the wall can be written as
where and are components of the velocity vector in the local wall tangent plane and normal, respectively. Similar expressions were also reported in other contexts [62,63,64,65,66,67,68]. In this work we will look at the wall shear stress () as our measure of near-wall tangential velocity component, and the divergence of wall shear stress () as our measure of near-wall normal velocity component, denoting these respectively by WSS and WSSdiv. Consequently, negative values of WSSdiv indicate flow towards the wall and postive values of WSSdiv indicates flow away from the wall.
Integration of the wall shear stress on the surface of the conduits results in surface shear lines, which are aligned with the tangential component of the viscous traction exerted by the flow on the wall. They indicate the limit in the direction of the flow velocity vector as the wall is approached, and are useful in describing the near-wall tangential flow, highlighting zones of attachment, separation, and critical points (where ).
Taking the wall shear stress as a planar two-dimensional vector field , one can compute the local instantaneous surface shear lines, hence describing locally the motion of the near-wall tangential flow. In order to derive these, we could perform a Taylor expansion as detailed in [16], or an alternative (but mathematically identical) approach would be to locally approximate the vector field to be linear. Denoting the wall shear stress vector field by and the local coordinate system by , we find
where matrix is the velocity gradient tensor
The set of equations can be seen as a linear system of ODEs, hence , or explicitly
whose solution involves either real or imaginary eigenvalues (, ):
In a two-dimensional vector field, there are five possible cases of solutions which are discussed in [69], with a corresponding discussion of existence of a unique critical point and degenerate cases. These are the local instantaneous streamlines, hence describing locally the motion of the flow [70,71]. In unsteady flow, the approximation in Equation (3) is applied at a moment in time, such that the solution trajectories (Equation (6)) correspond to particle paths, which do not generally coincide with streamlines except at an instant.
For clarity we will order the eigenvalues such that, if they are all real then , while if the solution comprises of a complex conjugate pair then . The corresponding unit eigenvectors are denoted by . The solution trajectories osculate the plane on the no-slip wall and the eigenvectors indicate the principal directions of motion of the flow locally. In the case of two real eigenvalues, the eigenvectors will indicate direction of dividing streamlines. In the case of a complex conjugate solution, the eigenvectors will indicate radii of rotation while the axis of swirl is that of the wall normal.
The ratio of the eigenvalues, if real will indicate the level of stretching and compressing of the flow along the eigenvectors, and if complex provide the spiralling compactness by , since from Equation (6) the time period of one revolution in the spiralling plane is given by [64,72]. Also, we note that the solution trajectories are exponential functions, and consequently two points initially located at a close distance will be separating (or converging, depending on the sign of the eigenvalues) at an exponential rate [48,64,73,74].
In the case that a critical point does exist from the solution Equation (6), the classification can be expressed (following [62]) as
We can evidently see that the unstable node/focus will result in a near-wall flow moving towards the wall (negative values of WSSdiv) and the stable node/focus will result in a near-wall flow moving away from the wall (positive values of WSSdiv).
Finally, in order to find the critical points, which are locations where we can rewrite the above linear system as
where are the critical points to be found.
2.5. Numerical Computation of the Near-Wall Flow
In practice, the wall shear stress field is assumed locally linear on piecewise linear mesh elements, hence consistent with the numerical scheme’s spatial interpolation. All analysis of critical points and computation of WSSdiv are therefore performed on an element-by-element basis. We briefly now present the numerical steps to compute these parameters.
Consider a piecewise linear triangle element on the no-slip boundary of the computational domain. Since the planar triangle element is embedded in a three-dimensional space, the first step involves creating a local coordinate system which preserves the triangle element shape, in which we denote the vertices of the triangle element by . We also note that the wall shear stress values are defined at the triangle vertices, and hence the local tangent plane at the vertex is not the same as the plane of the triangle element. The second step therefore involves projecting (using a simple inner product) the wall shear stress at each vertex onto the plane of the triangle element, denoting these by . Finally, we can write a linear system from Equation (3) as
This linear system can be solved for the unknown coefficient vector , and the critical points can then be found by rearranging Equation (8) as
One must then perform a check if the critical point lies within the triangle element, and a barycentric coordinate system is employed.
The computation of can also be computed on an element-by-element basis. Since each triangle element is piecewise linear, the spatial derivatives of any variable will be constant for that element. For each triangle element, in the local two dimensional coordinate system, we compute
Now, since the measure will be stored at the mesh vertices, and vertices belong to other mesh elements also, a simple averaging is finally performed, with constant weights since the mesh quality is locally nearly uniform.
Before presenting the results for the six patient cases, it is worth providing an example of the near-wall flow presented above. In Figure 3 we have traced the surface shear lines (surface integral of WSS) and the streamlines (volume integral of velocity), and plotted the WSS critical points. In the left plot, we see that even though points are traced from a set of seed points initially in close proximity, as the streamlines move away from the surface their trajectories are then defined by the free-stream flow, which cannot be represented by the near-wall flow field. In the middle and right plots, corresponding respectively to a stable focus (with positive WSSdiv) and unstable node (with negative WSSdiv), we can visually appreciate the physical meaning behind the above presentation of the near-wall flow. These examples also elucidate how effective the techniques outlined are at deconstructing and analysing the near-wall flow field, and how this then relates to the free-stream flow field. Further examples of streamlines configurations in the vicinity of wall shear stress critical points can be found in works including [47,64,67,75,76].

Figure 3.
Detail of surface shear lines, instantaneous streamlines and wall shear stress critical points. Wall shear stress critical points are marked by coloured dots, such that green indicates a focus, hence complex conjugate pair solution, blue indicates a saddle or node, hence real solution, and red are locations a small distance along the eigenvectors (hence principal directions of dividing surface shear lines), see Equation (6). Left plot: solution for Case 1 at time = 0.181 s; velocity streamlines are coloured blue if originating near a focus WSS critical point, and red if originating near a saddle/node WSS critical point. Middle plot: detail of stable focus, showing how the flow moves in a spiral manner in the plane of the wall, gradually moving away from the wall. The red streamline indicates the spiralling core. We observe an interaction with the free-stream flow soon after, the vortex compresses before stretching again and continuing further into the aneurysm. Right plot: detail of an unstable node, showing how flow impinges on the wall and spreads out. The red streamline ends at the stagnation point. Red dots indicate direction of principal axes (the eigenvectors) on one side only of the critical point.
3. Results and Discussion
Results of the simulations, with a Newtonian viscosity model and inflow flow rate boundary condition for Patient 5 (see Figure 2), are presented in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 at three instances in the cardiovascular cycle representing peak systole, end systole (dicrotic notch) and end diastole. In these figures, the wall shear stress critical points are marked by coloured dots, such that green indicates a focus, hence complex conjugate pair solution (spiralling motion), blue indicates a saddle or node, hence real solution, and red are locations a small distance along the eigenvectors (hence principal directions of dividing surface shear lines). It is apparent that the near-wall flow field is very complex for all cases, though some particularly so such as Case 3, while others are simpler such as Case 2. We observe that the WSSdiv patterns, which describes the normal component of the velocity, tends to be more stable than the WSS, which describes the horizontal component of the velocity. This was also reported in [16].
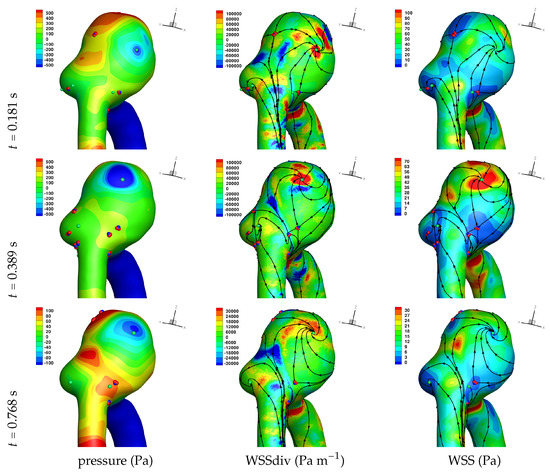
Figure 4.
Solution for Case 1. Plots of surface shear lines and WSS critical points (colouring scheme as in Figure 3).
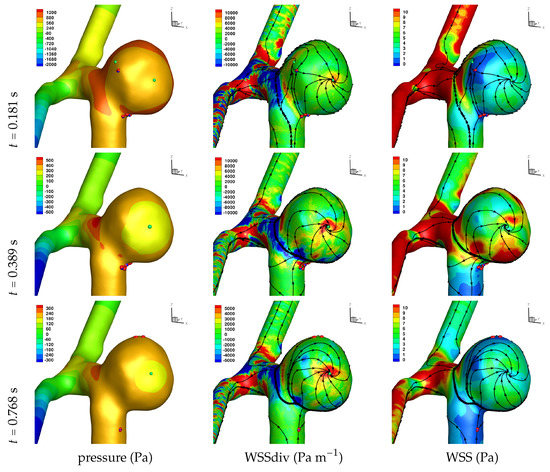
Figure 5.
Solution for Case 2. Plots of surface shear lines and WSS critical points (colouring scheme as in Figure 3).
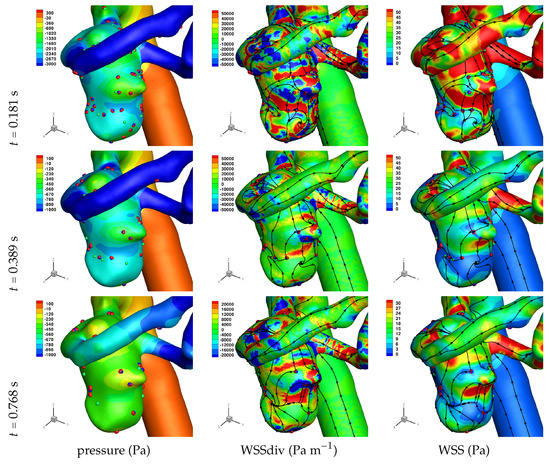
Figure 6.
Solution for Case 3. Plots of surface shear lines and WSS critical points (colouring scheme as in Figure 3).
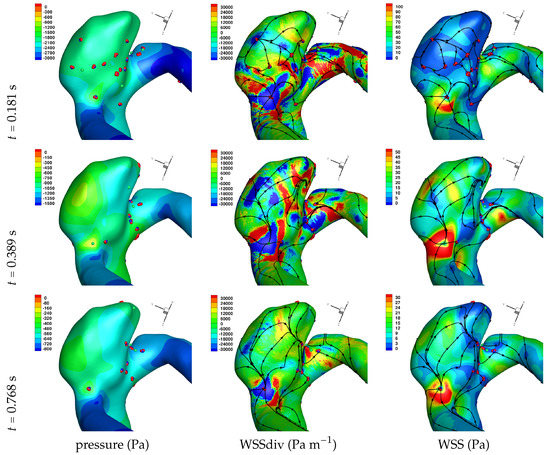
Figure 7.
Solution for Case 4. Plots of surface shear lines and WSS critical points (colouring scheme as in Figure 3).
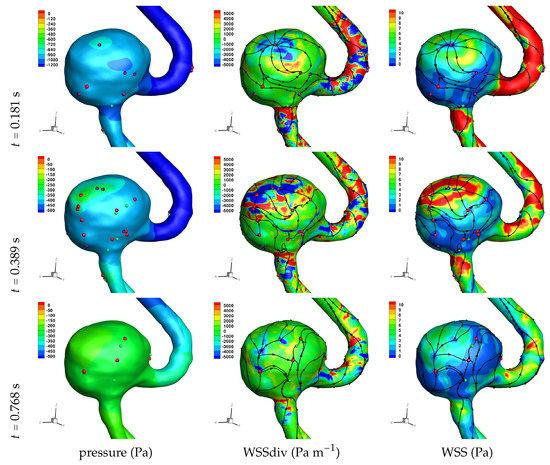
Figure 8.
Solution for Case 5. Plots of surface shear lines and WSS critical points (colouring scheme as in Figure 3).
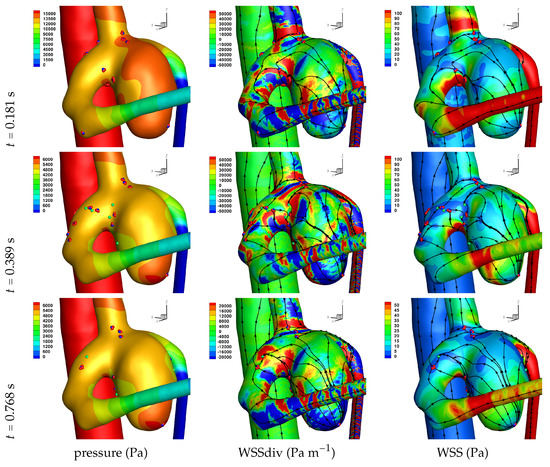
Figure 9.
Solution for Case 6. Plots of surface shear lines and WSS critical points (colouring scheme as in Figure 3).
A common feature to most cases is that of a persistent focus, which is present throughout the cardiac cycle. In Table 2 the strongest persistent focus is reported, based on WSSdiv magnitude, throughout the three instances of the cardiac cycle. When present, these anchored (on the no-slip wall) vortices help stabilise the flow within the aneurysm. For Case 4 there is no evident persistent focus, while for Case 6 (Newtonian rheology) the focus appears only in the decelerating phase of the cardiac cycle. These focii are located in a region of positive WSSdiv, and hence indicate the near-wall flow is moving away from the wall. This is also identifiable by the negative sign of the real component of the complex eigenvalue pair which form the solution (see Equation (6)), indicating these are stable focii. Consequently, the flow moves from the near-wall region into the main free-stream flow, along a vortex which is anchored at the wall. If we take as example Case 1, at time 0.181 s, from Table 2 we have WSSdiv = 420,000 Pa m and can approximate the normal velocity component at a distance using Equation (2): for m then m s, and for mm then m s, highlighting that these vortices are indeed comprised of fast moving flow. The spiralling compactness () is also reported in Table 2, and the observed general trend is a reduction (or negligible change) in spiralling compactness between peak systole and end diastole. For high values of spiralling compactness, there is a rapid motion to the focus centre without many rotations about the centre, while a zero spiralling compactness indicates purely circular motion about the centre with no radial change [72]. As one would expect from physical principles, we observe similar trends in positive WSSdiv and negative . The magnitude of the negative indicates the attractor strength of the stable focus, and since mass in conserved, as the flow approaches the focus it must also move away from the wall with a positive WSSdiv, at a similar rate.

Table 2.
Results for the strongest (based on maximum |WSSdiv|) persistent focus critical point located within the aneurysm. Note: for Case 4 no persistent focus critical point was present and hence different points are reported; for Case 6 the persistent focus critical point only appeared from end systole to end diastole. The total number of critical points within the aneurysm are also reported at each time instance (right column). Units: WSSdiv (Pa m), WSS (Pa). Results are presented to three significant figures.
The number of critical points within the aneurysm are also reported in Table 2. We observe an overall trend of a decrease in number, between peak systole and end diastole, however at end systole both an increase and decrease are observed. The reason for this is that at end systole there is a deceleration of the flow, which will require dissipation, and commonly this results in eddy formation. This consequently affects the near-wall flow field as vorticity is generated at the wall and is diffused and transported into the free-stream flow field. While one should not confuse vorticity (hence angular velocity) with eddies, this simplified description of the process is useful here. The question then is at what stage of the overall dissipation due to deceleration does the end systole time instance lie. This will be case dependent, as the aneurysm shape and flow field will affect this. We in fact see that for some cases the number of critical points has increased, which suggests significant eddy motion within the aneurysm is still present at this time, while for other cases there is a decrease in number of critical points, which suggests that the deceleration of the flow has largely already occurred, though there is a further reduction in number of critical points by the end diastole stage. The decrease in spiralling compactness of the strongest persistent focus critical point during the deceleration phase of the cardiac cycle, supports this discussion of increased eddy motion as a dissipation mechanism. It is also interesting to observe the shear rate magnitude () through the cardiac cycle, since viscosity diffuses momentum by means of the rate of strain tensor (D), and results for Case 3 and 6 are shown respectively in Figure 10 and Figure 11. From these we observe a decrease in shear rate from peak systole through to end diastole for Case 3, however for Case 6 we observe an increase in shear rate from peak systole to end systole and then a subsequent decrease at end diastole. This trend is similarly seen in the number of critical points from Table 2.
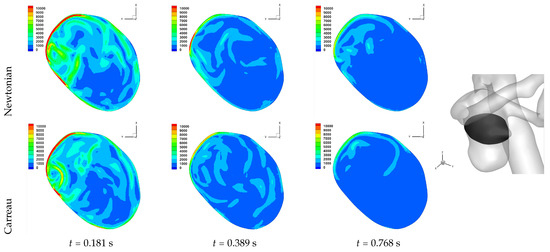
Figure 10.
Cross-section plots of shear rate magnitude (s) of Case 3, for Newtonian and Carreau rheological models. Location of the cross-section is shown.
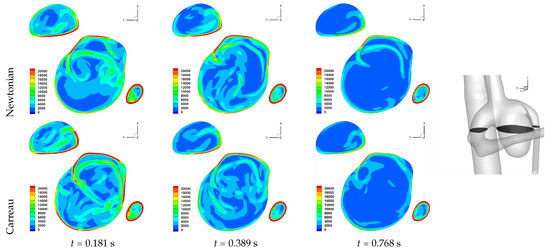
Figure 11.
Cross-section plots of shear rate magnitude (s) of Case 6, for Newtonian and Carreau rheological models. Location of the cross-section is shown.
An aneurysm’s surface area can been partitioned based on the near-wall flow field characteristics, and results are presented in Table 3. We should first highlight that while partitioning the aneurysm surface by values of WSS and WSSdiv, the values of WSS and WSSdiv at a given point are uncorrelated, as previously reported in [15]. The reason for the lack of correlation is due to the fact that they describe fluid motion in mutually orthogonal directions. In order to investigate the nature of the near-wall flow field for each aneurysm, we have chosen the threshold values of WSS = 1 Pa and WSSdiv = ±1000 Pa m based on previous work [15]. The WSS = 1 Pa threshold is widely used to indicate propensity for disease [4]. The different near-wall flow regimes covered in Table 3 are listed here again for clarity, together with the shorthand notation adopted.

Table 3.
Percentage area of aneurysm which satisfies conditions on WSS and WSSdiv. WSS < 1 suggests slow tangential flow (→), WSS > 1 suggests faster tangential flow (⇉), WSSdiv < −1000 suggests fast perpendicular flow to the wall (⇊), WSSdiv > 1000 suggests fast perpendicular flow from the wall (⇈), |WSSdiv| < 1000 suggests slow flow perpendicular to the wall (⇵). The partitioning of the area is based on the underlying discrete surface mesh, the vertices of which hold the function values. If any vertex of a mesh element did not satisfy the partitioning criteria, it was not included. Consequently the sum of the areas in the rows does not add to 100%, as we have in effect also excluded partial perimeters to the partitioned regions. This does not affect the analysis. Units: WSSdiv (Pa m), WSS (Pa). Results are presented to two decimal places.
- WSS < 1 Pa suggests slow tangential flow, (→)
- WSS > 1 Pa suggests faster tangential flow, (⇉)
- WSSdiv < -1000 Pa m suggests fast perpendicular flow to the wall, (⇊)
- WSSdiv > 1000 Pa m suggests fast perpendicular flow from the wall, (⇈)
- |WSSdiv| < 1000 Pa m suggests slow perpendicular flow, (⇵)
We observe that a threshold of WSS = 1 Pa biases the results to lie in the WSS > 1 Pa regions, except for Case 5 which is a large scaccular basilar aneurysm. From Equation (2) we can approximate the tangential velocity component for WSS = 1 Pa, and for m we have m s, and for mm we have m s. Given these approximations of very low near-wall tangential flow, it is worth reconsidering the various WSS thresholds associated with diseases reported in the literature [4].
While a value of m s at mm is indeed not negligible so close to the wall, the values reported above for the normal component of the velocity for a persistent strong focus at the same distance is m s, which is clearly substantially larger. At the smaller distance of m, the normal and tangential components of velocity for a strong persistent vortex and what is considered to be a slow tangential flow, are now similar. The discrepancy in magnitude of and at larger arises from the approximation of and , from which we can see the influence of the order of . These equations are the leading order terms of a Taylor expansion, and it may be beneficial to include higher order terms to match the order of .
Let us return to Table 3, and focus on the associated percentage aneurysm area for WSS > 1 and |WSSdiv| > 1000, hence for the more prevalent situations occurring within the aneurysm dome. We observe that for WSSdiv < −1000 the trend is a decrease in percentage area, from peak systole to end systole and then to end diastole. On the other hand we observe that for WSSdiv > 1000 the trend is an increase in percentage area between peak systole and end systole, and then a decrease between end systole and end diastole. The reasons for this are as follows. During the deceleration of the fluid (from peak systole to end diastole), we expect a decrease in magnitude of flow impingement on the wall, hence less observed percentage area for WSSdiv < −1000. Also, during the deceleration phase, we typically have an increase in eddying motion in order to diffuse momentum, and since the focii critical points tend to be of stable type, hence locations of positive WSSdiv, we observe the increase in percentage area with WSSdiv > 1000 from peak systole to end systole. By the time we reach end diastole the flow has further decelerated and diffused much of the momentum, consequently the eddying motion has decreased and so has the number of stable focii, resulting in less percentage area associated with WSSdiv > 1000.
Let us now consider the average values of WSSdiv when WSS < 1 Pa and WSS > 1 Pa, as presented in Table 4. We note that the average values of negative WSSdiv (near-wall flow moving to the wall) are greater in magnitude than the counterpart positive WSSdiv (near-wall flow moving away from the wall). This is due to the fact that flow moving to the wall will have higher momentum, and hence velocity (we are assuming constant density). This fluid volume will subsequently run along the wall before moving away again, decreasing its momentum by means of the viscous forces during this trajectory. In this table, and from the plots shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, we observe that some aneurysms exhibit higher WSS and average WSSdiv magnitude, namely Case 1, Case 3 and Case 6, and the reason for this is not apparent based on the geometric characterisations presented in Table 1, nor from qualitative analysis. One therefore needs to investigate the entire flow field to understand how the fluid is entering the aneurysm, promoting the large near-wall WSSdiv and WSS values observed. For near-wall transport both to and from the wall, the average WSSdiv magnitude drops between peak systole and end diastole due to the flow having decelerated, but it typically increases at end systole, indicating a higher transfer between free-stream and near-wall regions.

Table 4.
Average values of WSSdiv as partitioned by WSS = 1 threshold. Only the aneurysm surface is considered. Units: WSSdiv (Pa m), WSS (Pa). Results are presented to three significant figures.
We now report on the effects of rheology, between Newtonian and Carreau generalised Newtonian models, for Case 2, Case 3 and Case 6. Overall we do not observe marked changes in patterns of WSS and WSSdiv, indicating that the free-stream flow field is unlikely to have altered considerably also. This has been reported in previous works [54,60]; namely that in large artery haemodynamic the non-Newtonian rheological models do not affect the flow field and the wall shear stress field significantly, and variations in boundary conditions (inflow/outflow, no-slip domain) have a greater effect.
In Table 2 we observe the same trends as discussed above if the Carreau model is adopted. We also observe greater and WSSdiv for results with the Carreau model in comparison to the Newtonian model, indicating faster flow leaving the wall at the strongest persistent focus critical point, and in general either no significant change or an increase in the number of critical point. These are seen throughout the cardiac cycle.
In Table 3 we see that there is no pronounced change in the percentage area covered by the WSS and WSSdiv partitions if the Newtonian or the Carreau model is adopted. On closer inspection we do observe a general modest increase in the percentage area covered by WSS > 1 Pa and WSSdiv < −1000 Pa m (i.e., non-stagnant flow moving to the wall). In fact there is also a general increase in the percentage area covered by WSS > 1 Pa and WSSdiv > 1000 Pa m (i.e., non-stagnant flow moving from the wall), but to a lesser extent. The Carreau model adopted is a shear thinning model, and since we can in general expect higher shear rates closer to the walls, we would have a lower apparent viscosity close to the no-slip domain. This will lead to smaller boundary layers, hence effectively bringing the far field free-stream flow closer to the no-slip wall. Additionally, as the flow moving to the wall has higher momentum (as indicated in Table 4) since it comes from the faster flowing free-stream domain, as it encounters the rigid wall with no-slip condition the fluid will be subjected to higher strain rates. Now, since the flow moving towards the wall is subjected to higher strain rate it will correspondingly have lower viscosity if the shear-thinning non-Newtonian model is used, and as such it will also flow less inhibited and cover a larger surface area. These may be some of the reason for the modest increase in observed flow moving to the wall, which interestingly occurs throughout the cardiac cycle. Similar reasoning can be applied for the flow moving away from the wall, though the flow has lost some of its momentum by means of viscosity during its near-wall trajectory (involving approaching the wall, moving along it, and finally moving away from it), and will consequently have a lower shear rate magnitude and the apparent viscosity will be more similar to the Newtonian value. Results for a cross-section of the domain near a set of unstable node critical points provide a visual aid in understanding the above discussion, as shown in Figure 12. We note the higher shear rate magnitude in the non-Newtonian solution, as well as the wider extent of the velocity moving to the wall, as compared to the Newtonian solution.
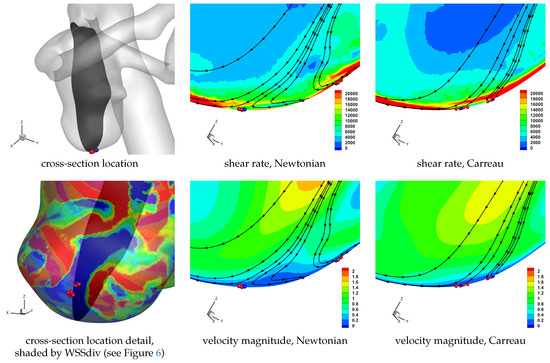
Figure 12.
Detail of aneurysm dome for Case 3 at s. Cross-section location and selection of unstable node critical points are shown in left column. Detail of cross-sections present a snapshot of in-plane velocity streamlines, with plots of velocity magnitude and shear rate magnitude, for Newtonian and Carreau rheological models.
In Table 4 we again observe the same trends as discussed above if the Carreau model is adopted. The differences between shear-thinning and constant viscosity models reported in Table 4 suggest a general reduction (or effectively unaltered) magnitude of average WSSdiv throughout the cardiac cycle. As discussed above, the higher shear rates are expected to occur at the no-slip domain, resulting in a reduced apparent viscosity at the wall for the Carreau model, allowing the fluid to flow more easily. This will allow the flow to align tangentially to the wall more easily, resulting in a lower magnitude of near-wall normal velocity. This is also observed in Figure 12.
The results presented thus far have considered a limited cohort of six patient cases, a single Reynolds number to define the flow regime, and two rheological models. To generalise the results, allowing for greater robustness of the findings and easier translation to other patient cases, we have also undertaken simulations for different cardiac profiles as shown in Figure 2 for Case 2, Case 3 and Case 6. The results of these simulations have been tabulated in a similar fashion to the results discussed above, and can be found in the Appendix A in Table A1, Appendix A in Table A1, Table A2 and Table A3. Without providing detailed discussion, we summarise the main findings. On changing the inlet flow rate profiles, the flow field has also noticeably changed and the values reported can be seen to differ considerably from those in Table 2, Table 3 and Table 4. The trends between peak systole, end systole and end diastole however still hold, with the ‘Healthy’ flow rate profile (see Figure 2) reporting the greatest deviation in trends. The ‘Healthy’ flow rate profile exhibits greater acceleration and deceleration phases, as compared to the ‘Patient’ cases. Please note that since the flow field has changed, the strongest persistent focus critical point reported in Table A1 will not be the same as in Table 2, and hence a direct comparison of values is not meaningful.
4. Conclusions
In this paper, we have presented simple, yet effective means to describe the near wall-flow field, as velocity components tangential to the wall or perpendicular to it, based on previous work [15]. These velocity components are effectively proportional to the wall shear stress (WSS) and the divergence of wall shear stress (WSSdiv), respectively. The tangential velocity component (hence WSS) is then further analysed to observe the local instantaneous surface shear lines, including locations of critical points and the principal directions of motion at these points, based on previous work [16]. This physically meaningful description, the mathematical tool set developed and simple numerical formulations, together provide the means to efficiently deconstruct the near-wall flow field, in a computationally inexpensive manner. These measures are not intended to substitute the existing correlators to disease [4,11,27,49], but rather they complement those findings and provide a simple and practical means of observing the near-wall flow field.
The analysis of the near-wall flow field was performed on six cerebral aneurysms. Unsteady numerical simulations of the haemodynamics were effected, and the aneurysm wall was partitioned into regions based on the the magnitude and direction of the tangential and perpendicular velocity components. Changes in the percentage surface area covered by the different regions, together with the average WSSdiv within each partition, were reported during the cardiac cycle at peak systole, end systole and end diastole. The WSS critical points were also analysed during the cardiac cycle, with respect to their type, the relative numbers and the persistence of the strongest stable focus. Together these provide extensive detail into the dynamics of the near-wall flow, and overall trends between the six patients cases analysed can be seen, and importantly the outliers also. Flow deceleration during the cardiac cycle promotes the formation of eddies as a momentum dissipation mechanism, and the effects of this are evident in the near-wall flow field, with an increase in WSS critical points, changes in percentage area associated with a flow characteristic and in mean WSS and WSSdiv values.
A comparison of Newtonian versus non-Newtonian rheological models was carried out on three aneurysms. The results indicate a very modest changes in the near-wall velocity field. Higher shear rate magnitude at the wall leads to lower effective viscosities at the near-wall region, resulting in smaller boundary layers, as well as flow aligning more readily to the no-slip wall tangent plane.
Since WSSdiv and WSS are related to orthogonal components of the near-wall velocity, they provide independent forms of information. The current literature on cardiovascular research commonly makes use of WSS and derived measures (such as: time averaged wall shear stress, residence times, oscillatory motion), however this only covers information of the near-wall tangential velocity, and it is certainly worth including WSSdiv in the analysis in order to describe the near-wall perpendicular velocity. This physical understanding of the measures provides greater insight into how to analyse and develop a better understanding of disease occurrence and progression.
In [45,46,49] the analysis of the near-wall flow was incorporated with the analysis method of Lagrangian Coherent Structures (LCS) in the context of cardiovascular flows. This time-evolved partitioning of the flow, together with the effects of transport and diffusion in the near-wall region, does indeed provide additional physically motivated information, important in understanding the near-wall flow field. Interestingly however, it was shown in these works that the near-wall flow LCS in fact showed good correlation to the WSS critical points of a time-averaged WSS field. Therefore, even with the simple methods outlined in this work one can obtain insight into time-evolved results, by simply performing a time average WSS and WSSdiv field to analyse.
A sensitivity analysis was carried out to quantify the error and its propagation through the data analysis. Six patient specific cases were investigated, adopting a Newtonian viscosity model and an inlet flow rate profile (‘Patient 5’, Figure 2). Additionally, three Cases were selected for further investigation, including using a shear-thinning non-Newtonian model for viscosity and three further flow rate profiles (also shown in Figure 2). Overall, similar general trends were reported, for three time instances in the cardiac cycle. The difference between Newtonian and non-Newtonian rheological models was not as marked as when changing the flow rate waveform. The ‘Healthy’ flow rate profile reported the greatest difference in computed solution. This sensitivity study provides greater robustness of the findings and easier translation to other patient cases.
We expect the methods outlined in the paper to be directly transferable to other problems where the near-wall region plays an important role, acting effectively as interface domain between wall and free-stream fluid. This is common in biological and physiological flows, where mass transport and signalling are important phenomena.
Author Contributions
Conceptualization, A.M.G.; methodology, A.M.G., V.G.A. and X.T.; validation, R.P., V.G.A. and I.V., formal analysis, A.M.G., V.G.A. and X.T.; investigation, A.M.G., V.G.A. and X.T.; resources, A.M.G., J.T. and R.P.; data curation, V.G.A., R.P., A.M.G. and J.T.; writing–original draft preparation, A.M.G.; writing–review and editing, A.M.G.; visualization, A.M.G., V.G.A., and X.T.; supervision, A.M.G. and J.T.; project administration, A.M.G. and J.T.; funding acquisition, A.M.G., J.T., A.S. and R.P.
Funding
This research was funded by University of Bristol though Ph.D. scholarships; Fundação para a Ciência e a Tecnologia (FCT) through the project UID/Multi/04621/2013 and scholarship SFRH/BD/90339/2012.
Acknowledgments
Vahid Goodarzi Ardakani gratefully acknowledges support from the University of Bristol to carry out his Ph.D. studies. The authors would also like to thank Centro Hospitalar e Universitário de Coimbra for the medical data, and the University of Bristol for the computer resources. The work of Iolanda Velho, Jorge Tiago and Adelia Sequeira has been partially supported by FCT—Fundação para a Ciência e a Tecnologia, through the project UID/Multi/04621/2013 of CEMAT—Center for Computational and Stochastic Mathematics, Instituto Superior Técnico of the University of Lisbon. Iolanda Velho has been supported by FCT scholarship SFRH/BD/90339/2012.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WSS | Wall shear stress—indication of near-wall flow in the plane of the wall |
| WSSdiv | Divergence of wall shear stress—indication of near-wall flow normal to the wall |
Appendix A. Tabulated Results for Different Flow Rate Profiles

Table A1.
Continuation of Table 2, for Case 2, Case 3 and Case 6 with flow rate profiles shown in Figure 2.
| Time (s) | WSSdiv | Num. Critical Points | ||||
|---|---|---|---|---|---|---|
| (Strongest Persistent Focus Critical Point) | (Node/Saddle)-(Focus) | |||||
| 0.051 | - | - | - | - | 9-0 | |
| Case 2 | 0.261 | −2200 | 3170 | −0.70 | 4260 | 10-1 |
| Healthy | 0.794 | −7910 | 5880 | −1.34 | 17,000 | 3-1 |
| Carreau | 0.051 | −3810 | 2430 | −1.57 | 6900 | 7-2 |
| Case 2 | 0.261 | −6990 | 3160 | −2.21 | 14,800 | 8-4 |
| Healthy | 0.794 | −9630 | 7420 | −1.30 | 19,300 | 7-3 |
| 0.246 | −11,200 | 7550 | −1.49 | 20,700 | 3-2 | |
| Case 2 | 0.330 | −12,500 | 8610 | −1.46 | 25,000 | 4-1 |
| Patient1 | 0.800 | −8770 | 7450 | −1.18 | 20,200 | 3-1 |
| 0.086 | −7750 | 5440 | −1.42 | 14,100 | 3-2 | |
| Case 2 | 0.298 | −22,100 | 9300 | −2.38 | 49,500 | 4-1 |
| Patient3 | 0.800 | −9340 | 4490 | −2.08 | 17,100 | 3-1 |
| 0.051 | −650,000 | 304,000 | −2.14 | 1,220,000 | 92-23 | |
| Case 3 | 0.261 | −90,800 | 49,300 | −1.84 | 144,000 | 44-12 |
| Healthy | 0.794 | −4200 | 2990 | −1.40 | 9040 | 35-7 |
| 0.246 | −119,000 | 70,600 | −1.69 | 243,000 | 82-19 | |
| Case 3 | 0.330 | −139,000 | 56,800 | −2.44 | 232,000 | 65-20 |
| Patient1 | 0.800 | −28,800 | 1440 | −2.00 | 60,500 | 44-11 |
| 0.086 | −81,200 | 37,500 | −2.17 | 145,000 | 67-16 | |
| Case 3 | 0.298 | −45,700 | 10,900 | −4.18 | 88,300 | 44-13 |
| Patient3 | 0.800 | −36,800 | 8570 | −4.3 | 95,900 | 37-10 |
| 0.051 | −689,000 | 768,000 | −0.90 | 998,000 | 37-10 | |
| Case 6 | 0.261 | - | - | - | - | 27-3 |
| Healthy | 0.794 | −104,000 | 59,600 | −1.75 | 195,000 | 19-4 |
| 0.246 | −317,000 | 117,000 | −2.71 | 608,000 | 42-5 | |
| Case 6 | 0.330 | −111,000 | 61,100 | −1.82 | 228,000 | 31-5 |
| Patient1 | 0.800 | −45,800 | 48,600 | −0.94 | 101,000 | 20-5 |
| 0.086 | −105,000 | 54,600 | −1.93 | 185,000 | 16-1 | |
| Case 6 | 0.298 | −46,100 | 27,600 | −1.67 | 96,800 | 27-3 |
| Patient3 | 0.800 | −104,000 | 111,000 | −0.93 | 184,000 | 13-4 |

Table A2.
Continuation of Table 3, for Case 2, Case 3 and Case 6 with flow rate profiles shown in Figure 2.
| Time (s) | WSS < 1 | WSS > 1 | ||||||
|---|---|---|---|---|---|---|---|---|
| WSSdiv < −1000 | |WSSdiv| < 1000 | WSSdiv > 1000 | WSSdiv < −1000 | |WSSdiv| < 1000 | WSSdiv > 1000 | |||
| (→ ⇊) | (→ ⇵) | (→ ⇈) | (⇉ ⇊) | (⇉ ⇵) | (⇉ ⇈) | |||
| 0.051 | 0.37 | 21.43 | 1.34 | 14.05 | 41.90 | 9.48 | ||
| Case 2 | 0.261 | 0.16 | 0.80 | 0.80 | 32.20 | 11.57 | 38.97 | |
| Healthy | 0.794 | 0.40 | 1.83 | 0.64 | 21.43 | 31.38 | 27.99 | |
| Carreau | 0.051 | 0.41 | 4.70 | 0.83 | 26.59 | 25.14 | 28.63 | |
| Case 2 | 0.261 | 0.18 | 0.26 | 0.77 | 32.45 | 12.14 | 39.98 | |
| Healthy | 0.794 | 0.42 | 4.99 | 1.73 | 24.81 | 29.48 | 25.93 | |
| 0.246 | 0.00 | 0.00 | 0.09 | 29.35 | 7.61 | 46.80 | ||
| Case 2 | 0.330 | 0.00 | 0.03 | 0.63 | 33.10 | 7.66 | 41.98 | |
| Patient1 | 0.800 | 0.82 | 4.83 | 1.75 | 21.25 | 29.79 | 25.20 | |
| 0.086 | 0.90 | 3.24 | 0.56 | 20.70 | 36.07 | 20.98 | ||
| Case 2 | 0.298 | 0.30 | 0.21 | 0.72 | 31.75 | 8.91 | 40.98 | |
| Patient3 | 0.800 | 0.99 | 5.93 | 1.33 | 21.05 | 27.28 | 27.18 | |
| 0.051 | 0.05 | 0.00 | 0.01 | 39.77 | 0.10 | 47.32 | ||
| Case 3 | 0.261 | 0.93 | 0.35 | 0.52 | 38.88 | 1.82 | 43.26 | |
| Healthy | 0.794 | 0.15 | 3.65 | 2.31 | 26.20 | 11.36 | 39.83 | |
| 0.246 | 0.38 | 0.14 | 0.07 | 38.81 | 1.08 | 46.50 | ||
| Case 3 | 0.330 | 0.20 | 0.31 | 0.49 | 36.37 | 1.22 | 46.93 | |
| Patient1 | 0.800 | 0.61 | 2.00 | 1.60 | 33.11 | 3.14 | 44.36 | |
| 0.086 | 0.10 | 0.06 | 0.49 | 38.73 | 1.19 | 46.95 | ||
| Case 3 | 0.298 | 0.14 | 0.03 | 0.49 | 34.71 | 2.17 | 46.69 | |
| Patient3 | 0.800 | 0.16 | 4.14 | 0.66 | 32.89 | 4.39 | 42.27 | |
| 0.051 | 0.00 | 0.00 | 0.00 | 40.65 | 0.00 | 51.80 | ||
| Case 6 | 0.261 | 0.00 | 0.00 | 0.05 | 41.37 | 0.36 | 49.57 | |
| Healthy | 0.794 | 0.01 | 0.00 | 0.37 | 36.57 | 1.22 | 51.68 | |
| 0.246 | 0.00 | 0.00 | 0.00 | 43.40 | 0.07 | 48.16 | ||
| Case 6 | 0.330 | 0.03 | 0.00 | 0.13 | 42.12 | 0.06 | 49.15 | |
| Patient1 | 0.800 | 0.00 | 0.00 | 0.06 | 39.83 | 0.64 | 50.40 | |
| 0.086 | 0.00 | 0.00 | 0.00 | 40.35 | 0.11 | 51.18 | ||
| Case 6 | 0.298 | 0.01 | 0.00 | 0.09 | 38.43 | 0.32 | 52.19 | |
| Patient3 | 0.800 | 0.02 | 0.01 | 0.03 | 37.71 | 0.60 | 51.20 | |

Table A3.
Continuation of Table 4, for Case 2, Case 3 and Case 6 with flow rate profiles shown in Figure 2.
| Time (s) | Average WSSdiv if WSS <1 | Average WSSdiv if WSS >1 | |||
|---|---|---|---|---|---|
| if WSSdiv < −1000 | if WSSdiv > 1000 | if WSSdiv < −1000 | if WSSdiv > 1000 | ||
| 0.051 | −5250 | 1710 | −8610 | 3450 | |
| Case 2 | 0.261 | 1660 | 3650 | −5080 | 4240 |
| Healthy | 0.794 | −2150 | 3440 | −3580 | 2650 |
| Carreau | 0.051 | −1460 | 2080 | −7220 | 4330 |
| Case 2 | 0.261 | −3160 | 3180 | −5530 | 4460 |
| Healthy | 0.794 | −1660 | 1930 | −3090 | 2880 |
| 0.246 | - | 7020 | 5390 | ||
| Case 2 | 0.330 | −1520 | 3550 | −7000 | 5420 |
| Patient1 | 0.800 | −1910 | 1740 | −3670 | 2780 |
| 0.086 | −1780 | 2380 | −3750 | 2510 | |
| Case 2 | 0.298 | −3120 | 3470 | −6530 | 5170 |
| Patient3 | 0.800 | −1880 | 1850 | −3750 | 2700 |
| 0.051 | −8210 | 16,100 | −75,700 | 73,400 | |
| Case 3 | 0.261 | −13,500 | 25,000 | −18,600 | 16,400 |
| Healthy | 0.794 | −4130 | 2920 | −9850 | 7270 |
| 0.246 | −33,900 | 28,000 | −34,400 | 27,600 | |
| Case 3 | 0.330 | −9630 | 6000 | −23,200 | 18,000 |
| Patient1 | 0.800 | −8600 | 6840 | −14,000 | 10,800 |
| 0.086 | −30,800 | 9300 | −26,700 | 23,800 | |
| Case 3 | 0.298 | −7580 | 8190 | −21,000 | 16,700 |
| Patient3 | 0.800 | −5520 | 4430 | −12,900 | 10,200 |
| 0.051 | - | - | −41,500 | 57,200 | |
| Case 6 | 0.261 | - | - | −62,000 | 68,700 |
| Healthy | 0.794 | −1140 | 5290 | −21,700 | 31,100 |
| 0.246 | −45,800 | 33,900 | −78,200 | 61,200 | |
| Case 6 | 0.330 | −20,200 | 13,600 | −60,100 | 44,800 |
| Patient1 | 0.800 | −7980 | 8290 | −63,000 | 54,000 |
| 0.086 | −13,800 | 53,800 | −65,400 | 53,400 | |
| Case 6 | 0.298 | −34,900 | 14,500 | −51,900 | 37,500 |
| Patient3 | 0.800 | −14,200 | 15,700 | −67,700 | 53,600 |
References
- Cebral, J.R.; Mut, F.; Gade, P.; Cheng, F.; Tobe, Y.; Frosen, J.; Robertson, A.M. Combining data from multiple sources to study mechanisms of aneurysm disease: Tools and techniques. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3133. [Google Scholar] [CrossRef] [PubMed]
- Nixon, A.M.; Gunel, M.; Sumpio, B.E. The critical role of hemodynamics in the development of cerebral vascular disease: A review. J. Neurosurg. 2010, 112, 1240–1253. [Google Scholar] [CrossRef] [PubMed]
- Sforza, D.M.; Putman, C.M.; Cebral, J.R. Hemodynamics of cerebral aneurysms. Ann. Rev. Fluid Mech. 2009, 41, 91–107. [Google Scholar] [CrossRef]
- Xiang, J.; Tutino, V.M.; Snyder, K.V.; Meng, H. CFD: Computational fluid dynamics or confounding factor dissemination? The role of hemodynamics in intracranial aneurysm rupture risk assessment. Am. J. Neuroradiol. 2014, 35, 1849–1857. [Google Scholar] [CrossRef]
- Shojima, M.; Oshima, M.; Takagi, K.; Torii, R.; Hayakawa, M.; Katada, K.; Morita, A.; Kirino, T. Magnitude and role of wall shear stress on cerebral aneurysm: Computational fluid dynamic study of 20 middle cerebral artery aneurysms. Stroke 2004, 35, 2500–2505. [Google Scholar] [CrossRef]
- Shimogonya, Y.; Ishikawa, T.; Imai, Y.; Mori, D.; Matsuki, N.; Yamaguchi, T. Formation of saccular cerebral aneurysms may require proliferation of the arterial wall: Computational investigation. J. Biomech. Sci. Eng. 2008, 3, 431–442. [Google Scholar] [CrossRef][Green Version]
- Miura, Y.; Ishida, F.; Umeda, Y.; Tanemura, H.; Suzuki, H.; Matsushima, S.; Shimosaka, S.; Taki, W. Low wall shear stress is independently associated with the rupture status of middle cerebral artery aneurysms. Stroke 2013, 44, 519–521. [Google Scholar] [CrossRef] [PubMed]
- Jamous, M.A.; Nagahiro, S.; Kitazato, K.T.; Satoh, K.; Satomi, J. Vascular corrosion casts mirroring early morphological changes that lead to the formation of saccular cerebral aneurysm: An experimental study in rats. J. Neurosurg. 2005, 102, 532–535. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Wang, Z.; Hoi, Y.; Gao, L.; Metaxa, E.; Swartz, D.D.; Kolega, J. Complex hemodynamics at the apex of an arterial bifurcation induces vascular remodeling resembling cerebral aneurysm initiation. Stroke 2007, 38, 1924–1931. [Google Scholar] [CrossRef]
- Kadirvel, R.; Ding, Y.H.; Dai, D.; Zakaria, H.; Robertson, A.M.; Danielson, M.A.; Lewis, D.A.; Cloft, H.J.; Kallmes, D.F. The influence of hemodynamic forces on biomarkers in the walls of elastase-induced aneurysms in rabbits. Neuroradiology 2007, 49, 1041–1053. [Google Scholar] [CrossRef]
- Cebral, J.R.; Mut, F.; Weir, J.; Putman, C. Quantitative characterization of the hemodynamic environment in ruptured and unruptured brain aneurysms. Am. J. Neuroradiol. 2011, 32, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Ojha, M. Wall shear stress temporal gradient and anastomotic intimal hyperplasia. Circ. Res. 1994, 74, 1227–1231. [Google Scholar] [CrossRef] [PubMed]
- Kleinstreuer, C.; Lei, M.; Archie, J.P. Flow input waveform effects on the temporal and spatial wall shear stress gradients in a femoral graft-artery connector. J. Biomech. Eng. 1996, 118, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Wootton, D.M.; Ku, D.N. Fluid mechanics of vascular systems, diseases, and thrombosis. Annu. Rev. Biomed. Eng. 1999, 1, 299–329. [Google Scholar] [CrossRef] [PubMed]
- Gambaruto, A.M.; Doorly, D.J.; Yamaguchi, T. Wall Shear Stress and Near-Wall Convective Transport: Comparisons with Vascular Remodelling in a Peripheral Graft Anastomosis. J. Comput. Phys. 2010, 229, 5339–5356. [Google Scholar] [CrossRef]
- Gambaruto, A.M.; Joao, A. Flow structures in cerebral aneurysms. Comput. Fluids 2012, 65, 56–65. [Google Scholar] [CrossRef]
- Goubergrits, L.; Thamsen, B.; Berthe, A.; Poethke, J.; Kertzscher, U.; Affeld, K.; Petz, C.; Hege, H.C.; Hoch, H.; Spuler, A. In vitro study of near-wall flow in a cerebral aneurysm model with and without coils. Am. J. Neuroradiol. 2010, 31, 1521–1528. [Google Scholar] [CrossRef] [PubMed]
- Mantha, A.; Karmonik, C.; Benndorf, G.; Strother, C.; Metcalfe, R. Hemodynamics in a cerebral artery before and after the formation of an aneurysm. Am. J. Neuroradiol. 2006, 27, 1113–1118. [Google Scholar]
- Ku, D.N.; Giddens, D.P.; Zarins, C.K.; Glagov, S. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arteriosclerosis 1985, 5, 293–302. [Google Scholar] [CrossRef]
- Shimogonya, Y.; Ishikawa, T.; Imai, Y.; Matsuki, N.; Yamaguchi, T. Can temporal fluctuation in spatial wall shear stress gradient initiate a cerebral aneurysm? A proposed novel hemodynamic index, the gradient oscillatory number (GON). J. Biomech. 2009, 42, 550–554. [Google Scholar] [CrossRef]
- Peiffer, V.; Sherwin, S.J.; Weinberg, P.D. Computation in the rabbit aorta of a new metric-the transverse wall shear stress-to quantify the multidirectional character of disturbed blood flow. J. Biomech. 2013, 46, 2651–2658. [Google Scholar] [CrossRef]
- Qian, Y.; Takao, H.; Umezu, M.; Murayama, Y. Risk analysis of unruptured aneurysms using computational fluid dynamics technology: Preliminary results. Am. J. Neuroradiol. 2011, 32, 1948–1955. [Google Scholar] [CrossRef]
- Takao, H.; Murayama, Y.; Otsuka, S.; Qian, Y.; Mohamed, A.; Masuda, S.; Yamamoto, M.; Abe, T. Hemodynamic differences between unruptured and ruptured intracranial aneurysms during observation. Stroke 2012, 43, 1436–1439. [Google Scholar] [CrossRef] [PubMed]
- Papaharilaou, Y.; Ekaterinaris, J.A.; Manousaki, E.; Katsamouris, A.N. A decoupled fluid structure approach for estimating wall stress in abdominal aortic aneurysms. J. Biomech. 2007, 40, 367–377. [Google Scholar] [CrossRef] [PubMed]
- Oeltze-Jafra, S.; Cebral, J.R.; Janiga, G.; Preim, B. Cluster analysis of vortical flow in simulations of cerebral aneurysm hemodynamics. IEEE Trans. Vis. Comput. Graph. 2016, 22, 757–766. [Google Scholar] [CrossRef] [PubMed]
- Morbiducci, U.; Gallo, D.; Cristofanelli, S.; Ponzini, R.; Deriu, M.A.; Rizzo, G.; Steinman, D.A. A rational approach to defining principal axes of multidirectional wall shear stress in realistic vascular geometries, with application to the study of the influence of helical flow on wall shear stress directionality in aorta. J. Biomech. 2015, 48, 899–906. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Antiga, L.; Steinman, D.A. Correlations among indicators of disturbed flow at the normal carotid bifurcation. J. Biomech. Eng. 2009, 131, 061013. [Google Scholar] [CrossRef] [PubMed]
- Baek, H.; Jayaraman, M.V.; Richardson, P.D.; Karniadakis, G.E. Flow instability and wall shear stress variation in intracranial aneurysms. J. R. Soc. Interface 2009, 7, 967–988. [Google Scholar] [CrossRef] [PubMed]
- Cebral, J.R.; Castro, M.A.; Burgess, J.E.; Pergolizzi, R.S.; Sheridan, M.J.; Putman, C.M. Characterization of cerebral aneurysms for assessing risk of rupture by using patient-specific computational hemodynamics models. Am. J. Neuroradiol. 2005, 26, 2550–2559. [Google Scholar]
- Sangalli, L.M.; Secchi, P.; Vantini, S.; Veneziani, A. A case study in exploratory functional data analysis: Geometrical features of the internal carotid artery. J. Am. Stat. Assoc. 2009, 104, 37–48. [Google Scholar] [CrossRef]
- Cebral, J.R.; Mut, F.; Weir, J.; Putman, C.M. Association of hemodynamic characteristics and cerebral aneurysm rupture. Am. J. Neuroradiol. 2011, 32, 264–270. [Google Scholar] [CrossRef]
- Sasaki, T.; Kakizawa, Y.; Yoshino, M.; Fujii, Y.; Yoroi, I.; Ichikawa, Y.; Horiuchi, T.; Hongo, K. Numerical Analysis of Bifurcation Angles and Branch Patterns in Intracranial Aneurysm Formation. Neurosurgery 2018. [Google Scholar] [CrossRef]
- Millan, R.D.; Dempere-Marco, L.; Pozo, J.M.; Cebral, J.R.; Frangi, A.F. Morphological characterization of intracranial aneurysms using 3-D moment invariants. IEEE Trans. Med Imaging 2007, 26, 1270–1282. [Google Scholar] [CrossRef]
- Tiago, J.; Gambaruto, A.; Sequeira, A. Patient-specific blood flow simulations: Setting Dirichlet boundary conditions for minimal error with respect to measured data. Math. Model. Nat. Phenom. 2014, 9, 98–116. [Google Scholar] [CrossRef]
- Sequeira, A.; Tiago, J.; Guerra, T. Boundary Control Problems in Hemodynamics. In Trends in Biomathematics: Modeling, Optimization and Computational Problems; Springer: Cham, Switzerland, 2018; pp. 27–48. [Google Scholar]
- Tricerri, P.; Dedè, L.; Gambaruto, A.; Quarteroni, A.; Sequeira, A. A numerical study of isotropic and anisotropic constitutive models with relevance to healthy and unhealthy cerebral arterial tissues. Int. J. Eng. Sci. 2016, 101, 126–155. [Google Scholar] [CrossRef]
- Torii, R.; Oshima, M.; Kobayashi, T.; Takagi, K.; Tezduyar, T.E. Fluid–structure interaction modeling of blood flow and cerebral aneurysm: Significance of artery and aneurysm shapes. Comput. Methods Appl. Mech. Eng. 2009, 198, 3613–3621. [Google Scholar] [CrossRef]
- Lei, M.; Giddens, D.P.; Jones, S.A.; Loth, F.; Bassinouny, H. Pulsatile flow in an end-to-side vascular graft model: Comparison of computations with experimental data. ASME J. Biomech. Eng. 2001, 123, 80–87. [Google Scholar] [CrossRef]
- Meng, H.; Tutino, V.M.; Xiang, J.; Siddiqui, A. High WSS or low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: Toward a unifying hypothesis. Am. J. Neuroradiol. 2014, 35, 1254–1262. [Google Scholar] [CrossRef] [PubMed]
- Hansen, K.B.; Arzani, A.; Shadden, S.C. Mechanical platelet activation potential in abdominal aortic aneurysms. J. Biomech. Eng. 2015, 137, 041005. [Google Scholar] [CrossRef] [PubMed]
- Hansen, K.B.; Shadden, S.C. A reduced-dimensional model for near-wall transport in cardiovascular flows. Biomech. Model. Mechanobiol. 2016, 15, 713–722. [Google Scholar] [CrossRef] [PubMed]
- Cebral, J.; Ollikainen, E.; Chung, B.J.; Mut, F.; Sippola, V.; Jahromi, B.R.; Tulamo, R.; Hernesniemi, J.; Niemelä, M.; Robertson, A.; et al. Flow conditions in the intracranial aneurysm lumen are associated with inflammation and degenerative changes of the aneurysm wall. Am. J. Neuroradiol. 2017, 38, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Chalouhi, N.; Ali, M.S.; Jabbour, P.M.; Tjoumakaris, S.I.; Gonzalez, L.F.; Rosenwasser, R.H.; Koch, W.J.; Dumont, A.S. Biology of intracranial aneurysms: Role of inflammation. J. Cereb. Blood Flow Metab. 2012, 32, 1659–1676. [Google Scholar] [CrossRef] [PubMed]
- Orr, A.W.; Helmke, B.P.; Blackman, B.R.; Schwartz, M.A. Mechanisms of mechanotransduction. Dev. Cell 2006, 10, 11–20. [Google Scholar] [CrossRef]
- Arzani, A.; Gambaruto, A.M.; Chen, G.; Shadden, S.C. Lagrangian wall shear stress structures and near-wall transport in high-Schmidt-number aneurysmal flows. J. Fluid Mech. 2016, 790, 158–172. [Google Scholar] [CrossRef]
- Arzani, A.; Gambaruto, A.M.; Chen, G.; Shadden, S.C. Wall shear stress exposure time: A Lagrangian measure of near-wall stagnation and concentration in cardiovascular flows. Biomech. Model. Mechanobiol. 2017, 16, 787–803. [Google Scholar] [CrossRef]
- Perry, A.E.; Chong, M.S. A series-expansion study of the Navier-Stokes equations with applications to three-dimensional separation patterns. J. Fluid Mech. 1986, 173, 207–223. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Arzani, A.; Shadden, S.C. Wall shear stress fixed points in cardiovascular fluid mechanics. J. Biomech. 2018, 73, 145–152. [Google Scholar] [CrossRef] [PubMed]
- Gambaruto, A.M. Processing the image gradient field using a topographic primal sketch approach. Int. J. Numer. Methods Biomed. Eng. 2015, 31, e02706. [Google Scholar] [CrossRef]
- João, A.; Gambaruto, A.M.; Pereira, R.; Sequeira, A. Robust and effective automatic parameter choice for medical image filtering. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2009. under review. [Google Scholar]
- Gambaruto, A.M.; Taylor, D.J.; Doorly, D.J. Modelling nasal airflow using a Fourier descriptor representation of geometry. Int. J. Numer. Methods Fluids 2009, 59, 1259–1283. [Google Scholar] [CrossRef]
- Ramalho, S.; Moura, A.; Gambaruto, A.M.; Sequeira, A. Sensitivity to outflow boundary conditions and level of geometry description for a cerebral aneurysm. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 697–713. [Google Scholar] [CrossRef] [PubMed]
- Ramalho, S.; Moura, A.B.; Gambaruto, A.M.; Sequeira, A. Influence of blood rheology and outflow boundary conditions in numerical simulations of cerebral aneurysms. In Mathematical Methods and Models in Biomedicine; Springer: New York, NY, USA, 2013; pp. 149–175. [Google Scholar]
- Pedley, T.J. Mathematical modelling of arterial fluid dynamics. J. Eng. Math. 2003, 47, 419–444. [Google Scholar] [CrossRef]
- Moyle, K.R.; Antiga, L.; Steinman, D.A. Inlet conditions for image-based CFD models of the carotid bifurcation: Is it reasonable to assume fully developed flow? J. Biomech. Eng. 2006, 128, 371–379. [Google Scholar] [CrossRef]
- Stamatopoulos, C.; Papaharilaou, Y.; Mathioulakis, D.S.; Katsamouris, A. Steady and unsteady flow within an axisymmetric tube dilatation. Exp. Therm. Fluid Sci. 2010, 34, 915–927. [Google Scholar] [CrossRef]
- He, X.; Ku, D.N. Unsteady entrance flow development in a straight tube. J. Biomech. Eng. 1994, 116, 355–360. [Google Scholar] [CrossRef]
- Marzo, A.; Singh, P.; Larrabide, I.; Radaelli, A.; Coley, S.; Gwilliam, M.; Wilkinson, I.D.; Lawford, P.; Reymond, P.; Patel, U.; et al. Computational hemodynamics in cerebral aneurysms: The effects of modeled versus measured boundary conditions. Ann. Biomed. Eng. 2011, 39, 884–896. [Google Scholar] [CrossRef] [PubMed]
- Gambaruto, A.M.; Janela, J.; Moura, A.; Sequeira, A. Sensitivity of hemodynamics in a patient specific cerebral aneurysm to vascular geometry and blood rheology. Math. Biosci. Eng. MBE 2011, 8, 409–423. [Google Scholar]
- Gambaruto, A.M.; Janela, J.; Moura, A.; Sequeira, A. Shear-thinning effects of hemodynamics in patient-specific cerebral aneurysms. Math. Biosci. Eng. MBE 2013, 10, 649–665. [Google Scholar] [CrossRef] [PubMed]
- Bandaru, V.; Kolchinskaya, A.; Padberg-Gehle, K.; Schumacher, J. Role of critical points of the skin friction field in formation of plumes in thermal convection. Phys. Rev. 2015, 92, 043006. [Google Scholar] [CrossRef] [PubMed]
- Surana, A.; Grunberg, O.; Haller, G. Exact theory of three-dimensional flow separation. Part 1. Steady separation. J. Fluid Mech. 2006, 564, 57–103. [Google Scholar] [CrossRef]
- Chong, M.S.; Perry, A.E.; Cantwell, B.J. A general classification of three-dimensional flow fields. Phys. Fluids Fluid Dyn. 1990, 2, 765–777. [Google Scholar] [CrossRef]
- Chong, M.S.; Monty, J.P.; Chin, C.; Marusic, I. The topology of skin friction and surface vorticity fields in wall-bounded flows. J. Turbul. 2012, 13, N6. [Google Scholar] [CrossRef]
- Hornung, H.; Perry, A.E. Some aspects of three-dimensional separation. i-streamsurface bifurcations. Z. Flugwiss. Weltraumforsch. 1984, 8, 77–87. [Google Scholar]
- Tobak, M.; Peake, D.J. Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 1982, 14, 61–85. [Google Scholar] [CrossRef]
- Lighthill, M.J. Attachment and separation in three-dimensional flow. In Laminar Boundary Layers; Rosenhead, L., Ed.; Oxford University Press: Oxford, UK, 1963; pp. 72–82. [Google Scholar]
- Nielson, M.N.; Jung, I.H. Tools for computing tangent curves for linearly varying vector fields over tetrahedral domains. IEEE Trans. Vis. Comput. Graph. 1999, 5, 360–372. [Google Scholar] [CrossRef]
- Kipfer, P.; Reck, F.; Greiner, G. Local exact particle tracing on unstructured grids. Comput. Graph Forum 2003, 22, 133–142. [Google Scholar] [CrossRef]
- Scheuermann, G.; Bobach, T.; Hagen, H.; Mahrous, K.; Hamann, B.; Joy, K.I.; Kollmann, W. A tetrahedra-based stream surface algorithm. In Proceedings of the IEEE Visualization, San Diego, CA, USA, 21–26 October 2001. [Google Scholar]
- Chakraborty, P.; Balachandar, S.; Adrian, R.J. On the relationships between local vortex identification schemes. J. Fluid Mech. 2005, 535, 189–214. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Ottino, J.M. Mixing, chaotic advection, and turbulence. Annu. Rev. Fluid Mech. 1990, 22, 207–254. [Google Scholar] [CrossRef]
- Dallmann, U. Topological Structures of Three-Dimensional Flow Separation; DFVLR Report IB 221-82-A07; Institut fuer Theoretische Stroemungsmechanik: Göttingen, Germany, 1983. [Google Scholar]
- Oswatitsch, K. Die Ablösungsbedingung von Grenzschichten. In Grenzschichtforschung/Boundary Layer Research; Springer: Berlin/Heidelberg, Germany, 1958; pp. 357–367. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).