3.2. Improving the Inner Wall Shape of the Recirculation Channel
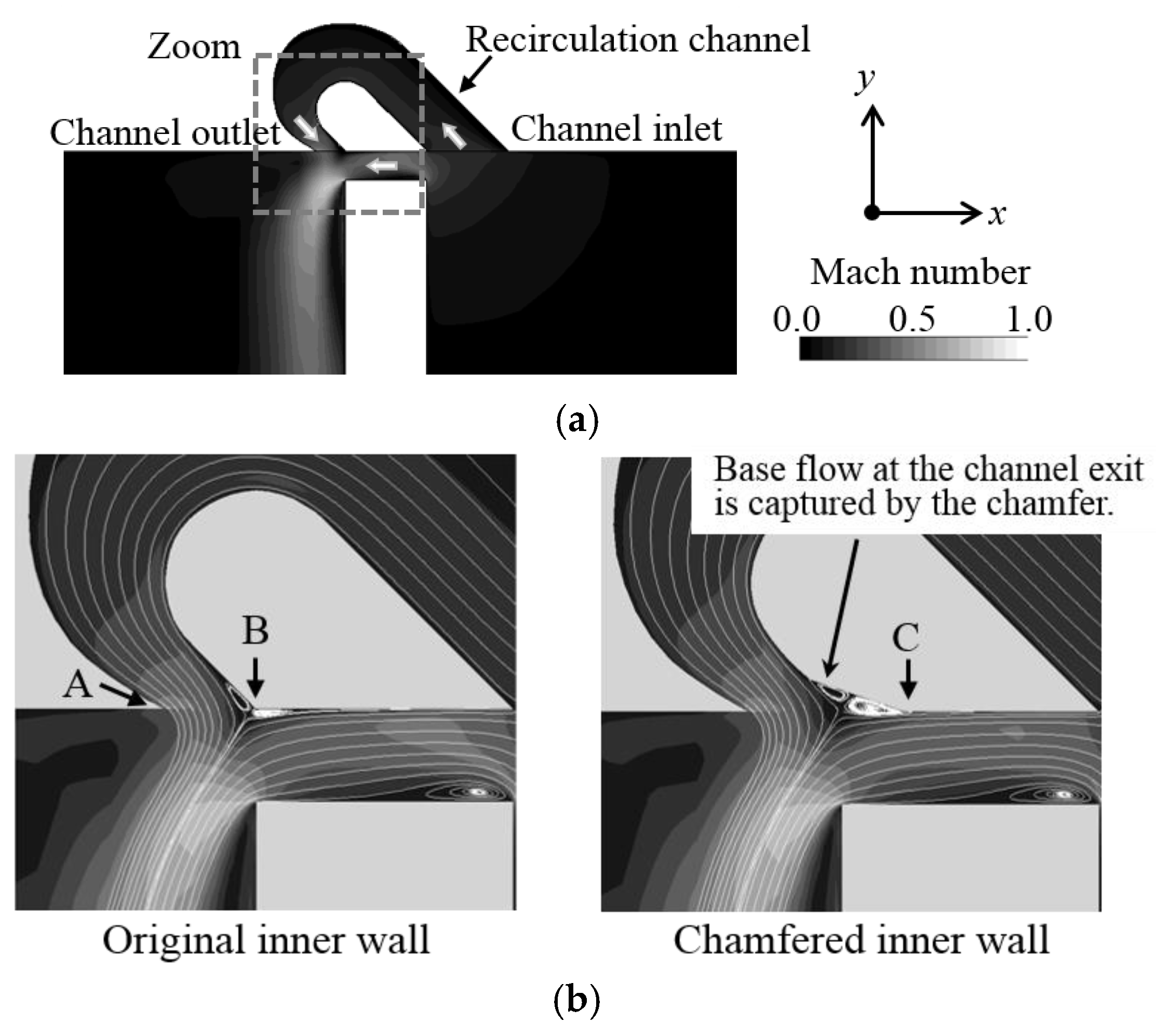
The overview of the recirculation channel flow structure is shown in
Figure 4a by Mach number grayscale iso-levels, captured by two-dimensional (2D) simulations. The flow conditions of this 2D calculation are specified by the results of corresponding 3D calculations on the computational domain of
Figure 2. In the absence of any casing treatment, the pressure difference across the blade thickness, which is modeled by imposing different pressures along the left and right boundaries of the computational domain of
Figure 4a, generates a leakage flow over the tip clearance. In the simulation shown in
Figure 4a, the right-hand side boundary is set at a higher pressure than the left boundary, so that the elevated pressure to the right of the modeled blade thickness creates a leakage jet over it that runs from right to left, as indicated by the white arrow. By applying the recirculation channel over the rotor blade, the fluid is sucked at the channel inlet and it is injected into the main passage at the channel outlet. The leakage flow from the rotor tip is diverted downwards, which indicates a significant interaction from the confluence of the two flows. As a result of the channel activation, the tip flow over the tip clearance directed towards the left computational domain boundary is substantially obstructed.
Figure 4b shows an attempt to improve the inner wall shape by two-dimensional numerical simulations.
Figure 4b compares the two-dimensional streamlines and Mach number distributions in the gray dashed square inset of
Figure 4a between the original inner wall shape and a chamfered inner wall. With the original inner wall shape, the recirculating flow separates at the RC outlet at the confluence of the leakage flow at Position B in
Figure 4b. This interaction causes a blockage of the recirculating flow at the channel outlet, which undesirably weakens the effect of this casing treatment design. In the chamfered inner wall case, a larger flow separation occurs at the Position C in
Figure 4b. Nevertheless, as the separation bubble is accommodated into the chamfer of the channel inner wall, the saddle point between the recirculating flow and the tip leakage flow shifts upward.
Figure 4c shows the change of the
y velocity profiles across the channel outlet plane by applying the chamfered inner wall. The
y velocity corresponds to the radial velocity in the three-dimensional configuration shown in
Figure 2. The negative value of the
y velocity in
Figure 4c indicates injection into the main flow passage. With the original inner wall shape, the
y velocity is positive in the vicinity of the Position B and this denotes and unwanted recirculation bubble. This bubble causes a blockage of
y velocity at the channel outlet. By applying the chamfered inner wall, a mitigation of the blockage at the channel outlet is obtained so that the recirculated flow from the channel is injected into the main flow passage through a wider effective outflow area.
Following this two-dimensional analysis on the potential benefit of the inner wall chamfer, the influence on the compressor SM defined by Equation (1) is evaluated on the three-dimensional passage geometry of
Figure 2. The three-dimensional steady RANS predicted the improvement of the compressor SM by 0.35% without adiabatic efficiency penalty by applying the chamfered inner wall. Thus, the chamfered inner wall was shown to be a more beneficial feature for the compressor tip flow than the original sharp inner wall. All subsequent evaluations of the recirculation channel design shown in this paper were conducted with the chamfered inner wall.
3.3. Parametric Study on the Channel Position: Half-Stage Performance
As stated in
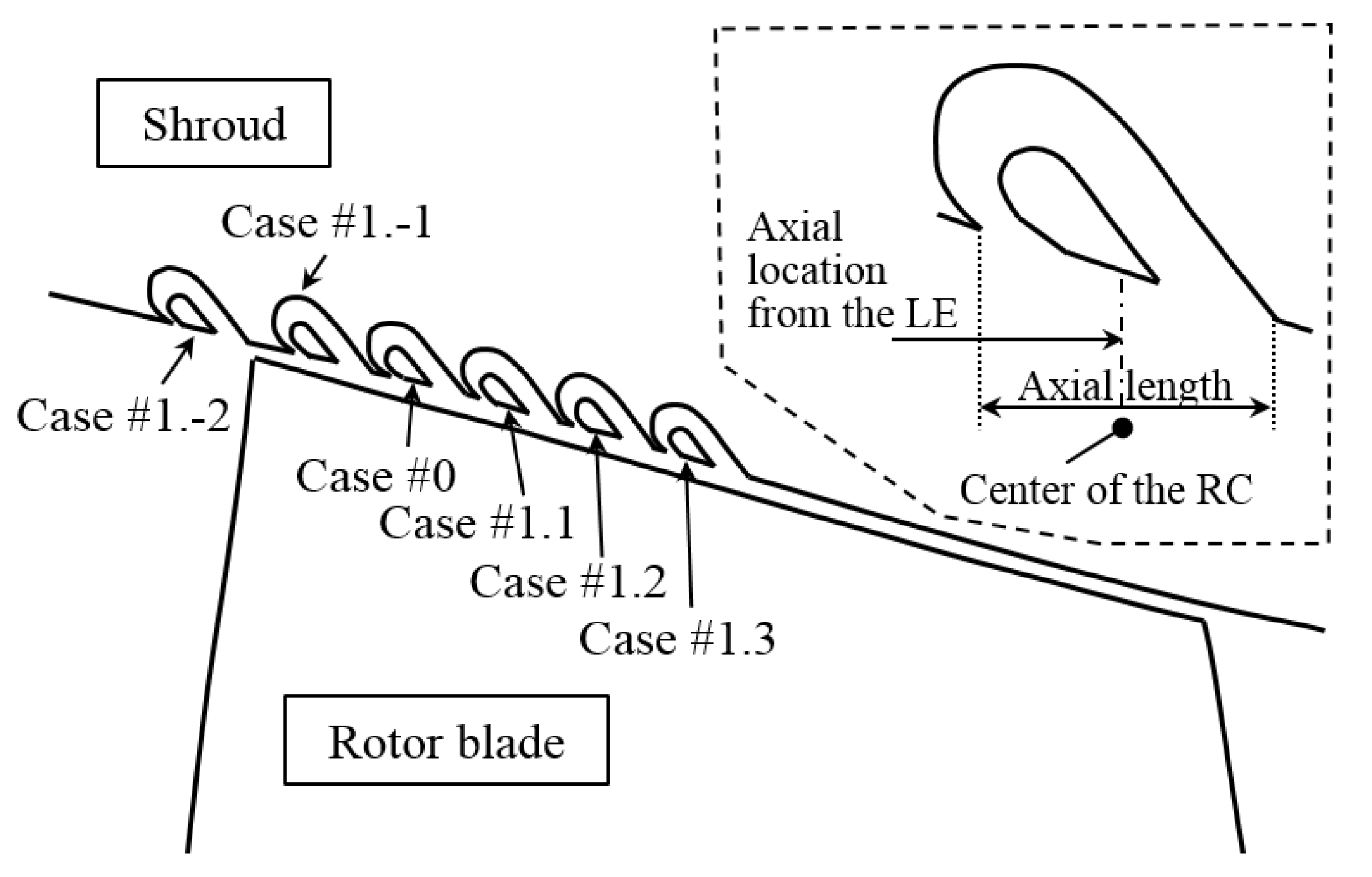
Section 2, the RC is designed to activate recirculating flow by the pressure difference between the channel inlet and the channel outlet. The static pressure at the channel inlet and at the channel outlet depends on the axial location of the RC. Hence, the axial position of the RC is likely to be an important factor in determining the RC performance. Therefore, a parametric study on the RC axial position is carried out to evaluate its effect on the compressor performance. Six different RC axial positions are tested, as shown by the meridional plane schematic of
Figure 5.
Table 3 lists the axial location and the axial length of each of them. The Case #0 RC in
Figure 5 is located as in
Figure 1. This datum recirculation channel is applied at about 0.2 axial chord lengths axially downstream from the blade leading edge, which is where the circumferential groove design gave the best stall margin in [
8]. The stall inception is determined numerically for all six cases by progressively increasing the exit pressure boundary condition.
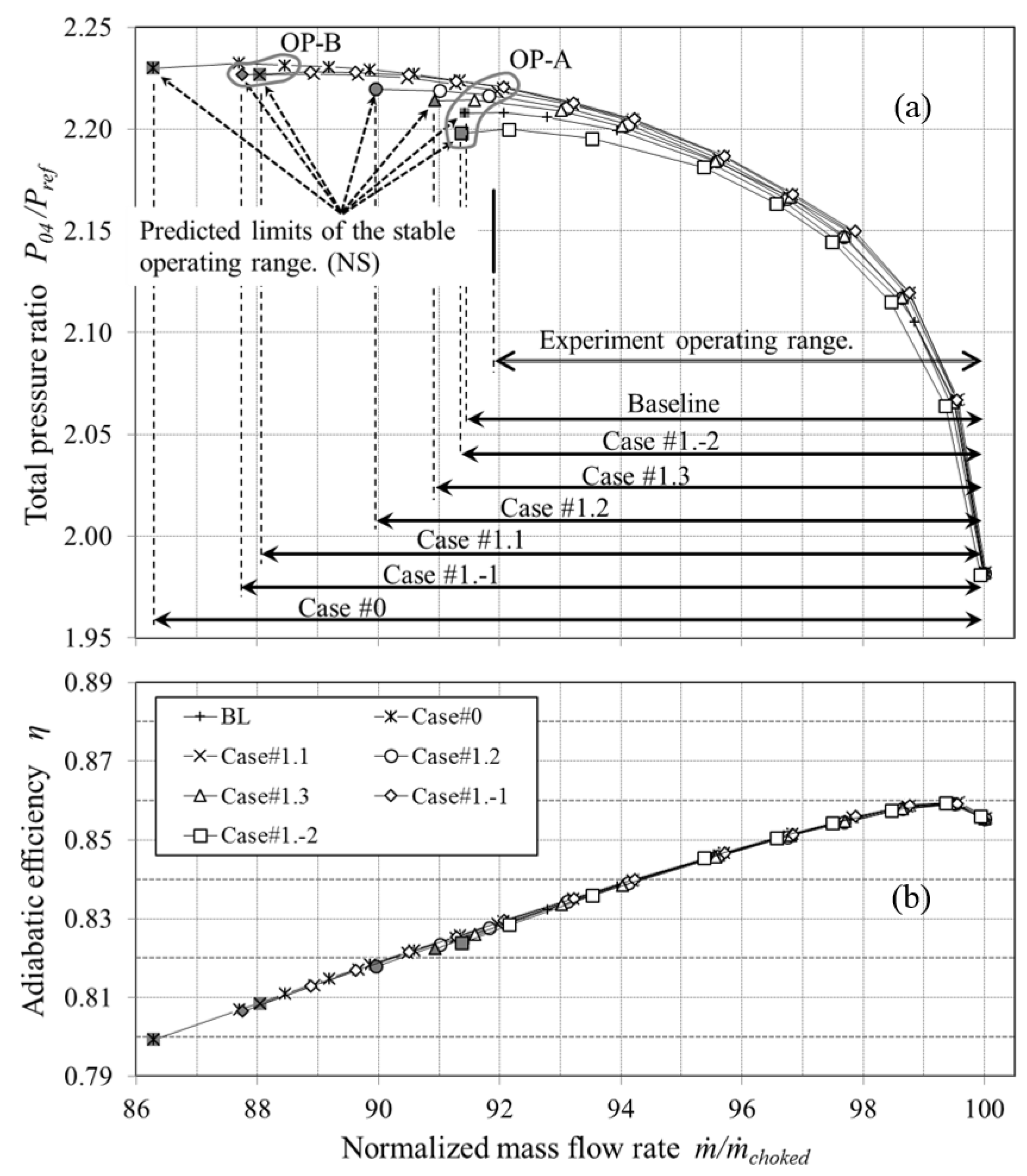
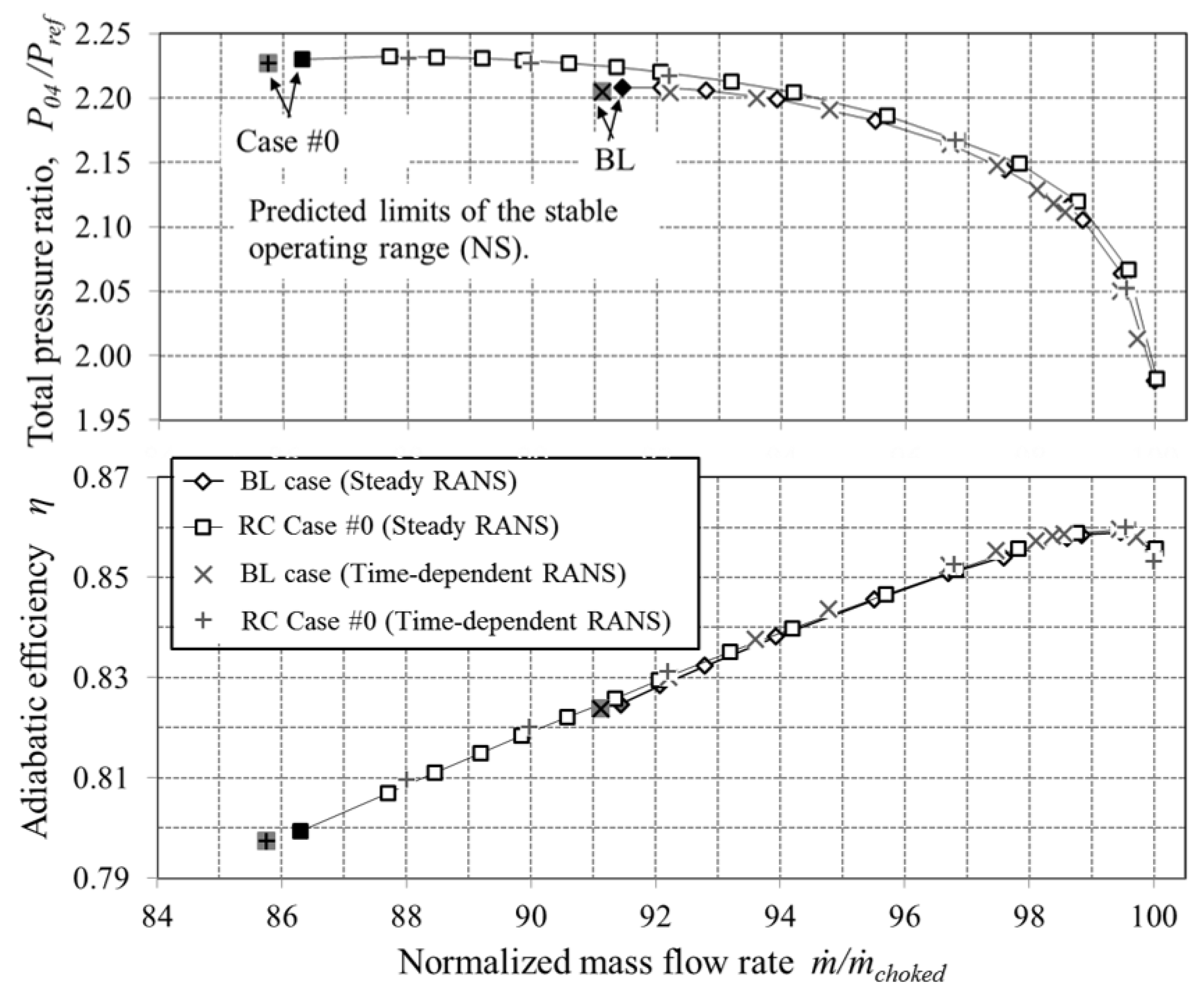
Figure 6 shows the comparison of the compressor performance characteristics among the six test cases.
Figure 6a uses the same legend and abscissa as
Figure 6b. The total pressure ratio in
Figure 6a is calculated by the ratio of the total pressure predicted at the Station 4 to the reference upstream total pressure given in [
18]. The adiabatic efficiency is calculated by Equation (2). The choked mass flow rate
predicted in the CFD of the baseline (BL) case is used to normalize the mass flow rate values of the abscissa. The final increment of the back pressure to detect the stall inception is 0.3% of the atmospheric pressure in all the calculations. The predicted limit of the stable operating range for each case is marked by the gray-filled symbol. The stable operating range in mass flow rate is highlighted by the arrow for each case at the bottom of
Figure 6a. Among these test cases, Case #0 is predicted to have the widest operating range. The predicted stable operating range of the compressor rotor decreases as the RC is moved axially either way from the Case #0 position.
Figure 6b shows that the rotor adiabatic efficiency is substantially unaffected by the presence of the RC, unlike with the casing treatments [
6,
7].
Figure 7a summarizes the variation of the compressor performance among the test cases. All values of the ordinate are calculated as the difference from the value of the BL case. The SM is calculated by Equation (1).
Figure 7b shows the variation in the injected axial momentum over the compressor operating range. The normalized axial momentum
M is calculated by
. A positive momentum means flow injection from the RC toward the main flow passage. All the cases except Case #1.-2 provides a better SM than the BL case. As shown in
Figure 7b, the injected momentum in Case #1.-2 is much smaller than in the other cases, which indicates that Case #1.-2 RC does not work as intended in
Figure 4. Both the Case #0 outlet pressure at the NS operating condition and the Case #0 adiabatic efficiency at the PE condition are the highest among the test cases. In
Figure 7b, the intensity of the injected momentum in Case #0 increases almost monotonically up to the stall inception. This feature shows an interesting and welcome self-regulating property of the recirculation channel. Similarly, in Cases #1.1 to1.3, the intensity of the injected momentum tends to rise with compressor loading. At the same back pressure setting, the intensity of the injected momentum tends to decrease monotonically as the RC is placed axially more downstream than in Case #0. Placing the RC upstream than in Case #0 generates a different trend. In Case #1.-1, significant axial momentum injection occurs at low loading conditions.
M increases with the outlet static pressure up to the outlet static pressure value 122 kPa. Above 122 kPa, the axial momentum injection intensity starts to decrease. At the NS condition of Case #1.-1, the intensity of the injected momentum is almost same as that of Case #0. This may explain why the operating range of Case #1.-1 is not wider than that of Case #0, although intense injection occurs in Case #1.-1 at low loading conditions. This difference is investigated further by the analysis of the corresponding flow structures presented in the next chapter.
3.4. Flow Structures over the Casing Wall with Recirculation Channel
Figure 8a shows the distribution of the normalized momentum injected in the axial direction at the RC inlet and at the RC outlet. In all the cases shown in
Figure 8a, the peak of the injected momentum in the axial direction is predicted at the channel outlet near the blade suction surface. The most intense flow injection is predicted at this point in Case #1.-1 at the operating condition OP-A. This reduces by increasing the compressor loading to the condition OP-B.
Figure 8b visualizes the streamlines inside the RC, which are drawn from the absolute velocity field of Case #1.-1 at OP-A. In
Figure 8b, the inner and outer walls of the casing channel are displayed transparent to show the trajectory of the streamlines. The streamlines related to the intense flow injection of
Figure 8a come from the PS of the rotor blade. This indicates the recirculation flow inside the casing channel is driven by the pressure difference between the blade SS and the blade PS.
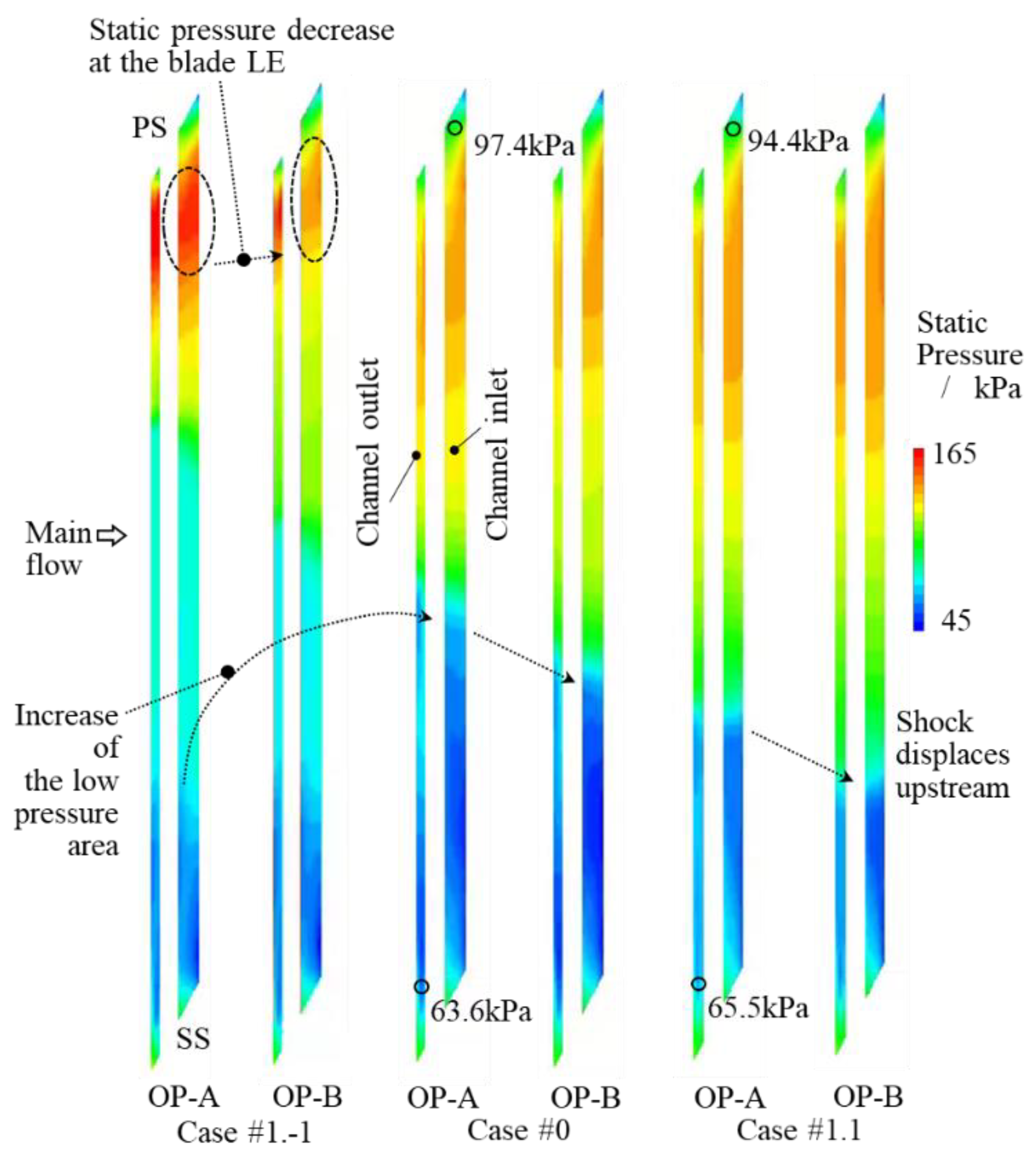
Figure 9 shows the static pressure distribution at the RC inlet and outlet. This is mainly determined by the positioning of the main passage flow structures, such as the passage shock front. In Case #1.-1, high static pressure sits in at the channel inlet at the operating condition OP-A because of the RC inlet being just behind the leading edge shock. This high pressure promotes the recirculating flow inside the casing channel. By increasing the compressor loading to the operating condition OP-B, the location of the passage shock front shifts upstream of the compressor rotor leading edge, pulling the high static pressure behind the shock with it, away from the channel inlet. This causes the static pressure at the channel inlet to decrease, as shown in
Figure 9. This is likely to be the main reason for the decrease in axial momentum injection at the high loading condition in Case #1.-1 shown in
Figure 8a. The predicted static pressure distribution at the channel outlet across one blade pitch is shown for Case#0 and Case #1.1 in
Figure 9. A region of high pressure, encircled by a dashed line ellipse for Case #1.-1 in
Figure 9, is located close to the blade pressure side. This location is pitchwise just ahead of the advancing blade that pressurizes air by a scooping action. The pressure difference between the channel inlet and the channel outlet across the blade thickness created by this action is lower with a casing treatment located more downstream, as shown by Case #0 and Case #1.1 in
Figure 9. This is likely to be the reason why the momentum injection in
Figure 7 is lower in Case #1.1, Case #1.2, and the Case #1.3 than in Case #0 at the same operating condition.
Figure 8 and
Figure 9 highlighted how the flow through the recirculation channel inlet and outlet responds to changes in the main passage flow structures.
Figure 10 shows how the near-casing flow structure changes more in detail, by surface streamlines and specific entropy color iso-levels near the casing wall. The surface streamlines are drawn by the absolute velocity field. The specific entropy
s is calculated as:
where
is the total temperature,
is the total pressure,
is the specific heat capacity at constant pressure,
is the specific gas constant, and subscript
denotes the computational domain inlet condition.
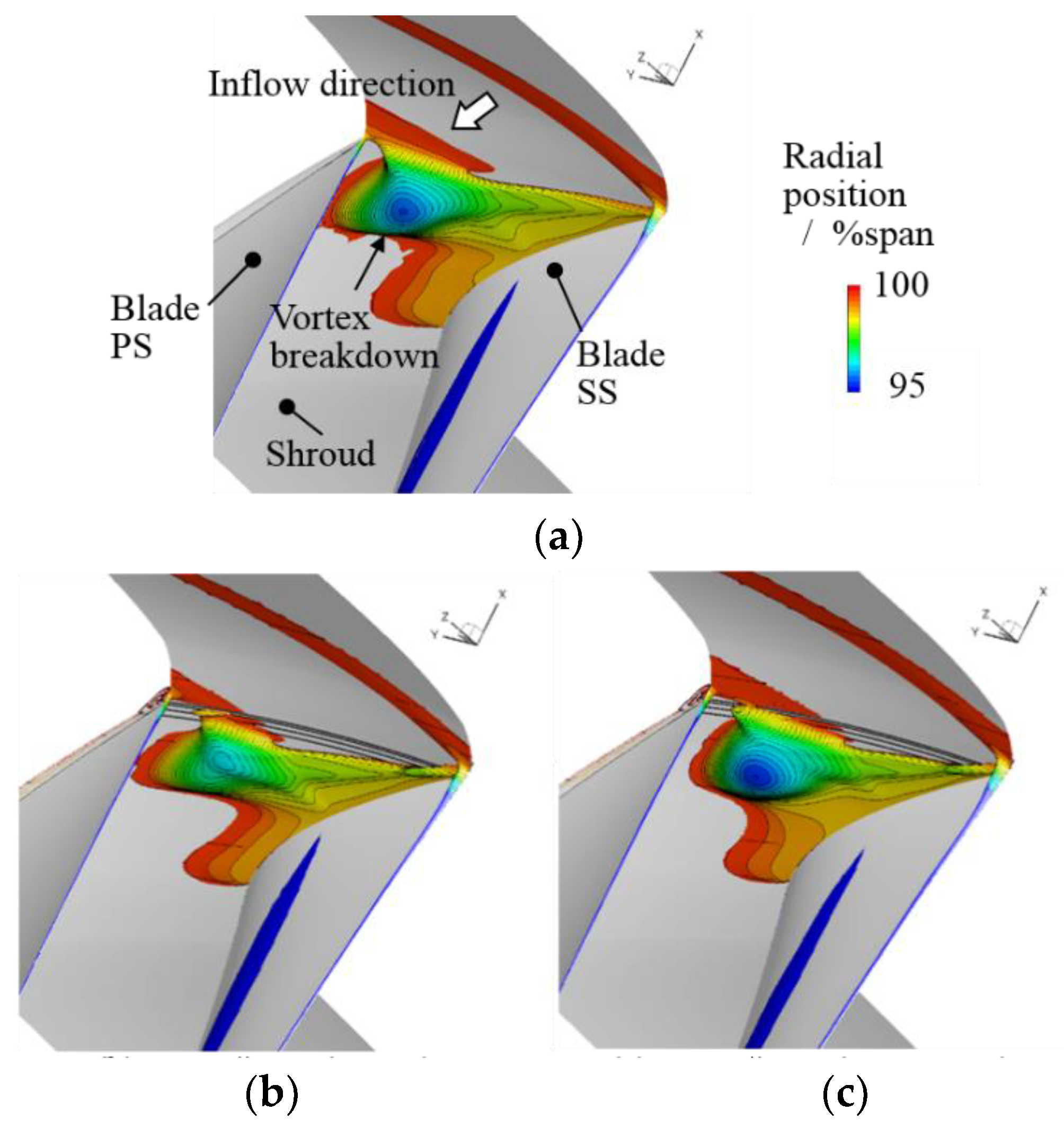
The surface streamlines and the specific entropy color iso-levels near the casing wall of the BL case, Case #1.-1, Case #0, and Case #1.1 are compared at the same operating condition (OP-A). In the BL case of
Figure 10a, an interface, or confluence, forms between the inflow and the reversed tip leakage flow from the rotor tip clearance, which is labelled “Interface” in
Figure 10. Over the casing wall, a substantial area is wetted by reversed flow from the blade PS, which causes the near-casing specific entropy between the blades to be high. In the BL case, this high specific entropy region extends to the immediate vicinity of the blade LE, as shown by the arrow in
Figure 10a. In Case #1.-1 of
Figure 10b, the interface displaces slightly downstream. By this, the reversed flow area reduces in Case #1.-1 compared to the BL case. The high specific entropy distribution near the blade PS LE is also mitigated in Case #1.-1 compared to the BL case. As the operating condition OP-A for Case #1.-1 is still away from the operating-range left limit of
Figure 6a, the passage shock front sits closer to the blade LE than in the BL case.
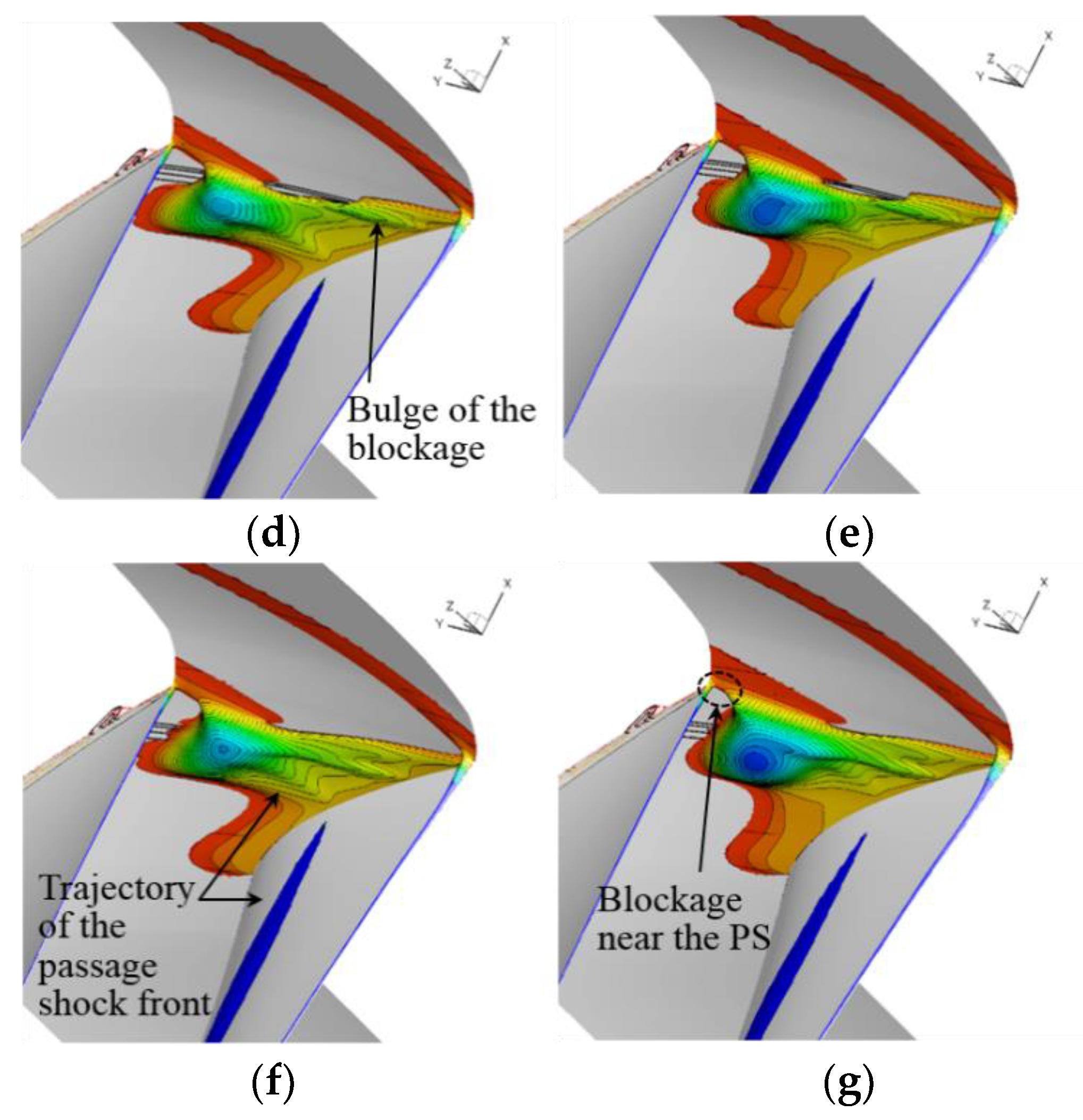
Figure 10c shows that the interface of
Figure 10a is split into two separate interfaces in Case #0. The second interface is created further downstream than in
Figure 10a, at a greater axial distance from the rotor blade LE axial plane. The location of the second interface corresponds to the position of the channel outlet. The predicted specific entropy is high around the channel outlet, due to the interaction between the main passage flow and the injected flow from the casing channel. However, the specific entropy near the blade LE in Case #0 reduces compared to the BL case of
Figure 10a. A flow structure with two interfaces is also predicted in Case #1.1. Compared to Case #0, the first interface of Case #1.1 in
Figure 10d is longer and the specific entropy level near the blade LE is higher. This indicates the RC in Case #1.1 provides a less beneficial change to the flow structure over the casing wall compared to Case #0.
3.5. Effect on the Passage Flow Structures
Figure 11 shows how the flow blockage created in the main passage changes with the axial location of the RC. The boundary surfaces of the flow blockage are identified by iso-surfaces of zero axial velocity. These boundary surfaces are colored by the radial distance from the casing wall of the BL geometry normalized by the radial height of the main flow passage. The rotor tip clearance is about 0.8% of the passage radial height. The blockage created by the rotor tip leakage is visualized at two different operating points: OP-A and OP-B of
Figure 6a.
Figure 11a visualizes the flow blockage in the BL case at its near-stall condition (OP-A). This blockage is caused by the volume between the zero-velocity iso-surface of
Figure 11a and the casing becoming filled by low-velocity fluid from the breakdown of the tip leakage vortex. This is an unwanted feature. In the cases with the RC (Case #1.-1, Case #0, and Case #1.1), the predicted blockage volume at the same operating condition (OP-A) is visibly smaller than in the BL case. Furthermore, at this operating condition, the blockage volume of Case #1.-1 looks smaller than that of Case #0 and of Case #1.1. This clarifies the effect of the RC injection described in
Figure 7 and
Figure 8 on the main passage flow. Case #1.-1 provides the most intense injection of axial momentum that adds to the main passage flow. This transfers axial momentum to the main passage flow, so that a greater portion of the main passage fluid moves in the positive axial direction, toward the passage exit. This reduces the reverse flow volume close to the casing, as shown in
Figure 11b. In Case #0, the flow blockage is partly suppressed at the middle pitch of the RC outlet, while it is bulged at the channel outlet near the blade LE. This is probably caused by the radial velocity component of the injected flow from the casing channel, which locally deflects the flow in the negative radial direction just below the RC outlet in the two-dimensional numerical prediction of
Figure 4a. At the higher loading condition (OP-B), the volume of separated flow near the casing is larger than that at OP-A for the three cases (Case #1.-1, Case #0, and Case #1.1). This most likely causes a higher blockage. The size of the volume of separated flow in Case #1.1 is larger than that of Case #0 and a larger blockage appears to be generated around the blade LE on the blade pressure side in Case #1.1. This is consistent with the earlier stall inception predicted in Case #1.1 in
Figure 6a than in Case #0.
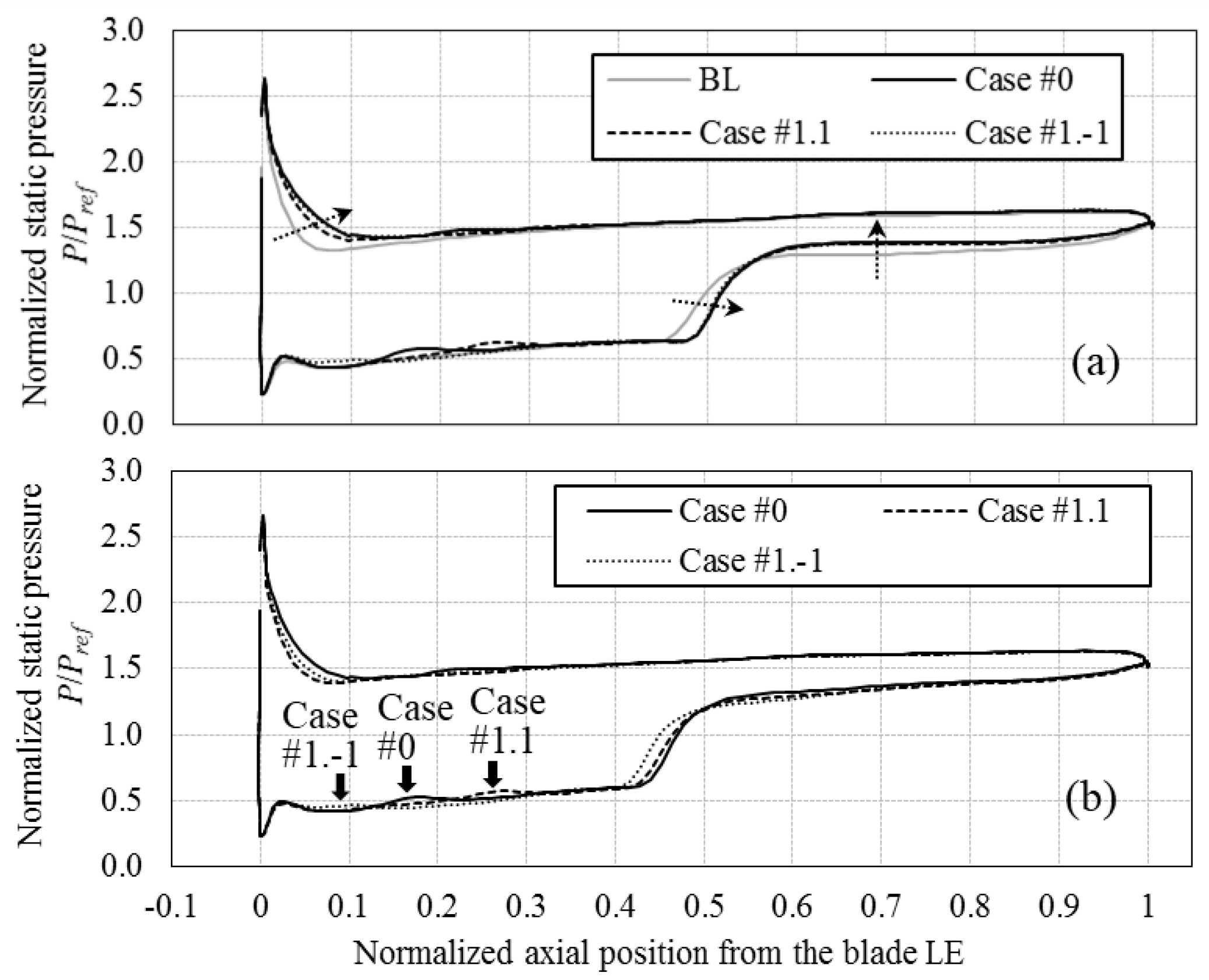
Figure 12 shows how the blade loading near the casing is changed by the action of the RC. Specifically,
Figure 12 shows the normalized static pressure distribution at 0.98 span from the rotor blade root.
Figure 12a compares the blade loadings among four cases at the operating condition OP-A, which corresponds to the stable operating range limit of the BL case.
Figure 12a shows that adding the RC reduces the sharpness of the normalized static pressure peak on the PS leading edge. The flow induced through the channel requires a positive pressure difference between the channel inlet and outlet. The broadening of the pressure peak towards the blade trailing edge provides pressure at the channel inlet and therefore benefits the production of the controlling flow through the RC. Over the blade suction side,
Figure 12a shows that adding the RC moves the axial location where the passage shock impinges on the blade surface from about 0.46 axial chords to about 0.49 axial chords. The pressure rise across the shock, as indicated by the vertical arrow in
Figure 12a, slightly increases.
Figure 12b shows corresponding results of blade loading at the operating condition OP-B. This figure does not include the result of the BL case, as the BL case stalls at a lower pressure ratio and therefore never reaches this operating condition.
Figure 12b shows that changing the RC axial position affects the location where the passage shock impinges on the blade suction side (SS). This is displayed in
Figure 12b by the sharp rise in static pressure that takes place between 0.4 and 0.5 axial chords. Specifically, Case #0 gives the most downstream shock impingement location, whereas both Case#1.-1 and Case #1.1 locate the passage shock wave upstream.
In all three RC cases, the static pressure on the blade SS increases at the RC, where indicated by the filled arrow for each case in
Figure 12b. This shows a local reduction in the blade loading by flow injection between 0.1 and 0.3 axial chords. In spite of this localized reduction in blade loading,
Figure 12 shows that introducing the RC maintains and possibly increases the rotor tip blade loading. This effect is quite different with respect to more conventional rotor tip treatments that off-load the rotor tip to reduce secondary flow losses and increase the stall margin, such as circumferential lean, sweep, or taper. This sets the RC treatment described in this work apart from three-dimensional blade treatment reported in the literature, as it enables to gain stall margin without compromising on performance, by retaining good blade loading in the rotor tip region.
Figure 12 indicates that the largest area endorsed by the normalized pressure distribution, hence the highest loading, is achieved at both OP-A and OP-B with the RC positioned as in Case #0.