Abstract
Among the most important variables in the design of falling film microreactors (FFMRs) is the liquid film thickness as well as the gas/liquid interfacial area, which dictate the mass and heat transfer rates. In a previous work conducted in our lab the characteristics of a free-falling Newtonian liquid film have been studied and appropriate correlations have been proposed. In this work the geometrical characteristics of a non-Newtonian shear thinning liquid, flowing in an inclined open microchannel, have been experimentally investigated and design correlations that can predict with reasonable accuracy the features of a FFMR have been proposed. The test section used was an open μ-channel with square cross section (WO = 1200 μm) made of brass which can be set to various inclination angles. The liquid film characteristics were measured by a non-intrusive technique that is based on the features of a micro Particle Image Velocimetry (μ-PIV) system. Relevant computational fluid dynamics (CFD) simulations revealed that the volume average dynamic viscosity over the flow domain is practically the same as the corresponding asymptotic viscosity value, which can thus be used in the proposed design equations. Finally, a generalized algorithm for the design of FFMRs, containing non-Newtonian shear thinning liquids, is suggested.
Keywords:
free-flowing film; FFMR; inclined μ-channel; non-Newtonian; shear thinning; μ-PIV; meniscus 1. Introduction
The term process intensification describes the methodology which aims to build smaller, more compact and cheaper systems. Microfluidics, i.e., the technology that concerns the manipulation of fluids at the submillimeter scale, has shown considerable promise for improving diagnostics and biology research [1]. Among other potential applications, microfluidics includes fluid handling and quantitative analysis in healthcare and veterinary medicine [2]. During the last decades, engineers have developed various micro-devices which have at least one characteristic dimension less than 1 mm and can be potentially used in biological and medical applications. These microdevices are also characterized by low consumption of reagents and multifunctionality, as various unit operations can be combined in a single piece of equipment.
Microreactors are among the widely studied microdevices, since they have significant advantages over conventional ones [3]. Falling film microreactors (FFMRs) are liquid–gas phase contact devices in which the aim is to generate thin liquid films and to achieve large contact areas between the two phases. The large gas/liquid interface which provides enhanced mass transfer rates between the phases is included between the main advantages of micro-reactors [4]. Biomedical applications involve body fluids, such as blood, saliva, semen, mucus, that are fluids which exhibit non-Newtonian shear thinning behavior.
Most of the published work concerning FFMR deals with the conversion rate of specific reactions (e.g., [4,5]), while limited work [6,7] has been published on the characteristics of the interface in such devices. For example, Ishikawa et al. [8], have studied the CO2 absorption into a wavy falling film of NaOH aqueous solution on a micro-baffled plate using two methods for visualizing the liquid film thickness. The first method uses the light reflection from a small angle (5°), that illuminates the liquid surface of a liquid film at another angle (45°). The second one is a particle injection method. More specifically the particles are PMMA slurry that can be detected and form the liquid film layer. Lokhat et al. [9], also studied, via CO2 absorption experiments, the influence of a reaction plate orientation and gas flow rate on liquid phase mass transfer coefficient. They proposed correlations that are based on Nusselt’s condensation theory. Tourvieille et al. [6], have visualized the liquid film thickness using fluorescence confocal microscopy, and they proposed correlations for determining the mass transfer coefficient, using Nusselt and Kapitza numbers. Yang et al. [10], who have investigated the liquid film thickness and the shape of the interface on an open channel FFMR using stereo digital microscopy, also proposed an empirical correlation, that predicts their experimentally measured liquid film thickness with 7% deviation. Patel et al. [11], have proposed another technique for the characterization of the interface between the liquid and the gas phase in a microchannel, using tracing particles and a microscope, and proved that this technique can reach the accuracy of 1.06 μm, without proposing any correlations for this specific method. Yu et al. [7], have experimentally measured the meniscus shape and the characteristics of the flow in inclined open rectangular microgrooves heat sinks using micro Particle Image Velocimetry (μ-PIV), and found that the meniscus shape is a parabolic arc.
In a previous work conducted in our lab the characteristics of a free falling Newtonian liquid film have been studied [12] and correlations have been proposed [13]. The aim of the present study is to extend our previous work [12,13] by performing experiments with non-Newtonian shear-thinning liquids and to check whether these correlations are valid for this type of fluids. Our ultimate goal is to propose an algorithm for the design of FFMRs.
2. Experimental Procedure
In a previous work of our group [12], a μ-PIV system, i.e., a non-intrusive method intended for measuring 2D velocity fields in microfluidics, was suitably adapted to measure the liquid film thickness and to reconstruct the shape of the interface of a free-flowing Newtonian liquid layer in an open μ-channel. In the proposed technique the area covered by the liquid phase is identified by recording the fluorescent particles used in μ-PIV for measuring the velocity field.
2.1. Experimental Setup
The experimental setup (Figure 1) comprises the test section, i.e., the open microchannel, which is connected to a syringe pump (AL-2000, World Precision Instruments®, Sarasota, FL, USA) to feed the liquid and the μ-PIV system. The μ-PIV system used consists of a high sensitivity charge-coupled device (CCD) camera (Hisense MkII, Dantec Dynamics®, Skovlunde, Denmark), which is connected to a microscope (Nikon Eclipse LV150, Nikon Corporation®, Tokyo, Japan), while the acquired images were processed by the Flow Manager Software (Dantec Dynamics, v4.00). Prior to measurements the fluids were traced by adding Nile red fluorescent carboxylate microspheres (Invitrogen, Carlsbad, MA, USA) with mean diameter of 1 μm. The measurements were conducted 30 diameters downstream from the inlet of the microchannel, where fully developed flow is established. The test section was placed on the microscope stage, which can be moved along its vertical axis with ten-micron accuracy. To obtain sufficiently magnified images a 20× air immersion objective with numerical aperture (NA) equal to 0.45 was used, which results in 3 μm depth of field. The maximum recording frame rate of the camera is 12.2 fps and that restricts the maximum frequency of the measurements to 12 Hz. The field of view was covering the whole channel width.
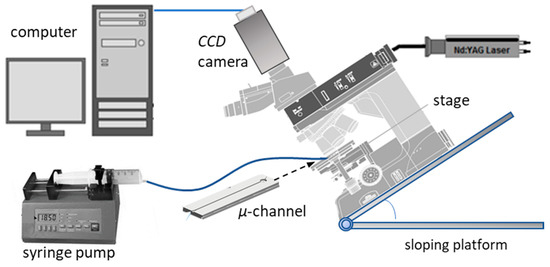
Figure 1.
The experimental setup.
The test section used (Figure 2) was an open μ-channel, with square cross section (WO = 1200 μm), made of brass. The test section was constructed by employing ultrahigh precision micromachining techniques, which have the unique advantage of being able to manufacture geometrically complex miniature components to high accuracy, with fine surface finish, in a wide range of engineering materials. The test-section used in the present was constructed using a five-axis ultra-precision micro milling machine that ensures both minimal surface roughness and straightness of the channels. Typical overall values of repeatability, surface finish and straightness achievable by this procedure are in the range of 1.0 μm, 0.040 μm Ra, and 0.2 μm over 100 mm of travel respectively. The channel was milled using a 500 μm cutter at 200 μm steps, while to ensure minimal surface roughness, a final 20 μm cut was performed.
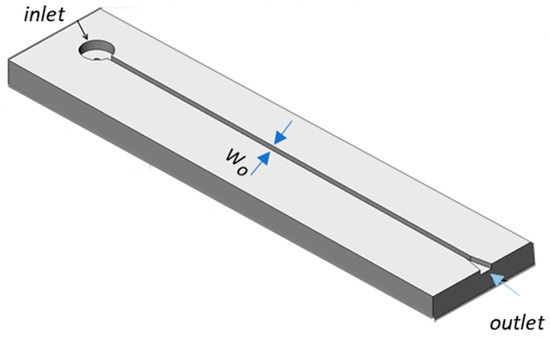
Figure 2.
Details of the brass μ-channel.
To assure continuous free flow, the liquid phase enters by overflowing a circular region preceding the inlet of the microchannel. To conduct the measurements, the lens axis must be perpendicular to the test section and so the microscope was placed on platform that can be tilted up to 45° from the horizontal position (Figure 1). The measurements were conducted at three inclination angles, namely 20°, 25°, and 30°.
Two non-Newtonian shear thinning fluids were used. Presented in Table 1 are their physical properties, i.e., density, ρ, surface tension, σ, and the contact angle (for brass) measured by a tensiometer (KSV Cam200, KSV Instruments®, Helsinki, Finland), and dynamic viscosity, μ, measured by a magnetic rheometer (AR-G2, TA Instruments, Sussex, UK). All properties were evaluated at room temperature (20–22 °C), and the experiments were conducted under the same conditions. The viscosity of the shear-thinning non-Newtonian fluids used can be accurately described by the Herschel–Bulkley model [14]:
where, , is the yield stress, K, the viscosity consistency and n, the power law index. The physical properties of the fluids are shown in Table 1, while, for the liquids employed, Figure 3 presents the dependence of viscosity on shear rate.

Table 1.
Physical properties of liquids used.
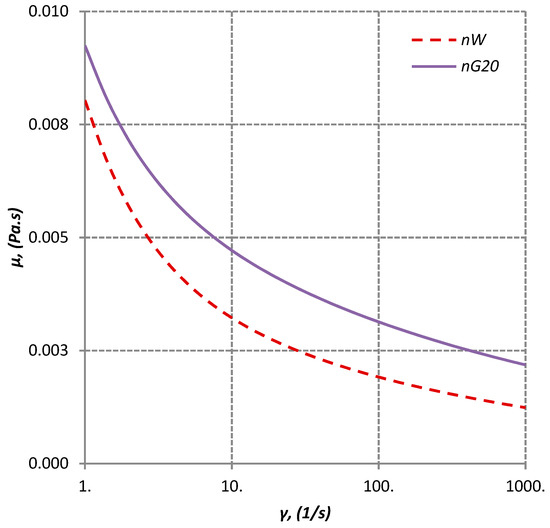
Figure 3.
Viscosity curves of the two non-Newtonian liquids used.
2.2. Measuring Procedure
As already mentioned at the experimental set-up section, μ-PIV measurements require the injection of fluorescent tracing particles into the fluid. Consequently, in each focusing plane, the liquid phase corresponds to areas where light spots are visible, the external dark areas are identified as the walls of the microchannel, whereas the inner dark area corresponds to the gas phase (Figure 4). The use of proper microscope objectives ensures a narrow depth of field, which in turn increases the measuring accuracy, since the focus plane can be moved with a steady step of 10–20 μm resulting in to the recording of 20–25 planes per measurement.
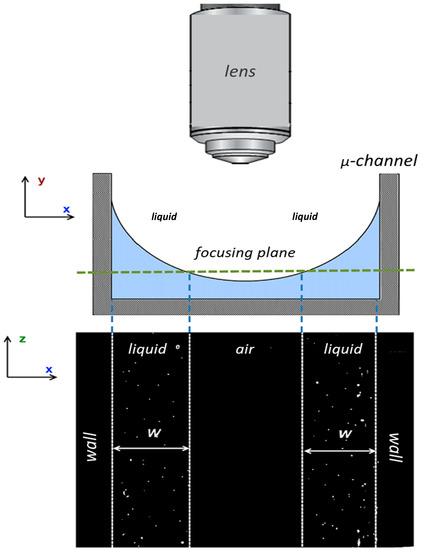
Figure 4.
Identification of the liquid phase using fluorescent particles.
The measuring system was calibrated by measuring a known liquid film thickness, i.e., by measuring the thickness of the liquid layer obtained when a known liquid volume is placed in a vessel with known cross-section. It must be noted that during the measurements the displacement of the focusing plane due to refraction was also considered.
During each measurement, the plane, where the tracing particles are initially visible, is recognized as the first plane of the measurements. When the bottom of the meniscus, i.e., the plane where the liquid covers the entire area, is reached, no dark regions are observed. By further moving the focusing plane, an area where no particles are visible in reached, which is identified as the bottom of the microchannel. The liquid film thickness is the distance between the bottom of the meniscus and the bottom of the microchannel. The shape of the meniscus can be reconstructed by combining the results corresponding to the various focusing planes. A typical reconstruction of the film is presented in Figure 5. As expected, the film is symmetrical with respect to the center plane of the channel and thus, to minimize effort, the measurements were taken only at one half of the channel. Figure 6 shows the main geometrical characteristics of the liquid film and a typical photo of it.
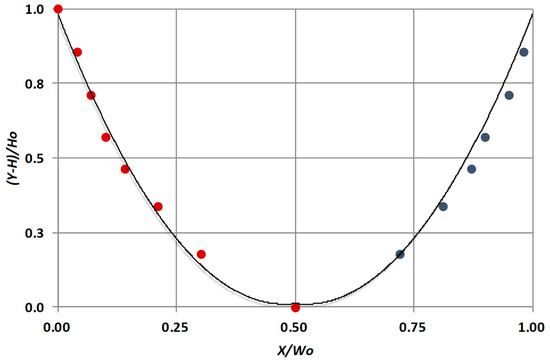
Figure 5.
Typical measurements of the liquid film (nW, 40 mL/h, inclination angle 25°) where X is the distance from vertical wall and Y the distance from the channel bottom.
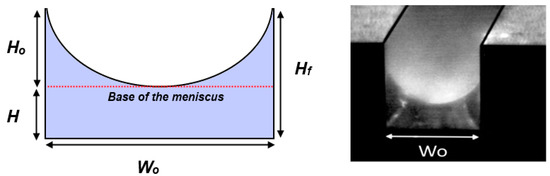
Figure 6.
(a) Geometrical characteristics of the liquid film; (b) Typical photo of the film at the channel exit.
3. Results and Discussion
3.1. Liquid Film Thickness Calculation
In our previous work [13], according to the Rayleigh method of dimensional analysis, it was found that the film thickness H can be calculated as a function of modified dimensionless numbers, i.e., Reynolds (Re), Froude (Fr) and Capillary (Ca) number.
The dimensionless numbers use the channel width (WO) as the characteristic length and the superficial velocity (US) defined as the volumetric flow rate divided by cross section of the meniscus. By inserting the aforementioned quantities, the dimensionless numbers are defined as follows:
with gφ being the component of the acceleration of gravity that acts in the direction of flow, i.e., gφ = g sin(φ) and φ is the inclination angle from the horizontal.
where ρ, μ and σ are the density, the viscosity and the surface tension of the fluid. In our case, where non-Newtonian liquids are used, an effective viscosity, i.e., a representative viscosity value along the whole domain, must be specified. To evaluate this viscosity, we have performed relevant CFD simulations.
3.2. Effective Viscosity Prediction
For the sake of computational simplicity, simulations were performed by forcibly imposing on the computational model the geometrical features of the liquid falling film, which are experimentally obtained. Namely, the experimentally measured parabolic surface profile was manually modeled and set as a free-slip wall boundary condition. At the bottom and at the two side walls of the domain the no-slip wall boundary condition was applied (Figure 7). Two liquid flow rate values were tested, i.e., 40 mL/h and 80 mL/h.
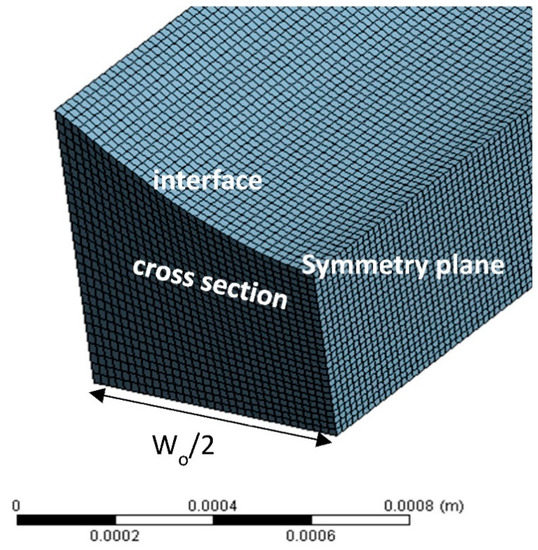
Figure 7.
Grid density of the simulation.
The governing equations for the fluid flow are the Navier–Stokes equations and the continuity equation for incompressible and non-Newtonian flow. The fluid domain was discretized using tetrahedral elements and a symmetry plane was used to halve the problem for lowering computational costs. Total cell number varied for every case tested; from about 180,000 to about 240,000 cells. All simulations were performed using a commercial CFD code, the ANSYS CFX® (v. 19, ANSYS Inc., Canonsburg, PA, USA). ANSYS CFX® provides a finite volume method, a fully coupled solver for pressure and velocity coupling. The Direct Numerical Simulation (DNS) method for laminar flow was employed for the solution, as the flow in the μ-channel does not present any turbulent phenomena. Figure 8, shows the dynamic viscosity distribution at cross section, which was placed 100 widths downstream from the inlet to minimize inlet disturbances.
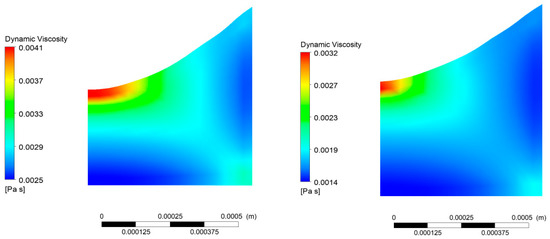
Figure 8.
Dynamic viscosity distribution on a cross section located 30 WO downstream from the channel entrance (left to right): nW_40; nG20_40.
Figure 8 presents typical dynamic viscosity distributions, calculated by CFD simulation, at a plane perpendicular to the flow direction and located 30 hydraulic diameters downstream from the liquid entrance. It worth mentioning that there are areas near the interface where the viscosity attains its higher value.
The volume averaged viscosity values predicted by the CFD simulation were compared with the asymptotic viscosity of the liquid, proving that the maximum difference is less than 8% (Table 2). We must also consider that the viscosity measurement has an inherent uncertainty of 8%. Consequently, the asymptotic viscosity, which is known a priori, can be used in Equations (3)–(5).

Table 2.
Average and asymptotic viscosity for the liquids tested.
The acquired data were appropriately fitted and the constants of Equation (2) were estimated (Table 3) and compared with the ones found for the same substrate type (i.e., brass) but for Newtonian fluids. It has been reported that for Newtonian fluids the constant C of Equation (2) depends on the type of the substrate material [15]. The present work proves that it also depends of the nature of the fluid, i.e., Newtonian or non-Newtonian, because for the same substrate type the non-Newtonian fluids result in thicker films. Although the volume averaged viscosity over the domain is almost the same as the corresponding asymptotic viscosity (Table 2), there are areas near the interface, where the viscosity values are much higher (Figure 8). Consequently, the liquid flow is expected to decelerate resulting in thicker films. As it can be seen in Figure 9, Equation (2) can predict with reasonable accuracy (less than ±15%) the liquid film thickness for the fluids, flow rates and inclination angles tested.

Table 3.
Constants of Equation (2) for film thickness correlation.
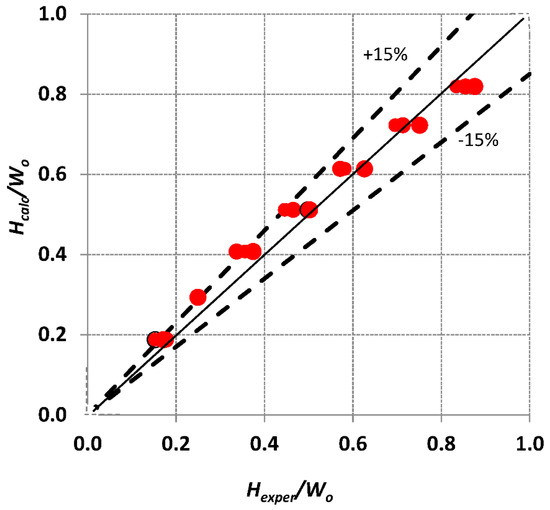
Figure 9.
Comparison between experimental and calculated by Equation (2) liquid film thickness, H, normalized with respect to the channel width for the various non-Newtonian liquids, liquid flow rates and inclination angles tested.
3.3. Meniscus Shape
It is obvious that in FFMRs the concave shape of the interface augments the interfacial area. Thus, a characteristic that we must be able to determine during the design of an FFMRs is the shape and length of the gas–liquid interface (Figure 6a). In our previous work [13] it was shown that the shape of the meniscus can be accurately represented by a second order polynomial:
where X is the distance from the side wall, while the constants of the equation are defined as:
where, Hf is the height where the three-phase contact is pinned, which for shallow μ-channels equals the channel’s depth and H is the height of the meniscus (Figure 6a) that can be calculated by Equation (2).
C = Hf − H
A = −BWO
Figure 10 presents the variation the meniscus height over the substrate divided by its maximum height along the channel width for the liquids, flow rates, and inclination angles studied. Figure 11 presents a comparison between the experimentally obtained meniscus profile and the one calculated by Equation (6). It is proved that Equation (6) can estimate the meniscus shape with reasonable accuracy (less than ±10%), for all the cases studied.
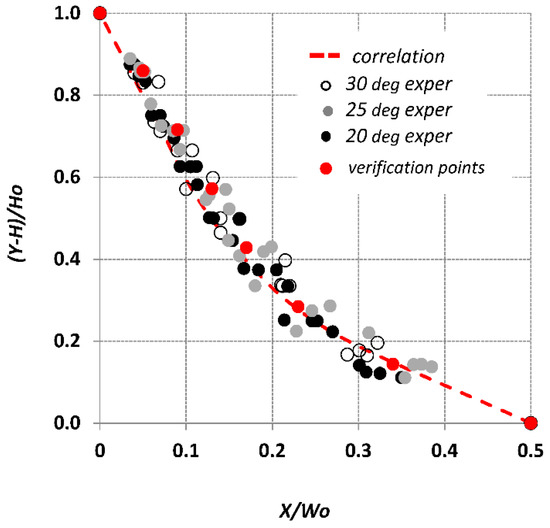
Figure 10.
Comparison of the shape of the interface calculated by Equation (6) with relevant experimental data.
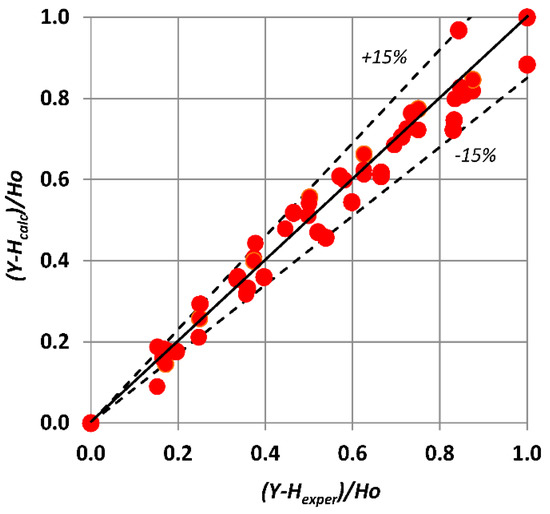
Figure 11.
Comparison between experimental and estimated local meniscus height.
Figure 12 verifies the assumption that the asymptotic viscosity (μ∞) can be used for calculating the liquid layer characteristics in place of volume averaged viscosity (μave), estimated by CFD. More precisely, the shape of the meniscus calculated by Equations (2)–(7) using either μ∞ or μave, is compared with the one defined experimentally. Although the curve corresponding to μave fits the experimental data better, the curve calculated using μ∞, which is a priori known, can also predict the meniscus shape with reasonable accuracy, i.e., ±8%, compared with the one based on the experimental data.
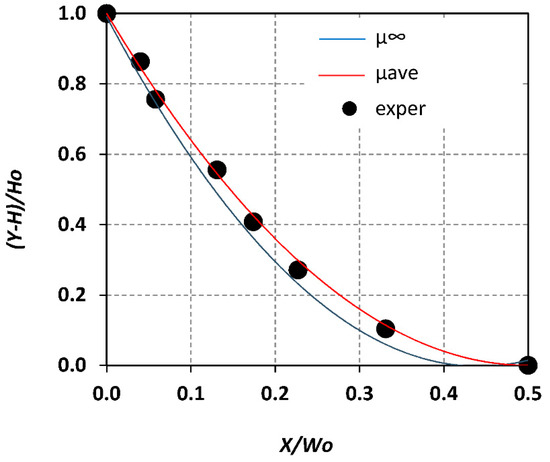
Figure 12.
Comparison of experimental data with curves calculated using asymptotic and effective viscosity (nW, 40 mL/h, 25°).
The length of the parabolic arc (L), i.e., the length of the meniscus (Figure 6a), can be calculated with the following formula [16]:
where HO and WO are parameters defined in Figure 6a. The liquid phase cross section (A) was calculated by:
Consequently, the specific surface (a) is the gas–liquid interfacial area (S) divided by the total fluid volume (V) in the reactor, that is:
whereas the fluid residence time per unit length of the reactor (τ) can be calculated by:
τ = A/Q
Figure 13 and Figure 14 present the effect of flow rate and inclination angle on the specific area and the residence time respectively. It is obvious that for a given flow rate both the specific area and the corresponding residence time can be controlled by altering the inclination angle.
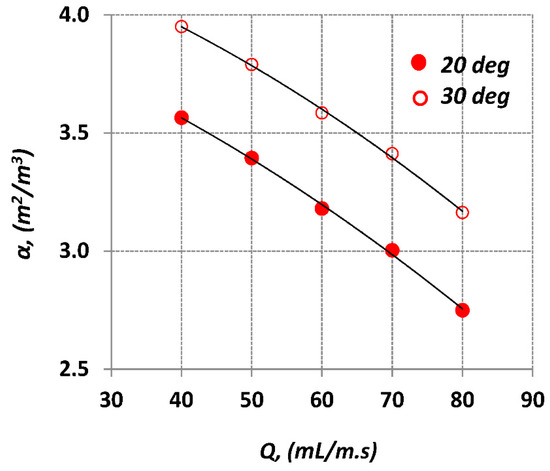
Figure 13.
Effect of liquid flow rate and inclination on the specific surface, for nW.
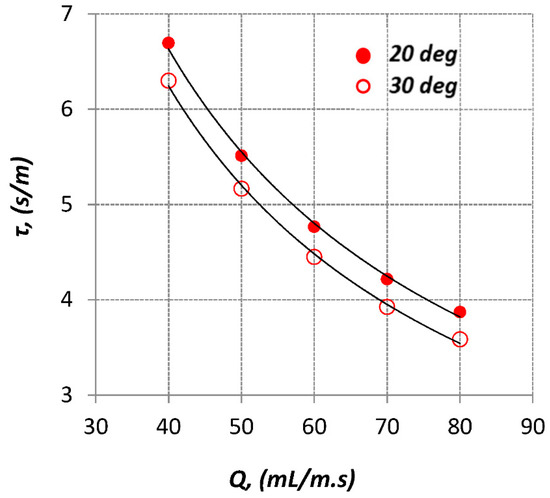
Figure 14.
Effect of liquid flow rate and inclination on the residence time (for nW).
Figure 15 presents a typical meniscus shape that corresponds to a flow rate of 40 mL/h and 25° inclination angle. The interfacial area calculated by the suggested procedure, i.e., Equations (6)–(11), is 15% lower than the one estimated using the experimental data. However, the deviation is considerably higher (i.e., around 30%), if a flat interface is assumed.
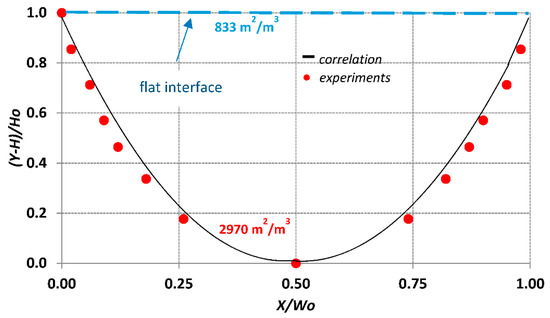
Figure 15.
Comparison of specific surface between the flat interface and the meniscus shape calculated by the proposed correlation Equation (6) for nW, 40 mL/h, 25°.
As a capstone of this study, a generalized algorithm for the design of FFMRs, is proposed (Figure 16). The input parameters of the algorithm are the physical properties and the flow rate of the liquid phase as well as the geometrical characteristics and the inclination angle of the μ-channel. Initially, the film thickness (H) is calculated by Equation (2). Subsequently, the shape of the interface can be determined by Equation (6) using the calculated film thickness (H) and the characteristics of the μ-channel. Finally, based on the calculated shape of the meniscus, the liquid phase cross section (A) can be calculated. Derived from this, important reactor design parameters, i.e., the specific surface (α) and the residence time (τ), can be specified.

Figure 16.
A general strategy for the design of falling film microreactors (FFMRs).
4. Conclusions
The most important features that must be considered during the design of FFMRs are the residence time of the liquid phase as well as the interfacial area per volume of fluid. Consequently, the thickness of the liquid film and the shape of the interface are key parameters for the design of such devices. In this work the geometrical characteristics of the liquid film, created when a non-Newtonian shear-thinning liquid flows in an inclined open microchannel made of brass, have been experimentally investigated.
Based on the experimental data, design correlations that can predict with reasonable accuracy the features of an FFMR design for biomedical applications have been proposed. The mean viscosity of the non-Newtonian fluid is calculated using relevant CFD simulations. It is also proved that the characteristics of the liquid film can be predicted with reasonable accuracy if the asymptotic viscosity (a priori known) is used in place of the calculated average one.
As a matter of fact, the design engineer could apply the proposed methodology to construct or rate an FFMR. Various input parameters, e.g., the inclination angle, can be changed and operating parameters (film thickness, interfacial area, residence time) can be recalculated by the same procedure. More work is certainly needed to investigate the dependence of the constant C (Equation (2)) on the channel material.
Author Contributions
A.A.M. had the initial conception of this work and designed the experiments; A.T.K. performed the experiments; Y.G.S. designed and performed the CFD simulations; A.A.M. interpreted the results; A.A.M., A.T.K. and Y.G.S. drafted the manuscript; A.A.M. reviewed and edited the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Spiros V. Paras for his helpful comments.
Conflicts of Interest
All authors state that there is no conflict of interest.
Nomenclature
| A | liquid phase cross section | μm2 |
| Ca | capillary number | Dimensionless |
| Fr | Froude number | Dimensionless |
| g | acceleration of gravity | m/s2 |
| Hf | height of the microchannel | μm |
| Ho | height of the meniscus | μm |
| H | liquid film thickness | μm |
| L | length of the interface (meniscus) | μm |
| M | objective lenses magnitude | Dimensionless |
| m | mass flow rate | kg/s |
| NA | numerical aperture | Dimensionless |
| Q | volumetric flow rate | mL/h |
| Re | Reynolds number | Dimensionless |
| S | gas–liquid interfacial area | μm2 |
| V | total fluid volume | μm3 |
| X | distance from vertical wall | μm |
| Y | distance from the channel bottom | μm |
| WO | width of microchannel | μm |
| Greek symbols | ||
| α | specific surface | m2/m3 |
| μ | liquid viscosity | Pa·s |
| σ | surface tension | N/m |
| τ | residence time/channel length | s/m |
| ρ | liquid density | kg/m3 |
| φ | inclination angle | ° |
References
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Yetisen, A.K.; Akram, M.S.; Lowe, C.R. Paper-based microfluidic point-of-care diagnostic devices. Lab Chip 2013, 13, 2210–2251. [Google Scholar] [CrossRef] [PubMed]
- Hessel, V.; Löwe, H.; Schönfeld, F. Micromixers—A review on passive and active mixing principles. Chem. Eng. Sci. 2005, 60, 2479–2501. [Google Scholar] [CrossRef]
- Chambers, R.D.; Holling, D.; Spink, R.C.; Sandford, G. Elemental fluorine. Part 13. Gas-liquid thin film microreactors for selective direct fluorination. Lab Chip 2001, 1, 132–137. [Google Scholar] [CrossRef] [PubMed]
- Stavarek, P.; Le Doan, T.V.; Loeb, P.; De Bellefon, C. Flow visualization and mass transfer characterization of falling film reactor. In Proceedings of the 8th World Congress of Chemical Engineering, Montreal, QC, Canada, 23–27 August 2009. [Google Scholar]
- Tourvieille, J.-N.; Bornette, F.; Philippe, R.; Vandenberghe, Q.; de Bellefon, C. Mass transfer characterisation of a microstructured falling film at pilot scale. Chem. Eng. J. 2013, 227, 182–190. [Google Scholar] [CrossRef]
- Yu, D.; Hu, X.; Guo, C.; Wang, T.; Xu, X.; Tang, D.; Nie, X.; Hu, L.; Gao, F.; Zhao, T. Investigation on meniscus shape and flow characteristics in open rectangular microgrooves heat sinks with micro-PIV. Appl. Therm. Eng. 2013, 61, 716–727. [Google Scholar] [CrossRef]
- Ishikawa, H.; Ookawara, S.; Yoshikawa, S. A study of wavy falling film flow on micro-baffled plate. Chem. Eng. Sci. 2016, 149, 104–116. [Google Scholar] [CrossRef]
- Lokhat, D.; Domah, A.K.; Padayachee, K.; Baboolal, A.; Ramjugernath, D. Gas–liquid mass transfer in a falling film microreactor: Effect of reactor orientation on liquid-side mass transfer coefficient. Chem. Eng. Sci. 2016, 155, 38–44. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, T.; Wang, D.; Tang, S. Investigation of the liquid film thickness in an open-channel falling film micro-reactor by a stereo digital microscopy. J. Taiwan Inst. Chem. Eng. 2018. [Google Scholar] [CrossRef]
- Patel, R.S.; Garimella, S.V. Technique for quantitative mapping of three-dimensional liquid–gas phase boundaries in microchannel flows. Int. J. Multiph. Flow 2014, 62, 45–51. [Google Scholar] [CrossRef]
- Anastasiou, A.D.; Makatsoris, C.; Gavriilidis, A.; Mouza, A.A. Application of μ-PIV for investigating liquid film characteristics in an open inclined microchannel. Exp. Therm. Fluid Sci. 2013, 44, 90–99. [Google Scholar] [CrossRef]
- Anastasiou, A.D.; Gavriilidis, A.; Mouza, A.A. Study of the hydrodynamic characteristics of a free flowing liquid film in open inclined microchannels. Chem. Eng. Sci. 2013, 101, 744–754. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Oxford, UK, 2011; ISBN 978-0-08-095160-7. [Google Scholar]
- Anastasiou, A.D.; Al-Rifai, N.; Gavriilidis, A.; Mouza, A.A. Prediction of the characteristics of the liquid film in open inclined micro-channels. In Proceedings of the 4th Micro and Nano Flow Conference 2014, London, UK, 6–10 September 2014. [Google Scholar]
- Spiegel, M.R.; Liu, J. Mathematical Handbook of Formulas and Tables; McGraw-Hill: New York, NY, USA, 1999; ISBN 978-0-07-038203-9. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).