Abstract
We consider steady, laminar, compressible lubrication flows in a high-speed two-dimensional journal bearing governed by the appropriate Reynolds equation. The thermodynamic states correspond to pressurized gases and are in the single-phase regime. Simple explicit formulas for the load capacity, power loss, and attitude angle are derived by applying the virial (or small density) expansions of pressure and shear viscosity to results developed in previous studies. The present virial approximation was compared to the exact numerical solutions to the Reynolds equation. It was shown that the results based on our virial expansions are quite accurate at thermodynamic states corresponding to dense and supercritical gases. The first virial correction is seen to significantly improve predictions based on the ideal gas theory.
1. Introduction
The canonical equation governing many lubrication flows is the Reynolds equation [1]. Since its introduction in the late 19th Century, it has been generalized to include the effects of three-dimensional unsteady flow, turbulence, non-Newtonian constitutive laws, two-phase flow, and wall slip [2,3,4,5]. Conditions under which the Reynolds equation is valid are satisfied in many devices [6,7,8,9,10]. An important motivation for the use of the Reynolds equation is that it provides a relatively simple, computationally-efficient, and easily-reproducible context in which to examine physical effects and mathematical models.
Recent interest in novel power systems have motivated the use of gases rather than highly viscous oils [11,12,13,14,15]. The advantages of gases over liquids include weight reduction, elimination of complications associated with fouling due to leaks and complications due to phase changes, and the compatibility with working fluids of the parent power system.
Because the viscosity of gases is smaller than that of oils, gas lubrication requires high speeds to support reasonable loads, and the resultant flows are very often compressible. The overall compressibility of the flow is usually characterized by the speed or bearing number defined as a non-dimensional measure of the flow speed; a precise definition of the version of the speed number used here will be given in the next section.
In most of the previous investigations of gas lubrication, the ideal gas model was employed [3,11,16]. One of the first analytical studies is due to Gross et al. [3], who developed approximations to the Reynolds equation valid for large speed numbers and ideal gases. It was shown that the first correction for finite speed number to the lowest-order, i.e., that corresponding to an infinite speed number, load and loss of a simple journal bearing is of the order of the inverse square of the speed number. For journal bearings lubricated with ideal gases, Gross et al. [3] provided explicit formulas for load and loss in terms of the speed number and eccentricity.
When the pressures are on the order of those of the thermodynamic critical point, the gas can no longer be regarded as ideal, and more complex gas models must be employed. In order to investigate the effects of pressurized gases on bearing performance, previous studies [17,18,19,20] have numerically solved the Reynolds equation along with digital table look-ups to capture the real gas behavior. Conboy [17], Kim [18] and Qin [19] used the NIST REFPROPdatabase [21], while Guenat and Schiffmann [20] employed the COOLPROPdatabase [22].
At the thermodynamic critical point, properties such as the specific heat at constant pressure and the thermal expansivity are singular; as a result, the Prandtl number is also singular at the thermodynamic critical point. Additionally, the bulk modulus:
where , T > 0, and p = p(,T) are the fluid density, absolute temperature, and thermodynamic pressure, is seen to be zero at the thermodynamic critical point and has a non-monotone variation with density at constant temperature.
A plot of a scaled version of Equation (1) is provided in Figure 1. Recognition of the singular behavior of high pressure gases has led [23] to examine the validity of the Reynolds equation in the general single-phase regime. These authors have given a careful derivation of the Reynolds equation and corresponding temperature equation valid for compressible flows of pressurized gases. The usual constraints of a thin fluid layer and small lubrication Reynolds number were imposed along with mild conditions on any imposed temperature differences. The resultant form of their Reynolds equation is given in the next section. The Reynolds and temperature equations of [23] were found to be valid over most of thermodynamic states corresponding to ideal, dense, and supercritical fluids, but were seen to break down simultaneously in the near-critical regime. The size of this near-critical region was given in terms of the lubrication Reynolds number; see, e.g., Section IV of [23]. It was shown by [23,24] that, within the stated region of validity, the solutions to the Reynolds and temperature equation of [23] were found to be in excellent agreement with the Navier–Stokes equations.
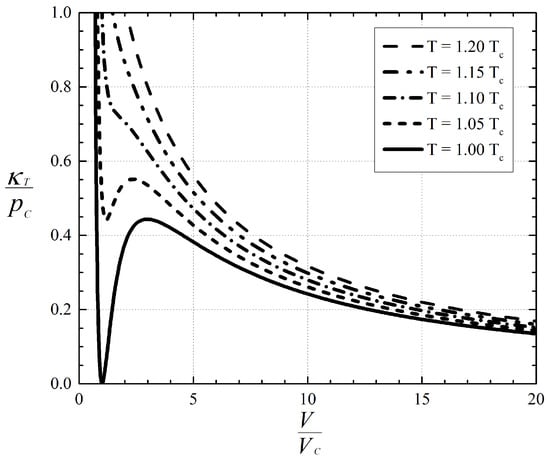
Figure 1.
Variation of the scaled bulk modulus with reduced specific volume for CO. Subscripts “c” will always denote quantities evaluated at the thermodynamic critical point and V = the specific volume. The curves were generated using the Redlich–Kwong–Soave (RKS) equation of state. Details of the RKS equation are given in [25] along with the physical constants for CO.
Chien and Cramer [26] derived approximate solutions to the Reynolds and temperature equation of [23] valid for pressurized gases and large speed numbers. Explicit expressions for the local density, pressure, temperature, and heat flux were given in terms of the bulk modulus, shear viscosity, thermal conductivity, thermal expansivity, Prandtl number, speed number, and the film thickness. In [27], Chien and Cramer used approximations, which are second-order in the speed number, to derive general expressions for the load, loss, and attitude angle for a two-dimensional journal bearing. For convenience, the relevant results of [27] are recorded in the next section. While the results are explicit, the results require the numerical evaluation of a number of integrals if the gas model is more complicated than that of an ideal gas. Numerical integration will also be required if the fluid properties are supplied by digital table look-ups.
The goal of the present investigation is to develop a simplified model for the load, loss, and attitude angle based on virial, i.e., small density, expansions of the pressure and shear viscosity. The resultant expressions will obviate the need for numerical evaluations of the integrals and provide explicit expressions for the load, loss, and attitude angle in terms of the first virial coefficient for pressure and a reference viscosity.
2. General Formulas
We begin with the general formulas for the load, loss, and attitude angle derived in [27] for large speed number. These formulas were derived by finding the second-order approximations to the Reynolds equation of [23,24] and then integrating the results for pressure over the journal bearing configuration sketched in Figure 2. The Reynolds equation is valid for steady, two-dimensional, compressible, laminar, single-phase flows at thermodynamic states sufficiently far from those of the thermodynamic critical point. Again, we refer the reader to [23,27] for details, derivations, and validation of these results. In the following, we summarize the principal results of [27], which form the basis for the present study.
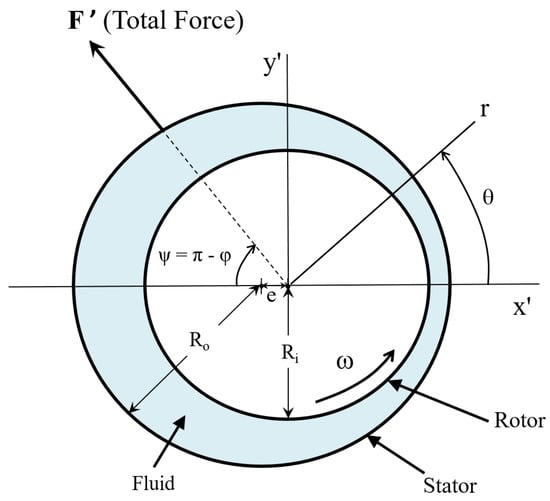
Figure 2.
Sketch of two-dimensional journal bearing. The angular velocity of the rotor = constant. The angle is the angle between the force F and the positive x axis. The angle .
The configuration considered in this study is a two-dimensional, infinitely-long journal bearing as sketched in Figure 2. The inner cylinder corresponds to the rotor, which has a radius R and is centered at x = 0 and y = 0. The rotor rotates at a rate of = U/R, where the constant U is the speed of the surface of the inner cylinder. The outer cylinder represents a stator, which is stationary and has a radius = R R. The center of the stator is located at x = − e ≡ − (R − R), y = 0. Here, is the eccentricity.
We take the gap between the rotor and stator to be sufficiently small compared to their radii. We can then approximate the flow using the unwrapped configuration sketched in Figure 3. The film thickness is given by the function h(x); the surface of the stator is taken to be y = h(x); and the surface of the rotor is to be given by y = 0. The coordinate x is the distance taken along the inner cylinder, i.e., the rotor, and is related to the angle by 2 where L ≡ 2R is the circumference of the rotor. The coordinate y is taken to be normal to the rotor. The minimum film thickness occurs at the origin and is given by , and the maximum thickness is h = h( = 2). Because of the periodicity of the physical configuration and the choice of the coordinate system,
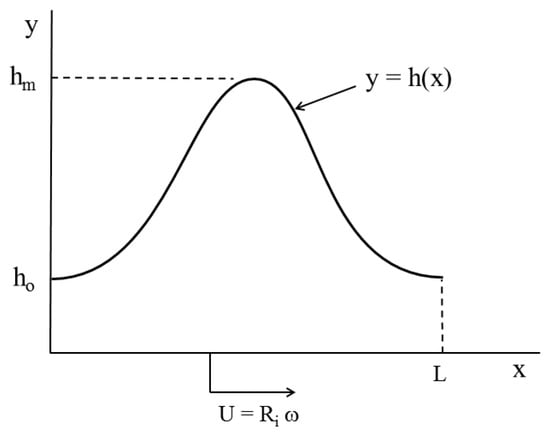
Figure 3.
Unwrapped configuration: The surface y = 0 corresponds to the surface of the inner cylinder, i.e., the rotor. The surface corresponds to the surface of the outer cylinder, i.e., the stator. The minimum film thickness is taken to be h(0), and the maximum film thickness is taken to be h .
The general results of [27] were obtained using the relatively weak condition on that it is symmetric about or = , i.e.,
The formulas derived in Section 5 use an explicit form of corresponding to a two-dimensional journal bearing sketched in Figure 2. When the gap width is small compared to the radii of the rotor and stator, we find that can be approximated by:
where = , and the parameter is related to the eccentricity by .
In terms of the unwrapped configuration of Figure 3, the non-dimensional form of the Reynolds equation derived by Chien and Cramer [23] is:
subjected to the periodicity condition:
Here, , and:
is the scaled fluid density. The subscript “ref” will always refer to a reference thermodynamic state; throughout this study, we take this reference state to be that at the minimum gap thickness, i.e., at = 0, 1 or, equivalently, = 0, 2. The thermodynamic function:
is the effective bulk modulus, which gives a measure of the relative strength of the local fluid stiffness to the fluid friction. The quantity = (,T) > 0 is the shear viscosity. The scaled version of the effective bulk modulus, i.e., Equation (11), is:
As in the classical lubrication theory, the flow may be regarded as isothermal for the purposes of computing the density and pressure. The temperature is therefore taken to be T throughout this calculation. The constant:
is the speed number. This form is the one that arises naturally during the non-dimensionalization process when pressurized gases are of interest.
For 1, the work in [27] has shown that the net force on the rotor seen in Figure 2 can be written as:
where F is the dimensional force, p is the pressure at the thermodynamic critical point, and b is the length of the bearing in the axial direction, i.e., the direction orthogonal to the diagrams of Figure 2 and Figure 3. The quantities I, I, and I arise naturally in the course of the derivation of [27] and are defined as:
where:
The subscripts “o” denote quantities evaluated at the lowest order density /, e.g.,
The attitude angle () is defined as the angle between F and the positive x axis seen in Figure 2, and was found to be:
Because both I and I are always < 0, the force on the rotor will always lie in the second quadrant of the x − y plane sketched in Figure 2. It will therefore be convenient to define the associated acute angle .
Under the same conditions, the work in [27] has shown that the scaled power loss can be written as:
where P is the dimensional power loss having units of energy per time, and negative if fluid friction opposes the motion of the rotor. The quantity:
is the shear viscosity scaled with the reference value. The evaluation of the scaled viscosity in the first integral on the right-hand side of Equation (21) can be done by using the second-order expression for density derived by [27] or by expanding (,T) in a Taylor series. In [27], the first approach was used in detailed numerical examples. Each approach will give approximations that are consistent with the accuracy of [27]. Here, it will be convenient to use the second approach. We first expand in a Taylor series for densities near the lowest-order density distribution, i.e., near . This expansion reads:
where, as pointed out above,
and the derivatives are to be evaluated at 1/ and T = T. If we further use the second-order expansion for the density, we have:
where and are O(1) expressions given in [27]. Substitution in Equation (23) and the first integral on the right hand side of Equation (21) yields:
where the symmetry condition, i.e., Equation (5), has been used to show that the O() contribution is identically zero.
3. Virial Expansion of Pressure and Bulk Modulus
The ideal gas theory is valid at low pressures. In particular, the densities are taken to be small compared to those at the thermodynamic critical point, i.e., when:
where the subscript “c” will always denote quantities evaluated at the thermodynamic critical point. Thus, the expansion of pressure in a power series for small density and constant temperature can be written as:
where the B = B(T) are referred to as the virial constants and R = the gas constant. In order that p = p(,T) RT as 0, we require that B = 1, so that:
Here, B will be referred to as the first virial coefficient. We now define a nondimensional version of this factor as:
so that:
Here, we have chosen to rescale B with a minus sign due to the fact that the first effect of intermolecular forces is to lower the pressure relative to the ideal gas value as the density is increased from zero.
The bulk modulus, i.e., Equation (1), is calculated to be:
At the reference density and temperature, the bulk modulus is:
where:
is the small parameter associated with the virial expansion. The quantity:
4. Virial Expansion of the Shear Viscosity
We now expand the shear viscosity in a virial, i.e., small density, expansion,
In order that as 0, we require that a(T), so that Equation (39) can be written as:
where:
We refer to a as the first virial coefficient of and Equation (41) as the scaled first virial coefficient of . When the viscosity is evaluated at the reference state, we have:
where . For future use, we note that:
5. Virial Expansions of Load, Loss, and Attitude Angle
We now substitute our virial expansions of the scaled bulk modulus and viscosity in Equations (14)–(17), (21), (48), and (20). We will retain only terms that are first-order in the small density expansion, i.e., those of order , and only terms that are second-order in the speed number , except in the case of the attitude angle, where we drop all terms o(). We therefore will provide the first corrections to the theory of ideal gases. Note that any terms multiplied by can be evaluated in the ideal gas state, i.e., at = 0. Thus, Equations (15)–(17) become:
If we now substitute the explicit expression for the film thickness, i.e., Equation (6), in Equations (49)–(51), we find:
where the factors:
Through substitution of Equations (52)–(54) in Equation (14) and straightforward manipulation, we then obtain the virial expansion of the load,
where:
and we have recognized that Equation (33) can be rewritten as:
Here:
is the critical compressibility.
If we substitute Equations (52) and (54) in Equation (20), we obtain the virial approximation to the attitude angle:
where we have used Equation (43).
The expression for virial expansion of the power loss is obtained by substituting Equations (7), (37), and (45) in Equations (48) and (21), yielding:
Equations (57), (61), and (62) give the dependence of the load, attitude angle, and power loss in terms of the eccentricity (through ), the specific gas model, the speed number, and the degree of pressurization. In the ideal gas limit, i.e., as 0, , Equations (57) and (62) become:
Because 0 and , further inspection of Equations (57) and (62) shows that the load and loss will always be less than that predicted by the ideal gas theory when 0. That is, the ideal gas theory will always overpredict the value of the load and loss, at least in the near-ideal and dense gas regime.
Because the shear viscosity increases with pressurization along isotherms, Equation (62) is consistent with the observations of [27] that undergoes a weak decrease as the fluid is pressurized, at least in the near-ideal and dense gas regimes. At this level of approximation, the effect of pressurization on the scaled loss, i.e., Equation (62), is determined by the ratio:
which [27] have pointed out tends to be nearly independent of temperature, particularly in the near-ideal and dense gas regime. This fact is illustrated in the next section as well. The independence of the scaled loss with temperature is consistent with the more comprehensive computations of [27].
In the ideal gas limit, the attitude angle, i.e., Equation (61), reduces to:
A comparison of Equations (65) to (61) reveals that isothermal pressurizations will increase the deviation of the attitude angle from the ideal gas result.
Once the fluid is chosen, fluid properties such as the critical pressure and temperature and the molecular weight can be obtained from widely-available references; in the following examples, we will use the data found in [25]. Once the degree of pressurization, i.e., and T, is chosen, the only remaining material parameters are the scaled virial constant and . These parameters are computed by different approaches depending on the nature of the gas model. If the equation of state and viscosity is determined by tabular data or is computed by using a digital property bank, the values of and T are used to compute or interpolate the corresponding p and . The value of (T) is estimated by using a sufficiently small value of / from the tabular data or property bank. It is then a straightforward matter to compute:
If the equation of state and shear viscosity are modeled by explicit known formulas, the same approach as for the case of tabular data could be used. That is, we could simply compute p, , (T) from , T. Alternatively, formulas for the required parameters can be computed by expanding these explicit functions for small values of . It is this latter approach that we will employ for the numerical calculations in the next section.
6. Numerical Results
For the purpose of illustration, we take the Redlich–Kwong–Soave (RKS) equation of state described in [25] and the viscosity model of Chung et al. [28,29] as our exact gas models (EGM). The fluid is chosen to be carbon dioxide (CO) and the physical parameters of CO were taken from Reid et al. [25].
If we expand the pressure for small density and constant temperature, we then obtain the scaled first virial coefficient for the pressure, i.e., Equation (30), corresponding to the RKS equation of state. The details are straightforward. In order to conserve journal space, we record only the final result here. The value of was found to be:
Internally consistent values of the nondimensional constants seen in Equation (66) were found to be k = 0.427480, b = 0.08664, Z = 1/3. The reduced temperature T and:
is a dimensionless function of T and the acentric factor = constant.
We have plotted the scaled version of virial expansion of :
combined with Equation (66) along with its exact value calculated using the EGM and Equation (1) in Figure 4 at temperatures equal to 1.25 T, 1.15 T, and 1.05 T. The lines represent the exact ; the symbols denote the virial expansion of , i.e., Equation (68). As V, 2 becomes O(1) such that the virial expansion is no longer valid. As a result, we will only consider the cases where 2 0.5 in all that follows. Examination of Figure 4 reveals that the agreement is very good over most of the dense gas regime. The differences between the exact and the virial expansion of are found to be less than 5% for each temperature and V ≥ 5 V.
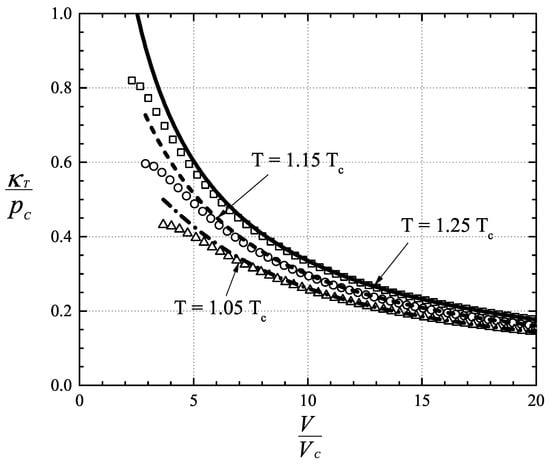
Figure 4.
Scaled bulk modulus vs. V/V at T = 1.25 T, 1.15 T, and 1.05 T. The lines represent the exact bulk modulus obtained from the exact gas model (EGM) and Equation (1). The symbols denote the virial expansion of the bulk modulus computed using Equations (68) and (66).
In a similar manner, a small density approximation is carried out for the viscosity model of Chung et al. [28,29]. The details of this expansion are straightforward. We again only record the final result. The scaled virial coefficient for the viscosity (43) was found to be:
where the quantities E, i = 1–5, were given in [25,28,29], as functions of the acentric factor, dipole moment, and association factor of the fluid in question. Thus, is independent of the temperature for the Chung et al. model [28,29].
The local form of the shear viscosity can be obtained from Equation (40). The result was found to be:
In all that follows, we take (T) to be given by Equation (69), so that is a constant. We have plotted this approximation to the viscosity along with that generated by the exact Chung et al. [28,29] model for temperatures of 1.25 T, 1.15 T, and 1.05 T in Figure 5. Examination of Figure 5 shows good agreement between the exact and the virial expansion of for V ≥ 5V. The difference is found to be approximately 6.8% at V = 5V. Because = constant for the Chung et al. model, the curve corresponding to the virial expansion is the same for every isotherm. The exact solution for / is also seen to have only a weak variation with temperature for the temperatures and densities in Figure 5.
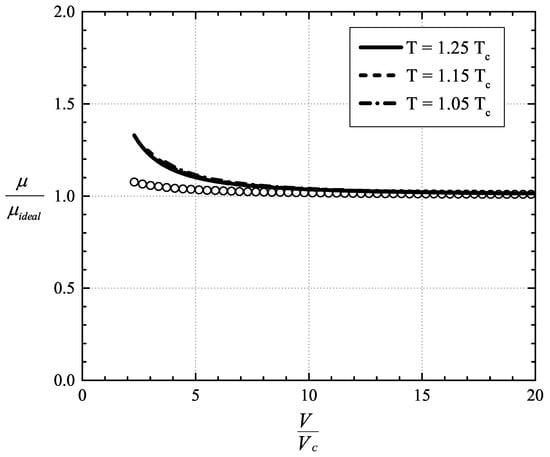
Figure 5.
Scaled shear viscosity vs. V/V at temperatures = 1.25 T, 1.15 T, and 1.05 T. The lines denote the exact viscosity resulting from the viscosity model of Chung et al. [28,29]. The symbol ◯ denotes the virial expansion of viscosity computed using Equations (69) and (70).
We now compare the load, loss, and attitude angle predicted by our virial approximations to the more general integrals, i.e., Equations (14)–(17) and (20)–(21), derived by [27]. We also compare the virial approximations of the load, loss, and attitude angle to those obtained with the simplification of the ideal gas theory. For context, we also compare the results based on each of these approximations to those based on numerical solutions to the exact Reynolds equation, i.e., Equation (8). For the convenience of the reader, we have summarized these approximations in Table 1.

Table 1.
Acronyms and approximations.
We regard the exact solutions to be the numerical integrations of the Reynolds equation derived and validated in [23,24] and used by [26,27]. The RKS gas model and Chung et al. [28,29] viscosity models will be employed in the integration of the Reynolds equation. A shooting method is used to solve the resultant two-point boundary value problem. The procedure for the calculation of the load and loss from the numerical solutions to the Reynolds equation is described in [27]. Checks on the tolerance for the shooting method and the resolution in the streamwise direction were carried out to ensure that the results displayed here are independent of the tolerance and number of points in . Further details regarding the solution to the exact Reynolds equation can be found in [23,24,27]. We will refer to this case as numerical solution to the Reynolds equation with the exact gas model (REGM).
The next level of accuracy is associated with the large theory of [27]. The load, loss, and attitude angle are given by Equations (14)–(17) and (20)–(21). The integrals are evaluated using Simpson’s rule. Checks on the number of points have been done to ensure that any results presented here are independent of the discretization. The material functions in Equations (14)–(17) and (20)–(21) were evaluated using the RKS equation of state and the full Chung et al. [28,29] models. This large (LL) approximation using the exact gas model (EGM) will be referred to as LLEGM.
The third set of results is based on the virial approximation scheme developed here, i.e., on the Equations (57), (61), and (62) with , (T) estimated by Equations (66)–(67) and (43) combined with Equation (69). In the following, we refer to this case as the virial expansion applied to LLEGM, i.e., LLV.
Finally, we compare each of these results to those obtained in the ideal gas theory. The formulas corresponding to the ideal gas theory are given by Equations (63)–(65). We refer to this case as ideal gas approximation applied to LLEGM or LLV, i.e., LLIG.
The accuracy of the virial expansions developed here will be seen by comparing the LLV results to the integral formulas on which LLEGM theory is based; that is, it provides a measure of the accuracy of the approximation of the material functions in the context of the load, loss, and attitude angle. The inclusion of the results of the exact Reynolds equation, i.e., REGM, will give a measure of the total error due to the large approximation and the virial approximation. The comparison of each of these theories to the ideal gas theory will give an indication of the error in the ideal gas theory at higher pressures in the context of load, loss, and attitude angle.
In these examples, we consider the unwrapped journal bearing sketched in Figure 3. The ratio h/L = 1.989 , and the speed number is taken to be = 50. Unless stated otherwise, = 0.5. Throughout this study, we take the reference thermodynamic state to be that at x = 0 and L.
The variation of the scaled load at T = 1.05 T and 1.25 T with the reference specific volume is plotted in Figure 6 and Figure 7, respectively. In all that follows, we only present results for reference thermodynamic states having 2 0.5. Inspection of Figure 6 and Figure 7 reveals that the LLV model is in excellent agreement with the LLEGM and REGM models for all the given reference thermodynamic states. As indicated in Section 5, the use of the ideal gas model will result in an overestimation of the load when the gas is pressurized. A comparison of Figure 6 and Figure 7 shows that the error in the ideal gas model is larger when T = 1.05 T than when T = 1.25 T for fixed V. This can be explained by the fact that the first correction term in Equation (57), i.e., , decreases as the reference temperature increases. The maximum difference between the LLV and LLIG model for the case of T = 1.05 T and 1.25 T occurs at V = 3.45 V and 2.27 V, respectively, and its value was found to be 53.7% and 41.2%, respectively.
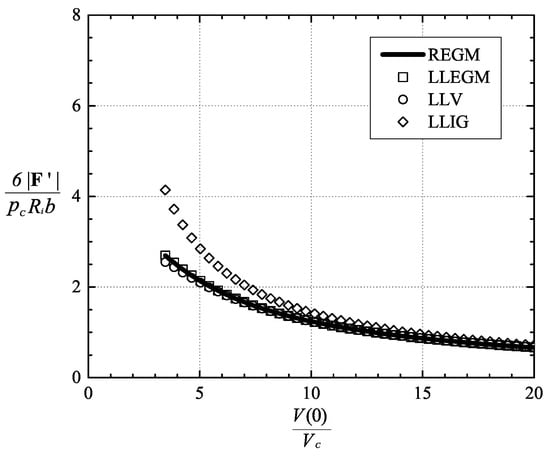
Figure 6.
Scaled load vs. reference specific volume V/V at T = 1.05 T. The speed number = 50 and the parameter = 0.5.
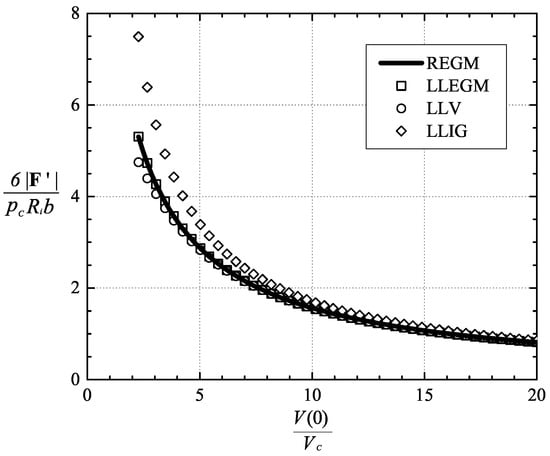
Figure 7.
Scaled load vs. reference specific volume V/V at T = 1.25 T. The speed number = 50 and the parameter = 0.5.
Observation of Figure 6 and Figure 7 also indicates that the scaled load increased with the pressurization and the increase of the reference temperature. This is due to the fact that the load is dominated by the variation of the bulk modulus for fixed and . These results are consistent with the findings of [27].
Because it was shown that the effects of the temperature on the scaled loss were insignificant [27], we have only plotted the variation of the scaled loss corresponding to the case of T = 1.25 T; our results are recorded in Figure 8. We have multiplied the scaled loss by (1 + ) in concert with the conventional practice in which the film thickness is scaled with the radial clearance. Examination of Figure 8 reveals that the agreement between the LLV model and the REGM and LLEGM models is seen to be excellent even at V = 2.27 V where the fluids can be considered to be dense gases or slightly supercritical fluids. As discussed in [27], the monotone increase of the viscosity with increasing pressure or decreasing specific volume leads to the decrease of the scaled loss for fixed and . As is clear from Equation (64), the scaled loss predicted by the LLIG model remains constant with isothermal pressurization. This is due to the fact that the ideal gas viscosity is a function of the reference temperature only. Again, the LLIG model overestimates the scaled loss in the pressurized gas regimes. The maximum difference between the LLV and LLIG models was found to be 8% for the cases considered in Figure 8.
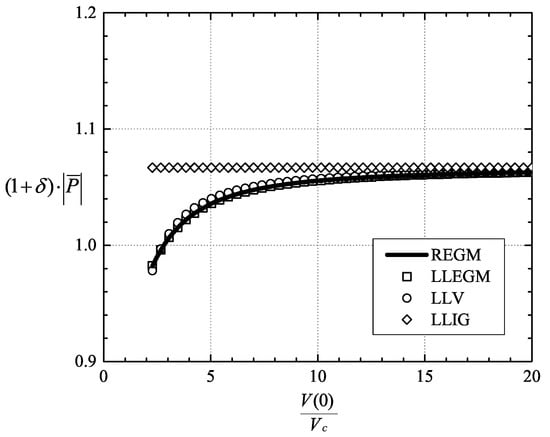
Figure 8.
Scaled loss vs. reference specific volume V(0)/V at T = 1.25 T. The speed number = 50 and the parameter = 0.5.
We note further that the loss is scaled with the zero-load loss, i.e., when = 0. Inspection of Figure 8 shows that the scaled loss of ideal gases will always be larger than one. On the other hand, because of the density dependence of the shear viscosity, the scaled loss can become ≤1 at higher pressures. This result is consistent with [27], but can be easily revealed by Equation (62), at least where the virial expansion is valid.
The variation of the scaled version of the attitude angle at T = 1.25 T is plotted as a function of the reference specific volume in Figure 9. Here, we use the associated attitude angle , i.e., the angle between the direction of the total force and the negative x axis seen in Figure 2. The agreement between the LLV, LLEGM, and REGM models is seen to be excellent. The attitude angle resulting from the LLV, LLEGM, and REGM models increased as the reference density rose. Inspection of Equation (65) reveals that is dependent only on and for ideal gases. Thus, the scaled attitude angle corresponding to the LLIG model remained constant, and its value was smaller than that predicted by the LLV, LLEGM, and REGM models at higher pressures. The maximum discrepancy between the LLV and LLIG models was found to be 25.6% for the reference states considered in Figure 9.
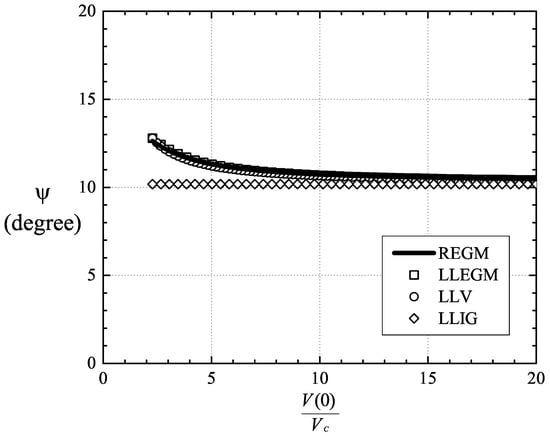
Figure 9.
Scaled attitude angle vs. reference specific volume V(0)/V at T = 1.25 T. The speed number = 50 and the parameter = 0.5.
We also have plotted the variation of the scaled load as a function of for V = 5 V, 10 V, and 15 V at T = 1.05 T in Figure 10. Results obtained from the LLV, LLEGM, and REGM models were found to be in excellent agreement. Inspection of Figure 10 reveals that the differences between the LLV and LLIG models increased with the increase of and reference pressure. The maximum differences between the LLV and the LLIG models at V = 5 V, 10 V, and 15 V were found to be 23.1%, 12.1%, and 7.4%, respectively, and occurred at = 1.
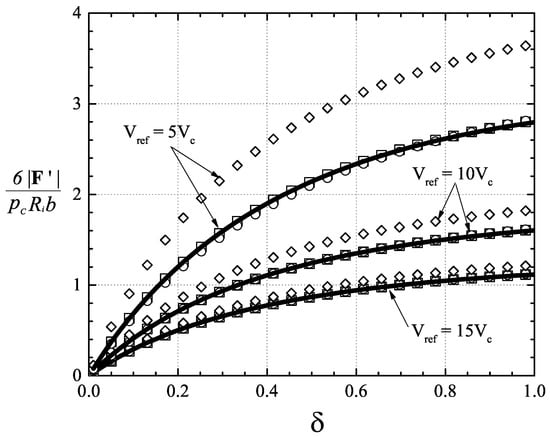
Figure 10.
Scaled load vs. at V = 5 V, 10 V and 15 V for T = 1.05 T. The speed number = 50. The solid lines represent the scaled load obtained from the REGM model; the symbols □, ◯, and ⋄ denote the scaled load computed by the LLEGM, LLV, and LLIG approximations, respectively.
The variation of the scaled loss is plotted against at T = 1.05 T for V = 10 V and 5 V in Figure 11 and Figure 12, respectively. Examination of Figure 11 and Figure 12 indicates that the LLV model is in very good agreement with the LLEGM and REGM models for a range of in both cases. The effects of the first virial correction term became more significant as increased for fixed pressure. The maximum discrepancy between the LLV and LLIG models for the case of V = 10 V and 5 V was found to be approximately 1% and 3%, respectively. The effects of the first virial correction on the scaled loss, i.e., Equation (62), seems to be smaller than that on the scaled load, i.e., Equation (57). This is due to the fact the variation of with the density is stronger than that of , as shown in Figure 4 and Figure 5.
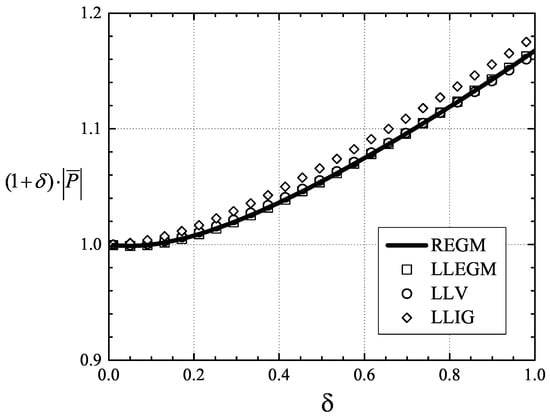
Figure 11.
Scaled loss vs. at V = 10 V and T = 1.05 T. The speed number = 50.
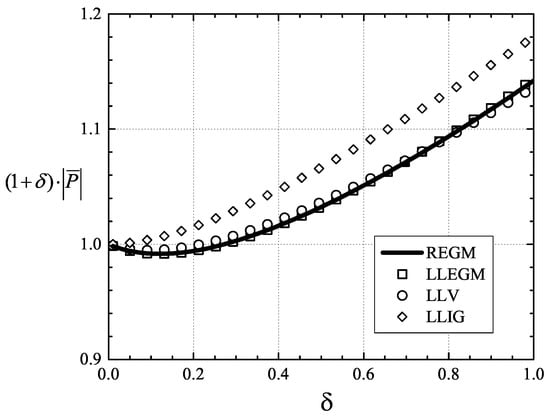
Figure 12.
Scaled loss vs. at V = 5 V and T = 1.05 T. The speed number = 50.
Inspection of Figure 12 also shows that the scaled loss had a local minimum at = 0.103 for the V = 5 V case. In general, it is easily shown that a local minimum of (1 + ) occurs when:
if we consider only the lowest-order approximation in , i.e, , for the loss, i.e., Equation (62). From Equation (71), it is easily shown that the minimum scaled loss of ideal gases will always be at = 0. For pressurized gases, the location of the minimum scaled loss will depend on the ratio of to . It can be shown that:
increases monotonically from 0 to 2 as . Thus, if is a constant and 1, a local minimum in the scaled loss, i.e., (1 + ) , occurs iff:
We have also plotted the variation of the scaled attitude angle as a function of at V = 5 V and T = 1.05 T in Figure 13. Observation of Figure 13 reveals the good agreement between the LLV, LLEGM, and REGM models, and the predicted attitude angle increased as increased. The maximum difference between the LLV and REGM models was found to be 6.4% and occurred at = 1.0. As is clear from Equation (61), the LLIG model, on the other hand, resulted in underestimation of the scaled attitude angle and deviated from the LLV model by 23.1% at = 1.0. In addition, we note that both F and F⟶ 0 at the same rate as goes to zero; this result is consistent with the findings of [30] for ideal gases.
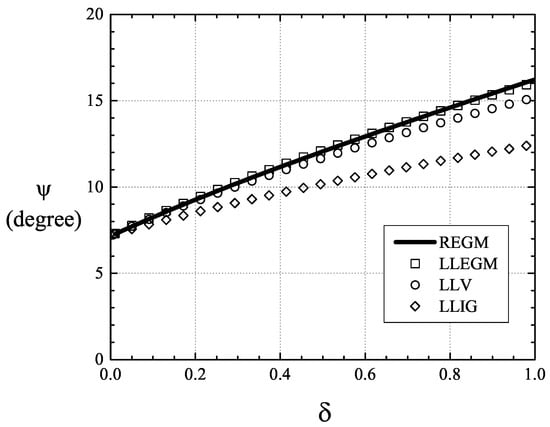
Figure 13.
Scaled attitude angle vs. at T = 1.05 T and V = 5 V. The speed number = 50.
7. Summary
The main goal of the present study was to provide simple explicit formulas for the load, power loss, and attitude angle for moderately-pressurized gases. We have applied a virial expansion, i.e., a / 1 approximation, to the large speed number approximations developed in [27]. The general results for the load, attitude angle, and loss are given by Equations (57), (61), and (62). The numerical results of Section 6 suggests that our virial expansions yield excellent agreement with both exact solutions to the Reynolds equation and the large approximations of [27] well into the dense gas and supercritical fluid regime. For example, for CO at a reference specific volume of 5 V and a reference temperature of 1.05 T 43.2 °C, the RKS equation of state predicts a reference pressure of 0.55 p 40.5 bar. Inspection of Figure 6 and Figure 10, Figure 11, Figure 12 and Figure 13 reveals that our approximations are quite good even at these elevated reference pressures. The results based on our simple virial expansions are also seen to be a a significant improvement over those of the ideal gas theory.
Once the virial coefficients, i.e., Equations (30) and (41), are determined from experiment, tabulated data, or analytical gas models, the formulas presented here can be used to gain intuition regarding the effects of pressurization, to carry out engineering estimates, and reduce computation time in large-scale numerical studies involving moderate pressures. The approach taken here was to replace complex material functions, i.e., complex equations of state and viscosity models, with a simple approximation. Thus, virial expansions such as that employed here should be equally effective for unsteady, fully-three-dimensional, and turbulent lubrication flows at moderate pressures.
Author Contributions
Both authors have contributed equally to the writing and physical/mathematical development. Computations and plotting were carried out by S.Y.C.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp Tower’s experiments, including an experimental determination of the viscosity of olive oil. Proc. R. Soc. Lond. 1886, 40, 191–203. [Google Scholar]
- Pinkus, O.; Sternlicht, B. Theory of Hydrodynamic Lubrication; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Gross, W.A.; Matsch, L.A.; Castelli, V.; Eshel, A.; Vohr, J.H.; Wildmann, M. Fluid Film Lubrication; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1980. [Google Scholar]
- Szeri, A.Z. Fluid Film Lubrication; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hamrock, B.J.; Schmidt, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Johansen, P.; Roemer, D.B.; Andersen, T.O.; Pedersen, H.C. On the application of Reynolds theory to thermo-piezo-viscous lubrication in oil hydraulics. In Proceedings of the 2015 International Conference on Fluid Power and Mechatronics, Harbin, China, 5–7 August 2015; pp. 58–62. [Google Scholar]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- Dupuy, F.; Bou-Saïd, B.; Tichy, J. High-speed subsonic compressible lubrication. J. Tribol. 2015, 137, 041702. [Google Scholar] [CrossRef]
- Dupuy, F.; Bou-Saïd, B.; Garcia, M.; Grau, G.; Rocchi, J.; Crespo, M.; Tichy, J. Tribological study of a slider bearing in the supersonic regime. J. Tribol. 2016, 138, 041702. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Wang, Q. Discussion on the Reynolds equation for the slipper bearing modeling in axial piston pumps. Tribol. Int. 2018, 118, 140–147. [Google Scholar] [CrossRef]
- DellaCorte, C.; Radil, K.C.; Bruckner, R.J.; Howard, S.A. Design, fabrication, and performance of open source generation I and II compliant hydrodynamic gas foil bearings. Tribol. Trans. 2008, 51, 254–264. [Google Scholar] [CrossRef]
- Dostal, V.; Driscoll, M.J.; Hejzlar, P. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors; Technical Report, MIT-ANP-TR-100; MIT Center for Advanced Nuclear Energy Systems: Cambridge, MA, USA, 2004. [Google Scholar]
- Wright, S.A.; Radel, R.F.; Vernon, M.E.; Rochau, G.E.; Pickard, P.S. Operation and Analysis of a Supercritical CO2 Brayton Cycle; Sandia Report, No. SAND2010-0171; Sandia National Laboratories: Albuquerque, NM, USA, 2010. [Google Scholar]
- Conboy, T.M.; Wright, S.A.; Pasch, J.; Fleming, D.; Rochau, G.; Fuller, R. Performance characteristics of an operating supercritical CO2 Brayton cycle. J. Eng. Gas Turbines Power 2012, 134, 111703. [Google Scholar] [CrossRef]
- Crespi, F.; Gavagnin, G.; Sánchez, D.; Martínez, G.S. Supercritical carbon dioxide cycles for power generation: A review. Appl. Energy 2017, 195, 152–183. [Google Scholar] [CrossRef]
- Peng, Z.C.; Khonsari, M.M. On the limiting load-carrying capacity of foil bearings. J. Tribol. 2004, 126, 817–818. [Google Scholar] [CrossRef]
- Conboy, T.M. Real-gas effects in foil thrust bearings operating in the turbulent regime. J. Tribol. 2013, 135, 031703. [Google Scholar] [CrossRef]
- Kim, D. Design space of foil bearings for closed-loop supercritical CO2 power cycles based on three-dimensional thermohydrodynamic analyses. J. Eng. Gas Turbines Power 2016, 138, 032504. [Google Scholar] [CrossRef]
- Qin, K. Development and Application of Multiphysics Simulation Tools for Foil Thrust Bearings Operating with Carbon Dioxide. Ph.D. Thesis, University of Queensland, Brisbane, Australia, 2017. [Google Scholar]
- Guenat, E.; Schiffmann, J. Real-gas effects on aerodynamic bearings. Tribol. Int. 2018, 120, 358–368. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Reference Fluid Thermodynamic and Transport Properties—REFPROP; Version 7; NIST Standard Ref. Database; National Institute of Standards and Technology Standard Reference Data Program: Gaithersburg, MD, USA, 2002; Volume 23. [Google Scholar]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- Chien, S.Y.; Cramer, M.S.; Untaroiu, A. Compressible Reynolds equation for high-pressure gases. Phys. Fluids 2017, 29, 116101. [Google Scholar] [CrossRef]
- Chien, S.Y.; Cramer, M.; Untaroiu, A. A compressible thermohydrodynamic analysis of journal bearings lubricated With supercritical CO2. In Proceedings of the ASME 2017 Fluids Engineering Division Summer Meeting, Waikoloa, HI, USA, 30 July–3 August 2017. Paper No. FEDSM2017-69310. [Google Scholar]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Chien, S.Y.; Cramer, M.S. Pressure, temperature, and heat flux in high speed lubrication flows of pressurized gases. Tribol. Int. 2019, 129, 468–475. [Google Scholar] [CrossRef]
- Chien, S.Y.; Cramer, M.S. Load and loss for high speed lubrication flows of pressurized gases between non-concentric cylinders. J. Fluid Mech. 2019. accepted. [Google Scholar]
- Chung, T.H.; Lee, L.L.; Starling, K.E. Applications of kinetic gas theories and multiparameter correlation for prediction of dilute gas viscosity and thermal conductivity. Ind. Eng. Chem. Fundam. 1984, 23, 8–13. [Google Scholar] [CrossRef]
- Chung, T.H.; Ajlan, M.; Lee, L.L.; Starling, K.E. Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Eng. Chem. Res. 1988, 27, 671–679. [Google Scholar] [CrossRef]
- Gross, W.; Zachmanoglou, E. Perturbation solutions for gas-lubricating films. J. Basic Eng. 1961, 83, 139–144. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).