Abstract
We put forth a robust reduced-order modeling approach for near real-time prediction of mesoscale flows. In our hybrid-modeling framework, we combine physics-based projection methods with neural network closures to account for truncated modes. We introduce a weighting parameter between the Galerkin projection and extreme learning machine models and explore its effectiveness, accuracy and generalizability. To illustrate the success of the proposed modeling paradigm, we predict both the mean flow pattern and the time series response of a single-layer quasi-geostrophic ocean model, which is a simplified prototype for wind-driven general circulation models. We demonstrate that our approach yields significant improvements over both the standard Galerkin projection and fully non-intrusive neural network methods with a negligible computational overhead.
1. Introduction
The growing advancements in computational power, technological breakthrough, algorithmic innovation, and the availability of data resources have started shaping the way we model physical problems now and for years to come. Many of these physical phenomena, whether it be in natural sciences and engineering disciplines or social sciences, are described by a set of ordinary differential equations (ODEs) or partial differential equations (PDEs) which is referred as the mathematical model of a physical system. Thus far, many computational approaches are based on solving these sets of equations of a mathematical model after applying suitable discretization schemes and numerical tools which may be referred to as a physics-based solution approach. Despite the advances in software engineering and processor technologies, the computational burden of high-fidelity simulation is still a limiting factor for many practical problems in different areas of research, specifically for the large-scale physical problems with high spatiotemporal variabilities such as turbulence modeling of geophysical flows, weather forecasting, and climate modeling. Indeed, low-fidelity models such as large eddy simulation (LES) [1] and Reynolds-averaged Navier–Stokes (RANS) [2] are introduced with additional approximations to neglect some of the physical aspects for closure modeling, and, as a result, the computational cost is reduced. However, these techniques require parameter calibration to approximate the true solution to any degree of confidence and may thus increase costs related to model validation and benchmark data generation.
As a first attempt to perform efficient physics-based surrogate modeling, projection based implementations of model order reduction strategies have proven to be successful in reducing computational cost significantly with little compromise in physical accuracy, and have been extensively utilized in the literature to address challenging fluid flow problems. In contrast to the physics-based modeling technique, the non-intrusive, data-driven modeling has recently become extremely popular in turbulence modeling because of the abundance of data resources from both high-fidelity simulations and experiments [3,4]. Until recently, fully non-intrusive artificial intelligence and machine learning algorithms have been considered one of the most promising fields to benefit greatly from existing datasets. Because of their black box nature in predicting the solution, the data-driven techniques are yet to be fully accepted in the community. This has led to the development of a new and fast emerging hybrid modeling approach (i.e., hybrid analytics) that combines a physics-based modeling strategy with a data-driven model to develop a robust scheme with significantly enhanced potential for performance than the component models alone. In this paper, we propose a hybrid framework to develop a robust and improved reduced-order model by combining a standard projection based reduced-order modeling with a simple artificial neural network architecture. This approach is applied to a single-layer quasi-geostrophic ocean model.
The study of ocean circulation, specifically the wind-driven circulation, is one of the most demanding areas of research from engineering and scientific points of view because of the energy potential in the motions of water masses within oceans in the form of heat and strong currents as well as the connection between ocean currents and climate dynamics [5,6,7]. Since ocean circulation is a significant part of climate systems, it is extremely important to study and understand the underlying physics to get the benefits from the rich potential of oceans. There have been many efforts put on developing models for ocean dynamics in the last few decades [8,9,10,11,12,13]. However, it is computationally challenging to model the ocean dynamics because of its large range of spatiotemporal scales and sporadic random transitions between coexisting eddies and vortices [14,15]. In our study, we use a two-dimensional single layer quasi-geostrophic ocean model as a test case for our proposed reduced-order model and consider the barotropic vorticity equation (BVE) with dissipative and forcing terms which is one of the most commonly used models for the double-gyre wind-driven geophysical flows. The BVE model is a simplified version of the full-fledged geophysical flow equations by considering the hydrostatic balance, geostrophic balance, the -plane approximation, and horizontal eddy viscosity parameterizations. However, the computational cost of simulation and analysis of the BVE model is high which makes this model a suitable test case to investigate an improved and robust reduced-order model.
Reduced-order modeling (ROM) techniques have been commonly introduced to reduce the computational cost of obtaining high-fidelity simulation results by generating a lower dimensional system with a similar range of accuracy through a variety of mathematical operations. Based on the approach, there have been a considerable number of promising reduced-order modeling techniques introduced, such as proper orthogonal decomposition (POD), Koopman mode decomposition (KMD), dynamic mode decomposition (DMD), reduced bases, etc. A detailed overview of such techniques and recent developments can be found in Refs. [16,17]. To predict the flow behavior in reduced-order space, we utilize the POD framework to generate the POD basis function and then use the Galerkin projection to find a set of ODEs that yield a low dimensional dynamical system [18]. Even though the Galerkin projection based ROMs have been successfully used in various areas of work [19,20,21,22], they are limited by modeling errors and numerical instabilities due to the truncation of POD modes for complex systems, such as the ocean circulation system considered in this study. See Refs. [23,24,25,26,27,28] to find some recent developments made to improve physics-based ROM techniques by stabilizing the numerical instabilities and taking into account the truncated mode contributions. Furthermore, Table 1 summarizes our descriptions for classifying several ROM approaches.

Table 1.
A classification of reduced-order modeling approaches.
In the present study, we utilize an artificial neural network (ANN) to develop our ROM framework. Neural networks, one of many machine learning (ML) strategies, have become an area of interest for researchers from diverse fields of study because of their self-adaptive and flexible nature, while approximating complex functions of any physical process with a high degree of accuracy. Even though ML tools such as ANN have been utilized in flow control community for the last couple of decades [29,30], the data-driven idea has recently been popular in computational fluid dynamics community for modeling and solving complex fluid flow problems [31,32,33,34,35,36]. These data-driven models can be developed either in a black box fashion or in combination with existing models. We utilize a simple single hidden layer feedforward network (SLFN), known as extreme learning machine (ELM), in this paper for both fully data-driven model and hybrid model. The resolved reduced-order model coefficients and full order simulation data are used to train the ELM architecture. The descriptive idea on ELM and its implementations can be found in Refs. [37,38,39].
The purpose of this paper is to develop a robust and efficient ROM framework using a hybrid approach, and test the performance of the proposed model with respect to the component models, i.e., physics-based and data-driven models. Recently, several promising works have been conducted to develop more efficient and improved reduced-order model frameworks using the hybridization of traditional projection based ROMs and data-driven ROMs [40,41,42]. The proposed hybrid framework is developed by combining two component models, the standard projection based ROM and an ANN framework. Our main motivation of this study comes from addressing the strengths and weaknesses of the component models to find a bridge between both models to benefit from the strength of both approaches. Combining an imperfect physics-based model with a data-driven technique to get a hybrid scheme is not an entirely new idea in scientific research [43,44]. Even though the hybridization approach varies with respect to the physical problem, selection of ML architecture, approach to find the solution, and the associated physics-based models, the main idea remains similar for most of the works. We then choose a challenging test problem for model order reduction for validation and comparison purpose, and perform a number of statistical analyses on the hybrid model as well as on the component models. The results of our tests suggest that the proposed model is robust and can be extremely useful for complex flow problems.
The rest of this manuscript is outlined as follows: in Section 2, we review the underlying governing equation of the physical problem considered in this study to generate data bank in full order space for POD basis construction and training the ANN architecture as well as the numerical schemes used for full order simulation. We briefly discuss the standard Galerkin projection based ROM approach and fully non-intrusive data-driven ROM approach in Section 3 and Section 4, respectively. In Section 5, we introduce our proposed hybrid ROM framework. In Section 6, we perform a variety of analyses to assess the performance and viability of the proposed model with respect to the performance of its physics-based component or data-driven component alone. We also include the full order simulation results as reference. Finally, we summarize our findings in Section 7.
2. Full Order Model (FOM)
In FOM, we solve the underlying governing equations using a suitable numerical model and generate the data bank of snapshots for ROM. In this section, we introduce the quasi-geostrophic ocean model as a test case and provide a brief description of the numerical schemes employed in this study.
2.1. Quasi-Geostrophic (QG) Ocean Model
Since it is well established that much of the world’s ocean circulation is wind-driven in large-scale, and oceanic mesoscale processes are also extremely prevalent in the large-scale oceanic circulations, studies of wind-driven circulation using an idealized double gyre wind forcing have become increasingly important in understanding various aspects of ocean and climate dynamics, such as the role of mesoscale eddies and their effect on mean circulation [15,45,46,47,48]. However, the numerical simulation of oceanic and atmospheric flows, up to this point, still requires approximations and simplifications of the full model to resolve some of the enormous range of spatial and temporal scales of the full form of the general circulation models. Even though remarkable advances in developing simplified models have been made during the last few decades in producing increasingly accurate results [8,49], an additional computational challenge is in being able to implement them in long time integration such as those required by the climate modeling [14,50]. Therefore, with this in mind, we consider the simple single-layer QG model, also known as barotropic vorticity equation (BVE) that can capture the random inter-decade and inter-annual transitions in large-scale ocean basins [51]. This mathematical model shares many analogies with the two-dimensional Euler equation and Navier–Stokes equation [52] and has been extensively used over the years to describe various aspects of the largest scales of turbulent geophysical fluid dynamics [53,54,55]. The dimensionless BVE for QG single-layer ocean model can be written as [34,56]
where the left hand side terms account for local acceleration and nonlinear advection, respectively, and the right hand side terms represent the rotational, dissipative, and forcing effects, respectively, in the governing equation. Here, is the kinematic vorticity, expressed as
where is the velocity vector. For two-dimensional flow in the x-y plane, the kinematic vorticity becomes
Here, the flow velocity components can be found from the stream function, , using the following definition:
In Cartesian co-ordinates,
The kinematic equation connecting the vorticity and stream function can be found by substituting the velocity components in terms of stream function in Equation (3), which forms the following divergence-free constraint satisfying Poisson equation:
where is the standard two-dimensional Laplacian operator. The dimensionless formulation of BVE in Equation (1) contains Reynolds number (Re) and Rossby number (Ro), two dimensionless numbers which are related to the physical parameters and non-dimensional variables in the following way:
where is the horizontal eddy viscosity coefficient for ocean basin and is the Rossby parameter. It should be noted that the BVE model presented here uses the beta-plane approximation, valid for most mid-latitude simplified ocean basins, i.e., the Coriolis parameter to account for Earth’s rotational effect is approximated by , where is the constant mean Coriolis parameter and is the gradient of the Coriolis parameter at the basin center. The characteristic horizontal length scale, L (for the non-dimensional purpose) is the basin dimension in x-direction in this study and the reference Sverdrup velocity scale, V, is given by
where is the maximum amplitude of the sinusoidal double-gyre wind stress, and and H are the reference fluid density and depth of the ocean basin, respectively. In our study, we consider the benchmark four-gyre circulation problem where the time average of the statistically steady equilibrium state exhibits a four-gyre circulation pattern for relatively high Re instead of the symmetric double-gyre standard structure [10,56,57]. Based on reference literature [10,58,59,60,61], we use slip boundary condition for the velocity, which translates into homogeneous Dirichlet boundary condition for the vorticity and corresponding , where symbolizes all the Cartesian boundaries. We initiate our computations from a quiescent state (i.e., and ) and integrate Equation (1) until a statistically steady state is obtained.
2.2. Numerical Schemes
Since for most of the physically relevant ocean circulation models, such as the QG models, the solutions remain in a quasi-stationary state as time goes to infinity [62], schemes designed for the numerical integration of such phenomena should be suited for quasi-stationary behavior of the solutions as well as for the long time integration. In our study, we use the second-order central finite difference schemes in linear terms. For the modeling of nonlinear term, we use second-order skew-symmetric, energy- and enstrophy-conserving Arakawa scheme [63] to avoid computational instabilities arising from nonlinear interactions for the Jacobian term, in Equation (1), defined as
where
Here, and are the step size in x- and y-directions, respectively. The detailed derivation of higher-order Arakawa schemes can be found in Ref. [23]. To implement the Runge–Kutta scheme, we use the method of lines to cast our system in the following form:
Here, subscripts i and j represent the discrete spatial indices in x and y directions, respectively. denotes the discrete spatial derivative operators. For our time advancement scheme, we use the optimal third order accurate total variation diminishing Runge–Kutta (TVDRK3) scheme given as [64]:
where is the adaptive time step, which can be computed at the end of each time step satisfying the stability criteria through the Courant–Freidrichs–Lewy (CFL) number. Finally, taking advantage of the simple Cartesian domain, an efficient fast Fourier transform (FFT) method is utilized for the solution of the elliptic Poisson equation which is the most computationally expensive part of the QG models [12]. Details of the aforementioned numerical methods used for this study can be found in Refs. [10,58].
3. Galerkin Projection Based Reduced-Order Model (ROM-GP)
Similar to the area of interest in the present study, many areas of physical science and engineering often require iterative computations, data assimilation, and finer scale simulation for large dynamical systems to resolve the underlying physical phenomena [65,66,67,68]. The efficiency of these large-scale simulations decreases with increasing computational complexity of the full order models due to the accumulation of the less significant intermediate results. Hence, the reduced-order models (ROMs) have come into wide use in large-scale simulations to replace large dynamical systems with lower dimensional systems having a similar range of validity and input/output characteristics. Proper orthogonal decomposition (POD), also referred as Karhunen–Loève transform (KLT), principal component analysis (PCA) or singular value decomposition (SVD), is a widely applied snapshot-based ROM technique in science and engineering applications with large dimensional systems of nonlinear ODEs or PDEs [69,70,71]. In this section, we develop a standard projection methodology for Equation (1) where a POD-GP ROM framework is developed from the field variables, and on the flow domain, and based on the method of snapshots [72]. The snapshots are obtained from the stored sample solution of FOM. The main procedure of ROM in the current study consists of generating low-dimensional orthogonal basis functions from snapshots and next, performing Galerkin projection to obtain the ROM. For POD basis construction, we first obtain N number of snapshots and denote the vorticity field, as for at pseudo-time . Then, we decompose the solution field by following way into a time-invariant mean, and a fluctuating part, to represent the full field with only fluctuating part [73]:
for where stands for the two-dimensional domain and the mean of the snapshot is
The following algorithm describes the POD-GP procedure:
- POD basis construction:
- *
- Construct a data correlation matrix of the fluctuating part, from the snapshots where . Here, i and j refer to the snapshot indices.
- *
- Compute the optimal POD basis functions by solving where is the diagonal eigenvalue matrix and refers to right eigenvector matrix whose columns are eigenvectors of . In general, most of the subroutines for solving above eigenvalue equation give with all of the eigenvectors normalized to unity.
- *
- Using the eigenvalues stored in a descending order in the diagonal matrix, , define the orthogonal POD basis functions for the vorticity field aswhere is the kth eigenvalue, is the nth component of the kth eigenvector, and is the kth POD mode. We must mention that the eigenvectors must be normalized in such a way that the basis functions satisfy the orthogonality condition.
- *
- Obtain the kth mode for the stream function, , utilizing the linear dependence between stream function and vorticity given by Equation (6): .
- *
- Span the fluctuating component of the field variables into the POD modes by doing the separation of variable aswhere is the time-dependent modal coefficients and and refer to the POD modes. It should be noted that the same accounts for both stream function and vorticity based on the kinematic relation given by Equation (6).
- *
- Retain R modes where , such that these R largest energy containing modes correspond to the largest eigenvalues (). The resulting full expression for the field variables can be written as
- Galerkin projection to obtain ROM:
- *
- Perform an orthogonal Galerkin projection by multiplying the governing equation with the POD basis functions and integrating over the domain [74], which yields the following dynamical system for :where
We can define the right hand side of Equation (22) as to express the equation in the following form:
The system given by above algorithm consists of R coupled ODEs for modal coefficients, which can be solved numerically by any suitable time integration scheme. Additionally, the POD basis functions and ROM coefficients can be precomputed from the data, which makes the system more efficient. Defining the vorticity field, at time , a complete specification of the dynamical system given by Equation (22) can be calculated by the following projection of the initial condition:
It is worth mentioning that there are occasions in our POD-GP ROM framework where we compute the inner product of two functions and as
In the present study, we compute the inner products by taking the integral of the product over the domain, using the dual integration method for Simpson’s rule. We refer to Ref. [75] for the details of the integration technique.
4. Artificial Neural Network Based Non-Intrusive Reduced-Order Model (ROM-ANN)
The study of artificial neural networks (ANN) was introduced in the 1990s as a multilayered perceptron based on the idea of mimicking the functions of neurons in human brain [76]. ANNs consist of layers possessing a predefined number of unit cells called neurons and connections between the neurons called weights to establish a map between an input layer and an output layer. Other than the input and output layers, an ANN architecture also contains at least one hidden layer which is independent of the training data. The learning can be supervised or unsupervised. In unsupervised learning, the network extracts data features without knowing the target output and input label [77]. On the other hand, we have used a supervised learning network named single-hidden layer feedforward neural networks (SLFNs) based on the precomputed inputs from ROM-GP model which discovers the mapping between inputs and outputs from provided labeled sample. Mathematically, the input layer distributes input signals to the Q dimensional hidden layer feature space (i.e., Q is the number of hidden neurons). Let represent the outputs from J number of output neurons. are the weights connecting the neurons in input and hidden layers, are the output weights between the hidden and output layers, and and are the random biases operating as thresholds for the hidden and output layers. Then, the feed-forward operation can be written as:
where differentiable functions F and G are the transfer or activation functions [78,79] which can be log-sigmoid, hyperbolic tangent sigmoid, or linear transfer function. The training process of ANN is adjusting the weights to reproduce the desired outputs when the given inputs are fed forward. In the present study, we use Extreme Learning Machine (ELM) architecture which randomly chooses weights for the hidden nodes and bias terms and analytically determines the output weights of SLFNs [80]. Huang et al. [37] first introduced ELM with a goal to achieve a learning speed thousands time faster than the traditional feedforward network learning algorithm while producing a better generalization performance. Later, several extensions of general ELM method are developed in different works [38,81,82]. In our study, the ANN architecture is trained by utilizing an ELM approach which requires no biases in the output layer () as well as the weights () and biases () are initialized randomly from a uniform distribution between and and no longer modified. Therefore, weights are only unknown to be determined in this case. We note that we utilized the tan-sigmoid activation function for the hidden layer neurons given by
and a linear activation function for the output layer neurons which is . Finally, from Equation (26), the output of ELM can be written as for N sample training data examples,
where and refer to training input–output data pairs. To illustrate further, we can show our problem in following matrix form:
where the superscript “T” refers to “Transpose”. In our study, the value of J is always 1 since there is only one output neuron. on the right hand side of the above equation is given by
By taking the transpose of Equation (29), the solution for the weights can be computed by
Here, is the pseudo-inverse of and “†” refers to “pseudo-inverse”. Since for matrix, we can apply following single value decomposition (SVD) to to compute the pseudo-inverse,
where and are column-orthogonal and orthogonal matrices, and is a diagonal matrix whose elements (i.e., where ) are non-negative and called singular values. To minimize the numerical instability introduced while calculating the inverse of by taking the reciprocal of each non-zero element, a well-known Tikhonov-type regularization [83] is used as
We choose for the present study which indicates the trade-off between the least-squares error and the penalty term for regularization [84]. The unknown weights can be calculated by using Equation (31).
In the present study, our ELM layers and architecture are devised with five inputs () and a single output () mechanism, as shown in Figure 1. Here, “LT” refers to “linear term”, “NT” refers to “nonlinear term”, and “TP” refers to “true projection” in the figure. The inputs are resolved ROM-GP variables in each time integration step which can be denoted from Equation (22) as
and the single true solution output for training set can be expressed as
which is the Galerkin projection to the FOM given by Equation (1). We denote the ANN predicted solution output as for the rest of this paper. Using the ANN prediction, , we can compute the modal coefficients, , for fully non-intrusive ROM using the following equation similar to Equation (23):
where is computed using Equation (28) in our neural network model deployment. We use the trained weights from the model to get the outputs (denoted as , i.e., in our study) for corresponding inputs of each time integration steps. We note that we normalize the computed ROM variables before using them as inputs for ELM training set to stabilize the system from any kind of numerical errors or biases, and to ensure that all the input variables are at a similar range. The normalized input sets in our study can be expressed as
where
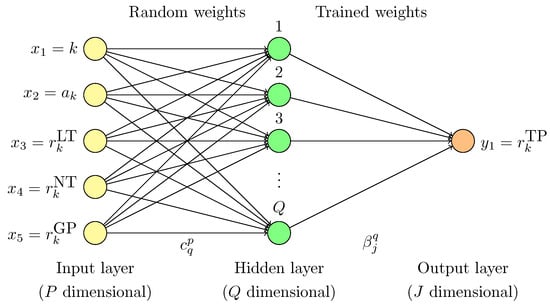
Figure 1.
Schematic representation of the extreme learning machine (ELM) neural network architecture utilized for the data-driven reduced-order modeling framework in this study.
Finally, we normalize our training set input and output in limit as
The physical output, is then recovered from the ANN predicted output, , by following unnormalization method for the normalized data:
This normalization ensures that the input variables lie in the data range of the tan-sigmoid activation function, i.e., to [85,86].
5. Hybrid Modeling (ROM-GP + ROM-ANN) Based Reduced-Order Model (ROM-H)
Hybrid modeling, as a combination of physics-based and data-driven modeling, is a fast emerging modeling approach in fluids community since both of these distinct modeling approaches are well-established in the community at this point. As illustrated in the left part of Figure 2, the traditional physics-based modeling approach can be described as understanding a part of the full physics (full physics is represented by the black colored region whereas the orange colored region displays the understood physics), developing a mathematical understanding through equations (green colored region in the figure), and finally resolving some part of the true physics (represented by the blue colored region) by using further assumptions and computational constraints. On the other hand, data-driven modeling works as a black box where we make an estimation of the true solution by using available observed data snapshots without having any knowledge of the governing physics. For model order reduction, the physics-based approach is widely applied as mentioned in previous sections, and nowadays, with the rapid growth of the availability of data, data-driven approach has become a popular route for reduced-order modeling. A comparative representation of these two approaches has been outlined in Table 2. Considering the pros and cons of both sides, our hybrid reduced-order modeling (ROM-H) comes up with the idea to address the negative aspects of both approaches, whereas the positive aspects can be leveraged simultaneously. Similar to any kind of hybrid approach, the primary goal of this paper is to establish a robust hybrid ROM framework which aims at making the model more efficient as compared to either the physics-based or data-driven ROM models.

Figure 2.
A schematic representation of the two distinct modeling approaches: (a) physics-based modeling approach; and (b) data-driven modeling approach.

Table 2.
Physics-based ROM vs. data-driven ROM.
We build our ROM-H framework by introducing a free parameter to dynamically account for the contribution of the physics-based ROM and data-driven ROM. The ROM-H methodology can be summarized by following key steps:
- Step 1 (offline):
- Generate a set of basis functions for from the snapshot data obtained from FOM.
- Step 2 (offline):
- Apply Galerkin projection to compute the coefficients required for ROM-GP.
- Step 3 (offline):
- Train the ELM network using the resolved ROM-GP coefficients and true projections datasets.
- Step 4 (online):
- Compute by solving the following ordinary differential equations in reduced-order space:where we define as a free weighting parameter in a range of to establish a relationship between the standard ROM-GP and non-intrusive ROM-ANN models. If , we recover Equation (23), whereas, for , Equation (40) can be obtained.
- Step 5 (offline):
- Obtain the full order solution by transferring data from reduced-order space by using Equation (20) as a post-processing task if needed.
The hybridization between the physics-based and data-driven based ROM happens in Step 4, where, in each time step, is calculated using Equation (23), and is obtained from Equation (40). The parameter gives us a freedom to benefit from both modeling techniques mentioned above rather than fully depending on a single modeling technique, and, as we show in Section 6, the hybrid model with optimal contribution from both modeling approaches gives a better prediction of the true solution than the individual modeling approaches. The limiting values of will result in the standard ROM-GP and ROM-ANN model solutions, respectively, and any value between the limits of 0 to 1 will give a solution with contribution from both ROM-GP and ROM-ANN models. Based on the working physical problem, we assume that either more physics-based model contribution or more data-driven model contribution can produce a better estimation of the truth. Keeping this in mind, instead of forcing an arbitrary value to specify for hybridization, we apply the following dynamic optimization strategy based on the values of and in each time integration steps:
Here, we utilize the absolute value of hyperbolic tangent function, which always produces a value for between 0 and 1. If the values of and are closely related (), the value of parameter will be 0, i.e., it indicates the use of ANN prediction for that particular case will be redundant. Similarly, if the values are far away, the ANN prediction contribution will be more dominant. However, we emphasize that the estimation technique we utilized here for calculation is on an ad-hoc basis for the present study. On this hybrid framework, the process of finding the optimal can be a potential topic for another research direction where optimization techniques such as trust-region method, conjugate gradient methods, or quasi-Newton methods can be used [87,88].
6. Numerical Results
For validation purpose, our reduced-order model resulting from the hybridization of the standard ROM-GP approach and fully non-intrusive ROM-ANN approach has been used to model a four-gyre barotropic ocean circulation problem. In this section, we present the numerical results and analyses demonstrating the computation and prediction performance of our proposed hybrid framework as well as the component models (ROM-GP and ROM-ANN) and FOM simulation for comparisons. We select this particular test problem (as many other studies do [10,56,61,89,90]) because of its complexity induced by the symmetric double-gyre wind forcing developing a four-gyre circulation pattern which makes this problem challenging enough to assess the viability of proposed models. Based on the following results, it is apparent that the ROM-H model provides a better estimation of the true solution as compared to the individual component model solutions. Indeed, it was shown before that adding a stabilization to the standard ROM-GP improves the model prediction and resolve more mean dynamics [23]. However, our proposed hybrid model idea is data-driven without taking any additional phenomenological arguments (e.g., eddy viscosity) to stabilize the model, and can be applied to most of the flow phenomena. On the other hand, we would like to note that the ROM-GP model can be cured with nonlinear modal eddy viscosities, i.e., with an energy-flow correction [91] or other closure approaches [92,93].
6.1. Case Setup Specifications for FOM Simulations
In the present work, we consider the dimensionless form of the BVE describing the QG problem in the Cartesian domain as a reference. The FOM simulation is conducted starting from to using a fixed time step of on a Munk layer resolving grid resolution. We collect 900 data snapshot from time to to avoid collecting data from initial transition period for POD basis generation and ELM training, i.e., the sampling time is . We use dimensionless parameters Re and constant Ro for all the simulations throughout the paper.
6.2. Analysis of the Standard ROM-GP Method
We first construct the POD data correlation matrix using the snapshots data from FOM simulation to generate the POD basis function for all the ROM approach in this paper. Hence, it is important to observe the characteristics and distribution of the eigenvalues with respect to modal index as presented in Figure 3. To estimate the total kinetic energy accumulation of the system, we compute the percentage of each eigenvalue by
where is the total number of snapshots. Since higher Re incorporates more stratification or, to be specific, as more energy is added to the system, more modes are required to capture majority percentage of the energies in the system. Figure 3 shows that, while only around 10 modes is enough to capture most of the system’s kinetic energy for Re , a large percentage of energies (close to and ) are accumulated in the first 30 and 40 modes for Re and Re cases, respectively. However, the percentage of captured energy is lower in higher Re cases which indicates the challenges associated with model order reduction of this test case in higher Re. These findings are supported by Figure 4 where we present the first few POD basis functions, the most important ones regarding the captured information, for Re . We can identify the increase in the equal number of smaller structures (maxima and minima) which correspond to higher POD indices. Using more POD bases will result in better approximation until the corresponding eigenvalue stagnation point reaches. Based on the POD analysis, we develop the rest of our studies using POD modes up to 40 to incorporate most of the physics within the system.
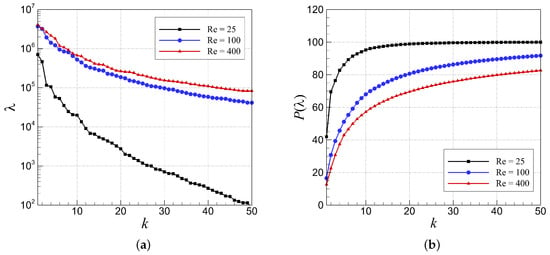
Figure 3.
Proper orthogonal decomposition (POD) analysis by using 900 equally distributed snapshots for Re : (a) Eigenvalue spectrum of the correlation matrix, ; and (b) Eigenvalue percentage energy accumulation with respect to modal index.

Figure 4.
Contour plots of some illustrative examples of POD basis functions for Re generated by the method of snapshots: (a) ; (b) ; (c) ; (d) ; and (e) .
Figure 5, Figure 6 and Figure 7 show the mean stream function field evolution with respect to increasing modes, R using standard ROM-GP approach for Re , respectively. It is apparent in Figure 5 that, for Re case, even shows a good prediction of the FOM solution. We can also notice in the figure that the mean stream function plot shows a consistent result for with respect to result, but we get a worse result for . This can be explained as an over-fitting, as we have seen in Figure 3 that, for Re = 25, modes contain more than 99% of the system’s total kinetic energy. It has also been noted in [94] that adding more modes might yield worse solutions due to the noise in the system. The inaccurate result for is understandable in a sense that the previous modes contain most of the energies (more than ) of the system which is considered a sufficient total kinetic energy for the optimal number of modes in most of the POD studies [83]. Even though modes shows a very good estimation of FOM result, it is recommended not to use more than the optimal number of POD modes to avoid instabilities in the solution field. This occurrence can also be seen in Figure 8 and Figure 9 for Re = 25. On the other hand, for Re case, shows a nonphysical two-gyre circulation pattern in Figure 6 similar to the plots of coarse truncated modes ( and ) for Re case in Figure 7. We further illustrate the effect of R and Re for ROM-GP approach in the prediction of true solution in Figure 8 and Figure 9. For the purpose of comparison, we include the FOM data projection to reduced-order space using corresponding POD basis functions for Re . In Figure 8, we show the non-dimensional time evolution of the first modal coefficient, in reduced-order space for different Re and R. The plot supports the conclusions drawn from the POD analysis and the mean stream function plots that for Re , 10 POD modes provide an unphysical result. For even higher Re , 20 POD modes show the numerical instabilities as we can see a sudden burst of random oscillations in much higher scales. To put extra emphasis on our findings, we present the results for tenth modal coefficient in Figure 9 where we can observe the same scenario as Figure 8 on a different scale. We can notice that the scales for tenth modal coefficient are much smaller than the first modal coefficient time series which is expected for higher modes, but the performance of the ROM-GP model is consistent.
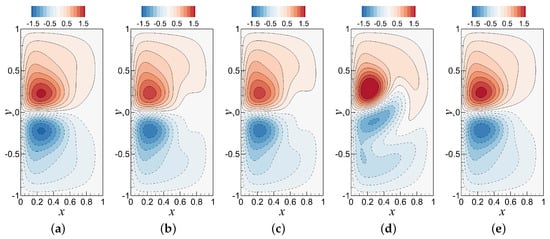
Figure 5.
Mean stream function contour plots between and obtained by reference FOM and standard ROM-GP simulations for Re : (a) at a resolution of ; (b) with modes; (c) with modes; (d) with modes; and (e) with modes. Note that a stable and well-estimated solution can be found using modes and adding more modes might yield worse solutions due to a possible over-fitting as occurred in case.

Figure 6.
Mean stream function contour plots between and obtained by reference FOM and standard ROM-GP simulations for Re : (a) at a resolution of ; (b) with modes; (c) with modes; (d) with modes; and (e) with modes. Note that a stable and well-estimated solution can be found within or 40 modes for this case.

Figure 7.
Mean stream function contour plots between and obtained by reference FOM and standard ROM-GP simulations for Re : (a) at a resolution of ; (b) with modes; (c) with modes; (d) with modes; and (e) with modes. Note that a stable and well-estimated solution can be found within modes for this case.

Figure 8.
Time series evolution of the first modal coefficient, between and for FOM projection and standard ROM-GP with varying Re (Re ) and POD modes (). modes for Re = 100, and modes for Re = 400.

Figure 9.
Time series evolution of the tenth modal coefficient, between and for FOM projection and standard ROM-GP with varying Re (Re ) and POD modes ().
6.3. Assessments of the Prediction Performance of ROM-GP, ROM-ANN, ROM-H
We observed the inability of the standard ROM-GP model to estimate the correct physics using coarse truncated modes ( or 20) for Re in Section 6.2. For this reason, we consider modes only for the rest of the analyses to assess the predictive performances of the models. As we can see in Figure 10 for Re , all models capture the two-gyre pattern, which is consistent with the true solution as well as previous observations. Similar to Section 6.2, the ROM-GP model fails to capture four-gyre pattern for Re and combination, as shown in Figure 11, but the ROM-ANN and ROM-H models exhibit a successful prediction. Nevertheless, Figure 12 demonstrates the most promising findings that the ROM-H model successfully predicts the four-gyre pattern while the other two basic ROM approaches fail for Re and combination. To support this finding, we again plot the time series evolution for both and , as presented in Figure 13 and Figure 14, to find that the ROM-H model shows an impressive prediction of the FOM projected time series for even higher Re. The prediction of ROM-ANN model is better than the ROM-GP model using same values for the parameters, but not as accurate as the ROM-H model for Re . As we can see, the ROM-H model is capable of capturing the physics utilizing only 10 modes, which leads to an excellent development of a more efficient ROM than the standard ROM-GP, which requires higher modes to capture the physics for Re . A summary of computational overhead is presented in Table 3.

Figure 10.
Mean stream function contour plots between and obtained by reference FOM and different ROM simulations for Re and modes: (a) at a resolution of ; (b) ; (c) ; and (d) . This figure clearly illustrates that all models have captured the two-gyre circulation pattern successfully.
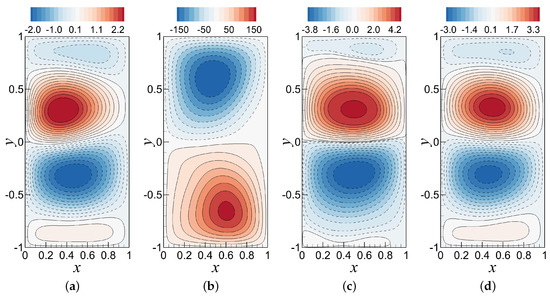
Figure 11.
Mean stream function contour plots between and obtained by reference FOM and different ROM simulations for Re and modes: (a) at a resolution of ; (b) ; (c) ; and (d) . The figure shows that ROM-ANN and ROM-H have captured the four-gyre circulation pattern similar to the FOM solution while ROM-GP has shown an unphysical two-gyre pattern.

Figure 12.
Mean stream function contour plots between and obtained by reference FOM and different ROM simulations for Re and modes: (a) at a resolution of ; (b) ; (c) ; and (d) . Note that only the proposed ROM-H model has successfully captured the four-gyre circulation.

Figure 13.
Time series evolution of the first modal coefficient, , between and for FOM projection and different ROM approaches (ROM-GP, ROM-ANN, and ROM-H) with varying Re (Re ) and POD modes ().

Figure 14.
Time series evolution of the tenth modal coefficient, , between and for FOM projection and different ROM approaches (ROM-GP, ROM-ANN, and ROM-H) with varying Re (Re ) and POD modes ().

Table 3.
The computational CPU time in seconds required for ROM simulations between and . Note that the FOM simulation is 4.82 h and offline POD basis generation takes about 23.38 min. The offline training time for ANN is less than one second due to the extremely fast ELM approach.
6.4. Sensitivity Analysis with Respect to ELM Neurons
Based on the results in Section 6.3, we can state that the prediction performance of our proposed ROM-H model is better than the ROM-ANN model for this test case. However, sensitivity analysis of the ANN architecture should be performed before reaching any conclusion to verify whether the network output alters with the change in the total number of neurons in hidden layer, Q [95]. Because of the black box nature of ANN, we perform a sensitivity analysis with respect to neurons for both ROM-ANN and ROM-H models. It can be clearly seen in Figure 15 of mean stream function results that the ROM-ANN model is showing similar performance improvements for all different number of neurons for and Re cases. Furthermore, in Figure 16, the ROM-H model is showing an excellent agreement with FOM solution for all different number of neurons. On the other hand, the time series of modal coefficient plots for ROM-ANN model in Figure 17 and Figure 18 exhibit some noticeably unusual traits in a number of cases, for example, (, Re ), (, Re ), (, Re ). In addition, the ROM-H model displays satisfactory consistency in its predictive behavior with respect to the variation of Q, as shown in Figure 19 and Figure 20. This suggests that the ROM-H model is robust with respect to the change in total number of neurons included in the hidden layer.
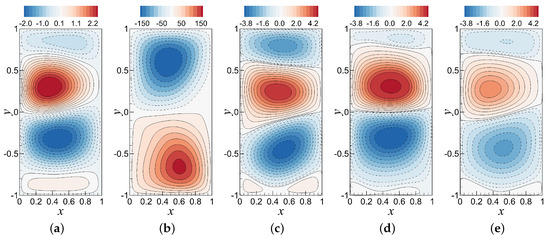
Figure 15.
Sensitivity analysis with respect to the number of neurons in ELM of fully non-intrusive ROM-ANN approach using mean stream function contour plots ( and Re ): (a) ; (b) ; (c) with neurons; (d) with neurons; and (e) with neurons.

Figure 16.
Sensitivity analysis with respect to the number of neurons in ELM of ROM-H approach using mean stream function contour plots ( and Re ): (a) ; (b) ; (c) with neurons; (d) with neurons; and (e) with neurons.

Figure 17.
Sensitivity analysis with respect to the number of ELM neurons of fully non-intrusive ROM-ANN approach using time series of the first modal coefficient, for Re and .
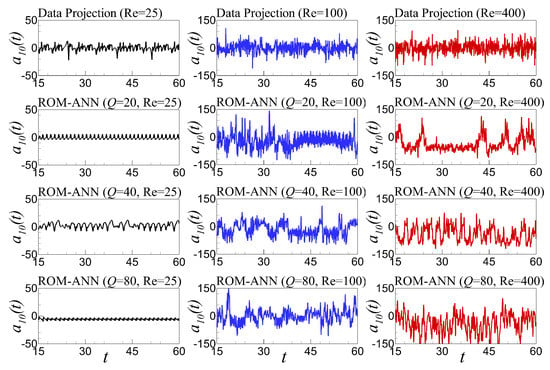
Figure 18.
Sensitivity analysis with respect to the number of ELM neurons of fully non-intrusive ROM-ANN approach using time series of the tenth modal coefficient, for Re and .

Figure 19.
Sensitivity analysis with respect to the number of ELM neurons of ROM-H approach using time series of the first modal coefficient, for Re and .

Figure 20.
Sensitivity analysis with respect to the number of ELM neurons of ROM-H approach using time series of the tenth modal coefficient, for Re and .
6.5. Time Series Evolution and Out-of-Sample Forecasting
To further illustrate the robustness and enhanced potential of the proposed model, here we present a couple more analyses on the ROM-GP, ROM-ANN, and ROM-H approaches. In Figure 21, we present the temporal evolution of obtained by ROM-GP, ROM-ANN and ROM-H model along with FOM projection for Re . The figure displays the forecasting capability of ROM models for a long period of time up to even though the data snapshots were taken between and . For Re and 400 in Figure 22 and Figure 23, respectively, the ROM-ANN and ROM-H models still show a stable time series results, whereas the ROM-GP prediction becomes unphysical. The long time forecasting can be a very useful property of the ROM-H model to reduce the computational cost, and can be applied for practical applications related to forecasting. An out-of-sample a posteriori analysis is also performed where the snapshot data and training dataset are prepared at a particular physical condition to predict the performance of the models at different physical condition. In this study, we conduct two out-of-sample analyses: in one case, we generate the snapshots and training data at Re (lower value than the target prediction state) to predict the performance at Re and, in the other case, we generate the snapshots and training data at Re (higher value than the target prediction state) to predict the performance at Re . As displayed in Figure 24 for the time series of , the ROM-GP again fails to capture the underlying physics for R . The ROM-ANN prediction seems not so random but still does not represent the true statistics. However, the ROM-H prediction series matches the scales of the time series of FOM data projection. We can get a clear idea of this quantitative analysis by observing the visual representation of the mean stream function field in Figure 25. It is apparent that only the ROM-H prediction matches the FOM result since the underlying four-gyre dynamics is captured. Finally, we analyze the prediction performance at Re by using the data collected at Re . The time series plot in Figure 26 reveals that neither ROM-GP nor ROM-ANN can capture the true scales while once again, the ROM-H model shows an impressive prediction of the true physics at Re using Re data. Figure 27 shows the mean field representation which indicates the ROM-H model is capable of out-of-sample forecasting using data from higher Re. These analyses of longer time forecasting and out-of-sample validation puts more strength on the conclusion drawn above that the proposed ROM-H method is more robust in predicting the underlying full order physics than the fully non-intrusive ROM-ANN and standard ROM-GP methods.

Figure 21.
Forecasting of temporal mode evolution of for Re . Note that ROMs are trained by the data snapshots obtained between and .
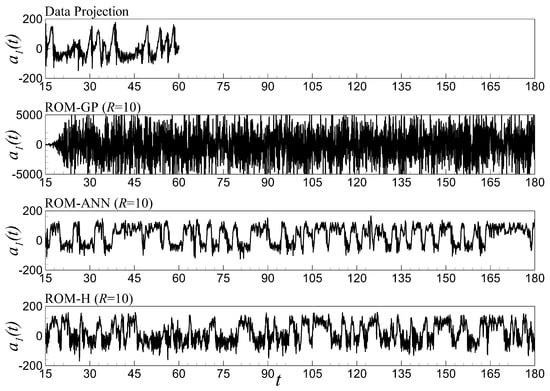
Figure 22.
Forecasting of temporal mode evolution of for Re . Note that all ROMs are trained by the data snapshots obtained between and . Although the ROM-GP approach provides reasonable (physical) results at the beginning (i.e., ), the error then is amplified exponentially.
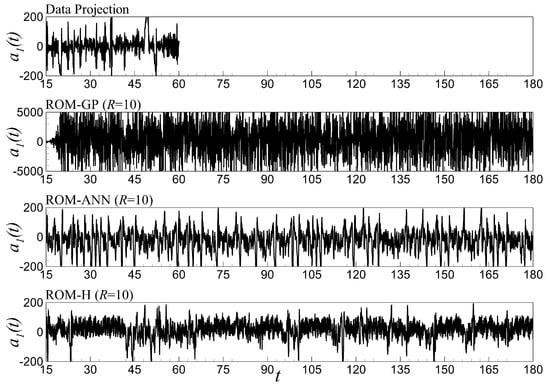
Figure 23.
Forecasting of temporal mode evolution of for Re . Note that all ROMs are trained by the data snapshots obtained between and . Although the ROM-GP approach provides reasonable (physical) results at the beginning (i.e., ), the error is then amplified exponentially.
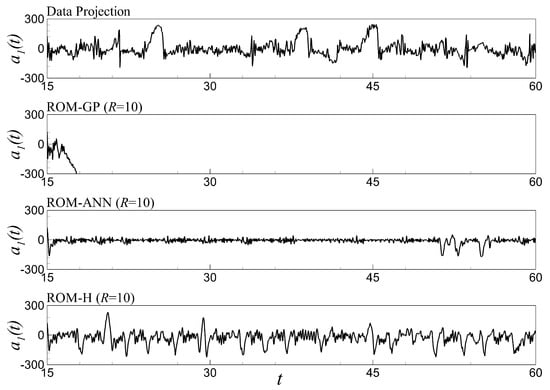
Figure 24.
Time series evolution of the first temporal coefficient for the out-of-sample forecast by FOM and different ROM approaches (ROM-GP, ROM-ANN, and ROM-H) using POD modes. Predictive performance is shown for Re while the training has been performed using the data generated at Re .
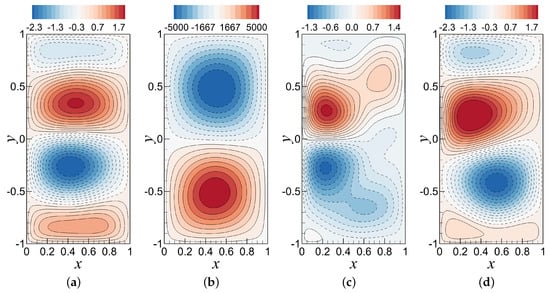
Figure 25.
Out-of-sample forecast of mean stream function by: (a) FOM; (b) ROM-GP; (c) ROM-ANN; and (d) ROM-H using POD modes. Predictive performance is shown for Re while the training has been performed using the data generated at Re . This figure clearly illustrates that the ROM-H model has successfully predicted the FOM solution while the ROM-GP model prediction is unphysical and the ROM-ANN prediction is not as accurate as the ROM-H prediction.

Figure 26.
Time series evolution of the first temporal coefficient for the out-of-sample forecast by FOM and different ROM approaches (ROM-GP, ROM-ANN, and ROM-H) using POD modes. Predictive performance is shown for Re while the training has been performed using the data generated at Re .

Figure 27.
Out-of-sample forecast of mean stream function by: (a) FOM; (b) ROM-GP; (c) ROM-ANN; and (d) ROM-H using POD modes. Predictive performance is shown for Re while the training has been performed using the data generated at Re . Similar to the previous results, this figure also shows that the ROM-H prediction is better than the other two model predictions.
7. Summary
In this work, we propose a reliable and robust reduced-order modeling technique using a hybrid framework. The hybridization is done by combining the standard Galerkin projection based ROM and ELM neural network architecture. We consider an ocean circulation problem governed by a single-layer quasi-geostrophic model as a test platform to analyze the prediction performance and robustness of the model compared to the physics-based and data-driven models. The training and snapshots data for POD basis construction are generated using a FOM simulation. The resolved ROM coefficients are utilized as inputs for the simple feedforward ELM network. We then introduce a weighting parameter to dynamically account for contributions from the physics-based and data-driven models. In other words, we propose a hybrid reduced-order model (ROM) comprising a first principle Galerkin model and a data driven ANN model for the dynamics based on POD mode amplitudes. Therefore, the key novelty of this hybrid ROM is a simple weighting between first-principle and data-driven model. Furthermore, we show an ad-hoc dynamical approach to estimate this weighting parameter which provides a freedom in the hybridization procedure to come up with a good possible combination of component model contributions.
To assess the performance of our proposed model, we perform a number of analyses based on the mean stream function field variable and time series evolution statistics. Our study reveals that the proposed hybrid ROM model can successfully capture the underlying physics using a small number of modes which means the hybrid model is capable of performing a robust model order reduction process than the standard projection based ROM and data-driven ROM approaches. To validate the fidelity of the results obtained by the hybrid framework, we conduct a sensitivity analysis which reveals that the hybrid model is consistent with respect to the total number of hidden layer neurons of the ELM network. To show the robustness of the model, we also perform a long time forecasting and out-of-sample validation analysis. The hybrid model successfully captures the flow dynamics for these cases, while the other two component models fail to predict the true physics for higher Re and lower number of modes. Overall, our primary goal of leveraging the advantages of two basic reduced-order modeling techniques is fulfilled by the proposed hybrid ROM model in a sense that the model is data-driven and can be generalized for complex fluid flow problems, the model is robust and capable of reducing the total computational cost significantly, and the model neither requires any extra stabilization modification to account for numerical instabilities nor is it fully dependent on black box predictions.
Author Contributions
Conceptualization, O.S. and A.R.; Data curation, S.M.R. and O.S.; Formal analysis, S.M.R. and O.S.; Methodology, O.S.; Supervision, O.S.; Writing—original draft, S.M.R.; and Writing—review and editing, S.M.R., O.S. and A.R.
Funding
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research under Award Number DE-SC0019290. Disclaimer: This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
Acknowledgments
The computing for this project was performed by using resources from the High Performance Computing Center (HPCC) at Oklahoma State University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada Flintridge, CA, USA, 1998. [Google Scholar]
- Durbin, P.A. Some recent developments in turbulence closure modeling. Ann. Rev. Fluid Mech. 2018, 50, 77–103. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence modeling in the age of data. arXiv, 2018; arXiv:1804.00183. [Google Scholar]
- Munk, W.H. On the wind-driven ocean circulation. J. Meteorol. 1950, 7, 80–93. [Google Scholar] [CrossRef]
- Pelc, R.; Fujita, R.M. Renewable energy from the ocean. Mar. Policy 2002, 26, 471–479. [Google Scholar] [CrossRef]
- Esteban, M.; Leary, D. Current developments and future prospects of offshore wind and ocean energy. Appl. Energy 2012, 90, 128–136. [Google Scholar] [CrossRef]
- McWilliams, J.C. Fundamentals of Geophysical Fluid Dynamics; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Berloff, P. Dynamically consistent parameterization of mesoscale eddies. Part I: Simple model. Ocean Model. 2015, 87, 1–19. [Google Scholar] [CrossRef]
- San, O.; Staples, A.E.; Wang, Z.; Iliescu, T. Approximate deconvolution large eddy simulation of a barotropic ocean circulation model. Ocean Model. 2011, 40, 120–132. [Google Scholar] [CrossRef]
- Berloff, P. Dynamically consistent parameterization of mesoscale eddies—Part II: Eddy fluxes and diffusivity from transient impulses. Fluids 2016, 1, 22. [Google Scholar] [CrossRef]
- Miller, R.N. Numerical Modeling of Ocean Circulation; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Kondrashov, D.; Chekroun, M.D.; Berloff, P. Multiscale Stuart–Landau emulators: Application to wind-driven ocean gyres. Fluids 2018, 3, 21. [Google Scholar] [CrossRef]
- Lynch, P. The origins of computer weather prediction and climate modeling. J. Comput. Phys. 2008, 227, 3431–3444. [Google Scholar] [CrossRef]
- Laurie, J.; Bouchet, F. Computation of rare transitions in the barotropic quasi-geostrophic equations. New J. Phys. 2015, 17, 015009. [Google Scholar] [CrossRef]
- Rowley, C.W.; Dawson, S.T. Model reduction for flow analysis and control. Ann. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef]
- Taira, K.; Brunton, S.L.; Dawson, S.T.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef]
- Ito, K.; Ravindran, S. A reduced-order method for simulation and control of fluid flows. J. Comput. Phys. 1998, 143, 403–425. [Google Scholar] [CrossRef]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-order modeling: New approaches for computational physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef]
- Brenner, T.A.; Fontenot, R.L.; Cizmas, P.G.; O’Brien, T.J.; Breault, R.W. A reduced-order model for heat transfer in multiphase flow and practical aspects of the proper orthogonal decomposition. Comput. Chem. Eng. 2012, 43, 68–80. [Google Scholar] [CrossRef]
- Iollo, A.; Lanteri, S.; Désidéri, J.A. Stability properties of POD–Galerkin approximations for the compressible Navier–Stokes equations. Theor. Comput. Fluid Dyn. 2000, 13, 377–396. [Google Scholar] [CrossRef]
- Freno, B.A.; Cizmas, P.G. A proper orthogonal decomposition method for nonlinear flows with deforming meshes. Int. J. Heat Fluid Flow 2014, 50, 145–159. [Google Scholar] [CrossRef]
- San, O.; Iliescu, T. A stabilized proper orthogonal decomposition reduced-order model for large scale quasigeostrophic ocean circulation. Adv. Comput. Math. 2015, 41, 1289–1319. [Google Scholar] [CrossRef]
- Behzad, F.; Helenbrook, B.T.; Ahmadi, G. On the sensitivity and accuracy of proper-orthogonal-decomposition-based reduced order models for Burgers equation. Comput. Fluids 2015, 106, 19–32. [Google Scholar] [CrossRef]
- Cizmas, P.G.; Richardson, B.R.; Brenner, T.A.; O’Brien, T.J.; Breault, R.W. Acceleration techniques for reduced-order models based on proper orthogonal decomposition. J. Comput. Phys. 2008, 227, 7791–7812. [Google Scholar] [CrossRef]
- Bistrian, D.; Navon, I. An improved algorithm for the shallow water equations model reduction: Dynamic Mode Decomposition vs. POD. Int. J. Numer. Methods Fluids 2015, 78, 552–580. [Google Scholar] [CrossRef]
- Behzad, F.; Helenbrook, B.T.; Ahmadi, G. Multilevel Algorithm for Obtaining the Proper Orthogonal Decomposition. AIAA J. 2018. [Google Scholar] [CrossRef]
- Bistrian, D.A.; Navon, I.M. Randomized dynamic mode decomposition for nonintrusive reduced order modelling. Int. J. Numer. Methods Eng. 2017, 112, 3–25. [Google Scholar] [CrossRef]
- Gautier, N.; Aider, J.L.; Duriez, T.; Noack, B.; Segond, M.; Abel, M. Closed-loop separation control using machine learning. J. Fluid Mech. 2015, 770, 442–457. [Google Scholar] [CrossRef]
- Lee, C.; Kim, J.; Babcock, D.; Goodman, R. Application of neural networks to turbulence control for drag reduction. Phys. Fluids 1997, 9, 1740–1747. [Google Scholar] [CrossRef]
- Gamahara, M.; Hattori, Y. Searching for turbulence models by artificial neural network. Phys. Rev. Fluids 2017, 2, 054604. [Google Scholar] [CrossRef]
- Duraisamy, K.; Zhang, Z.J.; Singh, A.P. New approaches in turbulence and transition modeling using data-driven techniques. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1284. [Google Scholar]
- Maulik, R.; San, O. A neural network approach for the blind deconvolution of turbulent flows. J. Fluid Mech. 2017, 831, 151–181. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Extreme learning machine for reduced order modeling of turbulent geophysical flows. Phys. Rev. E 2018, 97, 042322. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.L.; Xiao, H.; Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys. Rev. Fluids 2018, 3, 074602. [Google Scholar] [CrossRef]
- Moosavi, A.; Stefanescu, R.; Sandu, A. Efficient construction of local parametric reduced order models using machine learning techniques. arXiv, 2015; arXiv:1511.02909. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L. Convex incremental extreme learning machine. Neurocomputing 2007, 70, 3056–3062. [Google Scholar] [CrossRef]
- Xiang, J.; Westerlund, M.; Sovilj, D.; Pulkkis, G. Using extreme learning machine for intrusion detection in a big data environment. In Proceedings of the 2014 Workshop on Artificial Intelligent and Security Workshop, Scottsdale, AZ, USA, 3–7 November 2014; pp. 73–82. [Google Scholar]
- Williams, M.O.; Schmid, P.J.; Kutz, J.N. Hybrid reduced-order integration with proper orthogonal decomposition and dynamic mode decomposition. Multiscale Model. Simul. 2013, 11, 522–544. [Google Scholar] [CrossRef]
- Xie, X.; Mohebujjaman, M.; Rebholz, L.; Iliescu, T. Data-driven filtered reduced order modeling of fluid flows. SIAM J. Sci. Comput. 2018, 40, B834–B857. [Google Scholar] [CrossRef]
- Mohebujjaman, M.; Rebholz, L.; Iliescu, T. Physically-constrained data-driven, filtered reduced order modeling of fluid flows. arXiv, 2018; arXiv:1806.0035. [Google Scholar]
- Wan, Z.Y.; Vlachas, P.; Koumoutsakos, P.; Sapsis, T. Data-assisted reduced-order modeling of extreme events in complex dynamical systems. PLoS ONE 2018, 13, e0197704. [Google Scholar] [CrossRef] [PubMed]
- Pathak, J.; Wikner, A.; Fussell, R.; Chandra, S.; Hunt, B.R.; Girvan, M.; Ott, E. Hybrid forecasting of chaotic processes: Using machine learning in conjunction with a knowledge-based model. Chao Interdiscip. J. Nonlinear Sci. 2018, 28, 041101. [Google Scholar] [CrossRef]
- Siedler, G.; Griffies, S.M.; Gould, J.; Church, J.A. Ocean Circulation and Climate: A 21st Century Perspective; Academic Press: Cambridge, MA, USA, 2013; Volume 103. [Google Scholar]
- Byrne, D.; Münnich, M.; Frenger, I.; Gruber, N. Mesoscale atmosphere ocean coupling enhances the transfer of wind energy into the ocean. Nat. Commun. 2016, 7, ncomms11867. [Google Scholar] [CrossRef] [PubMed]
- Holland, W.R. The role of mesoscale eddies in the general circulation of the ocean—Numerical experiments using a wind-driven quasi-geostrophic model. J. Phys. Oceanogr. 1978, 8, 363–392. [Google Scholar] [CrossRef]
- Hogg, A.M.C.; Dewar, W.K.; Berloff, P.; Kravtsov, S.; Hutchinson, D.K. The effects of mesoscale ocean–atmosphere coupling on the large-scale ocean circulation. J. Clim. 2009, 22, 4066–4082. [Google Scholar] [CrossRef]
- Hua, B.; Haidvogel, D. Numerical simulations of the vertical structure of quasi-geostrophic turbulence. J. Atmos. Sci. 1986, 43, 2923–2936. [Google Scholar] [CrossRef]
- Ghil, M.; Chekroun, M.D.; Simonnet, E. Climate dynamics and fluid mechanics: Natural variability and related uncertainties. Phys. D Nonlinear Phenom. 2008, 237, 2111–2126. [Google Scholar] [CrossRef]
- Charney, J.G.; Fjörtoft, R.; Neumann, J.V. Numerical integration of the barotropic vorticity equation. Tellus 1950, 2, 237–254. [Google Scholar] [CrossRef]
- Bouchet, F.; Simonnet, E. Random changes of flow topology in two-dimensional and geophysical turbulence. Phys. Rev. Lett. 2009, 102, 094504. [Google Scholar] [CrossRef] [PubMed]
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects; Academic Press: Waltham, MA, USA, 2011. [Google Scholar]
- Majda, A.; Wang, X. Nonlinear Dynamics and Statistical Theories for Basic Geophysical Flows; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Greatbatch, R.J.; Nadiga, B.T. Four-gyre circulation in a barotropic model with double-gyre wind forcing. J. Phys. Oceanogr. 2000, 30, 1461–1471. [Google Scholar] [CrossRef]
- Nadiga, B.T.; Margolin, L.G. Dispersive–dissipative eddy parameterization in a barotropic model. J. Phys. Oceanogr. 2001, 31, 2525–2531. [Google Scholar] [CrossRef]
- San, O. Numerical assessments of ocean energy extraction from western boundary currents using a quasi-geostrophic ocean circulation model. Int. J. Mar. Energy 2016, 16, 12–29. [Google Scholar] [CrossRef]
- San, O.; Staples, A.E. An efficient coarse grid projection method for quasigeostrophic models of large-scale ocean circulation. Int. J. Multiscale Comput. Eng. 2013, 11, 463–495. [Google Scholar] [CrossRef]
- Özgökmen, T.M.; Chassignet, E.P. Emergence of inertial gyres in a two-layer quasigeostrophic ocean model. J. Phys. Oceanogr. 1998, 28, 461–484. [Google Scholar] [CrossRef]
- Holm, D.D.; Nadiga, B.T. Modeling mesoscale turbulence in the barotropic double-gyre circulation. J. Phys. Oceanogr. 2003, 33, 2355–2365. [Google Scholar] [CrossRef]
- Medjo, T.T. Numerical simulations of a two-layer quasi-geostrophic equation of the ocean. SIAM J. Numer. Anal. 2000, 37, 2005–2022. [Google Scholar] [CrossRef]
- Arakawa, A. Computational design for long-term numerical integration of the equations of fluid motion: Two-dimensional incompressible flow. Part I. J. Comput. Phys. 1966, 1, 119–143. [Google Scholar] [CrossRef]
- Gottlieb, S.; Shu, C.W. Total variation diminishing Runge–Kutta schemes. Math. Comput. Am. Math. Soc. 1998, 67, 73–85. [Google Scholar] [CrossRef]
- Wedi, N.P. Increasing horizontal resolution in numerical weather prediction and climate simulations: Illusion or panacea? Philos. Trans. R. Soc. A 2014, 372, 20130289. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Noack, B.R. Closed-loop turbulence control: Progress and challenges. Appl. Mech. Rev. 2015, 67, 050801. [Google Scholar] [CrossRef]
- Navon, I.M.; Zou, X.; Derber, J.; Sela, J. Variational data assimilation with an adiabatic version of the NMC spectral model. Mon. Weather Rev. 1992, 120, 1433–1446. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Lumley, J.L. Stochastic Tools in Turbulence; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Kosambi, D.D. Statistics in function space. In D D Kosambi; Ramaswamy, R., Ed.; Springer: New Delhi, India, 2016; pp. 115–123. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Noack, B.R.; Afanasiev, K.; Morzński, M.; Tadmor, G.; Thiele, F. A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 2003, 497, 335–363. [Google Scholar] [CrossRef]
- Rapún, M.L.; Vega, J.M. Reduced order models based on local POD plus Galerkin projection. J. Comput. Phys. 2010, 229, 3046–3063. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Frankel, S. Numerical Methods for Engineers and Scientists; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesús, O. Neural Network Design; Pws Pub.: Boston, MA, USA, 1996; Volume 20. [Google Scholar]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-fuzzy and soft computing; a computational approach to learning and machine intelligence. IEEE Trans. Autom. Control 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Lapedes, A.S.; Farber, R.M. How neural nets work. In Neural Information Processing Systems; Springer: Berlin, Germany, 1988; pp. 442–456. [Google Scholar]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme learning machines: A survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Zhou, H.; Soh, Y.C.; Jiang, C.; Wu, X. Compressed representation learning for fluid field reconstruction from sparse sensor observations. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–16 July 2015. [Google Scholar]
- Kasun, L.L.C.; Zhou, H.; Huang, G.B.; Vong, C.M. Representational learning with extreme learning machine for big data. IEEE Intell. Syst. 2013, 28, 31–34. [Google Scholar]
- Cordier, L.; El Majd, B.A.; Favier, J. Calibration of POD reduced-order models using Tikhonov regularization. Int. J. Numer. Methods Fluids 2010, 63, 269–296. [Google Scholar] [CrossRef]
- Cancelliere, R.; Deluca, R.; Gai, M.; Gallinari, P.; Rubini, L. An analysis of numerical issues in neural training by pseudoinversion. Comput. Appl. Math. 2017, 36, 599–609. [Google Scholar] [CrossRef]
- Huang, G.B.; Babri, H.A. Upper bounds on the number of hidden neurons in feedforward networks with arbitrary bounded nonlinear activation functions. IEEE Trans. Neural Netw. 1998, 9, 224–229. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.L.; Choi, T.M.; Au, K.F.; Yu, Y. Sales forecasting using extreme learning machine with applications in fashion retailing. Decis. Support Syst. 2008, 46, 411–419. [Google Scholar] [CrossRef]
- Wright, S.; Nocedal, J. Numerical Optimization; Springer Science: Berlin, Germany, 1999; Volume 35, p. 7. [Google Scholar]
- Lin, C.J.; Weng, R.C.; Keerthi, S.S. Trust region newton method for logistic regression. J. Mach. Learn. Res. 2008, 9, 627–650. [Google Scholar]
- Cushman-Roisin, B.; Manga, M. Introduction to Geophysical Fluid Dynamics. Pure Appl. Geophys. 1995, 144, 177–178. [Google Scholar]
- Cummins, P.F. Inertial gyres in decaying and forced geostrophic turbulence. J. Mar. Res. 1992, 50, 545–566. [Google Scholar] [CrossRef]
- Östh, J.; Noack, B.R.; Krajnović, S.; Barros, D.; Borée, J. On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body. J. Fluid Mech. 2014, 747, 518–544. [Google Scholar] [CrossRef]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 237, 10–26. [Google Scholar] [CrossRef]
- San, O.; Iliescu, T. Proper orthogonal decomposition closure models for fluid flows: Burgers equation. Int. J. Numer. Anal. Model. Ser. B 2014, 5, 217–237. [Google Scholar]
- Giere, S.; Iliescu, T.; John, V.; Wells, D. SUPG reduced order models for convection-dominated convection–diffusion–reaction equations. Comput. Methods Appl. Mech. Eng. 2015, 289, 454–474. [Google Scholar] [CrossRef]
- Montano, J.; Palmer, A. Numeric sensitivity analysis applied to feedforward neural networks. Neural Comput. Appl. 2003, 12, 119–125. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).