A Numerical Study of the Sound and Force Production of Flexible Insect Wings
Abstract
1. Introduction
2. Materials and Methods
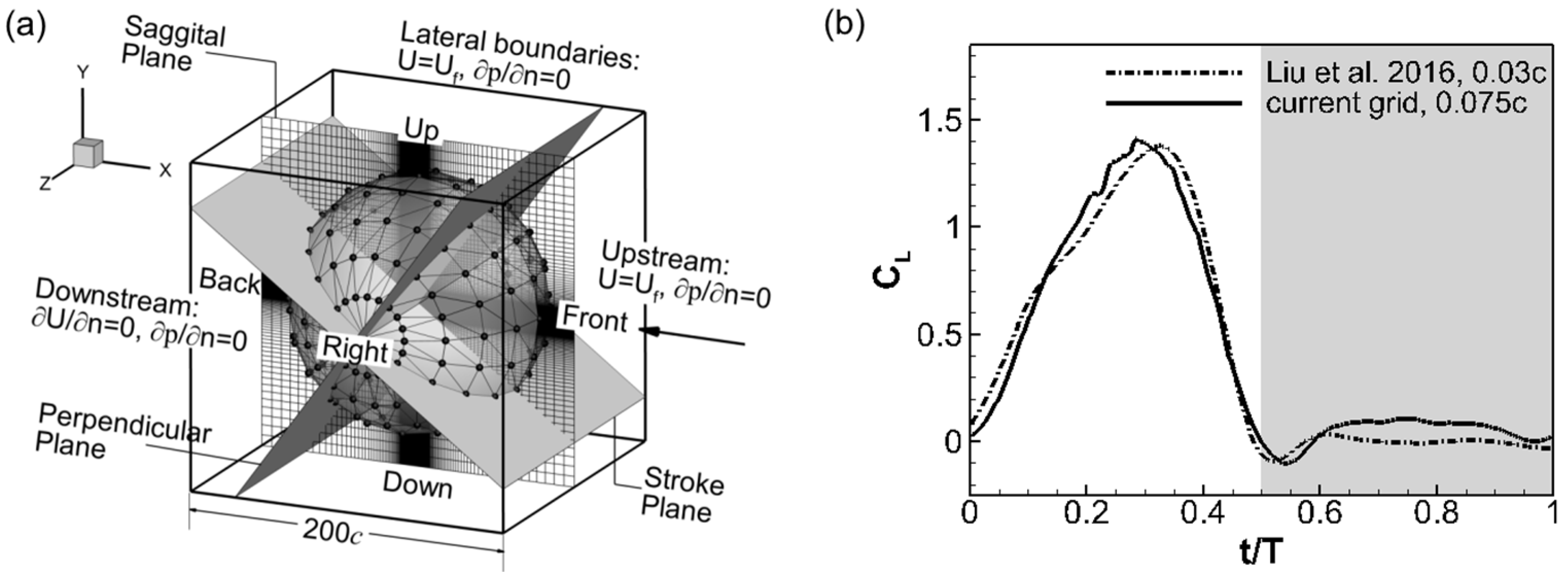
2.1. Computational Methodology
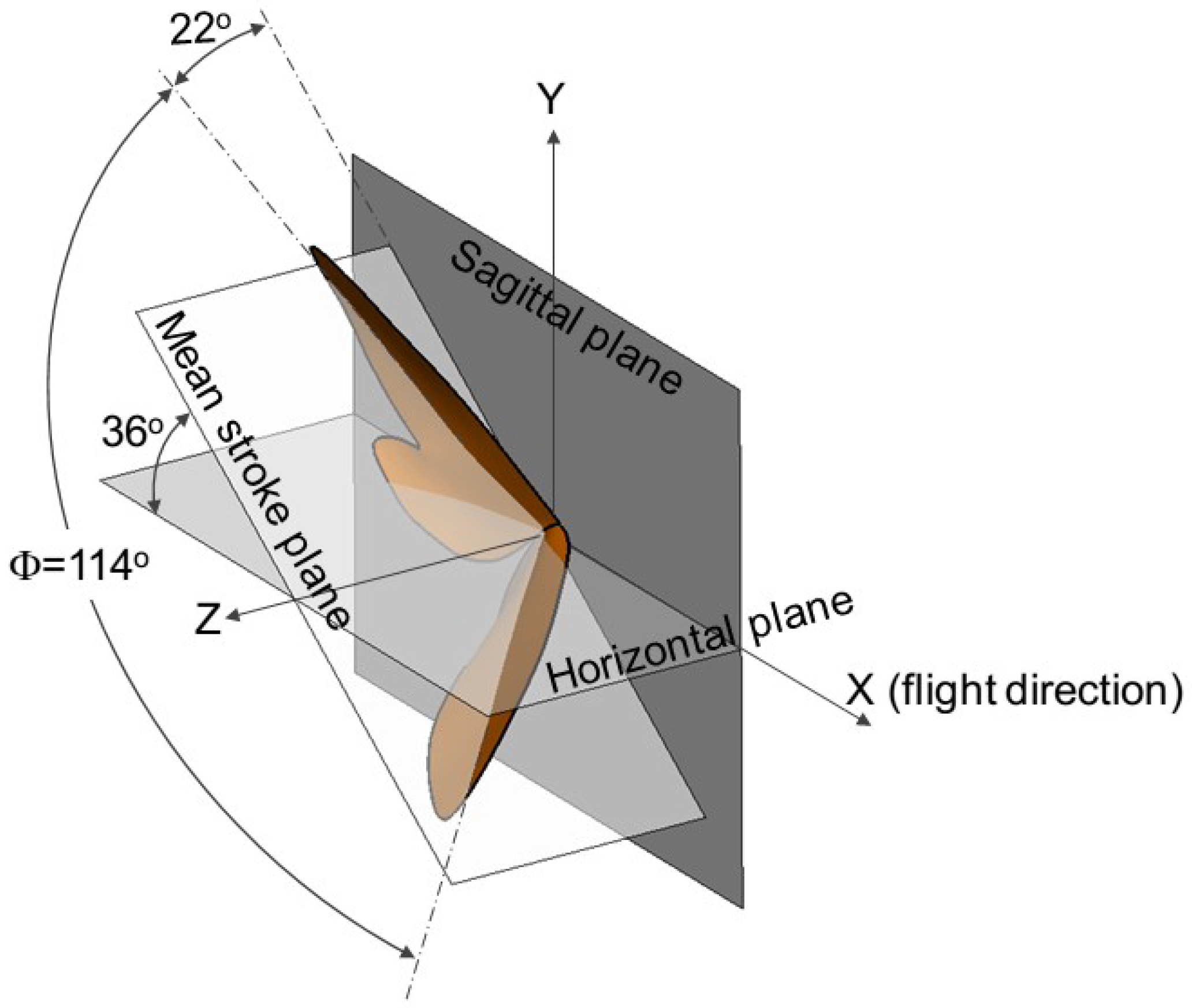
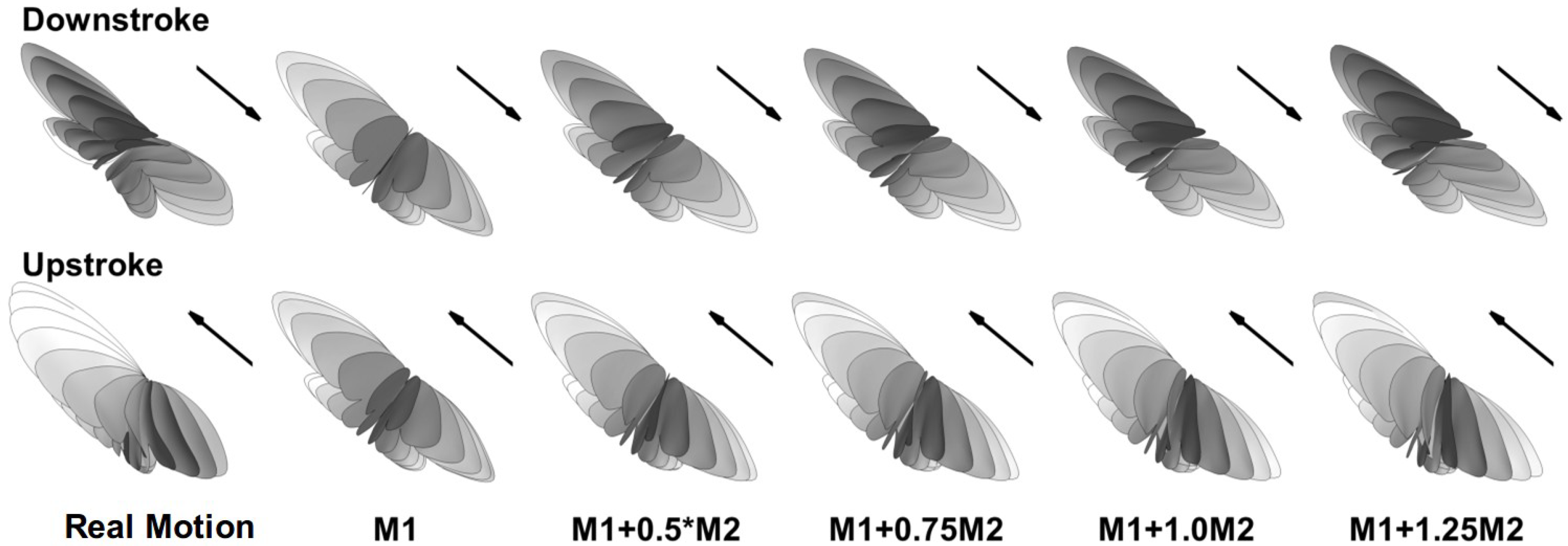
2.2. Wing Models and Simulation Setup
3. Results and Discussion
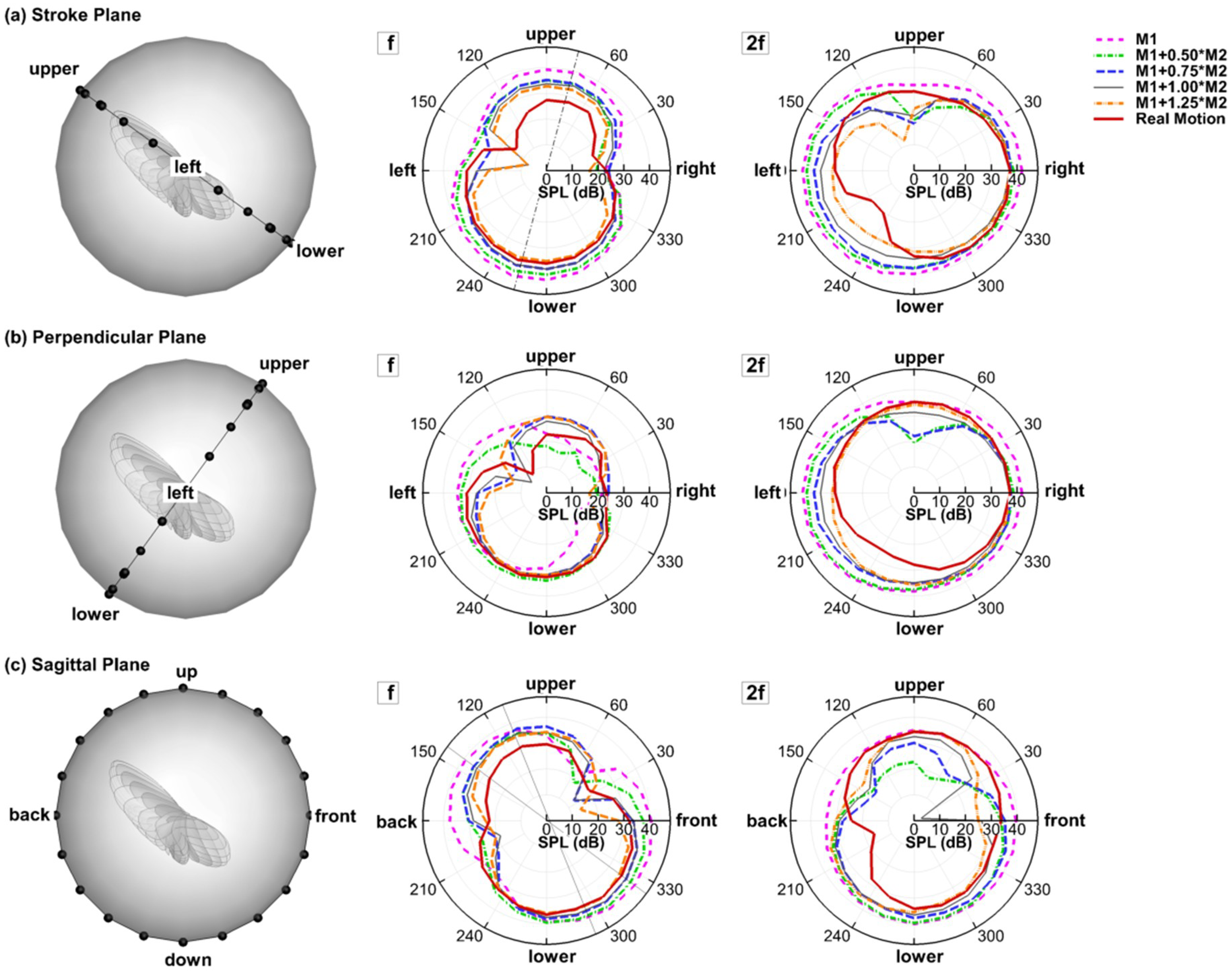
3.1. Generation of the Flapping Tune
3.2. Aerodynamic Force Scaling with Dynamic Pressure Force
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, M. Insect flight dynamics: Stability and control. Rev. Mod. Phys. 2014, 86, 615. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. I. The quasi-steady analysis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1984, 305, 1–15. [Google Scholar] [CrossRef]
- Ellington, C.P.; Van Den Berg, C.; Willmott, A.P.; Thomas, A.L.R. Leading-edge vortices in insect flight. Nature 1996, 384, 626. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.-O.; Sane, S.P. Wing Rotation and the Aerodynamics Basis of Insect Flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Tang, J. Lift and power requirements of hovering flight in Drosophila virilis. J. Exp. Biol. 2002, 205, 2413–2427. [Google Scholar] [PubMed]
- Usherwood, J.R.; Ellington, C.P. The aerodynamics of revolving wings I. Model hawkmoth wings. J. Exp. Biol. 2002, 205, 1547–1564. [Google Scholar] [PubMed]
- Usherwood, J.R.; Ellington, C.P. The aerodynamics of revolving wings II. Propeller force coefficients from mayfly to quail. J. Exp. Biol. 2002, 205, 1565–1576. [Google Scholar] [PubMed]
- Dickson, W.B.; Dickinson, M.H. The effect of advance ratio on the aerodynamics of revolving wings. J. Exp. Biol. 2004, 207, 4269–4281. [Google Scholar] [CrossRef] [PubMed]
- Ewing, A.W. Arthropod Bioacoustics: Neurobiology and Behaviour; Comstock Publishing Associates: Ithaca, NY, USA, 1989. [Google Scholar]
- Jackson, J.C.; Robert, D. Nonlinear auditory mechanism enhances female sounds for male mosquitoes. Proc. Natl. Acad. Sci. USA 2006, 103, 16734–16739. [Google Scholar] [CrossRef] [PubMed]
- Srygley, R.B. Evolution of the wave: Aerodynamic and aposematic functions of butterfly wing motion. Proc. R. Soc. Lond. B Biol. Sci. 2007, 274, 913–917. [Google Scholar] [CrossRef] [PubMed]
- Pitcher, T.J. Behaviour of Teleost Fishes; Fish & Fisheries Series; Springer: Dordrecht, The Netherlands, 1992; ISBN 9780412429309. [Google Scholar]
- Pitcher, T.J.; Partridge, B.L.; Wardle, C.S. A blind fish can school. Science 1976, 194, 963–965. [Google Scholar] [CrossRef] [PubMed]
- Partridge, B.L.; Pitcher, T.J. The sensory basis of fish schools: Relative roles of lateral line and vision. J. Comp. Physiol. 1980, 135, 315–325. [Google Scholar] [CrossRef]
- Robert, D.; Göpfert, M.C. Acoustic sensitivity of fly antennae. J. Insect Physiol. 2002, 48, 189–196. [Google Scholar] [CrossRef]
- Clark, C.J. Locomotion-Induced Sounds and Sonations: Mechanisms, Communication Function, and Relationship with Behavior. In Vertebrate Sound Production and Acoustic Communication; Suthers, R., Fitch, W., Fay, R., Popper, A., Eds.; Springer Handbook of Auditory Research; Springer: Cham, Switzerland, 2016; Volume 53. [Google Scholar]
- Sueur, J.; Tuck, E.J.; Robert, D. Sound radiation around a flying fly. J. Acoust. Soc. Am. 2005, 118, 530–538. [Google Scholar] [CrossRef] [PubMed]
- Bae, Y.; Moon, Y.J. Aerodynamic sound generation of flapping wing. J. Acoust. Soc. Am. 2008, 124, 72–81. [Google Scholar] [CrossRef] [PubMed]
- Inada, Y.; Aono, H.; Liu, H.; Aoyama, T. Numerical Analysis of Sound Generation of Insect Flapping Wings. Theor. Appl. Mech. Jpn. 2009, 57, 437–447. [Google Scholar]
- Geng, B.; Xue, Q.; Zheng, X.; Liu, G.; Ren, Y.; Dong, H. The effect of wing flexibility on sound generation of flapping wings. Bioinspir. Biomim. 2017, 13, 16010. [Google Scholar] [CrossRef] [PubMed]
- Combes, S.A.; Daniel, T.L. Into thin air: Contributions of aerodynamic and inertial-elastic forces to wing bending in the hawkmoth Manduca sexta. J. Exp. Biol. 2003, 206, 2999–3006. [Google Scholar] [CrossRef] [PubMed]
- Eldredge, J.D.; Toomey, J.; Medina, A. On the roles of chord-wise flexibility in a flapping wing with hovering kinematics. J. Fluid Mech. 2010, 659, 94–115. [Google Scholar] [CrossRef]
- Heathcote, S.; Wang, Z.; Gursul, I. Effect of spanwise flexibility on flapping wing propulsion. J. Fluids Struct. 2008, 24, 183–199. [Google Scholar] [CrossRef]
- Kang, C.-K.; Aono, H.; Cesnik, C.E.S.; Shyy, W. Effects of flexibility on the aerodynamic performance of flapping wings. J. Fluid Mech. 2011, 689, 32–74. [Google Scholar] [CrossRef]
- Du, G.; Sun, M. Effects of wing deformation on aerodynamic forces in hovering hoverflies. J. Exp. Biol. 2010, 213, 2273–2283. [Google Scholar] [CrossRef] [PubMed]
- Young, J.; Walker, S.M.; Bomphrey, R.J.; Taylor, G.K.; Thomas, A.L.R. Details of insect wing design and deformation enhance aerodynamic function and flight efficiency. Science 2009, 325, 1549–1552. [Google Scholar] [CrossRef] [PubMed]
- Hardin, J.C.; Pope, D.S. An acoustic/viscous splitting technique for computational aeroacoustics. Theor. Comput. Fluid Dyn. 1994, 6, 323–340. [Google Scholar] [CrossRef]
- Seo, J.-H.; Moon, Y.J. Perturbed compressible equations for aeroacoustic noise prediction at low Mach numbers. AIAA J. 2005, 43, 1716–1724. [Google Scholar] [CrossRef]
- Seo, J.H.; Moon, Y.J. Linearized perturbed compressible equations for low Mach number aeroacoustics. J. Comput. Phys. 2006, 218, 702–719. [Google Scholar] [CrossRef]
- Mittal, R.; Dong, H.; Bozkurttas, M.; Najjar, F.M.; Vargas, A.; von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 2008, 227, 4825–4852. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Xue, Q.; Mittal, R.; Beilamowicz, S. A coupled sharp-interface immersed boundary-finite-element method for flow-structure interaction with application to human phonation. J. Biomech. Eng. 2010, 132, 111003. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.H.; Mittal, R. A high-order immersed boundary method for acoustic wave scattering and low-Mach number flow-induced sound in complex geometries. J. Comput. Phys. 2011, 230, 1000–1019. [Google Scholar] [CrossRef] [PubMed]
- Koehler, C.; Liang, Z.; Gaston, Z.; Wan, H.; Dong, H. 3D reconstruction and analysis of wing deformation in free-flying dragonflies. J. Exp. Biol. 2012. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Dong, H. Low-dimensional Modeling and Aerodynamics of Flexible Wings in Flapping Flight. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 4168. [Google Scholar]
- Liu, G.; Dong, H.; Li, C. Vortex dynamics and new lift enhancement mechanism of wing–body interaction in insect forward flight. J. Fluid Mech. 2016, 795, 634–651. [Google Scholar] [CrossRef]
- Wan, H.; Dong, H.; Gai, K. Computational investigation of cicada aerodynamics in forward flight. J. R. Soc. Interface 2014, 12, 20141116. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, Q.; Deng, X.; Sane, S.P. Aerodynamic effects of flexibility in flapping wings. J. R. Soc. Interface 2010, 7, 485–497. [Google Scholar] [CrossRef] [PubMed]
- Leishman, G.J. Principles of Helicopter Aerodynamics with CD Extra; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
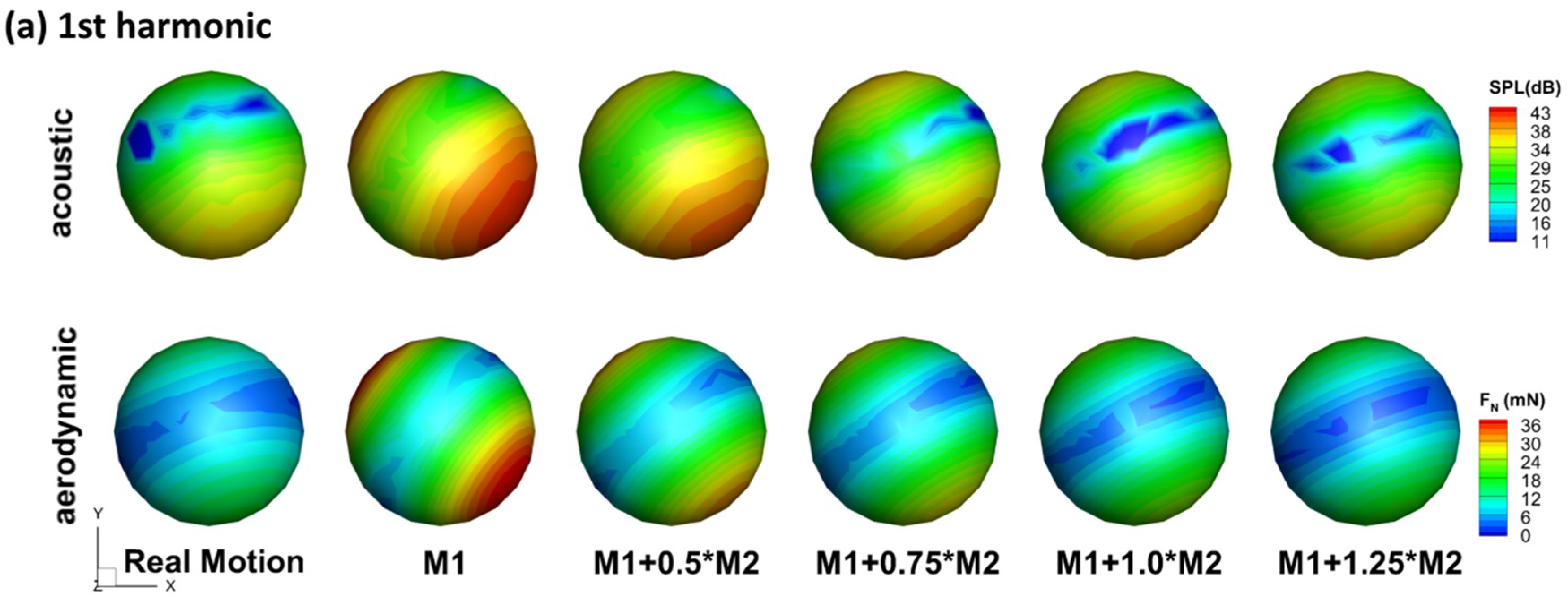
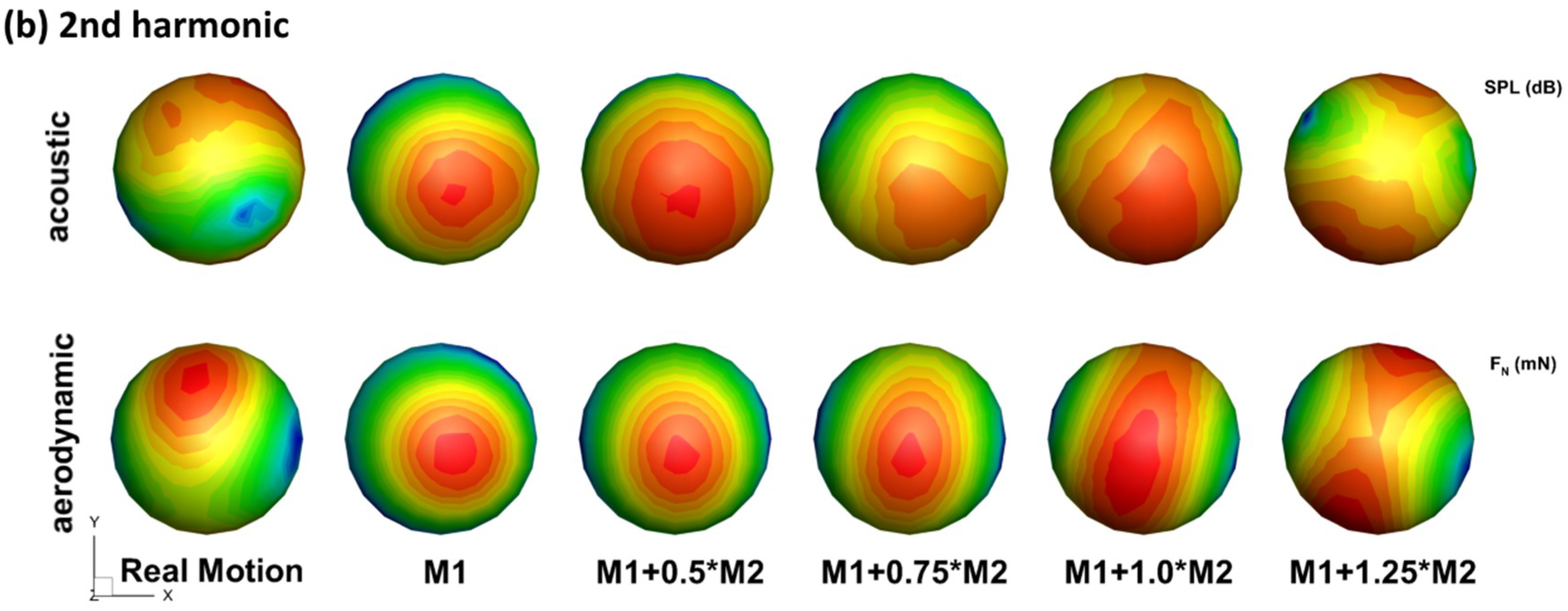
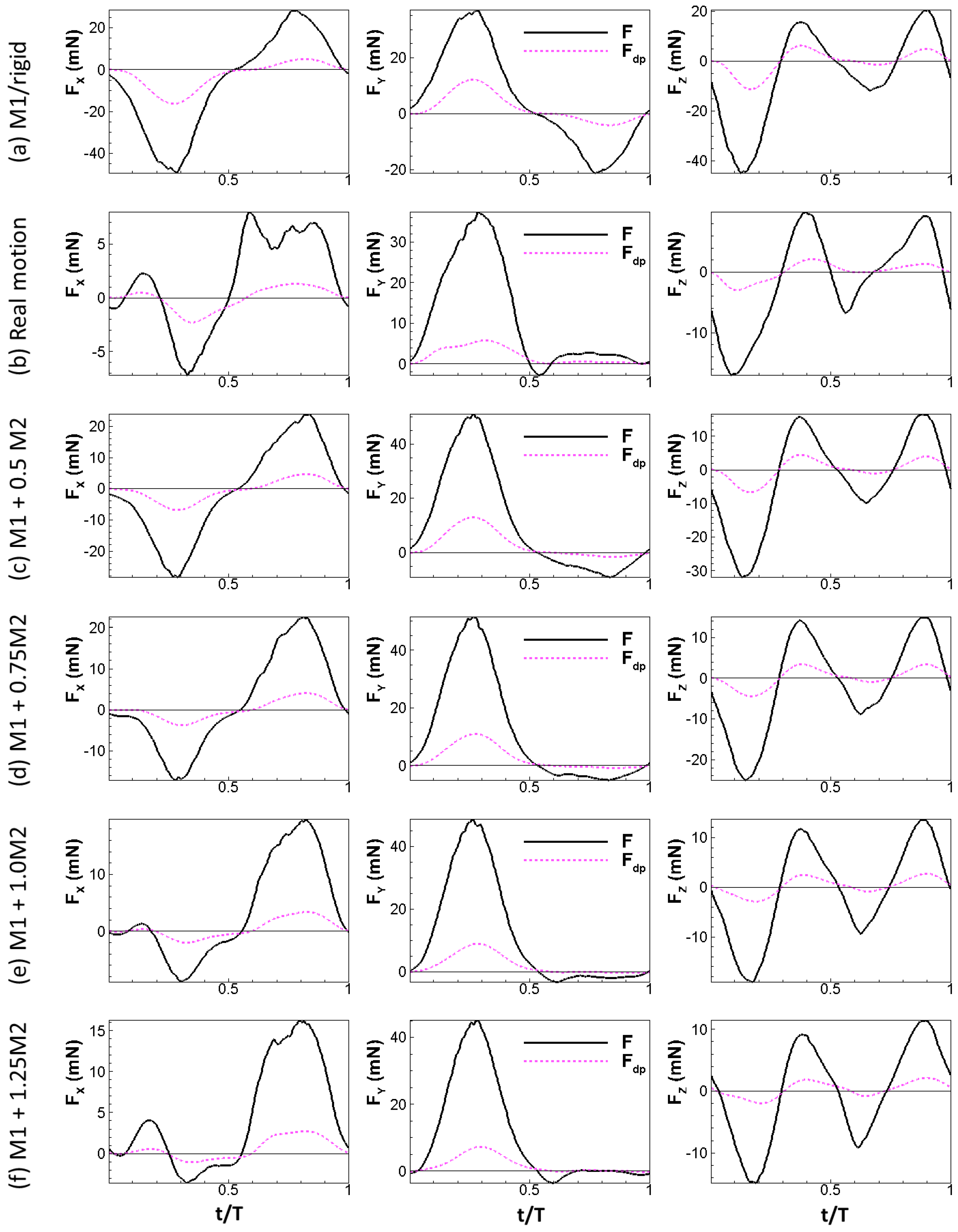
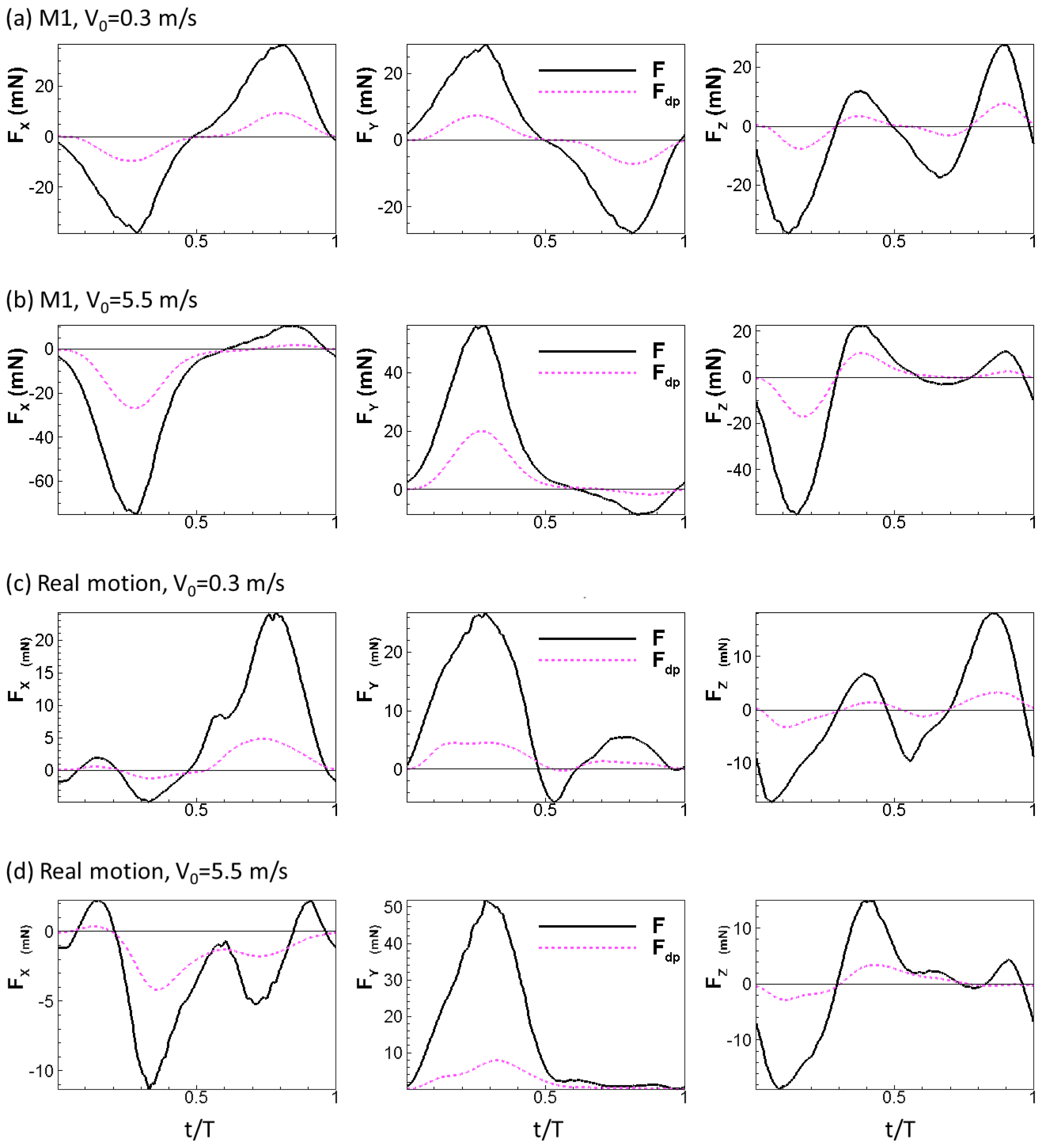
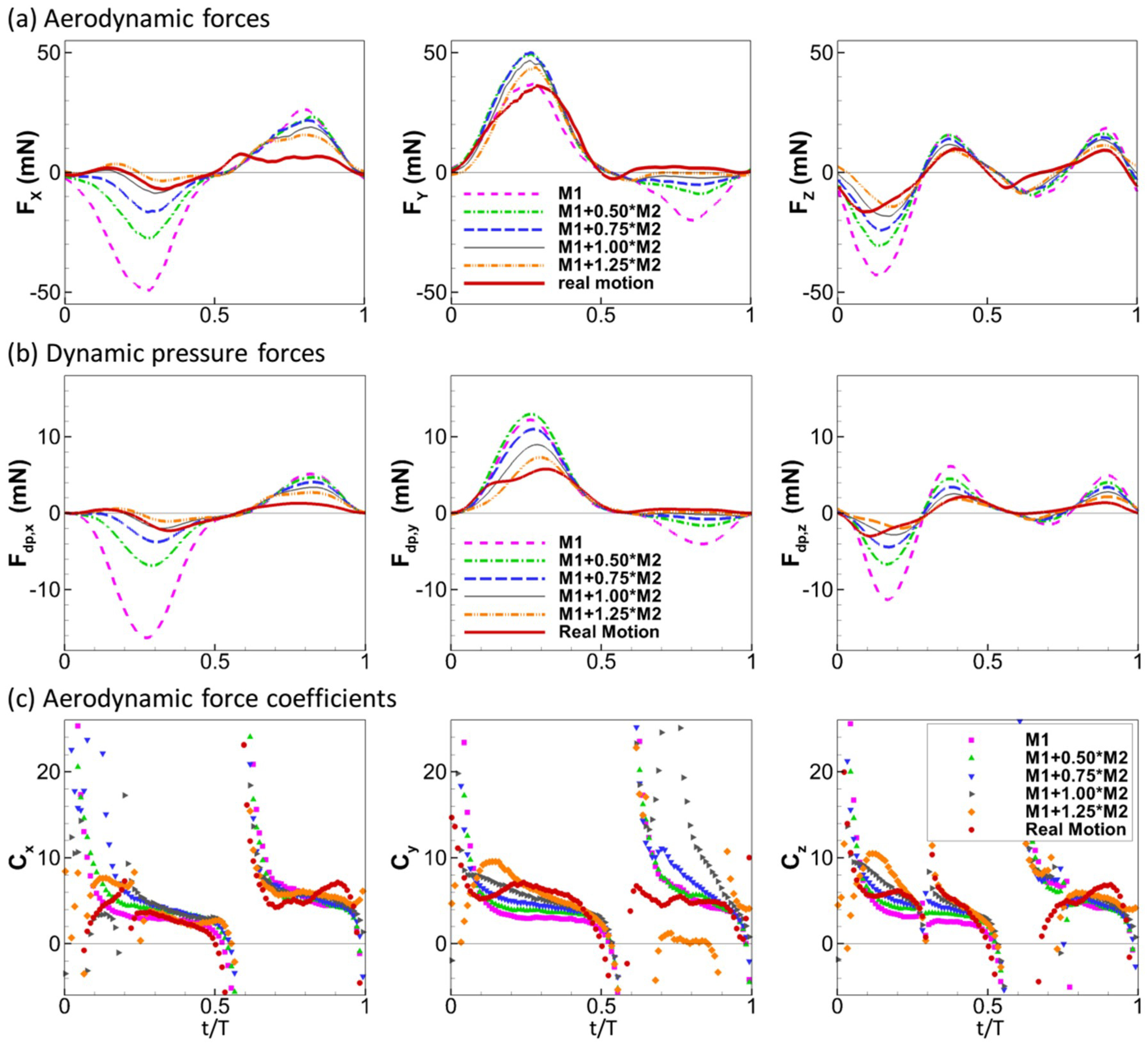
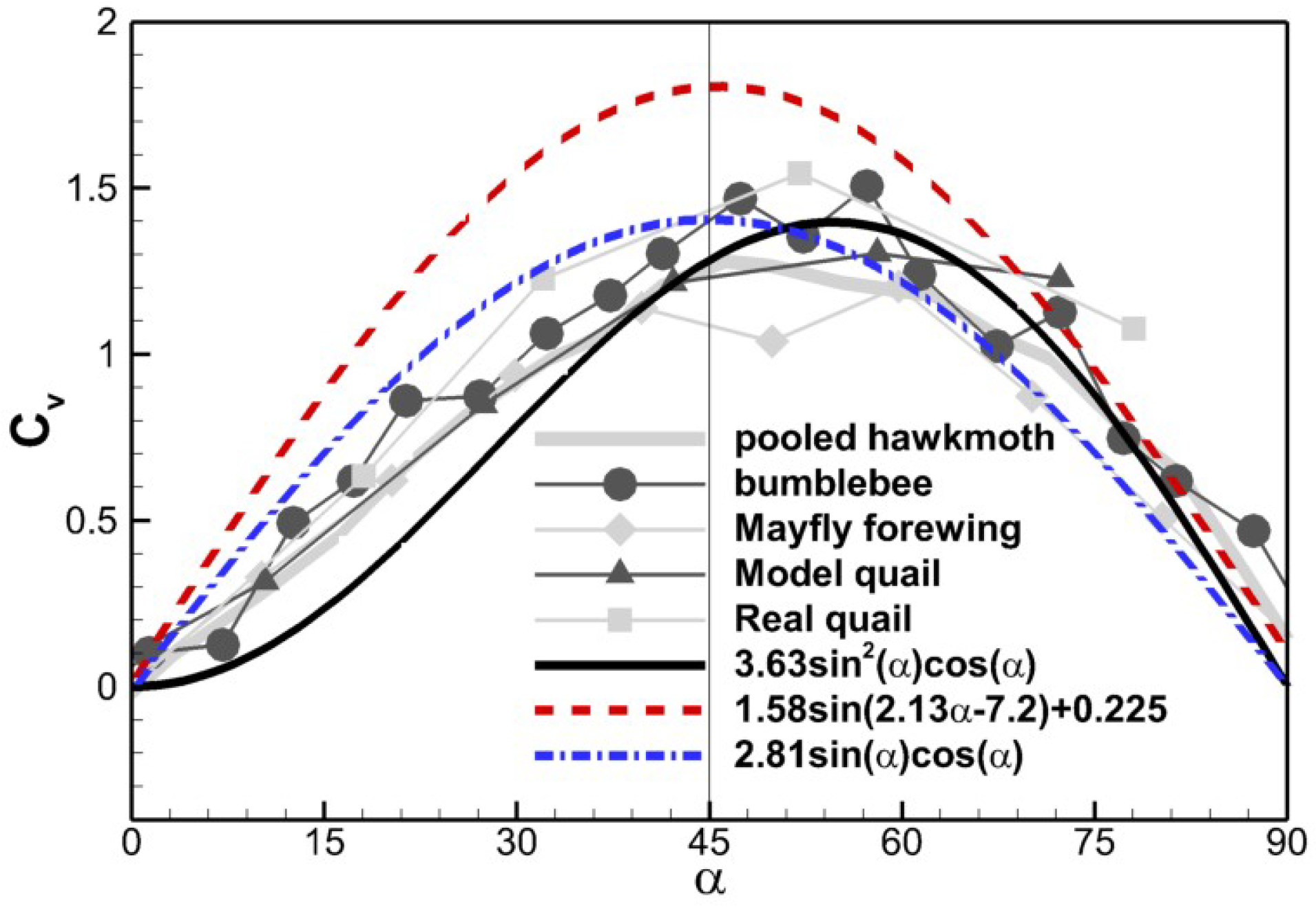
| Force Component | M1 | M1 + 0.5M2 | M1 + 0.75M2 | M1 + 1.0M2 | M1 + 1.25M2 | Real Motion |
|---|---|---|---|---|---|---|
| Fx | 0.973 | 0.899 | 0.985 | 0.982 | 0.980 | 0.981 |
| Fy | 0.976 | 0.982 | 0.991 | 0.991 | 0.984 | 0.968 |
| Fz | 0.945 | 0.930 | 0.971 | 0.979 | 0.976 | 0.956 |
| Force Component | M1 at 0.3 m/s | M1 at 5.5 m/s | Real at 0.3 m/s | Real at 5.5 m/s |
|---|---|---|---|---|
| Fx | 0.986 | 0.981 | 0.949 | 0.925 |
| Fy | 0.985 | 0.986 | 0.971 | 0.975 |
| Fz | 0.943 | 0.958 | 0.916 | 0.924 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, B.; Zheng, X.; Xue, Q.; Liu, G.; Dong, H. A Numerical Study of the Sound and Force Production of Flexible Insect Wings. Fluids 2018, 3, 87. https://doi.org/10.3390/fluids3040087
Geng B, Zheng X, Xue Q, Liu G, Dong H. A Numerical Study of the Sound and Force Production of Flexible Insect Wings. Fluids. 2018; 3(4):87. https://doi.org/10.3390/fluids3040087
Chicago/Turabian StyleGeng, Biao, Xudong Zheng, Qian Xue, Geng Liu, and Haibo Dong. 2018. "A Numerical Study of the Sound and Force Production of Flexible Insect Wings" Fluids 3, no. 4: 87. https://doi.org/10.3390/fluids3040087
APA StyleGeng, B., Zheng, X., Xue, Q., Liu, G., & Dong, H. (2018). A Numerical Study of the Sound and Force Production of Flexible Insect Wings. Fluids, 3(4), 87. https://doi.org/10.3390/fluids3040087







