The Impact of Stenosis Severity on Hemodynamic Parameters in the Iliac Artery: A Fluid–Structure Interaction Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Population
2.2. Geometry Reconstruction
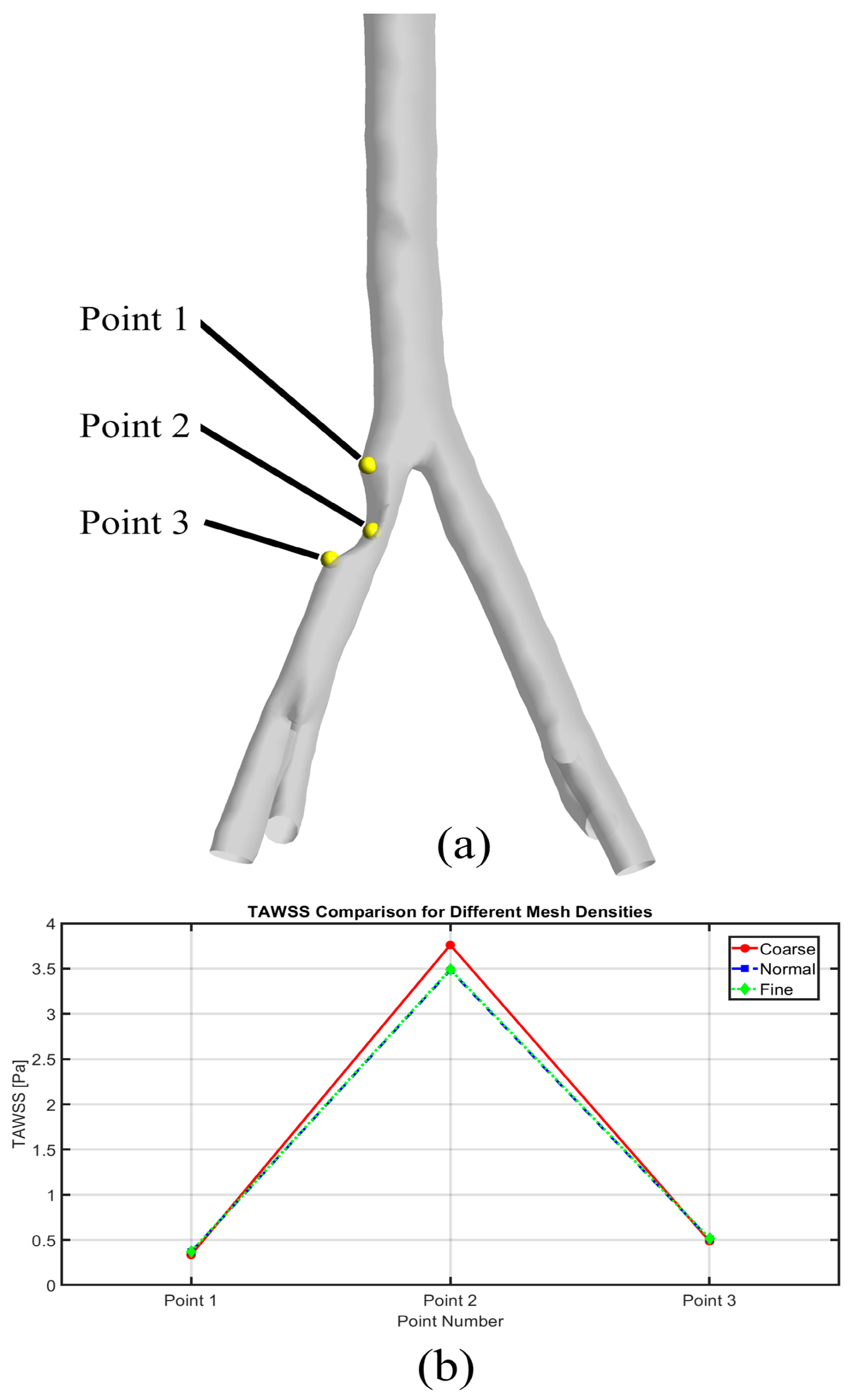
2.3. Mesh Generation
2.4. Computational Analysis
2.5. Hemodynamic Parameters
2.5.1. TAWSS
2.5.2. OSI
2.5.3. HOLMES
2.5.4. ECAP
2.6. Model Assumptions
- The arterial wall is assumed to be a homogeneous, isotropic, and linear elastic material.
- Blood is modeled as an incompressible, non-Newtonian fluid, with its behavior described by the Carreau–Yasuda model.
- The inlet flow profile is assumed to be a representative physiological waveform based on previously published and validated data for the aortic bifurcation.
- The complex downstream vasculature is represented using 3-element Windkessel models coupled to each outlet, capturing the essential resistance and compliance of the peripheral circulation.
- The stenoses are geometrically modeled as smooth, asymmetric narrowing of the arterial lumen, allowing for a controlled parametric study of stenosis severity.
3. Results
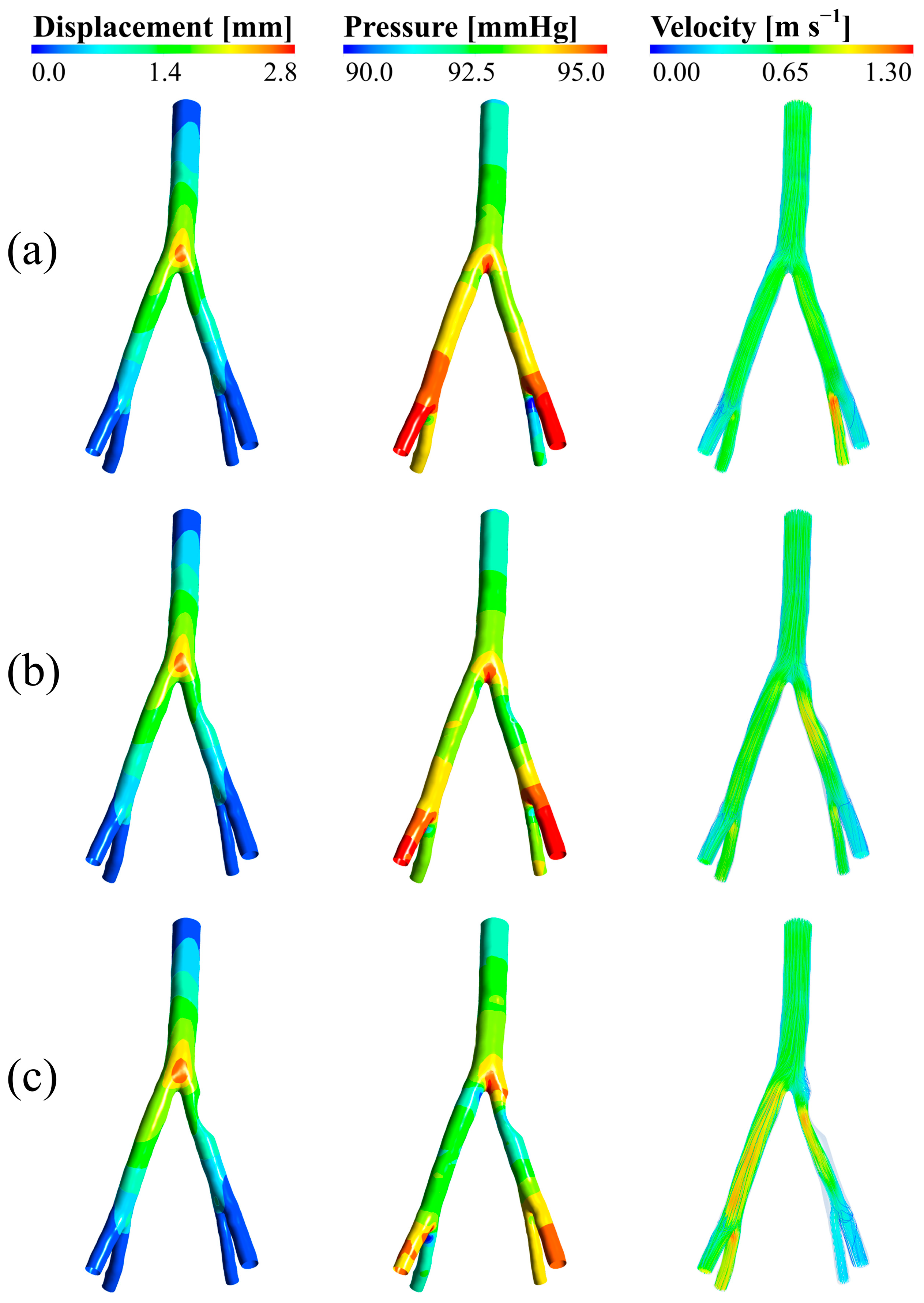
3.1. Wall Displacement, Pressure, and Velocity
3.2. TAWSS
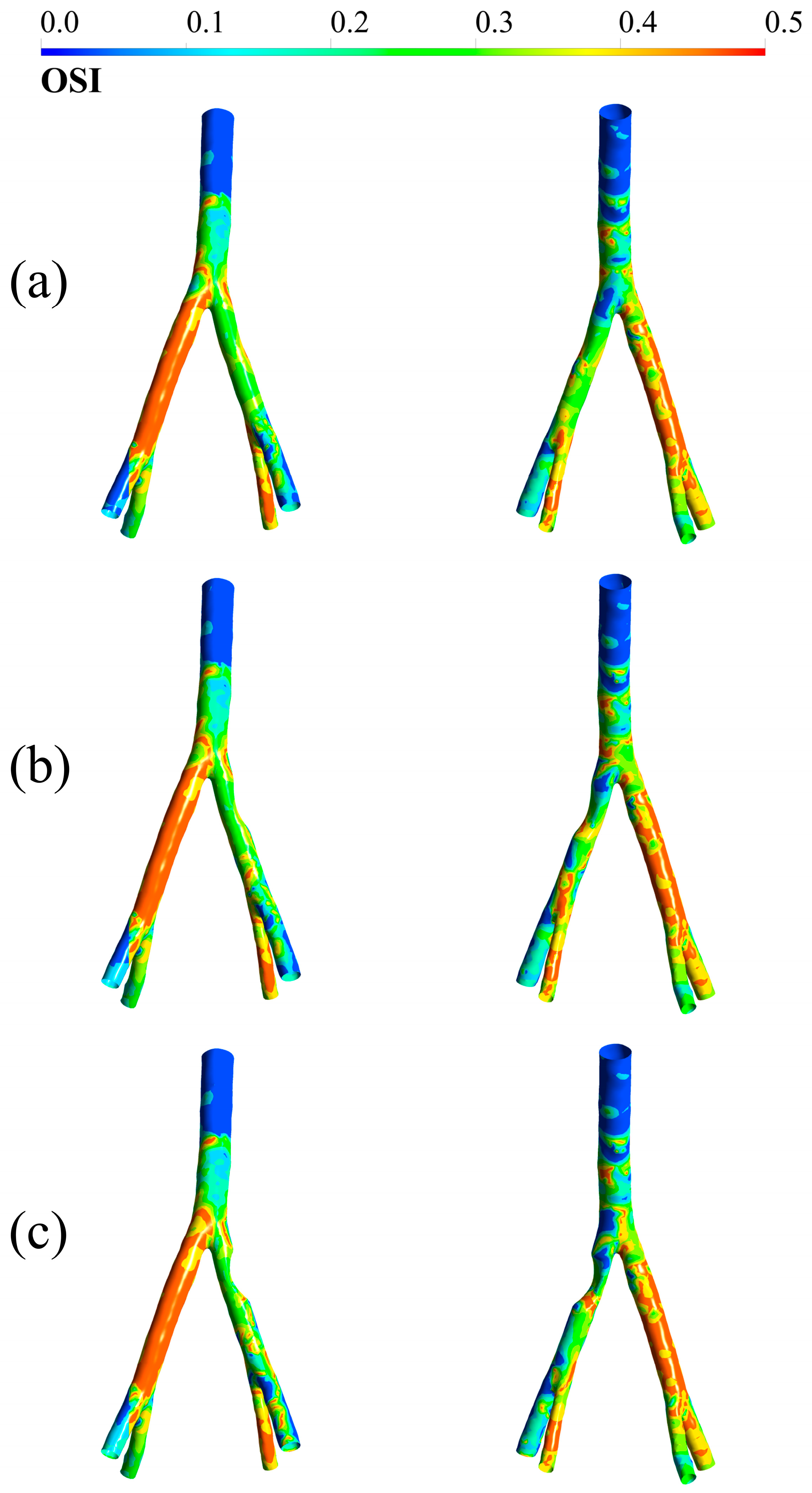
3.3. OSI
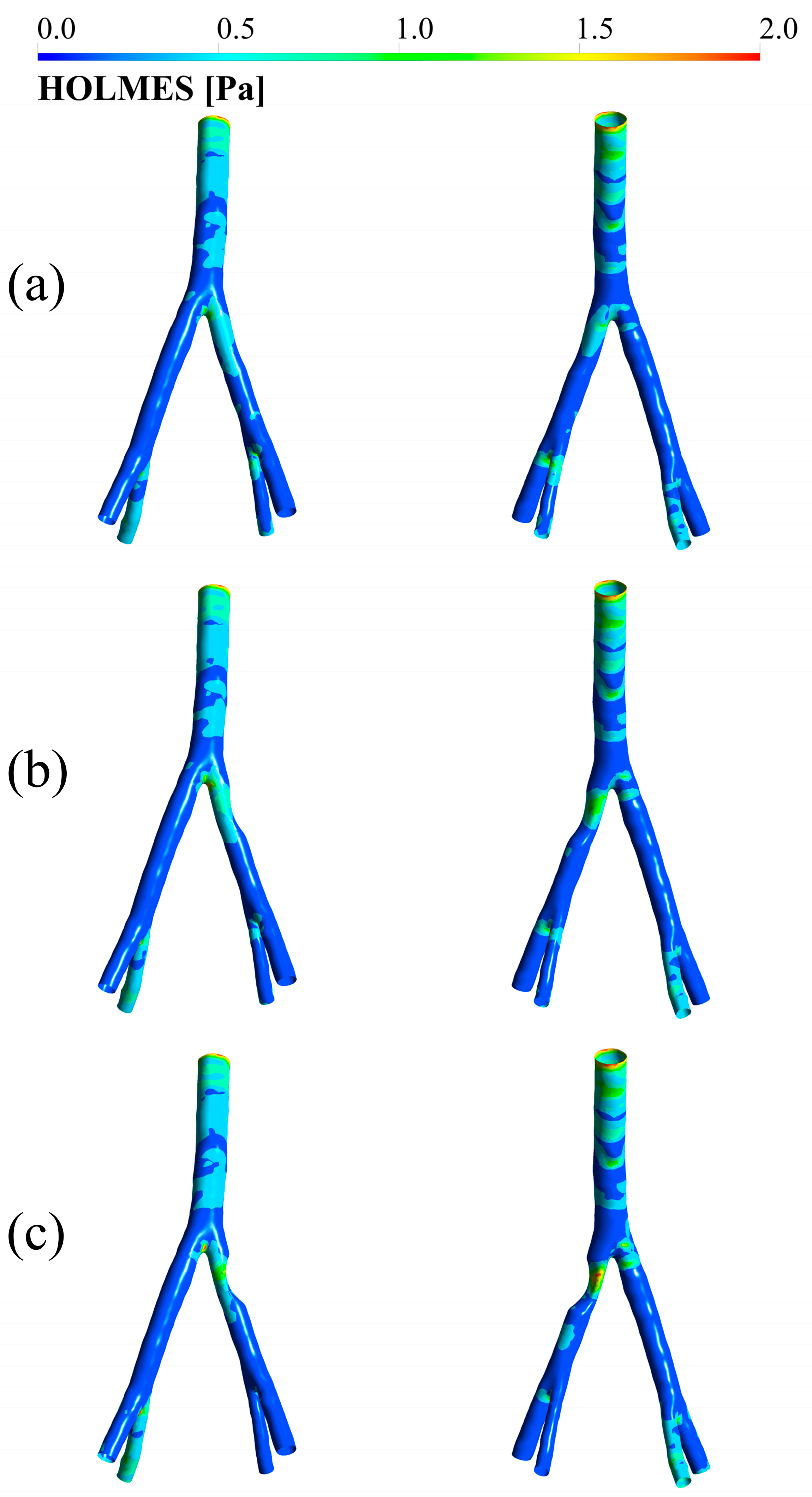
3.4. HOLMES
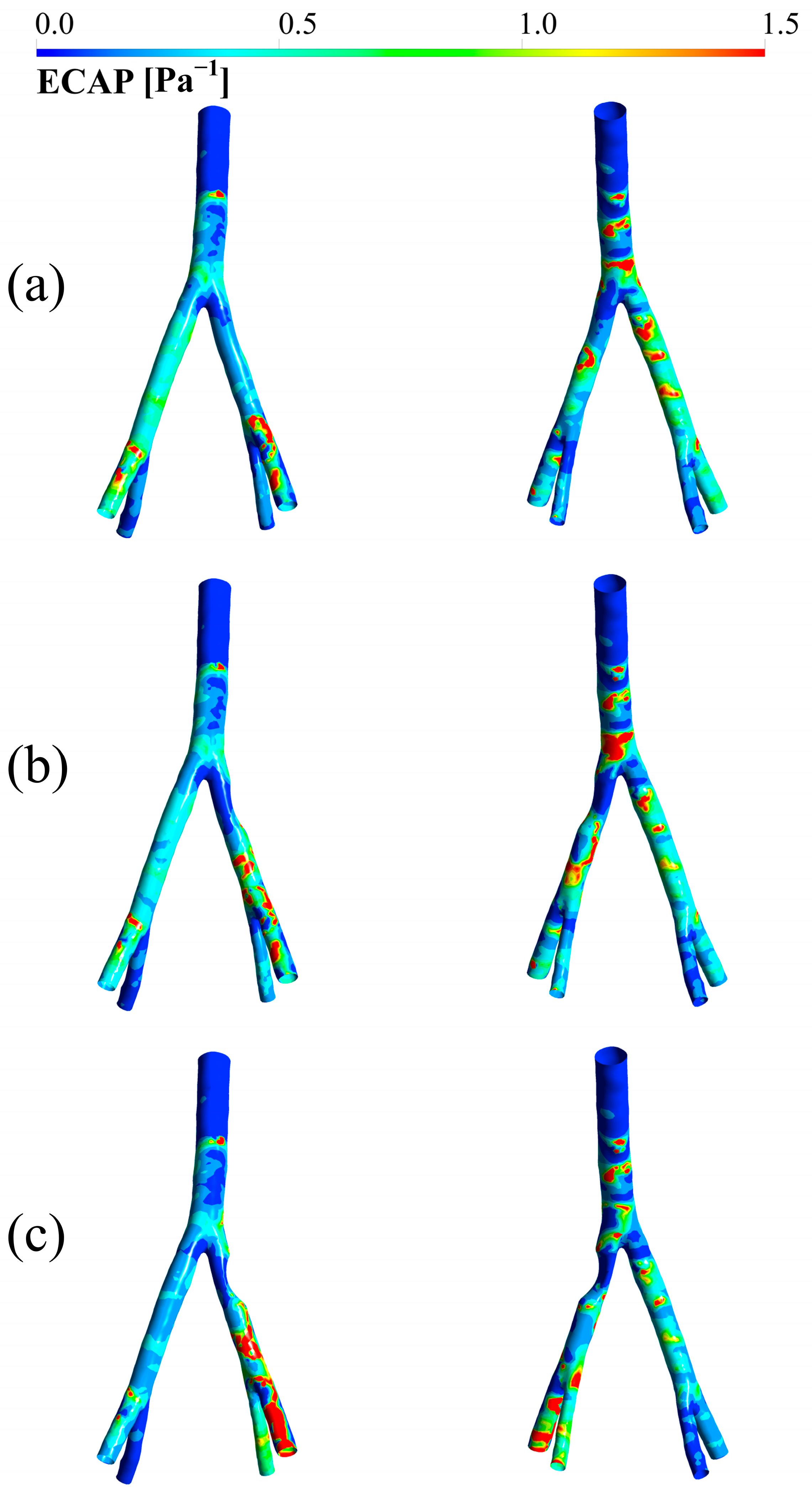
3.5. ECAP
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tsao, C.W.; Aday, A.W.; Almarzooq, Z.I.; Anderson, C.A.M.; Arora, P.; Avery, C.L.; Baker-Smith, C.M.; Beaton, A.Z.; Boehme, A.K.; Buxton, A.E.; et al. Heart Disease and Stroke Statistics—2023 Update: A Report from the American Heart Association. Circulation 2023, 147, e93–e621. [Google Scholar] [CrossRef]
- World Heart Report 2023. Confronting the World’s Number One Killer. 2023. Available online: https://medbox.org/document/world-heart-report-2023-confronting-the-worlds-number-one-killer (accessed on 23 April 2024).
- Sörös, P.; Hachinski, V. Cardiovascular and Neurological Causes of Sudden Death after Ischaemic Stroke. Lancet Neurol. 2012, 11, 179–188. [Google Scholar] [CrossRef]
- Dieter, R.S.; Chu, W.W.; Pacanowski, J.P.; McBride, P.E.; Tanke, T.E. The Significance of Lower Extremity Peripheral Arterial Disease. Clin. Cardiol. 2002, 25, 3–10. [Google Scholar] [CrossRef]
- Nakamura, E.; Sato, Y.; Iwakiri, T.; Yamashita, A.; Moriguchi-Goto, S.; Maekawa, K.; Gi, T.; Asada, Y. Asymptomatic Plaques of Lower Peripheral Arteries and Their Association with Cardiovascular Disease: An Autopsy Study. J. Atheroscler. Thromb. 2017, 24, 921–927. [Google Scholar] [CrossRef]
- Lanzino, G.; Rabinstein, A.A.; Brown, R.D., Jr. Treatment of Carotid Artery Stenosis: Medical Therapy, Surgery, or Stenting? Mayo Clin. Proc. 2009, 84, 362–368. [Google Scholar] [CrossRef]
- Velissaris, I.; Kiskinis, D.; Anastasiadis, K. Synchronous Carotid Artery Stenting and Open Heart Surgery. J. Vasc. Surg. 2011, 53, 1237–1241. [Google Scholar] [CrossRef] [PubMed]
- Mehra, A.; Mohan, B. Value of FFR in Clinical Practice. Indian Heart J. 2015, 67, 77–80. [Google Scholar] [CrossRef] [PubMed]
- Angelini, P.; Uribe, C. Stent Angioplasty in Coronary Artery Anomalies with Intramural Course: When, Why, How, With What Results? J. Soc. Cardiovasc. Angiogr. Interv. 2023, 2, 100595. [Google Scholar] [CrossRef]
- Moore, J.A.; Steinman, D.A.; Prakash, S.; Johnston, K.W.; Ethier, C.R. A Numerical Study of Blood Flow Patterns in Anatomically Realistic and Simplified End-to-Side Anastomoses. J. Biomech. Eng. 1999, 121, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Ong, C.W.; Wee, I.; Syn, N.; Ng, S.; Leo, H.L.; Richards, A.M.; Choong, A.M.T.L. Computational Fluid Dynamics Modeling of Hemodynamic Parameters in the Human Diseased Aorta: A Systematic Review. Ann. Vasc. Surg. 2020, 63, 336–381. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Pichardo-Almarza, C.; Di Tomaso, G.; Balabani, S.; Agu, O.; Diaz-Zuccarini, V. Predicting Atherosclerotic Plaque Location in an Iliac Bifurcation Using a Hybrid CFD/Biomechanical Approach. In Bioinformatics and Biomedical Engineering; IWBBIO 2015; Springer: Cham, Switzerland, 2015; Volume 9044, pp. 594–606. [Google Scholar] [CrossRef]
- Carvalho, V.; Carneiro, F.; Ferreira, A.C.; Gama, V.; Teixeira, J.C.; Teixeira, S. Numerical Study of the Unsteady Flow in Simplified and Realistic Iliac Bifurcation Models. Fluids 2021, 6, 284. [Google Scholar] [CrossRef]
- Carneiro, F.; Silva, A.E.; Teixeira, S.F.C.F.; Teixeira, J.C.F.; Lobarinhas, P.A.M.; Ribeiro, V.G. The Influence of Renal Branches on the Iliac Arteries Blood Flow. In Proceedings of the ASME 2008 3rd Frontiers in Biomedical Devices Conference, Irvine, CA, USA, 18–20 June 2008; pp. 91–96. [Google Scholar] [CrossRef]
- Harris, J.; Paul, A.; Ghosh, B. Numerical Simulation of Blood Flow in Aortoiliac Bifurcation with Increasing Degree of Stenosis. J. Appl. Fluid Mech. 2023, 16, 1601–1614. [Google Scholar] [CrossRef]
- Luo, K.; Jiang, W.; Yu, C.; Tian, X.; Zhou, Z.; Ding, Y. Fluid-Solid Interaction Analysis on Iliac Bifurcation Artery: A Numerical Study. Int. J. Comput. Methods 2019, 16, 1850112. [Google Scholar] [CrossRef]
- Skopalik, S.; Hall Barrientos, P.; Matthews, J.; Radjenovic, A.; Mark, P.; Roditi, G.; Paul, M.C. Image-Based Computational Fluid Dynamics for Estimating Pressure Drop and Fractional Flow Reserve across Iliac Artery Stenosis: A Comparison with in-Vivo Measurements. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3437. [Google Scholar] [CrossRef]
- Heinen, S.G.H.; van den Heuvel, D.A.F.; de Vries, J.P.P.M.; van de Vosse, F.N.; Delhaas, T.; Huberts, W. A Geometry-Based Model for Non-Invasive Estimation of Pressure Gradients over Iliac Artery Stenoses. J. Biomech. 2019, 92, 67–75. [Google Scholar] [CrossRef]
- Heinen, S.G.H.; van den Heuvel, D.A.F.; Huberts, W.; de Boer, S.W.; van de Vosse, F.N.; Delhaas, T.; de Vries, J.P.P.M. In Vivo Validation of Patient-Specific Pressure Gradient Calculations for Iliac Artery Stenosis Severity Assessment. J. Am. Heart Assoc. 2017, 6, e007328. [Google Scholar] [CrossRef]
- Birn, J.; Vedantham, S. May-Thurner Syndrome and Other Obstructive Iliac Vein Lesions: Meaning, Myth, and Mystery. Vasc. Med. 2015, 20, 74–83. [Google Scholar] [CrossRef]
- Aboyans, V.; Ricco, J.-B.; Bartelink, M.-L.E.L.; Björck, M.; Brodmann, M.; Cohnert, T.; Collet, J.-P.; Czerny, M.; De Carlo, M.; Debus, S.; et al. 2017 ESC Guidelines on the Diagnosis and Treatment of Peripheral Arterial Diseases, in Collaboration with the European Society for Vascular Surgery (ESVS): Document Covering Atherosclerotic Disease of Extracranial Carotid and Vertebral, Mesenteric, Renal. Eur. Heart J. 2018, 39, 763–816. [Google Scholar] [CrossRef]
- Gijsen, F.J.H.; Wentzel, J.J.; Thury, A.; Lamers, B.; Schuurbiers, J.C.H.; Serruys, P.W.; van der Steen, A.F. A New Imaging Technique to Study 3-D Plaque and Shear Stress Distribution in Human Coronary Artery Bifurcations in Vivo. J. Biomech. 2007, 40, 2349–2357. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Pichardo-Almarza, C.; Agu, O.; Díaz-Zuccarini, V. A Multiscale Modelling Approach to Understand Atherosclerosis Formation: A Patient-Specific Case Study in the Aortic Bifurcation. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2017, 231, 378–390. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Agu, O.; Balabani, S.; Díaz-Zuccarini, V. Development of a Patient-Specific Simulation Tool to Analyse Aortic Dissections: Assessment of Mixed Patient-Specific Flow and Pressure Boundary Conditions. Med. Eng. Phys. 2014, 36, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Alimohammadi, M. Aortic Dissection: Simulation Tools for Disease Management and Understanding; Springer: Cham, Switzerland, 2018; ISBN 0-262-00274-4. [Google Scholar]
- Eskandari, A.; Malek, S.; Jabbari, A.; Javari, K.; Rahmati, N.; Nikbakhtian, B.; Mohebbi, B.; Parhizgar, S.E.; Alimohammadi, M. Enhancing Cardiac Assessments: Accurate and Efficient Prediction of Quantitative Fractional Flow Reserve. Front. Bioeng. Biotechnol. 2025, 13, 1438253. [Google Scholar] [CrossRef] [PubMed]
- Gijsen, F.J.; van de Vosse, F.N.; Janssen, J.D. The Influence of the Non-Newtonian Properties of Blood on the Flow in Large Arteries: Steady Flow in a Carotid Bifurcation Model. J. Biomech. 1999, 32, 601–608. [Google Scholar] [CrossRef] [PubMed]
- Skacel, P.; Bursa, J. Poisson’s Ratio and Compressibility of Arterial Wall–Improved Experimental Data Reject Auxetic Behaviour. J. Mech. Behav. Biomed. Mater. 2022, 131, 105229. [Google Scholar] [CrossRef]
- Camasão, D.B.; Mantovani, D. The Mechanical Characterization of Blood Vessels and Their Substitutes in the Continuous Quest for Physiological-Relevant Performances. A Critical Review. Mater. Today Bio 2021, 10, 100106. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Sherwood, J.M.; Karimpour, M.; Agu, O.; Balabani, S.; Díaz-Zuccarini, V. Aortic Dissection Simulation Models for Clinical Support: Fluid-Structure Interaction vs. Rigid Wall Models. Biomed. Eng. Online 2015, 14, 34. [Google Scholar] [CrossRef]
- Peiffer, V.; Sherwin, S.J.; Weinberg, P.D. Does Low and Oscillatory Wall Shear Stress Correlate Spatially with Early Atherosclerosis? A Systematic Review. Cardiovasc. Res. 2013, 99, 242–250. [Google Scholar] [CrossRef]
- Dadras, R.; Jabbari, A.; Asl, N.K.; Soltani, M.; Rafiee, F.; Parsaee, M.; Golchin, S.; Pouraliakbar, H.; Sadeghipour, P.; Alimohammadi, M. In-Silico Investigations of Haemodynamic Parameters for a Blunt Thoracic Aortic Injury Case. Sci. Rep. 2023, 13, 8355. [Google Scholar] [CrossRef]
- Rafieianzab, D.; Abazari, M.A.; Soltani, M.; Alimohammadi, M. The Effect of Coarctation Degrees on Wall Shear Stress Indices. Sci. Rep. 2021, 11, 12757. [Google Scholar] [CrossRef]
- Mutlu, O.; Salman, H.E.; Al-Thani, H.; El-Menyar, A.; Qidwai, U.A.; Yalcin, H.C. How Does Hemodynamics Affect Rupture Tissue Mechanics in Abdominal Aortic Aneurysm: Focus on Wall Shear Stress Derived Parameters, Time-Averaged Wall Shear Stress, Oscillatory Shear Index, Endothelial Cell Activation Potential, and Relative Residence Time. Comput. Biol. Med. 2023, 154, 106609. [Google Scholar] [CrossRef]
- Boniforti, M.A.; Magini, R.; Orosco Salinas, T. Hemodynamic Investigation of the Flow Diverter Treatment of Intracranial Aneurysm. Fluids 2023, 8, 189. [Google Scholar] [CrossRef]
- Ong, C.W.; Wee, I.J.Y.; Toma, M.; Cui, F.; Xu, X.Y.; Richards, A.M.; Leo, H.L.; Choong, A.M.T.L. Haemodynamic Changes in Visceral Hybrid Repairs of Type III and Type V Thoracoabdominal Aortic Aneurysms. Sci. Rep. 2023, 13, 13760. [Google Scholar] [CrossRef] [PubMed]
- Yadav, M.K.; Mohammed, A.K.M.; Puramadathil, V.; Geetha, D.; Unni, M. Lower Extremity Arteries. Cardiovasc. Diagn. Ther. 2019, 9, S174–S182. [Google Scholar] [CrossRef]
- Morrison, T.M.; Stitzel, J.D.; Levine, S.M. Modeling and Simulation in Biomedical Engineering: Regulatory Science and Innovation for Advancing Public Health. Ann. Biomed. Eng. 2023, 51, 1–5. [Google Scholar] [CrossRef]
- Dake, P.G.; Mukherjee, J.; Sahu, K.C.; Pandit, A.B. Computational Fluid Dynamics in Cardiovascular Engineering: A Comprehensive Review. Trans. Indian Natl. Acad. Eng. 2024, 9, 335–362. [Google Scholar] [CrossRef]
- Okazaki, S.; Shirahama, M.; Hashida, R.; Matsuura, M.; Yoshida, S.; Nakama, K.; Matsuse, H.; Shiba, N. Iliac Intramedullary Stabilization for Type IIIA Fragility Fractures of the Pelvis. Sci. Rep. 2020, 10, 20380. [Google Scholar] [CrossRef]
- Totorean, A.F.; Totorean, I.C.; Bernad, S.I.; Ciocan, T.; Malita, D.C.; Gaita, D.; Bernad, E.S. Patient-Specific Image-Based Computational Fluid Dynamics Analysis of Abdominal Aorta and Branches. J. Pers. Med. 2022, 12, 1502. [Google Scholar] [CrossRef] [PubMed]
- Javadzadegan, A.; Yong, A.S.C.; Chang, M.; Ng, A.C.C.; Yiannikas, J.; Ng, M.K.C.; Behnia, M.; Kritharides, L. Flow Recirculation Zone Length and Shear Rate Are Differentially Affected by Stenosis Severity in Human Coronary Arteries. Am. J. Physiol.-Heart Circ. Physiol. 2013, 304, H559–H566. [Google Scholar] [CrossRef]
- Górski, G.; Kucab, K. Time-Dependent Simulation of Blood Flow through an Abdominal Aorta with Iliac Arteries. Eur. Biophys. J. 2023, 53, 429–445. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, P.D. Haemodynamic Wall Shear Stress, Endothelial Permeability and Atherosclerosis—A Triad of Controversy. Front. Bioeng. Biotechnol. 2022, 10, 836680. [Google Scholar] [CrossRef]
- Taylor, C.A.; Hughes, T.J.; Zarins, C.K. Finite Element Modeling of Three-Dimensional Pulsatile Flow in the Abdominal Aorta: Relevance to Atherosclerosis. Ann. Biomed. Eng. 1998, 26, 975–987. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, J.R.; Kleinstreuer, C.; Truskey, G.A.; Lei, M. Relation between Non-Uniform Hemodynamics and Sites of Altered Permeability and Lesion Growth at the Rabbit Aorto-Celiac Junction. Atherosclerosis 1999, 143, 27–40. [Google Scholar] [CrossRef] [PubMed]


| Outlet | Proximal Resistance (R1) (mmHg·s/m3) | Distal Resistance (R2) (mmHg·s/m3) | Compliance (C) (m3/mmHg) |
|---|---|---|---|
| RIIA | 2.9982 × 104 | 1.0002 × 10−10 | 1.5804 × 10−2 |
| REIA | 2.0584 × 104 | 1.0002 × 10−10 | 1.3246 × 10−1 |
| LIIA | 3.7549 × 104 | 1.0002 × 10−10 | 2.5142 × 10−2 |
| LEIA | 2.6417 × 104 | 1.001 × 10−10 | 2.3328 × 10−1 |
| 22 | 2.2 | 0.644 | 0.392 | 0.110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmati, N.; Pouraliakbar, H.; Eskandari, A.; Javari, K.; Jabbarinick, A.; Sadeghipour, P.; Soltani, M.; Alimohammadi, M. The Impact of Stenosis Severity on Hemodynamic Parameters in the Iliac Artery: A Fluid–Structure Interaction Study. Bioengineering 2025, 12, 1042. https://doi.org/10.3390/bioengineering12101042
Rahmati N, Pouraliakbar H, Eskandari A, Javari K, Jabbarinick A, Sadeghipour P, Soltani M, Alimohammadi M. The Impact of Stenosis Severity on Hemodynamic Parameters in the Iliac Artery: A Fluid–Structure Interaction Study. Bioengineering. 2025; 12(10):1042. https://doi.org/10.3390/bioengineering12101042
Chicago/Turabian StyleRahmati, Nima, Hamidreza Pouraliakbar, Arshia Eskandari, Kian Javari, Alireza Jabbarinick, Parham Sadeghipour, Madjid Soltani, and Mona Alimohammadi. 2025. "The Impact of Stenosis Severity on Hemodynamic Parameters in the Iliac Artery: A Fluid–Structure Interaction Study" Bioengineering 12, no. 10: 1042. https://doi.org/10.3390/bioengineering12101042
APA StyleRahmati, N., Pouraliakbar, H., Eskandari, A., Javari, K., Jabbarinick, A., Sadeghipour, P., Soltani, M., & Alimohammadi, M. (2025). The Impact of Stenosis Severity on Hemodynamic Parameters in the Iliac Artery: A Fluid–Structure Interaction Study. Bioengineering, 12(10), 1042. https://doi.org/10.3390/bioengineering12101042







