Outdoor Ice Rinks in Ontario, Canada—An Oversimplified Model for Ice Water Equivalent and Operational Duration to Evaluate Changing Climate
Abstract
1. Introduction
2. Study Area and Methods
2.1. Study Area
2.2. Initial Testing of the Ice Rink Model
2.3. Assumptions or Prior Settings for the Ice Rink and Its Modelling
2.4. Physically Based Ice Rink Model
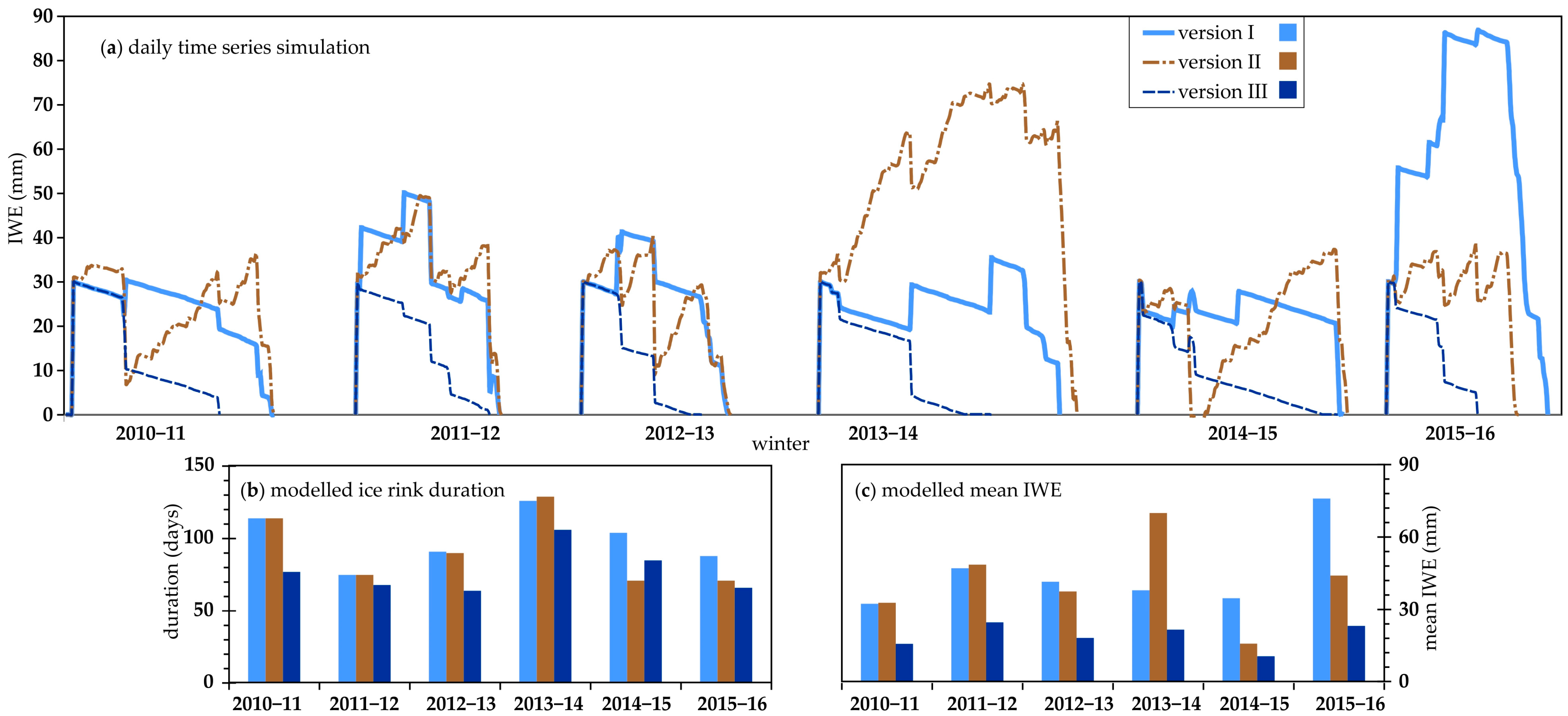
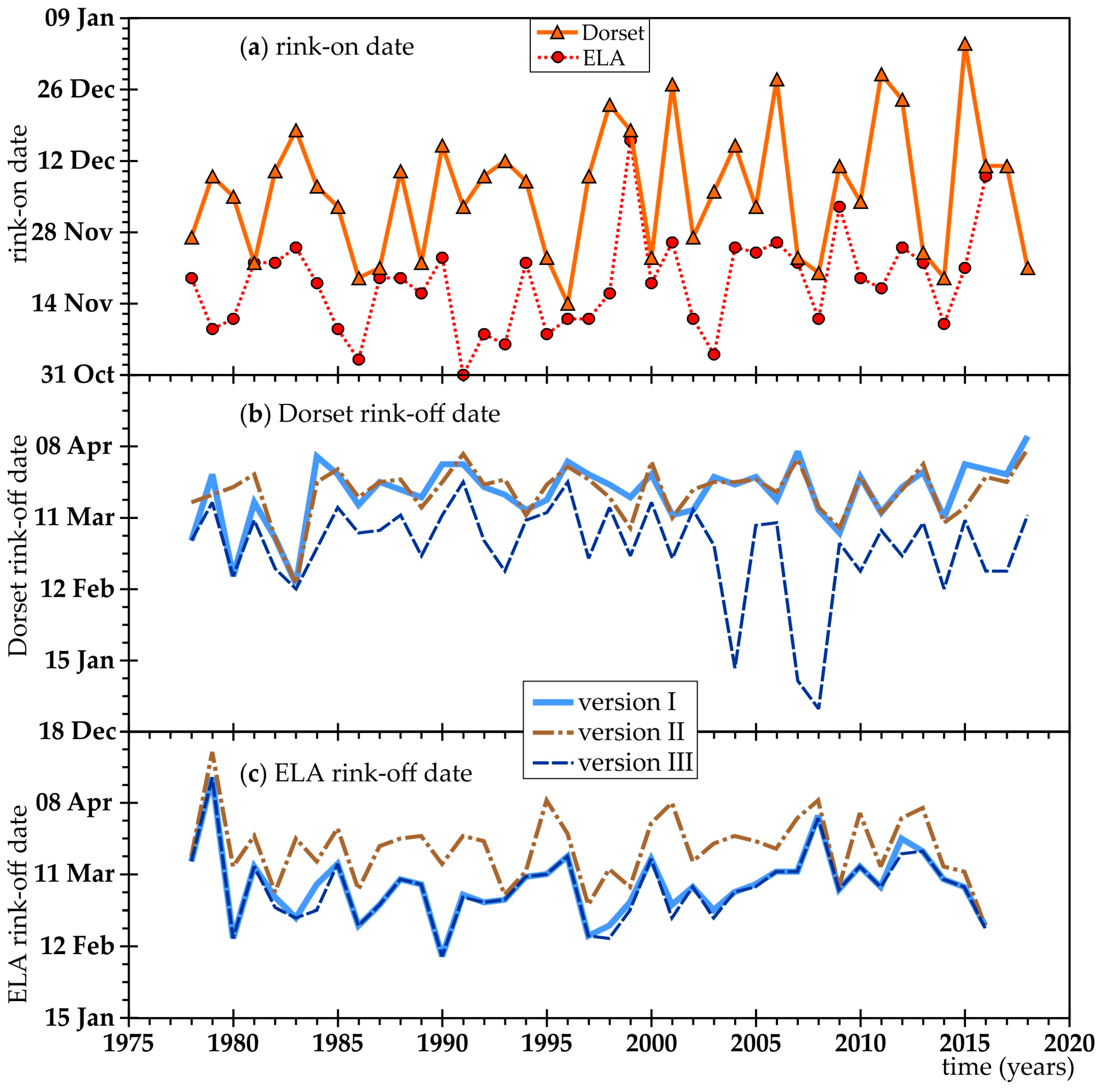
2.5. Model Versions with Varying Scenarios
2.5.1. Version I: Adding Rain as Ice and Ignoring Snow
2.5.2. Version II: No Rain Addition and Adding Some Snow as Ice
2.5.3. Version III: Neither Rain nor Snow Addition
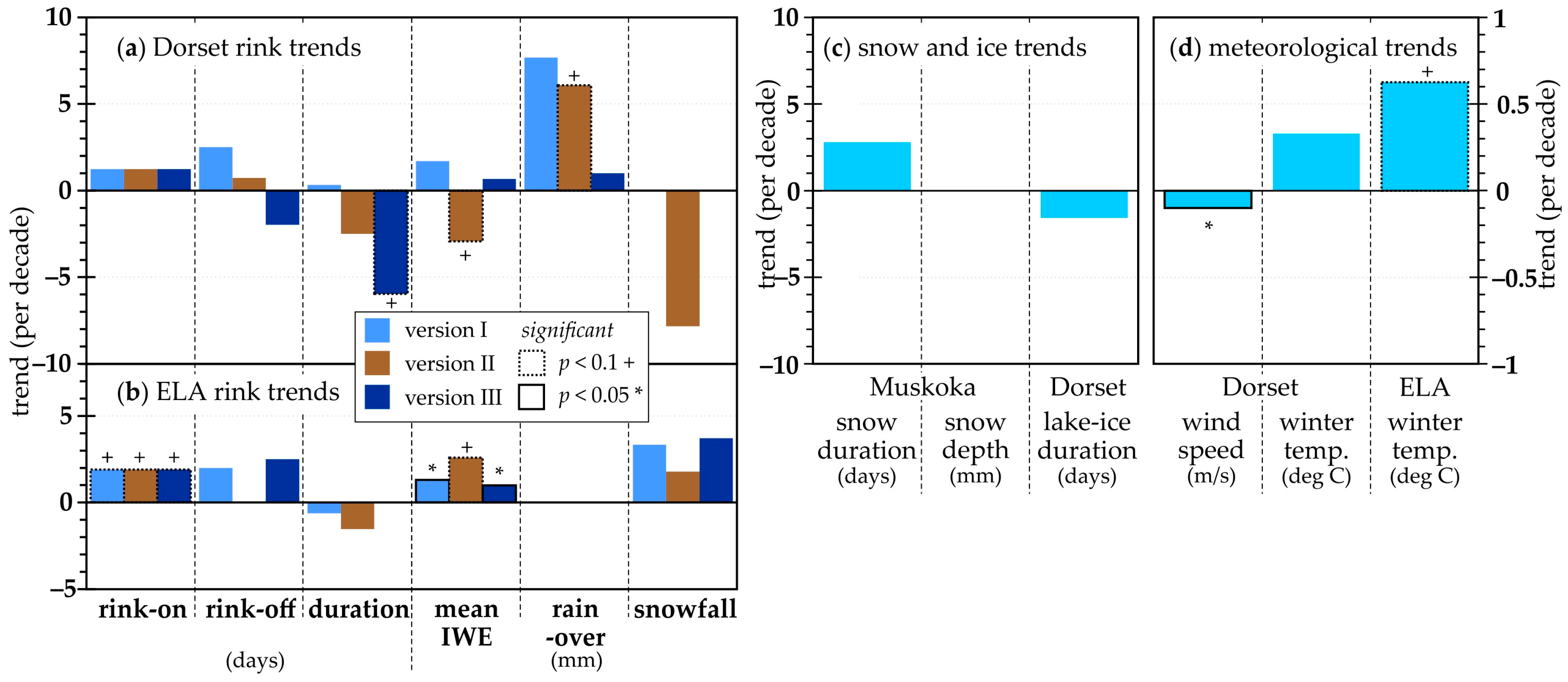
2.6. Trend Analysis
3. Results
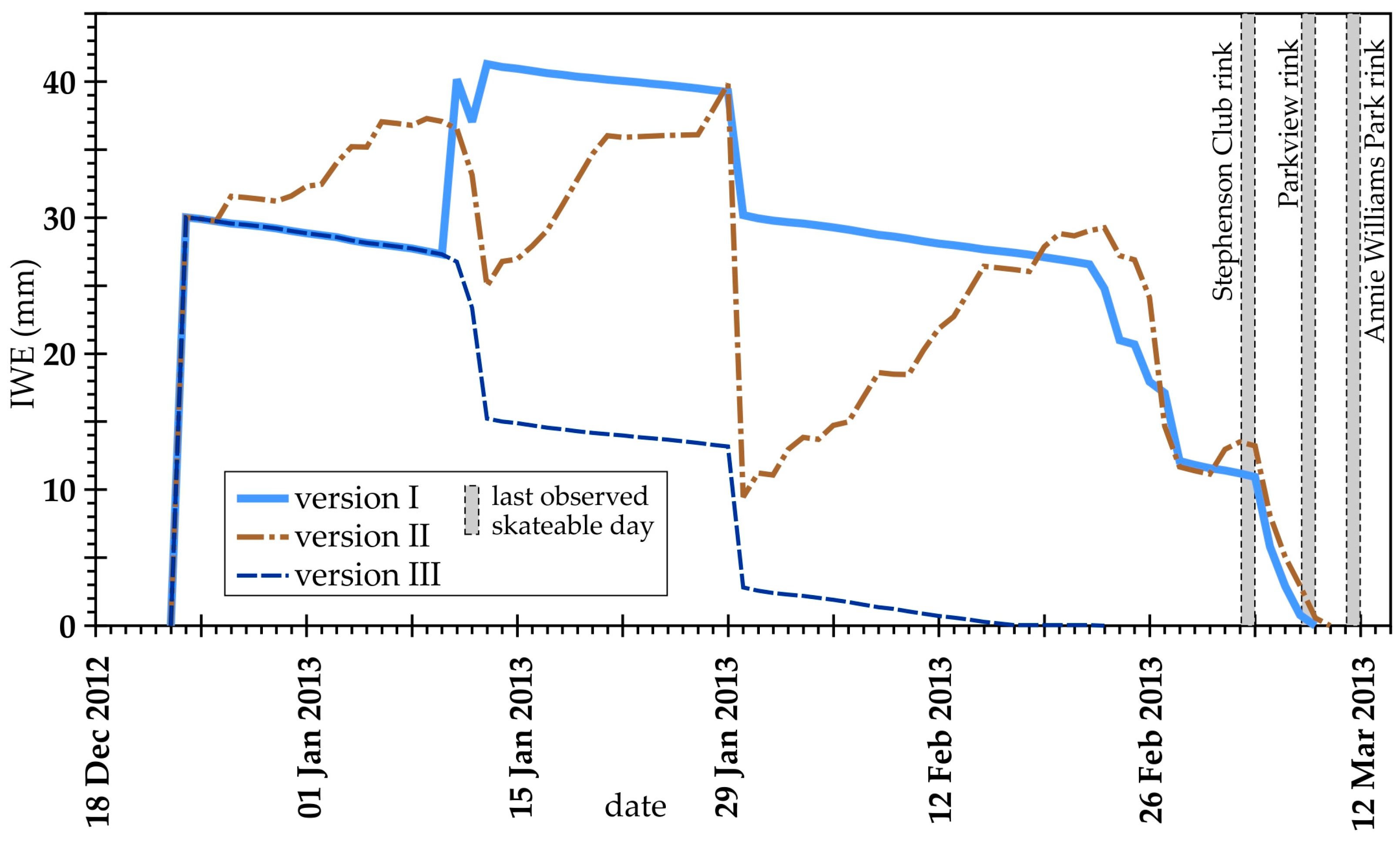
3.1. Model Testing
3.2. Comparing Three Versions by Simulations of Six Winters (2011 to 2016)
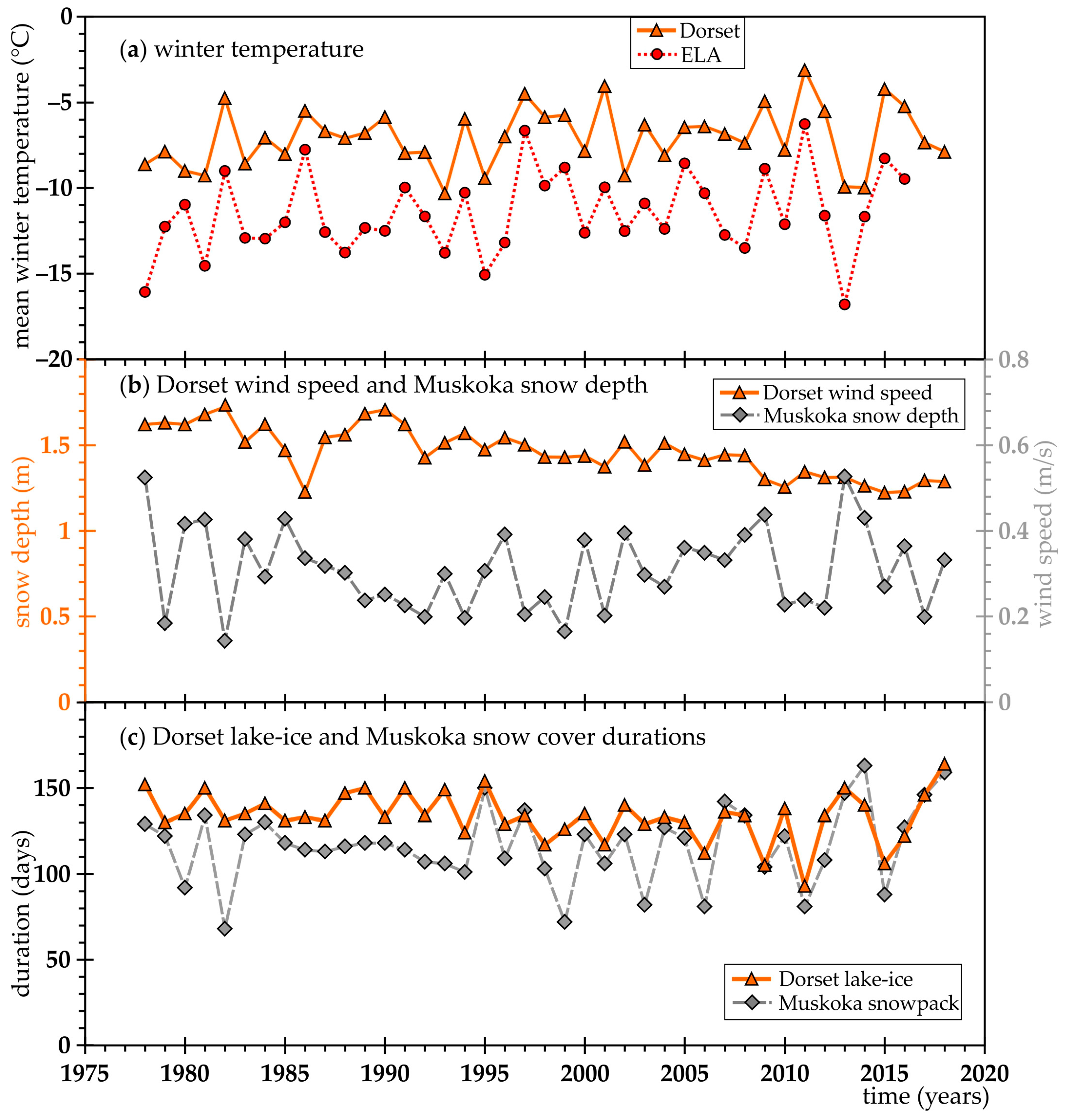
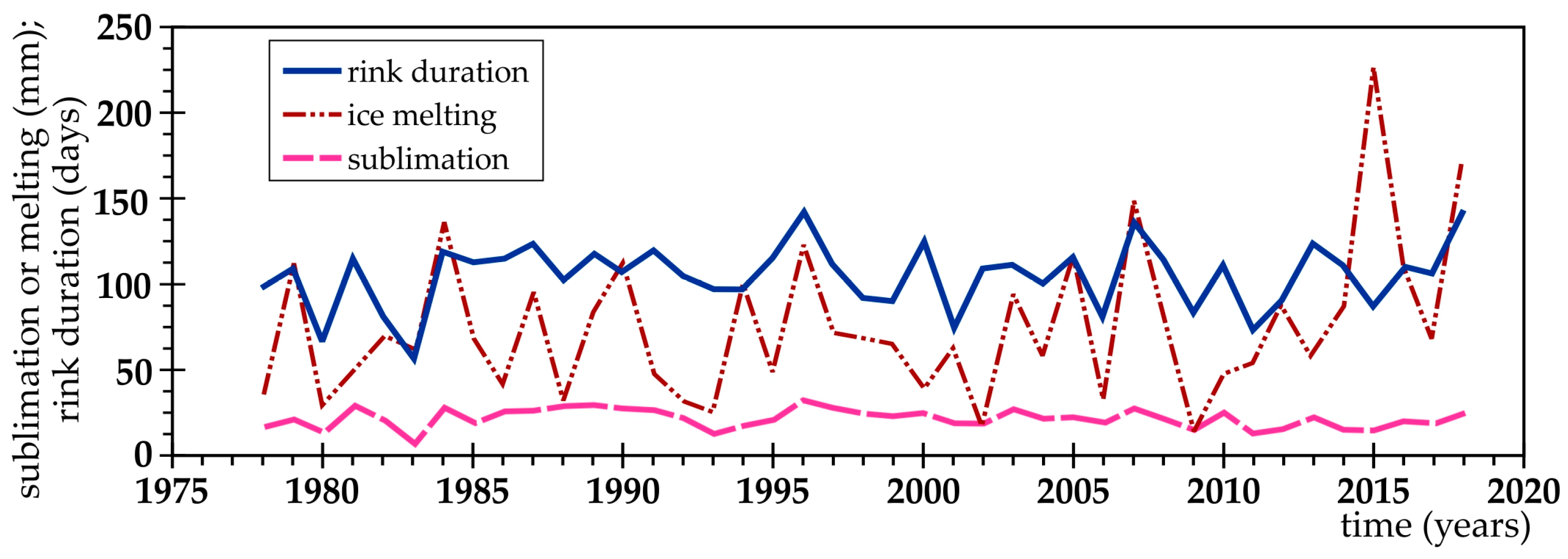
3.3. Long-Term Simulation at Dorset and ELA
3.4. Trend over Time
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IWE | Ice Water Equivalent |
Appendix A. Model Results Summary
| Statistic | Rink-On | Rink-Off | Duration | Mean IWE | Total Rain-On | Total Snow-On |
|---|---|---|---|---|---|---|
| Dorset | ||||||
| Version I: mean | 6 December | 2 March | 106 | 40.4 | 75.7 | N/A |
| Std. Dev. | 12.8 | 12.0 | 18.6 | 15.7 | 48.3 | N/A |
| SD 1st 20 yrs | 9.7 | 14.1 | 18.6 | 12.7 | 43.5 | N/A |
| SD 2nd 20 yrs | 14.8 | 9.6 | 19.3 | 18.2 | 54.3 | N/A |
| Version II: mean | 6 December | 21 March | 105.5 | 47.4 | 70.2 | 187 |
| Std. Dev. | 12.8 | 10.0 | 19.8 | 13.6 | 37.1 | 56.2 |
| SD 1st 20 yrs | 9.7 | 11.1 | 17.3 | 12.7 | 32.7 | 61.2 |
| D 2nd 20 yrs | 14.8 | 9.3 | 22.0 | 15.0 | 42.0 | 46.8 |
| Version III: mean | 6 December | 28 February | 84.5 | 19.8 | 48.8 | N/A |
| Std. Dev. | 12.8 | 18.8 | 22.4 | 3.9 | 32.4 | N/A |
| SD 1st 20 yrs | 9.7 | 11.9 | 18.1 | 4.0 | 35.4 | N/A |
| SD 2nd 20 yrs | 14.8 | 22.8 | 23.8 | 3.8 | 30.8 | N/A |
| ELA | ||||||
| Version I: mean | 17 November | 6 March | 108.7 | 20.9 | 3.0 | 97.7 |
| Std. Dev. | 9.5 | 13.1 | 14.3 | 4.0 | 5.8 | 33.3 |
| SD 1st 20 yrs | 7.3 | 15.0 | 13.8 | 3.5 | 2.8 | 33.0 |
| SD 2nd 20 yrs | 10.1 | 11.6 | 14.5 | 3.7 | 7.3 | 35.3 |
| Version II: mean | 17 November | 21 March | 2 May | 45.7 | 5.0 | 111 |
| Std. Dev. | 9.5 | 13.3 | 16.2 | 9.1 | 6.8 | 35.2 |
| SD 1st 20 yrs | 7.3 | 13.7 | 13.3 | 8.4 | 6.0 | 32.1 |
| SD 2nd 20 yrs | 10.1 | 13.9 | 18.2 | 9.7 | 7.5 | 38.8 |
| Version III: mean | 17 November | 5 March | 107.7 | 19.7 | 2.5 | 97.4 |
| Std. Dev. | 9.5 | 13.4 | 14.7 | 3.6 | 4.1 | 33.3 |
| SD 1st 20 yrs | 7.3 | 15.1 | 14.1 | 4.0 | 2.8 | 33.0 |
| SD 2nd 20 yrs | 10.1 | 12.0 | 15.0 | 2.5 | 4.8 | 35.5 |
Appendix B. Example of Daily Energy Budgets
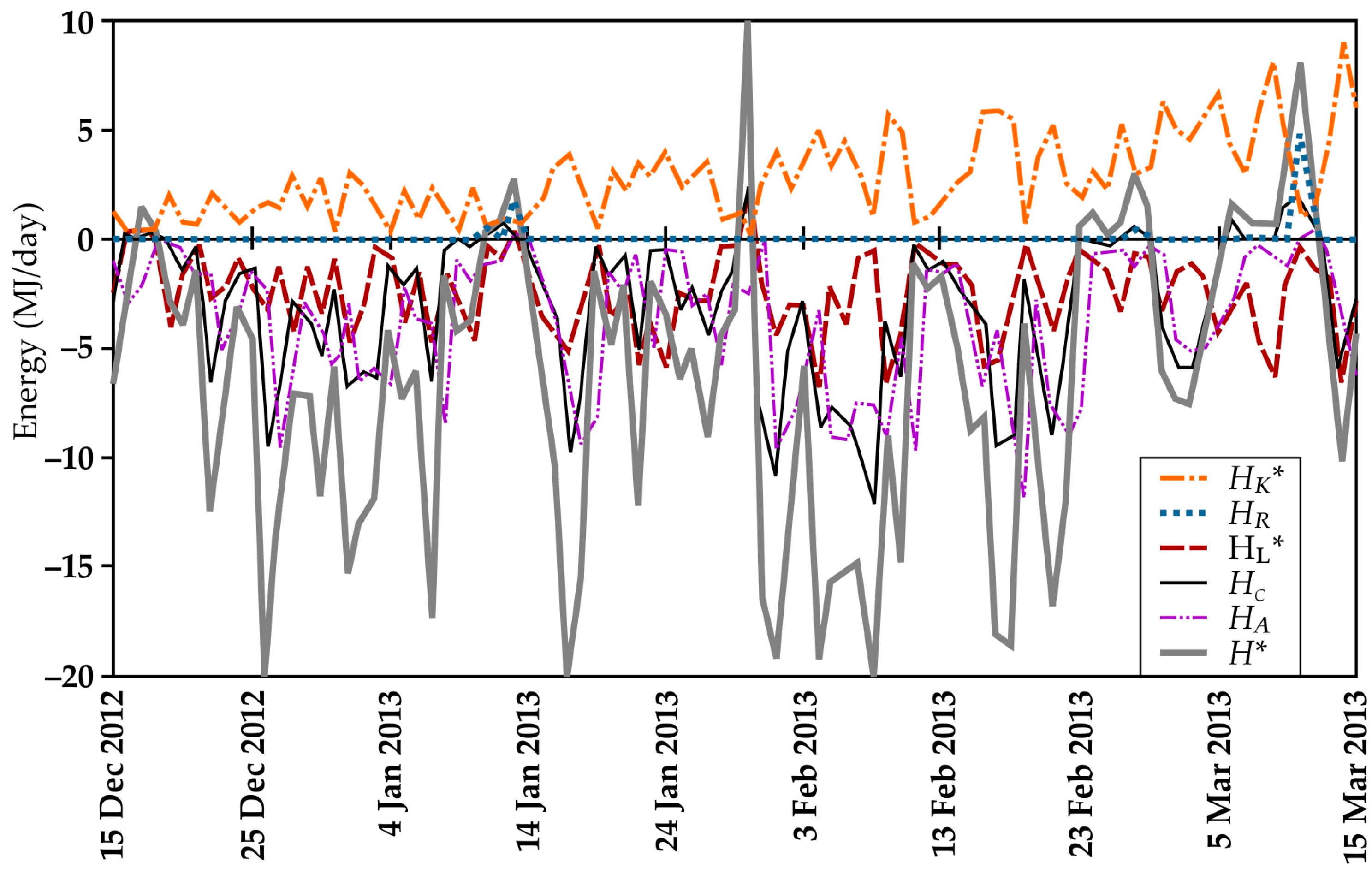
References
- Hardy, S. Memory, performance, and history: The making of American ice hockey at St. Paul’s School, 1860–1915. Int. J. Hist. Sport 1997, 14, 97–115. [Google Scholar] [CrossRef]
- Robidoux, M.A. Stickhandling Through the Margins: First Nations hockey in Canada; University of Toronto Press: Toronto, ON, Canada, 2012. [Google Scholar]
- Lorenz, S.L. Constructing a Cultural History of Canadian Hockey. Int. J. Hist. Sport 2015, 32, 2107–2113. [Google Scholar] [CrossRef]
- Bennett, P. Re-Imagining the Creation: Popular Mythology, the Mi’kmaq, and the Origins of Canadian Hockey. In Hockey: Challenging Canada’s Game; Ellison, J., Anderson, J., Eds.; Canadian Museum of History/University of Ottawa Press: Gatineau, QC, Canada, 2018; pp. 45–60. [Google Scholar]
- Hardy, S.; Holman, A.C. Hockey: A Global History; University of Illinois Press: Champaign, IL, USA, 2018. [Google Scholar]
- Koller, C. The Beginnings of the International Ice Hockey Federation. Int. J. Hist. Sport 2024, 41, 1249–1266. [Google Scholar] [CrossRef]
- Clark, M.J. Making ‘Mr. Hockey’: Race, Gender, Class, and Nation in Media Representations of Gordie Howe. Ph.D. Thesis, School of Kinesiology & Health Studies, Queen University, Kingston, ON, Canada, 2018. Available online: http://hdl.handle.net/1974/25662 (accessed on 2 October 2025).
- Field, R. Representing “The Rocket”: The Filmic Use of Maurice Richard in Canadian History. J. Sport Hist. 2014, 41, 15–28. [Google Scholar] [CrossRef]
- Gretzky, W. On Family, Hockey and Healing; Random House Canada: Toronto, ON, Canada, 2001; ISBN 978-0-679-31114-0. [Google Scholar]
- Doeden, M. Wayne Gretzky; Twenty-First Century Books: Tunbridge Wells, UK, 2007; ISBN 978-0822571650. [Google Scholar]
- Allain, K.A. Kid Crosby or Golden Boy: Sidney Crosby, Canadian national identity, and the policing of hockey masculinity. Int. Rev. Sociol. Sport 2011, 46, 3–22. [Google Scholar] [CrossRef]
- Cantelon, H. Have Skates, Will Travel: Canada, International Hockey, and the Changing Hockey Labour Market. In Artificial Ice: Hockey, Culture, and Commerce; Whitson, D., Gruneau, R., Eds.; University of Toronto Press: Toronto, ON, Canada, 2006; Chapter 11; pp. 215–236. [Google Scholar] [CrossRef]
- Holman, A.C. The Canadian hockey player problem: Cultural reckoning and national identities in American collegiate sport, 1947–1980. Can. Hist. Rev. 2007, 88, 439–468. [Google Scholar] [CrossRef]
- Brown, L.C.; Duguay, C.R. The response and role of ice cover in lake-climate interactions. Prog. Phys. Geogr. 2010, 34, 671–704. [Google Scholar] [CrossRef]
- Chen, Y.; She, Y. Long-term variations of river ice breakup timing across Canada and its response to climate change. Cold Reg. Sci. Technol. 2020, 176, 103091. [Google Scholar] [CrossRef]
- Sharma, S.; Richardson, D.C.; Woolway, R.I.; Imrit, M.A.; Bouffard, D.; Blagrave, K.; Daly, J.; Filazzola, A.; Granin, N.; Korhonen, J.; et al. Loss of ice cover, shifting phenology, and more extreme events in Northern Hemisphere lakes. J. Geophys. Res. Biogeosci. 2021, 126, e2021JG006348. [Google Scholar] [CrossRef]
- Damyanov, N.N.; Matthews, H.D.; Mysak, L.A. Observed decreases in the Canadian outdoor skating season due to recent winter warming. Environ. Res. Lett. 2012, 7, 014028. [Google Scholar] [CrossRef]
- Dickau, M.; Matthews, D.; Guertin, É.; Seto, D. Projections of declining outdoor skating availability in Montreal due to global warming. Environ. Res. Commun. 2020, 2, 051001. [Google Scholar] [CrossRef]
- McLeman, R.; Golian, S.; Murphy, C.; Robertson, C. Future prospects for backyard skating rinks look bleak in a warming climate. Can. Geogr./Géographies Can. 2023, 68, 247–255. [Google Scholar] [CrossRef]
- International Institute for Sustainable Development. Experimental Lakes Area data provided by Scott Higgins; International Institute for Sustainable Development: Winnipeg, MB, Canada, 2024. [Google Scholar]
- Wilfred Laurier University. RinkWatch. Available online: https://www.rinkwatch.org/ (accessed on 21 December 2024).
- King’s Printer for Ontario. Ontario’s Data Catalogue: Ontario Ministry of Environment, Conservation and Parks: Inland Lakes and Streams—Physical Conditions 2024. Available online: https://data.ontario.ca/dataset/inland-lakes-and-streams-physical-conditions (accessed on 23 December 2024).
- Yao, H.; Field, T.; McConnell, C.; Beaton, A.; James, A.L. Comparison of five snow water equivalent estimation methods across categories. Hydrol. Process. 2018, 32, 1894–1908. [Google Scholar] [CrossRef]
- Buck, A.L. New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Yao, H.; Samal, N.R.; Joehnk, K.D.; Fang, X.; Bruce, L.C.; Pierson, D.C.; Rusak, J.A. Comparing ice and temperature simulations by four dynamic lake models in Harp Lake: Past performance and future predictions. Hydrol. Process. 2014, 28, 4587–4601. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Proc. R. Neth. Acad. Sci. 1950, 53, 386–392. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. Am. Stat. Assoc. J. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trends. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.; Gibbons, J.D. Rank Correlation Methods, 5th ed.; Edward Arnold: London, UK, 1990. [Google Scholar]
- Environment Canada and Climate Change. Historical Climate Data. Available online: https://climate.weather.gc.ca/ (accessed on 23 December 2024).
- Roos, J. Breaking the Ice: Slowly Warming to the Topic of Climate Change. Ph.D. Thesis, Lund University, Lund, Sweden, 2017. [Google Scholar]
- Anisimov, O.; Orttung, R. Climate change in Northern Russia through the prism of public perception. Ambio 2019, 48, 661–671. [Google Scholar] [CrossRef]
- Ahmed, S.I.; Rudra, R.; Goel, P.; Amili, A.; Dickinson, T.; Singh, K.; Khan, A. Change in Winter Precipitation Regime across Ontario, Canada. Hydrology 2022, 9, 81. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Kouwen, N.; Soulis, E.D. Surface temperature adjustments to improve weather radar representation of multi-temporal winter precipitation accumulations. J. Hydrol. 2001, 253, 148–168. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Venable, N.B.H.; Khishigbayar, J.; Cherry, M.L. The Probability of Precipitation as Snow Derived from Daily Air Temperature for High Elevation Areas of Colorado, United States. In Proceedings of the Cold and Mountain Region Hydrological Systems Under Climate Change: Towards Improved Projections, Gothenburg, Sweden, 22 July 2013; Volume 360, pp. 65–70. [Google Scholar]
- Fassnacht, S.R.; Soulis, E.D. Implications during transitional periods of improvements to the snow processes in the Land Surface Scheme—Hydrological Model WATCLASS. Atmosphere-Ocean 2002, 40, 389–403. [Google Scholar] [CrossRef]
- Wright, R.; Wright, J. The End of All Things. In Wrong, Alternative Tentacle; Alternative Tentacles: Vancouver, BC, Canada, 1989; Chapter 6. [Google Scholar]


| Input Item | Unit | Remark |
|---|---|---|
| Precipitation | mm/day | |
| Mean temperature | °C | |
| Minimum temperature | °C | |
| Relative humidity | % | |
| Wind speed | km/h | |
| Shortwave radiation | KJ/day | |
| Longwave radiation | KJ/day | measured or estimated |
| Snowfall | mm/day | estimated |
| Rainfall | mm/day | estimated |
| Rink | Observed | Model I | Model II | Model III |
|---|---|---|---|---|
| Stephenson Lions | 5 March 2013 | 8 March 2013 (3) | 9 March 2013 (4) | 22 February 2013 (−13) |
| Annie Williams | 13 March 2013 | 8 March 2013 (−5) | 9 March 2013 (−4) | 22 February 2014 (−19) |
| Parkview NIR | 8 March 2013 | 8 March 2013 (0) | 9 March 2013 (1) | 22 March 2013 (14) |
| 24 March 2014 | 28 March 2014 (4) | 5 April 2014 (12) | 20 February 2014 (−32) | |
| 9 March 2015 | 11 March 2015 (2) | 14 March 2015 (5) | 1 March 2015 (−8) | |
| 21 February 2016 | 26 March 2016 (33) | 11 March 2016 (18) | 19 February 2016 (−2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, H.; Fassnacht, S.R. Outdoor Ice Rinks in Ontario, Canada—An Oversimplified Model for Ice Water Equivalent and Operational Duration to Evaluate Changing Climate. Hydrology 2025, 12, 263. https://doi.org/10.3390/hydrology12100263
Yao H, Fassnacht SR. Outdoor Ice Rinks in Ontario, Canada—An Oversimplified Model for Ice Water Equivalent and Operational Duration to Evaluate Changing Climate. Hydrology. 2025; 12(10):263. https://doi.org/10.3390/hydrology12100263
Chicago/Turabian StyleYao, Huaxia, and Steven R. Fassnacht. 2025. "Outdoor Ice Rinks in Ontario, Canada—An Oversimplified Model for Ice Water Equivalent and Operational Duration to Evaluate Changing Climate" Hydrology 12, no. 10: 263. https://doi.org/10.3390/hydrology12100263
APA StyleYao, H., & Fassnacht, S. R. (2025). Outdoor Ice Rinks in Ontario, Canada—An Oversimplified Model for Ice Water Equivalent and Operational Duration to Evaluate Changing Climate. Hydrology, 12(10), 263. https://doi.org/10.3390/hydrology12100263








