Abstract
Extraction of Pb(II) with picrate ion [Pic−] and 0, 0.58, 15, 48, or 97 mmol·dm−3 Cd(NO3)2 by benzo-18-crown-6 ether (B18C6; L as its symbol) into benzene (Bz) was studied. Three kinds of extraction constants, Kex, Kex±, and KPb/PbL (or Kex2±), were determined at 298 K: these constants were defined as [PbLPic2]Bz/P, [PbLPic+]Bz[Pic−]Bz/P, and [PbL2+]Bz/[Pb2+][L]Bz (or [PbL2+]Bz([Pic−]Bz)2/P), respectively. The symbol P shows [Pb2+][L]Bz[Pic−]2 and the subscript “Bz” denotes the Bz phase, Bz saturated with water. Simultaneously, conditional distribution constants, KD,Pic (=[Pic−]Bz/[Pic−]), of Pic− with distribution equilibrium-potential differences (dep) were determined. Then, based on the above four constants and others, the component equilibrium constants of K1,Bz (=[PbLPic+]Bz/[PbL2+]Bz[Pic−]Bz), K2,Bz (=[PbLPic2]Bz/[PbLPic+]Bz[Pic−]Bz), and KD,PbL (=[PbL2+]Bz/[PbL2+]) were obtained. Using these constants, the Pb(II) extraction with B18C6 under the co-presence of Cd(II) in the water phase was characterized. In such a characterization, I and IBz dependences on the constants were mainly discussed, where their symbols denote the ionic strength of the water phase and that of the Bz one, respectively.
1. Introduction
In extraction systems with crown compounds (L), some extraction constants, such as Kex and Kex±, have been employed for evaluating their extraction-abilities and -selectivities [1,2,3,4,5,6]. Here, the constants Kex and Kex± have been generally defined as [MLAz]org/P and [MLAz−1+]org[A−]org/P, respectively, with P = [Mz+][L]org[A−]z at z = 1 and 2 [1,7,8,9]. The symbols Mz+, A−, and the subscript “org” denote a metal ion with the formal charge of z+, a univalent pairing anion, and an organic phase, respectively. For evaluating the ability and selectivity of L for its extraction, many studies have been present [1,2,3,4,5,6,7,8,9], but those for clarifying ionic strength (I) dependences of the equilibrium constants seemed to be few [10,11]. Recently, one of the authors reported the I and IDCE (with HNO3 as an I conditioner) dependences of the Kex and Kex± values in the silver picrate (AgPic) extraction with benzo-18-crown-6 ether (B18C6) into 1,2-dichloroethane (DCE), where IDCE refers to the I value for the DCE phase [12]. At the same time, conditional distribution constants (KD,A = [A−]org/[A−]) of the picrate ion Pic− (=A−) into the DCE (=org) phases have been determined [12] and thereby distribution equilibrium potential-differences (dep; Δφeq as a symbol in an equation) have been evaluated [7,8,12].
In the present paper, to expand such characterization [12] for the AgPic extraction system to that for an MIIPic2 extraction one, we determined at 298 K the Kex, Kex±, and KD,Pic values for PbPic2 extraction with B18C6 into benzene (Bz) under a co-presence of Cd(NO3)2 in a water phase. Then, I and IBz dependences of these equilibrium constants were mainly examined [12]. Similar examinations were performed for other overall or component equilibrium-constants, such as KPb/PbL, Kex,ip, and K1,Bz (see Equations (6)–(8) for their definitions), derived from the above equilibrium constants. This study is expected to be useful for comparisons between the Kex and Kex± values, because magnitudes of their comparable values depend on I [10,11] or IBz in general. Consequently, such data relevant to I and IBz can make more precise comparisons between the values possible.
In addition, it had been pointed out that the presence of alkali metal and transition metal ions by high concentrations may cause significant interferences in the removal of Pb in acidic waste streams [13]. Similarly, the Mz+ separation with solvent extraction [13] and membrane transport experiments has been studied [14,15]. However, these quantitative considerations based on any equilibrium constants have not been reported. This situation reveals the importance of these fundamental studies [10,11,12] and this work as well, which can make a prediction for their separation more precise.
As well as the previous paper [12], the dep values which were fundamentally based on the ion transfer of Pic− at the water/Bz interfaces were evaluated from the determined KD,Pic values [16]. Moreover, the relationship between log Kex± and dep was quantitatively discussed [7,16].
The both M(II) ions are well-known as toxic metals to living things in nature [17], but were employed here as simply model metal ones. Additionally, Bz was selected because a lot of data for the extraction of these M(II) ions with B18C6 or 18-crown-6 ether (18C6) is available [1,3,6,8,18,19,20].
A competitive extraction between Pb(II) and Cd(II) with B18C6 into Bz had been assumed with the addition of Cd(II) in the water phase in the beginning of this study, compared with the log (Kex,Pb/Kex,Cd) value of 9.73 for the Pb(II) and Cd(II) extraction with 18C6 [9]. However, against our plan, such an extraction behavior was not observed here.
2. Results and Discussion
2.1. Determination of Composition of Extracted Species with Pb(II) at Some [Cd]t/[Pb]t Values
Determination of an M(II):L composition is based on the following Kex or Kex± definition [1,8,19,21]: Kex = [MLA2]org/P and Kex± = [MLA+]org[A−]org/P with P = [M2+][L]org[A−]2 at z = 2. Taking common logarithms of both sides of these definitions and then rearranging them, we can easily obtain
with D0 = [MLA20]org/[M2+], D+ = [MLA+]org/[M2+] (see the Section 2.9), and Kex+ (=Kex±/KD,A) = [MLA+]org/[M2+][L]org[A−] [1,8,19]. From applying the approximate that D0 and D+ nearly equal D for Equations (1) and (2), respectively, the following equations were derived:
where D is an experimental distribution ratio and defined as [Pb(II)](species analyzed by AAS measurement)/([Pb(II)]t − [Pb(II)](species analyzed by AAS measurement))org. In addition, [Pb(II)]t refers to a total concentration of Pb(NO3)2 employed. Therefore, in terms of a plot of log (D/[A−]2) versus log [L]Bz come from Equation (1a) or that of log (D/[A−]) from Equation (2a), we can determine the Pb(II):L compositions in the extraction systems from their slopes [9]. Figure 1 shows such plots based on Equation (1a).
log (D0/[A−]2) = log Kex + log [L]org
and log (D+/[A−]) = log Kex+ + log [L]org
log (D/[A−]2) ≈ log Kex + log [L]org
and log (D/[A−]) ≈ log Kex+ + log [L]org
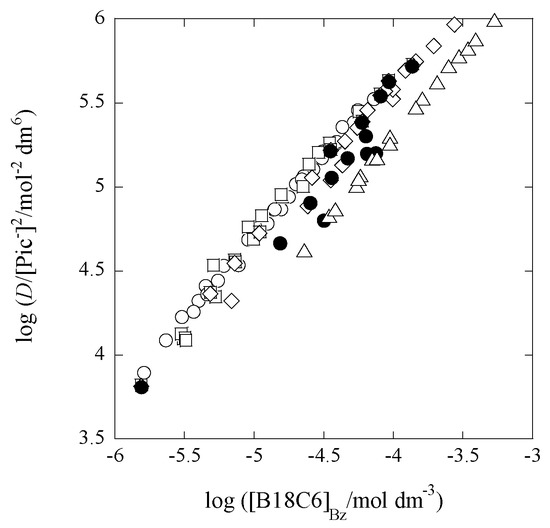
Figure 1.
Plots for composition determination based on Equation (1a) under the conditions of [Cd]t/[Pb]t = 0 (open circle), 1.06 (square), 26.6 (diamond), 88.5 (full circle), and 178 (triangle).
Experimentally-obtained slopes were 0.98 for the Pb(II)–B18C6 extraction system with 0 mmol·dm−3 of Cd(II) (or [Cd]t/[Pb]t = 0), 1.0 for that with 0.58 of Cd(II) (or 1.06), 0.97 for that with 14 of Cd(II) (or 26.6), 0.98 for that with 48 of Cd(II) (or 88.4), and 1.0 for that with 97 of Cd(II) (or 178). From these results, we can see easily that the compositions of Pb(II):B18C6 are 1:1 for all the systems. In the present study, there was no need of employing Equation (2a). The compositions of Pb(II):Pic(−I) were speculated to be 1:2 from similarity to the systems [3] reported before for M(II) extraction with 18C6 into Bz and from a charge balance in the Bz phases [1,8,19,21]: approximately [PbLPic+]Bz ≈ [Pic−]Bz from more-precisely 2[Pb2+]Bz + 2[PbL2+]Bz + [PbLPic+]Bz + [PbPic+]Bz ≈ [Pic−]Bz + [NO3−]Bz, because it was expected that [PbLPic+]Bz >> 2[Pb2+]Bz + 2[PbL2+]Bz + [PbPic+]Bz and [Pic−]Bz >> [NO3−]Bz [9,21].
2.2. Determination of Kex, Kex±, and KD,Pic
According to previous papers [1,8,9,22], the extraction-constant parameter (Kexmix) has been proposed:
with KD,A ≈ [MLA+]org/[A−]. Using this equation, we can immediately obtain the Kex and KD,A values from a plot of log Kexmix versus −log ([M2+][L]org[A−]). In addition, Equation (3) can be rewritten as:
log Kexmix = log {([MLA2]org + [MLA+]org + [ML2+]org + …)/P}
≈ log {Kex + (KD,A/[M2+][L]org[A−])}
≈ log {Kex + (KD,A/[M2+][L]org[A−])}
Similarly, the Kex± value (with the Kex one; see Table 1) can be obtained from a plot of log Kexmix versus −log P1/2. Figure 2 and Figure 3 show examples of such plots.

Table 1.
Basic data for the Pb(II) extraction by B18C6 from the water phase with co-presence of Cd(NO3)2 into Bz at 298 K.
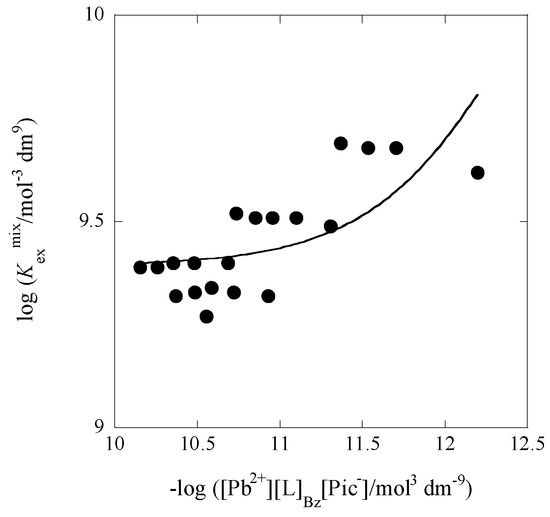
Figure 2.
Plot of log Kexmix versus −log ([Pb2+][L]Bz[Pic−]) with L = B18C6 at [Cd]t/[Pb]t = 88.5. The line is based on Equation (3).
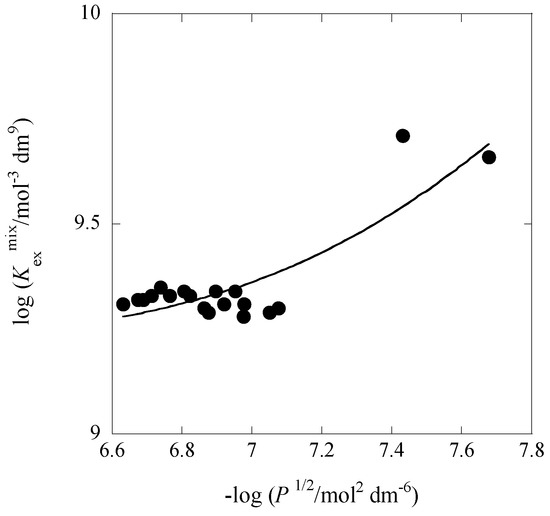
Figure 3.
Plot of log Kexmix versus −log P1/2 with B18C6 at [Cd]t/[Pb]t = 88.5. The line is based on Equation (4).
From these plots, the KD,Pic, Kex±, and Kex values were determined at 298 K. Table 1 lists these extraction constants, Kex and Kex±, and the conditional distribution constants, KD,Pic, with averaged ionic strength-values (I) for the water phase in the five [Cd]t/[Pb]t conditions. The Kex values determined with Equation (4) were equal or close to those with Equation (3). This fact raises the credibility of the values themselves and also shows the effects of Equations (3) and (4) on evaluation. The Kex and Kex± values at [Cd]t/[Pb]t = 0 were smaller than those (1011.712 mol−3·dm9 and 104.1 mol−2·dm6 [9]) reported before at I = 0.0059 mol·dm−3 for the PbPic2 extraction with 18C6 into Bz.
2.3. Dep Determination from KD,Pic
From the log KD,Pic values listed in Table 1, using the following equation and a standardized distribution constant (KD,PicS), we can easily obtain the dep (or Δφeq) values for the five [Cd]t/[Pb]t conditions at 298 K:
Δφeq = −0.05916(log KD,Pic − log KD,PicS) = ΔφPic0′ − 0.05916log KD,Pic
Here, the KD,PicS value is defined as the KD,Pic one at Δφeq = 0 V, equals antilog (ΔφPic0′/0.05916) (=exp (ΔφPic0′/0.02569) [23]), and, as its common logarithmic value, −8.208 or −7.4473 is available from references [24,25]. In addition, the minus sign of −0.05916 (=−2.303RT/F ) and the symbol ΔφPic0′ denote the formal charge of Pic− and the standard formal potential for the Pic− transfer across the water/Bz interface, respectively. We mainly employed the former value for the evaluation described below. Table 1 lists the dep/V values evaluated from log KD,PicS = −8.208 [24].
2.4. Determination of KPb/PbL, Kex,ip, K1,Bz, K2,Bz, and KD,PbL
These constants can be evaluated from the following relations [1,18,26,27,28].
log KPb/PbL = log ([PbL2+]Bz/[Pb2+][L]Bz) ≈ log (D/[L]Bz),
log Kex,ip = log ([PbLPic2]Bz/[PbL2+][Pic−]2) = log (KexKD,L/KPbL),
log K1.Bz = log ([PbLPic+]Bz/[PbL2+]Bz[Pic−]Bz) ≈ log {Kex±/KPb/PbL(KD,Pic)2}
= log (Kex±/Kex2±),
log K2,Bz = log ([PbLPic2]Bz/[PbLPic+]Bz[Pic−]Bz) = log (Kex/Kex±),
and log KD,PbL = log ([PbL2+]Bz/[PbL2+]) ≈ log (KPb/PbLKD,L/KPbL).
Only for the KPb/PbL values, they were obtained as the averages of D/[B18C6]Bz at every [Cd]t/[Pb]t value [27]. For the above evaluation at 298 K, 0.943 [2] and 3.19 [29] were used as the logarithmic values of KD,B18C6 (=[B18C6]Bz/[B18C6]) and KPbB18C6 (=[PbB18C62+]/[Pb2+][B18C6]), respectively. These five logarithmic K-values are summarized in Table 2, together with the ionic strength-values (IBz) for the Bz phase.

Table 2.
Some equilibrium constants obtained from the Pb(II) extraction experiments by L = B18C6 from the water phase with co-presence of Cd(NO3)2 into Bz at 298 K.
2.5. Correlation between log Kex± and Dep
We can obtain the following relation from the thermodynamic cycle of the PbLPic+ extraction with Pic−.
log Kex± = 2log KD,Pic + log KPb/PbL + log K1,Bz
= 2log KD,PicS − 2(F/2.303RT)Δφeq + log KPb/PbL·K1,Bz
= 2log KD,PicS − 2(F/2.303RT)Δφeq + log KPb/PbL·K1,Bz
Here, the log KPb/PbL·K1,Bz term was in the range of 8.7 to 9.1 (see the data in Table 2) and log KD,PicS (=−8.208 [24] or −7.4473 [25]) equals log KD,Pic at Δφeq = 0 V. Hence, we obtained to be −7.7 to −7.3 for the former KD,PicS value or the −6.2 to −5.8 for the latter one as the term of 2log KD,PicS + log KPb/PbL⋅K1,Bz (see Table 1 and Table 2). In addition, 2F/2.303RT becomes 33.80 V−1 at T = 298.15 K. Rearranging Equation (11), we can immediately derive
log Kex± ≈ (−7.7 to −7.3) − 33.80ΔφEquation
From the regression analysis of an experimental plot in Figure 4, the following line was obtained: log Kex± = (−5.3 ± 1.4) − (27.3 ± 4.2)Δφeq at |R| = 0.967, where the symbol R denotes a correlation coefficient. This regression line is close to Equation (11a) which was estimated from the experimental K values. This fact indicates the presence of dep, as similar to the results reported previously [7,8,12,16,21,22].
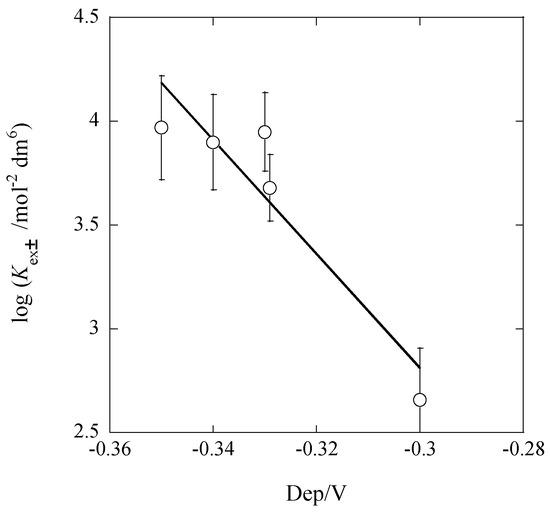
Figure 4.
Plot of log Kex± versus dep for the Pb(II) extraction with Cd(NO3)2 and B18C6 into Bz. The line corresponds to Equation (11a).
2.6. I Dependences of log Kex and log Kex,ip
The thermodynamic extraction constant of Kex is Kex0 = [PbLPic2]Bz/aPb[L]Bz(aPic)2, where aPb and aPic refer to activities of Pb2+ and Pic− in the water phase, respectively, and it was assumed that [PbLPic2]Bz is equal to the activity in the Bz phase, because PbL2+(Pic−)2 is charge-less. The same is true of [B18C6]Bz too. Taking the common logarithms of both sides of the Kex0 definition, we can obtain
log Kex0 = log Kex − log {yPb(yPic)2}
with yPb = aPb/[Pb2+] and yPic = aPic/[Pic−]. Introducing the extended Debye–Hückel (DH) equation [30,31] in Equation (12) and arranging it, the following equation was obtained:
Here, the DH equation was based on the mean activity coefficient and the symbol denote the ion-size parameter [30] in Å unit. Although the extended DH equation holds in the I range of ≤0.1 mol·dm−3 [30] as you know, we approximately employed it for the condition of I = 0.29 (see Table 1). Figure 5 shows curve-fittings of the plots for Equation (12a).
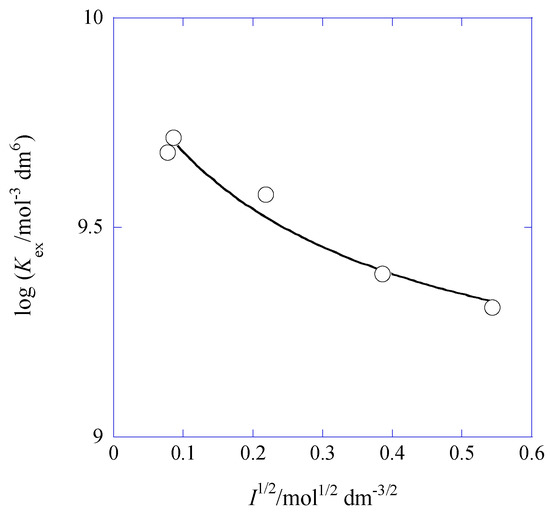
Figure 5.
Plot of log Kex versus I1/2 for the Pb(II) extraction with Cd(NO3)2 and B18C6 into Bz. The line is based on Equation (12a).
Its regression line was log Kex = (9.91 ± 0.03) − 6 × (0.5114)/(1 + (3.40 ± 0.46)) at R = 0.980, where the coefficient A was fixed to 0.5114 mol−1/2·dm3/2 [30] and the value in water was evaluated to be 10 Å (=3.40/0.3291) at 298 K.
Similarly, the log Kex,ip values were analyzed. Their constants were expressed as
with Kex,ip0 = [PbLPic2]Bz/aPbL(aPic)2 = Kex,ip/yPbL(yPic)2
The regression analysis of the plots yielded log Kex,ip = (7.66 ± 0.03) − 6 × (0.5114)/(1 + (3.41 ± 0.51)) at R = 0.975 and then the a± value was evaluated to be 10 Å. The accordance between Pb2+–Pic− distance and PbB18C62+–Pic− one suggests that the former interaction between the Pb2+ and Pic− ions in water saturated with Bz is equivalent with the latter one between PbB18C62+ and Pic−.
It is interesting that the evaluated values are close to the sum (=11.5 Å) of the ion-size parameters [32] between Pb2+ (4.5 Å) and Pic− (7 Å) for water. This Kex,ip0 value was well in accord with that (=107.66 mol−1·dm3) calculated from the thermodynamic cycle of Kex,ip0 ≈ Kex0KD,L/KPbL (=109.91 × 100.943/103.19).
Considering that the Kex values are most precise ones of the some extraction constants determined here (see their errors in Table 1), the fair dependences of log Kex on I indicate a simple role of Cd(NO3)2 only as the ionic strength conditioner in the present extraction systems. In other words, the authors were not be able to clearly find out positive or negative effects of Cd(NO3)2 on the present Pb(II) extraction with B18C6 into Bz.
2.7. IBz Dependences of log K1,Bz and log K2,Bz
Using IBz and the DH limiting law [30], both log K1,Bz0 and log K2,Bz0 can be expressed as
with yPbLPic,Bz ≈ yPic,Bz and
Rearranging Equations (14) and (15), we can obtain
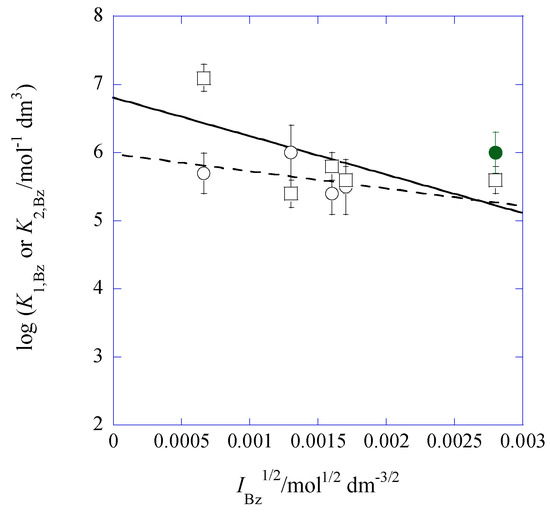
Figure 6.
Plots of log K1,Bz (circle) and log K2,Bz (square) versus IBz1/2 for the Pb(II) extraction with Cd(NO3)2 and B18C6 into Bz. The regression lines were based on Equations (14a) and (15a). The full circle was omitted from the regression analysis of log K1,Bz.
At the same time, these plots were analyzed by using the both equations. Their regression lines were log K1,Bz = (5.98 ± 0.49) − 4 × (63 ± 89) at R = 0.449 except for the point of [Cd]t/[Pb]t = 178 and log K2,Bz = (6.81 ± 0.68) − 2 × (282 ± 195) at R = 0.641. These lines intersected with each other at IBz1/2 = 2.7 × 10−3 mol1/2·dm−3/2, yielding log K1,Bz = log K2,Bz = 5.31. This fact indicates that, in the lower IBz range less than 7.1 × 10−6 mol·dm−3, the K2,Bz values are larger than the K1,Bz ones. The latter values may be estimated to actually be the smaller values because of the approximation [33] for the K1,Bz determination (see Equation (8)). Unlike the case of the CdPic2–B18C6 extraction system [33], unfortunately, we do not have the procedure which corrects such deviations for the present extraction systems, because of a lack of adequate data used for the correction.
In addition, we tried curve-fittings to the two plots using the following equations:
with the approximation of 1 >> (see Table 2). Here, the symbols b1 and b2 denote empirical curve-fitting parameters [30,31] which were simply predicted in this study from the plot shapes (see Figure 6). The regression analyses of the plots at 298 K gave log K1,Bz = (6.16 ± 0.80) − 4 × (179 ± 247) + (2.3 ± 2.7) × 105IBz at R = 0.569 and log K2,Bz = (8.80 ± 0.98) − 2 × (1625 ± 603) + (7.6 ± 3.3) × 105IBz at 0.914 (see Figure 7). Modifying these equations like the Davies one [30,31], their 2nd and 3rd terms became −4 × (179 ± 247)( − (3.2 ± 5.9) × 102IBz) and −2 × (1625 ± 603)( − (2.3 ± 1.3) × 102IBz), respectively. These b1/4ABz and b2/2ABz values of about 320 and 230 mol−1/2·dm3/2 for the Bz phases are much larger than 0.3 [31] for the aqueous solution at 298 K. Equation (14b) intersects Equation (15b) around IBz1/2 = 3.3 × 10−3 mol1/2·dm−3/2, yielding log K1,Bz = log K2,Bz = 6.30, and then their two lines equal with each other within the experimental errors (see the plots in Figure 7).
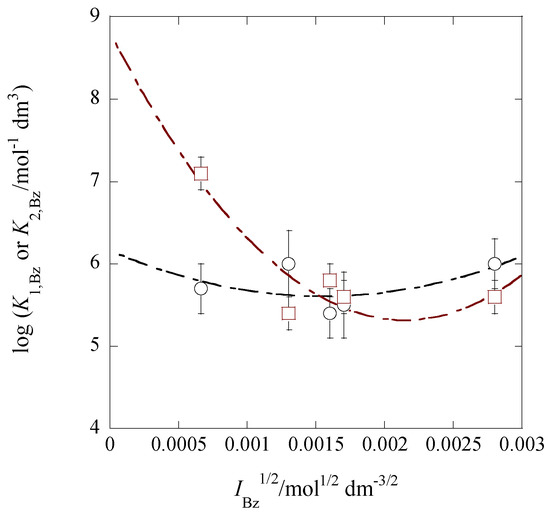
Figure 7.
Plots of log K1,Bz (circle) and log K2,Bz (square) versus IBz1/2 for the Pb(II) extraction with Cd(NO3)2 and B18C6 into Bz. The regression lines were based on Equations (14b) and (15b).
In comparison of Equations (14a) and (15a) with Equations (14b) and (15b), the point of intersection changed from IBz1/2/mol1/2·dm−3/2 = 0.0027 to 0.0033, while their corresponding log K1,Bz (=log K2,Bz) value changed from 5.3 to 6.3.
At least in the lower IBz range less than 1.1 × 10−5 mol·dm−3, the K2,Bz values are larger than the K1,Bz ones. From the results of the calculation based on Equations (14a,b) and (15a,b), the relation of K1,Bz < K2,Bz holds in the range less than (0.71 − 1.1) × 10−5 mol·dm−3 (see above). According to the paper [8], such a fact suggests a structural change around Pb(II) in the reaction of Pb(B18C6)Pic+Bz + Pic−Bz ⇌ Pb(B18C6)Pic2,Bz, such as Cd(18C6)Pic2,Bz of the Cd(II) extraction systems [33]. Trends similar to K1,Bz < K2,Bz are observed in the reactions of Cd18C62+ with Pic−, Cl−, and Br− in the Bz phases for fixed IBz values [1,8]. The higher IBz range may lead to the formation of ion-pair complexes with other coordination structures around Pb(II), although their structures are not clear.
Table 3 shows results for the both estimated values from Equations (14a) and (15a) and those from Equations (14b) and (15b). In comparison with differences, |dif.|, in K1,Bz and K2,Bz between the experimental and estimated values, the |dif.| values estimated from Equations (14b) and (15b) were essentially smaller than those done from Equations (14a) and (15a). Especially, the former equations seem to be superior to the latter ones in the IBz range, namely the present experimental [Cd]t/[Pb]t range, of 4 × 10−7 to 8 × 10−6 mol·dm−3 in the cases of the prediction of K2,Bz. Unfortunately, chemical and physical meanings of b1 and b2 are not clear still now.

Table 3.
Comparison between Equations (14a) and (15a) and Equations (14b) and (15b) in the re-production of the experimental K1,Bz and K2,Bz values 1 at 298 K.
2.8. IBz Dependences of log Kex±0′, log KD,Pic0′, and log KPb/PbL0
The thermodynamic equilibrium constant Kex±0 is equal to (y±,Bz)2Kex±0′, with y±,Bz = (yPbLPic,Bz·yPic,Bz)1/2 and Kex±0′ = [PbLPic+]Bz[Pic−]Bz/(aPb[L]Bz(aPic)2). Taking the common logarithms of the both sides in this equation and rearranging it with the DH limiting law, we can easily obtain
Figure 8 shows the plot of log Kex±0′ versus IBz1/2 based on Equation (16). The regression analysis of this plot gave the equation of log Kex±0′ = (3.11 ± 0.69) + 2 × (315 ± 196) at R = 0.680. From this Kex,±0 value and the Kex0 one, we calculated log K2,Bz0 to be 6.80 ± 0.69, being in good agreement with that (=6.8) evaluated from Equation (15a).
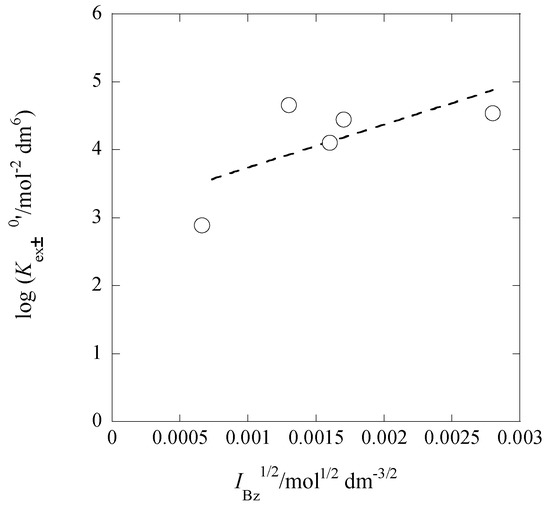
Figure 8.
Plot of log Kex±0′ versus IBz1/2 based on Equation (16) for the Pb(II) extraction with Cd(NO3)2 and B18C6 into Bz. The symbol Kex±0′ was defined as Kex±/yPb(yPic)2.
Similarly, the plot of log KD,Pic0′ versus IBz1/2 was performed in Figure 9, where KD,Pic0′ is defined as [Pic−]Bz/aPic. This plot is based on the equation
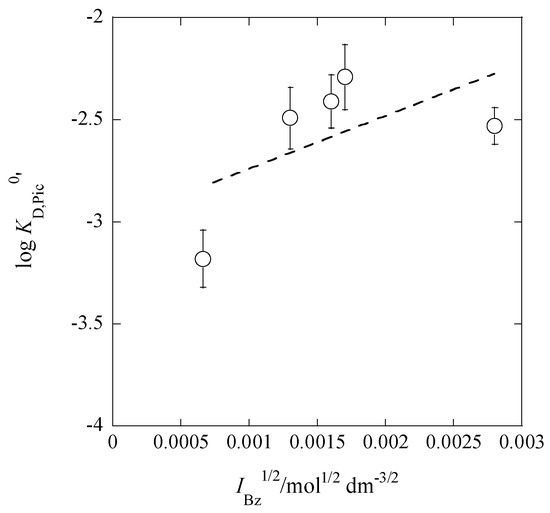
Figure 9.
Plot of log KD,Pic0′ versus IBz1/2 based on Equation (17) for the Pb(II) extraction with Cd(NO3)2 and B18C6 into Bz. The symbol KD,Pic0′ was defined as KD,Pic/yPic. The error bars in the figure are those of the log KD,Pic values.
The regression analysis yielded log KD,Pic0′ = (−3.00 ± 0.36) + (258 ± 210) at R = 0.578.
In addition, the analysis was tried by using an equation similar to Equations (14b) and (15b) with 1 >> Its regression line was
at R = 0.995. Here, the latter two terms are rearranged into (1949 ± 154)( − (245 ± 29)IBz). This value, 245 mol−1/2·dm3/2, is comparable to the b1/4ABz (=~320) and b2/2ABz (=~230) values estimated above.
Lastly, the log KPb/PbL0′ (=log ([PbL2+]Bz/aPb[L]Bz)) values were analyzed. This constant was related with the log KPb/PbL0 (=log (aPbL,Bz/aPb[L]Bz)) value by the following equation:
The log KPb/PbL0′ values were plotted against the IBz1/2 ones. The regression line based on Equation (18) was log KPb/PbL0′ = (3.546 ± 0.001) + 4 × (2.16 ± 0.16) at R = 0.997, except for the two points of IBz = 4.4 × 10−7 and 1.7 × 10−6 mol·dm−3 (see Table 2). These two log KPb/PbL0′ values excluded from the regression analysis are included in the regression line within experimental errors. However, the ABz value is much smaller than the others. In addition, the analysis was tried by using an equation similar to Equations (14b) and (15b). However, its regression line showed the result of ABz < 0.
By a combination with log KD,Pic0, the log KPb/PbL0 can be changed into log Kex2±0 (=log (aPbL,Bz(aPic,Bz)2/aPb[L]Bz(aPic,Bz)2)) = log KPb/PbL0 + 2log KD,Pic0. Thus, the log Kex2±0 value was estimated to be −2.45 ± 0.37 from Equation (17) (the linear type) or −4.96 ± 0.13 from Equation (17a) (the f (p) = a + bp + cp2 type). Using log Kex±0 = 3.11 obtained from Equation (16) and log K1,Bz0 = 5.98 from Equation (14a) (the linear type), the log Kex2±0 value was calculated to be −2.87 ± 0.85. On the other hand, the log Kex2±0 value became −3.1 ± 1.1 in the calculation with log K1,Bz0 = 6.16 from Equation (14b) (the f (p) = a + bp + cp2 type). Except for −4.9 from Equation (17a), the values calculated from the three equations agreed with each other within their calculation errors. According to the thermodynamic cycle, the relation of Kex± = KPb/PbLK1,Bz(KD,Pic)2 holds. From this relation, we obtained log Kex±0 = 3.54 ± 0.72 (=log KPb/PbL0 + log K1,Bz0 + 2log KD,Pic0). This value is in agreement with that (=3.1) calculated from Equation (16) within the calculation error of ±0.7. In addition, the same calculation was performed with the values obtained from the polynomial Equations (14b) and (17a). Its value was 1.20 ± 0.83, being much smaller than 3.1. These results suggest that the linear-type equation is the more reliable than the polynomial-type one, from the thermodynamic points of view.
From the four experimental ABz/mol−1/2·dm3/2 values based on Equations (14a), (15a), (16), and (17), except for the value obtained from Equation (18), their average value was estimated to be 230. Consequently, this ABz value for Bz saturated with water was about 2-times larger than that (=103.3 mol−1/2·dm3/2) calculated for pure Bz with εr = 2.275 [2] at 298.15 K. To agree with this conclusion, however, a reasonable reason will be required for the omission of the result of Equation (18).
2.9. A Try for Estimation of Detailed Separation Factor
According to the previous papers [8,33], the following relations hold for given Pic− and L.
with
log (Kex,Pb/Kex,Cd) = log (D0,Pb/D0,Cd),
log (Kex±,Pb/Kex±,Cd) = log (D+,Pb/D+,Cd),
and log (KPb/PbL/KCd/CdL) = log (D2+,Pb/D2+,Cd)
D0,Pb = [PbLPic2]Bz/[Pb2+] = Kex[L]Bz[Pic−]2,
D+,Pb = [PbLPic+]Bz/[Pb2+] = Kex±[L]Bz[Pic−]/KD,Pic,
and D2+,Pb = [PbL2+]Bz/[Pb2+] = KPb/PbL[L]Bz.
Here, D0,Pb, D+,Pb, and D2+,Pb show the values of M = Pb at z = 0, 1, and 2, respectively. The same is true of the definitions for the Cd(II) (=M(II)) extraction system with B18C6.
For example, Equation (19) can be expressed as:
log (D0,Pb/D0,Cd) = log ([PbLPic2]Bz/[CdLPic2]Bz) + log ([Cd2+]/[Pb2+])
Assuming that [Cd2+]/[Pb2+] approximately equals [Cd2+]t/[Pb2+]t, then we can estimate the more detailed value than the separation factor. In the Pb(II) extraction with Cd(II) by B18C6 into Bz, the log (D0,Pb/D0,Cd) value was 7.09 in which the log Kex value (=9.448) was estimated at I = 0.095 [33] from the regression line of Figure 5. From Equation (25) and [Cd2+]t/[Pb2+]t = 55.5 estimated from a correlation between [Cd]t/[Pb]t and I in Table 1, the log ([PbLPic2]Bz/[CdLPic2]Bz) value became 5.35. At least this result shows that the actual separation of Pb(II) from a test solution with an 56 excess amount of Cd(II) is possible. The same can be true of an application based on the handling for D+,Pb/D+,Cd and D2+,Pb/D2+,Cd, if the Kex±,Cd and KCd/CdL values are determined about the CdPic2 extraction with B18C6 (=L) into Bz.
2.10. Relative Concentrations of the Three Species Extracted into Bz
We can immediately calculate relative concentrations of PbLPic2, PbLPic+, and PbL2+ in the Bz phases from the D0,Pb, D+,Pb, and D2+,Pb values, respectively [8,24,30]. For example, the percentage of the relative concentration of PbLPic2 can be obtained from 100D0,Pb/(D0,Pb + D+,Pb + D2+,Pb). In addition, the concentrations of PbLPic+ and PbL2+ were evaluated from similar equations. The thus-calculated values were: 46% for PbLPic2, 10% for PbLPic+, and 44% for PbL2+ at I = 0.0074 mol·dm−3 (or [Cd]t/[Pb]t = 0); 38%, 25%, and 37% at 0.0060 (or 1.061), respectively; 35%, 32%, and 34% at 0.048 (or 26.63), respectively; 24%, 53%, and 23% at 0.15 (or 88.48), respectively; and 26%, 49%, and 25% at 0.29 (or 177.5), respectively.
One can see easily that the distribution of PbLPic2 and PbL2+ into Bz is dominant in the lower I or [Cd]t/[Pb]t values, while that of CdLPic+ is dominant in the higher I ones. That is, in the I range more than 0.15 mol·dm−3, the distribution of PbLPic+ with Pic− may be dominant, compared with those of both PbLPic20 and PbL2+ with 2Pic−. Now, the authors cannot clearly explain this result; namely, in the higher I range, why is the univalent cationic complex more extractable to the Bz phase than the other complexes are? Conversely, can they call this phenomenon “salting out effect”? However, these data can be useful for the discussion of membrane transport phenomena with L [34]. That is, what species mainly transfer through the membrane?
3. Materials and Methods
3.1. Materials
Purities of the reagents Pb(NO3)2 (Wako, 99.9%) and Cd(NO3)2·4H2O (Kanto, Guaranteed pure reagent (GR), >98.0%) were determined by an EDTA titration with Na2EDTA·2H2O (Dojin, Kumamoto in Japan, >99.5%): their purities obtained were 98.3% for Pb(II) and 96.6–98.7% for Cd(II). A basic aqueous solution (pH > 10) of picric acid, HPic·mH2O, (Wako, GR, >99.5%: added water 15–25%) was analyzed at 355 or 356 nm by using a Hitachi UV–Visible spectrophotometer (type U-2001) (Hitachi High-Technologies Corporation, Tokyo, Japan) and then its concentration was determined with the calibration curve (ε356 = 1.45 × 104 cm−1·mol−1·dm3 [35]) for Pic−. Using a calibration curve (ε273 = 2.50 × 103·cm−1 mol−1·dm3 [6]) of B18C6 at 273 nm, a concentration of an aqueous solution with its ether (Tokyo Chemical Industry, Co. Ltd., Tokyo, Japan, >98.0% and others) was determined spectrophotometrically. The diluent Bz (Wako Pure Chemical Industries, Ltd., Osaka, Japan, or Kanto Chemical Co., Ltd., Tokyo, Japan) was washed three times with pure water and then saturated with water. Other chemicals were of the GR grades. Pure water was prepared as follows: a tap water was distilled once with a stainless-steel still and then passed through the Autopure system (Yamato/Millipore, type WT 101 UV) (Tokyo, Japan).
3.2. Extraction Procedures
Aqueous solution containing 5.478 × 10−4 mol·dm−3 Pb(NO3)2, 1.272 × 10−3 HPic, x Cd(NO3)2, 0.0198 HNO3, and y B18C6 was prepared and mixed with the equal volume (10 or 12 cm3) of Bz saturated with water in a stoppered glass tube of about 30 cm3. Here, x was fixed at 0 mol·dm−3, 5.810 × 10−4, 0.01459, 0.04847, or 0.09726 and, at a fixed x, y was changed in the ranges of 6.5 × 10−6 to 1.6 × 10−4 mol·dm−3 (see circle in Figure 1), 3.9 × 10−6 to 1.9 × 10−4 (square), 1.3 × 10−5 to 4.4 × 10−4 (diamond), 3.9 × 10−6 to 2.6 × 10−4 (full circle), or 3.7 × 10−5 to 7.4 × 10−4 (triangle), respectively. The glass tubes with some kinds of the L concentrations were agitated for 2 min. by hands and then mechanically shaken for 2 h in a water bath thermostated at 25 ± 0.3 °C. After it, the mixtures were centrifuged. The Bz phases were separated at 25 °C, transferred into the other tubes, and some cubic centimeters of 0.1 mol·dm−3 HNO3 were added to them. These mixtures in the tubes were handled with the same manner as that described above. The Pb(II) amounts of the acidic water phases, into which the Pb(II) species normally-extracted into Bz was back-extracted, were determined at 283.3 nm by the atomic absorption spectrophotometer (Hitachi, type Z-6100) (Hitachi High-Technologies Corporation, Tokyo, Japan) with an air–C2H2 flame. At the same time, the amounts of Cd(II) in all the acidic phases were atomic-absorption-spectrophotometrically measured at 228.8 nm, but its element was not detected.
3.3. Extraction Model Employed for the Analysis of the System
Since significant amounts of Cd(II) in the Bz phases were not detected with the AAS measurements, the following extraction model was employed for the analysis of the present system: (1) Pb2+ + L ⇌ PbL2+ [29] (KCdL = 0.89 mol−1·dm3 [18] was omitted; (2) Pb2+ + Pic− ⇌ PbPic+ [21]; (3) Cd2+ + Pic−⇌ CdPic+ [1]; and (4) H+ + Pic− ⇌ HPic [33] in the water phase; (5) Pic− ⇌ Pic−Bz; (6) HPic ⇌ HPicBz [36]; (7) L ⇌ LBz [2]; and (8) PbL2+ ⇌ PbL2+Bz between the water and Bz phases; and (9) PbL2+Bz + Pic−Bz ⇌ PbLPic+Bz; and (10) PbLPic+Bz + Pic−Bz ⇌ PbLPic2,Bz in the Bz phase. Except for the Processes (5), (8)–(10), the equilibrium constants of the above processes at 298 K were available from References [1,2,18,21,29,36,37]. Analytic method of the extraction system based on this model was essentially the same as that reported before [1,9] (see Section 2.2).
4. Conclusions
The thermodynamic values for Kex, Kex±, KPb/PbL, Kex,ip, and KD,Pic were determined at 298 K. The same is also true of the K1,Bz0 and K2,Bz0 values at IBz → 0 for the simple Bz phases. It was demonstrated that the thermodynamic relations, Kex0 ≈ Kex,ip0KPbL/KD,L, K2,Bz0 = Kex0/Kex±0, Kex2±0 = KPb/PbL0(KD,Pic0)2, Kex2±0 = Kex±0/K1,Bz0, and Kex±0 = KPb/PbL0K1,Bz0(KD,Pic0)2, hold in the system. It seems that the linear equation is superior to the polynomial-type one for the IBz dependences of the above equilibrium constants, although the R values with the former were less than those with the latter. Consequently, these results make comparisons between the Kex, Kex±, or K1,Bz values reported in different I or Iorg conditions possible. However, there may be a fact that this study must be applied to the more practical extraction and separation systems. Moreover, it was clarified experimentally that log Kex± is proportional to dep.
At least, the separation of Pb(II) by B18C6 into the Bz phase from the mixtures at [Cd]t/[Pb]t ≈ 60 was confirmed experimentally and theoretically. This condition exceeds [PbLPic2]Bz/[CdLPic2]Bz = 2.2 × 105 at B18C6 (=L) and satisfies a measure (=104) of the separation factor. The Kex,Pb/Kex,Cd ratio at the fixed I condition can promise more precise evaluation of Pb(II) selectivity of L against Cd(II), compared with the ratio calculated at different I conditions. While, the co-presence of Cd(NO3)2 less than 180 of [Cd]t/[Pb]t has no clear effect to the experimental Pb(II) extraction with B18C6 into Bz. This Cd(II) salt in the present system acted only as the ionic strength conditioner in the water phases.
Author Contributions
Y.K. and C.N. conceived and designed the experiments; T.N. performed the experiments; Y.K. and T.N. analyzed the data; C.N. and Y.K. contributed reagents/materials/analysis tools; and Y.K. wrote the paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Kex | Extraction constant for MLA2 |
| Kex± | Extraction constant for MLA+ with A− |
| I | Ionic strength for the water phase |
| KD,A | Conditional distribution constant of A− into the org phase |
| KM/ML | Incorporative constant of M2+ with L into the org phase |
| Kex,ip | Ion-pair extraction constant for MLA2 |
| K1,org | Ion-pair formation constant for ML2+ with A− in the org phase |
| D0, D+, D | Distribution ratio for MLA2, that for MLA+, that for mixture |
| Kex+ | Extraction constant for MLA+ |
| Kexmix | Extraction-constant parameter |
| Dep, Δϕeq | Distribution equilibrium potential between the bulk water and org phases |
| KD,PicS | Standard distribution constant of Pic− into the org phase |
| ΔϕPic0′ | Standard formal potential for the Pic− transfer across the water/org interface |
| K2,org | Ion-pair formation constant for MLA+ with A− in the org phase |
| KD,PbL | Conditional distribution constant of PbL2+ into the org phase |
| Kex2± | Extraction constant for ML2+ with 2A− |
| KD,L | Distribution constant of L into the org phase |
| KPbL | Complex formation constant of Pb2+ with L in water |
| Kex0 | Thermodynamic extraction constant of Kex |
| å± | Ion-size parameter, a mean value |
| Kex,ip0 | Thermodynamic ion-pair extraction constant of Kex,ip |
| K1,Bz0 | Thermodynamic ion-pair formation constant for ML2+ with A− in the Bz phase |
| K2,Bz0 | Thermodynamic ion-pair formation constant for MLA+ with A− in the Bz phase |
| Kex±0 | Thermodynamic extraction constant of Kex± |
| KPb/PbL0 | Thermodynamic incorporative constant of Pb2+ with L into the org phase |
| Kex2±0 | Thermodynamic extraction constant of Kex2± |
| D2+,Pb | Distribution ratio for PbL2+ |
References
- Kudo, Y.; Horiuchi, N.; Katsuta, S.; Takeda, Y. Extraction of cadmium bromide and picrate by 18-crown-6 ether into various less-polar diluents: Analysis of overall extraction equilibria based on their component equilibria with formation of their ion pairs in water. J. Mol. Liquids 2013, 177, 257–266. [Google Scholar] [CrossRef]
- Takeda, Y. Extraction of alkali metal picrate with 18-crown-6, benzo-18-crown-6, and dibenzo-18-crown-6 into various organic solvents. Elucidation of fundamental equilibria governing extraction-ability and -selectivity. Bunseki Kagaku 2002, 51, 515–525. (In Japanese) [Google Scholar] [CrossRef]
- Takeda, Y.; Katō, H. The solvent extraction of bivalent metal picrates by 15-crown-5, 18-crown-6, and dibenzo-18-crown-6. Bull. Chem. Soc. Jpn. 1979, 52, 1027–1030. [Google Scholar] [CrossRef]
- Levitskaia, T.G.; Maya, L.; Van Berkel, G.J.; Moyer, B.A. Anion partitioning and ion pairing behavior of anions in the extraction of cesium salts by 4,5″-bis(tert-octylbenzo)dibenzo-24-crown-8 in 1,2-dichloroethane. Inorg. Chem. 2007, 46, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Takeda, Y.; Nishida, M. Solvent extraction of various metal picrates with benzo-18-crown-6 into CHCl3. Bull. Chem. Soc. Jpn. 1989, 62, 1468–1471. [Google Scholar] [CrossRef]
- Takeda, Y.; Kawarabayashi, A.; Takahashi, K.; Kudo, Y. Extraction of alkali metal picrates with benzo-18-crown-6 into various organic solvents. Fundamental equilibria which govern the highest extraction selectivity for K+ among alkali metal ions. Bull. Chem. Soc. Jpn. 1995, 68, 1309–1314. [Google Scholar] [CrossRef]
- Kudo, Y.; Amano, T.; Ikeda, S. Determination of distribution equilibrium-potential differences based on extraction with several crown ethers by nitrobenzene, 1,2-dichloroethane and dichloromethane. Int. J. Chem. 2017, 9, 110–123. [Google Scholar] [CrossRef]
- Kudo, Y.; Tomokata, S. Extraction of cadmium chloride by 18-crown-6 ether into various diluents: A comparative study with bromide and picrate extraction systems. J. Mol. Liquids 2018, 249, 904–911. [Google Scholar] [CrossRef]
- Kudo, Y.; Takahashi, Y.; Numako, C.; Katsuta, S. Extraction of lead picrate by 18-crown-6 ether into various diluents: Examples of sub-analysis of overall extraction equilibrium based on component equilibria. J. Mol. Liquids 2014, 194, 121–129. [Google Scholar] [CrossRef]
- Kolthoff, I.M. Ionic strength effect on extraction of potassium complexed with crown ether 18-crown-6. Preliminary communication. Can. J. Chem. 1981, 59, 1548–1551. [Google Scholar] [CrossRef]
- Kolthoff, I.M.; Chantooni, M.K., Jr. Crown ether complexed alkali metal picrate ion pairs in water saturated dichloromethane as studied by electrolytic conductance and by partitioning into water. Effect of lithium chloride on partitioning. J. Chem. Eng. Data 1997, 42, 49–53. [Google Scholar] [CrossRef]
- Kudo, Y.; Ikeda, S.; Morioka, S.; Tomokata, S. Silver(I) extraction with benzo-18-crown-6 ether from water into 1,2-dichloroethane: Analyses on ionic strength of the phases and their equilibrium potentials. Inorganics 2017, 5, 42. [Google Scholar] [CrossRef]
- Wood, D.J.; Law, J.D.; Tullock, P.A. Extraction of lead and strontium from hazardous waste streams by solvent extraction with 4, 4’,(5’)-di-(t-butyldicyclohexano)-18-crown-6. Solvent Extr. Ion Exch. 1997, 15, 65–78. [Google Scholar] [CrossRef]
- Kazemi, S.Y.; Hamidi, A.S. Competitive removal of lead(II), copper(II), and cadmium(II) ions through a bulk liquid membrane containing macrocyclic crown ethers and oleic acid as ion carriers. J. Chem. Eng. Data 2011, 56, 222–229. [Google Scholar] [CrossRef]
- Bhatluri, K.K.; Manna, M.S.; Saha, P.; Ghoshal, A.K. Supported liquid membrane-based simultaneous separation of cadmium and lead from wastewater. J. Membr. Sci. 2014, 459, 256–263. [Google Scholar] [CrossRef]
- Kudo, Y.; Nakamori, T.; Numako, C. Extraction of sodium picrate by 3m-crown-m ethers and their mono-benzo derivatives (m = 5, 6) into benzene: Estimation of their equilibrium-potential differences at the less-polar diluent/water interface by an extraction method. J. Chem. 2016, 2016, 5175746. [Google Scholar] [CrossRef]
- Panich-Pat, T.; Upatham, S.; Pokethitiyook, P.; Krautrachue, M.; Lanza, G.R. Phytoextraction of metal contaminants by Typha angustifolia: Interaction of lead and cadmium in soil-water microcosms. J. Environ. Prot. 2010, 1, 431–437. [Google Scholar] [CrossRef]
- Katsuta, S.; Tsuchiya, F.; Takeda, Y. Equilibrium studies on complexation in water and solvent extraction of zinc(II) and cadmium(II) with benzo-18-crown-6. Talanta 2000, 51, 637–644. [Google Scholar] [CrossRef]
- Kudo, Y.; Kobayashi, Y.; Katsuta, S.; Takeda, Y. Ion-pair formation of cadmium-18-crown-6 ether complex ions with picrate and chloride ions in water and distribution of its picrate ion-pair complex into benzene. J. Mol. Liquids 2009, 146, 60–65. [Google Scholar] [CrossRef]
- Dernini, S.; Scrugli, A.; Palmas, S.; Polcaro, A.M. Competitive extraction of Pb2+ by dicyclohexano-18-crown-6 from heavy metal aqueous solutions. J. Chem. Eng. Data 1996, 41, 1388–1391. [Google Scholar] [CrossRef]
- Kudo, Y.; Takahashi, Y.; Katsuta, S.; Takeda, Y. Extraction of several divalent metal picrates by 18-crown-6 ether derivatives into benzene: A refinements for analyzing extraction equilibria. Int. J. Chem. 2013, 5, 90–102. [Google Scholar] [CrossRef]
- Kudo, Y.; Katsuta, S.; Ohsawa, Y.; Nozaki, K. Solvent extraction of cadmium picrate by 18-crown-6 ether into several less-polar diluents and nitrobenzene: Re-evaluation of corresponding overall extraction systems. J. Thermodyn. Catal. 2015, 6, 146. [Google Scholar]
- Sanchez Vallejo, L.J.; Ovejero, J.M.; Fernández, R.A.; Dassie, E.A. Single ion transfer at liquid/liquid interface. J. Chem. 2012, 2012, 462197. [Google Scholar]
- Fyles, T.M. Extraction and transport of alkali metal salts by crown ethers and cryptands: Estimation of extraction constants and their relationship to transport flux. Can. J. Chem. 1987, 65, 884–891. [Google Scholar] [CrossRef]
- Abraham, M.H.; Liszi, J. Calculation of ionic solvation—V The calculation of partition coefficients of ions. J. Inorg. Nucl. Chem. 1981, 43, 143–151. [Google Scholar] [CrossRef]
- Kudo, Y.; Takeda, Y.; Matsuda, H. Ion-transfer-polarographic study of distribution equilibrium of metal complex cations with several crown ethers between nitrobenzene and water. Bunseki Kagaku 1991, 40, 779–784. (In Japanese) [Google Scholar] [CrossRef]
- Kudo, Y. An approximation method for determining key extraction constants in the equilibrium-analysis of Cd(II) extraction with 18-crown-6 ether into some diluents. J. Anal. Pharm. Res. 2017, 5, 00144. [Google Scholar] [CrossRef]
- Kudo, Y.; Miyakawa, T.; Takeda, Y.; Matsuda, H. Ion-transfer polarographic study of the distribution of alkali and alkaline-earth metal complexes with 3m-crown-m ether derivatives (m = 5, 6) between water and nitrobenzene phases. J. Incl. Phenom. Mol. Recog. Chem. 1996, 26, 331–341. [Google Scholar] [CrossRef]
- Takeda, Y.; Kohno, R.; Kudo, Y.; Fukada, N. Stabilities in water and transfer activity coefficients from water to nonaqueous solvents of benzo-18-crown-6-metal ion complexes. Bull. Chem. Soc. Jpn. 1989, 62, 999–1003. [Google Scholar] [CrossRef]
- Tamamushi, R. Denki Kagaku (Electrochemistry), 2nd ed.; Tokyo Kagaku Dojin: Tokyo, Japan, 1991; pp. 29–33. [Google Scholar]
- De Levie, R. Aqueous Acid-Base Equilibria and Titrations; Oxford Chemistry Primers; Davies, S.G., Compton, R.G., Evans, J., Gladden, L.F., Eds.; Oxford University Press: Oxford, UK, 1999; pp. 59–63. [Google Scholar]
- Kielland, J. Individual activity coefficients of ions in aqueous solutions. J. Am. Chem. Soc. 1937, 59, 1675–1678. [Google Scholar] [CrossRef]
- Kudo, Y.; Tanaka, Y.; Ichikawa, T.; Katsuta, S. Determination of some component equilibrium-constants by Cd(II) picrate extraction with benzo-18-crown-6 ether into various diluents and their evaluation. J. Anal. Bioanal. Tech. 2017, 8, 391. [Google Scholar] [CrossRef]
- Suljkanoć, M.; Nurković, E.; Suljagić, J. Influence of nonionic surfactants as competitive carriers in bulk liquid membrane transport of metal cations using macrocyclic ligands. J. Chem. Biol. Phys. Sci. Sect. A 2017, 8, 77–89. [Google Scholar]
- Takeda, Y.; Kawarabayashi, A.; Endō, K.; Yahata, T.; Kudo, Y.; Katsuta, S. Solvent extraction of alkali metal (Li–Cs) picrates with 18-crown-6 into various diluents. Elucidation of fundamental equilibria which govern the extraction-ability and -selectivity. Anal. Sci. 1998, 14, 215–223. [Google Scholar] [CrossRef]
- Kudo, Y.; Takahashi, Y.; Katsuta, S. Distribution of picric acid into various diluents. J. Chem. 2013, 2013, 869506. [Google Scholar] [CrossRef]
- Kortüm, G.; Vogel, W.; Andrussow, K. Dissociation Constants of Organic Acids in Aqueous Solution; IUPAC, Section of Analytical Chemistry Commission on Electrochemical Data: Butterworths, London, UK, 1961; p. 454. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).