Abstract
A mixture of nonlabeled (14N2H4) and 15N labeled hydrazine (15N2H4) in an aqueous solution is oxidized to 15N2, 14N2, and 14N15N molecules, indicating the intermediate existence of the 14NH2-14NH-15NH-15NH2 with subsequent hydrogen transfers and splitting of side N-N bonds. The structures, thermodynamics and electron characteristics of various N4H6 molecules in aqueous solutions are investigated using theoretical treatment at the CCSD/cc-pVTZ level of theory to explain the crucial part of the hydrazine oxidation reaction. Most N4H6 structures in aqueous solutions are decomposed during geometry optimization. Splitting the bond between central nitrogen atoms is the most frequent method, but the breakaway of the side nitrogen is energetically the most preferred one. The N-N fissions are enabled by suitable hydrogen rearrangements. Gibbs free energy data indicate the dominant abundance of NH3... N2... NH3 species. The side N atoms have very high negative charges, which should support hydrogen transfers in aqueous solutions. The only stable cyclo-(NH)4…H2 structure has a Gibbs energy that is too high and breaks the H2 molecule. The remaining initial cyclic structures are split into hydrazine and HN≡NH or H2N≡N species, and their relative abundance in aqueous solutions is vanishing.
1. Introduction
Hydrazine N2H4 is a colorless flammable liquid that is used in industry and agriculture due to its reducing properties. It is used as a corrosion inhibitor in boilers, as a rocket propellant, antioxidant, catalyst, and pesticide precursor. In boiler water, it serves as an oxygen scavenger that reacts with oxygen into nitrogen and water only, which does not cause corrosion of ferrous metals. Unreacted hydrazine can be decomposed into ammonia, which can be corrosive to copper and copper-containing alloys [1]. Thus, the knowledge of the exact mechanism of its oxidation is of practical importance so far.
Higginson and Sutton [2] studied the oxidation of 15N-enriched hydrazine by an excess of various oxidizing agents in aqueous solutions. Mass spectroscopic analysis of the evolved nitrogen for 28, 29 and 30 mass-number abundance (i.e., incidence of 14N2, 15N14N and 15N2 molecules, respectively) has shown that the proportion of 15N2 molecules decreased while that of 15N14N molecules increased depending on the oxidizing agent used. If the nitrogen produced by the reaction
involves no N-N fission, the evolved N2 molecule originates in the same N2H4 molecule, and therefore it must have the same distribution of 15N isotopes as the hydrazine reactant. This implies that some of the nitrogen molecules are formed by a mechanism involving a N-N fission and the formation of nitrogen-containing radicals from two different hydrazine molecules as follows:
2 N2H4 → N2 + 2 NH3
15NH2-15NH2 + 14NH2-14NH2 → 15NH2-15NH• + •14NH-14NH2 → 15NH2-15NH-14NH-14NH2
15NH2-15NH-14NH-14NH2 → 15NH3 + 15NH = 14N-14NH2 → 15NH3 + 15N14N + 14NH3
15NH2-15NH-14NH-14NH2 → 15NH2-15N = 14NH + 14NH3 → 15NH3 + 15N14N + 14NH3
Cahn and Powell [3] confirmed the randomized 15N14N composition obtained by one-electron oxidation of 15N enriched hydrazines with a number of oxidizing agents unlike exclusively four-electron oxidizing agents (acid iodate, alkaline ferricyanide) that produced unrandomized N2 molecules (all four hydrogen atoms must be removed from a single hydrazine molecule). Petek and Bruckenstein [4] observed that the electrooxidation of 15N labelled hydrazine (96.7% enrichment) at the Pt electrode produced N2 molecules with the ratio of 14N15N/15N15N = 0.07 ± 0.01 while in Ce(IV) solutions it was 0.9 ± 0.2. A ratio of both isotopic forms between these two limits was produced by simultaneous electrooxidation and homogeneous oxidation with electrogenerated Ce(IV).
A bright yellow substance, stable under −178 °C, is formed after thermal decomposition of hydrazine at high temperatures (~850 °F) and low pressures (~0.5 mm Hg) in a flowing system [5]. The authors suppose that it is tetrazane N4H6.
Based on polarographic and voltammetric studies of hydrazine in alkali solutions, Karp and Meites [6] suggested its two-electron oxidation to diimide with subsequent dimerization and decomposition as follows
2 N2H2 → N4H4 → NH4+ + N3−
The proposed mechanism is also capable of explaining the randomized 15N14N composition.
Ball [7] investigated the structure and some thermochemical properties of the cis- and trans-conformations of tetrazane NH2-NH-NH-NH2 using various-level ab initio methods. Unlike nearly planar trans-conformation, the cis-conformation should be denoted as a gauche structure (N-N-N-N dihedral angle of ca 90°).
The decomposition of hydrazine was studied at the CCSD(T)-F12a/aug-ccpVTZ//ωB97x-D3/6-311++G(3df,3pd) level of theory [8]. A comprehensive analysis of the N4H6 singlet potential energy surfaces was performed. Three stable isomers, NH2-NH-NH-NH2, NH2-NH-NH2=NH and NH2-NH2-N=NH2, and the transition states for H transfers between them were obtained as well. Stabilized NH2-NH-NH-NH2 formation becomes significant only at relatively high pressures and low temperatures due to its decomposition into N2H3• + N2H3•. No direct reaction between NH2-NH-NH-NH2 and NH2-NH2-N=NH2 was found. NH3 eliminations from NH2-NH-NH-NH2 and NH2-NH2-N=NH2 are energetically preferred, but only NH2-NH2-N=NH2 has relatively small activation energy for this reaction (see Table 1).

Table 1.
Reaction, ΔEr, and activation, Ea, energy data from elementary reactions on the N4H6 potential energy surface [8].
It is evident that the decomposition of N4H6 is crucial for hydrazine oxidation with subsequent 15N14N molecule formation. It depends on the suitable N4H6 site of N-N bond splitting. At first, the NH2-NH-NH-NH2 isomer is formed by the reaction
N2H3• + N2H3• → NH2-NH-NH-NH2
In the next steps, H transfers and possible N-N bond splitting may proceed. The main aim of this study is a quantum-chemical study of N4H6 isomers in aqueous solutions solely at the Coupled Cluster level of theory and to determine the sites of the possible N-N fission within them. The thermodynamic properties of the decomposition reaction products enable us to predict the possible formation of 15N14N molecules in real systems. The electronic structure of the optimized structures will also be discussed.
2. Results and Discussion
We consider possible linear isomers of N4H6 with an N1-N2-N3-N4 backbone and the composition of N1Hm-N2Hn-N3Hp-N4Hq, where subscripts m, n, p and q denote the number of H atoms bonded to individual Ni; i = 1→ 4, atoms, and m + n + p + q = 6. We started geometry optimizations from anti- and syn-conformations of N1-N2-N3-N4. The optimized structures usually correspond to gauche conformers, or some N-N bonds are split (see Table 2). If N1 and N2 correspond to 15N atoms, while N3 and N4 correspond to the 14N ones, then N1-N2 and N3-N4 fissions would lead to 15N14N molecules, unlike the N2-N3 fissions.

Table 2.
N1-N2-N3-N4 dihedral angles (Θ1234), absolute (G298) and relative (ΔG298) Gibbs free energies at 298.15 K for the optimized N4H6 structures obtained from the starting ones. The most stable structure is highlighted in bold. The different structures with the same notation are distinguished by additional letters a, b, c, or d.
In the case of cyclo-N4H6 isomers we can use the same notation, but any N-N fission can lead to 15N14N molecules because of suitable H transfers within the cycle.
We introduce the notation Xmnpq for the individual systems under study, where X = A, B and C, and D stands for anti-, syn-, cyclic and gauche-structures and the indices m, n, p and q are explained above. X = E denotes structures with N-N fissions, i.e., consisting of two or three molecules after geometry optimization. X = F stands for structures with N2-N3 fissions and subsequent N1-N4 bond formations. The N-N fissions in E and F systems are denoted by round brackets where the mutually bonded N atoms are included in the same bracket couple. The different structures with the same Xmnpq notation can be distinguished by additional letters a, b, c, etc. For example, E(22)(11)a and E(22)(11)b denote two different structures composed of H2N-NH2 and HN=NH molecules.
The N4H6 structures under study are shown in Table 2 and are divided into three groups according to the initial N1-N2-N3-N4 conformations. The H atom rearrangements during geometry optimizations are less frequent in the anti-conformations (starting A structures) than in the syn-conformations (starting B structures). In both groups the probability of N-N fissions is approximately 50%, and N2-N3 fissions prevail. On the other hand, the N1-N2 fissions lead to energetically preferred products such as E(3)(201), E(3)(102) and especially E(3)(00)(3). In the B1221 syn-conformation the mutual interaction of N1 and N4 causes the formation of the N1-N4 bond and N2-N3 fission leading to the structure of H2N2-N1H-N4H-N3H2, i.e., F12)(21, in gauche conformation or decomposition to more stable HN1=N4H and H2N2-N3H2 species denoted as the F1)(22)(1 system.
The relative Gibbs free energies in Table 2 are related to the structure D2112a obtained by the reaction (6) in the first step. According to these data, the system E(3)(00)(3), which corresponds to 15NH3, 14NH3 and 15N14N molecules, is dominant among all N4H6 structures in aqueous solutions under normal conditions and the relative abundance of the remaining systems vanishes. In general, the decomposed E systems are more stable than the remaining structures (see Table 2, Table 3 and Table 4, Figure 1 and Figure 2).

Table 3.
Interatomic distances (in Å) in the optimized Amnpq and Dmnpq structures. The different structures with the same notation are distinguished by additional letters a, b, c, or d.

Table 4.
Interatomic distances (in Å) in the optimized Emnpq and Fmnpq systems. The different structures with the same notation are distinguished by additional letters a, b, c, or d.
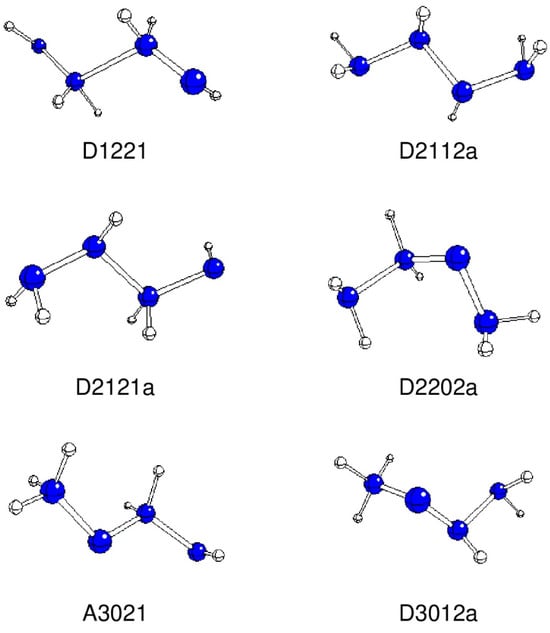
Figure 1.
Optimized geometries of stable A and D structures (N—blue, H—white).
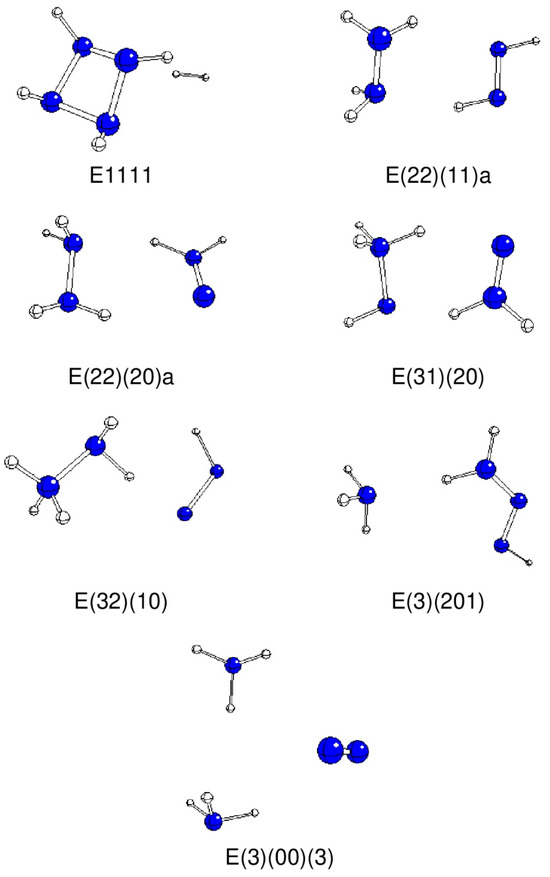
Figure 2.
Optimized geometries of stable E systems (N—blue, H—white).
During the geometry optimization of the starting cyclic C structures (Table 2), only the least stable cyclo-(NH)4 structure, denoted as E1111, preserves its tetraatomic ring after removing an H2 molecule. The remaining C structures split into hydrazine and HN=NH in E(22)(11)d or H2N=N in E(22)(02). The disadvantage of cyclic structure preservation is indicated by preferring the above-mentioned F structures after N1-N4 bonding within geometry optimization of the starting B1221 syn-conformation.
The bonding within N4H6 structures can be described by individual bond lengths d (Table 3 and Table 4) as well as by the corresponding electron density ρ (Table 5 and Table 6) and ellipticity ε (Table 7 and Table 8) at their bond-critical points (BCP) [9]. Bond strengths decrease with bond lengths d and increase with their BCP electron densities ρBCP. Their double bond character in acyclic structures increases with their BCP ellipticities εBCP.

Table 5.
BCP electron density (in e/Bohr3) of N-N and N-H bonds in the optimized Amnpq and Dmnpq structures. The different structures with the same notation are distinguished by additional letters a, b, c, or d.

Table 6.
BCP electron density (in e/Bohr3) of N-N and N-H bonds in the optimized Emnpq and Fmnpq systems. The different structures with the same notation are distinguished by additional letters a, b, c, or d.

Table 7.
BCP ellipticity of N-N and N-H bonds in the optimized Amnpq and Dmnpq structures. The different structures with the same notation are distinguished by additional letters a, b, c, or d.

Table 8.
BCP ellipticity of N-N and N-H bonds in the optimized Emnpq and Fmnpq systems. The different structures with the same notation are distinguished by additional letters a, b, c, or d.
The D1221 structure has an extremely long N2-N3 bond, and the remaining N-N bonds are shorter than the average N4H6 ones. The ρBCP(N2-N3)~0.1 e/Bohr3 corresponds to a very weak bond, and the remaining N-N bonds are approximately three times stronger. The εBCP(N2-N3)~0.1 is relatively high, and the remaining double N-N bonds have a ca. two times higher ellipticity.
The D2112a-c structures differ in N1-N2-N3-N4 dihedral angles, and their bond length alternation decreases with non-planarity of their backbone. Their ρBCP(N-N) values vary by about ~0.3 e/Bohr3, as in single N-N bonds. The εBCP(N2-N3) values decrease with non-planarity (~0.1 and less), while they are very small for the remaining N-N bonds, which correspond to single bonds.
Similarly, the D2121a-d structures differ in the N1-N2-N3-N4 dihedral angles, with the N2-N3 bond length being longer and weaker than the remaining ones’. The ρBCP(N-N) values that vary by about ~0.3 e/Bohr3 correspond to single N-N bonds. The εBCP(N2-N3) values decrease with non-planarity (~0.1 and less); εBCP(N3-N4)~0.2 is typical for double bonds.
The N-N bond properties in the A2202, D2202a-b and D2022 structures (aside from reverse numbering of N atoms) vary with the N1-N2-N3-N4 dihedral angles. The N2-N3 bonds are the shortest in all these systems. The ρBCP(N-N) values that vary by about ~0.3 e/Bohr3 are typical for single N-N bonds but the εBCP(N2-N3)~0.3 in all structures indicate the double-bond character of this bond.
In A3021 the N-N bond lengths decrease with the distance from N1, and the BCP ellipticity values indicate the same trend in decreasing double-bond character. However, the ρBCP(N-N) values of about 0.3 e/Bohr3 correspond to single N-N bonds.
Analogous trends are observed for D3012a-b structures.
In E1111 with N-N bond lengths of ca. 1.5 Å and ρBCP(N-N)~0.3 e/Bohr3 typical for single N-N bonds, the εBCP(N-N) values of 0.108 can be explained by mechanical strain in its four-membered ring rather than by its double-bond character.
The remaining E systems consist of two or three independent molecules, interacting through weak hydrogen bonds only, which can be treated independently of their parent E structures. The possible biradical character of E(32)(10) can be excluded on the basis of its atomic charges (see later) which indicate the existence of [NH3-NH2]+ and [HN≡N]− charged species.
H2N-NH2 with an N-N distance of 1.45 Å, ρBCP(N-N) = 0.295 e/Bohr3 and εBCP(N-N) = 0.008 in all E systems is typical for a single N-N bond.
HN=NH with an N-N distance of 1.245 Å, ρBCP(N-N) = 0.486 e/Bohr3 and εBCP(N-N) = 0.189 in all E systems corresponds to the double N-N bond.
Its isomer H2N=N has a N-N distance of 1.23 Å and ρBCP(N-N) = 0.497 e/Bohr3 which correspond to the double N-N bond in contradiction with εBCP(N-N) = 0.020, which corresponds to single or triple bonds.
On the other hand, NH3-NH has a N-N distance of 1.47 Å and ρBCP(N-N) = 0.27 e/Bohr3, which corresponds to the single N-N bond in contrast to the high εBCP(N-N) value of 0.156.
The [NH3-NH2]+ cation with an N-N distance of 1.446 Å, ρBCP(N-N) = 0.293 e/Bohr3 and εBCP(N-N) = 0.089 corresponds to a single N-N bond.
Its counterpart [HN≡N]− has a N-N distance of 1.242 Å and ρBCP(N-N) = 0.48 e/Bohr3 which correspond to the double N-N bond in contradiction with its too low εBCP(N-N) = 0.072.
N2 has a N-N distance of 1.096 Å, ρBCP(N-N) = 0.714 e/Bohr3 and εBCP(N-N) = 0.000, which is typical for the triple bond.
Finally, H2N-N=NH with N-N distances of 1.36 and 1.24 Å, ρBCP(N-N) values of 0.37 and 0.48 e/Bohr3 as well as εBCP(N-N) values of 0.23 and 0.13, respectively, probably correspond to nearly-double N-N bonds.
The F(11)(22) system is explained within the HN≡NH and H2N-NH2 structures above.
The F12)(21 structure H2N2-N1H-N4H-N3H2 (aside from different numbering of N atoms) corresponds to the D2112 structures explained above.
We have not discussed N-H bonding in the systems under study because the differences in their bond lengths and BCP electron densities are too small. However, their BCP electron densities are higher than those of N-N bonds except HN=NH, H2N=N, [HN≡N]− and N2. Increased εBCP(N-H) values can mostly be ascribed to the double-bond character of neighboring N-N bonds, except εBCP(N-H) = 0.3 in NH3 molecules within the E(3)(102) systems.
The nitrogen atomic charges in the A and D structures (Table 9) on the N1 and N4 atoms are more negative (−0.65 to −0.82) than on the central N2 and N3 atoms (−0.35 to −0.50). Positive hydrogen atomic charges bonded to side N1 and N4 atoms increase with the number of bonded H atoms. The same trend holds for H atoms bonded to central N2 and N3 atoms which are more positive than the side hydrogens.

Table 9.
Atomic charges of N and H (bonded to N in brackets) in the optimized Amnpq and Dmnpq structures. The asterisks denote the atoms also included in hydrogen bonds. The different structures with the same notation are distinguished by additional letters a, b, c, or d.
In the decomposed E systems (Table 10), negative N charges increase with the number of bonded H atoms. An analogous trend for positive H charges cannot be confirmed. Atomic charges are only slightly affected by hydrogen bonding. In the E(32)(10) system, the charges of its [NH3-NH2]+ and [HN≡N]− subsystems are +0.97 and −0.68, respectively (the ideal charges are +1.00 and −1.00, respectively). The errors can be ascribed to numerical integration of electron density up to 0.001 e/Bohr3 (instead of 0.000 e/Bohr3). A significantly higher error of [HN≡N]− is caused by the higher diffusive character of the electron density of anionic species. When accounting for the errors in the electron density integration over atomic basins, the alternative biradical structure of the neutral E(32)(10) subsystems (the ideal charges of both species should be 0.00) seems to be less probable.

Table 10.
Atomic charges of N and H (bonded to N in bracket) in the optimized Emnpq and Fmnpq systems. Asterisks denote atoms also included in hydrogen bonds. The different structures with the same notation are distinguished by additional letters a, b, c, or d.
3. Method
Geometry optimizations for various isomers of neutral N4H6 molecules were performed at the CCSD (Coupled Cluster using Single and Double substitutions from the Hartree-Fock determinant) [10] level of theory and cc-pVTZ basis sets [11]. The effects of the aqueous solution were taken into account within the SMD (Solvation Model based on the solute electron Density) solvation model [12]. The optimized structures were tested by vibrational analysis for the absence of imaginary vibrations. Gaussian16 (Revision B.01) software [13] was used for all quantum-chemical calculations.
The electron structures of the systems under study were evaluated in terms of Quantum Theory of Atoms-in-Molecules (QTAIM) [9] using AIM2000 (Version 1.0) software [14]. The bond strengths were compared according to the electron densities ρ at the bond-critical points (BCP). The BCP bond ellipticities εBCP were evaluated as
where λi are the eigenvalues of the Hessian of the BCP electron density within the sequence λ1 < λ2 < 0 < λ3. Atomic charges were obtained by integration over atomic basins up to 0.001 e/Bohr3.
εBCP = λ1/λ2 − 1
Visualization and geometry modification were performed using MOLDRAW (Release 2.0) software (https://www.moldraw.software.informer.com, accessed on 9 September 2019) [15].
4. Conclusions
We have shown that most N4H6 structures in aqueous solutions are decomposed during geometry optimization. Splitting the bond between central nitrogen atoms is the most frequent method, but the breakaway of the side nitrogen is energetically the most preferred one. The N-N fissions are enabled by suitable hydrogen rearrangements. The initial H2N-NH-NH-NH2 structure (D2112) has a very weak central N-N bond, which explains the high degree of reversibility for the reaction (6). The most stable system NH3…N2…NH3 (E(3)(00)(3) system) might be obtained by transfers of both H atoms bonded with central nitrogens to the side N atoms. According to [8], such double H transfer was not found by quantum-chemical calculations in vacuo, and so must be decomposed into several steps and this instantaneous decomposition should be slowed down. Furthermore, our calculations show that the transfer of the third H atom to the side nitrogen is very energetically disadvantageous, as indicated by the Gibbs energies of the structures NH3-N=NH2-NH and NH3-N=NH-NH2 (A3021 and D3012, respectively, see Table 2). In aqueous solutions, H atom transfers can be mediated by H2O, H3O+ and/or OH− species. We have shown that side N atoms have very high negative charges that should support such hydrogen transfers.
The experimentally observed formation of 15N14N molecules [1,2,3,4] is enabled by side N-N fissions. We have shown that the Gibbs free energy data (Table 2) indicate the dominant abundance of the NH3... N2... NH3 species (E(3)(00)(3) system) in aqueous solutions, which explains the mentioned observations.
The 15N14N molecules can also be created by the decomposition of cyclic N4H6 structures. We have shown the high instability of such species. The only stable cyclo-(NH)4…H2 structure (E1111) has a too-high Gibbs energy and breaks the H2 molecule instead. The remaining initial cyclic structures are split into hydrazine and HN≡NH (E(22)(11)d) or H2N≡N species (E(22)(02), see Table 2), and their relative abundance in aqueous solutions vanishes.
We can deduce from the QTAIM analysis of our systems that single, double and triple N-N bonds exhibit BCP electron densities of ca. 0.2, 0.5 and 0.7 e/Bohr3 with BCP ellipticities of ca 0, 0.2 and 0, respectively. The bonds in the N4H6 structures often exhibit significant deviations from these values.
Our study did not solve all of the problems related to hydrazine oxidation in aqueous solutions. The role of various water forms and the corresponding transition states should also be investigated. The transition states can possibly be of extremely high-energy. Thus, the thermodynamic stability of the products means less if their formation is kinetically hindered. Moreover, directly accounting for the solvent molecules is required. An alternative reaction pathway through N4H4 [6] according to reaction (5) is worth studying as well. Further theoretical studies in these fields are desirable.
Author Contributions
Methodology, software, investigation, writing—original draft preparation, writing—review and editing, M.B.; conceptualization, supervision, project administration, funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This publication was supported by the Competence Center for SMART Technologies for Electronics and Informatics Systems and Services under the project no. ITMS 26240220072.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All necessary research data are presented in the article.
Acknowledgments
M.B. thanks the HPC center at the Slovak University of Technology in Bratislava, which is a part of the Slovak Infrastructure of High Performance Computing (SIVVP Project No. 26230120002, funded by the European Region Development Funds), for computing facilities.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lauko, L.; Hudec, R.; Lenghartova, K.; Manova, A.; Cacho, F.; Beinrohr, E. Simple Electrochemical Determination of Hydrazine in Water. Pol. J. Environ. Stud. 2015, 24, 1659–1666. [Google Scholar] [CrossRef] [PubMed]
- Higginson, W.C.E.; Sutton, D. The Oxidation of Hydrazine in Aqueous Solution. Part II. The Use of 15N as a Tracer in the Oxidation of Hydrazine. J. Chem. Soc. 1953, 1402–1406. [Google Scholar] [CrossRef]
- Cahn, J.W.; Powell, R.E. Oxidation of Hydrazine in Solution. J. Am. Chem. Soc. 1954, 76, 2568–2572. [Google Scholar] [CrossRef]
- Petek, M.; Bruckenstein, S. An Isotopic Labeling Investigation of the Mechanism of the Electrooxidation of Hydrazine at Platinum. An Electrochemical Mass Spectrometric Study. Electroanal. Chem. Interrac. Electrochem. 1973, 47, 329–333. [Google Scholar] [CrossRef]
- Rice, F.O.; Sherber, F. The Hydrazino Radical and Tetrazane. J. Am. Chem. Soc. 1955, 77, 291–293. [Google Scholar] [CrossRef]
- Karp, S.; Meites, L. The Voltammetric Characteristics and Mechanism of Electrooxidation of Hydrazine. J. Am. Chem. Soc. 1962, 84, 906–912. [Google Scholar] [CrossRef]
- Ball, D.W. Tetrazane: Hartree-Fock, Gaussian-2 and -3, and Complete Basis Set Predictions of Some Thermochemical Properties of N4H6. J. Phys. Chem. A 2001, 105, 465–470. [Google Scholar] [CrossRef]
- Dana, A.G.; Moore, K.B., III; Jasper, A.W.; Green, W.H. Large Intermediates in Hydrazine Decomposition: A Theoretical Study of the N3H5 and N4H6 Potential Energy Surfaces. J. Phys. Chem. A 2019, 123, 4679–4692. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990; ISBN 9780198558651. [Google Scholar]
- Scuseria, G.E.; Janssen, C.L.; Schaefer, H.F., III. An efficient reformulation of the closed-shell coupled cluster single and double excitation (CCSD) equations. J. Chem. Phys. 1988, 89, 7382–7387. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Frisch, G.W.; Trucks, M.J.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Biegler-König, F.; Schönbohm, J.; Bayles, D. AIM2000—A Program to Analyze and Visualize Atoms in Molecules. J. Comput. Chem. 2001, 22, 545–559. [Google Scholar]
- Ugliengo, P. MOLDRAW: A Program to Display and Manipulate Molecular and Crystal Structures, University Torino, Torino. 2012. Available online: https://www.moldraw.software.informer.com (accessed on 9 September 2019).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).