Abstract
N-ary gray-level (nGL) coding strategy is an effective method for absolute phase retrieval in the fringe projection technique. However, the conventional nGL method contains many unwrapping errors at the boundaries of codewords. In addition, the number of codewords is limited in only one pattern. Consequently, this paper proposes a new gray-level coding method based on half-period coding, which can improve both these two deficiencies. Specifically, we embed every period with a 2-bit codeword, instead of a 1-bit codeword. Then, special correction and decoding methods are proposed to correct the codewords and calculate the fringe orders, respectively. The proposed method can generate n2 codewords with n gray levels in one pattern. Moreover, this method is insensitive to moderate image blurring. Various experiments demonstrate the robustness and effectiveness of the proposed strategy.
1. Introduction
Optical three-dimensional (3D) measurement technology is now a hot research topic in many fields such as industrial inspection, biomedicine, virtual reality and reverse engineering [1,2,3]. Among various optical methods, digital fringe projection (DFP) is widely used for its characteristics of high speed, high accuracy and easy set-up [4,5,6,7,8]. In a typical DFP system, a projector projects some predesigned fringe patterns onto the measured object, and a camera is used to capture the deformed patterns modulated by the object’s profile. Then, a suitable digital fringe analysis method is selected to calculate the phase map which reveals the relationship between the depth and the distribution of the object’s surface. After system calibration [9,10,11], the real 3D world coordinates of the object surface can be recovered based on the phase map.
Many digital fringe analysis methods have been developed for phase retrieval, among which Fourier transform profilometry (FTP) [12,13,14] and phase shifting profilometry (PSP) [15,16,17,18] are the most widely used. FTP is suitable for dynamic measurement because it only projects one single-shot pattern, so the speed can be as fast as the camera frame rate. However, the accuracy of FTP will drop sharply when facing complex surfaces with abrupt changes. In contrast to FTP, PSP, which requires more than one pattern (normally at least three) to reconstruct the 3D shape of the object, has high accuracy at the cost of speed. As a result, it is often applied for static and low-speed measurement. Unfortunately, due to the use of arctangent function, the phase map recovered by both FTP and PSP ranges from 0 to 2π with 2π discontinuities, known as the wrapped phase. Furthermore, phase discontinuities turn the originally continuous absolute phase into the range of [0, 2π]. After each cycle, the phase value decreases by 2π. In other words, the wrapped phase loses the information of fringe order k of every cycle. Therefore, phase unwrapping techniques are necessary to calculate the fringe order k and then recover the absolute phase.
The existing phase unwrapping algorithms can be classified into two principle categories: spatial algorithms and temporal algorithms [7]. Spatial algorithms such as reliability-guided [19] and quality-guided methods [20,21] tend to fail when dealing with large discontinuities and isolated objects. Unlike spatial algorithms, temporal algorithms project extra patterns to provide additional information on the fringe order; thus, the accuracy of temporal methods is much higher than spatial methods. Currently, popular temporal unwrapping methods include two-wavelength [22,23], multiple-wavelength [24], gray-code [25,26] and phase-coding methods [27,28,29]. Among them, the gray-code method which encodes patterns with binary intensity values has a wide range of application for its easy-to-understand principles and robustness. Yet, only two intensities being employed limit the number of codewords. Concretely, m patterns can only generate 2m codewords. In order to expand the amount of codewords, the n-ary gray-level (nGL) method [30,31,32,33,34,35,36] that uses n > 2 intensity values was developed. In the nGL method, the number can be broadened to nm with the same m patterns.
However, in real measurement, it is likely that some of the codewords at the 2π boundaries would be calculated inaccurately and would thus lead to unwrapping errors, which has become a major challenge to be solved in gray-level methods. Many methods were proposed to improve this deficiency. Chen et al. [31] modified the sequences of the nGL method’s codewords in a way that is similar to gray-code. Specifically, two neighboring codewords are arranged to differ only by one gray-level, so that the boundary unwrapping errors can be removed in principle. Zheng [26] improved this deficiency of the gray-code method when measuring step-heights, based on an adaptive median filter. Wu [34] proposed a shifting gray-code method to eliminate boundary errors in the defocused scene. Cai et al. [32] proposed a half-period correction method which can correct wrong boundary codewords in both noisy and defocused situations. In this method, two half-period masks are generated combining the wrapped phase. Then, each mask can be utilized to align and correct halves of the codewords. However, this method still requires the projection of six fringe patterns, which is too many for high-speed measurement. Inspired by Cai’s method, we propose a new gray-level coding method based on half-period coding. Specifically, Cai uses two half-period masks to divide a 1-bit codeword into two halves for alignment and correction, but the code of each half is actually the same. Yet, we consider that each half might not always have to be the same. In fact, each half-period mask can be utilized to determine its own half-code. Therefore, we embed every half-period with a code, so that each period is assigned with a 2-bit codeword, thus generating more codewords in one pattern. The proposed unwrapping method guarantees more robust unwrapping results. In addition, the proposed method requires the projection of only one additional pattern to unwrap the wrapped phase when compared to other temporal unwrapping methods, which has the potential to be applied in high-speed measurement.
2. Principles
2.1. Three-Step Phase-Shifting Method
PSP is one of the most widely used methods in fringe projection for phase recovery due to its high accuracy and fast speed. Among various PSP algorithms, the three-step phase-shifting method requires the least number of patterns, thus becoming the best choice in high-speed measurement. Three sinusoidal phase-shift patterns with 2π/3 shifts captured by camera can be mathematically described as:
where A(x,y) denotes the average intensity of the image, B(x,y) represents the fringe contrast or the so-called intensity modulation, and φ(x,y) is the wrapped phase waiting to be solved. Combining Equations (1)–(3), the three variables mentioned above can be calculated as:
A and B can be utilized to generate a mask which can remove the background, according to a suitable threshold. The mask can be calculated by:
Due to the use of arctangent function from Equation (6), the wrapped phase will be limited in the range of [0, 2π] with 2π jumps. In order to gain the absolute phase, phase unwrapping must be applied to remove these discontinuities. Once the fringe order is determined by the appropriate unwrapping method, the absolute phase can be solved by:
where Φ(x,y) is the absolute phase and k(x,y) is the fringe order calculated by the phase unwrapping method.
2.2. The Proposed Method
2.2.1. Coding Strategy
The proposed method encodes every half-period with a code, so each period has a 2-bit codeword. In general, n intensity levels are able to generate n2 different codewords. Without loss of generality, this paper selects n = 4 intensity levels, generating 16 fringe orders. The specific codewords for each period are listed in Table 1. C1 cycles in the loop of ‘1234’ four times and C2 is arranged as ‘1234234134124123’. C1 and C2 can form a unique 2-bit codeword C1C2 together to determine the fringe order. Figure 1 shows the designed codewords, where C1 and C2 are plotted in green and red, respectively. From this picture, we can see that every period is embedded with a 2-bit codeword. Let C1 and C2 be the sequences shown in Table 1. Then, the codes can be mathematically described as:
where x represents the horizontal location of the pattern and P denotes the number of pixels per period. If x lies in the first half-period, code is assigned to C1. In contrast, if x lies in the second half-period, code is assigned to C2. Consequently, the coded pattern can be described by:
where A(x,y) and B(x,y) are the average intensity and intensity modulation, respectively. Generally, both A(x,y) and B(x,y) are set to 0.5 to generate four gray levels of {0, 1/3, 2/3, 1}.

Table 1.
The designed codewords of the proposed method.
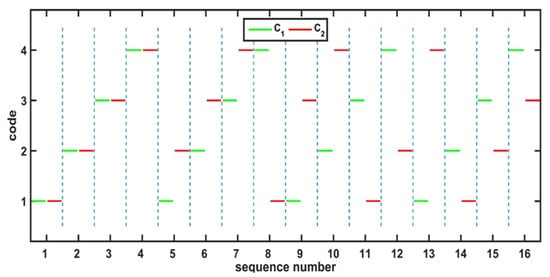
Figure 1.
The designed codewords of the proposed method.
The four fringe patterns to be projected are presented in Figure 2. Figure 2a shows the three sinusoidal patterns, which are used to obtain the wrapped phase. Figure 2b displays the pattern of the proposed method, which is employed to compute the fringe order.
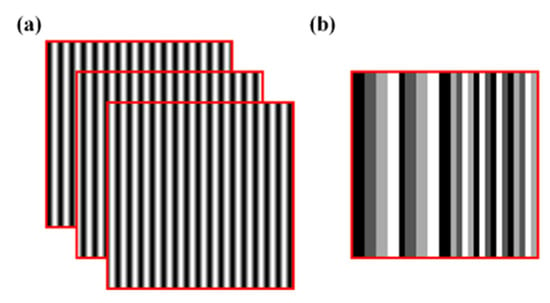
Figure 2.
Patterns used in the proposed method. (a)Three sinusoidal patterns. (b) The coded pattern.
2.2.2. Unwrapping Strategy
The procedure of the unwrapping strategy is presented in Figure 3, and the detailed steps of the method are described as follows:
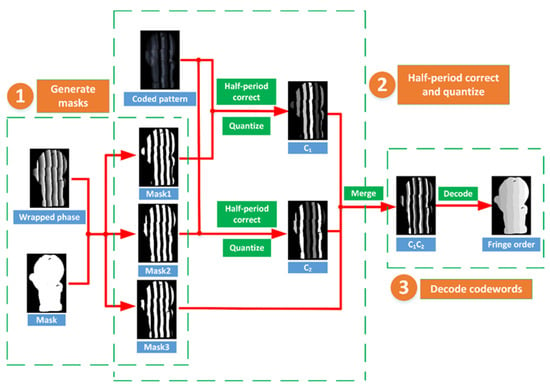
Figure 3.
The procedure of the unwrapping strategy.
Step 1: Generate masks. As Equations (6) and (7) indicate, we can obtain the wrapped phase and Mask to remove the background. Afterwards, three masks can be produced by the wrapped phase and Mask. The process is shown in Figure 3 and the three masks can be mathematically presented by:
Mask1 and Mask2 are used to correct and quantize C1 and C2, while Mask3 is used to merge them into a 2-bit codeword C1C2.
Step 2: Correct and quantize half-period. Due to sharp changes between the intensities of C1 and C2, some of the boundary pixels would be calculated inaccurately. For example, the codeword of the 13th period is assigned as ‘14’, but in practice some pixels in the boundary of C1 and C2 might be computed as ‘2’ or ‘3’. Different from Cai’s method that corrects two identical parts of a 1-bit codeword, the half-period correction method is applied to correct two different bits of a 2-bit codeword. In detail, we first multiply the captured coded pattern with Mask1 and Mask2 to align the maps of C1 and C2 with the wrapped phase at every boundary. Then, we use a bwlabel function in Matlab to segment and mark the connected regions. After that, we compute the average intensity value of every labeled region and replace each region with the average value. Thus, the wrong boundary codewords can be corrected. Briefly, this correction method makes use of characteristics of the wrapped phase to align the codewords at each boundary, and then employs an averaging operation to reduce the errors brought about by noises and reduce defocusing to the least level. As a result, it can eliminate the errors at the boundaries to a great extent.
After correcting, we quantize these regions into four gray levels {1, 2, 3, 4} according to their mean values by suitable thresholds. In this way, we obtain the corrected and quantized maps of C1 and C2. Next, we use an AND function among the two maps and Mask3. Then, we can acquire the map of 2-bit codewords C1C2. It is clear to see in Figure 3 that this map is split into many stripes and each stripe corresponds to a 2-bit codeword.
Step 3: Decode codewords. The codewords include normal codewords and defective codewords. Figure 4 gives the detailed process. The normal codewords represent those complete codewords that have both C1 and C2 in one period. For this kind of codeword, it is easy to find the corresponding fringe orders by the look-up table given in Table 1.
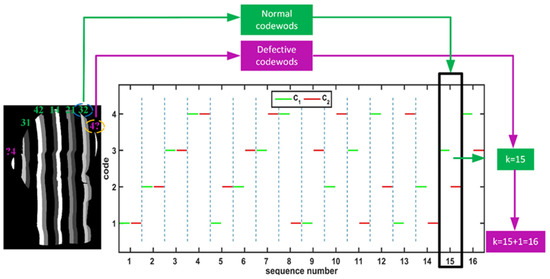
Figure 4.
The process of decoding.
The defective codewords are the incomplete codewords which lose either C1 or C2, due to the location of the objects or the inappropriate thresholds. These defective codewords cannot be determined directly but can be calculated by referring to their adjacent codewords. In other words, if we have calculated the fringe order of the previous codeword or the next codeword, the fringe order of the current defective codeword can be obtained by its previous fringe order plus one or the next fringe order minus one. Once all the codewords are decoded, the absolute phase can be recovered based on Equation (8).
3. Simulation
In this section, the hypothesis that the proposed coding method is able to correctly calculate the fringe order in defocused scenes was validated in simulations. In general, the image blurring can be obtained through a convolution operation with the point spread function (PSF) which can be approximated by a 2D Gaussian filter [37]:
where σ denotes the standard deviation and its value determines the degree of blurring. Therefore, different degrees of image blurring can be obtained by setting different values of σ. The 2D Gaussian filters can be easily generated by the use of the fspecial function in Matlab. In this simulation, the period of the coded patterns was 36 pixels. Three Gaussian filters with σ = 5, σ = 10 and σ = 15 were generated, which can be seen in Figure 5a,d,g, respectively. To test the feasibility of the proposed method, the three patterns of different degrees were utilized to solve the fringe order and the absolute phase through our method. The results are shown in Figure 5b,c, Figure 5e,f and Figure 5h,I, respectively. We can see that in the first two situations of σ = 5 and σ = 10, our method could still correctly obtain the fringe order and reconstruct the reference plane. However, in the last situation when the σ increased to 15, the image became severely blurred and our method failed. From this simulation, we can draw the conclusion that the proposed method is applicable in moderate defocused scenes. When the blurring becomes severe, the proposed method will be likely to fail.
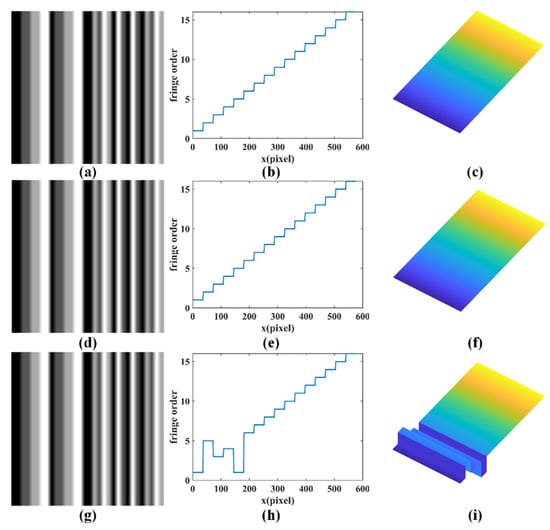
Figure 5.
Blurred reference patterns and results of simulation with different standard deviation σ. (a–c) Blurred reference pattern, one section of fringe order and reconstruction of reference plane with σ = 5, respectively. (d–f) Blurred reference pattern, one section of fringe order and reconstruction of reference plane with σ = 10, respectively. (g–i) Blurred reference pattern, one section of fringe order and reconstruction of reference plane with σ = 15, respectively.
4. Experiments
To verify the performance of the proposed method, a DFP system was set up including a digital projector (LightCrafter4500), a CMOS camera (Point Grey Chameleon3) and a computer. The resolution of the projector is 912 × 1140 pixels, whereas the resolution of the camera is 1280 × 1024 pixels. The focal length of the lens mounted on the camera is 8 mm. The projector projected the predesigned fringe patterns onto the objects, and in the meantime the camera simultaneously captured the deformed images. Afterwards, the images were sent to a computer and the 3D shape could be acquired by suitable algorithms. Figure 6 shows the experimental set-up.
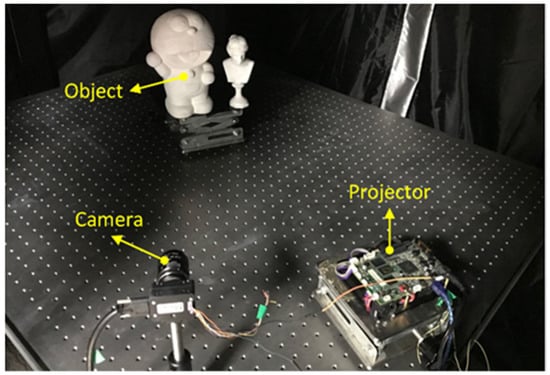
Figure 6.
The experimental set-up.
4.1. Measurement of Complex Object
The first experiments tested the performance of the proposed method to measure a sculpture of Doraemon. The result is displayed in Figure 7. Figure 7a shows the captured coded pattern. Figure 7b,c present the maps of C1 and C2, obtained by Mask1 and Mask2, respectively. C1 is labelled in red and C2 is labelled in blue. In Figure 7d, the normal codewords consisting of both C1 and C2 are labelled in green. Obviously, there are two defective codewords on the left and right edges of Doraemon, which lost their half-code. The normal codewords can easily find their corresponding fringe orders by Table 1, whereas the fringe orders of defective codewords need to be calculated by referring to their neighbors. For example, the codeword on the right edge lost its right half-code. The left adjacent codeword is ‘31’, whose corresponding fringe order is 11. Consequently, we could acquire the fringe order of the defective codeword by 11 plus1, and that is 12. The map of fringe orders and the result of 3D reconstruction are shown in Figure 7e,f, respectively. The 400th cross-section of two objects is presented in Figure 8. Although some codewords are defective, we can still obtain the right fringe order.
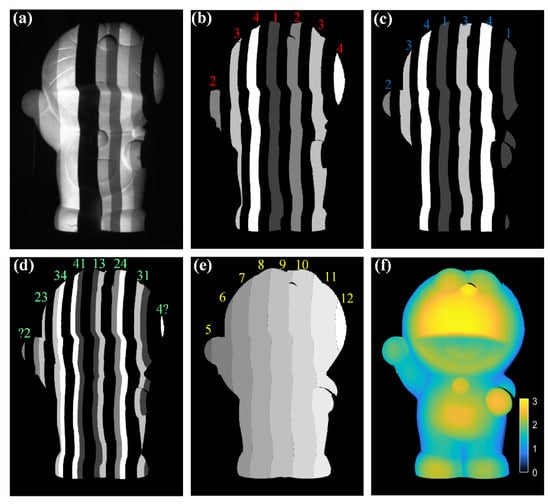
Figure 7.
Processing of the sculpture of Doraemon. (a) Captured coded pattern. (b) The map of C1. (c) The map of C2. (d) The map of 2-bit codewords C1C2. (e) The map of fringe orders. (f) The result of 3D reconstruction.
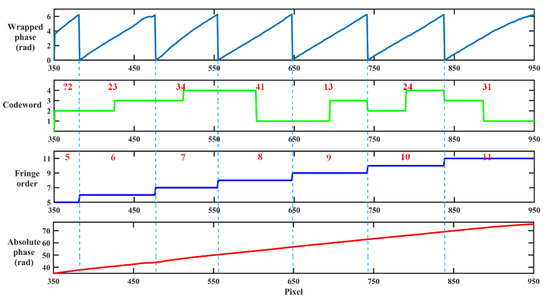
Figure 8.
The 400th cross-section of two isolated sculptures.
The comparative experiments in the proposed method and the method in Ref. [32] were also set up. The results of the two methods are presented in Figure 9a,b. It can be seen that both methods can reconstruct Doraemon well and the reconstructions have a smooth surface, confirming the good performance of the proposed method when measuring a complex object.
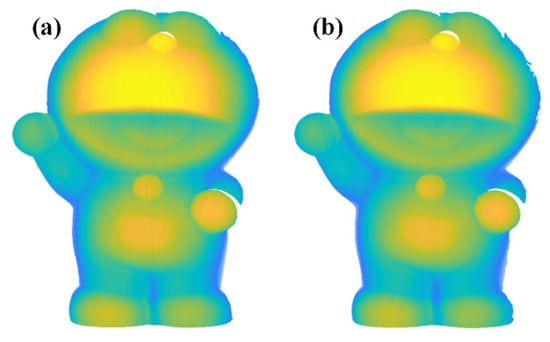
Figure 9.
Three-dimensional reconstruction of the sculpture of Doraemon. (a) The proposed method. (b) Method in Ref. [32].
4.2. Measurement of the Standard Ball
The second experiment measured a standard ball to test the accuracy of the proposed method. We compared our method with Ref. [32] and the 20-step phase-shifting method. The 20-step phase-shifting method was treated as the ground truth to analyze the accuracy quantitatively. Figure 10a,b,c display the results of the 20-step phase-shifting method, the proposed method and the method in Ref. [32], respectively. It is clear that the reconstruction of the three approaches has a smooth surface. Then, the root-mean-square errors (RMSE) were computed, listed in Table 2. The two values are very close to zero and similar, indicating good accuracy of both approaches.
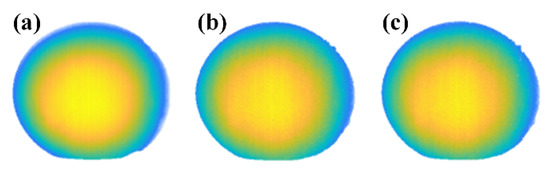
Figure 10.
Three-dimensional reconstruction of the standard ball; (a) 20-step phase-shifting method. (b) The proposed method. (c) Method in Ref. [32].

Table 2.
Root-mean-square errors (RMSE) between nGL and the proposed method.
4.3. Measurement under Defocused Scenes
The simulation in Section 3 demonstrates the validation of the proposed method to reconstruct objects under moderate defocused scenes. The last experiment manifests this point in real data. We take photos of the proposed method, the method in Ref. [32] and the conventional nGL method in clear scenes. Then, the pictures are slightly blurred using Equation (14) of σ = 10. Figure 11 shows the reconstruction results. Clearly, there are many white lines in the conventional nGL method, indicating inaccurate unwrapping values. On the other hand, methods of this paper and Ref. [32] could overcome the camera defocusing and obtain good results for reconstruction. Therefore, the proposed method is able to reconstruct objects in moderately defocused scenes.
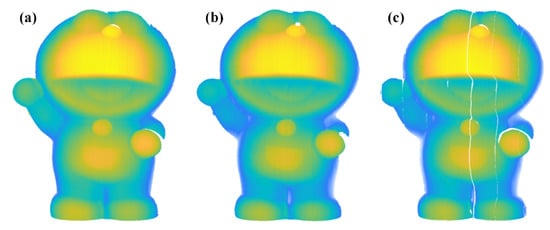
Figure 11.
Three-dimensional reconstructions under defocused scenes; (a) 3D reconstruction of the proposed method; (b) 3D reconstruction of Ref. [32]; (c) 3D reconstruction of the conventional nGL method.
5. Conclusions
This paper proposes an improved gray-level method based on half-period coding, which embeds two codes in one period; thus, each period corresponds to a 2-bit codeword. The 2-bit codewords can be corrected and quantized by three masks based on the wrapped phase. Through the proposed unwrapping algorithms, fringe orders can be calculated. Various experiments demonstrate the robustness and accuracy of the proposed method. Compared with conventional gray-level methods, the proposed method only requires projection of four patterns combined with the three-step phase-shifting method, enhancing the measurement speed. In addition, this method has the ability to reconstruct objects in the defocused scene.
Author Contributions
Conceptualization, X.C.; Data curation, B.T.; Formal analysis, L.Z.; Investigation, B.T.; Methodology, Z.R.; Project administration, X.C.; Resources, X.C.; Software, Z.R.; Supervision, B.T.; Validation, Z.R.; Visualization, L.Z.; Writing—original draft, Z.R.; Writing—review and editing, X.C. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Natural Science Foundation of China (NSFC) (51905005, 51605130), Natural Science Foundation of Anhui Province (2008085QF318), Open Fund of the Key Laboratory for Metallurgical Equipment and Control Technology of Ministry of Education in Wuhan University of Science and Technology (MECOF2021B03) and Open Fund of the Key Laboratory of Icing and Anti/De-icing (Grant No. IADL20200308).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhong, K.; Li, Z.; Zhou, X.; Li, Y.; Shi, Y.; Wang, C. Enhanced phase measurement profilometry for industrial 3D inspection automation. Int. J. Adv. Manuf. Technol. 2014, 76, 1563–1574. [Google Scholar] [CrossRef]
- Heist, S.; Zhang, C.; Reichwald, K.; Kuhmstedt, P.; Notni, G.; Tunnermann, A. 5D hyperspectral imaging: Fast and accurate measurement of surface shape and spectral characteristics using structured light. Opt. Express 2018, 26, 23366–23379. [Google Scholar] [CrossRef]
- Inanç, A.; Kösoğlu, G.; Yüksel, H.; Naci Inci, M. 3-D optical profilometry at micron scale with multi-frequency fringe projection using modified fibre optic Lloyd’s mirror technique. Opt. Lasers Eng. 2018, 105, 14–26. [Google Scholar] [CrossRef]
- Van der Jeught, S.; Dirckx, J.J.J. Real-time structured light profilometry: A review. Opt. Lasers Eng. 2016, 87, 18–31. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Zhang, S. Absolute phase retrieval methods for digital fringe projection profilometry A review. Opt. Lasers Eng. 2018, 107, 28–37. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Lasers Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Cai, B.; Wang, Y.; Wang, K.; Ma, M.; Chen, X. Camera Calibration Robust to Defocus Using Phase-Shifting Patterns. Sensors 2017, 17, 2361. [Google Scholar] [CrossRef] [Green Version]
- Lu, P.; Sun, C.; Liu, B.; Wang, P. Accurate and robust calibration method based on pattern geometric constraints for fringe projection profilometry. Appl. Opt. 2017, 56, 784–794. [Google Scholar] [CrossRef]
- Cai, B.; Wang, Y.; Wu, J.; Wang, M.; Li, F.; Ma, M.; Chen, X.; Wang, K. An effective method for camera calibration in defocus scene with circular gratings. Opt. Lasers Eng. 2019, 114, 44–49. [Google Scholar] [CrossRef]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 1983, 22, 3977. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Jing, Z.; Wang, Z.; Kuang, D. Comparison of Fourier transform, windowed Fourier transform, and wavelet transform methods for phase calculation at discontinuities in fringe projection profilometry. Opt. Lasers Eng. 2012, 50, 1152–1160. [Google Scholar] [CrossRef]
- Kemao, Q. Applications of windowed Fourier fringe analysis in optical measurement: A review. Opt. Lasers Eng. 2015, 66, 67–73. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Tao, B.; Liu, Y.; Huang, L.; Chen, G.; Chen, B. 3D reconstruction based on photoelastic fringes. Concurr. Comput. Pract. Exp. 2021, 34, e6481. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, J.; Liu, Y.; Chen, X.; Wang, Y. Motion-induced error reduction for phase-shifting profilometry with phase probability equalization. Opt. Lasers Eng. 2022, 156, 107088. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, J.; Zhang, D.; Chen, X.; Wang, Y. Nonlinear Correction for Fringe Projection Profilometry With Shifted-Phase Histogram Equalization. IEEE Trans. Instrum. Meas. 2022, 71, 5005509. [Google Scholar] [CrossRef]
- Cui, H. Reliability-guided phase-unwrapping algorithm for the measurement of discontinuous three-dimensional objects. Opt. Eng. 2011, 50, 063602. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Yau, S.T. Multilevel quality-guided phase unwrapping algorithm for real-time three-dimensional shape reconstruction. Appl. Opt. 2007, 46, 50–57. [Google Scholar] [CrossRef]
- Zhong, H.; Tang, J.; Zhang, S.; Chen, M. An Improved Quality-Guided Phase-Unwrapping Algorithm Based on Priority Queue. IEEE Geosci. Remote Sens. Lett. 2011, 8, 364–368. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Z.; Liu, Q.; Wang, Y.; Wang, Y.; Gu, Y.; Chen, X. Two-wavelength phase-shifting method with four patterns for three-dimensional shape measurement. Opt. Eng. 2020, 59, 024107. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.; Lau, D.L.; Hao, Q.; Hassebrook, L.G. Dual-frequency pattern scheme for high speed 3-D shape measurement. Opt. Express 2010, 18, 5229–5244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, L.; Dong, X.; Xi, J.; Yu, Y.; Yang, C. A new phase unwrapping algorithm based on Three Wavelength Phase Shift Profilometry method. Opt. Laser Technol. 2013, 45, 319–329. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, X.; Xiang, L.; Sun, X. 3-D shape measurement based on complementary Gray-code light. Opt. Lasers Eng. 2012, 50, 574–579. [Google Scholar] [CrossRef]
- Zheng, D.; Da, F.; Kemao, Q.; Seah, H.S. Phase-shifting profilometry combined with Gray-code patterns projection: Unwrapping error removal by an adaptive median filter. Opt. Express 2017, 25, 4700–4713. [Google Scholar]
- Wang, Y.; Zhang, S. Novel phase-coding method for absolute phase retrieval. Opt. Lett. 2012, 37, 2067–2069. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Wang, Y.; Ma, M.; Zeng, C. Quantized phase coding and connected region labeling for absolute phase retrieval. Opt. Express 2016, 24, 28613–28624. [Google Scholar] [CrossRef]
- Chen, X.; Wu, J.; Fan, R.; Liu, Q.; Xiao, Y.; Wang, Y.; Wang, Y. Two-digit phase-coding strategy for fringe projection profilometry. IEEE Trans. Instrum. Meas. 2020, 91, 242–256. [Google Scholar] [CrossRef]
- Porras-Aguilar, R.; Falaggis, K.; Ramos-Garcia, R. Optimum projection pattern generation for grey-level coded structured light illumination systems. Opt. Lasers Eng. 2017, 91, 242–256. [Google Scholar] [CrossRef]
- Chen, X.; Chen, S.; Luo, J.; Ma, M.; Wang, Y.; Wang, Y.; Chen, L. Modified Gray-Level Coding Method for Absolute Phase Retrieval. Sensors 2017, 17, 2383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, B.; Yang, Y.; Wu, J.; Wang, Y.; Wang, M.; Chen, X.; Wang, K.; Zhang, L. An improved gray-level coding method for absolute phase measurement based on half-period correction. Opt. Lasers Eng. 2020, 128, 106012. [Google Scholar] [CrossRef]
- Ma, M.; Yao, P.; Deng, J.; Deng, H.; Zhang, J.; Zhong, X. A morphology phase unwrapping method with one code grating. Rev. Sci. Instrum. 2018, 89, 073112. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Wu, J.; Chen, X.; Wang, Y. Spatial binary coding method for stripe-wise phase unwrapping. Appl. Opt. 2020, 59, 4279–4285. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, W.; Zhang, Q. High-speed three-dimensional shape measurement based on shifting Gray-code light. Opt. Express 2019, 27, 22631–22644. [Google Scholar] [CrossRef]
- Wu, Z.; Zuo, C.; Guo, W.; Tao, T.; Zhang, Q. High-speed three-dimensional shape measurement based on cyclic complementary Gray-code light. Opt. Express 2019, 27, 1283–1297. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Hou, C.; Song, Z. Defocus map estimation from a single image via spectrum contrast. Opt. Lett. 2013, 38, 1706–1708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).