The Effect of Non-Uniform Irradiation on Laser Photovoltaics: Experiments and Simulations

Abstract

Laser wireless power transmission (LWPT) has various applications for mobile devices and specific equipment under extreme conditions. The light spot received by laser photovoltaics is usually non-uniform, resulting in system efficiency reduction. The output characteristics of 1 × 1 cm² GaAs laser photovoltaics were measured under various illuminated areas. The experimental results showed that the efficiency decreased from 40.8% at the full irradiated area to 26.7% at 1/10 irradiated area. Furthermore, the drop in short-circuit current was the main factor for decreasing the efficiency. A three-dimensional (3D) finite element model was used to investigate this factor. The simulation results indicated that non-uniform irradiation could increase the total non-radiative recombination rate. The recombination rate of the absorption region increased from 6.0 × 10²⁰ cm⁻³/s to 2.5 × 10²¹ cm⁻³/s, reducing the short-circuit current.

1. Introduction

Laser wireless power transmission (LWPT) has the outstanding advantages of high transmission power density, high immunity to electromagnetic interference, and good mobile flexibility, which is suitable for continuous power supply for mobile devices such as unmanned aerial vehicles, airships, and robots [1,2,3,4]. Unlike PV devices, which transform sunlight into electricity, laser photovoltaics convert monochromatic light into electrical power. The laser beam is often non-uniformly irradiated on the laser photovoltaics, limiting the system conversion efficiency. As the basic unit of the laser receiving system, the output performance of laser photovoltaics determines the overall system efficiency. Therefore, it is of great scientific and practical value to study the effects of non-uniform illumination on laser photovoltaics output performance.

In fact, laser power transmission systems primarily use two transmission media: one that transmits optical power via optical fibers (power-over-fiber) and the other, which transmits optical power through free space or the atmosphere (wireless systems). Carlos Algora et al. provided a theoretical model for GaAs laser photovoltaics under non-uniform irradiation [5]. Their research revealed that non-uniform irradiation decreased laser photovoltaics conversion efficiency by increasing series resistance. Christopher E. Valdivia et al. changed the uniformity of the spot by modulating the full width at half maxima (FWHM) of the Gaussian beam [6]. He discovered that non-uniform irradiation degraded laser photovoltaics performance, primarily caused by fill factor reduction due to lateral current spreading. Yuki Komuro et al. also reported that non-uniform luminous flux distribution decreased photovoltaic conversion efficiency by reducing the fill factor [7]. Furthermore, increased lateral spreading resistance resulted in a decrease in fill factor. Although numerous studies were conducted on the effect of spot uniformity on laser photovoltaics, the majority of them used optical fibers to transmit a Gaussian beam to the whole surface of laser photovoltaics and then adjusted the FWHM of the laser beam. However, changing the FWHM of the Gaussian beam is mainly suitable for the application of power-over-fiber [8,9]. The laser spot received by the laser photovoltaics is not Gaussian in wireless systems, and laser spots may deviate from the laser photovoltaics center, resulting in extremely non-uniform irradiation on laser photovoltaics [10].

Wireless systems’ inherent problems, such as transmission loss through the environment, human eye safety issues, and accurate alignment between light transmitter and receiver, have led to little research. Some application scenarios are extremely important, such as power supply for sensitive electrical equipment in areas of high electromagnetic noise (nuclear plants) [9]. To simulate the above wireless systems, we tested the output characteristics of laser photovoltaics under non-uniform illumination. Luminous flux distribution on laser photovoltaics was changed by modulating the baffle position. Therefore, the purpose of this work is to analyze the fundamental reason for laser photovoltaics performance degradation caused by the non-uniform spot.

2. Experimental Method and Results

2.1. Experimental Scheme

We used homemade 808 nm single-junction GaAs laser photovoltaics (area: 1 × 1 cm²), combined with a temperature-controlled platform for the experiments, and the test platform is shown in Figure 1.

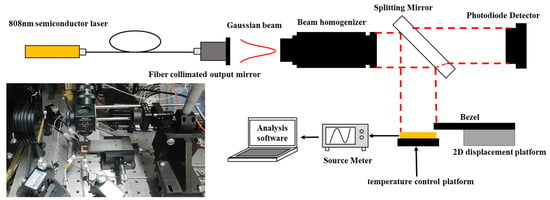
Figure 1. The test platform of laser photovoltaics.

The laser beam was generated by an 808 nm semiconductor laser, and the output power was always set to 1 W. After fiber transmission, the beam entered the fiber collimator and became the Gaussian spot. Then, the homogenizer converted the Gaussian spot into a square flat-topped spot with nearly uniform energy distribution, as shown in Figure 2. Finally, the laser beam was illuminated on the surface of the laser photovoltaics through a 45-degree reflector.

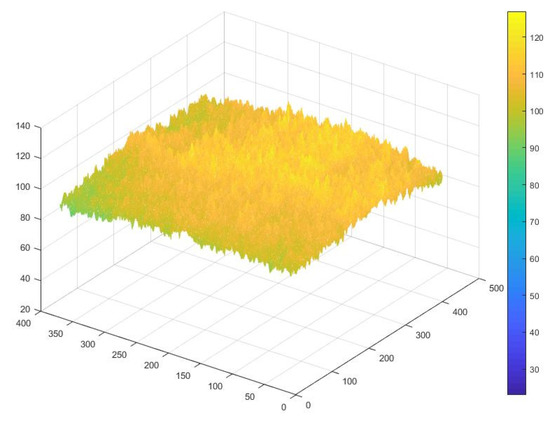
Figure 2. Light spot intensity distribution after homogenization.

As shown in Figure 3, the irradiated area of the laser photovoltaics ranged from 100% to 10% by controlling the displacement platform. The I–V curves of the laser photovoltaics under different irradiated areas were tested by the four-probe technique using a Keithley 2400 digital source meter.

Figure 3. Test laser photovoltaics under different area irradiation percentages; (a) 20% irradiation; (b) 50% irradiation; (c) 90% irradiation.

2.2. Experimental Results and Discussion

To avoid experimental variation, multiple chips on the same wafer were selected for the experiments. Figure 4 shows the I–V curves of the laser photovoltaics measured under different irradiated area percentages.

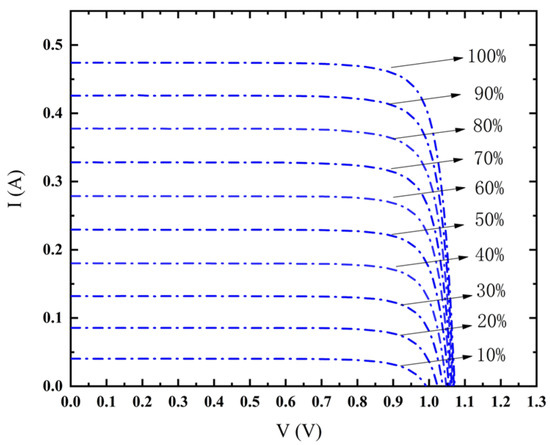
Figure 4. I–V curves under different illumination area percentages.

The parameters, such as open-circuit voltage (V_oc), short-circuit current (I_sc), fill factor(FF), and maximum output power (P_m), were extracted from the I–V curves of multiple laser photovoltaics with different irradiated areas and plotted as box and whisker chart in Figure 5. Figure 5a showed that the I_sc decreased from 0.436 A at 100% illuminated area to 0.032 A at 10% illuminated area. Moreover, I_sc varied linearly with the irradiation percentage, mainly because it is proportional to the incident light intensity. Figure 5b illustrated that the variation of P_m with illumination area corresponded to the variation of I_sc; Figure 5c showed that the V_oc increased from 0.99 V at 10% illuminated area to 1.07 V at 100% illuminated area. Besides, the V_oc increased logarithmically with the increase of irradiation percentage, mainly due to the logarithmic relationship between V_oc and I_sc, as follows:

$$V_{oc}=\frac{n\mathrm{k}T}{q}\ln \left(1+\frac{I_{ph}}{I_0}\right)$$

(1)

where, n is the ideal factor, taken between 1 and 2. k is the Boltzmann constant, T is the temperature, q is the electron charge, I_ph is the photogenerated current, and I₀ is the reverse saturation current of the equivalent diode. Figure 5d showed that the FF decreased from 84% at 100% illuminated area to 78% at 10% illuminated area. It could be explained that non-uniform irradiation caused a rise in series resistance, reducing FF [11,12].

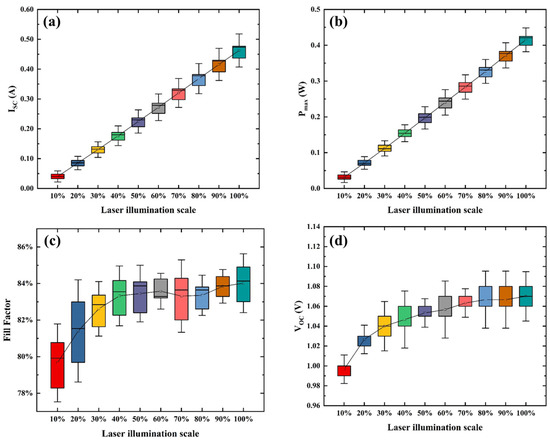
Figure 5. The relationship between the key parameters of laser photovoltaics and the proportion of area irradiation (a) I_sc; (b) P_m; (c) FF; (d) V_oc. The box defines the 25th and 75th percentiles and the median value of the set, the hollow square is the mean value, and the whiskers show the range.

The incident laser power is reduced as the irradiated area decreases, lowering the efficiency. Therefore, we performed another set of control experiments to distinguish between the FF drop caused by non-uniform illumination vs that caused by the lower intensity illumination. In this experiment, a laser photovoltaic was randomly selected. First, as shown in Figure 6a, with a “full spot irradiation”, we tested the output characteristics of laser photovoltaics when the power is changed from 100 mw to 1000 mw under full spot irradiation. Then, as shown in Figure 6a with “scaled irradiation”, we tested the output characteristics of laser photovoltaics under 1 W/cm² when the irradiation area varied from 10% to 100%. As shown in Figure 6a, FF reduction in “full spot irradiation” only includes the factor of the lower intensity illumination, whereas FF reduction in “scaled irradiation” includes two factors, non-uniform irradiation, and lower intensity illumination; the difference between the two curves at the same power is FF drop caused by non-uniformity. The larger the unilluminated region, the greater the reduction in FF. Figure 6b showed that the efficiency decreased from 40.8% at the full irradiated area to 26.7% at 1/10 irradiated area, a reduction of 14.1%, resulting from a combination of the reduced incident laser power and non-uniform irradiation. Comparing Figure 6b with Figure 5c,d, it was found that variations in conversion efficiency corresponded to variations in V_oc and FF. In other words, the main factors decreasing laser photovoltaics conversion efficiency were V_oc and FF, which is consistent with the efficiency calculation equation:

$$\eta =\frac{P_m}{P_{in}}=\frac{I_m\ast V_m}{P_{in}}=\frac{I_{sc}\ast V_{oc}}{P_{in}}\ast FF$$

(2)

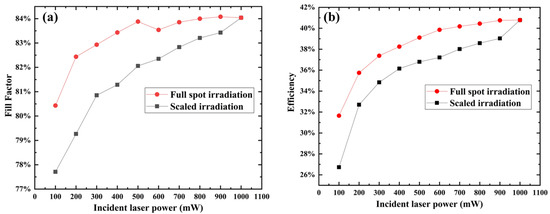
Figure 6. A comparison of the output characteristics of laser photovoltaics under different irradiation methods; (a) Fill factor; (b) Efficiency.

However, further analysis showed that the V_oc was a function of the I_sc, as shown in (1), and that the FF variation was caused by the series resistance, which affected the I_sc [13]. We calculated the variation in series resistance by means of fitting and presented the value of series resistance in Table 1. The fitting method for calculated series resistance is described in Ref. [8] in detail.

Table 1. Series resistance of laser photovoltaics under different laser illumination scales.

Laser Illumination Scale	100%	90%	80%	70%	60%	50%	40%	30%	20%	10%
series resistance (Ω)	0.32	0.44	0.46	0.49	0.69	0.74	1.02	1.54	2.23	5.17

As a result, the most important reason for decreasing efficiency was the reduction of the I_sc. To explain this experimental phenomenon, we developed a 3D model and analyzed the fundamental reason for the drop in I_sc.

3. Results Simulation Results and Discussion

3.1. Theoretical Models for Numerical Simulations

We used APSYS software to simulate the effect of non-uniform irradiation on the output performance of laser photovoltaics. The software contains typical physical models such as the heterojunction model, tunneling model, hydrodynamic model, and quantum mechanical fluctuation model, covering basic equations such as Poisson’s equation, current continuity equation, hot carrier energy transport equation, quantum mechanical fluctuation equation, and heat flow equation. The I–V characteristics of laser photovoltaics can be obtained by solving the Poisson equation and the current continuity equation under certain boundary conditions [14]. The Poisson equation is as follows [14]:

$$-\nabla \left(\frac{{\epsilon }_0{\epsilon }_{dc}}{q}\nabla V\right)=-n+p+N_D\left(1-f_D\right)-N_A{f}_A+{\displaystyle \sum _j^{}{N}_{tj}}\left({\delta }_j-f_{tj}\right)$$

(3)

In the above equation, V is the electric potential, ${\epsilon }_0$ is the vacuum permittivity, ${\epsilon }_{dc}$ is the low-frequency permittivity, q is the electron charge, n is the electron concentration, p is the hole concentration, N_D is the shallow donor density, N_A is the shallow acceptor density, f_D is the donor energy level, f_A is the occupancy probability of the acceptor energy level, N_tj is the density of the jth deep trap level, f_tj is the occupancy probability of the jth deep trap level, δ_j is 1 for donor-like traps and 0 for acceptor-like traps. The current continuity equations for electrons and holes are expressed as [14]:

$$\nabla \cdot J_n-{\displaystyle \sum _j^{}{R}_n^{tj}}-R_{sp}-R_{st}-R_{au}+G_{opt}\left(t\right)=\frac{\partial n}{\partial t}+N_D\frac{\partial f_D}{\partial t}$$

(4)

$$\nabla \cdot J_p-{\displaystyle \sum _j^{}{R}_p^{tj}}-R_{sp}-R_{st}-R_{au}+G_{opt}\left(t\right)=-\frac{\partial p}{\partial t}+N_A\frac{\partial f_A}{\partial t}$$

(5)

where $J_n$ and $J_p$ represent the current densities of electrons and holes, respectively; $R_n^{tj}$ and $R_p^{tj}$ are the electron and hole recombination rates per unit volume through the jth deep trap respectively; $G_{opt}$ is the photon generation rate; $R_{sp}$, $R_{au}$ and $R_{st}$ are the spontaneous recombination rate, the Auger recombination rate and the stimulated recombination rate per unit volume, respectively.

3.2. Simulation Details

The 3D laser photovoltaics model was developed to simulate the effect of non-uniform irradiation on the output performance of laser photovoltaics. The model used a typical laser photovoltaics structure [15,16], which is shown in Figure 7. Table 2 listed the doping and thickness of the structure. The antireflection coating (ARC) layer consisted of 60 nm SiO₂ and 90 nm TiO₂, which could minimize reflectivity under illumination with an 808 nm laser beam. The Base and Emitter layers formed the absorption region, absorbing incident photons and separating photogenerated carriers. The Window and BSF layers formed diffusion barriers with the Base and Emitter layers, which could inhibit the diffusion and reduce the recombination rate of minority carriers at the interface. The Cap layer was highly doped GaAs, which formed a good ohmic contact with the upper metal layer.

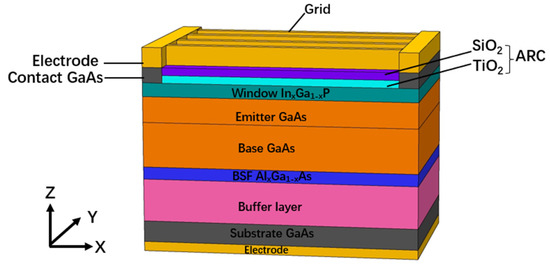
Figure 7. The simulated structure of laser photovoltaics.

Table 2. The thickness and doping of laser photovoltaics.

Layer	Material	Doping Type	Doping (cm−3)	Thickness (nm)
Buffer	GaAs	p+	5.00 × 1018	1000
BSF	AlxGa(1−x)As(x = 30%)	p+	5.00 × 1018	50
Base	GaAs	p	1.00 × 1017	3500
Emitter	GaAs	n	2.00 × 1018	500
Window	InxGa(1−x)P(x = 49%)	n+	5.00 × 1018	50
Cap	GaAs	n++	5.00 × 1019	200
ARC		90 nm TiO2 + 60 nmSiO2 (R = 0.8%)

3.3. Simulation Results and Analysis

Figure 8 compared the simulated and measured I–V characteristics. Figure 8a is 500 mW irradiated on 0.5 cm² area, Figure 8b is 500 mW irradiated on 1 cm² area. Under the same incident power, the current under 50% illumination is 207 mA, which is much lower than the current under full-spot illumination, 227 mA. However, the V_oc varies slightly. The model matched the output characteristics well.

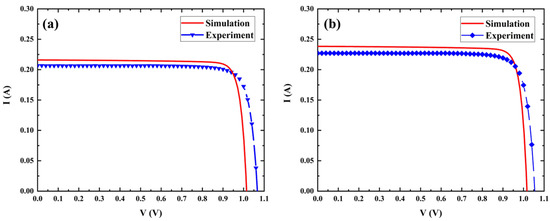
Figure 8. A simulation and experiment of I–V characteristics (a) under 50% illumination; (b) under full-spot illumination.

Figure 8 showed that the FF of the simulation result was slightly higher than that of the experimental result. This is because the model used simplified boundary conditions to represent the electrical characteristics of contact. It excluded metal light absorption and resistance. For photovoltaic devices, the metal-semiconductor contact generates series resistance, lowering the FF. The optical thickness of the ARC layer may deviate from the theoretical value, which reduces the photogenerated current. Therefore, the simulation result of I_sc was slightly higher than the experimental result.

The experimental results showed that the primary factor of significant conversion efficiency decrease was the reduction in I_sc. Therefore, we analyzed the I_sc variation with non-uniform illumination by studying the longitudinal carrier generation and recombination on the cross-section parallel to the direction of the incident light. The cross-section was shown with the red dashed line in Figure 9.

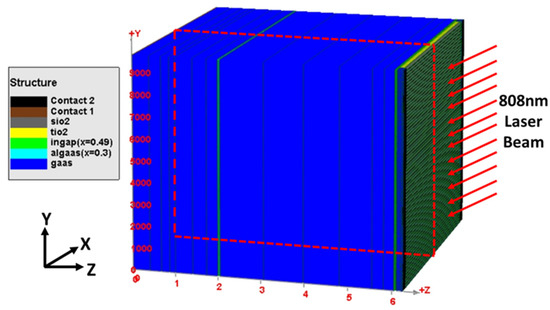
Figure 9. The cross-section of the laser photovoltaic in the YZ direction.

Figure 10 shows the carrier recombination rate and the distribution of photogenerated carriers on the cross-section under two different irradiation conditions; one is 500 mW irradiated on 0.5 cm² area, and the other is 500 mW irradiated on 1 cm² area. Comparing Figure 10a,c, it was found that the unilluminated area hardly generated photogenerated carriers. In addition, photogenerated carriers were generated faster under 50% area illumination than under 100% area illumination. Comparing Figure 10b,d, the overall carrier recombination rate was higher under 50% area illumination, around 2.5 × 10²¹ cm−³/s. This is because more carriers were generated in a smaller area, and the carrier recombination rate increased as the number of carriers increased. More carriers failed to be transported through the electrodes to the external circuit; therefore, the I_sc of the laser photovoltaics was as low as 207 mA in Figure 8a, with a conversion efficiency of 36.8% in Figure 6b. On the other side, the carrier recombination rate was relatively low under 100% area illumination, being around 6.0 × 10²⁰ cm−³/s. The I_sc of laser photovoltaics was relatively high, reaching 227 mA in Figure 8b, with a conversion efficiency of 39.1% in Figure 6b. When the laser photovoltaics was illuminated non-uniformly, the unilluminated area could be equated to a dark diode in the equivalent circuit model [17,18]. Additionally, the unilluminated region had no photogenerated carriers and consumed photogenerated current, reducing I_sc. Therefore, the conversion efficiency of laser photovoltaics decreased. We also predicted that the performance of the laser photovoltaics would be further degraded by non-uniform irradiation when the incident power was further increased.

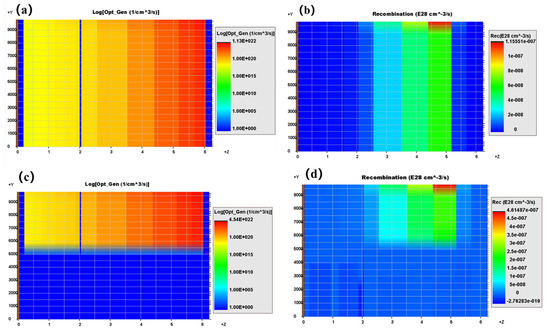
Figure 10. (a) The photogenerated carrier rate under 100% area illumination; (b) Carrier recombination rate distribution under 100% area illumination; (c) Photogenerated carrier rate under 50% area illumination; (d) Carrier recombination rate under 50% area illumination.

4. Conclusions

An experiment was carried out for the LWPT application situation in which the laser photovoltaics was non-uniformly irradiated. Experimental results demonstrated that incident laser beam uniformity had a considerable influence on the conversion efficiency of laser photovoltaics, with an efficiency variation of up to 14.1%. The 3D model was developed to simulate the effect of non-uniform irradiation on the output performance of laser photovoltaics. Based on the experimental and simulation results, we concluded that the decrease in I_sc was the main factor for the decrease in efficiency under non-uniform illumination. Furthermore, non-uniform illumination increased the overall carrier recombination rate. When the laser photovoltaics was illuminated non-uniformly, the dark area could be equated to a dark diode in the equivalent circuit model, which had no photogenerated carriers and consumed photogenerated current.