Dynamics of Fractional Vortex Beams at Fraunhofer Diffraction Zone

Abstract

Fractional vortex beams (FVBs) possess unique topological properties that are manifested in the vortex distribution. However, there are still discrepancies in the value of the vortex strength of FVBs at the far field. In this work we present a complete picture of the behavior of the phase singularities of non-integer (commonly known as fractional) beams in the Fraunhofer diffraction region and demonstrate a very good correspondence between experiments and simulations. As shown in the text, the original beam waist ${\omega }_0$ was found to be a key factor relating to the beam profile topology. This variable was measured in the process of calibrating the experiment. Finally, an experimental method to obtain the non-integer topological charge is proposed. This method only requires an analysis of the intensity, knowledge of the transition behaviors, and the beam waist.

1. Introduction

Singular beams with circularly symmetric transverse profiles—along the axis of propagation—are characterized by an angular phase dependence of the form $exp\left(i\alpha \theta \right)$, where $\alpha$ is the integer topological charge. Light fields with non-integer $\alpha$ values are known as fractional vortex beams (FVBs) and have interesting applications and properties due to the behavior of their phase singularities. Research on FVBs includes particle trapping [1], perfect FVBs [2], topologically structured darkness [3], and even a representation of Hilbert’s hotel paradox [4].

Despite these recent advances, there are some inconsistencies in the studies on FVBs due to their complex propagation properties. Basistiy et al. [5] presented an analytical approach to the fractional topological charge problem, but only for the particular case of $\alpha =1/2$. Berry has developed an analytical model for integer and non-integer topological charges for vortex beams propagating in free space [6] and the results of his work have been confirmed experimentally [7,8]. According to these studies, FVBs do not maintain their strength during propagation and remain fractional only in the near field. That is, depending on the initial topological charge they evolve from fractional to the nearest integer, since the non-integer part generates systemically opposite unitary charge vortexes that cancel each other out [6]. Therefore, it can be said that the vortex strength evolves from fractional to a “topological charge (TC) staircase”.

The current works have focused their attention on the value of the total vortex strength of FVBs at the Fraunhofer diffraction zone. However, at this point different authors have proposed divergent interpretations. According to Jesus-Silva et al. [9], the vortex strength increases by one only at a number slightly larger than an integer. However, more recently, it has been found theoretically and experimentally that the total strength of FVBs at the far field exhibits two unitary jumps only when a non-integer $\alpha$ is in the close vicinity of any even-integer number [10]. The total strength of the FBVs depends not only on the initial charge $\alpha$, but also on the incident light source; therefore, considering a Gaussian beam instead of an ideal plane wave produces a different output. This is of the utmost importance because in many practical applications a Gaussian beam is incident upon a spatial light modulator (SLM) to generate an optical vortex.

Some aspects of this vortex transition have produced different opinions and views among authors. For example, Wen et al. discovered that the “staircase” of vortex strength vs. initial topological charge $\alpha$ is always an odd integer in the far field. Their results pose a discrepancy with previous works such as [4,6,9] that obtain the “TC staircase” but with different values. Recently, this debate led to a further study by Kotlyar et al. [11,12], who developed an analytical model for vortex propagation, and they also supported their discoveries with numerical simulations and experiments.

Even though many scholars agree on the staircase scenario, its values for practical non-integer beams are highly dependent on the experimental conditions. For that reason, in this work we intended to study the behavior of non-integer vortex transition experimentally for different transitions and beam waists. To this end, a practical application is proposed to determine vortex strength experimentally given certain parameters.

A complete list of all the work carried out on fractional and non-integer vortex beams can be found in a recent review conducted by Zhang et al. [13].

2. Theoretical Insights and Numerical Results

To analyze fractional vortex beams in the Fraunhofer diffraction zone of practical optical fields (optical beams with finite width), it is necessary to consider a monochromatic Gaussian beam as a normally incident light source on an SLM with transmission function $exp\left(i\alpha \theta \right)$ in the initial transverse plane $\mathbf{r}=(r,\theta )$. Then the initial field is expressed as $U_{\alpha }(r,\theta )=exp(-r^2/{\omega }_0^2)exp\left(i\alpha \theta \right)$, where ${\omega }_0$ is the beam waist radius and $\alpha$ is the topological charge. Under the paraxial regime, the field in the Fraunhofer diffraction zone—aside from multiplicative phase factors—is the two-dimensional Fourier transform of the initial field, evaluated at the frequency $\rho /\lambda z$, i.e., $U_{\alpha }(\rho ,\varphi )\propto \mathcal{F}\left[U_{\alpha }(r,\theta )\right]$ [9]. A non-integer $\alpha$ in the initial field produces a step discontinuity in addition to the central singularity [6]. The propagated field is then calculated with a non-integer $\alpha$, by means of an expansion of the fractional transmission function in Fourier series. The result is the equation [6]

$$U_{\alpha }(r,\theta )=\frac{e^{i\pi \alpha }sin\left(\pi \alpha \right)}{\pi }\sum _{n=-\infty }^{\infty }\frac{U_n(r,\theta )}{\alpha -n},$$

(1)

where $U_n(r,\theta )$ is the initial complex field associated with a beam with an integer topological charge. The two-dimensional Fourier transform of Equation (1), together with multiplicative phase factors, produces the far-field expression [11]

$$\begin{array}{c}{U}_{\alpha }(\rho ,\varphi )=\frac{e^{i\pi \alpha }sin\left(\pi \alpha \right)}{\sqrt{\pi }}\frac{\rho k^2{\omega }_0^3}{8z^2}exp\left(ikz\right)exp\left(i\frac{k{\rho }^2}{2z}\right)exp(-\gamma )\hfill \\ \hfill \times \sum _{n=-\infty }^{\infty }\frac{{(-i)}^{\left|n\right|+1}}{\alpha -n}exp\left(in\varphi \right)\left[I_{\frac{\left|n\right|-1}{2}}\left(\gamma \right)-I_{\frac{\left|n\right|+1}{2}}\left(\gamma \right)\right],\end{array}$$

(2)

where $I_m(·)$ is the modified Bessel function of the first kind of order m and $\gamma ={[k{\omega }_0\rho \sqrt{2}/4z]}^2$. A strictly fractional $\alpha$ breaks the circular symmetry in the far field but, in return, an axial symmetry appears, where all the vortex dynamics is observed. Figure 1 presents numerical results for the particular case $\alpha =2.15$ and $\alpha =3.63$. The initial phase with a fractional step is shown in Figure 1a.1,b.1. Assuming a collimated Gaussian beam as an incident light source, the far-field phase and intensity are shown in Figure 1a.2,b.2 and Figure 1a.3,b.3, respectively. The far-field phase exhibits three unit vortices (five for case $\alpha =3.63$), which implies three local minima in the amplitude. To better visualize this distribution of unit vortices, Figure 1a.4,b.4 shows the intensity in logarithmic scale. The distribution of the unit vortex depends on $\alpha$, ${\omega }_0$ and the orientation of the symmetry axis (for simplicity, this is chosen to be vertical). At this point, it is interesting to analyze the distribution of unit vortices during a phase transition between two integer values of $\alpha$. A complete phase transition is considered to be the process that occurs when $\alpha$ goes from an integer value n to the next one, $n+1$, with fractional (non integer) values in between them. These phase transitions involve an interesting $\pm 1$ charge vortex dynamics, in which it is possible to distinguish two types of unit vortices. The first one—from hereon called the resident vortex—has a charge of an equal sign to that of the nucleus charge. This resident vortex enters (or leaves from) the center from (towards) infinity. The second one—henceforth called the tourist vortex—has a charge of the opposite sign to that of the nucleus. This tourist vortex comes from infinity, reaches a minimum distance from the center, and returns. This is well documented in [10]. Therefore, the distance of the unit vortices to the optical axis in the far field is a parameter of great interest which has not been studied yet and can be related to the fractional topological charge $\alpha$. The dimensionless value $\mathrm{d}/{\mathrm{d}}_0$ is defined as the normalized distance of the unit vortices from the center to their positions, where ${\mathrm{d}}_0$ is the radius of the beam or the real beam extension. Those distances are calculated by tracking the dark spots present in the intensity distributions. The center is obtained from the regular integer vortices position at the beginning (or end) of the transition, whereas the beam extension is determined by the experimental conditions (i.e., the camera aperture). A visual example can be seen in Figure 1a.4,b.4. Figure 1c shows the distance $\mathrm{d}/{\mathrm{d}}_0$ as a function of the fractional topological charge $\alpha$, for a fixed ${\omega }_0$ and $\lambda$. All transitions have resident-type vortices, as can be seen in Figure 1c.1. The tourist vortices only appear in intermediate transitions, as shown in Figure 1c.2. This behavior is related to the parity of the integer topological charges at the borders of a transition [10].

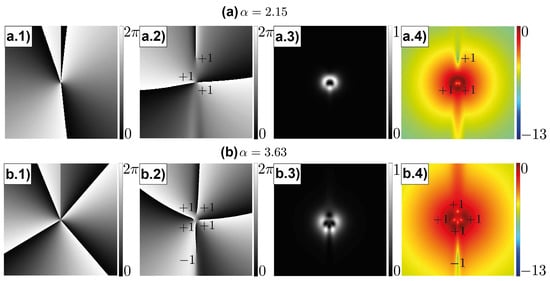
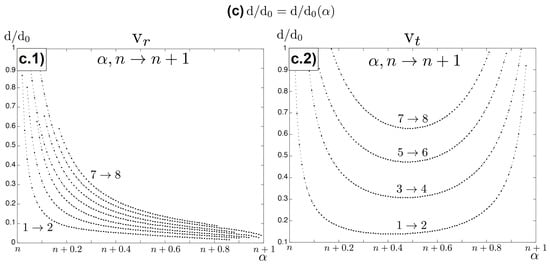
Figure 1. Numerical simulations. (a) Fractional vortex beam with $\alpha =2.15$: (a.1) initial phase profile, (a.2) far-field phase profile, (a.3) far-field intensity profile, and (a.4) far-field intensity profile in logarithmic scale. (b) Fractional vortex beam with $\alpha =3.63$: (b.1) initial phase profile, (b.2) far-field phase profile, (b.3) far-field intensity profile, and (b.4) far-field intensity profile in logarithmic scale. (c) Normalized distance measured from the position of the unit vortices to the center. (c.1) Distance for the resident vortices ${\mathrm{v}}_r$ in transitions from $1\to 2$ to $7\to 8$. (c.2) Distance for the tourist vortices ${\mathrm{v}}_t$, present only in transitions starting with odd n, from $1\to 2$ to $7\to 8$.

3. Experimental Results and Discussion

By means of the experimental setup shown in Figure 2a, the intensity patterns can be obtained, and based on these, one can obtain the unit vortex distances. Utilizing a 2f lens focusing system, it is possible to measure far-field intensity distributions of FVBs, since the complex amplitude distribution in the focal plane of a lens corresponds to the Fraunhofer diffraction pattern. A collimated Gaussian beam (HeNe, $\lambda =633$ nm), with reduced power by means of a neutral filter (NF), passes through a beam splitter (BS) and reaches a reflective SLM (Holoeye Pluto II, with $1920\times 1080$-pixel resolution). The SLM is programmed with one of the phase profiles (Figure 1a.1 to produce practical FVBs, and the blazing order is filtered by means of a variable diameter aperture (AP). After the field is reflected by a beam splitter (BS), the intensity distributions of the FVBs are detected using a CMOS camera (EO-5012M, pixel size 2.2 µm × 2.2 µm) positioned at the focal plane of a convex lens (f = 400 mm). Samples of the experimental intensity profiles (logarithmic scale) for transitions [$\alpha ,1\to 2$] and [$\alpha ,2\to 3$] are shown in Figure 2b,c. Figure 2b.1,b.2 shows the far-field intensity profile corresponding to $\alpha =1.38$ and $\alpha =1.82$ respectively. In the same way, Figure 2c.1,c.2 shows the far-field intensity profile corresponding to $\alpha =2.34$ and $\alpha =2.88$, respectively. These results are in agreement with those presented in [10].

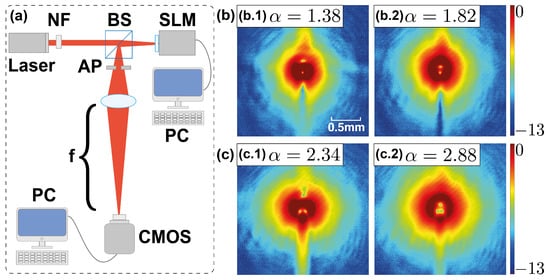
Figure 2. (a) Experimental setup: a collimated beam (HeNe, $\lambda =632.8$ nm) hits the SLM programmed with one of the phase profiles. The focused field is imaged by means of the CMOS camera through a 2f system (f $=400$ mm). Notation: NF, neutral filter; BS, beam splitter; AP, aperture. (b,c) Sample intensity profiles (logarithmic scale) for transition [$\alpha ,1\to 2$], (b.1) $\alpha =1.38$, and (b.2) $\alpha =1.82$. Transition [$\alpha ,2\to 3$], (c.1) $\alpha =2.34$, and (c.2) $\alpha =2.88$.

From the intensity profiles obtained experimentally, it is possible to calculate the distances of the unit vortices in the focal plane as $\alpha$ changes in the initial input field. This analysis is started by measuring the distances in the intermediate steps of each transition, i.e., for the transition [$\alpha$,$3\to 4$], $\alpha =3.5$; for [$\alpha$,$4\to 5$], $\alpha =4.5$, and so on. The experimental results are shown in Figure 3a, marked with green triangles. The distances are measured by means of an algorithm—using MATLAB software—that calculates the position of the local minima in the intensity profiles (logarithmic scale) and subsequently the distance with respect to the central position in which all the vortices are located together for the integer $\alpha$. The top right of Figure 3a shows the experimental intensity profile at the focal plane for $\alpha =1.50$ as a sample. Carrying out numerical simulations with the parameters of the experiment, it is possible to estimate the range of values between which the experimental beam waist is located. Following Figure 3a, it is possible to calculate the distances for beam waists ${\omega }_0=0.3$ (red squares), $0.6$ (blue circles), and $0.9$ mm (black asterisks). Considering what was obtained in the simulations and the experimental measurements (green triangles), the beam waist value should be located between $0.6$ and $0.9$ mm. Figure 3b shows the experimental beam profile at the SLM position. By measuring the full width at half maximum (FWHM) and using the relation ${\omega }_0=\mathrm{FWHM}/2\sqrt{ln\left(2\right)}$, an experimental beam waist of $0.77\pm 0.01$ mm can be obtained, which is in agreement with the theoretical value using the data provided by the manufacturer. Using ${\omega }_0=0.77$ mm, and setting intermediate $\alpha$ values of $0.5$, the simulations provide the distances for each half-integer transition. Figure 4a shows a comparison between the numerical (red squares) and the experimental (green triangles) results. The difference $\Delta$ between the distances calculated in the simulations and those calculated based on the experimental data is represented by the blue bars. The numerical simulations are in good agreement with the experimental results, as can be observed in the low error obtained for the first ten phase transitions. As an example, Figure 4b,c shows the intensity and logarithmic scale profiles for $\alpha =3.50$, respectively (${\omega }_0=0.77$ mm). Figure 4b.1 presents the intensity profile at the focal plane and Figure 4b.2 presents its respective experimental profile. In the same way, Figure 4c.1 presents the intensity profile (logarithmic scale) at the focal plane and Figure 4c.2 presents its respective experimental profile.

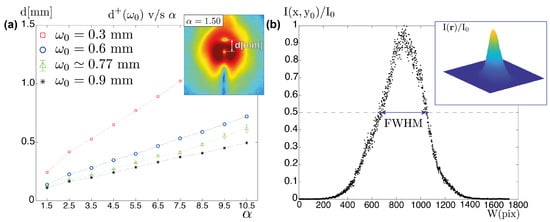
Figure 3. Distances of resident vortices ${\mathrm{v}}_r$ with fractional steps of $0.5$. (a) Numerical simulations for different waists ${\omega }_0$: $0.3$ (red square), $0.6$ (blue circle), and $0.9$ mm (black asterisk). Experimental results (green triangle) for the measured waist ${\omega }_0=0.77$ mm. Top right: focal plane intensity profile sample (logarithmic scale) for $\alpha =1.50$. (b) Experimental Gaussian beam profile (HeNe, THORLABS HNL100L, $\lambda =632.8$ nm).

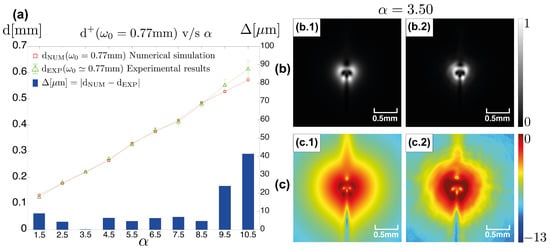
Figure 4. (a) Distances of resident vortices with fractional steps of $0.5$; numerical simulation (red square), and experimental measurements (green triangle) comparison. (b) Normalized focal-plane intensity profiles for $\alpha =3.50$, ${\omega }_0=0.77$ mm, $\lambda =632.8$ nm. (b.1) Numerical simulation and (b.2) experimental results. (c) Normalized focal plane intensity profiles (logarithmic scale) for $\alpha =3.50$, ${\omega }_0=0.77$ mm, $\lambda =632.8$ nm. (c.1) Numerical simulation and (c.2) experimental results.

After obtaining the beam waist, the intensity profiles at the focal plane are recorded experimentally by means of the CCD camera. Then, every distance from the center of the beam to the $\mathit{resident}$ vortex can be obtained by varying $\alpha$ in steps of 0.02. Figure 5a presents a comparison between the numerical simulation results and the experimental results considering the transitions $[\alpha ,2\to 3]$ and $[\alpha ,4\to 5]$ as examples. The distances ${\mathrm{d}}_{\mathrm{SIM}}$, calculated based on the numerical simulations, are represented by red circles for $[\alpha ,2\to 3]$ and green squares for $[\alpha ,4\to 5]$. The experimental results are represented by black triangles for $[\alpha ,2\to 3]$ and blue asterisks for $[\alpha ,4\to 5]$. This comparison shows a very good agreement between the numerical simulations and the experimental values. Figure 5b shows the experimental distances of the $\mathit{resident}$ vortices for phase transitions $1\to 2$, $2\to 3$, $3\to 4$, $4\to 5$, and $5\to 6$ with $\alpha$ steps of $0.02$. Because the size of a vortex beam increases with topological charge (consider that the experiment has a fixed field of view—about 2 mm × 2 mm—therefore ${\omega }_0$ is constant), the first experimental distance obtained for every transition occurs at higher fractional values. Then, as the transition increases, the initial measurement moves away from the origin. This can be seen in Figure 5, where, for example, the first measurement of the $\mathit{resident}$ vortex for transition $[\alpha ,2\to 3]$ occurs at $\alpha =2.10$ and at $\alpha =4.20$ for transition $[\alpha ,4\to 5]$. Furthermore, the transition $5\to 6$ starts with $\alpha \simeq 5.35$, resulting in a reduction of the values of $\alpha$ available for greater transitions. Nevertheless, this inconvenient can be overcome by changing the value of ${\omega }_0$ and keeping the beam extension intact. To clarify, observing Figure 3a, it can be inferred that the set of transition curves (e.g., Figure 1c.1) are transported farther from or nearer to the origin according to the beam waist. Then, to obtain a higher resolution at the origin (transitions with $\alpha >X.5$) it is better to have a low value of ${\omega }_0$. On the contrary, to obtain a greater measurement range, the curve has to start at lower values $\alpha <X.5$, which can be achieved by having a high value of ${\omega }_0$, which diminishes the resolution at the center. This compromise has to be performed in order to have a good range of non-integer values of $\alpha$.

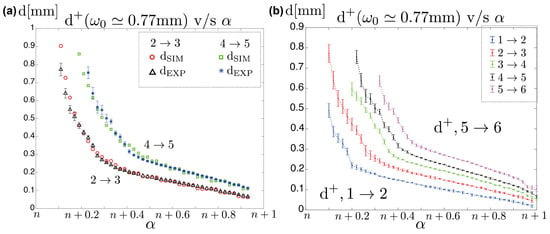
Figure 5. (a) Distances of resident vortices ${\mathrm{v}}_r$ (${\omega }_0=0.77$ mm, $\lambda =632.8$ nm), for phase transitions $2\to 3$ and $4\to 5$. Numerical simulations (red circles for $2\to 3$ and green square for $4\to 5$) and experimental results (black triangles for $2\to 3$ and blue asterisks for $4\to 5$) comparison. (b) Experimental results: distances of resident vortices for transitions $1\to 2$, $2\to 3$, $3\to 4$, $4\to 5$, and $5\to 6$ with $\alpha$ steps of $0.02$.

The curves presented in Figure 5b show that is possible to relate—with some degree of certainty—the distance of the $\mathit{resident}$ vortex with the magnitude of the original topological charge $\alpha$. In this case, original refers to the topological charge initially set up for any particular vortex. For example, $\mathrm{d}(\alpha =2.24)=0.4$ mm, whereas $\mathrm{d}(\alpha =2.26)=0.35$ mm. Using these curves, it is possible to estimate the non-integer value of $\alpha$ when knowing only two parameters, d and ${\omega }_0$. Figure 6 shows four experimental examples of two different transitions, $\alpha ,2\to 3$ and $\alpha ,4\to 5$. The estimation of d, considering the known value of ${\omega }_0$, is then interpolated in the corresponding curves of Figure 5. The result is the value of $\alpha$ with an error of approximately less than $1\%$ (see Table 1). Regarding the error, as can be seen in Figure 5, the zone composed of values $\alpha <X.5$ has greater error for d. On the other hand, the zone $\alpha >X.5$ has a small error. This is reflected in the values obtained for these examples (see Table 1). It is to be noted that, as shown in Figure 6a.1,b.1, the resident vortex is diffuse at values of $\alpha <X.5$. This is the reason for the greater error in the estimation of d. Even though the relative error for the estimation of d can be high as $7\%$ the estimation of $\alpha$ can still have a small error. In conclusion, it is possible to estimate $\alpha$ merely by extracting the value of d from the intensity profile of the vortex under known beam waist conditions. The TC estimation proposed here does not have a superhigh resolution, compared to the work of Liu et al. [14], but it is possible to detect TC at a fractional level without the need for a trained neural network. Even though the method proposed here is not direct it has potential due to its simplicity.

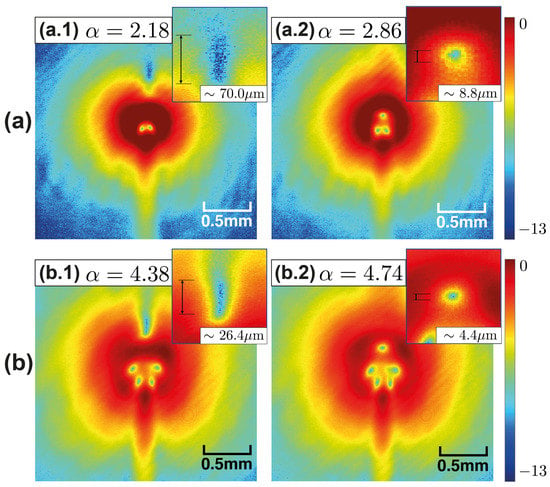
Figure 6. Experimental results: far-field intensity profiles (logarithmic scale). (a) Phase transition $\alpha ,2\to 3$. (a.1) $\alpha =2.18$. (a.2) $\alpha =2.86$. (b) Phase transition $\alpha ,4\to 5$. (b.1) $\alpha =4.38$. (b.2) $\alpha =4.74$. Top right: zoomed local minimum for resident vortex position.

Table 1. Estimated topological charge $\left|\alpha \right|$ via interpolation from resident vortex experimental distance curves, d${}_{exp}$(µm). Data correspond to Figure 6 samples: $\alpha =2.18$, $\alpha =2.86$, $\alpha =4.38$, and $\alpha =4.74$.

Input $\mathit{\alpha }$	d (µm)	d${}_{\mathit{exp}}$ (µm)	${\mathit{\alpha }}_{\mathit{exp}}$	Err $\mathbf{\Delta }\mathit{\alpha }$
2.18	462.3	462.0 ± 35.2	2.18 ± 0.02	<1%
2.86	88.0	83.6 ± 4.4	2.87 ± 0.01	<0.7%
4.38	352.3	358.6 ± 13.2	4.40 ± 0.04	<1%
4.74	176.1	176.0 ± 2.2	4.74 ± 0.02	<0.4%

4. Conclusions

The behavior of non-integer practical vortex beams in the Fraunhofer diffraction zone was studied thoroughly, according to the presented theoretical model and its experimental verification. A complete picture of each transition from topological charges 1 to 6, comparing the numerical and the experimental data, is presented here. The measurement of ${\omega }_0$ turned out to be a key part of this work, allowing the self-calibration of the experiment and matching it with the simulations with very low error. As mentioned in the text, when the resident enters the beam extension, its position is difficult to pinpoint, hindering the measurement of d, and therefore producing greater error. Moreover, it generates some minor discrepancies at approximately the middle point of the curve. This is also reflected in the measurement of ${\omega }_0$, where larger transitions have greater errors. It is to be noted that even though the transition curves for the resident vortex do not cross, the greater the transition, the shorter the interval. This inconvenience can be surpassed by changing the value of ${\omega }_0$ as the transition integer becomes larger. Finally, in this work we demonstrate a method of making a precise determination of the vortex strength of non-integer vortexes without the need of the phase. The vortex strength was estimated here with an error of less than $1\%$. This opens up new possibilities for the application of non-integer vortex beams in free-space optical communication using each vortex as a symbol, assuming the orthogonality of each one, as can be seen in [14].