Propagation Characteristics of Hermite–Gaussian Beam under Pointing Error in Free Space
Abstract
:1. Introduction
2. Modeling of the Average Irradiance under Pointing Error
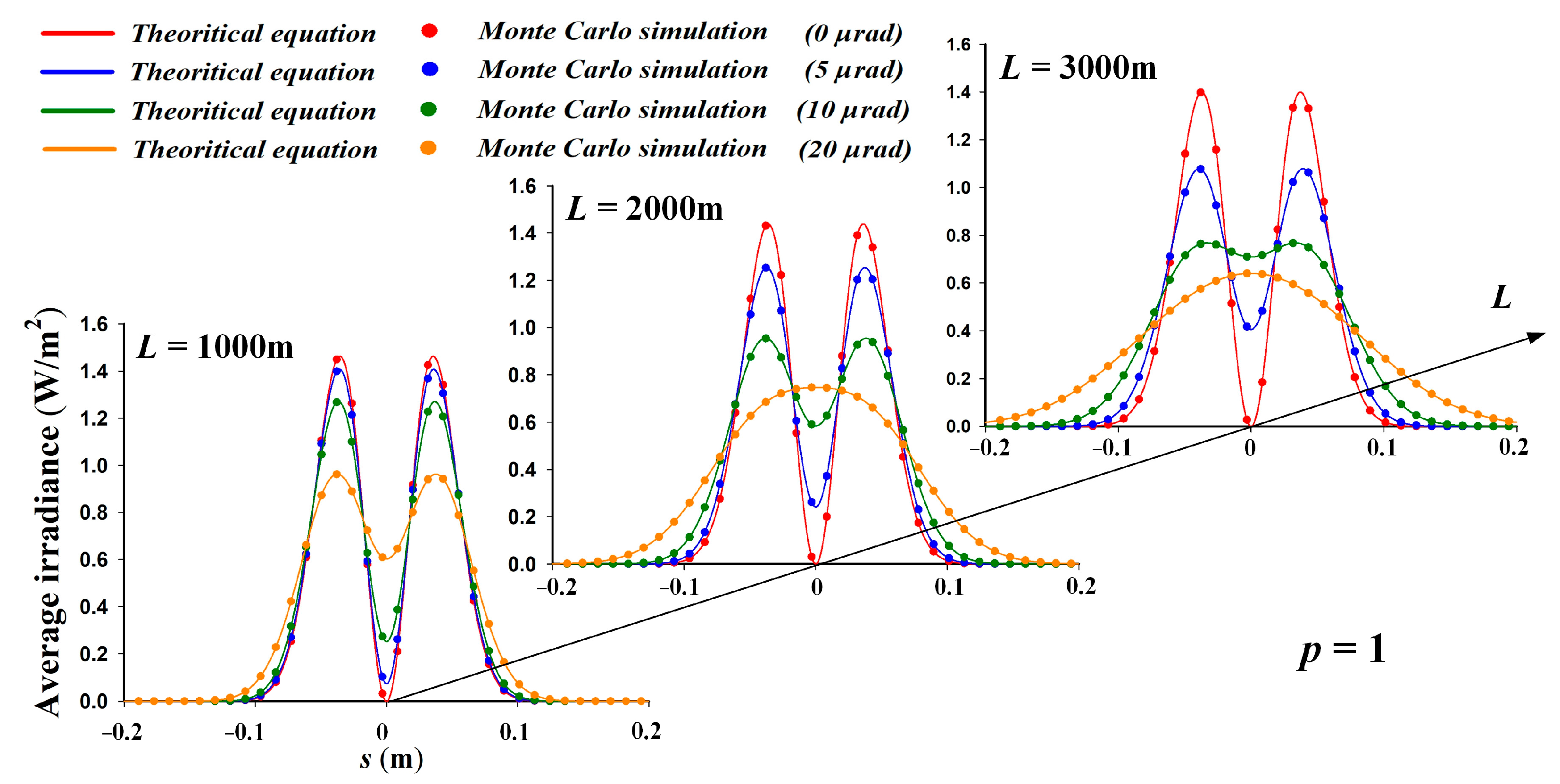
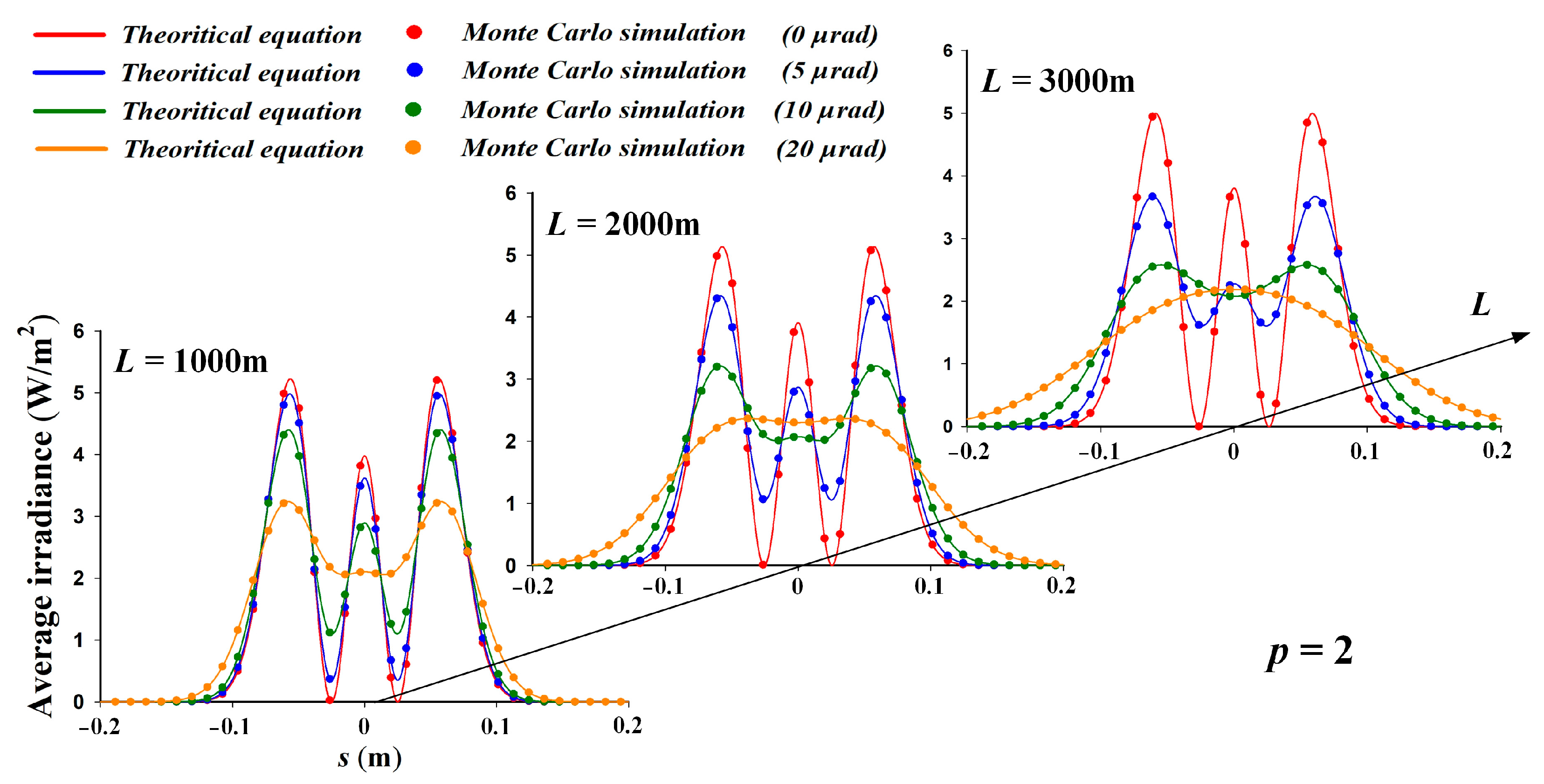
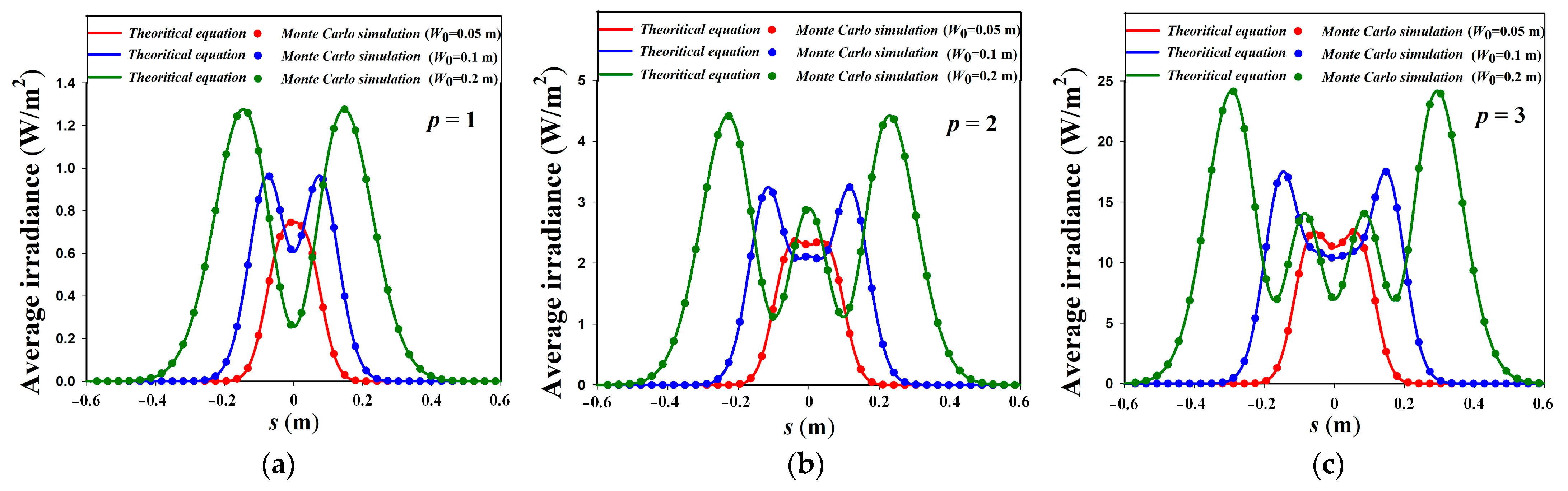
3. Numerical Simulation Results and Verification
4. Discussion
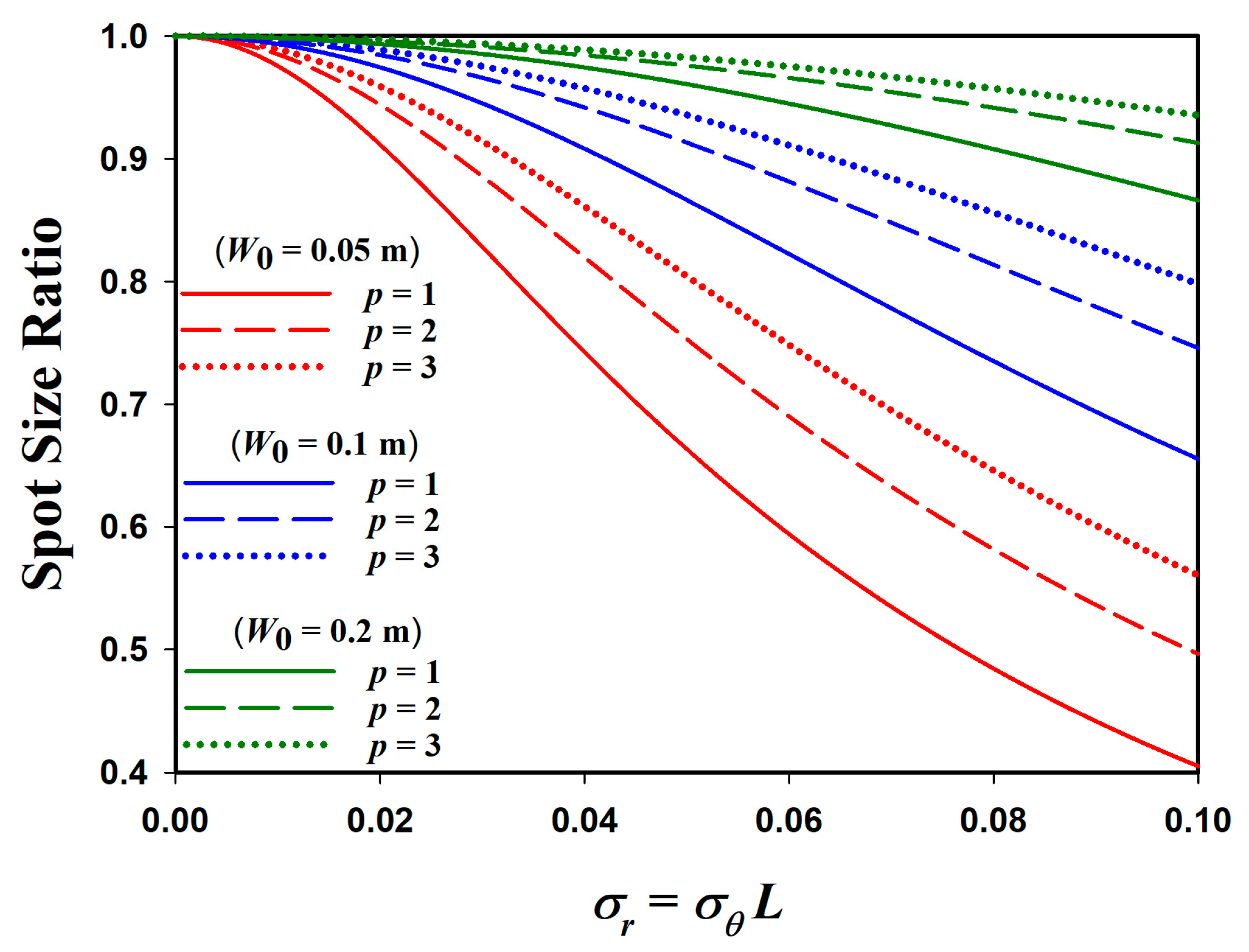
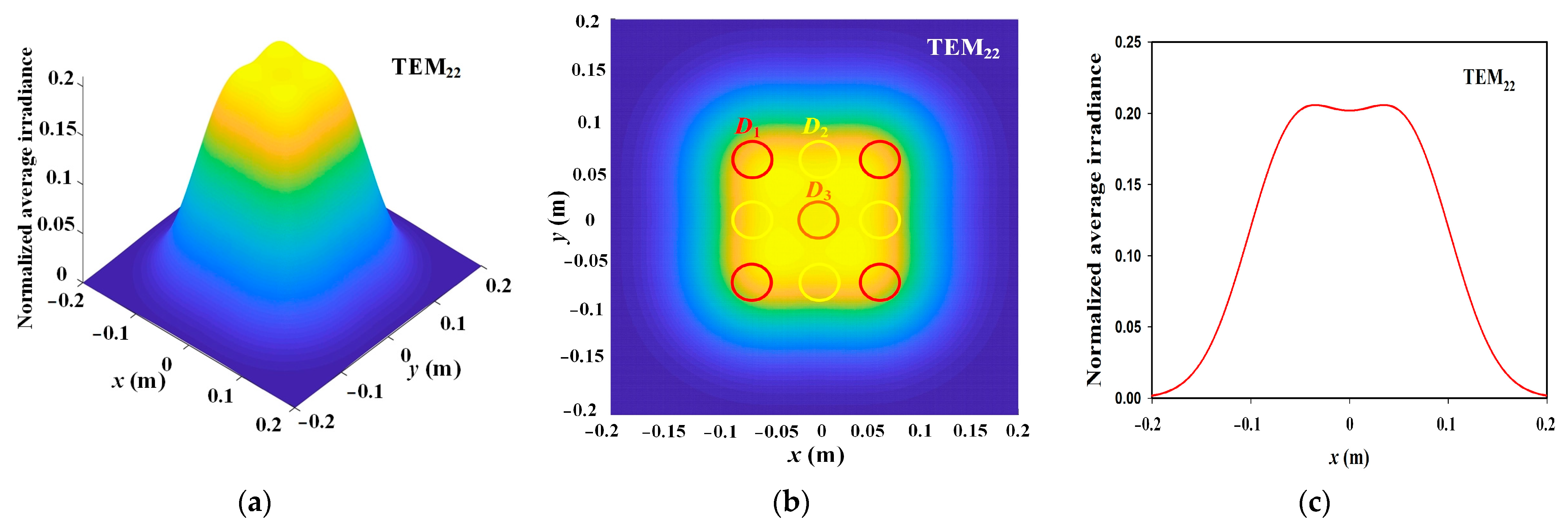
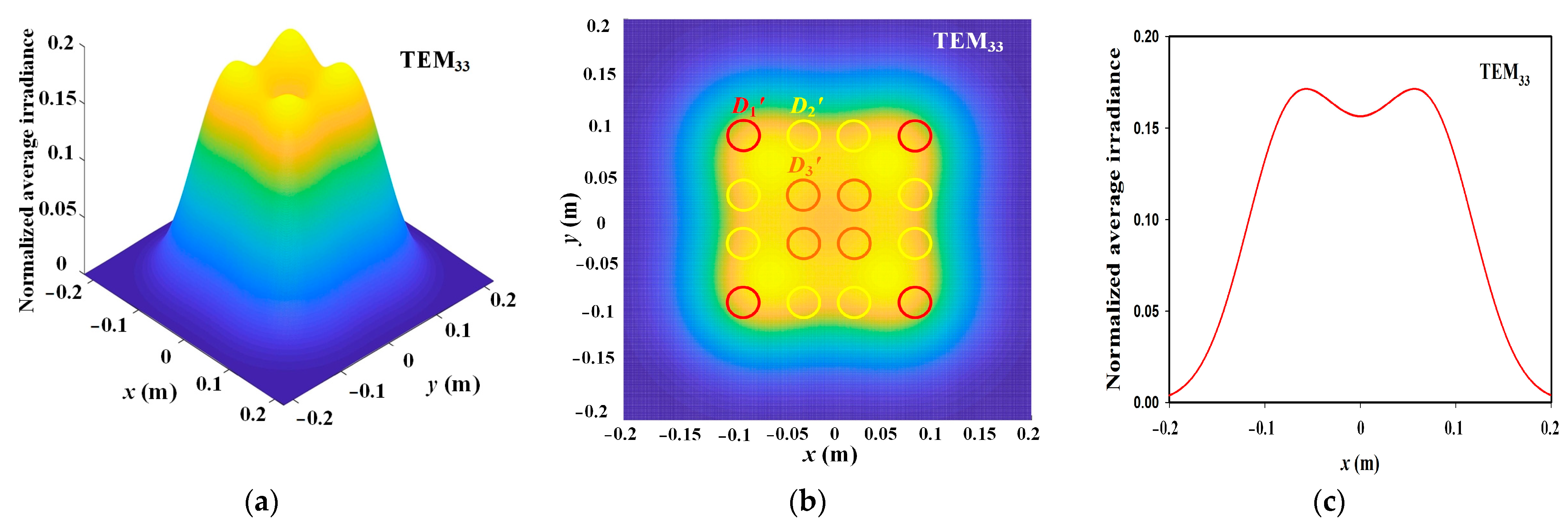
4.1. Effective Spot Size
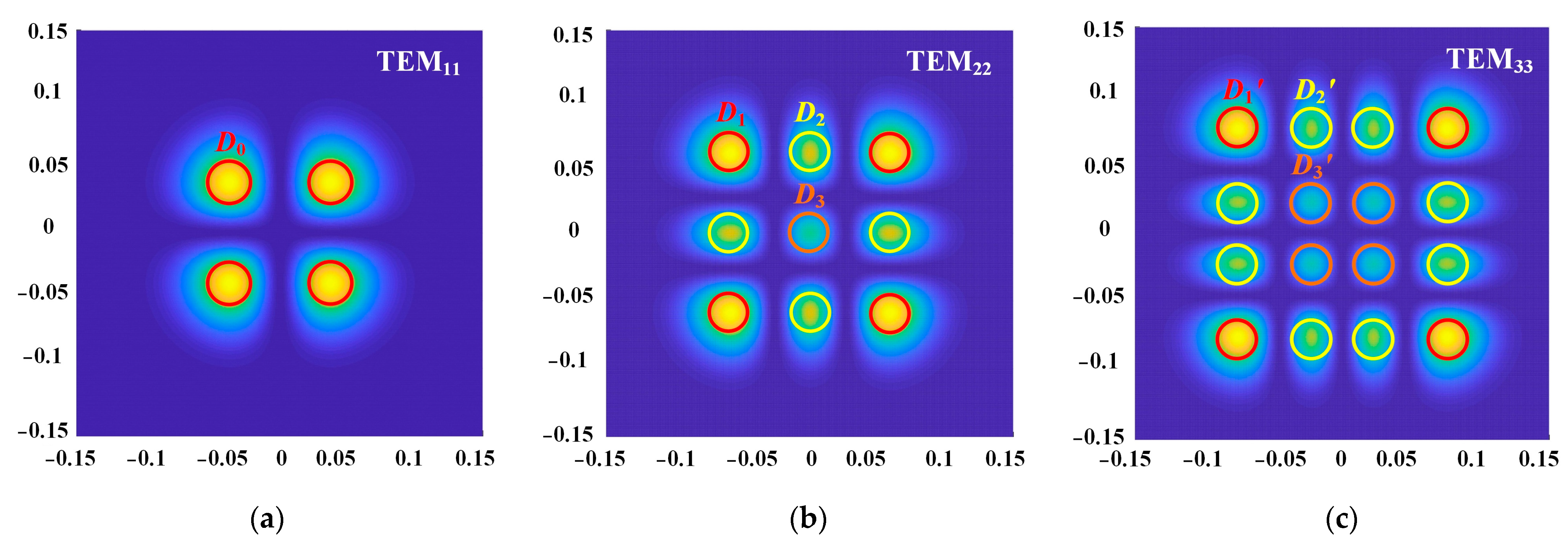
4.2. Location of the Local Extreme Value in the Average Irradiance under Pointing Error
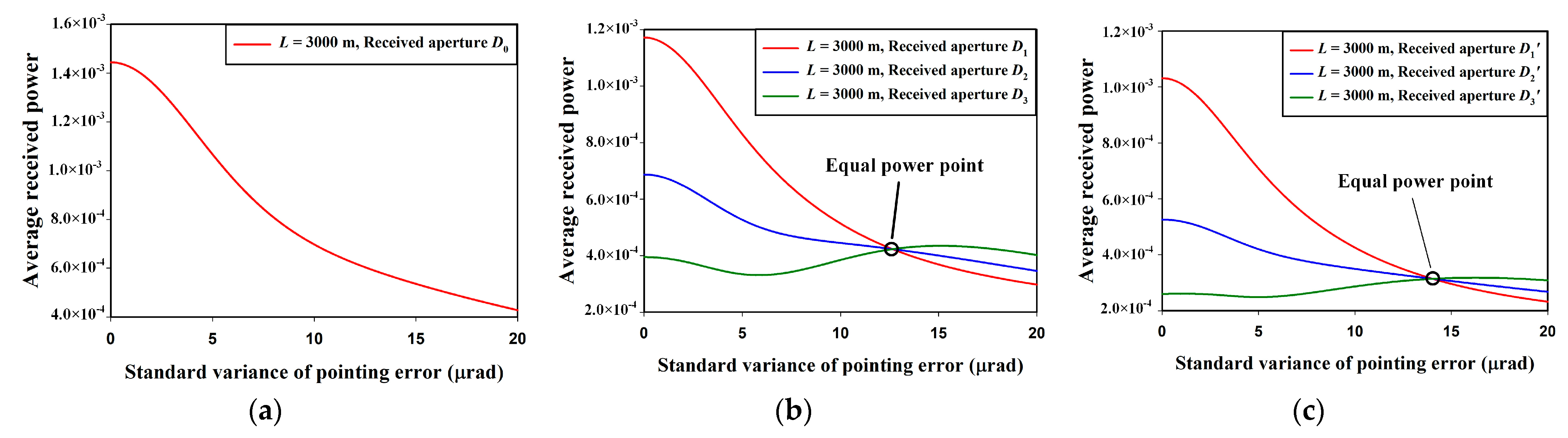
4.3. Average Received Power and SNR Loss
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- You, X.; Wang, C.; Huang, J.; Gao, X.; Zhang, Z.; Wang, M.; Huang, Y.; Zhang, C.; Jiang, Y.; Wang, J.; et al. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts. Sci. China Inf. Sci. 2021, 64, 110301. [Google Scholar] [CrossRef]
- Mansour, A.; Mesleh, R.; Abaza, M. New challenges in wireless and free space optical communications. Opt. Lasers Eng. 2017, 89, 95–108. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Hossan, M.T.; Islam, A.; Jang, Y.M. A Comparative Survey of Optical Wireless Technologies: Architectures and Applications. IEEE Access 2018, 6, 9819–9840. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef] [Green Version]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Laabs, H. Propagation of Hermite-Gaussian-beams beyond the paraxial approximation. Opt. Commun. 1998, 147, 1–4. [Google Scholar] [CrossRef]
- Young, C.Y.; Gilchrest, Y.V.; Macon, B.R. Turbulence induced beam spreading of higher order mode optical waves. Opt. Eng. 2002, 41, 1097–1103. [Google Scholar]
- Kiasaleh, K. Statistical Profile of Hermite-Gaussian Beam in the Presence of Residual Spatial Jitter in FSO Communications. IEEE Commun. Lett. 2016, 20, 656–659. [Google Scholar] [CrossRef]
- Kiasaleh, K. Spatial beam tracking for Hermite-Gaussian-based free-space optical communications. Opt. Eng. 2017, 56, 076106. [Google Scholar] [CrossRef]
- Kiasaleh, K. Probability density function of Hermite-Gaussian beam intensity in the presence of spatial error. Opt. Eng. 2016, 55, 095109. [Google Scholar] [CrossRef]
- Carter, W.H. Spot size and divergence for Hermite Gaussian beams of any order. Appl. Opt. 1980, 19, 1027–1029. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Chebaane, S.; Ben Khalifa, S.; Grover, A.; Dewra, S.; Angurala, M. Performance Evaluation of a 4 × 20-Gbps OFDM-Based FSO Link Incorporating Hybrid W-MDM Techniques. Front. Phys. 2021, 9, 746779. [Google Scholar] [CrossRef]
- Chaudhary, S.; Lin, B.; Tang, X.; Wei, X.; Zhou, Z.; Lin, C.; Zhang, M.; Zhang, H. 40 Gbps-80 GHz PSK-MDM based Ro-FSO transmission system. Opt. Quantum Electron. 2018, 50, 321. [Google Scholar] [CrossRef]
- Boobalan, S.; Prakash, S.A.; Angurala, M.; Malhotra, J.; Singh, M. Performance Enhancement of 3 × 20 Gbit/s MDM-Based OFDM-FSO System. Wirel. Pers. Commun. 2022, 122, 3137–3165. [Google Scholar] [CrossRef]
- Pang, K.; Song, H.; Zhao, Z.; Zhang, R.; Song, H.; Xie, G.; Li, L.; Liu, C.; Du, J.; Molisch, A.F.; et al. 400-Gbit/s QPSK free-space optical communication link based on four-fold multiplexing of Hermite-Gaussian or Laguerre-Gaussian modes by varying both modal indices. Opt. Lett. 2018, 43, 3889–3892. [Google Scholar] [CrossRef] [PubMed]
- Kaymak, Y.; Rojas-Cessa, R.; Feng, J.; Ansari, N.; Zhou, M.; Zhang, T. A Survey on Acquisition, Tracking, and Pointing Mechanisms for Mobile Free-Space Optical Communications. IEEE Commun. Surv. Tutor. 2018, 20, 1104–1123. [Google Scholar] [CrossRef]
- Kaushal, H.; Jain, V.K.; Kar, S. Free Space Optical Communication; Springer: New Delhi, India, 2017. [Google Scholar]
- Magidi, S.; Jabeena, A. Free Space Optics, Channel Models and Hybrid Modulation Schemes: A Review. Wirel. Pers. Commun. 2021, 119, 2951–2974. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Hu, Z.; Zeng, Q.; Qin, K. Single-Layer Phase Screen with Pointing Errors for Free Space Optical Communication. IEEE Access 2021, 9, 104070–104078. [Google Scholar] [CrossRef]
- Hu, S.; Liu, H.; Zhao, L.; Bian, X. The Link Attenuation Model Based on Monte Carlo Simulation for Laser Transmission in Fog Channel. IEEE Photonics J. 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Hu, Z.; Jiang, D.; Liu, X.; Zhu, B.; Zeng, Q.; Qin, K. Performance research on flat-topped beam-based small satellites free space optical communication. Opt. Commun. 2021, 487, 126802. [Google Scholar] [CrossRef]
- Bashir, M.; Alouini, M. Optimal Power Allocation Between Beam Tracking and Symbol Detection Channels in a Free-Space Optical Communications Receiver. IEEE Trans. Commun. 2021, 69, 7631–7646. [Google Scholar] [CrossRef]



| p | |
| 1 | |
| 2 | |
| 3 |
| Parameters | Value |
|---|---|
| Optical beam waist (W0) | 0.05 m |
| Wavelength (λ) | 850 nm |
| Propagation distance (L) | 1000, 2000 and 3000 m |
| Standard variance of pointing error angle () | 0, 5, 10 and 20 μrad |
| Grid points (N × N) | 1024 × 1024 |
| Simulated numbers (M) | 10,000 |
| Locations of the local maxima | p |
| ; (). | 1 |
| 0, ; 0, (). | 2 |
| , ; , (). | 3 |
| Locations of the local minima | p |
| 0 | 1 |
| ; (). | 2 |
| 0,; 0, (). | 3 |
| In the presence of pointing error | |
| , , , , , . | Coordinates of the local maximum irradiance |
| , , . | Coordinates of the local minimum irradiance |
| In the absence of pointing error | |
| , , , , , . | Coordinates of the local maximum irradiance |
| , , . | Coordinates of the local minimum irradiance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Jiang, D.; Zhang, Y.; Kong, L.; Zeng, Q.; Qin, K. Propagation Characteristics of Hermite–Gaussian Beam under Pointing Error in Free Space. Photonics 2022, 9, 478. https://doi.org/10.3390/photonics9070478
Liu X, Jiang D, Zhang Y, Kong L, Zeng Q, Qin K. Propagation Characteristics of Hermite–Gaussian Beam under Pointing Error in Free Space. Photonics. 2022; 9(7):478. https://doi.org/10.3390/photonics9070478
Chicago/Turabian StyleLiu, Xin, Dagang Jiang, Yu Zhang, Lingzhao Kong, Qinyong Zeng, and Kaiyu Qin. 2022. "Propagation Characteristics of Hermite–Gaussian Beam under Pointing Error in Free Space" Photonics 9, no. 7: 478. https://doi.org/10.3390/photonics9070478
APA StyleLiu, X., Jiang, D., Zhang, Y., Kong, L., Zeng, Q., & Qin, K. (2022). Propagation Characteristics of Hermite–Gaussian Beam under Pointing Error in Free Space. Photonics, 9(7), 478. https://doi.org/10.3390/photonics9070478





