Abstract
Analytical expressions for the cross-spectral density matrix of a partially coherent twisted Laguerre-Gaussian pulsed (PCTLGP) beam in anisotropic atmospheric turbulence are derived based on the extended Huygens–Fresnel principle. Numerical results indicate that the atmospheric turbulence induces the degeneration of the spectral intensity distribution of the PCTLGP beam, and the PCTLGP beam also shows different evolution properties on propagation in weaker turbulence and stronger turbulence. The PCTLGP beam with a negative twisted factor exhibits an advantage over the Laguerre-Gaussian pulsed beam for reducing the atmospheric turbulence-induced degeneration, and this advantage is further strengthened with increasing the topological charge, mode order and absolute value of the twisted factor. In addition, we also find that the pulse duration will affect the spectral intensity of the PCTLGP beam in turbulence. This kind of beam will show potential application value in free-space optical communications and remote sensing.
1. Introduction
Optical pulse has attracted enormous attention since the concept of the Gaussian Schell-Model pulsed (GSMP) beam was introduced by Paakkonen et al. [1,2]. Subsequently, the generation and propagation of various pulsed beams have been extensively studied [3,4,5,6,7,8,9]. In recent years, the partially coherent (PC) beams with a vortex phase carrying orbital angular momentum (OAM) have attracted considerable interest due to their various applications in free-space optical communications (FSOC), optical tweezers, astronomy [9,10,11,12,13,14,15,16], etc. The partially coherent Laguerre-Gaussian (PCLG) beam is a classical vortex beam that shows more obvious advantages in reducing the turbulence-induced scintillation [13,14,15]. A large number of studies have indicated that PCLG beams can be applied to the optical manipulation of Bose–Einstein condensates, optical imaging, biomedicine, quantum information coding and other fields [4,13,14,15,16,17,18,19,20]. Based on the merits of the OAM mode and the pulsed beam, the propagation of Laguerre-Gaussian pulsed (LGP) beams in the different channels have been investigated widely [4,21,22,23]. For examples, Martínez-Matos et al. studied the spatial pulse shaping of ultrashort Laguerre-Gaussian beams at the focal plane [21]. The time-varying of the pulse Laguerre-Gaussian beam propagating in free space has been analyzed by Gao et al. [22]. Li et al. investigated the probability distribution of OAM modes of the ultrashort LGP beam propagating through oceanic turbulence [23].
Many studies have been conducted on the propagation of PC beams through a turbulent atmosphere [6,7,9,13,14,15,20]. Researches have demonstrated that the anisotropic atmospheric turbulence will seriously affect the characteristics of the beam in practical applications [7,13,15]. Therefore, reducing the influence of turbulence on beam propagation is necessary. The modulation of the vortex phase and twist phase is one of the important methods to effectively suppress the influence of turbulence [24,25,26,27,28,29,30]. Peng et al. introduced a PC twisted beam, named the twisted Laguerre-Gaussian Schell-model beam, which carries both the vortex phase and twist phase. The results show that the influence of atmospheric turbulence on the propagation characteristics for this beam can be effectively reduced by adjusting the twisted factor, topological charge and mode order [13,16,28,29,30].
However, to the best of our knowledge, the evolution properties of a partially coherent twisted Laguerre-Gaussian pulsed (PCTLGP) beam propagating through anisotropic atmospheric turbulence are still unreported so far. In this paper, we focus on the evolution of the spectral intensity distribution for the PCTLGP beam in anisotropic non-Kolmogorov turbulence. Analytical expressions for the cross-spectral density matrix (CSDM) of the PCTLGP beam propagating through the turbulence are derived, and numerical results are illustrated in detail. The results have reference value for the application of beams in FSOC and other fields.
2. Theoretical Formulation
In the source plane (z = 0), the statistical properties of the partially coherent Laguerre-Gaussian pulsed (PCLGP) beam at points r1 = (r1x, r1y) and r2 = (r2x, r2y), and at different instant times t1 and t2, can be characterized by a two-point two-time mutual coherent function matrix (MCFM), which is given by [7,9,13,15,20]:
where H(·) being the Hermite polynomial, n and l denote the mode order and the topological charge, respectively. Their meanings are consistent throughout the paper. , , and are the binomial coefficients. σ and δ describe the waist width and the spatial coherence length, respectively. T0 and Tc are the pulse duration and the temporal coherence length, respectively. ω0 is the central angular frequency of the pulse. “*” describes the complex conjugate.
According to the Fourier-transform [9]
the two-point two-frequency CSDM of an PCLGP beam at z = 0 plane can be expressed as [7,13,20]:
where and denote the spectral width and the spectral coherent width of the pulse, respectively.
According to the extended Huygens–Fresnel principle, the two-point two-frequency CSDM at the arbitrary two points ρ1 = (x1, y1) and ρ2 = (x2, y2) in the received plane (z = L) can be expressed as [7,9]:
where L is the propagation distance, and c is the speed of light in a vacuum. ⟨·⟩ denotes the ensemble average, and the turbulent factor ⟨exp[ψ1 + ]⟩ is given by [3,13,15,20]:
where ρ0 denotes the coherence length of a spherical wave propagating in turbulence and is given by [3,13,16]:
where k = 2π/λ, is the wave number, with λ as the wavelength. Φn(κ) represents the spatial power spectrum of the refractive-index fluctuations of anisotropic atmospheric turbulence with κ = (κx, κy, κz) denoting the spatial wavenumber, and is given by [7,13]:
where α is the spectral power law, is the generalized refractive structure constant with units m3−α. ξx and ξy are the anisotropic factors that can describe the asymmetry of turbulence cells. A(α) = cos(απ/2)Γ(α−1)/(4π2), c(α) = [2πA(α)Γ(5/2−α/2)/3]1/(α−5) with Γ(·) represents the Gamma function. κx, κy and κz are three components of the κ along the x, y and z directions. κm = c(α)/l0 and κ0 = 2π/L0. l0 and L0 are the turbulence inner and outer scales, respectively.
After the twist phase modulation is applied to PCLGP beam, with the setting ω1 = ω2 = ω, the CSDM of a PCTLGP beam in the received plane can be obtained [7,9,13]:
where η denotes the twisted factor.
Substituting Equations (5)–(7) into Equation (8), we can obtain the expression of the CSDM for a PCTLGP beam propagating through the anisotropic atmospheric turbulence:
with
In the above derivations, we have used the following formulas [13,20]:
The spectral density along the observation plane at the “coincident point” ρ1 = ρ2 = ρ = (x, y) is given by the formula [7,9,13]:
According to Equations (9), (10) and (15), the spectral density of a PCTLGP beam is mainly determined by the twisted factor η, topological charge l, mode order n, pulse duration T0 and turbulence parameters.
3. Numerical Simulation and Discussion
In this section, we numerically calculate the spectral intensity of the PCTLGP beam propagating through the anisotropic non-Kolmogorov turbulence by using the above analyses. The parameters in the following calculations were set as λ = 1550 nm, σ = 20 mm, δ = 10 mm, ω0 = 2.9788 rad/fs, ω = 1.02ω0, T0 = 100 fs, Tc = 50 fs, α = 3.4, L0 = 50 m, l0 = 10 mm; the other parameters were specified in the figure captions.
To understand the twist phase induced evolution of the spectral intensity distribution on propagation, Figure 1 shows both the 3D-normalized spectral intensity distribution of the PCLGP beam (η = 0 m−1) and the PCTLGP beam (η = −5 × 10−4 m−1) at several propagation distances in anisotropic non-Kolmogorov turbulence. In Figure 1(a1,b1), one finds that the initial beam profiles of the PCLGP beam and the PCTLGP beam show a multi-ring dark hollow beam profile. From Figure 1(a1–a8), the evolution process of the PCLGP beam can be seen: the spectral intensity in the dark center region gradually increases with the increase in the propagation distance, and the dark ring gradually disappears, and the outer ring gradually degenerates, and finally the beam spot evolves into a Gaussian shape. Similarly, for a PCTLGP beam (see Figure 1(b1–b8)), the spectral intensity distribution gradually evolves to a flat-top distribution, and eventually converges into a Gaussian-like distribution. This is consistent with the conclusions in Refs. [15,31,32,33]: The Kurtosis parameters of the arbitrary beams will converge to a constant 2 as the propagation distance L→∞, which means that arbitrary beams will evolve into a Gaussian shape in atmospheric turbulence with the increase in L. Compared to Figure 1a,b, it can be found that the PCLGP beam evolves into Gaussian distribution more quickly than the PCTLGP beam during transmission, which indicates that the twist phase plays an important role in resistance to the turbulence-induced degeneration.
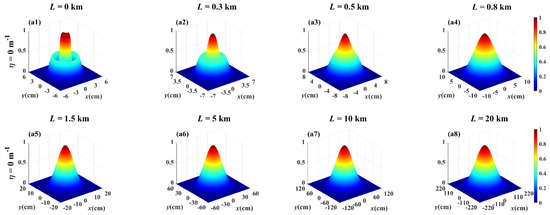
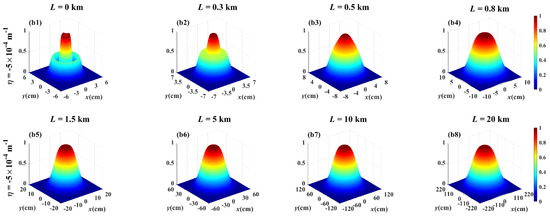
Figure 1.
Normalized spectral intensity distribution of (a1–a8) the PCLGP beam and (b1–b8) the PCTLGP beam at several propagation distances in anisotropic turbulence (ξx = ξy = 3, l = 1, n = 1, = 1 × 10−14 m3−α).
Next, we focus on the influence of the topological charge on the evolution properties during propagation. Figure 2 shows the normalized spectral intensity distribution of the PCTLGP beam propagating through the anisotropic non-Kolmogorov turbulence ( = 1 × 10−17 m3−α) at several propagation distances for the different topological charges. Figure 2a,c,d presents that the normalized spectral intensity distribution of the PCTLGP beam gradually evolves from a dark hollow distribution to a flat-topped distribution when n = 0, and finally converges into a Gaussian-like distribution. Figure 2b displays the normalized spectral intensity distribution of the PCTLGP beam when n ≠ 0, and the results shown agree with those discussed in Figure 1. Importantly, we find that the evolution of the PCTLGP beam can be accelerated with the decrease in l, indicating that the PCTLGP beam with a larger l has a stronger ability to resist the degeneration caused by the turbulent atmosphere. In Ref. [14], the partially coherent radially polarized vortex beam studied by Yu et.al. also showed a similar phenomenon. Furthermore, it can be seen that the progress of the beam evolving into a Gaussian-like shape will not be accelerated with the increase in the propagation distance when it propagates for a long distance (L > 3 km), which is caused by the too weak turbulence, but the beam spot is larger with the increase in L.
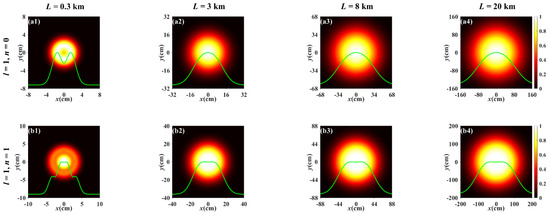
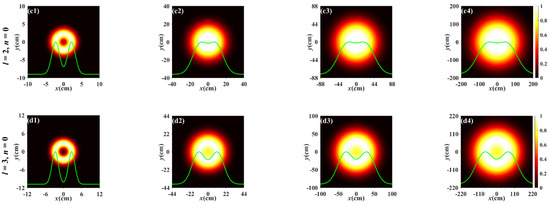
Figure 2.
Normalized spectral intensity distribution of the PCTLGP beam at several propagation distances in anisotropic turbulence for different mode orders and topological charges (ξx = ξy = 3, = 1 × 10−17 m3−α, η = −5 × 10−4 m−1).
For comparison, Figure 3 depicts the normalized spectral intensity distribution of the PCTLGP beam propagating through the anisotropic non-Kolmogorov turbulence ( = 1 × 10−13 m3−α) at the same propagation distances and the topological charges with Figure 2. Figure 3a–d shows the progress of the normalized spectral intensity distribution for the PCTLGP beam gradually evolves to a Gaussian-like distribution under different mode orders and topological charges. It can be easily found that the degeneration of the PCTLGP beam is accelerated by the stronger turbulence by comparing Figure 2 and Figure 3. It is also found that the PCTLGP beam shows different evolution properties when propagating in weaker turbulence and stronger turbulence. The degradation progress of the beam is accelerated with increasing L when propagating for L > 3 km in stronger atmospheric turbulence, and it eventually converges to a Gaussian-like distribution, while the weakly turbulent atmosphere has little effect on the progress of the beam evolving into a Gaussian-like shape, and only the beam spot becomes lager with the increase in L.
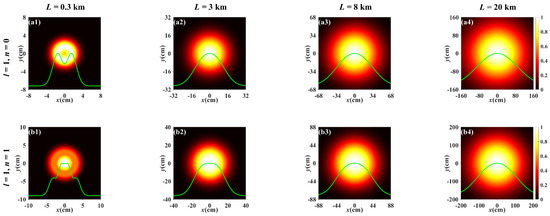
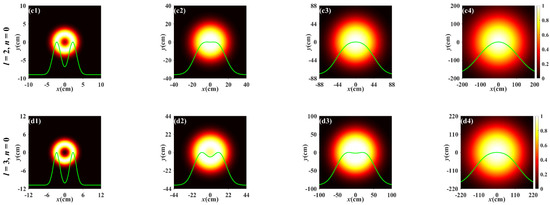
Figure 3.
Normalized spectral intensity distribution of the PCTLGP beam at several propagation distances in anisotropic turbulence for different mode orders and topological charges (ξx = ξy = 3, = 1 × 10−13 m3−α, η = −5 × 10−4 m−1).
To explore the influence of the twisted factor on the evolution of the beam, Figure 4 studies the normalized spectral intensity distribution of the PCTLGP beam with η = −1 × 10−3 m−1 propagating through the weaker turbulence ( = 1 × 10−17 m3−α). Figure 4a–d illustrates the evolution of the PCTLGP beam in the turbulent atmosphere, and it can be seen that the degeneration of the PCTLGP beam will be suppressed with the increase in l. Compared to Figure 2 and Figure 4, it can be found that the PCTLGP beam with the smaller η has a stronger ability to maintain the dark hollow distribution when propagating in the weaker turbulence, meaning that the PCTLGP beam has an advantage over the PCLGP beam for resisting the degeneration caused by turbulence, and the advantage is further enhanced with decreasing η.
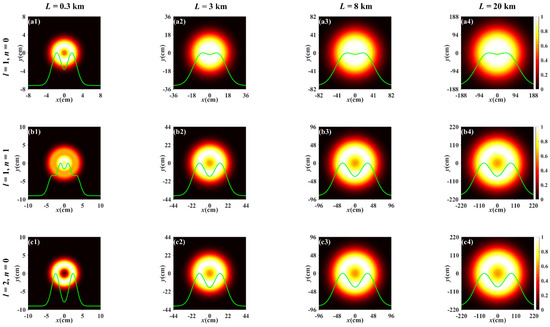

Figure 4.
Normalized spectral intensity distribution of the PCTLGP beam at several propagation distances in anisotropic turbulence for different mode orders and topological charges (ξx = ξy = 3, = 1 × 10−17 m3−α, η = −1 × 10−3 m−1).
Figure 5 illustrates the evolution of the normalized spectral intensity distribution for a PCTLGP beam with η = −1 × 10−3 m−1 propagating through the stronger turbulence ( = 1 × 10−13 m3−α). Figure 5a–d depicts the degeneration of the PCTLGP beam with different l and n in the turbulent atmosphere. Compared to Figure 3 and Figure 5, it can be seen that the above conclusions obtained from comparing Figure 2 and Figure 4 are also applicable to the stronger turbulence, that is to say, whether in stronger turbulence or weaker turbulence, the PCTLGP beam with a smaller η can more effectively resist the influence of the turbulence on the degeneration. Next, we focus on the effect of the joint modulation of the twist factor and the topological charge on the beam evolution.
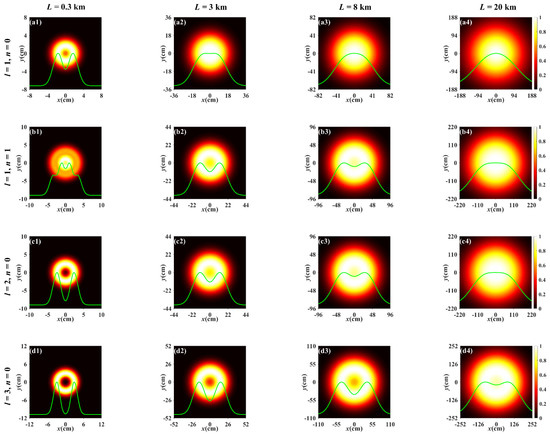
Figure 5.
Normalized spectral intensity distribution of the PCTLGP beam at several propagation distances in anisotropic turbulence for different mode orders and topological charges (ξx = ξy = 3, = 1 × 10−13 m3−α, η = −1 × 10−3 m−1).
Figure 6 gives the evolution of the normalized spectral intensity distribution of the PCTLGP beam on propagation through anisotropic non-Kolmogorov turbulent atmosphere for the different topological charges and twisted factors. Figure 6a–c studies the influence of the sign of the twisted factor on the beam evolution, and the results present that the process of the beam evolving into a Gaussian shape is accelerated by modulating the sign of twisted factor is “+”. Conversely, the evolution process is suppressed when the sign is “−”. In addition, Figure 6c,d shows that the values of l and η will affect the degeneration of the PCTLGP beam, and one finds that the beam degenerates more slowly when both l and |η| are larger, which means that the PCTLGP beam with a negative twisted factor shows an advantage in resisting the turbulence-induced degeneration, and this advantage is further enhanced with increasing l and |η|.
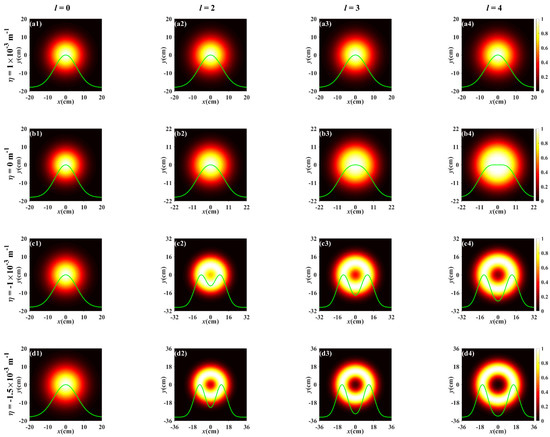
Figure 6.
Normalized spectral intensity distribution of the PCTLGP beam propagating through the anisotropic turbulence for different twisted factors and topological charges ( = 5 × 10−14 m3−α, ξx = ξy = 2, L = 2 km, n = 0).
For comparison, we introduce the normalized spectral intensity S(T0) = S(ρ, L; ω)/Smax(ρ, L; ω), where Smax(ρ, L; ω) is the maximum spectral intensity at the points ρ = (x, y) when the pulse duration is 100 fs. Figure 7 illustrates the S(T0) of the PCTLGP beam propagating for 0.3 km in anisotropic non-Kolmogorov turbulent atmosphere under the different pulse durations. Obviously, Figure 7 shows that the overall S(T0) increases with increasing T0. Figure 7a–c illustrates the influence of the twisted factor, the topological charge and the mode order on S(T0), respectively. It can be found that the ability of the PCTLGP beam to maintain the dark hollow shape is enhanced with increasing l, and the dark ring of the beam is more obvious when n is larger. Moreover, the PCTLGP beam degrades more slowly when the sign of the twisted factor is “−”. Therefore, we can draw a conclusion: the PCTLGP beam with a negative twisted factor can more effectively resist the influence of turbulence, and this resistance ability is further enhanced with increasing l, n.
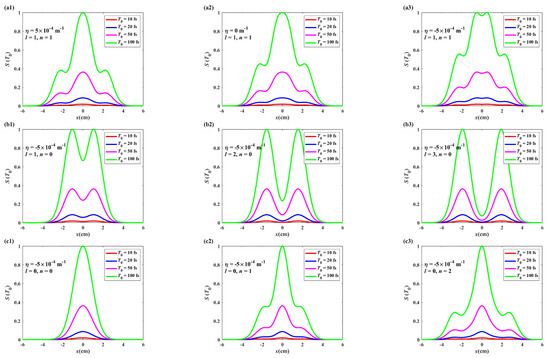
Figure 7.
The relationship between the normalized spectral intensity with pulse duration of the PCTLGP beam propagating through the anisotropic turbulence for different (a1–a3) twisted factors, (b1–b3) topological charges, (c1–c3) mode orders (ξx = ξy = 3, L = 0.3 km, = 1 × 10−14 m3−α).
4. Conclusions
In this paper, we have derived the analytical expressions for the diagonal elements of the CSDM for a PCTLGP beam in anisotropic turbulent atmosphere. The evolution properties of the PCTLGP beam on propagation are numerically discussed in detail. It is found that the initial beam profile of the PCTLGP beam (n ≠ 0) shows a multi-ring dark hollow beam profile, and it will degenerate into a flat-top distribution with the increase in the propagation distance and eventually evolves into a Gaussian-like distribution in the far field. In addition, the influence of the twisted factor η, topological charge l, mode order n, pulse duration T0 and turbulence parameters on the spectral intensity of the PCTLGP beam propagating through the turbulent atmosphere have been studied, and we find the most important parameters affecting the spectral intensity are the twisted factor η and topological charge l. Numerical results show that the PCTLGP beam with a negative twisted factor shows an advantage over the PCLGP beam in resisting the turbulence-induced degeneration, and this advantage is further strengthened with increasing l and |η|. Moreover, the ability of the PCTLGP beam to resist turbulence also increases with the increase in n, and the pulse duration will affect the value of the spectral intensity, which increases with increasing T0. It is also found that the PCTLGP beam shows different evolution properties when propagating in weaker turbulence and stronger turbulence. When the PCTLGP beam propagates for long distances in a weakly turbulent atmosphere, the progress of the beam evolving into a Gaussian-like shape will not be accelerated with the increase in the propagation distance, and only the beam spot will become lager. However, the degradation progress of the beam is accelerated with increasing L when propagating for long distances in stronger atmospheric turbulence, and it eventually converges to the Gaussian-like distribution. Compared with the general PCLGP beam, the PCTLGP beam shows some advantages. Therefore, the PCTLGP beam will be useful in free-space optical communications and remote sensing.
Author Contributions
Writing—original draft, Y.X. (Ying Xu); writing—review and editing, Y.X. (Ying Xu), Y.X. (Yonggen Xu); supervision, Y.X. (Ying Xu), Y.X. (Yonggen Xu) and T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Sichuan Provincial University Key Laboratory of Detection and Application of Space Effect in Southwest Sichuan (ZDXM202201003); Department of Science and Technology of Sichuan Province (2019YJ0470); NSAF (U2130123); International Partnership Program of Chinese Academy of Sciences (181231KYSB20200033); and Shanghai Science and Technology Program (21511105000 and 19ZR1464100).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Exclude this statement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Paakkonen, P.; Turunen, J.; Vahimaa, P.; Friberg, A.; Wyrowski, F. Partially coherent Gaussian pulses. Opt. Commun. 2002, 204, 53–58. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, L.; Zhu, S. Partially coherent light pulse and its propagation. Opt. Commun. 2003, 219, 65–70. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Wang, G.; Yin, H.; Wang, J. The influence of oceanic turbulence on the spectral properties of chirped Gaussian pulsed beam. Opt. Laser Technol. 2016, 82, 76–81. [Google Scholar] [CrossRef]
- Ding, C.; Korotkova, O.; Horoshko, D.; Zhao, Z.; Pan, L. Evolution of Spatiotemporal Intensity of Partially Coherent Pulsed Beams with Spatial Cosine-Gaussian and Temporal Laguerre-Gaussian Correlations in Still, Pure Water. Photonics 2021, 8, 102. [Google Scholar] [CrossRef]
- Wang, H.; Yan, X.; Feng, X.; Zhao, Z.; Pan, L. Intensity Evolution of Cosine-Gaussian-Correlated Schell-Model Pulse Scattered by a Medium. Appl. Sci. 2020, 10, 1825. [Google Scholar] [CrossRef]
- Liu, D.; Luo, X.; Wang, G.; Wang, Y. Spectral and Coherence Properties of Spectrally Partially Coherent Gaussian Schell-model Pulsed Beams Propagating in Turbulent Atmosphere. Curr. Opt. Photonics 2017, 1, 271–277. [Google Scholar]
- Li, Y.; Gao, M.; Lv, H.; Wang, L.; Ren, S.; Hu, X. Anisotropic turbulence-induced statistical properties evolution of a radially polarized partially coherent pulsed beam on propagation. Opt. Commun. 2020, 466, 125669. [Google Scholar] [CrossRef]
- Wang, X.; Tang, J.; Wang, Y.; Liu, X.; Liang, C.; Zhao, L.; Hoenders, B.; Cai, Y.; Ma, P. Complex and phase screen methods for studying arbitrary genuine Schell-model partially coherent pulses in nonlinear media. Opt. Express 2022, 30, 24222–24231. [Google Scholar] [CrossRef]
- Li, Y.; Gao, M.; Li, B. Vortex phase induced evolution of propagation properties of a spatiotemporally partially coherent partially polarized pulsed beam in atmospheric turbulence. Opt. Commun. 2022, 518, 128385. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, G.; Ma, X.; Zhong, H.; Yin, H.; Wang, Y.; Liu, D. Intensity and Coherence Characteristics of a Radial Phase-Locked Multi-Gaussian Schell-Model Vortex Beam Array in Atmospheric Turbulence. Photonics 2021, 8, 5. [Google Scholar] [CrossRef]
- Guo, Z. Coherent Property Evolution of Partially Coherent Elliptical Vortex Beam Propagation Through Turbulence. Laser Optoelectron. Prog. 2021, 58, 0901001. [Google Scholar]
- Liu, D.; Wang, Y.; Wang, G.; Yin, H. Propagation properties of a partially coherent anomalous hollow vortex beam in uniaxial crystal orthogonal to the optical axis. J. Mod. Opt. 2018, 65, 1442–1449. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, L.; Yang, N.; Xu, Y. Propagation characteristics of partially coherent twisted Laguerre-Gaussian beam in atmospheric turbulence with anisotropy. J. Mod. Opt. 2022, 69, 200–209. [Google Scholar] [CrossRef]
- Yu, J.; Huang, Y.; Wang, F.; Liu, X.; Gbur, R.; Cai, Y. Scintillation properties of a partially coherent vector beam with vortex phase in turbulent atmosphere. Opt. Express 2019, 27, 26676–26688. [Google Scholar] [CrossRef]
- Zhao, L.; Xu, Y.; Dan, Y. Evolution properties of partially coherent radially polarized Laguerre-Gaussian vortex beams in an anisotropic turbulent atmosphere. Opt. Express 2021, 29, 34986–35002. [Google Scholar] [CrossRef]
- Peng, X.; Liu, L.; Wang, F.; Popov, S.; Cai, Y. Twisted Laguerre-Gaussian Schell-model beam and its orbital angular moment. Opt. Express 2018, 26, 33956–33969. [Google Scholar] [CrossRef]
- Zhong, W.; Yang, Z.; Belic, M.; Zhong, W. Two-dimensional asymmetric Laguerre-Gaussian diffraction-free beams. Phys. Lett. A 2022, 423, 127818. [Google Scholar] [CrossRef]
- Zhong, W.P.; Zhong, W.; Belic, M.; Yang, Z. Controllable two-dimensional diffraction-free polygon beams. Phys. Lett. A 2022, 432, 128009. [Google Scholar] [CrossRef]
- Pan, X.; Wu, J.; Li, Z.; Zhang, C.; Deng, C.; Zhang, Z.; Wen, H.; Gao, Q.; Yang, J.; Yi, Z.; et al. Laguerre-Gaussian mode purity of Gaussian vortex beams. Optik 2021, 230, 166320. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Zhao, X. Intensity and effective beam width of partially coherent Laguerre–Gaussian beams through a turbulent atmosphere. J. Opt. Soc. Am. A 2015, 32, 1623–1630. [Google Scholar] [CrossRef]
- Martínez-Matos, Ó.; Vaveliuk, P.; Izquierdo, J.; Loriot, V. Femtosecond spatial pulse shaping at the focal plane. Opt. Express 2013, 21, 25010–25025. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, Y.; Gao, C. Study on the time-varying and propagating characteristics of ultrashort pulse Laguerre-Gaussian beam. Opt. Express 2010, 18, 12104–12110. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, Y.; Zhu, Y. Probability distribution of the orbital angular momentum mode of the ultrashort Laguerre-Gaussian pulsed beam propagation in oceanic turbulence. Results Phys. 2018, 11, 698–705. [Google Scholar] [CrossRef]
- Liu, Z.; Wan, L.; Zhou, Y.; Zhang, Y.; Zhao, D. Progress on Studies of Beams Carrying Twist. Photonics 2021, 8, 92. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, D. Propagation properties of a twisted rectangular multi-Gaussian Schell-model beam in free space and oceanic turbulence. Appl. Opt. 2018, 57, 8978–8983. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, F.; Cai, Y. Propagation of a twist Gaussian-Schell model beam in non-Kolmogorov turbulence. Opt. Commun. 2014, 324, 108–113. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Liang, C.; Liu, L.; Wang, F.; Cai, Y. Statistical Characteristics of a Twisted Anisotropic Gaussian Schell-Model Beam in Turbulent Ocean. Photonics 2020, 7, 37. [Google Scholar]
- Liu, Y.; Lin, R.; Wang, F.; Cai, Y.; Yu, J. Propagation properties of Laguerre-Gaussian Schell-model beams with a twist phase. J. Quant. Spectrosc. Radiat. Transf. 2021, 264, 107556. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, H.; Xie, C.; Zhu, S.; Li, Z. Twisted rectangular Laguerre-Gaussian correlated sources in anisotropic turbulent atmosphere. Opt. Commun. 2020, 459, 125004. [Google Scholar] [CrossRef]
- Madhu, V.; Ivan, J. Robustness of the twist parameter of Laguerre-Gaussian mode superpositions against atmospheric turbulence. Phys. Rev. A 2017, 95, 043836. [Google Scholar]
- Xu, Y.; Dan, Y.; Yu, J.; Cai, Y. Kurtosis parameter K of arbitrary electromagnetic beams propagating through non-Kolmogorov turbulence. J. Mod. Opt. 2017, 64, 1976–1987. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Y.; Wang, S.; Deng, X.; Liu, Y.; Wang, S. Kurtosis parameter and coupling coefficient of partially-coherent twisted Gaussian beam propagating through non-Kolmogorov atmospheric turbulence. J. Russ. Laser Res. 2022, 43, 509–519. [Google Scholar] [CrossRef]
- Zhou, Y.; Cheng, K.; Zhu, B.; Yao, N.; Zhong, X. Beam spreading, kurtosis parameter and Strehl ratio of partially coherent cosh-Airy beams in atmospheric turbulence. Optik 2019, 183, 656–663. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).