Laguerre-Gaussian Beams with an Increased Dark Area and Autofocusing
Abstract
:1. Introduction
2. Fourier-Invariant Laguerre-Gaussian Beams with an Increased Dark Area
3. Fresnel Transform of the Laguerre-Gaussian Beam with an Increased Dark Area
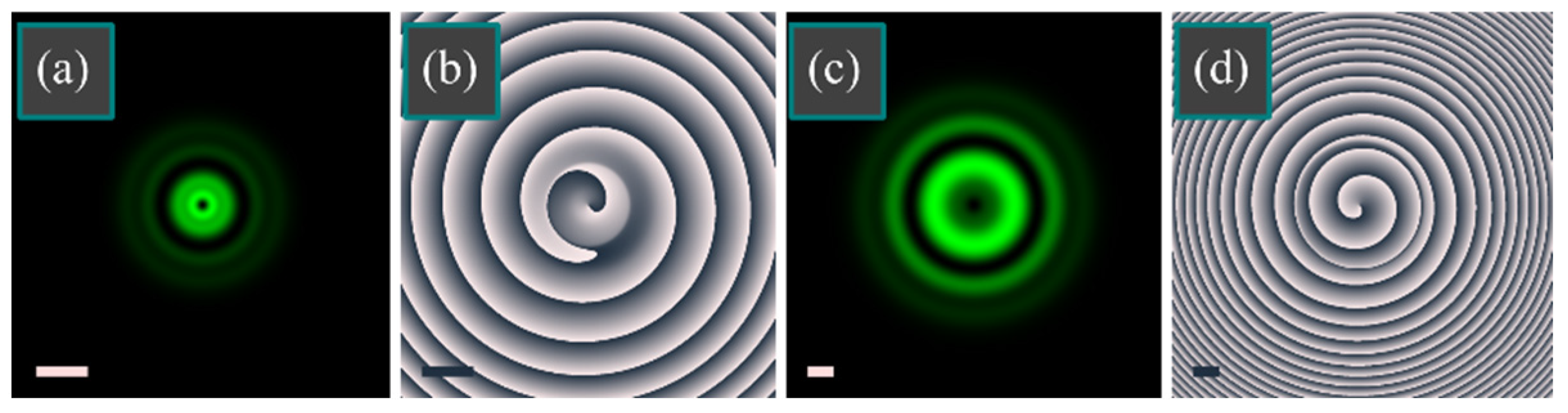
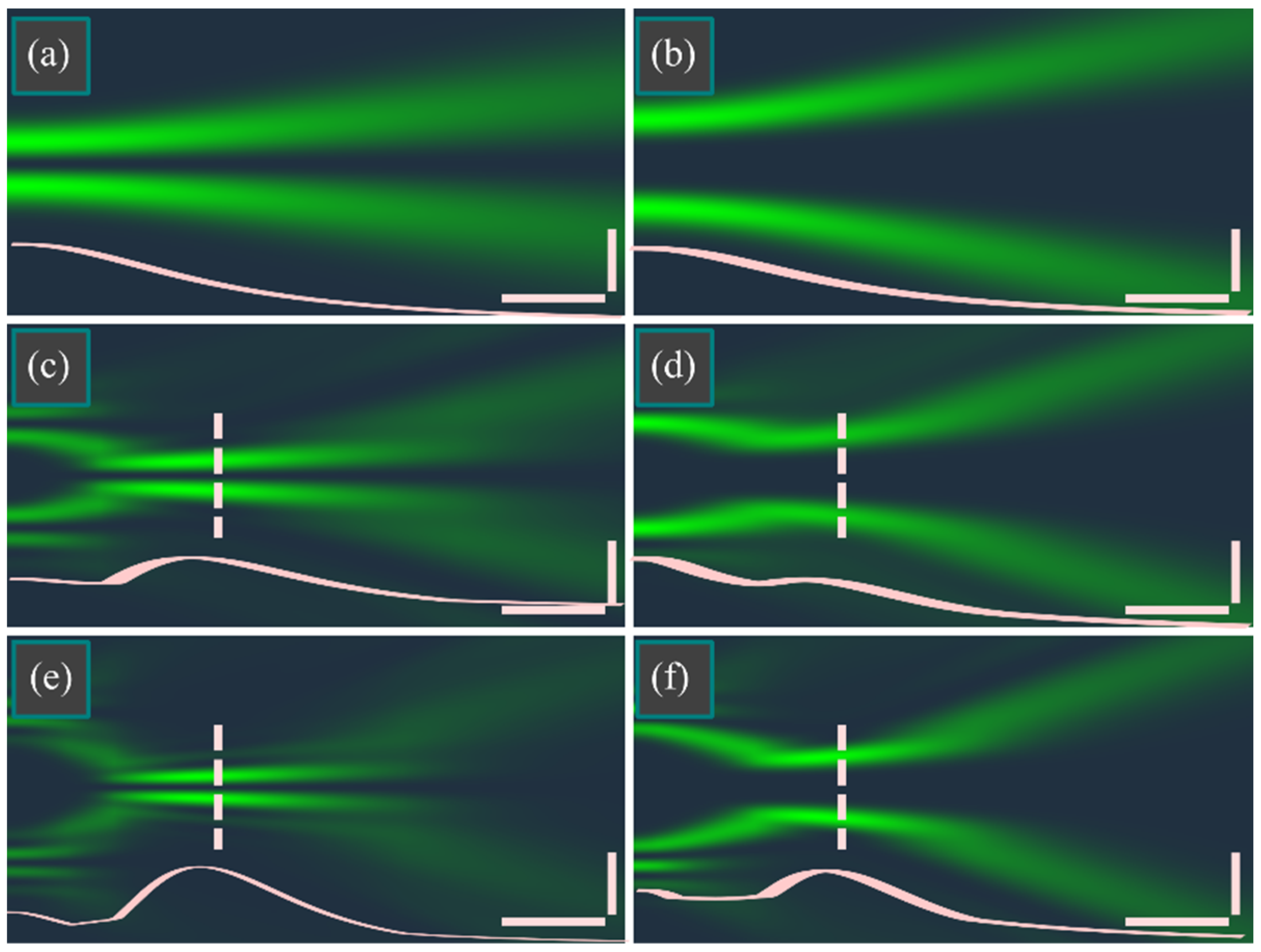
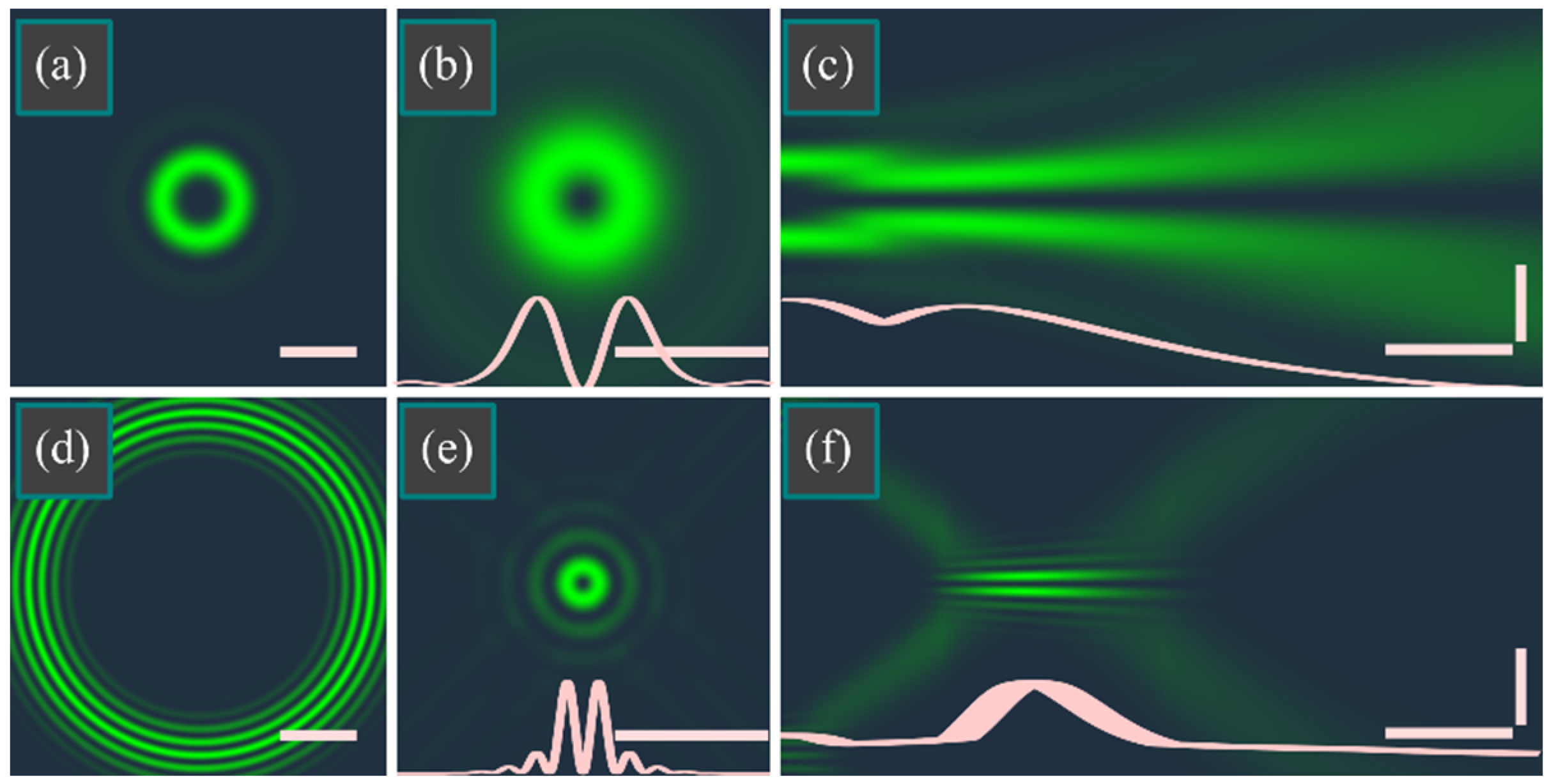
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prentice, P.A.; MacDonald, M.P.; Frank, T.G.; Cuschieri, A.; Spalding, G.C.; Sibbett, W.; Campbell, P.A.; Dholakia, K. Manipulation and filtration of low index particles with holographic Laguerre-Gaussian optical trap arrays. Opt. Express 2004, 12, 593–600. [Google Scholar] [CrossRef] [PubMed]
- Doster, T.; Watnik, A.T. Laguerre–Gauss and Bessel–Gauss beams propagation through turbulence: Analysis of channel efficiency. Appl. Opt. 2016, 55, 10239–10246. [Google Scholar] [CrossRef] [PubMed]
- Ferlic, N.A.; van Iersel, M.; Paulson, D.A.; Davis, C.C. Propagation of Laguerre-Gaussian and Im Bessel beams through atmospheric turbulence: A computational study. In Proceedings of the Laser Communication and Propagation through the Atmosphere and Oceans IX, Online, 22 August 2020; p. 115060H. [Google Scholar] [CrossRef]
- Abad, M.G.G.; Mahmoudi, M. Laguerre-Gaussian modes generated vector beam via nonlinear magneto-optical rotation. Sci. Rep. 2021, 11, 5972. [Google Scholar] [CrossRef]
- Cao, M.; Yu, Y.; Zhang, L.; Ye, F.; Wang, Y.; Wei, D.; Zhang, P.; Guo, W.; Zhang, S.; Gao, H.; et al. Demonstration of CNOT gate with Laguerre Gaussian beams via four-wave mixing in atom vapor. Opt. Express 2014, 22, 20177–20184. [Google Scholar] [CrossRef]
- Dedecker, P.; Muls, B.; Hofkens, J.; Enderlein, J.; Hotta, J. Orientational effects in the excitation and de-excitation of single molecules interacting with donut-mode laser beams. Opt. Express 2007, 15, 3372–3383. [Google Scholar] [CrossRef] [PubMed]
- Bokor, N.; Iketaki, Y.; Watanabe, T.; Fujii, M. Investigation of polarization effects for high-numerical-aperture first-order Laguerre-Gaussian beams by 2D scanning with a single fluorescent microbead. Opt. Express 2005, 13, 10440–10447. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Ru, G. Orbital angular momentum density of an elegant Laguerre–Gaussian beam. Prog. Electromagn. Res. 2013, 141, 751–768. [Google Scholar] [CrossRef]
- Abramochkin, E.; Razueva, E.; Volostnikov, V. General astigmatic transform of Hermite–Laguerre–Gaussian beams. J. Opt. Soc. Am. A 2010, 27, 2506–2513. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. Asymmetric Laguerre-Gaussian beams. Phys. Rev. A 2016, 93, 063858. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Abramochkin, E.G.; Kovalev, A.A.; Savelyeva, A.A. Product of two Laguerre–Gaussian beams. Photonics 2022, 9, 496. [Google Scholar] [CrossRef]
- Bisson, J.F.; Senatsky, Y.; Ueda, K.I. Generation of Laguerre-Gaussian modes in Nd:YAG laser using diffractive optical pumping. Laser Phys. Lett. 2005, 2, 327–333. [Google Scholar] [CrossRef]
- Lin, D.; Daniel, J.M.O.; Clarkson, W.A. Controlling the handedness of directly excited Laguerre–Gaussian modes in a solid-state laser. Opt. Lett. 2014, 39, 3903–3906. [Google Scholar] [CrossRef] [PubMed]
- Thirugnanasambandam, M.P.; Senatsky, Y.; Ueda, K. Generation of very-high order Laguerre-Gaussian modes in Yb:YAG ceramic laser. Laser Phys. Lett. 2010, 7, 637–643. [Google Scholar] [CrossRef]
- Wang, M.; Ma, Y.; Sheng, Q.; He, X.; Liu, J.; Shi, W.; Yao, J.; Omatsu, T. Laguerre-Gaussian beam generation via enhanced intracavity spherical aberration. Opt. Express 2021, 29, 27783–27790. [Google Scholar] [CrossRef] [PubMed]
- Abramochkin, E.; Volostnikov, V. Beam transformations and nontransformed beams. Opt. Commun. 1991, 83, 123–135. [Google Scholar] [CrossRef]
- Matsumoto, N.; Ando, T.; Inoue, T.; Ohtake, Y.; Fukuchi, N.; Hara, T. Generation of high-quality higher-order Laguerre-Gaussian beams using liquid-crystal-on-silicon spatial light modulators. J. Opt. Soc. Am. A 2008, 25, 1642–1651. [Google Scholar] [CrossRef] [PubMed]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Gori, F.; Guattari, G.; Padovani, C. Bessel-Gauss beams. Opt. Commun. 1987, 64, 491–495. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotlyar, V.V.; Abramochkin, E.G.; Kovalev, A.A.; Savelyeva, A.A. Laguerre-Gaussian Beams with an Increased Dark Area and Autofocusing. Photonics 2022, 9, 708. https://doi.org/10.3390/photonics9100708
Kotlyar VV, Abramochkin EG, Kovalev AA, Savelyeva AA. Laguerre-Gaussian Beams with an Increased Dark Area and Autofocusing. Photonics. 2022; 9(10):708. https://doi.org/10.3390/photonics9100708
Chicago/Turabian StyleKotlyar, Victor V., Eugeny G. Abramochkin, Alexey A. Kovalev, and Alexandra A. Savelyeva. 2022. "Laguerre-Gaussian Beams with an Increased Dark Area and Autofocusing" Photonics 9, no. 10: 708. https://doi.org/10.3390/photonics9100708
APA StyleKotlyar, V. V., Abramochkin, E. G., Kovalev, A. A., & Savelyeva, A. A. (2022). Laguerre-Gaussian Beams with an Increased Dark Area and Autofocusing. Photonics, 9(10), 708. https://doi.org/10.3390/photonics9100708




