Abstract
A new family of partially coherent pulsed beams with spatial cosine-Gaussian and temporal Laguerre–Gaussian correlations, named spatial cosine-Gaussian and temporal Laguerre–Gaussian correlated Schell-model (SCTLGSM) pulsed beams, is introduced. An analytic propagation formula is derived for the SCTLGSM pulsed beam through the spatiotemporal ABCD optical system characterizing a continuous dispersive medium. As an example, the evolution of spatiotemporal intensity of the SCTLGSM pulsed beam in a still, pure water column is then investigated. It is found that the SCTLGSM pulsed beams simultaneously exhibit spatiotemporal self-splitting and self-focusing phenomena, which can be attributed to the special spatial/temporal coherence structures and the presence of pulse chirper in the source plane. The physical interpretation of the obtained phenomena is given. The results obtained in this paper will be of interest in underwater optical technologies, e.g., directed energy and communications.
1. Introduction
In the past few years, a great deal of attention has been paid to partially coherent beams radiated by sources with non-Gaussian correlation functions [1,2,3,4,5,6,7,8,9]. This is due to a variety of extraordinary features that these beams exhibit on free-space propagation, such as self-splitting [10,11,12], self-focusing [13], self-steering [14], and useful shapes they acquire in the far field: flat-tops [15], rings [7,16], rectangles [17], grids [18], and dark-hollow intensity profiles [19]. These new properties have already stimulated new applications in optical particle trapping, free-space optical communications [20], classic imaging [21] and remote sensing [22]. It was also recently revealed that partially coherent sources with complex coherence states (non-trivial phase distributions) can be used for fine directional control of the produced far-field spectral density and polarization distributions [23,24].
All of the aforementioned investigations are confined to statistically stationary light sources/beams in the spatial domain. More recently, non-stationary optical pulses, i.e., those with partial temporal/spectral and spatial coherence states were introduced [25,26,27,28]. Such pulses are envisioned to benefit applications in pulse shaping, laser micromachining, medical diagnosis, ghost imaging, etc. Conventionally, in time domain, a partially coherent light pulse was characterized by Schell model with a temporal Gaussian correlation function. In 2013, Lajunen et al. introduced the non-uniformly partially coherent pulse sources, i.e., sources with a non-Gaussian correlation function [29]. The generated pulsed beams were shown to lead to self-focusing upon propagation in time domain. Subsequently, other models for partially coherent pulsed sources were developed [30,31,32,33,34] to illustrate temporal self-splitting, multispot self-focusing and formation of flat far-fields, among other effects. Partially coherent pulses with the structured phase of the correlation function were also recently studied to demonstrate the control in the average pulse arrival time [35]. However, investigations in [27,28,29,30,31,32,33,34,35,36] were solely confined to the time domain while spatial pulse profiles were assumed to be constant. The non-stationary pulses can be realized experimentally. A stationary, spatially partially coherent beam with a prescribed profile of the coherence function can be first realized with the help of a spatial light modulator or Fourier optics 2f system [12]. Then the spatial correlation can be converted to temporal correlation with the direct space-to-time pulse shaper [37].
Thus, an interesting question arises: what new phenomena can one observe on propagation of partially coherent pulsed beams radiated from sources having non-Gaussian, and in general different, profiles in temporal and spatial correlation functions at the same time? In fact, partially coherent pulses with both spatial and temporal/spectral structured correlations were already considered [38,39] but the analysis relied on Gaussian distributions alone. It would be interesting to consider non-Gaussian but analytically tractable models for the spatial and temporal partial coherence.
In this paper, we choose a combination of the cosine-Gaussian Schell model for the spatial correlations and the Laguerre–Gaussian correlated Schell-model for the temporal ones. Each of these two types of partial coherence was studied separately in the literature. The cosine-Gaussian Schell model for the spatial correlations was studied both theoretically [10] and experimentally [12] and it was demonstrated that the initially Gaussian intensity distribution changes to the dark-hollow distribution and remains shape-invariant in the far field. It was shown also that this model is much simpler for analytical treatment compared to other non-Gaussian models. The Laguerre–Gaussian correlated Schell-model for the temporal correlations was studied theoretically [31] and it was found that it exhibits temporal self-splitting into n + 1 lobes upon propagation in a dispersive medium, where n is the order of the Laguerre polynomial. A potentially high number of lobes distinguishes this model from the alternative ones, which may be attractive for some applications. Thus, we introduce a new family of spatially and temporally partially coherent pulsed beams with spatial cosine-Gaussian and temporal Laguerre–Gaussian correlations, named SCTLGSM pulses. The mathematical consistency and physical feasibility of such beams are briefly discussed in the Appendix A. We then explore the evolution of the spatiotemporal intensity of a typical SCTLGSM pulsed beam through an ABCD optical system describing a diffractive and a dispersive medium, generalizing the particular media considered in Refs. [10,12,31]. Using the second-order optical coherence theory of the non-stationary optical fields, we derive, in Section 2, the analytical expressions for the spatiotemporal intensity of the SCTLGSM pulsed beams passing through the ABCD optical systems. In Section 3, the detailed numerical results regarding the SCTLGSM pulse evolution are presented and the corresponding physical interpretations are given. In Section 4, the main results obtained in this paper are summarized. The self-splitting/self-focusing of a non-stationary pulse in the temporal and spatial domains can be potentially used in optical communication systems operating in dispersive environments, e.g., underwater, for information encoding. This phenomenon can also be applied in temporal ghost imaging [40,41] and optical coherence tomography [42] for obtaining the pulse replicas that can be used for further manipulation of imaged/sensed fields.
2. Theory and Method
In the space–time domain, the second-order correlation properties of a partially coherent pulsed beam are described by the mutual coherence function (MCF) [39,43,44]. Let for the SCTLGSM pulsed beam, the mutual coherence function at the source plane z = 0 be defined as
where S and T characterize the spatial and the temporal parts, respectively:
Here and are the two-dimensional transverse position vectors, τ1 and τ2 are two time instants, cos(•) is the cosine function, and m is the beam order parameter. Further, Ln(•) denotes the Laguerre polynomial of mode order n, ω0 is the pulse’s carrier frequency, while w0 and δ denote the r.m.s. spatial beam width and the r.m.s. beam transverse coherence width, respectively. T0 and Tc represent the pulse duration and the temporal coherence length, respectively. The pulsed beam expressed by Equation (1) is therefore the spatial cosine-Gaussian and temporal Laguerre–Gaussian correlated Schell-model (SCTLGSM) pulsed beam. The SCTLGSM pulsed beam reduces to the conventional Gaussian Schell-model (GSM) pulsed beam when m = 0 and n = 0. For m ≠ 0 and n ≠ 0, the spatial and the temporal coherence parts of the mutual coherence function are modulated by the cosine function and the Laguerre function, respectively. The details of the model can be found in the Appendix A.
We will now consider propagation of the SCTLGSM pulsed beam in the spatiotemporal domain by means of the extended Collins formula, under the paraxial approximation. We consider an additional linear chirp s imposed on the pulse before it enters the dispersive medium [45]. This chirp is described by the factor in the field amplitude, can be realized by an amplitude modulator, and results in pulse compression upon propagation in a dispersive medium in the case of Gaussian Schell model [26]. A similar effect is expected for the SCTLGSM pulsed beam. Adopting the ABCD characterization of the optical system embedded in a dispersive medium in the absence of spatiotemporal coupling, we employ the following integral formula [46,47]
here k(ω0) = n(ω0)ω0/c denotes the wave number, in which n(ω0) is the refractive index of the medium at carrier frequency ω0, c is the speed of light in vacuum, r1 = (x1, y1) and r2 = (x2, y2) are position vectors in any plane z > 0 and t1 and t2 are two time instants of the pulse profile. Further, AS, BS and DS are the transfer matrix elements of the optical system in the spatial domain [48], while AT, BT and DT are those in the temporal domain [45].
On substituting from Equations (1)–(3) into Equation (4), one can derive the following simplified expression
where
After tedious calculation, one can obtain the following expression, for the spatial domain:
where
and
with the spatial ABCD matrix in the form
On the other hand, in the temporal domain, one can obtain the expression
where H2q is Hermite polynomial of order 2q, and
with the temporal ABCD matrix given by expression
Here we assume that the refractive index of the dispersive medium is given by expression n(ω) = naω + nb, where na = β2c and nb = c/vg − 2β2ω0c. Here β2 denotes the group velocity dispersion and vg is the group velocity of the pulse [49]. Furthermore, the time coordinate is a retarded time with respect to a frame moving with group velocity vg and s is the chirp coefficient of the pulse.
Let r1 = r2 = r and t1 = t2 = t in Equations (8) and (15), respectively. Then the spatiotemporal intensity of the SCTLGSM pulsed beam becomes
where cosh(•) is the hyperbolic cosine function. Equation (20) is the main formula derived in this paper. It can be used to investigate the spatiotemporal intensity evolution of the SCTLGSM pulsed beams in any diffractive and dispersive medium.
3. Spatiotemporal Intensity Evolution of the SCTLGSM Pulsed Beams in Water
In this section, the interaction of the SCTLGSM pulsed beams in a column of still, pure water is examined by means of numerical examples. The group velocity refractive index of water at 20 °C and the standard atmospheric pressure is ng = c/vg = 1.3591 and its group velocity dispersion coefficient is β2 = 58.174 ps2km−1 [50]. In the following calculation, the pulses’ and medium’s parameters are chosen to be w0 = 2 mm, σ = 2 mm, T0 = 4 ps, Tc = 2 ps, ω0 = 3.667 rad/fs (λ0 = 514 nm [51]), unless different values are specified. Because of still water absorption [52] the propagation distances will be limited to 100 m throughout the text.
Figure 1a–d shows the evolution of the spatiotemporal intensity I(x, y, t, z) of the SCTLGSM pulsed beam as a function of propagation distance z and horizontal coordinate x with different beam orders, m = 0, 1, 2 and 3. The other values of parameters are y = 0, t = 0, s =0 and n = 0. Figure 2a,b shows the same as Figure 1 but at different time instants t = 2 ps, 5 ps, and for m = 1. As can be seen, beam order plays an important role in the spatial splitting of the SCTLGSM pulsed beam. Of course, for the GSM pulsed beam (m = 0), there is no beam splitting upon propagation. However, for m = 1, the beam splits into two sub-beams when the propagation distance z exceeds 30 m. For larger beam orders (see m = 2 and m = 3), the starting point of the split moves closer to the source plane z = 0. Note that time t has no impact on the beam splitting position. For larger time instants t, the spatiotemporal intensity is gradually reduced (see t = 2 ps and 5 ps in Figure 2). These results can be interpreted physically as follows. Equation (20) can be expressed as
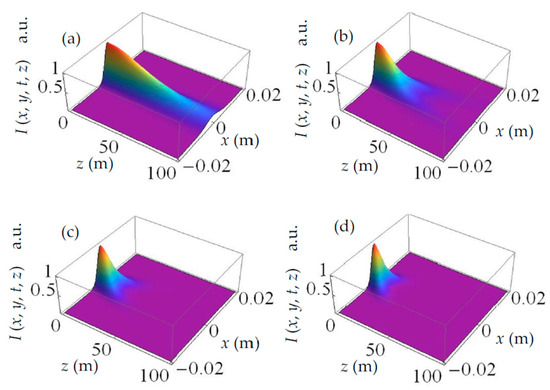
Figure 1.
Evolution of spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam as a function of propagation distance z and horizontal coordinate x with different beam orders: (a) m = 0, (b) m = 1, (c) m = 2 and (d) m = 3.
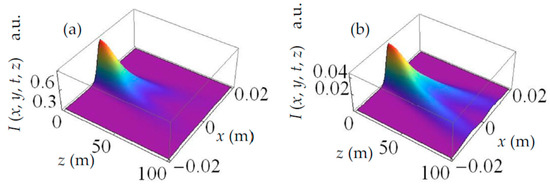
Figure 2.
Evolution of spatiotemporal intensity I(x, y, t, z) (Equation (20)) of spatial cosine-Gaussian and temporal Laguerre–Gaussian correlated Schell-model (SCTLGSM) pulsed beam as a function of propagation distance z and horizontal coordinate x with different time (a) t = 2 ps and (b) t = 5 ps, and for m = 1, s = 0.
Further, when y = 0, t = 0 and n = 0, Equation (21) can be expressed as
It can be seen from Equation (22) that the spatiotemporal intensity I(x, y, t, z) is a superposition of two exponential functions symmetric with respect to the coordinate axis x = 0. When the propagation distance z is short, the two exponential functions are similar, hence the two beams cannot be distinguished. However, when z grows large enough, the two beams become visibly different. Further, when beam order m increases, the position where the beam starts to split moves closer to the source plane z = 0. Moreover, when t ≠ 0, the decrease of the spatiotemporal intensity is attributed to the last exponential function in Equation (21), which plays an important role in determining the value of spatiotemporal intensity.
Figure 3 and Figure 4 show the density plots for the normalized spatiotemporal intensity I(x, y, t, z) of the SCTLGSM pulsed beam in the x–y plane at some propagation distances z = 0, 30 m, 40 m, 60 m and for m = 1 (Figure 3) and m = 2 (Figure 4), respectively. The other values of parameters are t = 0, s = 0 and n = 0. It is shown that the SCTLGSM pulsed beam exhibits self-splitting properties upon propagation in water, i.e., the initial beam spot evolves into four sub-beam spots in the far field depending on the value of beam order m. For larger m, the self-splitting time is smaller. These results can be explained from the Equation (22). When m increases, coefficient (2π)1/2m/δk of z in the exponential function increases as well. Hence, the rate of change in the spatiotemporal intensity increases with the increasing propagation distance.
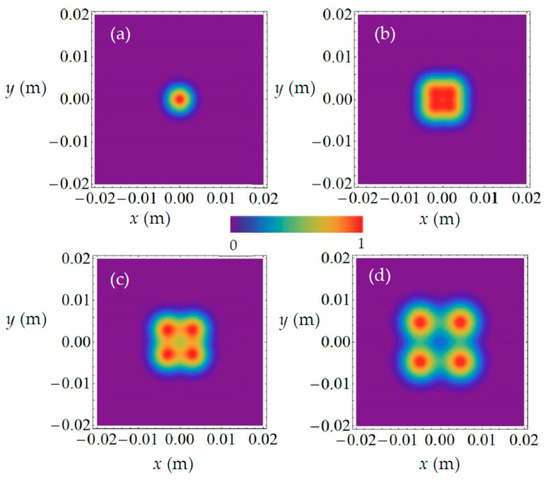
Figure 3.
Density plots for the normalized spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam in the x–y plane at some propagation distances: (a) z = 0, (b) z = 30 m, (c) z = 40 m, (d) z = 60 m and for t = 0, s = 0, m = 1.
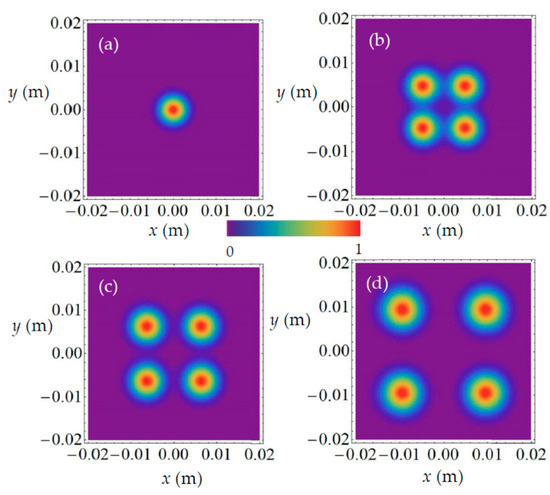
Figure 4.
Density plots for the normalized spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam in the x–y plane at some propagation distances (a) z = 0, (b) z = 30 m, (c) z = 40 m, (d) z = 60 m and for t = 0, s = 0, m = 2.
Figure 5 illustrates the evolution of the spatiotemporal intensity I(x, y, t, z) of the SCTLGSM pulsed beam as a function of propagation distance z and time t, with different beam orders n = 0, 1, 2 and 3. The other calculation parameters are x = 0, y = 0, s = −0.4ps−2 and m = 0. One can see from Figure 5 that the beam exhibits self-splitting behavior when n > 0. Specifically, the beam splits into n + 1 sub-beams with increasing propagation distance z, being in good agreement with the results of the Laguerre–Gaussian Schell-model pulsed beam in time domain [31]. While for n = 0, i.e., for the conventional Gaussian-correlated Schell-model pulsed beam, there is no self-splitting upon propagation. These results can be interpreted as follows. For n = 0, the last term of Equation (21) can be re-expressed as
while for n=1,
and for n = 2,
here Equations (24) and (25) can be re-written as:
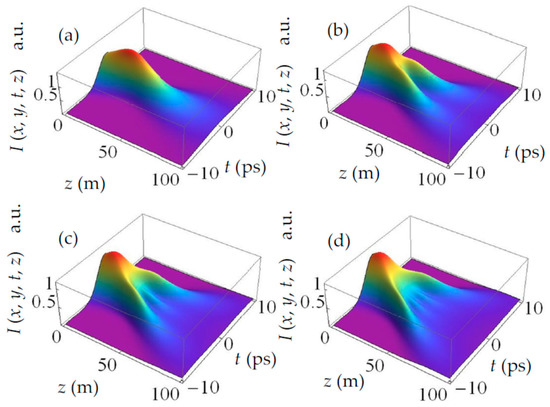
Figure 5.
Evolution of spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam as a function of propagation distance z and time t with different beam orders (a) n = 0, (b) n =1, (c) n =2 and (d) n =3.
From Equation (24) we see that In=1 is a product of functions and . Thus, letting
and solving Equation (30), In=1 will obtain two symmetric intensity maxima at when . Therefore, the beam starts splitting into two sub-beams in Figure 5b. In addition, when z is very short, the influence of term ξ1 t2+Ψ1 can be neglected compared with that of exp(−φt2). This is why there is only one beam when z is much closer to the source plane. Similarly, for n = 2 and n = 3, we can obtain 3 intensity maxima and 4 intensity maxima in the far field, respectively.
Figure 6 shows the evolution of spatiotemporal intensity I(x, y, t, z) of the SCTLGSM pulsed beam as a function of propagation distance z and time t with different values of chirp coefficient s = 0, −0.4ps−2, −0.8ps−2, −1.2ps−2, and for n = 0, m = 0, x = 0, y = 0. It is shown that the self-focusing phenomenon takes place upon propagation when chirp coefficient s < 0, and it becomes more noticeable with decreasing chirp coefficient s, while the position of the focus shifts towards the source plane. This result can be explained as follows. When n = 0, m = 0, x = 0, y = 0, Equation (23) can be expressed as
where
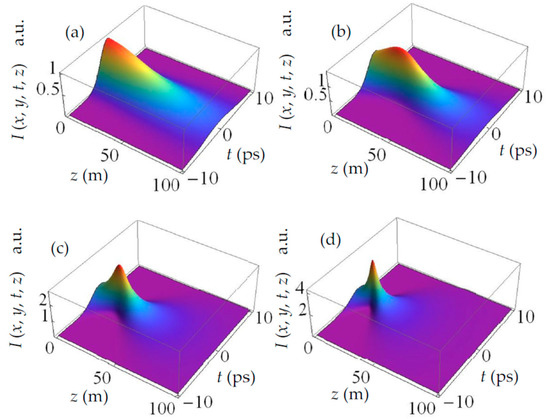
Figure 6.
Evolution of spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam as a function of propagation distance z and time t with different chirp coefficients (a) s = 0, (b) s =−0.4 ps−2, (c) s =−0.8 ps−2, (d) s =−1.2 ps−2 and for n = 0, m = 0.
One can see from Equation (32) that is a quadratic function of z, and will reach minima when
Hence, the self-focusing phenomenon appears upon propagation when chirp coefficient s < 0. Moreover, with increasing |s|, zmin will decrease, which can be seen from Equation (33), because for large |s|, can be omitted. Equation (33) can be expressed as zmin ≈ β2/|s| which is why the position of focus shifts towards the source plane with increasing |s|. Here the influence of s on propagation in the temporal ABCD matrix is equivalent to a lens. Hence, the self-focusing phenomenon appears.
Figure 7 shows the evolution of spatiotemporal intensity I(x, y, t, z) of SCTLGSM pulsed beam as a function of propagation distance z and time t with different chirp coefficients s = 0, −0.4ps−2, −0.8ps−2, −1.2ps−2, and for n = 1, m = 0, x = 0, y = 0. It is shown that the self-focusing and the self-splitting phenomena take place at the same time when chirp coefficient s < 0. Due to the shift of the position of self-focusing, there are three intensity peaks appearing for larger |s|.
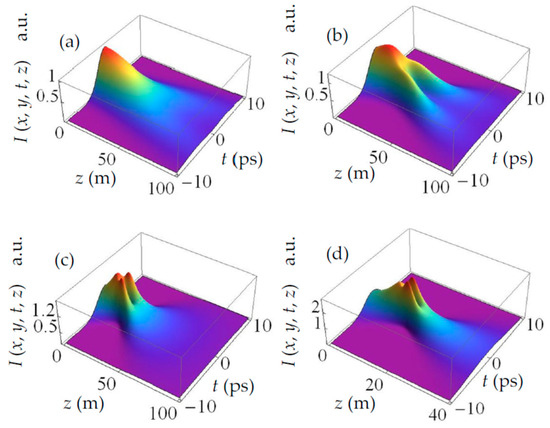
Figure 7.
Evolution of spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam as a function of propagation distance z and time t with different chirp coefficients (a) s = 0, (b) s =-0.4 ps−2, (c) s =-0.8 ps−2, (d) s =−1.2 ps−2 and for n = 1, m = 0.
Figure 8a–e shows the density plots for the normalized spatiotemporal intensity I(x, y, t, z) of the SCTLGSM pulsed beam in the x–t plane at fixed propagation distances z = 0, 20 m, 30 m, 40 m, 50 m and for s = −0.4ps−2, n = 0, m = 0, y = 0. As can be seen, there is a circular intensity distribution in the x–t plane for z = 0. With the increasing propagation distance z, the circular intensity distribution becomes elliptical (Figure 8c–e), where the self-focusing appears in the coordinate axis t. Figure 8f shows the normalized spatiotemporal intensity I(x, y, t, z) of the SCTLGSM pulsed beam as a function of propagation distance z for different values of the chirp coefficient s = 0, −0.4ps−2, −0.8ps−2, −1.2ps−2, where n = 0, m = 0, x = 0, y = 0. One can see that the self-focusing phenomenon becomes more and more noticeable with increasing chirp coefficient |s|. Moreover, for the case of m = n = 1, shown in Figure 9a–c, the beam splits first in the coordinate axis t, and then splits in the coordinate axis x (Figure 9d). In the far field, the beam splits into four sub-beam spots in the x–t plane. Figure 9f shows the normalized spatiotemporal intensity I(x, y, t, z) of the SCTLGSM pulsed beam as a function of propagation distance z for different chirp coefficient values: s = 0, −0.4ps−2, −0.8ps−2, −1.2ps−2, where n = 1, m = 1, x = 0, y = 0, t = 0. One can find that the self-focusing phenomenon is more noticeable for s = −1.2ps−2. Comparison of Figure 8 with Figure 9 implies that the beam orders m and n play an important role in determining the spatiotemporal intensity distribution in x–t plane.
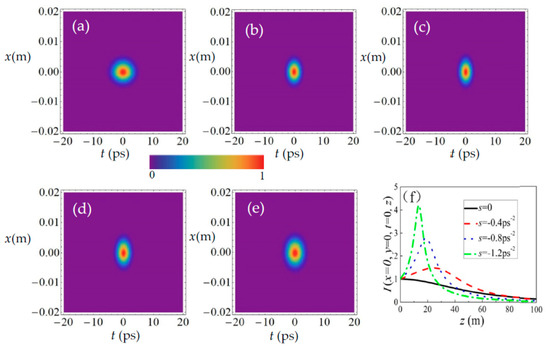
Figure 8.
Density plots for the normalized spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam in the x–t plane at some propagation distances (a) z = 0, (b) z =20 m, (c) z =30 m, (d) z =40 m, (e) z =50 m and for s = −0.4ps−2, n = 0, m = 0. (f) Normalized intensity I(x, y, t, z) (Equation (22)) of SCTLGSM pulsed beam as a function of propagation distance z for different chirp coefficients s = 0, −0.4ps−2, −0.8ps−2, −1.2ps−2.
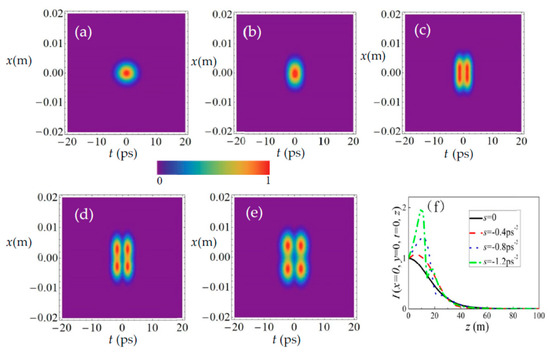
Figure 9.
Density plots for the normalized spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam in the x–t plane at some propagation distances (a) z = 0, (b) z =20 m, (c) z = 30 m, (d) z = 40 m, (e) z = 50 m and for s = −0.4, n = 1, m = 1. (f) Normalized intensity I(x, y, t, z) (Equation (22)) of SCTLGSM pulsed beam as a function of propagation distance z for different chirp coefficients s = 0, −0.4 ps−2, −0.8 ps−2 and −1.2 ps−2.
Figure 10a–d includes the density plots for the normalized spatiotemporal intensity I(x, y, t, z) of the SCTLGSM pulsed beam in the x–t plane for different beam orders m = n = 0, m = n = 1, m = n = 2, m = n = 3 at z = 50 m, and for s = −0.4 ps−2, y = 0. It is shown that no beam splitting occurs in the far field for m = n = 0. However, for m = n = 1, the initial beam starts to split into two sub-beams in coordinate axis t and coordinate axis x, respectively. With increasing beam order, such as m = n = 2, the initial beam starts to split into three sub-beams in coordinate axis t and two sub-beams in coordinate axis x, respectively. In addition, for m = n = 3, the initial beam starts to split into four sub-beams in coordinate axis t and two sub-beams coordinate axis x, respectively. These results are consistent with those of Figure 5.
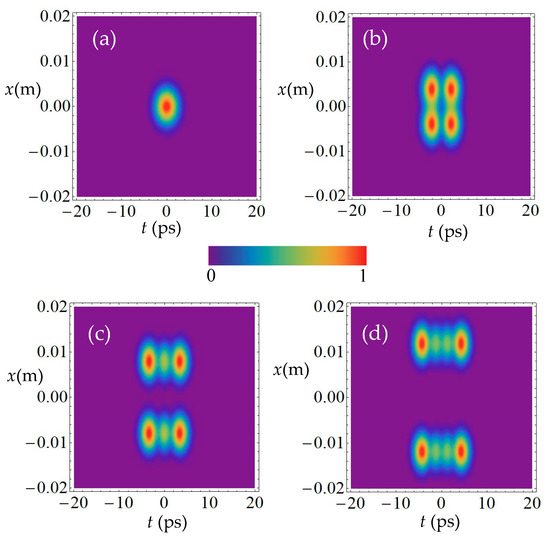
Figure 10.
Density plots for the normalized spatiotemporal intensity I(x, y, t, z) (Equation (20)) of SCTLGSM pulsed beam in the x–t plane for different beam orders (a) m = n = 0, (b) m = n = 1, (c) m = n = 2, (d) m = n = 3 at z = 50 m with s = −0.4ps−2.
4. Concluding Remarks
In this paper, a new class of partially coherent pulsed beams with spatial cosine-Gaussian and temporal Laguerre–Gaussian correlations is introduced. The analytical expressions of the spatiotemporal intensity of the SCTLGSM pulsed beam through the ABCD optical system on passing in a diffractive/dispersive medium are obtained and used to investigate the evolution of the spatiotemporal intensity of the SCTLGSM pulsed beam in still, pure water. It is found that the SCTLGSM pulsed beam exhibits the phenomena of simultaneous spatiotemporal self-splitting and self-focusing. When the chirp coefficient is trivial, s = 0, in the x–z plane, the beam always splits into two sub-beams, when m > 0, while in the t–z plane, the beam splits into n + 1 sub-beams. When s < 0, the spatiotemporal self-focusing phenomenon takes place. The influence of s on propagation in a dispersive medium is equivalent to the effect of a lens in a diffractive medium. Physically, the special structuring of the spatial coherence and temporal coherence states result in the spatiotemporal self-splitting phenomenon of the SCTLGSM pulsed beam. Furthermore, the pulse chirp leads to the spatiotemporal self-focusing phenomenon of the SCTLGSM pulsed beam. The results obtained in this paper can be readily extended to other dispersive media and/or other temporal ABCD optical systems.
More importantly, we have explored the possibility of shaping of optical pulsed signals by source correlations in one of the most frequently encountered natural environments—pure water. Such a method can be of interest for rapidly developing underwater optical technologies, including wireless communications and directed energy. In particular, one can obtain the desired beam profiles delivered at suitable time instants by modulating the spatial and temporal coherence structures of the pulsed beams and/or adding a linear chirp.
It should be stressed that our work was carried out under the assumption that the refractive index of the dispersive medium is linear. The self-focusing effect comes from the source-induced spatial and temporal interference effects (pulse chirp) and should not be associated with the medium’s non-linear effects. In cases when the dispersive medium is nonlinear, the four-wave-mixing [53] and formation of optical solitons must be additionally discussed [54]. We note that there is a report available on propagation of the spatially partially coherent beams with non-Gaussian correlation in oceanic turbulence [55] in which the correlation-induced phenomenon of self-focusing also appears, confirming the validity of our results.
Author Contributions
C.D. (Investigation, Methodology, Writing—Original Draft Preparation, Writing—Review & Editing); O.K. (Formal Analysis, Writing—Review & Editing); D.H. (Formal Analysis, Validation); Z.Z. (Formal Analysis, Validation); L.P. (Resources, Formal Analysis, Project Administration). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded partially by the National Natural Science Foundation of China (61575091), China Scholarship Council (202008410578), 2020 Central Plains Talents Program of Henan, High-level talents international training program and Excellent Overseas Visiting Scholar Program of Henan.
Institutional Review Board Statement
This study did not involve humans or animals.
Informed Consent Statement
This study did not involve humans.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this appendix, we will justify the validity of adopted mutual coherence function with spatial cosine-Gaussian and temporal Laguerre–Gaussian correlations. The mutual coherence function of the SCTLGSM pulsed beam at the source plane z = 0 is defined as
where the spatial and the temporal mutual coherence functions can be written in the following forms, respectively,
where pS and pT are non-negative weight functions, and H(ρ, ε) and h(t, v) are arbitrary kernels in the space domain and the time domain, respectively. We assume that
and choose the weighting functions pS and pT as follows:
where parameter σ is a factor relating to beam width [12], and Hn is a Hermite polynomial of order n [31]. Here, we choose the mutual coherence functions in the spatial domain and in time domain from Refs. [12,31], respectively.
The cross-spectral density function is obtained from the mutual coherence function using the generalized Wiener–Khintchine theorem
After tedious calculation and considering the specific Equations (2) and (3), one obtains
where
and the pulse duration T0, temporal coherence length Tc, spectral bandwidth Ω and the spectral coherence width Ωc are related by
On the one hand, Equations (A2) and (A3) guarantee that the mutual coherence function of the SCTLGSM pulsed beam is a non-negative kernel and is therefore physically realizable [56]. On the other hand, they show how such a pulsed beam can be realized by transformations of an incoherent field with the mutual coherence function
The field can be obtained from a perfectly spatially and temporally incoherent source, e.g., a broadband light-emitting diode, by spatial and temporal amplitude modulation with the modulation profiles and respectively.
In order to obtain the SCTLGSM pulsed beam, we need to pass the field through a spatial and temporal imaging system with the transfer function so that the output field becomes
which, according to Equations (A2), (A3) and (A12), will give us a field with the desired mutual coherence function , given by Equation (A1). The spatial transfer function, Equation (A4), can be regarded as a product of three terms (up to an irrelevant constant factor) [12]: (i) the transfer function corresponding to diffraction at a distance L, , (ii) the phase factor of a thin lens with the focal distance f, , and (iii) the transmission coefficient of a Gaussian amplitude filter with the intensity standard deviation , , where k is the wave number corresponding to the carrier frequency and . The above considerations are valid for the fields of bandwidth much less than the carrier frequency.
In a similar way, the temporal transfer function, Equation (A5), can be regarded as a product of three terms corresponding to standard components of a temporal imaging system [57] (again, up to a constant factor): (i) the transfer function corresponding to propagation through a dispersive medium with the total group delay dispersion (GDD) D, , (ii) the phase factor of a time lens with the focal GDD , , and (iii) the transmission coefficient of a Gaussian amplitude modulator with the intensity standard deviation , , where .
Thus, a combination of elementary transformations described above gives a possible way of generation of a SCTLGSM pulsed beam.
In the Figure A1, we present an explanatory figure for the source of SCTLGSM pulsed beam with spatial cosine-Gaussian and temporal Laguerre–Gaussian correlations and show the spectral density profiles of the source.
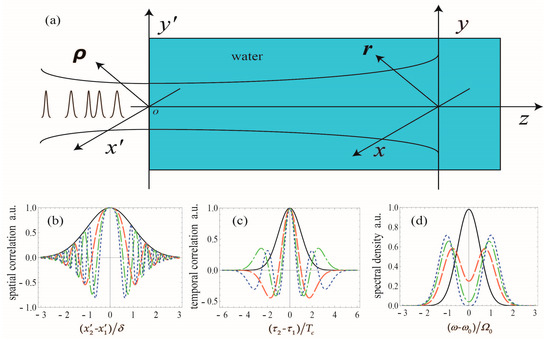
Figure A1.
(a) Illustrating figure of the SCTLGSM pulsed beam propagating in water. (b) Spatial degree of coherence of the pulsed beam source as a function of . Solid black: m = 0; Dashed red: m = 1; Dash-dotted green: m = 2; Dotted blue: m = 3. (c) Temporal degree of coherence of the pulsed beam source as a function of . Solid black: n = 0; Dashed red: n = 1; Dash-dotted green: n = 2; Dotted blue: n = 3. (d) Spectral density of the pulsed beam source as a function of (ω − ω0)/Ω0. Solid black: Ωc/Ω0 =1; Dashed red: Ωc/Ω0 = 1; Dash-dotted green: Ωc/Ω0 = 0.5; Dotted blue: Ωc/Ω0 = 0.1.
References
- Korotkova, O. Random Light Beams: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Cai, Y.J.; Chen, Y.H.; Wang, F. Generation and propagation of partially coherent beams with nonconventional correlation functions: A review [Invited]. J. Opt. Soc. Am. A 2014, 31, 2083–2096. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.J.; Wang, F.; Chen, Y.H.; Liu, X.L. Recent advances in partially coherent beams with prescribed degrees of coherence. Sci. Found. China 2017, 25, 38–60. [Google Scholar]
- Cai, Y.J.; Chen, Y.H.; Yu, J.Y.; Liu, X.L.; Liu, L. Generation of Partially Coherent Beams. Prog. Opt. 2017, 62, 157–223. [Google Scholar]
- Wan, L.P.; Zhao, D.M. Controllable rotating Gaussian Schell-model beams. Opt. Lett. 2019, 44, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.P.; Wang, J.; Huang, H.K.; Wang, H.Y.; Zhu, S.J.; Li, Z.H.; Lu, J. Propagation Characteristics of a Twisted Cosine-Gaussian Correlated Radially Polarized Beam. Appl. Sci. 2018, 8, 1485. [Google Scholar] [CrossRef]
- Zheng, S.M.; Yuan, C.F.; Ji, X.L.; Wang, T. Ring-shaped twisted Gaussian Schell-model array beams. J. Opt. Soc. Am. A 2020, 37, 444–449. [Google Scholar] [CrossRef]
- Hyde IV, M.W.; Bose-Pillai, S.; Voelz, D.G.; Xiao, X. A fast and efficient method for producing partially coherent sources. J. Opt. 2017, 19, 025601. [Google Scholar] [CrossRef]
- Wang, J.; Yang, S.; Guo, M.J.; Feng, Z.F.; Li, J.H. Change in phase singularities of a partially coherent Gaussian vortex beam propagating in a GRIN fiber. Opt. Express 2020, 28, 4661–4673. [Google Scholar] [CrossRef]
- Mei, Z.R.; Korotkova, O. Cosine-Gaussian Schell-model sources. Opt. Lett. 2013, 38, 2578–2580. [Google Scholar] [CrossRef]
- Chen, Y.H.; Gu, J.X.; Wang, F.; Cai, Y.J. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam. Phys. Rev. A 2015, 91, 013823. [Google Scholar] [CrossRef]
- Liang, C.H.; Wang, F.; Liu, X.L.; Cai, Y.J.; Korotkova, O. Experimental generation of cosine-Gaussian-correlated Schell-model beams with rectangular symmetry. Opt. Lett. 2014, 39, 769–772. [Google Scholar] [CrossRef] [PubMed]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.H.; Ponomarenko, S.A.; Cai, Y.J. Self-steering partially coherent beams. Sci. Rep. 2017, 7, 39957. [Google Scholar] [CrossRef]
- Sahin, S.; Korotkova, O. Light sources generating far fields with tunable flat profiles. Opt. Lett. 2012, 37, 2970–2972. [Google Scholar] [CrossRef]
- Liang, C.H.; Khosravi, R.; Liang, X.; Kacerovská, B.; Monfared, Y.E. Standard and elegant higher-order Laguerre-Gaussian correlated Schell-model beams. J.Opt. 2019, 21, 085607. [Google Scholar] [CrossRef]
- Korotkova, O. Random sources for rectangular far fields. Opt. Lett. 2014, 39, 64–67. [Google Scholar] [CrossRef]
- Wan, L.P.; Zhao, D.M. Optical coherence grids and their propagation characteristics. Opt. Express 2018, 26, 2168–2180. [Google Scholar] [CrossRef]
- Chen, Y.H.; Wang, F.; Zhao, C.L.; Cai, Y.J. Experimental demonstration of a Laguerre-Gaussian correlated Schell-model vortex beam. Opt. Express 2014, 22, 5826–5838. [Google Scholar] [CrossRef]
- Gbur, G. Partially coherent beam propagation in atmospheric turbulence [Invited]. J. Opt. Soc. Am. A 2014, 31, 2038–2045. [Google Scholar] [CrossRef]
- Singh, M.; Lajunen, H.; Tervo, J.; Turunen, J. Imaging with partially coherent light: Elementary-field approach. Opt. Express 2015, 23, 28132–28140. [Google Scholar] [CrossRef]
- Wu, G.F.; Cai, Y.J. Detection of a semirough target in turbulent atmosphere by a partially coherent beam. Opt. Lett. 2011, 36, 1939–1941. [Google Scholar] [CrossRef]
- Korotkova, O.; Chen, X. Phase structuring of the complex degree of coherence. Opt. Lett. 2018, 43, 4727–4730. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O.; Chen, X.; Setälä, T. Electromagnetic Schell-model beams with arbitrary complex correlation states. Opt. Lett. 2019, 44, 4945–4948. [Google Scholar] [CrossRef] [PubMed]
- Pääkkönen, P.; Turunen, J.; Vahimaa, P.; Friberg, A.T.; Wyrowski, F. Partially coherent Gaussian pulses. Opt. Commun. 2002, 204, 53–58. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, L.G.; Zhu, S.Y. Partially coherent light pulse and its propagation. Opt. Commun. 2003, 219, 65–70. [Google Scholar] [CrossRef]
- Turunen, J. Low-coherence laser beams. In Laser Beam Propagation: Generation and Propagation of Customized Light; Forbes, A., Ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Bourassin-Bouchet, C.; Couprie, M.E. Partially coherent ultrafast spectrography. Nat. Commun. 2015, 6, 6465. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Non-uniformly correlated partially coherent pulses. Opt. Express 2013, 21, 190–195. [Google Scholar] [CrossRef]
- Ding, C.L.; Korotkova, O.; Pan, L.Z. The control of pulse profiles with tunable temporal coherence. Phys. Lett. A 2014, 378, 1687–1690. [Google Scholar] [CrossRef]
- Ding, C.L.; Koivurova, M.; Turunen, J.; Pan, L.Z. Temporal self-splitting of optical pulses. Phys. Rev. A 2018, 97, 053838. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhao, D.M.; Tian, K.H.; Pan, W.Q.; Zhang, K.W. Gaussian temporal modulation for the behavior of multi-sinc Schell-model pulses in dispersive media. Opt. Commun. 2018, 416, 160–165. [Google Scholar] [CrossRef]
- Tang, M.M.; Zhao, D.M.; Zhu, Y.B.; Ang, L.-K. Electromagnetic sinc Schell-model pulses in dispersive media. Phys. Lett. A 2016, 380, 794–797. [Google Scholar] [CrossRef]
- Ding, C.L.; Korotkova, O.; Zhao, D.M.; Li, D.L.; Zhao, Z.G.; Pan, L.Z. Propagation of temporal coherence gratings in dispersive medium with a chirper. Opt. Express 2020, 28, 7463–7474. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Ding, C.L.; Hyde, M.W., IV; Korotkova, O. Non-stationary pulses with complex-valued temporal degree of coherence. J.Opt. 2020, 22, 105607. [Google Scholar] [CrossRef]
- Ding, C.L.; Korotkova, O.; Zhang, Y.T.; Pan, L.Z. Cosine-Gaussian correlated Schell-model pulsed beams. Opt. Express 2014, 22, 931–942. [Google Scholar] [CrossRef] [PubMed]
- Torres-Company, V.; Mínguez-Vega, G.; Lancis, J.; Friberg, A.T. Controllable generation of partially coherent light pulses with direct space-to-time pulse shaper. Opt. Lett. 2007, 32, 1608–1610. [Google Scholar] [CrossRef] [PubMed]
- Christov, I.P. Propagation of Partially Coherent Light Pulses. Opt. Acta Int. J. Opt. 1986, 33, 63–72. [Google Scholar] [CrossRef]
- Lajunen, H.; Vahimaa, P.; Tervo, J. Theory of spatially and spectrally partially coherent pulses. J. Opt. Soc. Am. A 2005, 22, 1536–1545. [Google Scholar] [CrossRef]
- Torres-Company, V.; Lajunen, H.; Lancis, J.; Friberg, A.T. Ghost interference with classical partially coherent light pulses. Phys. Rev. A 2008, 77, 043811. [Google Scholar] [CrossRef]
- Shirai, T.; Setälä, T.; Friberg, A.T. Temporal ghost imaging with classical non-stationary pulsed light. J. Opt. Soc. Am. B 2010, 27, 2549–2555. [Google Scholar] [CrossRef]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef]
- Bertolotti, M.; Ferrari, A.; Sereda, L. Coherence properties of nonstationary polychromatic light sources. J. Opt. Soc. Am. B 1995, 12, 341–347. [Google Scholar] [CrossRef]
- Sereda, L.; Bertolotti, M.; Ferrari, A. Coherence properties of nonstationary light wave fields. J. Opt. Soc. Am. A 1998, 15, 695–705. [Google Scholar] [CrossRef]
- Dijaili, S.P.; Dienes, A.; Smith, J.S. ABCD matrices for dispersive pulse propagation. IEEE J. Quantum Elect. 1990, 26, 1158–1164. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University: Cambridge, UK, 1995. [Google Scholar]
- Luo, M.L.; Zhao, D.M. Characterizing the polarization and cross-polarization of electromagnetic vortex pulses in the space-time and space-frequency domain. Opt. Express 2015, 23, 4153–4162. [Google Scholar] [CrossRef]
- Turunen, J.; Friberg, A.T. Matrix representation of Gaussian Schell-model beams in optical systems. Opt. Laser Technol. 1986, 18, 259–267. [Google Scholar] [CrossRef]
- Lajunen, H.; Turunen, J.; Vahimaa, P.; Tervo, J.; Wyrowski, F. Spectrally partially coherent pulse trains in dispersive media. Opt. Commun. 2005, 255, 12–22. [Google Scholar] [CrossRef]
- Daimon, M.; Masumura, A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811–3820. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Liu, L.R.; Sun, J.F. Influence of temperature and salinity fluctuations on propagation behaviour of partially coherent beams in oceanic turbulence. J. Opt. A Pure Appl. Opt. 2006, 8, 1052. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Schnebelin, C.; Cassagne, C.; de Araújo, C.B.; Boudebs, G. Measurements of the third- and fifth-order optical nonlinearities of water at 532 and 1064 nm using the D4σ method. Opt. Lett. 2014, 39, 5046–5049. [Google Scholar] [CrossRef]
- Sedov, E.V.; Redyuk, A.A.; Fedoruk, M.P.; Gelash, A.A.; Frumin, L.L.; Turitsyn, S.K. Soliton content in the standard optical OFDM signal. Opt. Lett. 2018, 43, 5985–5988. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, J.; Wang, J. Propagation characteristics of non-uniformly Sinc-correlated blue-green laser beam through oceanic turbulence. Infrared Laser Eng. 2020, 49, 20190370. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef] [PubMed]
- Patera, G.; Horoshko, D.B.; Kolobov, M.I. Space-time duality and quantum temporal imaging. Phys. Rev. A 2018, 98, 053815. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).